Finite-temperature critical behaviors in 2D long-range quantum Heisenberg model

Abstract

The Mermin-Wagner theorem states that spontaneous continuous symmetry breaking is prohibited in systems with short-range interactions at spatial dimension D ≤ 2. For long-range interactions with a power-law form (1/r^α), the theorem further forbids ferromagnetic or antiferromagnetic order at finite temperature when α ≥ 2D. However, the situation for α ∈ (2, 4) at D = 2 is not covered by the theorem. To address this, we conduct large-scale quantum Monte Carlo simulations and field theoretical analysis. Our findings show spontaneous breaking of SU(2) symmetry in the ferromagnetic Heisenberg model with 1/r^α-form long-range interactions at D = 2. We determine critical exponents through finite-size analysis for α < 3 (above the upper critical dimension with Gaussian fixed point) and 3 ≤ α < 4 (below the upper critical dimension with non-Gaussian fixed point). These results reveal new critical behaviors in 2D long-range Heisenberg models, encouraging further experimental studies of quantum materials with long-range interactions beyond the Mermin-Wagner theorem’s scope.

Introduction

In recent years, the importance of the studies on long-range (LR) lattice models have been gradually noticed, due to the fact that they exhibit intrinsically different properties from their short-ranged (SR) counterparts. For example, LR Heisenberg models at spatial dimension D = 2 acquires anomalous magnon dispersion different from the linear and quadratic spin-waves in the SR antiferromagnetic and ferromagnetic models^1,2. In addition, the violation of Mermin-Wagner theorem and unconventional critical properties in LR systems also attracted much attention in investigations of both quantum spin models and interacting fermionic models^{3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23}.

These phenomena also have immediate experimental relevance. Due to the fast development in the Rydberg atom arrays^{24,25,26,27,28}, the magic angle twisted bilayer Graphene and other 2D quantum moiré materials^{29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66} and the programmable quantum simulators^67,68 such as quantum gases coupled to optical cavities⁶⁹. LR interactions in the forms of van der Waals, dipole-dipole and Coulomb have given rise to a plethora of correlated topological and quantum phases of matter beyond the semi-classical or mean-field type descriptions, and new theoretical paradigm that could cope with these fast emergent experimental facts are critically called for.

One particularly interesting direction is to explore the critical properties of phase transitions with continuous symmetry breaking, outside the realm of the established Mermin-Wagner theorem. For 1D LR antiferromagnetic Heisenberg chain²³ and Heisenberg ladders¹⁴ with 1/r^α-form LR interactions, the phase diagram as well as the critical exponents have been addressed and it has been found that there is an upper critical value α_c above which there is no phase transitions for these systems. Below α_c, the transition exists and the critical exponents are dependent on α, as identified by both field theory analysis and numerical evidence. However, for 2D LR Heisenberg models with finite-temperature transitions, it was only known that, for D = 2 Heisenberg model with ferromagnetic LR interaction 1/r^α, a finite-temperature ferromagnetic phase will not exist when α ≥ 4 which has been proved analytically in Ref. ⁷⁰, and for α ≤ 2 the system is gapped due to the generalized Higgs mechanism^1,2 and the finite-temperature ferromagnetic order should be allowed. However, the situation in α ∈ (2, 4) is not well understood. Although there are classical field theory predictions and renormalization group analysis on this issue^3,4,7, which state there is a Gaussian fix-point for 2 < α < 3 and a non-Gaussian fixed-point for 3 ≤ α < 4, a thorough numerical treatment on the 2D quantum Heisenberg model has not been performed to date. Such unbiased numerical analysis of this model is crucial not only because the field-theory scenario needs to be impartially examined on the realistic lattice models, but also due to the fact that the Heisenberg model is one of the most central toy models in condensed matter and statistic physics and a complete clarification of the critical properties of this model will serve as the cornerstone of further studies on LR quantum many body systems.

Here we bridge these gaps by large-scale QMC simulations and field theory analysis. We find clear evidence of the breakdown of the Mermin-Wagner theorem with finite-temperature phase transitions in α ∈ (2, 4), as shown in Fig. 1. By performing the state-of-the-art finite-size scaling analysis, as illustrated in Fig. 2, we obtain the accurate critical exponents of the phase transition as a function of α as shown in Fig. 3, and demonstrate these results nicely satisfy the field-theory predictions both for α < 3 where the system is above the upper critical dimension with Gaussian fixed point and for 3 ≤ α < 4 where the system is below the upper critical dimension with non-Gaussian fixed point. Our results explicitly show the critical behaviors for α ∈ (2, 4) in LR Heisenberg model at D = 2 and will intrigue further theoretical and experimental physics and even mathematics studies of systems with LR interactions beyond the realm of the Mermin-Wagner theorem^{3,4,5,6,7,8,71}.

Fig. 1: Phase diagram of the 2D LR ferromagnetic Heisenberg model.

As the temperature is reduced, the system undergoes a continuous phase transition from paramagnetic phase to the ferromagnetic phase in the entire region of α ∈ (2, 4). The black dots are the critical points determined from QMC simulations, as exemplified in Figs. 2 and 3. The standard error of the mean (SEM) is used when estimating the errors of the physical quantities.

Fig. 2: The determination of the critical point and exponents at α = 2.5.

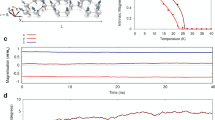
a Binder ratio U(T, L) versus temperature T for different system sizes. b Crossing points of Binder ratios T^*(L) versus 1/L. The solid line represents a fitting of the data points with Eq. (9). The fitted curve is T^*(L) = − 2.935L^−1.491 + 3.5776. c Data collapse of the order parameter 〈m²〉 near the critical point T_c. Notice here we replace the correlation length exponent ν with ${\nu }^{{\prime} }$ as in Eq. (13). d $\ln [G(L/2)]$ versus $\ln (L)$ for different system sizes L = 16, 24, 36, 54, 80, 120, 180. The data is fitted with a straight line as in Eq. (14) and the fitted result is $\ln [G(L/2)]=-0.999(1)\ln (L)$. The errors of $\ln [G(L/2)]$ are smaller than the symbol sizes and SEM is used when estimating the errors of the physical quantities.

Fig. 3: Critical exponents ${\nu }^{{\prime} }$, β and η_Q in the region of α ∈ [2.3, 3.7] obtained from data collapse and from fitting to the correlation function G(r).

The black and blue solid lines in a–c are the predictions of LR Gaussian theory (α < 3) and two-loop perturbative RG predictions (3 ≤ α < 4) for Gaussian and interacting (non-Gaussian) fixed points^3,4,6. SEM is used when estimating the errors of the physical quantities.

Results

Model

The Hamiltonian of the LR ferromagnetic Heisenberg model is

$${{{\mathcal{H}}}}=-\mathop{\sum}\limits_{i < j}{J}_{ij}{{{{\bf{S}}}}}_{i}{{{{\bf{S}}}}}_{j},$$

(1)

where ${J}_{ij}=\frac{1}{{r}_{ij}^{\alpha }}$ denotes the LR coupling and r_ij is the nearest distance between site i and site j under the periodic boundary condition. In order to alleviate the strong finite-size effects in systems with LR interactions arising from the cut-off of LR interactions under the periodic boundary condition, we replace J_ij with the Ewald-corrected coupling ${\tilde{J}}_{ij}$^19,72 which takes the form of

$${\tilde{J}}_{ij}=\mathop{\sum }\limits_{m,n=-\infty }^{\infty }\frac{1}{| {{{\bf{i}}}}-{{{\bf{j}}}}+m{L}_{x}{{{{\bf{e}}}}}_{x}+n{L}_{y}{{{{\bf{e}}}}}_{y}{| }^{\alpha }}.$$

(2)

This modified coupling parameter ${\tilde{J}}_{ij}$ counts all the possible distances between two sites under the periodic boundary condition, so that the effect of cutting off the tail of LR interactions is minimized, and this trick has been shown to be very useful in the simulation of many LR systems^14,18,19,72. For 2D there is no closed form for Eq. (2), so we truncate the summation at ∣m∣_max, ∣n∣_max = 1000 for α < 3 which is large enough to have the well-converged finite-size scaling behavior, as shown in Fig. 2. For α ≥ 3 the finite-size effects are mainly from crossovers to SR case, and we find the original coupling J_ij is fine to obtain converged results.

When α ≥ 2D the system reduces to the SR case where there is no spontaneously continuous symmetry breaking phase at finite-temperature. When α ≤ D, the Hamiltonian is no longer extensive and there is no well-defined thermodynamic limit. Between α ∈ (2, 4) we carry out the QMC simulations^73,74,75 up to the linear system size of L = 256, as shown in Fig. 2, to determine the precise phase boundary as well as the critical exponents ν, β, and η. Note that because of strong finite-size effects, we only compute the region of α ∈ [2.3, 3.7] where our QMC simulations can obtain well-converged results. The origins of finite-size effects as α approaches the two boundaries, α = 2 and α = 4, exhibit inherent distinctions. When α → 2, the finite-size effect arises from the escalating intensity of LR (long-range) interactions, which fundamentally reduces the efficiency of the Ewald-corrected scheme. Conversely, as α → 4, the system approaches the regime where finite-temperature phase transitions do not exist. Consequently, near this boundary, the convergence of data points becomes exceedingly slow to be overcome. The results are shown in Figs. 1 and 3 and will be discussed in the critical exponents section. The QMC implementation is explained in the Supplementary Note 1.

Note that when α ≤ D, the Hamiltonian defined in Eq. (1) can actually be Kac-normalized^10,76 to be extensive with the addition of a factor $\frac{N-1}{{\sum }_{i < j}{J}_{ij}}$ to the Hamiltonian. Although this is not the focus of our paper, we examine the Kac-normalized Hamiltonian and the results are shown in Supplementary Note 2.

Critical exponents

Figure 2 shows our results at α = 2.5. We first use the crossing points of the Binder ratios to locate the critical temperature T_c. The crossing points of U(T, L) with U(T, 2L) are denoted as T^*(L), and through fitting to Eq. (9) the precise value of T_c can be obtained. We then use the value of T_c to perform data collapse according to Eq. (10) and Eq. (13) separately for 3 ≤ α < 4 and α < 3, to obtain the critical exponents ${\nu }^{{\prime} }$ and β. To obtain the anomalous dimension η_Q, we measure the correlation function G(L/2) at the obtained critical temperature T_c and obtain the anomalous dimension separately by fitting to Eq. (11) for 3 ≤ α < 4 and Eq. (14) for α < 3.

According to the conventions defined in Eq. (16) and field theory results of the mean-field critical exponents in Eq. (7), we can extract the expression for the three critical exponents in the Gaussian region which are ${\nu }^{{\prime} }=1$, $\beta =\frac{1}{2}$ and η_Q = 1. Outside the Gaussian region, we have η = 4 − α and γ defined in Eq. (8), and the value of β and ν can be obtained via solving the scaling relations between the critical exponents with $\nu =\frac{\gamma }{2-\eta }$ and $\beta =\frac{\gamma \eta }{2(2-\eta )}$.

The critical exponents we have obtained are shown in Fig. 3. We find that within the region we simulated, our QMC-obtained critical exponents ${\nu }^{{\prime} }(\alpha ),\beta (\alpha )$, and η_Q(α) match nicely with the prediction of both LR Gaussian theory (for α < 3) and the two-loop perturbative RG (for 3 ≤ α < 4), although there is a sign of deviating from two-loop RG predictions when α approaches 4. The possible deviation might be explained by the increasing finite-size effects near the boundary or the inefficiency of two-loop perturbative RG predictions when α is away from α = 3. The results can be further improved by either considering higher-order RG corrections or by pushing the QMC simulations to larger system sizes. Notably, the predicted form of anomalous dimension η receives no corrections at any α ∈ (2, 4)³ and our results confirm this argument with η matching with η = 4−α well in the whole region.

Discussions

Our investigation reveals a finite-temperature phase transition point in the 2D LR Heisenberg model, occurring for values of α within the range of α ∈ (2, 4), which separates the ferromagnetic phase from the paramagnetic phase. We observe that the phase transition point exhibits distinct behaviors: a Gaussian fixed point characterizes the transition for α ≤ 3, while a non-Gaussian fixed point emerges for 3 < α < 4. Similar phenomena have been observed in various LR systems^{6,7,8,9,10,14,18,19,23}. However, it is important to note that LR Ising-like systems differ intrinsically from LR Heisenberg-like systems. The former does not adhere to the Mermin-Wagner theorem, guaranteeing a finite-temperature transition for all α > 0, while the latter exhibits an upper critical value α_c beyond which the Mermin-Wagner theorem precludes the existence of phase transitions. In conclusion, our results clearly point out the LR quantum many-body system exhibit unconventional critical properties beyond the realm of the Mermin-Wagner theorem, which are also worthwhile to pursue in future experimentalrealizations, such as the quantum simulators.

Methods

Field theory analysis

We review here the field theory description of the model at the thermodynamic limit dating back to Ref. ³. The action can be written as

$$S=\int{d}^{D}x{d}^{D}{x}^{{\prime} }\frac{{\sum }_{i}{\phi }^{i}(x){\phi }^{i}({x}^{{\prime} })}{| x-{x}^{{\prime} }{| }^{d+\sigma }}+\lambda \int{d}^{D}x\mathop{\sum}\limits_{i}{\phi }^{i}{(x)}^{4},$$

(3)

to match the lattice model, we need α = d + σ. Under the scaling symmetry

$$x\to sx,{\phi }^{i}\to {s}^{-{{{\Delta }}}_{\phi }}{\phi }^{i},$$

(4)

the kinetic term remains unchanged when ${{{\Delta }}}_{\phi }=\frac{D-\sigma }{2}$. The coupling constant of ϕ⁴ interaction, on the other hand, scales as

$$\lambda \to {s}^{2\alpha -3D}\lambda .$$

(5)

When $\alpha \,< \frac{3D}{2}$, the coupling constant decays at larger length scale, which means the λϕ⁴ term is an irrelevant operator. The Gaussian fixed point at λ = 0 is a stable fixed point. Notice when λ = 0, the action is in a purely quadratic form, hence named “Gaussian" fixed point. This was established mathematically in Ref. ⁶. When $\alpha \,> \frac{3D}{2}$, the λϕ⁴ term becomes relevant, which triggers a renormalization group towards a different non-Gaussian fixed point³. One can perform standard renormalization technique to calculate the scaling dimension of various operators, by evaluating Feynman diagrams with non-conventional propagators. Such a calculation was first performed in³. Since the kinetic term in Eq. (3) is no-local, which can not receive corrections from any local counter terms, the scaling dimension of ϕ will not be renormalized (This can be easily seen by analyzing the Callan-Symanzik equation for the two-point function 〈ϕ(x)ϕ(y)〉, see for example, Ref. ⁷⁷). Equivalently, we have η = 2Δ_ϕ − D + 2. Our numerical result clearly confirms such a theoretical prediction. For a fixed σ in Eq. (3), we can define the upper critical dimension as the space-time dimension at which the ϕ⁴ term is marginal. The ${{{\Delta }}}_{{\phi }^{4}}=4{{{\Delta }}}_{\phi }={D}_{uc}$ gives us

$${D}_{uc}=2\sigma =2(\alpha -D).$$

(6)

We now focus on the D = 2 case. When α < 3, the critical behavior is controlled by the λ = 0 Gaussian fixed point. The critical behavior is similar to the usual Ising model at D > 4, due to the effect of dangerously irrelevant operators⁷⁸, the critical exponents are given by

$$\nu =\frac{1}{\alpha -2},\quad \beta =\frac{1}{2},\quad \eta =4-\alpha .$$

(7)

For example, the β = 1/2 exponent can be seen from the following argument. Deform the action (3) by a mass term ∫dx^Dtϕ(x)² with negative t and minimize the potential, we get 〈ϕ〉 ∝ (−t/λ)^β, with β = 1/2. The other exponents can be calculated by similar mean field theory analysis. The critical exponent η controls the two point function 〈ϕ(x)ϕ(y)〉 only at the strict thermodynamic limit. At finite sizes, the power law behavior will be modified to (14), which follows from analysing the effect of dangerously irrelevant operators carefully⁷⁹.

When α > 3, on the other hand, the second term in Eq. (3) becomes relevant, and renormalization group flows towards a different non-Gaussian fixed point³. The critical exponent η will remain at its mean field theory value³ as in Eq. (7). The other exponents, on the other hand receives correction at ${{{\mathcal{O}}}}\left({(\alpha -3)}^{2}\right)$. The two-loop perturbation results for γ is

$$\frac{1}{\gamma }=1-\left(\frac{n+2}{n+8}\right)\frac{\epsilon }{\sigma }-\frac{(n+2)(7n+20)}{{(n+8)}^{3}}Q(\sigma ){\left(\frac{\epsilon }{\sigma }\right)}^{2}+O\left({\epsilon }^{3}\right)$$

(8)

with $Q(\sigma )=\sigma \left[\psi (1)-2\psi \left(\frac{1}{2}\sigma \right)+\psi (\sigma )\right]$ where ψ(z) is the logarithmic derivative of the gamma function. The other critical exponents can be obtained by scaling relations between them.

When α > 4, the long-range model becomes equivalent to short-range models, due to the Mermin-Wagner theorem^80,81,82, the system will be gapped at finite-temperature. In the field-theory language, the value of α at which such a long-range to short-range crossover happens when the scaling dimension of ϕ equals to the scaling dimension of the short range model. In two dimensions, this gives α = 4^3,4.

Finite-size scaling analysis

To identify the phase transitions and obtain the critical exponents, we compute the square magnetization 〈m²〉, the correlation function G(r), and the Binder ratio $U(T,L)=\frac{5}{2}(1-\frac{1}{3}\frac{\langle {m}^{4}\rangle }{{\langle {m}^{2}\rangle }^{2}})$ in the QMC simulation. The crossing point of U(T, L) with U(T, 2L) is denoted as T^*(L) and it is expected to converge to the thermodynamic limit critical temperature T_c following the scaling relation:

$${T}^{* }(L)=a{L}^{-b}+{T}_{c}.$$

(9)

Given the values of T*(L) with sufficiently small errors and large enough system sizes L, the critical point T_c can be precisely located as shown in Fig. 2. To obtain the critical exponents ν, β and η, when D ≤ D_uc, the standard finite-size scaling behavior (FSS)^3,83 allows us to perform a data collapse near the critical points with the relation

$${m}^{2} \sim {L}^{-2\beta /\nu }\cdot f\left[{L}^{1/\nu }\left(T-{T}_{c}\right)\right],\quad T \sim {T}_{c}.$$

(10)

The anomalous dimension can also be obtained by fitting to the correlation function at the critical point T_c

$$G(r)=\langle {S}_{{{{{\bf{r}}}}}^{{\prime} }}^{z}{S}_{{{{{\bf{r}}}}}^{{\prime} }+{{{\bf{r}}}}}^{z}\rangle \sim {r}^{-D+2-\eta }.$$

(11)

However, when D > D_uc, which is our case when α < 3, the system enters the mean-field region where the hyperscaling relation breaks down, famously due to the effect of dangerously irrelevant operator^79,84,85. The scaling of the correlation length in this region shall follow the relation ${\xi }_{L} \sim {L}^{\frac{{D}_{{{\rm{uc}}}}}{D}}$ instead of ξ_L ~ L^{10,18,19,79,84,85,86}, and this leads to the modification of hyperscaling relation with

$${\nu }^{{\prime} }d=2-{\alpha }_{H},$$

(12)

where ${\nu }^{{\prime} }=\frac{{D}_{{{\rm{uc}}}}}{D}\nu$ and α_H is the critical exponent associated with the specific heat. For our system Eq. (1), the upper critical dimension is D_uc = 2(α − D), which we will explain later in the field theory analysis section. Accordingly, Eq. (10) also needs to be modified and the correct relation for data collapse in mean field region is^{10,18,19,79,84}

$${m}^{2} \sim {L}^{-2\beta /{\nu }^{{\prime} }}\cdot f\left[{L}^{1/{\nu }^{{\prime} }}\left(T-{T}_{c}\right)\right],\quad T \sim {T}_{c}.$$

(13)

The scaling of correlation function for α < 3 is also modified with

$$G(r)=\langle {S}_{{{{{\bf{r}}}}}^{{\prime} }}^{z}{S}_{{{{{\bf{r}}}}}^{{\prime} }+{{{\bf{r}}}}}^{z}\rangle \sim {r}^{-D+2-{\eta }_{Q}},$$

(14)

where

$${\eta }_{Q}=\frac{D}{{D}_{{{\mbox{uc}}}}}\eta -\frac{2D}{{D}_{{{\mbox{uc}}}}}+2.$$

(15)

By fitting to Eq. (14), the modified anomalous dimension η_Q as well as η can be obtained.

To unify the conventions, we define

$${\eta }_{Q}=\left\{\begin{array}{l}{\displaystyle\frac{D}{{D}_{{{\rm{uc}}}}}\eta -\frac{2D}{{D}_{{{\rm{uc}}}}}}+2,\quad\,{{\mbox{if}}}\,\,D \,>\, {D}_{{{\mbox{uc}}}},\\ \eta ,\qquad\qquad \qquad\qquad\,{{\mbox{if}}}\,\,D\le {D}_{{{\mbox{uc}}}}.\end{array}\right.$$

(16)

and

$${\nu }^{{\prime} }=\left\{\begin{array}{l}\frac{{D}_{{{\rm{uc}}}}}{D}\nu ,\quad\,{{\mbox{if}}}\,\,D \,>\, {D}_{{{\mbox{uc}}}},\\ \nu ,\quad \,{{\mbox{if}}}\,\,D\le {D}_{{{\mbox{uc}}}}.\end{array}\right.$$

(17)

Then ${\nu }^{{\prime} }$, β and η_Q will be obtained with the same scaling functions for both α < 3 and 3 ≤ α < 4.