Skip to main content
SpringerLink
Log in

Frequency theorem and inertial manifolds for neutral delay equations

  • Published:
Journal of Evolution Equations Aims and scope Submit manuscript

Abstract

We study the infinite-horizon quadratic regulator problem for linear control systems in Hilbert spaces, where the cost functional is in some sense unbounded. Our motivation comes from delay equations with the feedback part containing discrete delays or, in other words, measurements given by \(\delta \)-functionals, which are unbounded in \(L_{2}\). Working in an abstract context in which such (and many others, including parabolic boundary control problems) equations can be treated, we obtain a version of the Frequency Theorem. It guarantees the existence of a unique optimal process and shows that the optimal cost is given by a quadratic Lyapunov-like functional. In our adjacent works it is shown that such functionals can be used to construct inertial manifolds and allow to treat and extend many works in the field in a unified manner. Here we concentrate on applications to delay equations and especially mention the works of R.A. Smith on developments of convergence theorems and the Poincaré-Bendixson theory; and also the works of Yu.A. Ryabov, R.D. Driver and C. Chicone on inertial manifolds for equations with small delays and their recent generalization for equations of neutral type given by S. Chen and J. Shen.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Notes

  1. We use the convention that a sesquilinear form is linear in the first and conjugate-linear in the second argument.

  2. Note that in this case the solution \(v(\cdot )\) is classical and, in particular, we have \(v(\cdot ) \in C([0,T];\mathcal {D}(A))\) (see Theorem 6.5, Chapter I in [33]).

  3. A proper argument for this should use the (non-quadratic!) functionals

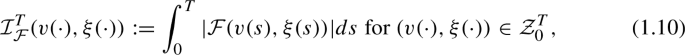
    figure a

    which can be also defined by continuity on \(\mathcal {Z}^{T}_{0}\).

  4. Note that Theorem 3 from [9] requires a clarification of its statement which is concerned with replacing formula (3.6) therein to an analog of (1.24) from the present work.

  5. Note that R.A. Smith used quadratic functionals and a “pocket” version of the Frequency Theorem in his works for ODEs [46], but he probably abandoned this approach for infinite-dimensional systems due to inability of obtaining optimal conditions for their existence [47]. Returning to this approach is our main motivation for this and adjacent works.

  6. Recall that the multiplication by a scalar in \(\mathbb {E}^{*}_{0}\) is given by the multiplication of functional’s values by scalar’s complex-conjugate.

  7. Here and below, the complexification of a real vector space \(\mathbb {E}_{0}\) is denoted by \(\mathbb {E}_{0}^\mathbb {C}\). For convenience, we use the same notations for the corresponding complexifcations of the operators.

  8. In fact, the Hilbert space structure is required only when we are studying the Fourier transform.

  9. Recall that \(\langle v, f \rangle := f(v)\) for any \(v \in \mathbb {E}\) and \(f \in \mathbb {E}^{*}\).

  10. This name comes from the Ancient Greek word \(\alpha \gamma \alpha \lambda \mu \alpha \) (agalma) that means an offering to a deity that, by its worth or artistic value, gives him/her special significance. So, “agalmanated” semantically can be understood as “glorified” or “adorned with glory”.

  11. In fact, the consideration of the operator S from (4.18) with \(\eta (\cdot ) = 0\) in \(L_{2}(-\tau ,T;\mathbb {R}^{n})\) and applying similar arguments to investigate its fixed point along with the fact that \(S^{2}\) is a uniform (in initial conditions) contraction show that A generates a \(C_{0}\)-semigroup.

  12. Here, for convenience, we put \((\mathcal {I}_{C}v)(\cdot ):= (\mathcal {I}_{C}\varPi _{2}v)(\cdot ) = (\mathcal {I}_{C}\phi )(\cdot )\) for \(v(\cdot )=(y(\cdot ),\phi (\cdot ))\). Moreover, as always, we omit emphasizing complexifications of the operators.

  13. That is \(\vartheta \) is the family of mappings \(\vartheta ^{t} :\mathbb {R} \rightarrow \mathbb {R}\) such that \(\vartheta ^{t}(s):=t+s\) for any \(t, s \in \mathbb {R}\)

  14. If there exists at least one bounded complete trajectory.

  15. For this it is required to satisfy (4.71) for two distinct values of \(\nu _{0}\) separating the same j roots. Clearly, if (4.71) is satisfied for some \(\nu _{0}\), it is also satisfied for all sufficiently close to \(\nu _{0}\) values due to the first resolvent identity combined with (4.31) and (4.38).

  16. Strictly speaking, the operator \(D_{0}\) also depends on \(\tau \) since it acts in the space \(C([-\tau ,0];\mathbb {R}^{n})\). In applications, we usually have \(M:=\sup _{\tau }\Vert D_{0}(\tau )\Vert < 1\). For example, \(D_{0}\phi = \alpha \phi (-\tau )\) with \(|\alpha | < 1\). This allows to vary \(\tau \rightarrow 0\) and \(\nu _{0} \rightarrow +\infty \) such that \(\tau \nu _{0} < -\ln M\).

References

  1. Adams R.A. Sobolev Spaces. Academic Press (1975)

  2. Anikushin M.M., Romanov A.O. Frequency conditions for the global stability of nonlinear delay equations with several equilibria. arXiv preprint, arXiv:2306.04716v2 (2023)

  3. Anikushin M.M. Variational description of uniform Lyapunov exponents via adapted metrics on exterior products. arXiv preprint, arXiv:2304.05713v2 (2023)

  4. Anikushin M.M. Spectral comparison of compound cocycles generated by delay equations in Hilbert spaces. arXiv preprint, arXiv:2302.02537v2 (2023)

  5. Anikushin M.M., Romanov A.O. Hidden and unstable periodic orbits as a result of homoclinic bifurcations in the Suarez-Schopf delayed oscillator and the irregularity of ENSO. Phys. D: Nonlinear Phenom., 445, 133653 (2023)

    Article  MathSciNet  Google Scholar 

  6. Anikushin M.M. Nonlinear semigroups for delay equations in Hilbert spaces, inertial manifolds and dimension estimates, Differ. Uravn. Protsessy Upravl., 4, (2022)

  7. Anikushin M.M. Inertial manifolds and foliations for asymptotically compact cocycles in Banach spaces. arXiv preprint, arXiv:2012.03821v3 (2022)

  8. Anikushin M.M. On the compactness of solutions to certain operator inequalities arising from the Likhtarnikov-Yakubovich frequency theorem. Vestnik St. Petersb. Univ. Math., 54(4), 301–310 (2021)

    Article  MathSciNet  Google Scholar 

  9. Anikushin M.M. Frequency theorem for parabolic equations and its relation to inertial manifolds theory. J. Math. Anal. Appl., 505(1), 125454 (2021)

    Article  MathSciNet  Google Scholar 

  10. Anikushin M.M. Almost automorphic dynamics in almost periodic cocycles with one-dimensional inertial manifold. Differ. Uravn. Protsessy Upravl., 2, 13–48 (2021), in Russian

    MathSciNet  Google Scholar 

  11. Anikushin M.M. A non-local reduction principle for cocycles in Hilbert spaces. J. Differ. Equations, 269(9), 6699–6731 (2020)

    Article  MathSciNet  Google Scholar 

  12. Anikushin M.M. On the Liouville phenomenon in estimates of fractal dimensions of forced quasi-periodic oscillations. Vestnik St. Petersb. Univ. Math., 52(3), 234–243 (2019)

    Article  MathSciNet  Google Scholar 

  13. Anikushin M.M., Reitmann V., Romanov A.O. Analytical and numerical estimates of the fractal dimension of forced quasiperiodic oscillations in control systems. Differ. Uravn. Protsessy Upravl., 2 (2019), in Russian

  14. Anikushin M.M. On the Smith reduction theorem for almost periodic ODEs satisfying the squeezing property. Rus. J. Nonlin. Dyn., 15(1), 97–108 (2019)

    MathSciNet  Google Scholar 

  15. Arov D.Z., Staffans O.J. The infinite-dimensional continuous time Kalman-Yakubovich-Popov inequality. Operator Theory: Advances and Applications, Birkhäuser Verlag Basel, Switzerland, 37–72 (2006)

  16. Bátkai A., and Piazzera S. Semigroups for Delay Equations. A K Peters, Wellesley (2005)

    Book  Google Scholar 

  17. Boutet de Monvel L., Chueshov I.D., Rezounenko A.V. Inertial manifolds for retarded semilinear parabolic equations, Nonlinear Anal. Theory Methods Appl., 34(6), 907–925 (1998)

  18. Burns J.A., Herdman T.L., Stech H.W. Linear functional differential equations as semigroups on product spaces. SIAM J. Math. Anal., 14(1), 98–116 (1983)

    Article  MathSciNet  Google Scholar 

  19. Chen S., Shen J. Smooth inertial manifolds for neutral differential equations with small delays. J. Dyn. Diff. Equat. (2021)

    Google Scholar 

  20. Chicone C. Inertial flows, slow flows, and combinatorial identities for delay equations. J. Dyn. Diff. Equat., 16(3), 805–831 (2004)

    Article  MathSciNet  Google Scholar 

  21. Chicone C. Inertial and slow manifolds for delay equations with small delays. J. Differ. Equations, 190(2), 364–406 (2003)

    Article  MathSciNet  Google Scholar 

  22. Chueshov I. Dynamics of Quasi-stable Dissipative Systems. Berlin: Springer (2015)

    Book  Google Scholar 

  23. Driver R.D. On Ryabov’s asymptotic characterization of the solutions of quasi-linear differential equations with small delays. SIAM Rev., 10(3), 329–341 (1968)

    Article  MathSciNet  Google Scholar 

  24. Dunford N., Schwartz J.T. Linear Operators, Part 1: General Theory. John Wiley & Sons (1988)

  25. Engel K.-J., Nagel R. One-Parameter Semigroups for Linear Evolution Equations. Springer-Verlag (2000)

  26. Gelig A.Kh., Leonov G.A., Yakubovich V.A. Stability of Nonlinear Systems with Non-Unique Equilibrium State. Nauka, Moscow (1978)

    Google Scholar 

  27. Hale J.K. Theory of Functional Differential Equations. Springer-Verlag, New York (1977)

    Book  Google Scholar 

  28. Koksch N., Siegmund S. Pullback attracting inertial manifolds for nonautonomous dynamical systems. J. Dyn. Differ. Equ., 14(4), 889–941 (2002)

    Article  MathSciNet  Google Scholar 

  29. Kostianko A., Zelik S. Kwak transform and inertial manifolds revisited. J. Dyn. Differ. Equ., 1–21 (2021)

  30. Kostianko A., Li X., Sun C., Zelik S. Inertial manifolds via spatial averaging revisited. SIAM J. Math. Anal., 54(1) (2022)

  31. Kostianko A. Zelik S. Inertial manifolds for 1D reaction-diffusion-advection systems. Part II: periodic boundary conditions, Commun. Pure Appl. Anal., 17(1), 285–317 (2018)

  32. Kostianko A. Zelik S. Inertial manifolds for 1D reaction-diffusion-advection systems. Part I: Dirichlet and Neumann boundary conditions, Commun. Pure Appl. Anal., 16(6), 2357–2376 (2017)

  33. Krein S.G. Linear Differential Equations in Banach Space, AMS (1971)

  34. Kuznetsov N.V., Reitmann V. Attractor Dimension Estimates for Dynamical Systems: Theory and Computation. Switzerland: Springer International Publishing AG (2020)

    Google Scholar 

  35. Likhtarnikov A.L., Yakubovich V.A. The frequency theorem for continuous one-parameter semigroups. Math. USSR-Izv. 41(4), 895–911 (1977), in Russian

    MathSciNet  Google Scholar 

  36. Likhtarnikov A.L., Yakubovich V.A. The frequency theorem for equations of evolutionary type. Sib. Math. J., 17(5), 790–803 (1976)

    Article  Google Scholar 

  37. Lions J.-L. Optimal Control of Systems Governed by Partial Differential Equations. Springer Verlag (1971)

  38. Louis J.-Cl., Wexler D. The Hilbert space regulator problem and operator Riccati equation under stabilizability. Annales de la Société Scientifique de Bruxelles, 105(4), 137–165 (1991)

  39. Miklavčič M. A sharp condition for existence of an inertial manifold. J. Dyn. Differ. Equ., 3(3), 437–456 (1991)

    Article  MathSciNet  Google Scholar 

  40. Pandolfi L. The standard regulator problem for systems with input delays. An approach through singular control theory. Appl. Math. Optim., 31(2), 119–136 (1995)

  41. Pritchard A., Salamon D. The linear-quadratic control problem for retarded systems with delays in control and observation. IMA J. Math. Control., 2(4), 335–362 (1985)

    Article  Google Scholar 

  42. Proskurnikov A.V. A new extension of the infinite-dimensional KYP lemma in the coercive case. IFAC-PapersOnLine, 48(1), 246–251 (2015)

    Article  Google Scholar 

  43. Romanov A.V. Sharp estimates of the dimension of inertial manifolds for nonlinear parabolic equations. Izvestiya: Mathematics, 43(1), 31–47 (1994)

  44. Ryabov Yu.A. Asymptotic properties of solutions of weakly nonlinear systems with small delay. Trudy Sem. Teor. Differential. Uravnenii s Otklon. Argumentom Univ. Druzhby Narodov Patrisa Lumumby, 5, 213–222 (1967), in Russian

  45. Smith R.A. Poincaré-Bendixson theory for certain retarded functional-differential equations. Differ. Integral Equ., 5(1), 213–240 (1992)

    Google Scholar 

  46. Smith R.A. Orbital stability for ordinary differential equations. J. Differ. Equations. 69(2), 265–287 (1987)

    Article  MathSciNet  Google Scholar 

  47. Smith R.A. Existence of periodic orbits of autonomous retarded functional differential equations. Math. Proc. Cambridge Philos. Soc., 88(1) (1980)

  48. Suarez M.J., Schopf P.S. A delayed action oscillator for ENSO. J. Atmos. Sci., 45(21), 3283–3287 (1988)

    Article  Google Scholar 

  49. Zelik S. Attractors. Then and now. Uspekhi Mat. Nauk, 78(4), 53–198 (2023)

    MathSciNet  Google Scholar 

  50. Zelik S. Inertial manifolds and finite-dimensional reduction for dissipative PDEs. P. Roy. Soc. Edinb. A, 144(6), 1245–1327 (2014)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author is grateful to the anonymous referee for careful reading and valuable suggestions, which particularly revealed technical flaws and led to significant improvements in the overall exposition.

Funding

The reported study was funded by the Russian Science Foundation (Project 22-11-00172).

Author information

Authors and Affiliations

  1. Department of Applied Cybernetics, Faculty of Mathematics and Mechanics, St Petersburg University, 28 Universitetskiy prospekt, Peterhof, Russia, 198504

    Mikhail Anikushin

Authors
  1. Mikhail Anikushin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mikhail Anikushin.

Ethics declarations

Conflict of interest

The author has no conflicts of interest to declare that are relevant to the content of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Anikushin, M. Frequency theorem and inertial manifolds for neutral delay equations. J. Evol. Equ. 23, 66 (2023). https://doi.org/10.1007/s00028-023-00915-w

Download citation

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00028-023-00915-w

Keywords

Mathematics Subject Classification

Search

Navigation