Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-28T06:58:53.124Z Has data issue: false hasContentIssue false
  • English
  • Français

On the ergodicity of unitary frame flows on Kähler manifolds

Part of: Complex manifolds Ergodic theory Global differential geometry

Published online by Cambridge University Press:  16 October 2023

MIHAJLO CEKIĆ ,
THIBAULT LEFEUVRE ,
ANDREI MOROIANU  and
UWE SEMMELMANN
MIHAJLO CEKIĆ
Affiliation:
Institut für Mathematik, Universität Zürich, Winterthurerstrasse 190, CH-8057 Zürich, Switzerland (e-mail: mihajlo.cekic@math.uzh.ch)
THIBAULT LEFEUVRE*
Affiliation:
Université de Paris and Sorbonne Université, CNRS, IMJ-PRG, F-75006 Paris, France
ANDREI MOROIANU
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire de mathématiques d’Orsay, 91405, Orsay, France (e-mail: andrei.moroianu@math.cnrs.fr)
UWE SEMMELMANN
Affiliation:
Institut für Geometrie und Topologie, Fachbereich Mathematik, Universität Stuttgart, Pfaffenwaldring 57, 70569 Stuttgart, Germany (e-mail: uwe.semmelmann@mathematik.uni-stuttgart.de)
*
e-mail: tlefeuvre@imj-prg.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 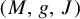$(M,g,J)$ be a closed Kähler manifold with negative sectional curvature and complex dimension 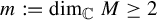$m := \dim _{\mathbb {C}} M \geq 2$. In this article, we study the unitary frame flow, that is, the restriction of the frame flow to the principal 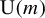$\mathrm {U}(m)$-bundle 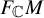$F_{\mathbb {C}}M$ of unitary frames. We show that if 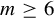$m \geq 6$ is even and 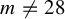$m \neq 28$, there exists 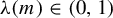$\unicode{x3bb} (m) \in (0, 1)$ such that if 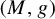$(M, g)$ has negative 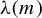$\unicode{x3bb} (m)$-pinched holomorphic sectional curvature, then the unitary frame flow is ergodic and mixing. The constants 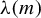$\unicode{x3bb} (m)$ satisfy 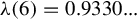$\unicode{x3bb} (6) = 0.9330...$, $\lim _{m \to +\infty } \unicode{x3bb} (m) = {11}/{12} = 0.9166...$, and 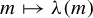$m \mapsto \unicode{x3bb} (m)$ is decreasing. This extends to the even-dimensional case the results of Brin and Gromov [On the ergodicity of frame flows. Invent. Math. 60(1) (1980), 1–7] who proved ergodicity of the unitary frame flow on negatively curved compact Kähler manifolds of odd complex dimension.

Keywords

partially hyperbolic flowsKähler manifoldsergodic theoryframe flowsPestov identity

MSC classification

Primary: 37A05: Measure-preserving transformations 37A20: Orbit equivalence, cocycles, ergodic equivalence relations 37A25: Ergodicity, mixing, rates of mixing 32Q15: Kähler manifolds
Secondary: 53C10: $G$-structures 53C22: Geodesics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 30
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amirov, A.. Existence and uniqueness theorems for the solution of an inverse problem for the transfer equation. Sibirsk. Mat. Zh. 27(6) (1986), 3–20.Google Scholar
Anosov, D. V.. Geodesic flows on closed Riemannian manifolds of negative curvature. Tr. Mat. Inst. Steklova 90 (1967), 209.Google Scholar
Berger, M.. Pincement riemannien et pincement holomorphe. Ann. Sc. Norm. Super. Pisa Cl. Sci. (3) 14 (1960), 151–159.Google Scholar
Berger, M.. Sur quelques variétés riemanniennes suffisamment pincées. Bull. Soc. Math. France 88 (1960), 57–71.CrossRefGoogle Scholar
Bishop, R. L. and Goldberg, S. I.. On the topology of positively curved Kähler manifolds. Tohoku Math. J. (2) 15 (1963), 359–364.CrossRefGoogle Scholar
Brin, M. and Gromov, M.. On the ergodicity of frame flows. Invent. Math. 60(1) (1980), 1–7.CrossRefGoogle Scholar
Bourguignon, J.-P. and Karcher, H.. Curvature operators: pinching estimates and geometric examples. Ann. Sci. Éc. Norm. Supér. (4) 11(1) (1978), 71–92.CrossRefGoogle Scholar
Brin, M. and Karcher, H.. Frame flows on manifolds with pinched negative curvature. Compos. Math. 52(3) (1984), 275–297.Google Scholar
Brin, M. and Pesin, Y. B.. Partially hyperbolic dynamical systems. Izv. Akad. Nauk SSSR Ser. Mat. 38 (1974), 170–212.Google Scholar
Burns, K. and Pollicott, M.. Stable ergodicity and frame flows. Geom. Dedicata 98 (2003), 189–210.CrossRefGoogle Scholar
Brin, M.. Topological transitivity of a certain class of dynamical systems, and flows of frames on manifolds of negative curvature. Funktsional. Anal. i Prilozhen. 9(1) (1975), 9–19.CrossRefGoogle Scholar
Brin, M.. The topology of group extensions of $C$ -systems. Mat. Zametki 18(3) (1975), 453–465.Google Scholar
Brin, M.. Ergodic theory of frame flows. Ergodic Theory and Dynamical Systems, II (College Park, MD, 1979/1980) (Progress in Mathematics, 21). Ed. Katok, A.. Birkhäuser, Boston, MA, 1982, pp. 163–183.CrossRefGoogle Scholar
Bott, R. and Tu, L. W.. Differential Forms in Algebraic Topology (Graduate Texts in Mathematics, 82). Springer-Verlag, New York–Berlin, 1982.CrossRefGoogle Scholar
Čadek, M. and Crabb, M.. $G$ -structures on spheres. Proc. Lond. Math. Soc. (3) 93(3) (2006), 791–816.CrossRefGoogle Scholar
Cekić, M. and Lefeuvre, T.. The Holonomy inverse problem. J. Eur. Math. Soc. (JEMS), to appear.Google Scholar
Cekić, M., Lefeuvre, T., Moroianu, A. and Semmelmann, U.. On the ergodicity of the frame flow on even-dimensional manifolds. Preprint, 2023, arXiv:2111.14811.Google Scholar
Cekić, M., Lefeuvre, T., Moroianu, A. and Semmelmann, U.. Towards Brin’s conjecture on frame flow ergodicity: new progress and perspectives. Math. Res. Rep. 3 (2022), 21–34.Google Scholar
Guillarmou, C., Paternain, G. P., Salo, M. and Uhlmann, G.. The X-ray transform for connections in negative curvature. Comm. Math. Phys. 343(1) (2016), 83–127.CrossRefGoogle Scholar
Howe, R. E. and Moore, C. C.. Asymptotic properties of unitary representations. J. Funct. Anal. 32(1) (1979), 72–96.CrossRefGoogle Scholar
Hopf, E.. Fuchsian groups and ergodic theory. Trans. Amer. Math. Soc. 39(2) (1936), 299–314.CrossRefGoogle Scholar
Hasselblatt, B. and Pesin, Y.. Partially hyperbolic dynamical systems. Handbook of Dynamical Systems. Volume 1B. Eds. Katok, A. and Hasselblatt, B.. Elsevier, Amsterdam, 2006, pp. 1–55.Google Scholar
Jakobson, D. and Strohmaier, A.. High energy limits of Laplace-type and Dirac-type eigenfunctions and frame flows. Comm. Math. Phys. 270(3) (2007), 813–833.CrossRefGoogle Scholar
Jakobson, D., Strohmaier, A. and Zelditch, S.. On the spectrum of geometric operators on Kähler manifolds. J. Mod. Dyn. 2(4) (2008), 701–718.CrossRefGoogle Scholar
Kobayashi, S. and Nomizu, K.. Foundations of Differential Geometry. Volume I (Wiley Classics Library, 62). John Wiley & Sons, Inc., New York, 1996; reprint of the 1963 original, A Wiley-Interscience Publication.Google Scholar
Lefeuvre, T.. Isometric extensions of Anosov flows via microlocal analysis. Comm. Math. Phys. 399(1) (2023), 453–479.CrossRefGoogle Scholar
Leonard, P.. $G$ -structures on spheres. Trans. Amer. Math. Soc. 157 (1971), 311–327.Google Scholar
Mukhometov, R. G.. Inverse kinematic problem of seismic on the plane. Akad. Nauk. SSSR 6 (1975), 243–252.Google Scholar
Mukhometov, R. G.. On a problem of reconstructing Riemannian metrics. Sibirsk. Mat. Zh. 22(3) (1981), 119–135, 237.Google Scholar
Paternain, G. P.. Geodesic Flows (Progress in Mathematics, 180). Birkhäuser Boston, Inc., Boston, MA, 1999.CrossRefGoogle Scholar
Pestov, L. N. and Sharafutdinov, V. A.. Integral geometry of tensor fields on a manifold of negative curvature. Sibirsk. Mat. Zh. 29(3) (1988), 114–130, 221.Google Scholar
Paternain, G. P., Salo, M. and Uhlmann, G.. Invariant distributions, Beurling transforms and tensor tomography in higher dimensions. Math. Ann. 363(1–2) (2015), 305–362.CrossRefGoogle Scholar
Sharafutdinov, V. A.. Integral Geometry of Tensor Fields (Inverse and Ill-Posed Problems Series, 1). VSP, Utrecht, 1994.CrossRefGoogle Scholar