Labor Supply Flexibility and Portfolio Selection with Early Retirement Option

Abstract

In this paper, we study the optimal consumption, investment, and life insurance problem of an economic agent who can choose a flexible labor supply and has an option to retire early with the existence of a mandatory retirement date. We model the agent’s preference as the Cobb–Douglas utility, which is a function of consumption and leisure, and consider the agent’s unit wage rate as a stochastic process. The optimization problem has a feature of combining both stochastic control and optimal stopping. To attack this problem, we adopt a dual-martingale approach and derive a dual problem, which is a finite-horizon optimal stopping problem choosing the early retirement date. Based on the partial differential equation techniques, we fully analyze the variational inequality arising from the dual problem. We show that the optimal early retirement time is characterized as the free boundary of the agent’s wealth-to-wage ratio. Finally, we establish a duality theorem and obtain an integral equation representation of optimal strategies.

Appendices

Appendix

Proof of Proposition 3.2

First, we use the following transformation to transform the degenerate backward parabolic problem in the VI (39) into a familiar forward non-degenerate parabolic problem:

$$\begin{aligned} \tau = T-t, \qquad \xi = \log z, \qquad \phi (\tau ,\xi ) = \Phi (t,z). \end{aligned}$$

(74)

Then we have the following VI:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \partial _\tau \phi (\tau ,\xi ) -{{{\mathcal {L}}}}_3\phi (\tau ,\xi ) \ge \psi (\xi ),\;\;\;&{}\text{ if }\;\;\phi (\tau ,\xi )=0,\\ \partial _\tau \phi (\tau ,\xi ) -{{{\mathcal {L}}}}_3\phi (\tau ,\xi ) = \psi (\xi ),\;\;\;&{}\text{ if }\;\;\phi (\tau ,\xi )>0,\\ \phi (0,\xi ) =0,\;\;\;\forall \xi \in (-\infty ,\infty ), \end{array}\right. } \end{aligned} \end{aligned}$$

(75)

where ${{{\mathcal {L}}}}_3$ and $\psi (\xi )$ are given by

$$\begin{aligned} {{{\mathcal {L}}}}_3 = \dfrac{\sigma _z^2}{2}\dfrac{\partial ^2}{\partial x^2} +\left( \beta _w-r_w+\dfrac{\sigma _z^2}{2} \right) \dfrac{\partial }{\partial x}-r_w \end{aligned}$$

(76)

and

$$\begin{aligned} \psi (\xi )&= \left[ \dfrac{\gamma }{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^{\frac{\gamma _1-\gamma }{\gamma }}e^{-\frac{1}{\gamma }\xi }+{\bar{L}}\right] \textbf{1}_{\{ {\log z_L}<\xi \}}\nonumber \\&\quad +\left[ \dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}e^{-\frac{1}{\gamma _1}\xi }+\big ({\bar{L}}-L\big )\right] \textbf{1}_{\{ \xi \le {\log z_L}\}} \end{aligned}$$

(77)

$$\begin{aligned}&\quad -\dfrac{\gamma _1}{1-\gamma _1}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}e^{-\frac{1}{\gamma _1}\xi }. \end{aligned}$$

(78)

We denote by ${{{{\mathcal {D}}}}_T^2}$ the domain of the problem (75), that is, ${{{{\mathcal {D}}}}_T^2}:= (0,T] \times {\mathbb {R}}$.

Proposition A.1

The VI (75) has a unique strong solution $\phi$ satisfying the following properties:

• (a) $\phi \in W^{1,2}_{p,\textrm{loc}}({{{{\mathcal {D}}}}_T^2}) \cap C(\overline{{{{{\mathcal {D}}}}_T^2}})$ for any $p \ge 1$, and $\partial _{\xi } \phi \in C(\overline{{{{{\mathcal {D}}}}_T^2}})$.

• (b) $\partial _{\xi } \phi \ge 0$ in ${{{{\mathcal {D}}}}_T^2}$ and $\partial _\tau \phi \ge 0$ a.e. in ${{{{\mathcal {D}}}}_T^2}$.

Proof

(a) From the properties of $\Psi (z)$, we know that

$$\begin{aligned} \Psi \in C^1(0,\infty ), \qquad \Psi \in W^{2,p}_{\textrm{loc}}(0,\infty ), \ \, \forall p \ge 1, \quad \text {and} \quad \Psi '(z)>0, \ \, \forall z \in (0,\infty ). \end{aligned}$$

Therefore, $\psi (\xi )=\Psi (e^\xi )$ satisfies

$$\begin{aligned} \psi \in C^1({\mathbb {R}}), \qquad \psi \in W^{2,p}_{\textrm{loc}}({\mathbb {R}}), \ \, \forall p \ge 1, \quad \text {and} \quad \psi '(\xi )>0, \ \, \forall \xi \in {\mathbb {R}}. \end{aligned}$$

(79)

Since the lower obstacle and the initial value of the problem (75) are zero functions, and the inhomogeneous term $\psi (\xi )$ satisfies (79), the problem (75) has a unique strong solution $\phi$ with $\phi \in W^{1,2}_{p,\textrm{loc}}({{{{\mathcal {D}}}}_T^2}) \cap C(\overline{{{{{\mathcal {D}}}}_T^2}})$ for any $p \ge 1$ and $\partial _{\xi } \phi \in C(\overline{{{{{\mathcal {D}}}}_T^2}})$ (see for instance p. 77 in Friedman [14]).

(b) We set $\phi _1(\tau ,\xi ):= \phi (\tau ,\xi +\varsigma )$ for $\varsigma >0$. Then $\phi _1$ satisfies the VI

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \partial _\tau \phi _1(\tau ,\xi ) -{{{\mathcal {L}}}}_3\phi _1(\tau ,\xi ) \ge \psi (\xi +\varsigma ),\;\;\;&{}\text{ if }\;\;\phi _1(\tau ,\xi )=0,\\ \partial _\tau \phi _1(\tau ,\xi ) -{{{\mathcal {L}}}}_3\phi _1(\tau ,\xi ) = \psi (\xi +\varsigma ),\;\;\;&{}\text{ if }\;\;\phi _1(\tau ,\xi )>0,\\ \phi _1(0,\xi ) =0,\;\;\;\forall \xi \in (-\infty ,\infty ). \end{array}\right. } \end{aligned} \end{aligned}$$

(80)

We see from (79) that $\psi$ is an increasing function. Therefore, $\psi (\xi +\varsigma ) > \psi (\xi )$ for all $x \in {\mathbb {R}}$. Since the lower obstacle and the initial condition for $\phi$ and $\phi _1$ are the same, by the comparison principle for VIs (see Friedman [13]), we obtain that $\phi _1(\tau ,\xi ) = \phi (\tau ,\xi +\varsigma ) \ge \phi (\tau ,\xi )$ for all $(\tau ,\xi ) \in {{{{\mathcal {D}}}}_T^2}$. Since this holds for any small $\varsigma >0$, we deduce that $\partial _{\xi } \phi \ge 0$ in ${{{{\mathcal {D}}}}_T^2}$.

We now set $\phi _2(\tau ,\xi ):=\phi (\tau +\varsigma ,\xi )$ for small $\varsigma >0$. Then $\phi _2$ satisfies

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \partial _\tau \phi _2(\tau ,\xi ) -{{{\mathcal {L}}}}_3\phi _2(\tau ,\xi ) \ge \psi (\xi ),\;\;&{}\text{ if }\;\;\phi _2(\tau ,\xi )=0\;\;\text{ and }\;\;(\tau ,\xi )\in {{{\mathcal {D}}}}_{T-\varsigma }^2\\ &{}\quad :=(\delta ,T]\times {\mathbb {R}},\\ \partial _\tau \phi _2(\tau ,\xi ) -{{{\mathcal {L}}}}_3\phi _2(\tau ,\xi ) = \psi (\xi ),\;\;&{}\text{ if }\;\;\phi _2(\tau ,\xi )>0\;\;\text{ and }\;\;(\tau ,\xi )\in {{{\mathcal {D}}}}_{T-\varsigma }^2,\\ \phi _2(0,\xi )=\phi (\varsigma ,\xi ) \ge 0,\;\;\;\forall \xi \in (-\infty ,\infty ). \end{array}\right. }\qquad \quad \end{aligned} \end{aligned}$$

(81)

By the comparison principle, we obtain $\phi _2(\tau ,\xi ) = \phi (\tau +\varsigma ,\xi ) \ge \phi _2(\tau ,\xi )$ for all $(\tau ,\xi ) \in {{{\mathcal {D}}}}_{T-\varsigma }^2$. Since this holds for any small $\varsigma >0$, we conclude that $\partial _\tau \phi \ge 0$ a.e. in ${{{{\mathcal {D}}}}_T^2}$. $\square$

By Proposition A.1, $\phi$ is monotone increasing. Therefore, we can define the free boundary as

$$\begin{aligned} \lambda (\tau ) = \inf \{ \xi \in {\mathbb {R}}: \phi (\tau ,\xi )>0 \}, \quad \tau \in (0,T]. \end{aligned}$$

Lemma A.1

  The following statements are true:

• (a) There exists a unique $z_T>0$ such that

  $$\begin{aligned} \Psi (z_T)=0. \end{aligned}$$

• (b) $\Psi (z_L)>0$. Hence, $z_T<z_L$ holds and $z_T$ is given by

  $$\begin{aligned} z_T=\left( \dfrac{{\bar{L}}-L}{\frac{\gamma _1}{1-\gamma _1}\Bigg ({\bar{L}}^ {\frac{\gamma _1-\gamma }{\gamma _1}}-{L}^{\frac{\gamma _1-\gamma }{\gamma _1}}\Bigg )}\right) ^{-\gamma _1}. \end{aligned}$$

Proof

(a) By the definition of $\Psi (z)$, we see that

$$\begin{aligned} \lim _{z \rightarrow 0+} \Psi (z) = -\infty \qquad \text {and} \qquad \lim _{z \rightarrow +\infty } \Psi (z) = {\bar{L}}. \end{aligned}$$

Since $\Psi '(z)>0$ for all $z>0$, we deduce that there exists a unique $z_T>0$ such that $\Psi (z_T)=0$.

(b) Note that

$$\begin{aligned} \Psi (z_L)&= \frac{\gamma }{\gamma _1-\gamma }L + {\bar{L}} - \frac{\gamma _1}{\gamma _1-\gamma }L^{\frac{\gamma }{\gamma _1}}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}\nonumber \\&={\bar{L}}\left( \frac{\gamma }{\gamma _1-\gamma }\dfrac{L}{{\bar{L}}} + 1 - \frac{\gamma _1}{\gamma _1-\gamma }\left( \dfrac{L}{{\bar{L}}}\right) ^\frac{\gamma }{\gamma _1}\right) . \end{aligned}$$

(82)

Let us temporarily denote ${\widehat{\Psi }}(\nu )$ by

$$\begin{aligned} {\widehat{\Psi }}(\nu )=\frac{\gamma }{\gamma _1-\gamma }\nu + 1 - \frac{\gamma _1}{\gamma _1-\gamma }\nu ^\frac{\gamma }{\gamma _1} \end{aligned}$$

for $0<\nu <1$.

Then,

$$\begin{aligned} {\widehat{\Psi }}'(\nu )&=\dfrac{\gamma }{\gamma _1-\gamma }-\dfrac{\gamma }{\gamma _1-\gamma }\nu ^{\frac{\gamma }{\gamma _1}-1}\\&=\dfrac{\gamma }{\gamma _1-\gamma }\left( 1-\nu ^{-\frac{\gamma _1-\gamma }{\gamma _1}}\right)<0\;\;\;\;\text{ for }\;\;0<\nu <1. \end{aligned}$$

Thus, ${\widehat{\Psi }}(\nu )$ is strictly decreasing in $0<\nu <1$. It follows that

$$\begin{aligned} {\widehat{\Psi }}(\nu )>{\widehat{\Psi }}(1)=0\;\;\text{ for }\;\;0<\nu <1. \end{aligned}$$

Since $0<L<{\bar{L}}$, we deduce that

$$\begin{aligned} \Psi (z_L) = {\bar{L}}{\widehat{\Psi }}\left( \dfrac{L}{{\bar{L}}}\right) >0. \end{aligned}$$

Finally, since $\Psi (z_T)=0$, $\Psi (z_L) > 0$, and $\Psi '(z)>0$ for all $z>0$, it is clear that $z_T<z_L$. $\square$

Lemma A.2

The free boundary $\lambda (\tau )$ is strictly decreasing in (0, T] and satisfies $\lambda (\tau ) \le \log z_T$ in (0, T].

Proof

From Proposition A.1, we know that $\partial _\tau \phi \ge 0$ a.e. in ${{{{\mathcal {D}}}}_T^2}$. Therefore, the free boundary $\lambda (\tau )$ is decreasing in (0, T].

We claim that $\lambda (\tau ) \le \log z_T$ in (0, T]. If there exists $\tau _0 \in (0,T]$ such that $\lambda (\tau _0)>\log z_T$, we would have $\lambda (\tau ) \ge \xi _0:= \lambda (\tau _0) > \log z_T$ for all $\tau \in (0,\tau _0)$. Then

$$\begin{aligned} \phi (\tau ,\xi )=0 \quad \, \text {in} \ \, (0,\tau _0) \times (-\infty ,\xi _0). \end{aligned}$$

(83)

By (75), (83) and the definition of $\lambda (\tau )$, we see that

$$\begin{aligned} 0 = \partial _\tau \phi (\tau ,\xi ) -{{{\mathcal {L}}}}_3\phi (\tau ,\xi ) \ge \psi (\xi ) \quad \, \text {in} \ \, (0,\tau _0) \times (-\infty ,\xi _0). \end{aligned}$$

(84)

Since $\psi (\xi )=\Psi (e^\xi )$, it follows from Lemma A.1 that

$$\begin{aligned} \psi (\xi ) \le 0 \quad \Longleftrightarrow \quad \xi \le \log z_T. \end{aligned}$$

(85)

Therefore, it follows from (84) and (85) that $\xi _0 \le \log z_T$. This is a contradiction. Hence, $\lambda (\tau ) \le \log z_T$ in (0, T].

Let us now show that $\lambda (\tau )$ is strictly decreasing in (0, T]. To show this, suppose that $\lambda (\tau )$ is not strictly decreasing in (0, T]. Then we would have $\lambda (\tau _1)=\lambda (\tau _2)=\xi _0$ for some $0< \tau _1 < \tau _2 \le T$. By the definition of $\lambda$, we obtain $\phi (\tau ,\xi _0)=0$ for all $\tau \in [\tau _1,\tau _2]$. Hence, $\partial _\tau \phi (\tau ,\xi _0)=0$ for all $\tau \in (\tau _1,\tau _2)$. Meanwhile, we see that

$$\begin{aligned} \partial _\tau \phi -{{{\mathcal {L}}}}_3\phi = \psi (\xi ) \quad \, \text {in} \ \, (\tau _1, \tau _2) \times (\xi _0, +\infty ), \end{aligned}$$

and hence

$$\begin{aligned} \partial _\tau (\partial _\tau \phi ) -{{{\mathcal {L}}}}_3(\partial _\tau \phi ) = 0 \quad \, \text {in} \ \, (\tau _1, \tau _2) \times (\xi _0, +\infty ). \end{aligned}$$

Since $\partial _\tau \phi \ge 0$, the function $\partial _\tau \phi$ achieves its minimum at $\xi =\xi _0$. Applying the Hopf lemma (see p. 349 in Evans [10]), we deduce that $\partial _{\xi } (\partial _\tau \phi )(\tau ,\xi _0) > 0$. However, we obtain from the definition of $\lambda$ that $\partial _{\xi } \phi (\tau , \xi _0)=0$ for all $\tau \in [\tau _1,\tau _2]$, and so $\partial _{\tau \xi } \phi (\tau , \xi _0)=0$ for all $\tau \in (\tau _1,\tau _2)$. This is a contradiction. Therefore, $\lambda (\tau )$ is strictly decreasing in (0, T]. $\square$

Proposition A.2

The limit of the free boundary $\lambda (\tau )$ is given by

$$\begin{aligned} \lambda (0):= \lim _{\tau \rightarrow 0+} \lambda (\tau ) = \log z_T. \end{aligned}$$

(86)

Proof

From Lemma A.2, we know that there exists some limit $\displaystyle \lambda (0):= \lim _{\tau \rightarrow 0+} \lambda (\tau ) \le \log z_T$. Suppose, contrary to our claim, that $\displaystyle \lambda (0) = \lim _{\tau \rightarrow 0+} \lambda (\tau ) < \log z_T$. Since $\lambda (\tau )$ is strictly decreasing, we then have $\lambda (\tau ) \le \xi _0$ for all $\tau \in [0,T]$, where $\xi _0:=\lambda (0)<\log z_T$. It follows from (75) and the definition of $\lambda (\tau )$ that

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \partial _\tau \phi (\tau ,\xi ) -{{{\mathcal {L}}}}_3\phi (\tau ,\xi ) = \psi (\xi ) \quad &{} \text {in} \ (0,T) \times (\xi _0, \log z_T),\\ \phi (0,\xi )=0 &{}\text {on} \ (\xi _0, \log z_T). \end{array}\right. } \end{aligned} \end{aligned}$$

Note that for $\xi _0<\xi<\frac{1}{2}(\xi _0+\log z_T) < \log z_T$, we have

$$\begin{aligned} \psi (\xi )< \psi \left( \frac{\xi _0+\log z_T}{2} \right) < \psi (\log z_T)=0. \end{aligned}$$

This yields that

$$\begin{aligned} \partial _\tau \phi (0,\xi ) \le {{{\mathcal {L}}}}_3\phi (0,\xi ) + \psi \left( \frac{\xi _0+\log z_T}{2} \right) < 0, \end{aligned}$$

which is a contradiction. Therefore, we conclude that $\lambda (0) = \log z_T$. $\square$

Proposition A.3

The free boundary $\lambda (\tau )$ is smooth in (0, T].

Proof

We first show that the free boundary $\lambda (\tau )$ is continuous in (0, T]. If not, there exist $\tau _0 \in (0,T]$, $\xi _0 \in {\mathbb {R}}$ and small $\varepsilon _0, \iota _0 > 0$ such that $\lambda (\tau _0-\varepsilon ) \ge \xi _0+\iota _0$ and $\lambda (\tau _0+\varepsilon ) \le \xi _0$ for all $\varepsilon \in (0,\varepsilon _0)$. By the definition of $\lambda (\tau )$, we see that for any $\varepsilon \in (0,\varepsilon _0)$,

$$\begin{aligned} \phi (\tau _0-\varepsilon ,\xi ) = 0, \qquad \forall \xi \le \xi _0+\iota _0, \end{aligned}$$

(87)

and

$$\begin{aligned} \phi (\tau _0+\varepsilon ,\xi )> 0, \qquad \forall \xi > \xi _0. \end{aligned}$$

(88)

Moreover, by (87) and the continuity of $\phi$, we have

$$\begin{aligned} \phi (\tau _0,\xi ) = 0, \qquad \forall \xi \le \xi _0+\iota _0. \end{aligned}$$

(89)

Therefore, it follows from (88) and (89) that

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \partial _\tau \phi -{{{\mathcal {L}}}}_3\phi = \psi (\xi ),\;\;\;&{}\text{ in }\;\;(\tau _0,\tau _0+\varepsilon _0) \times (\xi _0,\xi _0+\iota _0),\\ \phi (\tau _0,\xi )=0,\;\;\;&{}\text{ on }\;\;(\xi _0,\xi _0+\iota _0). \end{array}\right. } \end{aligned} \end{aligned}$$

Since $\lambda (\tau )$ is strictly decreasing in (0, T], we note from Lemma A.2 that $\lambda (\tau _0)<\log z_T$. Since $\psi (\xi )$ is increasing, we have $\psi (\xi ) \le \psi (\xi _0+\iota _0) \le \psi (\lambda (\tau _0)) < \psi (\log z_T)=\psi (z_T)=0$ for all $\xi \le \xi _0+\iota _0$, by (89). Thus, it follows that $\partial _\tau \phi (\tau _0,\xi ) \le \psi (\lambda (\tau _0)) < 0$ for any $x \in (\xi _0,\xi _0+\iota _0)$, which is a contradiction. Hence, the free boundary $\lambda (\tau )$ is continuous in (0, T].

Moreover, since $\partial _\tau \phi \ge 0$ and 0 is the lower obstacle, it can be proved that $\lambda (\tau ) \in C^{0,1}((0,T])$ by the method developed by Friedman [13]. At this point, it follows from the bootstrap argument (see also Jiang [21] and Schaeffer [30]) that $\lambda (\tau ) \in C^{\infty }((0,T])$. $\square$

Let us define $\Lambda (t)$ by

$$\begin{aligned} \Lambda (t)\equiv e^{\lambda (T-t)}\;\;\text{ for }\;\;t\in [0,T]. \end{aligned}$$

(90)

That is,

$$\begin{aligned} \Lambda (t)= \inf \{ z \in {\mathbb {R}}_+: \Phi (t,z)>0 \}, \quad t \in [0,T). \end{aligned}$$

In terms of $\Lambda (t)$ and $\Phi (t,z)$, from A.1 to A.3 and Lemma A.2, we have just obtained the desired results.

Proof of Lemma 3.2

Let us denote

$$\begin{aligned}&\Phi _\infty (t,z)\\&:= {\left\{ \begin{array}{ll} 0,\quad &{}\text{ for }\;\;(t,z)\in [0,T]\times [0,z_\infty ],\\ \displaystyle Dz^{n_2}+\dfrac{2}{\sigma _z^2(n_1-n_2)}\\ \quad \times \left[ z^{n_2}\int _0^z\xi ^{-n_2-1}\Psi (\xi )d\xi +z^{n_1}\int _z^\infty \xi ^{-n_1-1}\Psi (\xi )d\xi \right] ,\quad &{}\text{ for }\;\;(t,z)\in [0,T]\times [z_\infty ,\infty ), \end{array}\right. } \end{aligned}$$

where $n_2$ is a negative root of the quadratic equation (44) and

$$\begin{aligned} D=-\dfrac{2}{\sigma _z^2(n_1-n_2)}\int _0^{z_\infty }\xi ^{-n_2-1}\Psi (\xi ) \, d\xi . \end{aligned}$$

It is easy to confirm that

$$\begin{aligned} \partial _t \Phi _{\infty }(t,z)+{{{\mathcal {L}}}}_2 \Phi (t,z) + \Psi (z) =0\;\;\text{ for }\;\;z>z_\infty \end{aligned}$$

and

$$\begin{aligned} \Phi _\infty (t,z_\infty ) = \partial _z \Phi _\infty (t,z_\infty )=0. \end{aligned}$$

Note that for $z>z_\infty$

$$\begin{aligned} \partial _z\Phi _\infty (t,z)&=n_2 D z^{n_2-1}+\dfrac{2}{\sigma _z^2(n_1-n_2)}\left[ n_2z^{n_2-1}\int _0^z\xi ^{-n_2-1}\Psi (\xi )d\xi \right. \\&\quad \left. +n_1z^{n_1-1}\int _z^\infty \xi ^{-n_1-1}\Psi (\xi )d\xi \right] \\&=\dfrac{2}{\sigma _z^2(n_1-n_2)}\left[ n_2z^{n_2-1}\int _{z_\infty }^z\xi ^{-n_2-1}\Psi (\xi )d\xi \right. \\&\quad \left. +n_1z^{n_1-1}\int _z^\infty \xi ^{-n_1-1}\Psi (\xi )d\xi \right] . \end{aligned}$$

Since $z_\infty <z_T$, $\Psi '(z)>0$, and $\Psi (z_T)=0$, we deduce that $\partial _z\Psi (t,z)$ is strictly increasing in $z\in (z_\infty ,z_T)$ and strictly decreasing in $z\in (z_T,\infty )$.

Moreover, it is easy to check that

$$\begin{aligned} \lim _{z\rightarrow +\infty }\partial _z \Phi _\infty (t,z)=\frac{{\bar{L}}}{r_w}>0. \end{aligned}$$

It follows from $\Phi _\infty (t,z_\infty ) = \partial _z \Phi _\infty (t,z_\infty )=0.$ that $\partial _z \Phi _\infty (t,z)>0$ and $\Phi _\infty (t,z)>0$ for $z>z_\infty$.

Thus,

$$\begin{aligned} \Phi _\infty (t,z)>0\;\;\text{ for }\;\;z>z_\infty ,\;\;\;\text{ and }\;\;\;\Phi _\infty (t,z)=0\;\;\text{ for }\;\;z\le z_\infty . \end{aligned}$$

Moreover, for $z\le z_\infty$

$$\begin{aligned} \partial _t \Phi _\infty (t,z)+{{{\mathcal {L}}}}_2 \Phi _\infty (t,z) +\Psi (z)=\Psi (z)\le \Psi (z_\infty )<\Psi (z_T)=0, \end{aligned}$$

where we have used the fact that $z_\infty <z_T$ and $\Psi '(z)>0$.

Hence, we can conclude that $\Phi _\infty (t,z)$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} -\partial _t \Phi _\infty - {{{\mathcal {L}}}}_2\Phi _\infty \ge \Psi (z)\;\;\;&{}\text{ for }\;\;\Phi _\infty (t,z)=0,\\ -\partial _t \Phi _\infty - {{{\mathcal {L}}}}_2\Phi _\infty = \Psi (z)\;\;\;&{}\text{ for }\;\;\Phi _\infty (t,z)>0,\\ \Phi _\infty (T,z) \ge 0, \;\;\;\forall \,z>0. \end{array}\right. } \end{aligned}$$

By the comparison principle for VI, we have

$$\begin{aligned} \Phi _\infty (t,z) \ge \Phi (t,z). \end{aligned}$$

Since $\Lambda (t)$ is strictly increasing in $t\in [0,T]$, it follows from the definition of $\Lambda (t)$ that

$$\begin{aligned} \Lambda (t)> z_\infty . \end{aligned}$$

From Lemma A.2, clearly $\Lambda (t)<z_T$.

Proof of Lemma 3.3

Let us define an equivalent martingale measure $\widetilde{{\mathbb {Q}}}^{a_1}$ by

$$\begin{aligned} \dfrac{d\widetilde{{\mathbb {Q}}}^{a_1}}{d\widetilde{{\mathbb {Q}}}}=e^{-\frac{1}{2}a_1^2\sigma _z^2(s-t)+a_1 \sigma _z\Big (B_s^{\widetilde{{\mathbb {Q}}}}-B_t^{\widetilde{{\mathbb {Q}}}}\Big )}. \end{aligned}$$

Then, Girsanov’s theorem implies that $B_s^{\widetilde{{\mathbb {Q}}}^a_1}=B_s^{\widetilde{{\mathbb {Q}}}}-a_1\sigma _z B_s^{\widetilde{{\mathbb {Q}}}}\;(t\le s \le T)$ is a standard Brownian motion under the measure $\widetilde{{\mathbb {Q}}}^{a_1}$.

Under the measure $\widetilde{{\mathbb {Q}}}^{a_1}$, the dynamics of ${{{\mathcal {Z}}}}$ follow

$$\begin{aligned} \dfrac{d{{{\mathcal {Z}}}}_s^{t,z}}{{{{\mathcal {Z}}}}_s^{t,z}} = \Big (\beta _w-r_w+\sigma _z^2(1+a_1)\Big )ds+\sigma _z dB_s^{\widetilde{{\mathbb {Q}}}^{a_1}}. \end{aligned}$$

Since

$$\begin{aligned} \big ({{{\mathcal {Z}}}}_s^{t,z}\big )^{a_1}&=z^{a_1}e^{a_1\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2\big )(s-t)+a_1 \sigma _z\big (B_s^{\widetilde{{\mathbb {Q}}}}-B_t^{\widetilde{{\mathbb {Q}}}}\big )}\\&=z^{a_1}e^{\big (a_1(\beta _w-r_w)+a_1(a_1+1)\frac{1}{2}\sigma _z^2\big )(s-t)}e^{-\frac{1}{2}a_1^2\sigma _z^2(s-t)+a_1 \sigma _z\big (B_s^{\widetilde{{\mathbb {Q}}}}-B_t^{\widetilde{{\mathbb {Q}}}}\big )}, \end{aligned}$$

we deduce that

$$\begin{aligned}&{\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \big ({{{\mathcal {Z}}}}_s^{t,z}\big )^{a_1} \textbf{1}_{\{{{{\mathcal {Z}}}}_s>a_2\}}\right] \end{aligned}$$

(91)

$$\begin{aligned}&\quad =z^{a_1}e^{\big (a_1(\beta _w-r_w)+a_1(a_1+1)\frac{1}{2}\sigma _z^2\big )(s-t)}{\mathbb {E}}^{\widetilde{{\mathbb {Q}}}^{a_1}}\left[ \textbf{1}_{\{{{{\mathcal {Z}}}}_s^{t,z}>a_2\}}\right] \nonumber \\&\quad =z^{a_1}e^{\big (a_1(\beta _w-r_w)+a_1(a_1+1)\frac{1}{2}\sigma _z^2\big )(s-t)} \widetilde{{\mathbb {Q}}}^{a_1}\left( {{{\mathcal {Z}}}}_s^{t,z}>a_2\right) \nonumber \\&\quad =z^{a_1}e^{\big (a_1(\beta _w-r_w)+a_1(a_1+1)\frac{1}{2}\sigma _z^2\big )(s-t)}\nonumber \\&\qquad {{{\mathcal {N}}}}\left( \dfrac{\log {(z/a_2)}+\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2+a_1\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) . \end{aligned}$$

(92)

Similarly, we have

$$\begin{aligned}{} & {} {\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \big ({{{\mathcal {Z}}}}_s^{t,z}\big )^{a_1} \textbf{1}_{\{{{{\mathcal {Z}}}}_s^{t,z}\le a_2\}}\right] =z^{a_1}e^{\big (a_1(\beta _w-r_w)+a_1(a_1+1)\frac{1}{2}\sigma _z^2\big )(s-t)}\nonumber \\{} & {} \quad {{{\mathcal {N}}}}\left( -\dfrac{\log {(z/a_2)}+\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2+a_1\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) . \end{aligned}$$

(93)

Moreover,

$$\begin{aligned} {\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \big ({{{\mathcal {Z}}}}_ s^{t,z}\big )^{a_1}\right] =z^{a_1}e^{\big (a_1(\beta _w-r_w)+a_1(a_1+1)\frac{1}{2}\sigma _z^2\big )(s-t)}. \end{aligned}$$

(94)

Proof of Lemma 3.4

From the variational inequality (VI) (39), we deduce that

$$\begin{aligned} {\left\{ \begin{array}{ll} -\partial _t (z \partial _z \Phi ) - {{{\mathcal {L}}}}_2(z \partial _z \Phi ) = z\Psi '(z)\;\;&{}\text{ in }\;\;\{(t,z)\mid \Phi (t,z)>0\},\\ \Phi (T,z)=0,\;\;\forall \;z\ge \Lambda (t),\quad \Phi (t,\Lambda (t))=0,\;\;\forall \;t\in [0,T]. \end{array}\right. } \end{aligned}$$

Let us denote $\Xi (t,z)$ by

$$\begin{aligned} \Xi (t,z)\equiv {\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^T e^{-r_w (s-t)}{{{\mathcal {Z}}}}_s^{t,z} \Psi '\big ({{{\mathcal {Z}}}}_s^{t,z}\big )ds \right] , \end{aligned}$$

where the measure $\widetilde{{\mathbb {Q}}}$ is defined in (35).

Note that

$$\begin{aligned} \Xi (t,z)\ge 0, \qquad \forall \, t\in [0,T]. \end{aligned}$$

Then, we can easily derive that $\Xi (t,z)$ satisfies the following PDE:

$$\begin{aligned} {\left\{ \begin{array}{ll} -\partial _t \Xi -{{{\mathcal {L}}}}_2 \Xi =z\Psi '(z)\;\;\;&{}\text{ for }\;\;z\in (0,\infty )\;\;\text{ and }\;\;0\le t <T,\\ \Xi (T,z)=0. \end{array}\right. } \end{aligned}$$

The comparison principle for the VI implies that

$$\begin{aligned} z \partial _z \Phi (t,z) \le \Xi (t,z). \end{aligned}$$

(95)

By Lemma 3.3, it follows that

$$\begin{aligned} \Xi (t,z)&={\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^T e^{-r_w (s-t)}{{{\mathcal {Z}}}}_s^{t,z} \Psi '\big ({{{\mathcal {Z}}}}_s^{t,z} \big )ds \right] \\&=-\dfrac{1}{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^{\frac{\gamma _1-\gamma }{\gamma }}z^ {-\frac{1}{\gamma }}e^{-K(T-t)}\\&\qquad {{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{z_L}}+\big (\beta _w-r_w +\frac{1}{2}\sigma _z^2-\frac{1}{\gamma }\sigma _z^2\big )(T-t)}{\sigma _z\sqrt{T-t}}\right) \\&\quad -\dfrac{1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}e^{-K_1(T-t)}\\&\qquad {{{\mathcal {N}}}}\left( -\dfrac{\log {\frac{z}{z_L}}+\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2 -\frac{1}{\gamma _1}\sigma _z^2\big )(T-t)}{\sigma _z\sqrt{T-t}}\right) \\&\quad +\dfrac{1}{1-\gamma _1}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}e^{-K_1(T-t)}, \end{aligned}$$

where we have used fact that

$$\begin{aligned} K&= r_w +\dfrac{\beta _w-r_w}{\gamma } +\dfrac{\gamma -1}{\gamma ^2}\dfrac{\sigma _z^2}{2} \qquad \text{ and } \qquad K_1 = r_w +\dfrac{\beta _w-r_w}{\gamma _1} +\dfrac{\gamma _1-1}{\gamma _1^2}\dfrac{\sigma _z^2}{2}. \end{aligned}$$

Thus, we can easily deduce that there exist positive constants $C_1$ and $C_2$ such that

$$\begin{aligned} |\Xi (t,z)|\le C_1 z^{-\frac{1}{\gamma }} + C_2 z^{-\frac{1}{\gamma _1}}. \end{aligned}$$

(96)

It follows from (95) and (96) that

$$\begin{aligned} 0\le z\partial _z\Phi (t,z)\le C_1 z^{-\frac{1}{\gamma }} + C_2 z^{-\frac{1}{\gamma _1}}. \end{aligned}$$

(97)

Proof of Proposition 3.3

(a) Since

$$\begin{aligned} \Phi \in W^{1,2}_{p,\textrm{loc}}\big ({{{{\mathcal {D}}}}_T^1}\big ) \cap C\big (\overline{{{{{\mathcal {D}}}}_T^1}}\big )\;\;\text{ for } \text{ any }\;\;p \ge 1, \end{aligned}$$

it follows from Itô’s lemma for the Sobolev space (see Theorem 1 in p. 122 of Krylov [24]) that for any $\tau \in {{{\mathcal {S}}}}(t,T)$

$$\begin{aligned}{} & {} e^{-r_w(\tau -t)}\Phi \big (\tau ,{{{\mathcal {Z}}}}_\tau ^{t,z}\big )-\Phi (t,z)=\int _t^\tau e^{-r_w(s-t)}\left( \partial _s \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )+{{{\mathcal {L}}}}_2 \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )\right) ds\nonumber \\{} & {} \quad +\int _t^\tau e^{-r_w(s-t)}\sigma _z{{{\mathcal {Z}}}}_s^{t,z}\partial _z \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )\,dB^{\widetilde{{\mathbb {Q}}}}. \end{aligned}$$

(98)

By Lemma 3.4, there exist positive constants $C_1$ and $C_2$ such that

$$\begin{aligned} 0\le z\partial _z \Phi (t,z)\le C_1 z^{-\frac{1}{\gamma }} + C_2 z^{-\frac{1}{\gamma _1}}. \end{aligned}$$

Thus, we deduce that

$$\begin{aligned}&{\mathbb {E}}^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^{\tau }\left( e^{-r_w(s-t)}\sigma _z{{{\mathcal {Z}}}}_s^{t,z}\partial _z \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )\right) ^2ds\right] \\&\quad \le {\mathbb {E}}^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^{T}\left( e^{-r_w(s-t)}\sigma _z{{{\mathcal {Z}}}}_s^{t,z}\partial _z \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )\right) ^2ds\right] \\&\quad \le \sigma _z^2 {\mathbb {E}}^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^{T} \left( C_1\big ({{{\mathcal {Z}}}}_s^{t,z}\big )^{-\frac{1}{\gamma }} + C_2 \big ({{{\mathcal {Z}}}}_ s^{t,z}\big )^{-\frac{1}{\gamma _1}}\right) ^2ds\right] \\&\quad <\infty . \end{aligned}$$

That is, the term

$$\begin{aligned} \int _t^\tau e^{-r_w(s-t)}\sigma _z{{{\mathcal {Z}}}}_s^{t,z}\partial _z \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )\,dB^{\widetilde{{\mathbb {Q}}}} \end{aligned}$$

is a ${{{\mathcal {F}}}}_t$-martingale.

By taking the expectation ${\mathbb {E}}^{\widetilde{{\mathbb {Q}}}}[\cdot ]$ on the both-sides of the Eq. (98), we have

$$\begin{aligned}{} & {} \Phi (t,z)+{\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^\tau e^{-r_w(s-t)}\left( \partial _s \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )+{{{\mathcal {L}}}}_2 \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )+\Psi \big ({{{\mathcal {Z}}}}_s^{t,z}\big )\right) ds\right] \qquad \nonumber \\{} & {} \qquad \qquad ={\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \Phi \big (\tau ,{{{\mathcal {Z}}}}_{\tau }^{t,z}\big )+\int _t^\tau e^{-r_w(s-t)}\Psi \big ({{{\mathcal {Z}}}}_s^{t,z}\big )ds\right] . \end{aligned}$$

(99)

Since $\Phi (t,z)$ satisfies the variational inequality (VI) (39), it follows that

$$\begin{aligned} \Phi (t,z)&\ge {\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \Phi \big (\tau ,{{{\mathcal {Z}}}}_{\tau }^{t,z}\big )+\int _t^\tau e^{-r_w(s-t)}\Psi \big ({{{\mathcal {Z}}}}_s^{t,z}\big )ds\right] \nonumber \\&={\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^\tau e^{-r_w(s-t)}\dfrac{1}{{{{\mathcal {Z}}}}_s^{t,z}}\left( {\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^{t,z}, 1\big )-{\tilde{u}}_A\big ({{{\mathcal {Z}}}}_s^{t,z}\big )\right) ds\right] , \end{aligned}$$

(100)

for any $\tau \in {{{\mathcal {S}}}}(t,T)$.

Let us consider the stopping time ${\hat{\tau }}_t(z)$ given by

$$\begin{aligned} {\hat{\tau }}_t(z)=\inf \big \{s\ge t \mid {{{\mathcal {Z}}}}_s^{t,z} \le \Lambda (s) \big \}\wedge T. \end{aligned}$$

• (i) If $z > \Lambda (t)$, it is clear that

  $$\begin{aligned} {\left\{ \begin{array}{ll} \partial _s \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big ) +{{{\mathcal {L}}}}_2 \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big ) +\Psi \big ({{{\mathcal {Z}}}}_s^{t,z}\big )=0\;\;\;&{}\text{ for }\;\;s\in [t,{\hat{\tau }}_t(z)),\\ \Phi \Big ({\hat{\tau }}_t(z), {{{\mathcal {Z}}}}_{{\hat{\tau }}_t(z)}^{t,z}\Big )=0. \end{array}\right. } \end{aligned}$$

  (101)

• (ii) If $z\le \Lambda (t)$, we deduce that ${\hat{\tau }}_t(z)=t$. Thus,

  $$\begin{aligned} \Phi (t,z)= & {} 0 ={\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\Bigg [\int _t^{{\hat{\tau }}_t(z)} e^{-r_w(s-t)}\dfrac{1}{{{{\mathcal {Z}}}}_s^{t,z}}\Bigg ({\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^{t,z}, 1\big )\nonumber \\{} & {} \qquad \qquad \quad -{\tilde{u}}_A\big ({{{\mathcal {Z}}}}_s^{t,z}\big )\Bigg )ds\Bigg ]. \end{aligned}$$

  (102)

It follows from (100), (101) and (102) that

$$\begin{aligned} \Phi (t,z)&=\sup _{\tau \in {{{\mathcal {S}}}}(t,T)}{\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^\tau e^{-r_w(s-t)}\dfrac{1}{{{{\mathcal {Z}}}}_s^{t,z}}\left( {\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^{t,z}, 1\big )-{\tilde{u}}_A\big ({{{\mathcal {Z}}}}_s^{t,z}\big )\right) ds\right] \\&={\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^{{\hat{\tau }}_t(z)} e^{-r_w(s-t)}\dfrac{1}{{{{\mathcal {Z}}}}_s^{t,z}}\left( {\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^{t,z}, 1\big )-{\tilde{u}}_A\big ({{{\mathcal {Z}}}}_s^{t,z}\big )\right) ds\right] . \end{aligned}$$

(b) Replacing $\tau$ by T in (99), it follows from $\Phi (T, z) =0$ that

$$\begin{aligned} \Phi (t,z)=-{\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^T e^{-r_w(s-t)}\left( \partial _s \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )+{{{\mathcal {L}}}}_2 \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )\right) ds\right] . \end{aligned}$$

(103)

From the VI (42), we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _s \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )+{{{\mathcal {L}}}}_2\Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )+\Psi \big ({{{\mathcal {Z}}}}_s^{t,z}\big ) =0\;\;\;&{}\text{ for }\;\;{{{\mathcal {Z}}}}_s^{t,z} >\Lambda (s),\\ \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )=0\;\;\;&{}\text{ for }\;\;0<{{{\mathcal {Z}}}}_s^{t,z}\le \Lambda (s) \end{array}\right. } \end{aligned}$$

(104)

for all $s\in [t,T]$.

It follows that

$$\begin{aligned} \Phi (t,z)&=-{\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^Te^{-r_w(s-t)}\big (\partial _s \Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )+{{{\mathcal {L}}}}_2\Phi \big (s,{{{\mathcal {Z}}}}_s^{t,z}\big )\big )ds \right] \nonumber \\&={\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^Te^{-r_w(s-t)}\Psi \big ({{{\mathcal {Z}}}}_s^{t,z} \big )\textbf{1}_{\{{{{\mathcal {Z}}}}_s^{t,z}>\Lambda (s) \}}ds \right] . \end{aligned}$$

(105)

Note that

$$\begin{aligned} \Lambda (t)<z_T <z_L\;\;\text{ for } \text{ all }\;\;t\in [0,T). \end{aligned}$$

Thus,

$$\begin{aligned} \Phi (t,z)&={\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^Te^{-r_w(s-t)} \left( \dfrac{\gamma }{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^{\frac{\gamma _1-\gamma }{\gamma }}\big ({{{\mathcal {Z}}}}_ s^{t,z}\big )^{-\frac{1}{\gamma }}+{\bar{L}}\right) \textbf{1}_{\{{{{\mathcal {Z}}}}_s^{t,z}>z_L \}}ds \right] \\&\quad +{\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^Te^{-r_w(s-t)}\left( \dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}\big ({{{\mathcal {Z}}}}_s^{t,z}\big )^{-\frac{1}{\gamma _1}}+({\bar{L}}-L)\right) \textbf{1}_{\{\Lambda (s)<{{{\mathcal {Z}}}}_s^{t,z}<z_L \}}ds \right] \\&\quad -{\mathbb {E}}_t^{\widetilde{{\mathbb {Q}}}}\left[ \int _t^Te^{-r_w(s-t)}\dfrac{\gamma _1}{1-\gamma _1} {\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}\big ({{{\mathcal {Z}}}}_s^{t,z}\big )^{-\frac{1}{\gamma _1}}\textbf{1}_{\{\Lambda (s)<{{{\mathcal {Z}}}}_s^{t,z} \}}ds\right] . \end{aligned}$$

It follows from (91), (93) and (94) that

$$\begin{aligned}&\Phi (t,z)=\int _t^T\left\{ e^{-K(s-t)}\dfrac{\gamma }{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^{\frac{\gamma _1-\gamma }{\gamma }}\right. \\&\quad \left. z^{-\frac{1}{\gamma }}{{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{z_L}}+\big (\beta _w-r_w+\frac{1}{2} \sigma _z^2-\frac{1}{\gamma }\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right. \\&\quad +\left. e^{-r_w(s-t)}{\bar{L}}{{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{z_L}} +\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right. \\&\quad -\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^ {-\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{z_L}}+\big (\beta _w-r_w +\frac{1}{2}\sigma _z^2-\frac{1}{\gamma _1}\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right. \\&\quad -\left. e^{-r_w(s-t)}\big ({\bar{L}}-L\big ){{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{z_L}} +\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right. \\&\quad +\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{ -\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{\Lambda (s)}} +\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2-\frac{1}{\gamma _1}\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right. \\&\quad +\left. e^{-r_w(s-t)}({\bar{L}}-L){{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{\Lambda (s)}} +\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right. \\&\quad -\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}} {{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{\Lambda (s)}}+\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2-\frac{1}{\gamma _1}\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right\} ds. \end{aligned}$$

Since $\Phi \in C(\overline{{{{{\mathcal {D}}}}_T^1}})$ (see Proposition 3.2), we have

$$\begin{aligned} \Phi (t,\Lambda (t))=\partial _z \Phi (t,\Lambda (t))=0. \end{aligned}$$

Proof of Proposition 3.4

(a) Recall that

$$\begin{aligned} \Upsilon (t,z) =\sup _{\tau \in {{{\mathcal {S}}}}({t,T})} {\mathbb {E}}_t^{{\mathbb {Q}}}\left[ \int _t^\tau e^{-\beta _w(s-t)}{\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^{t,z}, 1\big )ds+e^{-\beta _w(\tau -t)}J_A\big ({{{\mathcal {Z}}}}_{\tau }^{t,z}\big ) \right] , \end{aligned}$$

Since $\Upsilon (t,z)=J_A(z)$ for $z\le \Lambda (t)$, it is clear that $\Upsilon (t,z)$ is strictly convex in $\{z\in {\mathbb {R}}_+ \mid z\le \Lambda (t)\}$. Now we show that $\Upsilon (t,z)$ is strictly convex in $\{z\in {\mathbb {R}}_+ \mid z >\Lambda (t)\}$.

Let $z_1>0$ and $z_2>0$ such that

$$\begin{aligned} z_1>\Lambda (t), \;z_2>\Lambda (t)\;\;\text{ with }\;\;z_1 \ne z_2. \end{aligned}$$

For some $\zeta \in (0,1)$, let us denote $z_3$ by

$$\begin{aligned} z_3 = \zeta z_1 + (1-\zeta )z_2. \end{aligned}$$

Note that

$$\begin{aligned} z_3= \zeta z_1 + (1-\zeta )z_2>\Lambda (t). \end{aligned}$$

It follows that ${\hat{\tau }}(z_3)>0$ a.s..

Since ${\tilde{u}}_B(z,1)$ and $J_A(z)$ are strictly convex in $z>0$, we obtain that

$$\begin{aligned} {\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^{t,z_3},1\big )<\zeta {\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^ {t,z_1},1\big )+(1-\zeta ){\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^{t,z_2},1\big )\;\;\text{ for }\;\;s\in [t,{\hat{\tau }}_t(z_3)) \end{aligned}$$

and

$$\begin{aligned} J_A\big ({{{\mathcal {Z}}}}_\tau ^{t,z_3}\big )<\zeta J_A\big ({{{\mathcal {Z}}}}_\tau ^{t,z_1}\big )+ (1-\zeta )J_A\big ({{{\mathcal {Z}}}}_\tau ^{t,z_2}\big ). \end{aligned}$$

Then, we have

$$\begin{aligned} \Upsilon (t,z_3)&=\sup _{\tau \in {{{\mathcal {S}}}}(t,T)}{\mathbb {E}}\left[ \int _t^\tau e^{-\beta (s-t)}{\tilde{u}}_B\big ({{{\mathcal {Z}}}}_s^{t,z_3},1\big )dt+e^{-\beta (\tau -t)} J_A\big ({{{\mathcal {Z}}}}_\tau ^{t,z_3}\big ) \right] \\&={\mathbb {E}}\left[ \int _t^{{\hat{\tau }}_t(z_3)} e^{-\beta (s-t)}{\tilde{u}}_ B\big ({{{\mathcal {Z}}}}_s^{t,z_3},w_t\big )ds+e^{-\beta \big ({{\hat{\tau }}_t({z_3})}-t\big )} J_A\big ( {{{\mathcal {Y}}}}_{{\hat{\tau }}_0({y_3}w^{\gamma _1})}^{y_3}\big ) \right] \\&<\zeta {\mathbb {E}}\left[ \int _t^{{\hat{\tau }}_t(z_3)} e^{-\beta (s-t)}{\tilde{u}}_ B\big ({{{\mathcal {Z}}}}_s^{t,z_1},1\big )ds+e^{-\beta \big ({{\hat{\tau }}_t({z_3})}-t\big )} J_A\big ({{{\mathcal {Z}}}}_ {{\hat{\tau }}_t({z_3})}^{t,z_1}\big ) \right] \\&\quad +(1-\zeta ){\mathbb {E}}\left[ \int _t^{{\hat{\tau }}_t(z_3)} e^{-\beta (s-t)}{\tilde{u}}_B \big ({{{\mathcal {Z}}}}_s^{t,z_2},1\big )ds+e^{-\beta \big ({{\hat{\tau }}_t({z_3})}-t\big )} J_A\big ( {{{\mathcal {Z}}}}_{{\hat{\tau }}_t({z_3})}^{t,z_2}\big ) \right] \\&\le \zeta \Upsilon (t, z_1)+ (1-\zeta )\Upsilon (t,z_2). \end{aligned}$$

Thus, $\Upsilon (t,z)$ is also strictly convex in $\{z\in {\mathbb {R}}_+ \mid z >\Lambda (t)\}$.

(b) By direct computation, we have

$$\begin{aligned}&\partial _z \Upsilon (t,z)=-\int _t^T\left\{ e^{-K (s-t)}\dfrac{1-\gamma }{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^{\frac{\gamma _1-\gamma }{\gamma }}z^ {-\frac{1}{\gamma }}{{{\mathcal {N}}}}\left( d_{\gamma -}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad -\left. e^{-K (s-t)}\dfrac{\gamma }{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^ {\frac{\gamma _1-\gamma }{\gamma }}z^{-\frac{1}{\gamma }}{} \textbf{n}\left( d_{\gamma -}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}} \right. \\&\quad \left. - e^{-r_w (s-t)}{L}{{{\mathcal {N}}}}\left( d_{1+}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad -\left. e^{-r_w t}{L}{} \textbf{n}\left( d_{1+}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. -e^{-K_1(s-t)}L^{ \frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad +\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}\textbf{n}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. +e^{-K_1(s-t)}L^ {\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \right. \\&\quad -\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}\textbf{n}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. -e^{-r_w (s-t)}\big ({\bar{L}}-L\big ){{{\mathcal {N}}}}\left( d_{1+}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \right. \\&\quad -\left. e^{-r_w (s-t)}\big ({\bar{L}}-L\big )\textbf{n}\left( d_{1+}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. e^{-K_1(s-t)}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{{{\mathcal {N}}}} \left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \right. \\&\quad +\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}\textbf{n}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right\} dt\\&\quad -{\left( {\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}+\delta k_M^{\frac{1-\gamma _1}{\gamma _1}}\right) }\dfrac{1}{K_1}z^{-\frac{1}{\gamma _1}} \end{aligned}$$

It follows from Lemma 3.5 that

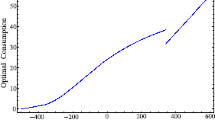
$$\begin{aligned} \lim _{z\rightarrow \infty }\partial _z \Upsilon (t,z)&=\lim _{z \rightarrow \infty }\int _t^T\left( e^{-r_w (s-t)}{L} {{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{z_L}}+\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right. \\&\quad +\left. e^{-r_w (s-t)}\big ({\bar{L}}-L\big ){{{\mathcal {N}}}}\left( \dfrac{\log {\frac{z}{\Lambda (s)}}+\big (\beta _w-r_w+\frac{1}{2}\sigma _z^2\big )(s-t)}{\sigma _z\sqrt{s-t}}\right) \right) ds\\&={\bar{L}}\dfrac{1-e^{-r_w (T-t)}}{r_w}. \end{aligned}$$

and

$$\begin{aligned} \lim _{z\rightarrow +\infty }\partial _z \Upsilon (t,z)=-\infty . \end{aligned}$$

Proof of Theorem 3.1

(a) By Corollary 3.1, we deduce that for given $x>-w{\bar{L}}(1-e^{-r_wT})/r_w$ there exists a unique $y^*>0$ such that

$$\begin{aligned} x = -\partial _y J(y^*,w). \end{aligned}$$

Let us denote ${\hat{\tau }}$ and $\widehat{{{\mathcal {X}}}}(t,{{{\mathcal {Y}}}}_t^{y^*},w_t)$ by

$$\begin{aligned} {\hat{\tau }}={\hat{\tau }}_0(y^*w^{\gamma _1})=\inf \Big \{t\ge 0 \mid {{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}={{{\mathcal {Y}}}}_t^{y*}( w_t)^{\gamma _1}\le \Lambda (t)\Big \}\wedge T \end{aligned}$$

and

$$\begin{aligned} \widehat{{{\mathcal {X}}}}(t,{{{\mathcal {Y}}}}_t^{y^*},w_t)= & {} {\mathbb {E}}_t\left[ \int _t^{{\hat{\tau }}\wedge t}\dfrac{{{{\mathcal {H}}}}_s}{{{{\mathcal {H}}}}_t}\left( {\widehat{c}}_s+{\delta {\widehat{M}}_s}-w_s({\bar{L}}-{\widehat{l}}_s)\right) ds\right. \nonumber \\{} & {} \left. +\int _{{\hat{\tau }}\wedge t}^\infty \dfrac{{{{\mathcal {H}}}}_s}{{{{\mathcal {H}}}}_t}\left( {\widehat{c}}_s+{\delta {\widehat{M}}_s}\right) ds\right] \;\;\text{ for }\;\;0\le t <\tau _D, \end{aligned}$$

(106)

respectively, where the candidate of optimal consumption ${\widehat{c}}_t={\widehat{c}}({{{\mathcal {Y}}}}_t^{y^*},w_t)$, bequest ${\widehat{M}}_t={\widehat{M}}({{{\mathcal {Y}}}}_t^y)$ and leisure ${\widehat{l}}_t={\widehat{l}}({{{\mathcal {Y}}}}_t^{y^*},w_t)$ for ${\hat{\tau }}$ are given in (26)–(28).

By Proposition 3.1, there exists an admissible portfolio ${\widehat{\pi }}_t$ such that

$$\begin{aligned} dX_t^{{\widehat{c}},{\widehat{l}}, {\widehat{M}}, {\hat{\tau }},{\widehat{\pi }}}= & {} \Bigg [(r+\delta )X_t^{{\widehat{c}},{\widehat{l}},{\widehat{M}},{\hat{\tau }},{\widehat{\pi }}} +(\mu -r){\widehat{\pi }}_t -\delta {\widehat{M}}_t\nonumber \\{} & {} \quad - {\widehat{c}}_t +\textbf{1}_{\{t< {\hat{\tau }}\}}w_t\big ({\bar{L}}-{\widehat{l}}_t\big )\Bigg ]dt\nonumber \\{} & {} \quad +\sigma {\widehat{\pi }}_t dB_t\;\;\text{ for }\;\;0\le t <\tau _D, \end{aligned}$$

(107)

where $X_t^{{\widehat{c}},{\widehat{l}},{\widehat{M}},{\hat{\tau }},{\widehat{\pi }}}= \widehat{{{\mathcal {X}}}}(t,{{{\mathcal {Y}}}}_t^{y^*},w_t)$ with $X_0^{{\widehat{c}},{\widehat{l}},{\widehat{M}},{\hat{\tau }}, {\widehat{\pi }}}=\widehat{{{\mathcal {X}}}}(0,{y^*},w)$

Note that

$$\begin{aligned} J(y^*,w)&= \sup _{\tau \in {{{\mathcal {S}}}}(0,T)}{\mathbb {E}}\left[ \int _0^\tau e^{-\beta t} {\tilde{u}}_B\big ({{{\mathcal {Y}}}}_t^{y^*},w_t\big )dt+e^{-\beta \tau } J_A\big ({{{\mathcal {Y}}}}_\tau ^{y^*}\big ) \right] \\&={\mathbb {E}}\left[ \int _0^{{\hat{\tau }}} e^{-\beta t}{\tilde{u}}_B\big ({{{\mathcal {Y}}}}_t^{y^*},w_t\big )dt+e^{-\beta {{\hat{\tau }}}} J_A\big ({{{\mathcal {Y}}}}_{{\hat{\tau }}}^{y^*}\big ) \right] . \end{aligned}$$

It follows that

$$\begin{aligned} \begin{aligned}&y^*\widehat{{{\mathcal {X}}}}(0,y^*,w)=y^*{\mathbb {E}}\left[ \int _0^ {{\hat{\tau }}}{{{{\mathcal {H}}}}_t}\left( {\widehat{c}}_t+{\delta {\widehat{M}}_t}-w_t\big ({\bar{L}}-{\widehat{l}}_t\big )\right) dt+\int _{{\hat{\tau }}} ^\infty {{{{\mathcal {H}}}}_t}\left( {\widehat{c}}_t+{\delta {\widehat{M}}_t}\right) dt\right] \\&\quad ={\mathbb {E}}\left[ \int _0^{{\hat{\tau }}}e^{-\beta t}{{{\mathcal {Y}}}}_t^{y^*} \left( {\widehat{c}}_t +{\delta {\widehat{M}}_t}-w_t\big ({\bar{L}}-{\widehat{l}}_t\big )\right) dt +\int _{{\hat{\tau }}}^\infty e^{-\beta t} {{{\mathcal {Y}}}}_t^{y^*}\left( {\widehat{c}}_t+{\delta {\widehat{M}}_t}\right) dt\right] \\&\quad ={\mathbb {E}}\left[ \int _0^{{\hat{\tau }}}e^{-\beta t}\left( u\big ({\widehat{c}}_t, {\widehat{l}}_t\big )+{\delta U\big ({\widehat{M}}_t\big )}-{\tilde{u}}_B\big ({{{\mathcal {Y}}}}_t^{y^*},w_t\big ) \right) dt\right. \\&\quad \quad \left. +\int _{{\hat{\tau }}}^\infty e^{-\beta t} \big (u\big ({\widehat{c}}_t,{\bar{L}}\big )+{\delta U\big ({\widehat{M}}_t\big )}-{\tilde{u}}_A\big ({{{\mathcal {Y}}}}_t^{y^*}\big )\big )dt\right] \\&\quad ={\mathbb {E}}\left[ \int _0^{{\hat{\tau }}}e^{-\beta t}\left( u\big ({\widehat{c}}_t,{\widehat{l}}_t\big )+{\delta U\big ({\widehat{M}}_t\big )}\right) dt+\int _{{\hat{\tau }}}^\infty e^{-\beta t} \left( u\big ({\widehat{c}}_t,{\bar{L}}\big )+{\delta U\big ({\widehat{M}}_t\big )}\right) dt\right] \\&\quad \quad -J(y^*,w). \end{aligned} \end{aligned}$$

(108)

Thus, we have

$$\begin{aligned}&J(y^*,w)+y^*\widehat{{{\mathcal {X}}}}(0,y^*,w) \\&\quad ={\mathbb {E}}\left[ \int _0^ {{\hat{\tau }}}e^{-\beta t}\left( u\big ({\widehat{c}}_t,{\widehat{l}}_t\big )+{\delta U\big ({\widehat{M}}_t\big )} \right) dt\right. \\&\quad \quad \left. +\int _{{\hat{\tau }}}^\infty e^{-\beta t} \left( u\big ({\widehat{c}}_t,{\bar{L}}\big )+{\delta U\big ({\widehat{M}}_t\big )}\right) dt\right] \\&\quad \le \sup _{(c,l,M,\pi ,\tau )\in {\mathcal {A}}\big (t,\widehat{{{\mathcal {X}}}}(0,y^*,w) \big )} {\mathbb {E}}\left[ \int _0^{{\tau }}e^{-\beta t}\left( u({c}_t,{l}_t)+{\delta U(M_t)}\right) dt\right. \\&\quad \quad \left. +\int _{{\tau }}^\infty e^{-\beta t} \left( u\big ({c}_t,{\bar{L}}\big )+{\delta U(M_t)}\right) dt\right] \\&\quad \le \inf _{y>0}\left( J(y,w)+y\widehat{{{\mathcal {X}}}}(0,y^*,w)\right) \\&\quad \le J(y^*,w)+y^*\widehat{{{\mathcal {X}}}}(0,y^*,w). \end{aligned}$$

This implies that

$$\begin{aligned} V(\widehat{{{\mathcal {X}}}}(0,y^*,w),w)=&\inf _{y>0}\left( J(y,w)+y \widehat{{{\mathcal {X}}}}(0,y^*,w)\right) =J(y^*,w)+y^*\widehat{{{\mathcal {X}}}}(0,y^*,w). \end{aligned}$$

Since J(y, w) is strictly convex in $y>0$ and $y^*=-\partial _y J(y,w)$, we deduce that

$$\begin{aligned} x=\widehat{{{\mathcal {X}}}}(0,y^*,w) = -\partial _y J(y^*,w). \end{aligned}$$

Hence,

$$\begin{aligned} V(x,w)&={\mathbb {E}}\left[ \int _0^{{\hat{\tau }}}e^{-\beta t}\left( u\big ({\widehat{c}}_t,{\widehat{l}}_t\big )+{\delta U\big ({\widehat{M}}_t\big )}\right) dt\right. \\&\quad \left. +\int _{{\hat{\tau }}}^\infty e^{-\beta t} \left( u\big ({\widehat{c}}_t,{\bar{L}}\big )+{\delta U({\widehat{M}}_t)}\right) dt\right] . \end{aligned}$$

(b) By the proof of part (a), $({\widehat{c}},{\widehat{l}}, {\widehat{M}}, {\widehat{\pi }},{\widehat{\tau }})$ is the optimal strategy for Problem 2.1, i.e.,

$$\begin{aligned} (c^*,l^*,M^*, \pi ^*,\tau ^*)=\big ({\widehat{c}},{\widehat{l}},{\widehat{M}}, {\widehat{\pi }},{\widehat{\tau }}\big ). \end{aligned}$$

Hence,

$$\begin{aligned} dX_t^{c^*,l^*,M^*,\pi ^*,\tau ^*}= & {} \Big [(r+\delta )X_t^{c^*,l^*, M^*,\pi ^*,\tau ^*} +(\mu -r)\pi ^* \nonumber \\{} & {} - c_t^*-\delta M_t^{*}+\textbf{1}_{\{t< {\hat{\tau }}\}}w_t\big ({\bar{L}}-{l}_t^*\big )\Big ]dt \nonumber \\{} & {} +\sigma {\pi }_t^* dB_t\;\;\text{ for }\;\;0\le t <\tau _D. \end{aligned}$$

(109)

and

$$\begin{aligned} x= & {} \widehat{{{\mathcal {X}}}}(0,{y^*},w) = -\partial _y J(y^*,w)\\= & {} {\mathbb {E}}\left[ \int _0^{{\tau }^*}{{{{\mathcal {H}}}}_t}\left( c_t^* + {\delta M_t^*}-w_t\big ({\bar{L}}-{l}_t^*\big )\right) dt+\int _{{\tau }^*}^\infty {{{{\mathcal {H}}}}_t}\left( {c}_t^* + {\delta {{{\mathcal {M}}}}_t^*}\right) dt\right] , \end{aligned}$$

It follows from the strong Markov Property that

$$\begin{aligned} X_t^{c^*,l^*,\pi ^*,\tau ^*}= & {} \widehat{{{\mathcal {X}}}}\big (t,{{{\mathcal {Y}}}}_t^{y^*},w_t\big ) = -\partial _y J\big ({{{\mathcal {Y}}}}_t^{y^*},w_t\big )\nonumber \\= & {} w_t\big (-\partial _z\Upsilon \big (t,{{{\mathcal {Z}}}}_t^{y^*w^ {\gamma _1}}\big )\big )=w_t{{{\mathcal {X}}}}\big (t,{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big ). \end{aligned}$$

(110)

Note that $\Upsilon (t,z)$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _t \Upsilon (t,z) +{{{\mathcal {L}}}}\Upsilon (t,z)+{\tilde{u}} _B(z,1)=0\;\;&{}\text{ for }\;\;z>\Lambda (t),\\ \Upsilon (t,z) = J_A(z), \end{array}\right. } \end{aligned}$$

(111)

where the elliptic differential operator ${{{\mathcal {L}}}}$ is given by

$$\begin{aligned} {{{\mathcal {L}}}} = \dfrac{\sigma _z^2}{2}z^2\dfrac{\partial ^2}{\partial z^2} +(\beta _w-r_w)z\dfrac{\partial }{\partial z}-\beta _w. \end{aligned}$$

By differentiating the both sides of the Eq. (111) with respect to z, we find that ${{{\mathcal {X}}}}(t,z)$ satisfies

$$\begin{aligned} \partial _t {{{\mathcal {X}}}}(t,z) + {{{\mathcal {L}}}}_2 {{{\mathcal {X}}}}(t,z) + {\widehat{c}}(z,1)+{\delta {\widehat{M}}(z)}-\big ({\bar{L}}-{\widehat{l}}(z,1)\big )=0\;\;\text{ for }\;\;z>\Lambda (t). \end{aligned}$$

(112)

Note that

$$\begin{aligned} c_t^*= & {} {\widehat{c}}\big ({{{\mathcal {Y}}}}_t^{y^*},w_t\big )=w_t{\widehat{c}} \big ({{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}},1\big ),\;\;{\widehat{M}}\big ({{{\mathcal {Y}}}}_t^{y^*}\big )=w_t {\widehat{M}}\big ({{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big )\nonumber \\ \text{ and }\;\;l_t^*= & {} {\widehat{l}} \big ({{{\mathcal {Y}}}}_t^{y^*},w_t\big )=w_t{\widehat{l}}\big ({{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}},1\big ). \end{aligned}$$

(113)

Since the inhomogeneous terms of the PDE (112) are $C^{0.\alpha }$ for some $\alpha \in (0,1)$, we see from the Schauder estimates that ${{{\mathcal {X}}}}(t,z)$ is $C^{2,\alpha }$ in $\{(t,z)\mid z>\Lambda (t)\}$. Therefore, we can apply Itô’s lemma to $X_t^{c^*,l^*,\pi ^*,\tau ^*}=w_t{{{\mathcal {X}}}}\big (t,{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big )$ for $t\in [0,\tau ^*)$.

It follows from the Eq. (112) that

$$\begin{aligned} dX_t^{c^*,l^*,M^*,\pi ^*,\tau ^*}&= w_t\partial _t {{{\mathcal {X}}}}\big (t,{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big )dt + w_t \partial _z {{{\mathcal {X}}}}\big (t, {{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big )d{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\\&\quad + w_t \partial _{zz}{{{\mathcal {X}}}}\big (t,{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big ) (d{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}})^2\\&\quad + {{{\mathcal {X}}}}\big (t,{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big )dw_t+\partial _z{{{\mathcal {X}}}}(t, {{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}})dw_td{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\\&=\Bigg [rX_t^{c^*,l^*, M^*,\pi ^*,\tau ^*} +(\mu -r)w_t\Pi \big (t,{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big )\\&\qquad - c_t^* - {\delta M_t^*}+\textbf{1}_{\{t< {\hat{\tau }}\}}w_t\big ({\bar{L}}-{l}_t^*\big )\Bigg ]dt\\&\quad +\sigma w_t\Pi \big (t,{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big ) dB_t, \end{aligned}$$

where we have used the fact that for any $z>0$

$$\begin{aligned} \dfrac{d{{{\mathcal {Z}}}}_t^z}{{{{\mathcal {Z}}}}_t^z}=(\beta _w-r_w)dt + \sigma _z dB_t^{{\mathbb {Q}}}=\big (\beta _w-r_w-(1-\gamma _1)\sigma _w\sigma _z\big )dt + \sigma _z dB_t. \end{aligned}$$

Comparing the above equation with the dynamics of wealth in (109), we have

$$\begin{aligned} \pi _t^*=w_t\Pi \big (t,{{{\mathcal {Z}}}}_t^{y^*w^{\gamma _1}}\big ). \end{aligned}$$

The Integral Equation Representation of ${{{\mathcal {X}}}}(t,y)$ and $\Pi (t,y)$ in Theorem 3.1

Recall that

$$\begin{aligned} d_{1\pm }(t,z)&=\dfrac{\log {z}+\big (\beta _w-r_w\pm \frac{1}{2}\sigma _z^2\big )t}{\sigma _z\sqrt{t}},\; \;d_{\gamma \pm }(t,z)=\dfrac{\log {z}+\big (\beta _w-r_w\pm \frac{1}{2}\sigma _z^2\pm \frac{1-\gamma }{\gamma }\sigma _z^2\big )t}{\sigma _z\sqrt{t}},\\&\quad \text{ and }\;\;d_{\gamma _1\pm }(t,z)=\dfrac{\log {z}+\big (\beta _w-r_w\pm \frac{1}{2}\sigma _ z^2\pm \frac{1-\gamma _1}{\gamma _1}\sigma _z^2\big )t}{\sigma _z\sqrt{t}}. \end{aligned}$$

Then, ${{{\mathcal {X}}}}(t,z)$ and $\Pi (t,z)$ has the following integral equation representation:

$$\begin{aligned}&{{{\mathcal {X}}}}(t,z)=-\partial _z \Upsilon (t,z) =\int _t^T\left\{ e^{-K (s-t)} \dfrac{1-\gamma }{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^{\frac{\gamma _1-\gamma }{\gamma }}z^{-\frac{1}{\gamma }}{{{\mathcal {N}}}}\left( d_{\gamma -}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad \left. - e^{-K (s-t)}\dfrac{\gamma }{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^ {\frac{\gamma _1-\gamma }{\gamma }}z^{-\frac{1}{\gamma }}{} \textbf{n}\left( d_{\gamma -}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. - e^{-r_w (s-t)}{L}{{{\mathcal {N}}}}\left( d_{1+}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad \left. -e^{-r_w t}{L}\textbf{n}\left( d_{1+}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. -e^{-K_1(s-t)}L^{\frac{\gamma _1 -\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad \left. +e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}\textbf{n}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. +e^{-K_1(s-t)}L^ {\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \right. \\&\quad \left. -e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}\textbf{n}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. -e^{-r_w (s-t)}\big ({\bar{L}}-L\big ){{{\mathcal {N}}}}\left( d_{1+}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \right. \\&\quad \left. -e^{-r_w (s-t)}\big ({\bar{L}}-L\big )\textbf{n}\left( d_{1+}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right. \\&\quad \left. e^{-K_1(s-t)}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{{{\mathcal {N}}}} \left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \right. \\&\quad \left. +e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}\textbf{n}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \dfrac{1}{\sigma _z\sqrt{s-t}}\right\} dt\\&\quad +{\left( {\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}+\delta k_M^{\frac{1-\gamma _1}{\gamma _1}}\right) }\dfrac{1}{K_1}z^{-\frac{1}{\gamma _1}} \end{aligned}$$

and

$$\begin{aligned} \Pi (t,z)&=\dfrac{(\theta -\gamma _1 \sigma _w)}{\sigma }z\partial _{zz}\Upsilon (t,z)-\dfrac{\sigma _w}{\sigma }\partial _z \Upsilon (t,z)\\&=-\dfrac{\sigma _z}{\sigma }z\partial _{zz}\Upsilon (t,z)+\dfrac{\sigma _w}{\sigma }{{{\mathcal {X}}}}(t,z), \end{aligned}$$

respectively, where

$$\begin{aligned} z\partial _{zz}\Upsilon (t,z)&=\int _t^T\left\{ e^{-K(s-t)}\dfrac{1}{\gamma }\dfrac{1-\gamma }{1-\gamma _1} \left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^{\frac{\gamma _1-\gamma }{\gamma }}z^{-\frac{1}{\gamma }}{{{\mathcal {N}}}} \left( d_{\gamma -}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad -\left. e^{-K(s-t)}\dfrac{\gamma }{1-\gamma _1}\left( \dfrac{\gamma _1-\gamma }{1-\gamma _1}\right) ^{\frac{\gamma _1-\gamma }{\gamma }}z^{-\frac{1}{\gamma _1}}{} \textbf{n}\left( d_{\gamma -}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) d_{\gamma +}\right. \\&\quad \left. \Bigg (s-t,\frac{z}{z_L}\Bigg )\dfrac{1}{\sigma _z^2(s-t)}\right. \\&\quad -\left. e^{-r_w(s-t)}L\textbf{n}\left( d_{1+}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) d_{1-} \Bigg (s-t,\frac{z}{z_L}\Bigg )\dfrac{1}{\sigma _z^2(s-t)}\right. \\&\quad \left. -e^{-K_1(s-t)}\frac{1}{\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad +\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{} \textbf{n}\right. \\&\quad \left. \left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) d_{\gamma _1+}\Bigg (s-t,\frac{z}{z_L}\Bigg ) \dfrac{1}{\sigma _z^2(s-t)}\right. \\&\quad +\left. e^{-K_1(s-t)}\frac{1}{\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^ {-\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \right. \\&\quad -\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}L^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{} \textbf{n} \left( d_{\gamma _1-}\Bigg (s-t,\frac{z}{z_L}\Bigg )\right) \right. \\&\quad \left. d_{\gamma _1+}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\dfrac{1}{\sigma _z^2(s-t)}\right. \\&\quad -\left. e^{-r_w(s-t)}\big ({\bar{L}}-L\big )\textbf{n}\left( d_{1+}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg ) \right) d_{1-}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\dfrac{1}{\sigma _z^2(s-t)}\right. \\&\quad -\left. e^{-K_1(s-t)} \frac{1}{\gamma _1}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}{{{\mathcal {N}}}}\left( d_{\gamma _1-} \Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\right) \right. \\&\quad +\left. e^{-K_1(s-t)}\dfrac{\gamma _1}{1-\gamma _1}{\bar{L}}^{\frac{\gamma _1-\gamma }{\gamma _1}}z^{-\frac{1}{\gamma _1}}\textbf{n}\left( d_{\gamma _1-}(s-t,\frac{z}{z_L})\right) \right. \\&\quad \left. d_{\gamma _1+}\Bigg (s-t,\frac{z}{\Lambda (s)}\Bigg )\dfrac{1}{\sigma _z^2(s-t)} \right\} dt. \end{aligned}$$