1 Introduction

Liquid crystal elastomers (LCEs) are advanced multifunctional materials that combine elasticity with orientational order [32]. Specifically, mechanical strains give rise to changes in liquid crystalline order and, conversely, changes in the orientational order generate mechanical stresses and strains. Because of their large reversible deformations and complex material responses in the presence of external stimuli, such as heat, light, electric or magnetic fields, LCEs are suitable for a wide range of applications in science, manufacturing, and medical research [4].

LCEs can be synthesized by various methods. Without special aligning mechanisms, polydomain samples are typically obtained where the material contains multiple subdomains, each of them with their own nematic alignment, termed the “director”. Monodomain LCEs can be achieved by a secondary cross-linking after electric or magnetic fields are applied or the material is mechanically deformed to induce the desired nematic orientation.

Sitting between the world of elastomers and that of liquid crystals, the analysis of LCEs can take advantage of developments in both these fields [22]. For unconstrained isotropic hyperelastic materials, it is well known that the only controllable deformations that can be maintained universally, i.e., independently of the material parameters, by application of surface tractions only, are those characterized by a constant deformation gradient in Cartesian coordinates, the so-called homogeneous deformations. This fundamental result due to Ericksen (1955) [8] (see also [29] for an alternative proof) has been central to the phenomenological study of many elastic materials for which constitutive parameters are derived from macroscopic experimental tests. The problem of controllable deformations for incompressible homogeneous isotropic hyperelastic materials is much more involved and was examined in [7, 17, 21]. We refer also to [28] for a review of these results. Extensions of the analysis to anisotropic elasticity are presented in [34, 35] and to anelasticity in [15, 33].

In addition, nematic elastomers can sustain large reversible deformations under small applied forces [9, 14, 16, 18, 19, 26, 27, 31, 36]. For ideal LCEs, the theoretical explanation is that the energy depending isotropically on the macroscopic deformation only through the relative strain of the microstructure is minimized by these materials through a force-free state, resulting in the so-called soft-elasticity phenomenon, where the microstructure consists of many homogeneously deformed parts, known as shear striping [1, 2, 5, 6]. Strain-energy densities depending also on the macroscopic strain to realistically account for semi-soft elasticity where the applied force required is small were proposed in [11–13] (see also [23, 24]).

In this paper, we consider ideal unconstrained uniaxial nematic LCEs characterized by a homogeneous isotropic hyperelastic strain-energy density and subject to surface tractions only, i.e., in the absence of body forces. We prove that, in Cartesian coordinates, assuming that the deformation gradient is sufficiently smooth, the deformation is always homogeneous, i.e., it has a constant deformation gradient, while the liquid crystal director is either uniformly aligned or oriented randomly. If we weaken the smoothness assumption, then multiple solutions with locally constant deformation gradients can exist, such as the classical shear striping. This result is a direct extension of Ericksen’s theorem for compressible elastic materials [8] to ideal LCEs. The case where LCEs are modelled as incompressible materials [1, 20, 24] is also of considerable interest, but will not be discussed here.

2 Ideal Liquid Crystal Elastomers

An ideal uniaxial nematic LCE can be described by a homogeneous strain-energy density function of the form [22]

$$ W^{(nc)}(\textbf{F},\textbf{n})=W(\textbf{A}), $$
(1)

where \(\textbf{F}\) represents the macroscopic deformation gradient from the cross-linking state, \(\textbf{n}\) is the nematic director (a unit vector for the localized direction of uniaxial nematic alignment) in the present configuration, and \(W(\textbf{A})\) is the strain-energy density of the isotropic polymer network, depending only on the (local) elastic deformation tensor \(\textbf{A}\). The tensors \(\textbf{F}\) and \(\textbf{A}\) satisfy the following relation [32],

$$ \textbf{F}=\textbf{G}\textbf{A}\textbf{G}_{0}^{-1}, $$
(2)

where

$$ \textbf{G}=\left (a^{1/3}-a^{-\nu /3}\right )\textbf{n}\otimes \textbf{n}+a^{-\nu /3}\textbf{I} $$
(3)

is the nematically-induced (natural) deformation tensor defining a change of frame of reference from the isotropic to a nematic phase. In equation (3), \(a>0\) is a light- or temperature-dependent shape parameter, \(\nu \) represents the optothermal analogue to the Poisson ratio relating responses in directions parallel or perpendicular to the director \(\textbf{n}\), ⊗ denotes the tensor product of two vectors, and \(\textbf{I}=\mathrm{diag}(1,1,1)\) is the identity tensor, with \(\mathrm{diag}(\cdot , \cdot , \cdot )\) denoting the diagonal second order tensor. We assume both \(a\) and \(\nu \) to be spatially independent. The tensor \(\textbf{G}_{0}\) has a similar expression to that of \(\textbf{G}\), with \(\textbf{n}_{0}\) instead of \(\textbf{n}\), \(a_{0}\) instead of \(a\), and \(\nu _{0}\) instead of \(\nu \), corresponding to the reference cross-linking state. The director \(\textbf{n}\) is an observable (spatial) quantity, and may differ from \(\textbf{n}_{0}\) by a rotation.

The square of the natural deformation tensor, known as the step-length tensor, takes the equivalent form [10] (see also [25]),

$$ \textbf{G}^{2}=c\left (\textbf{I}+2\textbf{Q}\right ), $$
(4)

where \(c\) is the effective step length of the polymeric chain and \(\textbf{Q}\) is the symmetric traceless order parameter tensor describing orientational order in nematic liquid crystals [3, 32]. In an isotropic phase, where the liquid crystal molecules are randomly oriented, \(\textbf{Q}=\textbf{0}\).

In practice, LCEs can be modeled as incompressible materials at the cost of imposing an extra constraint, namely \(\det \textbf{F}=1\). However, here we consider universal solutions for unconstrained LCEs, i.e., incompressibility is not enforced.

In equation (1), the elastic strain-energy density \(W\) is minimized by any deformation satisfying \(\textbf{A}\textbf{A}^{T}=\textbf{I}\), and the nematic strain-energy function \(W^{(nc)}\) is minimized by any deformation satisfying \(\left (\textbf{F}\textbf{G}_{0}\right )\left (\textbf{F}\textbf{G}_{0} \right )^{T}=\textbf{G}^{2}\). Without loss of generality, we assume that the strain-energy density described by equation (1) vanishes in the reference state where \(\textbf{F}=\textbf{I}\) and \(\textbf{G}=\textbf{G}_{0}\).

By (3), if \(\textbf{R}\) is a rigid-body rotation, then the following identity holds

$$ \textbf{R}^{\mathsf{T}}\textbf{G}\textbf{R}=\left (a^{1/3}-a^{-\nu /3} \right )\left (\textbf{R}^{\mathsf{T}}\textbf{n}\right )\otimes \left ( \textbf{R}^{\mathsf{T}}\textbf{n}\right )+a^{-\nu /3}\textbf{I}. $$
(5)

Since nematic elastomers are weakly cross-linked, the nematic director can rotate freely, and the material displays isotropic mechanical properties. Then, the strain-energy density given by (1) satisfies the following conditions inherited from isotropic finite elasticity [22]:

(C1):

Objectivity/Frame-indifference. The constitutive equation is unaffected by a superimposed rigid-body transformation (which involves a change of position after deformation). As \(\textbf{n}\) is defined with respect to the deformed configuration, it transforms when this configuration is rotated, whereas \(\textbf{n}_{0}\) does not. Material objectivity is guaranteed by defining strain-energy functions in terms of the scalar invariants.

This is because, by the material frame indifference of \(W\),

$$ W(\textbf{R}^{\mathsf{T}}\textbf{A})=W(\textbf{A}), $$
(6)

and by (2),

$$ \textbf{R}^{\mathsf{T}}\textbf{F}=\left (\textbf{R}^{\mathsf{T}} \textbf{G}\textbf{R}\right )\left (\textbf{R}^{\mathsf{T}}\textbf{A} \right )\textbf{G}_{0}^{-1}. $$
(7)

Then (1), (5), (6) and (7) imply

$$ W^{(nc)}(\textbf{R}^{\mathsf{T}}\textbf{F},\textbf{R}^{\mathsf{T}} \textbf{n})=W(\textbf{R}^{\mathsf{T}}\textbf{A})=W(\textbf{A})=W^{(nc)}( \textbf{F},\textbf{n}). $$
(8)
(C2):

Isotropy. The constitutive equation is unaffected by a rigid-body transformation prior to deformation. As \(\textbf{n}\) is defined with respect to the deformed configuration, it does not change when the reference configuration is rotated, whereas \(\textbf{n}_{0}\) does. For isotropic materials, the strain-energy function is a symmetric function of the principal stretch ratios.

This is because, since \(W\) is isotropic, i.e.,

$$ W(\textbf{A})=W(\textbf{A}\textbf{R}), $$
(9)

and (2) holds, it follows that

$$ \textbf{F}\textbf{R}=\textbf{G}\left (\textbf{A}\textbf{R}\right )\left ( \textbf{R}^{\mathsf{T}}\textbf{G}_{0}^{-1}\textbf{R}\right ). $$
(10)

Then, by (1), (9) and (10),

$$ W^{(nc)}(\textbf{F}\textbf{R},\textbf{n})=W(\textbf{A}\textbf{R})=W( \textbf{A})=W^{(nc)}(\textbf{F},\textbf{n}). $$
(11)

Under the frame-indifference condition (C1), the LCE model defined by (1) can be expressed equivalently in terms of the scalar invariants [30], as follows:

$$ W^{(nc)}\left (I^{(nc)}_{1},I^{(nc)}_{2},I^{(nc)}_{3},I^{(nc)}_{4},I^{(nc)}_{5} \right )= W(I_{1},I_{2},I_{3}), $$
(12)

where

$$\begin{aligned} &I^{(nc)}_{1}=\mathrm{tr}\left (\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{ \mathsf{T}}\right )=\mathrm{tr}\left (\textbf{F}^{\mathsf{T}} \textbf{G}_{0}^{2}\textbf{F}\right ), \end{aligned}$$
(13)
$$\begin{aligned} &I^{(nc)}_{2}=\mathrm{tr}\left [\mathrm{Cof}\left (\textbf{F} \textbf{G}_{0}^{2}\textbf{F}^{\mathsf{T}}\right )\right ]=\mathrm{tr} \left [\mathrm{Cof}\left (\textbf{F}^{\mathsf{T}}\textbf{G}_{0}^{2} \textbf{F}\right )\right ], \end{aligned}$$
(14)
$$\begin{aligned} &I^{(nc)}_{3}=\det \left (\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{ \mathsf{T}}\right )=\det \left (\textbf{F}^{\mathsf{T}}\textbf{G}_{0}^{2} \textbf{F}\right ), \end{aligned}$$
(15)
$$\begin{aligned} &I^{(nc)}_{4}=\textbf{n}\cdot \textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{ \mathsf{T}}\textbf{n}, \end{aligned}$$
(16)
$$\begin{aligned} &I^{(nc)}_{5}=\textbf{n}\cdot \left (\textbf{F}\textbf{G}_{0}^{2} \textbf{F}^{\mathsf{T}}\right )^{2}\textbf{n}, \end{aligned}$$
(17)

and \(\{I_{1},I_{2},I_{3}\}\) are the principal invariants of the elastic Cauchy-Green tensors \(\textbf{A}\textbf{A}^{\mathsf{T}}\) and \(\textbf{A}^{\mathsf{T}}\textbf{A}\).

The following relations between \(\left \{I^{(nc)}_{1},I^{(nc)}_{2},I^{(nc)}_{3},I^{(nc)}_{4},I^{(nc)}_{5} \right \}\) and \(\{I_{1},I_{2},I_{3}\}\) are obtained:

$$ I_{3}=\left (\det \textbf{A}\right )^{2}=\left [\det \textbf{G}^{-1} \det \left (\textbf{F}\textbf{G}_{0}\right )\right ]^{2}=a^{2(2\nu -1)/3}I^{(nc)}_{3}, $$
(18)

where \(\det \textbf{G}=a^{(1-2\nu )/3}\),

$$ \begin{aligned} I_{1}&=\mathrm{tr}\left (\textbf{A}^{\mathsf{T}} \textbf{A}\right ) \\ &=\mathrm{tr}\left [\left (\textbf{F}\textbf{G}_{0}\right )^{\mathsf{T}} \textbf{G}^{-2}\left (\textbf{F}\textbf{G}_{0}\right )\right ] \\ &=a^{2\nu /3}\left [\mathrm{tr}\left (\textbf{F}\textbf{G}_{0}^{2} \textbf{F}^{\mathsf{T}}\right )-\left (1- a^{-2(\nu +1)/3}\right ) \textbf{n}\cdot \left (\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{\mathsf{T}} \right )\textbf{n}\right ] \\ &=a^{2\nu /3}\left [I^{(nc)}_{1}-\left (1- a^{-2(\nu +1)/3}\right )I^{(nc)}_{4} \right ], \end{aligned} $$
(19)

and, using (18),

$$ \begin{aligned} I_{2}&=I_{3}\ \mathrm{tr}\left (\textbf{A}^{\mathsf{T}} \textbf{A}\right )^{-\mathsf{T}} \\ &=a^{2(2\nu -1)/3}I^{(nc)}_{3}\mathrm{tr}\left [\left (\textbf{F} \textbf{G}_{0}\right )^{-1}\textbf{G}^{2}\left (\textbf{F}\textbf{G}_{0} \right )^{-\mathsf{T}}\right ] \\ &=a^{2(2\nu -1)/3}I^{(nc)}_{3}a^{-2\nu /3}\left [\mathrm{tr}\left ( \textbf{F}^{-\mathsf{T}}\textbf{G}_{0}^{-2}\textbf{F}^{-1}\right )- \left (1- a^{2(\nu +1)/3}\right )\textbf{n}\cdot \left (\textbf{F}^{- \mathsf{T}}\textbf{G}_{0}^{-2}\textbf{F}^{-1}\right )\textbf{n}\right ] \\ &=a^{2(\nu -1)/3}\left [I^{(nc)}_{2}-\left (1-a^{2(\nu +1)/3}\right ) \left (I^{(nc)}_{5}-I^{(nc)}_{1}I^{(nc)}_{4}+I^{(nc)}_{2}\right ) \right ]. \end{aligned} $$
(20)

Note that the above expression for \(I_{2}\) holds since, by the Cayley-Hamilton theorem, we have

$$ \left (\textbf{F}\textbf{G}_{0}\textbf{F}^{\mathsf{T}}\right )^{3}-I^{(nc)}_{1} \left (\textbf{F}\textbf{G}_{0}\textbf{F}^{\mathsf{T}}\right )^{2}+I^{(nc)}_{2} \left (\textbf{F}\textbf{G}_{0}\textbf{F}^{\mathsf{T}}\right )-I^{(nc)}_{3} \textbf{I}=0, $$
(21)

and multiplying the above equation by \(\left (\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{\mathsf{T}}\right )^{-1}\) gives

$$ I^{(nc)}_{3}\left (\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{\mathsf{T}} \right )^{-1}=\left (\textbf{F}\textbf{G}_{0^{2}}\textbf{F}^{\mathsf{T}} \right )^{2}-I^{(nc)}_{1}\left (\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{ \mathsf{T}}\right )+I^{(nc)}_{2}\textbf{I}. $$
(22)

Hence,

$$ \begin{aligned} \textbf{n}\cdot \textbf{F}^{-\mathsf{T}}\textbf{G}_{0}^{-2} \textbf{F}^{-1}\textbf{n} &=\textbf{n}\cdot \left (I^{(nc)}_{3}\right )^{-1} \left [\left (\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{\mathsf{T}}\right )^{2}-I^{(nc)}_{1} \left (\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{\mathsf{T}}\right )+I^{(nc)}_{2} \textbf{I}\right ]\textbf{n} \\ &=\left (I^{(nc)}_{3}\right )^{-1}\left (I^{(nc)}_{5}-I^{(nc)}_{1}I^{(nc)}_{4}+I^{(nc)}_{2} \right ). \end{aligned} $$
(23)

By the isotropy condition (C2), the LCE model given by (1) can be written equivalently as

$$ W^{(nc)}(\lambda _{1},\lambda _{2},\lambda _{3},\textbf{n})= W(\alpha _{1}, \alpha _{2},\alpha _{3}), $$
(24)

where \(\lambda _{1}^{2}\), \(\lambda _{2}^{2}\), \(\lambda _{3}^{2}\) are the principal eigenvalues of \(\textbf{F}\textbf{G}_{0}^{2}\textbf{F}^{\mathsf{T}}\) and \(\alpha _{1}^{2}\), \(\alpha _{2}^{2}\), \(\alpha _{3}^{2}\) are the principal eigenvalues of \(\textbf{A}^{\mathsf{T}}\textbf{A}\). The following relations between these principal eigenvalues and the corresponding principal invariants hold,

$$ I^{(nc)}_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}, \qquad I^{(nc)}_{2}=\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2} \lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2},\qquad I^{(nc)}_{3}= \lambda _{1}^{2}\lambda _{2}^{2}\lambda _{3}^{2}, $$
(25)

and

$$ I_{1}=\alpha _{1}^{2}+\alpha _{2}^{2}+\alpha _{3}^{2},\qquad I_{2}= \alpha _{1}^{2}\alpha _{2}^{2}+\alpha _{2}^{2}\alpha _{3}^{2}+\alpha _{3}^{2} \alpha _{3}^{2}\qquad I_{3}=\alpha _{1}^{2}\alpha _{2}^{2}\alpha _{3}^{2}, $$
(26)

as usual.

3 Stresses and Stress-Free Configurations

For nematic LCEs, the director is ‘free’ to rotate, hence \(\textbf{F}\) and \(\textbf{n}\) are independent variables. Since \(\textbf{G}\) and \(\textbf{G}_{0}\) are symmetric, the Cauchy stress tensor for the nematic material with the strain-energy function described by (1) is calculated as follows [22],

$$ \begin{aligned} \textbf{T}^{(nc)} &=J^{-1} \frac{\partial W^{(nc)}}{\partial \textbf{F}}\textbf{F}^{T} \\ &=J^{-1}\textbf{G}^{-1}\frac{\partial W}{\partial \textbf{A}} \textbf{A}^{T}\textbf{G} \\ &=\left (\det \textbf{G}^{-1}\det \textbf{G}_{0}\right )\textbf{G}^{-1} \textbf{T}\textbf{G}, \end{aligned} $$
(27)

where \(J=\det \textbf{F}=\det \textbf{G}\det \textbf{A}\det \textbf{G}_{0}^{-1} \) and

$$ \textbf{T}=\left (\det \textbf{A}\right )^{-1} \frac{\partial W}{\partial \textbf{A}}\textbf{A}^{T} $$
(28)

is the Cauchy stress tensor from isotropic finite elasticity. Equivalently,

$$ \textbf{T}=\beta _{0}\ \textbf{I}+\beta _{1}\ \textbf{B}+\beta _{-1}\ \textbf{B}^{-1}, $$
(29)

where

$$ \beta _{0}=\frac{2}{\sqrt{I_{3}}}\left (I_{2} \frac{\partial W}{\partial I_{2}}+I_{3} \frac{\partial W}{\partial I_{3}}\right ),\qquad \beta _{1}= \frac{2}{\sqrt{I_{3}}}\frac{\partial W}{\partial I_{1}},\qquad \beta _{-1}=-2 \sqrt{I_{3}}\frac{\partial W}{\partial I_{2}} $$
(30)

are scalar functions of the principal invariants \(\{I_{1}, I_{2}, I_{2}\}\) of \(\textbf{B}=\textbf{A}\textbf{A}^{T}\).

The first Piola-Kirchhoff stress tensor for the nematic material is equal to

$$ \textbf{P}^{(nc)}=\textbf{T}^{(nc)}\ \mathrm{Cof}\ \textbf{F} = \frac{\partial W^{(nc)}}{\partial \textbf{F}} =\textbf{G}^{-1} \frac{\partial W}{\partial \textbf{A}} =\textbf{G}^{-1}\textbf{P}, $$
(31)

where \(\mathrm{Cof}\ \textbf{F}=J\textbf{F}^{-T}\) and

$$ \textbf{P}=\frac{\partial W}{\partial \textbf{A}} $$
(32)

is the first Piola-Kirchhoff stress tensor from isotropic elasticity.

The corresponding second Piola-Kirchhoff stress tensor is

$$ \textbf{S}^{(nc)}=\textbf{F}^{-1}\textbf{P}^{(nc)}=\textbf{G}_{0} \textbf{A}^{-1}\textbf{G}^{-2}\textbf{P}\textbf{G}_{0}=\textbf{G}_{0} \textbf{A}^{-1}\textbf{G}^{-2}\textbf{A}\textbf{S}\textbf{G}_{0}, $$
(33)

where \(\textbf{S}=\textbf{A}^{-1}\textbf{P}\) is the second Piola-Kirchhoff from isotropic elasticity.

Since the relation (29) between the Cauchy stress tensor \(\textbf{T}\) and the Cauchy-Green tensor \(\textbf{B}\) is not invertible in general, more than one deformation gradient \(\textbf{A}\) may induce the same stress tensor \(\textbf{T}\). Thus the Cauchy stress tensor \(\textbf{T}^{(nc)}\) in a nematic LCE may also be generated by more than one deformation gradient \(\textbf{F}\). Such deformations corresponding to the same stress tensor can also alternate in LCE materials to produce inhomogeneous patterns. In this case, for geometric compatibility, any two different gradient tensors \(\textbf{F}\) and \(\widehat{\textbf{F}}\) corresponding to two alternating phases must be rank-one connected, i.e., \(\mathrm{rank}\left (\textbf{F}-\widehat{\textbf{F}}\right )=1\).

For example, assuming that \(\textbf{T}=\textbf{0}\) for rigid-body rotations, i.e., when \(\textbf{A}=\textbf{R}\), then \(\textbf{T}^{(nc)}=\textbf{0}\) when \(\textbf{F}=\textbf{G}\textbf{R}\textbf{G}_{0}^{-1}\). In particular, in the absence of elastic deformations, such that \(\textbf{A}=\textbf{I}\) and \(\textbf{G}=\textbf{G}_{0}\), the undeformed configuration, with \(\textbf{F}=\textbf{I}\), is stress free, i.e., \(\textbf{T}^{(nc)}=\textbf{0}\). However, since it is possible for a stress-free state to be generated by more than one deformation, when these deformations are geometrically compatible, they can also alternate in the same material, producing an inhomogeneous pattern.

More generally, if \(\textbf{T}=p\textbf{I}\), where \(p\) is constant, while \(\textbf{A}=c \textbf{R}\), where \(c\) is constant and \(\textbf{R}\) is a rigid-body rotation, then \(\textbf{T}^{(nc)}=p\left (\det \textbf{G}^{-1}\det \textbf{G}_{0} \right )\textbf{I}\) for \(\textbf{F}=c \textbf{G}\textbf{R}\textbf{G}_{0}^{-1}\). As it is possible for the same stress to be generated by different deformations, if these are geometrically compatible, then they can also alternate in the same material to produce inhomogeneous patterns.

Our result concerning controllable deformation in ideal nematic elastomers is established in the next section.

4 Controllable Deformations

Theorem 1

For an ideal unconstrained uniaxial nematic LCE characterized by equation (1), such that \(\textbf{G}_{0}\) is constant in Cartesian coordinates, a deformation with gradient \(\textbf{F}(\textbf{X})\) of differentiability class \(\mathcal{C}^{2}\), such that \(\det \textbf{F}(\textbf{X})>0\), can be maintained for all \(W^{(nc)}\) by the application of surface tractions only (without body forces) if and only if both \(\textbf{F}\) and \(\textbf{G}\) are constant in Cartesian coordinates.

Proof

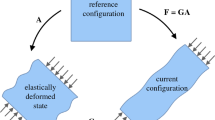
We set the notation \(\overline{\textbf{F}}=\textbf{F}\textbf{G}_{0}\), so that \(\overline{\textbf{F}}=\textbf{G}\textbf{A}\) (see Fig. 1). Since \(\textbf{G}_{0}\) is constant, this amounts to a change of coordinates from the cross-linking state, with coordinates \((X_{1},X_{2},X_{3})\), to a virtual isotropic state, with coordinates \((\overline{X}_{1},\overline{X}_{2},\overline{X}_{3})\), such that

$$ G_{0ij}=\frac{\partial X_{i}}{\partial \overline{X}_{j}},\qquad i,j=1, 2, 3. $$
(34)

Henceforth, all calculations are carried out within this new system of coordinates.

Fig. 1
figure 1

Schematic of multiplicative decomposition \(\textbf{F}=\textbf{G}\textbf{A}\textbf{G}_{0}^{-1}\) and adopted notation \(\textbf{F}\textbf{G}_{0}=\overline{\textbf{F}}=\textbf{G}\textbf{A}\)

Full size image

The first Piola-Kirchhoff stress takes the form

$$ \overline{\textbf{P}}^{(nc)}= \frac{\partial W^{(nc)}}{\partial \overline{\textbf{F}}}=\sum _{i=1}^{5} \frac{\partial W^{(nc)}}{\partial I^{(nc)}_{i}} \frac{\partial I^{(nc)}_{i}}{\partial \overline{\textbf{F}}}. $$
(35)

In the absence of body forces, the equation of elastostatic equilibrium is

$$ \mathrm{Div} \ \overline{\textbf{P}}^{(nc)}=\textbf{0}. $$
(36)

Equivalently,

$$ \sum _{i=1}^{5}\frac{\partial W^{(nc)}}{\partial I^{(nc)}_{i}} \mathrm{Div}\left ( \frac{\partial I^{(nc)}_{i}}{\partial \overline{\textbf{F}}}\right )+ \sum _{i=1}^{9}\sum _{j=1}^{3} \frac{\partial ^{2} W^{(nc)}}{\partial I^{(nc)}_{i}\partial I^{(nc)}_{j}} \left (\mathrm{Grad}\ I^{(nc)}_{j}\right ) \frac{\partial I^{(nc)}_{i}}{\partial \overline{\textbf{F}}}= \textbf{0}. $$
(37)

By the standard argument, if this holds for arbitrary \(W^{(nc)}\), then

$$ \mathrm{Div}\left ( \frac{\partial I^{(nc)}_{i}}{\partial \overline{\textbf{F}}}\right )= \textbf{0}, \qquad i=1, \ldots, 5, $$

and

$$ \left (\mathrm{Grad}\ I^{(nc)}_{j}\right ) \frac{\partial I^{(nc)}_{i}}{\partial \overline{\textbf{F}}}+\left ( \mathrm{Grad}\ I^{(nc)}_{i}\right ) \frac{\partial I^{(nc)}_{j}}{\partial \overline{\textbf{F}}}= \textbf{0}, \qquad i,j=1, \ldots, 5. $$

In particular, if \(i=j\), then

$$ \mathrm{Grad}\ I^{(nc)}_{i}=0,\qquad i=1, \ldots, 5. $$

For \(i=1\), \(\partial I^{(nc)}_{1}/\partial \overline{\textbf{F}}=2 \overline{\textbf{F}}\), hence

$$ \mathrm{Grad}\ I^{(nc)}_{1}=\textbf{0}\qquad \text{and}\quad \mathrm{Div}\left ( \frac{\partial I^{(nc)}_{1}}{\partial \overline{\textbf{F}}}\right )=2 \ \mathrm{Div}\ \overline{\textbf{F}}=\textbf{0}. $$
(38)

If the components of the deformation gradient are expressed in Cartesian coordinates as

$$ \overline{F}_{ij}=\frac{\partial x_{i}}{\partial \overline{X}_{j}}, \qquad i,j=1, 2, 3, $$

then \(\mathrm{Div}\ \overline{\textbf{F}}=\textbf{0}\) takes the form

$$ \sum _{k=1}^{3} \frac{\partial ^{2} x_{i}}{\partial \overline{X}_{k}^{2}}=0,\quad i=1, 2, 3, $$

and \(\mathrm{Grad}\ I^{(nc)}_{1}=\textbf{0}\) can be written as

$$ \sum _{i=1}^{3}\sum _{j=1}^{3} \frac{\partial x_{i}}{\partial \overline{X}_{j}} \frac{\partial ^{2} x_{i}}{\partial \overline{X}_{j}\partial \overline{X}_{k}}=0, \qquad k=1, 2, 3. $$

Therefore,

$$ 0=\sum _{k=1}^{3}\frac{\partial}{\partial \overline{X}_{k}}\left ( \sum _{i=1}^{3}\sum _{j=1}^{3} \frac{\partial x_{i}}{\partial \overline{X}_{j}} \frac{\partial ^{2} x_{i}}{\partial \overline{X}_{j}\partial \overline{X}_{k}} \right ) =\sum _{i=1}^{3}\sum _{j=1}^{3}\sum _{k=1}^{3} \frac{\partial ^{2} x_{i}}{\partial \overline{X}_{j}\partial \overline{X}_{k}} \frac{\partial ^{2} x_{i}}{\partial \overline{X}_{j}\partial \overline{X}_{k}}. $$

Noting that the right-hand side of the above equality is a sum of squares, it follows that

$$ \frac{\partial ^{2} x_{i}}{\partial \overline{X}_{j}\partial \overline{X}_{k}}=0, \qquad i,j,k=1, 2, 3. $$

Hence \(\overline{\textbf{F}}\) is constant in the Cartesian coordinates \((\overline{X}_{1},\overline{X}_{2},\overline{X}_{3})\), and since \(\textbf{G}_{0}\) is constant, \(\textbf{F}\) is also constant in the Cartesian coordinates \((X_{1},X_{2},X_{3})\).

Next, we show that \(\textbf{G}\) is constant as well. For \(i=4\),

$$ \mathrm{Grad}\ I^{(nc)}_{4}=\textbf{0}\qquad \text{and}\quad \mathrm{Div}\left ( \frac{\partial I^{(nc)}_{4}}{\partial \overline{\textbf{F}}}\right )= \textbf{0}. $$
(39)

Taking any finite deformation with \(\overline{\textbf{F}}\) constant, we choose the Cartesian coordinates along its principal directions, such that \(\overline{\textbf{F}}=\mathrm{diag}\left (\overline{F}_{11}, \overline{F}_{22}, \overline{F}_{33}\right )\). Then the first equation in \(I^{(nc)}_{4}\) implies:

$$ \begin{aligned} \overline{F}_{11} \frac{\partial n_{1}^{2}}{\partial \overline{X}_{1}}+\overline{F}_{22} \frac{\partial n_{2}^{2}}{\partial \overline{X}_{1}}+\overline{F}_{33} \frac{\partial n_{3}^{2}}{\partial \overline{X}_{1}}&=0, \\ \overline{F}_{11}\frac{\partial n_{1}^{2}}{\partial \overline{X}_{2}}+ \overline{F}_{22}\frac{\partial n_{2}^{2}}{\partial \overline{X}_{2}}+ \overline{F}_{33}\frac{\partial n_{3}^{2}}{\partial \overline{X}_{2}}&=0, \\ \overline{F}_{11}\frac{\partial n_{1}^{2}}{\partial \overline{X}_{3}}+ \overline{F}_{22}\frac{\partial n_{2}^{2}}{\partial \overline{X}_{3}}+ \overline{F}_{33}\frac{\partial n_{3}^{2}}{\partial \overline{X}_{3}}&=0, \end{aligned} $$

while the second equation implies

$$ \frac{\partial n_{1}^{2}}{\partial \overline{X}_{1}}=0,\qquad \frac{\partial n_{2}^{2}}{\partial \overline{X}_{2}}=0,\qquad \frac{\partial n_{3}^{2}}{\partial \overline{X}_{3}}=0. $$

From the above equations, we infer that \(n_{i}\) is independent of \(\overline{X}_{i}\), for \(i=1,2,3\), and the following conditions are satisfied simultaneously:

$$ \begin{aligned} &\left (\overline{F}_{11}-\overline{F}_{33}\right ) \frac{\partial n_{1}^{2}}{\partial \overline{X}_{2}}=0,\qquad \left ( \overline{F}_{11}-\overline{F}_{22}\right ) \frac{\partial n_{1}^{2}}{\partial \overline{X}_{3}}=0, \\ &\left (\overline{F}_{22}-\overline{F}_{33}\right ) \frac{\partial n_{2}^{2}}{\partial \overline{X}_{1}}=0,\qquad \left ( \overline{F}_{22}-\overline{F}_{11}\right ) \frac{\partial n_{2}^{2}}{\partial \overline{X}_{3}}=0, \\ &\left (\overline{F}_{33}-\overline{F}_{22}\right ) \frac{\partial n_{3}^{2}}{\partial \overline{X}_{1}}=0,\qquad \left ( \overline{F}_{33}-\overline{F}_{11}\right ) \frac{\partial n_{3}^{2}}{\partial \overline{X}_{2}}=0. \end{aligned} $$

By the isotropy condition (C2), we can apply any rotation \(\textbf{R}\) prior to the deformation, such that \(\left \{\overline{F}_{11}, \overline{F}_{22}, \overline{F}_{33} \right \}\) permute along the diagonal, while \(\textbf{n}\) does not rotate. After replacing \(\mathrm{diag}\left (\overline{F}_{11}, \overline{F}_{22}, \overline{F}_{33}\right )\) first with \(\mathrm{diag}\left (\overline{F}_{22}, \overline{F}_{33}, \overline{F}_{11}\right )\) and second with \(\mathrm{diag}\left (\overline{F}_{33}, \overline{F}_{11}, \overline{F}_{22}\right )\), we also obtain, respectively:

$$ \begin{aligned} &\left (\overline{F}_{22}-\overline{F}_{11}\right ) \frac{\partial n_{1}^{2}}{\partial \overline{X}_{2}}=0,\qquad \left ( \overline{F}_{22}-\overline{F}_{33}\right ) \frac{\partial n_{1}^{2}}{\partial \overline{X}_{3}}=0, \\ &\left (\overline{F}_{33}-\overline{F}_{11}\right ) \frac{\partial n_{2}^{2}}{\partial \overline{X}_{1}}=0,\qquad \left ( \overline{F}_{33}-\overline{F}_{22}\right ) \frac{\partial n_{2}^{2}}{\partial \overline{X}_{3}}=0, \\ &\left (\overline{F}_{11}-\overline{F}_{33}\right ) \frac{\partial n_{3}^{2}}{\partial \overline{X}_{1}}=0,\qquad \left ( \overline{F}_{11}-\overline{F}_{22}\right ) \frac{\partial n_{3}^{2}}{\partial \overline{X}_{2}}=0, \end{aligned} $$

and

$$ \begin{aligned} &\left (\overline{F}_{33}-\overline{F}_{22}\right ) \frac{\partial n_{1}^{2}}{\partial \overline{X}_{2}}=0,\qquad \left ( \overline{F}_{33}-\overline{F}_{11}\right ) \frac{\partial n_{1}^{2}}{\partial \overline{X}_{3}}=0, \\ &\left (\overline{F}_{11}-\overline{F}_{22}\right ) \frac{\partial n_{2}^{2}}{\partial \overline{X}_{1}}=0,\qquad \left ( \overline{F}_{11}-\overline{F}_{33}\right ) \frac{\partial n_{2}^{2}}{\partial \overline{X}_{3}}=0, \\ &\left (\overline{F}_{22}-\overline{F}_{11}\right ) \frac{\partial n_{3}^{2}}{\partial \overline{X}_{1}}=0,\qquad \left ( \overline{F}_{22}-\overline{F}_{33}\right ) \frac{\partial n_{3}^{2}}{\partial \overline{X}_{2}}=0. \end{aligned} $$

We distinguish the following two cases. First, if at least two of the three diagonal values \(\left \{\overline{F}_{11}, \overline{F}_{22}, \overline{F}_{33} \right \}\) are different from each other, then \(\mathrm{Grad}\ \textbf{n}=\textbf{0}\), i.e., \(\textbf{n}\) is uniform in the Cartesian coordinates \((\overline{X}_{1},\overline{X}_{2},\overline{X}_{3})\), and since \(\textbf{G}_{0}\) is constant, \(\textbf{n}\) is also uniform in the Cartesian coordinates \((X_{1},X_{2},X_{3})\) (see also [34]). Thus \(\textbf{G}\) is constant. Second, if \(\overline{F}_{11}=\overline{F}_{22}=\overline{F}_{33}=\overline{F}\), then \(\overline{\textbf{F}}=\overline{F}\textbf{I}\), where \(\overline{F}\) is a constant scalar in the Cartesian coordinates \((\overline{X}_{1},\overline{X}_{2},\overline{X}_{3})\). Hence, the current configuration is an isotropic state, i.e., \(\textbf{G}\) is constant, in the Cartesian coordinates \((\overline{X}_{1},\overline{X}_{2},\overline{X}_{3})\). Because \(\textbf{G}_{0}\) is constant, it follows that \(\textbf{G}\) is constant also in the Cartesian coordinates \((X_{1},X_{2},X_{3})\), i.e., either \(\textbf{n}=\textbf{n}_{0}\) or both the reference and current configurations are isotropic.

Conversely, when \(\textbf{F}\) and \(\textbf{G}\) are constant in the Cartesian coordinates, given that \(\textbf{G}_{0}\) is constant, the equation of elastostatic equilibrium in the absence of body forces is automatically satisfied. □

We note that, when equal and opposite homogeneous shear deformations generate alternating shear stripes in LCEs as in soft (or semi-soft) elastic phenomena, the deformation gradient in two adjacent stripes are geometrically compatible (see, e.g., [22, Chap. 6]). Therefore, by assuming that, the deformation gradient is piecewise of differentiability class \(\mathcal{C}^{2}\), the result of the above theorem can be extended to shear-striping patterns, which can also be maintained universally by the application of surface tractions only in ideal nematic elastomers. This is formally presented in the next result.

Corollary 1

For an ideal unconstrained uniaxial nematic LCE characterized by equation (1), such that \(\textbf{G}_{0}\) is constant in Cartesian coordinates, a deformation with gradient \(\textbf{F}(\textbf{X})\) which is piecewise of differentiability class \(\mathcal{C}^{2}\), such that \(\det \textbf{F}(\textbf{X})>0\), can be maintained for all \(W^{(nc)}\) by the application of surface tractions only (without body forces) if and only if both \(\textbf{F}\) and \(\textbf{G}\) are piecewise constant in Cartesian coordinates. In two adjacent subdomains, the deformation gradient, \(\textbf{F}_{+}\) and \(\textbf{F}_{-}\), must be rank-one connected, i.e., \(\mathrm{rank}\left (\textbf{F}_{+}-\textbf{F}_{-}\right )=1\), for geometric compatibility.

5 Conclusion

For unconstrained uniaxial nematic LCEs described by a homogeneous isotropic strain-energy density function, we proved that the only deformations that are independent of the material parameters and can be maintained by the application of traction forces on the boundary of the body, assuming that the deformation gradient is sufficiently smooth, are the homogeneous deformations, i.e., those for which the deformation gradient is constant and the director is either uniform or randomly oriented in the Cartesian coordinates. This result is consistent with the classical Ericksen’s theorem for nonlinear homogeneous isotropic hyperelastic materials, which is directly applicable to ideal LCEs in an isotropic phase. However, in a nematic phase, the constitutive strain-energy density is a function of five invariants instead of three, to account also for the liquid crystal orientation.

Since LCEs are to a large extent incompressible materials, and we know from the elastic case that this extra constraint guarantees the existence of additional universal solutions, there are also important inhomogeneous deformations that can be controlled by the application of surface tractions and are independent of the constitutive parameters. We refer to [1, 20, 24] where such deformations have been examined.