1 Introduction

Computer simulation is of great importance in science and engineering fields along with experiments and theories. This computational approach enables us to predict the structure, dynamics, and other material properties of complex macromolecules. With significant advances in computation, there have been considerable efforts in polymer modeling and simulation from the atomistic to the macroscopic level [1, 2]. The fully atomistic or united atom model (considering specific units as one site) [3] is used to describe detailed atomistic information of nanomaterials [4, 5]; however, it is unfeasible for large-scale applications, due to a significant amount of computing time cost. Mapping atomistic into coarse-grained (CG) representation (as illustrated in Fig. 1) can, therefore, extend to complicated macromolecular systems by simplifying the physical system through a reduction in degrees of freedom.

Fig. 1
figure 1

Schemes illustrating mapping atomistic representation into CG beads

Full size image

With the development of suitable mapping schemes, they can still capture the fundamental physical characteristics of phenomena observed in high-resolution models or experimental data [6,7,8]. This CG simulation offers an attractive opportunity to describe complicated phenomena, such as phase separation [9], crystalline behavior [10], biomolecules [11, 12], self-assembly [13, 14], etc. Yet, there have been reports that inappropriate CG parameterization and methods may result in artifacts (e.g., thermodynamic inconsistency, fast dynamics, etc.) [15, 16], leading to an invalid thermodynamic expression with inexact preservation of experimental observables. Accordingly, it is a continual challenge to adopt or develop effective CG models or techniques for each system to minimize inaccuracies induced by lost atomistic details.

Polymer, a connection of repetitive monomers, has been well known to have its own internal microstructure, showing a hierarchy of different lengths and corresponding time scales [17, 18]. The time scales of the polymer span a wide range from femtoseconds to even seconds (also for length scales ranging from nanometers to millimeters or larger); thus, this cannot be described by just a single model or simulation. In this regard, multiscale molecular simulation, bridging atomistic and CG force fields, would efficiently help to directly demonstrate macroscopic properties and behaviors from underlying molecular phenomena in polymeric materials [19,20,21,22]. Particularly, this computational technique would be beneficial to understand the properties and morphologies of polymeric materials blended with multiple components. There have been many efforts to study mixtures of polymeric materials [23,24,25,26,27], which often exhibit enhanced properties compared to a single polymer. Such studies are necessary for developing the polymer industry in that mixtures can be more economical and tailor product properties. Most polymer pairs, however, are immiscible, and thus tend to show phase separation behavior, leading to deteriorated properties [28]. These thermodynamic behaviors of polymer blends significantly affect their morphology and rheological features; thus, it is crucial to identify the characteristics of interfacial properties and structures between each blend component to improve their miscibility.

The present paper is a review of the current status and trends in the field of polymer blends via computer simulation. This includes computational methodologies at various time and length scales including polymer blend models and theories. We organize the review as follows. Section 2 briefly overviews the basics of polymer blends covering experimental observations, theories, and models. Also, Sect. 3 introduces widely well-known computational methodologies used in the field of polymeric materials, from molecular scales (molecular dynamics and Monte Carlo) to macromolecular scales (coarse-graining models, dissipative particle dynamics, etc.). In Sect. 4, we discuss the structural, rheological, and mechanical properties of polymer blends, with a detailed analysis of current published experimental and computational researches. This paper also deals with how we can properly construct a polymer blend model and compute its properties based on computer simulation. Finally, we conclude the review by stating the current challenges in the modeling and simulation of polymer blend system and future direction.

2 Background: polymer blend theory

2.1 Polymer miscibility

Polymer blends can exhibit either homogenous or heterogeneous. This polymer miscibility is known to be governed by the Gibbs free energy of mixing \(\Delta G\) as defined by

$$\Delta G = \Delta H - T\Delta S,$$
(1)

where \(\Delta H\) and \(\Delta S\) are the enthalpy and entropy of mixing at a given temperature T, respectively. In Eq. (1), when the value of \(\Delta G\) is negative, then components in a mixture become miscible. Since the contribution of entropy of mixing becomes negligibly small for higher molecular weight due to the restricted number of possible configurations, \(\Delta G\) is primarily influenced by \(\Delta H\). Flory and Huggins [29,30,31] introduced the formula for the entropy and enthalpy of mixing based on the mean-field lattice model (Fig. 2), deriving an estimate of the miscibility of polymers.

Fig. 2
figure 2

Schematic drawing of the lattice chain model representing a mixture of polymers A (blue) and B (red)

Full size image

This model describes a macromolecule as a random walk on a lattice consisting of N sites of equal volume. Each bead of the polymer occupies one lattice, and a bond connecting adjacent beads of the molecule represents a link of the lattice. For a binary mixture of polymer chains A and B, each consisting of NA and NB segments per chain, respectively, the researchers obtained the following expression for the change in the free energy of mixing \(\Delta F\) at a given temperature T:

$$\Delta F = N{k_B}T\left[ {\frac{{{\phi _A}}}{{{N_A}}}\ln {\phi _A} + \frac{{{\phi _B}}}{{{N_B}}}\ln {\phi _B} + \chi {\phi _A}{\phi _B}} \right].$$
(2)

Here, \(k_{B}\) is Boltzmann constant and \(\phi_{i}\) is the volume fraction of chain i, respectively, while \(\chi\) is a dimensionless quantity, so called the Flory–Huggins interaction parameter, expressed by:

$$\chi = z[\varepsilon_{AB} - (\varepsilon_{AA} + \varepsilon_{BB} )/2]/k_{B} T,$$
(3)

where z represents the coordination number of species and εij represents the interaction energy between the species i and j, respectively. The initial two terms in Eq. (2) arise from the entropy of mixing, while the last term is based on the enthalpy of mixing. The \(\Delta F\) depends on the value of \(\chi\) parameter as well as on the degrees of polymerization of the species [31,32,33]. The \(\chi\) parameter in Eq. (3) describes the phase behavior (mixed or unmixed) of polymer–polymer or polymer–solvent systems. It represents the energetic contribution to the free energy of mixing in a polymer mixture, in other words, a parameter of the differences in the strength of interaction energies between components in a mixture. A positive value indicates favorable interaction, while a negative value denotes unfavorable interaction, resulting in phase separation or immiscibility. The Flory–Huggins parameter is related to the solubility parameter \(\delta\) [34]. The \(\delta\) is an important property that defines the ability to be dissolved, determined by the square root of the cohesive energy density CED as below.

$$\delta = \sqrt {CED} = \left[ {\frac{{\Delta H_{vap} - RT}}{{V_{m} }}} \right]^{1/2} .$$
(4)

Here, \(\Delta H_{vap}\) denotes the heat of vaporization and \(R\) denotes the gas constant, respectively, while \(V_{m}\) is the molar volume of species. According to the Hansen solubility parameter [35], CED is generated by molecular forces (e.g., dispersion force, dipole–dipole interaction, or hydrogen bond interaction), thus this often determines the degree of solubility in a mixture. The relationship between the \(\chi\) parameter and the solubility parameter is defined by

$$\chi = \frac{{V_{m} }}{kT}(\delta_{A} - \delta_{B} )^{2} .$$
(5)

This implies that the difference in \(\delta\) of species A and B in a mixture can connote the polymer miscibility. However, the value of \(\chi\) parameter computed from the Hildebrand solubility parameter via Eq. (5) is often invalid for mixtures containing polar and hydrogen bond interaction. Instead, the Hansen solubility parameter has proven to be useful for estimating the Flory–Huggins parameter. This is expressed in terms of the three solubility parameters from dispersion forces (d), polar forces (p), and hydrogen bond interactions (h):

$$\delta = \sqrt {\delta_{d}^{2} + \delta_{p}^{2} + \delta_{h}^{2} } .$$
(6)

This is based on the idea that a molecule can be dissolved by overcoming surrounding molecular interactions. Tables 1 and 2 present the values of two solubility parameters and \(\chi\) parameter for various polymeric materials [36,37,38,39,40,41,42,43].

Table 1 Hildebrand solubility parameter values of polymer modifiers/segments/blocks studied by works [36,37,38,39,40,41,42,43]. Reproduced from [36]
Full size table
Table 2 Hansen solubility parameter values of polymers studied by works [35, 44,45,46,47]. Reproduced from [44]
Full size table

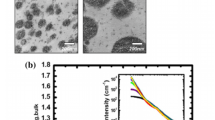
While these findings offer insightful information of miscibility, these methodologies are often inadequate for certain polymers and solvents [48, 49]. This can be attributed to intrinsic interactions such as hydrogen bonding or other complicated interactions. Furthermore, \(\chi\) parameter also shows dependence on the concentration of components as shown in Fig. 3a [50,51,52].

Fig. 3
figure 3

Behaviors of the Flory–Huggins interaction parameters with a composition and b temperature for various polymer blend: polystyrene/poly(p-methylstyrene (dPS/PpMS), PS/dPS, deuterated poly(methylbutylene)/poly(ethylbutylene) (dPMB/PEB), polypropylene/deuterated head-to-head polypropylene (PP/dhhPP), PS/polybutadiene (PB), dPS/poly(tetramethyl bisphenol A polycarbonate (TMPC), and dPS/poly(vinyl methyl ether) (PVME). Reproduced from [51]

Full size image

2.2 Phase behavior of polymer blend

Empirically, it has been well established that \(\chi\) is a function of T (Fig. 3b), as shown below [31, 52]:

$$\chi (T) \approx A + B/T.$$
(7)

The temperature-independent term A contributes to the entropic part of \(\chi\), while the second term represents its enthalpic part. This observation aligns well with polymer blends [50, 53,54,55]. Generally, polymer blend systems exhibit two critical solubility temperatures: an upper critical solution temperature (UCST), which is the critical temperature for phase separation occurring at low temperatures, and a lower critical solution temperature (LCST) where phase separation occurs at higher temperatures. These two solubility boundaries define a region of miscibility gap where phase separation takes place. For miscible polymer blends, it is common for them to undergo segregation at elevated temperatures (LCST behavior), whereas UCST behavior is relatively less observed [56, 57]. This can be understood through Eq. (1). The majority of solutions have a positive value of \(\Delta S\), attributed to increased configurational entropy. This leads to a critical temperature (UCST) at which \(\Delta G\) becomes zero. However, since the value of \(\Delta H\) for most polymers is typically negative (indicating exothermic mixing), they tend to exhibit LCST behavior rather than UCST. Figure 4 presents a schematic representation of the phase diagram for polymer blends with LCST and UCST.

Fig. 4
figure 4

Schematic phase diagram of LCST and UCST blends. Binodal curve is depicted as solid line and spinodal curve as dashed line

Full size image

However, it should be noted that relying solely on the negative value of the \(\Delta G\) is insufficient to determine the stability of a mixture against phase separation with varying compositions. This merely indicates that the mixture will not segregate into two distinct phases consisting of pure components. Phase separation can still occur even when \(\Delta G\) is negative; thus, it is imperative to take into account the second derivative of the free energy \(\left( {\frac{{\partial^{2} \Delta G}}{{\partial \Delta \phi^{2} }}} \right)_{P,T}\). The binodal curve (known as the coexistence curve) refers to the phenomenon of distinct nucleation and subsequent growth in small spherical domains of the second phase, which gradually increase in size over a period of time. When \(\left( {\frac{{\partial^{2} \Delta G}}{{\partial \Delta \phi^{2} }}} \right)_{P,T}\) becomes negative within the binodal boundary, it enters the spinodal region. Notably, the binodal and spinodal points coincide at the critical temperature, as depicted in Fig. 4. The regions between the binodal and spinodal points can be characterized as metastable regions, wherein minor fluctuations fail to induce phase separations.

Figure 5 shows the nonlinear behavior of \(\chi\) parameter for many polymeric materials at various temperatures [58,59,60]. In cases where nonlinearity is observed in Eq. (7), \(\chi\) can be fitted to a quadratic function of 1/T as following Eq. (8) [61,62,63].

$$\chi (T) \approx A + B/T + C/T^{2} .$$
(8)
Fig. 5
figure 5

a Flory–Huggins interaction parameter as a function of 1/T, and b the reduced value \(\chi - A - B/T - C/T^{2}\) as a function of p/T for deuterated poly(ethylbutylene)/poly(methylbutylene) (PEB/DPMB) done by Lefebvre et al. [59] The symbols represent the volume fractions of dPMB equal to 0.414 (pink and purple triangles), 0.161 (yellow and mustard diamonds), and 0.099 (orange and maroon circles) from the one-phase and equal to 0.161 (green and forest squares) and 0.099 (blue and navy circles) from the metastable at p = 0.01 and 0.86 kbar. Reproduced from [58]

Full size image

There are various methods to estimate the value of \(\chi\) parameter, including techniques such as small angle X-ray and neutron scattering [59], viscometry [64], differential scanning calorimetry (DSC) [53], or gas chromatography [65] (we will discuss computational methods for calculating \(\chi\) parameter later). Each method for estimating \(\chi\) parameter has its own advantages and limitations; thus, the selection of an appropriate method for measurement should be based on the specific characteristics of the system and the objectives of the research. Moreover, combining multiple experimental approaches can often yield accurate and comprehensive results. As such, the utilization of those approaches can achieve a deeper understanding of the phase behaviors of polymer blends, leading to more robust interpretations of the experimental data.

3 Background: computer simulation of the polymer

Since their pioneering efforts in 1953 by Metropolis [66] with Monte Carlo (MC) simulations and in 1957 by Alder and Wainwright [67] with molecular dynamics (MD) simulations, computer simulation methods, and algorithms have made significant progress. MD and MC methods, based on Newtonian dynamics and statistical mechanics, facilitate the direct measurement of physical properties and phenomena at the atomistic and molecular levels. Consequently, computer simulations serve as an important tool that supplements existing experimental findings and even offers a means to explore properties that are difficult to access through experimentation alone. Diverse computational techniques corresponding various time and length scales are illustrated in Fig. 6.

Fig. 6
figure 6

Time- and length-scale representation of various computational techniques

Full size image

In general, atomistic methods include MD and MC simulations, while mesoscale methods include coarse-grained (CG) simulation [12, 68, 69], dissipative particle dynamics (DPD) [70, 71], or Brownian dynamics (BD) [72]. Continuum methods, including the finite element method (FEM) [73], are governed by appropriate constitutive equations, such as the Navier–Stokes equation [74]. These methods are based on the assumption that the properties of the system can be represented by continuous fields, such as temperature, pressure, and velocity. In this section, we provide a concise overview of simulation techniques of polymeric materials, covering integration schemes, thermostats, barostats, and force fields. The discussion consists of two parts: (i) molecular scale modeling (with an emphasis on MD simulation) and (ii) macromolecular scale modeling.

3.1 Molecular scale modeling

Polymer exhibits a diverse range of phenomena spanning multiple length and time scales, facing challenges in the investigation of their intrinsic characteristics. In general, it is observed ranging from the atomic scale of monomers (angstroms) to the larger scale of polymer radius of gyration (nanometers), and time scales encompassing femtoseconds up to seconds, minutes, or even years [52]. In this regard, atomistically detailed computer-aided simulations could be a useful tool for studying the molecular mechanisms of polymers and moreover help to provide insights into underlying characteristics by bridging the gap between the atomic scale and meso/macro-phenomena. One of the most widely used simulations, MD simulation calculates the time-dependent variables of a system of particles by integrating their equations of motion as shown in Eq. (9).

$${\mathbf{F}}_{i} = m_{i} {\mathbf{a}}_{i} .$$
(9)

Here, \(m_{i}\) is atomic mass, \({\mathbf{a}}_{i}\) is its acceleration, and \({\mathbf{F}}_{i}\) is the force acting upon particle i, in a system consisting of N particles, respectively. There are various algorithms for integrating the equations of motion: Verlet [75], Velocity Verlet [76], Leap-frog [77], Beeman’s algorithm [78], etc. The widely utilized algorithm, Velocity Verlet (as an extension of the Verlet algorithm) is a numerical algorithm in which both the position and the velocity are updated at each time step. The basic equations are as follows:

$$\begin{gathered} {\mathbf{r}}(t + \delta t) = {\mathbf{r}}(t) + {\mathbf{v}}(t)\delta t + \frac{{{\mathbf{F}}(t)}}{2m}\delta t^{2} , \hfill \\ {\mathbf{v}}(t + \delta t) = {\mathbf{v}}(t) + \frac{1}{2m}\left[ {{\mathbf{F}}(t) + {\mathbf{F}}(t + \delta t)} \right]\delta t, \hfill \\ \end{gathered}$$
(10)

where \({\mathbf{r}}\) is the position vector, \({\mathbf{v}}\) is the velocity vector, and \({\mathbf{F}}\) is the force vector with time t, respectively. This algorithm makes it possible to achieve energy conservation, thereby reinforcing the accuracy in simulation and proving its suitability for capturing the intricate dynamics of molecules. The selection of an appropriate integration scheme in MD simulation requires a thorough consideration of the characteristics of the target system to obtain reliable results in simulation. Additionally, temperature and pressure controls are achieved by introducing additional dynamic variables into the original system, effectively acting as a thermostat (e.g., Velocity scaling [79], Nosé-Hoover [80, 81], or Langevin [82, 83]) or barostat (e.g., Berendson [84], Anderson [85]). These supplementary variables play a crucial role in regulating and maintaining the desired temperature or pressure conditions throughout the simulation.

Once a suitable molecular scale model has been identified, we should find an appropriate force-field for the polymer system from established libraries. Polymer exhibits both bonded and non-bonded interactions. Bonded interactions refer to chemical bonding including bond stretching, bond angle, and dihedral angle interactions. Non-bonded interactions, on the other hand, which include van der Waals forces, hydrogen bond interaction, and electrostatic interaction, arise from intermolecular forces between chains. Specifically, these interactions occur among loosely interacting groups of atoms. Each force-field comprises a set of parameters and functions, consisting of multiple terms with distinct characteristics, as represented in the formula for the total interaction potential \(U\) of particle i in Eq. (11).

$$U({\mathbf{R}}_{i} ) = U_{{{\text{bond}}}} + U_{{{\text{angle}}}} + U_{{{\text{dihedral}}}} + U_{vdW} + U_{{{\text{elec}}}} ,$$
(11)

where the first three terms represent bond, angle, and dihedral interaction energy and the other two terms are van der Waals and electrostatic interaction energy, respectively. \({\mathbf{R}}_{i}\) is the position vector of atoms in a polymeric system. There are many functional formulas for each interaction, for instance, COMPASS [86], CHARMM [87], AMBER [88], etc.; however, the details are not covered in this article.

In particular, nonequilibrium molecular dynamics (NEMD) techniques have been developed as an extension of traditional MD, providing a means to investigate significant physical properties within a system subjected to an external field, such as shear or extensional flow. Therefore, it enables us to enhance our understanding of the intricate phenomena of materials departing from equilibrium. NEMD requires thoroughly considered equations of motion along with the appropriate boundary conditions and thermostat settings for each flow field in the system. Under the assumption of applying the proper methodologies, NEMD has proven to be an effective tool for predicting transport properties such as shear viscosity, diffusivity, and thermal conductivity. The first requirement for incorporating a field into the equations of motion of the system is that it should be consistent with the periodic boundary conditions (PBCs) to maintain the homogeneity of the system. PBCs effectively mitigate surface effects that can occur in a fixed simulation box, thereby reducing the computational cost of simulations. Specifically, the simulation box can become deformed imposed by the flow field, leading to numerical instability in the simulation [89]. One well-known approach is the Lees–Edwards boundary conditions [90] which allows to investigate the bulk properties of molecules undergoing shear flow. Such a scheme involves duplicating the simulation cell through periodic images, thereby accounting for the translation of molecules, and accurately representing the boundary effects under actual flow. The Kraynik–Reinelt [91, 92] boundary conditions control the unit lattice vectors under the planar elongational flow, facilitating the remapping of the simulation cell from the extended to undeformed state.

The first NEMD algorithm, so-called DOLLS [93], was suitable in the limit of linear strain rates, but exhibited remarkable errors in properties at high flow fields [94]. Therefore, Evans and Morriss [95] and Ladd [96] proposed the SLLOD algorithm for planar Couette flow which has been shown to be exact for all values of the flow field. Also, Hoover et al. [97] explored the validity of both the DOLLS and SLLOD algorithms in conjunction with boundary conditions for simple shear. According to Baig et al. [98], they developed p-SLLOD algorithm, which is compatible with Lagrangian and Hamiltonian mechanics [99]. It contains the following equations of motion.

$$\begin{gathered} {\dot{\mathbf{q}}}_{i} = \frac{{{\mathbf{p}}_{i} }}{{m_{i} }} + {\mathbf{q}}_{i} \cdot \nabla {\mathbf{u}}, \hfill \\ {\dot{\mathbf{p}}}_{i} = {\mathbf{F}}_{i} - {\mathbf{p}}_{i} \cdot \nabla {\mathbf{u}} - m_{i} {\mathbf{q}}_{i} \cdot \nabla {\mathbf{u}} \cdot \nabla {\mathbf{u}}, \hfill \\ \end{gathered}$$
(12)

where \({\mathbf{q}}_{i}\) and \({\mathbf{p}}_{i}\) are the position vector and the peculiar momentum vector (except external flow field), whereas \(m_{i}\) and \({\mathbf{F}}_{i}\) are the mass and the force vector of atom i, respectively. \({\mathbf{u}}\) is the streaming velocity. They demonstrated its capability to model the system under both shear and extensional flow, enabling the direct calculation of a variety of structural, thermodynamic, and rheological properties.

As previously mentioned, the use of inappropriate algorithms or thermostatting techniques can lead to the artifacts, such as unstable values of properties, energy non-conservation, or convergence problems during NEMD simulation. Delhommelle et al. [100] addressed the occurrence of unphysically observable phenomena under an assumed flow profile. The work stressed the importance of employing a configurational thermostat (without assumption of flow field in NEMD) to realistically represent the system under flow conditions. In line with the findings by Delhommelle et al. Baranyai [101] also demonstrated anisotropy between configurational and kinetic temperatures. Li et al. [102] stressed that it should be employed to different formulations for thermal transport depending on the thermostat method through a comparison between the Nosé–Hoover thermostat with the Langevin approach. Additionally, Ke et al. [103] conducted a comprehensive investigation into the widely used thermostats and barostats in terms of accuracy in physical properties and fluctuations, thus emphasizing on the importance of considering effective thermostats/barostats in contrast with equilibrium MD. To prevent issues arising from the incorrect construction of simulation methodologies, careful attention should be paid to the selection of the suitable thermostats and algorithms based on relevant literatures. Furthermore, it is needed to meticulously organize NEMD simulation strategies depending on the specific characteristics of the systems for the desired physical properties. As pointed by Anstine et al. [104], they estimated the mechanical properties of glassy polymers, concluding that physical properties of polymers can be significantly influenced by modeling techniques, such as force-field and polymer builder. Hence, one has to be very cautious in applying thermostats/barostats in conjunction with other algorithms in NEMD simulation to accurately estimate values of physical properties.

The MC technique, also known as the Metropolis method [66], involves generating a sample of the population using random numbers. The key steps in MC simulation can be summarized as follows: (i) Formulating the physics problem of interest into a probabilistic model. (ii) Numerically sampling the probability model to obtain representative configurations. (iii) Analyzing the collected data using statistical models. The fundamental principle of MC involves estimating the average characteristics of system based on the probability distribution, associated with the ensembles in statistical mechanics. While MD simulations track the evolution of a system over time, MC simulations enable the estimation of ensemble-averaged properties through statistical sampling. By employing random sampling, MC simulations efficiently explore the phase space and provide valuable information in equilibrium thermodynamics and statistical mechanics.

3.2 Macromolecular scale modeling

CG methods are based on hierarchies of overlapping length or time scales, where the majority of degrees of freedom are reduced by grouping or averaging atoms into larger entities. These models aim to capture the essential features and collective behavior of the system while reducing computational costs. In CG, multiple atoms are typically combined into a single interaction site, referred to as a CG particle or bead. These beads represent a collection of atoms with similar properties and behavior. The interactions between beads are described by effective potentials which can unveil the thermodynamic and structural characteristics of the system at the CG level. Similar to atomistic models, bonded potentials within a CG bead can be depicted by several empirical models, such as finite extensible nonlinear elastic (FENE) bond potential [105]. The FENE potential follows the expression:

$$U_{FENE} = \left\{ \begin{gathered} - 0.5kR_{0} \ln (1 - R_{ij} /R_{0} )^{2} ,\,\,R_{ij} \le R_{0} \hfill \\ \infty ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,R_{ij} > R_{0} , \hfill \\ \end{gathered} \right.$$
(13)

where \(R_{0}\) is the maximum bond extension length, \(k\) is the spring constant, and \(R_{ij}\) is the bond vector between particle i and j, respectively.

Most commonly used CG models in polymer systems are Martini [106, 107], united-atom [3], Kremer–Grest (KG) [105, 108], etc. The Martini model is mainly employed for biosystems such as proteins and lipids. This model typically makes a group of four heavy atoms into one CG bead, allowing for the investigation of large-scale conformational changes, self-assembly processes, and membrane behaviors [13, 109, 110]. Furthermore, this model with its high computational efficiency, is suitable for calculating interactions within polymer blends, even those involving large molecules [111,112,113]. The united-atom model simplifies the representation of molecules by merging hydrogen atoms with their adjacent heavy atoms. In other words, hydrogen atoms are treated as parts of the heavy atoms they are bonded to, effectively reducing the total number of particles in the system. This model has been extensively employed in simulating polymers, enabling investigation into phase transition, diffusion processes, and other dynamic characteristics [114, 115]. The KG model, a bead-spring model, represents a chain as successive beads connected by springs. Each bead interacts with neighboring beads through potential energy function (e.g., Weeks–Chandler–Anderson interactions [116], FENE potential, or a bending potential introduced by Faller and Müller-Plathe [117,118,119]) including the bond, angle, and dihedral interactions. One of the key features of the KG model is its ability to simulate entanglements and topological constraints between polymer chains; thus, it can express the realistic behavior of polymers, including their conformational changes, chain relaxation, and diffusion dynamics. Consequently, the model is effective for studying various aspects of polymer blends, such as melt dynamics, phase transition, or miscibility [120, 121].

Dissipative Particle Dynamics (DPD) [70, 71] is a mesoscale simulation method that has gained significant popularity in the field of soft matter and complex fluids. In DPD, particles represent groups of atoms, and interactions are governed by conservative (c), dissipative (d), and random forces (r) between particle i and j as described by Eq. (14).

$$F_{ij} = F_{ij}^{c} + F_{ij}^{d} + F_{ij}^{r} .$$
(14)

Here, the conservative force represents long-range interactions, while the dissipative force dissipates energy, thereby describing the effects of viscosity. The random force accounts for thermal fluctuations. DPD has been applied to studying self-assembly processes, micellar systems, and flow behavior, offering the details of collective behavior and dynamics of complex systems [122, 123].

Brownian Dynamics (BD) simulations [72] are stochastic simulation methods that focus on modeling diffusion processes. In contrast to MD simulations, BD operates on a much larger time scale, typically up to a few nanoseconds. It is commonly employed in investigating solvent–polymer interactions using an implicit continuum solvent description. The governing equation in BD, known as the Langevin equation [82, 83], incorporates dissipative and random force terms that account for the effects of polymer–solvent interactions, including the influence of solvent removal from the polymer. The Langevin equation can be expressed as:

$$F_{i} (t) = - \gamma p_{i} + \sigma \xi_{i} (t),$$
(15)

where \(\gamma\) is the friction coefficient, \(p_{i}\) is the momentum, and \(\xi_{i} (t)\) is the random force with the coupling coefficient \(\sigma\) of the particle i at time t, respectively. By employing BD simulations, researchers can investigate the diffusion and mixing behavior of polymer blends [124]. The motion of each polymer chain is influenced by both conservative and stochastic forces, describing the effects of the surrounding solvent and thermal fluctuations. Based on this algorithm, it allows us to predict the macroscopic properties of polymer blends, such as viscosity, diffusion coefficients, and phase separation behavior [125].

The aforementioned CG techniques, which go beyond atomistic simulations, are valuable approaches in molecular modeling, offering perspectives into the collective behavior and properties of complicated systems. Therefore, it is desirable to perform multiscale simulations by combining atomistic and CG scale models to demonstrate phenomena occurring across various scales. This approach contributes to a deeper understanding of molecular system behavior.

4 Characteristics of the polymer blend

4.1 Morphology and miscibility

Over the years, it has been widely reported that polymers do not readily mix to form a homogeneous mixture. Accordingly, their morphologies significantly dictate the physical properties of these phase-separated polymers, such as toughness, flowability, and optical properties. Therefore, it is crucial to establish the relationship between them and to predict the morphology. Recent advancements in microscopy techniques, including scanning electron microscopy (SEM), atomic force microscopy (AFM), and transmission electron microscopy (TEM) have allowed for more detailed observations of the morphology of polymer blends.

For high-molecular-weight polymer blends, miscibility is primarily dependent on the values of \(\Delta H\) and \(\chi\) parameter, due to the low contribution of the entropy of mixing as previously mentioned in Eq. (1). There have been numerous studies aiming to quantify the \(\chi\) parameter of polymer blends. Lee et al. [126] determined the miscibility for polystyrene (PS)– polybutadiene (PBD) blends investigated by DSC. They investigated values of the Flory–Huggins interaction parameter, which ranged from 0.0040 to 0.0102, for different molecular weights and compositions of the PS–PBD blends. Roe et al. [127] also calculated the \(\chi\) parameter of PS–PBD blends under various conditions including temperature, via light scattering measurement. Additionally, the surface morphology of UCST blend [isotactic polystyrene (iPS)–poly(4-methyl styrene) (P4MS) blend] was studied by Chang and Woo [128] through AFM and DSC. The values of \(\chi\) parameter for Ips–P4MS blends are found to be in the range of 0.0163 – 0.0232 depending on the composition. All these values are greater than the values at the critical points, indicating that iPS–P4MS blends are immiscible for all compositions. Such immiscible or miscible phenomena are closely correlated with the interface of morphology between each component in a mixture. The study conducted by Li et al. [129] investigates the role of the interface in the morphologies of three different categories of blend: (i) high-density polyethylene (HDPE)/styrene–ethylene–butylene–styrene (SEBS) and HDPE/styrene–ethylene–butylene (SEB), (ii) an incompatible binary system comprised of HDPE/PS, and (iii) compatible ternary systems comprised of HDPE/PS compatibilized by SEBS and SEB, respectively. The results conclude high interfacial tension shows a strong dependency on the composition of pore size of co-continuous microstructure. According to Taguet et al. [130], the detailed interface–morphology relationship in PE–thermoplastic starch (TPS) blends is elucidated by the formation of a thin glycerol-rich layer at the PE–TPS interface, which plays a role as an interfacial modification. They added the quantity of poly(ethylene-g-maleic anhydride) (PE-g-MA) copolymer (a compatibilizer) allowing to place itself at the interface of PE–TPS and improve adhesion between phases. Therefore, they suggested a potential approach to modify interfaces in polymer blend using plasticized polymers and small molecule modifiers.

There are several efforts to supplement the miscibility parameter. Tambasco et al. [51] suggested the temperature- and concentration-independent parameter, which would be more characteristic indicator of blend system than the \(\chi\) parameter, by analyzing experimental data from neuron scattering, cloud point curves, and pressure–volume–temperature (PVT) surfaces for several blends [131,132,133,134,135,136,137,138]. Based on the Born–Green–Yvon (BGY) theory [139], the authors attempted to quantify the binary interactions of polymer blends, offering a feasible substitute for the Flory–Huggins interaction parameter.

Since these experimental methods are quite complicated, many groups have devoted to observing the morphology and interaction parameters based on semi-empirical approaches or computer simulations [140,141,142]. Estridge and Jayaraman [143] performed CG simulations of AB diblock copolymer grafted particles in an immiscible A–B blend (DBCGPs) (Fig. 7).

Fig. 7
figure 7

Representative snapshots (Top and side view) of interfacial configurations with different volume fractions of DBCGP equal to a, f 7.3 \(\times\) 10–4, b, g 3.6 \(\times\) 10–3, c, h 7.3 \(\times\) 10–3, d, i 1.0 \(\times\) 10–2, and e, j 1.4 \(\times\) 10–2. Reproduced from [143]

Full size image

Polymers are represented as a bead-spring model with the Weeks − Chandler − Andersen (WCA) [116] and 6–12 Lennard–Jones (LJ) [144, 145] potentials. This study has revealed that DBCGPs are effective alternatives to AB diblock copolymers (BCPs), which are well known as compatibilizers in a blend of A and B polymers. The researchers calculated the probability of DBCGP distribution at the blend interface, desorption energy, and interfacial tension. The results show a higher desorption energy and a reduction in the interfacial tension compared to that of BCPs. Additionally, Kozuch et al. [146] performed MD simulations of bead-spring chains with different stiffness, demonstrating good agreement with experimental values by mapping real polymer chains onto their bead-spring chains.

Here, it is necessary to focus on studies that combine atomistic and mesoscale simulations to accurately compute the miscibility and morphology of polymer blends [22]. The study reported by Luo and Jiang [147] investigates the miscibility of poly(ethylene oxide) (PEO)–poly(vinyl chloride) (PVC) blends via both atomistic MD and mesoscale DPD. They determined the Flory–Huggins interaction parameter from CED and intermolecular radial distribution function, concluding that a larger degree of hydrogen bonding interaction was observed in PEO–PVC blends with a weight ratio at 70/30 and 30/70 compared to 50/50, as shown in Figs. 8 and 9. These features are supported by the morphologies of PEO–PVC blends, where the 50/50 blend exhibits a weak phase separation.

Fig. 8
figure 8

Flory–Huggins interaction parameter of PEO–PVC blends with weight ratios at 70/30, 50/50, and 30/70. The filled squares represent the values obtained by Eq. (5). Reproduced from [147]

Full size image
Fig. 9
figure 9

Radial distribution functions of the intermolecular carbon–carbon pairs of like- and unlike-components in PEO–PVC blends with corresponding morphologies from DPD simulation (PEO: red, PVC: green). Reproduced from [147]

Full size image

In addition, Spyriouni and Vergelati [148] conducted the molecular simulations at the atomistic and mesoscopic level for the binary blend of polyamide 6 (PA6) with poly(vinyl alcohol) (PVOH), poly-(vinyl acetate) (PVAC), and partially hydrolyzed PVAC for a wide range of compositions. They calculated CED of the pure components and mixture from the atomistic simulation, and then derived the \(\chi\) parameter as a function of composition for blends. Moreover, the interaction parameter, along with structural parameters, was applied to the CG simulation, thus enabling the examination of the behaviors of high-molecular-weight blends and long-time scales that allowed the observation of phase separation. For all mixtures, the highest \(\chi\) parameters were observed for the 50/50 composition. The PVAC–PA6 mixtures had the smallest, while the highest values were observed for PVOH-PA6. This is attributed to the low hydrolysis degree, in other words, a reduction in the hydrogen bonds and an increase in the portion of extended conformations. In this way, it is evident that applying the parameters obtained through atomistic-level simulations to mesoscopic-level simulations would provide substantial information and profound considerations in the morphology of polymer blends.

4.2 Rheology

Generally, quantifying the rheology of polymer blends is challenging due to the presence of viscoelastic and nonlinear effects within multiphase systems. As mentioned earlier, their structures and interactions play a crucial role in determining their rheological properties. Specifically, the proportion of components in a blend significantly influences its elasticity, viscosity, and flow behavior [149]. Moreover, the formation of networks between different phases can profoundly impact the rheological characteristics [150]. Thus, it is evident that the rheological characteristics of polymer blends are predominantly controlled by their morphology, which is distinct from that of homopolymers. Several researches have been devoted to demonstrating the rheology of polymer blends. According to Hamad et al. [151], the rheological and mechanical properties of poly(lactic acid) (PLA)–PS blends were investigated for different ratios of each component. The results show that PLA–PS blend exhibits a shear-thinning behavior. Also, the viscosity of the blend decreases with an increasing composition of PLA, which is attributed to the complicated molecular structure (high viscosity) of PS. Huang et al. [152] conducted a study that phase behavior could be regulated by altering the blend composition and, in particular, the deformation or stress history. These findings are analogous to the research reported by Peng et al. [153], wherein blend morphologies significantly affect the rheological properties. It was elucidated by conducting MD simulations on two distinct blends: a well-mixed blend and a phase-separated blend (Fig. 10a). They clearly revealed the effect of characteristics of blend components (chain length) on the diffusion and storage modulus (Fig. 10b and c). Notably, it was observed that stiff chains had the ability to slow down the dynamics of soft chains, resulting in a higher storage modulus of homogenously mixed blends, as shown below in Fig. 10c.

Fig. 10
figure 10

a Snapshots of mixed (left) and unmixed (right) blend configurations. Red spheres represent A chains (stiffer chains using FENE, LJ, and many-body interaction), and blue spheres represent B chains (softer chains using only FENE). b Plot of the center of mass (COM) and monomer (bead) mean-square displacements (MSD) of B chains in B melts and A–B blends. c Storage modulus as a function of shear frequency for A melts (black), B melts (green), mixed A–B blend (red), and unmixed A–B blend (blue). Reproduced from [153]

Full size image

Iza et al. [154] found that interfacial modification significantly affected the rheological behaviors of PS–PE immiscible blends under transient flow. More precisely, it was observed that the quantity and structure of the compatibilizer, capable of modifying the blend morphology, had a significant impact on the rheological response to a suddenly imposed shear rate. Also, Huang and Hua [155] performed mesoscale simulations of Nylon 6–elastomer (ACM) blends, revealing an impact of flow history on the blend morphology. They clearly provided detailed information on the relationship between flow-induced morphology and blend rheology by computing the stress relaxation and topological properties. Wang et al. [156] studied the storage modulus and viscosity for PP–ultrahigh molecular weight polyethylene (UMWPE) blends. By combining DPD simulations and experimental measurements, it was explored that changes in the morphology led to a decrease in the miscibility and storage modulus under extension–shear coupled flow, showing good agreement with experimental results. Furthermore, Hajizadeh et al. [157] investigated the structure and rheology of the linear–dendrimer polymer blends under planar elongational flow via nonequilibrium MD simulations, revealing the effect of blend structure on rheology. Besides, there are other studies conducted on rheological properties of Polymethyl methacrylate (PMMA) – PS [158], poly(3-hexylthiophene) (P3HT)–[6, 6]-phenyl-C61-butyric acid methyl ester (PCBM) [159], protein–water or polymer [160, 161], n-alkanes–polymers [162], or poly(vinylphenol)–poly(ethylene terephthalate) [163], PS–polyisoprene [164] blends, etc.

Simulating the deformation of polymer blends under external forces requires a multiscale approach; thus, several studies have endeavored to explore the rheology of polymer blend through multiscale simulation [152, 155, 156, 159, 165]. Deng et al. [165] investigated the properties of polymer blends with shear processing by employing a combined simulation. The model systems here corresponded to PS-b-polyacrylonitrile (PAN) block copolymer systems. They observed that the morphology became anisotropic structure with applied shear stress. This phenomenon aligned with the results of normal stress field (Fig. 11), wherein the stress was relieved by the soft phase.

Fig. 11
figure 11

Normal stress field in x–z plane of PAN block copolymer blends for shear rates equal to a 0, b 2 \(\times\) 103 s−1, c 1 \(\times\) 104 s−1, and d 2 \(\times\) 105 s.−1. Corresponding morphologies are shown on the top-left corner (the hard phase is displayed in red, and the soft matrix is colored blue). Reproduced from [165]

Full size image

The rheological properties of the polymer blends are significantly involved with polymer entanglements or dynamic behaviors. O’Connor et al. [166] conducted a study on the entanglement topology and nonlinear rheology of ring-linear polymer blends with varied ring fractions as depicted in Fig. 12a. Based on the primitive path analysis [167, 168], the authors quantified the degree of ring–linear threading and linear–linear entanglement. These computations then were utilized to validate rheological properties. Interestingly, the study observed an extensional stress overshoot for different ring fractions, as shown in Fig. 12b. They demonstrated that this phenomenon was attributed to overstretching and recoil of ring polymers caused by unthreading from linear chains. This implies that simply changing composition allows the stress overshoot to be varied for nonlinear strain rates.

Fig. 12
figure 12

a Primitive path chain topologies during extensional flow for linear (red)–ring (green) blends at different volume fraction of ring polymer \(\phi_{R}\) = 30% (top) and 88% (bottom). Configurations are shown at equilibrium (left) and the overshoot strain \(\varepsilon_{H}\) = 3.0 (center) and 7.5 (right). b Stress curves (at the same \(\dot{\varepsilon }_{H}\)) under startup extensional flow for blends and pure melts. Reproduced from [166]

Full size image

Young et al. [125] also investigated the influence of topological constraints on the rheology of ring–linear blends. They showed ring polymers in the blend exhibited considerable conformational fluctuation, leading to a stress overshoot.

4.3 Mechanical properties

It is generally known that combining various polymers become enables the achievement of a variety of mechanical properties that are not easily attainable with individual polymers alone. These blends can exhibit distinctive behaviors, such as enhanced tensile strength, improved impact resistance, increased flexibility, and enhanced durability; whereas, improper blending can lead to phase separation or reduced mechanical performance. Hence, it would be worthwhile to understand the relationship between the molecular factors and mechanical properties of the polymer blend. Ge et al. [169] demonstrated the mechanical weakness of the interface of immiscible polymer blends via large-scale MD simulations. According to their results, the lack of entanglements at the interface induces chains to be easily pulled out from the opposite side; thus, there is a minimum interdiffusion depth required for significant entanglement formation which enables to enhance an interfacial strength. Huang and Hua also [155] provided an in-depth understanding of blend elasticity for immiscible Nylon 6–elastomer (ACM) blends based on interfacial relaxation analysis. According to study done by Salahhoori et al. [170], using MD simulations, the blend compatibility, miscibility, and mechanical behavior of poly (vinyl fluoride) (PVF), poly (vinyl chloride) (PVC), and poly (vinyl acetate) (PVAc) with Pebax-1657 (Px) were examined. They calculated the shear modulus, bulk modulus, and Young’s modulus under different stress conditions. Researchers demonstrated that due to the chemical bonding of Px with PVAc, PVC, and PVF, miscibility was improved, and notably, the Px–PVC blend effectively formed a cross-linked network, resulting in enhanced mechanical properties. Also, Wei et al. [171] attempted to compute the mechanical properties of nature rubber-graft-rigid-polymer and rigid-polymer blend systems based on computational approaches. Their results showed that a higher strain rate gave rise to a higher stress modulus or yield stress. They also found that systems with increasing internal structure factors, such as nonbonding interaction or architecture (length and the number of graft chains), exhibited a better mechanical performance (Fig. 13).

Fig. 13
figure 13

a Stress–strain curves for various strain rates (at the interaction parameter within rigid-polymer beads \(\varepsilon_{RR}\) = 5.0) and b tensile modulus as a function of \(\varepsilon_{RR}\) for nature rubber-graft-rigid-polymer and rigid-polymer blend systems. \(\varepsilon_{PP}\) denotes the interaction parameter within polymer. Reproduced from [171]

Full size image

There is another study on mechanical characteristics where PMMA and dibutyl phthalate (DBP) binary systems are simulated by MD simulation [172]. They calculated the mechanical properties, based on the Reuss mean method [173], revealing the effect of temperature and DBP ratio on Young’s modulus, bulk modulus, shear modulus, and Poisson’s ratio. The trend reflects the addition of DBP can improve the ductility of PMMA. Moreover, Zhao et al. [174] predicted the mechanical properties of A–B polymer blend film by MC simulation combined with the lattice spring model. As they applied the force perpendicular to the film surface, it was observed that the stress-field distribution closely matched the film’s morphology. Those kinds of work may help us to find useful information for designing and fabricating high-performance polymer blends.

5 Conclusion

This review summarizes the theories, simulation methodologies, and properties (morphology, rheology, and mechanical characteristics) of various polymer blend systems. Numerous studies regarding polymer blends via computational approaches from atomistic to macromolecular scale have been reported for molecular weight, molecular architecture, blending composition, or plasticizers. In general, most polymer blends used to be immiscible; thus, the degree of miscibility significantly determines the blend characteristics. Therefore, it is beneficial to employ multiscale simulations to get the molecular features of polymer blends across various scales. In most cases, computational methods easily calculate the value of \(\chi\) parameter, also correlating with the miscibility or morphology of many polymer blend systems. These show a good agreement with experimental results, and furthermore successfully associated with molecular structure predicted from the simulations. In particular, the rheological and mechanical properties of polymer blends are closely related to their morphology as well; many studies provide insight into controlling its properties. But still, there are difficulties in modeling and simulating complicated polymer blends such as multiphase blends or crystalline components; thus, significant effort has been devoted to predicting them, in terms of rheological or mechanical properties via computer simulations.

Also, one has to bear in mind, the conditions necessary for accurate molecular simulation of polymeric materials. That is, efficiently linking the atomistic and CG force fields is the key to multiscale simulation of polymer blend systems. There are many related studies mentioned; however, we carefully consider the computational methodologies for desired systems by linking atomistic and CG methods to match the realistic or experimental phenomena.