1 Introduction

STEM (Science, Technology, Engineering, and Mathematics) has been emphasised in economic policy, educational policy, and educational practice in recent years (Li et al., 2020). This integrated approach is essential given the fast-paced technological, industrial, and societal transformations in our world (Roehrig et al., 2021). Mathematics plays a crucial role across all the mentioned disciplines, as scientific, technological, and engineering applications often rely on (complex) mathematical models. Understanding the applicability of math in STEM disciplines empowers learners to engage actively and knowledgeably in their personal, civic, and professional endeavours (e.g. Maaß et al., 2019; Niss & Blum, 2020).

The interdisciplinary and therefore integrated nature of STEM (e.g. Roehrig et al., 2021) can be introduced to students through mathematical modelling (MM), enabling students to gain an understanding of mathematics within STEM fields (Kohen & Orenstein, 2021; Cohen-Nissan & Kohen, 2023). In our contribution, MM is understood as a crucial link to computer science, the sciences and technology and can thus be considered (very) relevant to society (Kohen & Nitzan, 2022). The student, as a modeller, must understand a real-world situation and (re)construct its underlying elements in order to simplify the situation and develop a comprehensible mathematical representation of the problem. Individual STEM disciplines generally have their own culture and approach to modelling domain-specific phenomena. Therefore, we attempt here an integrative merging from a mathematics didactics perspective.

There is a scarcity of research evidence concerning the utilisation of MM within formal school mathematics, specifically when integrated within a STEM context. In publications of the last five years addressing STEM integration in school studies, an increasingly holistic view of it as a subject field is taken, mainly from a science perspective, however not from a mathematical or mathematics education perspective (e.g. Just & Siller, 2022). MM instruction in a STEM context is a challenging task, as it demands informed adaptation of the interdisciplinary STEM-related aspect of the MM tasks to school mathematics (Maaß et al., 2019).

It is particularly the teachers’ role to support their students in effective engagement with MM tasks in class (Schukajlow et al., 2018), particularly in a STEM context (Geiger, 2011). Yet little is known about the practices that scaffold modelling instruction in such contexts. Although several studies have contributed to our understanding of how modelling instruction can be supported (e.g. Borromeo Ferri, 2018; Greefrath et al., 2022), there are no clear definitions of MM-oriented scaffolding practices, especially in relation to modelling in STEM-related contexts. Moreover, there is ambiguity as to the role of teachers’ expertise in scaffolding practices for modelling instruction.

In this article, we suggest recognising instances of scaffolding practices in implementing MM tasks in a STEM-related context. The role that teachers play in such instruction is then problematised through a data-driven approach, comparing them according to their professional teaching experience, i.e. contrasting novice (pre-service) and expert (in-service) teachers.

2 Theoretical background

2.1 Mathematical modelling in STEM-related contexts

Mathematical modelling is a sub-field of applied mathematics (e.g. Blum & Niss, 1991; Niss & Blum, 2020; Pollak, 1979), which has manifold relations to the STEM subjects. The modelling process is described as a cycle, which starts in the real-world, moving forward to the mathematical world, and then coming back to the real-world. We view MM from a didactical perspective, which seeks to integrate modelling into mathematics education fully in order to enhance mathematics learning (Kaiser & Sriraman, 2006). This perspective is visualised in the modelling cycle, suggested by Kaiser and Stender (2013) (e.g. Fig. 1).

Fig. 1
figure 1

The didactical modelling cycle (Kaiser & Stender, 2013, p.279)

Full size image

First, one has to understand the real situation, while making assumptions based on the essential conditions of the problem at hand and distinguishing them from less important features (understand and simplify). Then, a translation process into a mathematical representation of the real problem can take place––the mathematical model, which can have different manifestations, such as an equation, a diagram, or a function (mathematise). These steps lead the modellers from the real-world realm to the mathematical realm, in which mathematical results are obtained while using mathematical procedures and algorithms (mathematical work), then are interpreted back in the real-world context (interpret), and finally validated against the real-world model and situation (validate). When applied in STEM contexts, an interdisciplinary approach to modelling is required, which means that mathematical and extra-mathematical activities must be fully integrated (Kaiser et al., 2013; Maaß et al., 2019). Through this approach of MM, essential criteria of an integrated STEM formulated by Roehrig et al., (2021, p. 4) are met, of which five are explicitly and directly addressed by our approach: focus on real-world problems, centrality of engineering, context integration, content integration and STEM-practices. In particular, the requirement to incorporate real-world problems or real-world contexts in STEM instruction is very prominent in the literature (e.g. Kelley & Knowles, 2016; Moore et al., 2020). As these are usually quite complex, MM is not only an end in itself, but a necessity from a mathematics didactics perspective.

The MM tasks in this study are grounded in authentic technological applications from the STEM workplace. Accordingly, the tasks present a scientific problem based on concepts and terms from the fields of physics, computer science, etc., where the solution is based on the use of mathematics in the middle school level. This demands high-level extra-mathematical knowledge, particularly when engaging the first two phases which occur in the reality domain that represent a STEM-related real-world situation which needs to be understood and structured in a simplified way (Kohen & Orenstein, 2021). In order to make the tasks accessible to students (and their teachers) who are not expected to be STEM experts, the structure of the tasks in our study is consistent with the four-step solution process as defined in previous studies as the solution plan (Schukajlow et al., 2015).

In summary, MM-in our understanding-is (inspired by Kohen & Nitzan, 2022) a guiding link to computer science, natural sciences and engineering. It is thus of central importance as an interdisciplinary bracket in the STEM context, and which emphasises the role of the M in this context both from a mathematical perspective and from a modelling-specific perspective-in both senses. This also underlines the role of mathematics in the STEM disciplines-in contrast to its representation in the curriculum.

2.2 The solution plan as a strategy for scaffolding modelling instruction

Scaffolding, according to Stone (1998), describes a framework for learners to overcome difficulties. Numerous frameworks and interventions have been researched for scaffolding MM learning, such as the foreshadowing and feedback framework for beginning modellers (Stillman et al., 2015), the scaffolding and intervention activities investigated for promoting independent students’ modelling activities (Stender, 2016), or an adaptive teacher intervention in the modelling process, classified by trigger, level, and intention (Leiß, 2007).

The solution plan, developed by Blum and others (Schukajlow et al., 2015) as a scaffolding tool for the DISUM research project (Blum & Leiß, 2007, 2007), consists of four steps, understanding task, searching mathematics, using mathematics, and explaining results, with the aim to support students within the solution process of MM tasks. The solution plan was chosen for this study, since this approach coincides with the didactic view of a modelling cycle (Greefrath & Vorhölter, 2016). This process for diagnosing within the steps of the modelling cycle, provides an explicit relationship between the modelling cycle and a solution plan as a “strategic aid” (p. 1245). Understanding task is the first step, in parallel to the first modelling step of understanding, involving the understanding of a given problem situation; searching mathematics is the second step, in which the situation is structured through making assumptions based on relevant variables and the real-world model is configured into a mathematical model, thus this step is in line with the combination of the modelling steps of simplifying/structuring and mathematising; using mathematics is the third step, involving working mathematically, in parallel to the modelling step of working mathematically; and explaining results is the fourth step, in which the mathematical results are interpreted and validated in relation to the real-world situation, and the final solution is presented. Therefore, this step corresponds to the modelling steps of interpreting, validating and exposing. Though designed to be applicable to a variety of content areas, it provides teachers with a clear operational-strategic structure for scaffolding students, such as visualising or sketching in order to understand the task. Our aim in this paper is to use the theoretical lens of the solution plan as a methodological aid for analysing teachers’ scaffolding practices, rather than implementing it as a resource for an appropriate intervention for teachers. Thus, our inquiry adopts the solution plan as an appropriate framework to help demonstrate the scaffolding practices employed by teachers when instructing MM tasks in STEM contexts.

Yet, to use such a scaffolding tool for MM tasks under a STEM focus, it makes sense also to consider general strategic processing, which can be supplemented with content-oriented hints depending on the use of the tool (Schukajlow et al., 2015). Consequently, this study examines the extent of teacher-provided scaffolding during the resolution of MM problems in a STEM context as the primary instructional focus, along with the application of general teaching practices.

There have been numerous publications, providing lists of effective teaching practices (e.g. Loewenberg Ball & Forzani, 2009; National Council of Teachers of Mathematics, 2014). In this study, we frame effective teaching practices based on the three dimensions of the quality teaching framework (Klieme & Rakoczy, 2008), by which effective instruction is based on effective classroom management, the facilitation of cognitive activation of learners, and the provision of student learning support. This framework has been widely used in various teaching contexts, including instruction-based modelling (e.g. Baumert & Kunter, 2013) and mathematics teaching (e.g. Lipowsky et al., 2009), making it relevant and applicable to our research.

2.3 Expertise in modelling instruction

Research has highlighted that expertise is characterised by a deep understanding and extensive knowledge in a specific domain, which is applicable within specific contexts (Boshuizen et al., 2020; Ericsson et al., 2006). Research suggests that attaining expertise in the field of teaching is strongly dependent on both teaching experience and teachers’ professional development (PD) (Caspari-Sadeghi & König, 2018; Sternberg & Horvath, 1995).

In this particular study, experts are defined as individuals who are likely to possess fundamental mathematical knowledge and contextual knowledge related to MM due to their general teaching experience.

To date, studies have demonstrated that novice teachers, i.e. pre-service teachers, exhibit less developed skills in modelling instruction compared to expert teachers (Didis et al., 2016). For instance, a recent study by Bastian et al., (2023) indicates that experienced teachers outperform novice teachers in their ability to handle the cognitive demands associated with teacher noticing and its various aspects. Another study conducted by Cai et al., (2022) compared expert and novice teachers in terms of modelling competencies as well their ability to recognise and address written artifacts of student thinking during the solving process—as we know from Borromeo Ferri and Blum (2010) both factors play a vital role while teaching MM. Cai et al., (2022) revealed that expert teachers were more aware of the characteristics of modelling tasks, particularly the need to make assumptions while solving them, and were more adept at responding to students’ responses by asking questions rather than simply pointing out and correcting mistakes.

The disparities between experts and non-experts primarily stem from the experts' quick access to relevant knowledge (Ericsson, 2018). Actual expertise lies in the ability to continuously assess a class situation, monitor students’ progress or challenges, and make necessary adjustments and decisions in real-time (Stigler & Miller, 2018). These skills become evident when observing teachers’ instructional practices in real-time. However, there is currently a gap in the literature regarding the identification of teachers' practices aimed at scaffolding students during the process of solving modelling tasks, particularly in STEM-related contexts that require more intricate contextual knowledge expertise (Kohen & Orenstein, 2021; Kaiser et al., 2013; Maaß et al., 2019). Therefore, the objective of our study is to compare experts (in-service) and novice (pre-service) teachers in their capacity to scaffold students during the instruction of modelling tasks in such contexts.

3 Research questions

In light of the above, the research questions are as follows:

  1. 1.

    What scaffolding practices can be recognised in teachers’ MM instruction in a STEM context?

  2. 2.

    What (if any) are the differences in type and quantity of the recognised scaffolding practices, while comparing MM task instruction in a STEM context of expert in-service teachers, and novice pre-service teachers?

4 Methodology

An in-depth study of scaffolding practices implemented during MM instruction in ten different lessons was conducted using a multiple case study design (Yin, 2017). The cases explored are ten mathematics lessons that were held by expert and novice teachers in 9th grade classes. The lessons are based on three MM tasks in a STEM context, four on the ‘Mobileye’ task, three on the ‘Gamma correction’ task, and three on the ‘GPS’ task, as described below. The instruction of all tasks was observed in the current study according to the four-step solution process of the solution plan. Moreover, teachers’ scaffolding practices were explored as part of a collaborative effort among all students in class for solving the MM tasks.

4.1 Participants

A total of six female teachers and two male teachers participated in our study, of which three were expert in-service teachers––Tamar, Abigail, and Noa (pseudo), and five were novice pre-service teachers––Liz, Eli, David, Maya, and Emma (pseudo). All expert teachers have similar mathematics teaching experience (M = 8 years, SD = 1.5) in the education system in Israel, and have participated in a practice-based PD program designed to train them in the instruction of MM tasks in a STEM context.

The study was conducted for the novice teachers in the last year of their professional training as part of their practicum course, therefore, this was their first year of practical experience in teaching.

Both the PD program and the practicum course were taught by expert math educators who are also experts in the field of MM, as they were part of the development team of the MM tasks used in this study. Participants, both expert and novice teachers, were exposed to the theoretical framework of MM as part of the PD program and practicum course, respectively. Further, they were experiencing the solution process of a variety of MM tasks in a STEM context, from which they had to select at least two to implement in class within a frame of a 50 min lesson. Both groups were not explicitly guided regarding effective instructional practices for MM instruction; rather, they were expected to implement the MM task in class according to their experience, either as expert teachers, or as novice teachers experiencing first-time teaching as part of their practicum year at school. However, as part of the support provided to teachers on the various platforms, they could consult with the PD program facilitators and the course lecturer regarding the construction of the lesson plan. The study follows three different MM tasks taught by the two groups of teachers. Table 1 presents a summary of the tasks that were implemented by the participants in this study.

Table 1 Summary of MM tasks employed by the study participants
Full size table

4.2 The MM tasks in a STEM context

The MM tasks in a STEM context are based on real-world STEM applications, through which students are exposed to the practical application of mathematics in their daily lives. The tasks are designed by mathematical researchers and educators, and are verified for authenticity with high-tech engineers and scientists in the STEM domains. This study focuses on three MM tasks in a STEM context, which facilitated our inquiry in this paper for scaffolding practices based on the solution plan scaffolding tool: the “Mobileye” task which presents an innovative technology for collision prevention (Dagan et al., 2004), the “Gamma correction” task which presents a technological challenge of correcting the brightness of a digital image based on Gamma correction (Amiri & Hassanpour, 2012), and the “GPS” task which presents the global positioning system for tracking the location of a person anywhere on earth (Bajaj et al., 2002). Here, we describe in detail the ‘Mobileye’ MM task that served as the basis of the scaffolding practices presented in the results. Elaboration on the other two MM tasks, namely the “Gamma correction” and “GPS” MM tasks appear in the supplementary materials. The full tasks can be retrieved from the last author’s website at https://mted.technion.ac.il/en/ (see the i-MAT program).

4.2.1 The ‘Mobileye’ MM task

An opening question serves as a trigger for the task: How can you maintain a safe distance between vehicles? In accordance with the first step, understanding task, an introduction to the Mobileye system is then presented with the aim of simplifying the main scientific and technology terms related to this system. In essence, the Mobileye system uses one camera to measure the distance between the car on which the camera is installed and the vehicle driving in front of it. At any given moment, it displays the time until a possible collision with the vehicle in front, and issues a warning when the time to collide is less than 0.9 s. In this step, assumptions are also made to simplify the real-world model, as a means of ensuring that the student is able to comprehend the real-world model in the STEM context, such as disregarding cases in which the vehicle is travelling along a winding road (Fig. 2).

Fig. 2
figure 2

The Mobileye system: simplification of main technology concepts

Full size image

The second step, searching mathematics, ensures that the students have the necessary mathematical knowledge required to accomplish the mathematisation step. The students are asked to inquire mathematically how the distance between cars can be measured using a single camera. To be able to build the real-world model, they must understand the manufacturer's data that are as used in the diagram; for example, the height at which the camera is installed in relation to the road. Identifying variables in the diagram is also necessary; for example, the image plane which depends on the distance between the cars. Afterwards, the real-world model is transformed into a mathematical model that is based on the calculation of the similarity of triangles. Figure 3 presents a summary for the mathematical model that is in line with the Mobileye technological challenge.

Fig. 3
figure 3

The mathematical model for solving the authentic technological challenge of Mobileye

Full size image

In the third step, using mathematics, students are asked to solve questions using mathematical procedures while referring to assumptions according to the real-world model (for example, the similarity ratio) that yield mathematical results, such as the distance between cars. The mathematical procedures required in the MM tasks in this study are fully incorporated into the curriculum and can be implemented in formal school lessons in a whole-class format (Kohen & Orenstein, 2021; Kohen & Nitzan, 2022). As a final step, explaining results, the results are interpreted according to the real-world context, e.g. the Mobileye's technological model, and the solution is validated according to the assumptions made. For example, does the calculated distance represent a safe distance or should the system sound an alarm?

4.3 Data sources and analyses

Observations of the ten case study lessons were the primary data source for this study. The observations covered an entire lesson lasting approximately 50 min and were recorded and transcribed verbatim. Aiming to recognise the teachers’ scaffolding practices, the observations were divided into units of analysis, each of which indicated a teachers’ statement (or a group of statements), i.e. students’ statements were not considered for analysis. In addition, teachers’ statements that were not related to modelling instruction that followed the solution plan steps, were coded as general practices (Praetorius et al., 2018): a) classroom management instances, such as “quiet now”; b) student support, such as teachers giving students enough time to think about a solution to a question, e.g. "I see there are already some students who have finished, that's great. Take a few more minutes to think about the solution and we will continue"; and c) cognitive activation, such as teachers’ rehearsal of well-known mathematical concepts, e.g. "what angles are these? What are they called? […] right. Vertically opposite angles”.

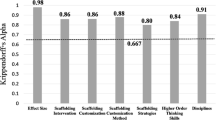
To address RQ1, we coded and analyzed MM scaffolding practices, which were revealed from the data based on content analysis (Shkedi, 2005). A detailed description of the practices appears in the results section. Inter-coder agreement for reliability purposes was established by two of the authors of this paper. We coded one observation of a teacher who did not participate in this study, but was also a participant of the designated PD program for MM instruction. Initially, we divided the observation into units of analysis, and reached a 96% agreement regarding the units’ distribution. Next, we independently coded the first quarter of these analysis units, then came together to create consensus coding. Three more rounds of coding were conducted for the remaining units of analysis in order to clarify code descriptions and add relevant examples. Inter-rater agreement was 90% at the end of this process. Following that, as an overall calculation of the four observations, we calculated the frequency for each scaffolding practice.

To address RQ2, we first calculated the frequencies of the combination between the type of scaffolding practices and type of task, i.e. ‘Mobileye’, ‘Gamma correction’, and ‘GPS’ tasks, using chi-squared analysis. In order to determine whether MM scaffolding practices vary by task type, this analysis was conducted independently of the two groups of participants. We then performed chi-squared analysis for calculating the frequencies of the combination between the type of scaffolding practices and teachers’ teaching experience, i.e. expert, vs novice teachers. We further calculated chi-squared adjudged residuals (AdjRes) for cells in the contingency frequency tables, for revealing which cell significantly contributes to the rejection of the omnibus chi-squared statistics (MacDonald & Gardner, 2000). AdjRes values higher than 1.96 or lower than − 1.96 indicated overrepresentation or underrepresentation (respectively) of specific scaffolding practices.

5 Results

This study identified three key themes of MM scaffolding practices. While the solution plan framework suggests a process for diagnosis within each of the steps, in accordance with the modelling cycle phases (Schukajlow et al., 2015), we revealed instances of scaffolding processes employed by the teachers not just within the solution plan steps, but also the practices used to bridge between the solution plan steps. A third theme that was revealed relates to scaffolding practices aimed to motivate students’ MM learning.

As a first step, we conducted a chi-squared test for Independence to determine whether the MM scaffolding practices differed by task, i.e. ‘Mobileye,’ vs ‘Gamma correction’, vs ‘GPS’ MM tasks. The analysis revealed a similar distribution of the MM scaffolding practices among the different tasks independently of the different groups, \({\chi }^{2}\left(4\right)=6.09, p>.05\). Also, examination of the distribution in the use of MM scaffolding practices between the various tasks for each group separately revealed that there were no significant differences among the expert teachers, \({\chi }^{2}\left(4\right)=5.84, p>.05\), and the novice teachers, \({\chi }^{2}\left(4\right)=2.64, p>.05\). Therefore, the results presented below combine the three tasks together.

Results indicated that both groups demonstrated an average of about 47% MM scaffolding practices out of the total number of teaching practices that were observed in class. The most common MM scaffolding practice was found to be the within scaffolding practice. It was used 2.5 times more compared to the between scaffolding practices, and 6 times more compared to the motivational scaffolding practices (Fig. 4).

Fig. 4
figure 4

Distribution of MM and general scaffolding practices in lessons around MM tasks in a STEM context

Full size image

Below we present each of the MM scaffolding practices.

5.1 MM practices within the solution plan steps

As we investigated the within MM scaffolding practices, we revealed three main practices: ‘basing mathematics’, ‘basing real-world’, and ‘extracting information’. Findings indicate that ‘basing real-world’ was the most dominant practice, about 1.4 times more than ‘basing mathematics’ practice, and almost 2.7 times more than ‘extracting information’ practice (Fig. 5).

Fig. 5
figure 5

Distribution of the major themes of the within MM scaffolding practices in lessons around MM tasks in a STEM context

Full size image

5.1.1 Basing real-world

This theme refers to teachers’ MM practices that involve establishing the scientific terms that are at the heart of the real-world model and basing students’ understanding of the real-world model. Having a clear understanding of these real-world terms is a necessary step for progressing in the modelling cycle, such as building or recognising the appropriate mathematical model and extracting relevant information for it. This practice was observed in all the solution plan steps, but mainly while supporting students during the understanding task step, since this step is critical for understanding the real-world model, and proceed to the next step of configuring the mathematical model. For example, during the understanding task step, Emma scaffolded the students’ understanding of the scientific term of “camera lens”, which is important, since without fully grasping that concept, students would not be able to figure out what information can be retrieved from the camera in order to understand the real-world model and make a sketch accordingly that would lead to the appropriate mathematical model. As such (referring to Fig. 2, above), she was saying: What do we have inside the camera? […] We have got the lens, Okay? The camera lens. And we have here the image that is captured by the lens and is formed on the image plane, and we have the focal length, this is the distance between the lens and the image plane. Additionally, Tamar aimed at basing the real-world model in the Mobileye task, which involved understanding the operating principle of the Mobileye system, based on the distance proportion between at least two objects. Thus, in order to illustrate the real-world model, Tamar showed the students photos that made use of the relationship between size and distances from the camera lens, so that small objects appeared disproportionately large compared to large objects (Fig. 6). For example, showing them a picture of the Eiffel Tower held between human fingers, Tamar explicitly mentioned that: When we photograph an object, an object that is far from us will appear small, and when we bring something close to the camera, the closer we get to the camera or to our eye, the larger it will appear.

Fig. 6
figure 6

An illustration of the real-world model as a trigger for the Mobileye task

Full size image

5.1.2 Basing mathematics

This theme refers to teachers’ MM practices that involved establishing the mathematical terms that are at the heart of the mathematical model, as well as basing students’ understanding of the mathematical model. In order to ensure student understanding of the mathematical model and further the ability to solve the mathematical problem, the relevant terms, such as proportion, corresponding angles, and ratio of similarity, must be well-established. This practice was observed while supporting students during the 'searching mathematics' and 'using mathematics' steps of the solution plan. For example, in the searching mathematics step, Abigail's scaffolding was applied to make sure that the students were familiar with how to prove triangle similarity, which is further used to inquire the distance between the two vehicles. Showing them Fig. 7, she was saying: Those two angles in grey represent equal corresponding angles between parallel lines, and in order to say that two triangles are similar we need two angles. Okay? And this is the proof that the two triangles obtained here are similar triangles.

Fig. 7
figure 7

The process of proving triangles similarity in the Mobileye task

Full size image

Another example relating to the using mathematics step, included Tamar's scaffolding which focused on understanding the geometric theorem of alternating angles between parallel lines, which is necessary for proving similarity of triangles. Accordingly, Tamar confirmed that the students were familiar with this geometric concept and under what conditions the alternating angles are equal:

Tamar: We need two pairs of corresponding equal angles to prove that these two triangles are similar. What pairs of equal angles do we have here?

A: We have corresponding angles

Tamar: You said corresponding angles, why? After all, corresponding angles don't have to be equal, right?

A: Right, I suppose so.

Tamar: What equal corresponding angles do we have?

D: Between the parallel lines.

Tamar: Right! So if the lines are not parallel the corresponding angles will not be equal.

5.1.3 Extracting information

This theme refers to teachers’ MM scaffolding practices in identifying and extracting information from a variety of sources and representations. This practice scaffolds in the understanding of the meaning of the data used in the MM task, which cannot be viewed as separate from the STEM context. This practice is particularly important in the aspect of searching mathematics and using mathematics steps, which involve the adaptation of the mathematical model according to the real-world model and the application of the mathematical model in order to achieve mathematical results, respectively. For example, extracting information during the searching mathematics step involves structuring the appropriate mathematical model by extracting certain data, e.g. equality of angles and parallel lines to prove triangle similarity, and making assumptions based on extracted data, such that the vehicle is driving on a straight road only and the back of the camera is perpendicular to the road. When Maya directed the students to prove the similarity between the triangles, she helped them extract information from the drawing (e.g. Fig. 7) according to the terms from the real-world, and for this purpose, she also made assumptions that assisted in the construction of the appropriate mathematical model, by saying: First of all let's assume that the car is driving on a straight road, without bends, ups or downs. What does it give us? […] Nice, so AB is perpendicular to the road, okay? That is, there is a right angle between the road and AB. Is there another right angle in the drawing? […]. EC is also perpendicular to CA. Great, what does that give us? […] Excellent, equality of angles. This brings us closer to the proof of similarity.

Extracting information during the using mathematics step involves extracting the relevant data and fitting it to the given mathematical model, such as applying the equation of similarity while solving a question based on Mobileye task. Authentic data regarding the Mobileye camera was provided to students so they could inquire the model using mathematical tools (Fig. 8). Accordingly, Abigail said: Well then let's see what we have here. According to the manufacturer's data, the camera in the private car is located at a height of 120 cm in relation to the road, i.e. AB is 120 cm. As for the focal length of the camera, CA, we're told that it’s 0.4 cm, and it’s constant, correct?

Fig. 8
figure 8

An example of authentic data of the Mobileye camera that allows investigation of the model using mathematical tools

Full size image

5.2 MM practices between the solution plan steps

Looking into the between MM scaffolding practices, we revealed two instances of practices: 'building up' (40% of total between practices) and 'connecting context and math' (60% of total between practices).

5.2.1 Building-up

This theme scaffolds students in building up attention toward a certain step in the solution plan. Using real-world terms with an allusion to mathematics, the following example taken from Tamar’s instruction directs the students to use the mathematical concepts (such as ratio) to structure the mathematical model based on the real-world model. Hence, her scaffolding illustrates the building up from the understanding task step to the subsequent searching mathematics step. Tamar illustrates the real-world model using photos of optical illusions based on the distances of the objects in the pictures from the camera lens, so that small objects appear disproportionately large compared to large objects (see Fig. 6 above). This illustration leads the students to use mathematical terms found in the basis of the appropriate mathematical model, as she was saying: What do we see in the pictures? How does that happen? How can you photograph people standing on the palm of a person’s hand? […] Right, so there is a matter of size. What else? […] You say distance from the camera, can you measure the distance of the objects in the picture from the camera? […] Does anyone have an idea how can we measure distance using a single camera? […] Excellent! We can base on ratio here, you are really aiming at the right place. Let's dive into the task and see how it all comes together.

5.2.2 Connecting context and math

This theme is more holistic, in which the teacher scaffolds students’ understanding through connecting between the real-world model and the mathematical model and vice versa. In addition, this theme includes moving back and forth to a certain step in the solution plan to emphasise or summarise terms and assumptions or to provide reasoning for previous actions. This practice can be observed in the transition between the different steps of the solution step. As an example for moving from the mathematical model to the real-world model is the following scaffolding question of Tamar, who pushed the students to find the connection between the use of the mathematical model of similarity of triangles to measuring the distance between two vehicles that relate to the real-world model: …the angle-angle similarity theorem tells us that these triangles are similar […] Okay, so the triangles are similar, but we want to measure the distance between the two vehicles. How are the two related?

An additional example for the teacher’s scaffolding through connecting can be found when Maya provides reasoning for interpreting a mathematical result during the explaining results step, which was based on an indication she made at the beginning of the lesson, following the understanding task step. She stated then that changing the vehicle's parameters can lead to incorrect measurements of distance between vehicles if the changes affect the parameters measured by the camera, for example raising the vehicle influences the height of the camera in relation to the road. Thus, while interpreting a mathematical result that dealt with changes in the camera's data in relation to the road, she was saying: Do you remember earlier that I mentioned how crucial it is to calibrate the camera and its device? Meaning that if we change something in the camera without making suitable adjustments, we will probably get an incorrect distance. Why does it matter? […] Right. The system will not alert you in time.

5.3 MM practices that motivate students’ MM learning

Looking at the motivational MM scaffolding practices, we revealed two practices: 'real-world motivation' (about 60% of total motivational practices) and 'mathematics motivation' (about 40% of total motivational practices).

5.3.1 Real-world motivation

This theme refers to attracting students to engage in the MM task through relevance of the real-world context to their lives. The following dialogue illustrates the way Abigail scaffolded her students’ motivation toward engaging in the MM task, from the very beginning of the lesson, attracting them to the subject through their personal connection to the 'Mobileye' technology and where they encounter it in their daily lives:

Abigail: It's about Mobileye's technology. Have you heard about it?

Y: Yes, it's the one in the cars.

Abigail: Right, what is it? What is "the one in cars"? What is that?

D: ... that detects potential accidents.

Abigail: Right. What else do you know about it?

A: It makes sounds if it detects danger coming… when you approach another vehicle too closely.

Abigail: Right!

5.3.2 Mathematics motivation

This theme refers to attracting students to engage in the MM task through relevance of the mathematics explored to their lives. For example, after establishing the main concepts involved with the invention of Mobileye system, Tamar was aiming to scaffold her students with the ultimate question of “why do we study mathematics?”, saying: Professor Amnon Shashua made billions out of it, he is actually the inventor of the Mobileye […] And it is based on a mathematical principle that you all know.

5.4 Comparison between expert and novice teachers

Moving forward to the comparison between the two groups examined in this study, namely expert in-service teachers and novice pre-service teachers, results based on a chi-squared test for independence indicated that the distribution of the use of MM scaffolding practices and general teaching practices for each group did not achieve significance \({\chi }^{2}\left(3\right)=0.36, p>.05\). According to these findings, the MM scaffolding practices were distributed similarly between the two groups, as was their overall frequency compared to the general teaching practices (see Table 2).

Table 2 Distribution of the MM scaffolding and general practices by the two groups
Full size table

Examining the distribution of the use of different MM scaffolding practices, the same trend of practices distribution that was generally revealed (Fig. 4 above) was evident among the two groups. A closer look at the major themes within each of the MM scaffolding practices, further revealed a similar trend in the frequency of scaffolding practices between the groups for each of the themes separately, as the chi-squared test for Independence did not achieve significance for the within practices \({\chi }^{2}\left(2\right)=1.74, p>.05\), for the between practices \({\chi }^{2}\left(1\right)=0.09, p>.05\), and for the motivational practices \({\chi }^{2}\left(1\right)=0.39, p>.05\).

6 Discussion

This study presents MM scaffolding practices for modelling instruction in a STEM context, which illustrate how teachers scaffold students within each of the solution plan steps, in the transition between them, and in motivating students for MM learning. Figure 9 presents visually the relation we found between the scaffolding practices for MM in a STEM context, and the solution plan steps.

Fig. 9
figure 9

The scaffolding practices for modelling in a STEM context, and their relation to the solution plan steps

Full size image

From a borrowed perspective on modelling competencies, Fig. 9 which illustrates teachers' scaffolding practices may be seen from a holistic or atomistic approach. On the one hand, the scaffolding practices revealed that the between solution plan steps fit in with a more holistic view of the modelling cycle, which requires the teacher to have an insight of the full-scale process of modelling and connect between the two entities of reality and mathematics. On the other hand, the scaffolding practices revealed for the within solution plan steps are in line with a more atomistic perspective, by which the teacher should scaffold each of the individual steps of the modelling cycle. Last, the motivational scaffolding practices may be seen from a social perspective as part of the global view of the modelling cycle (Barbosa, 2006; Cevikbas et al., 2021).

As the within scaffolding practices were found to be the most dominant in all observed lessons, it seems that the teachers found it important to scaffold students within each of the solution plan steps. This finding accords with previous studies, by which the solution process of a modelling problem requires completing each step of the modelling cycle correctly and in a purposeful manner. Nevertheless, these studies indicate difficulties completing each phase (Kaiser, 2007). Little research has indicated that such difficulties are found to be prominent in MM instruction which involves a STEM context (Just & Siller, 2022), thus further studies are required in this area. This study provides an initial view of the practices involved in instructing such MM tasks, and besides that––it presents the sub-practices that comprise them. In particular, the practice of basing real-world was found to be the most frequent, indicating that great emphasis is required to support students’ understanding of the main scientific terms of the real-world model. This is clearly a significant finding, as this understanding is mainly reflected in the first step of the solution plan steps, namely understanding task, which forms the basis on which the entire solution process of the modelling task is built.

Further, although less indicated, the scaffolding practices of basing students’ understanding of the mathematical model and extracting information also appeared intensively in teachers’ observations. These two practices must be performed while still being connected to the STEM context, yet they are more characterised as practices that teachers are used to in standard math lessons (Niss & Blum, 2020). Accordingly, in relation to the solution plan steps, these practices were more characterised with the searching and using mathematics steps. As complementary to the teachers’ massive use of the ‘basing real-world’ scaffolding practice, these findings point to their profound understanding of the modelling process, which was demonstrated in their attempt to support students in the understanding of both models and the relation between them, which is an indispensable step toward completing the full modelling cycle (Blomhøj & Højgaard Jensen, 2007).

We further discovered that the practices that scaffold students’ progress in the solution plan steps, through the transition between the different steps, were also an important factor in successfully completing each of the MM tasks. These include iterative repetition of steps, which is necessary for completing a follow-up solution plan step. In particular, it was found that the practice of connecting context and math was significantly manifested in teachers’ observed lessons. We particularly find this practice to be a complex one, as it demands a holistic view of the real-world model and the mathematical model, and emphasises the balance that needs to be made between the two, as well as the ability to express it to students to facilitate their overall understanding as well (Borromeo Ferri, 2018). This finding is in line with previous studies which establish the expertise of the teachers as a first necessary step toward qualifying their students (Geiger, 2011; Schukajlow et al., 2018).

Our aim in this study was on revealing didactical MM practices that scaffold students’ engagement with MM tasks in STEM context, yet we clearly discovered practices that motivate students to engage in MM tasks through both demonstrating the relevance of the real-world context and mathematics to their lives. These are two complementary perspectives that together fulfill the basic two realms that comprise the modelling cycle, i.e. the real-world realm, and the mathematical realm (Blum & Leiß, 2007, 2007). Generally it can be said that these two types of motivating practices are not documented in the maths education literature as frequent in math lessons, which may possibly explain the students’ ultimate question of “why do we study mathematics?” (Siller et al., in press; Kohen & Nitzan, 2022). This finding is of much significance, since students’ motivation to study mathematics is a crucial factor in their future choice in STEM fields for study and their careers (Siller et al., in press; Just & Siller 2022). The unique authentic context of the MM tasks that further exemplified the applicability of mathematics studies in STEM fields to the students, may further attract students to these fields (Geiger, 2011; Siller et al., in press).

Identifying practices for modelling instruction is not a straightforward matter, yet we managed to discover these practices among both experts and novice teachers. Intriguingly, both groups demonstrated similar scaffolding practices, as opposed to previous studies which found a benefit for expert teachers in relation to modelling instruction (Bastian et al., 2023; Cai et al., 2022; Didis et al., 2016). Nevertheless, we can affirm that the STEM context of the MM task demands expertise which is not just related to teaching experience, but also contextual knowledge expertise to handle the extra-mathematical aspect of teaching those tasks fully, as well as its integration with the mathematical aspect (Kohen & Orenstein, 2021; Kaiser et al., 2013; Maaß et al., 2019). Previous studies which establish the expertise of the teachers as a first necessary step toward qualifying their students (Geiger, 2011; Schukajlow et al., 2018), have also mentioned the importance of teachers’ professional training (e.g. Caspari-Sadeghi & König, 2018). The support given to both expert teachers through a designated PD program for MM instruction, and the novice teachers through their professional teacher training, may have prepared them well for scaffolding their students during MM instruction. This points to the need to support teachers in being professionals in modelling––both as modellers themselves, and as teachers who need to support their students in coping with MM tasks (Geiger, 2011; Schukajlow et al., 2018; Siller et al., in press; Kohen & Nitzan, 2022).

7 Study limitations

The general instructional practices were coded in this study only in cases in which no scaffolding practices for MM were revealed, however there may be double coding for teachers’ statements regarding both general and MM-specific practices. This can be a subject for future study, which may explore how MM instruction and effective math instruction may be intertwined, not just as complementary aspects, but as a single integrated one.

Another limitation of this study is the focus merely on observations. It may be possible that a triangulation of data with other sources of information, such as teachers’ self-reports, would provide a more sensitive view of the differences between these two groups.

Moreover, there is a limitation pertaining to the challenge posed by the tasks and their respective contexts. Specifically, it is possible that the complexity of the context may have added an additional burden for students, and thus an increased reliance on mathematical modelling practices, compared to the general ones. However, we maintain the assumption that this matter does not impact our findings, as we detected no discernible differences in the instructional scaffolding approaches employed for each task. Rather, we assert that the instruction of MM tasks that involve an interdisciplinary connection to STEM fields requires substantial scaffolding. This was realised, in particular, in the emphasis on the basing real-world scaffolding practice in each of the solution plan steps, as well as the emphasis placed on the ‘between solution plan steps’ practice of connecting context and math, which indicates the teachers’ effort in focusing on the practices that are more directed to supporting students with the unique context of the tasks.

8 Conclusion and study contribution

In summary, our study indicates that MM plays a central role in STEM, emphasising its mathematical essence (Siller et al., in press). Our study provides an important theoretical contribution to defining specific scaffolding practices for MM instruction in a STEM context. It reveals how a constitutive link between mathematics and industrial workplace applications is implemented in the classroom through MM.

In addition, the practices which were exemplified in formal lessons, held as plenary sessions, point to both theoretical and practical contributions of the study, indicating that effective modelling instruction can take place in a variety of learning contexts, with the appropriate scaffolding (Puntambekar & Hübscher, 2005; Smit et al., 2013). Supporting modelling activities with the help of the scaffolding concept has great potential. Ideally, these activities help to acquire heuristics which can be applied in further contexts, enabling the modelling process to be performed independently in the future.

From a practical viewpoint, this study provides a valuable insight into MM scaffolding practices that may be used in training pre- and in-service teachers for MM instruction in a STEM context. Viewing the findings from the perspective of this unique context of the tasks, it is evident that, in addition to appropriate teacher training for MM instruction, the use of modelling tasks that are consistent with the solution plan encourages the use of MM scaffolding practices that improve the adaptive support provided by teachers, regardless of their prior teaching experience. Thus, a thorough understanding of the modelling process is essential to teach those tasks effectively, which requires an interdisciplinary knowledge regarding both mathematics and STEM contexts.