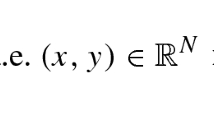Optimal regularity for degenerate Kolmogorov equations in non-divergence form with rough-in-time coefficients

Abstract

We consider a class of degenerate equations in non-divergence form satisfying a parabolic Hörmander condition, with coefficients that are measurable in time and Hölder continuous in the space variables. By utilizing a generalized notion of strong solution, we establish the existence of a fundamental solution and its optimal Hölder regularity, as well as Gaussian estimates. These results are key to study the backward Kolmogorov equations associated to a class of Langevin diffusions.

1 Introduction

We study existence and optimal regularity properties of the fundamental solution to a Kolmogorov operator that satisfies a parabolic Hörmander condition. The coefficients of the operator are Hölder continuous in the space variables, but only measurable in time.

Precisely, for fixed $d\le N$ and $T_0>0$, we consider the second order operator in non-divergence form $\mathscr {A}+ Y$ with

$$\begin{aligned} \begin{aligned} \mathscr {A}&= \frac{1}{2}\sum _{i,j=1}^{d} a_{ij}(t,x)\partial _{x_i x_j}+ \sum _{i=1}^{d} a_{i}(t,x)\partial _{x_i} +a(t,x),\qquad (t,x)\in \mathscr {S}_{T_0}:=]0,T_0[\times \mathbb {R}^N, \\ Y&= \partial _t + \langle B x,\nabla \rangle = \partial _{t} + \sum _{i,j=1}^{N}b_{ij}x_{j}\partial _{x_{i}}, \qquad x\in \mathbb {R}^N, \end{aligned} \end{aligned}$$

(1.1)

where B is a constant matrix of dimension $N\times N$. Here, $\mathscr {A}$ is an elliptic operator on $\mathbb {R}^d$ and Y is a first order differential operator on $\mathbb {R}\times \mathbb {R}^N$, also called transport or drift term. The focus of this paper is mainly on the case $d<N$, that is when $\mathscr {A}+ Y$ is fully degenerate, namely no coercivity condition on $\mathbb {R}^N$ is satisfied.

Throughout the paper, $\mathscr {A}+ Y$ verifies the following two structural

Assumption 1.1

(Coercivity on $\mathbb {R}^{d}$) For $1\le i,j\le d$, the coefficients $a_{ij},a_{i},a$ are in $L^\infty ([0,T_0];C_{b}(\mathbb {R}^N))$, where $C_{b}(\mathbb {R}^N)$ denotes the space of bounded continuous functions on ${\mathbb {R}}^{N}$. The diffusion matrix $\left( a_{ij}\right) _{i,j=1,\ldots ,d}$ is symmetric and there exists a positive constant $\mu$ such that

$$\begin{aligned} {\mu ^{-1}}{|\xi |^2} \le \sum _{i,j=1}^{d}a_{ij}(t,x)\xi _i \xi _j \le \mu |\xi |^2,\qquad x\in \mathbb {R}^N,\ \xi \in \mathbb {R}^{d}, \end{aligned}$$

for almost every $t\in [0,T_0]$.

Assumption 1.2

(Hörmander condition) The vector fields $\partial _{x_1},\ldots ,\partial _{x_{d}}$ and Y satisfy

$$\begin{aligned} \text {rank } \text {Lie}(\partial _{x_1},\ldots ,\partial _{x_{d}},Y) = N+1. \end{aligned}$$

(1.2)

We refer to (1.2) as a parabolic Hörmander condition since the drift term Y plays a key role in the generation of the Lie algebra. Under Assumption 1.2, the prototype Kolmogorov operator

$$\begin{aligned} \frac{\delta }{2}\sum _{i=1}^{d}\partial _{x_{i}x_{i}} + Y \end{aligned}$$

(1.3)

is hypoelliptic for any $\delta >0$. Kolmogorov [19] (see also [15]) constructed the explicit Gaussian fundamental solution for (1.3), which is the transition density of a linear stochastic differential equation.

Motivations for the study of $\mathscr {A}+ Y$ come from physics and finance. In its most basic form, with $N=2$ and $d=1$,

$$\begin{aligned} \frac{1}{2}\partial _{x_{1}x_{1}}+x_{1}\partial _{x_{2}}+\partial _{t} \end{aligned}$$

(1.4)

is the backward Kolmogorov operator of the system of stochastic equations

$$\begin{aligned} {\left\{ \begin{array}{ll} dV_{t}=dW_{t}&{}\\ dX_{t}=V_{t}dt&{} \end{array}\right. } \end{aligned}$$

(1.5)

where W is a real Brownian motion. In the classical Langevin model, (V, X) describes the velocity and position of a particle in the phase space and it is the prototype of more general kinetic models (cf. [17, 18, 22]). In mathematical finance, (V, X) represents the log-price and average processes used in modeling path-dependent financial derivatives, such as Asian options (cf. [2, 31]).

1.1 Overview of the results: motivations and comparison with the literature

The study of the fundamental solution and its regularity properties is a relevant task in the theory of partial differential equations. In this regard, we point out that the global Schauder estimates recently proved in [25] strongly rely on the results of this paper (see Sect. 4 for a brief anticipation of the results in [25]). The study of the fundamental solution is also crucial in tackling the martingale problem for the corresponding stochastic differential equations (SDEs) (see [29]). For instance, it is known that uniform bounds on the first and second order derivatives of the solutions to the Cauchy problem can be utilized to prove weak and pathwise well-posedness of the SDE, respectively. We point out that the matter of pathwise uniqueness for the SDE is still partially open in the Hölder setting (see [5]). These issues will be addressed in a future work.

The innovative aspects of our contribution revolve around the regularity assumptions on the coefficients and the regularity properties that we prove for the solutions. For Kolmogorov operators with coefficients that are Hölder continuous (in both space and time) in a classical sense, the study of the existence of a fundamental solution goes back to the early papers [16, 28, 38, 39]. More modern and natural approaches make use of different Hölder spaces, which better adapt to the geometric properties of the operator and of the underlying diffusion processes. Deferring the precise definitions until Sect. 1.2, we may identify two main notions of Hölder space:

• Anisotropic these are the Hölder spaces utilized in [26] and later adopted by several authors (see [24, 37] among others). They comprise functions $g:{\mathbb {R}}^{N}\rightarrow \mathbb {R}$ that are Hölder continuous with respect to an anisotropic norm $| \cdot |_B$ related to the scaling properties of the underlying diffusion process (cf. [6, 21]). For example, the anisotropic norm for the Langevin operator (1.4) reads as $|(v,x)|_B = |v| + |x|^{\frac{1}{3}}$ for $(v,x)\in \mathbb {R}^{2}$ and reflects the time-scaling behavior of the stochastic system (1.5), i.e. $(\Delta V )^2 \approx \Delta t$ and $(\Delta X)^2 \approx (\Delta t)^3$.

• Intrinsic these are the Hölder spaces introduced in [36] and then studied by several authors (see [30] among others). They are defined for functions $f:\mathbb {R}\times {\mathbb {R}}^{N}\rightarrow \mathbb {R}$, by specifying the regularity along the Hörmander vector fields $\partial _{x_1}, \ldots , \partial _{x_d}$ and Y. The Hörmander condition then allows to recover joint Hölder regularity in both time and space with respect to an intrinsic distance on $\mathbb {R}\times {\mathbb {R}}^{N}$, which reduces to the anisotropic distance when restricted to ${\mathbb {R}}^{N}$, i.e. $| t-s |^{1/2} + | x - e^{(t-s)B} y |_B$ for $(t,x),(s,y)\in \mathbb {R}\times {\mathbb {R}}^{N}$ (cf. Remarks 1.1 and 1.2).

In regards to these Hölder spaces, we recognize two main streams of literature that consider anisotropic or intrinsic regularity for both the data and the solutions:

• Anisotropic-to-anisotropic in this approach, initiated in [26], the coefficients of the operator are assumed anisotropically Hölder continuous in space and only measurable in time, and the same type of regularity is proved for the solutions. These are typically defined in the distributional sense and do not benefit from the time-smoothing effect that is typical of parabolic equations (see, for instance, Theorem 4.3 in [37]). In particular, no regularity along Y, and thus in the time-variable, is provided.

• Intrinsic-to-intrinsic in this approach, initiated by [36] and then developed by several authors (e.g. [1, 7, 13, 32] among others), the data are typically assumed to be intrinsically Hölder continuous in time-space. Solutions are defined in the Lie sense, regarding Y as a directional derivative. In this approach, regularity properties in space and time are strictly intertwined: this allows to fully exploit the smoothing effect of the equation. However, the regularity assumptions on the data makes the analysis less suitable for applications to stochastic equations.

Only recently (see [3, 10]), the last two approaches have been combined into a third one, which we refer to as anisotropic-to-intrinsic and provides intrinsic regularity of the solutions under anisotropic regularity of the coefficients. Our contributions go exactly in this direction. In particular:

• Theorem 1.1 establishes the existence of the fundamental solution, together with Gaussian estimates for the solution and its derivatives. It generalizes the results in [7] by relaxing the regularity hypotheses on the coefficients: as pointed out in [10], intrinsic Hölder continuity is a rather restrictive assumption and simple smooth bounded functions like $f(t,x_1,x_2) =\sin x_2$ fail to satisfy this condition. Theorem 1.1 is also comparable with the results in [6]: however, in the latter reference, it is not proved that the kernel constructed with the parametrix method is a fundamental solution, which would require careful potential estimates; on the other hand, the framework considered in [6] is more general because the drift Y is not necessarily linear in x.

• Theorem 1.2 contains global intrinsic Hölder estimates on the fundamental solution. At the level of the fundamental solution, this result extends some partial results in [8, Theorem 3.2] obtained for Hölder continuous coefficients in the intrinsic sense. Most importantly, the estimates of Theorem 1.2, together with the intermediate estimates their proof rely on, are key to obtain the optimal global Schauder estimates in [25] (cf. Sect. 4 below). The latter are stronger than previous results obtained in the anisotropic-to-anisotropic and the intrinsic-to-intrinsic settings (e.g. [9, 14, 17, 24, 26, 37] among others) and also refine the estimates of intrinsic-to-intrinsic type recently obtained in [3, 10]. We refer to [25, Section 1] for a detailed comparison for the literature on Schauder estimates for degenerate Kolmogorov equations.

Finally, the anisotropic Hölder regularity of solutions to $\mathscr {A}+Y$ unveils the full smoothing effect of the the differential operator in both the space and time variables. A notable implication is the possibility to prove intrinsic Taylor formulas like those proved in [30] (cf. Remark 1.2), on which stochastic tools like the Itô formula rely (see [21]). Furthermore, the setting of coefficients that are rough in the time variable naturally arises in the study of stochastic partial differential equations (see, for example, [20, 35]).

1.2 Anisotropic and intrinsic Hölder spaces

We start by noticing that condition (1.2) is equivalent to the well-known Kalman rank condition for controllability in linear systems theory (cf., for instance, [33]). Also, it was shown in [23] that (1.2) is equivalent to B having the block-form

$$\begin{aligned} B=\begin{pmatrix} *&{} *&{} \cdots &{} *&{} *\\ B_1 &{} *&{}\cdots &{} *&{} *\\ 0 &{} B_2 &{}\cdots &{} *&{} *\\ \vdots &{} \vdots &{}\ddots &{} \vdots &{}\vdots \\ 0 &{} 0 &{}\cdots &{} B_{q}&{} *\end{pmatrix} \end{aligned}$$

(1.6)

where the $*$-blocks are arbitrary and $B_j$ is a $(d_{j-1}\times d_j)$-matrix of rank $d_j$ with

$$\begin{aligned} d\equiv d_{0}\ge d_1\ge \cdots \ge d_{q}\ge 1,\qquad \sum _{i=0}^{q} d_i=N. \end{aligned}$$

This allows to introduce natural definitions of anisotropic norm and Hölder continuity on $\mathbb {R}^{N}$.

Definition 1.1

(Anisotropic norm and anisotropic Hölder spaces) For any $x\in {\mathbb {R}}^{N}$ let

$$\begin{aligned} |x|_B:= \sum _{j=0}^{q}\, \sum _{i=\bar{d}_{j-1}+1}^{\bar{d}_j} |x_{i}|^{\frac{1}{2j+1}}, \qquad {\bar{d}_j:= \sum _{k=0}^j d_k}. \end{aligned}$$

(1.7)

For $\alpha \in \,]0,1]$ we denote by $C^{\alpha }_{B}({\mathbb {R}}^{N})$ the set of functions $g\in C_{b}({\mathbb {R}}^{N})$ such that

$$\begin{aligned} \Vert g\Vert _{C^{\alpha }_{B}({\mathbb {R}}^{N})}:=\sup _{x\in {\mathbb {R}}^{N}} |g(x)|+ \sup _{x,y\in {\mathbb {R}}^{N}} \frac{|g(x) - g(y)| }{ |x - y|^{\alpha }_B } < \infty , \end{aligned}$$

and by $L^{\infty }([0,T_0];C^{\alpha }_{B}({\mathbb {R}}^{N}))$ the set of measurable functions $f:[0,T_0] \longrightarrow C^{\alpha }_{B}({\mathbb {R}}^{N})$ such that

$$\begin{aligned} \Vert f \Vert _{L^{\infty }( [0,T_0];C^{\alpha }_{B}({\mathbb {R}}^{N}))}:= \sup _{t\in [0,T_0]} \Vert f(t) \Vert _{C^{\alpha }_{B}({\mathbb {R}}^{N})} < \infty . \end{aligned}$$

To give the precise definition of the Hölder space $C_{B}^{2,\alpha }$ we first introduce the intrinsic Hölder regularity along the vector fields appearing in the Hörmander condition (1.2). As it is standard in the framework of functional analysis on homogeneous groups (cf. [11]), the idea is to weight the Hölder exponent in terms of the formal degree of the vector fields, which is equal to 1 for $\partial _{x_1},\ldots ,\partial _{x_d}$ and equal to 2 for Y.

Definition 1.2

Let $\alpha \in \,]0,1]$, $\beta \in \, ]0,2]$ and $T>0$. We denote respectively by $C_{d}^{\alpha }(\mathscr {S}_{T})$ and $C_{Y}^{\beta }(\mathscr {S}_{T})$ the set of the functions $f:\mathscr {S}_{T} \rightarrow \mathbb {R}$ such that the following semi-norms are finite

$$\begin{aligned} \left\| f\right\| _{C_{d}^{\alpha }(\mathscr {S}_{T})}&:= \sum _{i=1}^{d} \sup _{(t,x)\in \mathscr {S}_{T}\atop h\in \mathbb {R}}\frac{\left| f (t,x +h \textbf{e}_i ) - f(t,x)\right| }{|h|^{\alpha }}, \\ \left\| f\right\| _{C_{Y}^{\beta }(\mathscr {S}_{T})}&:=\sup _{t,s\in [0,T]\atop x\in {\mathbb {R}}^{N}}\frac{\left| f(s,e^{(s-t) B}x) - f(t,x)\right| }{|t-s|^{\frac{\beta }{2}}}. \end{aligned}$$

Here $\textbf{e}_i$ denotes the i-th element of the canonical basis of $\mathbb {R}^N$.

Moreover, we say that f is a.e. Lie differentiable along Y on $\mathscr {S}_{T}$ if there exists $F\in L_{\textrm{loc}}^{1}(]0,T[;C_b({\mathbb {R}}^{N}))$ such that

$$\begin{aligned} f(s,e^{(s - t) B}x) = f(t,x) + \int _{t}^{s} F(r, e^{(r - t) B} x )d r, \qquad (t,x)\in \mathscr {S}_{T},\ s\in \,]0,T[.\nonumber \\ \end{aligned}$$

(1.8)

In that case, we set $Yf=F$ and call it an a.e. Lie derivative of f on $\mathscr {S}_{T}$.

Next we recall the intrinsic Hölder spaces of order 0 and 1 introduced in [30, 31].

Definition 1.3

(Intrinsic Hölder spaces: orders 0 and 1) For $\alpha \in \,]0,1]$, $C_{B}^{0,\alpha }(\mathscr {S}_T)$ and $C_{B}^{1,\alpha }(\mathscr {S}_T)$ denote, respectively, the set of the functions $f:\mathscr {S}_{T} \rightarrow \mathbb {R}$ such that the following semi-norms are finite

$$\begin{aligned} \Vert f\Vert _{C^{0,\alpha }_{B}(\mathscr {S}_T)}&:=\Vert f\Vert _{C^{\alpha }_{Y}(\mathscr {S}_T)}+\Vert f\Vert _{C^{\alpha }_{d}(\mathscr {S}_T)},\\ \Vert {f}\Vert _{C^{1,\alpha }_{B}(\mathscr {S}_T)}&:=\Vert f\Vert _{C^{1+\alpha }_{Y}(\mathscr {S}_T)}+\sum \limits _{i=1}^{d} \Vert {\partial _{x_i}f}\Vert _{C_{B}^{0,\alpha }(\mathscr {S}_T)}\\&={\Vert f\Vert _{C^{1+\alpha }_{Y}(\mathscr {S}_T)}+\sum \limits _{i=1}^{d} \big ( \Vert \partial _{x_i}f \Vert _{C^{\alpha }_{Y}(\mathscr {S}_T)}+\Vert \partial _{x_i}f \Vert _{C^{\alpha }_{d}(\mathscr {S}_T)} \big )} . \end{aligned}$$

Remark 1.1

It is standard to show (see [30]) that, if $f\in C_{B}^{0,\alpha }(\mathscr {S}_T)$, then f is $\alpha$-Hölder continuous w.r.t. the intrinsic distance, namely

$$\begin{aligned} |f(t,x) - f(t,y)| \le C\big ( |t-s|^{\frac{\alpha }{2}}+|x-e^{(t-s)B}y|^{\alpha }_{B} ), \qquad (t,x)(s,t)\in \mathscr {S}_T, \end{aligned}$$

where C is a positive constant that depends only on the matrix B and T. In particular, f enjoys anisotropic Hölder regularity, and thus also regularity in the degenerate variables $x_{i}$ for $i>d$, namely

$$\begin{aligned} \sup _{x,y\in \mathbb {R}^N } \frac{|f(t,x) - f(t,y)| }{ |x - y|^{\alpha }_B } \le C \Vert f\Vert _{C^{0,\alpha }_{B}(\mathscr {S}_T)}, \qquad t\in [0,T[. \end{aligned}$$

Remark 1.2

In [30] it was also shown that if $f\in C_{B}^{1,\alpha }(\mathscr {S}_T)$ then the following intrinsic Taylor formula holds:

$$\begin{aligned}{} & {} \Big | f(s, y) - f(t,x) - \sum _{i=1}^d \partial _{x_i} f(t, x ) (y - e^{(s-t) B }x)_i \Big | \\{} & {} \le C \big ( |s-t|^{\frac{1}{2}}+|y - e^{(s-t) B }x|_{B} \big )^{1+\alpha }, \qquad (t,x),(s,y)\in \mathscr {S}_T. \end{aligned}$$

where C is a positive constant that depends only on the matrix B. We stress that the Taylor “polynomial” above only contains the first derivatives of f w.r.t. the first d components of x.

To cope with the lack of regularity of the coefficients in the time-direction, the definition of $C_{B}^{2,\alpha }(\mathscr {S}_T)$ differs from the one given in [30], specifically with regards to the regularity along Y.

Definition 1.4

(Intrinsic Hölder spaces: order 2) For $\alpha \in \,]0,1]$, $C_{B}^{2,\alpha }(\mathscr {S}_T)$ is the set of functions $f:\mathscr {S}_{T} \rightarrow \mathbb {R}$ such that following semi-norm is finite:

$$\begin{aligned} \Vert {f}\Vert _{C^{2,\alpha }_{B}(\mathscr {S}_T)}&= \sum _{i=1}^{d}\Vert {\partial _{x_i}f}\Vert _{C_{B}^{1,\alpha }(\mathscr {S}_T)}+ \Vert Yf \Vert _{L^{\infty }([0,T];C^{\alpha }_{B}({\mathbb {R}}^{N}))} \nonumber \\&= \sum _{i=1}^{d} \Vert \partial _{x_i}f\Vert _{C^{1+\alpha }_{Y}(\mathscr {S}_T)}+\sum \limits _{i,j=1}^{d} \big ( \Vert \partial _{x_i x_j}f \Vert _{C^{\alpha }_{Y}(\mathscr {S}_T)} + \Vert \partial _{x_i x_j}f \Vert _{C^{\alpha }_{d}(\mathscr {S}_T)} \big )\nonumber \\&\quad + \Vert Yf \Vert _{L^{\infty }([0,T];C^{\alpha }_{B}({\mathbb {R}}^{N}))} . \end{aligned}$$

(1.9)

Here Yf is the a.e. Lie derivative as in Definition 1.2.

Remark 1.3

Definition 1.4 is similar in spirit to that proposed in [9, 27, 30] for the study of Kolmogorov operators with Hölder coefficients: according to their definition, if f belongs to $C^{2,\alpha }$ then Yf belongs to $C^{0,\alpha }_B$.

This is the regularity the fundamental solution enjoys in case the coefficients of $\mathscr {A}$ are Hölder continuous in both space and time, namely if they belong to $C^{0,\alpha }_B$. By contrast, if $f\in C_{B}^{2,\alpha }$ in the sense of Definition 1.4 then f is generally at most Lipschitz continuous along Y: this is the optimal result one can prove without assuming further regularity of the coefficients in the time variable other than measurability, as it was shown in [4] in the case of coefficients only dependent on time.

For reader’s convenience, we recall that we shall always denote by $\mathscr {S}_{T}$ the strip $]0,T[\times {\mathbb {R}}^{N}$; also, in the following table we collect the notations used for the main functional spaces (Table 1):

Table 1 Functional spaces

1.3 Main results

As previously explained, major questions in the study of Kolmogorov equations are the very definition of solution and its optimal regularity properties. It is well-known that, in general, the fundamental solution is not regular enough to support the derivatives $\partial _{x_{i}}$, for $d<i\le N$, appearing in the transport term Y. Indeed, under the Hörmander condition (1.2), these derivatives are of order three and higher in the intrinsic sense. For this reason, even for equations with Hölder coefficients, weak notions of solution have been introduced. We employ a notion of solution, recently proposed in [35] with the aim of studying Langevin stochastic PDEs with rough coefficients. In accordance with the intrinsic Hölder space $C_{B}^{2,\alpha }(\mathscr {S}_T)$ in Definition 1.4, this solution supports the existence of an a.e. Lie derivative and is the strongest possible under our regularity assumptions on the coefficients.

Definition 1.5

(Strong Lie solution) Let $0<T\le T_0$ and $f\in L_{\textrm{loc}}^{1}([0,T[;C_{b}({\mathbb {R}}^{N}))$. A solution to equation

$$\begin{aligned} \mathscr {A}u+ Yu = f\ \text { on }\mathscr {S}_{T} \end{aligned}$$

(1.10)

is a continuous function u such that there exist $\partial _{x_{i}}u,\partial _{x_i x_j}u\in L_{\textrm{loc}}^{1}([0,T[;C_{b}({\mathbb {R}}^{N}))$, for $i,j=1,\ldots ,d$, and $f - \mathscr {A}u$ is an a.e. Lie derivative of u in the sense of Definition 1.2, i.e.

$$\begin{aligned} u(s,e^{(s-t)B}x)= & {} u(t,x)-\int _t^{s}\left( \mathscr {A}u(\tau ,e^{(\tau -t)B}x)-f(\tau ,e^{(\tau -t)B}x)\right) d\tau , \nonumber \\{} & {} \quad (t, x)\in \mathscr {S}_{T},\ s<T. \end{aligned}$$

(1.11)

Remark 1.4

Notice that $s\mapsto (s,e^{(s-t)B}x)$ is the integral curve of Y starting from (t, x): for any suitably regular function u the limit

$$\begin{aligned} Yu(t,x):= \lim _{s\rightarrow t}\frac{u(s,e^{(s-t)B}x)-u(t,x)}{s-t} \end{aligned}$$

(1.12)

is the directional (or Lie) derivative along Y of u at (t, x). Thus, if the integrand in (1.11) is continuous then u is a classical (pointwise) solution of (1.10). However, as noticed in Remark 2.6, in general a solution u in the sense of Definition 1.5 is only a.e. differentiable along Y and Eq. (1.10) is satisfied for almost every $(t,x)\in \mathscr {S}_{T}$.

In order to state our first main result, we give the following

Definition 1.6

(Fundamental solution) A fundamental solution of $\mathscr {A}+ Y$ is a function $p=p(t,x;T,y)$ defined for $t<T$ and $x,y\in \mathbb {R}^N$ such that, for any fixed $(T,y)\in \mathscr {S}_{T_0}$, we have:

• (i) $p(\cdot ,\cdot ;T,y)$ is a solution of equation $\mathscr {A}u+Y u=0$ on $\mathscr {S}_{T}$ in the sense of Definition 1.5;

• (ii) For any $g\in C_{b}({\mathbb {R}}^{N})$ we have

  $$\begin{aligned} \lim _{\begin{array}{c} (t,x)\rightarrow (T,y)\\ t<T \end{array}} \int _{\mathbb {R}^N}p(t,x;T,\eta )g(\eta )d\eta =g(y). \end{aligned}$$

Before stating our main results, we introduce our last standing assumption, which is concerned with the regularity of the coefficients of $\mathscr {A}$.

Assumption 1.3

The coefficients $a_{ij},a_i,a$ of $\mathscr {A}$ belong to $L^{\infty }([0,T_0];C^{\alpha }_{B}({\mathbb {R}}^{N}))$ for some $\alpha \in \, ]0,1]$.

Remark 1.5

The boundedness requirement in Assumption 1.3 is a crucial ingredient of the parametrix method: it is used to get the preliminary Gaussian estimates (cf. Proposition A.1) on which the entire technique relies. In particular, the key property is boundedness in space for any fixed time. On the other hand, a detailed examination of the proof reveals the possibility for an extension that includes coefficients that are only locally integrable, as opposed to bounded, in the time variable. We aim to investigate this extension in a future work.

The following result states the existence of the fundamental solution p of $\mathscr {A}+ Y$, as well as uniform Gaussian bounds for p and its derivatives with respect to the non-degenerate variables $x_1,\ldots ,x_{d}$.

Theorem 1.1

(Existence and Gaussian bounds) Under Assumptions 1.1, 1.2 and 1.3, $\mathscr {A}+Y$ has a fundamental solution $p=p(t,x;T,y)$ in the sense of Definition 1.6. For every $\varepsilon >0$ there exists a positive constant C, only dependent on $T_0,\mu ,B,\varepsilon ,\alpha$ and the $\alpha$-Hölder norms of the coefficients, such that

$$\begin{aligned} p(t,x;T,y)&\le C \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(1.13)

$$\begin{aligned} \left| \partial _{x_i}p(t,x;T,y)\right|&\le \frac{C}{\sqrt{T-t}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(1.14)

$$\begin{aligned} \left| \partial _{x_i x_j}p(t,x;T,y)\right|&\le \frac{C}{T-t} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(1.15)

for any $(T,y)\in \mathscr {S}_{T_0}$, $(t,x)\in \mathscr {S}_{T}$ and $i,j=1,\ldots ,d$, where $\Gamma ^\delta$ is the Gaussian fundamental solution of (1.3), whose explicitly expression is given in (2.4). Moreover, there exist two positive constants $\bar{\mu },\bar{c}$ such that

$$\begin{aligned} \bar{c}\, \Gamma ^{\bar{\mu }}(t,x;T,y) \le p(t,x;T,y), \end{aligned}$$

(1.16)

for any $(T,y)\in \mathscr {S}_{T_0}$ and $(t,x)\in \mathscr {S}_{T}$.

In Sect. 4 we present several results for the Cauchy problem that are straightforward consequences of Theorem 1.1. The proof of Theorem 1.1 is based on a modification of Levi’s parametrix technique, which allows to deal with the lack of regularity of the coefficients along the drift term Y. The main tool is the fundamental solution of a Kolmogorov operator with time-dependent measurable coefficients, also recently studied in [4]. This approach allows for a careful analysis of the optimal regularity properties of the fundamental solution p: Theorem 1.2 below states that p belongs to the intrinsic Hölder space $C_{B}^{2,\alpha }$ as given by Definition 1.4. As the notation could be misleading, we explicitly remark that for $u\in C_{B}^{2,\alpha }$ not even the first order derivatives $\partial _{x_{i}}u$, for $i>d$, necessarily exist. However, in general we cannot expect higher regularity properties for solutions to (1.10) and $C_{B}^{2,\alpha }$-regularity is indeed optimal. The following theorem refines the known results about the smoothness of the fundamental solution in [26, 27] and [9] and exhibits its maximal regularity properties.

Theorem 1.2

(Regularity of the fundamental solution) Under the assumptions of Theorem 1.1, $p(\cdot ,\cdot ;T,y)\in C_{B}^{2,{\beta }}(\mathscr {S}_{\tau })$ for every $(T,y)\in \mathscr {S}_{T_0}$, $0<\tau <T$ and $\beta <\alpha$. Precisely, there exists a positive constant C only dependent on $T_0,\mu ,B,\beta ,\alpha$ and the $\alpha$-Hölder norms of the coefficients, such that

$$\begin{aligned} \Vert p(\cdot ,\cdot ;T,y) \Vert _{C_{B}^{2,\beta }(\mathscr {S}_{\tau })} \le \frac{C}{(T-\tau )^{\frac{Q+{2+\beta }}{2}}}, \end{aligned}$$

where Q is the so-called homogeneous dimension of $\mathbb {R}^N$ with respect to the quasi-norm $|\cdot |_B$ defined by

$$\begin{aligned} Q=\sum _{i=0}^{q} (2i+1) d_{i}. \end{aligned}$$

(1.17)

Remark 1.6

As previously explained, the Hölder space $C^{2+\alpha }$ introduced in [26] (and adopted in [24, 37] to prove Schauder estimates), consists of functions f that, together with their second order derivatives $\partial _{x_{i}x_{j}}f$ in the non-degenerate directions $i,j=1,\ldots ,d$, are Hölder continuous w.r.t. the anisotropic norm (1.7). This notion is weaker than Definition 1.4 both in terms of the regularity of $\partial _{x_{i}}f$ and, more importantly, in terms of the Lipschitz continuity of f along Y (cf. (1.8)) which reveals the regularizing effect of the associated evolution semigroup.

The rest of the paper is structured as follows. Section 2 contains the construction of the fundamental solution by means of the parametrix method: in particular, Sect. 2.2 includes the proof of Theorem 1.1. In Sect. 3 we prove the regularity estimates of the fundamental solution, in particular Theorem 1.2. In Sect. 4, we anticipate some results for the Cauchy problem for $\mathscr {A}+Y$, namely well-posedness and Schauder estimates, which can be derived by utilizing our results on the fundamental solution. The appendices contain the Gaussian and potential estimates that are employed in the proofs.

2 Parametrix construction

The parametrix method, introduced by E. Levi in 1907, is a constructive technique to prove the existence of the fundamental solution to an elliptic operator, later extended by several authors to numerous parabolic settings. The monograph [12] is a classical reference for the application of the method to uniformly parabolic operators; the case of degenerate operators of the form (1.1) with Hölder continuous coefficients was studied in [7, 36]. We refer to [4] for a derivation of the fundamental solution via classical Fourier methods, in the case of time-depending measurable coefficients.

Let Assumptions 1.1, 1.2 and 1.3 be satisfied. The first step of the parametrix method is to set a kernel $\textbf{P}=\textbf{P}(t,x;T,y)$ that serves as proxy for the fundamental solution, called parametrix. We denote by $\mathscr {A}^{(s,v)}$ the operator obtained by freezing the second-order coefficients of $\mathscr {A}$ along the integral curve of the vector field Y passing through $(s,v)\in \mathscr {S}_{T_0}$ and neglecting the lower order terms. Namely we consider the operator

$$\begin{aligned} \mathscr {A}^{(s,v)}:= \frac{1}{2}\sum _{i,j=1}^{d} a_{ij}(t,e^{(t-s)B}v)\partial _{x_i x_j}, \qquad (t,x) \in \mathscr {S}_{T_0}. \end{aligned}$$

(2.1)

One can directly prove that the fundamental solution of

$$\begin{aligned} \mathscr {A}^{(s,v)} + Y, \end{aligned}$$

in the sense of Definition 1.6, is given by

$$\begin{aligned} \Gamma ^{(s,v)}(t,x;T,y)=\textbf{G}(\mathscr {C}^{(s,v)}(t,T),y-e^{(T-t)B}x),\qquad (T,y)\in \mathscr {S}_{T_0},\ (t,x)\in \mathscr {S}_T, \end{aligned}$$

where

$$\begin{aligned} \textbf{G}(\mathscr {C},z):= \frac{1}{\sqrt{(2\pi )^{N}\det \mathscr {C}}}e^{-\frac{1}{2}\langle \mathscr {C}^{-1}z,z\rangle } \end{aligned}$$

is the Gaussian kernel on ${\mathbb {R}}^{N}$ and

$$\begin{aligned} \mathscr {C}^{(s,v)}(t,T)&:= \int _{t}^{T} e^{(T-\tau ) B} A^{(s,{v})} (\tau ) e^{(T-\tau ) B^*}d\tau , \end{aligned}$$

(2.2)

$$\begin{aligned} A^{(s,v)}(\tau )&:=\begin{pmatrix} A_0(\tau ,e^{(\tau -s)B}v)&{} 0 \\ 0 &{} 0\end{pmatrix},\qquad A_{0}=\left( a_{ij}\right) _{i,j=1,\ldots ,d}. \end{aligned}$$

(2.3)

Remark 2.1

Clearly $\Gamma ^{(s,v)}(t,x;T,y)$ is of class $C^{\infty }$ as a function of x and only absolutely continuous along the integral curves of Y as a function of (t, x).

Remark 2.2

In the particular case of $A_{0}\equiv \delta I_{d}$ for some $\delta >0$, where $I_{d}$ is the $(d\times d)$-identity matrix, the Kolmogorov operator $\mathscr {A}^{(s,v)} + Y$ reads as in (1.3) and its fundamental solution reduces to

$$\begin{aligned} \Gamma ^{\delta }(t,x;T,y):=\textbf{G}(\delta \mathscr {C}(T-t),y-e^{(T-t)B}x), \end{aligned}$$

(2.4)

with

$$\begin{aligned} \mathscr {C}(t)= \int _{0}^{t} e^{(t-\tau ) B} \begin{pmatrix} I_{d} &{} 0 \\ 0 &{} 0\end{pmatrix} e^{(t-\tau ) B^*}d\tau . \end{aligned}$$

(2.5)

Proceeding as in [29, 35], we define the parametrix function $\textbf{P}(t,x;T,y)$ as

$$\begin{aligned} \textbf{P}(t,x;T,y):=\Gamma ^{(T,y)}(t,x;T,y),\qquad (T,y)\in \mathscr {S}_{T_0}, \ (t,x)\in \mathscr {S}_T, \end{aligned}$$

(2.6)

and we refer to it as to the time-dependent parametrix in order to emphasize the fact that it is obtained by freezing only the space variable of the coefficients of $\mathscr {A}$.

Remark 2.3

Since $\Gamma ^{(s,v)}$ is the fundamental solution of $\mathscr {A}^{(s,v)} + Y$, we have

$$\begin{aligned} (\mathscr {A}^{(T,y)}+Y) \textbf{P}(\cdot ,\cdot ;T,y) = 0 \quad \text {on } \mathscr {S}_T, \end{aligned}$$

(2.7)

in the sense of Definition 1.5, for any $(T,y)\in \mathscr {S}_{T_0}$.

Remark 2.4

In [7], where the variable coefficients of $\mathscr {A}$ are assumed intrinsically Hölder continuous in space and time, the parametrix is defined as the fundamental solution of the operator obtained by freezing the second order coefficients of $\mathscr {A}$ in both time and space variables, i.e.

$$\begin{aligned} \frac{1}{2}\sum _{i,j=1}^{d} a_{ij}(s,v)\partial _{x_i x_j} + Y. \end{aligned}$$

As we shall see below, the choice of freezing the coefficients only in the space variable, along the integral curve of Y as in (2.1), is necessary in order to deal with the lack of regularity in the time variable.

Once the parametrix function is defined, the parametrix construction prescribes that a fundamental solution of $\mathscr {A}+Y$ is sought in the form

$$\begin{aligned} p(t,x;T,y)= \textbf{P}(t,x;T,y)+ \int _t^T\int _{\mathbb {R}^N} \textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y)d\eta d\tau , \end{aligned}$$

(2.8)

where $\phi$ is an unknown function. We now perform some heuristic computations that will lead to a fixed-point equation for $\phi$. Assuming that $p(t,x;T,y)$ in (2.8) is a fundamental solution of $\mathscr {A}+Y$, we obtain

$$\begin{aligned} 0=(\mathscr {A}+Y) p(t,x;T,y)= & {} (\mathscr {A}+Y)\textbf{P}(t,x;T,y)+(\mathscr {A}+Y)\\{} & {} \times \int _t^T\int _{\mathbb {R}^N} \textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y) d\eta d\tau . \end{aligned}$$

Furthermore, by formally differentiating and employing $p(t,x;t, \cdot )= \delta _x$ we also have

$$\begin{aligned} \begin{aligned}&(\mathscr {A}+Y)\int _t^T\int _{\mathbb {R}^N} \textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y) d\eta d\tau \\&\quad = \int _t^T\int _{\mathbb {R}^N} (\mathscr {A}+Y)\textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y) d\eta d\tau - \phi (t,x;T,y). \end{aligned} \end{aligned}$$

Therefore, $\phi (t,x;T,y)$ must solve the Volterra integral equation

$$\begin{aligned} \phi (t,x;T,y)= (\mathscr {A}+Y)\textbf{P}(t,x;T,y)+\int _t^T\int _{\mathbb {R}^N} (\mathscr {A}+Y)\textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y) d\eta d\tau .\nonumber \\ \end{aligned}$$

(2.9)

Now, owing to Remark 2.3, Eq. (2.9) can be written as

$$\begin{aligned} \phi (t,x;T,y)= & {} (\mathscr {A}-\mathscr {A}^{(T,y)}) \textbf{P}(t,x;T,y)+\int _t^T\int _{\mathbb {R}^N} (\mathscr {A}-\mathscr {A}^{(\tau ,\eta )})\nonumber \\{} & {} \textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y) d\eta d\tau , \end{aligned}$$

(2.10)

whose solution can be determined by an iterative procedure, which leads to the series representation

$$\begin{aligned} \phi (t,x;T,y)=\sum \limits _{k\ge 1} \phi _k(t,x;T,y) \end{aligned}$$

(2.11)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _1(t,x;T,y):= \left( \mathscr {A}-\mathscr {A}^{(T,y)}\right) \textbf{P}(t,x;T,y),\\ \displaystyle \phi _{k+1}(t,x;T,y):= \int _t^T\int _{\mathbb {R}^N} (\mathscr {A}-\mathscr {A}^{(\tau ,\eta )}) \textbf{P}(t,x;\tau ,\eta ) \phi _k(\tau ,\eta ;T,y) d\eta d\tau , \qquad k\in \mathbb {N}. \end{array}\right. }\nonumber \\ \end{aligned}$$

(2.12)

In order to make the previous arguments rigorous one has to prove that:

• The series defined by (2.11)–(2.12) is uniformly convergent on $\mathscr {S}_T$. At this stage one also obtains a uniform upper bound and a Hölder estimate for $\phi$;

• p defined by (2.8) is actually a fundamental solution of $\mathscr {A}+Y$. In this step one also establishes the Gaussian estimates on $p$ and its derivatives that appear in Theorem 1.1.

2.1 Convergence of the series and estimates on $\phi$

Proposition 2.1

For every $(T,y)\in \mathscr {S}_{T_0}$ the series in (2.11) converges uniformly in $(t,x)\in \mathscr {S}_T$ and the function $\phi =\phi (t,x;T,y)$ solves the integral Eq. (2.10) on $\mathscr {S}_T$. Furthermore, for every $\varepsilon >0$ and $0<\delta <\alpha$, there exists a positive constant C, only dependent on $T_0, \mu , B, \delta ,\alpha , \varepsilon$ and the $\alpha$-Hölder norms of the coefficients, such that

$$\begin{aligned} \left| \phi (t,x;T,y)\right|&\le \frac{C}{(T-t)^{1-\frac{\alpha }{2}}}\Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(2.13)

$$\begin{aligned} \left| \phi (t,x;T,y)-\phi (t,v;T,y)\right|&\le \frac{C|x-v|^{\alpha -\delta }_B}{(T-t)^{1-\frac{\delta }{2}}}\left( \Gamma ^{\mu +\varepsilon }(t,x;T,y)+\Gamma ^{\mu +\varepsilon }(t,v;T,y)\right) , \end{aligned}$$

(2.14)

for any $(T,y)\in \mathscr {S}_{T_0}$ and $(t,x),(t,v)\in \mathscr {S}_{T}$.

To avoid repeating the arguments already used in [7], we limit ourselves to highlighting the parts of the proof that differ significantly from the classical case.

Proof

We first prove that there exists a positive $\kappa$ such that

$$\begin{aligned} | (\mathscr {A}-\mathscr {A}^{(T,y)} ) \textbf{P}(t,x;T,y) |\le & {} \frac{ \kappa }{(T-t)^{1-\alpha /2}}\Gamma ^{\mu +\varepsilon }(t,x;T,y), \nonumber \\{} & {} \qquad (T,y)\in \mathscr {S}_{T_0},\ (t,x)\in \mathscr {S}_{T}. \end{aligned}$$

(2.15)

Assume for simplicity that $a_i,a \equiv 0$, the general case being a straightforward extension. By definition (2.1) we have

$$\begin{aligned} |(\mathscr {A}-\mathscr {A}^{(T,y)}) \textbf{P}(t,x;T,y)|&\le \frac{1}{2}\sum _{i,j=1}^{d} | a_{ij}(t,x) - a_{ij}(t,e^{-(T-t)B}y)| \nonumber \\&\quad \times | \partial _{x_i x_j} \textbf{P}(t,x;T,y)|\le \end{aligned}$$

(2.16)

(by the Hölder regularity of $a_{ij}$ and the Gaussian estimate (A.11))

$$\begin{aligned}&\le \kappa \frac{| x - e^{-(T-t)B}y |^{\alpha }_{B}}{T-t}\,\Gamma ^{\mu +\varepsilon /2}(t,x;T,y). \end{aligned}$$

(2.17)

The estimate (A.9) then yields (2.15).

For any $(T,y)\in \, \mathscr {S}_{T_0}$ and $(t,x)\in \mathscr {S}_T$, (2.12) and (2.15) imply

$$\begin{aligned} | \phi _1(t,x;T,y) | \le \frac{ \kappa }{(T-t)^{1-\alpha /2}}\,\Gamma ^{\mu +\varepsilon }(t,x;T,y) \end{aligned}$$

and

$$\begin{aligned} | \phi _{2}(t,x;T,y) |&\le \int _t^T\int _{\mathbb {R}^N} \left| \left( \mathscr {A}-\mathscr {A}^{(\tau ,\eta )}\right) \textbf{P}(t,x;\tau ,\eta )\right| \times | \phi _1(\tau ,\eta ;T,y)| d\eta d\tau \\ {}&\le \kappa ^2 \int _t^T \frac{ 1}{(\tau -t)^{1-\alpha /2}} \frac{ 1}{(T-\tau )^{1-\alpha /2}}\\&\quad \times \int _{\mathbb {R}^N} \Gamma ^{\mu +\varepsilon }(t,x;\tau ,\eta )\Gamma ^{\mu +\varepsilon }(\tau ,\eta ;T,y) d\eta d\tau = \end{aligned}$$

(by the Chapman–Kolmogorov identity and solving the integral in $d\tau$)

$$\begin{aligned}&= \kappa ^2\, \frac{ \Gamma ^2_{\text {Euler}}\left( \frac{\alpha }{2}\right) }{ (T-t)^{1 - \alpha }\Gamma _{\text {Euler}}( \alpha ) } \Gamma ^{\mu +\varepsilon }(t,x;T,y). \end{aligned}$$

Proceeding by induction, it is straightforward to verify that

$$\begin{aligned} | \phi _{n}(t,x;T,y) | \le \kappa ^{n}\frac{\Gamma _{\text {Euler}}^{n}\left( \frac{\alpha }{2}\right) }{(T-t)^{1-\frac{\alpha }{2}}\Gamma _{\text {Euler}} (\frac{\alpha }{2}) }\Gamma ^{\mu +\varepsilon }(t,x;T,y), \qquad n\in \mathbb {N}. \end{aligned}$$

This proves the uniform convergence of the series on $\mathscr {S}_T$, which in turn implies that $\phi$ satisfies (2.10), as well as the estimate (2.13).

The proof of (2.14) is a technical modification of the arguments in [7, Lemma 6.1], which is necessary to account for the different parametrix function. For sake of brevity, we leave the details to the reader. $\square$

Remark 2.5

The proof above is particularly informative to understand the choice of the parametrix function in relation to the lack of regularity of the coefficients with respect to the time variable. In particular, in passing from (2.17) to (2.15), we take advantage of the increment $| x - e^{-(T-t)B}y |_B^{\alpha }$ in order to recover the integrability of the singularity in time. In the classical case, namely when the coefficient $a_{ij}$ is also Hölder continuous in time, the parametrix function is obtained by freezing the variable coefficients in both space and time (see Remark 2.4). In (2.16), this choice leads to increments of type

$$\begin{aligned} \big | a_{ij}(t,x) - a_{ij}( T, y ) \big |, \end{aligned}$$

which is clearly not helpful if $a_{ij}$ does not exhibit any regularity in time.

Furthermore, note that the coefficients have to be frozen in the space variable along the integral curve of Y: freezing the coefficients at a fixed point y would yield an increment of type $| x - y |_B^{\alpha }$ in (2.17), which does not allow to employ the Gaussian estimates in (A.9) to control the singularity.

2.2 Proof that p is a fundamental solution and Gaussian bounds

We now prove the first part of Theorem 1.1, concerning the existence of the fundamental solution of $\mathscr {A}+Y$. This is achieved by proving that the candidate solution $p=p(t,x;T,y)$ defined through (2.8) satisfies points i) and ii) of Definition 1.6. The innovative part of the proof consists in showing point i), which is $p(\cdot ,\cdot ;T,y)$ solves the equation

$$\begin{aligned} \mathscr {A}u +Y u=0\quad \hbox { on}\ \mathscr {S}_T \end{aligned}$$

(2.18)

in the integral sense of Definition 1.5. Once more, we provide the details of the parts that significantly depart from the classical case.

For any $(T,y)\in \mathscr {S}_{T_0}$, let us rewrite $p(t,x;T,y)$ as

$$\begin{aligned} p(t,x;T,y) = \textbf{P}(t,x;T,y) + \Phi (t,x;T,y), \qquad (t,x)\in \mathscr {S}_T, \end{aligned}$$

where we set

$$\begin{aligned} \Phi (t,x;T,y):=\int _t^T\int _{\mathbb {R}^N} \textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y)d\eta d\tau . \end{aligned}$$

(2.19)

The strategy of the proof is to first show that $p$ possesses the regularity required in order to qualify as a fundamental solution, and then to check that it actually solves Eq. (2.18). As pointed out in Remark 2.7, the parametrix $\textbf{P}=\textbf{P}(t,x;T,y)$ is an integral solution to (2.7). In particular, it is smooth in the variable x and absolutely continuous along Y. As for $\Phi =\Phi (t,x;T,y)$, the next result shows that it is twice differentiable w.r.t. $x_1,\ldots ,x_{d}$ and states some Gaussian bounds on the derivatives.

Proposition 2.2

For any $(T,y)\in \mathscr {S}_{T_0}$, $(t,x)\in \mathscr {S}_T$ and $i,j = 1,\ldots ,d$, there exist

$$\begin{aligned} \partial _{x_i } \Phi (t,x;T,y)&= \int _t^T\int _{\mathbb {R}^N} \partial _{x_i} \textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y)d\eta d\tau ,\\ \partial _{x_i x_j } \Phi (t,x;T,y)&= \int _t^T\int _{\mathbb {R}^N} \partial _{x_{i}x_{j}} \textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y)d\eta d\tau , \end{aligned}$$

and, for any $\varepsilon >0$ we have

$$\begin{aligned} \left| {\Phi }(t,x;T,y)\right|&\le C (T-t)^{\frac{\alpha }{2}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \\ \left| \partial _{x_i}{\Phi }(t,x;T,y)\right|&\le \frac{C}{(T-t)^{\frac{1-\alpha }{2}}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \\ \left| \partial _{x_i x_j}{\Phi }(t,x;T,y)\right|&\le \frac{C}{(T-t)^{\frac{2-\alpha }{2}}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

where C denotes a positive constant, only dependent on $T_0, \mu , B,\alpha , \varepsilon$ and the $\alpha$-Hölder norms of the coefficients.

Proof

By the definition of $\Phi$ in (2.19) we have

$$\begin{aligned} \Phi (t,x;T,y) = \int _t^T J(t,x;\tau ;T,y) d\tau , \end{aligned}$$

with J defined as in (B.1). The potential estimates of Proposition B.1 upon integrating in $\tau$, yield the result. $\square$

The following result shows that $\Phi (\cdot ,\cdot ;T,y)$ is also Lipschitz continuous along the integral curves of Y.

Lemma 2.1

For every $(T,y)\in \mathscr {S}_{T_0}$ and $(t,x)\in \mathscr {S}_T$, we have

$$\begin{aligned} \Phi \big (s,e^{(s-t)B}x;T,y\big )-\Phi (t,x;T,y)=-\int _t^s F(\tau ,x;T,y)d\tau , \qquad s\in [t,T[, \end{aligned}$$

where

$$\begin{aligned} F(\tau ,x;T,y):= & {} \int _\tau ^T\int _{\mathbb {R}^N} \mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big )\phi (r,\eta ;T,y)d\eta dr \nonumber \\{} & {} + \phi \big (\tau ,e^{(\tau -t)B}x;T,y\big ). \end{aligned}$$

(2.20)

Proof

For any $s\in [t,T[$ one can write

$$\begin{aligned} \begin{aligned}&\Phi \big (s,e^{(s-t)B}x;T,y\big )-\Phi (t,x;T,y)\\&= \underbrace{\int _{s}^{T}\int _{\mathbb {R}^N} \left( \textbf{P}\big (s,e^{(s-t)B}x;r,\eta \big )-\textbf{P}(t,x;r,\eta )\right) \phi (r,\eta ;T,y)d\eta dr} _{=:G(t,x)}\\&\quad -\underbrace{\int _{t}^{s}\int _{\mathbb {R}^N} \textbf{P}(t,x;r,\eta )\phi (r,\eta ;T,y) d\eta dr}_{=:H(t,x)}. \end{aligned} \end{aligned}$$

First, we study the term G(t, x). Remark 2.3 yields

$$\begin{aligned} G(t,x)={\int _{s}^{T}\int _{\mathbb {R}^N} \left( \int _t^{s}-\mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big )d\tau \right) \phi (r,\eta ;T,y)d\eta dr}. \end{aligned}$$

By (A.11) and Assumption 1.3, for every $\varepsilon >0$ we have

$$\begin{aligned} \left| \mathscr {A}^{(r,\eta )}\textbf{P}(\tau ,e^{(\tau -t)B}x;r,\eta ) \right| \le \frac{C}{r-\tau } \Gamma ^{\mu +\varepsilon }(\tau ,e^{(\tau -t)B}x;r,\eta ), \qquad t< \tau<s< r< T. \end{aligned}$$

Therefore, considering also (2.13), for any $r\in \,]s,T]$, the function

$$\begin{aligned} (\tau ,\eta )\mapsto | \mathscr {A}^{(r,\eta )}\textbf{P}(\tau ,e^{(\tau -t)B}x;r,\eta ) \phi (r,\eta ;T,y) | \end{aligned}$$

is integrable on $[t,s]\times \mathbb {R}^N$. Thus Fubini’s theorem yields

$$\begin{aligned}{} & {} \int _{\mathbb {R}^N}\left( \int _t^{s}\mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big ) d\tau \right) \phi (r,\eta ;T,y) d\eta \\{} & {} \quad = \int _t^{s} \int _{\mathbb {R}^N} \mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big )\phi (r,\eta ;T,y)d\eta d\tau . \end{aligned}$$

Moreover, by the potential estimate (B.3) with $\delta =\frac{\alpha }{2}$, for any $\varepsilon >0$ we have

$$\begin{aligned} \begin{aligned}&\left| \int _{\mathbb {R}^N}\mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big )\phi (r,\eta ;T,y)d\eta \right| \\&\le {\frac{C}{(T-r)^{1-\frac{\alpha }{4}}(r-\tau )^{1-\frac{\alpha }{4}}} }\Gamma ^{\mu +\varepsilon }\big (\tau ,e^{(\tau -t)B}x;T,y\big ). \end{aligned} \end{aligned}$$

(2.21)

As the right-hand side term is integrable over $[t,s]\times [s,T]$ as a function of $(\tau ,r)$, we can apply once more Fubini’s theorem to conclude that

$$\begin{aligned} G(t,x) =-\int _t^{s} \int _{s}^{T} \int _{\mathbb {R}^N} \mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big )\phi (r,\eta ;T,y)d\eta dr d\tau .\nonumber \\ \end{aligned}$$

(2.22)

Let us consider H(t, x). For every $n\in \mathbb {N}$, we define $\varepsilon _n(r):=\frac{1}{n}(r-t)$. Note that, for every $r\in \,]t,s[$ we have $r-\varepsilon _n(r)\ge t$. Hence

$$\begin{aligned} \begin{aligned} H(t,x) =&\underbrace{ \int _{t}^{s}\int _{\mathbb {R}^N} \textbf{P}\big (r-\varepsilon _n(r),e^{(r-\varepsilon _n(r)-t)B}x;r,\eta \big )\phi (r,\eta ;T,y) d\eta dr }_{=:{\tilde{H}}_n(t,x)}\\&-\underbrace{\int _{t}^{s}\int _{\mathbb {R}^N} \left( \textbf{P}\big (r-\varepsilon _n(r),e^{(r-\varepsilon _n(r)-t)B}x;r,\eta \big )-\textbf{P}(t,x;r,\eta )\right) \phi (r,\eta ;T,y) d\eta dr} _{ =:H_n(t,x)}. \end{aligned} \end{aligned}$$

Once more, Remark 2.3 yields

$$\begin{aligned} H_{n}(t,x)&= \int _{t}^{s}\int _{\mathbb {R}^N}\bigg ( \int _{t}^{r-\varepsilon _n(r)}\mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big )d\tau \bigg ) \phi (r,\eta ;T,y)d\eta dr \end{aligned}$$

(applying Fubini’s theorem as above)

$$\begin{aligned}&= \int _{t}^{s} \int _{t}^{r-\varepsilon _n(r)} \int _{\mathbb {R}^N}\mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big ) \phi (r,\eta ;T,y)d\eta d\tau dr \end{aligned}$$

(setting $\delta _n(\tau )=\frac{\tau -t}{n-1}$ and applying Fubini’s theorem again)

$$\begin{aligned}&= \int _{t}^{s-\varepsilon _n(s)}\int _{\tau +\delta _n(\tau )}^{s}\int _{\mathbb {R}^N} \mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big ) \phi (r,\eta ;T,y)d\eta dr d\tau \end{aligned}$$

(by (2.21) and applying Lebesgue’s dominated convergence theorem)

$$\begin{aligned}&\xrightarrow [n\rightarrow \infty ]{} \int _{t}^{s}\int _{\tau }^{s} \int _{\mathbb {R}^N} \mathscr {A}^{(r,\eta )}\textbf{P}\big (\tau ,e^{(\tau -t)B}x;r,\eta \big ) \phi (r,\eta ;T,y)d\eta dr d\tau . \end{aligned}$$

On the other hand, by the potential estimate (B.2), for any $n\in \mathbb {N}$ we have

$$\begin{aligned}{} & {} \left| \int _{\mathbb {R}^N} \textbf{P}\big (r-\varepsilon _n(r),e^{(r-\varepsilon _n(r)-t)B}x;r,\eta \big )\phi (r,\eta ;T,y) d\eta \right| \le C\frac{\Gamma ^{\mu +\varepsilon }(\tau ,e^{(\tau -t)B}x;T,y)}{(T-r)^{1-\frac{\alpha }{2}}(T-r)^{\frac{Q}{2}}},\\{} & {} \qquad r\in [t,s]. \end{aligned}$$

Thus Lebesgue’s dominated convergence theorem yields

$$\begin{aligned} \lim _{n\rightarrow \infty } {\tilde{H}}_n(t,x)&= \int _t^{s} \lim _{n\rightarrow \infty } \int _{\mathbb {R}^N} \textbf{P}\big (r-\varepsilon _n(r),e^{(r-\varepsilon _n(r)-t)B}x;r,\eta \big ) \phi (r,\eta ;T,y) d\eta \, dr \end{aligned}$$

(by (2.24), since $\eta \mapsto \phi (r,\eta ;T,y)$ is a bounded and continuous function for every $r\in [t,s]$)

$$\begin{aligned}&=\int _t^s \phi \big (r,e^{(r-t)B}x;T,y\big ) dr. \end{aligned}$$

We have proved that

$$\begin{aligned} H(t,x)= & {} \int _{t}^{s}\int _{\tau }^{s} \int _{\mathbb {R}^N} \mathscr {A}^{(r,\eta )}\textbf{P}(\tau ,e^{(\tau -t)B}x;r,\eta ) \phi (r,\eta ;T,y)d\eta dr d\tau \\{} & {} +\int _t^s \phi (\tau ,e^{(\tau -t)B}x;T,y) d\tau . \end{aligned}$$

This and (2.22) prove the statement. $\square$

We are now in the position to prove Theorem 1.1, namely that $p=p(t,x;T,y)$ defined by (2.8) is a fundamental solution of $\mathscr {A}+ Y$ in the sense of definition Definition 1.6, and that the Gaussian bounds from (1.13) to (1.16) are satisfied.

Proof of Theorem 1.1

Let $p=p(t,x;T,y)$ be defined by (2.8).

Step 1. We show that $p=p(t,x;T,y)$ satisfies point i) of Definition 1.6, namely that $p(\cdot ,\cdot ;T,y)$ is an integral solution to (2.18) on $\mathscr {S}_T$ in the sense of Definition 1.5. By Lemma 2.1, we have

$$\begin{aligned}&p\big (s,e^{(s-t)B}x;T,y\big )-p(t,x;T,y)\nonumber \\&= \textbf{P}(s,e^{(s-t)B}x;T,y)-\textbf{P}(t,x;T,y)+\Phi (s,e^{(s-t)B}x;T,y)\nonumber \\&\quad -\Phi (t,x;T,y)\nonumber \\&=- \int _t^{s} \Big ( \mathscr {A}^{(r,\eta )}\textbf{P}(\tau ,e^{(\tau -t)B}x;r,\eta ) + F(\tau ,x;T,y) \Big ) d\tau . \end{aligned}$$

(2.23)

Furthermore, by (2.20) and since $\phi (t,x;T,y)$ solves the integral Eq. (2.9), we obtain

$$\begin{aligned}&\mathscr {A}^{(r,\eta )}\textbf{P}(\tau ,e^{(\tau -t)B}x;r,\eta ) + F(\tau ,x;T,y) = \mathscr {A}\textbf{P}(\tau ,e^{(\tau -t)B}x;T,y) \\&\quad + \int _{\tau }^{T}\int _{\mathbb {R}^N}\mathscr {A}\textbf{P}(\tau ,e^{(\tau -t)B}x;r,\eta )\phi (r,\eta ;T,y)d\eta dr \end{aligned}$$

(by Proposition 2.2)

$$\begin{aligned}&= \mathscr {A}\textbf{P}(\tau ,e^{(\tau -t)B}x;T,y)+\mathscr {A}\Phi (\tau ,e^{(\tau -t)B}x;T,y) = \mathscr {A}p(\tau ,e^{(\tau -t)B}x;T,y) , \end{aligned}$$

which, together with (2.23), concludes the proof.

Step 2. We show that $p=p(t,x;T,y)$ satisfies point ii) of Definition 1.6. In light of the estimate (2.13), it is straightforward to see that

$$\begin{aligned} | \Phi (t,x;T,y) | \le C (T-t)^{\frac{\alpha }{2}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \qquad (T,y)\in \mathscr {S}_{T_0}, \ (t,x)\in \mathscr {S}_T. \end{aligned}$$

Therefore, it is enough to prove that, for any fixed $(T,y)\in ]0,T_0[ \times \mathbb {R}^N$, we have

$$\begin{aligned} \lim _{\begin{array}{c} (t,x)\rightarrow (T,y)\\ tau<T \end{array}} \int _{\mathbb {R}^N}\textbf{P}(t,x;T,\eta )f(\eta )d\eta =f(y), \qquad f\in C_b(\mathbb {R}^N). \end{aligned}$$

(2.24)

Recalling the definition of the parametrix $\textbf{P}$, we add and subtract to obtain

$$\begin{aligned} \begin{aligned} \int _{\mathbb {R}^N}\textbf{P}(t,x;T,\eta )f(\eta )d\eta&=\int _{\mathbb {R}^N} \Gamma ^{(T,\eta )} (t,x;T,\eta )f(\eta )d\eta \\&=\int _{\mathbb {R}^N}\Gamma ^{(T,y)} (t,x;T,\eta )f(\eta )d\eta \\&\quad + \underbrace{\int _{\mathbb {R}^N}\left( \Gamma ^{(T,\eta )} (t,x;T,\eta )-\Gamma ^{(T,y)} (t,x;T,\eta )\right) f(\eta )d\eta }_{=:J(t,x)}. \end{aligned} \end{aligned}$$

Furthermore, by estimate (A.12), for every $\varepsilon >0$ one has

$$\begin{aligned} |J(t,x)|\le C\int _{\mathbb {R}^N} |y-\eta |_B^\alpha \Gamma ^{\mu +\varepsilon }(t,x;T,\eta )d\eta . \end{aligned}$$

Eventually, (2.24) follows from classical arguments.

Step 3. We show the upper Gaussian bounds (1.13)–(1.14)–(1.15) for p and its derivatives. The proof of the lower Gaussian bound (1.16) is similar to that of Theorem 4.7 in [34] and Section 5.1.4. in [35], thus we omit it for sake of brevity.

The Gaussian bounds of Proposition A.1 and the definition of parametrix (2.6) yield the estimates (1.13)–(1.14)–(1.15) for $\textbf{P}=\textbf{P}(t,x;T,y)$. The estimates of Proposition 2.2 and the fact that $p = \textbf{P}+ \Phi$ conclude the proof. $\square$

Remark 2.6

Any integral solution u to Eq. (1.11) on $\mathscr {S}_T$ in the sense of Definition 1.5, is Lie differentiable along Y almost everywhere on $\mathscr {S}_T$. Indeed, the set $H_T$ of $(t,x)\in \mathscr {S}_T$ such that Yu(t, x) in (1.12) exists finite, is measurable as the limit

$$\begin{aligned} \limsup _{\tau \rightarrow t^+} \frac{u\big ( \tau , e^{(\tau - t) B} x \big ) - u(t,x)}{\tau - t} \end{aligned}$$

is a measurable function of (t, x) and the same holds for $\liminf$. This is a straightforward consequence of the continuity of u along the integral curves of Y. The fact that $H_T$ has null Lebesgue measure stems from Fubini’s theorem, as u is absolutely continuous along the integral curves of Y and the map

$$\begin{aligned} (\tau ,y)\mapsto (\tau ,e^{\tau B} y) \end{aligned}$$

is a diffeomorphism on $\mathscr {S}_T$.

3 Regularity of the fundamental solution

In this section we prove Theorem 1.2. Since $p(\cdot ,\cdot ;T,y)$ can be represented as in (2.8), we need to study the regularity of $\textbf{P}(\cdot ,\cdot ;T,y)$ and $\Phi (\cdot ,\cdot ;T,y)$. While the former term can be easily dealt with by means of the Gaussian estimates of Appendix A, the latter has to be treated more carefully. We start with the proof of Theorem 1.2, which is based on the regularity estimates for $\Phi (\cdot ,\cdot ;T,y)$ and $\textbf{P}(\cdot ,\cdot ;T,y)$ proved in Sects. 3.1 and 3.2, respectively.

Proof of Theorem 1.2

Let $\beta <\alpha$. For fixed $(T,y)\in \mathscr {S}_{T_0}$, we set

$$\begin{aligned} f(t,x):=p(t,x;T,y), \qquad (t,x) \in {\mathscr {S}}_T. \end{aligned}$$

We first note that, by definition of fundamental solution, (1.8) is satisfied with $Yf = - \mathscr {A}f$. Furthermore, for any $t\in ]0,T[$, by (1.9) and the representation (2.8) we have

$$\begin{aligned} \Vert f \Vert _{C_{B}^{2,\beta }(\mathscr {S}_{t})}&= N_{\textbf{P},1} + N_{\textbf{P},2} + N_{\Phi ,1} + N_{\Phi ,2} , \end{aligned}$$

where

$$\begin{aligned} N_{\textbf{P},1}&:= \sum _{i=1}^{d} \Vert \partial _{x_i} \textbf{P}(\cdot ,\cdot ;T,y) \Vert _{C^{1+\beta }_{Y}(\mathscr {S}_t)} +\sum \limits _{i,j=1}^{d} \big ( \Vert \partial _{x_i x_j} \textbf{P}(\cdot ,\cdot ;T,y) \Vert _{C^{\beta }_{Y}(\mathscr {S}_t)}\\&\quad + \Vert \partial _{x_i x_j} \textbf{P}(\cdot ,\cdot ;T,y) \Vert _{C^{\beta }_{d}(\mathscr {S}_t)} \big ), \\ N_{\textbf{P},2}&:= \Vert \mathscr {A}\textbf{P}(\cdot ,\cdot ;T,y) \Vert _{L^{\infty }([0,t];C^{\beta }_{B}({\mathbb {R}}^{N}))} , \\ N_{\Phi ,1}&:= \sum _{i=1}^{d} \Vert \partial _{x_i} \Phi (\cdot ,\cdot ;T,y) \Vert _{C^{1+\beta }_{Y}(\mathscr {S}_t)}+\sum \limits _{i,j=1}^{d} \big ( \Vert \partial _{x_i x_j} \Phi (\cdot ,\cdot ;T,y) \Vert _{C^{\beta }_{Y}(\mathscr {S}_t)} \\&\quad + \Vert \partial _{x_i x_j} \Phi (\cdot ,\cdot ;T,y) \Vert _{C^{\beta }_{d}(\mathscr {S}_t)} \big ),\\ N_{\Phi ,2}&:= \Vert \mathscr {A}\Phi (\cdot ,\cdot ;T,y) \Vert _{L^{\infty }([0,t];C^{\beta }_{B}({\mathbb {R}}^{N}))} . \end{aligned}$$

Now, the estimates of Lemma 3.2 yield

$$\begin{aligned} N_{\textbf{P},1} \le \frac{C}{(T-t)^{\frac{Q+{2+\beta }}{2}}}. \end{aligned}$$

(3.1)

To bound $N_{\textbf{P},2}$, first fix $i,j=1,\ldots , d$ and note that, by estimate (A.11), we obtain

$$\begin{aligned} \sup _{x\in \mathbb {R}^N} \big | \partial _{x_i x_j} \textbf{P}(s,x;T,y) \big | \le \frac{C}{(T-t)^{\frac{Q+2}{2}}}, \qquad s<t. \end{aligned}$$

(3.2)

Furthermore, (3.1) combined with Remark 1.1 yield

$$\begin{aligned} \sup _{x,v\in \mathbb {R}^N} \frac{| \partial _{x_i x_j} \textbf{P}(s,x;T,y) - \partial _{x_i x_j} \textbf{P}(s,v;T,y)| }{ |x - v|^{\beta }_B } \le \frac{C}{(T-t)^{\frac{Q+{2+\beta }}{2}}}, \qquad s<t.\nonumber \\ \end{aligned}$$

(3.3)

Thus, by (3.2)–(3.3) we obtain

$$\begin{aligned} \Vert \partial _{x_i x_j} \textbf{P}(s,\cdot ;T,y) \Vert _{C^{\beta }_{B}({\mathbb {R}}^{N})} \le \frac{C}{(T-t)^{\frac{Q+{2+\beta }}{2}}}, \qquad s<t, \end{aligned}$$

which in turn implies

$$\begin{aligned} \Vert \partial _{x_i x_j} \textbf{P}(\cdot ,\cdot ;T,y) \Vert _{L^{\infty }([0,t];C^{\beta }_{B}({\mathbb {R}}^{N}))} \le \frac{C}{(T-t)^{\frac{Q+{2+\beta }}{2}}}. \end{aligned}$$

This, together with Assumption 1.3, prove

$$\begin{aligned} N_{\textbf{P},2} \le \frac{C}{(T-t)^{\frac{Q+{2+\beta }}{2}}}. \end{aligned}$$

The bound for $N_{\Phi ,1}$ stems from the estimates of Proposition 3.1, which yield

$$\begin{aligned} N_{\Phi ,1} \le \frac{C}{(T-t)^{\frac{Q+{2-(\alpha -\beta )}}{2}}} \le \frac{C}{(T-t)^{\frac{Q+{2+\beta }}{2}}}. \end{aligned}$$

Eventually, the bound for $N_{\Phi ,2}$ follows from the same arguments used to bound $N_{\textbf{P},2}$.

$\square$

The rest of this section is devoted to the results utilized in the proof of Theorem 1.2. It is useful to introduce the following

Notation 3.1

Let $f=f(t,x;T,y)$ be a function defined for $(T,y)\in \mathscr {S}_{T_0}$ and $(t,x)\in {\mathscr {S}}_T$, suitably differentiable w.r.t. x. For any $i =1,\ldots , N$, we set

$$\begin{aligned} \partial _{i} f(t,x;T,y):= \partial _{x_i} f(t,x;T,y), \end{aligned}$$

and we adopt analogous notations for the higher-order derivatives.

This notation is useful in order to compose partial derivatives with other functions. For instance, if $g=g(t,x)$ is a given function, then

$$\begin{aligned} \partial _{i} f\big (t,g(t,x);T,y\big ) = \partial _{z_i} f(t,z;T,y)|_{z=g(t,x)}. \end{aligned}$$

3.1 Regularity estimates of $\Phi$

Now prove the Hölder estimates for $\Phi (\cdot ,\cdot ;T,y)$. We recall that Q denotes the homogeneous dimension of ${\mathbb {R}}^{N}$ as in (1.17).

Proposition 3.1

For every $\varepsilon >0$ and $0<\beta <\alpha$ there exists a positive constant C, only dependent on $T_0,\mu , B, \varepsilon ,\alpha , \beta$ and the $\alpha$-Hölder norms of the coefficients, such that, for any $i,j,k=1,\ldots ,d$, we have

$$\begin{aligned}&\big |\partial _i\Phi (s,e^{(s-t)B}x;T,y)-\partial _i\Phi (t,x;T,y)\big |\nonumber \\&\le C(s-t)^{\frac{1+\beta }{2}} \frac{(T-t)^{{Q}/{2}}}{(T-s)^{\frac{Q+2-(\alpha -\beta ) }{2}}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(3.4)

$$\begin{aligned}&\big |\partial _{ij}\Phi (s,e^{(s-t)B}x;T,y)-\partial _{ij}\Phi (t,x;T,y)\big |\nonumber \\&\le C (s-t)^{\frac{\beta }{2}}\frac{(T-t)^{{Q}/{2}}}{(T-s)^{\frac{Q+2-(\alpha -\beta ) }{2}}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(3.5)

$$\begin{aligned}&\left| \partial _{ij}\Phi (t,x +h \textbf{e}_k ;T,y)-\partial _{ij}\Phi (t,x;T,y)\right| \nonumber \\ {}&\le C |h|^{\beta } {\frac{\Gamma ^{\mu +\varepsilon }(t,x +h \textbf{e}_k ;T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)}{(T-t)^{\frac{2- (\alpha -\beta ) }{2}}} }, \end{aligned}$$

(3.6)

for every $(T,y)\in \mathscr {S}_{T_0}$, $(t,x)\in \mathscr {S}_{T}$, $t< s<T$ and $h\in \mathbb {R}$.

The proof of estimates (3.4)–(3.5) relies on the following

Lemma 3.1

Let $(T,y)\in \mathscr {S}_{T_0}$. Then, for any $i=1,\ldots , d$, the function $u:=\partial _i \textbf{P}(\cdot ,\cdot ;T,y)$ is a strong Lie solution to the equation

$$\begin{aligned} \mathscr {A}u+ Yu = - \sum _{j=1}^{d+d_1} b_{ji} \partial _j\textbf{P}(\cdot ,\cdot ;T,y) \ \text { on }\mathscr {S}_{T}, \end{aligned}$$

in the sense of Definition 1.5.

Proof

We note that

$$\begin{aligned}{}[\partial _i,Y]\textbf{P}(t,x;T,y) = [\partial _i, \langle B x, \nabla \rangle + \partial _t ] \textbf{P}(t,x;T,y) =\sum _{j=1}^{d+d_1} b_{ji}\partial _j \textbf{P}(t,x;T,y), \end{aligned}$$

for every $x\in \mathbb {R}^N$ and for almost every $t\in [0,T[$, where, in the last equality, we used that $b_{ji}=0$ if $j>d+d_1$. While it is obvious that the previous identity holds for smooth functions of (t, x), one can directly check that $\partial _i\partial _t \textbf{P}(t,x;T,y)=\partial _t\partial _i \textbf{P}(t,x;T,y)$ and thus the identity holds for the parametrix too. Therefore, we obtain

$$\begin{aligned}&\partial _i\textbf{P}(s,e^{(s-t)B}x;\tau ,\eta )-\partial _i\textbf{P}(t,x;\tau ,\eta )\\&=\int _t^s (Y\partial _i\textbf{P})(r,e^{(r-t)B}x;\tau ,\eta )dr \\&=\int _t^s \Big ( ( \partial _iY\textbf{P})(r,e^{(r-t)B}x;\tau ,\eta )-[\partial _i,Y]\textbf{P}(r,e^{(r-t)B}x;\tau ,\eta ) \Big )dr \end{aligned}$$

(by Remark 2.3)

$$\begin{aligned} =&- \int _t^s \Big ( ( \partial _i\mathscr {A}^{(\tau ,\eta )}\textbf{P})(r,e^{(r-t)B}x;\tau ,\eta )+\sum _{j=1}^{d+d_1} b_{ji}\partial _j\textbf{P}(r,e^{(r-t)B}x;\tau ,\eta ) \Big ) dr \end{aligned}$$

(since $\partial _i\mathscr {A}^{(\tau ,\eta )}=\mathscr {A}^{(\tau ,\eta )}\partial _i$)

$$\begin{aligned} =&- \int _t^s \Big ( \big (\mathscr {A}^{(\tau ,\eta )}\partial _i\textbf{P}\big )(r,e^{(r-t)B}x;\tau ,\eta )+\sum _{j=1}^{d+d_1} b_{ji}\partial _j\textbf{P}(r,e^{(r-t)B}x;\tau ,\eta ) \Big ) dr. \end{aligned}$$

$\square$

We are now in the position to prove Proposition 3.1.

Proof of Proposition 3.1

Let $(T,y)\in \mathscr {S}_{T_0}$, $(t,x)\in \mathscr {S}_{T}$, $t< s<T$ and $h\in \mathbb {R}$ be fixed. Also fix $i,j,k\in \{1,\ldots , d\}$. First we prove (3.4). By adding and subtracting, we have

$$\begin{aligned} \begin{aligned}&\partial _i\Phi (s,e^{(s-t)B}x;T,y)-\partial _i\Phi (t,x;T,y)\\&\quad =\int _{s}^T\int _{\mathbb {R}^N} \underbrace{ \Big (\partial _i\textbf{P}(s,e^{(s-t)B}x;\tau ,\eta )-\partial _i\textbf{P}(t,x;\tau ,\eta )\Big ) }_{=: I(\tau ,\eta )} \phi (\tau ,\eta ;T,y)d\eta d\tau \\&\qquad -\underbrace{\int _{t}^{s}\int _{\mathbb {R}^N} \partial _{i}\textbf{P}(t,x;\tau ,\eta ) \phi (\tau ,\eta ;T,y)d\eta d\tau }_{=: L}. \end{aligned} \end{aligned}$$

We consider the first term. By Lemma 3.1 and swapping the integrals as in the proof of Proposition 2.1, we have

$$\begin{aligned}&\int _{s}^T\int _{\mathbb {R}^N} { I(\tau ,\eta )} \phi (\tau ,\eta ;T,y)d\eta d\tau \\&\quad = - \int _{s}^T \int _t^s \int _{\mathbb {R}^N} \bigg ( \big ( \mathscr {A}^{(\tau ,\eta )} \partial _i\textbf{P}\big )(r,e^{(r-t)B}x;\tau ,\eta ) \\&\quad \quad + \sum _{j=1}^{d+d_1} b_{ji}\partial _j\textbf{P}(r,e^{(r-t)B}x;\tau ,\eta ) \bigg ) \phi (\tau ,\eta ;T,y)d\eta dr d\tau . \end{aligned}$$

Therefore, the estimates of Proposition B.1 with $\delta = (\alpha -\beta ) /2$ yield

$$\begin{aligned}&\bigg |\int _{s}^T\int _{\mathbb {R}^N} { I(\tau ,\eta )} \phi (\tau ,\eta ;T,y)d\eta d\tau \bigg | \\&\quad \le \int _{s}^T \int _t^s \frac{C}{(T-\tau )^{1-\frac{\alpha -\beta }{4}}({\tau -r})^{\frac{3}{2}-\frac{\alpha +\beta }{4}}} \Gamma ^{\mu +\varepsilon }(r,e^{(r-t)B}x;T,y)dr d\tau \end{aligned}$$

(by a standard estimate on $\Gamma ^{\mu +\varepsilon }(r,e^{(r-t)B}x;T,y)$)

$$\begin{aligned}&\le C\underbrace{\int _{s}^T \int _t^s \frac{1}{(T-\tau )^{1-\frac{\alpha -\beta }{4}}({\tau -r})^{\frac{3}{2}-\frac{\alpha +\beta }{4}}} dr d\tau } _{=:K } \left( \frac{T-t}{T-s}\right) ^{{Q}/{2}} \Gamma ^{\mu +\varepsilon }(t,x;T,y). \end{aligned}$$

(3.7)

We now bound K:

$$\begin{aligned} K&= \int _t^s \int _{s}^T \frac{1}{(T-\tau )^{1-\frac{\alpha -\beta }{4}}({\tau -r})^{\frac{3}{2}-\frac{\alpha +\beta }{4}}} d\tau dr \\&\le \int _t^s \int _{s}^T \frac{1}{(T-\tau )^{1-\frac{\alpha - \beta }{4}}(\tau -r)^{1-\frac{\alpha - \beta }{4}}} d\tau \frac{1}{({s-r})^{\frac{1}{2}-\frac{\beta }{2}}} dr \end{aligned}$$

(solving the integral in $d \tau$)

$$\begin{aligned}&\le C \int _t^s \frac{1}{(T-r)^{1-\frac{\alpha -\beta }{2}}} \frac{1}{({s-r})^{\frac{1}{2}-\frac{\beta }{2}} }dr \le \frac{C}{(T-s)^{1-\frac{\alpha -\beta }{2}}} \int _t^s \frac{1}{({s-r})^{\frac{1 - \beta }{2}} }dr \nonumber \\&\quad \le \frac{C}{(T-s)^{1-\frac{\alpha -\beta }{2}}} (s-t)^{\frac{1+\beta }{2}}. \end{aligned}$$

(3.8)

On the other hand, estimate (B.3) with $\delta = \alpha - \beta$ yields

$$\begin{aligned} |L|&\le \int _t^s \frac{C}{(T-\tau )^{1-\frac{\alpha - \beta }{2}}(\tau -t)^{\frac{1}{2} -\frac{\beta }{2}}} d\tau \, \Gamma ^{\mu +\varepsilon }(t,x;T,y) \\&\le \frac{C}{(T-s)^{1-\frac{\alpha - \beta }{2}}} \int _t^s \frac{1}{(\tau -t)^{\frac{1-\beta }{2}}} d\tau \, \Gamma ^{\mu +\varepsilon }(t,x;T,y)\\&\le \frac{C}{(T-s)^{1-\frac{\alpha - \beta }{2}}}(s-t)^{\frac{1+\beta }{2}} \Gamma ^{\mu +\varepsilon }(t,x;T,y). \end{aligned}$$

This, together with (3.7)–(3.8), proves (3.4). Estimate (3.5) can be obtained following the same arguments.

We finally prove (3.6). By Proposition 2.2 we have

$$\begin{aligned}&\partial _{ij}(t,x +h \textbf{e}_k ;T,y) - \partial _{ij}\Phi (t,x;T,y)\\&\quad =\int _t^T \underbrace{\int _{\mathbb {R}^N}\big ( \partial _{ij}\textbf{P}(t,x +h \textbf{e}_k ;\tau ,\eta ) - \partial _{ij}\textbf{P}(t,x;\tau ,\eta )\big )\phi (\tau ,\eta ;T,y)d\eta }_{=:I(\tau )} d\tau . \end{aligned}$$

We first prove that

$$\begin{aligned}{} & {} |I(\tau )|\le C \frac{|h|^{\beta }}{(T-\tau )^{1-\frac{\alpha - \beta }{4}}({\tau -t})^{1-\frac{\alpha - \beta }{4}}}\left( \Gamma ^{\mu +\varepsilon }(t, x + h \textbf{e}_k;T,y)+\Gamma ^{\mu +\varepsilon }(t,{x};T,y)\right) , \\{} & {} \qquad \tau \in ]t,T[. \end{aligned}$$

We consider the case $\tau -t\ge h^2$. By the mean-value theorem, there exists a real ${\bar{h}}$ with $|{\bar{h}}|\le |h|$ such that

$$\begin{aligned} \left| \partial _{ij}\textbf{P}(t,x + h \textbf{e}_k;\tau ,\eta ) - \partial _{ij}\textbf{P}(t,x;\tau ,\eta )\right| =|h| \left| \partial _{ijk}\textbf{P}(t,x +{\bar{h}} \textbf{e}_k;\tau ,\eta )\right| . \end{aligned}$$

Therefore, by the estimate (B.3) with $\delta = (\alpha -\beta ) /2$, we have

$$\begin{aligned} |I(\tau )|&\le C \frac{|h|}{(T-\tau )^{1-\frac{\alpha - \beta }{4}}({\tau -t})^{\frac{3}{2}-\frac{\alpha + \beta }{4}}}\Gamma ^{\mu +\varepsilon }(t,x +{\bar{h}} \textbf{e}_k ;T,y) \end{aligned}$$

(since $\tau -t\ge h^2$)

$$\begin{aligned}&\le C \frac{|h|^{\beta }}{(T-\tau )^{1-\frac{\alpha - \beta }{4}}({\tau -t})^{1-\frac{\alpha - \beta }{4}}}\Gamma ^{\mu +\varepsilon }(t,x +{\bar{h}} \textbf{e}_k ;T,y) \end{aligned}$$

(by standard estimates on $\Gamma ^{\mu +\varepsilon }(t,x +{\bar{h}} \textbf{e}_k;T,y)$ with $\tau -t\ge h^2$)

$$\begin{aligned}&\le C \frac{|h|^{\beta }}{(T-\tau )^{1-\frac{\alpha - \beta }{4}}({\tau -t})^{1-\frac{\alpha - \beta }{4}}}\big (\Gamma ^{\mu +\varepsilon }(t, x+h \textbf{e}_k;T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)\big ). \end{aligned}$$

We now consider the case $\tau -t< h^2$. Employing triangular inequality and estimate (B.3) with $\delta = (\alpha - \beta ) /2$, we get

$$\begin{aligned} |I(\tau )|&\le \frac{C}{(T-\tau )^{1-\frac{\alpha -\beta }{4}}({\tau -t})^{1-\frac{\alpha +\beta }{4}}}\big (\Gamma ^{\mu +\varepsilon }(t, x+ h \textbf{e}_k;T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)\big ) \end{aligned}$$

(since $\tau -t<h^2$)

$$\begin{aligned}&\le C \frac{|h|^{\beta }}{(T-\tau )^{1-\frac{\alpha -\beta }{4}}({\tau -t})^{1-\frac{\alpha -\beta }{4}}} \big (\Gamma ^{\mu +\varepsilon }(t, x+ h \textbf{e}_k;T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)\big ). \end{aligned}$$

Therefore, combining the previous estimates, we obtain

$$\begin{aligned} \bigg |\int _t^T I(\tau )d\tau \bigg |&\le C{|h|^{\beta }} \int _t^T\frac{1}{(T-\tau )^{1-\frac{\alpha -\beta }{4}}({\tau -t})^{1-\frac{\alpha -\beta }{4}}}d\tau \big (\Gamma ^{\mu +\varepsilon }(t, x+ h \textbf{e}_k;T,y)\\&\quad +\Gamma ^{\mu +\varepsilon }(t,x;T,y)\big ) \\ {}&\le C{|h|^{\beta }} \frac{1}{(T-t)^{1-\frac{\alpha -\beta }{2}}} \big (\Gamma ^{\mu +\varepsilon }(t, x+ h \textbf{e}_k;T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)\big ), \end{aligned}$$

which proves (3.6). $\square$

3.2 Regularity estimates for the parametrix

We have the following Hölder estimates for $\textbf{P}$. Notice that Notation 3.1 remains in force.

Lemma 3.2

Let $0\le \beta \le \alpha$. Then for every $\varepsilon >0$ there exists a positive constant C, only dependent on $T_0,\mu , B, \varepsilon , \alpha , \beta$ and the $\alpha$-Hölder norms of the coefficients, such that for any $i,j,k=1,\ldots ,d$ we have

$$\begin{aligned} \big |\partial _i\textbf{P}(s,e^{(s-t)B}x;T,y)- \partial _i\textbf{P}(t,x;T,y)\big |&\le C(s-t)^{\frac{1+\beta }{2}}\frac{(T-t)^{{Q}/{2}}}{(T-s)^{\frac{Q+2+\beta }{2}}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(3.9)

$$\begin{aligned} \big |\partial _{ij}\textbf{P}(s,e^{(s-t)B}x;T,y)- \partial _{ij}\textbf{P}(t,x;T,y)\big |&\le C (s-t)^{\frac{\beta }{2}}\frac{(T-t)^{{Q}/{2}}}{(T-s)^{\frac{Q+2+\beta }{2}}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(3.10)

$$\begin{aligned} \big |\partial _{ij}\textbf{P}(t, x+ h \textbf{e}_k;T,y)- \partial _{ij}\textbf{P}(t,x;T,y)\big |&\le C |h|^{\beta } \frac{1}{(T-t)^{\frac{2+\beta }{2}}} \left( \Gamma ^{\mu +\varepsilon }(t, x+ h \textbf{e}_k;T,y)\right. \nonumber \\&\quad \left. +\Gamma ^{\mu +\varepsilon }(t,x;T,y)\right) , \end{aligned}$$

(3.11)

for any $(T,y)\in \mathscr {S}_{T_0}$, $(t,x)\in \mathscr {S}_{T}$, $t< s<T$ and $h\in \mathbb {R}$.

Proof

We first consider (3.9). By Lemma 3.1 we have

$$\begin{aligned} \partial _i\textbf{P}(s,e^{(s-t)B}x;T,y)-\partial _i\textbf{P}(t,x;T,y)&= - \int _t^s \Big ( \mathscr {A}^{(T,y)}\partial _i\textbf{P}(r,e^{(r-t)B}x;T,y) \\&\quad + \sum _{j=1}^{d+d_1} b_{ji}\partial _j\textbf{P}(r,e^{(r-t)B}x;T,y)\Big )dr. \end{aligned}$$

Therefore, by boundedness of the coefficients of $\mathscr {A}^{(T,y)}$ and the estimates of Proposition A.1, we obtain

$$\begin{aligned}&\big |\partial _i\textbf{P}(s,e^{(s-t)B}x;T,y)-\partial _i\textbf{P}(t,x;T,y)\big | \\&\le \int _t^s \frac{C}{(T-r)^\frac{3}{2}}\Gamma ^{\mu +\varepsilon }(r,e^{(r-t)B}x;T,y)dr\\&\le \int _t^s \frac{C}{(T-r)^\frac{3}{2}}dr\left( \frac{T-t}{T-s}\right) ^{{Q}/{2}}\Gamma ^{\mu +\varepsilon }(t,x;T,y) \end{aligned}$$

(for any $\beta \le 1$)

$$\begin{aligned}&\le C \frac{(s-t)^{\frac{1+\beta }{2}}}{(T-s)^{1+\frac{\beta }{2}}}\left( \frac{T-t}{T-s}\right) ^{{Q}/{2}} \Gamma ^{\mu +\varepsilon }(t,x;T,y). \end{aligned}$$

The proof of (3.10) is based on analogous arguments.

We finally prove (3.11). As for (3.6), we first consider the case $T-t\ge h^2$. By the mean-value theorem, there exists a real $\bar{h}$ with $|\bar{h}|\le |h|$ such that

$$\begin{aligned} \left| \partial _{ij}\textbf{P}(t, x+ h \textbf{e}_k; T, y)- \partial _{ij}\textbf{P}(t,x; T, y)\right|&= |h|\left| \partial _{ijk}\textbf{P}(t, x+{\bar{h}} \textbf{e}_k ; T, y)\right| \end{aligned}$$

(by estimate (A.11))

$$\begin{aligned}&\le C \frac{|h|}{({T-t})^{\frac{3}{2}}}\Gamma ^{\mu +\varepsilon }(t, x+{\bar{h}} \textbf{e}_k ;T,y) \end{aligned}$$

(since $T-t\ge h^2$ and by standard estimates on $\Gamma ^{\mu +\varepsilon }(t, x+{\bar{h}} \textbf{e}_k;T,y)$)

$$\begin{aligned}&\le C \frac{|h|^{\beta }}{({ T-t})^{1+\frac{\beta }{2}}}\left( \Gamma ^{\mu +\varepsilon }(t, x+ h \textbf{e}_k;T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)\right) . \end{aligned}$$

We now consider $T-t< h^2$. Employing triangular inequality and estimate (A.11) yields

$$\begin{aligned}&\left| \partial _{ij}\textbf{P}(t, x+ h \textbf{e}_k ; T, y)- \partial _{ij}\textbf{P}(t,x; T, y)\right| \\&\le \frac{C}{{T-t}}\left( \Gamma ^{\mu +\varepsilon }(t, x+ h \textbf{e}_k;T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)\right) \end{aligned}$$

(since $T-t< h^2$)

$$\begin{aligned}&\le C \frac{|h|^{\beta }}{({ T-t})^{1+\frac{\beta }{2}}}\left( \Gamma ^{\mu +\varepsilon }(t, x+ h \textbf{e}_k;T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)\right) . \end{aligned}$$

This concludes the proof of (3.11). $\square$

4 Cauchy problem

In this section we anticipate some of the results on the Cauchy problem, namely well-posedness and Schauder estimates, which can be derived by utilizing the existence and the regularity estimates on the fundamental solution. We refer the reader to [25] for the details.

Consider the Cauchy problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathscr {A}u+Yu = f &{}\text {on }\mathscr {S}_T,\\ u(T,\cdot )= g &{}\text {on }\mathbb {R}^N, \end{array}\right. } \end{aligned}$$

(4.1)

with $T>0$ being fixed hereafter.

Assumption 4.1

For some $\alpha \in ]0,1]$ and $\nu \in [0,2+\alpha ]$, we have $f\in L^{\infty }( [0,T];C^{\alpha }_{B}({\mathbb {R}}^{N}))$ and $g\in C^{\nu }_{B}({\mathbb {R}}^{N})$.

When $\nu >1$, the definition of the anisotropic space $C^{\nu }_{B}({\mathbb {R}}^{N})$ is a standard extension of that in Definition 1.1. Once more, we refer to [25] for the details.

Theorem 4.1

(Well-posedness and Schauder estimate) Under Assumptions 1.1, 1.2, 1.3 and 4.1, the function

$$\begin{aligned} u(t,x):=\int _{\mathbb {R}^N}p(t,x;T,y)g(y)dy-\int _t^T\int _{\mathbb {R}^N} p(t,x;s,y)f(s,y)dy ds \end{aligned}$$

is the unique bounded solution of the Cauchy problem (4.1), in the sense of Definition 1.5. Furthermore, for any $\beta \in ]0,\alpha [$, u satisfies

$$\begin{aligned} \Vert u \Vert _{C_{B}^{2,\beta }(\mathscr {S}_t)} \le C \big ( (T-t)^{-\frac{2+\beta -\nu }{2}} \Vert g \Vert _{C^{\nu }_{B}({\mathbb {R}}^{N})} + \Vert f \Vert _{L^{\infty }( [0,t];C^{\beta }_{B}({\mathbb {R}}^{N}))} \big ), \qquad t\in ]0,T[. \end{aligned}$$

Remark 4.1

In [25] it is allowed for f to be unbounded with respect to the time variable, namely $\Vert f \Vert _{L^{\infty }( [0,t];C^{\alpha }_{B}({\mathbb {R}}^{N}))} \sim (T-t)^{-\gamma }$ as $t\rightarrow T^-$, for some $\gamma \in [0,1[$. Furthermore, the proofs in [25] can be extended to include the case of f and g with exponential growth in the space variable, namely:

$$\begin{aligned} |f(t,x)|+|g(x)|&\le C e^{C |x|^2},\qquad x\in {\mathbb {R}}^{N}. \end{aligned}$$

As a consequence of Proposition 4.1, we have the following result, which contains further useful properties that allow to view the fundamental solution as the transition probability density of a Markovian process.

Corollary 4.1

Under the assumptions of Theorem 1.1 we have:

• (i) The Chapman–Kolmogorov identity

  $$\begin{aligned} p(t,x;T,y)= & {} \int _{\mathbb {R}^N}p(t,x;s,\eta )p(s,\eta ;T,y)d\eta , \\{} & {} 0<t< s< T<T_0,\ x,y\in \mathbb {R}^N; \end{aligned}$$

• (ii) If the zero-th order coefficient a of $\mathscr {A}$ is constant, i.e. $a(t,x)= \bar{a}$, then

  $$\begin{aligned} \int _{\mathbb {R}^N}p(t,x;T,y)dy=e^{\bar{a}(T-t)},\qquad 0< t<T<T_0,\ x\in \mathbb {R}^N. \end{aligned}$$

Appendices

A Gaussian estimates

We prove Gaussian estimates that are crucial in the analysis of Sects. 2 and 3. Here we follow the ideas in [7, Section 3], but with some technical difference. Namely, in the aforementioned paper the Kolmogorov operator acts on the forward variables of $\Gamma ^{(s,v)}(t,x;T,y)$, whereas here we consider $\mathscr {A}+Y$ acting on the backward variables (t, x). This has an impact on the spatial derivatives, which contain additional factors that require a careful analysis.

Throughout the appendix we suppose that Assumptions 1.1, 1.2 and 1.3 are satisfied and fix $(s,v)\in \mathscr {S}_{T_0}$. Denoting by $B_0$ the matrix B with null $*$-blocks, we define the $N\times N$ matrices

$$\begin{aligned} \mathscr {C}_0(t):=&\int _{0}^{t} e^{(t-\tau ) B_0} \begin{pmatrix} I_{d} &{} 0 \\ 0 &{} 0\end{pmatrix} e^{(t-\tau ) B_0^*}d\tau , \\ \mathscr {C}_0^{(s,v)}(t,T):=&\int _{t}^{T} e^{(T-\tau ) B_0} A^{(s,v)} (\tau ) e^{(T-\tau ) B_0^*}d\tau , \end{aligned}$$

with $A^{(s,v)}$ as defined in (2.3). As an immediate consequence of Assumption 1.1 we can compare the quadratic forms associated to $\mathscr {C}^{(s,v)}$ (as in (2.2)), $\mathscr {C}_0^{(s,v)}$ with $\mathscr {C}(T-t)$ (as in (2.5)), $\mathscr {C}_0(T-t)$, respectively:

$$\begin{aligned} \frac{1}{\mu }\mathscr {C}(T-t)\le \mathscr {C}^{(s,v)}(t,T)\le \mu \mathscr {C}(T-t),\nonumber \\ \frac{1}{\mu }\mathscr {C}_0(T-t)\le \mathscr {C}_0^{(s,v)}(t,T)\le \mu \mathscr {C}_0(T-t), \end{aligned}$$

(A.1)

for any $t \le T$. Moreover, an asymptotic comparison near 0 of $\mathscr {C}^{(s,v)}$ and $\mathscr {C}_0^{(s,v)}$ holds:

Lemma A.1

There exist two positive constants C and $\delta$, only dependent on $\mu$ and B, such that

$$\begin{aligned} \frac{1}{2\mu }\mathscr {C}_0(T-t)&\le \mathscr {C}^{(s,v)}(t,T)\le 2\mu \mathscr {C}_0(T-t),\\ \frac{1}{\left( 2\mu \right) ^{N}}\det \mathscr {C}_0(T-t)&\le \det \mathscr {C}^{(s,v)}(t,T)\le \left( 2\mu \right) ^{N}\det \mathscr {C}_0(T-t), \end{aligned}$$

for any $0<T-t< \delta$. Analogous estimates hold for $\big (\mathscr {C}^{(s,v)}(t,T)\big )^{-1}$.

Proof

It follows from the same arguments of [23, Lemma 3.1]: the proof is only based on the properties of the matrices A and B, and it is not relevant whether A has constant or time-dependent entries. $\square$

Remark A.1

We note that $|\cdot |_B$ is homogeneous with respect to the family of dilations defined by the matrices

$$\begin{aligned} D(\lambda ):=\text {diag}(\lambda I_{d},\lambda ^3 I_{d_1},\ldots ,\lambda ^{2q+1}I_{d_{q}}), \qquad \lambda \ge 0. \end{aligned}$$

In [23, Proposition 2.3] it is proved that

$$\begin{aligned} \mathscr {C}_0(t)= D(\sqrt{t})\mathscr {C}_0(1)D(\sqrt{t}), \qquad t\ge 0. \end{aligned}$$

(A.2)

Therefore, for $0<T-t<\delta$ with $\delta$ as in Lemma A.1,

$$\begin{aligned} \frac{(T-t)^Q}{\left( 2\mu \right) ^{N}}\det \mathscr {C}_0(1)\le \det \mathscr {C}^{(s,v)}(t,T)\le \left( 2\mu \right) ^{N}(T-t)^Q\det \mathscr {C}_0(1). \end{aligned}$$

To compute the spatial derivatives of $\Gamma ^{(s,v)}(t,x;T,y)$ it is useful noticing that

$$\begin{aligned} \Gamma ^{(s,v)}(t,x;T,y)=\textbf{G}\big ( H^{(s,v)}(t,T), e^{-(T-t)B}y-x \big ),\qquad {(T,y)\in \mathscr {S}_{T_0}, \ (t,x)\in {\mathscr {S}}_T,} \end{aligned}$$

where

$$\begin{aligned} H^{(s,v)}(t,T):= e^{-(T-t)B}\mathscr {C}^{(s,v)}(t,T)e^{-(T-t)B^*}. \end{aligned}$$

Since $\mathscr {C}^{(s,v)}(t,T)$ is symmetric positive definite and $e^{-(T-t)B}$ is non-singular, then $H^{(s,v)}(t,T)$ is symmetric and positive definite for every $0\le t < T$.

In order to give estimates on the matrix $H^{(s,v)}$ we need to study the elements of $e^{tB}$. We recall the block partition (1.6) of the matrix B: for $h,k=0,\ldots ,q$, we denote the $d_h\times d_k$ block of B by

$$\begin{aligned} \mathscr {Q}_{hk}:=\left( b_{ij}\right) _{ i={\bar{d}}_{h-1}+1,\ldots ,{\bar{d}}_h\atop j={\bar{d}}_{k-1}+1,\ldots ,{\bar{d}}_k}, \end{aligned}$$

with ${\bar{d}}_{h}$ as in (1.7). Note that by (1.6) we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \mathscr {Q}_{hk}=0_{d_h\times d_k} &{}\text {if } h>k+1,\\ \mathscr {Q}_{hk}=B_h &{}\text {if } h=k+1,\\ \mathscr {Q}_{hk}=*&{}\text {if } h<k+1. \end{array}\right. } \end{aligned}$$

(A.3)

Analogously, for $n\in \mathbb {N}$, we can consider the same block decomposition for $B^n$. We denote by $\mathscr {Q}_{hk}^{(n)}$ the $d_h\times d_k$ block of $B^n$.

Lemma A.2

Let $h,k=0,\ldots ,q$ and $n\in \mathbb {N}$. Then

$$\begin{aligned} \mathscr {Q}^{(n)}_{hk}=0_{d_h\times d_k}, \qquad h>k+n, \end{aligned}$$

(A.4)

which is $\left( B^n\right) _{ij}=0$ if $i\in \{{\bar{d}}_{h-1}+1,\ldots ,{\bar{d}}_h\}$ and $j\in \{{\bar{d}}_{k-1}+1,\ldots ,{\bar{d}}_k\}$.

Proof

We proceed by induction on n. The case of $n=1$ is obvious (see (A.3)). Now we assume that (A.4) holds for a certain $n\in \mathbb {N}$. For $h>k+n+1$ we have

$$\begin{aligned} \mathscr {Q}^{(n+1)}_{hk} = \sum _{m=0}^{q} \mathscr {Q}^{(n)}_{hm}\mathscr {Q}_{mk}. \end{aligned}$$

If $m < h- n$, then $\mathscr {Q}^{(n)}_{hm}=0_{d_h\times d_m}$ by inductive hypothesis; if $m\ge h- n$, then $m>k+1$ and $\mathscr {Q}_{mk}=0_{d_m\times d_k}$. Therefore $\mathscr {Q}^{(n+1)}_{hk}=0_{d_h\times d_k}$. $\square$

Lemma A.3

Let $h,k=1,\ldots ,q$ such that $h-k=: n \in \mathbb {N}$. For any $i\in \{\bar{d}_{h-1}+1,\ldots ,\bar{d}_h\}$ and $j\in \{\bar{d}_{k-1}+1,\ldots ,\bar{d}_k\}$ we have

$$\begin{aligned} \left( e^{tB}\right) _{ij}=O(t^n),\quad \text {as }t\rightarrow 0. \end{aligned}$$

Proof

From Lemma A.2 we have that $(B^m)_{ij}=0$ for every $m=0,\ldots ,n-1$, since $\mathscr {Q}^{(m)}_{hk}=0_{d_h \times d_k}$ for $h-k=n>m$. Therefore

$$\begin{aligned} (e^{tB})_{ij}=\frac{t^n(B^n)_{ij}}{n!} + O(t^{n+1}),\quad \text {as } t\rightarrow 0. \end{aligned}$$

$\square$

Lemma A.4

There exists a positive constant C that only depends on $\mu$, B and $T_0$ such that, for every $i,j=1,\ldots ,d$ and $k=d +1,\ldots ,d + d_1$,

$$\begin{aligned} \big |\big ( H^{(s,v)}(t,T)^{-1} x\big )_i\big |&\le \frac{C}{\sqrt{T-t}} \big | D( \sqrt{T-t})^{-1} e^{(T-t)B}x\big |, \end{aligned}$$

(A.5)

$$\begin{aligned} \big |(H^{(s,v)}(t,T)^{-1}\big )_{ij}\big |&\le \frac{C}{T-t}, \end{aligned}$$

(A.6)

$$\begin{aligned} \big |\big ( H^{(s,v)}(t,T)^{-1} x\big )_k\big |&\le \frac{C}{(T-t)^{\frac{3}{2}}} \big | D( \sqrt{T-t})^{-1} e^{(T-t)B}x\big |, \end{aligned}$$

(A.7)

$$\begin{aligned} \big |\big (H^{(s,v)}(t,T)^{-1}\big )_{ik}\big |&\le \frac{C}{(T-t)^2}, \end{aligned}$$

(A.8)

for any $0<T<T_0$ and $(t,x)\in {\mathscr {S}}_T$.

Proof

We prove the first inequality. Setting $\tau = T-t$, we have

$$\begin{aligned} \left| \left( H^{(s,v)}(t,T)^{-1} x\right) _i\right|&= \frac{1}{\sqrt{\tau }} \left| \Big ( D( \sqrt{\tau }) e^{\tau B^*} \mathscr {C}^{(s,v)}(t,T)^{-1} e^{\tau B}x \Big )_i\right| \\&\le \frac{1}{\sqrt{\tau }} \sum _{n=1}^N \Big | \big (D(\sqrt{\tau }) e^{\tau B^*} D( \sqrt{\tau })^{-1}\big )_{in}\Big | \\&\quad \left\| D( \sqrt{\tau }) \mathscr {C}^{(s,v)}(t,T)^{-1} D( \sqrt{\tau })\right\| \\&\left| D( \sqrt{\tau })^{-1} e^{\tau B}x\right| . \end{aligned}$$

By Lemma A.1 there exists a positive constant $\delta$ such that, if $0<\tau <\delta$, we have

$$\begin{aligned} \left\| D( \sqrt{\tau }) \mathscr {C}^{(s,v)}(t,T)^{-1} D( \sqrt{\tau })\right\|&\le \sup \limits _{| y|=1}\langle D( \sqrt{\tau }) \mathscr {C}^{(s,v)}(t,T)^{-1} D( \sqrt{\tau }) y, y\rangle \\&\le 2\mu \sup \limits _{| y|=1}\langle \mathscr {C}_0(\tau )^{-1} D( \sqrt{\tau }) y,D( \sqrt{\tau }) y\rangle \\&=2\mu \Vert \mathscr {C}_0(1)^{-1} \Vert , \end{aligned}$$

where the last equality follows from (A.2). If $\delta \le \tau < T_0$, by Eq. (A.1) we have

$$\begin{aligned} \left\| D( \sqrt{\tau }) \mathscr {C}^{(s,v)}(t,T)^{-1} D( \sqrt{\tau })\right\| \le \mu \left\| D( \sqrt{\tau }) \mathscr {C}(\tau )^{-1} D( \sqrt{\tau })\right\| , \end{aligned}$$

which is bounded by a constant that depends only on $\mu$, $T_0$ and B.

In order to conclude the proof of (A.5), we let $h_n$ be the only $h\in \{0,\ldots ,q\}$ such that ${\bar{d}}_{h-1}+1\le n\le {\bar{d}}_h$. Then, by Lemma A.3, since $i\in \{1,\ldots ,d\}$, we obtain

$$\begin{aligned} \big (D( \sqrt{\tau }) e^{\tau B^*} D( \sqrt{\tau })^{-1}\big )_{in}= & {} D( \sqrt{\tau })_{ii}\big (e^{\tau B^*}\big )_{in} D( \sqrt{\tau })^{-1}_{nn} \\= & {} {{\tau }^{\frac{1}{2}}} \left( e^{\tau B}\right) _{ni} {\tau ^{-\frac{2h_n +1}{2}}} =O(1) \qquad \text {as } \tau \rightarrow 0. \end{aligned}$$

Estimate (A.6) follows from (A.5) choosing $x=\textbf{e}_j$. Estimates (A.7) and (A.8) can be proved following the same arguments, noticing that for $k=d+1,\ldots ,d+d_1$ we have $D(\tau )_{kk}=\tau ^{3}$. $\square$

Finally, we provide Gaussian estimates for $\Gamma ^{(s,v)}(t,x;T,y)$ and its derivatives up to the fourth order that will be used to study the Hölder regularity of the second order derivatives of the fundamental solution via the representation (2.8)–(2.12). The following result can be proved as [7, Proposition 3.5].

Lemma A.5

For every $\beta \ge 0$ and $\varepsilon >0$ there exists a positive constant C, only dependent on $T_0,\mu ,B,\varepsilon$ and $\beta$, such that

$$\begin{aligned}{} & {} |w_i|^{\beta } \, \Gamma ^{(s,v)}(t,x;T,y) \le C\Gamma ^{\mu +\varepsilon }(t,x;T, y), \nonumber \\ {}{} & {} (T,y)\in \mathscr {S}_{T_0},\ (t,x)\in {\mathscr {S}}_T,\ i=1,\ldots ,N, \end{aligned}$$

(A.9)

where

$$\begin{aligned} w=D(\sqrt{T-t})^{-1}\left( y-e^{(T-t)B} x\right) . \end{aligned}$$

Notation A.1

Let $\nu =(\nu _1,\ldots ,\nu _N)\in \mathbb {N}_0^N$ be a multi-index. We define the B-length of $\nu$ as

$$\begin{aligned}{}[\nu ]_B:= \sum _{j=0}^{q}(2j+1)\sum _{i=\bar{d}_{j-1}+1}^{\bar{d}_j}\nu _{i}. \end{aligned}$$

Moreover, as usual $\partial ^\nu _x=\partial _{x_1}^{\nu _1}\cdots \partial _{x_N}^{\nu _N}.$

Combining Lemmas A.4 and A.5 with [7, Proposition 3.1, 3.6 and Lemma 5.2], some lengthy but straightforward computations show the following

Proposition A.1

We have

$$\begin{aligned} \frac{1}{\mu ^N}\Gamma ^{\frac{1}{\mu }}(t,x;T,y) \le \Gamma ^{(s,v)}(t,x;T,y) \le \mu ^N \Gamma ^\mu (t,x;T,y). \end{aligned}$$

(A.10)

for any $(T,y)\in \mathscr {S}_{T_0}$ and $(t,x)\in {\mathscr {S}}_T$. Moreover, for every $\varepsilon >0$ and $\nu \in \mathbb {N}^N_0$ with $[\nu ]_B\le 4$, there exists a positive constant C, only dependent on $T_0, \mu , B$ and $\varepsilon$, such that

$$\begin{aligned} |\partial _{x}^\nu \Gamma ^{(s,v)}(t,x;T,y)|&\le \frac{C}{(T-t)^{\frac{[\nu ]_B}{2}}}\Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(A.11)

$$\begin{aligned} \left| \partial _{x}^\nu \Gamma ^{(s,v)}(t,x;T,y)-\partial _{x}^\nu \Gamma ^{(s,w)}(t,x;T,y)\right|&\le C \frac{|v-w|_B^\alpha }{(T-t)^{\frac{[\nu ]_B}{2}}} \Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(A.12)

for any $(T,y)\in \mathscr {S}_{T_0}$, $(t,x)\in {\mathscr {S}}_T$ and $w\in \mathbb {R}^N$.

B potential estimates

We study $\Phi =\Phi (t,x;T,y)$ in (2.19) and its derivatives w.r.t. to the variables $x_1,\ldots ,x_d$. To do so, we have to deal with some singular integrals. We follow the steps in [7, Section 5], but we remark that the estimates of Proposition B.1 extend the ones in the aforementioned paper to higher order derivatives. This is needed to prove the optimal regularity of $\Phi (t,x;T,y)$ and thereafter of $p(t,x;T,y)$.

We set

$$\begin{aligned} J(t,x;\tau ;T,y):= & {} \int _{\mathbb {R}^N} \textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y) d\eta , \nonumber \\ {}{} & {} \quad (T,y)\in \mathscr {S}_{T_0},\ (t,x)\in \mathscr {S}_T, \ \tau \in ]t,T[. \end{aligned}$$

(B.1)

Proposition B.1

For every $\varepsilon >0$, $\nu \in \mathbb {N}^N_0$ with $[\nu ]_B\le 4$ and $0<\delta <\alpha$, there exists a positive constant C, only dependent on $N, T_0, \mu , B, \delta ,\alpha$ and $\varepsilon$, such that,

$$\begin{aligned} \left| J(t,x;\tau ;T,y)\right|&\le \frac{C}{(T-\tau )^{1-\frac{\alpha }{2}}}\Gamma ^{\mu +\varepsilon }(t,x;T,y) \end{aligned}$$

(B.2)

$$\begin{aligned} \left| \partial _x^\nu J(t,x;\tau ;T,y)\right|&\le \frac{C}{(T-\tau )^{1-\frac{\delta }{2}}(\tau -t)^{\frac{[\nu ]_B-(\alpha -\delta )}{2}}}\Gamma ^{\mu +\varepsilon }(t,x;T,y), \end{aligned}$$

(B.3)

for every $(T,y)\in \mathscr {S}_{T_0}$, $(t,x)\in \mathscr {S}_T$ and $\tau \in ]t,T[$.

Proof

The proof relies on Proposition 2.1: (B.2) can be easily obtained by applying estimate (A.10) to $\textbf{P}(t,x;\tau ,\eta )$, estimate (2.13) to $\phi (\tau ,\eta ;T,y)$ and the Chapman–Kolmogorov identity.

We provide a full proof of (B.3) in the case of $\partial _x^\nu =\partial _{x_i x_j}$, with $i,j\le d$, the proof for higher order derivatives being analogous. The idea is to combine (2.14) with the techniques in [7, Proposition 5.3] and [36, Proposition 3.2]. Let $(t,x)\in \mathscr {S}_T$ and $\tau \in ]t,T[$ be fixed. By estimates (A.11) and (2.13), we have

$$\begin{aligned} \partial _{x_i x_j}J(t,x;\tau ;T,y)=\int _{\mathbb {R}^N} \partial _{x_i x_j}\textbf{P}(t,x;\tau ,\eta )\phi (\tau ,\eta ;T,y) d\eta . \end{aligned}$$

We set $=\frac{t+T}{2}$ and consider two separate cases:

Case $<\tau < T$. By (A.11) and (2.13), we have that for every $\varepsilon >0$ and $0<\delta <\alpha$ there exists a positive constant C such that

$$\begin{aligned} |\partial _{x_i x_j}J(t,x;\tau ;T,y)|&\le \int _{\mathbb {R}^N}\frac{C}{(T-\tau )^{1-\frac{\alpha }{2}}(\tau -t)}\Gamma ^{\mu +\varepsilon }(t,x;\tau ,\eta ) \Gamma ^{\mu +\varepsilon }(\tau ,\eta ;T,y)d\eta \end{aligned}$$

(by the Chapman–Kolmogorov equation)

$$\begin{aligned}&\le \frac{C}{(T-\tau )^{1-\frac{\alpha }{2}}(\tau -t)}\Gamma ^{\mu +\varepsilon }(t,x;T,y) \end{aligned}$$

(since $T-\tau <\tau -t$)

$$\begin{aligned}&\le \frac{C}{(T-\tau )^{1-\frac{\delta }{2}}(\tau -t)^{1-\frac{\alpha -\delta }{2}}}\Gamma ^{\mu +\varepsilon }(t,x;T,y). \end{aligned}$$

Case $t<\tau \le$. Here we need to handle with care the singularity of $\partial _{x_i x_j}\textbf{P}(t,x;\tau ,\eta )$ for small $\tau -t$. Note that in this case the following inequalities hold true:

$$\begin{aligned} \tau -t \le \frac{T-t}{2}\le T-\tau < T-t. \end{aligned}$$

(B.4)

We have

$$\begin{aligned} \partial _{x_i x_j}J(t,x;\tau ;T,y)=K_1 +K_2 +K_3, \end{aligned}$$

where, setting ${\xi }=e^{(\tau -t)B}x$,

$$\begin{aligned} K_1&:=\int _{\mathbb {R}^N} \partial _{x_i x_j}\Gamma ^{(\tau ,\eta )}(t,x;\tau ,\eta )\big (\phi (\tau ,\eta ;T,y)-\phi (\tau ,{\xi };T,y)\big ) d\eta ,\\ K_2&:= \phi (\tau ,{\xi };T,y) \int _{\mathbb {R}^N} \left( \partial _{x_i x_j}\Gamma ^{(\tau ,\eta )}(t,x;\tau ,\eta )-\partial _{x_i x_j}\Gamma ^{(\tau ,v)}(t,x;\tau ,\eta )\big |_{v={\xi }}\right) d\eta ,\\ K_3&:= \phi (\tau ,x;T,y) \int _{\mathbb {R}^N} \partial _{x_i x_j}\Gamma ^{(\tau ,v)}(t,x;\tau ,\eta )\big |_{v={\xi }}d\eta . \end{aligned}$$

We first consider $K_1$. By (2.14) and (A.11), for every $\varepsilon >0$ and $0<\delta <\alpha$ there exists a positive constant C such that

$$\begin{aligned} |K_1 |&\le \frac{C}{(T-\tau )^{1-\frac{\delta }{2}}} \int _{\mathbb {R}^N}\frac{|\eta -{\xi }|^{\alpha -\delta }_B}{(\tau -t)}\Gamma ^{\mu +\frac{\varepsilon }{2}}(t,x;\tau ,\eta )\\&\quad \times \left( \Gamma ^{\mu +\varepsilon }(\tau ,{\xi };T,y)+\Gamma ^{\mu +\varepsilon }(\tau ,\eta ;T,y)\right) d\eta \end{aligned}$$

(by (A.9))

$$\begin{aligned}&\le \frac{C}{(T-\tau )^{1-\frac{\delta }{2}}} \int _{\mathbb {R}^N}\frac{1}{(\tau -t)^{1-\frac{\alpha -\delta }{2}}}\Gamma ^{\mu +\varepsilon }(t,x;\tau ,\eta )\\&\quad \times \left( \Gamma ^{\mu +\varepsilon }(\tau ,{\xi };T,y)+\Gamma ^{\mu +\varepsilon }(\tau ,\eta ;T,y)\right) d\eta \end{aligned}$$

(integrating in $\eta$ and by the Chapman–Kolmogorov identity)

$$\begin{aligned}&\le \frac{C}{(T-\tau )^{1-\frac{\delta }{2}}(\tau -t)^{1-\frac{\alpha -\delta }{2}}} \left( \Gamma ^{\mu +\varepsilon }(\tau ,{\xi };T,y)+\Gamma ^{\mu +\varepsilon }(t,x;T,y)\right) \end{aligned}$$

(by (B.4))

$$\begin{aligned}&\le \frac{C}{(T-\tau )^{1-\frac{\delta }{2}}(\tau -t)^{1-\frac{\alpha -\delta }{2}}} \Gamma ^{\mu +\varepsilon }(t,x;T,y). \end{aligned}$$

Consider now $K_2$. By (2.13) and (A.12), we obtain

$$\begin{aligned} |K_2 |&\le C{\frac{\Gamma ^{\mu +\varepsilon }(\tau ,{\xi };T,y)}{(T-\tau )^{1-\frac{\alpha }{2}}}} \int _{\mathbb {R}^N}\frac{|\eta -{\xi }|^{\alpha }_B}{\tau -t}\Gamma ^{\mu +\varepsilon }(t,x;\tau ,\eta )d\eta \\ \end{aligned}$$

(by (A.9) and integrating in $\eta$)

$$\begin{aligned}&\le \frac{C}{(T-\tau )^{1-\frac{\alpha }{2}}(\tau -t)^{1-\frac{\alpha }{2}}} \Gamma ^{\mu +\varepsilon }(\tau ,{\xi };T,y) \end{aligned}$$

(again by (B.4))

$$\begin{aligned}&{\le \frac{C}{(T-\tau )^{1-\frac{\delta }{2}}(\tau -t)^{1-\frac{\alpha -\delta }{2}}} }\Gamma ^{\mu +\varepsilon }(t,x;T,y). \end{aligned}$$

Finally, $K_{3}=0$ since

$$\begin{aligned} \int _{\mathbb {R}^N} \partial _{x_i x_j}\Gamma ^{(\tau ,v)}(t,x;\tau ,\eta )d\eta =\partial _{x_i x_j}\int _{\mathbb {R}^N}\Gamma ^{(\tau ,v)}(t,x;\tau ,\eta )d\eta =0 \end{aligned}$$

for any $v\in {\mathbb {R}}^{N}$. $\square$