When to Share My First-party Content: the Role of Membership Bundles in Content Platforms

Abstract

Content platforms suffer from declining subscriber growth. To address this issue, we examine an interesting strategy that competing platforms jointly launch a membership bundle, which provides consumers with simultaneous access to them at a reduced price. We investigate how the bundle approach interacts with first-party content production in shaping platforms’ pricing and content-sharing decisions. By solving a game-theoretical model, we illustrate that: first, competing platforms offer the bundle only when they are less differentiated. Second, in stark contrast with the consequence of keeping the content exclusive without the bundle, the platform is more likely to share its content with the membership bundle. Third, despite the exclusivity of first-party content, with the membership bundle, the rival platform may generate higher profit instead of always being harmed without the bundle. We enrich the understanding of how platform coopetition interacts with first-party content production and draw practical implications for platform owners.

Appendices

Appendix 1. Proofs of Lemmas and Propositions

Proof of Lemma 1

By taking the first- and second-order conditions of ${\pi }_{i}$ with respect to ${p}_{i}$, we have $\frac{\partial\pi_i}{\partial p_i}=\frac{\alpha p_{-i}-2tp_i+(t-\alpha)(\alpha+\lambda)}{(t-\alpha)(t+\alpha)},\;\frac{\partial^2\pi_i}{\partial p_i^2}=\frac{2t}{\alpha^2-t^2}.$ It is obvious that $\frac{{\partial }^{2}{\pi }_{i}}{\partial {p}_{i}^{2}}<0$ with $t>\alpha$. Then, by jointly solving $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=0$, and $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=0$, we obtain ${p}_{i}^{*}=\frac{(t-\alpha )(\alpha +\lambda )}{2t-\alpha }$, by substituting ${p}_{i}^{*}$ into ${n}_{i}$, ${n}_{M}$, and ${\pi }_{i}$, we finish the proof.

Proof of Lemma 2

Firstly, by taking the first- and second-order conditions of ${\pi }_{A}+{\pi }_{B}$ with respect to ${p}_{M}$, we have $\frac{\partial(\pi_A+\pi_B)}{\partial p_M}=\frac{2p_A+{2p}_B-4p_M-t+\alpha+2\lambda}{t+\alpha},\;$, $\frac{\partial^2(\pi_A+\pi_B)}{\partial p_M^2}=-\frac4{t+\alpha}$. It’s obvious that $\frac{{\partial }^{2}({\pi }_{A}+{\pi }_{B})}{\partial {{p}_{M}}^{2}}<0$, let $\frac{\partial ({\pi }_{A}+{\pi }_{B})}{\partial {p}_{M}}=0$, we have ${p}_{M}=\frac{2{p}_{A}+2{p}_{B}-t+\alpha +2\lambda }{4}$, substituting ${p}_{M}$ into ${\pi }_{i}$, and take the first- and second-order conditions of ${\pi }_{i}$ with respect to ${p}_{i}$, we have $\frac{\partial {\pi }_{i}}{\partial {p}_{i}}=\frac{{p}_{i}}{2(t-\alpha )}-\frac{{p}_{-i}}{t-\alpha }+\frac{5t+3\alpha -2\lambda }{8(t+\alpha )}$, $\frac{{\partial }^{2}{\pi }_{i}}{\partial {p}_{i}^{2}}=\frac{1}{\alpha -t}<0$, by jointly solving $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=0$, and $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=0$, we obtain ${p}_{i}^{*}=\frac{(t-\alpha )(5t+3\alpha -2\lambda )}{4(t+\alpha )}$. Substituting ${p}_{i}^{*}$ into ${p}_{M}$, ${n}_{i}$, ${n}_{M}$, and ${\pi }_{i}$, we finish the proof.

Proof of Corollary 1

With the membership bundle, ${n}_{M}^{*}=\frac{2\lambda +\alpha -t}{2(t+\alpha )}$, without the membership bundle, ${n}_{M}^{*}=\frac{{\alpha }^{2}+t\left(\alpha +2\lambda \right)-2{t}^{2}}{\left(2t-\alpha \right)(t+\alpha )}$. Let $\Delta =\frac{2\lambda +\alpha -t}{2(t+\alpha )}-\frac{{\alpha }^{2}+t\left(\alpha +2\lambda \right)-2{t}^{2}}{\left(2t-\alpha \right)(t+\alpha )}$, we can easily find that $\Delta >0$ with $-\frac{\alpha }{2}-\frac{{\alpha }^{2}}{2t}<\lambda <\frac{3t}{2}-\frac{\alpha }{2}-\frac{{\alpha }^{2}}{t}$. Further, we have $\frac{\partial\Delta }{\partial \alpha }=-\frac{t{\alpha }^{2}+{\alpha }^{2}\lambda +2{t}^{2}\left(2\alpha +\lambda \right)}{{\left(2{t}^{2}+t\alpha -{\alpha }^{2}\right)}^{2}}<0$, and $\frac{\partial\Delta }{\partial \lambda }=-\frac{\alpha }{2{t}^{2}+t\alpha -{\alpha }^{2}}<0$.

Proof of Corollary 2

With the membership bundle, ${p}_{i}^{*}=\frac{(t-\alpha )(5t+3\alpha -2\lambda )}{4(t+\alpha )}$, without the membership bundle, ${p}_{i}^{*}=\frac{(t-\alpha )(\alpha +\lambda )}{2t-\alpha }$. Let $\Delta =\frac{(t-\alpha )(5t+3\alpha -2\lambda )}{4(t+\alpha )}-\frac{(t-\alpha )(\alpha +\lambda )}{2t-\alpha }$, we can have when $\lambda<\frac{(t-\alpha)(10t+7\alpha)}{8t+2\alpha},\;\Delta>0$, otherwise, $\Delta<0.$

Proof of Proposition 1

In Stage 1, if the platforms decide to offer the membership bundle, we need to have that the profits for both platforms when they offer the membership bundle should be higher than the condition when they do not offer the bundle. Consequently, let $\Delta =\frac{11{t}^{2}-6t\alpha -5{\alpha }^{2}-8t\lambda -8\alpha \lambda +4{\lambda }^{2}}{16(t+\alpha )}-\frac{t(t-\alpha ){(\alpha +\lambda )}^{2}}{{\left(2t-\alpha \right)}^{2}(t+\alpha )}$, we can easily have when $\lambda<\frac{8t^3-8t^2\alpha+2t\alpha^2-2\alpha^3-\sqrt{\left(2t^2-3t\alpha+\alpha^2\right)^2(16t^2+16t\alpha+9\alpha^2)}}{2\alpha^2},\;\Delta>0$, or else, $\Delta<0.$

Proof of Lemma 3

By taking the first- and second-order conditions of ${\pi }_{i}$ with respect to ${p}_{i}$, we have $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=\frac{\alpha {p}_{B}-2{p}_{A}t+t\alpha -{\alpha }^{2}+t\delta +t\lambda -\alpha \lambda }{(t-\alpha )(t+\alpha )}$, $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=\frac{\alpha {p}_{A}-2{p}_{B}t+t\alpha -{\alpha }^{2}-\alpha \delta +t\lambda -\alpha \lambda }{(t-\alpha )(t+\alpha )}$, $\frac{{\partial }^{2}{\pi }_{i}}{\partial {p}_{i}^{2}}=\frac{2t}{{\alpha }^{2}-{t}^{2}}<0$. By jointly solving $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=0$ and $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=0$, we obtain ${p}_{A}^{*}=\frac{2{t}^{2}\left(\alpha +\delta +\lambda \right)-t\alpha \left(\alpha +\lambda \right)-{\alpha }^{2}(\alpha +\delta +\lambda )}{4{t}^{2}-{\alpha }^{2}}$, ${p}_{B}^{*}=\frac{2{t}^{2}\left(\alpha +\lambda \right)-t\alpha \left(\alpha +\delta +\lambda \right)-{\alpha }^{2}(\alpha +\lambda )}{4{t}^{2}-{\alpha }^{2}}$. Substituting ${p}_{i}^{*}$ into ${n}_{i}$, ${n}_{M}$, and ${\pi }_{i}$, we finish the proof.

Proof of Corollary 3

The proof is straightforward with $t>\alpha$.

Proof of Lemma 4

First, when ${\pi }_{B}^{*}>\overline{{\pi }_{B}^{*}}$, i.e., platform B can acquire higher profit when the additional content is exclusively kept, regardless of platform A’s content-sharing decision and the level of $w$, platform B never purchases the additional content. Second, when ${\pi }_{B}^{*}<\overline{{\pi }_{B}^{*}}$, i.e., platform B's profit is harmed by content exclusivity, platform B purchases the additional content when $w<\overline{{\pi }_{B}^{*}}-{\pi }_{B}^{*}$ if platform A sell the content. platform A then sets $w$ to be slightly lower than $\overline{{\pi }_{B}^{*}}-{\pi }_{B}^{*}$ and the two platforms end up with $\overline{{\pi }_{A}^{*}}+\overline{{\pi }_{B}^{*}}-{\pi }_{B}^{*}$, and ${\pi }_{B}^{*}$, respectively. Consequently, regarding platform A’s decision, if $\overline{{\pi }_{A}^{*}}+\overline{{\pi }_{B}^{*}}-{\pi }_{B}^{*}>{\pi }_{A}^{*}$, platform A shares the content and platform B purchases, otherwise, platform A does not share.

Proof of Lemma 5

The proof is straightforward with $t>\alpha.$

Proof of Proposition 2

With $t>\alpha$, and on the basis of Lemma 5, it is easy to have ${\pi }_{A}^{*}-\overline{{\pi }_{A}^{*}}>\overline{{\pi }_{B}^{*}}-{\pi }_{B}^{*}$, and the content is kept exclusive by platform A.

Proof of Lemma 6

First, by taking the first- and second-order conditions of ${\pi }_{A}+{\pi }_{B}$ with respect to ${p}_{M}$, we have $\frac{\partial ({\pi }_{A}+{\pi }_{B})}{\partial {p}_{M}}=\frac{2{p}_{A}+{2p}_{B}-4{p}_{M}-t+\alpha +\delta +2\lambda }{t+\alpha }$, $\frac{\partial^2(\pi_A+\pi_B)}{\partial p_M^2}=-\frac4{t+\alpha}.$ It’s obvious that $\frac{{\partial }^{2}({\pi }_{A}+{\pi }_{B})}{\partial {{p}_{M}}^{2}}<0$, let $\frac{\partial ({\pi }_{A}+{\pi }_{B})}{\partial {p}_{M}}=0$, we have ${p}_{M}=\frac{2{p}_{A}+2{p}_{B}-t+\alpha +\delta +2\lambda }{4}$, substituting ${p}_{M}$ into ${\pi }_{i}$, and take the first- and second-order conditions of ${\pi }_{i}$ with respect to ${p}_{i}$, we have $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=\frac{{p}_{B}}{2(t-\alpha )}-\frac{{p}_{A}}{t-\alpha }+\frac{5t+3\alpha -2\lambda }{8\left(t+\alpha \right)}+\frac{3t\delta +5\alpha \delta }{8\left(t+\alpha \right)(t-\alpha )}$, $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=\frac{{p}_{A}}{2(t-\alpha )}-\frac{{p}_{B}}{t-\alpha }+\frac{5t+3\alpha -2\lambda }{8\left(t+\alpha \right)}-\frac{5t\delta +3\alpha \delta }{8\left(t+\alpha \right)(t-\alpha )}$, $\frac{{\partial }^{2}{\pi }_{i}}{\partial {p}_{i}^{2}}=\frac{1}{\alpha -t}<0$, by jointly solving $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=0$, and $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=0$, we obtain ${p}_{A}^{*}=\frac{15{t}^{2}+t\left(\delta -6\alpha -6\lambda \right)+\alpha (7\delta +6\lambda -9\alpha )}{12(t+\alpha )}$, ${p}_{B}^{*}=\frac{15{t}^{2}-t\left(7\delta +6\alpha +6\lambda \right)-\alpha (\delta -6\lambda +9\alpha )}{12(t+\alpha )}$. Substituting ${p}_{i}^{*}$ into ${p}_{M}$, ${n}_{i}$, ${n}_{M}$, and ${\pi }_{i}$, we finish the proof.

Proof of Corollary 4

$\Delta {n}_{A}^{C}=\frac{(5\alpha -t)\delta }{12(t-\alpha )(t+\alpha )}$, with $t>\alpha$, if $\alpha >\frac{t}{5}$, $\Delta {n}_{A}^{C}>0$, if $\alpha <\frac{t}{5}$, $\Delta {n}_{A}^{C}<0$. The other relationships are also straightforward with $t>\alpha.$

Proof of Lemma 7

The proof is straightforward with $t>\alpha.$

Proof of Proposition 3

On the basis of Lemmas 4 and 7, first, when $\lambda >\frac{102{t}^{2}-108t\alpha +6{\alpha }^{2}-35t\delta +19\alpha \delta }{72(t-\alpha )}$, platform B never purchases the content, and the content is exclusively kept by platform A. Second, when $\lambda <\frac{102{t}^{2}-108t\alpha +6{\alpha }^{2}-35t\delta +19\alpha \delta }{72(t-\alpha )}$, we can find that when $\lambda>t-\alpha+\frac{\alpha\delta-17t\delta}{36(t-\alpha)}\left(t-\alpha+\frac{\alpha\delta-17t\delta}{36\left(t-\alpha\right)}<\frac{102t^2-108t\alpha+6\alpha^2-35t\delta+19\alpha\delta}{72(t-\alpha)}\right)$, ${\pi }_{A}^{C*}-\overline{{\pi }_{A}^{C*}}>\overline{{\pi }_{B}^{C*}}-{\pi }_{B}^{C*}$, platform A exclusively keeps the content. Otherwise, when $\lambda <t-\alpha +\frac{\alpha \delta -17t\delta }{36(t-\alpha )}$, the content is nonexclusively shared. And $w^\ast=\overline{\pi_B^{C\ast}}-\pi_B^{C\ast}=\frac{\delta\lbrack102t^2+\alpha\left(6\alpha+19\delta+72\lambda\right)-t(108\alpha+35\delta+72\lambda)\rbrack}{144(t-\alpha)(t+\alpha)}.$ The proof of the threshold of $\delta$ is consistent with the above process.

Proof of Proposition 4

In equilibrium, the content is always exclusive regardless of the membership bundle offering decision, the two platforms end up with ${\pi }_{A}^{C*}$, ${\pi }_{B}^{C*}$ with the bundle, and ${\pi }_{A}^{N*}$, ${\pi }_{B}^{N*}$ without the bundle, respectively. If the two platforms offer the membership bundle, their profits with the membership bundle should both be higher that of without the bundle, i.e., ${\pi }_{A}^{C*}>{\pi }_{A}^{N*}$, ${\pi }_{B}^{C*}>{\pi }_{B}^{N*}$. Let

$$\begin{array}{l}{\pi }_{A}^{C*}-{\pi }_{A}^{N*}={A}_{1}{\lambda }^{2}+{B}_{1}\lambda +{C}_{1}\\ {\pi }_{B}^{C*}-{\pi }_{B}^{N*}={A}_{2}{\lambda }^{2}+{B}_{2}\lambda +{C}_{2}\end{array}$$

wherein ${A}_{1}=\frac{{\alpha }^{2}}{4{\left(\alpha -2t\right)}^{2}(t+\alpha )}$, ${B}_{1}=\frac{-8{t}^{4}+2{t}^{2}{\alpha }^{2}+{\alpha }^{4}+4{t}^{3}\left(\alpha -2\delta \right)+t{\alpha }^{2}(\alpha +4\delta )}{2{\left(\alpha -2t\right)}^{2}(t+\alpha )(2t+\alpha )}$, ${C}_{1}=\frac{1}{144(t+\alpha ){({\alpha }^{2}-{4t}^{2})}^{2}}[1584{t}^{6}-96{t}^{5}\left(9\alpha -5\delta \right)+16{t}^{3}\alpha \left(27{\alpha }^{2}-51\alpha \delta -20{\delta }^{2}\right)+{\alpha }^{4}\left(-45{\alpha }^{2}+66\alpha \delta -17{\delta }^{2}\right)+2t{\alpha }^{3}\left(45{\alpha }^{2}+159\alpha \delta +64{\delta }^{2}\right)-8{t}^{4}\left(261{\alpha }^{2}+12\alpha \delta +74{\delta }^{2}\right)+3{t}^{2}{\alpha }^{2}\left(297{\alpha }^{2}+16\alpha \delta +88{\delta }^{2}\right)]$, ${A}_{2}=\frac{{\alpha }^{2}}{4{\left(\alpha -2t\right)}^{2}(t+\alpha )}$, ${B}_{2}=\frac{-8{t}^{4}+2{t}^{2}{\alpha }^{2}+{\alpha }^{3}(\alpha +\delta )+4{t}^{3}\left(\alpha +2\delta \right)+t{\alpha }^{2}(\alpha -2\delta )}{2{\left(\alpha -2t\right)}^{2}(t+\alpha )(2t+\alpha )}$, ${C}_{2}=\frac{99{t}^{3}-51{t}^{2}\left(3\alpha +2\delta \right)+\alpha \left(45{\alpha }^{2}-6\alpha \delta -19{\delta }^{2}\right)+t(9{\alpha }^{2}+108\alpha \delta +35{\delta }^{2})}{144(t-\alpha )(t+\alpha )}-\frac{t{\alpha }^{2}{[{\alpha }^{2}-2{t}^{2}+t(\alpha +\delta )]}^{2}}{(t-\alpha )(t+\alpha ){({\alpha }^{2}-4{t}^{2})}^{2}}$. We can have that when $\lambda <{\lambda }_{1}=\frac{-{B}_{1}-\sqrt{{{B}_{1}}^{2}-4{A}_{1}{C}_{1}}}{2{A}_{1}}$, ${\pi }_{A}^{C*}>{\pi }_{A}^{N*}$, and when $\lambda <{\lambda }_{2}=\frac{-{B}_{2}-\sqrt{{{B}_{2}}^{2}-4{A}_{2}{C}_{2}}}{2{A}_{2}}$, ${\pi }_{B}^{C*}>{\pi }_{B}^{N*}$, while for the two larger roots, i.e., $\frac{-{B}_{1}+\sqrt{{{B}_{1}}^{2}-4{A}_{1}{C}_{1}}}{2{A}_{1}}$ and $\frac{-{B}_{2}+\sqrt{{{B}_{2}}^{2}-4{A}_{2}{C}_{2}}}{2{A}_{2}}$, they exceed the upper bound of the feasible region and are eliminated. Consequently, we have that when $\lambda <\mathit{min}\{{\lambda }_{1},{\lambda }_{2}\}$, they offer the membership bundle, otherwise, they do not.

Appendix 2. Model Extensions

2.1 Extension 1–Strategic Content Production

In our main model, we consider the value of additional first-party content (i.e., $\delta$) to be exogenously given. Now, we present the condition when the platform, i.e., platform A, endogenously determines the value of additional content and discuss how the membership bundle will influence platform A’s strategic content production. We have platform A facing a quadratic cost function, i.e., $c\left(\delta \right)=\frac{1}{2}k{\delta }^{2}$, which is commonly used in the literature. Additionally, regarding the content value determination in events’ timeline, we have that in Stage 2, platform A first determines the value before the decision of content sharing and pricing, while the other stages are consistent with the main model. We can summarize platform A’s optimal value of additional content in the following lemma. Note that we have $k>\frac{2t{(2{t}^{2}-{\alpha }^{2})}^{2}}{({t}^{2}-{\alpha }^{2}){(4{t}^{2}-{\alpha }^{2})}^{2}}$, i.e., the content production cost cannot be too low, to ensure the second-order condition to be negative and the optimal additional content value to be positive.

Lemma A1

When platforms do not offer the membership bundle, the optimal value of platform A’s additional first-party content is ${\delta }^{N*}=\frac{2\left(t-\alpha \right)(2t+\alpha )(2{t}^{3}-t{\alpha }^{2})(\alpha +\lambda )}{16k{t}^{6}-8{t}^{5}+8{t}^{3}{\alpha }^{2}-24k{t}^{4}{\alpha }^{2}-2t{\alpha }^{4}+9k{t}^{2}{\alpha }^{2}-k{\alpha }^{6}}$; when platforms offer the membership bundle, the optimal value of platform A’s additional first-party content is $\delta^{C\ast}=\frac{3(t-\alpha)(5t+11\alpha)}{t+72kt^2-17\alpha-72k\alpha^2}.$.

Consequently, we further have the membership bundle’s influence on platform A’s strategic content production strategy. Due to the high nonlinearity of the equilibrium outcomes, we seek to numerical method to obtain the optimal value of additional first-party content, as shown in Table 3, with $t=1$, and the results remain unchanged if we assign other values. From this, we can make the following observation.

Table 3 The optimal value of additional first-party content

Observation A1

The introduction of a membership bundle reduces the optimal value of the platform’s first-party content.

According to Table 3 and Observation A1, the membership bundle approach reduces platforms’ intention to produce first-party content. This may be because the membership bundle approach limits the effectiveness of additional content exclusivity in further seizing the market share. The result also suggests that with the membership bundle, the platforms become less likely to expand their level of differentiation, in terms of both first-party content production and content sharing.

2.2 Extension 2–Platform Asymmetry

In the main model, we demonstrate the symmetric case in which each platform holds the same amount of exclusive content (i.e., ${\lambda }_{A}={\lambda }_{B}=\lambda$). Now, we relax the assumption to examine the role of platform asymmetry. Without loss of generality, we consider that platform A holds more exclusive content values $\rho$ than platform B (i.e., ${\lambda }_{A}-{\lambda }_{B}=\rho$), and other aspects remain consistent with the main model. Regarding the additional first-party content production and content-sharing decision, we may have two possible scenarios: the stronger platform, i.e., platform A, produces the additional content and decides whether to share with the weaker platform, i.e., platform B, or inversely, platform B produces the additional content and chooses whether to share with platform A.

2.2.1 The Stronger Platform Produces Additional First-Party Content

In this subsection, we present the case in which platform A, the stronger platform, produces additional content, and illustrate when it chooses to share the content with platform B, as well as the conditions for the two platforms to offer the membership bundle.

When the platforms do not offer the membership bundle, in line with the main model, we directly present the equilibrium outcomes according to the content-sharing decision.

Lemma B1

When the additional content is exclusively held by platform A, each platform’s equilibrium price is $p_A^{S1\ast}=\frac{2t^2\left(\alpha+\delta+\lambda+\rho\right)-t\alpha\left(\alpha+\lambda\right)-\alpha^2(\alpha+\delta+\lambda+\rho)}{4t^2-\alpha^2}$, $p_B^{S1\ast}=\frac{2t^2\left(\alpha+\lambda\right)-t\alpha\left(\alpha+\delta+\lambda+\rho\right)-\alpha^2(\alpha+\lambda)}{4t^2-\alpha^2}$. The number of consumers joining one platform is $n_A^{S1\ast}=\frac{4t^4+\alpha^4-2t^3\left(\alpha+\lambda\right)+t^2\alpha(\delta+\lambda+\rho-4\alpha)+t\alpha^2\left(\alpha+\lambda\right)}{4t^4-5t^2\alpha^2+\alpha^4}$, $n_B^{S1\ast}=\frac{4t^4+\alpha^4-2t^3\left(\alpha+\delta+\lambda+\rho\right)+t^2\alpha(\lambda-4\alpha)+t\alpha^2\left(\alpha+\delta+\lambda+\rho\right)}{4t^4-5t^2\alpha^2+\alpha^4}$ , respectively, and the number of consumers joining both platforms is $n_M^{S1\ast}=\frac{\alpha^2+t\left(\alpha+\delta+2\lambda+\rho\right)-2t^2}{(2t-\alpha)(t+\alpha)}$. Each platform’s profit is $\pi_A^{S1\ast}=\frac{t{\lbrack t\alpha\left(\alpha+\lambda\right)+\alpha^2(\alpha+\delta+\lambda+\rho)-2t^2(\alpha+\delta+\lambda+\rho)\rbrack}^2}{(t-\alpha)(t+\alpha){(\alpha^2-4t^2)}^2}$, and $\pi_B^{S1\ast}=\frac{t{\lbrack t\alpha\left(\alpha+\delta+\lambda+\rho\right)+\alpha^2(\alpha+\lambda)-2t^2(\alpha+\lambda)\rbrack}^2}{(t-\alpha)(t+\alpha){(\alpha^2-4t^2)}^2}.$

In this case, we have $\mathrm{max}\{\frac{\alpha t\left(\delta +\rho \right)}{2{t}^{2}-t\alpha -{\alpha }^{2}}-\alpha ,t-\frac{\alpha +\delta +\rho }{2}-\frac{{\alpha }^{2}}{2t}\}<\lambda <\frac{2{t}^{2}-{\alpha }^{2}}{t}-\frac{\delta +\rho }{2{t}^{2}-t\alpha -{\alpha }^{2}}$ to ensure $0<n_i^{S1\ast},n_M^{S1\ast}<1.$

Lemma B2

When the additional content of platform A is shared with platform B, each platform’s equilibrium price is ${p}_{A}^{S2*}=\frac{2{t}^{2}\left(\alpha +\lambda +\rho \right)-t\alpha \left(\alpha +\lambda \right)-{\alpha }^{2}(\alpha +\lambda +\rho )}{4{t}^{2}-{\alpha }^{2}}$, and ${p}_{B}^{S2*}=\frac{2{t}^{2}\left(\alpha +\lambda \right)-t\alpha \left(\alpha +\lambda +\rho \right)-{\alpha }^{2}(\alpha +\lambda )}{4{t}^{2}-{\alpha }^{2}}$. The number of consumers joining one platform is ${n}_{A}^{S2*}=\frac{4{t}^{4}+{\alpha }^{4}-2{t}^{3}\left(\alpha +\lambda \right)+{t}^{2}\alpha (\lambda +\rho -4\alpha )+t{\alpha }^{2}\left(\alpha +\lambda \right)}{4{t}^{4}-5{t}^{2}{\alpha }^{2}+{\alpha }^{4}}$, ${n}_{B}^{S2*}=\frac{4{t}^{4}+{\alpha }^{4}-2{t}^{3}\left(\alpha +\lambda +\rho \right)+{t}^{2}\alpha (\lambda -4\alpha )+t{\alpha }^{2}\left(\alpha +\lambda +\rho \right)}{4{t}^{4}-5{t}^{2}{\alpha }^{2}+{\alpha }^{4}}$, respectively, and the number of consumers joining both platforms is ${n}_{M}^{S2*}=\frac{{\alpha }^{2}+t\left(\alpha +2\lambda +\rho \right)-2{t}^{2}}{(2t-\alpha )(t+\alpha )}$. Each platform’s profit is ${\pi }_{A}^{S2*}=\frac{t{[t\alpha \left(\alpha +\lambda \right)+{\alpha }^{2}(\alpha +\lambda +\rho )-2{t}^{2}(\alpha +\lambda +\rho )]}^{2}}{(t-\alpha )(t+\alpha ){({\alpha }^{2}-4{t}^{2})}^{2}}$, and $\pi_B^{S2\ast}=\frac{t{\lbrack t\alpha\left(\alpha+\lambda+\rho\right)+\alpha^2(\alpha+\lambda)-2t^2(\alpha+\lambda)\rbrack}^2}{(t-\alpha)(t+\alpha){(\alpha^2-4t^2)}^2}.$

In this case, we have $\mathrm{max}\{\frac{\alpha t\rho }{2{t}^{2}-t\alpha -{\alpha }^{2}}-\alpha ,t-\frac{\alpha +\rho }{2}-\frac{{\alpha }^{2}}{2t}\}<\lambda <\frac{2{t}^{2}-{\alpha }^{2}}{t}-\frac{\rho }{2{t}^{2}-t\alpha -{\alpha }^{2}}$ to guarantee that $0<n_i^{S2\ast},n_M^{S2\ast}<1.$

On the basis of the platforms’ equilibrium profits under the two scenarios, we first have that $\pi_A^{S1\ast}>\pi_A^{S2\ast},\;\pi_B^{S1\ast}<\pi_B^{S2\ast}$, from which we can identify platform A’s content-sharing decision from Lemma 4, as shown in the following proposition.

Proposition B1

Without the membership bundle, platform A’s additional first-party content is always exclusively held.

When the platforms offer the membership bundle, we can summarize the equilibrium outcomes in the following lemmas according to the content-sharing decision.

Lemma B3

When the additional content is exclusively held by platform A, the price for the membership bundle is ${p}_{M}^{S3*}=\frac{2{t}^{2}-t\alpha +\alpha (2\lambda +\delta +\rho -\alpha )}{2(t+\alpha )}$, the price for each platform’s stand-alone service is ${p}_{A}^{S3*}=\frac{15{t}^{2}+t\left(\delta +\rho -6\alpha -6\lambda \right)+\alpha (7\delta +7\rho +6\lambda -9\alpha )}{12(t+\alpha )}$, and ${p}_{B}^{S3*}=\frac{15{t}^{2}-t\left(7\delta +7\rho +6\alpha +6\lambda \right)-\alpha (\delta +\rho -6\lambda +9\alpha )}{12(t+\alpha )}$. The number of consumers joining one platform is ${n}_{A}^{S3*}=\frac{9{t}^{2}-t\left(6\alpha +\delta +\rho +6\lambda \right)+\alpha (5\delta +5\rho +6\lambda -3\alpha )}{12({t}^{2}-{\alpha }^{2})}$, ${n}_{B}^{S3*}=\frac{9{t}^{2}-t\left(6\alpha +5\delta +5\rho +6\lambda \right)+\alpha (\delta +\rho +6\lambda -3\alpha )}{12({t}^{2}-{\alpha }^{2})}$, and the number of consumers joining both platforms is ${n}_{M}^{S3*}=\frac{2\lambda +\alpha +\delta +\rho -t}{2(t+\alpha )}$. Each platform’s profit is ${\pi }_{A}^{S3*}=\frac{1}{144(t-\alpha )(t+\alpha )}\{99{t}^{3}-3{t}^{2}\left(51\alpha -10\delta -10\rho +24\lambda \right)+\alpha [45{\alpha }^{2}-66\alpha \delta -66\alpha \rho +17{\left(\delta +\rho \right)}^{2}-72\alpha \lambda -36{\lambda }^{2}]+t[9{\alpha }^{2}-{\left(\delta +\rho \right)}^{2}+36{\lambda }^{2}+36\alpha \delta +36\alpha \rho +144\alpha \lambda ]\}$, and ${\pi }_{B}^{S3*}=\frac{1}{144\left(t-\alpha \right)\left(t+\alpha \right)}\{99{t}^{3}-3{t}^{2}\left(51\alpha +34\delta +34\rho +24\lambda \right)+\alpha [45{\alpha }^{2}-19({\delta +\rho )}^{2}-72\delta \lambda -72\rho \lambda -36{\lambda }^{2}-6\alpha \delta -6\alpha \rho -72\alpha \lambda ]+t[9{\alpha }^{2}+35{\left(\delta +\rho \right)}^{2}+72\delta \lambda +72\rho \lambda +36{\lambda }^{2}+108\alpha \delta +108\alpha \rho +144\alpha \lambda ]\}$.

In this case, we have $\mathrm{max}\left\{\frac{\alpha \left[9\alpha +5\left(\delta +\rho \right)\right]-t\left(6\alpha +\delta +\rho \right)-3{t}^{2}}{6\left(t-\alpha \right)},\frac{t}{2}-\frac{\alpha }{2}+\frac{\delta +\rho }{6}\right\}<\lambda <\mathrm{min}\{\frac{9{t}^{2}-6t\alpha -5t\left(\delta +\rho \right)+\alpha \left(\alpha +\rho -3\alpha \right)}{6\left(t-\alpha \right)},\frac{3{t}^{2}-2{\alpha }^{2}-t(\alpha +\delta +\rho )}{2t}\}$ to guarantee $0<{n}_{i}^{S3*}, {n}_{M}^{S3*}<1$ and $\max\left\{p_A^{S3\ast},p_B^{S3\ast}\right\}<p_M^{S3\ast}<p_A^{S3\ast}+p_B^{S3\ast}.$

Lemma B4

When the additional content of platform A is shared with platform B, the price for the membership bundle is ${p}_{M}^{S4*}=\frac{2{t}^{2}-t\alpha +\alpha (\rho +2\lambda -\alpha )}{2(t+\alpha )}$, the price for each platform’s stand-alone service is ${p}_{A}^{S4*}=\frac{15{t}^{2}+t\left(\rho -6\alpha -6\lambda \right)+\alpha (7\rho +6\lambda -9\alpha )}{12(t+\alpha )}$, and ${p}_{B}^{S4*}=\frac{15{t}^{2}-t\left(7\rho +6\alpha +6\lambda \right)-\alpha (\rho -6\lambda +9\alpha )}{12(t+\alpha )}$. The number of consumers joining one platform is ${n}_{A}^{S4*}=\frac{9{t}^{2}-t\left(6\alpha +\rho +6\lambda \right)+\alpha (5\rho +6\lambda -3\alpha )}{12({t}^{2}-{\alpha }^{2})}$, ${n}_{B}^{S4*}=\frac{9{t}^{2}-t\left(6\alpha +5\rho +6\lambda \right)+\alpha (\rho +6\lambda -3\alpha )}{12({t}^{2}-{\alpha }^{2})}$, and the number of consumers joining both platforms is ${n}_{M}^{S4*}=\frac{2\lambda +\alpha +\rho -t}{2(t+\alpha )}$. Each platform’s profit is ${\pi }_{A}^{S4*}=\frac{1}{144(t-\alpha )(t+\alpha )}\{99{t}^{3}-3{t}^{2}\left(51\alpha +24\lambda -10\rho \right)+\alpha \left(45{\alpha }^{2}-72\alpha \lambda -36{\lambda }^{2}-66\alpha \rho +17{\rho }^{2}\right)+t[9{\alpha }^{2}+36{\lambda }^{2}-{\rho }^{2}+36\alpha (4\lambda +\rho )]\}$, and ${\pi }_{B}^{S4*}=\frac{1}{144(t-\alpha )(t+\alpha )}\left\{99{t}^{3}-3{t}^{2}\left(51\alpha +24\lambda +34\rho \right)+\alpha \left[45{\alpha }^{2}-36{\lambda }^{2}-72\lambda \rho -19{\rho }^{2}-6\alpha \left(12\lambda +\rho \right)\right]+t\left[9{\alpha }^{2}+36{\lambda }^{2}+72\lambda \rho +35{\rho }^{2}+36\alpha \left(4\lambda +3\rho \right)\right]\right\}$.

In this case, we have $\mathrm{max}\left\{\frac{9{\alpha }^{2}+5\alpha \rho -6t\alpha -t\rho -3{t}^{2}}{6\left(t-\alpha \right)},\frac{t}{2}-\frac{\alpha }{2}+\frac{\rho }{6}\right\}<\lambda <\mathrm{min}\{\frac{9{t}^{2}-5t\rho -6t\alpha +\alpha \rho -3{\alpha }^{2}}{6\left(t-\alpha \right)},\frac{3{t}^{2}-2{\alpha }^{2}-t(\alpha +\rho )}{2t}\}$ to guarantee that $0<{n}_{i}^{S4*}, {n}_{M}^{S4*}<1$ and $\max\left\{p_A^{S4\ast},p_B^{S4\ast}\right\}<p_M^{S4\ast}<p_A^{S4\ast}+p_B^{S4\ast}.$

Then, regarding the platforms’ profit differential under the two scenarios, we can summarize the relevant outcomes in the following lemma.

Lemma B5

With the membership bundle, in equilibrium, ${\pi }_{A}^{S3*}>{\pi }_{A}^{S4*}$; if $\lambda<\frac{102t^2-108t\alpha+6\alpha^2-(35t-19\alpha)(\delta+2\rho)}{72(t-\alpha)}\left(\delta<\frac{102t^2+2\alpha\left(3\alpha+36\lambda+19\rho\right)-2t(54\alpha+36\lambda+35\rho)}{35t-19\alpha}\right)$, ${\pi }_{B}^{S3*}<{\pi }_{B}^{S4*}$, if $\lambda>\frac{102t^2-108t\alpha+6\alpha^2-(35t-19\alpha)(\delta+2\rho)}{72(t-\alpha)}\left(\delta>\frac{102t^2+2\alpha\left(3\alpha+36\lambda+19\rho\right)-2t(54\alpha+36\lambda+35\rho)}{35t-19\alpha}\right)$, $\pi_B^{S3\ast}>\pi_B^{S4\ast}.$

On the basis of Lemmas 4 and B5, we can further summarize the content-sharing decision of platform A in the following proposition.

Proposition B2

• (a) With the membership bundle, when $\lambda<\frac{36t^2-72t\alpha-17t\left(\delta+2\rho\right)+\alpha(36\alpha+\delta+2\rho)}{36(t-\alpha)}\left(\delta<\frac{36t^2+2\alpha\left(18\alpha+18\lambda+\rho\right)-2t(36\alpha+18\lambda+17\rho)}{36(t-\alpha)(t+\alpha)}\right)$, platform A shares its additional first-party content with platform B; when $\lambda>\frac{36t^2-72t\alpha-17t\left(\delta+2\rho\right)+\alpha(36\alpha+\delta+2\rho)}{36(t-\alpha)}\left(\delta>\frac{36t^2+2\alpha\left(18\alpha+18\lambda+\rho\right)-2t(36\alpha+18\lambda+17\rho)}{36(t-\alpha)(t+\alpha)}\right)$, platform A exclusively holds its additional first-party content.

• (b) When the additional content is nonexclusively shared with platform B (i.e., $\lambda <\frac{36{t}^{2}-72t\alpha -17t\left(\delta +2\rho \right)+\alpha (36\alpha +\delta +2\rho )}{36(t-\alpha )}$ or $\delta <\frac{36{t}^{2}+2\alpha \left(18\alpha +18\lambda +\rho \right)-2t(36\alpha +18\lambda +17\rho )}{36(t-\alpha )(t+\alpha )}$), platform A prices the additional content at ${w}^{*}=\frac{\delta [102{t}^{2}+\alpha \left(6\alpha +19\delta +72\lambda +38\rho \right)-t(108\alpha +35\delta +72\lambda +70\rho )]}{144(t-\alpha )(t+\alpha )}$. Each platform’s final profit is ${\pi }_{A}^{*}=\frac{1}{144(t-\alpha )(t+\alpha )}\{99{t}^{3}-3{t}^{2}\left(51\alpha -34\delta +24\lambda -10\rho \right)+t\left[9{\alpha }^{2}-35{\delta }^{2}-72\delta \lambda +36{\lambda }^{2}-36\alpha \left(3\delta -4\lambda -\rho \right)-70\delta \rho -{\rho }^{2}\right]+\alpha [45{\alpha }^{2}+19{\delta }^{2}+72\delta \lambda -36{\lambda }^{2}+6\alpha \left(\delta -12\lambda -11\rho \right)+38\delta \rho +17{\rho }^{2}]\}$, and $\pi_B^\ast=\frac1{144\left(t-\alpha\right)\left(t+\alpha\right)}\{99t^3-3t^2\left(51\alpha+34\delta+34\rho+24\lambda\right)+\alpha\lbrack45\alpha^2-19({\delta+\rho)}^2-72\delta\lambda-72\rho\lambda-36\lambda^2-6\alpha\delta-6\alpha\rho-72\alpha\lambda\rbrack+t\lbrack9\alpha^2+35\left(\delta+\rho\right)^2+72\delta\lambda+72\rho\lambda+36\lambda^2+108\alpha\delta+108\alpha\rho+144\alpha\lambda\rbrack\}.$

Finally, we present the boundary condition for the platforms to collaborate and offer the membership bundle. The result is summarized in the following proposition.

Proposition B3

When $\lambda <\mathrm{min}\{{\lambda }_{3},{\lambda }_{4}\}$, the platforms offer the membership bundle; when $\lambda >\mathrm{min}\{{\lambda }_{3},{\lambda }_{4}\}$, the platforms do not offer the membership bundle.

The expressions of ${\lambda }_{3}$ and ${\lambda }_{4}$ are too complex and relegated to Appendix 1. The above results suggest that with platform asymmetry, when the stronger platform produces the additional first-party content and makes the content-sharing decision, the corresponding equilibrium outcomes and findings are consistent with our main model, which proves the robustness of our findings.

2.2.2 The Weaker Platform Produces the Additional First-party Content

We now present the case in which platform B, the weaker platform, produces additional content and further discuss the content-sharing and membership bundle offering decision.

When the platforms do not offer the membership bundle, we summarize the platforms’ equilibrium demands and prices in the following lemmas according to the content-sharing decision.

Lemma B6

When the additional content is exclusively held by platform B, each platform’s equilibrium price is ${p}_{A}^{W1*}=\frac{2{t}^{2}\left(\alpha +\lambda +\rho \right)-t\alpha \left(\alpha +\delta +\lambda \right)-{\alpha }^{2}(\alpha +\lambda +\rho )}{4{t}^{2}-{\alpha }^{2}}$, and ${p}_{B}^{W1*}=\frac{2{t}^{2}\left(\alpha +\delta +\lambda \right)-t\alpha \left(\alpha +\lambda +\rho \right)-{\alpha }^{2}(\alpha +\delta +\lambda )}{4{t}^{2}-{\alpha }^{2}}$. The number of consumers joining one platform is ${n}_{A}^{W1*}=\frac{4{t}^{4}+{\alpha }^{4}-2{t}^{3}\left(\alpha +\delta +\lambda \right)+{t}^{2}\alpha (\lambda +\rho -4\alpha )+t{\alpha }^{2}\left(\alpha +\delta +\lambda \right)}{4{t}^{4}-5{t}^{2}{\alpha }^{2}+{\alpha }^{4}}$, ${n}_{B}^{W1*}=\frac{4{t}^{4}+{\alpha }^{4}-2{t}^{3}\left(\alpha +\lambda +\rho \right)+{t}^{2}\alpha (\lambda +\delta -4\alpha )+t{\alpha }^{2}\left(\alpha +\lambda +\rho \right)}{4{t}^{4}-5{t}^{2}{\alpha }^{2}+{\alpha }^{4}}$, and the number of consumers joining both platforms is ${n}_{M}^{W1*}=\frac{{\alpha }^{2}+t\left(\alpha +\delta +2\lambda +\rho \right)-2{t}^{2}}{(2t-\alpha )(t+\alpha )}$. Each platform’s profit is ${\pi }_{A}^{W1*}=\frac{t{[t\alpha \left(\alpha +\delta +\lambda \right)+{\alpha }^{2}(\alpha +\lambda +\rho )-2{t}^{2}(\alpha +\lambda +\rho )]}^{2}}{(t-\alpha )(t+\alpha ){({\alpha }^{2}-4{t}^{2})}^{2}}$, and $\pi_B^{W1\ast}=\frac{t{\lbrack t\alpha\left(\alpha+\lambda+\rho\right)+\alpha^2(\alpha+\delta+\lambda)-2t^2(\alpha+\delta+\lambda)\rbrack}^2}{(t-\alpha)(t+\alpha){(\alpha^2-4t^2)}^2}.$

In this case, regarding the constraints to keep $0<{n}_{i}^{W1*}, {n}_{M}^{W1*}<1$, we may have two sets of conditions: first, when $\delta >\rho$, we have $\mathrm{max}\{\frac{t\alpha \left(\delta -\rho \right)}{2{t}^{2}-t\alpha -{\alpha }^{2}}-\left(\alpha +\rho \right),t-\frac{{\alpha }^{2}}{2t}-\frac{\alpha +\delta +\rho }{2}\}<\lambda <\frac{4{t}^{4}+{\alpha }^{4}-2{t}^{3}\left(\alpha +\delta \right)+t{\alpha }^{2}\left(\alpha +\delta \right)+{t}^{2}\alpha (\rho -4\alpha )}{t(2{t}^{2}-t\alpha -{\alpha }^{2})}$; second, when $\delta <\rho$, we have $\max\left\{\frac{t\alpha\left(\rho-\delta\right)}{2t^2-t\alpha-\alpha^2}-\left(\alpha+\delta\right),t-\frac{\alpha^2}{2t}-\frac{\alpha+\delta+\rho}2\right\}<\lambda<\frac{4t^4+\alpha^4-2t^3\left(\alpha+\rho\right)+t\alpha^2\left(\alpha+\rho\right)+t^2\alpha(\delta-4\alpha)}{t(2t^2-t\alpha-\alpha^2)}.$

When the additional content of platform B is shared with platform A, the equilibrium outcomes are consistent with Lemma B2.

Regarding the two platforms’ equilibrium profits in the two scenarios, we have ${\pi }_{B}^{W1*}>{\pi }_{B}^{S2*}$, ${\pi }_{A}^{W1*}<{\pi }_{A}^{S2*}$; then, on the basis of Lemma 4, we summarize platform B’s content-sharing decision in the following proposition.

Proposition B4

• (a) Without the membership bundle, when $\lambda<\frac{\left(8t^3\alpha-4t\alpha^2\right)\left(\alpha+\rho\right)-(4t^2+3t^2\alpha^2+\alpha^4)(2\alpha+\delta+2\lambda)}{2{(t-\alpha)}^2{(2t+\alpha)}^2}\left(\delta<\frac{\left(8t^3\alpha-4t\alpha^3\right)\left(\alpha+\lambda+\rho\right)+(-8t^4+6t^2\alpha^2-2\alpha^4)(\alpha+\lambda)}{4t^4-3t^2\alpha^2+\alpha^4}\right)$, platform B shares its additional first-party content with platform A; when $\lambda>\frac{\left(8t^3\alpha-4t\alpha^2\right)\left(\alpha+\rho\right)-(4t^2+3t^2\alpha^2+\alpha^4)(2\alpha+\delta+2\lambda)}{2{(t-\alpha)}^2{(2t+\alpha)}^2}\left(\delta>\frac{\left(8t^3\alpha-4t\alpha^3\right)\left(\alpha+\lambda+\rho\right)+(-8t^4+6t^2\alpha^2-2\alpha^4)(\alpha+\lambda)}{4t^4-3t^2\alpha^2+\alpha^4}\right)$, platform B exclusively holds its additional first-party content.

• (b) When the additional content is nonexclusively shared with platform A (i.e., $\lambda <\frac{\left(8{t}^{3}\alpha -4t{\alpha }^{2}\right)\left(\alpha +\rho \right)-(4{t}^{2}+3{t}^{2}{\alpha }^{2}+{\alpha }^{4})(2\alpha +\delta +2\lambda )}{2{(t-\alpha )}^{2}{(2t+\alpha )}^{2}}$ or $\delta <\frac{\left(8{t}^{3}\alpha -4t{\alpha }^{3}\right)\left(\alpha +\lambda +\rho \right)+(-8{t}^{4}+6{t}^{2}{\alpha }^{2}-2{\alpha }^{4})(\alpha +\lambda )}{4{t}^{4}-3{t}^{2}{\alpha }^{2}+{\alpha }^{4}}$), platform B prices the additional content at ${w}^{*}=\frac{{t}^{2}\alpha \delta [4{t}^{2}\left(\alpha +\lambda +\rho \right)-2{\alpha }^{2}\left(\alpha +\lambda +\rho \right)-t\alpha (2\alpha +\delta +2\lambda )]}{(t-\alpha )(t+\alpha ){({\alpha }^{2}-4{t}^{2})}^{2}}$, and each platform’s final profit is ${\pi }_{A}^{*}=\frac{t{[t\alpha \left(\alpha +\delta +\lambda \right)+{\alpha }^{2}(\alpha +\lambda +\rho )-2{t}^{2}(\alpha +\lambda +\rho )]}^{2}}{(t-\alpha )(t+\alpha ){({\alpha }^{2}-4{t}^{2})}^{2}}$, $\pi_B^\ast=\frac t{(t-\alpha)(t+\alpha){(\alpha^2-4t^2)}^2}\{\left[-2t^2\left(\alpha+\lambda\right)+\alpha^2\left(\alpha+\lambda\right)+t\alpha\left(\alpha+\lambda+\rho\right)\right]^2+t\alpha\delta\lbrack4t^2\left(\alpha+\lambda+\rho\right)-2\alpha^2\left(\alpha+\lambda+\rho\right)-t\alpha(2\alpha+\delta+2\lambda)\rbrack\}.$  

From proposition B4, we find that even without the membership bundle, platform B, as the weaker one, may choose to nonexclusively share its additional first-party content with platform A, instead of keeping it exclusive to mitigate its value disadvantage compared to platform A. This may be because with the content-sharing choice, platform B’s final profit is composed of both the revenue from consumers and the income of selling the first-party content, wherein the latter depends on platform A’s profit differential under the two cases. As in our model, each platform’s demand and the corresponding price lie on the value differential between the two platforms. When $\lambda$ or $\delta$ is low, the efficiency of content exclusivity in demand enhancement and disadvantage mitigation is limited. As a result, platform B relies on the content-sharing revenue and chooses to share with platform A. In contrast, when $\lambda$ or $\delta$ is large, content exclusivity can significantly mitigate platform B’s content differential with platform A or even make it the dominant platform. This significantly increases platform B’s demand and revenue from consumers. Consequently, platform B chooses to keep the content exclusive.

When the platforms offer the membership bundle, we can also present the equilibrium strategies in the following lemmas.

Lemma B7

When the additional content is exclusively held by platform A, the price for the membership bundle is ${p}_{M}^{W2*}=\frac{2{t}^{2}-t\alpha +\alpha (2\lambda +\delta +\rho -\alpha )}{2(t+\alpha )}$, and the price for each platform’s stand-alone service is ${p}_{A}^{W2*}=\frac{15{t}^{2}+t\left(-7\delta +\rho -6\alpha -6\lambda \right)-\alpha (\delta -7\rho -6\lambda +9\alpha )}{12(t+\alpha )}$, ${p}_{B}^{W2*}=\frac{15{t}^{2}+t\left(\delta -7\rho -6\alpha -6\lambda \right)-\alpha (-7\delta +\rho -6\lambda +9\alpha )}{12(t+\alpha )}$, respectively. The number of consumers joining one platform is ${n}_{A}^{W2*}=\frac{9{t}^{2}-t\left(6\alpha +5\delta +\rho +6\lambda \right)+\alpha (\delta +5\rho +6\lambda -3\alpha )}{12({t}^{2}-{\alpha }^{2})}$, ${n}_{B}^{W2*}=\frac{9{t}^{2}-t\left(6\alpha +\delta +5\rho +6\lambda \right)+\alpha (5\delta +\rho +6\lambda -3\alpha )}{12({t}^{2}-{\alpha }^{2})}$, and the number of consumers joining both platforms is ${n}_{M}^{W2*}=\frac{2\lambda +\alpha +\delta +\rho -t}{2(t+\alpha )}$. Each platform’s profit is ${\pi }_{A}^{W2*}=\frac{1}{144(t-\alpha )(t+\alpha )}\{99{t}^{3}-3{t}^{2}\left(51\alpha +34\delta -10\rho +24\lambda \right)+\alpha [45{\alpha }^{2}-19{\delta }^{2}-72\delta \lambda -36{\lambda }^{2}-34\delta \rho +17{\rho }^{2}-6\alpha \delta -72\alpha \lambda -66\alpha \rho ]+t[9{\alpha }^{2}+35{\delta }^{2}+72\delta \lambda +36{\lambda }^{2}+2\delta \rho -{\rho }^{2}+108\alpha \delta +36\alpha \rho +144\alpha \lambda ]\}$, and $\pi_B^{W2\ast}=\frac1{144\left(t-\alpha\right)\left(t+\alpha\right)}\{99t^3-3t^2\left(51\alpha-10\delta+34\rho+24\lambda\right)+\alpha\lbrack45\alpha^2+17\delta^2-36\lambda^2-34\delta\rho-72\lambda\rho-19\rho^2-66\alpha\delta-6\alpha\rho-72\alpha\lambda\rbrack+t\lbrack9\alpha^2-\delta^2+36\lambda^2+2\delta\rho+72\rho\lambda+35\rho^2+36\alpha\delta+108\alpha\rho+144\alpha\lambda\rbrack\}.$

In this case, regarding the constraints for $0<{n}_{i}^{W2*}, {n}_{M}^{W2*}<1$ and $\mathrm{max}\left\{{p}_{A}^{W2*},{p}_{B}^{W2*}\right\}<{p}_{M}^{W2*}<{p}_{A}^{*}+{p}_{B}^{*}$, we still have two sets of conditions to be met, when $\delta >\rho$, $\mathrm{max}\{\frac{\alpha \left(9\alpha +5\delta +\rho \right)-t\left(6\alpha +\delta +5\rho \right)-3{t}^{2}}{6\left(t-\alpha \right)},\frac{t-\alpha }{2}+\frac{\delta -7\rho }{6}\}<\lambda <\mathrm{min}\{\frac{9{t}^{2}-t\left(6\alpha +5\delta +\rho \right)+\alpha \left(-3\alpha +\delta +5\rho \right)}{6\left(t-\alpha \right)},\frac{3t}{2}-\frac{{\alpha }^{2}}{t}-\frac{\alpha +\delta +\rho }{2}\}$; when $\delta <\rho$, $\max\left\{\frac{\alpha\left(9\alpha+\delta+5\rho\right)-t\left(6\alpha+5\delta+\rho\right)-3t^2}{6\left(t-\alpha\right)},\frac{t-\alpha}2+\frac{\rho-7\delta}6\right\}<\lambda<\min\{\frac{9t^2-t\left(6\alpha+\delta+5\rho\right)+\alpha\left(-3\alpha+5\delta+\rho\right)}{6\left(t-\alpha\right)},\frac{3t}2-\frac{\alpha^2}t-\frac{\alpha+\delta+\rho}2\}.$

When the additional content of platform B is shared with platform A, the equilibrium outcomes are consistent with Lemma B4.

Then, we can compare the two platforms’ equilibrium profits under the two cases, as shown in the following lemma.

Lemma B8

With the membership bundle, in equilibrium, if $\alpha <\frac{t}{17}$, when $\delta <\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\pi }_{B}^{W2*}>{\pi }_{B}^{S4*}$, when $\delta >\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\pi }_{B}^{W2*}<{\pi }_{B}^{S4*}$; if $\alpha >\frac{t}{17}$, when $\delta <\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\pi }_{B}^{W2*}<{\pi }_{B}^{S4*}$, when $\delta >\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\pi }_{B}^{W2*}>{\pi }_{B}^{S4*}$. When $\delta <\frac{102{t}^{2}-2t\left(54\alpha +36\lambda +\rho \right)+2\alpha (3\alpha +36\lambda +17\rho )}{35t-19\alpha }$, ${\pi }_{A}^{S4*}>{\pi }_{A}^{W2*}$, and when $\delta >\frac{102{t}^{2}-2t\left(54\alpha +36\lambda +\rho \right)+2\alpha (3\alpha +36\lambda +17\rho )}{35t-19\alpha }$, $\pi_A^{S4\ast}<\pi_A^{W2\ast}.$

Consequently, on the basis of Lemmas 4 and B7, we summarize platform B’s content-sharing decision in the following proposition.

Proposition B5

• (a) If $t>\frac{3\sqrt{3328{\alpha }^{2}+992\alpha \left(\lambda +\rho \right)+{(\lambda +\rho )}^{2}}-145\alpha -3\lambda -3\rho }{79}$, when $\delta <\frac{36{t}^{2}-2t\left(36\alpha +18\lambda +\rho \right)+2\alpha (18\alpha +18\lambda +17\rho )}{17t-\alpha }$, platform B shares its additional first-party content with platform A; when $\delta >\frac{36{t}^{2}-2t\left(36\alpha +18\lambda +\rho \right)+2\alpha (18\alpha +18\lambda +17\rho )}{17t-\alpha }$, platform B exclusively holds its additional first-party content; if $t<\frac{3\sqrt{3328{\alpha }^{2}+992\alpha \left(\lambda +\rho \right)+{(\lambda +\rho )}^{2}}-145\alpha -3\lambda -3\rho }{79}$, when $\delta <\frac{102{t}^{2}-2t\left(54\alpha +36\lambda +\rho \right)+2\alpha (3\alpha +36\lambda +17\rho )}{35t-19\alpha }$, platform B shares its additional first-party content with platform A; when $\delta >\frac{102{t}^{2}-2t\left(54\alpha +36\lambda +\rho \right)+2\alpha (3\alpha +36\lambda +17\rho )}{35t-19\alpha }$, platform B exclusively holds its additional first-party content.

• (b) When the additional content is nonexclusively shared with platform A, platform B prices the additional content at ${w}^{*}=\frac{\delta [102{t}^{2}-t\left(108\alpha +35\delta +72\lambda +2\rho \right)+\alpha (6\alpha +19\delta +72\lambda +34\rho )]}{144(t-\alpha )(t+\alpha )}$. Each platform’s final profit is ${\pi }_{A}^{*}=\frac{1}{144(t-\alpha )(t+\alpha )}\{99{t}^{3}-3{t}^{2}\left(51\alpha +34\delta -10\rho +24\lambda \right)+\alpha [45{\alpha }^{2}-19{\delta }^{2}-72\delta \lambda -36{\lambda }^{2}-34\delta \rho +17{\rho }^{2}-6\alpha \delta -72\alpha \lambda -66\alpha \rho ]+t[9{\alpha }^{2}+35{\delta }^{2}+72\delta \lambda +36{\lambda }^{2}+2\delta \rho -{\rho }^{2}+108\alpha \delta +36\alpha \rho +144\alpha \lambda ]\}$, and $\pi_B^\ast=\frac1{144(t-\alpha)(t+\alpha)}\{99t^3-3t^2\left(51\alpha-34\delta+24\lambda+34\rho\right)+\alpha\left[45\alpha^2+19\delta^2+72\delta\lambda-36\lambda^2+6\alpha\left(\delta-12\lambda-\rho\right)+34\delta\rho-72\lambda\rho-19\rho^2\right]+t\lbrack9\alpha^2+36\lambda^2+72\lambda\rho+35\rho^2+36\alpha(4\lambda+3\rho)\rbrack\}.$

In line with our main model, Proposition B5 suggests that with the membership bundle, platform B tends to share its additional first-party content with platform A when $\delta$ is relatively low.

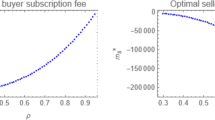
Finally, regarding the membership bundle offering decision, on the basis of content sharing outcomes, we may have four possible scenarios, i.e., the content is kept exclusive regardless of the membership bundle, the content is nonexclusive regardless of the membership bundle, the content is exclusive without the bundle but is nonexclusive with the bundle, and the content is nonexclusive without the bundle but is exclusive with the bundle. Theoretically, we can have that in the four possible scenarios, each platform’s profit differential between the condition with and without the bundle can be expressed by a quadratic function of $\lambda$ with an upward opening. We may have two roots characterizing the relevant thresholds regarding the membership bundle offering decision, and the larger root exceeds the upper bound of the feasible region. Consequently, we have that under each scenario, when $\lambda$ is relatively small, the platforms choose to collaborate and offer the membership bundle, which is also in line with our main model. However, due to the high nonlinearity of the profit functions, the relevant thresholds are extremely hard to characterize, so, we still seek to numerical method to obtain the relevant results, as shown in Fig. 5. Note that the major findings remain unchanged if we assign other values over the parameters.

Fig. 5

The membership bundle offering decision and content distribution outcome when the weaker platform produces additional first-party content ($t=1$). a $\delta >\rho$ ($\delta =0.3$, $\rho =0.2$), b $\delta <\rho$ ($\delta =0.2$, $\rho =0.3$). Notes: In subfigure (a), the content is always exclusive. In subfigure (b), the two platforms offer the membership bundle in regions II and III, but do not offer the bundle in regions I and VI. The additional content is exclusive in regions I and II, but goes nonexclusive in regions III and VI

As shown in Fig. 5, we can find that when the weaker platform produces some additional first-party content and makes the content-sharing decision, the two platforms will collaborate and offer the membership bundle when $\lambda$ is relatively low. Additionally, the content is nonexclusively shared under low $\lambda$, but goes exclusive when $\lambda$ is large. The above results are in line with what we have in the main model, suggesting that our findings are robust.

2.3 Extension 3–Revenue Sharing by a Nash-Bargaining Process

In the main model, we assume the revenue from multihoming consumers who purchase the membership bundle to be split equally between the two platforms, as The Information and Bloomberg Media do, and for the sake of simplicity. In this section, we relax this assumption, and consider the two platforms share the revenue using a Nash-bargaining process, which has been widely introduced in relevant research, we use a “ ~ ” above the variables to represent this case. Now, we illustrate the new revenue-sharing contract. With the membership bundle, platform A occupies a faction $\mu , \mu \in (\mathrm{0,1})$ of the revenue generated from the bundle, as a result of Nash-bargaining, and platform B receives the rest $1-\mu$. Then the two platforms’ profit function is updated to $\widetilde{{\pi }_{A}}=\widetilde{{p}_{A}}\widetilde{{n}_{A}}+\mu \widetilde{{p}_{M}}\widetilde{{n}_{M}}$, ${\pi }_{B}=\widetilde{{p}_{B}}\widetilde{{n}_{B}}+(1-\mu )\widetilde{{p}_{M}}\widetilde{{n}_{M}}$, respectively. Furthermore, for the sake of simplicity, we consider the two platforms to have equal bargaining power, which has also been widely introduced in previous works (Chiang & Jhang-Li, 2020). The Nash-bargaining process shapes the timeline of events as follows: in Stage 1, the two platforms negotiate on $\mu$, and make up the bundle offering decision. The following stages remain consistent with the main model.

Solving the model by backward induction, we have the equilibrium outcomes in Stages 2–4. If without the membership bundle, the equilibrium outcomes (Lemmas 1 and 3) remain valid, and in equilibrium, the additional first-party content is always kept exclusive, as shown in Proposition 2. When the platforms offer the bundle, we can summarize the corresponding outcomes in the following lemmas.

Lemma C1

When the additional first-party content is exclusively held by platform A, the price for the membership bundle is $\widetilde{{p}_{M}^{1*}}=\frac{2{t}^{2}-t\alpha +\alpha (2\lambda +\delta -\alpha )}{2(t+\alpha )}$, and the price for each platform’s stand-alone service is $\widetilde{{p}_{A}^{1*}}=\frac{{t}^{2}\left(8-\mu \right)+t\left[2\left(\alpha +\lambda \right)\left(\mu -2\right)+\delta \mu \right]-\alpha [\delta \left(\mu -4\right)+2\lambda \left(\mu -2\right)+\alpha (\mu +4)]}{6(t+\alpha )}$, $\widetilde{{p}_{B}^{1*}}=\frac{{t}^{2}\left(7+\mu \right)-t\left[2\left(\alpha +\lambda \right)\left(\mu +1\right)+\delta \left(3+\mu \right)\right]+\alpha [\delta \left(\mu -1\right)+2\lambda \left(\mu +1\right)+\alpha (\mu -5)]}{6(t+\alpha )}$. The number of consumers joining one platform is $\widetilde{{n}_{A}^{1*}}=\frac{{t}^{2}\left(\mu +4\right)-t\left[2\left(\alpha +\lambda \right)\left(\mu +1\right)+\delta \mu \right]+\alpha [\delta \left(\mu +2\right)+2\lambda \left(\mu +1\right)+\alpha (\mu -2)]}{6({t}^{2}-{\alpha }^{2})}$, $\widetilde{{n}_{B}^{1*}}=\frac{{t}^{2}\left(5-\mu \right)+t\left[2\left(\alpha +\lambda \right)\left(\mu -2\right)+\delta (\mu -3)\right]-\alpha [\delta \left(\mu -1\right)+2\lambda \left(\mu -2\right)+\alpha (\mu +1)]}{6({t}^{2}-{\alpha }^{2})}$, and the number of consumers joining both platforms is $\widetilde{{n}_{M}^{1*}}=\frac{2\lambda +\alpha +\delta -t}{2(t+\alpha )}$. Each platform’s profit is $\widetilde{{\pi }_{A}^{1*}}=\widetilde{{p}_{A}^{1*}}\widetilde{{n}_{A}^{1*}}+\mu \widetilde{{p}_{M}^{1*}}\widetilde{{n}_{M}^{1*}}$, $\widetilde{\pi_B^{1\ast}}=\widetilde{p_B^{1\ast}}\widetilde{n_B^{1\ast}}+(1-\mu)\widetilde{p_M^{1\ast}}\widetilde{n_M^{1\ast}}.$

Lemma C2

When the additional first-party content is shared with platform B, the price for the membership bundle is $\widetilde{{p}_{M}^{2*}}=\frac{2{t}^{2}-t\alpha -\alpha (\alpha -2\lambda )}{2(t+\alpha )}$, and the price for each platform’s stand-alone service is $\widetilde{{p}_{A}^{2*}}=\frac{\left(t-\alpha \right)[t\left(8-\mu \right)+2\lambda \left(\mu -2\right)+\alpha (\mu +4)]}{6(t+\alpha )}$, $\widetilde{{p}_{B}^{2*}}=\frac{\left(t-\alpha \right)[t\left(\mu +7\right)-2\lambda \left(\mu +1\right)-\alpha (\mu -5)]}{6(t+\alpha )}$. The number of consumers joining one platform is $\widetilde{{n}_{A}^{2*}}=\frac{t\left(\mu +4\right)-2\lambda \left(\mu +1\right)-\alpha (\mu -2)}{6(t+\alpha )}$, $\widetilde{{n}_{B}^{2*}}=\frac{t\left(5-\mu \right)+2\lambda \left(\mu -2\right)+\alpha (\mu +1)}{6(t+\alpha )}$, and the number of consumers joining both platforms is $\widetilde{{n}_{M}^{2*}}=\frac{2\lambda +\alpha -t}{2(t+\alpha )}$. Each platform’s profit is $\widetilde{{\pi }_{A}^{2*}}=\widetilde{{p}_{A}^{2*}}\widetilde{{n}_{A}^{2*}}+\mu \widetilde{{p}_{M}^{2*}}\widetilde{{n}_{M}^{2*}}$, $\widetilde{{\pi }_{B}^{2*}}=\widetilde{{p}_{B}^{2*}}\widetilde{{n}_{B}^{2*}}+(1-\mu )\widetilde{{p}_{M}^{2*}}\widetilde{{n}_{M}^{2*}}$.

In the above two cases, we still have that $0<\widetilde{{n}_{i}^{*}}, \widetilde{{n}_{M}^{*}}<1$ and $\mathrm{max}\left\{\widetilde{{p}_{A}^{*}},\widetilde{{p}_{B}^{*}}\right\}<\widetilde{{p}_{M}^{*}}<\widetilde{{p}_{A}^{*}}+\widetilde{{p}_{B}^{*}}$ in equilibrium.

Further, we can characterize the content-sharing decision with the membership bundle. First, regarding the two platforms’ profit under the two subgames, we have the following lemma.

Lemma C3

With the membership bundle, in equilibrium, $\widetilde{{\pi }_{A}^{1*}}>\widetilde{{\pi }_{A}^{2*}}$; when $\lambda <{\lambda }^{a}$, $\widetilde{{\pi }_{B}^{1*}}<\widetilde{{\pi }_{B}^{2*}}$, and when $\lambda >{\lambda }^{a}$, $\widetilde{{\pi }_{B}^{1*}}>\widetilde{{\pi }_{B}^{2*}}$, wherein ${\lambda }^{a}=\frac{1}{2{\alpha }^{2}\left(2{\mu }^{2}-21\mu +19\right)-4t\alpha \left(2{\mu }^{2}-11\mu +5\right)+2{t}^{2}\left(2{\mu }^{2}-\mu -9\right)}\{-{\alpha }^{2}\left[\delta \left(\mu -10\right)+2\alpha \left(\mu -2\right)\right]\left(\mu -1\right)+2{t}^{3}\left({\mu }^{2}-8\mu -9\right)-{t}^{2}\left[\delta \left({\mu }^{2}-9\right)+2\alpha \left(3{\mu }^{2}-19\mu +8\right)\right]+t\alpha [\alpha \left(2{\mu }^{2}-11\mu +9\right)+\alpha \left(6{\mu }^{2}-28\mu +38\right)]\}$

Consequently, on the basis of Lemmas C3 and 4, we can summarize the platforms’ content-sharing decision in the following proposition.

Proposition C1

• (a) With the membership bundle, when $\lambda <{\lambda }^{b}$, platform A’s additional first-party content is shared with platform B; when $\lambda >{\lambda }^{b}$, platform A exclusively holds the additional first-party content, wherein ${\lambda }^{b}=\frac{1}{2\left(t-\alpha \right)[\alpha \left(6\mu -4{\mu }^{2}-11\right)+t(4{\mu }^{2}-2\mu -9)]}\{2{t}^{3}\left(2{\mu }^{2}-\mu -9\right)+{t}^{2}\left[\delta \left(9-2{\mu }^{2}\right)-2\alpha \left(6{\mu }^{2}-5\mu -9\right)\right]+t\alpha \left[\delta \left(9-4\mu +4{\mu }^{2}\right)+2\alpha \left(6{\mu }^{2}-7\mu +11\right)\right]-2{\alpha }^{2}[\delta {\left(\mu -1\right)}^{2}+\alpha \left(2{\mu }^{2}-3\mu +10\right)]\}$.

• (b) When the additional content is exclusively shared, platform A prices the additional first-party content at $w^\ast=\widetilde{\pi_B^{2\ast}}-\widetilde{\pi_B^{1\ast}}.$ The platform’s profit is $\widetilde{{\pi }_{A}^{3*}}=\widetilde{{\pi }_{A}^{2*}}+\widetilde{{\pi }_{B}^{2*}}-\widetilde{{\pi }_{B}^{1*}}$, $\widetilde{\pi_B^{3\ast}}=\widetilde{\pi_B^{1\ast}.}$

The above result is consistent with what we have in Proposition 3. Now, we can go backward to Stage 1 to analyze the bargaining process. If the two platforms reach an agreement and offer the membership bundle, the additional first-party content may be exclusively or nonexclusively distributed depending on $\lambda$; otherwise, if the two platforms fail to reach an agreement, platform A always exclusively holds the additional content, and the two platform ends up with ${\pi }_{A}^{N*}$, ${\pi }_{B}^{N*}$, respectively. Consequently, the bargaining problem can be described by the payoff pair $(\widetilde{{\pi }_{A}^{1*}},\widetilde{{\pi }_{B}^{1*}})$ if the additional content is exclusive and $(\widetilde{{\pi }_{A}^{3*}},\widetilde{{\pi }_{B}^{3*}})$ if the additional content is nonexclusive with the membership bundle, from the disagreement point $({\pi }_{A}^{N*},{\pi }_{B}^{N*})$. Therefore, the equilibrium revenue-sharing parameter $\mu$ satisfies:

$${\mu }^{1*}=\mathrm{argmax}{(\widetilde{{\pi }_{A}^{1*}}-{\pi }_{A}^{N*})}^{(1/2)}{(\widetilde{{\pi }_{B}^{1*}}-{\pi }_{B}^{N*})}^{(1/2)}$$

and

$${\mu }^{2*}=\mathrm{argmax}{(\widetilde{{\pi }_{A}^{3*}}-{\pi }_{A}^{N*})}^{(1/2)}{(\widetilde{{\pi }_{B}^{3*}}-{\pi }_{B}^{N*})}^{(1/2)}$$

, in constraint to $\widetilde{{\pi }_{i}^{1*}}\ge {\pi }_{i}^{N*}$, and $\widetilde{{\pi }_{i}^{3*}}\ge {\pi }_{i}^{N*}$, $i\in \{A,B\}$, respectively.

Due to the high non-linearity of the functions, the equilibrium revenue-sharing parameters are extremely complex to be analytically solved. Consequently, we seek to numerical method to illustrate how the Nash-bargaining process influences the equilibrium outcomes, as shown in Fig. 6, and the results remain unchanged when we assign other values over the parameters. Based on Fig. 6, we can have the following observation.

Observation 1

When $\lambda$ is relatively low, the two platforms offer the membership bundle; when $\lambda$ is relatively large, the two platforms do not offer the membership bundle.

Fig. 6

The membership bundle offering decision under a Nash-bargaining process ($t=1$). a $\alpha =0$, b $\alpha =0.1$, c $\alpha =0.2$

The result is in line with Propositions 1 and 4. Furthermore, in this case, regardless of the membership bundle offering decision, the additional first-party content is always exclusively held by platform A. The above results are consistent with what we have in the main model, showing that the revenue-sharing mechanism has little influence on our equilibrium outcomes, and suggesting that our findings are robust.

2.3.1 Proof of Lemmas and Propositions of Extensions 1–3

Proof of Lemma A1

By taking the first- and second-order conditions of ${\pi }_{A}^{N*}-\frac{1}{2}k{\delta }^{2}$ and ${\pi }_{A}^{C*}-\frac{1}{2}k{\delta }^{2}$ with respect to $\delta$, let $\frac{\partial {\pi }_{A}^{N*}-\frac{1}{2}k{\delta }^{2}}{\partial \delta }=0$ and $\frac{\partial {\pi }_{A}^{C*}-\frac{1}{2}k{\delta }^{2}}{\partial \delta }=0$, we can have ${\delta }^{N*}=\frac{2\left(t-\alpha \right)(2t+\alpha )(2{t}^{3}-t{\alpha }^{2})(\alpha +\lambda )}{16k{t}^{6}-8{t}^{5}+8{t}^{3}{\alpha }^{2}-24k{t}^{4}{\alpha }^{2}-2t{\alpha }^{4}+9k{t}^{2}{\alpha }^{2}-k{\alpha }^{6}}$, ${\delta }^{C*}=\frac{3(t-\alpha )(5t+11\alpha )}{t+72k{t}^{2}-17\alpha -72k{\alpha }^{2}}$, respectively. We also have $k>\frac{2t{(2{t}^{2}-{\alpha }^{2})}^{2}}{({t}^{2}-{\alpha }^{2}){(4{t}^{2}-{\alpha }^{2})}^{2}}$ to ensure that $\frac{{\partial }^{2}{\pi }_{A}^{N*}-\frac{1}{2}k{\delta }^{2}}{\partial {\delta }^{2}}<0$ and $\frac{\partial^2\pi_A^{C\ast}-\frac12k\delta^2}{\partial\delta^2}<0.$

The proofs of Lemmas B1 and B3 are consistent with the proofs of Lemmas 3 and 6 if we replace $\delta$ by $\delta +\rho$, and the proofs of Lemmas B2 and B4 are consistent with the proofs of Lemmas 3 and 6 if we replace $\delta$ by $\rho$. Consequently, to avoid duplication, we omit the proof process.

Proof of Proposition B1

The proof is straightforward with Lemma 4 and ${\pi }_{A}^{S1*}>{\pi }_{A}^{S2*}$, $\pi_B^{S1\ast}<\pi_B^{S2\ast}.$

Proof of Lemma B5

It is easily to find that ${\pi }_{A}^{S3*}>{\pi }_{A}^{S4*}$ with $t>\alpha$. Let $\Delta ={\pi }_{B}^{S4*}-{\pi }_{B}^{S3*}$, we can find that $\frac{\partial\Delta }{\partial \lambda }<0$, consequently, when $\lambda <\frac{102{t}^{2}-108t\alpha +6{\alpha }^{2}-(35t-19\alpha )(\delta +2\rho )}{72(t-\alpha )}$, $\Delta >0$, otherwise, $\Delta <0$. The proof of the condition for $\delta$ is consistent with this process.

Proof of Proposition B2

On the basis of Lemma 4, we first have that if $\lambda >\frac{102{t}^{2}-108t\alpha +6{\alpha }^{2}-(35t-19\alpha )(\delta +2\rho )}{72(t-\alpha )}$, both platforms benefit from content exclusivity, and the content is exclusively kept. If $\lambda <\frac{102{t}^{2}-108t\alpha +6{\alpha }^{2}-(35t-19\alpha )(\delta +2\rho )}{72(t-\alpha )}$, ${\pi }_{A}^{S3*}>{\pi }_{A}^{S4*}$ and ${\pi }_{B}^{S3*}<{\pi }_{B}^{S4*}$, when $\lambda <\frac{36{t}^{2}-72t\alpha -17t\left(\delta +2\rho \right)+\alpha (36\alpha +\delta +2\rho )}{36(t-\alpha )}$ ($\frac{36{t}^{2}-72t\alpha -17t\left(\delta +2\rho \right)+\alpha (36\alpha +\delta +2\rho )}{36(t-\alpha )}<\frac{102{t}^{2}-108t\alpha +6{\alpha }^{2}-(35t-19\alpha )(\delta +2\rho )}{72(t-\alpha )}$), ${\pi }_{A}^{S3*}-{\pi }_{A}^{S4*}<{\pi }_{B}^{S4*}-{\pi }_{B}^{S3*}$, platform A shares the content, otherwise, the content goes exclusive.

Proof of Proposition B3

In line with the main model, we have that the content always goes exclusive when considering the bundle offering decision in the feasible region. Consequently, the relevant conditions are consistent with the main model if we replace $\delta$ with $\delta +\rho$, and so do the expressions of ${\lambda }_{3}$ and ${\lambda }_{4}$.

Proof of Lemma B6

By solving the first- and second-order conditions of ${\pi }_{i}$ with respect to ${p}_{i}$, we first have that $\frac{{\partial }^{2}{\pi }_{i}}{\partial {p}_{i}^{2}}=-\frac{2t}{{t}^{2}-{\alpha }^{2}}<0$, then, by jointly solving $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=0$ and $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=0$, we can have ${p}_{A}^{*}=\frac{2{t}^{2}\left(\alpha +\lambda +\rho \right)-t\alpha \left(\alpha +\delta +\lambda \right)-{\alpha }^{2}(\alpha +\lambda +\rho )}{4{t}^{2}-{\alpha }^{2}}$, and ${p}_{B}^{*}=\frac{2{t}^{2}\left(\alpha +\delta +\lambda \right)-t\alpha \left(\alpha +\lambda +\rho \right)-{\alpha }^{2}(\alpha +\delta +\lambda )}{4{t}^{2}-{\alpha }^{2}}$, by substituting ${p}_{i}^{*}$ into ${n}_{i}$, ${n}_{M}$, and ${\pi }_{i}$, we finish the proof.

Proof of Proposition B4

With ${\pi }_{B}^{W1*}>{\pi }_{B}^{S2*}$, ${\pi }_{A}^{W1*}<{\pi }_{A}^{S2*}$, and on the basis of Lemma 4, we can have that when $\lambda <\frac{\left(8{t}^{3}\alpha -4t{\alpha }^{2}\right)\left(\alpha +\rho \right)-(4{t}^{2}+3{t}^{2}{\alpha }^{2}+{\alpha }^{4})(2\alpha +\delta +2\lambda )}{2{(t-\alpha )}^{2}{(2t+\alpha )}^{2}}$, ${\pi }_{B}^{W1*}-{\pi }_{B}^{S2*}<{\pi }_{A}^{S2*}-{\pi }_{A}^{W1*}$, platform B prices the content at ${w}^{*}={\pi }_{A}^{S2*}-{\pi }_{A}^{W1*}$, and shares the content, when $\lambda >\frac{\left(8{t}^{3}\alpha -4t{\alpha }^{2}\right)\left(\alpha +\rho \right)-(4{t}^{2}+3{t}^{2}{\alpha }^{2}+{\alpha }^{4})(2\alpha +\delta +2\lambda )}{2{(t-\alpha )}^{2}{(2t+\alpha )}^{2}}$, ${\pi }_{B}^{W1*}-{\pi }_{B}^{S2*}>{\pi }_{A}^{S2*}-{\pi }_{A}^{W1*}$, the content is exclusive.

Proof of Lemma B7

By taking the first- and second-order condition of ${\pi }_{A}+{\pi }_{B}$ with respect to ${p}_{M}$, we first have $\frac{{\partial }^{2}({\pi }_{A}+{\pi }_{B})}{\partial {p}_{M}^{2}}=-\frac{4}{t+\alpha }<0$, then, let $\frac{\partial ({\pi }_{A}+{\pi }_{B})}{\partial {p}_{M}}=0$, we have ${p}_{M}=\frac{2{p}_{A}+2{p}_{B}-t+\alpha +\delta +\rho +2\lambda }{4}$. Substituting ${p}_{M}$ into ${\pi }_{i}$, and take the first- and second-order conditions of ${\pi }_{i}$ with respect to ${p}_{i}$, we have $\frac{{\partial }^{2}{\pi }_{i}}{\partial {p}_{i}^{2}}=\frac{1}{\alpha -t}<0$, by jointly solving $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=0$ and $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=0$, we can have ${p}_{A}^{*}=\frac{15{t}^{2}+t\left(-7\delta +\rho -6\alpha -6\lambda \right)-\alpha (\delta -7\rho -6\lambda +9\alpha )}{12(t+\alpha )}$, ${p}_{B}^{*}=\frac{15{t}^{2}+t\left(\delta -7\rho -6\alpha -6\lambda \right)-\alpha (-7\delta +\rho -6\lambda +9\alpha )}{12(t+\alpha )}$. Substituting ${p}_{i}^{*}$ into ${p}_{M}$, ${n}_{i}$, ${n}_{M}$, and ${\pi }_{i}$, we finish the proof.

Proof of Lemma B8

Let ${\Delta }_{1}={\pi }_{B}^{W2*}-{\pi }_{B}^{S4*}=\frac{\delta [30{t}^{2}+\alpha \left(17\delta -34\rho -66\alpha \right)+t(36\alpha -\delta +2\rho )]}{144(t-\alpha )(t+\alpha )}$, when $\alpha <\frac{t}{17}$, $\frac{\partial {\Delta }_{1}}{\partial \delta }<0$, consequently, when $\delta >\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\Delta }_{1}<0$, and when $\delta <\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\Delta }_{1}>0$, when $\alpha >\frac{t}{17}$, $\frac{\partial {\Delta }_{1}}{\partial \delta }>0$, and thus, when $\delta >\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\Delta }_{1}>0$, and when $\delta <\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\Delta }_{1}<0$. Let ${\Delta }_{2}={\pi }_{A}^{S4*}-{\pi }_{A}^{W2*}=\frac{\delta [102{t}^{2}+\alpha \left(19\delta +34\rho +72\lambda +6\alpha \right)-t(108\alpha +35\delta +72\lambda +2\rho )]}{144(t-\alpha )(t+\alpha )}$, with $t>\alpha$, we can have $\frac{\partial {\Delta }_{2}}{\partial \delta }<0$, consequently, When $\delta <\frac{102{t}^{2}-2t\left(54\alpha +36\lambda +\rho \right)+2\alpha (3\alpha +36\lambda +17\rho )}{35t-19\alpha }$, ${\pi }_{A}^{S4*}>{\pi }_{A}^{W2*}$, and when $\delta >\frac{102{t}^{2}-2t\left(54\alpha +36\lambda +\rho \right)+2\alpha (3\alpha +36\lambda +17\rho )}{35t-19\alpha }$, $\pi_A^{S4\ast}<\pi_A^{W2\ast}.$

Proof of Proposition B5

Let ${\delta }_{1}=\frac{102{t}^{2}-2t\left(54\alpha +36\lambda +\rho \right)+2\alpha (3\alpha +36\lambda +17\rho )}{35t-19\alpha }$, ${\delta }_{2}=\frac{30{t}^{2}+36t\alpha -66{\alpha }^{2}+2t\rho -34\alpha \rho }{t-17\alpha }$, ${\delta }_{3}=\frac{36{t}^{2}-2t\left(36\alpha +18\lambda +\rho \right)+2\alpha (18\alpha +18\lambda +17\rho )}{17t-\alpha }$, with $t>\alpha$, if $\alpha <\frac{t}{17}$, ${\delta }_{3}<{\delta }_{1}<{\delta }_{2}$, when ${\delta >\delta }_{3}$, on the basis of Lemma 4, platform B exclusively keep the content, when ${\delta <\delta }_{3}$, platform B shares the content. While if $\alpha >\frac{t}{17}$, when $t>\frac{3\sqrt{3328{\alpha }^{2}+992\alpha \left(\lambda +\rho \right)+{(\lambda +\rho )}^{2}}-145\alpha -3\lambda -3\rho }{79}$, ${\delta }_{2}<{\delta }_{3}<{\delta }_{1}$, thus, when ${\delta >\delta }_{3}$, platform B exclusively keep the content, when ${\delta <\delta }_{3}$, platform B shares the content; when $t<\frac{3\sqrt{3328{\alpha }^{2}+992\alpha \left(\lambda +\rho \right)+{(\lambda +\rho )}^{2}}-145\alpha -3\lambda -3\rho }{79}$, ${\delta }_{3}<{\delta }_{1}<{\delta }_{2}$, when ${\delta >\delta }_{1}$, platform B exclusively keep the content, when ${\delta <\delta }_{1}$, platform B shares the content.

Proof of Lemma C1

By taking the first- and second-order conditions of ${\pi }_{A}+{\pi }_{B}$ with respect to ${p}_{M}$, we have $\frac{{\partial }^{2}({\pi }_{A}+{\pi }_{B})}{\partial {{p}_{M}}^{2}}=-\frac{4}{t+\alpha }<0$, and solving $\frac{\partial ({\pi }_{A}+{\pi }_{B})}{\partial {p}_{M}}=0$, we have ${p}_{M}=\frac{2{p}_{A}+2{p}_{B}-t+\alpha +\delta +2\lambda }{4}$, substituting ${p}_{M}$ into ${\pi }_{i}$, and take the first- and second-order conditions of ${\pi }_{i}$ with respect to ${p}_{i}$, we have $\frac{{\partial }^{2}{\pi }_{i}}{\partial {p}_{i}^{2}}=\frac{1}{\alpha -t}<0$, by jointly solving $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=0$, and $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=0$, we obtain ${p}_{A}^{*}=\frac{{t}^{2}\left(8-\mu \right)+t\left[2\left(\alpha +\lambda \right)\left(\mu -2\right)+\delta \mu \right]-\alpha [\delta \left(\mu -4\right)+2\lambda \left(\mu -2\right)+\alpha (\mu +4)]}{6(t+\alpha )}$, ${p}_{B}^{*}=\frac{{t}^{2}\left(7+\mu \right)-t\left[2\left(\alpha +\lambda \right)\left(\mu +1\right)+\delta \left(3+\mu \right)\right]+\alpha [\delta \left(\mu -1\right)+2\lambda \left(\mu +1\right)+\alpha (\mu -5)]}{6(t+\alpha )}$. Substituting ${p}_{i}^{*}$ into ${p}_{M}$, ${n}_{i}$, ${n}_{M}$, and ${\pi }_{i}$, we finish the proof.

Proof of Lemma C2

By taking the first- and second-order conditions of ${\pi }_{A}+{\pi }_{B}$ with respect to ${p}_{M}$, we have $\frac{{\partial }^{2}({\pi }_{A}+{\pi }_{B})}{\partial {{p}_{M}}^{2}}=-\frac{4}{t+\alpha }<0$, and solving $\frac{\partial ({\pi }_{A}+{\pi }_{B})}{\partial {p}_{M}}=0$, we have ${p}_{M}=\frac{2{p}_{A}+2{p}_{B}-t+\alpha +2\lambda }{4}$. Substituting ${p}_{M}$ into ${\pi }_{i}$, and take the first- and second-order conditions of ${\pi }_{i}$ with respect to ${p}_{i}$, we have $\frac{{\partial }^{2}{\pi }_{i}}{\partial {p}_{i}^{2}}=\frac{1}{\alpha -t}<0$, by jointly solving $\frac{\partial {\pi }_{A}}{\partial {p}_{A}}=0$, and $\frac{\partial {\pi }_{B}}{\partial {p}_{B}}=0$, we obtain ${p}_{A}^{*}=\frac{\left(t-\alpha \right)[t\left(8-\mu \right)+2\lambda \left(\mu -2\right)+\alpha (\mu +4)]}{6(t+\alpha )}$, ${p}_{B}^{*}=\frac{\left(t-\alpha \right)[t\left(\mu +7\right)-2\lambda \left(\mu +1\right)-\alpha (\mu -5)]}{6(t+\alpha )}$. Substituting ${p}_{i}^{*}$ into ${p}_{M}$, ${n}_{i}$, ${n}_{M}$, and ${\pi }_{i}$, we finish the proof.

Proof of Lemma C3

The proof is straightforward with $t>\alpha.$

Proof of Proposition C1

On the basis of Lemmas C3 and 4, we can find that when $\lambda >{\lambda }^{a}$, both platforms’ profit is higher under content exclusivity, and thus, the additional content is always exclusively held by platform A. Further, when $\lambda <{\lambda }^{a}$, platform A benefits from content exclusivity while platform B is harmed. Consequently, when $\lambda <{\lambda }^{b}$ (${\lambda }^{a}>{\lambda }^{b}$), $\widetilde{{\pi }_{A}^{1*}}-\widetilde{{\pi }_{A}^{2*}}<\widetilde{{\pi }_{B}^{2*}}-\widetilde{{\pi }_{B}^{1*}}$, the additional first-party content is shared at price $\widetilde{{\pi }_{B}^{2*}}-\widetilde{{\pi }_{B}^{1*}}$; when $\lambda >{\lambda }^{b}$, $\widetilde{{\pi }_{A}^{1*}}-\widetilde{{\pi }_{A}^{2*}}>\widetilde{{\pi }_{B}^{2*}}-\widetilde{{\pi }_{B}^{1*}}$, the additional content goes exclusive.