Value-added services decisions of bilateral platform with user expectation and resources constraint

Abstract

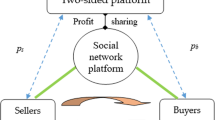
This paper studies the value-added services (VAS) investment and pricing strategies of monopoly bilateral platform with limited resources and asymmetric user information. By constructing a game theory model, we conclude that the platform earns higher profits when both of the bilateral users are informed than when the sellers are informed and the buyers are uninformed. The passive expectation of uninformed users weakens the monopoly power of platform pricing and causes lower platform profit. Additionally, the VAS investment and pricing strategies of the platform are jointly influenced by users’ cross-network externality and marginal utility. Among them, the platform investment is mainly related to marginal utility, and its pricing strategies depend heavily on the cross-network externality. Moreover,Uninformed users with passive expectation enforce the platform to invest all of the resources and higher service level in them when the cross-network externality of users on either side does not have a decisive advantage.

Appendix A: Proof

1.1 Appendix A.1: Proof of Theorem 1

Based on the profit function:

$$\begin{aligned} \pi&=(1+\alpha _{b}n_{s}^e+\beta _{b}x_{b}-p_{b})p_{b}+(\alpha _{s}+\alpha _{b}\alpha _{s}n_{s} ^e+\alpha _{s}\beta _{b}x_{b}-\alpha _{s}p_{b}\\&\quad +\beta _{s}x_{s}-p_{s})p_{s}-\frac{\phi }{2}x_{b}^2-\frac{\phi }{2}x_{b}^2 \end{aligned}$$

The first-order condition can be written as:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial \pi }{\partial p_{b}}=\alpha _{b}n_{s}^e-2p_{b}-\alpha _{s}p_{s}+x_{b}\beta _{b}+1 \\ \frac{\partial \pi }{\partial p_{s}}=\alpha _{s}-2p_{s}-\alpha _{s} p_{b} + \beta _{s} x_{s} +\alpha _{s}\alpha _{b}n_{s}^e+\alpha _{s} \beta _{b} x_{b} \\ \frac{\partial \pi }{\partial x_{b}}=-\phi x_{b}+p_{b}\beta _{b}+p_{s}\alpha _{s}\beta _{b}\\ \frac{\partial \pi }{\partial x_{s}}=p_{s}\beta _{s}-\phi x_{s}\\ \end{array} \right. \end{aligned}$$

(6)

The corresponding Hessian matrix are as following:

$$\begin{aligned} H(p_{b},p_{s},x_{b},x_{s})=\begin{pmatrix} \frac{\partial ^{2}\pi }{\partial p_{b}^{2}}&{} \frac{\partial ^{2}\pi }{\partial p_{b}\partial p_{s}} &{} \frac{\partial ^{2}\pi }{\partial p_{b}\partial x_{b}}&{} \frac{\partial ^{2}\pi }{\partial p_{b}\partial x_{s}}\\ \frac{\partial ^{2}\pi }{\partial p_{s}\partial p_{b}}&{} \frac{\partial ^{2}\pi }{\partial p_{s}^{2}} &{} \frac{\partial ^{2}\pi }{\partial p_{s}\partial x_{b}}&{} \frac{\partial ^{2}\pi }{\partial p_{s}\partial x_{s}}\\ \frac{\partial ^{2}\pi }{\partial x_{b}\partial p_{b}}&{} \frac{\partial ^{2}\pi }{\partial x_{b}\partial p_{s}} &{} \frac{\partial ^{2}\pi }{\partial x_{b}^{2}}&{} \frac{\partial ^{2}\pi }{\partial x_{b}\partial x_{s}}\\ \frac{\partial ^{2}\pi }{\partial p_{b}\partial x_{s}}&{} \frac{\partial ^{2}\pi }{\partial p_{s}\partial x_{s}} &{} \frac{\partial ^{2}\pi }{\partial x_{b}\partial x_{s}}&{} \frac{\partial ^{2}\pi }{\partial x_{s}^{2}} \end{pmatrix}=\begin{pmatrix} -2&{}-\alpha _{s}&{}\beta _{b}&{}0\\ -\alpha _{s}&{}-2&{}\alpha _{s}\beta _{b}&{}\beta _{s}\\ \beta _{b}&{}\alpha _{s}\beta _{b}&{}-\phi &{}0\\ 0&{}\beta _{s}&{}0&{}-\phi \end{pmatrix} \end{aligned}$$

It is easy to know that $\left| H_{1} \right| =\left| -2 \right| <0$, $\left| H_{2} \right| =\left| \begin{array}{ll} -2&{}\quad -\alpha _{s}\\ -\alpha _{s}&{} \quad -2 \end{array}\right| =4-\alpha _{s}^2>0$, $\left| H_{3} \right| =\left| \begin{array}{lll} -2&{}\quad -\alpha _{s}&{}\quad \beta _{b}\\ -\alpha _{s}&{}\quad -2&{}\quad \alpha _{s}\beta _{b}\\ \beta _{b}&{}\quad \alpha _{s}\beta _{b}&{}\quad -\phi \end{array}\right| =-4\phi +\phi \alpha _{s}^2+2\beta _{b}^2$ and $\left| H_{4} \right| =\left| \begin{array}{llll} -2&{}\quad -\alpha _{s}&{}\quad \beta _{b}&{}\quad 0\\ -\alpha _{s}&{}\quad -2&{}\quad \alpha _{s}\beta _{b}&{}\quad \beta _{s}\\ \beta _{b}&{}\quad \alpha _{s}\beta _{b}&{}\quad -\phi &{}\quad 0\\ 0&{}\quad \beta _{s}&{}\quad 0&{}\quad -\phi \end{array}\right| =4\phi ^2-\phi ^2\alpha _{s}^2-2\phi \beta _{b}^2-2\phi \beta _{s}^2+\beta _{b}^2\beta _{s}^2$.

We can verify that $\left| H_{3} \right| <0$, when $\phi >\frac{2\beta _{b}^2}{4-\alpha _{s}^2}$. $\left| H_{4} \right|$ can be taken as a function of $\phi$: $\left| H_{4} \right| =(4-\alpha _{s}^2)\phi ^2-2(\beta _{b}^2+\beta _{s}^2)\phi +\beta _{s}^2\beta _{b}^2$, let $a=4-\alpha _{s}^2, b=-2(\beta _{b}^2+\beta _{s}^2)$ and $c=\beta _{s}^2\beta _{b}^2$, the solutions of $\left| H_{4} \right| =0$ are $\phi ^{1}=\frac{\beta _{s}^2+\beta _{b}^2\pm \sqrt{(\beta _{s}^2+\beta _{b}^2)^2-(4-\alpha _{s}^2) \beta _{s}^2\beta _{b}^2}}{4-\alpha _{s}^2}$. It is easy to verify that:

$$\begin{aligned} \phi _{1}^{1}&=\frac{\beta _{s}^2+\beta _{b}^2+\sqrt{(\beta _{s}^2+\beta _{b}^2)^2-(4-\alpha _{s}^2) \beta _{s}^2\beta _{b}^2}}{4-\alpha _{s}^2}>\frac{2\beta _{b}^2}{4-\alpha _{s}^2},\\ 0<\phi _{2}^{1}&=\frac{\beta _{s}^2+\beta _{b}^2-\sqrt{(\beta _{s}^2+\beta _{b}^2)^2-(4-\alpha _{s}^2) \beta _{s}^2\beta _{b}^2}}{4-\alpha _{s}^2}<\frac{2\beta _{b}^2}{4-\alpha _{s}^2}. \end{aligned}$$

Therefore, the Hessian matrix is negative definite only when $\phi >\frac{\beta _{s}^2+\beta _{b}^2+\sqrt{(\beta _{s}^2+\beta _{b}^2)^2-(4-\alpha _{s}^2 )\beta _{s}^2\beta _{b}^2}}{4-\alpha _{s}^2}$.

Let $\overline{\phi }=\frac{\beta _{s}^2+\beta _{b}^2+\sqrt{(\beta _{s}^2+\beta _{b}^2)^2-(4-\alpha _{s}^2) \beta _{s}^2\beta _{b}^2}}{4-\alpha _{s}^2}$, then we can obtain the following conclusions:

• (1) If $\phi >\overline{\phi }$, the Hessian matrix is negative definite. The first-order can ensure the optimal solution from (A1).

  $$\begin{aligned} p_{b}^*&=\frac{\phi (\phi (-2+\alpha _{s}^2)+\beta _{s}^2)}{I},\; p_{s}^*=\frac{-\phi ^2\alpha _{s}}{I},\; x_{s}^*=\frac{-\phi \alpha _{s}\beta _{s}}{I}\quad {\textit{and}}\\ x_{b}^*&=\frac{\beta _{b}(-2\phi +\beta _{s}^2)}{I} \end{aligned}$$

  Let $I=\phi =(\phi (-4+\alpha _{s}(\alpha _{b}+\alpha _{s}))+2\beta _{b}^2)+(2\phi -\beta _{b}^2)\beta -_{s}^2$, $D_{1}=-\frac{\phi \alpha _{s}\beta _{s}}{I}$, $D_{2}=-\frac{\beta _{b}(-2\phi +\beta _{s}^2)}{I}$, $A=\alpha _{s}+(-2+\alpha _{s}(\alpha _{b}+\alpha _{s}))\beta _{s}$ and $\phi ^{'}=\frac{2\beta _{b}(1+\beta _{b})+2+\beta _{s}(\alpha _{s}+2\beta _{s}) +\sqrt{18\beta _{b}^3+4\beta _{b}^4+4\beta _{b}\beta _{s}A+4\beta _{b}^2(1+\beta _{s}A) +\beta _{s}^2(\alpha _{s}+2\beta _{s})^2}}{2(4-\alpha _{s}(\alpha _{s}+\alpha _{b}))}$. Because the platform has limited resources and the level of investment satisfies the condition $0< x_{b}+x_{s}\le 1$. There are the following two cases:

  • (i) When $D_{1}+D_{2}<1$, that is $\phi >\phi ^{'}$. It is obvious that the optimal investment $x_{b}^*+x_{s}^*<1$, the optimal solution and profit are $p_{b}^*=\frac{\phi (\phi (-2+\alpha _{s}^2)+\beta _{s}^2)}{I},$ $p_{s}^*=\frac{-\phi ^2\alpha _{s}}{I},$ $x_{s}^*=\frac{-\phi \alpha _{s}\beta _{s}}{I},$ $x_{b}^*=\frac{\beta _{b}(-2\phi +\beta _{s}^2)}{I},$ and $\pi ^*=-\frac{\phi (2\phi -\beta _{s}^2)(\phi ^2\alpha _{s}^2-(2\phi -\beta _{b}^2)(2\phi -\beta _{s}^2))}{2I^2}$.

  • (ii) When $D_{1}+D_{2}\ge 1$, that is $\phi \le \phi ^{'}$, the optimal investment $x_{b}^*+ x_{s}^* \ge 1$, based on the resource constraint $0< x_{b}^*+x_{s}^*\le 1$, the optimal investment are $x_{b}^*+x_{s}^*=1$.

• (2) If $\phi <\overline{\phi }$, the Hessian matrix is not negative definite. Since the profit function is a continuous and bounded function, the optimal solution can be obtained when investment is located in its boundary $(x_{b}=0, x_{s}=0)$, $(x_{b}=1, x_{s}=0)$ or $(x_{b}=0, x_{s}=1)$.

When $x_{b}=0, x_{s}=0$, the optimal profit can be obtained as following:

$$\begin{aligned} \pi _{x_{b}=0,\; x_{s}=0}=\frac{4-\alpha _{s}^2}{(-4+\alpha _{s}(\alpha _{b}+\alpha _{s}))^2} \end{aligned}$$

When $x_{b}=1, x_{s}=0$, the optimal profit can be obtained as following:

$$\begin{aligned} \pi _{x_{b}=1,\; x_{s}=0}=\frac{(4-\alpha _{s}^2)(2\phi \alpha _{b}\alpha _{s}+(2-4\phi +\phi \alpha _{s}^2+2\beta _{b} (2+\beta _{b})))}{2(-4+\alpha _{s}(\alpha _{b}+\alpha _{s}))^2} \end{aligned}$$

When $x_{b}=0, x_{s}=1$, the optimal profit can be obtained as following:

$$\begin{aligned}&\pi _{x_{b}=0,x_{s}=1}\\&\quad =\frac{-2\alpha _{b}(-4+\alpha _{s}^2)(\phi \alpha _{s}+\beta _{s})+\alpha _{b}^2 (-\phi \alpha _{s}^2+2\beta _{s}^2)-(-4+\alpha _{s}^2)(2-4\phi +\phi \alpha _{s}^2+2\alpha _{s}\beta _{s} +2\beta _{s}^2)}{2(-4+\alpha _{s}(\alpha _{b}+\alpha _{s}))^2}\\&\pi _{x_{b}=1,\; x_{s}=0}-\pi _{x_{b}=0,\; x_{s}=0}=-\frac{\phi }{2} -\frac{(-4+\alpha _{s}^2)\beta _{b}(2+\beta _{b})}{(-4+\alpha _{s}(\alpha _{b}+\alpha _{s}))^2} \end{aligned}$$

When $0<\phi <\phi _{6}$, then $\pi _{x_{b}=1, x_{s}=0}> \pi _{x_{b}=0, x_{s}=0}$.

$$\begin{aligned} \pi _{x_{b}=0,\; x_{s}=1}-\pi _{x_{b}=0,\ x_{s}=0}=-\frac{\phi }{2} +\frac{\beta _{s}(-(\alpha _{b}+\alpha _{s})(-4+\alpha _{s}^2)+(4+\alpha _{b}^2-\alpha _{s}^2) \beta _{s})}{(-4+\alpha _{s}(\alpha _{b}+\alpha _{s}))^2} \end{aligned}$$

When $0<\phi <\phi _{7}$, then $\pi _{x_{b}=0,\ x_{s}=1}> \pi _{x_{b}=0,\ x_{s}=0}$.

Where $\phi _{6}=\frac{16\beta _{b}-4\alpha _{s}^2\beta _{b} +8\beta _{b}^2-2\alpha _{b}^2\beta _{b}^2}{16-8\alpha _{b}\alpha _{s}-8\alpha _{s}^2+\alpha _{b} ^2\alpha _{s}^2+2\alpha _{b}\alpha _{s}^3+\alpha _{s}^4}$, $\phi _{7}=\frac{8\alpha _{b}\beta _{s}+8\alpha _{s}\beta _{s}-2\alpha _{b}\alpha _{s}^2\beta _{s} -2\alpha _{s}^3\beta _{s}+8\beta _{s}^3+2\alpha _{b}^2\beta _{s}^2-2\alpha _{s}^2\beta _{s}^2}{16-8\alpha _{b}\alpha _{s}-8\alpha _{s}^2+\alpha _{b}^2\alpha _{s} ^2+2\alpha _{b}\alpha _{s}^3+\alpha _{s}^4}$, in which $\phi _{6}>\overline{\phi }$, $\phi _{7}>\overline{\phi }$.

1.2 Appendix A.2: Proof of Proposition 1

In order to satisfy the condition that the investment amount is greater than 0, the following conditions must be met: $I<0$, $\phi (-4\phi +\phi (\alpha _{b}+\alpha _{s})^2+2\beta _{b}^2)+(2\phi -\beta _{b}^2)\beta _{s}^2<0$, $\phi >\frac{\beta _{b}^2}{2}$ and $\phi >\frac{\beta _{s}^2}{2}$.

From $I<0$, we can get: $\phi >\phi ^{*}$.

Where $\phi ^{*}=\frac{-\beta _{b}^2-\beta _{s}^2}{-4+\alpha _{b}\alpha _{s}+\alpha _{s}^2} +\sqrt{\frac{\beta _{b}^4-2\beta _{b}^2\beta _{s}^2+\alpha _{b}\alpha _{s}\beta _{b}^2\beta _{s} ^2+\alpha _{s}^2\beta _{b}^2\beta _{s}^2+\alpha _{s}^2\beta _{b}^2\beta _{s}^2+\beta _{s}^4}{(-4+\alpha _{b}\alpha _{s}+\alpha _{s}^2)^2}}$.

From $\phi (-4\phi +\phi (\alpha _{b}+\alpha _{s})^2+2\beta _{b}^2)+(2\phi -\beta _{b}^2)\beta _{s}^2<0$, we can get the constraint on the marginal investment cost of VAS as: $\phi >\phi _{1}$, where $\phi _{1}=\frac{-\beta _{b}^2-\beta _{s}^2}{-4+\alpha _{b}^2 +2\alpha _{b}\alpha _{s}+\alpha _{s}^2}+\sqrt{\frac{\beta _{b}^4-2 \beta _{b}^2\beta _{s}^2+\alpha _{b}^2\beta _{b}^2\beta _{s}^2+2\alpha _{b} \alpha _{s}\beta _{b}^2\beta _{s}^2+\alpha _{s}^2\beta _{b}^2\beta _{s}^2+\beta _{s} ^4}{(-4+\alpha _{b}^2+2\alpha _{b}\alpha _{s}+\alpha _{s}^2)^2}}$. Among these conditions, $\phi _{1}>\phi ^{*}$. So the final condition on cost is: $\phi >\phi _{1}$.

$$\begin{aligned} \pi _{UBIS}^*-\pi _{IB}^*=\frac{\phi ^3\alpha _{b}^2(2\phi -\beta _{b}^2) (-2\phi +\beta _{s}^2)^2}{2(\phi (-4\phi +\phi (\alpha _{b}+\alpha _{s})^2 +2\beta _{b}^2)+(2\phi -\beta _{b}^2)\beta _{s}^2) I^2} \end{aligned}$$

With the above conditions, it can be seen that $\pi _{UBIS}^*-\pi _{IB}^*<0$.

1.3 Appendix A.3: Proof of Proposition 2

• (1) When the platform invests their resources in bilateral users, the gaps between investment and price are as following:

  $$\begin{aligned} p_{b}^*- p_{s}^*=\frac{\phi (\phi (-2+\alpha _{s}+\alpha _{s}^2)+\beta _{s}^2)}{I}\; {\textit{and}}\; x_{b}^*-x_{s}^*=\frac{\phi \alpha _{s}\beta _{s}+\beta _{b}(-2\phi +\beta _{s}^2)}{I} \end{aligned}$$

  Since $I<0$, only the numerator $\phi (-2+\alpha _{s}+\alpha _{s}^2)+\beta _{s}^2$ and $\phi \alpha _{s}\beta _{s}+\beta _{b}(-2\phi +\beta _{s}^2)$ needs to be discussed. After calculation, the following results can be obtained: when $\frac{1}{4}(-3+\sqrt{33})\le \beta _{b}<1, 1<\frac{2\beta _{b}}{\beta _{s}}\le \alpha _{s}<1$, the numerators $\phi (-2+\alpha _{s}+\alpha _{s}^2)+\beta _{s}^2$ and $\phi \alpha _{s}\beta _{s}+\beta _{b}(-2\phi +\beta _{s}^2)$ in the formula $p_{b}^*- p_{s}^*$ and $x_{b}^*-x_{s}^*$ satisfy the condition of being greater than 0 at the same time, and also meet the conditions $\phi >\phi ^{*}$. Other conditions that make numerators larger than 0 at the same time are too complicated. Therefore, this article does not give too much description. Similarly, when $\beta _{s}\le \beta _{b},\ 1\le \alpha _{s}<2$, the numerator $\phi (-2+\alpha _{s}+\alpha _{s}^2)+\beta _{s}^2$ in formula $p_{b}^*- p_{s}^*$ satisfy the condition of being greater than 0, and the numerator $\phi \alpha _{s}\beta _{s}+\beta _{b}(-2\phi +\beta _{s}^2)$ in formula $x_{b}^*-x_{s}^*$ satisfy the condition of being less than 0 at the same time, the condition $\phi >\phi ^{*}$ also need to be met. When $\alpha _{s}\le \sqrt{\frac{\beta _{b}^2-\beta _{s}^2}{\beta _{b}^2}}, \beta _{s}<\beta _{b}$, the numerators $\phi (-2+\alpha _{s}+\alpha _{s}^2)+\beta _{s}^2$ and $\phi \alpha _{s}\beta _{s}+\beta _{b}(-2\phi +\beta _{s}^2)$ in the formula $p_{b}^*- p_{s}^*$ and $x_{b}^*-x_{s}^*$ satisfy the condition of being less than 0 at the same time, and also meet the condition $\phi >\phi ^{*}$.

• (2) When the platform invests all their resources in sellers($x_{s}^*=1, x_{b}^*=0$), the gap between price is as following:

  $$\begin{aligned} p_{b}^*-p_{s}^*=\frac{-2+\alpha _{s}+\alpha _{s}^2+(2-\alpha _{b}+\alpha _{s})\beta _{s}}{-4+\alpha _{s}(\alpha _{b}+\alpha _{s})} \end{aligned}$$

  It can be observed that the denominator is always less than 0, only the numerator $-2+\alpha _{s}+\alpha _{s}^2+(2-\alpha _{b}+\alpha _{s})\beta _{s}$ in the formula needs to be discussed. After calculation, it can be known that the condition $1<\alpha _{s}<2$ is met, the numerator $-2+\alpha _{s}+\alpha _{s}^2+(2-\alpha _{b}+\alpha _{s})\beta _{s}$ is greater than 0.

• (3) When the platform invests all their resources in buyers($x_{s}^*=0,\ x_{b}^*=1$), the gap between price is as following:

  $$\begin{aligned} p_{b}^*-p_{s}^*=\frac{(-2+\alpha _{s}+\alpha _{s}^2)(1+\beta _{b})}{-4+\alpha _{s}(\alpha _{b}+\alpha _{s})} \end{aligned}$$

Similarly, the denominator $-4+\alpha _{s}(\alpha _{b}+\alpha _{s})$ is less than 0, so only the numerator $(-2+\alpha _{s}+\alpha _{s}^2)$ in formula $p_{b}^*-p_{s}^*$ needs to be discussed. After calculation, it can be known that the condition $0<\alpha _{b}<1$ and $1<\alpha _{s}$ are met, the numerator $(-2+\alpha _{s}+\alpha _{s}^2)$ is greater than 0. Similarly, the condition $0<\alpha _{b}\le 1, 0<\alpha _{b}<2$ or $1<\alpha _{b}<2$ are met, the numerator$(-2+\alpha _{s}+\alpha _{s}^2)$ is greater than 0.

1.4 Appendix A.4: Proof of Proposition 3

Because the condition that the investment amount is greater than 0 must be satisfied, the following results can be obtained: $\phi >\frac{\beta _{b}^2}{2}$ and $\phi >\frac{\beta _{s}^2}{2}$.

• (a) When the buyers of platform have incomplete information and form the passive expectation: $\partial x_{s}^{*}/\partial \alpha _{s}=\frac{\phi \beta _{s}(\phi ^2\alpha _{s}^2+(2\phi -\beta _{b}^2) (2\phi -\beta _{s}^2))}{I^2}>0$, $\partial x_{s}^{*}/\partial \alpha _{b}=\frac{\phi ^3\alpha _{s}^2\beta _{s}}{I^2}>0$, $\partial x_{b}^{*}/\partial \alpha _{s}=-\frac{\phi ^2(\alpha _{b}+2\alpha _{s})\beta _{b}(-2\phi +\beta _{s}^2)}{I^2}>0$ and $\partial x_{b}^{*}/\partial \alpha _{b}=-\frac{\phi ^2\alpha _{s}\beta _{b}(-2\phi +\beta _{s}^2)}{I^2}>0$.

• (b) When the buyers of platform have incomplete information and form the passive expectation: $\partial x_{s}^{*}/\partial \beta _{s}=\frac{\phi \alpha _{s}(-\phi ^2\alpha _{b}\alpha _{s}-\phi ^2\alpha _{s}^2+ (2\phi -\beta _{b}^2) (2\phi +\beta _{s}^2))}{I^2}$.

The condition for making the numerator $-\phi ^2\alpha _{b}\alpha _{s}-\phi ^2\alpha _{s}^2+ (2\phi -\beta _{b}^2) (2\phi +\beta _{s}^2)$ in the formula $\partial x_{s}^{*}/\partial \beta _{s}$ greater than 0 are $\phi <\phi _{2}$ and $\phi >\phi _{3}$. Where $\phi _{2}=\frac{-\beta _{b}^2+\beta _{s}^2}{-4+\alpha _{b}\alpha _{s}+\alpha _{s}^2 }-\sqrt{\frac{\beta _{b}^4+2\beta _{b}^2\beta _{s}^2-\alpha _{s}\alpha _{b}\beta _{b}^2\beta _{s}^2 -\alpha _{s}^2\beta _{b}^2\beta _{s}^2+\beta _{s}^4}{(-4+\alpha _{b}\alpha _{s}+\alpha _{s}^2)^2}}$ and $\phi _{3}=\frac{-\beta _{b}^2+\beta _{s}^2}{-4+\alpha _{b}\alpha _{s}+\alpha _{s}^2} +\sqrt{\frac{\beta _{b}^4+2\beta _{b}^2\beta _{s}^2-\alpha _{s}\alpha _{b}\beta _{b}^2\beta _{s} ^2-\alpha _{s}^2\beta _{b}^2\beta _{s}^2+\beta _{s}^4}{(-4+\alpha _{b}\alpha _{s}+\alpha _{s}^2)^2}}$. And it also needs to meet the condition $\phi >\phi ^{*}$ that the investment amount is greater than 0 at the same time.

Because $\phi ^{*}>\phi _{3}$, it can be concluded that the investment amount is greater than 0, the numerator $-\phi ^2\alpha _{b}\alpha _{s}-\phi ^2\alpha _{s}^2+ (2\phi -\beta _{b}^2) (2\phi +\beta _{s}^2)$ in the formula $\partial x_{s}^{*}/\partial \beta _{s}$ will also be greater than 0, then $\partial x_{s}^{*}/\partial \beta _{s}>0$.

$\partial x_{s}^{*}/\partial \beta _{b}=\frac{2\phi \alpha _{s}\beta _{b}\beta _{s} (2\phi -\beta _{s}^2)}{I^2}>0$, $\partial x_{b}^{*}/\partial \beta _{s}=\frac{2\phi ^2\alpha _{s}(\alpha _{b}+\alpha _{s})\beta _{b}\beta _{s} }{I^2}>0$ and $\partial x_{b}^{*}/\partial \beta _{b}=-\frac{(2\phi -\beta _{s}^2)(\phi (\phi (-4+\alpha _{s} (\alpha _{b}+\alpha _{s}))-2\beta _{b}^2)+(2\phi +\beta _{b}^2)\beta _{s}^2) }{I^2}$,

The condition for making the numerator $(\phi (\phi (-4+\alpha _{s}(\alpha _{b}+\alpha _{s}))-2\beta _{b}^2)+(2\phi +\beta _{b}^2)\beta _{s}^2)$ in the formula $\partial x_{b}^{*}/\partial \beta _{b}$ less than 0 are $\phi <\phi _{4}$ and $\phi >\phi _{5}$.

Where $\phi _{4}=\frac{\beta _{b}^2-\beta _{s}^2}{-4+\alpha _{b}\alpha _{s} +\alpha _{s}^2}-\sqrt{\frac{\beta _{b}^4+2\beta _{b}^2\beta _{s}^2 -\alpha _{s}\alpha _{b}\beta _{b}^2\beta _{s}^2-\alpha _{s}^2\beta _{b} ^2\beta _{s}^2+\beta _{s}^4}{(-4+\alpha _{b}\alpha _{s}+\alpha _{s}^2)^2}}$, $\phi _{5}=\frac{\beta _{b}^2-\beta _{s}^2}{-4+\alpha _{b}\alpha _{s} +\alpha _{s}^2}+\sqrt{\frac{\beta _{b}^4+2\beta _{b}^2\beta _{s}^2 -\alpha _{s}\alpha _{b}\beta _{b}^2\beta _{s}^2-\alpha _{s}^2\beta _{b} ^2\beta _{s}^2+\beta _{s}^4}{(-4+\alpha _{b}\alpha _{s}+\alpha _{s}^2)^2}}$.

Similarly, it is calculated that $\phi ^{*}>\phi _{5}$.

Therefore, when $\phi >\phi ^{*}$, the numerator $(\phi (\phi (-4+\alpha _{s}(\alpha _{b}+\alpha _{s}))-2\beta _{b}^2)+(2\phi +\beta _{b}^2)\beta _{s}^2)$ in the formula $\partial x_{b}^{*}/\partial \beta _{b}$ is less than 0, then $\partial x_{b}^{*}/\partial \beta _{b}>0$.

1.5 Appendix A.5: Proof of Proposition 4

According to $\partial p_{b}^{*}/\partial \alpha _{s}=\frac{\phi ^2(\phi \alpha _{b}(\phi (2+\alpha _{s}^2)-\beta _{s}^2)+2\alpha _{s}(\phi -\beta _{b}^2) (-2\phi +\beta _{s}^2)) }{I^2}$ and $\partial p_{b}^{*}/\partial \alpha _{b}=-\frac{\phi ^3\alpha _{s} (\phi (-2+\alpha _{s}^2)+\beta _{s}^2) }{I^2}$, we can get the following conclusions.

After calculation, the following results can be obtained: when $\alpha _{b}^{'}<\alpha _{b}$, the numerator $(\phi \alpha _{b}(\phi (2+\alpha _{s}^2)-\beta _{s}^2)+2\alpha _{s}(\phi -\beta _{b}^2) (-2\phi +\beta _{s}^2)$ in the formula $\partial p_{b}^{*}/\partial \alpha _{s}$ is greater than 0, then $\partial p_{b}^{*}/\partial \alpha _{s}>0$. However, when $\alpha _{b}^{'}>\alpha _{b}$, the numerator $(\phi \alpha _{b}(\phi (2+\alpha _{s}^2)-\beta _{s}^2)+2\alpha _{s}(\phi -\beta _{b}^2) (-2\phi +\beta _{s}^2)$ in the formula $\partial p_{b}^{*}/\partial \alpha _{s}$ is less than 0, then $\partial p_{b}^{*}/\partial \alpha _{s}<0$.

Similarly, when $\alpha _{s}>\sqrt{2}$, the numerator $\phi (-2+\alpha _{s}^2)+\beta _{s}^2$ in the formula $\partial p_{b}^{*}/\partial \alpha _{b}$ is greater than 0, then $\partial p_{b}^{*}/\partial \alpha _{b}<0$. Other conditions are too complex to describe in this article.

$\partial p_{s}^{*}/\partial \alpha _{s}=\frac{\phi ^4\alpha _{s}^2+\phi ^2 (2\phi -\beta _{b}^2) (2\phi -\beta _{s}^2)) }{I^2} >0$, $\partial p_{s}^{*}/\partial \alpha _{b} =\frac{\phi ^4\alpha _{s}^2}{I^2} >0$.