Weak essentially undecidable theories of concatenation, part II

Abstract

We show that we can interpret concatenation theories in arithmetical theories without coding sequences by identifying binary strings with $2\times 2$ matrices with determinant 1.

1 Introduction

A computably enumerable first-order theory is called essentially undecidable if any consistent extension, in the same language, is undecidable (there is no algorithm for deciding whether an arbitrary sentence is a theorem). A computably enumerable first-order theory is called essentially incomplete if any recursively axiomatizable consistent extension is incomplete. Since a decidable consistent theory can be extended to a decidable complete consistent theory (see Chapter 1 of Tarski et al. [12]), a theory is essentially undecidable if and only if it is essentially incomplete. Two theories that are known to be essentially undecidable are Robinson arithmetic ${\textsf{Q}}$ and the related theory ${\textsf{R}}$ (see Fig. 1 for the axioms of ${\textsf{R}}$ and ${\textsf{Q}}$). The essential undecidability of ${\textsf{R}}$ and ${\textsf{Q}}$ is proved in Chapter 2 of [12]. In Chapter 1 of [12], Tarski introduces interpretability as an indirect way of showing that first-order theories are essentially undecidable. The method is indirect because it reduces the problem of essential undecidability of a theory T to the problem of essentially undecidability of a theory S which is known to be essentially undecidable. Interpretability between theories is a reflexive and transitive relation and thus induces a degree structure on the class of computably enumerable essentially undecidable first-order theories.

Fig. 1

Non-logical axioms of the first-order theories ${\textsf{R}}$, ${\textsf{Q}}$. The axioms of ${\textsf{R}}$ are given by axiom schemes where n, m, k are natural numbers and ${\overline{n}}$, ${\overline{m}}$, ${\overline{k}}$ are their canonical names

In [10], we introduce two theories of concatenation ${{\textsf{W}}}{{\textsf{D}}}$, ${\textsf{D}}$ and show that they are respectively mutually interpretable with ${\textsf{R}}$ and ${\textsf{Q}}$ (see Fig. 2 for the axioms of ${{\textsf{W}}}{{\textsf{D}}}$ and ${\textsf{D}}$). The language of ${{\textsf{W}}}{{\textsf{D}}}$ and ${\textsf{D}}$ is $\lbrace 0, 1, \circ , \preceq \rbrace$ where 0 and 1 are constant symbols, $\circ$ is a binary function symbol and $\preceq$ is a binary relation symbol. The intended model of ${{\textsf{W}}}{{\textsf{D}}}$ and ${\textsf{D}}$ is the free semigroup generated by two letters extended with the prefix relation. Extending finitely generated free semigroups with the prefix relation allows us to introduce $\Sigma _1$-formulas which are expressive enough to encode computations by Turing machines (see Kristiansen and Murwanashyaka [6]). $\Sigma _1$-formulas are formulas on negation normal form where universal quantifiers occur bounded, i.e., they are of the form $\forall x \preceq t$. Axioms ${\textsf{D}}_4 - {\textsf{D}}_7$ are essential for coding sequences in ${\textsf{D}}$ since they allow us to work with $\Sigma _0$-formulas, formulas where all quantifiers are of the form $\exists x \preceq t$, $\forall x \preceq t$. In [10], we show that ${\textsf{Q}}$ is interpretable in ${\textsf{D}}$ by using especially axioms ${\textsf{D}}_4 - {\textsf{D}}_7$ to restrict the universe of ${\textsf{D}}$ to a domain K on which the analogue of ${\textsf{Q}}_3$ holds, that is, the sentence ${\textsf{Q}}_3^{ \prime } \equiv \ \forall x \; [ \ x = 0 \; \vee \; x = 1 \; \vee \; \exists y \preceq x \; [ \ x = y0 \; \vee \; x = y 1 \ ] \ ]$. To improve readability, we use juxtaposition instead of the binary function symbol $\circ$ of the formal language. Due to the existential quantifier in ${\textsf{Q}}_3^{ \prime }$, we need to ensure that $\Sigma _0$-formulas are absolute for K.

Fig. 2

Non-logical axioms of the first-order theories ${{\textsf{W}}}{{\textsf{D}}}$, ${\textsf{D}}$. The axioms of ${{\textsf{W}}}{{\textsf{D}}}$ are given by axiom schemes where $\alpha , \beta , \gamma$ are nonempty binary strings and ${\overline{\alpha }}$, ${\overline{\beta }}$, ${\overline{\gamma }}$ are their canonical names. $\textsf{Pref} ( \alpha )$ is the set of all nonempty prefixes of $\alpha$

Since ${\textsf{D}}$ and ${\textsf{Q}}$ are mutually interpretable, we can identify differences between these two theories by investigating the interpretability degrees of the theories we obtain by weakening axioms ${\textsf{D}}_4 - {\textsf{D}}_7$, ${\textsf{Q}}_3$ which are essential for coding sequences in ${\textsf{D}}$ and ${\textsf{Q}}$. In addition to ${\textsf{D}}$ and ${{\textsf{W}}}{{\textsf{D}}}$, we introduce in [10] two theories ${{\textsf{I}}}{{\textsf{D}}}$, ${{\textsf{I}}}{{\textsf{D}}}^{ *}$ (called ${\textsf{C}}$, ${{\textsf{B}}}{{\textsf{T}}}$, respectively, in [10]) and prove that their interpretability degrees are strictly between the degrees of ${{\textsf{W}}}{{\textsf{D}}}$ and ${\textsf{D}}$. But we are not able to determine in [10] whether ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^*$ are mutually interpretable. We obtain ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ *}$ from ${\textsf{D}}$ by replacing axioms ${\textsf{D}}_4 - {\textsf{D}}_7$ with respectively the axiom schemas

$$\begin{aligned} {{\textsf{I}}}{{\textsf{D}}}_4 \equiv \ \forall x \; \left[ \ x \preceq {\overline{\alpha }} \leftrightarrow \bigvee _{ \gamma \in \textsf{Pref} ( \alpha ) } x= {\overline{\gamma }} \ \right] , \ \ {{\textsf{I}}}{{\textsf{D}}}_4^{ * } \equiv \ \forall x \left[ \ x \sqsubseteq _{ {\textsf{s}} } {\overline{\alpha }} \rightarrow \bigvee _{ \gamma \in \textsf{Sub} ( \alpha ) } x= {\overline{\gamma }} \ \right] \end{aligned}$$

where $\alpha$ is a nonempty binary string, ${\overline{\alpha }}$ is a canonical variable-free term that represents $\alpha$, $\textsf{Pref} ( \alpha )$ denotes the set of all nonempty prefixes of $\alpha$, $\textsf{Sub} ( \alpha )$ denotes the set of all nonempty substrings of $\alpha$ and $x \sqsubseteq _{ {\textsf{s}} } y$ is shorthand for

$$\begin{aligned} \begin{aligned} x = y \; \vee \; \exists u v \; \left[ \ y = ux \; \vee \; y = xv \; \vee \; y = uxv \ \right] . \end{aligned} \end{aligned}$$

In the standard model, $x \sqsubseteq _{ {\textsf{s}} } y$ holds if and only if $x \in \textsf{Sub} (y)$. It is easy to interpret ${{\textsf{I}}}{{\textsf{D}}}$ in ${{\textsf{I}}}{{\textsf{D}}}^*$ while it is less obvious whether ${{\textsf{I}}}{{\textsf{D}}}^*$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}$ since the axiom schema ${{\textsf{I}}}{{\textsf{D}}}_4^{ * }$ puts strong constraints on the concatenation operator while any model of ${\textsf{D}}_1 - {\textsf{D}}_3$ can always be extended to a model of ${{\textsf{I}}}{{\textsf{D}}}$. In Sect. 3, we show that ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ *}$ are mutually interpretable.

Given mutually interpretability of ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ *}$, a natural question is whether the arithmetical analogues of ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ *}$ are also mutually interpretable. We let ${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^*$ be the theories we obtain from ${\textsf{Q}}$ by replacing axiom ${\textsf{Q}}_3$ with respectively the axiom schemas

$$\begin{aligned} {{\textsf{I}}}{{\textsf{Q}}}_3 \equiv \ \forall x \; \left[ \ x \le {\overline{n}} \leftrightarrow \bigvee _{k \le n } x = {\overline{k}} \ \right] , \ \ {{\textsf{I}}}{{\textsf{Q}}}_3^* \equiv \ \forall x \; \left[ \ x \le _{ {\textsf{l}} } {\overline{n}} \rightarrow \bigvee _{k \le n } x = {\overline{k}} \ \right] \end{aligned}$$

where n is a natural number, ${\overline{n}}$ is a canonical variable-free term that represents n, $\le$ is a fresh binary relation symbol that is realized as the less than or equal relation in the standard model and $x \le _{ {\textsf{l}} } y \equiv \ \exists z \; [ \ z + x = y \ ]$. In Sect. 4, we show that ${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^{ *}$ are mutually interpretable.

We try to identify differences between concatenation theories and arithmetical theories by investigating the comparability of ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}$ with respect to interpretability. In Sect.  5, we show that ${{\textsf{I}}}{{\textsf{Q}}}$ is expressive enough to interpret the theory $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ we obtain by extending ${{\textsf{I}}}{{\textsf{D}}}$ with the axioms

$$\begin{aligned} \forall x y \; [ \ x \ne y \rightarrow ( \ 0x \ne 0y \; \wedge \; 1x \ne 1y \ ) \ ], \ \ \forall x y \; [ \ 0 x \ne 1 y \ ] . \end{aligned}$$

Since ${{\textsf{I}}}{{\textsf{Q}}}$ does not have enough resources for coding general sequences, the interpretation we give shows that we can think of concatenation theories as naturally contained in arithmetical theories. In Sect. 5.2, we show that the idea behind the interpretation of ${{\textsf{I}}}{{\textsf{D}}}$ in ${{\textsf{I}}}{{\textsf{Q}}}$ allows us to give a very simple interpretation of ${{\textsf{W}}}{{\textsf{D}}}$ in ${\textsf{R}}$. In Sect. 6, we show that our interpretation of ${{\textsf{I}}}{{\textsf{D}}}$ in ${{\textsf{I}}}{{\textsf{Q}}}$ extends in a natural way to an interpretation in ${\textsf{Q}}$ of Grzegorczyk’s theory of concatenation ${{\textsf{T}}}{{\textsf{C}}}$ [3] (see Fig. 3 for the axioms of ${{\textsf{T}}}{{\textsf{C}}}$). We can think of ${\textsf{D}}$ as a fragment of ${{\textsf{T}}}{{\textsf{C}}}$ since ${{\textsf{T}}}{{\textsf{C}}}$ proves all the axioms of ${\textsf{D}}$ when we let $x \preceq y \equiv \ x = y \; \vee \; \exists z \; [ \ y = x z \ ]$. The intended model of ${{\textsf{T}}}{{\textsf{C}}}$ is a finitely generated free semigroup with at least two generators. We have not been able to determine whether ${{\textsf{I}}}{{\textsf{Q}}}$ is interpretable in $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ and whether $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}$.

Fig. 3

Non-logical axioms of the first-order theory ${{\textsf{T}}}{{\textsf{C}}}$

We summarize our results in the following theorem. We let $S \le T$ mean that S is interpretable in T. We let $S < T$ mean $S \le T \; \wedge \; T \not \le S$. We let $S \cong T$ mean $S \le T \; \wedge \; T \le S$. We let $\overline{ {{\textsf{I}}}{{\textsf{D}}} }^{ * }$ denote the theory we obtain from $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ by replacing ${{\textsf{I}}}{{\textsf{D}}}_4$ with ${{\textsf{I}}}{{\textsf{D}}}_4^*$.

Theorem 1

$$\begin{aligned} {\textsf{R}} \cong {{\textsf{W}}}{{\textsf{D}}}< {{\textsf{I}}}{{\textsf{D}}} \cong {{\textsf{I}}}{{\textsf{D}}}^{*} \le \overline{ {{\textsf{I}}}{{\textsf{D}}} } \cong \overline{ {{\textsf{I}}}{{\textsf{D}}} }^{ * } \le {{\textsf{I}}}{{\textsf{Q}}} \cong {{\textsf{I}}}{{\textsf{Q}}}^{ * } < {\textsf{Q}} \cong {\textsf{D}} . \end{aligned}$$

It is not difficult to see that the two strict inequalities ${{\textsf{W}}}{{\textsf{D}}} < {{\textsf{I}}}{{\textsf{D}}}$, ${{\textsf{I}}}{{\textsf{Q}}} < {\textsf{Q}}$ hold. If ${{\textsf{I}}}{{\textsf{D}}}$ were interpretable in ${{\textsf{W}}}{{\textsf{D}}}$, then ${{\textsf{I}}}{{\textsf{D}}}_1 - {{\textsf{I}}}{{\textsf{D}}}_3$ would be interpretable in a finite subtheory of ${{\textsf{W}}}{{\textsf{D}}}$. Since any model of ${{\textsf{I}}}{{\textsf{D}}}_1 - {{\textsf{I}}}{{\textsf{D}}}_3$ is infinite while any finite subtheory of ${{\textsf{W}}}{{\textsf{D}}}$ has a finite model, ${{\textsf{I}}}{{\textsf{D}}}$ is not interpretable in ${{\textsf{W}}}{{\textsf{D}}}$. Similarly, if ${\textsf{Q}}$ were interpretable in ${{\textsf{I}}}{{\textsf{Q}}}$, it would be interpretable in a finite subtheory of ${{\textsf{I}}}{{\textsf{Q}}}$. But, any finite subtheory of ${{\textsf{I}}}{{\textsf{Q}}}$ is interpretable in the first-order theory of the field of real numbers $( {\mathbb {R}}, 0, 1, +, \times )$, which was shown to be decidable by Tarski [11]. Since ${\textsf{Q}}$ is essentially undecidable, it is not interpretable in ${{\textsf{I}}}{{\textsf{Q}}}$.

2 Preliminaries

In this section, we clarify a number of notions that we only glossed over in the previous section.

2.1 Notation and terminology

We consider the structures

$$\begin{aligned} \mathfrak {D}^{-} = ( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }, {\varvec{0}}, {\varvec{1}}, ^\frown ) \ \ \text{ and } \ \ {\mathfrak {D}} = ( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }, {\varvec{0}}, {\varvec{1}}, ^\frown , \preceq ^{ {\mathfrak {D}} } ) \end{aligned}$$

where $\lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ is the set of all finite nonempty strings over the alphabet $\lbrace {\varvec{0}}, {\varvec{1}} \rbrace$, the binary operator $^\frown$ concatenates elements of $\lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ and $\preceq ^{ {\mathfrak {D}} }$ denotes the prefix relation, i.e., $x \preceq ^{ {\mathfrak {D}} } y$ if and only if $y = x$ or there exists $z \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ such that $y = x ^\frown z$. The structure $\mathfrak {D}^{-}$ is thus the free semigroup with two generators. We call elements of $\lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ bit strings. The structures $\mathfrak {D}^{-}$ and ${\mathfrak {D}}$ are first-order structures over the languages ${\mathcal {L}}_{ {{\textsf{B}}}{{\textsf{T}}} }^{-} = \lbrace 0, 1, \circ \rbrace$ and ${\mathcal {L}}_{ {{\textsf{B}}}{{\textsf{T}}} } = \lbrace 0, 1, \circ , \preceq \rbrace$, respectively.

The language of first-order arithmetic is ${\mathcal {L}}_{ {{\textsf{N}}}{{\textsf{T}}} } = \lbrace 0, \textrm{S}, +, \times \rbrace$ and we denote by $( {\mathbb {N}}, 0, \textrm{S}, +, \times )$ the standard first-order structure. In first-order number theory, each natural number n is associated with a numeral ${\overline{n}}$ by recursion: ${\overline{0}} \equiv \ 0$ and $\overline{n+1} \equiv \ \textrm{S} {\overline{n}}$. Each non-empty bit string $\alpha \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ is associated by recursion with a unique ${\mathcal {L}}_{ {{\textsf{B}}}{{\textsf{T}}} }^{-}$-term ${\overline{\alpha }}$, called a biteral, as follows: $\overline{ {\varvec{0}} } \equiv 0$, $\overline{ {\varvec{1}} } \equiv 1$, $\overline{ \alpha {\varvec{0}} } \equiv ( {\overline{\alpha }} \circ 0 )$ and $\overline{ \alpha {\varvec{1}} } \equiv ( {\overline{\alpha }} \circ 1 )$. The biterals are important if we, for example, want to show that certain sets are definable since we then need to talk about elements of $\lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ in the formal theory.

A class is a formula with at least one free variable. Given a class I with n free variables, we write $(x_1, \ldots , x_n ) \in I$ for $I (x_1, \ldots , x_n)$. If I has two free variables, we also write xIy for I(x, y) . We let $( \exists x_1, \ldots , x_n ) \in I \; \left[ \ \phi \ \right]$ and $( \forall x_1, \ldots , x_n ) \in I \; \left[ \ \phi \ \right]$ be shorthand for the formulas $\exists x_1, \ldots , x_n \; [ \ I(x_1, \ldots , x_n) \; \wedge \; \phi \ ]$ and $\forall x_1, \ldots , x_n \; [ \ I(x_1, \ldots , x_n) \rightarrow \phi \ ]$, respectively. We let $\lbrace (x_1, \ldots , x_n) \in I: \ \psi \rbrace$ be shorthand for $I ( x_1, \ldots , x_n ) \; \wedge \; \psi$.

2.2 Translations and interpretations

We recall the method of relative interpretability introduced by Tarski [12] for showing that first-order theories are essentially undecidable. We restrict ourselves to many-dimensional parameter-free one-piece relative interpretations. Let ${\mathcal {L}}_{1}$ and ${\mathcal {L}}_{2}$ be computable first-order languages. A relative translation $\tau$ from ${\mathcal {L}}_{1}$ to ${\mathcal {L}}_{2}$ is a computable map given by:

• 1. An ${\mathcal {L}}_{2}$-formula $\delta (x_1, \ldots , x_m)$ with exactly m free variable. The formula $\delta (x_1, \ldots , x_m)$ is called a domain.

• 2. For each n-ary relation symbol R of ${\mathcal {L}}_{1}$, an ${\mathcal {L}}_{2}$-formula $\psi _{R}( \textbf{x}_1, \ldots , \textbf{x}_n )$ with exactly mn free variables. The equality symbol $=$ is treated as a binary relation symbol.

• 3. For each n-ary function symbol f of ${\mathcal {L}}_{1}$, an ${\mathcal {L}}_{2}$-formula $\psi _{f}( \textbf{x}_1, \ldots , \textbf{x}_n, \textbf{y} )$ with exactly $m(n+1)$ free variables.

• 4. For each constant symbol c of ${\mathcal {L}}_{1}$, an ${\mathcal {L}}_{2}$-formula $\psi _{c}( \textbf{y} )$ with exactly m free variables.

We extend $\tau$ to a translation of atomic ${\mathcal {L}}_{1}$-formulas by mapping an ${\mathcal {L}}_{1}$-term t to an ${\mathcal {L}}_{2}$-formula $( t )^{ \tau , \textbf{w} }$ with free variables $\textbf{w}$ that denote the value of t:

• 5. For each n-ary relation symbol R of ${\mathcal {L}}_{1}$

  $$\begin{aligned} \big ( R(t_1, \ldots , t_n ) \big )^{ \tau } \equiv \ \exists \textbf{v}_1 \ldots \textbf{v}_n \; \left[ \ \bigwedge _{ i = 1 }^{ n } \delta ( \textbf{v}_i ) \ \wedge \ \bigwedge _{ j = 1 }^{ n } ( t_j )^{ \tau , \textbf{v}_j } \ \wedge \ \psi _{ R } ( \textbf{v}_1 \ldots \textbf{v}_n ) \ \right] \end{aligned}$$

  where $\textbf{v}_1 \ldots \textbf{v}_n$ are distinct variable symbols that do not occur in $t_1, \ldots , t_n$ and

  • (a) for each variable symbol x of ${\mathcal {L}}_{1}$, $\; (x)^{ \tau , \textbf{w} } \equiv \ \bigwedge _{ i = 1 }^{ m } w_i = x_i \;$

  • (b) for each constant symbol c of ${\mathcal {L}}_{1}$, $\; (c)^{ \tau , \textbf{w} } \equiv \ \psi _{c} ( \textbf{w} ) \;$

  • (c) for each n-ary function symbol f of ${\mathcal {L}}_{1}$

    $$\begin{aligned}{} & {} \big ( f(t_1, \ldots , t_n ) \big )^{ \tau , \textbf{w} }\\{} & {} \quad \equiv \exists \textbf{w}_1 \ldots \textbf{w}_n \; \left[ \ \bigwedge _{ i = 1 }^{ n } \delta ( \textbf{w}_i ) \ \wedge \ \bigwedge _{ j = 1 }^{ n } ( t_j )^{ \tau , \textbf{w}_j } \ \wedge \ \psi _{ f } ( \textbf{w}_1 \ldots \textbf{w}_n, \textbf{w} ) \ \right] \end{aligned}$$

    where $\textbf{w}_1 \ldots \textbf{w}_n$ are distinct variable symbols that do not occur in $\bigwedge _{ j = 1 }^{ n } ( t_j )^{ \tau , \textbf{w} } \;$.

We extend $\tau$ to a translation of all ${\mathcal {L}}_{1}$-formulas as follows:

• 6. $( \lnot \phi )^{\tau } \equiv \ \lnot \phi ^{\tau }$

• 7. $( \phi \oslash \psi )^{\tau } \equiv \phi ^{\tau } \oslash \psi ^{\tau }$ for $\oslash \in \lbrace \wedge , \vee , \rightarrow , \leftrightarrow \rbrace$

• 8. $( \exists x \; \phi )^{\tau } \equiv \ \exists \textbf{x} \; [ \ \delta ( \textbf{x} ) \; \wedge \; \phi ^{\tau } \ ]$

• 9. $( \forall x \; \phi )^{\tau } \equiv \ \forall \textbf{x} \; [ \ \delta ( \textbf{x} ) \rightarrow \phi ^{\tau } \ ] \;$.

Let ${S}$ be an ${\mathcal {L}}_{1}$-theory and let ${T}$ be an ${\mathcal {L}}_{2}$-theory. We say that ${S}$ is (relatively) interpretable in ${T}$ if there exists a relative translation $\tau$ such that

• ${T} \vdash \exists {\textbf {x}} \; \left[ \ \delta ( {\textbf {x}} ) \ \right]$

• For each function symbol f of ${\mathcal {L}}_{1}$

  $$\begin{aligned} {T} \vdash \bigwedge _{i=1}^{n} \delta ( {\textbf {x}}_i ) \rightarrow \exists {\textbf {y}} \; \left[ \ \delta ( {\textbf {y}} ) \wedge \psi _{f}( {\textbf {x}}_1, \ldots , {\textbf {x}}_n, {\textbf {y}} ) \wedge \forall {\textbf {z}} \; \left[ \ \delta ( {\textbf {z}} ) \wedge \psi _{f} ( {\textbf {x}}_1, \ldots , {\textbf {x}}_n, {\textbf {z}} ) \rightarrow \psi _{=} ( {\textbf {y}} , {\textbf {z}}) \ \right] \ \ \right] . \end{aligned}$$

• For each constant symbol c of ${\mathcal {L}}_{1}$

  $$\begin{aligned} {T} \vdash \exists {\textbf {y}} \; \left[ \ \delta ( {\textbf {y}} ) \wedge \psi _{c}( {\textbf {y}} ) \wedge \forall {\textbf {z}} \; \left[ \ \delta ( {\textbf {z}} ) \wedge \psi _{c}( {\textbf {z}} ) \rightarrow \psi _{=} ( {\textbf {y}} , {\textbf {z}}) \ \right] \ \right] . \end{aligned}$$

• ${T}$ proves $\phi ^{\tau }$ for each non-logical axiom $\phi$ of ${S}$. If equality is not translated as equality, then ${T}$ must prove the translation of each equality axiom.

If ${S}$ is relatively interpretable in ${T}$ and ${T}$ is relatively interpretable in ${S}$, we say that ${S}$ and ${T}$ are mutually interpretable.

The following proposition summarizes important properties of relative interpretability (see Tarski et al. [12] for the details).

Proposition 2

Let ${S}$, ${T}$ and ${U}$ be computably enumerable first-order theories.

• 1. If ${S}$ is interpretable in ${T}$ and ${T}$ is consistent, then ${S}$ is consistent.

• 2. If ${S}$ is interpretable in ${T}$ and ${T}$ is interpretable in ${U}$, then ${S}$ is interpretable in ${U}$.

• 3. If ${S}$ is interpretable in ${T}$ and ${S}$ is essentially undecidable, then ${T}$ is essentially undecidable.

3 Mutual interpretability of ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{*}$

In this section, we show that ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{*}$ are mutually interpretable (see Fig. 4 for the axioms of ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{*}$). It is easy to see that ${{\textsf{I}}}{{\textsf{D}}}$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}^{*}$. We therefore need to focus on the more difficult task of proving that ${{\textsf{I}}}{{\textsf{D}}}^{*}$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}$. It is more difficult to interpret ${{\textsf{I}}}{{\textsf{D}}}^{*}$ in ${{\textsf{I}}}{{\textsf{D}}}$ because the axiom schema ${{\textsf{I}}}{{\textsf{D}}}^{*}_4$ puts strong constraints on the concatenation operator while it is always possible to extend any model of ${{\textsf{I}}}{{\textsf{D}}}_1$, ${{\textsf{I}}}{{\textsf{D}}}_2$, ${{\textsf{I}}}{{\textsf{D}}}_3$ to a model of ${{\textsf{I}}}{{\textsf{D}}}$. For example, we can have models of ${{\textsf{I}}}{{\textsf{D}}}$ where there exist infinitely many pairs x, y such that $x y = {\overline{\alpha }}$ for each nonempty string $\alpha$. Indeed, consider the model where the universe is the Cartesian product $\prod _{ i < \omega } \lbrace 0, 1 \rbrace ^*$, concatenation is componentwise and each binary string $\beta$ is mapped to the constant sequence $( \beta )_{ i < \omega }$.

Fig. 4

Non-logical axioms of the first-order theories ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^*$. ${{\textsf{I}}}{{\textsf{D}}}_4$ and ${{\textsf{I}}}{{\textsf{D}}}_4^{ *}$ are axiom schemas where $\alpha$ is a nonempty binary string, $\textsf{Pref} ( \alpha )$ is the set of all nonempty prefixes of $\alpha$ and $\textsf{Sub} ( \alpha )$ is the set of all nonempty substrings of $\alpha$. Furthermore, $x \sqsubseteq _{ {\textsf{s}} } y \equiv \ x = y \; \vee \; \exists u v \; [ \ y = ux \; \vee \; y = xv \; \vee \; y = uxv \ ]$

To interpret ${{\textsf{I}}}{{\textsf{D}}}^{*}$ in ${{\textsf{I}}}{{\textsf{D}}}$, we need to use the axiom schema ${{\textsf{I}}}{{\textsf{D}}}_4$ in an essential way to define a function $\star$ that provably in ${{\textsf{I}}}{{\textsf{D}}}$ satisfies the translation of each axiom of ${{\textsf{I}}}{{\textsf{D}}}^{*}$. The idea is to observe that since we have the right cancellation law in the weak form of ${{\textsf{I}}}{{\textsf{D}}}_2$, if we had an axiom schema for the suffix relation, denoted $\preceq _{ \textsf{suff} }$, analogues to ${{\textsf{I}}}{{\textsf{D}}}_4$, we could try to define $\star$ by requiring that $x \star y = xy$ only if $y \preceq _{ \textsf{suff} } xy$. If xy is a variable-free term and $y \preceq _{ \textsf{suff} } xy$, then the axiom schema for the suffix relation gives us a finite number of possibilities for the value of y. If we also knew that 0 and 1 were atoms/ indecomposable, we would be able to use ${{\textsf{I}}}{{\textsf{D}}}_2$ and ${{\textsf{I}}}{{\textsf{D}}}_3$ to determine that x and y are also variable-free terms. To make this idea work, we need to ensure that $\star$ is associative. Our solution is to show that extending ${{\textsf{I}}}{{\textsf{D}}}$ with an axiom schema for $\preceq _{ \textsf{suff} }$ and the axiom $\forall x y \; [ \ y \preceq _{ \textsf{suff} } x y \ ]$ does not change the interpretability degree.

This section is organized as follows: In Sect. 3.1, we show that we can extend ${{\textsf{I}}}{{\textsf{D}}}$ to a theory ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ with the same interpretability degree where 0 and 1 are atoms. In Sect. 3.2, we show that we can extend ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ to a theory ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ with the same interpretability degree where we have an axiom schema for the suffix relation $\preceq _{ \textsf{suff} }$ analogues to the axiom schema ${{\textsf{I}}}{{\textsf{D}}}_4$. In Sect. 3.3, we extended ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ to a theory ${{\textsf{I}}}{{\textsf{D}}}^{ (4) }$ with the same interpretability degree and where we have an axiom schema for the substring relation, analogues to ${{\textsf{I}}}{{\textsf{D}}}_4$. In Sect. 3.4, we use the axiom schema for the substring relation to extend ${{\textsf{I}}}{{\textsf{D}}}^{ (4) }$ to a theory ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$ with the same interpretability degree and where the suffix relation $\preceq _{ \textsf{suff} }$ satisfies additional properties. Finally, in Sect. 3.5, we show that ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$.

3.1 Atoms

It will prove useful later to know that 0 and 1 are atoms. So, let ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ be ${{\textsf{I}}}{{\textsf{D}}}$ extended with the axioms

$$\begin{aligned} \textsf{AT0} \equiv \ \forall xy \; [ \ xy \ne 0 \ ], \ \ \ \textsf{AT1} \equiv \ \forall xy \; [ \ xy \ne 1 \ ] . \end{aligned}$$

Lemma 3

${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ are mutually interpretable.

Proof

Since ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ is an extension of ${{\textsf{I}}}{{\textsf{D}}}$, it suffices to show that ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}$. Since the axioms of ${{\textsf{I}}}{{\textsf{D}}}$ are universal sentences, it suffices to relativize quantification to a domain K on which the sentences $\textsf{AT0}$, $\textsf{AT1}$ hold. We obtain K by successively restricting the universe to subclasses with nice properties.

Let

$$\begin{aligned} K_1 = \lbrace x: \ x = 0 \; \vee \; x= 1 \; \vee \; \exists y \; [ \ x = y0 \; \vee \; x = y1 \ ] \ \rbrace . \end{aligned}$$

Clearly, $0, 1 \in K_1$. Since concatenation is associative, $K_1$ is closed under concatenation.

Let

$$\begin{aligned} K_2 = \left\{ y \in K_1: \ \forall x \in K_1 \; \left[ \ \bigwedge _{ a \in \lbrace 0,1 \rbrace } x y \ne a \ \right] \ \right\} . \end{aligned}$$

We show that $0, 1 \in K_2$. Let $a, b \in \lbrace 0,1 \rbrace$ and let $x \in K_1$. We need to show $xb \ne a$. Assume for the sake of a contradiction that $xb = a$. Since $x \in K_1$, let $c \in \lbrace 0,1 \rbrace$ be such that $x = c$ or $x = uc$ for some u. Let $d \in \lbrace 0,1 \rbrace {\setminus } \lbrace c \rbrace$. Then, $xb = a$ implies $ddxb = dda$. By ${{\textsf{I}}}{{\textsf{D}}}_3$ and ${{\textsf{I}}}{{\textsf{D}}}_2$, $ddx = dd$, which contradicts ${{\textsf{I}}}{{\textsf{D}}}_3$. Thus, $0, 1 \in K_2$.

We now show that $K_2$ is closed under the maps $x \mapsto x0$, $x \mapsto x1$. Let $y \in K_2$ and let $b \in \lbrace 0,1 \rbrace$. We need to show that $yb \in K_2$. Since $y, b \in K_2 \subseteq K_1$ and $K_1$ is closed under concatenation, $yb \in K_1$. Now, let $a \in \lbrace 0,1 \rbrace$ and let $x \in K_1$. We need to show $x yb \ne a$. Assume for the sake of a contradiction that $x y b = a$. Then, $ax yb = aa$. By ${{\textsf{I}}}{{\textsf{D}}}_3$ and ${{\textsf{I}}}{{\textsf{D}}}_2$, we have $ax y = a$, which contradicts $y \in K_2$ since $ax \in K_1$ as $a, x \in K_1$ and $K_1$ is closed under concatenation. Thus, $K_2$ is closed under the maps $x \mapsto x0$, $x \mapsto x1$.

The class $K_2$ is not a domain since it may not be closed under concatenation. We obtain K by restricting $K_2$ to a subclass that contains 0 and 1 and is closed under concatenation. Let

$$\begin{aligned} K = \lbrace w \in K_2: \ \forall z \in K_2 \; [ \ zw \in K_2 \ ] \ \rbrace . \end{aligned}$$

We have $0, 1 \in K$ since $K_2$ contains 0, 1 and is closed under the maps $x \mapsto x0$, $x \mapsto x1$. We now show that K is closed under concatenation. Let $w_0, w_1 \in K$. We need to show that $w_0 w_1 \in K$. Since $w_0 \in K \subseteq K_2$ and $w_1 \in K$, we have $w_0 w_1 \in K_2$. Now, let $z \in K_2$. We need to show that $z w_0 w_1 \in K_2$. We do not worry about parentheses since ${{\textsf{I}}}{{\textsf{D}}}_1$ tells us that concatenation is associative. Since $w_0 \in K$, we have $z w_0 \in K_2$. Since $w_1 \in K$, we have $z w_0 w_1 \in K_2$. Hence, $w_0 w_1 \in K$. Thus, K is closed under concatenation. $\square$

3.2 Suffix relation

In this section, we show that we can extend ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ to a theory where we have an axiom schema for the suffix relation, analogues to ${{\textsf{I}}}{{\textsf{D}}}_4$, without changing the interpretability degree. We extend the language of ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ with a fresh binary relation symbol $\preceq _{ \textsf{suff} }$. Given a nonempty binary string $\alpha$, let $\textsf{Suff} ( \alpha )$ denote the set of all nonempty suffixes of $\alpha$: $\gamma \in \textsf{Suff} ( \alpha )$ if and only if $\alpha = \gamma$ or $\exists \delta \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + } \; [ \ \alpha = \delta \gamma \; \wedge \; \gamma \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + } \ ]$. Let ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ be ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$ extended with the following axiom schema

$$\begin{aligned} \forall x \; \left[ \ x \preceq _{ \textsf{suff} } {\overline{\alpha }} \leftrightarrow \bigvee _{ \gamma \in \textsf{Suff} ( \alpha ) } x= {\overline{\gamma }} \ \right] . \end{aligned}$$

Lemma 4

${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ are mutually interpretable.

Proof

Since ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ is an extension of ${{\textsf{I}}}{{\textsf{D}}}$, it suffices by Lemma 3 to show that the suffix relation is definable in ${{\textsf{I}}}{{\textsf{D}}}^{ (2) }$. We translate the suffix relation as follows: $x \preceq _{ \textsf{suff} } y$ if and only if

• (1) $y = x \; \vee \; \exists u \; [ \ y = ux \ ]$

• (2) $\forall u \preceq x \; \big [ \ u = 0 \; \vee \; u = 1 \; \vee \; \exists v \preceq u \; [ \ u = v 0 \; \vee \; u = v 1 \ ] \ \big ]$

• (3) $\preceq$ is reflexive and transitive on the class $I_x = \lbrace z: \ z \preceq x \rbrace$, $\ x \in I_x$ and $\forall z \in I_x \; \forall w \preceq z \; [ \ w \in I_x \ ]$.

Given a nonempty binary string $\alpha$, we need to show that

$$\begin{aligned} {{\textsf{I}}}{{\textsf{D}}}^{ (2) } \vdash \forall x \; \left[ \ x \preceq _{ \textsf{suff} } {\overline{\alpha }} \leftrightarrow \bigvee _{ \gamma \in \textsf{Suff} ( \alpha ) } x= {\overline{\gamma }} \ \right] . \end{aligned}$$

$( \Leftarrow )$

We show that

$$\begin{aligned} {{\textsf{I}}}{{\textsf{D}}}^{ (2) } \vdash \forall x \; \left[ \ \big ( \ \bigvee _{ \gamma \in \textsf{Suff} ( \alpha ) } x= {\overline{\gamma }} \ \big ) \rightarrow x \preceq _{ \textsf{suff} } {\overline{\alpha }} \ \right] . \end{aligned}$$

Let $\gamma \in \textsf{Suff} ( \alpha )$. We need to show that ${\overline{\gamma }} \preceq _{ \textsf{suff} } {\overline{\alpha }}$ holds. That is, we need to show that ${\overline{\gamma }}$ and ${\overline{\alpha }}$ satisfy (1)–(3). It is easy to prove by induction on the length of binary strings that

$$\begin{aligned} {{\textsf{I}}}{{\textsf{D}}} \vdash {\overline{\delta }} \, \; {\overline{\zeta }} = \overline{ \delta \zeta } \ \ \text{ for } \text{ all } \delta , \zeta \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + } \ . \qquad {(*)} \end{aligned}$$

By (*), ${\overline{\alpha }} = {\overline{\gamma }}$ or ${\overline{\alpha }} = {\overline{\delta }} \; {\overline{\gamma }}$ where $\delta$ is a prefix of $\alpha$. Hence, (1) holds. By (*) and the axiom schema ${{\textsf{I}}}{{\textsf{D}}}_4$ for the prefix relation, ${\overline{\gamma }}$ satisfies (2)–(3). Thus, ${\overline{\gamma }} \preceq _{ \textsf{suff} } {\overline{\alpha }}$ holds.

$( \Rightarrow )$

We need to show that

$$\begin{aligned} {{\textsf{I}}}{{\textsf{D}}}^{ (2) } \vdash \forall x \; \left[ \ x \preceq _{ \textsf{suff} } {\overline{\alpha }} \rightarrow \bigvee _{ \gamma \in \textsf{Suff} ( \alpha ) } x= {\overline{\gamma }} \ \right] . \qquad {(**)} \end{aligned}$$

We prove (**) by induction on the length of $\alpha$. Assume $\alpha \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace$ and $x \preceq _{ \textsf{suff} } {\overline{\alpha }}$ holds. By (1), $x = {\overline{\alpha }}$ or there exist u such that ${\overline{\alpha }} = u x$. By $\textsf{AT0}$ and $\textsf{AT1}$, we have $x = {\overline{\alpha }}$. Thus, (**) holds when $\alpha \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace$.

We consider the inductive case. Assume $\alpha = \beta a$ where $a \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace$, $\beta \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ and

$$\begin{aligned} {{\textsf{I}}}{{\textsf{D}}}^{ (2) } \vdash \forall x \; \left[ \ x \preceq _{ \textsf{suff} } {\overline{\beta }} \rightarrow \bigvee _{ \gamma \in \textsf{Suff} ( \beta ) } x= {\overline{\gamma }} \ \right] \ . \qquad {(***)} \end{aligned}$$

By definition, ${\overline{\alpha }} = \overline{ \beta a } = {\overline{\beta }} \, {\overline{a}}$. Assume $x \preceq _{ \textsf{suff} } {\overline{\alpha }}$ holds. By (1), $x = {\overline{\alpha }}$ or there exist u such that ${\overline{\alpha }} = u x$. If $x = {\overline{\alpha }}$, we are done. So, assume ${\overline{\alpha }} = u x$. By (3), we have $x \preceq x$. Then, by (2), we have one of the following cases: (i) there exists $b \in \lbrace 0, 1 \rbrace$ such that $b = x$, (ii) there exist $w \preceq x$ and $c \in \lbrace 0, 1 \rbrace$ such that $x = w c$. Assume (i) holds. We have ${\overline{\beta }} \, {\overline{a}} = {\overline{\alpha }} = ux = u b$. By ${{\textsf{I}}}{{\textsf{D}}}_3$, we have $\, {\overline{a}} = b = x$. Thus, $x= {\overline{\gamma }}$ where $\gamma \in \textsf{Suff} ( \alpha )$.

Assume (ii) holds. Then, ${\overline{\beta }} \, {\overline{a}} = {\overline{\alpha }} = ux = u w c$. By ${{\textsf{I}}}{{\textsf{D}}}_3$, we have ${\overline{a}} = c$. By ${{\textsf{I}}}{{\textsf{D}}}_2$, we have ${\overline{\beta }} = u w$. Furthermore

• $\forall u \preceq w \; \big [ \ u = 0 \; \vee \; u = 1 \; \vee \; \exists v \preceq u \; [ \ u = v 0 \; \vee \; u = v 1 \ ] \ \big ]$ since $u \preceq w \; \wedge \; w \preceq x$ implies $u \preceq x$ by (3)

• since $w \preceq x$ and (3) holds, $\preceq$ is reflexive and transitive on the class $I_w = \lbrace z: \ z \preceq w \rbrace$, $\ w \in I_w$ and $\forall z \in I_w \; \forall w \preceq z \; [ \ w \in I_w \ ]$.

Thus, $w \preceq _{ \textsf{suff} } {\overline{\beta }}$ holds. By (***), $w = {\overline{\delta }}$ where $\delta$ is a suffix of $\beta$. Then, $x = w {\overline{a}} = {\overline{\delta }} \, {\overline{a}} = \overline{ \delta a}$ and $\delta a$ is a suffix of $\alpha$. Thus, $\alpha$ satisfies (**).

Thus, by induction, (**) holds for all nonempty binary strings $\alpha$. $\square$

3.3 Substring relation

In this section, we show that we can extend ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ to a theory where we have an axiom schema for the substring relation, analogues to ${{\textsf{I}}}{{\textsf{D}}}_4$, without changing the interpretability degree. We extend the language of ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ with a fresh binary relation symbol $\preceq _{ \textsf{sub} }$. Given a nonempty binary string $\alpha$, let $\textsf{Sub} ( \alpha )$ denote the set of all nonempty substrings of $\alpha$: $\beta \in \textsf{Sub} ( \alpha )$ if and only if $\alpha = \beta$ or there exist $\gamma , \delta \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ such that $\beta \in \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }$ and $\alpha = \gamma \beta \; \vee \; \alpha = \beta \delta \; \vee \; \alpha = \gamma \beta \delta$. Let ${{\textsf{I}}}{{\textsf{D}}}^{ (4) }$ be ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ extended with the following axiom schema

$$\begin{aligned} \forall x \; \left[ \ x \preceq _{ \textsf{sub} } {\overline{\alpha }} \leftrightarrow \bigvee _{ \gamma \in \textsf{Sub} ( \alpha ) } x= {\overline{\gamma }} \ \right] . \end{aligned}$$

Lemma 5

${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ (4) }$ are mutually interpretable.

Proof

By Lemma 4, it suffices to show that the substring relation is definable in ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$. We translate the substring relation as follows

$$\begin{aligned} x \preceq _{ \textsf{sub} } y \equiv \ x \preceq y \; \vee \; x \preceq _{ \textsf{suff} } y \; \vee \; \exists u \preceq y \; [ \ x \preceq _{ \textsf{suff} } u \ ] . \end{aligned}$$

By the axiom schema for the prefix relation and the axiom schema for the suffix relation, it is easy to see that ${{\textsf{I}}}{{\textsf{D}}}^{ (3) }$ proves $\forall x \; [ \ x \preceq _{ \textsf{sub} } {\overline{\alpha }} \leftrightarrow \bigvee _{ \gamma \in \textsf{Sub} ( \alpha ) } x= {\overline{\gamma }} \ ]$ for each nonempty binary string $\alpha$. $\square$

3.4 Suffix relation II

We are finally ready to equip the suffix relation with two very important properties. Let ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$ be ${{\textsf{I}}}{{\textsf{D}}}^{ (4) }$ extended with the following axioms

$$\begin{aligned} \forall x \; \left[ \ \bigwedge _{ a \in \lbrace 0, 1 \rbrace } a \preceq _{ \textsf{suff} } xa \ \right] , \ \ \ \ \forall x y \; \left[ \ x \preceq _{ \textsf{suff} } y \rightarrow \bigwedge _{ a \in \lbrace 0, 1 \rbrace } xa \preceq _{ \textsf{suff} } ya \ \right] . \end{aligned}$$

To show that ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$ and ${{\textsf{I}}}{{\textsf{D}}}$ are mutually interpretable, we need the following lemma. Recall that a class is a formula with at least one free variable and that if I is a class with one free variable we occasionally write $x \in I$ for I(x) .

Lemma 6

There exists a class J with the following properties:

• (1) $\; {{\textsf{I}}}{{\textsf{D}}}^{ (4) } \vdash t \in J \$ for each variable-free term t

• (2) ${{\textsf{I}}}{{\textsf{D}}}^{ (4) } \vdash \forall x \; \forall z \in J \; \big [ \ \bigwedge _{ a \in \lbrace 0, 1 \rbrace } ( \ z = xa \rightarrow a \preceq _{ \textsf{suff} } z \ ) \ \big ]$

• (3) ${{\textsf{I}}}{{\textsf{D}}}^{ (4) } \vdash \forall x y \; \forall z \in J \; \big [ \ \bigwedge _{ a \in \lbrace 0, 1 \rbrace } \big ( \ ( \ z = ya \; \wedge \; x \preceq _{ \textsf{suff} } y \ ) \rightarrow ( \ xa \preceq _{ \textsf{suff} } z \ ) \ \big ) \big ]$

• (4) ${{\textsf{I}}}{{\textsf{D}}}^{ (4) } \vdash \forall z \in J \; \big [ \ z = 0 \; \vee \; z = 1 \; \vee \; \exists u \preceq _{ \textsf{sub} } z \; [ \ z = u0 \; \vee \; z = u 1 \ ] \ \big ]$

• (5) ${{\textsf{I}}}{{\textsf{D}}}^{ (4) } \vdash \forall z \in J \; \forall u \; \big [ \ u \preceq _{ \textsf{sub} } z \rightarrow u \in J \ \big ]$.

Proof

We define J as follows: $u \in J$ if and only if

• (i) $u \preceq _{ \textsf{sub} } u$

• (ii) $\forall w \preceq _{ \textsf{sub} } u \; [ \ w \preceq _{ \textsf{sub} } w \ ]$

• (iii) $\forall w \preceq _{ \textsf{sub} } u \; \forall v_0 \preceq _{ \textsf{sub} } w \; \forall v_1 \preceq _{ \textsf{sub} } v_0 \; [ \ v_1 \preceq _{ \textsf{sub} } w \ ] \;$

  • (A) $\forall w \preceq _{ \textsf{sub} } u \; [ \ w = 0 \; \vee \; w = 1 \; \vee \; \exists v \preceq _{ \textsf{sub} } w \; [ \ w = v0 \; \vee \; w = v1 \ ] \ ] \;$.

  • (B) $\forall w \preceq _{ \textsf{sub} } u \; \forall x \; [ \ w = x 0 \rightarrow 0 \preceq _{ \textsf{suff} } w \ ]$

  • (C) $\forall w \preceq _{ \textsf{sub} } u \; \forall x \; [ \ w = x 1 \rightarrow 1 \preceq _{ \textsf{suff} } w \ ]$

  • (D) $\forall w \preceq _{ \textsf{sub} } u \; \forall x y \; [ \ ( \ w = y 0 \; \wedge \; x \preceq _{ \textsf{suff} } y \ ) \rightarrow x0 \preceq _{ \textsf{sub} } w \ ]$

  • (E) $\forall w \preceq _{ \textsf{sub} } u \; \forall x y \; [ \ ( \ w = y 1 \; \wedge \; x \preceq _{ \textsf{suff} } y \ ) \rightarrow x1 \preceq _{ \textsf{sub} } w \ ] \;$.

It follows straight from the definition that J satisfies clauses (2)–(4). By the axiom schema for the substring relation, the axiom schema for the suffix relation, $\textsf{AT0}$, $\textsf{AT1}$, ${{\textsf{I}}}{{\textsf{D}}}_2$ and ${{\textsf{I}}}{{\textsf{D}}}_3$, J satisfies Clause (1). It remains to show that J also satisfies Clause (5). That is, we need to show that J is downward closed under $\preceq _{ \textsf{sub} }$. So, assume $u^{ \prime } \preceq _{ \textsf{sub} } u \in J$. We need to show that $u^{ \prime } \in J$. That is, we need to show that $u^{ \prime }$ satisfies (i)–(iii) and (A)–(E). We show that $u^{ \prime }$ satisfies (i). Since u satisfies (ii), $u^{ \prime } \preceq _{ \textsf{sub} } u$ implies $u^{ \prime } \preceq _{ \textsf{sub} } u^{ \prime }$. Thus, $u^{ \prime }$ satisfies (i).

We show that $u^{ \prime }$ satisfies (ii)–(iii) and (A)–(E). Consider one of these clauses. It is of the form $\forall w \preceq _{ \textsf{sub} } u^{ \prime } \; \phi (w)$. We need to show that $\forall w \preceq _{ \textsf{sub} } u^{ \prime } \; \phi (w)$ holds. Since $u \in J$, we know that $\forall w \preceq _{ \textsf{sub} } u \; \phi (w)$ holds. Let $w \preceq _{ \textsf{sub} } u^{ \prime }$. We need to show that $\phi (w )$ holds. Since $\forall w \preceq _{ \textsf{sub} } u \; \phi (w)$ holds, it suffices to show that $w \preceq _{ \textsf{sub} } u$ holds. By assumption

$$\begin{aligned} w \preceq _{ \textsf{sub} } u^{ \prime } \preceq _{ \textsf{sub} } u . \end{aligned}$$

Since u satisfies (i)

$$\begin{aligned} w \preceq _{ \textsf{sub} } u^{ \prime } \preceq _{ \textsf{sub} } u \preceq _{ \textsf{sub} } u . \end{aligned}$$

Then, $w \preceq _{ \textsf{sub} } u$ since u satisfies (iii). Hence, $\forall w \preceq _{ \textsf{sub} } u^{ \prime } \; \phi (w)$ holds. Thus, $u^{ \prime }$ satisfies clauses (ii)–(iii), (A)–(E).

Since $u^{ \prime }$ satisfies (i)–(iii) and (A)–(E), $u^{ \prime } \in J$. Thus, J is downward closed under $\preceq _{ \textsf{sub} }$. $\square$

Lemma 7

${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$ are mutually interpretable.

Proof

By Lemma 5, it suffices to show that ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}^{ ( 4 ) }$. Let J be the class given by Lemma 6. To interpret ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$ in ${{\textsf{I}}}{{\textsf{D}}}^{ ( 4 ) }$ it suffices to translate the suffix relation as follows

$$\begin{aligned} x \preceq _{ \textsf{suff} }^{ \tau } y \equiv \ ( \ y \in J \; \wedge \; x \preceq _{ \textsf{suff} } y \ ) \ \vee \ ( \ y \not \in J \; \wedge \; x = x \ ) . \end{aligned}$$

We need show that the translation of each instance of the axiom schema for the suffix relation is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ ( 4 ) }$. Let $\alpha$ be a nonempty binary string. We need to show that

$$\begin{aligned} \forall x \; \left[ \ x \preceq _{ \textsf{suff} }^{ \tau } {\overline{\alpha }} \leftrightarrow \bigvee _{ \gamma \in \textsf{Suff} ( \alpha ) } x= {\overline{\gamma }} \ \right] \end{aligned}$$

(A)

holds. By Clause (1) of Lemma 6, $\; {\overline{\alpha }} \in J$. Hence, by the definition of $\preceq _{ \textsf{suff} }^{ \tau }$, (A) holds if and only if

$$\begin{aligned} \forall x \; \left[ \ x \preceq _{ \textsf{suff} } {\overline{\alpha }} \leftrightarrow \bigvee _{ \gamma \in \textsf{Suff} ( \alpha ) } x= {\overline{\gamma }} \ \right] \end{aligned}$$

(B)

holds. Observe that (B) is an instance of the axiom schema for the suffix relation. Thus, the translation of each instance of the axiom schema for the suffix relation is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ ( 4 ) }$.

We need to show that the translation of the axiom

$$\begin{aligned} \forall x \; \left[ \ \bigwedge _{ a \in \lbrace 0, 1 \rbrace } a \preceq _{ \textsf{suff} } xa \ \right] \end{aligned}$$

(C)

is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ ( 4 ) }$. Let x be arbitrary and let $a \in \lbrace 0, 1 \rbrace$. We need to show that $a \preceq _{ \textsf{suff} }^{ \tau } xa$ holds. Assume $xa \in J$. Then, $a \preceq _{ \textsf{suff} }^{ \tau } xa$ holds if and only if $a \preceq _{ \textsf{suff} } xa$ holds. By Clause (2) of Lemma 6, $a \preceq _{ \textsf{suff} } xa$ holds. Hence, $a \preceq _{ \textsf{suff} }^{ \tau } xa$ holds when $xa \in J$. Assume now $xa \not \in J$. Then, $a \preceq _{ \textsf{suff} }^{ \tau } xa$ holds by the second disjunct in the definition of $\preceq _{ \textsf{suff} }^{ \tau }$. Thus, the translation of (C) is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ ( 4 ) }$.

We need to show that the translation of the axiom

$$\begin{aligned} \forall x y \; \left[ \ x \preceq _{ \textsf{suff} } y \rightarrow \bigwedge _{ a \in \lbrace 0, 1 \rbrace } xa \preceq _{ \textsf{suff} } ya \ \right] \end{aligned}$$

(D)

is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ ( 4 ) }$. Let $a \in \lbrace 0, 1 \rbrace$ and assume $x \preceq _{ \textsf{suff} }^{ \tau } y$. We need to show that $xa \preceq _{ \textsf{suff} }^{ \tau } ya$ holds. Assume first $ya \not \in J$. Then, $xa \preceq _{ \textsf{suff} }^{ \tau } ya$ holds by the second disjunct in the definition of $\preceq _{ \textsf{suff} }^{ \tau }$. Assume next $ya \in J$. Then, by Clause (4) of Lemma 6, $ya \in \lbrace 0, 1 \rbrace$ or there exist $u \preceq _{ \textsf{sub} } ya$ and $b \in \lbrace 0, 1 \rbrace$ such that $ya = u b$. By $\textsf{AT0}$, $\textsf{AT1}$ and ${{\textsf{I}}}{{\textsf{D}}}_3$, we have $ya = u a$ where $u \preceq _{ \textsf{sub} } ya$. By ${{\textsf{I}}}{{\textsf{D}}}_2$, we have $y = u$. Hence, $y \preceq _{ \textsf{sub} } ya$. By Clause (5) of Lemma 6, $y \in J$. Thus, since $x \preceq _{ \textsf{suff} }^{ \tau } y$ holds and $y \in J$, we have $x \preceq _{ \textsf{suff} } y$ by the definition of $\preceq _{ \textsf{suff} }^{ \tau }$. Then, by Clause (3) of Lemma  6, $xa \preceq _{ \textsf{suff} } ya$ holds. Thus, the translation of (D) is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ ( 4 ) }$. $\square$

3.5 Interpretation of ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ in ${{\textsf{I}}}{{\textsf{D}}}$

We are finally ready to show that ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ and ${{\textsf{I}}}{{\textsf{D}}}$ are mutually interpretable.

Theorem 8

The theories ${{\textsf{I}}}{{\textsf{D}}}$, ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ are mutually interpretable.

Proof

To interpret ${{\textsf{I}}}{{\textsf{D}}}$ in ${{\textsf{I}}}{{\textsf{D}}}^{ * }$, it suffices to translate $\preceq$ as follows

$$\begin{aligned} x \preceq y \equiv \ y =x \; \vee \; \exists z \; [ \ y = xz \ ] . \end{aligned}$$

Given a nonempty binary string $\alpha$, we have

$$\begin{aligned} \begin{aligned} x \preceq {\overline{\alpha }}&\Leftrightarrow {\overline{\alpha }} = x \vee \exists z \; [ \ {\overline{\alpha }} = x z \ ]\\&\Leftrightarrow {\overline{\alpha }} = x \; \vee \;\\&\quad \exists z \; [ \ x \sqsubseteq _{ {\textsf{s}} } {\overline{\alpha }} \; \wedge \; z \sqsubseteq _{ {\textsf{s}} } {\overline{\alpha }} \; \wedge \; {\overline{\alpha }} = x z \ ] \qquad ( \text{ def. } \text{ of } \sqsubseteq _{ {\textsf{s}} } \; )\\&\Leftrightarrow {\overline{\alpha }} = x \; \vee \;\\&\quad \bigvee _{ \beta , \gamma \in \textsf{Sub} ( \alpha ) } ( \ x= {\overline{\beta }} \wedge z = {\overline{\gamma }} \wedge {\overline{\beta }} \ {\overline{\gamma }} = {\overline{\alpha }} \ ) \qquad ( {{\textsf{I}}}{{\textsf{D}}}^{ * }_4 )\\&\Leftrightarrow \bigvee _{ \beta \in \textsf{Pref} ( \alpha ) } x = {\overline{\beta }}\qquad ( {{\textsf{I}}}{{\textsf{D}}}_1 - {{\textsf{I}}}{{\textsf{D}}}_3 ) . \end{aligned} \end{aligned}$$

This shows that the translation of each instance of the axiom schema ${{\textsf{I}}}{{\textsf{D}}}_4$ is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ * }$. Thus, ${{\textsf{I}}}{{\textsf{D}}}$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}^{ * }$.

Next, we show that ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}$. By Lemma 7, it suffices to show that ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$. Since the axioms of ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ are universal sentences or sentences where existential quantifiers occur in the antecedent (instances of ${{\textsf{I}}}{{\textsf{D}}}^{ * }_4$), to interpret ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ in ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$ it suffices to relativize quantification to a suitable domain K.

We start by defining an auxiliary class $K_1$ (this is why we extended ${{\textsf{I}}}{{\textsf{D}}}^{ (4) }$ to ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$). Let

$$\begin{aligned} K_1 = \lbrace u: \ \forall x \; [ \ u \preceq _{ \textsf{suff} } xu \ ] \ \rbrace . \end{aligned}$$

By the axiom $\forall x \; [ \ \bigwedge _{ a \in \lbrace 0, 1 \rbrace } a \preceq _{ \textsf{suff} } xa \ ]$, we have $0, 1 \in J$. We show that $K_1$ is closed under the maps $u \mapsto u0$, $\; u \mapsto u1$. Let $b \in \lbrace 0, 1 \rbrace$ and let $u \in K_1$. We need to show that $ub \in K_1$. That is, we need to show that $ub \preceq _{ \textsf{suff} } xu b$ for all x. Since $u \in K_1$, we know that

$$\begin{aligned} \forall x \; [ \ u \preceq _{ \textsf{suff} } xu \ ] \qquad {(*)} \end{aligned}$$

holds. Then, by (*) and the axiom

$$\begin{aligned} \forall x y \; \left[ \ x \preceq _{ \textsf{suff} } y \rightarrow \bigwedge _{ a \in \lbrace 0, 1 \rbrace } xa \preceq _{ \textsf{suff} } ya \ \right] \end{aligned}$$

we have

$$\begin{aligned} \forall x \; [ \ ub \preceq _{ \textsf{suff} } xub \ ] . \end{aligned}$$

Hence, $ub \in K_1$. Thus, $K_1$ is closed under the maps $u \mapsto u0$, $\; u \mapsto u1$.

The class $K_1$ is not a domain since it may not be closed under concatenation. We let

$$\begin{aligned} K = \lbrace u \in K_1: \ \forall v \in K_1 \; [ \ vu \in K_1 \ ] \ \rbrace . \end{aligned}$$

Since $K_1$ contains 0 and 1 and is closed under the maps $x \mapsto x0$, $\; x \mapsto x1$, we have $0,1 \in K$. We show that K is closed under concatenation. Let $u_0, u_1 \in K$. We need to show that $u_0 u_1 \in K$. We start by showing that $u_0 u_1 \in K_1$. We have $u_0 \in K \subseteq K_1$. Hence, $u_0 u_1 \in K_1$ since $u_1 \in K$. Next, we need to show that $\forall v \in K_1 [ \ v u_0 u_1 \in K_1 \ ]$. We do not need to worry about parentheses since ${{\textsf{I}}}{{\textsf{D}}}_1$ tells us that concatenation is associative. Let $v \in K_1$. We need to show that $v u_0 u_1 \in K_1$. Since $u_0 \in K$, we have $v u_0 \in K_1$. Since $u_1 \in K$, we have $v u_0 u_1 \in K_1$. Hence, $u_0 u_1 \in K$. Thus, K is closed under concatenation and therefore satisfies the domain conditions.

Since the axioms ${{\textsf{I}}}{{\textsf{D}}}_1$, ${{\textsf{I}}}{{\textsf{D}}}_2$, ${{\textsf{I}}}{{\textsf{D}}}_3$ are universal sentences, their restrictions to K are theorems of ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$. It remains to show that the restriction to K of each instance of

$$\begin{aligned} {{\textsf{I}}}{{\textsf{D}}}^{ * }_4 \equiv \ \forall x \left[ \ x \sqsubseteq _{ {\textsf{s}} } {\overline{\alpha }} \rightarrow \bigvee _{ \gamma \in \textsf{Sub} ( \alpha ) } x= {\overline{\gamma }} \ \right] \end{aligned}$$

is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$. It suffices to show that for each nonempty binary string $\alpha$

$$\begin{aligned} \forall x , y \in K \big [ \ xy = {\overline{\alpha }} \ \rightarrow \ \bigvee _{ \beta , \gamma \in \textsf{Sub} ( \alpha ) } ( \ x = {\overline{\gamma }} \; \wedge \; y = {\overline{\beta }} \ ) \ \big ]\ .\qquad {(**)} \end{aligned}$$

So, let $x, y \in K$ and assume $x y = {\overline{\alpha }}$. Since $y \in K \subseteq K_ 1$, we know that $y \preceq _{ \textsf{suff} } xy = {\overline{\alpha }}$. By the axiom schema for the suffix relation, $y = {\overline{\beta }}$ where $\beta$ is a nonempty suffix of $\alpha$. So, $x {\overline{\beta }} = {\overline{\alpha }} \;$. By ${{\textsf{I}}}{{\textsf{D}}}_1$, ${{\textsf{I}}}{{\textsf{D}}}_2$, ${{\textsf{I}}}{{\textsf{D}}}_3$, $\textsf{AT0}$, $\textsf{AT1}$, we have that $x = {\overline{\gamma }}$ where $\gamma$ is a nonempty prefix of $\alpha$ such that $\alpha = \gamma \beta$. Thus, (**) hols for all nonempty binary strings $\alpha$. Thus, the translation of each instance of ${{\textsf{I}}}{{\textsf{D}}}^{ * }_4$ is a theorem of ${{\textsf{I}}}{{\textsf{D}}}^{ (5) }$. $\square$

3.6 The theories $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$, $\overline{ {{\textsf{I}}}{{\textsf{D}}} }^{ * }$

The axioms ${{\textsf{I}}}{{\textsf{D}}}_1$, ${{\textsf{I}}}{{\textsf{D}}}_2$, ${{\textsf{I}}}{{\textsf{D}}}_3$ describe a right cancellative semigroup. It is also natural to consider semigroups that are also left cancellative, for example $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + }, {\varvec{0}}, {\varvec{1}}, ^\frown )$. Let $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ and $\overline{ {{\textsf{I}}}{{\textsf{D}}} }^{*}$ be ${{\textsf{I}}}{{\textsf{D}}}$ and ${{\textsf{I}}}{{\textsf{D}}}^{ * }$, respectively, extended with the axioms

$$\begin{aligned} \forall x y \; [ \ x \ne y \rightarrow ( \ 0x \ne 0y \; \wedge \; 1x \ne 1y \ ) \ ], \ \ \forall x y \; [ \ 0 x \ne 1 y \ ] . \end{aligned}$$

It is not difficult to see that ${{\textsf{T}}}{{\textsf{C}}}$ proves each axiom of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }^{*}$. It is easily seen that our interpretation of ${{\textsf{I}}}{{\textsf{D}}}^{*}$ in ${{\textsf{I}}}{{\textsf{D}}}$ is also an interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }^{*}$ in $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$. Thus, $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ and $\overline{ {{\textsf{I}}}{{\textsf{D}}} }^{*}$ are mutually interpretable. We have not been able to determine whether $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ is interpretable in ${{\textsf{I}}}{{\textsf{D}}}$.

Theorem 9

$\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ and $\overline{ {{\textsf{I}}}{{\textsf{D}}} }^{*}$ are mutually interpretable.

Open Problem 10

Is $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ interpretable in ${{\textsf{I}}}{{\textsf{D}}}$?

4 Mutual interpretability of ${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^*$

In this section, we show that ${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^{ * }$ are also mutually interpretable. Recall that ${{\textsf{I}}}{{\textsf{Q}}}^{ * }$ is the theory we obtain from ${{\textsf{I}}}{{\textsf{Q}}}$ by removing $\le$ from the language and replacing the axiom schema ${{\textsf{I}}}{{\textsf{Q}}}_3$ with the axiom schema

$$\begin{aligned} {{\textsf{I}}}{{\textsf{Q}}}^{ * }_3 \equiv \ \forall x \; \big [ \ x \le _{ {\textsf{l}} } {\overline{n}} \rightarrow \bigvee _{ k \le n } x = {\overline{k}} \ \big ] \end{aligned}$$

where $x \le _{ {\textsf{l}} } y \equiv \ \exists z \; [ \ z + x = y \ ]$.

Theorem 11

${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^*$ are mutually interpretable.

The proof strategy is similar to the one we used to interpret ${{\textsf{I}}}{{\textsf{D}}}^{ * }$ in ${{\textsf{I}}}{{\textsf{D}}}$. Since we obtain an interpretation of ${{\textsf{I}}}{{\textsf{Q}}}$ in ${{\textsf{I}}}{{\textsf{Q}}}^*$ by translating $\le$ as $\le _{ {\textsf{l}} }$, we just need to focus on proving that ${{\textsf{I}}}{{\textsf{Q}}}^*$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}$. The proof is structured as follows: In Sect. 4.1, we extend ${{\textsf{I}}}{{\textsf{Q}}}$ to a theory ${{\textsf{I}}}{{\textsf{Q}}}^+$ which proves that for each inductive class there exists a an inductive subclass that is closed under addition and multiplication. A class is inductive if it contains 0 and is closed under the successor function. In Sect. 4.2, we extend ${{\textsf{I}}}{{\textsf{Q}}}^+$ to a theory ${{\textsf{I}}}{{\textsf{Q}}}^{++}$ with the same interpretability degree as ${{\textsf{I}}}{{\textsf{Q}}}^+$ and where the ordering relation $\le$ satisfies additional properties. In Sect. 4.3, we show that ${{\textsf{I}}}{{\textsf{Q}}}^*$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}^+$. Finally, in Sect.  7, we show that ${{\textsf{I}}}{{\textsf{Q}}}$ is mutually interpretable with a theory ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ that is an extension of ${{\textsf{I}}}{{\textsf{Q}}}^+$.

4.1 Closure under addition and multiplication

A class X is called inductive if $0 \in X$ and $\forall x \in X \; [ \ \textrm{S}x \in X \ ]$. A class X is called a cut if it is inductive and $\forall x \in X \; \forall y \; [ \ y \le _{ {\textsf{l}} } x \rightarrow y \in X \ ]$. Let ${{\textsf{I}}}{{\textsf{Q}}}^{ + }$ and ${\textsf{Q}}^{ + }$ be respectively ${{\textsf{I}}}{{\textsf{Q}}}$ and ${\textsf{Q}}$ extended with the following axioms

• Associativity of addition $\forall x y z \; [ \ (x+y) + z = x + (y+z) \ ]$

• Left distributive law $\forall x y z \; [ \ x (y+z) = xy + xz \ ]$

• Associativity of multiplication $\forall x y z \; [ \ (xy) z = x (yz) \ ] \;$.

Lemma V.5.10 of Hajek and Pudlak [4] says that ${\textsf{Q}}^+$ proves that any inductive class has a subclass that is a cut and is closed under $+$ and $\times$. The proof of that lemma shows that ${{\textsf{I}}}{{\textsf{Q}}}^+$ proves that any inductive class has an inductive subclass that is closed under $+$ and $\times$ (see also Sect. 7).

Lemma 12

Let X be an inductive class. Then, ${{\textsf{I}}}{{\textsf{Q}}}^{ + }$ proves that there exists an inductive subclass Y that is closed under $+$ and $\times$.

4.2 Ordering relation

Let ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ be ${{\textsf{I}}}{{\textsf{Q}}}^{ + }$ extended with the following axioms

$$\begin{aligned} \forall x \; [ \ 0 \le x \ ], \ \ \ \forall x y \; [ \ x \le y \rightarrow Sx \le Sy \ ] \end{aligned}$$

Using the ideas of Sect. 3.4, we prove the following lemma.

Lemma 13

${{\textsf{I}}}{{\textsf{Q}}}^{ + }$ and ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ are mutually interpretable.

Proof

Since ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ is an extension of ${{\textsf{I}}}{{\textsf{Q}}}^{ + }$, it suffices to show that ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}^{ + }$. Furthermore, it suffices to show that we can translate $\le$ in such a way that ${{\textsf{I}}}{{\textsf{Q}}}^{ + }$ proves the translation of each instance of ${{\textsf{I}}}{{\textsf{Q}}}_3$ and the translation of $\forall x \; [ \ 0 \le x \ ]$ and $\forall x y \; [ \ x \le y \rightarrow Sx \le Sy \ ]$.

Let $u \in G$ if and only if

• (1) $u \le u$

• (2) $\forall w \le u \; [ \ w \le w \ ]$

• (3) $\forall w \le u \; \forall v_0 \le w \; \forall v_1 \le v_0 \; [ \ v_1 \le w \ ]$

  • (A) $\forall w \le u \; [ \ w = 0 \; \vee \; \exists v \le w \; [ \ w = \textrm{S} v \ ]$

  • (B) $\forall w \le u \; \forall x \; [ \ w = \textrm{S} x \rightarrow 0 \le w \ ]$

  • (C) $\forall w \le u \; \forall x y \; [ \ ( \ w = \textrm{S} y \; \wedge \; x \le y \ ) \rightarrow \textrm{S} x \le w \ ]$.

It can be verified that ${{\textsf{I}}}{{\textsf{Q}}}$ proves that $t \in G$ for each variable-free term t and that G is downward closed under $\le$.

We translate $\le$ as follows

$$\begin{aligned} x \le ^{ \tau } y \equiv \ ( \ y \in G \; \wedge \; x \le y \ ) \ \vee \ ( \ y \not \in G \; \wedge \; x = x \ ) . \end{aligned}$$

Since $t \in G$ for each variable-free term t, the translation of each instance of the axiom schema ${{\textsf{I}}}{{\textsf{Q}}}_3$ is a theorem of ${{\textsf{I}}}{{\textsf{Q}}}^+$.

We show that ${{\textsf{I}}}{{\textsf{Q}}}^+$ proves the translation of $\forall x \; [ \ 0 \le x \ ]$. Choose an arbitrary x. If $x \not \in G$, then $0 \le ^{ \tau } x$ holds by the second disjunct in the definition of $\le ^{ \tau }$. Otherwise, $x \in G$. We need to show that $0 \le x$ holds. If $x = 0$, then $0 \le x$ holds by ${{\textsf{I}}}{{\textsf{Q}}}_3$. Otherwise, by (A), there exists $v \le x$ such that $x = \textrm{S} v$. Then, by (B), $0 \le x$ holds. Thus, ${{\textsf{I}}}{{\textsf{Q}}}^+ \vdash \forall x \; [ \ 0 \le ^{ \tau } x \ ]$.

We show that ${{\textsf{I}}}{{\textsf{Q}}}^+$ proves the translation of $\forall x y \; [ \ x \le y \rightarrow \textrm{S} x \le \textrm{S} y \ ]$. Assume $x \le y$ holds. If $\textrm{S} y \not \in G$, then $\textrm{S} x \le ^{ \tau } \textrm{S} y$ holds by the second disjunct in the definition of $\le ^{ \tau }$. Otherwise, $\textrm{S} y \in G$. We need to show that $\textrm{S} x \le \textrm{S} y$ holds. By ${\textsf{Q}}_2$, $\textrm{S} y \ne 0$. Hence, by (A), there exists $v \le \textrm{S} y$ such that $\textrm{S} y = \textrm{S} v$. By ${\textsf{Q}}_1$, $y = v$. Hence, $y \le \textrm{S} y$. Since G is downward closed under $\le$, we have $y \in G$. Then, by (C), $\textrm{S} x \le \textrm{S} y$ holds. Thus, ${{\textsf{I}}}{{\textsf{Q}}}^+ \vdash \forall x y \; [ \ x \le ^{ \tau } y \rightarrow \textrm{S} x \le ^{ \tau } \textrm{S} y \ ]$. $\square$

4.3 Interpretation of ${{\textsf{I}}}{{\textsf{Q}}}^{ * }$ in ${{\textsf{I}}}{{\textsf{Q}}}^{ + }$

Lemma 14

${{\textsf{I}}}{{\textsf{Q}}}^{ * }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}^{ + }$.

Proof

By Lemma 13, it suffices to show that ${{\textsf{I}}}{{\textsf{Q}}}^{ * }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$. We interpret ${{\textsf{I}}}{{\textsf{Q}}}^{ * }$ in ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ by simply restricting the universe of ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ to an inductive subclass K that is closed under $+, \times$ and which is such that ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ proves that $\forall x, u \in K \; [ \ u \le x + u \ ]$.

Let

$$\begin{aligned} K_1 = \lbrace u: \ \forall x \; [ \ u \le x + u \ ] \ \rbrace \end{aligned}$$

We have $0 \in K_1$ by the axiom $\forall x \; [ \ 0 \le x \ ]$ and ${\textsf{Q}}_4$. We show that $K_1$ is closed under $\textrm{S}$. Let $u \in K_1$. We need to show that $\textrm{S} u \in K_1$. That is, we need to show that $\textrm{S} u \le x + \textrm{S}u$. Since $u \in K_1$, we have $u \le x+ u$. Then, $\textrm{S} u \le \textrm{S} (x+u)$ by the axiom $\forall x y \; [ \ x \le y \rightarrow \textrm{S} x \le \textrm{S} y \ ]$. By ${\textsf{Q}}_5$, we have

$$\begin{aligned} \textrm{S} u \le \textrm{S} (x+u) = x + \textrm{S} u . \end{aligned}$$

Hence, $\textrm{S} u \in K_1$. Thus, $K_1$ contains 0 and is closed under $\textrm{S}$. By Lemma 12, there exists an inductive subclass K of $K_1$ that is closed under $+$ and $\times$.

We interpret ${{\textsf{I}}}{{\textsf{Q}}}^{ * }$ in ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ by relativizing quantification to K. The translation of each one of the axioms ${\textsf{Q}}_1 - {\textsf{Q}}_2$, ${\textsf{Q}}_4 - {\textsf{Q}}_7$ is a theorem of ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ since universal sentences are absolute for K. It remains to show that each instance of ${{\textsf{I}}}{{\textsf{Q}}}_3^*$ is a theorem of ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$. Choose a natural number n. We need to show that

$$\begin{aligned} {{\textsf{I}}}{{\textsf{Q}}}^{ ++ } \vdash \forall x, y \in K \; \left[ \ x + y = {\overline{n}} \rightarrow \bigvee _{ k \le n } y = {\overline{k}} \ \right] . \end{aligned}$$

Assume $x, y \in K$ and $x + y = {\overline{n}}$. Since $y \in K \subseteq K_1$, we have $y \le {\overline{n}}$. By the axiom schema ${{\textsf{I}}}{{\textsf{Q}}}_3$, there exists $k \le n$ such that $y = {\overline{k}}$. Thus, ${{\textsf{I}}}{{\textsf{Q}}}^{ ++ }$ proves the translation of each instance of ${{\textsf{I}}}{{\textsf{Q}}}_3^*$. $\square$

Fig. 5

Non-logical axioms of the first-order theories $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ and ${{\textsf{I}}}{{\textsf{Q}}}$

5 Interpretability of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$

In this section, we show that $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}$ (see Fig. 5 for the axioms of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ and ${{\textsf{I}}}{{\textsf{Q}}}$). The most intuitive way to interpret concatenation theories in arithmetical theories is to construct a formula $\phi _{ \circ } (x, y, z )$ that given x and y defines an object that encodes a computation of $x \circ y$. Unfortunately, ${{\textsf{I}}}{{\textsf{Q}}}$ does not have the resources necessary to prove that we can find a domain I on which $\phi _{ \circ } (x, y, z )$ defines a function that satisfies ${{\textsf{I}}}{{\textsf{D}}}_1$, ${{\textsf{I}}}{{\textsf{D}}}_2$, ${{\textsf{I}}}{{\textsf{D}}}_3$, $\overline{ {{\textsf{I}}}{{\textsf{D}}} }_5$, $\overline{ {{\textsf{I}}}{{\textsf{D}}} }_6$. To prove correctness of recursive definition in Robinson Arithmetic ${\textsf{Q}}$, we rely on the axiom ${\textsf{Q}}_3 \equiv \ \forall x \; [ \ x = 0 \; \vee \; \exists y \; [ \ x = Sy \ ] \ ]$. The axiom schema ${{\textsf{I}}}{{\textsf{Q}}}_3 \equiv \ \forall x \; [ \ x \le {\overline{n}} \leftrightarrow \bigvee _{ k \le n } x= {\overline{k}} \ ]$ can only allow us to verify that $\phi _{ \circ } (x, y, z )$ gives a correct value z when x and y represent variable-free terms. Thus, to interpret $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$, we need a conception of strings as numbers that allows us to translate concatenation without coding sequences. The translation needs to also be simple enough that we can prove its correctness in ${{\textsf{I}}}{{\textsf{Q}}}$. In Lemma 4 of [2], Ganea explains how we can translate concatenation as a $\Delta _0$-formula in strong theories such as Peano Arithmetic ${{\textsf{P}}}{{\textsf{A}}}$ and $\mathsf {I \Delta }_0$.

Although we show that $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}$, we have not been able to determine whether the converse holds.

Open Problem 15

Is ${{\textsf{I}}}{{\textsf{Q}}}$ interpretable in $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$?

As mentioned, the main result of this section is the following theorem.

Theorem 16

$\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}$.

The proof of the theorem is structured as follows: In Sect. 5.1, we explain how we intend to interpret $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$. In Sect. 5.2, we use this idea to give a simple interpretation of ${{\textsf{W}}}{{\textsf{D}}}$ in ${\textsf{R}}$. In Sect. 5.3, we show that we can interpret $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in an extension of ${{\textsf{I}}}{{\textsf{Q}}}$ which we denote ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$. Finally, in Sect. 7, we show that ${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ are mutually interpretable.

5.1 Strings as matrices

The idea is to think of strings as $2 \times 2$ matrices and to translate concatenation as matrix multiplication. Let us first see how we can use this idea to give a 4-dimensional interpretation of $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * }, \varepsilon , {\varvec{0}}, {\varvec{1}}, ^\frown )$ in $( {\mathbb {N}}, 0, 1, +, \times )$, where $\varepsilon$ denotes the empty string and $\lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * } = \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ + } \cup \lbrace \varepsilon \rbrace$. Let

$$\begin{aligned} \varepsilon ^{ \tau }:= \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}, \ \ \ \ \ \ {\varvec{0}}^{ \tau }:= \begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}, \ \ \ \ \ \ {\varvec{1}}^{ \tau }:= \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix} . \end{aligned}$$

Let $\textbf{SL}_2 ( {\mathbb {N}} )$ denote the monoid generated by ${\varvec{0}}^{ \tau }$ and ${\varvec{1}}^{ \tau }$ under matrix multiplication. The monoid $\textbf{SL}_2 ( {\mathbb {N}} )$ is a substructure of the special linear group $\textbf{SL}_2 ( {\mathbb {Z}} )$ of $2 \times 2$ matrices with integer coefficients and determinant 1; the two matrices ${\varvec{0}}^{ \tau }$ and ${\varvec{1}}^{ \tau }$ generate $\textbf{SL}_2 ( {\mathbb {Z}} )$. Let $\times$ denote matrix multiplication. Then, $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * }, \varepsilon , {\varvec{0}}, {\varvec{1}}, ^\frown )$ is isomorphic to $( \textbf{SL}_2 ( {\mathbb {N}} ), \varepsilon ^{ \tau }, {\varvec{0}}^{ \tau }, {\varvec{1}}^{ \tau }, \times )$. Since $\textbf{SL}_2 ( {\mathbb {N}} )$ is the set of $2 \times 2$ matrices with natural number coefficients and determinant 1, the isomorphism defines a 4-dimensional interpretation of $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * }, \varepsilon , {\varvec{0}}, {\varvec{1}}, ^\frown )$ in $( {\mathbb {N}}, 0, 1, +, \times )$. The idea is to specify an interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$ by building on this interpretation of $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * }, \varepsilon , {\varvec{0}}, {\varvec{1}}, ^\frown )$ in $( {\mathbb {N}}, 0, 1, +, \times )$. But we need to be careful since the axioms ${{\textsf{I}}}{{\textsf{Q}}}_1 - {{\textsf{I}}}{{\textsf{Q}}}_2$, ${{\textsf{I}}}{{\textsf{Q}}}_4 - {{\textsf{I}}}{{\textsf{Q}}}_7$ have many models.

In Lemma 11 of [10], we use this idea of associating strings with matrices to prove that ${{\textsf{I}}}{{\textsf{D}}}_1 - {{\textsf{I}}}{{\textsf{D}}}_3$ has a decidable model. We prove this result by giving a 4-dimensional interpretation of ${{\textsf{I}}}{{\textsf{D}}}_1 - {{\textsf{I}}}{{\textsf{D}}}_3$ in the first-order theory of the real closed field $( {\mathbb {R}}, 0, 1, +, \times , \le )$, which is decidable (see Tarski [11]). At the time, we were investigating whether it is possible to remove some of the axioms of ${\textsf{D}}$ and obtain a theory that is essentially undecidable. The possibility of interpreting $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$ resulted from a careful investigation of the algebraic properties of $( {\mathbb {R}}, 0, 1, +, \times , \le )$ we need to interpret ${{\textsf{I}}}{{\textsf{D}}}_1 - {{\textsf{I}}}{{\textsf{D}}}_3$. Properties (I)–(VIII) in Fig. 6 are sufficient to interpret $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$. Extending ${{\textsf{I}}}{{\textsf{Q}}}$ with (I)–(VIII) allows us to reason about natural numbers in the standard way. In the rest of the paper, we use the Roman numerals (I)–(VIII) to refer exclusively to axioms (I)–(VIII) in Fig. 6.

The 4-dimensional interpretation of $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * }, \varepsilon , {\varvec{0}}, {\varvec{1}}, ^\frown )$ in $( {\mathbb {N}}, 0, 1, +, \times )$ we described is a many-to-one reduction that maps existential sentences to existential sentences. This means that unsolvability of equations over $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * }, \varepsilon , {\varvec{0}}, {\varvec{1}}, ^\frown )$ implies unsolvability of equations over $( {\mathbb {N}}, 0, 1, +, \times )$. The idea of associating $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * }, \varepsilon , {\varvec{0}}, {\varvec{1}}, ^\frown )$ with $\textbf{SL}_2 ( {\mathbb {N}} )$ dates back to Markov [9]. According to Lothaire [7] (see p. 387), in the 1950s, A. A. Markov hoped that Hilbert‘s 10th Problem could be solved by proving unsolvability of word equations, that is, equations over finitely generated free semigroups. In 1970, Yuri Matiyasevich proved that Hilbert‘s 10th Problem is undecidable using a completely different method (see for example Davis [1]). In 1977, Makanin [8] proved that the existential theory of a finitely generated free semigroup is decidable.

Fig. 6

Algebraic properties we need in order to interpret $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$

5.2 Interpretation of ${{\textsf{W}}}{{\textsf{D}}}$ in ${\textsf{R}}$

In this section, we show that the isomorphism between $( \lbrace {\varvec{0}}, {\varvec{1}} \rbrace ^{ * }, \varepsilon , {\varvec{0}}, {\varvec{1}}, ^\frown )$ and $\textbf{SL}_2 ( {\mathbb {N}} )$ defines a very simple interpretation of ${{\textsf{W}}}{{\textsf{D}}}$ in ${\textsf{R}}$.

Lemma 17

Let $\tau$ be the 4-dimensional translation of $\lbrace 0, 1, \circ \rbrace$ in $\lbrace 0, \textrm{S}, +, \times \rbrace$ defined as follows

• 0 and 1 are translated as $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}$, respectively

• $\circ$ is translated as matrix multiplication

• the domain is the class of all $2 \times 2$ matrices $\begin{pmatrix} x &{}\quad y \\ z &{}\quad w \end{pmatrix}$.

Then, $\tau$ extends to a translation of $\lbrace 0, 1, \circ , \preceq \rbrace$ in $\lbrace 0, \textrm{S}, +, \times , \le \rbrace$ that defines a 4-dimensional interpretation of ${{\textsf{W}}}{{\textsf{D}}}$ in ${\textsf{R}}$.

Proof

By the axiom schemas ${\textsf{R}}_1 \equiv \ {\overline{n}} + {\overline{m}} = \overline{n+m}$, ${\textsf{R}}_2 \equiv \ {\overline{n}} \times {\overline{m}} = \overline{n \times m}$, ${\textsf{R}}$ proves the translation of each instance of ${{\textsf{W}}}{{\textsf{D}}}_1 \equiv \ {\overline{\alpha }} \ {\overline{\beta }} = \overline{ \alpha \beta }$. By the axiom schema ${\textsf{R}}_3$, ${\textsf{R}}$ proves the translation of each instance of ${{\textsf{W}}}{{\textsf{D}}}_2$. It remains to give a translation of $\preceq$ that provably satisfies the axiom schema

$$\begin{aligned} {{\textsf{W}}}{{\textsf{D}}}_3 \equiv \ \forall x \left[ \ x \preceq {\overline{\alpha }} \leftrightarrow \bigvee _{ \gamma \in \textsf{Pref} ( \alpha ) } x= {\overline{\gamma }} \ \right] . \end{aligned}$$

This is where we use the axiom schema ${{\textsf{I}}}{{\textsf{Q}}}_3 \equiv \ \forall x \; [ \ x \le {\overline{n}} \leftrightarrow \bigvee _{ k \le n } x= {\overline{k}} \ ]$, which is a theorem of ${\textsf{R}}$.

Let

$$\begin{aligned} K = \left\{ \begin{pmatrix} x &{}\quad y \\ z &{}\quad w \end{pmatrix}: \ \ \begin{pmatrix} x &{}\quad y \\ z &{}\quad w \end{pmatrix} \ne \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix} \ \ \wedge \ \ xw = 1 + yz \ \right\} . \end{aligned}$$

Let

$$\begin{aligned} A = \begin{pmatrix} a_1 &{}\quad a_2 \\ a_3 &{}\quad a_4 \end{pmatrix} \ \ \text{ and } \ \ B = \begin{pmatrix} b_1 &{}\quad b_2 \\ b_3 &{}\quad b_4 \end{pmatrix} . \end{aligned}$$

Let $A \preceq B$ if and only if $A, B \in K$ and there exists a largest element $m(B) \in \lbrace b_1, b_2, b_3, b_4 \rbrace$ with respect to $\le$ such that

• (1) $A = B$ or

• (2) there exists $C \in K$ such that $a_i, c_i \le m(B)$ for all $1 \le i \le 4$ and $AC = B \;$.

Let ${{\textsf{S}}}{{\textsf{L}}}_2 ( {\mathbb {N}} )^+$ denote ${{\textsf{S}}}{{\textsf{L}}}_2 ( {\mathbb {N}} )$ minus the identity matrix. Assume B is the translation of a variable-free ${\mathcal {L}}_{ {{\textsf{B}}}{{\textsf{T}}} }$-term. Then, $B \in {{\textsf{S}}}{{\textsf{L}}}_2 ( {\mathbb {N}} )^+$. The bound in (2) tells that $A, C \in {{\textsf{S}}}{{\textsf{L}}}_2 ( {\mathbb {N}} )^+$. It is straightforward to verify that if $A, B, C \in {{\textsf{S}}}{{\textsf{L}}}_2 ( {\mathbb {N}} )^+$ are such that $AC = B$, then a bound such as the one in (2) holds. It is then clear that (1)–(2) capture what it means for a finite string to be a prefix of another string. Thus, ${\textsf{R}}$ proves the translation of each instance of ${{\textsf{W}}}{{\textsf{D}}}_3$. $\square$

5.3 Interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$

Let ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ be ${{\textsf{I}}}{{\textsf{Q}}}$ extended with axioms (I)–(VIII) in Fig. 6. We can reason in ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ about natural numbers in the standard way and will therefore occasionally not refer explicitly to the axioms of ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ we use. In this section, we show that $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$.

We start by making a few simple observations:

• Axiom (IV) tells us that addition is commutative. Hence, by ${\textsf{Q}}_4$, 0 is an additive identity. That is, ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) } \vdash \forall x \; [ \ 0 + x = x \; \wedge \; x + 0 = x \ ]$.

• Recall that $1 = \textrm{S} 0$. By ${\textsf{Q}}_7$ and ${\textsf{Q}}_6$

  $$\begin{aligned} x 1 = x 0 + x = 0 + x = x . \end{aligned}$$

  Since axiom (V) tells us that multiplication is commutative, 1 is a multiplicative identity. That is, ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) } \vdash \forall x \; [ \ 1x = x \; \wedge \; x1 = x \ ]$.

• Axiom (VI) tells us that addition is right-cancellative. Since addition is commutative, it is also left-cancellative. That is

  $$\begin{aligned} {{\textsf{I}}}{{\textsf{Q}}}^{ (2) } \vdash \forall x y z \; [ \ z+ x = z+ y \rightarrow x = y \ ] . \end{aligned}$$

• By ${\textsf{Q}}_6$ and (V), ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) } \vdash \forall x \; [ \ x0 = 0 \; \wedge \; 0x = 0 \ ]$.

Lemma 18

Let $\tau$ be the 4-dimensional translation of $\lbrace 0, 1, \circ \rbrace$ in $\lbrace 0, \textrm{S}, +, \times \rbrace$ defined as follows

• 0 and 1 are translated as $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}$, respectively

• $\circ$ is translated as matrix multiplication

• the domain J is the class of all $2 \times 2$ matrices $\begin{pmatrix} x &{}\quad y \\ z &{}\quad w \end{pmatrix}$ where $x \ne 0$.

Then, $\tau$ extends to a translation of $\lbrace 0, 1, \circ , \preceq \rbrace$ in $\lbrace 0, \textrm{S}, +, \times , \le \rbrace$ that defines a 4-dimensional interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$.

Proof

We verify that J satisfies the domain condition. It is clear that $0^{ \tau }, 1^{ \tau } \in J$. It remains to verify that J is closed under matrix multiplication. Let

$$\begin{aligned} A = \begin{pmatrix} a_1 &{}\quad a_2 \\ a_3 &{}\quad a_4 \end{pmatrix}, \ \ \ B = \begin{pmatrix} b_1 &{}\quad b_2 \\ b_3 &{}\quad b_4 \end{pmatrix}, \ \ \ AB = \begin{pmatrix} a_1 b_1 + a_2 b_3 &{}\quad a_1 b_2 + a_2 b_4 \\ a_3 b_1 + a_4 b_3 &{}\quad a_3 b_2 + a_4 b_4 \end{pmatrix} \end{aligned}$$

where $a_1, b_1 \ne 0$. We need to show that $a_1 b_1 + a_2 b_3 \ne 0$. Axiom (VIII) tells us that models of ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ do not have zero divisors. Hence, $a_1 b_1 \ne 0$. Axiom (VII) tells us that 0 is the only element with an additive inverse. Hence, $a_1 b_1 + a_2 b_3 \ne 0$, which implies $AB \in J$. Thus, J is closed under matrix multiplication.

It is straightforward to verify that (I)–(V) suffice to prove that matrix multiplication is associative. Thus, ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ proves the translation of ${{\textsf{I}}}{{\textsf{D}}}_1$.

Next, we show that the translation of ${{\textsf{I}}}{{\textsf{D}}}_2$ and $\overline{ {{\textsf{I}}}{{\textsf{D}}} }_5$ are theorems of ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$. We need to show that

• (1) $\forall A, B \in J \; [ \ ( \ A 0^{ \tau } = B 0^{ \tau } \; \vee \; 0^{ \tau } A = 0^{ \tau } B \ ) \rightarrow A = B \ ]$

• (2) $\forall A, B \in J \; [ \ ( \ A 1^{ \tau } = B 1^{ \tau } \; \vee \; 1^{ \tau } A = 1^{ \tau } B \ ) \rightarrow A = B \ ]$.

We verify (1). First, we show that $\forall A, B \in J \; [ \ A 0^{ \tau } = B 0^{ \tau } \rightarrow A = B \ ]$. Assume $x, a \ne 0$ and

$$\begin{aligned} \begin{pmatrix} x+ y &{}\quad y \\ z +w &{} \quad w \end{pmatrix} = \begin{pmatrix} x &{} \quad y \\ z &{}\quad w \end{pmatrix} 0^{ \tau } = \begin{pmatrix} a &{}\quad b \\ c &{}\quad d \end{pmatrix} 0^{ \tau } = \begin{pmatrix} a + b &{}\quad b \\ c + d &{} \quad d \end{pmatrix} . \end{aligned}$$

We need to show that $x = a$ and $z = c$. We have

$$\begin{aligned} x+ b = x + y = a+ b \ \wedge \ z+d = z + w = c +d . \end{aligned}$$

Since addition is right-cancellative, $x = a$ and $z = c$. Thus, for all $A, B \in J$, if $A 0^{ \tau } = B 0^{ \tau }$, then $A = B$.

We show that $\forall A, B \in J \; [ \ 0^{ \tau } A = 0^{ \tau } B \rightarrow A = B \ ]$. Assume $x, a \ne 0$ and

$$\begin{aligned} \begin{pmatrix} x &{}\quad y \\ x + z &{}\quad y + w \end{pmatrix} = 0^{ \tau } \begin{pmatrix} x &{}\quad y \\ z &{}\quad w \end{pmatrix} = 0^{ \tau } \begin{pmatrix} a &{}\quad b \\ c &{}\quad d \end{pmatrix} = \begin{pmatrix} a &{}\quad b \\ a+c &{}\quad b+d \end{pmatrix} . \end{aligned}$$

We need to show that $z = c$ and $w = d$. We have

$$\begin{aligned} a + z = x + z = a + c \ \wedge \ b + w = y + w = b + d . \end{aligned}$$

Since addition is left-cancellative, $z = c$ and $w = d$. Thus, for all $A, B \in J$, if $0^{ \tau } A = 0^{ \tau } B$, then $A = B$. Hence, (1) holds. By similar reasoning, (2) holds. Thus, ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ proves the translation of ${{\textsf{I}}}{{\textsf{D}}}_2$ and $\overline{ {{\textsf{I}}}{{\textsf{D}}} }_5$.

We show that the translation of ${{\textsf{I}}}{{\textsf{D}}}_3$ is a theorem of ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$. We need to show that $\forall A, B \in J \; [ \ A 0^{ \tau } \ne B 1^{ \tau } \ ]$. Assume for the sake of a contradiction $x, a \ne 0$ and

$$\begin{aligned} \begin{pmatrix} x+ y &{}\quad y \\ z +w &{}\quad w \end{pmatrix} = \begin{pmatrix} x &{}\quad y \\ z &{}\quad w \end{pmatrix} 0^{ \tau } = \begin{pmatrix} a &{}\quad b \\ c &{}\quad d \end{pmatrix} 1^{ \tau } = \begin{pmatrix} a &{}\quad a + b \\ c &{}\quad c + d \end{pmatrix} . \end{aligned}$$

Then

$$\begin{aligned} a = x + y = x + a + b \end{aligned}$$

where we have omitted parentheses since addition is associative. Since 0 is an additive identity and addition is commutative, $0 + a = x + b + a$. Since addition is right-cancellative, $0 = x + b$. Since 0 is the only element with an addititive inverse, $x = 0$, which contradicts the assumption that $x \ne 0$. Thus, ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ proves the translation of ${{\textsf{I}}}{{\textsf{D}}}_3$.

We show that the translation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }_6$ is a theorem of ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$. We need to show that $\forall A, B \in J \; [ \ 0^{ \tau } A \ne 1^{ \tau } B \ \ ]$. Assume for the sake of a contradiction $x, a \ne 0$ and

$$\begin{aligned} \begin{pmatrix} x &{}\quad y \\ x+z &{}\quad y+w \end{pmatrix} = 0^{ \tau } \begin{pmatrix} x &{}\quad y \\ z &{}\quad w \end{pmatrix} = 1^{ \tau } \begin{pmatrix} a &{}\quad b \\ c &{}\quad d \end{pmatrix} = \begin{pmatrix} a+c &{}\quad b + d \\ c &{}\quad d \end{pmatrix} . \end{aligned}$$

Then, $x = a+c = a + x + z$. Hence, $0 = a + z$. Since 0 is the only element with an addititive inverse, $a = 0$, which contradicts the assumption that $a \ne 0$. Thus, ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ proves the translation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }_6$.

Finally, we translate $\preceq$ as in the proof of Lemma 17. $\square$

6 Interpretation of ${{\textsf{T}}}{{\textsf{C}}}$ in ${\textsf{Q}}$

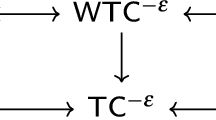
In this section, we show that our interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$ extends in a natural way to an interpretation of ${{\textsf{T}}}{{\textsf{C}}}$ in ${\textsf{Q}}$. Instead of interpreting ${{\textsf{T}}}{{\textsf{C}}}$, we interpret the variant ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ where we extend the language of ${{\textsf{T}}}{{\textsf{C}}}$ with a constant symbol $\varepsilon$ for the identity element. See Fig. 7 for the axioms of ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$. We choose to work with ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ because the identity matrix is naturally present in our interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$ and because we get a more compact form of the editor axiom (${{\textsf{T}}}{{\textsf{C}}}_2$ and ${{\textsf{T}}}{{\textsf{C}}}_3^{ \varepsilon }$). The interpretation we give can be turned into an interpretation of ${{\textsf{T}}}{{\textsf{C}}}$ by simply removing the identity matrix from the domain (see Appendix A of Visser [13] for mutual interpretability of ${{\textsf{T}}}{{\textsf{C}}}$ and ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$).

Fig. 7

Non-logical axioms of the first-order theory ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$

Recall that $x \le _{ {\textsf{l}} } y \equiv \ \exists r \; [ \ r + x = y \ ]$. Let $x <_{ {\textsf{l}} } y \equiv \ \exists r \; [ \ r \ne 0 \; \wedge \; r + x = y \ ]$. Let ${\textsf{Q}}^{ (2) }$ be ${\textsf{Q}}$ extended with axioms (I)–(VI) in Fig. 6 and the trichotomy law

$$\begin{aligned} \forall x y \; [ \ x<_{ {\textsf{l}} } y \; \vee \; x = y \; \vee \; y <_{ {\textsf{l}} } x \ ] . \end{aligned}$$

We make a few simple observations:

• Axiom (VII) $\forall x y \; [ \ x+y = 0 \rightarrow ( \ x = 0 \; \wedge \; y = 0 \ ) \ ]$ is a theorem of ${\textsf{Q}}^{ (2) }$. Indeed, assume $x+y = 0$. If $y = 0$, then $x = 0$ by ${\textsf{Q}}_4$. Thus, it suffices to show that $y = 0$. Assume for the sake of a contradiction that $y \ne 0$. Then, by ${\textsf{Q}}_3$, there exists v such that $y = \textrm{S} v$. By ${\textsf{Q}}_5$

  $$\begin{aligned} 0 = x+y = x + \textrm{S} v = \textrm{S} ( x+v ) \end{aligned}$$

  which contradicts ${\textsf{Q}}_2$. Thus, $x+y = 0$ implies $x =y = 0$.

• Axiom (VIII) $\forall x y \; [ \ x y = 0 \rightarrow ( \ x= 0 \; \vee \; y = 0 \ ) \ ]$ is a theorem of ${\textsf{Q}}^{ (2) }$. Indeed, assume $xy = 0$ and $y \ne 0$. By ${\textsf{Q}}_3$, there exists v such that $y = \textrm{S} v$. By ${\textsf{Q}}_7$

  $$\begin{aligned} 0 = xy = x v + x \end{aligned}$$

  which implies $x = 0$. Thus, $xy = 0$ implies $x= 0 \; \vee \; y = 0$.

• ${\textsf{Q}}^{ (2) }$ proves that 1 is the only element with a multiplicative inverse. Indeed, assume $xy = 1$. By commutativity of multiplication, ${\textsf{Q}}_2$ and ${\textsf{Q}}_5$, we have $x, y \ne 0$. Hence, by ${\textsf{Q}}_3$, there exist u, v such that $x = \textrm{S} u$ and $y = \textrm{S} v$. By commutativity of multiplication, ${\textsf{Q}}_7$ and ${\textsf{Q}}_5$

  $$\begin{aligned} 1 = x y = x v + x = {\textsf{S}} (xv + u) \ \wedge \ 1 = yx = yu + y = {\textsf{S}} ( yu + v) . \end{aligned}$$

  By ${\textsf{Q}}_1$

  $$\begin{aligned} 0 = xv + u \ \wedge \ 0 = yu + v \end{aligned}$$

  which implies $u = v = 0$. Hence, $x = y = 1$. Thus, $xy = 1$ implies $x = y = 1$.

This section as structured as follows: In Sect. 6.1, we show that that if we modify our interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ by choosing as the domain the class K of all $2 \times 2$ matrices with determinant 1, we obtain an interpretation in ${\textsf{Q}}^{ (2) }$ of the theory we obtain from ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ by replacing the editor axiom ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_2$ with the axioms ${\textsf{D}}_2$, ${\textsf{D}}_3$, $\overline{ {{\textsf{I}}}{{\textsf{D}}} }_5$, $\overline{ {{\textsf{I}}}{{\textsf{D}}} }_6$, $\forall x \; [ \ x = \varepsilon \; \vee \; \exists y \; [ \ x = y0 \; \vee \; x = y1 \ ]$. In Sect. 6.2, we extend our interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ to an interpretation of ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ in ${\textsf{Q}}^{ (2) }$ by restricting K to a subclass on which the editor axiom holds. Finally, in Sect. 8, we show that we can interpret ${\textsf{Q}}^{ (2) }$ in ${\textsf{Q}}$ by restricting the universe of ${\textsf{Q}}$ to a suitable subclass.

6.1 Atoms and predecessors

Let K denote the class all $2 \times 2$ matrices with determinant 1. That is

$$\begin{aligned} K = \left\{ \begin{pmatrix} x &{}\quad y\\ z &{} \quad w \end{pmatrix}: \ xw = 1 + yz \ \right\} . \end{aligned}$$

It is not difficult to verify that ${\textsf{Q}}^{ (2) }$ proves that $\det (AB) = 1$ if $\det (A) = \det (B) = 1$. We thus have the following lemma.

Lemma 19

${\textsf{Q}}^{ (2) }$ proves that K is closed under $\begin{pmatrix} 1 &{} \quad 0 \\ 0 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}$ and matrix multiplication.

Let us say that $A \in K$ is an atom in K if for all $B, C \in K$, $A = BC$ implies that one of B and C is the identity matrix. The proof of the following lemma is straightforward.

Lemma 20

${\textsf{Q}}^{ (2) }$ proves that $\begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$ and $\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}$ are atoms in K.

In [10], we introduce a theory $\textsf{BTQ}$ and show that ${\textsf{D}}$ interprets ${\textsf{Q}}$ by showing that it interprets $\textsf{BTQ}$. We obtain $\textsf{BTQ}$ from ${{\textsf{I}}}{{\textsf{D}}}$ by replacing ${{\textsf{I}}}{{\textsf{D}}}_4$ with the axiom $\forall x \; [ \ x = 0 \; \vee \; x = 1 \; \vee \; \exists y \; [ \ x = y0 \; \vee \; x = y1 \ ]$. The next lemma shows that if we modify the translation in Lemma 18 by choosing as the domain the class of all elements in K distinct from the identity matrix, we obtain an interpretation of $\textsf{BTQ}$ in ${\textsf{Q}}^{ (2) }$.

Lemma 21

Let $A \in K$. Then, ${\textsf{Q}}^{ (2) }$ proves that A is the identity matrix or that there exist $B, C \in K$ such that $A = BC$ and C is one of $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}$.

Proof

Let $K \ni A = \begin{pmatrix} a &{}\quad b \\ c &{}\quad d \end{pmatrix}$. By the trichotomy law, we have the following cases

• (1a) $a = b \; \wedge \; c <_{ {\textsf{l}} } d$, (1b) $a = b \; \wedge \; c = d$, (1c) $a = b \; \wedge \; d <_{ {\textsf{l}} } c$

• (2a) $a <_{ {\textsf{l}} } b \; \wedge \; c = d$, (2b) $b <_{ {\textsf{l}} } a \; \wedge \; c = d$

• (3a) $b<_{ {\textsf{l}} } a \; \wedge \; c <_{ {\textsf{l}} } d$, (3b) $a<_{ {\textsf{l}} } b \; \wedge \; d <_{ {\textsf{l}} } c$, (3c) $b<_{ {\textsf{l}} } a \; \wedge \; d <_{ {\textsf{l}} } c$, (3d) $a<_{ {\textsf{l}} } b \; \wedge \; c <_{ {\textsf{l}} } d \;$.

We consider Case (1a). Since $a = b \; \wedge \; c <_{ {\textsf{l}} } d$, let $d = r + c$ where $r \ne 0$. Since $ad = 1 + bc$ as $A \in K$, we have

$$\begin{aligned} ar + ac = a (r+c) = ad = 1 + bc = 1 + ac \end{aligned}$$

Since addition is right-cancellative, $ar = 1$, which implies $a = r = 1$. Thus

$$\begin{aligned} A = \begin{pmatrix} 1 &{}\quad 1 \\ c &{}\quad 1+c \end{pmatrix} = \begin{pmatrix} 1 &{}\quad 0 \\ c &{}\quad 1 \end{pmatrix} \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix} . \end{aligned}$$

We consider Case (1b). Since $a = b \; \wedge \; c = d$ and $A \in K$, we have

$$\begin{aligned} ad = 1+ bc = 1+ ad . \end{aligned}$$

Since 0 is an additive identity and addition is right-cancellative, $0 = 1$ which contradicts ${\textsf{Q}}_2$.

We consider Case (1c). Since $a = b \; \wedge \; d <_{ {\textsf{l}} } c$, let $c = s + d$ where $s \ne 0$. We have

$$\begin{aligned} ad = 1 + bc = 1 + a (s+d ) = 1 + as + ad . \end{aligned}$$

Hence, $0 = 1+ as$. Since addition is commutative, $0 = \textrm{S} ( as + 0 )$ by ${\textsf{Q}}_5$, which contradicts ${\textsf{Q}}_2$.

We consider Case (2a). Since $a <_{ {\textsf{l}} } b \; \wedge \; c = d$, let $b = r + a$ where $r \ne 0$. We have

$$\begin{aligned} ad = 1+ bc = 1 + (r+a) d = 1 + rd + ad . \end{aligned}$$

Hence, $0 = 1 + rd$ which contradicts ${\textsf{Q}}_2$.

We consider Case (2b). Since $b <_{ {\textsf{l}} } a \; \wedge \; c = d$, let $a = s + b$ where $s \ne 0$. We have

$$\begin{aligned} sd + bd = (s+b) d = ad = 1 +bc = 1 + bd . \end{aligned}$$

Hence, $sd = 1$ which implies $s = d = 1$. Thus

$$\begin{aligned} A = \begin{pmatrix} 1 +b &{}\quad b \\ 1 &{}\quad 1 \end{pmatrix} = \begin{pmatrix} 1 &{}\quad b \\ 0 &{} \quad 1 \end{pmatrix} \begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix} . \end{aligned}$$

We consider Case (3a). Since $b<_{ {\textsf{l}} } a \; \wedge \; c <_{ {\textsf{l}} } d$, there exist $r, s \ne 0$ such that $a = r + b$ and $d = s + c$. Since $ad = 1 + bc$, we have

$$\begin{aligned} rs + rc + bs + bc = (r+b) ( s+c) = ad = 1 + bc \end{aligned}$$

which implies

$$\begin{aligned} rs + rc + bs = 1 . \end{aligned}$$

Since $r, s \ne 0$, we conclude that $r = s = 1$ and $b = c = 0$. Thus, $A = \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}$.

We consider Case (3b). Since $a<_{ {\textsf{l}} } b \; \wedge \; d <_{ {\textsf{l}} } c$, there exist $p, q \ne 0$ such that $b = p + a$ and $c = q + d$. Since $ad = 1 + bc$, we have

$$\begin{aligned} ad = 1 + bc = 1 + (p+a) (q+d) = 1 + pq + pd + aq + ad . \end{aligned}$$

Hence, $0 = 1 + pq + pd + aq$ which contradicts ${\textsf{Q}}_2$.

We consider Case (3c). Since $b<_{ {\textsf{l}} } a \; \wedge \; d <_{ {\textsf{l}} } c$,

$$\begin{aligned} A = \begin{pmatrix} a &{} \quad b \\ c &{}\quad d \end{pmatrix} = E \begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix} \ \ \ \text{ where } E = \begin{pmatrix} a-b &{}\quad b \\ c-d &{}\quad d \end{pmatrix} . \end{aligned}$$

Since addition is right-cancellative in ${\textsf{Q}}^{ (2) }$, we write $a-b$ and $c-d$ for the unique elements r, s such that $a = r + b$ and $c = s + d$. We need to show that $E \in K$. That is, we need to show that $\det (E ) = 1$. First, observe that

$$\begin{aligned} (x-y) z = xy - yz \ \text{ and } \ ( 1 + xz ) - y z = 1 + ( xz - yz) \end{aligned}$$

since

$$\begin{aligned} (x-y) z + yz = \big ( (x-y) + y \big ) z = x z \ \text{ and } \ 1 + ( xz - yz ) + yz = 1 + xz . \end{aligned}$$

Since $\det (A) = 1$, we have

$$\begin{aligned} (a-b) d = ad - bd = ( 1+ bc) -bd = 1 + b ( c-d) . \end{aligned}$$

Thus, $E \in K$.

We consider Case (3d). Since $a<_{ {\textsf{l}} } b \; \wedge \; c <_{ {\textsf{l}} } d$

$$\begin{aligned} A = \begin{pmatrix} a &{}\quad b \\ c &{}\quad d \end{pmatrix} = G \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix} \ \ \ \text{ where } G = \begin{pmatrix} a &{}\quad b -a \\ c &{} \quad d -c \end{pmatrix} \end{aligned}$$

We need to show that $G \in K$. That is, we need to show that $\det (G) = 1$. Since $\det (A) = 1$, we have

$$\begin{aligned} a (d-c) = ad - ac = 1 + bc - ac = 1 + (b-a) c . \end{aligned}$$

Thus, $G \in K$. $\square$

By similar reasoning, ${\textsf{Q}}^{ (2) }$ proves that left predecessors also exist: if $A \in K$ is not the identity, then there exist $B, C \in K$ such that $A = C B$ and C is one of $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{} \quad 1 \\ 0 &{} \quad 1 \end{pmatrix}$. Since modified subtraction makes sense in ${\textsf{Q}}^{ (2) }$, we also get that the cancellation laws hold: if $A, B, C \in K$ and $AC = BC \; \vee \; C A = CB$, then $A = B$. In particular, in any model of ${\textsf{Q}}^{ (2) }$, K defines a model of the theory ${\textsf{F}}$ of Szmielew and Tarski (see Tarski et al. [12, p. 86]). The theory ${\textsf{F}}$ is given by the following non-logical axioms: concatenation is associative, every element is both left cancellative and right cancellative, the two maps $x \mapsto x0$ and $y \mapsto y1$ have disjoint images, every element different from 0 and 1 is in the image of one of the two maps $x \mapsto x0$ and $y \mapsto y1$. The intended model is the free semigroup with two generators.

6.2 Interpretation of ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$

We are finally ready to extend our interpretation of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ to an interpretation of ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ in ${\textsf{Q}}^{ (2) }$. All we need to do is to restrict the class K to a subclass on which the editor axiom holds.

Theorem 22

There exists a class I such that the 4-dimensional translation of $\lbrace \varepsilon , 0, 1, \circ \rbrace$ in $\lbrace 0, 1, S, +, \times \rbrace$ defined by

• $\varepsilon$, 0 and 1 are translated as $\begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}$, respectively

• $\circ$ is translated as matrix multiplication

• the domain is I

defines a 4-dimensional interpretation of ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ in ${\textsf{Q}}^{ (2) }$.

Proof

Let

$$\begin{aligned} K = \left\{ \begin{pmatrix} x &{}\quad y \\ z &{}\quad w \end{pmatrix}: \ xw = 1 + yz \ \right\} . \end{aligned}$$

Lemmas 18 and 20 tell us that the restriction of axioms ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_1 - {{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_2$, ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_4 - {{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_8$ to K are theorems of ${\textsf{Q}}^{ (2) }$. Since ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_1 - {{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_2$, ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_4 - {{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_8$ are universal sentences, to interpret ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ in ${\textsf{Q}}^{ (2) }$, it suffices to restrict the class K to a subclass I on which the editor axiom ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }_2$ holds. We need the following three properties that are given by Lemmas 18 and 21

$$\begin{aligned} \begin{array}{r l } {{\textsf{D}}}{{\textsf{J}}} &{} \forall A, B \in K \; \Big [ \ A \begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix} \ne B \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix} \ \Big ] \\ \\ {{\textsf{R}}}{{\textsf{C}}} &{} \forall A, B \in K \; \Bigg [ A \ne B \rightarrow \\ &{} \quad \quad \Bigg ( A \begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix} \ne B \begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix} \ \wedge \ A \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix} \ne B \begin{pmatrix} 1 &{}\quad 1 \\ 0 &{} \quad 1 \end{pmatrix} \Bigg ) \ \Bigg ] \\ \\ {{\textsf{P}}}{{\textsf{D}}} &{} \forall A \in K \; \Big [ \ A = \begin{pmatrix} 1 &{}\quad 0 \\ 0 &{} \quad 1 \end{pmatrix} \ \vee \ \\ &{} \quad \quad \exists B \in K \; \Bigg [ \ A = B \begin{pmatrix} 1 &{} 0 \\ 1 &{} \quad 1 \end{pmatrix} \ \vee \ A = B \begin{pmatrix} 1 &{} \quad 1 \\ 0 &{}\quad 1 \end{pmatrix} \ \Bigg ] \ \Bigg ] \end{array} \end{aligned}$$

Let

$$\begin{aligned} H= & {} \Big \lbrace W \in K: \ \forall X Z \; \forall Y \in K \big [ \ \ XY = ZW \rightarrow \exists U \in K \; [ \\{} & {} ( \ Z = XU \; \wedge \; UW = Y ) \vee ( \ X = ZU \; \wedge \; UY = W ) \ ] \ \big ] \ \Big \rbrace . \end{aligned}$$

It follows from ${{\textsf{D}}}{{\textsf{J}}}$, ${{\textsf{R}}}{{\textsf{C}}}$, ${{\textsf{P}}}{{\textsf{D}}}$ and associativity of matrix multiplication that $\begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}$ are elements of H. We show that H is closed under matrix multiplication. So, assume $W_0, W_1 \in H$. We need to show that $W_0 W_1 \in H$. First, we observe that $W_0 W_1 \in K$ since K is closed under matrix multiplication and $H \subseteq K$. Now, let X, Y, Z be such that $XY = Z W_0 W_1$ and $Y \in K$. Since $W_1 \in H$, we have the following two cases for some $U_1 \in K$

$$\begin{aligned} (1) \ X = Z W_0 U_1 \; \wedge \; U_1 Y = W_1 , \ \ \ (2) \ Z W_0 = X U_1 \; \wedge \; U_1 W_1 = Y . \end{aligned}$$

We consider (1). Since K is closed under matrix multiplication and $H \subseteq K$, we have

$$\begin{aligned} X = Z W_0 U_1 \ \wedge \ W_0 U_1 Y = W_0 W_1 \ \wedge \ W_0 U_1 \in K \ . \qquad {(*)} \end{aligned}$$

We consider (2). Since $W_0 \in H$ and $U_1 \in K$, we have one of the following two cases for some $U_0 \in K$

$$\begin{aligned}{} & {} (2a) \ Z = X U_0 \; \wedge \; U_0 W_0 = U_1 \; \wedge \; U_1 W_1 = Y, \\{} & {} (2b) \ X = Z U_0 \; \wedge \; U_0 U_1 = W_0 \; \wedge \; U_1 W_1 = Y . \end{aligned}$$

In case of (2a), we have

$$\begin{aligned} Z = X U_0 \ \wedge \ U_0 W_0 W_1 = U_1 W_1 = Y \ \wedge \ U_0 \in K\ . \qquad {(**)} \end{aligned}$$

In case of (2b), we have

$$\begin{aligned} X = Z U_0 \ \wedge \ W_0 W_1 = U_0 U_1 W_1 = U_0 Y \ \wedge \ U_0 \in K . \qquad {({*}{*}{*})} \end{aligned}$$

By (*), (**) and (***), we have $W_0 W_1 \in H$. Thus, H is closed under matrix multiplication.

We are finally ready to specify the class I. Let

$$\begin{aligned} I = \left\{ A \in H: \ \forall B \; [ \ B \preceq _{ K } A \rightarrow B \in H \ ] \ \right\} \end{aligned}$$

where

$$\begin{aligned} B \preceq _{ K } A \equiv \ \exists C \in K \; [ \ A = B C \ ] . \end{aligned}$$

It follows from Lemma 20 that $\begin{pmatrix} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 0 \\ 1 &{}\quad 1 \end{pmatrix}$, $\begin{pmatrix} 1 &{}\quad 1 \\ 0 &{}\quad 1 \end{pmatrix}$ are elements of I. To show that I defines a model of ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$, it suffices to show that I is closed under matrix multiplication and downward closed under $\preceq _{ K }$, where the latter ensures that the editor axiom holds restricted to I.

We show that I is closed under matrix multiplication. Assume $A_0, A_1 \in I$. We need to show that $A_0 A_1 \in I$. So, assume $B C = A_0 A_1$ where $C \in K$. We need to show that $B \in H$. Since $A_1 \in I \subseteq H$ and $C \in K$, we have one of the following cases for some $U \in K$

$$\begin{aligned} (i) \ A_0 = B U \; \wedge \; U A_1 = C \;, \ \ \ (ii) \ B = A_0 U \; \wedge \; U C = A_1 . \end{aligned}$$

In case of (i) we have $B \preceq _{ K } A_0$ which implies $B \in H$ since $A_0 \in I$. In case of (ii) we have $U \preceq _{ K } A_1$ which implies $U \in H$ since $A_1 \in I$. Since H is closed under matrix multiplication and $A_0 \in I \subseteq H$, we have $B = A_0 U \in H$. Hence, $A_0 A_1 \in I$. Thus, I is closed under matrix multiplication.

We show that I is downward closed under $\preceq _{ K }$. So, assume $B \preceq _{ K } A$ where $A \in I$. We need to show that $B \in I$. That is, we need to show that $B \in H$ and $\forall D \preceq _{ K } B \; [ \ D \in H \ ]$. Since $A \in I$ and $B \preceq _{ K } A$, it follows from the definition of I that $B \in H$. Assume now $B = DC$ where $C \in K$. We need to show that $D \in H$. Since $B \preceq _{ K } A$, there exists $E \in K$ such that $A = B E$. Hence, $DC E = BE = A$. Since $C, E \in K$ and K is closed under matrix multiplication, $CE \in K$. Hence, $D \preceq _{ K } A$. Then, $D \in H$ since $A \in I$. Thus, I is downward closed under $\preceq _{ K }$. $\square$

7 Commutative semirings I

We complete our proof of interpretability of $\overline{ {{\textsf{I}}}{{\textsf{D}}} }$ in ${{\textsf{I}}}{{\textsf{Q}}}$ by showing that ${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ are mutually interpretable.

Theorem 23

${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ are mutually interpretable.

Proof

Since ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ is an extension of ${{\textsf{I}}}{{\textsf{Q}}}$, we only need to show that ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}$. Our strategy is to first restrict the universe of ${{\textsf{I}}}{{\textsf{Q}}}$ to an inductive class $N_2$ which is such that each of the axioms (I)–(VIII) in Fig. 6 holds on $N_2$ when we restrict quantification to $N_2$ and treat addition and multiplication as partial functions. Recall that a class X is inductive if $0 \in X$ and $\forall x \in X \; [ \ \textrm{S} x \in X \ ]$. Now, since the axioms of ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ are all universal sentences, to interpret ${{\textsf{I}}}{{\textsf{Q}}}^{ (2) }$ in ${{\textsf{I}}}{{\textsf{Q}}}$, it suffices to relativize quantification to a subclass N of $N_2$ that is closed under $0, \textrm{S}, +, \times$.

We start by restricting the universe of ${{\textsf{I}}}{{\textsf{Q}}}$ to a subclass $N_0$ where 0 is the only element with an additive inverse, and addition is associative and right-cancellative. Let $u \in N_0$ if and only if

• (1) $0 + u = u$

• (2) $\forall x \; [ \ x+u = 0 \rightarrow ( \ x=0 \; \wedge \; u = 0 ) \ ]$

• (3) $\forall x \; [ \ \textrm{S} x + u = \textrm{S} ( x + u ) \ ]$

• (4) $\forall x y \; [ \ (x+y ) + u = x + (y+u ) \ ]$

• (5) $\forall x y \; [ \ x + u = y + u \rightarrow x= y \ ] \;$

• (6) $0 u = 0 \;$.

We verify that $0 \in N_0$. We need to show that 0 satisfies (1)–(6). By ${\textsf{Q}}_4 \equiv \ \forall x \; [ \ x+0 = x \ ]$, 0 satisfies (1)–(5). By ${\textsf{Q}}_6 \equiv \ \forall x \; [ \ x0 = 0 \ ]$, 0 satisfies (6). Thus, $0 \in N_0$.

We verify that $N_0$ is closed under $\textrm{S}$. Let $u \in N_0$. We need to show that $\textrm{S} u \in N_0$. That is, we need to show that $\textrm{S} u$ satisfies (1)–(6). We have

$$\begin{aligned} 0 + \textrm{S} u = \textrm{S} (0 + u ) = \textrm{S} u = \textrm{S} u + 0 \end{aligned}$$

where the first equality holds by ${\textsf{Q}}_5 \equiv \ \forall x y \; [ \ x+ \textrm{S} y = \textrm{S} (x+y ) \ ]$, the second equality holds since u satisfies (1) and the last equality holds by ${\textsf{Q}}_4$. Thus, $\textrm{S} u$ satisfies (1).

By ${\textsf{Q}}_5$ and ${\textsf{Q}}_2 \equiv \ \forall x \; [ \ \textrm{S} x \ne 0 \ ]$

$$\begin{aligned} x + \textrm{S} u = \textrm{S} (x+u ) \ne 0 . \end{aligned}$$

Thus, $\textrm{S} u$ satisfies (2).

We have

$$\begin{aligned} \textrm{S} x + \textrm{S} u = \textrm{S} ( \textrm{S} x + u ) = \textrm{SS} (x+u) = \textrm{S} ( x + \textrm{S} u ) \end{aligned}$$

where the first equality holds by ${\textsf{Q}}_5$, the second equality holds since u satisfies (3) and the last equality holds by ${\textsf{Q}}_5$. Thus, $\textrm{S} u$ satisfies (3).

We have

$$\begin{aligned} (x+y ) + \textrm{S} u = \textrm{S} ( (x+y) + u ) = \textrm{S} ( x + (y+u) ) = x + ( y + \textrm{S} u ) \end{aligned}$$

where the first equality holds by ${\textsf{Q}}_5$, the second equality holds since u satisfies (4), and the last equality holds by ${\textsf{Q}}_5$. Thus, $\textrm{S} u$ satisfies (4).

We have

$$\begin{aligned} \textrm{S} ( x+u ) = x + \textrm{S} u = y + \textrm{S} u = \textrm{S} ( y+u ) \ \Rightarrow \ x+u = y+u \ \Rightarrow \ x + y \end{aligned}$$

where the first implication follows from ${\textsf{Q}}_1 \equiv \ \forall xy \; [ \ \textrm{S} x = \textrm{S} y \rightarrow x = y \ ]$, and the last implication follows from the assumption that u satisfies (5). Thus, $\textrm{S} u$ satisfies (5).

By ${\textsf{Q}}_7 \equiv \ \forall x y \; [ \ x \times \textrm{S} y = x \times y + x \ ]$

$$\begin{aligned} 0 \times \textrm{S} u = 0u + 0 = 0 + 0 = 0 \end{aligned}$$

where the second equality follows from the assumption that u satisfies (6) and the last equality holds by ${\textsf{Q}}_4$. Thus, $\textrm{S} u$ satisfies (6).

Since Su satisfies (1)–(6), $\textrm{S} u \in N_0$. Thus, $N_0$ is closed under $\textrm{S}$. Since $N_0$ contains 0 and is closed under $\textrm{S}$, the class $N_0$ is inductive.

We restrict $N_0$ to a subclass $N_1$ where addition is commutative, the left distributive law holds, and there are no zero divisors. Let $u \in N_1$ if and only if $u \in N_0$ and

• (7) $\forall x \in N_0 \; [ \ x + u = u + x \ ]$

• (8) $\forall x \in N_0 \; \forall y \; [ \ x (y+u ) = xy + xu \ ]$

• (9) $\forall x \in N_0 \; [ \ x u = 0 \rightarrow ( \ x = 0 \; \vee \; u = 0 ) \ ]$

• (10) $\forall x \in N_0 \; [ \ \textrm{S} x \times u = xu + u \ ] \;$.

Verify that $N_1$ contains 0. We need to show that $0 \in N_0$ and that 0 satisfies (7)–(10). Since $N_0$ is inductive, $0 \in N_0$. By ${\textsf{Q}}_4$ and (1), 0 satisfies (7). By ${\textsf{Q}}_4$ and ${\textsf{Q}}_6$, 0 satisfies (8). It is obvious that 0 satisfies (9). By ${\textsf{Q}}_6$ and ${\textsf{Q}}_4$, 0 satisfies (10). Since 0 is an element of $N_0$ and satisfies (7)–(10), $0 \in N_1$.

We verify that $N_1$ is closed under $\textrm{S}$. Let $u \in N_1$. We need to show that $\textrm{S} u \in N_0$ and that $\textrm{S} u$ satisfies (7)–(10). Since $N_0$ is inductive and $u \in N_1 \subseteq N_0$, $\textrm{S} u \in N_0$. We verify that $\textrm{S} u$ satisfies (7). Let $x \in N_0$. Then

$$\begin{aligned} x + \textrm{S} u = \textrm{S} ( x+u ) = \textrm{S} ( u + x ) = \textrm{S} u + x \end{aligned}$$

where the first equality holds by ${\textsf{Q}}_5$, the second equality holds since u satisfies (7), and the last equality holds since x satisfies (3). Thus, $\textrm{S} u$ satisfies (7).

We verify that $\textrm{S} u$ satisfies (8). Let $x \in N_0$. We have

$$\begin{aligned} \begin{aligned} x ( y + \textrm{S} u )&= x \times \textrm{S} (y+ u )\quad ( {\textsf{Q}}_5 )\\&= x (y+u ) + x \quad ( {\textsf{Q}}_7 )\\&= ( xy+ xu ) + x \quad ( u \text{ satisfies } (8))\\&= xy+ ( xu + x ) \quad ( x \text{ satisfies } (4))\\&= xy+ ( x \times \textrm{S} u ) \quad ( {\textsf{Q}}_7 ) . \end{aligned} \end{aligned}$$

Thus, $\textrm{S} u$ satisfies (8).

We verify that $\textrm{S} u$ satisfies (9). Let $x \in N_0$ and assume $x \times \textrm{S} u = 0$. By ${\textsf{Q}}_7$, $x u + x = 0$. Since x satisfies (2), $x = 0$. Thus, $\textrm{S} u$ satisfies (9).

Finally, we verify that $\textrm{S} u$ satisfies (10). Let $x \in N_0$. We have

$$\begin{aligned} \begin{aligned} \textrm{S} x \times \textrm{S} u&= ( \textrm{S} x \times u ) + \textrm{S} x \quad ( {\textsf{Q}}_{7})\\&= ( xu + u ) + \textrm{S} x \quad ( u \text{ satisfies } (10))\\&= xu + (u + \textrm{S} x ) \quad ( \textrm{S} x \in N_0 \text{ satisfies } (4))\\&= xu + \textrm{S} (u + x ) \quad ( {\textsf{Q}}_{5})\\&= xu + \textrm{S} ( x + u ) \quad ( x \in N_0 \text{ and } u \text{ satisfies } (7))\\&= xu + ( x + \textrm{S} u ) \quad ( {\textsf{Q}}_{5})\\&= (xu + x ) + \textrm{S} u \quad ( \textrm{S} u \in N_0 \text{ satisfies } (4))\\&= ( x \times \textrm{S} u ) + \textrm{S} u \quad ( {\textsf{Q}}_7) . \end{aligned} \end{aligned}$$

Thus, $\textrm{S} u$ satisfies (10).

Since $\textrm{S} u$ is an element of $N_0$ and satisfies (7)–(10), $\textrm{S} u \in N_1$. Thus, $N_1$ is closed under $\textrm{S}$. Since $N_1$ contains 0 and is closed under $\textrm{S}$, the class $N_1$ is inductive.

We restrict $N_1$ to a subclass $N_2$ where multiplication is associative and commutative. Let $u \in N_2$ if and only if $u \in N_1$ and

• (11) $\forall x, y \in N_1 \; [ \ (xy ) u = x (yu) \ ]$

• (12) $\forall x \in N_1 \; [ \ x u = u x \ ] \;$.

We verify that $0 \in N_2$. We need to show that $0 \in N_1$ and that 0 satisfies (11)–(12). Since $N_1$ is inductive, $0 \in N_1$. By ${\textsf{Q}}_6$, 0 satisfies (11). By ${\textsf{Q}}_6$ and (6), 0 satisfies (12). Thus, $0 \in N_2$.

We verify that $N_2$ is closed under $\textrm{S}$. Let $u \in N_2$. We need to show that $\textrm{S} u \in N_1$ and that $\textrm{S} u$ satisfies (11)–(12). Since $N_{ 2} \subseteq N_1$ and $N_1$ is inductive, $\textrm{S} u \in N_1$. We verify that $\textrm{S} u$ satisfies (11). Let $x, y \in N_1$. We have

$$\begin{aligned} \begin{aligned} (xy) \times \textrm{S} u&= (xy)u + xy \quad ( {\textsf{Q}}_7 )\\&= x (yu) + xy \quad ( u \text{ satisfies } (11) )\\&= x ( yu + y ) \quad ( x \in N_0 \text{ and } y \in N_1 \text{ satisfies } (8) )\\&= x (y \times \textrm{S} u ) \quad ( {\textsf{Q}}_7 ) . \end{aligned} \end{aligned}$$

Thus, $\textrm{S} u$ satisfies (11).

We verify that $\textrm{S} u$ satisfies (12). Let $x \in N_1$. We have

$$\begin{aligned} \begin{aligned} x \times \textrm{S} u&= xu + x \quad ( {\textsf{Q}}_7 )\\&= ux + x \quad ( u \text{ satisfies } (12) \; )\\&= \textrm{S} u \times x \quad ( u \in N_0 \text{ and } x \in N_1 \text{ satisfies } (10) ) . \end{aligned} \end{aligned}$$

Thus, $\textrm{S} u$ satisfies (12).

Since $\textrm{S} u$ is an element of $N_1$ and satisfies (11)–(12), $\textrm{S} u \in N_2$. Thus, $N_2$ is closed under $\textrm{S}$. Since $N_2$ contains 0 and is closed under $\textrm{S}$, the class $N_2$ is inductive.

We are almost done. All that remains is to restrict $N_2$ to an inductive class that is closed under addition and multiplication. We start by ensuring closure under addition. Let

$$\begin{aligned} N_3 = \lbrace u \in N_2: \ \forall x \in N_2 \; [ \ x+u \in N_2 \ ] \ \rbrace . \end{aligned}$$

By ${\textsf{Q}}_4$, $0 \in N_3$. We show that that $N_3$ is closed under $\textrm{S}$. Let $u \in N_3$. Since $N_2$ is inductive and $u \in N_3 \subseteq N_2$, $\textrm{S} u \in N_2$. By ${\textsf{Q}}_5$, given $x \in N_2$, we have $x + \textrm{S} u = \textrm{S} (x + u )$. Since $u \in N_3$, $x+u \in N_2$. Since $N_2$ is inductive, $\textrm{S} (x + u ) \in N_2$. Hence, $\textrm{S} u \in N_3$. Thus, $N_3$ is closed under $\textrm{S}$.

We verify that $N_3$ is closed under $+$. Let $u, v \in N_3$. We need to show that $u+v \in N_2$ and $\forall x \in N_2 [ \ x + (u+v ) \in N_2 \ ]$. Since $u \in N_2$ and $v \in N_3$, $u+v \in N_2$. Now, let $x \in N_2$. Since $u \in N_3$, $x + u \in N_2$. Since $v \in N_3$, $(x+u) + v \in N_2$. Since $v \in N_2 \subseteq N_0$ satisfies (4), $(x+u) + v = x + (u+v)$. Hence, $u+ v \in N_3$ Thus, $N_3$ is closed under $+$.

Let

$$\begin{aligned} N = \lbrace u \in N_3: \ \forall x \in N_3 \; [ \ xu \in N_3 \ ] \ \rbrace . \end{aligned}$$

We show that N is an inductive class that is closed under $+$ and $\times$. We show that $0 \in N$. Since $N_3$ is inductive, $0 \in N_3$. Let $x \in N_3$. By ${\textsf{Q}}_6$, $x 0 = 0 \in N_3$. Thus, $0 \in N$.

We show that N is closed under $\textrm{S}$. Let $u \in N$. We need to show that $\textrm{S} u \in N$. Since $u \in N_3$ and $N_3$ is inductive, $\textrm{S} u \in N_3$. Let $x \in N_3$. By ${\textsf{Q}}_7$, $x \times \textrm{S} u = xu + x$. Since $u \in N$, $xu \in N$. Since $N_3$ is closed under addition, $xu + x \in N_3$. Hence, $\textrm{S} u \in N$. Thus, N is closed under $\textrm{S}$.

We show that N is closed under $+$. Let $u, v \in N \subseteq N_3$. Since $N_3$ is closed under addition, $u+v \in N_3$. Let $x \in N_3$. Since $u, v \in N$, $xu, xv \in N_3$. Since $N_3$ is closed under addition, $xu + xv \in N_3$. Since $x \in N_3 \subseteq N_0$ and $v \in N_3 \subseteq N_1$, $xu + xv = x (u+v )$. Hence, $u+v \in N$. Thus, N is closed under $+$.

We show that N is closed under $\times$. Let $u, v \in N \subseteq N_3$. Since $u \in N_3$ and $v \in N$, $uv \in N_3$. Let $x \in N_3$. Since $u \in N$, $xu \in N_3$. Since $v \in N$, $(xu ) v \in N_3$. Since $x, u \in N_3 \subseteq N_1$ and $v \in N_3 \subseteq N_2$ satisfies (11), $(xu) v = x (uv)$. Hence, $uv \in N$. Thus, N is closed under $\times$.

Since N satisfies the domain conditions and all the axioms of ${{\textsf{I}}}{{\textsf{Q}}}^{ (2 ) }$ hold restricted to N as they are universal sentences, ${{\textsf{I}}}{{\textsf{Q}}}^{ (2 ) }$ is interpretable in ${{\textsf{I}}}{{\textsf{Q}}}$. Since ${{\textsf{I}}}{{\textsf{Q}}}^{ (2 ) }$ is an extension of ${{\textsf{I}}}{{\textsf{Q}}}$, it follows that ${{\textsf{I}}}{{\textsf{Q}}}$ and ${{\textsf{I}}}{{\textsf{Q}}}^{ (2 ) }$ are mutually interpretable. $\square$

8 Commutative semirings II

It is clear that ${\textsf{Q}}^{ (2) }$ is interpretable in ${\textsf{Q}}$ since each axiom of ${\textsf{Q}}^{ (2) }$ is provable in $I \Delta _0$, which is ${\textsf{Q}}$ extended with an induction schema for $\Sigma _0$-formulas, and $I \Delta _0$ is interpretable in ${\textsf{Q}}$ (see Section V.5c of Hájek and Pudlák [4]). Lemma V.5.11 of [4] shows that we can interpret any finite subtheory of $I \Delta _0$ in ${\textsf{Q}}$ by restricting the universe of ${\textsf{Q}}$ to a suitable subclass. It then follows that our interpretation of ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ in ${\textsf{Q}}^{ (2) }$ really extends to a recursion-free interpretation of ${{\textsf{T}}}{{\textsf{C}}}^{ \varepsilon }$ in ${\textsf{Q}}$. For the benefit of the reader, we show that we can also prove this by building on the proof of Theorem 23.

Given a sentence $\phi$ and a class M, let $\phi ^M$ denote the sentence we obtain by restricting quantification to M.

Theorem 24

There exists a class M such that ${\textsf{Q}} \vdash \phi ^M$ for each axiom $\phi$ of ${\textsf{Q}}^{ (2) }$.

Proof

Let N be the class in the proof of Theorem 23. Let

$$\begin{aligned} u \le _{ N } v \equiv \ \exists r \in N \; [ \ u + r = v \ ] . \end{aligned}$$

We restrict N to an inductive subclass $M_0$ that is downward closed under $\le _{ N }$. Let

$$\begin{aligned} M_0 = \big \lbrace u \in N: \ \forall v \le _{ N } u \; [ \ v \in N \ ] \ \wedge \ \forall x, y \le _{ N } u \; [ \ x \le _{ N } y \; \vee \; y \le _{ N } x \ ] \ \big \rbrace . \end{aligned}$$

We show that $0 \in M_0$. Assume $v + r = 0$. If $r = 0$, then $v = 0$ by ${\textsf{Q}}_4$. If $r \ne 0$, then by ${\textsf{Q}}_3$ there exists t such $r = \textrm{S} t$. Then, by ${\textsf{Q}}_5$, $0 = v +r = \textrm{S} ( v + t )$ which contradicts ${\textsf{Q}}_2$. Thus, since $0 \in N$ and $0+ 0 = 0$, we have $0 \in M_0$.

We show that $M_0$ is closed under $\textrm{S}$. Let $u \in M_0$. We need to show that $\textrm{S} u \in M_0$. Since $u \in M_0 \subseteq N$ and N is inductive, $\textrm{S} u \in N$. We show that $\forall v \le _{ N } \textrm{S} u \; [ \ v \in N \ ]$. Assume $r \in N$ and $v + r = \textrm{S} u$. We need to show that $v \in N$. If $v = 0$, then $v \in N$ since N is an inductive class. Otherwise, by ${\textsf{Q}}_3$, there exists w such that $\textrm{S} w = v$. By Clause (3) in the proof of Theorem 23

$$\begin{aligned} \textrm{S} u = v+r = \textrm{S} w + r = \textrm{S} ( w + r ) . \end{aligned}$$

By ${\textsf{Q}}_1$, $w + r = u$. Hence, $w \le _{ N } u$. Since $u \in M_0$, we have $w \in N$. Since N is an inductive class, $v = \textrm{S} w \in N$. Thus, $\forall v \le _{ N } \textrm{S} u \; [ \ v \in N \ ]$.

We show that $\forall x, y \le _{ N } \textrm{S} u \; [ \ x \le _{ N } y \; \vee \; y \le _{ N } x \ ]$. Assume $x, y \le _{ N } \textrm{S} u$. By what we have just shown, $x, y \in N$. If $x = \textrm{S} u$ or $y = \textrm{S} u$, then x and y are comparable with respect to $\le _{ N }$ since $x, y \le _{ N } \textrm{S} u$. Otherwise, by ${\textsf{Q}}_4$

$$\begin{aligned} \textrm{S} u = x + r \ \ \wedge \ \ \textrm{S} u = y + t \ \ \text{ where } r, t \in N \setminus \lbrace 0 \rbrace . \end{aligned}$$

Since $x, y, r, t \in N$, we have

$$\begin{aligned} \textrm{S} u = x + r = r + x \ \ \wedge \ \ \textrm{S} u = y + t = t + y \end{aligned}$$

by Clause (7) in the proof of Theorem 23. By ${\textsf{Q}}_3$, there exist $r_0, t_0$ such that $r = \textrm{S} r_0$ and $t = \textrm{S} t_0$. Hence

$$\begin{aligned} \textrm{S} u = \textrm{S} r_0 + x = \textrm{S} ( r_0 + x ) \ \ \wedge \ \ \textrm{S} u = \textrm{S} t_0 + y = \textrm{S} ( t_0 + y) \end{aligned}$$

by Clause (3) in the proof of Theorem 23. By ${\textsf{Q}}_1$, $u = r_0 + x$ and $u = t_0 + y$. Hence, $r_0, t_0 \le _{ N } u$ which implies $r_0, t_0 \in N$ since $u \in M_0$. Then

$$\begin{aligned} u = r_0 + x = x + r_0 \ \ \wedge \ \ u = t_0 + y = y + t_0 \end{aligned}$$

by Clause (7) in the proof of Theorem 23. Hence, $x, y \le _{ N } u$ which implies that x and y are comparable with respect to $\le _{ N }$ since $u \in M_0$. Thus, we have $\forall x, y \le _{ N } \textrm{S} u \; [ \ x \le _{ N } y \; \vee \; y \le _{ N } x \ ]$. It then follows that $\textrm{S} u \in M_0$.

Since $\le _{ N }$ is transitive, $M_0$ is downward closed under $\le _{ N }$. Indeed, assume $w \le _{ N } v$ and $v \le _{ N } u$. Then, there exist $r, t \in N$ such that $v = w + r$ and $u = v + t$. Hence, $u = (w+r ) + t$. Since $t \in N \subseteq N_0$, we have

$$\begin{aligned} u = (w+r ) + t = w + (r + t ) \end{aligned}$$

by Clause (4) in the proof of Theorem 23. Since $r, t \in N$ and N is closed under addition, $r + t \in N$. Hence, $w \le _{ N } u$. Thus, $\le _{ N }$ is transitive.

We restrict $M_0$ to a subclass $M_1$ that is closed under addition. Let

$$\begin{aligned} M_1 = \big \lbrace u \in M_0: \ \forall x \in M_0 \; [ \ x+u \in M_0 \ ] \ \big \rbrace . \end{aligned}$$

The class $M_1$ is shown to be closed under $0, \textrm{S}$ and $+$ just as in the proof of Theorem 23. We show that $M_1$ is downward closed under $\le _{ N }$. Assume $u \in M_1$ and $u = v + r$ where $r \in N$. We need to show that $v \in M_1$. So, let $x \in M_0$. We need to show that $x + v \in M_0$. We have

$$\begin{aligned} M_0 \ni x + u = x + (v+r ) = (x+v ) + r \end{aligned}$$

by Clause (4) in the proof of Theorem 23. Then

$$\begin{aligned} x+v \le _{ N } x+u \in M_0 . \end{aligned}$$

Since $M_0$ is downward closed under $\le _{ N }$, we have $x+v \in M_0$. Hence, $v \in M_1$. Thus, $M_1$ is downward closed under $\le _{ N }$.

Finally, we restrict $M_1$ to a domain M. Let

$$\begin{aligned} M = \big \lbrace u \in M_1: \ \forall x \in M_1 \; [ \ xu \in M_1 \ ] \ \big \rbrace . \end{aligned}$$

The class M is shown to be closed under $0, \textrm{S}, +, \times$ just as in the proof of Theorem 23. We show that $M_1$ is downward closed under $\le _{ N }$. Assume $u \in M$ and $u = v + r$ where $r \in N$. We need to show that $v \in M$. So, let $x \in M_1$. We need to show that $x v \in M_1$. We have

$$\begin{aligned} M_1 \ni x u = x (v+r ) = xv + xr \end{aligned}$$

by Clause (8) in the proof of Theorem 23. Since $v \le _{ N } u$, $u \in M \subseteq M_1$ and $M_1$ is downward closed under $\le _{ N }$, we have $v \in M_1$. Then, by Clause (7) in the proof of Theorem 23

$$\begin{aligned} u = v +r = r + v . \end{aligned}$$

Hence, $r \le _{ N } u$ which implies $r \in M_1$. Since $x, r \in M_1$ and $M_1$ is closed under $\times$, we have $xr \in M_1 \subseteq N$. Then, $x u = xv + xr$ implies $xv \le _{ N } xu$. Since $xu \in M_1$ and $M_1$ is downward closed under $\le _{ N }$, we have $xv \in M_1$. Hence, $v \in M$. Thus, M is downward closed under $\le _{ N }$.

Axioms (I)–(VIII) in Fig. 6 and the axioms of ${\textsf{Q}}$ that are universal sentences hold on M when we restrict quantification to M since they hold on N when we restrict quantification to N. We show that ${\textsf{Q}}_3 \equiv \ \forall x \; \big [ \ x = 0 \; \vee \; \exists y \; [ \ x = \textrm{S} y \ ] \ \big ]$ holds on M. Assume $x \in M {\setminus } \lbrace 0 \rbrace$. By ${\textsf{Q}}_3$, there exists y such that $x = \textrm{S} y$. We need to show that $y \in M$. By ${\textsf{Q}}_4$ and ${\textsf{Q}}_5$, we have

$$\begin{aligned} x = \textrm{S} y = \textrm{S} y + 0 = \textrm{S} ( y + 0 ) = y + \textrm{S} 0 . \end{aligned}$$

Since M is an inductive class, $\textrm{S} 0 \in M \subseteq N$. Hence, $y \le _{ N } x$. Since M is downward closed under $\le _{ N }$, we have $y \in M$. Thus, ${\textsf{Q}}_3$ holds restricted to M.

Finally, we show the trichotomy law $\forall x y \; [ \ x<_{ {\textsf{l}} } y \; \vee \; x = y \; \vee \; y <_{ {\textsf{l}} } x \ ]$ holds restricted to M. Recall that $x <_{ {\textsf{l}} } y \equiv \ \exists r \; [ \ r \ne 0 \; \wedge \; r + x = y \ ]$. Let $x, y \in M$. Since M is closed under addition and addition on M is commutative

$$\begin{aligned} y +x = x+ y \in M . \end{aligned}$$

Then, $x, y \le _{ N } x+ y$. Since $M \subseteq M_0$, we have

$$\begin{aligned} x \le _{ N } y \; \vee \; y \le _{ N } x . \end{aligned}$$

Assume $y = x + r$ where $r \in N$. By Clause (7) in the proof of Theorem 23, $y = x+r = r +x$. Hence, $r \le _{ N } y$ which implies $r \in M$. Similarly, if $x = y +t$ where $t \in N$, then $t \in M$. Hence, since $x \le _{ N } y \; \vee \; y \le _{ N } x$ holds

$$\begin{aligned} \exists r, t \in M \; [ \ y = x + r \ \vee \ x = y + t \ ] . \end{aligned}$$

Thus, the trichotomy law holds restricted to M. $\square$