Modeling Closed-Loop Control of Installed Jet Noise Using Ginzburg-Landau Equation

Abstract

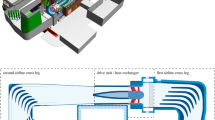
Installation noise is a dominant source associated with aircraft jet engines. Recent studies show that linear wavepacket models can be employed for prediction of installation noise, which suggests that linear control strategies can also be adopted for mitigation of it. We present here a simple model to test different control approaches and highlight the potential restrictions on a successful noise control in an actual jet. The model contains all the essential elements for a realistic representation of the actual control problem: a stochastic wavepacket is obtained via a linear Ginzburg-Landau model; the effect of the wing trailing edge is accounted for by introducing a semi-infinite half plane near the wavepacket; and the actuation is achieved by placing a dipolar point source at the trailing edge, which models a piezoelectric actuator. An optimal causal resolvent-based control method is compared against the classical wave-cancellation method. The effect of the causality constraint on the control performance is tested by placing the sensor at different positions. We demonstrate that when the sensor is not positioned sufficiently upstream of the trailing edge, which can be the case for the actual control problem due to geometric restrictions, causality reduces the control performance. We also show that this limitation can be moderated using the optimal causal control together with modelling of the forcing.

Appendices

Appendix A Solution of the Wiener-Hopf Problem

To solve the Wiener-Hopf problem defined in (25), we define two Wiener-Hopf factorisations

$$\begin{aligned} \hat{\textbf{D}}&=\hat{\textbf{D}}_-\hat{\textbf{D}}_+,\end{aligned}$$

(A1)

$$\begin{aligned} \hat{\textbf{D}}&=(\hat{\textbf{D}})_-+(\hat{\textbf{D}})_+, \end{aligned}$$

(A2)

that are multiplicative and additive, respectively, for a given matrix $\hat{\textbf{D}}$. Here, the subscripts − and $+$ denote being regular in the lower and upper complex plane, i.e., being entirely causal and non-causal, respectively. For a Wiener-Hopf problem given in the form

$$\begin{aligned} \hat{\textbf{D}}\hat{\textbf{K}}_+\hat{\textbf{E}} = \hat{\mathbf {\Lambda }}_- + \hat{\textbf{F}}, \end{aligned}$$

(A3)

the solution for the causal part is given by

$$\begin{aligned} \hat{\mathbf {\Gamma }}_+=\hat{\textbf{D}}_+^{-1}\big (\hat{\textbf{D}}_-^{-1}\hat{\textbf{F}}\hat{\textbf{E}}_-^{-1}\big )_+\hat{\textbf{E}}_+^{-1}. \end{aligned}$$

(A4)

Then, the causal gain matrix in (25) can be obtained by setting $\hat{\textbf{D}}\triangleq \hat{\textbf{G}}_a^H\hat{\textbf{G}}_a^{ }+\textbf{Q}$, $\hat{\textbf{E}}\triangleq \hat{\textbf{P}}_{yy}$ and $\hat{\textbf{F}}\triangleq -\hat{\textbf{G}}_a^H\hat{\textbf{P}}_{zy}^{ }$ and substituting these into (A3). We refer the reader to Martini et al. (2022) for details about how to achieve the Wiener-Hopf factorisations given in (A1) and (A2), where an efficient matrix-free method based on Hilbert transform is described to perform the multiplicative factorisation. The additive factorisation can be achieved by taking the inverse Fourier transform of $\hat{\textbf{D}}$ in (A2), splitting the resulting time-domain kernel $\textbf{D}$ into two parts such that $\textbf{D}_-(t<0)=0$ and $\textbf{D}_+(t>0)=0$, and finally taking the Fourier transforms of $\textbf{D}_-$ and $\textbf{D}_+$ to obtain $\hat{\textbf{D}}_-$ and $\hat{\textbf{D}}_+$, respectively.

Appendix B Spectral Proper Orthogonal Decomposition

SPOD (Towne et al. 2018) of a discrete-in-space stochastic variable $\hat{\textbf{q}}$ can be achieved by calculating the CSD matrix $\hat{\textbf{P}}_{qq}=\langle \hat{\textbf{q}}\hat{\textbf{q}}^H\rangle$ as in (7) and then solving the eigenvalue problem

$$\begin{aligned} \hat{\textbf{P}}_{qq}\textbf{W}{\varvec{\psi }}={\lambda }{\varvec{\psi }}, \end{aligned}$$

(B5)

where ${\varvec{\psi }}$ and ${\lambda }$ denote the eigenvector and the eigenvalue, respectively, and $\textbf{W}$ is a matrix to compute the energy norm, such that the energy of a given stochastic variable $\hat{{\xi }}(x)$ is calculated using the discretised vector $\hat{\varvec{\xi }}$ as

$$\begin{aligned} \langle \hat{\varvec{\xi }}^H\textbf{W}\hat{\varvec{\xi }}^H\rangle =\langle \int _S\hat{{\xi }}^*(x)W\hat{{\xi }}(x)dS\rangle , \end{aligned}$$

(B6)

where S denotes the domain $\hat{{\xi }}$ is defined, and W denotes the energy norm, which is chosen as 1 for this study. The SPOD modes are then obtained via the eigendecomposition

$$\begin{aligned} \textbf{W}^{1/2}\hat{\textbf{P}}_{qq}{{}\textbf{W}^{1/2}}^H=\tilde{\mathbf {\Psi }}\mathbf {\Lambda }\tilde{\mathbf {\Psi }}^H, \end{aligned}$$

(B7)

where $\mathbf {\Lambda }$ is a diagonal matrix containing the eigenvalues and $\tilde{\mathbf {\Psi }}\triangleq [\tilde{\varvec{\psi }}^{(1)}\,\tilde{\varvec{\psi }}^{(2)}\,\cdots ]$ denotes the matrix containing the eigenvectors. The eigenvectors given in (B5) that are orthogonal with respect to the norm defined in (B6) are then calculated as

$$\begin{aligned} {\varvec{\psi }}^{(i)}=\textbf{W}^{-1/2}\tilde{\varvec{\psi }}^{(i)}, \end{aligned}$$

(B8)

where the superscript (i) denotes the ith eigenvector. The optimal SPOD mode is defined as the eigenvector corresponding to the largest eigenvalue.