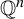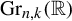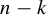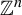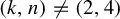1 Introduction
In this paper, we study the joint distribution of rational subspaces of a fixed discriminant (also called height by some authors) and of two naturally associated lattices: the integer lattice in the subspace and in its orthogonal complement together with some natural refinements.
Let Q be a positive definite integral quadratic form on
![]() $\mathbb {Q}^n$
and let
$\mathbb {Q}^n$
and let
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be a rational k-dimensional subspace. Here,
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be a rational k-dimensional subspace. Here,
![]() $\mathrm {Gr}_{n,k}$
is the projective variety of k-dimensional subspaces of the n-dimensional linear space. The discriminant
$\mathrm {Gr}_{n,k}$
is the projective variety of k-dimensional subspaces of the n-dimensional linear space. The discriminant
![]() $\mathrm {disc}_Q(L)$
of L with respect to Q is the discriminant of the restriction of Q to the integer lattice
$\mathrm {disc}_Q(L)$
of L with respect to Q is the discriminant of the restriction of Q to the integer lattice
![]() $L(\mathbb {Z}) = L\cap \mathbb {Z}^n$
. As a formula, this is
$L(\mathbb {Z}) = L\cap \mathbb {Z}^n$
. As a formula, this is
 $$ \begin{align*} \mathrm{disc}_Q(L) = \det \begin{pmatrix} \langle v_1,v_1\rangle_Q & \cdots & \langle v_1,v_k\rangle_Q \\ \vdots & & \vdots \\ \langle v_k,v_1\rangle_Q & \cdots & \langle v_k,v_k\rangle_Q \end{pmatrix}\!, \end{align*} $$
$$ \begin{align*} \mathrm{disc}_Q(L) = \det \begin{pmatrix} \langle v_1,v_1\rangle_Q & \cdots & \langle v_1,v_k\rangle_Q \\ \vdots & & \vdots \\ \langle v_k,v_1\rangle_Q & \cdots & \langle v_k,v_k\rangle_Q \end{pmatrix}\!, \end{align*} $$
where
![]() $\langle \cdot ,\cdot \rangle _Q$
is the bilinear form induced by Q and
$\langle \cdot ,\cdot \rangle _Q$
is the bilinear form induced by Q and
![]() $v_1,\ldots ,v_k$
is a basis of
$v_1,\ldots ,v_k$
is a basis of
![]() $L(\mathbb {Z})$
. We consider the finite set
$L(\mathbb {Z})$
. We consider the finite set
We attach to any
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
the restriction of Q to
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
the restriction of Q to
![]() $L(\mathbb {Z})$
represented in a basis. This is an integral quadratic form in k-variables which is well defined up to a change of basis, i.e. (in the language of quadratic forms), up to equivalence. In particular, it defines a well-defined point, which is also called the shape of
$L(\mathbb {Z})$
represented in a basis. This is an integral quadratic form in k-variables which is well defined up to a change of basis, i.e. (in the language of quadratic forms), up to equivalence. In particular, it defines a well-defined point, which is also called the shape of
![]() $L(\mathbb {Z})$
,
$L(\mathbb {Z})$
,
where
![]() $\mathcal {S}_{k}$
is the space of positive definite real quadratic forms on
$\mathcal {S}_{k}$
is the space of positive definite real quadratic forms on
![]() $\mathbb {R}^n$
up to similarity (i.e. up to equivalence and positive multiples). We may identify
$\mathbb {R}^n$
up to similarity (i.e. up to equivalence and positive multiples). We may identify
![]() $\mathcal {S}_{k}$
as
$\mathcal {S}_{k}$
as
which, in particular, equips
![]() $\mathcal {S}_{k}$
with a probability measure
$\mathcal {S}_{k}$
with a probability measure
![]() $m_{\mathcal {S}_{k}}$
arising from the Haar measures of the groups on the right. We will simply call
$m_{\mathcal {S}_{k}}$
arising from the Haar measures of the groups on the right. We will simply call
![]() $m_{\mathcal {S}_{k}}$
the Haar probability measure on
$m_{\mathcal {S}_{k}}$
the Haar probability measure on
![]() $\mathcal {S}_{k}$
.
$\mathcal {S}_{k}$
.
Analogously, one may define the point
![]() $[L^\perp (\mathbb {Z})]\in \mathcal {S}_{n-k}$
, where
$[L^\perp (\mathbb {Z})]\in \mathcal {S}_{n-k}$
, where
![]() $L^\perp $
is the orthogonal complement of L with respect to Q. Overall, we obtain a triple of points
$L^\perp $
is the orthogonal complement of L with respect to Q. Overall, we obtain a triple of points
![]() $(L,[L(\mathbb {Z})],[L^\perp (\mathbb {Z})])$
. The goal of this work is to study the distribution of these points in
$(L,[L(\mathbb {Z})],[L^\perp (\mathbb {Z})])$
. The goal of this work is to study the distribution of these points in
![]() $\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
as
$\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
as
![]() $\mathrm {disc}_Q(L)$
grows. In what follows,
$\mathrm {disc}_Q(L)$
grows. In what follows,
![]() $\mathrm {Gr}_{n,k}(\mathbb {R})$
is given the unique
$\mathrm {Gr}_{n,k}(\mathbb {R})$
is given the unique
![]() $\mathrm {SO}_Q(\mathbb {R})$
-invariant probability measure
$\mathrm {SO}_Q(\mathbb {R})$
-invariant probability measure
![]() $m_{\mathrm {Gr}_{n,k}(\mathbb {R})}$
.
$m_{\mathrm {Gr}_{n,k}(\mathbb {R})}$
.
Conjecture 1.1. Let
![]() $k,n \in \mathbb {N}$
be integers such that
$k,n \in \mathbb {N}$
be integers such that
![]() $k \geq 2$
and
$k \geq 2$
and
![]() $n-k \geq 2$
. Then the sets
$n-k \geq 2$
. Then the sets
equidistribute (implicitly, we mean with respect to the product ‘Haar’ measure, i.e. the product measure
![]() $m_{\mathrm {Gr}_{n,k}(\mathbb {R})} \otimes m_{\mathcal {S}_{k}} \otimes m_{\mathcal {S}_{n-k}}$
) in
$m_{\mathrm {Gr}_{n,k}(\mathbb {R})} \otimes m_{\mathcal {S}_{k}} \otimes m_{\mathcal {S}_{n-k}}$
) in
![]() $\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
as
$\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
as
![]() $D \to \infty $
along
$D \to \infty $
along
![]() $D \in \mathbb {N}$
satisfying
$D \in \mathbb {N}$
satisfying
![]() $\mathcal {H}^{n,k}_Q (D)\neq \emptyset $
.
$\mathcal {H}^{n,k}_Q (D)\neq \emptyset $
.
Remark 1.2. There exists an analogous conjecture for
![]() $k=1$
,
$k=1$
,
![]() $n-k \geq 2$
, where one only considers the pairs
$n-k \geq 2$
, where one only considers the pairs
![]() $(L,[L^\perp (\mathbb {Z})])$
(and, similarly, for
$(L,[L^\perp (\mathbb {Z})])$
(and, similarly, for
![]() $n-k=1$
,
$n-k=1$
,
![]() $k \geq 2$
). This has been studied extensively by the first named author with Einsiedler and Shapira in [Reference Aka, Einsiedler and ShapiraAES16a, Reference Aka, Einsiedler and ShapiraAES16b], where the conjecture is settled for
$k \geq 2$
). This has been studied extensively by the first named author with Einsiedler and Shapira in [Reference Aka, Einsiedler and ShapiraAES16a, Reference Aka, Einsiedler and ShapiraAES16b], where the conjecture is settled for
![]() $n \geq 6$
(i.e.
$n \geq 6$
(i.e.
![]() $n-k \geq 5$
), for
$n-k \geq 5$
), for
![]() $n = 4,5$
under a weak congruence condition and for
$n = 4,5$
under a weak congruence condition and for
![]() $n=3$
under a stronger congruence condition on D. We remark that, as it is written, [Reference Aka, Einsiedler and ShapiraAES16a, Reference Aka, Einsiedler and ShapiraAES16b] treat only the case where Q is the sum of squares (which we will sometimes call the standard form), but the arguments carry over without major difficulties. Using effective methods from homogeneous dynamics, Einsiedler, Rühr and Wirth [Reference Einsiedler, Rühr and WirthERW19] proved an effective version of the conjecture when
$n=3$
under a stronger congruence condition on D. We remark that, as it is written, [Reference Aka, Einsiedler and ShapiraAES16a, Reference Aka, Einsiedler and ShapiraAES16b] treat only the case where Q is the sum of squares (which we will sometimes call the standard form), but the arguments carry over without major difficulties. Using effective methods from homogeneous dynamics, Einsiedler, Rühr and Wirth [Reference Einsiedler, Rühr and WirthERW19] proved an effective version of the conjecture when
![]() $n=4,5$
, removing, in particular, all congruence conditions. The case
$n=4,5$
, removing, in particular, all congruence conditions. The case
![]() $n=3$
relies on a deep classification theorem for joinings by Einsiedler and Lindenstrauss [Reference Einsiedler and LindenstraussEL19]; effective versions of this theorem are well out of reach of current methods from homogeneous dynamics. Assuming the generalized Riemann hypothesis, Blomer and Brumley [Reference Blomer and BrumleyBB20] recently removed the congruence condition in [Reference Aka, Einsiedler and ShapiraAES16b].
$n=3$
relies on a deep classification theorem for joinings by Einsiedler and Lindenstrauss [Reference Einsiedler and LindenstraussEL19]; effective versions of this theorem are well out of reach of current methods from homogeneous dynamics. Assuming the generalized Riemann hypothesis, Blomer and Brumley [Reference Blomer and BrumleyBB20] recently removed the congruence condition in [Reference Aka, Einsiedler and ShapiraAES16b].
Remark 1.3. The case
![]() $k=2$
and
$k=2$
and
![]() $n-k=2$
of Conjecture 1.1 was settled in [Reference Aka, Einsiedler and WieserAEW22] by the first and the last named author together with Einsiedler under a (relatively strong) congruence condition when Q is the sum of four squares. The result in the paper is, in fact, stronger as it considers two additional shapes that one can naturally associate to L, essentially, thanks to the local isomorphism between
$n-k=2$
of Conjecture 1.1 was settled in [Reference Aka, Einsiedler and WieserAEW22] by the first and the last named author together with Einsiedler under a (relatively strong) congruence condition when Q is the sum of four squares. The result in the paper is, in fact, stronger as it considers two additional shapes that one can naturally associate to L, essentially, thanks to the local isomorphism between
![]() $\mathrm {SO}_4(\mathbb {R})$
and
$\mathrm {SO}_4(\mathbb {R})$
and
![]() $\mathrm {SO}_3(\mathbb {R}) \times \mathrm {SO}_3(\mathbb {R})$
. The arguments carry over without major difficulties to consider norm forms on quaternion algebras (equivalently, the forms Q for which
$\mathrm {SO}_3(\mathbb {R}) \times \mathrm {SO}_3(\mathbb {R})$
. The arguments carry over without major difficulties to consider norm forms on quaternion algebras (equivalently, the forms Q for which
![]() $\mathrm {disc}(Q)$
is a square in
$\mathrm {disc}(Q)$
is a square in
![]() $\mathbb {Q}^\times $
). In [Reference Aka and WieserAW21], the first and last named author extend the results of [Reference Aka, Einsiedler and WieserAEW22] to treat arbitrary quadratic forms.
$\mathbb {Q}^\times $
). In [Reference Aka and WieserAW21], the first and last named author extend the results of [Reference Aka, Einsiedler and WieserAEW22] to treat arbitrary quadratic forms.
In this article, we prove Conjecture 1.1 in the remaining cases, partially under congruence conditions. For integers
![]() $D,\ell $
, we write
$D,\ell $
, we write
![]() $D^{[\ell ]}$
for the
$D^{[\ell ]}$
for the
![]() $\ell $
-power free part of D, i.e. the largest divisor d of D with
$\ell $
-power free part of D, i.e. the largest divisor d of D with
![]() $a^\ell \nmid d$
for any
$a^\ell \nmid d$
for any
![]() $a>1$
.
$a>1$
.
Theorem 1.4. (Equidistribution of subspaces and shapes)
Let
![]() $2 \leq k \leq n$
be integers with
$2 \leq k \leq n$
be integers with
![]() $k \leq n-k$
and
$k \leq n-k$
and
![]() $n-k>3$
, and let p be an odd prime with
$n-k>3$
, and let p be an odd prime with
![]() $p \nmid \mathrm {disc}(Q)$
. Let
$p \nmid \mathrm {disc}(Q)$
. Let
![]() $D_i\in \mathbb {N}$
be a sequence of integers with
$D_i\in \mathbb {N}$
be a sequence of integers with
![]() $D_i^{[k]}\to \infty $
and
$D_i^{[k]}\to \infty $
and
![]() $\mathcal {H}_{Q}^{n,k}(D_i)\neq \emptyset $
for every i. Then the sets
$\mathcal {H}_{Q}^{n,k}(D_i)\neq \emptyset $
for every i. Then the sets
equidistribute in
![]() $\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
as
$\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
as
![]() $i \to \infty $
, assuming the following conditions.
$i \to \infty $
, assuming the following conditions.
-
•
 $p \nmid D_i$
if
$p \nmid D_i$
if
 $k \in \{3,4\}$
.
$k \in \{3,4\}$
. -
•
 $-D_i \,\mod\! p$
is a square in
$-D_i \,\mod\! p$
is a square in
 $\mathbb {F}_p^\times $
if
$\mathbb {F}_p^\times $
if
 $k=2$
.
$k=2$
.
Moreover, the analogous statement holds when the roles of k and
![]() $n-k$
are reversed.
$n-k$
are reversed.
Remark 1.5. Maass [Reference MaassMaa56, Reference MaassMaa59] in the 1960s and Schmidt [Reference SchmidtSch98] in the 1990s considered problems of this kind. They proved that the set of pairs
![]() $(L,[L(\mathbb {Z})])$
equidistributes in
$(L,[L(\mathbb {Z})])$
equidistributes in
![]() $\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k}$
, where
$\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k}$
, where
![]() $L\in \mathrm {Gr}_{n,k}(\mathbb {Q})$
varies over the rational subspaces with discriminant at most D. In this averaged set-up, Horesh and Karasik [Reference Horesh and KarasikHK20] recently verified Conjecture 1.1. Indeed, their version is polynomially effective in D.
$L\in \mathrm {Gr}_{n,k}(\mathbb {Q})$
varies over the rational subspaces with discriminant at most D. In this averaged set-up, Horesh and Karasik [Reference Horesh and KarasikHK20] recently verified Conjecture 1.1. Indeed, their version is polynomially effective in D.
Remark 1.6. (Congruence conditions)
As in the previous works referenced in Remarks 1.2 and 1.3, our proof is dynamical in nature and follows from an equidistribution result for certain orbits in an adelic homogeneous space. The congruence conditions at the prime p assert, roughly speaking, that one can use non-trivial dynamics at one fixed place for all D. The acting groups we consider here are (variations of) the
![]() $\mathbb {Q}_p$
-points of
$\mathbb {Q}_p$
-points of
for
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
. In particular, the cases
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
. In particular, the cases
![]() $k=2$
and
$k=2$
and
![]() $k>2$
are very different from a dynamical viewpoint.
$k>2$
are very different from a dynamical viewpoint.
-
• For
 $k>2$
, the group
$k>2$
, the group
 $\mathbf {H}_L$
is semisimple. The knowledge about measures on homogeneous spaces invariant under unipotents is vast (see Ratner’s seminal works [Reference RatnerRat91, Reference RatnerRat95]). In our situation, we use an S-arithmetic version of a theorem by Mozes and Shah [Reference Mozes and ShahMS95], proved by Gorodnik and Oh [Reference Gorodnik and OhGO11], which describes weak
$\mathbf {H}_L$
is semisimple. The knowledge about measures on homogeneous spaces invariant under unipotents is vast (see Ratner’s seminal works [Reference RatnerRat91, Reference RatnerRat95]). In our situation, we use an S-arithmetic version of a theorem by Mozes and Shah [Reference Mozes and ShahMS95], proved by Gorodnik and Oh [Reference Gorodnik and OhGO11], which describes weak
 ${}^\ast $
-limits of measures with invariance under a semisimple group. Roughly speaking, the theorem implies that any sequence of orbits under a semisimple subgroup is either equidistributed or sits (up to a small shift) inside an orbit of a larger subgroup. The flexibility that this method provides allows us to, in fact, prove a significantly stronger result; see Theorem 1.11 below.
${}^\ast $
-limits of measures with invariance under a semisimple group. Roughly speaking, the theorem implies that any sequence of orbits under a semisimple subgroup is either equidistributed or sits (up to a small shift) inside an orbit of a larger subgroup. The flexibility that this method provides allows us to, in fact, prove a significantly stronger result; see Theorem 1.11 below. -
• For
 $k=2$
and
$k=2$
and
 $n-k \geq 3$
, the group
$n-k \geq 3$
, the group
 $\mathbf {H}_L$
is reductive. Thus, one can apply the results mentioned in the previous bullet point only to the commutator subgroup of
$\mathbf {H}_L$
is reductive. Thus, one can apply the results mentioned in the previous bullet point only to the commutator subgroup of
 $\mathbf {H}_L$
, which is non-maximal and has intermediate subgroups.
$\mathbf {H}_L$
, which is non-maximal and has intermediate subgroups.
One of the novelties of this article is a treatment of this reductive case where we use additional invariance under the center to rule out intermediate subgroups ‘on average’ (see §4.3). Here, as well as for the second component of the triples in Theorem 1.4, we need equidistribution of certain adelic torus orbits; this is a generalized version of a theorem of Duke [Reference DukeDuk88] that builds on a breakthrough of Iwaniec [Reference IwaniecIwa87] (see, for example, [Reference Einsiedler, Lindenstrauss, Michel and VenkateshELMV11, Reference Harcos and MichelHM06, Reference WieserWie19]). Furthermore, to prove simultaneous equidistribution of the tuples in Theorem 1.4, we apply a new simple disjointness trick (see the following remark).
Remark 1.7. (Disjointness)
In the upcoming work, the first and last named author prove, together with Einsiedler, Luethi and Michel [Reference Ellenberg and VenkateshAEL+21], an effective version of Conjecture 1.1 when
![]() $k\neq 2$
. This removes, in particular, the congruence conditions. The technique consists of a method to ‘bootstrap’ effective equidistribution in the individual factors to simultaneous effective equidistribution (in some situations).
$k\neq 2$
. This removes, in particular, the congruence conditions. The technique consists of a method to ‘bootstrap’ effective equidistribution in the individual factors to simultaneous effective equidistribution (in some situations).
In the current article, we use an ineffective analogue of this to prove Theorem 1.4, namely, the very well-known fact that mixing systems are disjoint from trivial systems (see also Lemma 4.2). This simple trick has (to our knowledge) not yet appeared in the literature in a similar context. It is particularly useful when
![]() $k=2$
and
$k=2$
and
![]() $n-k\geq 3$
, in which case, we cannot rely solely on methods from unipotent dynamics (see Remark 1.6).
$n-k\geq 3$
, in which case, we cannot rely solely on methods from unipotent dynamics (see Remark 1.6).
Remark 1.8. (On the power assumption)
The assumption in Theorem 1.4 regarding the power free part of the discriminants should be considered a simplifying assumption only. Its purpose is automatically to rule out situations where, for most subspaces
![]() $L \in \mathcal {H}^{n,k}_Q(D)$
, the quadratic form
$L \in \mathcal {H}^{n,k}_Q(D)$
, the quadratic form
![]() $Q|_{L(\mathbb {Z})}$
(or
$Q|_{L(\mathbb {Z})}$
(or
![]() $Q|_{L^\perp (\mathbb {Z})}$
) is highly imprimitive (i.e. a multiple of a quadratic form of very small discriminant). We expect that such discriminants do not exist regardless of their factorization. A conjecture in this spirit is phrased in Appendix B. Moreover, Schmidt’s work [Reference SchmidtSch68] suggests that
$Q|_{L^\perp (\mathbb {Z})}$
) is highly imprimitive (i.e. a multiple of a quadratic form of very small discriminant). We expect that such discriminants do not exist regardless of their factorization. A conjecture in this spirit is phrased in Appendix B. Moreover, Schmidt’s work [Reference SchmidtSch68] suggests that
![]() $|\mathcal {H}^{n,k}_Q(D)| = D^{{n}/{2}-1+o(1)}$
, in which case one could remove the assumption that
$|\mathcal {H}^{n,k}_Q(D)| = D^{{n}/{2}-1+o(1)}$
, in which case one could remove the assumption that
![]() $D_i^{[k]}\to \infty $
in Theorem 1.4.
$D_i^{[k]}\to \infty $
in Theorem 1.4.
1.1 A strengthening
In the following, we present a strengthening of Conjecture 1.1 inspired by the notion of grids introduced in [Reference Aka, Einsiedler and ShapiraAES16a] and by Bersudsky’s construction of a moduli space [Reference BersudskyBer19] which refines the results of [Reference Aka, Einsiedler and ShapiraAES16a].
Consider the set of pairs
![]() $(L,\Lambda )$
, where
$(L,\Lambda )$
, where
![]() $L \subset \mathbb {R}^n$
is a k-dimensional subspace and where
$L \subset \mathbb {R}^n$
is a k-dimensional subspace and where
![]() $\Lambda \subset \mathbb {R}^n$
is a lattice of full rank with the property that
$\Lambda \subset \mathbb {R}^n$
is a lattice of full rank with the property that
![]() $L \cap \Lambda $
is a lattice in L (L is
$L \cap \Lambda $
is a lattice in L (L is
![]() $\Lambda $
-rational). We define an equivalence relation on these pairs by setting
$\Lambda $
-rational). We define an equivalence relation on these pairs by setting
![]() $(L,\Lambda )\sim (L',\Lambda ')$
whenever the following conditions are satisfied.
$(L,\Lambda )\sim (L',\Lambda ')$
whenever the following conditions are satisfied.
-
(1)
 $L=L'$
.
$L=L'$
. -
(2) There exists
 $g \in \mathrm {GL}_n(\mathbb {R})$
with
$g \in \mathrm {GL}_n(\mathbb {R})$
with
 $\det (g)> 0$
such that g acts on L and
$\det (g)> 0$
such that g acts on L and
 $L^{\perp }$
as scalar multiplication and
$L^{\perp }$
as scalar multiplication and
 $g\Lambda = \Lambda '$
.
$g\Lambda = \Lambda '$
.
We write
![]() $[L,\Lambda ]$
for the class of
$[L,\Lambda ]$
for the class of
![]() $(L,\Lambda )$
; elements of such a class are said to be homothetic along L or L-homothetic to
$(L,\Lambda )$
; elements of such a class are said to be homothetic along L or L-homothetic to
![]() $(L,\Lambda )$
. We refer to the set
$(L,\Lambda )$
. We refer to the set
![]() $\mathcal {Y}$
of such equivalence classes as the moduli space of basis extensions. Indeed, one can think of a lattice
$\mathcal {Y}$
of such equivalence classes as the moduli space of basis extensions. Indeed, one can think of a lattice
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $L\cap \Lambda $
is a lattice as one choice of complementing the lattice
$L\cap \Lambda $
is a lattice as one choice of complementing the lattice
![]() $L \cap \Lambda $
into a basis of
$L \cap \Lambda $
into a basis of
![]() $\mathbb {R}^n$
. The equivalence relation is not very transparent in this viewpoint; see §6 for further discussion.
$\mathbb {R}^n$
. The equivalence relation is not very transparent in this viewpoint; see §6 for further discussion.
The moduli space
![]() $\mathcal {Y}$
is designed to incorporate subspaces as well as both shapes. Clearly, we have a well-defined map
$\mathcal {Y}$
is designed to incorporate subspaces as well as both shapes. Clearly, we have a well-defined map
The restriction of Q to
![]() $L \cap \Lambda $
yields a well-defined element of
$L \cap \Lambda $
yields a well-defined element of
![]() $\mathcal {S}_{k}$
. Similarly, one may check that
$\mathcal {S}_{k}$
. Similarly, one may check that
![]() $L^\perp $
intersects the dual lattice
$L^\perp $
intersects the dual lattice
![]() $\Lambda ^\#$
in a lattice; the second shape is given by the restriction of Q to
$\Lambda ^\#$
in a lattice; the second shape is given by the restriction of Q to
![]() $L^\perp \cap \Lambda ^\#$
.
$L^\perp \cap \Lambda ^\#$
.
We note that there is a natural identification of
![]() $\mathcal {Y}$
with a double quotient of a Lie group (cf. Lemma 6.3) so that we may again speak of the ‘Haar measure’ on
$\mathcal {Y}$
with a double quotient of a Lie group (cf. Lemma 6.3) so that we may again speak of the ‘Haar measure’ on
![]() $\mathcal {Y}$
.
$\mathcal {Y}$
.
Conjecture 1.9. Let
![]() $k,n \in \mathbb {N}$
be integers such that
$k,n \in \mathbb {N}$
be integers such that
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $n-k \geq 3$
. Then the sets
$n-k \geq 3$
. Then the sets
equidistribute with respect to the Haar measure as
![]() $D \to \infty $
along
$D \to \infty $
along
![]() $D \in \mathbb {N}$
satisfying
$D \in \mathbb {N}$
satisfying
![]() $\mathcal {H}^{n,k}_Q(D)\neq \emptyset $
.
$\mathcal {H}^{n,k}_Q(D)\neq \emptyset $
.
Remark 1.10. (From Conjectures 1.9 to 1.1)
When Q is unimodular (i.e.
![]() $\mathrm {disc}(Q) = 1$
), Conjecture 1.9 implies Conjecture 1.1. Otherwise, Conjecture 1.9 implies equidistribution of the triples
$\mathrm {disc}(Q) = 1$
), Conjecture 1.9 implies Conjecture 1.1. Otherwise, Conjecture 1.9 implies equidistribution of the triples
![]() $(L,[L(\mathbb {Z})],[L^\perp \cap (\mathbb {Z}^n)^\#])$
, where
$(L,[L(\mathbb {Z})],[L^\perp \cap (\mathbb {Z}^n)^\#])$
, where
![]() $(\mathbb {Z}^n)^\#$
is the dual lattice to
$(\mathbb {Z}^n)^\#$
is the dual lattice to
![]() $\mathbb {Z}^n$
under the quadratic form Q: that is,
$\mathbb {Z}^n$
under the quadratic form Q: that is,
This is not significantly different, as the lattice
![]() $L^\perp \cap (\mathbb {Z}^n)^\#$
contains
$L^\perp \cap (\mathbb {Z}^n)^\#$
contains
![]() $L^\perp \cap \mathbb {Z}^n$
with index at most
$L^\perp \cap \mathbb {Z}^n$
with index at most
![]() $\mathrm {disc}(Q)$
; nevertheless, it is insufficient to deduce Conjecture 1.1. In §6, we introduce tuples
$\mathrm {disc}(Q)$
; nevertheless, it is insufficient to deduce Conjecture 1.1. In §6, we introduce tuples
![]() $[L,\Lambda _L]$
that satisfy an analogue of Conjecture 1.9; this adapted conjecture implies Conjecture 1.1
$[L,\Lambda _L]$
that satisfy an analogue of Conjecture 1.9; this adapted conjecture implies Conjecture 1.1
We prove the following theorem towards Conjecture 1.9.
Theorem 1.11. Let
![]() $k,n$
be integers with
$k,n$
be integers with
![]() $3 \leq k \leq n-k$
and let p be an odd prime with
$3 \leq k \leq n-k$
and let p be an odd prime with
![]() $p \nmid \mathrm {disc}(Q)$
. Let
$p \nmid \mathrm {disc}(Q)$
. Let
![]() $D_i\in \mathbb {N}$
be a sequence of integers with
$D_i\in \mathbb {N}$
be a sequence of integers with
![]() $D_i^{[k]}\to \infty $
and
$D_i^{[k]}\to \infty $
and
![]() $\mathcal {H}_{Q}^{n,k}(D_i)\neq \emptyset $
for every i. Then the sets
$\mathcal {H}_{Q}^{n,k}(D_i)\neq \emptyset $
for every i. Then the sets
equidistribute in
![]() $\mathcal {Y}$
as
$\mathcal {Y}$
as
![]() $i \to \infty $
assuming, in addition, that
$i \to \infty $
assuming, in addition, that
![]() $p \nmid D_i$
if
$p \nmid D_i$
if
![]() $k \in \{3,4\}$
.
$k \in \{3,4\}$
.
Remark 1.12. As mentioned in Remark 1.6, the assumption
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $n-k \geq 3$
asserts that the acting group underlying the problem is semisimple. There are instances where one could overcome this obstacle: Khayutin [Reference KhayutinKha21] proved equidistribution of grids when
$n-k \geq 3$
asserts that the acting group underlying the problem is semisimple. There are instances where one could overcome this obstacle: Khayutin [Reference KhayutinKha21] proved equidistribution of grids when
![]() $(k,n) = (1,3)$
, as conjectured in [Reference Aka, Einsiedler and ShapiraAES16a], using techniques from geometric invariant theory.
$(k,n) = (1,3)$
, as conjectured in [Reference Aka, Einsiedler and ShapiraAES16a], using techniques from geometric invariant theory.
1.2 Further refinements and questions
For an integral quadratic form q in k variables, a primitive representation of q by Q is a
![]() $\mathbb {Z}$
-linear map
$\mathbb {Z}$
-linear map
![]() $\iota : \mathbb {Z}^k \to \mathbb {Z}^n$
such that
$\iota : \mathbb {Z}^k \to \mathbb {Z}^n$
such that
![]() $Q(\iota (v)) = q(v)$
for all
$Q(\iota (v)) = q(v)$
for all
![]() $v \in \mathbb {Z}^k$
and such that
$v \in \mathbb {Z}^k$
and such that
![]() $\mathbb {Q}\iota (\mathbb {Z}^k) \cap \mathbb {Q}^n = \iota (\mathbb {Z}^k)$
. One can identify primitive representations of q with subspaces
$\mathbb {Q}\iota (\mathbb {Z}^k) \cap \mathbb {Q}^n = \iota (\mathbb {Z}^k)$
. One can identify primitive representations of q with subspaces
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
such that
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
such that
![]() $Q|_{L(\mathbb {Z})}$
is equivalent to q. Given this definition, one could ask about the distribution of the pairs
$Q|_{L(\mathbb {Z})}$
is equivalent to q. Given this definition, one could ask about the distribution of the pairs
inside
![]() $\mathrm {Gr}_{n,k}(\mathbb {R})\times \mathcal {S}_{n-k}$
when
$\mathrm {Gr}_{n,k}(\mathbb {R})\times \mathcal {S}_{n-k}$
when
![]() $\mathrm {disc}(q) \to \infty $
. The condition
$\mathrm {disc}(q) \to \infty $
. The condition
![]() $\mathrm {disc}(q) \to \infty $
here is not sufficient; for example, when q represents
$\mathrm {disc}(q) \to \infty $
here is not sufficient; for example, when q represents
![]() $1$
and Q represents
$1$
and Q represents
![]() $1$
only on, say,
$1$
only on, say,
![]() $\pm v \in \mathbb {Z}^n$
, then any primitive representation of q by Q must contain
$\pm v \in \mathbb {Z}^n$
, then any primitive representation of q by Q must contain
![]() $\pm v$
. However, the subspaces in
$\pm v$
. However, the subspaces in
![]() $\mathrm {Gr}_{n,k}(\mathbb {R})$
containing
$\mathrm {Gr}_{n,k}(\mathbb {R})$
containing
![]() $\pm v$
form a Zariski closed subset. Assuming that the minimal value represented by q goes to infinity, the above question is very strongly related to results of Ellenberg and Venkatesh [Reference Ellenberg and VenkateshEV08], as are indeed our techniques in this article. In principle, these techniques should apply to show that, under congruence conditions as in Theorems 1.4 and 1.11, the pairs in (1.2) are equidistributed when
$\pm v$
form a Zariski closed subset. Assuming that the minimal value represented by q goes to infinity, the above question is very strongly related to results of Ellenberg and Venkatesh [Reference Ellenberg and VenkateshEV08], as are indeed our techniques in this article. In principle, these techniques should apply to show that, under congruence conditions as in Theorems 1.4 and 1.11, the pairs in (1.2) are equidistributed when
![]() $q_i$
is a sequence of quadratic forms primitively representable by Q whose minimal values tend to infinity.
$q_i$
is a sequence of quadratic forms primitively representable by Q whose minimal values tend to infinity.
As alluded to in Remark 1.12, it would be interesting to know whether Khayutin’s technique applies to show the analogue of Theorem 1.11 when, say,
![]() $(k,n) = (2,5),(2,4)$
. The two cases are from quite different dynamical perspectives, as noted in Remark 1.6.
$(k,n) = (2,5),(2,4)$
. The two cases are from quite different dynamical perspectives, as noted in Remark 1.6.
Furthermore, we note that this paper has various clear directions of possible generalization. Most notably, this paper can be extended to indefinite forms. Let Q be an indefinite integral quadratic form on
![]() $\mathbb {Q}^n$
of signature
$\mathbb {Q}^n$
of signature
![]() $(r,s)$
. Here, we observe that
$(r,s)$
. Here, we observe that
![]() $\mathrm {SO}_Q(\mathbb {R})$
does not act transitively on
$\mathrm {SO}_Q(\mathbb {R})$
does not act transitively on
![]() $\mathrm {Gr}_{n,k}(\mathbb {R})$
. Indeed, the degenerate subspaces form a Zariski closed subset (the equation being
$\mathrm {Gr}_{n,k}(\mathbb {R})$
. Indeed, the degenerate subspaces form a Zariski closed subset (the equation being
![]() $\mathrm {disc}(Q|_L) = 0$
). The complement is a disjoint union of finitely many open sets on which
$\mathrm {disc}(Q|_L) = 0$
). The complement is a disjoint union of finitely many open sets on which
![]() $\mathrm {SO}_Q(\mathbb {R})$
acts transitively; for each tuple
$\mathrm {SO}_Q(\mathbb {R})$
acts transitively; for each tuple
![]() $(r',s')$
with
$(r',s')$
with
![]() $r'+s'= k$
and
$r'+s'= k$
and
![]() $r' \leq r,\ s' \leq s$
, such an open set is given by the subspaces L for which
$r' \leq r,\ s' \leq s$
, such an open set is given by the subspaces L for which
![]() $Q|_L$
has signature
$Q|_L$
has signature
![]() $(r',s')$
. The analogue of the above conjectures and theorems can then be formulated by replacing
$(r',s')$
. The analogue of the above conjectures and theorems can then be formulated by replacing
![]() $\mathrm {Gr}_{n,k}(\mathbb {R})$
with one of these open sets. The proofs generalize without major difficulties to this case; we refrain from doing so here for simplicity of the exposition. Other directions of generalization include the number field case, which is not addressed in any of the works prior to this article and is hence interesting in other dimensions as well.
$\mathrm {Gr}_{n,k}(\mathbb {R})$
with one of these open sets. The proofs generalize without major difficulties to this case; we refrain from doing so here for simplicity of the exposition. Other directions of generalization include the number field case, which is not addressed in any of the works prior to this article and is hence interesting in other dimensions as well.
1.3 Organization of the paper
This article consists of two parts. In Part
![]() $1$
—the ‘dynamical’ part—we establish the necessary results concerning equidistribution of certain adelic orbits. It is structured as follows.
$1$
—the ‘dynamical’ part—we establish the necessary results concerning equidistribution of certain adelic orbits. It is structured as follows.
-
• In §2.1, we prove various results concerning stabilizer subgroups of subspaces.
-
• In §3, we prove the homogeneous analogue of Theorem 1.11. The key ingredient of our proof is an S-arithmetic extension of a theorem of Mozes and Shah [Reference Mozes and ShahMS95] that was proved by Gorodonik and Oh [Reference Gorodnik and OhGO11]. The arguments used in this section only work when the dimension and codimension (that is, k and
 $n-k$
) are at least three.
$n-k$
) are at least three. -
• In §4, we prove the homogeneous analogue of Theorem 1.4 for two-dimensional subspaces (i.e. for
 $k=2$
). Contrary to the case of dimension and codimension at least three, the groups whose dynamics we use are not semisimple (see Remark 1.6). In particular, the theorem of Gorodonik and Oh [Reference Gorodnik and OhGO11] is not sufficient and more subtle arguments, relying on Duke’s theorem [Reference DukeDuk88] and the trick mentioned in Remark 1.7, are required.
$k=2$
). Contrary to the case of dimension and codimension at least three, the groups whose dynamics we use are not semisimple (see Remark 1.6). In particular, the theorem of Gorodonik and Oh [Reference Gorodnik and OhGO11] is not sufficient and more subtle arguments, relying on Duke’s theorem [Reference DukeDuk88] and the trick mentioned in Remark 1.7, are required.
In Part
![]() $2$
, we deduce Theorems 1.4 and 1.11 from the homogeneous dynamics results proved in §3 (
$2$
, we deduce Theorems 1.4 and 1.11 from the homogeneous dynamics results proved in §3 (
![]() $k>2$
) and §4 (
$k>2$
) and §4 (
![]() $k=2$
) of the first part. More precisely, it is structured as follows.
$k=2$
) of the first part. More precisely, it is structured as follows.
-
• In §5.1, we prove that the discriminant of the orthogonal complement of a subspace is equal to the discriminant of the subspace up to an essentially negligible factor.
-
• In §6, we study the moduli space of base extensions and show that it surjects onto
 $\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
. From this, we prove that a slight strengthening of Theorem 1.11 implies Theorem 1.4. In these considerations, it is useful to include subspaces together with an orientation.
$\mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
. From this, we prove that a slight strengthening of Theorem 1.11 implies Theorem 1.4. In these considerations, it is useful to include subspaces together with an orientation. -
• In §7, we finally establish Theorems 1.4 and 1.11. The technique here is by now standard—we interpret the sets in Theorem 1.11 as projections of the adelic orbits in Part
 $1$
(or a slight adaptation thereof).
$1$
(or a slight adaptation thereof).
In the appendix, we establish various complementary facts.
-
• In Appendix A, we discuss non-emptiness conditions for the set
 $\mathcal {H}^{n,k}_Q(D)$
when the quadratic form Q is the sum of squares. In particular, we prove that
$\mathcal {H}^{n,k}_Q(D)$
when the quadratic form Q is the sum of squares. In particular, we prove that
 $\mathcal {H}^{n,k}_Q(D) \neq \emptyset $
for all
$\mathcal {H}^{n,k}_Q(D) \neq \emptyset $
for all
 $n \geq 5$
. The techniques here are completely elementary and we do not provide any counting results.
$n \geq 5$
. The techniques here are completely elementary and we do not provide any counting results. -
• In Appendix B, we prove various facts complementing the discussion in §5.1. For example, we prove that if
 $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
is a subspace where
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
is a subspace where
 $k < n-k$
, then the quadratic form on the orthogonal complement
$k < n-k$
, then the quadratic form on the orthogonal complement
 $Q|_{L^\perp (\mathbb {Z})}$
is primitive up to negligible factors.
$Q|_{L^\perp (\mathbb {Z})}$
is primitive up to negligible factors.
1.4 Notation
Let
![]() $V_{\mathbb {Q}}$
be the set of places of
$V_{\mathbb {Q}}$
be the set of places of
![]() $\mathbb {Q}$
and denote by
$\mathbb {Q}$
and denote by
![]() $\mathbb {Q}_v$
for any
$\mathbb {Q}_v$
for any
![]() $v \in V_{\mathbb {Q}}$
the completion at v. Given a subset
$v \in V_{\mathbb {Q}}$
the completion at v. Given a subset
![]() $S \subset V_{\mathbb {Q}}$
, we define the ring
$S \subset V_{\mathbb {Q}}$
, we define the ring
![]() $\mathbb {Q}_S$
to be the restricted direct product of
$\mathbb {Q}_S$
to be the restricted direct product of
![]() $\mathbb {Q}_p$
for
$\mathbb {Q}_p$
for
![]() $p \in S$
with respect to the subgroups
$p \in S$
with respect to the subgroups
![]() $\mathbb {Z}_p$
for
$\mathbb {Z}_p$
for
![]() $p \in S\setminus \{\infty \}$
. Moreover, we set
$p \in S\setminus \{\infty \}$
. Moreover, we set
![]() $\mathbb {Z}^S := \mathbb {Z}[{1}/{p} : p \in S\setminus \{\infty \} \}$
. When
$\mathbb {Z}^S := \mathbb {Z}[{1}/{p} : p \in S\setminus \{\infty \} \}$
. When
![]() $S = V_{\mathbb {Q}}$
, we denote
$S = V_{\mathbb {Q}}$
, we denote
![]() $\mathbb {Q}_S$
by
$\mathbb {Q}_S$
by
![]() $\mathbb {A}$
and call it the ring of adeles. When, instead,
$\mathbb {A}$
and call it the ring of adeles. When, instead,
![]() $S= V_{\mathbb {Q}} \setminus \{\infty \}$
, we denote
$S= V_{\mathbb {Q}} \setminus \{\infty \}$
, we denote
![]() $\mathbb {Q}_S$
by
$\mathbb {Q}_S$
by
![]() $\mathbb {A}_f$
and call it the ring of finite adeles. Finally, we let
$\mathbb {A}_f$
and call it the ring of finite adeles. Finally, we let
![]() $\hat {\mathbb {Z}} = \prod _{p \in V_{\mathbb {Q}} \setminus \{\infty \}} \mathbb {Z}_p$
.
$\hat {\mathbb {Z}} = \prod _{p \in V_{\mathbb {Q}} \setminus \{\infty \}} \mathbb {Z}_p$
.
Let
![]() $\mathbf {G}< \mathrm {SL}_N$
be a connected algebraic group defined over
$\mathbf {G}< \mathrm {SL}_N$
be a connected algebraic group defined over
![]() $\mathbb {Q}$
. We identify
$\mathbb {Q}$
. We identify
![]() $\mathbf {G}(\mathbb {Z}^S) = \mathbf {G}(\mathbb {Q}_S) \cap \mathrm {SL}_N(\mathbb {Z}^S)$
with its diagonally embedded copy in
$\mathbf {G}(\mathbb {Z}^S) = \mathbf {G}(\mathbb {Q}_S) \cap \mathrm {SL}_N(\mathbb {Z}^S)$
with its diagonally embedded copy in
![]() $\mathbf {G}(\mathbb {Q}_S)$
. If
$\mathbf {G}(\mathbb {Q}_S)$
. If
![]() $\mathbf {G}$
has no non-trivial
$\mathbf {G}$
has no non-trivial
![]() $\mathbb {Q}$
-characters (for example, when the radical of
$\mathbb {Q}$
-characters (for example, when the radical of
![]() $\mathbf {G}$
is unipotent), the Borel–Harish–Chandra theorem (see [Reference Platonov and RapinchukPR94, Theorem 5.5]) yields that
$\mathbf {G}$
is unipotent), the Borel–Harish–Chandra theorem (see [Reference Platonov and RapinchukPR94, Theorem 5.5]) yields that
![]() $\mathbf {G}(\mathbb {Z}^S)$
is a lattice in
$\mathbf {G}(\mathbb {Z}^S)$
is a lattice in
![]() $\mathbf {G}(\mathbb {Q}_S)$
whenever
$\mathbf {G}(\mathbb {Q}_S)$
whenever
![]() $\infty \in S$
. In particular, the quotient
$\infty \in S$
. In particular, the quotient
![]() $\mathbf {G}(\mathbb {Q}_S)/\mathbf {G}(\mathbb {Z}^S)$
is a finite volume homogeneous space. For
$\mathbf {G}(\mathbb {Q}_S)/\mathbf {G}(\mathbb {Z}^S)$
is a finite volume homogeneous space. For
![]() $g \in \mathbf {G}(\mathbb {Q}_S)$
and
$g \in \mathbf {G}(\mathbb {Q}_S)$
and
![]() $v \in S$
,
$v \in S$
,
![]() $g_v$
denotes the v-adic component of g.
$g_v$
denotes the v-adic component of g.
Whenever
![]() $\mathbf {G}$
is semisimple, we denote by
$\mathbf {G}$
is semisimple, we denote by
![]() $\mathbf {G}(\mathbb {Q}_S)^+$
the image of the simply connected cover in
$\mathbf {G}(\mathbb {Q}_S)^+$
the image of the simply connected cover in
![]() $\mathbf {G}(\mathbb {Q}_S)$
(somewhat informally, this can be thought of as the part of
$\mathbf {G}(\mathbb {Q}_S)$
(somewhat informally, this can be thought of as the part of
![]() $\mathbf {G}(\mathbb {Q}_S)$
that is generated by unipotents).
$\mathbf {G}(\mathbb {Q}_S)$
that is generated by unipotents).
1.4.1 Quadratic forms
Throughout this article,
![]() $(V,Q)$
is a fixed non-degenerate quadratic space over
$(V,Q)$
is a fixed non-degenerate quadratic space over
![]() $\mathbb {Q}$
of dimension n. The induced bilinear form is denoted by
$\mathbb {Q}$
of dimension n. The induced bilinear form is denoted by
![]() $\langle \cdot ,\cdot \rangle _Q$
. We assume throughout that
$\langle \cdot ,\cdot \rangle _Q$
. We assume throughout that
![]() $(V,Q)$
is positive definite. We also identify V with
$(V,Q)$
is positive definite. We also identify V with
![]() $\mathbb {Q}^n$
and suppose that
$\mathbb {Q}^n$
and suppose that
![]() $\langle \cdot ,\cdot \rangle _Q$
takes integral values on
$\langle \cdot ,\cdot \rangle _Q$
takes integral values on
![]() $\mathbb {Z}^n \times \mathbb {Z}^n$
, in which case we say that Q is integral. Equivalently, the matrix representation
$\mathbb {Z}^n \times \mathbb {Z}^n$
, in which case we say that Q is integral. Equivalently, the matrix representation
![]() $M_Q$
in the standard basis of
$M_Q$
in the standard basis of
![]() $\mathbb {Z}^n$
has integral entries.
$\mathbb {Z}^n$
has integral entries.
We denote by
![]() $\mathrm {O}_Q$
(respectively,
$\mathrm {O}_Q$
(respectively,
![]() $\mathrm {SO}_Q$
) the orthogonal (respectively, special orthogonal) group for Q. Recall that
$\mathrm {SO}_Q$
) the orthogonal (respectively, special orthogonal) group for Q. Recall that
![]() $\mathrm {SO}_Q$
is abelian if
$\mathrm {SO}_Q$
is abelian if
![]() $\dim (V) = 2$
and semisimple otherwise. We denote by
$\dim (V) = 2$
and semisimple otherwise. We denote by
![]() $\mathrm {Spin}_Q$
the spin group for Q, which is the simply connected cover of
$\mathrm {Spin}_Q$
the spin group for Q, which is the simply connected cover of
![]() $\mathrm {SO}_Q$
if
$\mathrm {SO}_Q$
if
![]() $\dim (V)>2$
. Explicitly, the spin group may be constructed from the Clifford algebra of Q. We remark that this article contains certain technicalities that will use the Clifford algebra—we refer to [Reference KnusKnu88] for a thorough discussion. The spin group comes with an isogeny of
$\dim (V)>2$
. Explicitly, the spin group may be constructed from the Clifford algebra of Q. We remark that this article contains certain technicalities that will use the Clifford algebra—we refer to [Reference KnusKnu88] for a thorough discussion. The spin group comes with an isogeny of
![]() $\mathbb {Q}$
-groups
$\mathbb {Q}$
-groups
![]() $\rho _Q: \mathrm {Spin}_Q \to \mathrm {SO}_Q$
which satisfies that, for any field K of characteristic zero, we have an exact sequence (cf. [Reference KnusKnu88, p. 64])
$\rho _Q: \mathrm {Spin}_Q \to \mathrm {SO}_Q$
which satisfies that, for any field K of characteristic zero, we have an exact sequence (cf. [Reference KnusKnu88, p. 64])
where the second homomorphism is given by the spinor norm. The isogeny
![]() $\rho _Q$
induces an integral structure on
$\rho _Q$
induces an integral structure on
![]() $\mathrm {Spin}_Q$
. For example,
$\mathrm {Spin}_Q$
. For example,
![]() $\mathrm {Spin}_Q(\mathbb {Z})$
consists of elements
$\mathrm {Spin}_Q(\mathbb {Z})$
consists of elements
![]() $g \in \mathrm {Spin}_Q(\mathbb {Q})$
for which
$g \in \mathrm {Spin}_Q(\mathbb {Q})$
for which
![]() $\rho _Q(g) \in \mathrm {SO}_Q(\mathbb {Z})$
. To simplify notation, we will write
$\rho _Q(g) \in \mathrm {SO}_Q(\mathbb {Z})$
. To simplify notation, we will write
![]() $g.v$
for the action of
$g.v$
for the action of
![]() $\mathrm {Spin}_Q$
on a vector in n-dimensional linear space. Here, the action is naturally induced by the isogeny
$\mathrm {Spin}_Q$
on a vector in n-dimensional linear space. Here, the action is naturally induced by the isogeny
![]() $\rho _Q$
(and the standard representation of
$\rho _Q$
(and the standard representation of
![]() $\mathrm {SO}_Q$
).
$\mathrm {SO}_Q$
).
Furthermore, we let
![]() $\mathrm {Gr}_{n,k}$
denote the Grassmannian of k-dimensional subspaces of V. Note that this is a homogeneous variety for
$\mathrm {Gr}_{n,k}$
denote the Grassmannian of k-dimensional subspaces of V. Note that this is a homogeneous variety for
![]() $\mathrm {SO}_Q$
and (through the isogeny
$\mathrm {SO}_Q$
and (through the isogeny
![]() $\rho _Q$
) also for
$\rho _Q$
) also for
![]() $\mathrm {Spin}_Q$
. If we assume that Q is positive definite (as we always do), the action of
$\mathrm {Spin}_Q$
. If we assume that Q is positive definite (as we always do), the action of
![]() $\mathrm {SO}_Q(\mathbb {R})$
on
$\mathrm {SO}_Q(\mathbb {R})$
on
![]() $\mathrm {Gr}_{n,k}(\mathbb {R})$
is transitive. Furthermore, in this case, the spinor norm on
$\mathrm {Gr}_{n,k}(\mathbb {R})$
is transitive. Furthermore, in this case, the spinor norm on
![]() $\mathrm {SO}_Q(\mathbb {R})$
takes only positive values so that
$\mathrm {SO}_Q(\mathbb {R})$
takes only positive values so that
![]() $\mathrm {Spin}_Q(\mathbb {R})$
surjects onto
$\mathrm {Spin}_Q(\mathbb {R})$
surjects onto
![]() $\mathrm {SO}_Q(\mathbb {R})$
and, in particular, also acts transitively.
$\mathrm {SO}_Q(\mathbb {R})$
and, in particular, also acts transitively.
We denote the standard positive definite form (i.e. the sum of n squares) by
![]() $Q_0$
and write
$Q_0$
and write
![]() $\mathrm {SO}_n$
for its special orthogonal group. As
$\mathrm {SO}_n$
for its special orthogonal group. As
![]() $Q_0$
and Q have the same signature, there exists
$Q_0$
and Q have the same signature, there exists
![]() $\eta _Q \in \mathrm {GL}_n(\mathbb {R})$
with
$\eta _Q \in \mathrm {GL}_n(\mathbb {R})$
with
![]() $\det (\eta _Q)> 0$
such that
$\det (\eta _Q)> 0$
such that
![]() $\eta _Q^t \eta _Q = M_Q$
or, equivalently,
$\eta _Q^t \eta _Q = M_Q$
or, equivalently,
holds for all
![]() $x \in \mathbb {R}^n$
(similarly for the induced bilinear forms). In particular,
$x \in \mathbb {R}^n$
(similarly for the induced bilinear forms). In particular,
![]() $\eta _Q$
maps pairs of vectors in V that are orthogonal with respect to Q onto pairs of vectors that are orthogonal with respect to
$\eta _Q$
maps pairs of vectors in V that are orthogonal with respect to Q onto pairs of vectors that are orthogonal with respect to
![]() $Q_0$
. Also,
$Q_0$
. Also,
![]() $\eta _Q^{-1} \mathrm {SO}_n(\mathbb {R}) \eta _Q = \mathrm {SO}_Q(\mathbb {R})$
.
$\eta _Q^{-1} \mathrm {SO}_n(\mathbb {R}) \eta _Q = \mathrm {SO}_Q(\mathbb {R})$
.
1.4.2 Quadratic forms on sublattices and discriminants
For any finitely generated
![]() $\mathbb {Z}$
-lattice
$\mathbb {Z}$
-lattice
![]() $\Gamma < \mathbb {Q}^n$
(of arbitrary rank), the restriction of Q to
$\Gamma < \mathbb {Q}^n$
(of arbitrary rank), the restriction of Q to
![]() $\Gamma $
induces a quadratic form. We denote by
$\Gamma $
induces a quadratic form. We denote by
![]() $q_\Gamma $
the representation of this form in a choice of basis of
$q_\Gamma $
the representation of this form in a choice of basis of
![]() $\Gamma $
. Hence,
$\Gamma $
. Hence,
![]() $q_\Gamma $
is well defined up to equivalence (and not proper equivalence) of quadratic forms (i.e. up to change of basis).
$q_\Gamma $
is well defined up to equivalence (and not proper equivalence) of quadratic forms (i.e. up to change of basis).
If
![]() $\Gamma < \mathbb {Z}^n$
,
$\Gamma < \mathbb {Z}^n$
,
![]() $q_\Gamma $
is an integral quadratic form and we denote by
$q_\Gamma $
is an integral quadratic form and we denote by
![]() $\gcd (q_\Gamma )$
the greatest common divisor of its coefficients (which is independent of the choice of basis). Note that
$\gcd (q_\Gamma )$
the greatest common divisor of its coefficients (which is independent of the choice of basis). Note that
![]() $\gcd (q_\Gamma )$
is sometimes also referred to as the content of
$\gcd (q_\Gamma )$
is sometimes also referred to as the content of
![]() $q_\Gamma $
. We write
$q_\Gamma $
. We write
![]() $\tilde {q}_\Gamma = {1}/{\gcd (q_\Gamma )}q_\Gamma $
for the primitive multiple of
$\tilde {q}_\Gamma = {1}/{\gcd (q_\Gamma )}q_\Gamma $
for the primitive multiple of
![]() $q_\Gamma $
. If
$q_\Gamma $
. If
![]() $L \subset \mathbb {Q}^n$
is a subspace, we sometimes write
$L \subset \mathbb {Q}^n$
is a subspace, we sometimes write
![]() $q_L$
instead of
$q_L$
instead of
![]() $q_{L(\mathbb {Z})}$
for simplicity.
$q_{L(\mathbb {Z})}$
for simplicity.
The discriminant
![]() $\mathrm {disc}_Q(\Gamma )$
of a finitely generated
$\mathrm {disc}_Q(\Gamma )$
of a finitely generated
![]() $\mathbb {Z}$
-lattice
$\mathbb {Z}$
-lattice
![]() $\Gamma < \mathbb {Q}^n$
is the discriminant of
$\Gamma < \mathbb {Q}^n$
is the discriminant of
![]() $q_\Gamma $
. As at the beginning of the introduction, we write
$q_\Gamma $
. As at the beginning of the introduction, we write
![]() $\mathrm {disc}_Q(L)$
instead of
$\mathrm {disc}_Q(L)$
instead of
![]() $\mathrm {disc}_Q(L(\mathbb {Z}))$
for any subspace
$\mathrm {disc}_Q(L(\mathbb {Z}))$
for any subspace
![]() $L \subset \mathbb {Q}^n$
. Given a prime p, we also define
$L \subset \mathbb {Q}^n$
. Given a prime p, we also define
where
![]() $L(\mathbb {Z}_p) = L(\mathbb {Q}_p)\cap \mathbb {Z}_p^n$
. We have the following useful identity,
$L(\mathbb {Z}_p) = L(\mathbb {Q}_p)\cap \mathbb {Z}_p^n$
. We have the following useful identity,
where the product is taken over all primes p and
![]() $\nu _p$
denotes the standard p-adic valuation. Note that only primes dividing the discriminant contribute non-trivially.
$\nu _p$
denotes the standard p-adic valuation. Note that only primes dividing the discriminant contribute non-trivially.
1.4.3 Choice of a reference subspace
We fix an integer
![]() $k\leq n$
for which we always assume that one of the following holds:
$k\leq n$
for which we always assume that one of the following holds:
-
•
 $k \geq 3$
and
$k \geq 3$
and
 $n-k \geq 3$
;
$n-k \geq 3$
; -
•
 $k = 2$
and
$k = 2$
and
 $n-k \geq 3$
; or
$n-k \geq 3$
; or -
•
 $k \geq 3$
and
$k \geq 3$
and
 $n-k=2$
.
$n-k=2$
.
Let
![]() $L_0 \subset V$
be given by
$L_0 \subset V$
be given by
We adapt the choice of
![]() $\eta _Q$
to this reference subspace
$\eta _Q$
to this reference subspace
![]() $L_0$
and suppose that the first k column vectors in
$L_0$
and suppose that the first k column vectors in
![]() $\eta _Q^{-1}$
are an orthonormal basis of
$\eta _Q^{-1}$
are an orthonormal basis of
![]() $L_0$
. This choice asserts that
$L_0$
. This choice asserts that
![]() $\eta _Q$
maps
$\eta _Q$
maps
![]() $L_0(\mathbb {R})$
to
$L_0(\mathbb {R})$
to
![]() $L_0(\mathbb {R})$
and hence
$L_0(\mathbb {R})$
and hence
![]() $L_0^\perp (\mathbb {R})$
to
$L_0^\perp (\mathbb {R})$
to
![]() $\{(0,\ldots ,0)\} \times \mathbb {R}^{n-k}$
.
$\{(0,\ldots ,0)\} \times \mathbb {R}^{n-k}$
.
1.4.4 Ambient groups
The following subgroups of
![]() $\mathrm {SL}_n$
will be useful throughout this work: that is,
$\mathrm {SL}_n$
will be useful throughout this work: that is,
 $$ \begin{align*} \mathbf{P}_{n,k} &= \bigg\{\! \begin{pmatrix} A & B \\ 0 & D \end{pmatrix} \in \mathrm{SL}_n : \det(A) = \det(D) = 1 \bigg\},\\ \mathbf{D}_{n,k} &= \bigg\{\! \begin{pmatrix} A & 0 \\ 0 & D \end{pmatrix} \in \mathrm{SL}_n : \det(A) = \det(D) = 1 \bigg\}, \end{align*} $$
$$ \begin{align*} \mathbf{P}_{n,k} &= \bigg\{\! \begin{pmatrix} A & B \\ 0 & D \end{pmatrix} \in \mathrm{SL}_n : \det(A) = \det(D) = 1 \bigg\},\\ \mathbf{D}_{n,k} &= \bigg\{\! \begin{pmatrix} A & 0 \\ 0 & D \end{pmatrix} \in \mathrm{SL}_n : \det(A) = \det(D) = 1 \bigg\}, \end{align*} $$
where A is a
![]() $k \times k$
-matrix, D is an
$k \times k$
-matrix, D is an
![]() $(n-k)\times (n-k)$
-matrix and B is a
$(n-k)\times (n-k)$
-matrix and B is a
![]() $k \times (n-k)$
-matrix. We denote by
$k \times (n-k)$
-matrix. We denote by
![]() $\pi _1$
(respectively,
$\pi _1$
(respectively,
![]() $\pi _2$
) the projection of
$\pi _2$
) the projection of
![]() $\mathbf {P}_{n,k}$
onto the upper-left (respectively, bottom-right) block. We also define the group
$\mathbf {P}_{n,k}$
onto the upper-left (respectively, bottom-right) block. We also define the group
By
![]() $\bar {\mathbf {G}}$
, we denote the Levi subgroup of
$\bar {\mathbf {G}}$
, we denote the Levi subgroup of
![]() $\mathbf {G}$
with
$\mathbf {G}$
with
![]() $B =0$
: that is,
$B =0$
: that is,
Remark 1.13. With regard to the aforementioned groups we will need two well-known facts. First,
![]() $\mathbf {D}_{n,k}$
is a maximal subgroup of
$\mathbf {D}_{n,k}$
is a maximal subgroup of
![]() $\mathbf {P}_{n,k}$
(which means that there is no connected
$\mathbf {P}_{n,k}$
(which means that there is no connected
![]() $\mathbb {Q}$
-group
$\mathbb {Q}$
-group
![]() $\mathbf {M}$
with
$\mathbf {M}$
with
![]() $\mathbf {D}_{n,k} \subsetneq \mathbf {M} \subsetneq \mathbf {P}_{n,k}$
) (see, for example, [Reference Aka, Einsiedler, Luethi, Michel and WieserAELM20, Proposition 3.2]). Second, for any quadratic form q in d variables,
$\mathbf {D}_{n,k} \subsetneq \mathbf {M} \subsetneq \mathbf {P}_{n,k}$
) (see, for example, [Reference Aka, Einsiedler, Luethi, Michel and WieserAELM20, Proposition 3.2]). Second, for any quadratic form q in d variables,
![]() $\mathrm {SO}_q$
is maximal in
$\mathrm {SO}_q$
is maximal in
![]() $\mathrm {SL}_d$
(see, for example, [Reference Liebeck and SeitzLS98] for a modern discussion of maximal subgroups of the classical groups).
$\mathrm {SL}_d$
(see, for example, [Reference Liebeck and SeitzLS98] for a modern discussion of maximal subgroups of the classical groups).
1.4.5 Landau notation
In classical Landau notation, we write
![]() $f \asymp g$
for two positive functions if there exist constants
$f \asymp g$
for two positive functions if there exist constants
![]() $c,C>0$
with
$c,C>0$
with
![]() $cf \leq g\leq Cf$
. If the constants depend on another quantity a, we sometimes write
$cf \leq g\leq Cf$
. If the constants depend on another quantity a, we sometimes write
![]() $f \asymp _a g$
to emphasize the dependence.
$f \asymp _a g$
to emphasize the dependence.
2 Part 1: Homogeneous results
For an overview of the contents of this part, we refer the reader to §1.3.
2.1 Stabilizer groups
Recall that, throughout the article, Q is a positive definite integral quadratic form on
![]() $V = \mathbb {Q}^n$
. In particular, any subspace of
$V = \mathbb {Q}^n$
. In particular, any subspace of
![]() $\mathbb {Q}^n$
is non-degenerate with respect to Q.
$\mathbb {Q}^n$
is non-degenerate with respect to Q.
2.1.1 Stabilizers of subspaces
For any subspace
![]() $L \subset \overline {\mathbb {Q}}^n$
, we define the following groups.
$L \subset \overline {\mathbb {Q}}^n$
, we define the following groups.
-
•
 $\mathbf {H}_L<\mathrm {Spin}_Q$
is the identity component of the stabilizer group of L in
$\mathbf {H}_L<\mathrm {Spin}_Q$
is the identity component of the stabilizer group of L in
 $\mathrm {Spin}_Q$
for the action of
$\mathrm {Spin}_Q$
for the action of
 $\mathrm {Spin}_Q$
on
$\mathrm {Spin}_Q$
on
 $\mathrm {Gr}_{n,k}$
.
$\mathrm {Gr}_{n,k}$
. -
•
 $\mathbf {H}^{\prime }_L<\mathrm {SO}_Q$
is the identity component of the stabilizer group of L in
$\mathbf {H}^{\prime }_L<\mathrm {SO}_Q$
is the identity component of the stabilizer group of L in
 $\mathrm {SO}_Q$
for the action of
$\mathrm {SO}_Q$
for the action of
 $\mathrm {SO}_Q$
on
$\mathrm {SO}_Q$
on
 $\mathrm {Gr}_{n,k}$
.
$\mathrm {Gr}_{n,k}$
.
Note that we have an isogeny
![]() $\mathbf {H}_L \to \mathbf {H}^{\prime }_L$
. Furthermore, the restriction to L (respectively,
$\mathbf {H}_L \to \mathbf {H}^{\prime }_L$
. Furthermore, the restriction to L (respectively,
![]() $L^\perp $
) yields an isomorphism of
$L^\perp $
) yields an isomorphism of
![]() $\mathbb {Q}$
-groups
$\mathbb {Q}$
-groups
To see this, one needs to check that the image does indeed consist of special orthogonal transformations. This follows from the fact that the determinant of the restrictions is a morphism with finite image and hence its kernel must be everything by connectedness. In particular, we have the following cases.
-
• If
 $k \geq 3$
and
$k \geq 3$
and
 $n-k \geq 3$
,
$n-k \geq 3$
,
 $\mathbf {H}^{\prime }_L$
(and hence also
$\mathbf {H}^{\prime }_L$
(and hence also
 $\mathbf {H}_L$
) is semisimple.
$\mathbf {H}_L$
) is semisimple. -
• If
 $k = 2$
and
$k = 2$
and
 $n-k \geq 3$
(or
$n-k \geq 3$
(or
 $k\geq 3$
and
$k\geq 3$
and
 $n-k =2$
),
$n-k =2$
),
 $\mathbf {H}^{\prime }_L$
is reductive.
$\mathbf {H}^{\prime }_L$
is reductive. -
• If
 $k=2$
and
$k=2$
and
 $n-k=2$
(which is not a case this paper covers),
$n-k=2$
(which is not a case this paper covers),
 $\mathbf {H}^{\prime }_L$
is abelian.
$\mathbf {H}^{\prime }_L$
is abelian.
Remark 2.1. (Special Clifford groups and (2.1))
Although it might seem appealing to suspect that
![]() $\mathbf {H}_L$
is simply connected, this is actually false. The following vague and lengthy explanation is not needed in what follows. Denote by
$\mathbf {H}_L$
is simply connected, this is actually false. The following vague and lengthy explanation is not needed in what follows. Denote by
![]() $\mathbf {M}$
the special Clifford group of Q and similarly by
$\mathbf {M}$
the special Clifford group of Q and similarly by
![]() $\mathbf {M}_1$
(respectively
$\mathbf {M}_1$
(respectively
![]() $\mathbf {M}_2$
) the special Clifford groups of
$\mathbf {M}_2$
) the special Clifford groups of
![]() $Q|_L$
(respectively,
$Q|_L$
(respectively,
![]() $Q|_{L^\perp }$
) for the duration of this remark—cf. [Reference KnusKnu88]. These are reductive groups whose center is a one-dimensional
$Q|_{L^\perp }$
) for the duration of this remark—cf. [Reference KnusKnu88]. These are reductive groups whose center is a one-dimensional
![]() $\mathbb {Q}$
-isotropic torus. We identify
$\mathbb {Q}$
-isotropic torus. We identify
![]() $\mathbf {M}_1,\mathbf {M}_2$
as subgroups of
$\mathbf {M}_1,\mathbf {M}_2$
as subgroups of
![]() $\mathbf {M}$
and write
$\mathbf {M}$
and write
![]() $\mathbf {C}$
for the center of
$\mathbf {C}$
for the center of
![]() $\mathbf {M}$
which is, in fact, equal to
$\mathbf {M}$
which is, in fact, equal to
![]() $\mathbf {M}_1 \cap \mathbf {M}_2$
. The natural map
$\mathbf {M}_1 \cap \mathbf {M}_2$
. The natural map
![]() $\phi : \mathbf {M}_1 \times \mathbf {M}_2 \to \mathbf {M}$
has kernel
$\phi : \mathbf {M}_1 \times \mathbf {M}_2 \to \mathbf {M}$
has kernel
![]() $\{(x,y) \in \mathbf {C}\times \mathbf {C}: xy = 1\}$
so that
$\{(x,y) \in \mathbf {C}\times \mathbf {C}: xy = 1\}$
so that
Furthermore, we have the spinor norm which is a character
![]() $\chi : \mathbf {M} \to \mathbf {G}_m$
whose kernel is the spin group. Similarly, we have spinor norms
$\chi : \mathbf {M} \to \mathbf {G}_m$
whose kernel is the spin group. Similarly, we have spinor norms
![]() $\chi _1,\chi _2$
for
$\chi _1,\chi _2$
for
![]() $\mathbf {M}_1$
(respectively,
$\mathbf {M}_1$
(respectively,
![]() $\mathbf {M}_2$
), which are simply the restrictions of
$\mathbf {M}_2$
), which are simply the restrictions of
![]() $\chi $
. The above yields that
$\chi $
. The above yields that
which is isogenous (but not isomorphic) to
![]() $\mathrm {Spin}_{Q|_L} \times \mathrm {Spin}_{Q|_{L^\perp }}$
.
$\mathrm {Spin}_{Q|_L} \times \mathrm {Spin}_{Q|_{L^\perp }}$
.
The first result that we prove states that the group
![]() $\mathbf {H}_L$
totally determines the subspace L (up to orthogonal complements). This is given more precisely in the following proposition. Recall that a non-trivial subspace
$\mathbf {H}_L$
totally determines the subspace L (up to orthogonal complements). This is given more precisely in the following proposition. Recall that a non-trivial subspace
![]() $W \subset V$
is non-degenerate if
$W \subset V$
is non-degenerate if
![]() $\mathrm {disc}(Q|_W)\neq 0$
or, equivalently, if there is no non-zero vector
$\mathrm {disc}(Q|_W)\neq 0$
or, equivalently, if there is no non-zero vector
![]() $w \in W$
so that
$w \in W$
so that
![]() $\langle w,w'\rangle = 0$
for all
$\langle w,w'\rangle = 0$
for all
![]() $w' \in W$
. This notion is stable under extension of scalars.
$w' \in W$
. This notion is stable under extension of scalars.
Proposition 2.2. Let
![]() $L_1, L_2 \leq V$
be non-degenerate subspaces. If
$L_1, L_2 \leq V$
be non-degenerate subspaces. If
![]() $\mathbf {H}_{L_1} = \mathbf {H}_{L_2}$
, then
$\mathbf {H}_{L_1} = \mathbf {H}_{L_2}$
, then
![]() $L_1 = L_2$
or
$L_1 = L_2$
or
![]() $L_1 = L_2^{\perp }$
.
$L_1 = L_2^{\perp }$
.
The proposition follows directly from the following simple lemma.
Lemma 2.3. Let
![]() $L \subset V$
be a non-degenerate subspace and let
$L \subset V$
be a non-degenerate subspace and let
![]() $W \subset V$
be a non-trivial non-degenerate subspace invariant under
$W \subset V$
be a non-trivial non-degenerate subspace invariant under
![]() $\mathbf {H}^{\prime }_L$
. Then
$\mathbf {H}^{\prime }_L$
. Then
![]() $W \in \{L,L^\perp ,V\}$
.
$W \in \{L,L^\perp ,V\}$
.
Proof. First, we observe the following: over
![]() $\bar {\mathbb {Q}}$
,
$\bar {\mathbb {Q}}$
,
![]() $\mathbf {H}^{\prime }_{L}$
acts transitively on the set of anisotropic lines in L and in
$\mathbf {H}^{\prime }_{L}$
acts transitively on the set of anisotropic lines in L and in
![]() $L^\perp $
. Indeed, by Witt’s theorem [Reference CasselsCas78, p. 20], the special orthogonal group in dimension at least two acts transitively on vectors of the same quadratic value. In any two lines, one can find vectors of the same quadratic value by taking roots.
$L^\perp $
. Indeed, by Witt’s theorem [Reference CasselsCas78, p. 20], the special orthogonal group in dimension at least two acts transitively on vectors of the same quadratic value. In any two lines, one can find vectors of the same quadratic value by taking roots.
Let
![]() $w \in W$
be anisotropic and write
$w \in W$
be anisotropic and write
![]() $w = w_1 + w_2$
for
$w = w_1 + w_2$
for
![]() $w_1 \in L$
and
$w_1 \in L$
and
![]() $w_2 \in L^\perp $
. As w is anisotropic, one of
$w_2 \in L^\perp $
. As w is anisotropic, one of
![]() $w_1$
or
$w_1$
or
![]() $w_2$
must also be anisotropic; we suppose that
$w_2$
must also be anisotropic; we suppose that
![]() $w_1$
is anisotropic, without loss of generality. Let
$w_1$
is anisotropic, without loss of generality. Let
![]() $h \in \mathbf {H}^{\prime }_{L}(\bar {\mathbb {Q}})$
be such that
$h \in \mathbf {H}^{\prime }_{L}(\bar {\mathbb {Q}})$
be such that
![]() $hw_1 \neq w_1$
and
$hw_1 \neq w_1$
and
![]() $hw_2 = w_2$
. Then
$hw_2 = w_2$
. Then
We claim that we can choose h so that u is anisotropic. Indeed, as
![]() $w_1$
is anisotropic, its orthogonal complement in L is non-degenerate (as L is non-degenerate). We can thus choose h to map
$w_1$
is anisotropic, its orthogonal complement in L is non-degenerate (as L is non-degenerate). We can thus choose h to map
![]() $w_1$
to a vector orthogonal to it by the above variant of Witt’s theorem. Then
$w_1$
to a vector orthogonal to it by the above variant of Witt’s theorem. Then
Now note that
![]() $L \cap W$
is
$L \cap W$
is
![]() $\mathbf {H}^{\prime }_L$
-invariant. By a further application of the above variant of Witt’s theorem and the fact that L is spanned by anisotropic vectors (L is non-degenerate), we obtain that
$\mathbf {H}^{\prime }_L$
-invariant. By a further application of the above variant of Witt’s theorem and the fact that L is spanned by anisotropic vectors (L is non-degenerate), we obtain that
![]() $L \cap W = L$
or, equivalently,
$L \cap W = L$
or, equivalently,
![]() $L \subset W$
. Thus, we may write
$L \subset W$
. Thus, we may write
![]() $W = L \oplus W'$
, where
$W = L \oplus W'$
, where
![]() $W'$
is an orthogonal complement to L in W and, in particular, is contained in
$W'$
is an orthogonal complement to L in W and, in particular, is contained in
![]() $L^\perp $
. The subspace
$L^\perp $
. The subspace
![]() $W'$
must be non-degenerate because W and L are, and hence it is trivial or contains anisotropic vectors. If
$W'$
must be non-degenerate because W and L are, and hence it is trivial or contains anisotropic vectors. If
![]() $W'$
is trivial, then
$W'$
is trivial, then
![]() $W = L$
and the proof is complete. Otherwise, we apply the above variant of Witt’s theorem and obtain that
$W = L$
and the proof is complete. Otherwise, we apply the above variant of Witt’s theorem and obtain that
![]() $W' = L^\perp $
and
$W' = L^\perp $
and
![]() $W = V$
.
$W = V$
.
An analogous statement holds for the relationship between quadratic forms and their special stabilizer groups.
Proposition 2.4. Let
![]() $Q_1, Q_2$
be rational quadratic forms on V. If
$Q_1, Q_2$
be rational quadratic forms on V. If
![]() $\mathrm {SO}_{Q_1} = \mathrm {SO}_{Q_2}$
, then
$\mathrm {SO}_{Q_1} = \mathrm {SO}_{Q_2}$
, then
![]() $Q_1 = r Q_2$
for some
$Q_1 = r Q_2$
for some
![]() $r \in \mathbb {Q}$
.
$r \in \mathbb {Q}$
.
For a proof, see [Reference Aka, Einsiedler and ShapiraAES16a, Lemma 3.3].
2.1.2 Maximality
We now aim to prove that, for any non-degenerate subspace L, the connected
![]() $\mathbb {Q}$
-groups
$\mathbb {Q}$
-groups
![]() $\mathbf {H}^{\prime }_L$
and
$\mathbf {H}^{\prime }_L$
and
![]() $\mathbf {H}_L$
are maximal subgroups. Here, maximal means among connected and proper subgroups (as it was in Remark 1.13).
$\mathbf {H}_L$
are maximal subgroups. Here, maximal means among connected and proper subgroups (as it was in Remark 1.13).
Proposition 2.5. For any non-degenerate subspace
![]() $L \subset V$
, the groups
$L \subset V$
, the groups
![]() $\mathbf {H}^{\prime }_L$
and
$\mathbf {H}^{\prime }_L$
and
![]() $\mathbf {H}_L$
are maximal.
$\mathbf {H}_L$
are maximal.
The result above is well known and due to Dynkin, who classified the maximal subgroups of the classical groups in [Reference DynkinDyn52] (see also the work of Liebeck and Seitz, for example [Reference Liebeck and SeitzLS98]). We will give an elementary proof.
Proof. Note that it suffices to prove the statement for
![]() $\mathbf {H}^{\prime }_L$
. As L is non-degenerate, we may choose an orthogonal basis of V consisting of an orthogonal basis of L and an orthogonal basis of
$\mathbf {H}^{\prime }_L$
. As L is non-degenerate, we may choose an orthogonal basis of V consisting of an orthogonal basis of L and an orthogonal basis of
![]() $L^\perp $
. Let
$L^\perp $
. Let
 $$ \begin{align*} M_Q = \begin{pmatrix} M_1 & 0 \\ 0 & M_4 \end{pmatrix} \quad \text{with} \ M_1,M_4 \ \text{diagonal matrices} \end{align*} $$
$$ \begin{align*} M_Q = \begin{pmatrix} M_1 & 0 \\ 0 & M_4 \end{pmatrix} \quad \text{with} \ M_1,M_4 \ \text{diagonal matrices} \end{align*} $$
be the matrix representation of Q in this basis. Computing the Lie algebras of
![]() $\mathrm {SO}_Q$
and
$\mathrm {SO}_Q$
and
![]() $\mathbf {H}^{\prime }_L$
we obtain
$\mathbf {H}^{\prime }_L$
we obtain
and
 $$ \begin{align*} \mathfrak{h} := \mathrm{Lie}(\mathbf{H}^{\prime}_L) = \bigg\{ A \in \mathrm{Mat}(n) : A = \begin{pmatrix} A_1 & 0 \\ 0 & A_4 \end{pmatrix} \text{and } A_i^{T}M_i + M_iA_i = 0, i = 1,4 \bigg\}. \end{align*} $$
$$ \begin{align*} \mathfrak{h} := \mathrm{Lie}(\mathbf{H}^{\prime}_L) = \bigg\{ A \in \mathrm{Mat}(n) : A = \begin{pmatrix} A_1 & 0 \\ 0 & A_4 \end{pmatrix} \text{and } A_i^{T}M_i + M_iA_i = 0, i = 1,4 \bigg\}. \end{align*} $$
We may split
![]() $\mathfrak {g}$
in a direct sum
$\mathfrak {g}$
in a direct sum
![]() $\mathfrak {h} \oplus \mathfrak {r}$
, where
$\mathfrak {h} \oplus \mathfrak {r}$
, where
![]() $\mathfrak {r}$
is an invariant subspace under the adjoint action of
$\mathfrak {r}$
is an invariant subspace under the adjoint action of
![]() $\mathbf {H}^{\prime }_L$
on
$\mathbf {H}^{\prime }_L$
on
![]() $\mathfrak {g}$
. Explicitly, we may set
$\mathfrak {g}$
. Explicitly, we may set
 $$ \begin{align*} \mathfrak{r} = \bigg\{ \begin{pmatrix} 0 & A_2 \\ A_3 & 0 \\ \end{pmatrix} : A_2^TM_1 +M_4A_3 = 0 \bigg\}. \end{align*} $$
$$ \begin{align*} \mathfrak{r} = \bigg\{ \begin{pmatrix} 0 & A_2 \\ A_3 & 0 \\ \end{pmatrix} : A_2^TM_1 +M_4A_3 = 0 \bigg\}. \end{align*} $$
We claim that the representation of
![]() $\mathbf {H}^{\prime }_L$
on
$\mathbf {H}^{\prime }_L$
on
![]() $\mathfrak {r}$
is irreducible. Note that we may also show that the representation of
$\mathfrak {r}$
is irreducible. Note that we may also show that the representation of
![]() $\mathrm {SO}_{Q|_L} \times \mathrm {SO}_{Q|_{L^{\perp }}}$
on
$\mathrm {SO}_{Q|_L} \times \mathrm {SO}_{Q|_{L^{\perp }}}$
on
![]() $\mathrm {Mat}(k, n-k)$
given by
$\mathrm {Mat}(k, n-k)$
given by
is irreducible. Over
![]() $\bar {\mathbb {Q}}$
, we may apply Lemma 2.6 below, from which this follows.
$\bar {\mathbb {Q}}$
, we may apply Lemma 2.6 below, from which this follows.
Now let
![]() $\mathbf {M}$
be a connected group containing
$\mathbf {M}$
be a connected group containing
![]() $\mathbf {H}^{\prime }_L$
and let
$\mathbf {H}^{\prime }_L$
and let
![]() $\mathfrak {m}$
be its Lie algebra. Note that
$\mathfrak {m}$
be its Lie algebra. Note that
![]() $\mathfrak {m} \cap \mathfrak {r}$
is an invariant subspace under the adjoint action of
$\mathfrak {m} \cap \mathfrak {r}$
is an invariant subspace under the adjoint action of
![]() $\mathbf {H}^{\prime }_L$
on
$\mathbf {H}^{\prime }_L$
on
![]() $\mathfrak {r}$
. Since this representation is irreducible,
$\mathfrak {r}$
. Since this representation is irreducible,
![]() $\mathfrak {m} \cap \mathfrak {r} = \{0\}$
or
$\mathfrak {m} \cap \mathfrak {r} = \{0\}$
or
![]() $\mathfrak {m} \cap \mathfrak {r} =\mathfrak {r}$
. In the former case, we have that
$\mathfrak {m} \cap \mathfrak {r} =\mathfrak {r}$
. In the former case, we have that
![]() $\mathfrak {m} = \mathfrak {h}$
and in the latter
$\mathfrak {m} = \mathfrak {h}$
and in the latter
![]() $\mathfrak {m} = \mathfrak {g}$
. It follows that
$\mathfrak {m} = \mathfrak {g}$
. It follows that
![]() $\mathbf {H}^{\prime }_L$
is maximal and the proof is complete.
$\mathbf {H}^{\prime }_L$
is maximal and the proof is complete.
Lemma 2.6. For any
![]() $k,m \geq 3$
, the action of
$k,m \geq 3$
, the action of
![]() $\mathrm {SO}_k \times \mathrm {SO}_m$
on
$\mathrm {SO}_k \times \mathrm {SO}_m$
on
![]() $\mathrm {Mat}(k,m)$
by right-multiplication (respectively, left-multiplication) is irreducible.
$\mathrm {Mat}(k,m)$
by right-multiplication (respectively, left-multiplication) is irreducible.
Proof. We write a very elementary proof for the sake of completeness. First, assume that
![]() $k,m \geq 3$
. Note that the standard representation of
$k,m \geq 3$
. Note that the standard representation of
![]() $\mathrm {SO}_k$
(respectively,
$\mathrm {SO}_k$
(respectively,
![]() $\mathrm {SO}_m$
) is irreducible as (note that, whenever
$\mathrm {SO}_m$
) is irreducible as (note that, whenever
![]() $k=2$
, any isotropic vector is a fixed vector)
$k=2$
, any isotropic vector is a fixed vector)
![]() $k \geq 3$
(respectively,
$k \geq 3$
(respectively,
![]() $m \geq 3$
). It follows that the representation of
$m \geq 3$
). It follows that the representation of
![]() $\mathrm {SO}_k \times \mathrm {SO}_m$
on the tensor product of the respective standard representations is also irreducible (see, for example, [Reference Etingof, Golberg, Hensel, Liu, Schwendner, Vaintrob and YudovinaEGH+11, Theorem 3.10.2]); the latter is isomorphic to the representation in the lemma.
$\mathrm {SO}_k \times \mathrm {SO}_m$
on the tensor product of the respective standard representations is also irreducible (see, for example, [Reference Etingof, Golberg, Hensel, Liu, Schwendner, Vaintrob and YudovinaEGH+11, Theorem 3.10.2]); the latter is isomorphic to the representation in the lemma.
2.2 The isotropy condition
Here, we establish congruence conditions that imply isotropy of the stabilizer groups
![]() $\mathbf {H}_L$
. Recall that a
$\mathbf {H}_L$
. Recall that a
![]() $\mathbb {Q}_p$
-group
$\mathbb {Q}_p$
-group
![]() $\mathbf {G}$
is strongly isotropic if, for every connected non-trivial normal subgroup
$\mathbf {G}$
is strongly isotropic if, for every connected non-trivial normal subgroup
![]() $\mathbf {N} < \mathbf {G}$
defined over
$\mathbf {N} < \mathbf {G}$
defined over
![]() $\mathbb {Q}_p$
, the group
$\mathbb {Q}_p$
, the group
![]() $\mathbf {N}(\mathbb {Q}_p)$
is not compact. We say that a
$\mathbf {N}(\mathbb {Q}_p)$
is not compact. We say that a
![]() $\mathbb {Q}$
-group
$\mathbb {Q}$
-group
![]() $\mathbf {G}$
is strongly isotropic at a prime p if
$\mathbf {G}$
is strongly isotropic at a prime p if
![]() $\mathbf {G}$
is strongly isotropic as a
$\mathbf {G}$
is strongly isotropic as a
![]() $\mathbb {Q}_p$
-group.
$\mathbb {Q}_p$
-group.
Proposition 2.7. Let
![]() $(V',Q')$
be any non-degenerate quadratic space over
$(V',Q')$
be any non-degenerate quadratic space over
![]() $\mathbb {Q}_p$
. Then
$\mathbb {Q}_p$
. Then
![]() $Q'$
is isotropic if and only if
$Q'$
is isotropic if and only if
![]() $\mathrm {Spin}_{Q'}$
is strongly isotropic.
$\mathrm {Spin}_{Q'}$
is strongly isotropic.
Proof. If
![]() $Q'$
is isotropic,
$Q'$
is isotropic,
![]() $V'$
contains a hyperbolic plane H (see [Reference CasselsCas78, Ch. 2, Lemma 2.1]). Then
$V'$
contains a hyperbolic plane H (see [Reference CasselsCas78, Ch. 2, Lemma 2.1]). Then
![]() $\mathrm {Spin}_{Q'}$
contains
$\mathrm {Spin}_{Q'}$
contains
![]() $\mathrm {Spin}_{Q'|_H}$
, which is a split torus. Hence,
$\mathrm {Spin}_{Q'|_H}$
, which is a split torus. Hence,
![]() $\mathrm {Spin}_{Q'}$
is isotropic. Conversely, if
$\mathrm {Spin}_{Q'}$
is isotropic. Conversely, if
![]() $Q'$
is anisotropic, then
$Q'$
is anisotropic, then
![]() $\mathrm {Spin}_{Q'}(\mathbb {Q}_p)$
is compact as the hypersurface
$\mathrm {Spin}_{Q'}(\mathbb {Q}_p)$
is compact as the hypersurface
![]() $Q'(x) =1$
is compact. This proves that
$Q'(x) =1$
is compact. This proves that
![]() $Q'$
is isotropic if and only if
$Q'$
is isotropic if and only if
![]() $\mathrm {Spin}_{Q'}$
is isotropic. This is sufficient to prove the proposition if
$\mathrm {Spin}_{Q'}$
is isotropic. This is sufficient to prove the proposition if
![]() $\dim (V') =2$
(as the torus
$\dim (V') =2$
(as the torus
![]() $\mathrm {Spin}_{Q'}$
is one dimensional) and if
$\mathrm {Spin}_{Q'}$
is one dimensional) and if
![]() $\dim (V')> 2$
is not equal to
$\dim (V')> 2$
is not equal to
![]() $4$
as
$4$
as
![]() $\mathrm {Spin}_{Q'}$
is absolutely almost simple in these cases.
$\mathrm {Spin}_{Q'}$
is absolutely almost simple in these cases.
Suppose that
![]() $\dim (V') = 4$
. We freely use facts about Clifford algebras and spin groups from [Reference KnusKnu88] (mostly Ch.
$\dim (V') = 4$
. We freely use facts about Clifford algebras and spin groups from [Reference KnusKnu88] (mostly Ch.
![]() $9$
therein). Recall that
$9$
therein). Recall that
![]() $\mathrm {Spin}_{Q'}$
is equal to the norm one elements of the even Clifford algebra
$\mathrm {Spin}_{Q'}$
is equal to the norm one elements of the even Clifford algebra
![]() $\mathcal {C}^0$
of
$\mathcal {C}^0$
of
![]() $Q'$
. If the center
$Q'$
. If the center
![]() $\mathcal {Z}$
of
$\mathcal {Z}$
of
![]() $\mathcal {C}^0$
is a field over
$\mathcal {C}^0$
is a field over
![]() $\mathbb {Q}_p$
, then
$\mathbb {Q}_p$
, then
![]() $\mathcal {C}^0$
is a quaternion algebra over
$\mathcal {C}^0$
is a quaternion algebra over
![]() $\mathcal {Z}$
and
$\mathcal {Z}$
and
![]() $\mathrm {Spin}_{Q'}$
is simple. In this case, the proof works as in the case of
$\mathrm {Spin}_{Q'}$
is simple. In this case, the proof works as in the case of
![]() $\dim (V') \neq 4$
.
$\dim (V') \neq 4$
.
Suppose that the center is split, which is equivalent to
![]() $\mathrm {disc}(Q')$
being a square in
$\mathrm {disc}(Q')$
being a square in
![]() $\mathbb {Q}_p$
. Thus, there is a quaternion algebra
$\mathbb {Q}_p$
. Thus, there is a quaternion algebra
![]() $\mathcal {B}$
over
$\mathcal {B}$
over
![]() $\mathbb {Q}_p$
such that
$\mathbb {Q}_p$
such that
![]() $(V',Q')$
is similar to
$(V',Q')$
is similar to
![]() $(\mathcal {B},\mathrm {Nr})$
, where
$(\mathcal {B},\mathrm {Nr})$
, where
![]() $\mathrm {Nr}$
is the norm on
$\mathrm {Nr}$
is the norm on
![]() $\mathcal {B}$
. Then,
$\mathcal {B}$
. Then,
![]() $\mathrm {Spin}_{Q'} \simeq \mathrm {SL}_1(\mathcal {B}) \times \mathrm {SL}_1(\mathcal {B})$
, which is a product of two
$\mathrm {Spin}_{Q'} \simeq \mathrm {SL}_1(\mathcal {B}) \times \mathrm {SL}_1(\mathcal {B})$
, which is a product of two
![]() $\mathbb {Q}_p$
-simple groups. Note that
$\mathbb {Q}_p$
-simple groups. Note that
![]() $\mathcal {B}$
or
$\mathcal {B}$
or
![]() $\mathrm {SL}_1(\mathcal {B})$
are isotropic if and only if
$\mathrm {SL}_1(\mathcal {B})$
are isotropic if and only if
![]() $Q'$
is isotropic. This concludes the proof of the proposition.
$Q'$
is isotropic. This concludes the proof of the proposition.
By means of (2.1), we obtain the following corollary.
Corollary 2.8. Let
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
and let p be an odd prime. Then,
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
and let p be an odd prime. Then,
![]() $\mathbf {H}_{L}$
is strongly isotropic at p if and only if the quadratic spaces
$\mathbf {H}_{L}$
is strongly isotropic at p if and only if the quadratic spaces
![]() $(L,Q|_{L})$
and
$(L,Q|_{L})$
and
![]() $(L^{\perp },Q|_{L^{\perp }})$
are isotropic over
$(L^{\perp },Q|_{L^{\perp }})$
are isotropic over
![]() $\mathbb {Q}_p$
.
$\mathbb {Q}_p$
.
Using standard arguments (as in [Reference Aka, Einsiedler and ShapiraAES16a, Lemma 3.7], for example) we may deduce the following explicit characterization of isotropy.
Proposition 2.9. Let
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be a rational subspace and let p be an odd prime. Then,
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be a rational subspace and let p be an odd prime. Then,
![]() $\mathbf {H}_L$
is strongly isotropic at p if any of the following conditions hold.
$\mathbf {H}_L$
is strongly isotropic at p if any of the following conditions hold.
-
•
 $k \geq 5$
and
$k \geq 5$
and
 $n-k \geq 5$
.
$n-k \geq 5$
. -
•
 $3 \leq k < 5$
,
$3 \leq k < 5$
,
 $n- k \geq 5$
and
$n- k \geq 5$
and
 $p \nmid \mathrm {disc}_Q(L)$
.
$p \nmid \mathrm {disc}_Q(L)$
. -
•
 $k \geq 5$
,
$k \geq 5$
,
 $3 \leq n- k < 5$
and
$3 \leq n- k < 5$
and
 $p \nmid \mathrm {disc}_Q(L^{\perp })$
.
$p \nmid \mathrm {disc}_Q(L^{\perp })$
. -
•
 $3 \leq k < 5$
,
$3 \leq k < 5$
,
 $3 \leq n- k < 5$
,
$3 \leq n- k < 5$
,
 $p \nmid \mathrm {disc}_Q(L)$
and
$p \nmid \mathrm {disc}_Q(L)$
and
 $p \nmid \mathrm {disc}_Q(L^{\perp })$
.
$p \nmid \mathrm {disc}_Q(L^{\perp })$
. -
•
 $k=2$
,
$k=2$
,
 $n-k \geq 5$
and
$n-k \geq 5$
and
 $-\mathrm {disc}_Q(L) \in (\mathbb {F}_p^\times )^2$
(i.e.
$-\mathrm {disc}_Q(L) \in (\mathbb {F}_p^\times )^2$
(i.e.
 $-\mathrm {disc}_Q(L)$
is a non-zero square modulo p).
$-\mathrm {disc}_Q(L)$
is a non-zero square modulo p). -
•
 $k=2$
,
$k=2$
,
 $3 \leq n-k < 5$
,
$3 \leq n-k < 5$
,
 $p \nmid \mathrm {disc}_Q(L^{\perp })$
and
$p \nmid \mathrm {disc}_Q(L^{\perp })$
and
 $-\mathrm {disc}_Q(L)\in (\mathbb {F}_p^\times )^2$
.
$-\mathrm {disc}_Q(L)\in (\mathbb {F}_p^\times )^2$
. -
•
 $k\geq 5$
,
$k\geq 5$
,
 $n-k = 2$
and
$n-k = 2$
and
 $-\mathrm {disc}_Q(L^\perp )\in (\mathbb {F}_p^\times )^2$
.
$-\mathrm {disc}_Q(L^\perp )\in (\mathbb {F}_p^\times )^2$
. -
•
 $3 \leq k < 5$
,
$3 \leq k < 5$
,
 $n-k=2$
,
$n-k=2$
,
 $p \nmid \mathrm {disc}_Q(L)$
and
$p \nmid \mathrm {disc}_Q(L)$
and
 $-\mathrm {disc}_Q(L^{\perp })\in (\mathbb {F}_p^\times )^2$
.
$-\mathrm {disc}_Q(L^{\perp })\in (\mathbb {F}_p^\times )^2$
.
Although the list is lengthy, let us note that half of it consists of interchanging the roles of k and
![]() $n-k$
as well as L and
$n-k$
as well as L and
![]() $L^\perp $
. Also, whenever
$L^\perp $
. Also, whenever
![]() $p \nmid \mathrm {disc}(Q)$
, the conditions
$p \nmid \mathrm {disc}(Q)$
, the conditions
![]() $p \nmid \mathrm {disc}_Q(L)$
and
$p \nmid \mathrm {disc}_Q(L)$
and
![]() $p \nmid \mathrm {disc}_Q(L^\perp )$
are equivalent (see Proposition 5.4 and its corollary). When
$p \nmid \mathrm {disc}_Q(L^\perp )$
are equivalent (see Proposition 5.4 and its corollary). When
![]() $k=4$
or
$k=4$
or
![]() $n-k=4$
, the above criteria are sufficient but not necessary. For example, the form
$n-k=4$
, the above criteria are sufficient but not necessary. For example, the form
![]() $x_1^2+x_2^2+ x_3^2 + px_4^2$
is isotropic although its discriminant is divisible by p.
$x_1^2+x_2^2+ x_3^2 + px_4^2$
is isotropic although its discriminant is divisible by p.
2.3 Diagonal embeddings of stabilizer groups
In this section, we define a diagonally embedded copy
![]() $\boldsymbol {\Delta}{\mathbf H}_L < \mathrm {Spin}_Q\times \mathbf {P}_{n,k}$
of the stabilizer group of any subspace
$\boldsymbol {\Delta}{\mathbf H}_L < \mathrm {Spin}_Q\times \mathbf {P}_{n,k}$
of the stabilizer group of any subspace
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
.
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
.
With the arithmetic application in Part
![]() $2$
in mind, we must allow any rational subspace a choice of a full-rank
$2$
in mind, we must allow any rational subspace a choice of a full-rank
![]() $\mathbb {Z}$
-lattice
$\mathbb {Z}$
-lattice
![]() $\Lambda _L \subset \mathbb {Q}^n$
with
$\Lambda _L \subset \mathbb {Q}^n$
with
If Q is unimodular (i.e.
![]() $\mathrm {disc}(Q) =1$
), then
$\mathrm {disc}(Q) =1$
), then
![]() $\Lambda _L = \mathbb {Z}^n=(\mathbb {Z}^n)^\#$
. We emphasize that, for the arguments in the current Part
$\Lambda _L = \mathbb {Z}^n=(\mathbb {Z}^n)^\#$
. We emphasize that, for the arguments in the current Part
![]() $1$
, this choice of intermediate lattice
$1$
, this choice of intermediate lattice
![]() $\Lambda _L$
is inconsequential and the reader may safely assume that
$\Lambda _L$
is inconsequential and the reader may safely assume that
![]() $\Lambda _L = \mathbb {Z}^n$
at first.
$\Lambda _L = \mathbb {Z}^n$
at first.
Let
![]() $g_L \in \mathrm {GL}_n(\mathbb {Q})$
be such that
$g_L \in \mathrm {GL}_n(\mathbb {Q})$
be such that
![]() $g_L \mathbb {Z}^n = \Lambda _L$
, its first k columns are a basis of
$g_L \mathbb {Z}^n = \Lambda _L$
, its first k columns are a basis of
![]() $L \cap \Lambda _L$
and
$L \cap \Lambda _L$
and
![]() $\det (g_L)>0$
. In words, the columns of
$\det (g_L)>0$
. In words, the columns of
![]() $g_L$
complement a basis of
$g_L$
complement a basis of
![]() $L\cap \Lambda _L$
into an oriented basis of
$L\cap \Lambda _L$
into an oriented basis of
![]() $\Lambda _L$
. We then have a well-defined morphism with finite kernel
$\Lambda _L$
. We then have a well-defined morphism with finite kernel
Note that the morphism depends on the choice of
![]() $\Lambda _L$
, but we omit this dependency here to simplify notation. It also depends on the choice of basis; a change of basis conjugates
$\Lambda _L$
, but we omit this dependency here to simplify notation. It also depends on the choice of basis; a change of basis conjugates
![]() $\Psi _L$
by an element of
$\Psi _L$
by an element of
![]() $\mathbf {P}_{n,k}(\mathbb {Z})$
.
$\mathbf {P}_{n,k}(\mathbb {Z})$
.
One can restrict the action of an element of
![]() $\mathbf {H}_L$
to L and represent the so-obtained special orthogonal transformation in the basis contained in
$\mathbf {H}_L$
to L and represent the so-obtained special orthogonal transformation in the basis contained in
![]() $g_L$
. This yields an epimorphism (as in (2.1))
$g_L$
. This yields an epimorphism (as in (2.1))
Explicitly, the epimorphism is given by
Similarly to the above, one can obtain an epimorphism
![]() $\mathbf {H}_L \to \mathrm {SO}_{Q|_{L^\perp }}$
. To make this explicit, we would like to specify how to obtain a basis of
$\mathbf {H}_L \to \mathrm {SO}_{Q|_{L^\perp }}$
. To make this explicit, we would like to specify how to obtain a basis of
![]() $L^\perp \cap \Lambda _L^\#$
from
$L^\perp \cap \Lambda _L^\#$
from
![]() $g_L$
. To do this, observe first that the basis dual to the columns of
$g_L$
. To do this, observe first that the basis dual to the columns of
![]() $g_L$
is given by the columns of
$g_L$
is given by the columns of
![]() $M_Q^{-1} (g_L^{-1})^t$
. Note that the last
$M_Q^{-1} (g_L^{-1})^t$
. Note that the last
![]() $n-k$
columns of
$n-k$
columns of
![]() $M_Q^{-1} (g_L^{-1})^t$
are orthogonal to L so they form a basis of
$M_Q^{-1} (g_L^{-1})^t$
are orthogonal to L so they form a basis of
![]() $\Lambda _L^\# \cap L^\perp $
. Hence, we obtain an epimorphism
$\Lambda _L^\# \cap L^\perp $
. Hence, we obtain an epimorphism
Note that
which shows that
We define the group
By the definitions above, the morphism
induces a morphism
which is, in fact, an isogeny.
3 The dynamical version of the theorem in codimension at least three
As mentioned in the introduction, our aim is to translate the main theorems into a statement concerning weak
![]() ${}^\ast $
limits of orbit measures on an adequate adelic homogeneous space. In this and the next section, we shall establish these equidistribution theorems for orbit measures. This section treats the case
${}^\ast $
limits of orbit measures on an adequate adelic homogeneous space. In this and the next section, we shall establish these equidistribution theorems for orbit measures. This section treats the case
![]() $k, n-k \geq 3$
.
$k, n-k \geq 3$
.
In the following we call a sequence of subspaces
![]() $L_i \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
admissible if:
$L_i \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
admissible if:
-
(1)
 $\mathrm {disc}_Q(L_i) \to \infty $
as
$\mathrm {disc}_Q(L_i) \to \infty $
as
 $i \to \infty $
;
$i \to \infty $
; -
(2)
 $\mathrm {disc}(\tilde {q}_{L_i}) \to \infty $
as
$\mathrm {disc}(\tilde {q}_{L_i}) \to \infty $
as
 $i \to \infty $
;
$i \to \infty $
; -
(3)
 $\mathrm {disc}(\tilde {q}_{L_i^\perp }) \to \infty $
as
$\mathrm {disc}(\tilde {q}_{L_i^\perp }) \to \infty $
as
 $i \to \infty $
; and
$i \to \infty $
; and -
(4) there exists a prime p such that
 $\mathbf {H}_{L_i}(\mathbb {Q}_p)$
is strongly isotropic for all i.
$\mathbf {H}_{L_i}(\mathbb {Q}_p)$
is strongly isotropic for all i.
This section establishes the following theorem. Conjecturally, an analogous version should hold when
![]() $k=2$
or
$k=2$
or
![]() $n-k =2$
(see Remark 1.12).
$n-k =2$
(see Remark 1.12).
Theorem 3.1. Let
![]() $L_i \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be an admissible sequence of rational subspaces (with a choice of lattice
$L_i \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be an admissible sequence of rational subspaces (with a choice of lattice
![]() $\Lambda _{L_i}$
as in §2.3), let
$\Lambda _{L_i}$
as in §2.3), let
![]() $g_i \in \mathbf {G}(\mathbb {R})$
and let
$g_i \in \mathbf {G}(\mathbb {R})$
and let
![]() $\mu _i$
be the Haar probability measure on the closed orbit
$\mu _i$
be the Haar probability measure on the closed orbit
Then
![]() $\mu _i$
converges to the Haar probability measure on
$\mu _i$
converges to the Haar probability measure on
as
![]() $i \to \infty $
.
$i \to \infty $
.
The rest of the section is devoted to proving Theorem 3.1. We remark that the notion of admissible sequences here is an ad hoc notion that appeared in other instances (see, for example, [Reference Aka, Einsiedler and WieserAEW22]) to achieve a similar goal. The assumptions (1)–(3) in the definition of admissibility are, in fact, necessary for the above theorem to hold while (4) can conjecturally be removed.
3.1 A general result on equidistribution of packets
The crucial input to our results is an S-arithmetic extension of a theorem of Mozes and Shah [Reference Mozes and ShahMS95] by Gorodnik and Oh [Reference Gorodnik and OhGO11]. We state a version of it here for the reader’s convenience.
Let
![]() $\mathsf {G}$
be a simply connected connected semisimple algebraic group defined over
$\mathsf {G}$
be a simply connected connected semisimple algebraic group defined over
![]() $\mathbb {Q}$
and
$\mathbb {Q}$
and
![]() $Y_{\mathbb {A}} = \mathsf {G}(\mathbb {A})/\mathsf {G}(\mathbb {Q})$
. Let W be a compact open subgroup of
$Y_{\mathbb {A}} = \mathsf {G}(\mathbb {A})/\mathsf {G}(\mathbb {Q})$
. Let W be a compact open subgroup of
![]() $\mathsf {G}(\mathbb {A}_f)$
. We denote by
$\mathsf {G}(\mathbb {A}_f)$
. We denote by
![]() $C_c(Y_{\mathbb {A}}, W)$
the set of all continuous compactly supported functions on
$C_c(Y_{\mathbb {A}}, W)$
the set of all continuous compactly supported functions on
![]() $Y_{\mathbb {A}}$
which are W invariant. Consider a sequence
$Y_{\mathbb {A}}$
which are W invariant. Consider a sequence
![]() $(\mathsf {H}_i)_{i\in \mathbb {N}}$
of connected semisimple subgroups of
$(\mathsf {H}_i)_{i\in \mathbb {N}}$
of connected semisimple subgroups of
![]() $\mathsf {G}$
and let
$\mathsf {G}$
and let
![]() $\mu _i$
denote the Haar probability measure on the orbit
$\mu _i$
denote the Haar probability measure on the orbit
![]() $\mathsf {H}_i(\mathbb {A})^+ \mathsf {G}(\mathbb {Q}) \subset Y_{\mathbb {A}}$
, where
$\mathsf {H}_i(\mathbb {A})^+ \mathsf {G}(\mathbb {Q}) \subset Y_{\mathbb {A}}$
, where
![]() $\mathsf {H}_i(\mathbb {A})^+$
is the image of the adelic points of the simply connected cover of
$\mathsf {H}_i(\mathbb {A})^+$
is the image of the adelic points of the simply connected cover of
![]() $\mathsf {H}_i$
in
$\mathsf {H}_i$
in
![]() $\mathsf {H}_i(\mathbb {A})$
. For given
$\mathsf {H}_i(\mathbb {A})$
. For given
![]() $g_i \in \mathsf {G}(\mathbb {A})$
, we are interested in the weak* limits of the sequence of measures
$g_i \in \mathsf {G}(\mathbb {A})$
, we are interested in the weak* limits of the sequence of measures
![]() $g_i\mu _i$
.
$g_i\mu _i$
.
Theorem 3.2. (Gorodnik and Oh [Reference Gorodnik and OhGO11, Theorem 1.7])
Assume that there exists a prime p such that
![]() $\mathsf {H}_i$
is strongly isotropic at p for all
$\mathsf {H}_i$
is strongly isotropic at p for all
![]() $i \in \mathbb {N}$
. Then, for any weak
$i \in \mathbb {N}$
. Then, for any weak
![]() ${}^\ast $
limit of the sequence
${}^\ast $
limit of the sequence
![]() $(g_i\mu _i)$
with
$(g_i\mu _i)$
with
![]() $\mu (Y_{\mathbb {A}}) = 1$
, there exists a connected
$\mu (Y_{\mathbb {A}}) = 1$
, there exists a connected
![]() $\mathbb {Q}$
-group
$\mathbb {Q}$
-group
![]() $\mathsf {M}< \mathsf {G}$
such that the following hold.
$\mathsf {M}< \mathsf {G}$
such that the following hold.
-
(1) For all i large enough, there exist
 $\delta _i \in \mathsf {G}(\mathbb {Q})$
such that:
$\delta _i \in \mathsf {G}(\mathbb {Q})$
such that:  $$ \begin{align*} \delta_i^{-1} \mathsf{H}_i \delta_i \subset \mathsf{M}. \end{align*} $$
$$ \begin{align*} \delta_i^{-1} \mathsf{H}_i \delta_i \subset \mathsf{M}. \end{align*} $$
-
(2) For any compact open subgroup W of
 $\mathsf {G}(\mathbb {A}_f)$
, there exists a finite-index normal subgroup
$\mathsf {G}(\mathbb {A}_f)$
, there exists a finite-index normal subgroup
 $M_0 = M_0(W)$
of
$M_0 = M_0(W)$
of
 $\mathsf {M}(\mathbb {A})$
and
$\mathsf {M}(\mathbb {A})$
and
 $g \in \mathsf {G}(\mathbb {A})$
such that
$g \in \mathsf {G}(\mathbb {A})$
such that
 $\mu $
agrees with the Haar probability measure on
$\mu $
agrees with the Haar probability measure on
 $gM_0 \mathsf {G}(\mathbb {Q})$
when restricted to
$gM_0 \mathsf {G}(\mathbb {Q})$
when restricted to
 $C_c(Y_{\mathbb {A}},W)$
. Moreover, there exists
$C_c(Y_{\mathbb {A}},W)$
. Moreover, there exists
 $h_i \in \mathsf {H}_i(\mathbb {A})^+$
such that
$h_i \in \mathsf {H}_i(\mathbb {A})^+$
such that
 $g_i h_i \delta _i \rightarrow g$
as
$g_i h_i \delta _i \rightarrow g$
as
 $i \rightarrow \infty $
.
$i \rightarrow \infty $
. -
(3) If the centralizers of
 $\mathsf {H}_i$
are
$\mathsf {H}_i$
are
 $\mathbb {Q}$
-anisotropic for all
$\mathbb {Q}$
-anisotropic for all
 $i \in \mathbb {N}$
, then
$i \in \mathbb {N}$
, then
 $\mathsf {M}$
is semisimple. Moreover, for any compact open subgroup W,
$\mathsf {M}$
is semisimple. Moreover, for any compact open subgroup W,
 $M_0 = M_0(W)$
in 2 contains
$M_0 = M_0(W)$
in 2 contains
 $\mathsf {M}(\mathbb {A})^+ \mathsf {M}(\mathbb {Q})$
.
$\mathsf {M}(\mathbb {A})^+ \mathsf {M}(\mathbb {Q})$
.
We remark that the theorem as stated in [Reference Gorodnik and OhGO11] does not assume that
![]() $\mathsf {G}$
is simply connected; we will, however, need only this case.
$\mathsf {G}$
is simply connected; we will, however, need only this case.
3.2 Proof of Theorem 3.1
We prove Theorem 3.1 in several steps and start with a short overview. Note that we have a morphism
given by mapping
![]() $g \in \mathbf {P}_{n,k}$
to
$g \in \mathbf {P}_{n,k}$
to
![]() $(\pi _1(g),\pi _2(g^{-1})^t)$
and
$(\pi _1(g),\pi _2(g^{-1})^t)$
and
![]() $\mathrm {Spin}_Q$
to itself via the identity map (see also §2.3). The first step of the theorem establishes equidistribution of the projections to the respective homogeneous quotients for
$\mathrm {Spin}_Q$
to itself via the identity map (see also §2.3). The first step of the theorem establishes equidistribution of the projections to the respective homogeneous quotients for
![]() $\mathrm {Spin}_Q, \mathrm {SL}_k, \mathrm {SL}_{n-k}$
(henceforth called ‘individual equidistribution’). The second step is the analogous statement for
$\mathrm {Spin}_Q, \mathrm {SL}_k, \mathrm {SL}_{n-k}$
(henceforth called ‘individual equidistribution’). The second step is the analogous statement for
![]() $\bar {\mathbf {G}}$
. Note that the admissibility assumption on the sequence of subspaces
$\bar {\mathbf {G}}$
. Note that the admissibility assumption on the sequence of subspaces
![]() $L_i$
is used for individual equidistribution and, in fact, the different conditions (1)–(3) imply the corresponding individual equidistribution statements (i.e. (1) implies equidistribution in the homogeneous quotient
$L_i$
is used for individual equidistribution and, in fact, the different conditions (1)–(3) imply the corresponding individual equidistribution statements (i.e. (1) implies equidistribution in the homogeneous quotient
![]() etc.).
etc.).
To briefly outline the argument here, consider a sequence of orbits
As the groups
![]() $\mathbf {H}_{L_i}$
are maximal subgroups, the theorem of Gorodnik and Oh above implies that either the orbits are equidistributed or that there exist lattice elements
$\mathbf {H}_{L_i}$
are maximal subgroups, the theorem of Gorodnik and Oh above implies that either the orbits are equidistributed or that there exist lattice elements
![]() $\delta _i$
so that
$\delta _i$
so that
![]() $\delta _i\mathbf {H}_{L_i}\delta _i^{-1}$
is eventually independent of i. In the latter case, we also know that the lattice elements are up to a bounded amount in the stabilizer group; this will be shown to contradict the assumption that
$\delta _i\mathbf {H}_{L_i}\delta _i^{-1}$
is eventually independent of i. In the latter case, we also know that the lattice elements are up to a bounded amount in the stabilizer group; this will be shown to contradict the assumption that
![]() $\mathrm {disc}_Q(L_i) \to \infty $
.
$\mathrm {disc}_Q(L_i) \to \infty $
.
3.2.1 Applying Theorem 3.2
Consider the subgroup
![]() $\mathbf {J} = \mathrm {Spin}_Q \times \mathrm {SL}_n$
. Note that
$\mathbf {J} = \mathrm {Spin}_Q \times \mathrm {SL}_n$
. Note that
![]() $\mathbf {J}$
is semisimple and simply connected so that we may apply Theorem 3.2 given a suitable sequence of subgroups.
$\mathbf {J}$
is semisimple and simply connected so that we may apply Theorem 3.2 given a suitable sequence of subgroups.
The groups
![]() $\mathbf {H}_{L_i}$
are potentially not simply connected, so a little more care is needed in applying Theorem 3.2 to the orbit measures
$\mathbf {H}_{L_i}$
are potentially not simply connected, so a little more care is needed in applying Theorem 3.2 to the orbit measures
![]() $\mu _i$
. We fix, for any i, some
$\mu _i$
. We fix, for any i, some
![]() $h_i \in \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})$
and consider the orbit measures on
$h_i \in \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})$
and consider the orbit measures on
![]() $g_ih_i \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+\mathbf {G}(\mathbb {Q})$
. In view of the theorem, it suffices to show that these converge to the Haar probability measure on
$g_ih_i \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+\mathbf {G}(\mathbb {Q})$
. In view of the theorem, it suffices to show that these converge to the Haar probability measure on
![]() . Indeed, by disintegration, the Haar measure on
. Indeed, by disintegration, the Haar measure on
![]() $g_i\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A}) \mathbf {G}(\mathbb {Q})$
is the integral over the Haar measures on
$g_i\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A}) \mathbf {G}(\mathbb {Q})$
is the integral over the Haar measures on
![]() $g_ih_i \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+\mathbf {G}(\mathbb {Q})$
when
$g_ih_i \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+\mathbf {G}(\mathbb {Q})$
when
![]() $h_i$
is integrated with respect to the Haar probability measure on the compact group
$h_i$
is integrated with respect to the Haar probability measure on the compact group
![]() $\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})/\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+$
. In other words, the Haar measure on
$\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})/\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+$
. In other words, the Haar measure on
![]() $g_i\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A}) \mathbf {G}(\mathbb {Q})$
is a convex combination of the Haar measures on the orbits
$g_i\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A}) \mathbf {G}(\mathbb {Q})$
is a convex combination of the Haar measures on the orbits
![]() $g_ih_i\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+ \mathbf {G}(\mathbb {Q})$
. To simplify notation, we replace
$g_ih_i\boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+ \mathbf {G}(\mathbb {Q})$
. To simplify notation, we replace
![]() $g_i$
by
$g_i$
by
![]() $g_ih_i$
in order to omit
$g_ih_i$
in order to omit
![]() $h_i$
. Furthermore, we abuse notation and write
$h_i$
. Furthermore, we abuse notation and write
![]() $\mu _i$
for these ‘components’ of the original orbit measures.
$\mu _i$
for these ‘components’ of the original orbit measures.
We fix a compact open subgroup W of
![]() $\mathbf {G}(\mathbb {A}_f)$
in view of (2)(b) in Theorem 3.2 and an odd prime p as in the definition of admissibility of the sequence
$\mathbf {G}(\mathbb {A}_f)$
in view of (2)(b) in Theorem 3.2 and an odd prime p as in the definition of admissibility of the sequence
![]() $(L_i)_i$
.
$(L_i)_i$
.
Let
![]() $\mu $
be any weak
$\mu $
be any weak
![]() ${}^\ast $
-limit of the measures
${}^\ast $
-limit of the measures
![]() $\mu _i$
. Note that
$\mu _i$
. Note that
![]() $\mu $
is a probability measure. Indeed, the pushforward of the measures
$\mu $
is a probability measure. Indeed, the pushforward of the measures
![]() $\mu _i$
to
$\mu _i$
to
![]() $\mathrm {Spin}_Q(\mathbb {A})/\mathrm {Spin}_Q(\mathbb {Q})$
has to converge to a probability measure as
$\mathrm {Spin}_Q(\mathbb {A})/\mathrm {Spin}_Q(\mathbb {Q})$
has to converge to a probability measure as
![]() $\mathrm {Spin}_Q(\mathbb {A})/\mathrm {Spin}_Q(\mathbb {Q})$
is compact. We let
$\mathrm {Spin}_Q(\mathbb {A})/\mathrm {Spin}_Q(\mathbb {Q})$
is compact. We let
![]() $\mathbf {M} < \mathbf {J}$
be as in Theorem 3.2. Because
$\mathbf {M} < \mathbf {J}$
be as in Theorem 3.2. Because
![]() $g_i \in \mathbf {G}(\mathbb {A})$
and
$g_i \in \mathbf {G}(\mathbb {A})$
and
![]() $\boldsymbol {\Delta}{\mathbf H}_{L_i} < \mathbf {G}$
for all i, the support of the measures
$\boldsymbol {\Delta}{\mathbf H}_{L_i} < \mathbf {G}$
for all i, the support of the measures
![]() $\mu _i$
is contained in
$\mu _i$
is contained in
![]() . Thus,
. Thus,
![]() $\mathbf {M}< \mathbf {G}$
.
$\mathbf {M}< \mathbf {G}$
.
Claim. It suffices to show that
![]() $\mathbf {M} = \mathbf {G}$
.
$\mathbf {M} = \mathbf {G}$
.
Proof of the claim
Suppose that
![]() $\mathbf {M} = \mathbf {G}$
. Let
$\mathbf {M} = \mathbf {G}$
. Let
![]() $M_0 = M_0(W)$
be as in Theorem 3.2. Since
$M_0 = M_0(W)$
be as in Theorem 3.2. Since
![]() $\mathbf {G}(\mathbb {A})$
has no proper finite-index subgroups [Reference Borel and TitsBT73, Theorem 6.7], we have
$\mathbf {G}(\mathbb {A})$
has no proper finite-index subgroups [Reference Borel and TitsBT73, Theorem 6.7], we have
![]() $M_0 = \mathbf {G}(\mathbb {A})$
(independently of W). Therefore, for any W-invariant continuous compactly supported function f, the integral
$M_0 = \mathbf {G}(\mathbb {A})$
(independently of W). Therefore, for any W-invariant continuous compactly supported function f, the integral
![]() $\mu (f)$
agrees with the integral against the Haar measure on
$\mu (f)$
agrees with the integral against the Haar measure on
![]() $\mathbf {G}(\mathbb {A})/\mathbf {G}(\mathbb {Q})$
. But any continuous compactly supported function is invariant under some compact open subgroup W; hence, the claim follows.
$\mathbf {G}(\mathbb {A})/\mathbf {G}(\mathbb {Q})$
. But any continuous compactly supported function is invariant under some compact open subgroup W; hence, the claim follows.
We now focus on proving that
![]() $\mathbf {M} = \mathbf {G}$
. By Theorem 3.2, there exist
$\mathbf {M} = \mathbf {G}$
. By Theorem 3.2, there exist
![]() $\delta _i \in \mathbf {G}(\mathbb {Q})$
such that
$\delta _i \in \mathbf {G}(\mathbb {Q})$
such that
![]() $\delta _i^{-1}\boldsymbol {\Delta}{\mathbf H}_{L_i}\delta _i < \mathbf {M}$
for all
$\delta _i^{-1}\boldsymbol {\Delta}{\mathbf H}_{L_i}\delta _i < \mathbf {M}$
for all
![]() $i \geq i_0$
. Furthermore, we fix
$i \geq i_0$
. Furthermore, we fix
![]() $g \in \mathbf {G}(\mathbb {A})$
as well as
$g \in \mathbf {G}(\mathbb {A})$
as well as
![]() $\hat {h}_i = (h_i, \Psi _{L_i}(h_i))\in \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+$
, as in Theorem 3.2, such that
$\hat {h}_i = (h_i, \Psi _{L_i}(h_i))\in \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})^+$
, as in Theorem 3.2, such that
3.2.2 Individual equidistribution of subspaces and shapes
Consider the morphism
In the following step of the proof, we show that the image
![]() $\bar {\mathbf {M}}$
of the subgroup
$\bar {\mathbf {M}}$
of the subgroup
![]() $\mathbf {M}$
via (3.2) projects surjectively onto each of the factors of
$\mathbf {M}$
via (3.2) projects surjectively onto each of the factors of
![]() $\bar {\mathbf {G}}$
.
$\bar {\mathbf {G}}$
.
Proposition 3.3. The morphism obtained by restricting the projection of
![]() $\bar {\mathbf {G}}$
onto any almost simple factor of
$\bar {\mathbf {G}}$
onto any almost simple factor of
![]() $\bar {\mathbf {G}}$
to
$\bar {\mathbf {G}}$
to
![]() $\mathbf {M}$
is surjective.
$\mathbf {M}$
is surjective.
Proof. We prove the proposition for each factor separately. To ease notation,
![]() $\pi $
will denote the projection of
$\pi $
will denote the projection of
![]() $\bar {\mathbf {G}}$
onto the factor in consideration, which we extend to
$\bar {\mathbf {G}}$
onto the factor in consideration, which we extend to
![]() $\mathbf {G}$
by precomposition.
$\mathbf {G}$
by precomposition.
First factor: As
![]() $\pi (\boldsymbol {\Delta}{\mathbf H}_{L_i}) = \mathbf {H}_{L_i}$
, we have, for each i,
$\pi (\boldsymbol {\Delta}{\mathbf H}_{L_i}) = \mathbf {H}_{L_i}$
, we have, for each i,
Since
![]() $\mathbf {H}_{L_i}$
is a maximal subgroup of
$\mathbf {H}_{L_i}$
is a maximal subgroup of
![]() $\mathrm {Spin}_Q$
(see Proposition 2.5), there are two options: either
$\mathrm {Spin}_Q$
(see Proposition 2.5), there are two options: either
![]() $\pi _{1}(\mathbf {M}) = \mathrm {Spin}_Q$
or
$\pi _{1}(\mathbf {M}) = \mathrm {Spin}_Q$
or
![]() $\pi (\delta _i)^{-1} \mathbf {H}_{L_i} \pi (\delta _i) = \pi (\mathbf {M})$
for all
$\pi (\delta _i)^{-1} \mathbf {H}_{L_i} \pi (\delta _i) = \pi (\mathbf {M})$
for all
![]() $i\geq i_0$
.
$i\geq i_0$
.
Suppose the second option holds (as the proof is complete otherwise). Setting
![]() $\gamma _i = \pi (\delta _i\delta _{i_0}^{-1})$
and
$\gamma _i = \pi (\delta _i\delta _{i_0}^{-1})$
and
![]() $L = L_{i_0}$
,
$L = L_{i_0}$
,
By Proposition 2.2, we have
![]() $\gamma _i.L = L_i$
or
$\gamma _i.L = L_i$
or
![]() $\gamma _i.L^\perp = L_i$
; by changing to a subsequence and increasing
$\gamma _i.L^\perp = L_i$
; by changing to a subsequence and increasing
![]() $i_0$
, we may suppose that the former option holds for all
$i_0$
, we may suppose that the former option holds for all
![]() $i \geq i_0$
. By (3.1) there exist
$i \geq i_0$
. By (3.1) there exist
![]() $h_i \in \mathbf {H}_{L_i}(\mathbb {A})$
such that
$h_i \in \mathbf {H}_{L_i}(\mathbb {A})$
such that
![]() $\pi (g_i) h_i \gamma _i \to \pi (g')$
for some
$\pi (g_i) h_i \gamma _i \to \pi (g')$
for some
![]() $g' \in \mathbf {G}(\mathbb {A})$
. Roughly speaking, this implies that
$g' \in \mathbf {G}(\mathbb {A})$
. Roughly speaking, this implies that
![]() $L_i = h_i\gamma _i.L \to \pi (g).L$
as
$L_i = h_i\gamma _i.L \to \pi (g).L$
as
![]() $\mathbb {Q}_p$
-subspaces for any prime p contradicting the discriminant condition. More precisely, let
$\mathbb {Q}_p$
-subspaces for any prime p contradicting the discriminant condition. More precisely, let
![]() $\varepsilon _i\to e$
be such that
$\varepsilon _i\to e$
be such that
![]() $\pi (g_i) h_i \gamma _i= \varepsilon _i\pi (g')$
. Then, for any prime p, the local discriminant gives
$\pi (g_i) h_i \gamma _i= \varepsilon _i\pi (g')$
. Then, for any prime p, the local discriminant gives
If i is large enough such that
![]() $\varepsilon _i \in \mathrm {Spin}_Q(\mathbb {R}\times \widehat {\mathbb {Z}})$
,
$\varepsilon _i \in \mathrm {Spin}_Q(\mathbb {R}\times \widehat {\mathbb {Z}})$
,
 $$ \begin{align*} \mathrm{disc}_Q(L_i) = \prod_p p^{\nu_p(\mathrm{disc}_{p,Q}(L_i))} = \prod_pp^{\nu_p(\mathrm{disc}_{p,Q}(\pi(g_p').L))}, \end{align*} $$
$$ \begin{align*} \mathrm{disc}_Q(L_i) = \prod_p p^{\nu_p(\mathrm{disc}_{p,Q}(L_i))} = \prod_pp^{\nu_p(\mathrm{disc}_{p,Q}(\pi(g_p').L))}, \end{align*} $$
which is constant, contradicting that
![]() $\mathrm {disc}_Q(L_i) \to \infty $
.
$\mathrm {disc}_Q(L_i) \to \infty $
.
Second factor: The proof is very similar to the first case, so we will be brief. By maximality of special orthogonal groups (Remark 1.13) and as
![]() $\pi (\boldsymbol {\Delta}{\mathbf H}_{L_i}) = \mathrm {SO}_{q_{{ }_{L_i\cap \Lambda _{L_i}}}}$
, we may suppose, by contradiction, that, for all
$\pi (\boldsymbol {\Delta}{\mathbf H}_{L_i}) = \mathrm {SO}_{q_{{ }_{L_i\cap \Lambda _{L_i}}}}$
, we may suppose, by contradiction, that, for all
![]() $i \geq i_0$
,
$i \geq i_0$
,
We simplify notation and write
![]() $q_i$
for the least integer multiple of
$q_i$
for the least integer multiple of
![]() $q_{{ }_{L_i \cap \Lambda _{L_i}}}$
that has integer coefficients. Since
$q_{{ }_{L_i \cap \Lambda _{L_i}}}$
that has integer coefficients. Since
![]() $L_i \cap \Lambda _{L_i}$
and
$L_i \cap \Lambda _{L_i}$
and
![]() $L_i(\mathbb {Z})$
are commensurable with indices controlled by
$L_i(\mathbb {Z})$
are commensurable with indices controlled by
![]() $\mathrm {disc}(Q)$
, we have
$\mathrm {disc}(Q)$
, we have
![]() $\mathrm {disc}(q_{i}) \asymp \mathrm {disc}(q_{L_i})$
and
$\mathrm {disc}(q_{i}) \asymp \mathrm {disc}(q_{L_i})$
and
![]() $\mathrm {disc}(\tilde {q}_{i}) \asymp \mathrm {disc}(\tilde {q}_{L_i})$
. In particular, by our assumption,
$\mathrm {disc}(\tilde {q}_{i}) \asymp \mathrm {disc}(\tilde {q}_{L_i})$
. In particular, by our assumption,
![]() $\mathrm {disc}(\tilde {q}_{i}) \to \infty $
as
$\mathrm {disc}(\tilde {q}_{i}) \to \infty $
as
![]() $i \to \infty $
.
$i \to \infty $
.
Set
![]() $\gamma _i = \pi (\delta _i\delta _{i_0}^{-1})\in \mathrm {SL}_k(\mathbb {Q})$
so that
$\gamma _i = \pi (\delta _i\delta _{i_0}^{-1})\in \mathrm {SL}_k(\mathbb {Q})$
so that
By Proposition 2.4, there exist coprime integers
![]() $m_i,n_i$
such that
$m_i,n_i$
such that
Using (3.1), write
![]() $\pi (g_i) h_i \gamma _i = \varepsilon _i \pi (g')$
for some
$\pi (g_i) h_i \gamma _i = \varepsilon _i \pi (g')$
for some
![]() $g' \in \mathbf {G}(\mathbb {A})$
and
$g' \in \mathbf {G}(\mathbb {A})$
and
![]() $\varepsilon _i \to e$
. By (3.3),
$\varepsilon _i \to e$
. By (3.3),
![]() $h_i(\gamma _i\tilde {q}_{i_0}) = \gamma _i\tilde {q}_{i_0}$
. Thus, for any prime p,
$h_i(\gamma _i\tilde {q}_{i_0}) = \gamma _i\tilde {q}_{i_0}$
. Thus, for any prime p,
The form
![]() $\pi (g_p')\tilde {q}_{i_0}$
is a form over
$\pi (g_p')\tilde {q}_{i_0}$
is a form over
![]() $\mathbb {Q}_p$
with trivial denominators for all but finitely many p. Applying
$\mathbb {Q}_p$
with trivial denominators for all but finitely many p. Applying
![]() $\varepsilon _{i,p}$
for large i does not change this. Furthermore,
$\varepsilon _{i,p}$
for large i does not change this. Furthermore,
![]() $m_i$
needs to divide all denominators of
$m_i$
needs to divide all denominators of
![]() $\tilde {q}_{i_0}$
over
$\tilde {q}_{i_0}$
over
![]() $\mathbb {Z}_p$
for all i as
$\mathbb {Z}_p$
for all i as
![]() $\tilde {q}_{i}$
is primitive. Hence,
$\tilde {q}_{i}$
is primitive. Hence,
![]() $m_i$
can only assume finitely many values and, by reversing roles, one can argue the same for
$m_i$
can only assume finitely many values and, by reversing roles, one can argue the same for
![]() $n_i$
. For any prime p,
$n_i$
. For any prime p,
and hence
 $$ \begin{align*} \mathrm{disc}(\tilde{q}_{i}) = \dfrac{m_i}{n_i} \prod_{p} p^{\mathrm{ord}_p(\mathrm{disc}_p(\pi(g_p')\tilde{q}_{i_0}))}, \end{align*} $$
$$ \begin{align*} \mathrm{disc}(\tilde{q}_{i}) = \dfrac{m_i}{n_i} \prod_{p} p^{\mathrm{ord}_p(\mathrm{disc}_p(\pi(g_p')\tilde{q}_{i_0}))}, \end{align*} $$
which is in contradiction to
![]() $\mathrm {disc}(\tilde {q}_{i}) \to \infty $
.
$\mathrm {disc}(\tilde {q}_{i}) \to \infty $
.
Third factor: The proof here is the same as for the second factor. We do, however, point out that the morphism
![]() $\mathbf {G} \to \bar {\mathbf {G}}$
was constructed to satisfy that, for any
$\mathbf {G} \to \bar {\mathbf {G}}$
was constructed to satisfy that, for any
![]() $h \in \mathbf {H}_{L_i}$
, we have
$h \in \mathbf {H}_{L_i}$
, we have
![]() $\pi ((h,\Psi _{L_i}(h)) = \psi _{2,L_i}(h)$
and hence
$\pi ((h,\Psi _{L_i}(h)) = \psi _{2,L_i}(h)$
and hence
![]() $\pi (\boldsymbol {\Delta}{\mathbf H}_{L_i}) = \mathrm {SO}_{q_{L_i^\perp \cap \Lambda _{L_i}^\#}}$
.
$\pi (\boldsymbol {\Delta}{\mathbf H}_{L_i}) = \mathrm {SO}_{q_{L_i^\perp \cap \Lambda _{L_i}^\#}}$
.
Remark 3.4. We recall from the beginning of §3.2 that the first three conditions in admissibility were used in this order for the three factors in the above proof. This has a consequence: if
![]() $L_i\in \mathrm {Gr}_{n,k}(\mathbb {Q})$
is any sequence of subspaces satisfying properties (1) and (4), then, for any
$L_i\in \mathrm {Gr}_{n,k}(\mathbb {Q})$
is any sequence of subspaces satisfying properties (1) and (4), then, for any
![]() $g_i \in \mathrm {Spin}_Q(\mathbb {R})$
, the packets
$g_i \in \mathrm {Spin}_Q(\mathbb {R})$
, the packets
are equidistributed as
![]() $i \to \infty $
. This can be used to obtain equidistribution of
$i \to \infty $
. This can be used to obtain equidistribution of
![]() $\mathcal {H}^{n,k}_Q(D) \subset \mathrm {Gr}_{n,k}(\mathbb {R})$
without any restrictions on the k-power free part of D (as opposed to our main theorems in the introduction).
$\mathcal {H}^{n,k}_Q(D) \subset \mathrm {Gr}_{n,k}(\mathbb {R})$
without any restrictions on the k-power free part of D (as opposed to our main theorems in the introduction).
3.2.3 Simultaneous equidistribution of subspaces and shapes
Proposition 3.3 shows that the image
![]() $\bar {\mathbf {M}}$
of
$\bar {\mathbf {M}}$
of
![]() $\mathbf {M}$
under (3.2) satisfies that the projection onto each simple factor of
$\mathbf {M}$
under (3.2) satisfies that the projection onto each simple factor of
![]() $\bar {\mathbf {G}}$
is surjective. We claim that this implies that
$\bar {\mathbf {G}}$
is surjective. We claim that this implies that
![]() $\bar {\mathbf {M}} = \bar {\mathbf {G}}$
.
$\bar {\mathbf {M}} = \bar {\mathbf {G}}$
.
We first show that the projection of
![]() $\bar {\mathbf {M}}$
to
$\bar {\mathbf {M}}$
to
![]() $\mathrm {SL}_k \times \mathrm {SL}_{n-k}$
is surjective. Note that any proper subgroup of
$\mathrm {SL}_k \times \mathrm {SL}_{n-k}$
is surjective. Note that any proper subgroup of
![]() $\mathrm {SL}_k \times \mathrm {SL}_{n-k}$
with surjective projections is the graph of an isomorphism
$\mathrm {SL}_k \times \mathrm {SL}_{n-k}$
with surjective projections is the graph of an isomorphism
![]() $\mathrm {SL}_k \to \mathrm {SL}_{n-k}$
. In particular, the intermediate claim is finished if
$\mathrm {SL}_k \to \mathrm {SL}_{n-k}$
. In particular, the intermediate claim is finished if
![]() $k \neq n-k$
. Suppose that
$k \neq n-k$
. Suppose that
![]() $ k = n-k$
and choose, for some
$ k = n-k$
and choose, for some
![]() $i \geq i_0$
, an element
$i \geq i_0$
, an element
![]() $h \in \mathbf {H}_{L_i}$
acting trivially on
$h \in \mathbf {H}_{L_i}$
acting trivially on
![]() $L_i$
but not trivially on
$L_i$
but not trivially on
![]() $L_i^{\perp }$
. The projection of
$L_i^{\perp }$
. The projection of
![]() $g_{L_i}^{-1}\rho _Q(h)g_{L_i}$
to the first (respectively, the second)
$g_{L_i}^{-1}\rho _Q(h)g_{L_i}$
to the first (respectively, the second)
![]() $\mathrm {SL}_{k}$
is trivial (respectively, non-trivial); the projection of
$\mathrm {SL}_{k}$
is trivial (respectively, non-trivial); the projection of
![]() $\bar {\mathbf {M}}$
to
$\bar {\mathbf {M}}$
to
![]() $\mathrm {SL}_k \times \mathrm {SL}_{n-k}$
thus contains elements of the form
$\mathrm {SL}_k \times \mathrm {SL}_{n-k}$
thus contains elements of the form
![]() $(e,g)$
with
$(e,g)$
with
![]() $g \neq e$
. This rules out graphs under isomorphisms and concludes the intermediate claim.
$g \neq e$
. This rules out graphs under isomorphisms and concludes the intermediate claim.
Now note that
![]() $\bar {\mathbf {M}}$
projects surjectively onto
$\bar {\mathbf {M}}$
projects surjectively onto
![]() $\mathrm {Spin}_Q$
and
$\mathrm {Spin}_Q$
and
![]() $\mathrm {SL}_k \times \mathrm {SL}_{n-k}$
and that the latter two
$\mathrm {SL}_k \times \mathrm {SL}_{n-k}$
and that the latter two
![]() $\mathbb {Q}$
-groups do not have isomorphic simple factors. By an argument similar to that above, we deduce that
$\mathbb {Q}$
-groups do not have isomorphic simple factors. By an argument similar to that above, we deduce that
![]() $\bar {\mathbf {M}} = \bar {\mathbf {G}}$
.
$\bar {\mathbf {M}} = \bar {\mathbf {G}}$
.
3.2.4 Handling the unipotent radical
We now turn to proving that
![]() $\mathbf {M} = \mathbf {G}$
, which concludes the proof of the theorem. By §3.2.3, we know that
$\mathbf {M} = \mathbf {G}$
, which concludes the proof of the theorem. By §3.2.3, we know that
![]() $\mathbf {M}$
surjects to
$\mathbf {M}$
surjects to
![]() $\bar {\mathbf {G}}$
. In particular, by the Levi–Malcev theorem, there exists some element in the unipotent radical of
$\bar {\mathbf {G}}$
. In particular, by the Levi–Malcev theorem, there exists some element in the unipotent radical of
![]() $\mathbf {P}_{n,k}$
$\mathbf {P}_{n,k}$
 $$ \begin{align*} y_C = \begin{pmatrix} I_k & C \\ 0 & I_{n-k} \end{pmatrix} \in \mathbf{P}_{n,k}(\mathbb{Q}) \end{align*} $$
$$ \begin{align*} y_C = \begin{pmatrix} I_k & C \\ 0 & I_{n-k} \end{pmatrix} \in \mathbf{P}_{n,k}(\mathbb{Q}) \end{align*} $$
such that
![]() $\mathbf {M}$
contains
$\mathbf {M}$
contains
![]() $\mathrm {Spin}_Q \times y_C \mathbf {D}_{n,k} y_C^{-1}$
. By maximality of the latter group (cf. Remark 1.13),
$\mathrm {Spin}_Q \times y_C \mathbf {D}_{n,k} y_C^{-1}$
. By maximality of the latter group (cf. Remark 1.13),
![]() $\mathbf {M}$
is either equal to
$\mathbf {M}$
is either equal to
![]() $\mathbf {G}$
or
$\mathbf {G}$
or
Assume, by contradiction, the latter. The inclusion
![]() $\delta _i^{-1}\boldsymbol {\Delta}{\mathbf H}_{L_i}\delta _i \subset \mathbf {M}$
implies that
$\delta _i^{-1}\boldsymbol {\Delta}{\mathbf H}_{L_i}\delta _i \subset \mathbf {M}$
implies that
where
![]() $\delta _{2,i}$
denotes the second coordinate of the element
$\delta _{2,i}$
denotes the second coordinate of the element
![]() $\delta _i \in \mathbf {G}(\mathbb {Q}) = \mathrm {Spin}_Q(\mathbb {Q})\times \mathbf {P}_{n,k}(\mathbb {Q})$
. Since
$\delta _i \in \mathbf {G}(\mathbb {Q}) = \mathrm {Spin}_Q(\mathbb {Q})\times \mathbf {P}_{n,k}(\mathbb {Q})$
. Since
![]() $y_C \mathbf {D}_{n,k} y_C^{-1}$
stabilizes two subspaces, namely,
$y_C \mathbf {D}_{n,k} y_C^{-1}$
stabilizes two subspaces, namely,
![]() $y_C L_0 = L_0$
and
$y_C L_0 = L_0$
and
![]() $L' = y_C(\{(0,\ldots ,0)\}\times \mathbb {Q}^{n-k})$
, the conjugated group
$L' = y_C(\{(0,\ldots ,0)\}\times \mathbb {Q}^{n-k})$
, the conjugated group
![]() $g_{L_i}\delta _{i,2}y_C \mathbf {D}_{n,k} y_C^{-1} \delta _{i,2}^{-1}g_{L_i}^{-1}$
fixes the subspaces
$g_{L_i}\delta _{i,2}y_C \mathbf {D}_{n,k} y_C^{-1} \delta _{i,2}^{-1}g_{L_i}^{-1}$
fixes the subspaces
As
![]() $\mathbf {H}_{L_i}$
fixes exactly the subspaces
$\mathbf {H}_{L_i}$
fixes exactly the subspaces
![]() $L_i,L_i^\perp $
, we must have
$L_i,L_i^\perp $
, we must have
for all i. We denote by
![]() $v_{1}^i,\ldots ,v_n^i$
the columns of
$v_{1}^i,\ldots ,v_n^i$
the columns of
![]() $g_{L_i}$
, which is a basis of
$g_{L_i}$
, which is a basis of
![]() $\Lambda _{L_i}$
, and by
$\Lambda _{L_i}$
, and by
![]() $w_1^i,\ldots ,w_n^i$
its dual basis. Recall that
$w_1^i,\ldots ,w_n^i$
its dual basis. Recall that
![]() $w_{k+1}^i,\ldots , w_n^i$
form a basis of
$w_{k+1}^i,\ldots , w_n^i$
form a basis of
![]() $\Lambda _{L_i}^\# \cap L_i^{\perp }$
. By (3.4), there exists a rational number
$\Lambda _{L_i}^\# \cap L_i^{\perp }$
. By (3.4), there exists a rational number
![]() $\alpha _i\in \mathbb {Q}^\times $
such that
$\alpha _i\in \mathbb {Q}^\times $
such that
To simplify notation, we set
![]() $\eta _i = \delta _{i,2}y_C$
.
$\eta _i = \delta _{i,2}y_C$
.
We first control the numbers
![]() $\alpha _i$
. From (3.1), we know that there are
$\alpha _i$
. From (3.1), we know that there are
![]() $h_i \in \mathbf {H}_{L_i}$
such that
$h_i \in \mathbf {H}_{L_i}$
such that
for some
![]() $g' \in \mathbf {P}_{n,k}(\mathbb {A})$
. For i large enough, there exist
$g' \in \mathbf {P}_{n,k}(\mathbb {A})$
. For i large enough, there exist
![]() $\varepsilon _i \in \mathbf {P}_{n,k}(\mathbb {R} \times \widehat {\mathbb {Z}})$
with
$\varepsilon _i \in \mathbf {P}_{n,k}(\mathbb {R} \times \widehat {\mathbb {Z}})$
with
![]() $g_{2,i} g_{L_i}^{-1} \rho _Q(h_i) g_{L_i} \eta _i= \varepsilon _i g'$
. We now fix a prime p so that
$g_{2,i} g_{L_i}^{-1} \rho _Q(h_i) g_{L_i} \eta _i= \varepsilon _i g'$
. We now fix a prime p so that
![]() $\rho _Q(h_{i,p}) g_{L_i} \eta _i= g_{L_i}\varepsilon _{i,p} g^{\prime }_p$
(as
$\rho _Q(h_{i,p}) g_{L_i} \eta _i= g_{L_i}\varepsilon _{i,p} g^{\prime }_p$
(as
![]() $g_{2,i} \in \mathbf {G}(\mathbb {R})$
). Applying
$g_{2,i} \in \mathbf {G}(\mathbb {R})$
). Applying
![]() $\rho _Q(h_{i,p})$
to (3.4), we obtain
$\rho _Q(h_{i,p})$
to (3.4), we obtain
Considering that the vectors
![]() $w^{i}_{k+1}\wedge \cdots \wedge w^{i}_n$
and
$w^{i}_{k+1}\wedge \cdots \wedge w^{i}_n$
and
![]() $e_{k+1} \wedge \cdots \wedge e_n$
are primitive (see, for example, [Reference CasselsCas97, Ch. 1, Lemma 2]) and that
$e_{k+1} \wedge \cdots \wedge e_n$
are primitive (see, for example, [Reference CasselsCas97, Ch. 1, Lemma 2]) and that
![]() $g_{L_i}$
and
$g_{L_i}$
and
![]() $g_p'$
have bounded denominators, this shows that the denominators and numerators of the numbers
$g_p'$
have bounded denominators, this shows that the denominators and numerators of the numbers
![]() $\alpha _i$
are bounded independently of i.
$\alpha _i$
are bounded independently of i.
We now compute the discriminant of the lattice spanned by
![]() $w^{i}_{k+1}, \ldots , w^{i}_n$
in two ways. First, note that, as
$w^{i}_{k+1}, \ldots , w^{i}_n$
in two ways. First, note that, as
![]() $w^{i}_{k+1},\ldots , w^{i}_n$
is a basis of
$w^{i}_{k+1},\ldots , w^{i}_n$
is a basis of
![]() $\Lambda _{L_i}^\# \cap L_i^\perp $
, the discriminant in question is equal to the discriminant of
$\Lambda _{L_i}^\# \cap L_i^\perp $
, the discriminant in question is equal to the discriminant of
![]() $\Lambda _{L_i}^\# \cap L_i^\perp $
and hence
$\Lambda _{L_i}^\# \cap L_i^\perp $
and hence
![]() $\asymp \mathrm {disc}_Q(L_i)$
. For the second way, observe that, by (3.5), the discriminant of the lattice spanned by
$\asymp \mathrm {disc}_Q(L_i)$
. For the second way, observe that, by (3.5), the discriminant of the lattice spanned by
![]() $w^{i}_{k+1}, \ldots , w^{i}_n$
is given by
$w^{i}_{k+1}, \ldots , w^{i}_n$
is given by
![]() $\alpha _i^{-1}$
multiplied by the determinant of the matrix with entries
$\alpha _i^{-1}$
multiplied by the determinant of the matrix with entries
(One conceptual way to see this is the following: the bilinear form
![]() $\langle \cdot ,\cdot \rangle _Q$
induces a bilinear form
$\langle \cdot ,\cdot \rangle _Q$
induces a bilinear form
![]() $\langle \cdot ,\cdot \rangle _{\bigwedge ^{n-k}Q}$
on the wedge product
$\langle \cdot ,\cdot \rangle _{\bigwedge ^{n-k}Q}$
on the wedge product
![]() $\bigwedge ^{n-k}\mathbb {Q}^n$
by defining it on pure wedges through
$\bigwedge ^{n-k}\mathbb {Q}^n$
by defining it on pure wedges through
This definition asserts that the discriminant of a rank
![]() $n-k$
lattice is the quadratic value of the wedge product of any of its bases. Equation 3.6 is then obtained by replacing one of the wedges in
$n-k$
lattice is the quadratic value of the wedge product of any of its bases. Equation 3.6 is then obtained by replacing one of the wedges in
![]() $\langle w_{k+1}^i\wedge \cdots \wedge w_n^i,w_{k+1}^i\wedge \cdots \wedge w_n^i \rangle _{\bigwedge ^{n-k}Q}$
via (3.5).)
$\langle w_{k+1}^i\wedge \cdots \wedge w_n^i,w_{k+1}^i\wedge \cdots \wedge w_n^i \rangle _{\bigwedge ^{n-k}Q}$
via (3.5).)
To compute this determinant, write
![]() $\eta _i e_j = \sum _{\ell } a_{\ell j}^i e_\ell $
for all
$\eta _i e_j = \sum _{\ell } a_{\ell j}^i e_\ell $
for all
![]() $j> k$
so that
$j> k$
so that
Using that
![]() $\{w^{i}_l\}$
are dual vectors to
$\{w^{i}_l\}$
are dual vectors to
![]() $\{v^{i}_l\}$
, we compute
$\{v^{i}_l\}$
, we compute
for all
![]() $m,j> k$
. This implies that the determinant of the matrix with entries (3.6) is equal to the determinant of the lower right-hand block of the matrix
$m,j> k$
. This implies that the determinant of the matrix with entries (3.6) is equal to the determinant of the lower right-hand block of the matrix
![]() $\eta _i$
. As the latter is equal to one, we conclude that the discriminant of the lattice spanned by
$\eta _i$
. As the latter is equal to one, we conclude that the discriminant of the lattice spanned by
![]() $w^{i}_{k+1}\wedge \cdots \wedge w^{i}_n$
is equal to
$w^{i}_{k+1}\wedge \cdots \wedge w^{i}_n$
is equal to
![]() $\alpha _i^{-1}$
.
$\alpha _i^{-1}$
.
To summarize, we have established the identity
Since the left-hand side of this identity goes to infinity as
![]() $i \to \infty $
(because
$i \to \infty $
(because
![]() $\asymp \mathrm {disc}_Q(L_i)$
) whereas the right-hand side is bounded, we have reached a contradiction. It follows that
$\asymp \mathrm {disc}_Q(L_i)$
) whereas the right-hand side is bounded, we have reached a contradiction. It follows that
![]() $\mathbf {M} = \mathbf {G}$
, and hence the proof of Theorem 3.1 is complete.
$\mathbf {M} = \mathbf {G}$
, and hence the proof of Theorem 3.1 is complete.
4 The dynamical version of the theorem in codimension 2
In the following, we prove the analogue of Theorem 3.1 for the case
![]() $k =2 $
and
$k =2 $
and
![]() $n-k \geq 3$
(i.e.
$n-k \geq 3$
(i.e.
![]() $n \geq 5$
) ignoring the unipotent radical (cf. Remark 1.12); the case
$n \geq 5$
) ignoring the unipotent radical (cf. Remark 1.12); the case
![]() $n-k =2$
,
$n-k =2$
,
![]() $k \geq 3$
is completely analogous and can be deduced by passing to the orthogonal complement. Contrary to cases treated in §3, the groups whose dynamics we use are not semisimple and have a non-trivial central torus (see also Remark 1.6).
$k \geq 3$
is completely analogous and can be deduced by passing to the orthogonal complement. Contrary to cases treated in §3, the groups whose dynamics we use are not semisimple and have a non-trivial central torus (see also Remark 1.6).
Recall the following notation (for
![]() $k=2$
).
$k=2$
).
-
•
 $\bar {\mathbf {G}} = \mathrm {Spin}_Q \times \mathrm {SL}_2 \times \mathrm {SL}_{n-2}$
(here, the ambient group).
$\bar {\mathbf {G}} = \mathrm {Spin}_Q \times \mathrm {SL}_2 \times \mathrm {SL}_{n-2}$
(here, the ambient group). -
•
 $\boldsymbol{\Delta \bar {\mathbf H}}_L = \{ (h,\psi _{1,L}(h),\psi _{2,L}(h)): h \in \mathbf {H}_L\}$
(here, the acting group) for any
$\boldsymbol{\Delta \bar {\mathbf H}}_L = \{ (h,\psi _{1,L}(h),\psi _{2,L}(h)): h \in \mathbf {H}_L\}$
(here, the acting group) for any
 $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
, where
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
, where
 $\psi _{1,L}$
(respectively,
$\psi _{1,L}$
(respectively,
 $\psi _{2,L}$
) is roughly the restriction of the action of h to L (respectively,
$\psi _{2,L}$
) is roughly the restriction of the action of h to L (respectively,
 $L^\perp $
) (cf. §2.3).
$L^\perp $
) (cf. §2.3). -
• For any
 $L \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
, a choice of intermediate lattice
$L \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
, a choice of intermediate lattice
 $\mathbb {Z}^n \subset \Lambda _L \subset (\mathbb {Z}^n)^\#$
(also implicit in the definition of
$\mathbb {Z}^n \subset \Lambda _L \subset (\mathbb {Z}^n)^\#$
(also implicit in the definition of
 $\boldsymbol{\Delta \bar {\mathbf H}}_L $
). For simplicity, we also assume here that
$\boldsymbol{\Delta \bar {\mathbf H}}_L $
). For simplicity, we also assume here that
 $\Lambda _L \cap L = L(\mathbb {Z})$
and
$\Lambda _L \cap L = L(\mathbb {Z})$
and
 $\Lambda _L^\# \cap L^\perp = L^\perp (\mathbb {Z})$
; such a choice will be constructed later (cf. Proposition 6.6). Again, if Q is unimodular,
$\Lambda _L^\# \cap L^\perp = L^\perp (\mathbb {Z})$
; such a choice will be constructed later (cf. Proposition 6.6). Again, if Q is unimodular,
 $\Lambda _L = \mathbb {Z}^n$
satisfies this property.
$\Lambda _L = \mathbb {Z}^n$
satisfies this property.
Theorem 4.1. Let
![]() $L_i \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
for
$L_i \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
for
![]() $i \geq 1$
be an admissible sequence of rational subspaces and let
$i \geq 1$
be an admissible sequence of rational subspaces and let
![]() $g_i \in \bar {\mathbf {G}}(\mathbb {R})$
be such that
$g_i \in \bar {\mathbf {G}}(\mathbb {R})$
be such that
![]() $g_i \boldsymbol{\Delta \bar {\mathbf H}}_{L_i}(\mathbb {R}) g_i^{-1} = \boldsymbol{\Delta \bar {\mathbf H}}_{L_0}(\mathbb {R})$
. Let
$g_i \boldsymbol{\Delta \bar {\mathbf H}}_{L_i}(\mathbb {R}) g_i^{-1} = \boldsymbol{\Delta \bar {\mathbf H}}_{L_0}(\mathbb {R})$
. Let
![]() $\mu _i$
be the Haar probability measure on the closed orbit
$\mu _i$
be the Haar probability measure on the closed orbit
Then
![]() $\mu _i$
converges to the Haar probability measure on
$\mu _i$
converges to the Haar probability measure on
as
![]() $i \to \infty $
.
$i \to \infty $
.
We will structure the proof somewhat differently as equidistribution in the first component turns out to be the most difficult challenge in the proof. We fix an admissible sequence of subspaces
![]() $L_i$
and a prime p, as in the definition of admissibility.
$L_i$
and a prime p, as in the definition of admissibility.
Recall (cf. §2.1.1) that, for any
![]() $L \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
, the group
$L \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
, the group
![]() $\mathbf {H}_L$
is not semisimple but only reductive. Let us describe the center as well as the commutator subgroup of
$\mathbf {H}_L$
is not semisimple but only reductive. Let us describe the center as well as the commutator subgroup of
![]() $\mathbf {H}_L$
. Define the pointwise stabilizer subgroup
$\mathbf {H}_L$
. Define the pointwise stabilizer subgroup
The center of
![]() $\mathbf {H}_L$
is equal to
$\mathbf {H}_L$
is equal to
![]() $\mathbf {H}^{\mathrm {pt}}_{L^\perp }$
, which we denote by
$\mathbf {H}^{\mathrm {pt}}_{L^\perp }$
, which we denote by
![]() $\mathbf {T}_L$
for simplicity, as it is abelian in this case. The commutator subgroup of
$\mathbf {T}_L$
for simplicity, as it is abelian in this case. The commutator subgroup of
![]() $\mathbf {H}_L$
is the semisimple group
$\mathbf {H}_L$
is the semisimple group
![]() $\mathbf {H}^{\mathrm {pt}}_L$
and
$\mathbf {H}^{\mathrm {pt}}_L$
and
![]() $\mathbf {H}_L$
is isogenous to
$\mathbf {H}_L$
is isogenous to
![]() $\mathbf {H}^{\mathrm {pt}}_L \times \mathbf {T}_L$
(see Remark 2.1). As in §3, one can use the measure rigidity result of Gorodnik and Oh [Reference Gorodnik and OhGO11], this time for subgroups of the form
$\mathbf {H}^{\mathrm {pt}}_L \times \mathbf {T}_L$
(see Remark 2.1). As in §3, one can use the measure rigidity result of Gorodnik and Oh [Reference Gorodnik and OhGO11], this time for subgroups of the form
![]() $\mathbf {H}^{\mathrm {pt}}_L$
. These are, however, non-maximal so that we need to put in extra effort to rule out intermediate groups. (Roughly speaking, the obstacle to overcome are ‘short vectors’ in L. Ellenberg and Venkatesh [Reference Ellenberg and VenkateshEV08] prove the theorem we are alluding to here assuming that L does not contain ‘short vectors’ (see also Proposition 4.7).) Here, we use an averaging procedure involving the torus
$\mathbf {H}^{\mathrm {pt}}_L$
. These are, however, non-maximal so that we need to put in extra effort to rule out intermediate groups. (Roughly speaking, the obstacle to overcome are ‘short vectors’ in L. Ellenberg and Venkatesh [Reference Ellenberg and VenkateshEV08] prove the theorem we are alluding to here assuming that L does not contain ‘short vectors’ (see also Proposition 4.7).) Here, we use an averaging procedure involving the torus
![]() $\mathbf {T}_L$
as well as Duke’s theorem [Reference DukeDuk88] to show that these obstructions typically do not occur.
$\mathbf {T}_L$
as well as Duke’s theorem [Reference DukeDuk88] to show that these obstructions typically do not occur.
We now outline the structure of the proof.
-
• In §4.1, we show (in Lemma 4.4) that it is sufficient to prove equidistribution in each of the factors of
 $\bar {\mathbf {G}}$
, that is, to show equidistribution of the projections of the packets in Theorem 4.1 to (4.1)As mentioned in Remark 1.7, we use the elementary fact that ergodic systems are disjoint from trivial systems for this reduction (see Lemma 4.2).
$\bar {\mathbf {G}}$
, that is, to show equidistribution of the projections of the packets in Theorem 4.1 to (4.1)As mentioned in Remark 1.7, we use the elementary fact that ergodic systems are disjoint from trivial systems for this reduction (see Lemma 4.2).
-
• To prove equidistribution in each of the factors of
 $\bar {\mathbf {G}}$
, we first note that equidistribution in the third factor can be verified as in §3, Proposition 3.3. Equidistribution in the second factor turns out to be a variant of Duke’s theorem [Reference DukeDuk88], which we discuss in §4.2.
$\bar {\mathbf {G}}$
, we first note that equidistribution in the third factor can be verified as in §3, Proposition 3.3. Equidistribution in the second factor turns out to be a variant of Duke’s theorem [Reference DukeDuk88], which we discuss in §4.2. -
• Due to the difficulties described above, equidistribution in the first factor of
 $\bar {\mathbf {G}}$
is the hardest to prove (cf. §4.3) and implies Theorem 4.1 by the first two items in this list. In §4.3.2, we collect a useful corollary of the above variant of Duke’s theorem which we then use in Lemma 4.10 to prove that the subspaces in the packet do not contain short vectors on average.
$\bar {\mathbf {G}}$
is the hardest to prove (cf. §4.3) and implies Theorem 4.1 by the first two items in this list. In §4.3.2, we collect a useful corollary of the above variant of Duke’s theorem which we then use in Lemma 4.10 to prove that the subspaces in the packet do not contain short vectors on average.
4.1 Reduction to individual equidistribution
As explained, we begin by reducing Theorem 4.1 to the corresponding equidistribution statement in each of the factors of
![]() $\bar {\mathbf {G}}$
. To this end, we will use the following elementary fact from abstract ergodic theory.
$\bar {\mathbf {G}}$
. To this end, we will use the following elementary fact from abstract ergodic theory.
Lemma 4.2. Let
![]() $\mathsf {X}_1 = (X,\mathcal {B}_1,\mu _1,\kern-1pt T_1)$
and
$\mathsf {X}_1 = (X,\mathcal {B}_1,\mu _1,\kern-1pt T_1)$
and
![]() $ \mathsf {X}_2 = (X_2,\mathcal {B}_2,\mu _2,\kern-1pt T_2)$
be measure-preserving systems. Suppose that
$ \mathsf {X}_2 = (X_2,\mathcal {B}_2,\mu _2,\kern-1pt T_2)$
be measure-preserving systems. Suppose that
![]() $\mathsf {X}_1$
is ergodic and that
$\mathsf {X}_1$
is ergodic and that
![]() $\mathsf {X}_2$
is trivial (that is,
$\mathsf {X}_2$
is trivial (that is,
![]() $T_2(x) = x$
for
$T_2(x) = x$
for
![]() $\mu _2$
-almost every
$\mu _2$
-almost every
![]() $x \in X_2)$
. Then the only joining of
$x \in X_2)$
. Then the only joining of
![]() $\mathsf {X}_1$
and
$\mathsf {X}_1$
and
![]() $\mathsf {X}_2$
is
$\mathsf {X}_2$
is
![]() $\mu _1 \times \mu _2$
.
$\mu _1 \times \mu _2$
.
Proof. Let
![]() $\nu $
be a joining and let
$\nu $
be a joining and let
![]() $A_1 \times A_2 \subset X_1 \times X_2$
be measurable. It suffices to show that
$A_1 \times A_2 \subset X_1 \times X_2$
be measurable. It suffices to show that
![]() $\nu (A_1 \times A_2) = \mu _1(A_1)\mu _2(A_2)$
. By
$\nu (A_1 \times A_2) = \mu _1(A_1)\mu _2(A_2)$
. By
![]() $T_1 \times T_2$
-invariance of
$T_1 \times T_2$
-invariance of
![]() $\nu $
,
$\nu $
,
 $$ \begin{align*} \nu(A_1 \times A_2) &= \int_{X_1 \times X_2} 1_{A_1}(x_1) 1_{A_2}(x_2) \, \mathrm{d} \nu(x_1,x_2) \\ &= \frac{1}{M} \sum_{m=0}^{M-1} \int_{X_1 \times X_2} 1_{A_1}(T_1^{m}x_1) 1_{A_2}(T_2^{m}x_2) \, \mathrm{d} \nu(x_1,x_2). \end{align*} $$
$$ \begin{align*} \nu(A_1 \times A_2) &= \int_{X_1 \times X_2} 1_{A_1}(x_1) 1_{A_2}(x_2) \, \mathrm{d} \nu(x_1,x_2) \\ &= \frac{1}{M} \sum_{m=0}^{M-1} \int_{X_1 \times X_2} 1_{A_1}(T_1^{m}x_1) 1_{A_2}(T_2^{m}x_2) \, \mathrm{d} \nu(x_1,x_2). \end{align*} $$
As
![]() $\mathsf {X}_1$
is ergodic, there is a
$\mathsf {X}_1$
is ergodic, there is a
![]() $\mu _1$
-conull set
$\mu _1$
-conull set
![]() $B_1 \subset X_1$
with
$B_1 \subset X_1$
with
 $$ \begin{align*} \frac{1}{M} \sum_{m=0}^{M-1} 1_{A_1}(T_1^m(x)) \to \mu_1(A_1) \end{align*} $$
$$ \begin{align*} \frac{1}{M} \sum_{m=0}^{M-1} 1_{A_1}(T_1^m(x)) \to \mu_1(A_1) \end{align*} $$
for every
![]() $x \in B_1$
, by Birkhoff’s ergodic theorem. As
$x \in B_1$
, by Birkhoff’s ergodic theorem. As
![]() $\mathsf {X}_2$
is trivial, there is a
$\mathsf {X}_2$
is trivial, there is a
![]() $\mu _2$
-conull set
$\mu _2$
-conull set
![]() $B_2$
with
$B_2$
with
![]() $T_2(x) = x$
for all
$T_2(x) = x$
for all
![]() $x \in B_2$
. We let
$x \in B_2$
. We let
![]() $B = B_1 \times B_2$
and note that B has full measure as it is the intersection of the full-measure sets
$B = B_1 \times B_2$
and note that B has full measure as it is the intersection of the full-measure sets
![]() $B_1 \times X_2$
and
$B_1 \times X_2$
and
![]() $X_1 \times B_2$
(we use, here, that
$X_1 \times B_2$
(we use, here, that
![]() $\nu $
is a joining). Therefore,
$\nu $
is a joining). Therefore,
 $$ \begin{align*} \nu(A_1 \times A_2) &=\frac{1}{M} \sum_{m=0}^{M-1} \int_{B} 1_{A_1}(T_1^{m}x_1) 1_{A_2}(T_2^{m}x_2) \, \mathrm{d} \nu(x_1,x_2)\\ &= \frac{1}{M} \sum_{m=0}^{M-1} \int_{B} 1_{A_1}(T_1^{m}x_1) 1_{A_2}(x_2) \, \mathrm{d} \nu(x_1,x_2) \\ &= \int_{B} \frac{1}{M} \sum_{m=0}^{M-1} 1_{A_1}(T_1^{m}x_1) 1_{A_2}(x_2) \, \mathrm{d} \nu(x_1,x_2)\\ & \to \int_{B} \mu_1(A_1) 1_{A_2}(x_2) \, \mathrm{d} \nu(x_1,x_2) = \mu_1(A_1) \mu_2(A_2), \end{align*} $$
$$ \begin{align*} \nu(A_1 \times A_2) &=\frac{1}{M} \sum_{m=0}^{M-1} \int_{B} 1_{A_1}(T_1^{m}x_1) 1_{A_2}(T_2^{m}x_2) \, \mathrm{d} \nu(x_1,x_2)\\ &= \frac{1}{M} \sum_{m=0}^{M-1} \int_{B} 1_{A_1}(T_1^{m}x_1) 1_{A_2}(x_2) \, \mathrm{d} \nu(x_1,x_2) \\ &= \int_{B} \frac{1}{M} \sum_{m=0}^{M-1} 1_{A_1}(T_1^{m}x_1) 1_{A_2}(x_2) \, \mathrm{d} \nu(x_1,x_2)\\ & \to \int_{B} \mu_1(A_1) 1_{A_2}(x_2) \, \mathrm{d} \nu(x_1,x_2) = \mu_1(A_1) \mu_2(A_2), \end{align*} $$
as claimed.
We aim to apply Lemma 4.2 to any weak
![]() ${}^\ast $
-limit
${}^\ast $
-limit
![]() $\mu $
of the measures in Theorem 4.1. Thus, we need to establish some invariance of the latter. Let p be as in the definition of admissibility.
$\mu $
of the measures in Theorem 4.1. Thus, we need to establish some invariance of the latter. Let p be as in the definition of admissibility.
Lemma 4.3. There exists
![]() $g \in \mathrm {GL}_n(\mathbb {Q}_p)$
with the following property. Let
$g \in \mathrm {GL}_n(\mathbb {Q}_p)$
with the following property. Let
![]() $L \in \mathrm {Gr}_{n,2}(\mathbb {Q}_p)$
be the subspace spanned by the first two columns of g. Then
$L \in \mathrm {Gr}_{n,2}(\mathbb {Q}_p)$
be the subspace spanned by the first two columns of g. Then
![]() $\mu $
is invariant under the subgroup of
$\mu $
is invariant under the subgroup of
![]() $\boldsymbol{\Delta \bar {\mathbf H}}_L(\mathbb {Q}_p) \subset \bar {\mathbf {G}}(\mathbb {Q}_p)$
, where
$\boldsymbol{\Delta \bar {\mathbf H}}_L(\mathbb {Q}_p) \subset \bar {\mathbf {G}}(\mathbb {Q}_p)$
, where
Moreover, the
![]() $\mathbb {Q}_p$
-group
$\mathbb {Q}_p$
-group
![]() $\boldsymbol{\Delta \bar {\mathbf H}}_L$
is strongly isotropic.
$\boldsymbol{\Delta \bar {\mathbf H}}_L$
is strongly isotropic.
Proof. First, we prove that there exists a compact subset
![]() $K \subset \mathrm {GL}_n(\mathbb {Q}_p)$
such that
$K \subset \mathrm {GL}_n(\mathbb {Q}_p)$
such that
![]() $g_{L_i} \in K$
for all
$g_{L_i} \in K$
for all
![]() $i \in \mathbb {N}$
. Recall that
$i \in \mathbb {N}$
. Recall that
![]() $g_{L_i}$
consists of a basis of an intermediate lattice
$g_{L_i}$
consists of a basis of an intermediate lattice
![]() $\mathbb {Z}^n \subseteq \Lambda _{L_i} \subseteq (\mathbb {Z}^n)^\#$
(cf. §2.3). The set K of elements
$\mathbb {Z}^n \subseteq \Lambda _{L_i} \subseteq (\mathbb {Z}^n)^\#$
(cf. §2.3). The set K of elements
![]() $g \in \mathrm {GL}_n(\mathbb {Q}_p)$
with
$g \in \mathrm {GL}_n(\mathbb {Q}_p)$
with
![]() $\mathbb {Z}_p^n \subset g\mathbb {Z}_p^n \subset (\mathbb {Z}_p^n)^\#$
is compact (in fact, it consists of finitely many cosets modulo
$\mathbb {Z}_p^n \subset g\mathbb {Z}_p^n \subset (\mathbb {Z}_p^n)^\#$
is compact (in fact, it consists of finitely many cosets modulo
![]() $\mathrm {GL}_n(\mathbb {Z}_p)$
on the right).
$\mathrm {GL}_n(\mathbb {Z}_p)$
on the right).
By compactness of K, we may assume (by passing to a subsequence) that the sequence
![]() $(g_{L_i})_{i \in \mathbb {N}}$
converges to some
$(g_{L_i})_{i \in \mathbb {N}}$
converges to some
![]() $g \in K$
. Let L denote the
$g \in K$
. Let L denote the
![]() $\mathbb {Q}_p$
-plane spanned by the first two columns of g. Note that
$\mathbb {Q}_p$
-plane spanned by the first two columns of g. Note that
![]() $\mu $
is
$\mu $
is
![]() $\boldsymbol{\Delta \bar {\mathbf H}}_L(\mathbb {Q}_p)$
-invariant because each
$\boldsymbol{\Delta \bar {\mathbf H}}_L(\mathbb {Q}_p)$
-invariant because each
![]() $\mu _i$
is
$\mu _i$
is
![]() $\boldsymbol{\Delta \bar {\mathbf H}}_{L_i}(\mathbb {Q}_p)$
-invariant. Therefore, we are left to show that L is non-degenerate and
$\boldsymbol{\Delta \bar {\mathbf H}}_{L_i}(\mathbb {Q}_p)$
-invariant. Therefore, we are left to show that L is non-degenerate and
![]() $\boldsymbol{\Delta \bar {\mathbf H}}_L(\mathbb {Q}_p)$
is strongly isotropic.
$\boldsymbol{\Delta \bar {\mathbf H}}_L(\mathbb {Q}_p)$
is strongly isotropic.
We observe that L and
![]() $L^{\perp }$
are non-degenerate. Indeed, since
$L^{\perp }$
are non-degenerate. Indeed, since
![]() $g_{L_i} \rightarrow g$
, there exist
$g_{L_i} \rightarrow g$
, there exist
![]() $\mathbb {Z}_p$
-bases of the subspaces
$\mathbb {Z}_p$
-bases of the subspaces
![]() $L_i$
which converge towards a basis of L. Taking discriminants of
$L_i$
which converge towards a basis of L. Taking discriminants of
![]() $L_i$
and L with respect to these bases, we obtain
$L_i$
and L with respect to these bases, we obtain
Since
![]() $\mathbb {Z}_p^{\times }/(\mathbb {Z}_p^{\times })^2$
is discrete,
$\mathbb {Z}_p^{\times }/(\mathbb {Z}_p^{\times })^2$
is discrete,
![]() $\mathrm {disc}_{p,Q}(L_i)$
is eventually constant and therefore
$\mathrm {disc}_{p,Q}(L_i)$
is eventually constant and therefore
![]() $\mathrm {disc}_{p,Q}(L) = \mathrm {disc}_{p,Q}(L_i)$
for i large enough; non-degeneracy of L follows. In particular,
$\mathrm {disc}_{p,Q}(L) = \mathrm {disc}_{p,Q}(L_i)$
for i large enough; non-degeneracy of L follows. In particular,
![]() $L^\perp $
is non-degenerate.
$L^\perp $
is non-degenerate.
We may now use Corollary 2.8 to show that
![]() $\boldsymbol{\Delta \bar {\mathbf H}}_L$
or, equivalently, that
$\boldsymbol{\Delta \bar {\mathbf H}}_L$
or, equivalently, that
![]() $\mathbf {H}_{L}$
is strongly isotropic. Since
$\mathbf {H}_{L}$
is strongly isotropic. Since
![]() $\mathbf {H}_{L_i}$
is strongly isotropic at p, the quadratic spaces
$\mathbf {H}_{L_i}$
is strongly isotropic at p, the quadratic spaces
![]() $(Q|_{L_i}, L_i)$
and
$(Q|_{L_i}, L_i)$
and
![]() $(Q|_{L_i^{\perp }}, L_i^{\perp })$
are isotropic over
$(Q|_{L_i^{\perp }}, L_i^{\perp })$
are isotropic over
![]() $\mathbb {Q}_p$
. By isotropy of the spaces
$\mathbb {Q}_p$
. By isotropy of the spaces
![]() $(Q|_{L_i}, L_i)$
, we have a sequence of non-zero primitive vectors
$(Q|_{L_i}, L_i)$
, we have a sequence of non-zero primitive vectors
![]() $v_i \in L_i(\mathbb {Z}_p)$
such that
$v_i \in L_i(\mathbb {Z}_p)$
such that
![]() $Q(v_i)=0$
(after multiplying with denominators). By compactness of
$Q(v_i)=0$
(after multiplying with denominators). By compactness of
![]() $\mathbb {Z}_p^n \setminus p\mathbb {Z}_p^n$
, the sequence
$\mathbb {Z}_p^n \setminus p\mathbb {Z}_p^n$
, the sequence
![]() $v_i$
admits a limit
$v_i$
admits a limit
![]() $v\in \mathbb {Z}_p^n \setminus p\mathbb {Z}_p^n$
after passing to a subsequence. This limit clearly satisfies
$v\in \mathbb {Z}_p^n \setminus p\mathbb {Z}_p^n$
after passing to a subsequence. This limit clearly satisfies
![]() $v \in L(\mathbb {Z}_p)$
and
$v \in L(\mathbb {Z}_p)$
and
![]() $Q(v) =0$
, so
$Q(v) =0$
, so
![]() $(Q|_L, L)$
is isotropic. An identical argument proves that
$(Q|_L, L)$
is isotropic. An identical argument proves that
![]() $(Q|_{L^{\perp }}, L^{\perp })$
is also isotropic, which proves (cf. Corollary 2.8) that
$(Q|_{L^{\perp }}, L^{\perp })$
is also isotropic, which proves (cf. Corollary 2.8) that
![]() $\mathbf {H}_{L}$
is a strongly isotropic group. The proof is complete.
$\mathbf {H}_{L}$
is a strongly isotropic group. The proof is complete.
Recall that
![]() $\psi _{1,L},\psi _{2,L}$
denote the epimorphisms
$\psi _{1,L},\psi _{2,L}$
denote the epimorphisms
![]() $\mathbf {H}_{L_i} \to \mathrm {SO}_{q_{L_i}}$
,
$\mathbf {H}_{L_i} \to \mathrm {SO}_{q_{L_i}}$
,
![]() $\mathbf {H}_{L_i} \to \mathrm {SO}_{q_{L_i^\perp }}$
, respectively.
$\mathbf {H}_{L_i} \to \mathrm {SO}_{q_{L_i^\perp }}$
, respectively.
Lemma 4.4. Suppose that individual equidistribution holds, i.e. that:
-
(1)
 $g_{i,1}\mathbf {H}_{L_i}(\mathbb {A}) \mathrm {Spin}_Q(\mathbb {Q})$
is equidistributed in
$g_{i,1}\mathbf {H}_{L_i}(\mathbb {A}) \mathrm {Spin}_Q(\mathbb {Q})$
is equidistributed in
 ;
; -
(2)
 $g_{i,2}\psi _{1,L}(\mathbf {H}_{L_i}(\mathbb {A})) \mathrm {SL}_2(\mathbb {Q})$
is equidistributed in
$g_{i,2}\psi _{1,L}(\mathbf {H}_{L_i}(\mathbb {A})) \mathrm {SL}_2(\mathbb {Q})$
is equidistributed in
 ; and
; and -
(3)
 $g_{i,3}\psi _{2,L}(\mathbf {H}_{L_i}(\mathbb {A})) \mathrm {SL}_{n-2}(\mathbb {Q})$
is equidistributed in
$g_{i,3}\psi _{2,L}(\mathbf {H}_{L_i}(\mathbb {A})) \mathrm {SL}_{n-2}(\mathbb {Q})$
is equidistributed in
 .
.
Then Theorem 4.1 holds.
Proof. Let
![]() $\mu $
be a weak
$\mu $
be a weak
![]() ${}^\ast $
-limit and choose L as in Lemma 4.3. By assumption,
${}^\ast $
-limit and choose L as in Lemma 4.3. By assumption,
![]() $\mu $
is a joining with respect to the Haar measures on each factor. We proceed in two steps and apply Lemma 4.2 once in each step.
$\mu $
is a joining with respect to the Haar measures on each factor. We proceed in two steps and apply Lemma 4.2 once in each step.
For the first step, we choose
![]() $h \in \mathbf {H}_{L}(\mathbb {Q}_p)$
, which acts trivially on L but non-trivially on
$h \in \mathbf {H}_{L}(\mathbb {Q}_p)$
, which acts trivially on L but non-trivially on
![]() $L^\perp $
. As
$L^\perp $
. As
![]() $\mathbf {H}_{L}(\mathbb {Q}_p)$
is strongly isotropic, we can choose h so that it is unipotent and not contained in any normal subgroup of
$\mathbf {H}_{L}(\mathbb {Q}_p)$
is strongly isotropic, we can choose h so that it is unipotent and not contained in any normal subgroup of
![]() $\mathrm {Spin}_Q(\mathbb {Q}_p)$
. Since
$\mathrm {Spin}_Q(\mathbb {Q}_p)$
. Since
![]() $\mathrm {Spin}_Q$
is simply connected and
$\mathrm {Spin}_Q$
is simply connected and
![]() $\mathrm {Spin}_Q(\mathbb {Q}_p)$
is isotropic,
$\mathrm {Spin}_Q(\mathbb {Q}_p)$
is isotropic,
![]() $\mathrm {Spin}_Q$
has strong approximation with respect to
$\mathrm {Spin}_Q$
has strong approximation with respect to
![]() $\{p\}$
(see, for example, [Reference Platonov and RapinchukPR94, Theorem 7.12]). In particular,
$\{p\}$
(see, for example, [Reference Platonov and RapinchukPR94, Theorem 7.12]). In particular,
![]() $\mathrm {Spin}_Q(\mathbb {Q}_p)$
acts ergodically on
$\mathrm {Spin}_Q(\mathbb {Q}_p)$
acts ergodically on
![]() with respect to the Haar measure on
with respect to the Haar measure on
![]() $X_1$
. By Mautner’s phenomenon (see [Reference Margulis and TomanovMT96, §2] for this instance), h also acts ergodically. Embedding h diagonally (using the embedding in Lemma 4.3), we can apply Lemma 4.2 for
$X_1$
. By Mautner’s phenomenon (see [Reference Margulis and TomanovMT96, §2] for this instance), h also acts ergodically. Embedding h diagonally (using the embedding in Lemma 4.3), we can apply Lemma 4.2 for
![]() $X_1$
, as above, and for
$X_1$
, as above, and for
![]() and obtain that the pushforward of
and obtain that the pushforward of
![]() $\mu $
to
$\mu $
to
![]() $X_1 \times X_2$
is the Haar measure.
$X_1 \times X_2$
is the Haar measure.
For the second step, we proceed similarly. Choose
![]() $h \in \mathbf {H}_{L}(\mathbb {Q}_p)$
, which acts trivially on
$h \in \mathbf {H}_{L}(\mathbb {Q}_p)$
, which acts trivially on
![]() $L^\perp $
but non-trivially on L. One checks that h acts ergodically on
$L^\perp $
but non-trivially on L. One checks that h acts ergodically on
![]() $X_1 \times X_2$
(via
$X_1 \times X_2$
(via
![]() $\pi _2(g^{-1}\rho _Q(h^{-1})g)^t$
on the second factor; cf. Lemma 4.3). Applying Lemma 4.2 again for
$\pi _2(g^{-1}\rho _Q(h^{-1})g)^t$
on the second factor; cf. Lemma 4.3). Applying Lemma 4.2 again for
![]() $X_1 \times X_2$
and for
$X_1 \times X_2$
and for
![]() , we obtain the claim.
, we obtain the claim.
We prove the conditions of Lemma 4.4 in an order that is potentially peculiar at first sight. The third assertion can be proved exactly as in §3 by applying [Reference Gorodnik and OhGO11] (see Proposition 3.3) so we omit it here.
4.2 Individual equidistribution in the second factor
The aim of this section is to prove the second assertion of Lemma 4.4. It follows from Duke’s theorem [Reference DukeDuk88] and its generalizations (see, for example, [Reference Einsiedler, Lindenstrauss, Michel and VenkateshELMV11, Reference Harcos and MichelHM06]. Note that
Although the right-hand side is equidistributed by Duke’s theorem (specifically, for example, by [Reference Einsiedler, Lindenstrauss, Michel and VenkateshELMV11, Theorem 4.6] or—as we assume a splitting condition—by [Reference WieserWie19]), one needs to verify that the left-hand side has sufficiently large ‘volume’.
Proposition 4.5. For
![]() $L \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
and any field K of characteristic zero, the image
$L \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
and any field K of characteristic zero, the image
![]() $\psi _{1,L}(\mathbf {H}_{L}(K))$
contains the group of squares in the abelian group
$\psi _{1,L}(\mathbf {H}_{L}(K))$
contains the group of squares in the abelian group
![]() $\mathrm {SO}_{q_{L}}(K)$
.
$\mathrm {SO}_{q_{L}}(K)$
.
Proof. The proof is surprisingly involved. First, observe that
![]() $\psi _{1,L}(\mathbf {H}_L(K))$
contains
$\psi _{1,L}(\mathbf {H}_L(K))$
contains
![]() $\psi _{1,L}(\mathbf {T}_L(K))$
, which we now identify as the set of squares in
$\psi _{1,L}(\mathbf {T}_L(K))$
, which we now identify as the set of squares in
![]() $\mathrm {SO}_{q_{L}}(K)$
.
$\mathrm {SO}_{q_{L}}(K)$
.
We identify the torus
![]() $\mathbf {T}_{L}$
in terms of the Clifford algebra. Denote by
$\mathbf {T}_{L}$
in terms of the Clifford algebra. Denote by
![]() $\mathcal {C}$
(respectively,
$\mathcal {C}$
(respectively,
![]() $\mathcal {C}^0$
) the Clifford algebra of Q (respectively, the even Clifford algebra of Q). Let
$\mathcal {C}^0$
) the Clifford algebra of Q (respectively, the even Clifford algebra of Q). Let
![]() $v_1,v_2$
be an orthogonal basis of L and complete it into an orthogonal basis of
$v_1,v_2$
be an orthogonal basis of L and complete it into an orthogonal basis of
![]() $\mathbb {Q}^n$
. Consider
$\mathbb {Q}^n$
. Consider
![]() $X = v_1v_2 \in (\mathcal {C}^0)^\times $
(L is non-degenerate), which satisfies the relationships
$X = v_1v_2 \in (\mathcal {C}^0)^\times $
(L is non-degenerate), which satisfies the relationships
for all
![]() $i>2$
. Moreover,
$i>2$
. Moreover,
![]() $X^2 = -Q(v_1)Q(v_2) \in \mathbb {Q}^\times $
. Denote by
$X^2 = -Q(v_1)Q(v_2) \in \mathbb {Q}^\times $
. Denote by
![]() $\sigma $
the standard involution on
$\sigma $
the standard involution on
![]() $\mathcal {C}$
. Then
$\mathcal {C}$
. Then
![]() $\sigma (X) = v_2 v_1 = -X$
.
$\sigma (X) = v_2 v_1 = -X$
.
It follows directly from (4.2) that, for all
![]() $a,b\in K$
, the element
$a,b\in K$
, the element
![]() $t = a+bX$
satisfies
$t = a+bX$
satisfies
![]() $tv_i = v_i t$
for
$tv_i = v_i t$
for
![]() $i>2$
. Also,
$i>2$
. Also,
 $$ \begin{align*} t v_1 \sigma(t) &= (a+bX)v_1(a-bX) = a^2v_1 +ab Xv_1 -abv_1 X -b^2 Xv_1 X\\ &=a^2 v_1 -2abQ(v_1) v_2 - b^2Q(v_1)Q(v_2) v_1 \in L, \end{align*} $$
$$ \begin{align*} t v_1 \sigma(t) &= (a+bX)v_1(a-bX) = a^2v_1 +ab Xv_1 -abv_1 X -b^2 Xv_1 X\\ &=a^2 v_1 -2abQ(v_1) v_2 - b^2Q(v_1)Q(v_2) v_1 \in L, \end{align*} $$
and similarly for
![]() $v_2$
. Therefore,
$v_2$
. Therefore,
![]() $t \in \mathbf {T}_L$
if and only if
$t \in \mathbf {T}_L$
if and only if
We set
and embed F into
![]() $\mathcal {C}^0$
via
$\mathcal {C}^0$
via
![]() $\sqrt {-\mathrm {disc}_Q(L)} \mapsto X$
. The non-trivial Galois automorphism on F is then given by
$\sqrt {-\mathrm {disc}_Q(L)} \mapsto X$
. The non-trivial Galois automorphism on F is then given by
![]() $\sigma |_F$
. To summarize, we obtain
$\sigma |_F$
. To summarize, we obtain
Also, recall that the special Clifford group surjects onto
![]() $\mathrm {SO}_Q$
, so that one may show analogously that
$\mathrm {SO}_Q$
, so that one may show analogously that
The proposition then follows from Hilbert’s theorem 90, as in the proof of [Reference WieserWie19, Lemma 7.2].
Corollary 4.6. The orbits
equidistribute as
![]() $i \to \infty $
.
$i \to \infty $
.
Proof. We deduce the corollary from existing literature and Proposition 4.5. We first claim that, as
![]() $i \to \infty $
, the sets
$i \to \infty $
, the sets
are equidistributed. By Proposition 4.5, the abelian group
![]() $\mathrm {SO}_{q_{L_i}}(\widehat {\mathbb {Z}})\psi _{1,L}(\mathbf {H}_{L_i}(\mathbb {A}))$
contains the group
$\mathrm {SO}_{q_{L_i}}(\widehat {\mathbb {Z}})\psi _{1,L}(\mathbf {H}_{L_i}(\mathbb {A}))$
contains the group
![]() $\mathrm {SO}_{q_{{ }_{L_i}}}(\widehat {\mathbb {Z}})\mathrm {SO}_{q_{{ }_{L_i}}}(\mathbb {A})^2$
, where
$\mathrm {SO}_{q_{{ }_{L_i}}}(\widehat {\mathbb {Z}})\mathrm {SO}_{q_{{ }_{L_i}}}(\mathbb {A})^2$
, where
![]() $\mathrm {SO}_{q_{{ }_{L_i}}}(\mathbb {A})^2$
denotes the group of squares.
$\mathrm {SO}_{q_{{ }_{L_i}}}(\mathbb {A})^2$
denotes the group of squares.
The orbit (4.3) is then a union of suborbits of the same form associated to these subgroups. Any sequence of such suborbits is equidistributed, for example, by [Reference Harcos and MichelHM06] as the volume is of size
![]() $\mathrm {disc}_Q(L_i)^{1/2+o(1)}$
. (Since the
$\mathrm {disc}_Q(L_i)^{1/2+o(1)}$
. (Since the
![]() $2$
-torsion of the Picard group of the order of discriminant
$2$
-torsion of the Picard group of the order of discriminant
![]() $\mathrm {disc}_Q(L_i)$
has size
$\mathrm {disc}_Q(L_i)$
has size
![]() $\mathrm {disc}_Q(L_i)^{o(1)}$
(see, for example, [Reference CasselsCas78, p. 342]), the squares form a subgroup of size
$\mathrm {disc}_Q(L_i)^{o(1)}$
(see, for example, [Reference CasselsCas78, p. 342]), the squares form a subgroup of size
![]() $\mathrm {disc}_Q(L_i)^{1/2+o(1)}$
.) We note that the result in [Reference Harcos and MichelHM06] allows smaller volumes (where the exponent
$\mathrm {disc}_Q(L_i)^{1/2+o(1)}$
.) We note that the result in [Reference Harcos and MichelHM06] allows smaller volumes (where the exponent
![]() $\tfrac 12$
can be replaced by
$\tfrac 12$
can be replaced by
![]() $\tfrac 12-\eta $
for some not too large
$\tfrac 12-\eta $
for some not too large
![]() $\eta>0$
). In the case needed here, one can also apply Linnik’s ergodic method as we assume a splitting condition at a fixed prime (see [Reference WieserWie19, §7]). By averaging, the claim in (4.3) follows. The corollary is implied by (4.3) and ergodicity of the Haar measure on
$\eta>0$
). In the case needed here, one can also apply Linnik’s ergodic method as we assume a splitting condition at a fixed prime (see [Reference WieserWie19, §7]). By averaging, the claim in (4.3) follows. The corollary is implied by (4.3) and ergodicity of the Haar measure on
![]() $\mathrm {SL}_2(\mathbb {A})/\mathrm {SL}_2(\mathbb {Q})$
under any diagonal flow.
$\mathrm {SL}_2(\mathbb {A})/\mathrm {SL}_2(\mathbb {Q})$
under any diagonal flow.
4.3 Individual equidistribution in the first factor
In view of the discussion in §4.2 and Lemma 4.4, it suffices to show equidistribution of the packets
to prove Theorem 4.1. We proceed in several steps.
4.3.1 An equidistribution theorem for the pointwise stabilizers
We first establish the following proposition which shows that either orbits of the pointwise stabilizer are equidistributed or there is some arithmetic obstruction.
Proposition 4.7. Let
![]() $(L_i)_i$
be a sequence of two-dimensional rational subspaces such that there exists a prime p for which
$(L_i)_i$
be a sequence of two-dimensional rational subspaces such that there exists a prime p for which
![]() $\mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {Q}_p)$
is strongly isotropic for all i. Let
$\mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {Q}_p)$
is strongly isotropic for all i. Let
![]() $g_i \in \mathbf {G}(\mathbb {R})$
and assume that
$g_i \in \mathbf {G}(\mathbb {R})$
and assume that
![]() $\mathrm {disc}_Q(L_i)\to \infty $
as
$\mathrm {disc}_Q(L_i)\to \infty $
as
![]() $i \to \infty $
. Then one of the following statements is true.
$i \to \infty $
. Then one of the following statements is true.
-
(1) The packets
 $g_i\mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {A})\mathrm {Spin}_Q(\mathbb {Q})$
are equidistributed in
$g_i\mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {A})\mathrm {Spin}_Q(\mathbb {Q})$
are equidistributed in
 as
as
 $i \to \infty $
.
$i \to \infty $
. -
(2) There exists a rational vector
 $v \in \mathbb {Q}^n\setminus \{0\}$
and lattice elements
$v \in \mathbb {Q}^n\setminus \{0\}$
and lattice elements
 $\delta _i \in \mathrm {Spin}_Q(\mathbb {Q})$
such that The lattice elements, additionally, satisfy that there exist
$\delta _i \in \mathrm {Spin}_Q(\mathbb {Q})$
such that The lattice elements, additionally, satisfy that there exist $$ \begin{align*} \mathbb{Q} v = \bigcap_i \delta_i^{-1}.L_i(\mathbb{Q}). \end{align*} $$
$$ \begin{align*} \mathbb{Q} v = \bigcap_i \delta_i^{-1}.L_i(\mathbb{Q}). \end{align*} $$
 $h_i \in \mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {A})$
such that the sequence
$h_i \in \mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {A})$
such that the sequence
 $g_i h_i\delta _i$
is convergent as
$g_i h_i\delta _i$
is convergent as
 $i \to \infty $
.
$i \to \infty $
.
Proof. We prove the proposition in exactly the same way we proved the first case in Proposition 3.3; thus, we are brief. Let
![]() $\delta _i \in \mathrm {Spin}_Q(\mathbb {Q})$
and a connected
$\delta _i \in \mathrm {Spin}_Q(\mathbb {Q})$
and a connected
![]() $\mathbb {Q}$
-group
$\mathbb {Q}$
-group
![]() $\mathbf {M} < \bar {\mathbf {G}}$
be as in Theorem 3.2. In particular,
$\mathbf {M} < \bar {\mathbf {G}}$
be as in Theorem 3.2. In particular,
and it suffices for equidistribution to verify that
![]() $\mathbf {M} = \mathrm {Spin}_Q$
. One can see that
$\mathbf {M} = \mathrm {Spin}_Q$
. One can see that
![]() $\mathbf {M}$
strictly contains
$\mathbf {M}$
strictly contains
![]() $\delta _i^{-1} \mathbf {H}^{\mathrm {pt}}_{L_i} \delta _i$
for all i by using
$\delta _i^{-1} \mathbf {H}^{\mathrm {pt}}_{L_i} \delta _i$
for all i by using
![]() $\mathrm {disc}_Q(L_i) \to \infty $
and repeating the proof of the first case in Proposition 3.3.
$\mathrm {disc}_Q(L_i) \to \infty $
and repeating the proof of the first case in Proposition 3.3.
Contrary to the case treated in Proposition 3.3, the groups
![]() $\mathbf {H}^{\mathrm {pt}}_{L_i}$
are non-maximal. The intermediate groups can, however, be understood explicitly: they are of the form
$\mathbf {H}^{\mathrm {pt}}_{L_i}$
are non-maximal. The intermediate groups can, however, be understood explicitly: they are of the form
![]() $\mathbf {H}^{\mathrm {pt}}_{W}$
, where W is a rational line contained in
$\mathbf {H}^{\mathrm {pt}}_{W}$
, where W is a rational line contained in
![]() $\delta _i^{-1}.L_i$
for all i. For a proof of this fact, we refer to [Reference Ellenberg and VenkateshEV08, Proposition 4]; see also the arXiv version of the same paper, where the authors give an elementary proof in the case
$\delta _i^{-1}.L_i$
for all i. For a proof of this fact, we refer to [Reference Ellenberg and VenkateshEV08, Proposition 4]; see also the arXiv version of the same paper, where the authors give an elementary proof in the case
![]() $n-2 \geq 7$
. This concludes the proof of the proposition.
$n-2 \geq 7$
. This concludes the proof of the proposition.
Corollary 4.8. Let the notation and the assumptions be as in Proposition 4.7 and suppose that the second case holds. Then
is bounded as
![]() $i \to \infty $
.
$i \to \infty $
.
Proof. Let
![]() $v \in \mathbb {Q}^n$
be as in Proposition 4.7 and suppose, without loss of generality, that v is integral and primitive. Suppose, also, that
$v \in \mathbb {Q}^n$
be as in Proposition 4.7 and suppose, without loss of generality, that v is integral and primitive. Suppose, also, that
![]() $g_i h_i \delta _i \to g' \in \mathrm {Spin}_Q(\mathbb {A})$
and write
$g_i h_i \delta _i \to g' \in \mathrm {Spin}_Q(\mathbb {A})$
and write
![]() $g_i h_i \delta _i = \varepsilon _i g'$
, where
$g_i h_i \delta _i = \varepsilon _i g'$
, where
![]() $\varepsilon _i \to e$
. Let
$\varepsilon _i \to e$
. Let
![]() $i_0$
be large enough so that
$i_0$
be large enough so that
![]() $\varepsilon _i \in \bar {\mathbf {G}}(\mathbb {R} \times \widehat {\mathbb {Z}})$
for all
$\varepsilon _i \in \bar {\mathbf {G}}(\mathbb {R} \times \widehat {\mathbb {Z}})$
for all
![]() $i \geq i_0$
and let
$i \geq i_0$
and let
![]() $N \in \mathbb {N}$
be the smallest integer such that
$N \in \mathbb {N}$
be the smallest integer such that
![]() $Ng^{\prime }_p$
is integral for all primes p.
$Ng^{\prime }_p$
is integral for all primes p.
We claim that
![]() $v_i:= N \delta _i.v \in L_i(\mathbb {Z})$
. To see this, first note that
$v_i:= N \delta _i.v \in L_i(\mathbb {Z})$
. To see this, first note that
![]() $v_i\in L_i(\mathbb {Q})$
. Furthermore, for any prime p, the vector
$v_i\in L_i(\mathbb {Q})$
. Furthermore, for any prime p, the vector
![]() $v_i$
is contained in
$v_i$
is contained in
![]() $L(\mathbb {Z}_p)$
. Indeed,
$L(\mathbb {Z}_p)$
. Indeed,
![]() $h_{i,p} \in \mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {Q}_p)$
necessarily fixes
$h_{i,p} \in \mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {Q}_p)$
necessarily fixes
![]() $v_i$
and, as
$v_i$
and, as
![]() $g_{i,p} = e$
,
$g_{i,p} = e$
,
This proves the claim and hence the corollary as
![]() $Q(N\delta _i.v) = N^2 Q(v)$
.
$Q(N\delta _i.v) = N^2 Q(v)$
.
4.3.2 A corollary of equidistribution in the second factor
In the following, we would like to give an estimate of the measure of the set of points in
![]() $g_{i,1}\mathbf {T}_{L_i}(\mathbb {A})\mathrm {Spin}_Q(\mathbb {Q})$
whose associated point in
$g_{i,1}\mathbf {T}_{L_i}(\mathbb {A})\mathrm {Spin}_Q(\mathbb {Q})$
whose associated point in
![]() is ‘close’ to the cusp. This will allow us to ‘wash out’ the effect of the obstructions in Proposition 4.7 on average across the full stabilizer group. To obtain said estimate, we introduce a height function that suits our needs.
is ‘close’ to the cusp. This will allow us to ‘wash out’ the effect of the obstructions in Proposition 4.7 on average across the full stabilizer group. To obtain said estimate, we introduce a height function that suits our needs.
Let
![]() ${\mathcal {S}}_{2}$
be the space of positive definite real binary quadratic forms up to similarity and write
${\mathcal {S}}_{2}$
be the space of positive definite real binary quadratic forms up to similarity and write
![]() $[q]$
for the similarity class of a binary form q. (Two positive definite binary real quadratic forms
$[q]$
for the similarity class of a binary form q. (Two positive definite binary real quadratic forms
![]() $Q_1,Q_2$
are similar if there exist
$Q_1,Q_2$
are similar if there exist
![]() ${\unicode{x3bb} }>0$
and
${\unicode{x3bb} }>0$
and
![]() $g \in {\mathrm {GL}}_2({\mathbb {Z}})$
with
$g \in {\mathrm {GL}}_2({\mathbb {Z}})$
with
![]() $Q_2(\cdot ) = {\unicode{x3bb} } Q_1(g\cdot )$
. Note that the space
$Q_2(\cdot ) = {\unicode{x3bb} } Q_1(g\cdot )$
. Note that the space
![]() ${\mathcal {S}}_{2}$
will be discussed in more detail in §6.2.) For
${\mathcal {S}}_{2}$
will be discussed in more detail in §6.2.) For
![]() $\varepsilon>0$
, we define
$\varepsilon>0$
, we define
 $$ \begin{align*} \mathcal{S}_{2}(\varepsilon) = \left\{ [q]\in \mathcal{S}_{2}: \min_{w \in \mathbb{Z}^2 \setminus\{0\}} q(w)> \varepsilon \sqrt{\mathrm{disc}(q)}\right\}\!\hspace{-0.5pt}. \end{align*} $$
$$ \begin{align*} \mathcal{S}_{2}(\varepsilon) = \left\{ [q]\in \mathcal{S}_{2}: \min_{w \in \mathbb{Z}^2 \setminus\{0\}} q(w)> \varepsilon \sqrt{\mathrm{disc}(q)}\right\}\!\hspace{-0.5pt}. \end{align*} $$
Note that the condition is independent of the choice of representative of
![]() $[q]$
.
$[q]$
.
By Mahler’s compactness criterion [Reference MahlerMah46], these are compact subsets of
![]() $\mathcal {S}_{2}$
and any compact subset is contained in
$\mathcal {S}_{2}$
and any compact subset is contained in
![]() $\mathcal {S}_{2}(\varepsilon )$
for some
$\mathcal {S}_{2}(\varepsilon )$
for some
![]() $\varepsilon>0$
. Furthermore, one can show that the Haar measure of
$\varepsilon>0$
. Furthermore, one can show that the Haar measure of
![]() $\mathcal {S}_{2} \setminus \mathcal {S}_{2}(\varepsilon )$
is
$\mathcal {S}_{2} \setminus \mathcal {S}_{2}(\varepsilon )$
is
![]() $\ll \varepsilon $
by direct integration of the hyperbolic area measure on that region.
$\ll \varepsilon $
by direct integration of the hyperbolic area measure on that region.
We define
to be the preimage of
![]() $\mathcal {S}_{2}(\varepsilon )$
under the composition
$\mathcal {S}_{2}(\varepsilon )$
under the composition
By the previous discussion, this is a compact set whose complement has Haar measure
![]() $\ll \varepsilon $
. For
$\ll \varepsilon $
. For
, we call the supremum over all
![]() $\varepsilon>0$
with
$\varepsilon>0$
with
![]() $x \in K_\varepsilon $
the minimal quadratic value for x.
$x \in K_\varepsilon $
the minimal quadratic value for x.
The following is a direct corollary of equidistribution in the second factor.
Corollary 4.9. For any
![]() $\varepsilon \in (0,1)$
, there exists
$\varepsilon \in (0,1)$
, there exists
![]() $i_0 \geq 1$
so that the measure of the set of points
$i_0 \geq 1$
so that the measure of the set of points
![]() for which
for which
![]() $g_{2}\psi _{1,L_i}(t)\mathrm {SL}_2(\mathbb {Q}) \not \in K_\varepsilon $
is
$g_{2}\psi _{1,L_i}(t)\mathrm {SL}_2(\mathbb {Q}) \not \in K_\varepsilon $
is
![]() $\ll \varepsilon $
for all
$\ll \varepsilon $
for all
![]() $i \geq i_0$
.
$i \geq i_0$
.
4.3.3 Using the shape in the subspace
In the following, we identify the minimal quadratic value for the points on the orbits in the context of proving Theorem 4.1. As
![]() $\mathrm {Spin}_Q(\mathbb {R} \times \widehat {\mathbb {Z}})$
is a compact open subgroup, it has finitely many orbits on
$\mathrm {Spin}_Q(\mathbb {R} \times \widehat {\mathbb {Z}})$
is a compact open subgroup, it has finitely many orbits on
![]() $\mathrm {Spin}_Q(\mathbb {A})/\mathrm {Spin}_Q(\mathbb {Q})$
(these correspond to the spin genus of the quadratic form Q). We choose a finite set of representatives
$\mathrm {Spin}_Q(\mathbb {A})/\mathrm {Spin}_Q(\mathbb {Q})$
(these correspond to the spin genus of the quadratic form Q). We choose a finite set of representatives
![]() $\mathcal {R} \subset \mathrm {Spin}_Q(\mathbb {A}_f)$
such that
$\mathcal {R} \subset \mathrm {Spin}_Q(\mathbb {A}_f)$
such that
Note that, in
![]() $\mathrm {SL}_2$
(or
$\mathrm {SL}_2$
(or
![]() $\mathrm {SL}_{n-2}$
), any
$\mathrm {SL}_{n-2}$
), any
![]() $g \in \mathrm {SL}_2(\mathbb {A})$
can be written as
$g \in \mathrm {SL}_2(\mathbb {A})$
can be written as
![]() $g = b \gamma $
, where
$g = b \gamma $
, where
![]() $b \in \mathrm {SL}_2 (\mathbb {R} \times \widehat {\mathbb {Z}})$
and
$b \in \mathrm {SL}_2 (\mathbb {R} \times \widehat {\mathbb {Z}})$
and
![]() $\gamma \in \mathrm {SL}_2(\mathbb {Q})$
.
$\gamma \in \mathrm {SL}_2(\mathbb {Q})$
.
Lemma 4.10. Let
![]() $h \in \boldsymbol{\Delta \bar {\mathbf H}}_{L_i}(\mathbb {A})$
and write
$h \in \boldsymbol{\Delta \bar {\mathbf H}}_{L_i}(\mathbb {A})$
and write
![]() $h \gamma = b \mathsf {r}$
for some
$h \gamma = b \mathsf {r}$
for some
![]() $\gamma \in \bar {\mathbf {G}}(\mathbb {Q})$
,
$\gamma \in \bar {\mathbf {G}}(\mathbb {Q})$
,
![]() $b \in \bar {\mathbf {G}}(\mathbb {R} \times \widehat {\mathbb {Z}})$
and
$b \in \bar {\mathbf {G}}(\mathbb {R} \times \widehat {\mathbb {Z}})$
and
![]() $\mathsf {r} \in \mathcal {R}$
. Then
$\mathsf {r} \in \mathcal {R}$
. Then
![]() $\gamma _1^{-1}.L_i$
is a rational subspace of discriminant
$\gamma _1^{-1}.L_i$
is a rational subspace of discriminant
![]() $\asymp D$
. Furthermore, the minimum
$\asymp D$
. Furthermore, the minimum
 $$ \begin{align*} \min_{w \in \mathbb{Z}^2 \setminus\{0\}} \frac{q_{\gamma_1^{-1}.L_i}(w)}{\sqrt{\mathrm{disc}_Q(\gamma_1^{-1}.L_i)}} \end{align*} $$
$$ \begin{align*} \min_{w \in \mathbb{Z}^2 \setminus\{0\}} \frac{q_{\gamma_1^{-1}.L_i}(w)}{\sqrt{\mathrm{disc}_Q(\gamma_1^{-1}.L_i)}} \end{align*} $$
is comparable to the minimal quadratic value for
![]() $g_{i,2}\psi _{1,L}(h)\mathrm {SL}_2(\mathbb {Q})$
.
$g_{i,2}\psi _{1,L}(h)\mathrm {SL}_2(\mathbb {Q})$
.
Note that a lemma in this spirit will later be used to deduce the main theorems from their dynamical counterparts (cf. Proposition 7.1). The statement here is more technical in nature (as it needs to treat different genera) and the reader is encouraged to return to the proof after reading Proposition 7.1. We note that such a treatment has appeared in different contexts in the literature [Reference Aka, Luethi, Michel and WieserALMW22, Reference Ellenberg and VenkateshEV08].
Proof. The ingredients for this proof are all contained in the proof of Proposition 7.1, so we are brief. Write
![]() $L = L_i$
for simplicity. Note that
$L = L_i$
for simplicity. Note that
![]() $h_{1,p} \gamma _1 = b_{1,p}\mathsf {r}_p$
and hence
$h_{1,p} \gamma _1 = b_{1,p}\mathsf {r}_p$
and hence
 $$ \begin{align*} \mathrm{disc}_{p,Q}(\gamma_1^{-1}.L) &= \mathrm{disc}_{p,Q}(\gamma_1^{-1}h_{1,p}^{-1}.L) = \mathrm{disc}_{p,Q}(\mathsf{r}_p^{-1}b_{1,p}.L)\\ &\asymp_{\mathsf{r}} \mathrm{disc}_{p,Q}(b_{1,p}.L) = \mathrm{disc}_{p,Q}(L). \end{align*} $$
$$ \begin{align*} \mathrm{disc}_{p,Q}(\gamma_1^{-1}.L) &= \mathrm{disc}_{p,Q}(\gamma_1^{-1}h_{1,p}^{-1}.L) = \mathrm{disc}_{p,Q}(\mathsf{r}_p^{-1}b_{1,p}.L)\\ &\asymp_{\mathsf{r}} \mathrm{disc}_{p,Q}(b_{1,p}.L) = \mathrm{disc}_{p,Q}(L). \end{align*} $$
As the discriminant is a product of the local discriminants (1.5), this proves the first claim.
For the second claim, we let
![]() $L' = \gamma _1^{-1}.L$
and consider
$L' = \gamma _1^{-1}.L$
and consider
![]() $m = g_{L'}^{-1}\rho _Q(\gamma _1^{-1})g_L \gamma _2\in \mathrm {GL}_n(\mathbb {Q})$
. Observe that
$m = g_{L'}^{-1}\rho _Q(\gamma _1^{-1})g_L \gamma _2\in \mathrm {GL}_n(\mathbb {Q})$
. Observe that
As we will now see, m is ‘almost integral’ and invertible. For this, compute
This implies that there exists some
![]() $N \in \mathbb {N}$
independent of L such that
$N \in \mathbb {N}$
independent of L such that
![]() $N\rho _Q( \gamma _1^{-1})g_L \gamma _2$
and
$N\rho _Q( \gamma _1^{-1})g_L \gamma _2$
and
![]() $N\rho _Q(\gamma _1^{-1})g_L^{-1} \gamma _2$
are integral. Recall that
$N\rho _Q(\gamma _1^{-1})g_L^{-1} \gamma _2$
are integral. Recall that
![]() $\mathrm {disc}(Q)g_{L'},\mathrm {disc}(Q)g_{L'}^{-1}$
are integral so that
$\mathrm {disc}(Q)g_{L'},\mathrm {disc}(Q)g_{L'}^{-1}$
are integral so that
![]() $N\mathrm {disc}(Q) m$
and
$N\mathrm {disc}(Q) m$
and
![]() $N \mathrm {disc}(Q)m^{-1}$
are integral. This discussion implies that, for any two positive definite real binary quadratic forms
$N \mathrm {disc}(Q)m^{-1}$
are integral. This discussion implies that, for any two positive definite real binary quadratic forms
![]() $q,q'$
with the property that
$q,q'$
with the property that
![]() $\pi _1(m)q$
and
$\pi _1(m)q$
and
![]() $q'$
are similar,
$q'$
are similar,
 $$ \begin{align*} \min_{w \in \mathbb{Z}^2\setminus\{0\}} \frac{q(w)}{\sqrt{\mathrm{disc}(q)}} \asymp \min_{w \in \mathbb{Z}^2\setminus\{0\}} \frac{q'(w)}{\sqrt{\mathrm{disc}(q')}}. \end{align*} $$
$$ \begin{align*} \min_{w \in \mathbb{Z}^2\setminus\{0\}} \frac{q(w)}{\sqrt{\mathrm{disc}(q)}} \asymp \min_{w \in \mathbb{Z}^2\setminus\{0\}} \frac{q'(w)}{\sqrt{\mathrm{disc}(q')}}. \end{align*} $$
Here, recall that
![]() $\mathrm {GL}_2(\mathbb {R})$
acts on binary forms via
$\mathrm {GL}_2(\mathbb {R})$
acts on binary forms via
![]() $gq(x) = q(g^t x)$
.
$gq(x) = q(g^t x)$
.
Now, note that
whereas the similarity class belonging to
![]() $g_{2}\psi _{1,L}(t)\mathrm {SL}_2(\mathbb {Q})$
is
$g_{2}\psi _{1,L}(t)\mathrm {SL}_2(\mathbb {Q})$
is
The claim follows.
4.3.4 Proof of Theorem 4.1
As explained, it now suffices to prove that the packets for
![]() $L_i$
,
$L_i$
,
equidistribute as
![]() $\mathrm {disc}_Q(L_i) \to \infty $
. Similarly to the situation in the proof of Theorem 3.1, we need to circumvent the problem that
$\mathrm {disc}_Q(L_i) \to \infty $
. Similarly to the situation in the proof of Theorem 3.1, we need to circumvent the problem that
![]() $\mathbf {H}_L$
for
$\mathbf {H}_L$
for
![]() $L \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
is not exactly isomorphic to
$L \in \mathrm {Gr}_{n,2}(\mathbb {Q})$
is not exactly isomorphic to
![]() $\mathbf {H}^{\mathrm {pt}}_L \times \mathbf {T}_L$
(see Remark 2.1 for a more careful discussion). Denote by
$\mathbf {H}^{\mathrm {pt}}_L \times \mathbf {T}_L$
(see Remark 2.1 for a more careful discussion). Denote by
![]() $\mathbf {H}_L(\mathbb {A})^\star $
the image of
$\mathbf {H}_L(\mathbb {A})^\star $
the image of
![]() $\mathbf {H}^{\mathrm {pt}}_L(\mathbb {A}) \times \mathbf {T}_L(\mathbb {A}) \to \mathbf {H}_L(\mathbb {A})$
; this is a normal subgroup of
$\mathbf {H}^{\mathrm {pt}}_L(\mathbb {A}) \times \mathbf {T}_L(\mathbb {A}) \to \mathbf {H}_L(\mathbb {A})$
; this is a normal subgroup of
![]() $\mathbf {H}_L(\mathbb {A})$
with the property that
$\mathbf {H}_L(\mathbb {A})$
with the property that
is compact and abelian. By an argument as at the beginning of the proof of Theorem 3.1, it suffices to show that, for any
![]() $k_i \in K_{L_i}$
, the orbits
$k_i \in K_{L_i}$
, the orbits
are equidistributed as
![]() $i \to \infty $
. We let
$i \to \infty $
. We let
![]() $\mu _i$
be the Haar measure on the ith such orbit and let
$\mu _i$
be the Haar measure on the ith such orbit and let
be the Haar measure on the closed orbits of
![]() $\mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {A})$
(respectively,
$\mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {A})$
(respectively,
![]() $\mathbf {T}_{L_i}(\mathbb {A})$
). Then, for any function
$\mathbf {T}_{L_i}(\mathbb {A})$
). Then, for any function
,
In the following, we identify
![]() $k_i$
with a representative in a fixed bounded region of
$k_i$
with a representative in a fixed bounded region of
![]() $\mathbf {H}_{L_i}(\mathbb {A})$
.
$\mathbf {H}_{L_i}(\mathbb {A})$
.
For a fixed
![]() $t_i\in \mathbf {T}_{L_i}(\mathbb {A})$
, the inner integral is the integral over the orbit
$t_i\in \mathbf {T}_{L_i}(\mathbb {A})$
, the inner integral is the integral over the orbit
Writing
![]() $t_i\gamma _i = b_i\mathsf {r}$
as in (4.4), we see that
$t_i\gamma _i = b_i\mathsf {r}$
as in (4.4), we see that
 $$ \begin{align*} g_{i,1}k_i t_i\mathbf{H}^{\mathrm{pt}}_{L_i}(\mathbb{A}) \mathrm{Spin}_Q(\mathbb{Q}) &= g_{i,1}k_ib_i\mathsf{r} \gamma_i^{-1} \mathbf{H}^{\mathrm{pt}}_{L_i}(\mathbb{A}) \mathrm{Spin}_Q(\mathbb{Q})\\ &= g_{i,1}k_ib_i\mathsf{r} \mathbf{H}^{\mathrm{pt}}_{\gamma_i^{-1}.L_i}(\mathbb{A}) \mathrm{Spin}_Q(\mathbb{Q}), \end{align*} $$
$$ \begin{align*} g_{i,1}k_i t_i\mathbf{H}^{\mathrm{pt}}_{L_i}(\mathbb{A}) \mathrm{Spin}_Q(\mathbb{Q}) &= g_{i,1}k_ib_i\mathsf{r} \gamma_i^{-1} \mathbf{H}^{\mathrm{pt}}_{L_i}(\mathbb{A}) \mathrm{Spin}_Q(\mathbb{Q})\\ &= g_{i,1}k_ib_i\mathsf{r} \mathbf{H}^{\mathrm{pt}}_{\gamma_i^{-1}.L_i}(\mathbb{A}) \mathrm{Spin}_Q(\mathbb{Q}), \end{align*} $$
which is equidistributed if and only if
![]() $\mathbf {H}^{\mathrm {pt}}_{\gamma _i^{-1}.L_i}(\mathbb {A}) \mathrm {Spin}_Q(\mathbb {Q})$
is equidistributed (as
$\mathbf {H}^{\mathrm {pt}}_{\gamma _i^{-1}.L_i}(\mathbb {A}) \mathrm {Spin}_Q(\mathbb {Q})$
is equidistributed (as
![]() $g_{i,1}k_ib_i$
is bounded). By Proposition 4.7 and its corollary, it suffices to show that the minimal non-zero value of
$g_{i,1}k_ib_i$
is bounded). By Proposition 4.7 and its corollary, it suffices to show that the minimal non-zero value of
![]() $q_{\gamma _i^{-1}.L_i}$
goes to infinity. This minimum is comparable to the minimal quadratic value for
$q_{\gamma _i^{-1}.L_i}$
goes to infinity. This minimum is comparable to the minimal quadratic value for
![]() $g_{i,2} \psi _{1,L}(t_i) \mathrm {SL}_2(\mathbb {Q})$
by Lemma 4.10.
$g_{i,2} \psi _{1,L}(t_i) \mathrm {SL}_2(\mathbb {Q})$
by Lemma 4.10.
Motivated by this observation, we define, for
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
so that the complement of
![]() $\mathcal {B}_i(\varepsilon )$
has
$\mathcal {B}_i(\varepsilon )$
has
![]() $\mu _{i,2}$
-measure
$\mu _{i,2}$
-measure
![]() $\ll \varepsilon $
for all i large enough (depending on
$\ll \varepsilon $
for all i large enough (depending on
![]() $\varepsilon $
), by Corollary 4.9. In view of (4.5), this implies that
$\varepsilon $
), by Corollary 4.9. In view of (4.5), this implies that
 $$ \begin{align*} \int f \, \mathrm{d} \mu_i = \dfrac{1}{\mu_{i,2}(\mathcal{B}_i(\varepsilon))} \int_{\mathcal{B}_i(\varepsilon)} \int f(g_{i,1}k_i h t) \, \mathrm{d} \mu_{1,i}(h) \, \mathrm{d} \mu_{i,2}(t) + \mathcal{O}(\varepsilon). \end{align*} $$
$$ \begin{align*} \int f \, \mathrm{d} \mu_i = \dfrac{1}{\mu_{i,2}(\mathcal{B}_i(\varepsilon))} \int_{\mathcal{B}_i(\varepsilon)} \int f(g_{i,1}k_i h t) \, \mathrm{d} \mu_{1,i}(h) \, \mathrm{d} \mu_{i,2}(t) + \mathcal{O}(\varepsilon). \end{align*} $$
By the previous paragraph, the orbits
![]() $g_{i,1}k_i \mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {A})t_i \mathrm {Spin}_Q(\mathbb {Q})$
are equidistributed for any sequence
$g_{i,1}k_i \mathbf {H}^{\mathrm {pt}}_{L_i}(\mathbb {A})t_i \mathrm {Spin}_Q(\mathbb {Q})$
are equidistributed for any sequence
![]() $t_i \in \mathcal {B}_i(\varepsilon )$
. The integral on the right-hand side is a convex combination of such orbital integrals and hence must converge to the integral of f over the Haar measure. Letting
$t_i \in \mathcal {B}_i(\varepsilon )$
. The integral on the right-hand side is a convex combination of such orbital integrals and hence must converge to the integral of f over the Haar measure. Letting
![]() $\mu $
be any weak
$\mu $
be any weak
![]() ${}^*$
-limit of the measures
${}^*$
-limit of the measures
![]() $\mu _i$
, we obtain
$\mu _i$
, we obtain
As
![]() $\varepsilon $
is arbitrary, this implies the claim.
$\varepsilon $
is arbitrary, this implies the claim.
5 Part 2: From equidistribution of orbits to the main theorems
For the contents of this part, we refer the reader to the overview of this article in §1.3.
5.1 Discriminants and glue groups
Recall that Q is a positive definite integral quadratic form on
![]() $\mathbb {Q}^n$
and that
$\mathbb {Q}^n$
and that
![]() $\langle \cdot ,\cdot \rangle _Q$
is its symmetric bilinear form. By integrality, we mean that
$\langle \cdot ,\cdot \rangle _Q$
is its symmetric bilinear form. By integrality, we mean that
![]() $\langle \cdot ,\cdot \rangle _Q$
takes integer values on
$\langle \cdot ,\cdot \rangle _Q$
takes integer values on
![]() $\mathbb {Z}^n\times \mathbb {Z}^n$
. The goal of this section is to prove the following proposition.
$\mathbb {Z}^n\times \mathbb {Z}^n$
. The goal of this section is to prove the following proposition.
Proposition 5.1. For any subspace
![]() $L \subset \mathbb {Q}^n$
, there exist two positive divisors
$L \subset \mathbb {Q}^n$
, there exist two positive divisors
![]() $m_1,m_2$
of
$m_1,m_2$
of
![]() $\mathrm {disc}(Q)$
with
$\mathrm {disc}(Q)$
with
In particular,
To that end, we will use the notion of glue groups defined in §5.1.1 and, in fact, prove a significantly finer statement in Proposition 5.4 below.
5.1.1 Definitions
For any
![]() $\mathbb {Z}$
-lattice
$\mathbb {Z}$
-lattice
![]() $\Gamma \subset \mathbb {Q}^n$
, we define the dual lattice
$\Gamma \subset \mathbb {Q}^n$
, we define the dual lattice
If
![]() $\Gamma \subset \mathbb {Z}^n$
(or, more generally, if
$\Gamma \subset \mathbb {Z}^n$
(or, more generally, if
![]() $\langle \cdot ,\cdot \rangle _Q$
takes integral values on
$\langle \cdot ,\cdot \rangle _Q$
takes integral values on
![]() $\Gamma \times \Gamma $
), the dual lattice
$\Gamma \times \Gamma $
), the dual lattice
![]() $\Gamma ^\#$
contains
$\Gamma ^\#$
contains
![]() $\Gamma $
. Note that if
$\Gamma $
. Note that if
![]() $\Gamma _1 \subset \Gamma _2$
are any two
$\Gamma _1 \subset \Gamma _2$
are any two
![]() $\mathbb {Z}$
-lattices, then
$\mathbb {Z}$
-lattices, then
![]() $\Gamma _1^\#\supset \Gamma _2^\#$
.
$\Gamma _1^\#\supset \Gamma _2^\#$
.
For the purposes of this section, a very useful classical tool is the so-called glue group, which one could see as a concept generalizing the discriminant. We introduce only what is needed here; for better context, we refer the reader to [Reference Conway and SloaneCS99, Reference McMullenMcM11] (in particular, we do not introduce the fractional form). We define the glue group of a rational subspace L (or of the lattice
![]() $L(\mathbb {Z})$
) as
$L(\mathbb {Z})$
) as
Note that
![]() $L(\mathbb {Z})^\#$
contains
$L(\mathbb {Z})^\#$
contains
![]() $L(\mathbb {Z})$
by integrality. The glue group is a finite abelian group whose cardinality is exactly the discriminant (see, for example, [Reference KitaokaKit93, §5.1]). We remark that the glue group may be computed from local data—this is made explicit in §B.1 of the appendix.
$L(\mathbb {Z})$
by integrality. The glue group is a finite abelian group whose cardinality is exactly the discriminant (see, for example, [Reference KitaokaKit93, §5.1]). We remark that the glue group may be computed from local data—this is made explicit in §B.1 of the appendix.
Remark 5.2. For each discriminant D, one may consider the collection of subspaces
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
with discriminant D and glue group that is a fixed abelian group of order D. In principle, the results of the current article should carry over to prove equidistribution of these subspaces together with their shapes (cf. [Reference Aka, Einsiedler and WieserAEW22]). However, it is not clear when one expects such collections to be non-empty, even when Q is the sum of squares.
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
with discriminant D and glue group that is a fixed abelian group of order D. In principle, the results of the current article should carry over to prove equidistribution of these subspaces together with their shapes (cf. [Reference Aka, Einsiedler and WieserAEW22]). However, it is not clear when one expects such collections to be non-empty, even when Q is the sum of squares.
5.1.2 The glue group of the orthogonal complement
We study the relationship between the glue group of a subspace and that of its orthogonal complement. Any subspace
![]() $L\subset \mathbb {Q}^n$
contains various lattices which are (potentially) of interest and are natural:
$L\subset \mathbb {Q}^n$
contains various lattices which are (potentially) of interest and are natural:
-
• the intersections
 $L(\mathbb {Z}) = L(\mathbb {Q}) \cap \mathbb {Z}^n$
and
$L(\mathbb {Z}) = L(\mathbb {Q}) \cap \mathbb {Z}^n$
and
 $L(\mathbb {Q}) \cap (\mathbb {Z}^n)^\#$
;
$L(\mathbb {Q}) \cap (\mathbb {Z}^n)^\#$
; -
• the dual lattice
 $L(\mathbb {Z})^\#$
; and
$L(\mathbb {Z})^\#$
; and -
• the projection lattices
 $\pi _L(\mathbb {Z}^n)$
and
$\pi _L(\mathbb {Z}^n)$
and
 $\pi _L((\mathbb {Z}^n)^\#)$
, where
$\pi _L((\mathbb {Z}^n)^\#)$
, where
 $\pi _L: \mathbb {Q}^n \to L$
denotes the orthogonal projection.
$\pi _L: \mathbb {Q}^n \to L$
denotes the orthogonal projection.
Lemma 5.3. (Elementary properties)
The following relationships between the aforementioned lattices hold.
-
(i)
 $L(\mathbb {Z})^\# = \pi _L((\mathbb {Z}^n)^\#)$
and
$L(\mathbb {Z})^\# = \pi _L((\mathbb {Z}^n)^\#)$
and
 $(L \cap (\mathbb {Z}^n)^\#)^\# = \pi _L(\mathbb {Z}^n)$
.
$(L \cap (\mathbb {Z}^n)^\#)^\# = \pi _L(\mathbb {Z}^n)$
. -
(ii)
 $(L \cap (\mathbb {Z}^n)^\#) / L(\mathbb {Z}) \simeq L(\mathbb {Z})^\# / \pi _L(\mathbb {Z}^n)$
.
$(L \cap (\mathbb {Z}^n)^\#) / L(\mathbb {Z}) \simeq L(\mathbb {Z})^\# / \pi _L(\mathbb {Z}^n)$
.
Proof. We prove (i) first. Since the proofs of the two assertions in (i) are similar, we only detail the first. Let
![]() $v_1, \ldots , v_k$
be a
$v_1, \ldots , v_k$
be a
![]() $\mathbb {Z}$
-basis of
$\mathbb {Z}$
-basis of
![]() $L(\mathbb {Z})$
. Moreover, let
$L(\mathbb {Z})$
. Moreover, let
![]() $w_1, \ldots , w_k \in L$
be the dual basis to
$w_1, \ldots , w_k \in L$
be the dual basis to
![]() $v_1, \ldots , v_k$
. Extend
$v_1, \ldots , v_k$
. Extend
![]() $v_1, \ldots , v_k$
to a basis
$v_1, \ldots , v_k$
to a basis
![]() $v_1, \ldots , v_n$
of
$v_1, \ldots , v_n$
of
![]() $\mathbb {Z}^n$
and consider
$\mathbb {Z}^n$
and consider
![]() $y_1, \ldots , y_n$
, the dual basis to
$y_1, \ldots , y_n$
, the dual basis to
![]() $v_1, \ldots , v_n$
. Then
$v_1, \ldots , v_n$
. Then
![]() $\pi _L(y_i) = w_i$
for any
$\pi _L(y_i) = w_i$
for any
![]() $i \leq k$
as
$i \leq k$
as
whenever
![]() $j \leq k$
. Moreover,
$j \leq k$
. Moreover,
![]() $y_i \in L^\perp $
for
$y_i \in L^\perp $
for
![]() $i>k$
, by construction. Thus,
$i>k$
, by construction. Thus,
as claimed. The proof of the second equality is analogous.
For (ii), note that, for any two lattices
![]() $\Lambda _1 \subset \Lambda _2$
in L, one has
$\Lambda _1 \subset \Lambda _2$
in L, one has
so (ii) follows from (i). To construct such an isomorphism, one proceeds as follows. Fix a basis
![]() $v_1, \ldots , v_n$
of
$v_1, \ldots , v_n$
of
![]() $\Lambda _2$
such that
$\Lambda _2$
such that
![]() $d_1v_1, \ldots , d_nv_n$
is a basis (such a basis is sometimes called an ‘adapted basis’ (in geometry of numbers); the existence can be easily seen using Smith’s normal form) of
$d_1v_1, \ldots , d_nv_n$
is a basis (such a basis is sometimes called an ‘adapted basis’ (in geometry of numbers); the existence can be easily seen using Smith’s normal form) of
![]() $\Lambda _1$
with
$\Lambda _1$
with
![]() $d_i \in \mathbb {Z}$
and let
$d_i \in \mathbb {Z}$
and let
![]() $w_1, \ldots , w_n$
be the dual basis to
$w_1, \ldots , w_n$
be the dual basis to
![]() $v_1, \ldots , v_n$
. Then, the map
$v_1, \ldots , v_n$
. Then, the map
induces the desired isomorphism.
Proposition 5.4. We have an isomorphism
When Q is unimodular, i.e.
![]() $\mathrm {disc}(Q) = 1$
, this together with Lemma 5.3 shows that the glue groups of L and
$\mathrm {disc}(Q) = 1$
, this together with Lemma 5.3 shows that the glue groups of L and
![]() $L^\perp $
are isomorphic. Indeed, in this case,
$L^\perp $
are isomorphic. Indeed, in this case,
![]() $(\mathbb {Z}^n)^\# = \mathbb {Z}^n$
and hence
$(\mathbb {Z}^n)^\# = \mathbb {Z}^n$
and hence
![]() $\pi _L(\mathbb {Z}^n) = L(\mathbb {Z})^\#$
. In particular, L and
$\pi _L(\mathbb {Z}^n) = L(\mathbb {Z})^\#$
. In particular, L and
![]() $L^\perp $
have the same discriminant. When Q is not unimodular, the proposition gives an isomorphism between subgroups of the respective glue groups.
$L^\perp $
have the same discriminant. When Q is not unimodular, the proposition gives an isomorphism between subgroups of the respective glue groups.
Proof. We define a map f from
![]() $\pi _L(\mathbb {Z}^n)$
to
$\pi _L(\mathbb {Z}^n)$
to
![]() $\pi _{L^{\perp }}(\mathbb {Z}^n)/L^{\perp }(\mathbb {Z})$
as follows. For
$\pi _{L^{\perp }}(\mathbb {Z}^n)/L^{\perp }(\mathbb {Z})$
as follows. For
![]() $x \in \pi _L(\mathbb {Z}^n)$
, choose a lift
$x \in \pi _L(\mathbb {Z}^n)$
, choose a lift
![]() $\hat {x} \in \mathbb {Z}^n$
of x for the projection
$\hat {x} \in \mathbb {Z}^n$
of x for the projection
![]() $\pi _L$
and define
$\pi _L$
and define
Note that f is well defined since, if
![]() $\hat {x}, \hat {y} \in \mathbb {Z}^n$
are two lifts of
$\hat {x}, \hat {y} \in \mathbb {Z}^n$
are two lifts of
![]() $x\in \pi _L(\mathbb {Z}^n)$
, then
$x\in \pi _L(\mathbb {Z}^n)$
, then
![]() $\hat {x} - \hat {y} \in L^{\perp }(\mathbb {Z})$
, which implies that
$\hat {x} - \hat {y} \in L^{\perp }(\mathbb {Z})$
, which implies that
![]() $\pi _{L^{\perp }}(\hat {x}) + L^\perp (\mathbb {Z}) = \pi _{L^{\perp }}(\hat {y}) + L^\perp (\mathbb {Z})$
.
$\pi _{L^{\perp }}(\hat {x}) + L^\perp (\mathbb {Z}) = \pi _{L^{\perp }}(\hat {y}) + L^\perp (\mathbb {Z})$
.
We show that
![]() $\ker (f) = L(\mathbb {Z})$
. Obviously,
$\ker (f) = L(\mathbb {Z})$
. Obviously,
![]() $L(\mathbb {Z}) \subset \ker (f)$
since, for any
$L(\mathbb {Z}) \subset \ker (f)$
since, for any
![]() $x \in L(\mathbb {Z})$
, we can choose x itself as lift. On the other hand, if
$x \in L(\mathbb {Z})$
, we can choose x itself as lift. On the other hand, if
![]() $x \in \ker (f)$
, there is a lift
$x \in \ker (f)$
, there is a lift
![]() $\hat {x} \in \mathbb {Z}^n$
of x for
$\hat {x} \in \mathbb {Z}^n$
of x for
![]() $\pi _L$
such that
$\pi _L$
such that
![]() $\pi _{L^{\perp }}(\hat {x}) \in L^{\perp }(\mathbb {Z})$
. In particular,
$\pi _{L^{\perp }}(\hat {x}) \in L^{\perp }(\mathbb {Z})$
. In particular,
We deduce that
![]() $\ker (f) \subset L(\mathbb {Z})$
and hence equality. This proves the proposition.
$\ker (f) \subset L(\mathbb {Z})$
and hence equality. This proves the proposition.
Proof of Proposition 5.1
By Proposition 5.4,
 $$ \begin{align*} \mathrm{disc}_Q(L) = |\mathcal{G}(L)| &= |L(\mathbb{Z})^\#/\pi_L(\mathbb{Z}^n)| \cdot |\pi_L(\mathbb{Z}^n)/L(\mathbb{Z})|\\ &= |L(\mathbb{Z})^\#/\pi_L(\mathbb{Z}^n)| \cdot |\pi_{L^\perp}(\mathbb{Z}^n)/L^\perp(\mathbb{Z})|\\ &= \frac{|L(\mathbb{Z})^\#/\pi_L(\mathbb{Z}^n)|}{|L^\perp(\mathbb{Z})^\#/\pi_{L^\perp}(\mathbb{Z}^n)|} |\mathcal{G}(L^\perp)|. \end{align*} $$
$$ \begin{align*} \mathrm{disc}_Q(L) = |\mathcal{G}(L)| &= |L(\mathbb{Z})^\#/\pi_L(\mathbb{Z}^n)| \cdot |\pi_L(\mathbb{Z}^n)/L(\mathbb{Z})|\\ &= |L(\mathbb{Z})^\#/\pi_L(\mathbb{Z}^n)| \cdot |\pi_{L^\perp}(\mathbb{Z}^n)/L^\perp(\mathbb{Z})|\\ &= \frac{|L(\mathbb{Z})^\#/\pi_L(\mathbb{Z}^n)|}{|L^\perp(\mathbb{Z})^\#/\pi_{L^\perp}(\mathbb{Z}^n)|} |\mathcal{G}(L^\perp)|. \end{align*} $$
Using Lemma 5.3, note that the finite group
![]() $L(\mathbb {Z})^\#/\pi _L(\mathbb {Z}^n) = \pi _L((\mathbb {Z}^n)^\#)/\pi _L(\mathbb {Z}^n)$
is a quotient of
$L(\mathbb {Z})^\#/\pi _L(\mathbb {Z}^n) = \pi _L((\mathbb {Z}^n)^\#)/\pi _L(\mathbb {Z}^n)$
is a quotient of
![]() $(\mathbb {Z}^n)^\#/\mathbb {Z}^n$
and hence
$(\mathbb {Z}^n)^\#/\mathbb {Z}^n$
and hence
![]() $|L(\mathbb {Z})^\#/\pi _L(\mathbb {Z}^n)|$
is a divisor of
$|L(\mathbb {Z})^\#/\pi _L(\mathbb {Z}^n)|$
is a divisor of
![]() $\mathrm {disc}(Q)=|(\mathbb {Z}^n)^\#/\mathbb {Z}^n|$
. As the analogous statement holds for
$\mathrm {disc}(Q)=|(\mathbb {Z}^n)^\#/\mathbb {Z}^n|$
. As the analogous statement holds for
![]() $L^\perp $
, the proposition follows.
$L^\perp $
, the proposition follows.
Remark 5.5. When
![]() $\mathrm {disc}(Q) = 1$
, Proposition 5.4 states that
$\mathrm {disc}(Q) = 1$
, Proposition 5.4 states that
![]() $\mathcal {G}(L) \simeq \mathcal {G}(L^\perp )$
. In addition to the discriminants of L and
$\mathcal {G}(L) \simeq \mathcal {G}(L^\perp )$
. In addition to the discriminants of L and
![]() $L^\perp $
being the same, this includes information about the local coefficients of the quadratic forms on L and
$L^\perp $
being the same, this includes information about the local coefficients of the quadratic forms on L and
![]() $L^\perp $
. This is exploited, for example, in Proposition B.6. When
$L^\perp $
. This is exploited, for example, in Proposition B.6. When
![]() $k=n-k$
, one can ask whether this implies that
$k=n-k$
, one can ask whether this implies that
![]() $Q|_{L(\mathbb {Z})}$
and
$Q|_{L(\mathbb {Z})}$
and
![]() $Q|_{L^\perp (\mathbb {Z})}$
are in the same genus.
$Q|_{L^\perp (\mathbb {Z})}$
are in the same genus.
6 Moduli spaces
In this section, we study the moduli space
![]() $\mathcal {Y}$
of basis extensions that was introduced in §1.1 consisting of (certain) homothety classes
$\mathcal {Y}$
of basis extensions that was introduced in §1.1 consisting of (certain) homothety classes
![]() $[L,\Lambda ]$
, where L is a k-dimensional subspace,
$[L,\Lambda ]$
, where L is a k-dimensional subspace,
![]() $\Lambda $
is a full-rank lattice in
$\Lambda $
is a full-rank lattice in
![]() $\mathbb {R}^n$
and
$\mathbb {R}^n$
and
![]() $L \cap \Lambda $
is a lattice in L. We also discuss a slight refinement of Theorem 1.11 (Theorem 6.9 below) and see how it implies Theorem 1.4.
$L \cap \Lambda $
is a lattice in L. We also discuss a slight refinement of Theorem 1.11 (Theorem 6.9 below) and see how it implies Theorem 1.4.
6.1 Oriented subspaces
For the purposes of proving the main theorems from their dynamical analogues, it is convenient to work with subspaces with an orientation. In fact, the main theorems may be refined to include orientation.
Oriented subspaces of dimension k form an affine variety
![]() $\mathrm {Gr}^+_{n,k}$
(defined over
$\mathrm {Gr}^+_{n,k}$
(defined over
![]() $\mathbb {Q}$
) with a morphism (of algebraic varieties)
$\mathbb {Q}$
) with a morphism (of algebraic varieties)
![]() $\mathrm {Gr}^+_{n,k} \to \mathrm {Gr}_{n,k}$
, where the preimage of any point consists of two points corresponding to two choices of orientation.
$\mathrm {Gr}^+_{n,k} \to \mathrm {Gr}_{n,k}$
, where the preimage of any point consists of two points corresponding to two choices of orientation.
Remark 6.1. To construct
![]() $\mathrm {Gr}^+_{n,k}$
explicitly, observe that the positive definite form Q induces a rational form
$\mathrm {Gr}^+_{n,k}$
explicitly, observe that the positive definite form Q induces a rational form
![]() $\mathrm {disc}_Q$
on the exterior product
$\mathrm {disc}_Q$
on the exterior product
![]() $\bigwedge ^k \mathbb {Q}^n$
via
$\bigwedge ^k \mathbb {Q}^n$
via
 $$ \begin{align*} \mathrm{disc}_Q(v_1\wedge \cdots \wedge v_k) = \det \begin{pmatrix} \langle v_1,v_1\rangle_Q & \cdots & \langle v_1,v_k\rangle_Q \\ \vdots & & \vdots \\ \langle v_k,v_1\rangle_Q & \cdots & \langle v_k,v_k\rangle_Q \end{pmatrix}\! . \end{align*} $$
$$ \begin{align*} \mathrm{disc}_Q(v_1\wedge \cdots \wedge v_k) = \det \begin{pmatrix} \langle v_1,v_1\rangle_Q & \cdots & \langle v_1,v_k\rangle_Q \\ \vdots & & \vdots \\ \langle v_k,v_1\rangle_Q & \cdots & \langle v_k,v_k\rangle_Q \end{pmatrix}\! . \end{align*} $$
Note that this merely extends the previous definition of discriminant. The variety
![]() $\mathrm {Gr}^+_{n,k}$
is then the subvariety of the variety of pure wedges
$\mathrm {Gr}^+_{n,k}$
is then the subvariety of the variety of pure wedges
![]() $\mathcal{P} $
satisfying the additional equation
$\mathcal{P} $
satisfying the additional equation
![]() $\mathrm {disc}_Q(v_1\wedge \cdots \wedge v_k) = 1$
. Note that rational subspaces with an orientation do not correspond to rational points of
$\mathrm {disc}_Q(v_1\wedge \cdots \wedge v_k) = 1$
. Note that rational subspaces with an orientation do not correspond to rational points of
![]() $\mathrm {Gr}^+_{n,k}$
but rather to primitive integer points of the variety of pure wedges
$\mathrm {Gr}^+_{n,k}$
but rather to primitive integer points of the variety of pure wedges
![]() $\mathcal {P}$
. In that sense, it is often more natural to work with
$\mathcal {P}$
. In that sense, it is often more natural to work with
![]() $\mathcal {P}$
instead of
$\mathcal {P}$
instead of
![]() $\mathrm {Gr}^+_{n,k}$
.
$\mathrm {Gr}^+_{n,k}$
.
The orthogonal group
![]() $\mathrm {SO}_Q$
(and hence also
$\mathrm {SO}_Q$
(and hence also
![]() $\mathrm {Spin}_Q$
) acts on oriented subspaces. For an oriented rational subspace L, the stabilizer group in
$\mathrm {Spin}_Q$
) acts on oriented subspaces. For an oriented rational subspace L, the stabilizer group in
![]() $\mathrm {Spin}_Q$
under this action is exactly equal to the stabilizer group
$\mathrm {Spin}_Q$
under this action is exactly equal to the stabilizer group
![]() $\mathbf {H}_L$
defined in §2.1.1. Moreover, the action of
$\mathbf {H}_L$
defined in §2.1.1. Moreover, the action of
![]() $\mathrm {Spin}_Q(\mathbb {R})$
on
$\mathrm {Spin}_Q(\mathbb {R})$
on
![]() $\mathrm {Gr}^+_{n,k}(\mathbb {R})$
is transitive (as is the action of
$\mathrm {Gr}^+_{n,k}(\mathbb {R})$
is transitive (as is the action of
![]() $\mathrm {SO}_Q(\mathbb {R})$
).
$\mathrm {SO}_Q(\mathbb {R})$
).
Remark 6.2. (Orientation on the orthogonal complement)
For any oriented k-dimensional subspace L, the orthogonal complement inherits an orientation: if
![]() $v_1,\ldots ,v_k$
is an oriented basis of L, then a basis
$v_1,\ldots ,v_k$
is an oriented basis of L, then a basis
![]() $v_{k+1},\ldots ,v_n$
of
$v_{k+1},\ldots ,v_n$
of
![]() $L^\perp $
is oriented if
$L^\perp $
is oriented if
![]() $\det (v_1,\ldots ,v_n)>0$
. The orthogonal complement yields an isomorphism
$\det (v_1,\ldots ,v_n)>0$
. The orthogonal complement yields an isomorphism
![]() $\mathrm {Gr}^+_{n,k} \to \mathrm {Gr}^+_{n,n-k}$
that is explicitly realizable in Plücker coordinates, at least, when
$\mathrm {Gr}^+_{n,k} \to \mathrm {Gr}^+_{n,n-k}$
that is explicitly realizable in Plücker coordinates, at least, when
![]() $\mathrm {disc}(Q) = 1$
[Reference SchmidtSch67, §1].
$\mathrm {disc}(Q) = 1$
[Reference SchmidtSch67, §1].
6.2 Quotients of homogeneous spaces
6.2.1 The moduli space of oriented basis extensions
We extend the definition of the moduli space of basis extensions to include orientation. Consider the pairs
![]() $(L,\Lambda )$
, where L is an oriented subspace,
$(L,\Lambda )$
, where L is an oriented subspace,
![]() $\Lambda \subset \mathbb {R}^n$
is a full-rank lattice and
$\Lambda \subset \mathbb {R}^n$
is a full-rank lattice and
![]() $L \cap \Lambda $
is a lattice in L. Two such pairs
$L \cap \Lambda $
is a lattice in L. Two such pairs
![]() $(L,\Lambda ),(L',\Lambda ')$
are equivalent if
$(L,\Lambda ),(L',\Lambda ')$
are equivalent if
![]() $L=L'$
(including orientation) and if there exists
$L=L'$
(including orientation) and if there exists
![]() $g \in \mathrm {GL}_n(\mathbb {R})$
which acts by positive scalar multiplication of L and
$g \in \mathrm {GL}_n(\mathbb {R})$
which acts by positive scalar multiplication of L and
![]() $L^\perp $
such that
$L^\perp $
such that
![]() $g \Lambda = \Lambda '$
. The moduli space of oriented basis extensions
$g \Lambda = \Lambda '$
. The moduli space of oriented basis extensions
![]() $\mathcal {Y}^+$
is defined to be the set of such equivalence classes
$\mathcal {Y}^+$
is defined to be the set of such equivalence classes
![]() $[L,\Lambda ]$
. There exists a natural map
$[L,\Lambda ]$
. There exists a natural map
![]() $\mathcal {Y}^+ \to \mathcal {Y}$
(simply by forgetting orientation).
$\mathcal {Y}^+ \to \mathcal {Y}$
(simply by forgetting orientation).
We begin by realizing
![]() $\mathcal {Y}^+$
as a double quotient of a Lie group. We use the following notation.
$\mathcal {Y}^+$
as a double quotient of a Lie group. We use the following notation.
-
• The groups
 $\mathbf {P}_{n,k}$
and
$\mathbf {P}_{n,k}$
and
 $\mathbf {G}$
, as defined in §1.4.4:
$\mathbf {G}$
, as defined in §1.4.4:  $$ \begin{align*} \mathbf{P}_{n,k} &= \bigg\{\! \begin{pmatrix} A & B \\ 0 & D \end{pmatrix} \in \mathrm{SL}_n : \det(A) = \det(D)=1 \bigg\},\\ \mathbf{G} &= \mathrm{Spin}_Q \times \mathbf{P}_{n,k}. \end{align*} $$
$$ \begin{align*} \mathbf{P}_{n,k} &= \bigg\{\! \begin{pmatrix} A & B \\ 0 & D \end{pmatrix} \in \mathrm{SL}_n : \det(A) = \det(D)=1 \bigg\},\\ \mathbf{G} &= \mathrm{Spin}_Q \times \mathbf{P}_{n,k}. \end{align*} $$
-
• The reference subspace
 $L_0$
spanned by the first k standard basis vectors (1.6) as well as the ‘standardization’
$L_0$
spanned by the first k standard basis vectors (1.6) as well as the ‘standardization’
 $\eta _Q$
defined in (1.3). Note that
$\eta _Q$
defined in (1.3). Note that
 $L_0$
is oriented using the standard basis.
$L_0$
is oriented using the standard basis. -
• For any oriented subspace
 $L \subset \mathbb {Q}^n$
, we let
$L \subset \mathbb {Q}^n$
, we let
 $\mathbf {H}_L<\mathrm {Spin}_Q$
be the stabilizer group of L.
$\mathbf {H}_L<\mathrm {Spin}_Q$
be the stabilizer group of L. -
• The subgroup
 $\mathbf {H}_{L_0}<\mathrm {Spin}_Q$
maps to a subgroup of
$\mathbf {H}_{L_0}<\mathrm {Spin}_Q$
maps to a subgroup of
 $\mathbf {P}_{n,k}$
under the (spin) isogeny
$\mathbf {P}_{n,k}$
under the (spin) isogeny
 $\rho _Q$
; we again denote by
$\rho _Q$
; we again denote by
 $\boldsymbol {\Delta}{\mathbf H}_{L_0}<\mathbf {G}$
the diagonally embedded group (this agrees with the definition in §2.3 with the choice of the standard basis).
$\boldsymbol {\Delta}{\mathbf H}_{L_0}<\mathbf {G}$
the diagonally embedded group (this agrees with the definition in §2.3 with the choice of the standard basis).
Lemma 6.3. There is an identification
By Lemma 6.3, we may pull back the Haar quotient probability measure on the right-hand side to
![]() $\mathcal {Y}^+$
(and by pushforward on
$\mathcal {Y}^+$
(and by pushforward on
![]() $\mathcal {Y}$
).
$\mathcal {Y}$
).
Proof. The above identification runs as follows. If
![]() $(g_1,g_2)\in \mathbf {G}(\mathbb {R})$
is given, we set
$(g_1,g_2)\in \mathbf {G}(\mathbb {R})$
is given, we set
![]() $L = \rho _Q(g_1^{-1})g_2L_0(\mathbb {R}) = g_1^{-1}.L_0(\mathbb {R})$
and
$L = \rho _Q(g_1^{-1})g_2L_0(\mathbb {R}) = g_1^{-1}.L_0(\mathbb {R})$
and
![]() $\Lambda =\rho _Q(g_1^{-1})g_2 \mathbb {Z}^n$
. Clearly,
$\Lambda =\rho _Q(g_1^{-1})g_2 \mathbb {Z}^n$
. Clearly,
![]() $\Lambda $
intersects L in the lattice
$\Lambda $
intersects L in the lattice
![]() $\rho _Q(g_1^{-1})g_2L_0(\mathbb {Z})$
. As any element of
$\rho _Q(g_1^{-1})g_2L_0(\mathbb {Z})$
. As any element of
![]() $\mathbf {P}_{n,k}(\mathbb {Z})$
stabilizes
$\mathbf {P}_{n,k}(\mathbb {Z})$
stabilizes
![]() $L_0(\mathbb {R})$
and
$L_0(\mathbb {R})$
and
![]() $\mathbb {Z}^n$
, and as
$\mathbb {Z}^n$
, and as
![]() $\boldsymbol {\Delta}{\mathbf H}_{L_0}(\mathbb {R})$
is diagonally embedded, we obtain a well-defined map
$\boldsymbol {\Delta}{\mathbf H}_{L_0}(\mathbb {R})$
is diagonally embedded, we obtain a well-defined map
The injectivity of this map is clear from the definition of
![]() $\boldsymbol {\Delta}{\mathbf H}_{L_0}(\mathbb {R})$
, so let us argue for the surjectivity.
$\boldsymbol {\Delta}{\mathbf H}_{L_0}(\mathbb {R})$
, so let us argue for the surjectivity.
Let
![]() $[L,\Lambda ] \in \mathcal {Y}$
. By choosing the representative correctly, we may assume that
$[L,\Lambda ] \in \mathcal {Y}$
. By choosing the representative correctly, we may assume that
![]() $\Lambda $
as well as
$\Lambda $
as well as
![]() $L \cap \Lambda $
are unimodular. Choose
$L \cap \Lambda $
are unimodular. Choose
![]() $g_1 \in \mathrm {Spin}_Q(\mathbb {R})$
such that
$g_1 \in \mathrm {Spin}_Q(\mathbb {R})$
such that
![]() $g_1.L = L_0$
. Then
$g_1.L = L_0$
. Then
![]() $L_0(\mathbb {R})$
is
$L_0(\mathbb {R})$
is
![]() $g_1.\Lambda $
-rational. Pick a basis
$g_1.\Lambda $
-rational. Pick a basis
![]() $v_1,\ldots ,v_k$
of
$v_1,\ldots ,v_k$
of
![]() $g_1.\Lambda \cap L_0(\mathbb {R})$
and complete it into a basis
$g_1.\Lambda \cap L_0(\mathbb {R})$
and complete it into a basis
![]() $v_1,\ldots ,v_n$
of
$v_1,\ldots ,v_n$
of
![]() $g_1.\Lambda $
. Set
$g_1.\Lambda $
. Set
As
![]() $g_1.\Lambda \cap L_0(\mathbb {R})$
is unimodular, we have that
$g_1.\Lambda \cap L_0(\mathbb {R})$
is unimodular, we have that
![]() $g_2 \in \mathbf {P}_{n,k}(\mathbb {R})$
. Under these choices we have
$g_2 \in \mathbf {P}_{n,k}(\mathbb {R})$
. Under these choices we have
![]() $\rho _Q(g_1^{-1})g_2L_0(\mathbb {R}) = L$
and
$\rho _Q(g_1^{-1})g_2L_0(\mathbb {R}) = L$
and
![]() $\rho _Q(g_1^{-1})g_2 \mathbb {Z}^n = \Lambda $
; surjectivity follows.
$\rho _Q(g_1^{-1})g_2 \mathbb {Z}^n = \Lambda $
; surjectivity follows.
Remark 6.4. (Action of
 $\mathrm {Spin}_Q(\mathbb {Z})$
)
$\mathrm {Spin}_Q(\mathbb {Z})$
)
Note that
![]() $\mathrm {Spin}_Q(\mathbb {Z})$
acts on
$\mathrm {Spin}_Q(\mathbb {Z})$
acts on
![]() $\mathcal {Y}^+$
via
$\mathcal {Y}^+$
via
![]() $g[L,\Lambda ] = [g.L,g.\Lambda ]$
. In view of the identification in Lemma 6.3 (and its proof), this action of
$g[L,\Lambda ] = [g.L,g.\Lambda ]$
. In view of the identification in Lemma 6.3 (and its proof), this action of
![]() $\mathrm {Spin}_Q(\mathbb {Z})$
corresponds to the
$\mathrm {Spin}_Q(\mathbb {Z})$
corresponds to the
![]() $\mathrm {Spin}_Q(\mathbb {Z})$
-action from the right on the double quotient
$\mathrm {Spin}_Q(\mathbb {Z})$
-action from the right on the double quotient
. In particular,
Recall from the introduction that
![]() $\mathcal {S}_{k}$
is the space of positive definite real quadratic forms in k variables up to similarity. Here, we say that two forms
$\mathcal {S}_{k}$
is the space of positive definite real quadratic forms in k variables up to similarity. Here, we say that two forms
![]() $q,q'$
in k-variables are equivalent if there is
$q,q'$
in k-variables are equivalent if there is
![]() $g \in \mathrm {GL}_k(\mathbb {Z})$
such that
$g \in \mathrm {GL}_k(\mathbb {Z})$
such that
![]() $gq = q'$
and similar if q is equivalent to a multiple of
$gq = q'$
and similar if q is equivalent to a multiple of
![]() $q'$
. We may identify
$q'$
. We may identify
![]() $\mathcal {S}_{k}$
with
$\mathcal {S}_{k}$
with
Indeed, to any point
![]() $\mathrm {O}_k(\mathbb {R})g \mathrm {PGL}_k(\mathbb {Z})$
, one associates the similarity class of the form represented by
$\mathrm {O}_k(\mathbb {R})g \mathrm {PGL}_k(\mathbb {Z})$
, one associates the similarity class of the form represented by
![]() $g^tg$
. Conversely, given the similarity class of a form q and a matrix representation M of q, one can write
$g^tg$
. Conversely, given the similarity class of a form q and a matrix representation M of q, one can write
![]() $M = g^t g$
for some
$M = g^t g$
for some
![]() $g \in \mathrm {GL}_k(\mathbb {R})$
. Another way of viewing the quotient in (6.1) is as the space of lattices in
$g \in \mathrm {GL}_k(\mathbb {R})$
. Another way of viewing the quotient in (6.1) is as the space of lattices in
![]() $\mathbb {R}^k$
up to isometries and homothety. For a lattice
$\mathbb {R}^k$
up to isometries and homothety. For a lattice
![]() $\Gamma \subset \mathbb {R}^k$
, we denote by
$\Gamma \subset \mathbb {R}^k$
, we denote by
![]() $\langle \Gamma \rangle $
its equivalence class. The map
$\langle \Gamma \rangle $
its equivalence class. The map
is the desired bijection. In words, the class of lattices
![]() $\langle \Gamma \rangle $
is associated to the similarity class of the standard form
$\langle \Gamma \rangle $
is associated to the similarity class of the standard form
![]() $Q_0$
represented in a basis of the lattice
$Q_0$
represented in a basis of the lattice
![]() $\Gamma $
.
$\Gamma $
.
Note that we have a map
![]() $[L,\Lambda ] \in \mathcal {Y} \mapsto [Q|_{L \cap \Lambda }] \in \mathcal {S}_{k}$
already alluded to in the introduction. It is natural to ask what equivalence class of lattices corresponds to the similarity class (or shape)
$[L,\Lambda ] \in \mathcal {Y} \mapsto [Q|_{L \cap \Lambda }] \in \mathcal {S}_{k}$
already alluded to in the introduction. It is natural to ask what equivalence class of lattices corresponds to the similarity class (or shape)
![]() $[Q|_{L\cap \Lambda }]$
from the introduction under the identification (6.2). To answer this question, choose a rotation
$[Q|_{L\cap \Lambda }]$
from the introduction under the identification (6.2). To answer this question, choose a rotation
![]() $k_L \in \mathrm {SO}_Q(\mathbb {R})$
with
$k_L \in \mathrm {SO}_Q(\mathbb {R})$
with
![]() $k_L L(\mathbb {R}) = L_0(\mathbb {R})$
. Apply
$k_L L(\mathbb {R}) = L_0(\mathbb {R})$
. Apply
![]() $\eta _Q$
to the lattice
$\eta _Q$
to the lattice
![]() $k_L (L\cap \Lambda ) \subset L_0(\mathbb {R})$
. Recall that
$k_L (L\cap \Lambda ) \subset L_0(\mathbb {R})$
. Recall that
![]() $\eta _Q$
was chosen in §1.4.1 to preserve
$\eta _Q$
was chosen in §1.4.1 to preserve
![]() $L_0(\mathbb {R})$
so that
$L_0(\mathbb {R})$
so that
![]() $\eta _Q k_L (L \cap \Lambda ) \subset L_0(\mathbb {R})$
. Since
$\eta _Q k_L (L \cap \Lambda ) \subset L_0(\mathbb {R})$
. Since
the equivalence class of the lattice
![]() $\eta _Q k_L (L \cap \Lambda )$
corresponds to the similarity class or shape
$\eta _Q k_L (L \cap \Lambda )$
corresponds to the similarity class or shape
![]() $[Q|_{L\cap \Lambda }]$
. As we did in the introduction, we will also write
$[Q|_{L\cap \Lambda }]$
. As we did in the introduction, we will also write
![]() $[L\cap \Lambda ]$
for that shape.
$[L\cap \Lambda ]$
for that shape.
Lemma 6.5. There is a surjective map
given explicitly by
![]() $[L,\Lambda ] \mapsto (L, [L\cap \Lambda ],[L^\perp \cap \Lambda ^\#])$
. Moreover, the pushforward of the Haar (quotient) probability measure is the Haar probability measure on the target.
$[L,\Lambda ] \mapsto (L, [L\cap \Lambda ],[L^\perp \cap \Lambda ^\#])$
. Moreover, the pushforward of the Haar (quotient) probability measure is the Haar probability measure on the target.
Proof. Recall that
![]() $\mathbf {H}^{\prime }_{L_0}$
is the stabilizer of
$\mathbf {H}^{\prime }_{L_0}$
is the stabilizer of
![]() $L_0$
in
$L_0$
in
![]() $\mathrm {SO}_Q$
. Over
$\mathrm {SO}_Q$
. Over
![]() $\mathbb {R}$
, we have
$\mathbb {R}$
, we have
![]() $\mathbf {H}^{\prime }_{L_0} (\mathbb {R}) = \rho _Q(\mathbf {H}_{L_0}(\mathbb {R}))$
. Consider the (surjective) composition
$\mathbf {H}^{\prime }_{L_0} (\mathbb {R}) = \rho _Q(\mathbf {H}_{L_0}(\mathbb {R}))$
. Consider the (surjective) composition

where the first map is the identification in Lemma 6.3, the second map is the quotient map and the third map is multiplication by
![]() $\eta _Q$
in the second factor. Observe that
$\eta _Q$
in the second factor. Observe that
is identified with
![]() $\mathrm {Gr}^+_{n,k}(\mathbb {R})$
via
$\mathrm {Gr}^+_{n,k}(\mathbb {R})$
via
![]() $\mathbf {H}_{L_0}(\mathbb {R})g_0 \mapsto g_0^{-1}.L_0(\mathbb {R})$
. Note also that
$\mathbf {H}_{L_0}(\mathbb {R})g_0 \mapsto g_0^{-1}.L_0(\mathbb {R})$
. Note also that
![]() $\eta _Q\mathbf {H}^{\prime }_{L_0}(\mathbb {R}))\eta _Q^{-1}$
is equal to the group
$\eta _Q\mathbf {H}^{\prime }_{L_0}(\mathbb {R}))\eta _Q^{-1}$
is equal to the group
![]() $\mathrm {SO}_k(\mathbb {R}) \times \mathrm {SO}_{n-k}(\mathbb {R})$
embedded block-diagonally. We apply projections onto the blocks (
$\mathrm {SO}_k(\mathbb {R}) \times \mathrm {SO}_{n-k}(\mathbb {R})$
embedded block-diagonally. We apply projections onto the blocks (
![]() $\pi _1,\pi _2$
defined in §1.4.4) as well as inverse-transpose in the second block to obtain a surjective map
$\pi _1,\pi _2$
defined in §1.4.4) as well as inverse-transpose in the second block to obtain a surjective map
Overall, we have a surjection
![]() $\phi :\mathcal {Y}^+ \to \mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
.
$\phi :\mathcal {Y}^+ \to \mathrm {Gr}_{n,k}(\mathbb {R}) \times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
.
It remains to verify that this surjection is the map from the lemma. Let
![]() $[L,\Lambda ] \in \mathcal {Y}^+$
and let
$[L,\Lambda ] \in \mathcal {Y}^+$
and let
![]() $(g_1,g_2) \in \mathbf {G}(\mathbb {R})$
be a representative of its double coset in Lemma 6.3. It is clear from the proof of Lemma 6.3 that
$(g_1,g_2) \in \mathbf {G}(\mathbb {R})$
be a representative of its double coset in Lemma 6.3. It is clear from the proof of Lemma 6.3 that
![]() $\phi ([L,\Lambda ])_1 = g_1^{-1}.L_0(\mathbb {R}) = L(\mathbb {R})$
. For the second component, note that, using
$\phi ([L,\Lambda ])_1 = g_1^{-1}.L_0(\mathbb {R}) = L(\mathbb {R})$
. For the second component, note that, using
![]() $g_1^{-1}.L_0(\mathbb {R}) = L(\mathbb {R})$
,
$g_1^{-1}.L_0(\mathbb {R}) = L(\mathbb {R})$
,
For the third component, we observe that
![]() $L^\perp (\mathbb {R}) = g_1^{-1}.L_0(\mathbb {R})^\perp $
as well as
$L^\perp (\mathbb {R}) = g_1^{-1}.L_0(\mathbb {R})^\perp $
as well as
![]() $\Lambda ^\# = \rho _Q(g_1^{-1})(g_{2}^{-1})^t\mathbb {Z}^n$
. Hence,
$\Lambda ^\# = \rho _Q(g_1^{-1})(g_{2}^{-1})^t\mathbb {Z}^n$
. Hence,
 $$ \begin{align*} [Q|_{L^\perp \cap \Lambda^\#}] &= [Q_0|_{\eta_Q \rho_Q(g_1)(L^\perp \cap \Lambda^\#)}] = [Q_0|_{\eta_Q (L_0^\perp \cap (g_{2}^{-1})^t\mathbb{Z}^n})] = [Q_0|_{\pi_2(\eta_Q (g_{2}^{-1})^t) \mathbb{Z}^k}] \\ &= \phi([L,\Lambda])_3, \end{align*} $$
$$ \begin{align*} [Q|_{L^\perp \cap \Lambda^\#}] &= [Q_0|_{\eta_Q \rho_Q(g_1)(L^\perp \cap \Lambda^\#)}] = [Q_0|_{\eta_Q (L_0^\perp \cap (g_{2}^{-1})^t\mathbb{Z}^n})] = [Q_0|_{\pi_2(\eta_Q (g_{2}^{-1})^t) \mathbb{Z}^k}] \\ &= \phi([L,\Lambda])_3, \end{align*} $$
which concludes the lemma.
6.3 A construction of an intermediate lattice
As was already observed in Remark 1.10, equidistribution of the tuples
![]() $[L,\mathbb {Z}^n]$
for
$[L,\mathbb {Z}^n]$
for
![]() $L \in \mathcal {H}^{n,k}_Q(D)$
(Conjecture 1.9) does not necessarily imply equidistribution of the tuples
$L \in \mathcal {H}^{n,k}_Q(D)$
(Conjecture 1.9) does not necessarily imply equidistribution of the tuples
![]() $(L,[L(\mathbb {Z})],[L^\perp (\mathbb {Z})])$
when Q is not unimodular (Conjecture 1.1). Indeed, one can see from Lemma 6.5 that it implies equidistribution of the tuples
$(L,[L(\mathbb {Z})],[L^\perp (\mathbb {Z})])$
when Q is not unimodular (Conjecture 1.1). Indeed, one can see from Lemma 6.5 that it implies equidistribution of the tuples
![]() $(L,[L(\mathbb {Z})],[L^\perp \cap (\mathbb {Z}^n)^\#])$
for
$(L,[L(\mathbb {Z})],[L^\perp \cap (\mathbb {Z}^n)^\#])$
for
![]() $L \in \mathcal {H}^{n,k}_Q(D)$
. Here, we construct, for every L, a full-rank sublattice
$L \in \mathcal {H}^{n,k}_Q(D)$
. Here, we construct, for every L, a full-rank sublattice
![]() $\Lambda _L\subset \mathbb {Q}^n$
so that equidistribution of the tuples
$\Lambda _L\subset \mathbb {Q}^n$
so that equidistribution of the tuples
![]() $[L,\Lambda _L]$
does have this desired implication. For any subspace
$[L,\Lambda _L]$
does have this desired implication. For any subspace
![]() $L \subset \mathbb {Q}^n$
, write
$L \subset \mathbb {Q}^n$
, write
![]() $\pi _L$
for the orthogonal projection onto L.
$\pi _L$
for the orthogonal projection onto L.
Proposition 6.6. For any subspace
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
, there exists a full-rank
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
, there exists a full-rank
![]() $\mathbb {Z}$
-lattice
$\mathbb {Z}$
-lattice
![]() $\Lambda _L \subset \mathbb {Q}^n$
with the following properties.
$\Lambda _L \subset \mathbb {Q}^n$
with the following properties.
-
(1)
 $\mathbb {Z}^n \subset \Lambda _L \subset (\mathbb {Z}^n)^\#$
.
$\mathbb {Z}^n \subset \Lambda _L \subset (\mathbb {Z}^n)^\#$
. -
(2) We have
 $$ \begin{align*} L \cap \Lambda_L = L(\mathbb{Z}), \quad \pi_{L^\perp}(\Lambda_L) = L^\perp(\mathbb{Z})^\# \quad \text{and} \quad L^\perp(\mathbb{Z}) = \Lambda_L^\# \cap L^\perp. \end{align*} $$
$$ \begin{align*} L \cap \Lambda_L = L(\mathbb{Z}), \quad \pi_{L^\perp}(\Lambda_L) = L^\perp(\mathbb{Z})^\# \quad \text{and} \quad L^\perp(\mathbb{Z}) = \Lambda_L^\# \cap L^\perp. \end{align*} $$
-
(3) Suppose that
 $L'$
satisfies that there are
$L'$
satisfies that there are
 $\gamma \in \mathrm {Spin}_Q(\mathbb {Q})$
and
$\gamma \in \mathrm {Spin}_Q(\mathbb {Q})$
and
 $k_p \in \mathrm {Spin}_Q(\mathbb {Z}_p)$
for every prime p such that
$k_p \in \mathrm {Spin}_Q(\mathbb {Z}_p)$
for every prime p such that
 $\gamma. L = L'$
and
$\gamma. L = L'$
and
 $k_p. L(\mathbb {Z}_p) = L'(\mathbb {Z}_p)$
. Then
$k_p. L(\mathbb {Z}_p) = L'(\mathbb {Z}_p)$
. Then  $$ \begin{align*} \Lambda_{L'} = \bigcap_{p} k_p.(\Lambda_L \otimes \mathbb{Z}_p) \cap \mathbb{Q}^n. \end{align*} $$
$$ \begin{align*} \Lambda_{L'} = \bigcap_{p} k_p.(\Lambda_L \otimes \mathbb{Z}_p) \cap \mathbb{Q}^n. \end{align*} $$
We remark that, if Q is unimodular, one may simply take
![]() $\Lambda _L = \mathbb {Z}^n$
. For Q not unimodular, this choice generally satisfies (1) and (3) but not necessarily (2).
$\Lambda _L = \mathbb {Z}^n$
. For Q not unimodular, this choice generally satisfies (1) and (3) but not necessarily (2).
Remark 6.7. (Equivalence relation)
We write
![]() $L \sim L'$
for rational subspaces
$L \sim L'$
for rational subspaces
![]() $L,L'$
of dimension k if there are
$L,L'$
of dimension k if there are
![]() $\gamma \in \mathrm {Spin}_Q(\mathbb {Q})$
and
$\gamma \in \mathrm {Spin}_Q(\mathbb {Q})$
and
![]() $k_p \in \mathrm {Spin}_Q(\mathbb {Z}_p)$
for every prime p such that
$k_p \in \mathrm {Spin}_Q(\mathbb {Z}_p)$
for every prime p such that
![]() $\gamma. L = L'$
and
$\gamma. L = L'$
and
![]() $k_p .L(\mathbb {Z}_p) = L'(\mathbb {Z}_p)$
. This defines an equivalence relation. As
$k_p .L(\mathbb {Z}_p) = L'(\mathbb {Z}_p)$
. This defines an equivalence relation. As
![]() $L,L'$
are locally rotated into each other, they have the same discriminant (see Equation (1.5)).
$L,L'$
are locally rotated into each other, they have the same discriminant (see Equation (1.5)).
Proof of Proposition 6.6
In view of Remark 6.7 and the required property in (3), we first observe that if
![]() $L'$
is equivalent to L and if L satisfies (1) and (2), then
$L'$
is equivalent to L and if L satisfies (1) and (2), then
![]() $L'$
also does so. Hence, we may split
$L'$
also does so. Hence, we may split
![]() $\mathrm {Gr}_{n,k}(\mathbb {Q})$
into equivalence classes, choose a representative L in each equivalence class and construct
$\mathrm {Gr}_{n,k}(\mathbb {Q})$
into equivalence classes, choose a representative L in each equivalence class and construct
![]() $\Lambda _L$
with the properties in (1) and (2) but ignoring (3).
$\Lambda _L$
with the properties in (1) and (2) but ignoring (3).
So, let
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be such a representative. Choose a basis
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be such a representative. Choose a basis
![]() $v_1,\ldots ,v_k$
of
$v_1,\ldots ,v_k$
of
![]() $L(\mathbb {Z})$
. We consider the
$L(\mathbb {Z})$
. We consider the
![]() $\mathbb {Z}$
-module
$\mathbb {Z}$
-module
![]() that fits into the following exact sequence
that fits into the following exact sequence
As
![]() $L \cap (\mathbb {Z}^n)^\#$
is primitive (a sublattice
$L \cap (\mathbb {Z}^n)^\#$
is primitive (a sublattice
![]() $\Gamma $
of a lattice
$\Gamma $
of a lattice
![]() $\Lambda \subset \mathbb {Q}^n$
is primitive if it is not strictly contained in any sublattice of the same rank) in
$\Lambda \subset \mathbb {Q}^n$
is primitive if it is not strictly contained in any sublattice of the same rank) in
![]() $(\mathbb {Z}^n)^\#$
, the module on the far right is free of rank
$(\mathbb {Z}^n)^\#$
, the module on the far right is free of rank
![]() $n-k$
. We choose a basis of it as well as representatives
$n-k$
. We choose a basis of it as well as representatives
![]() $v_{k+1},\ldots ,v_n \in (\mathbb {Z}^n)^\#$
of these basis elements. Define
$v_{k+1},\ldots ,v_n \in (\mathbb {Z}^n)^\#$
of these basis elements. Define
It is not hard to see that this lattice contains
![]() $\mathbb {Z}^n$
and is contained in
$\mathbb {Z}^n$
and is contained in
![]() $(\mathbb {Z}^n)^\#$
so that (1) is satisfied.
$(\mathbb {Z}^n)^\#$
so that (1) is satisfied.
Suppose that
This implies that
![]() $\sum _{i>k}\alpha _i v_i \in L$
and so
$\sum _{i>k}\alpha _i v_i \in L$
and so
![]() $\sum _{i>k}\alpha _i v_i = 0$
by linear independence. The identity
$\sum _{i>k}\alpha _i v_i = 0$
by linear independence. The identity
![]() $L \cap \Lambda _L = L(\mathbb {Z})$
follows.
$L \cap \Lambda _L = L(\mathbb {Z})$
follows.
By Lemma 5.3, the projection
![]() $\pi _{L^\perp }:(\mathbb {Z}^n)^\# \to L^\perp (\mathbb {Z})^\#$
is surjective. Clearly, the kernel is
$\pi _{L^\perp }:(\mathbb {Z}^n)^\# \to L^\perp (\mathbb {Z})^\#$
is surjective. Clearly, the kernel is
![]() $L\cap (\mathbb {Z}^n)^\#$
and hence, by construction of
$L\cap (\mathbb {Z}^n)^\#$
and hence, by construction of
![]() $\Lambda _L$
, we have
$\Lambda _L$
, we have
![]() $\pi _{L^\perp }(\Lambda _L) = \pi _{L^\perp }((\mathbb {Z}^n)^\#) = L^\perp (\mathbb {Z})^\#$
.
$\pi _{L^\perp }(\Lambda _L) = \pi _{L^\perp }((\mathbb {Z}^n)^\#) = L^\perp (\mathbb {Z})^\#$
.
It remains to prove the last identity. As
![]() $\Lambda _L^\# \supset \mathbb {Z}^n$
, we have
$\Lambda _L^\# \supset \mathbb {Z}^n$
, we have
![]() $\Lambda _L^\# \cap L^\perp \supset L^\perp (\mathbb {Z})$
, so it suffices to show that
$\Lambda _L^\# \cap L^\perp \supset L^\perp (\mathbb {Z})$
, so it suffices to show that
For
![]() $v = \pi _{L^\perp }(v') \in \pi _{L^\perp }(\Lambda _L)$
and
$v = \pi _{L^\perp }(v') \in \pi _{L^\perp }(\Lambda _L)$
and
![]() $w \in L^\perp \cap \Lambda _L^\#$
, we have
$w \in L^\perp \cap \Lambda _L^\#$
, we have
![]() $\langle v,w\rangle = \langle v',w\rangle \in \mathbb {Z}$
, which proves the remaining claim.
$\langle v,w\rangle = \langle v',w\rangle \in \mathbb {Z}$
, which proves the remaining claim.
Remark 6.8. Observe that
![]() $\Lambda _L$
constructed above depends on the choice of basis for the free module
$\Lambda _L$
constructed above depends on the choice of basis for the free module
![]() which forms the ‘free part’ of
which forms the ‘free part’ of
![]() in the sense of (6.3). But the short exact sequence (6.3) does not split, in general, so that the basis elements have no canonical lifts to
in the sense of (6.3). But the short exact sequence (6.3) does not split, in general, so that the basis elements have no canonical lifts to
![]() ; different choices yield different lattices
; different choices yield different lattices
![]() $\Lambda _L$
. This dependency is inconsequential as the set of lattices
$\Lambda _L$
. This dependency is inconsequential as the set of lattices
![]() $\Lambda $
with
$\Lambda $
with
![]() $\mathbb {Z}^n \subset \Lambda \subset (\mathbb {Z}^n)^\#$
is finite.
$\mathbb {Z}^n \subset \Lambda \subset (\mathbb {Z}^n)^\#$
is finite.
6.4 A refinement of Theorem 1.11
We now present a refinement of Theorem 1.11, which is necessary to deduce the desired equidistribution theorem of shapes (i.e. Theorem 1.4).
Theorem 6.9. Let
![]() $k\geq 3$
with
$k\geq 3$
with
![]() $k \leq n-k$
and let p be a prime with
$k \leq n-k$
and let p be a prime with
![]() $p \nmid 2\mathrm {disc}(Q)$
. Let
$p \nmid 2\mathrm {disc}(Q)$
. Let
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q}) \mapsto \Lambda _L$
satisfy conditions (1) and (3) from Proposition 6.6. Suppose that
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q}) \mapsto \Lambda _L$
satisfy conditions (1) and (3) from Proposition 6.6. Suppose that
![]() $D_i \in \mathbb {N}$
is a sequence of integers with
$D_i \in \mathbb {N}$
is a sequence of integers with
![]() $D_i^{[k]}\to \infty $
,
$D_i^{[k]}\to \infty $
,
![]() $\mathcal {H}_{Q}^{n,k}(D_i)\neq \emptyset $
as well as
$\mathcal {H}_{Q}^{n,k}(D_i)\neq \emptyset $
as well as
![]() $p \nmid D_i$
if
$p \nmid D_i$
if
![]() $k \in \{3,4\}$
. Then the sets
$k \in \{3,4\}$
. Then the sets
equidistribute in
![]() $\mathcal {Y}^+$
as
$\mathcal {Y}^+$
as
![]() $i \to \infty $
$i \to \infty $
We observe that the special case
![]() $\Lambda _L= \mathbb {Z}^n$
for every
$\Lambda _L= \mathbb {Z}^n$
for every
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
in Theorem 6.9 implies Theorem 1.11 after projection
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
in Theorem 6.9 implies Theorem 1.11 after projection
![]() $\mathcal {Y}^+\to \mathcal {Y}$
.
$\mathcal {Y}^+\to \mathcal {Y}$
.
Proof of Theorem 1.4 from Theorem 6.9 when
 $k \geq 3$
$k \geq 3$
Let
![]() $\Lambda _L$
for
$\Lambda _L$
for
![]() $L\in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be defined as in Proposition 6.6. Let p be a prime and let
$L\in \mathrm {Gr}_{n,k}(\mathbb {Q})$
be defined as in Proposition 6.6. Let p be a prime and let
![]() $D_i\geq 1$
be a sequence of discriminants as in Theorem 1.4. Then Theorem 6.9 is applicable and the sets in (6.4) are equidistributed in
$D_i\geq 1$
be a sequence of discriminants as in Theorem 1.4. Then Theorem 6.9 is applicable and the sets in (6.4) are equidistributed in
![]() $\mathcal {Y}^+$
when
$\mathcal {Y}^+$
when
![]() $i \to \infty $
. By construction of
$i \to \infty $
. By construction of
![]() $\Lambda _L$
, the image of these sets under the map in Lemma 6.5 is exactly
$\Lambda _L$
, the image of these sets under the map in Lemma 6.5 is exactly
These images are equidistributed with respect to the pushforward measure, which is the Haar probability measure on
![]() $\mathrm {Gr}_{n,k}(\mathbb {R})\times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
.
$\mathrm {Gr}_{n,k}(\mathbb {R})\times \mathcal {S}_{k} \times \mathcal {S}_{n-k}$
.
Remark 6.10. (Theorem 1.4 for oriented subspaces)
Let
![]() $\mathcal {X}_k$
be the space of positive definite real quadratic forms in k variables up to proper similarity. Observe that the shape of an oriented k-dimensional subspace makes sense as a point in
$\mathcal {X}_k$
be the space of positive definite real quadratic forms in k variables up to proper similarity. Observe that the shape of an oriented k-dimensional subspace makes sense as a point in
![]() $\mathcal {X}_k$
. Very much related to this is the fact that the proof of Lemma 6.5 actually establishes a surjective map
$\mathcal {X}_k$
. Very much related to this is the fact that the proof of Lemma 6.5 actually establishes a surjective map
![]() $\mathcal {Y}^+ \to \mathrm {Gr}^+_{n,k}(\mathbb {R})\times \mathcal {X}_k \times \mathcal {X}_{n-k}$
. Theorem 1.4 may thus be generalized to this latter space. For
$\mathcal {Y}^+ \to \mathrm {Gr}^+_{n,k}(\mathbb {R})\times \mathcal {X}_k \times \mathcal {X}_{n-k}$
. Theorem 1.4 may thus be generalized to this latter space. For
![]() $k=1$
, this oriented version already appears in the works [Reference Aka, Einsiedler and ShapiraAES16a, Reference Aka, Einsiedler and ShapiraAES16b].
$k=1$
, this oriented version already appears in the works [Reference Aka, Einsiedler and ShapiraAES16a, Reference Aka, Einsiedler and ShapiraAES16b].
7 Proof of the main theorems from the dynamical versions
The aim of this section is to prove Theorems 6.9 and 1.4 for
![]() $k=2$
. We remark that any possible future upgrades to the dynamical versions (with regard to the congruence conditions at fixed primes) imply the analogous upgrades to the arithmetic versions.
$k=2$
. We remark that any possible future upgrades to the dynamical versions (with regard to the congruence conditions at fixed primes) imply the analogous upgrades to the arithmetic versions.
7.1 Notation
We recall and introduce here some notation used throughout this §7. In the following,
![]() $L \subset \mathbb {Q}^n$
is an arbitrary k-dimensional oriented subspace unless specified otherwise.
$L \subset \mathbb {Q}^n$
is an arbitrary k-dimensional oriented subspace unless specified otherwise.
-
•
 $\mathcal {Y}^+$
is the moduli space of oriented basis extensions defined in §6.2.1 (see also §1.1). Recall that
$\mathcal {Y}^+$
is the moduli space of oriented basis extensions defined in §6.2.1 (see also §1.1). Recall that
 $\mathrm {Spin}_Q(\mathbb {Z})$
acts on
$\mathrm {Spin}_Q(\mathbb {Z})$
acts on
 $\mathcal {Y}^+$
via
$\mathcal {Y}^+$
via
 $g[L,\Lambda ] = [g.L,g.\Lambda ]$
. Moreover, by Lemma 6.3 and the subsequent Remark 6.4, (7.1)
$g[L,\Lambda ] = [g.L,g.\Lambda ]$
. Moreover, by Lemma 6.3 and the subsequent Remark 6.4, (7.1) (7.2)where
(7.2)where
 $L_0 = \mathbb {Q}^k \times \{(0,\ldots ,0)\} \subset \mathbb {Q}^n$
is the fixed reference subspace (cf. (1.6)) and
$L_0 = \mathbb {Q}^k \times \{(0,\ldots ,0)\} \subset \mathbb {Q}^n$
is the fixed reference subspace (cf. (1.6)) and
 $\mathbf {G} = \mathrm {Spin}_Q \times \mathbf {P}_{n,k}$
(cf. 1.4.4).
$\mathbf {G} = \mathrm {Spin}_Q \times \mathbf {P}_{n,k}$
(cf. 1.4.4).
-
• The subgroup
 $\mathbf {H}_L < \mathrm {Spin}_Q$
is the identity component of the stabilizer group of L (cf. §2.1.1 and see also §6.1).
$\mathbf {H}_L < \mathrm {Spin}_Q$
is the identity component of the stabilizer group of L (cf. §2.1.1 and see also §6.1). -
• We fix a full-rank lattice
 $\mathbb {Z}^n \subset \Lambda _L \subset (\mathbb {Z}^n)^\#$
satisfying (1) and (3) in Proposition 6.6. The reader is encouraged to keep in mind the case
$\mathbb {Z}^n \subset \Lambda _L \subset (\mathbb {Z}^n)^\#$
satisfying (1) and (3) in Proposition 6.6. The reader is encouraged to keep in mind the case
 $\mathrm {disc}(Q) = 1$
, where one may take
$\mathrm {disc}(Q) = 1$
, where one may take
 $\Lambda _L = \mathbb {Z}^n$
for all L.
$\Lambda _L = \mathbb {Z}^n$
for all L. -
• We fix an oriented basis of
 $\Lambda _L$
, where the first k vectors are an oriented basis of
$\Lambda _L$
, where the first k vectors are an oriented basis of
 $L\cap \Lambda _L$
. Let
$L\cap \Lambda _L$
. Let
 $g_L \in \mathrm {GL}_n(\mathbb {Q})$
be the element whose columns consist of this basis.
$g_L \in \mathrm {GL}_n(\mathbb {Q})$
be the element whose columns consist of this basis. -
• The subgroup
 $\boldsymbol {\Delta}{\mathbf H}_L < \mathbf {G}$
is defined as in §2.3 using the basis in
$\boldsymbol {\Delta}{\mathbf H}_L < \mathbf {G}$
is defined as in §2.3 using the basis in
 $g_L$
.
$g_L$
. -
• For any
 $[L,\Lambda ] \in \mathcal {Y}^+$
(where L is not necessarily rational), to shorten notation, we write
$[L,\Lambda ] \in \mathcal {Y}^+$
(where L is not necessarily rational), to shorten notation, we write
 $[L, \Lambda ]_{\star }$
for the equivalence class
$[L, \Lambda ]_{\star }$
for the equivalence class
 .
. -
• Let
 $\mathsf {s}_L \in \mathbf {G}(\mathbb {R})$
be the representative of the double coset of
$\mathsf {s}_L \in \mathbf {G}(\mathbb {R})$
be the representative of the double coset of
 $[L,\Lambda _L]$
defined using
$[L,\Lambda _L]$
defined using
 $g_L$
(see also the proof of Lemma 6.3).
$g_L$
(see also the proof of Lemma 6.3). -
• For any
 $D \in \mathbb {N}$
with
$D \in \mathbb {N}$
with
 $\mathcal {H}^{n,k}_Q(D) \neq \emptyset $
we consider the finite set
$\mathcal {H}^{n,k}_Q(D) \neq \emptyset $
we consider the finite set
 $\mathcal {R}^{n,k}_Q(D)\subset \mathcal {Y}^+$
consisting of classes
$\mathcal {R}^{n,k}_Q(D)\subset \mathcal {Y}^+$
consisting of classes
 $[L,\Lambda _L]$
, where L runs over all oriented k-dimensional subspaces
$[L,\Lambda _L]$
, where L runs over all oriented k-dimensional subspaces
 $L \subset \mathbb {Q}^n$
with
$L \subset \mathbb {Q}^n$
with
 $\mathrm {disc}_Q(L)=D$
(see also (6.4)). The action of
$\mathrm {disc}_Q(L)=D$
(see also (6.4)). The action of
 $\mathrm {Spin}_Q(\mathbb {Z})$
on
$\mathrm {Spin}_Q(\mathbb {Z})$
on
 $\mathcal {Y}^+$
leaves
$\mathcal {Y}^+$
leaves
 $\mathcal {R}^{n,k}_Q(D)$
invariant.
$\mathcal {R}^{n,k}_Q(D)$
invariant.
7.2 Outline of the proof
Let
be the principal genus. (The genera (i.e. orbits of
![]() $\mathbf {G}(\mathbb {R})\times \mathbf {G}(\widehat {\mathbb {Z}})$
) correspond to classes in the spinor genus of Q. Recall that if Q is the sum of squares in
$\mathbf {G}(\mathbb {R})\times \mathbf {G}(\widehat {\mathbb {Z}})$
) correspond to classes in the spinor genus of Q. Recall that if Q is the sum of squares in
![]() $\leq 8$
variables, then the spinor genus consists of one class (cf. [Reference CasselsCas78, p. 232]) and hence
$\leq 8$
variables, then the spinor genus consists of one class (cf. [Reference CasselsCas78, p. 232]) and hence
.) There is a natural map
given by taking the quotient on the left of
![]() $\mathbf {G}(\mathbb {A})/\mathbf {G}(\mathbb {Q})$
by the maximal compact open subgroup
$\mathbf {G}(\mathbb {A})/\mathbf {G}(\mathbb {Q})$
by the maximal compact open subgroup
![]() $\mathbf {G}(\widehat {\mathbb {Z}})$
and
$\mathbf {G}(\widehat {\mathbb {Z}})$
and
![]() $\boldsymbol {\Delta}{\mathbf H}_{L_0}(\mathbb {R})$
. Consider an oriented subspace L of discriminant D and the orbit
$\boldsymbol {\Delta}{\mathbf H}_{L_0}(\mathbb {R})$
. Consider an oriented subspace L of discriminant D and the orbit
![]() $\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})$
. For any
$\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})$
. For any
![]() $L \in \mathcal {H}^{n,k}_Q(D)$
, the image of the intersection of
$L \in \mathcal {H}^{n,k}_Q(D)$
, the image of the intersection of
![]() $\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})$
with
$\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})$
with
![]() $\mathcal {U}$
under (7.3) is a subset of the collection
$\mathcal {U}$
under (7.3) is a subset of the collection
and contains
![]() $[L,\Lambda _L]$
(see Proposition 7.1). In other words, we have a commutative diagram
$[L,\Lambda _L]$
(see Proposition 7.1). In other words, we have a commutative diagram

Assuming that
![]() $k\geq 3$
, the intersection
$k\geq 3$
, the intersection
![]() $\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})\cap \mathcal {U}$
is equidistributed in
$\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})\cap \mathcal {U}$
is equidistributed in
![]() $\mathcal {U}$
with respect to the normalized restriction of the Haar measure (along any sequence of admissible subspaces). This immediately implies equidistribution of the pushforwards under the map in (7.3).
$\mathcal {U}$
with respect to the normalized restriction of the Haar measure (along any sequence of admissible subspaces). This immediately implies equidistribution of the pushforwards under the map in (7.3).
It remains to compare the pushforward of the Haar measure on the orbit with the measure on
![]() induced by the normalized counting measure on
induced by the normalized counting measure on
![]() $\mathcal {R}^{n,k}_Q(D)$
. (This technical argument constitutes a large part of this section §7.) To this end, we first note that the projection
$\mathcal {R}^{n,k}_Q(D)$
. (This technical argument constitutes a large part of this section §7.) To this end, we first note that the projection
![]() $\mathrm {P}(L)$
of
$\mathrm {P}(L)$
of
![]() $\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})\cap \mathcal {U}$
is not surjective but
$\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})\cap \mathcal {U}$
is not surjective but
![]() may be decomposed into such images for different subspaces L (see Remark 7.2). Thus, it is enough to determine the weights of individual points in
may be decomposed into such images for different subspaces L (see Remark 7.2). Thus, it is enough to determine the weights of individual points in
![]() $\mathrm {P}(L)$
(see Lemmas 7.3 and 7.4).
$\mathrm {P}(L)$
(see Lemmas 7.3 and 7.4).
7.3 Generating integer points from the packet
As a first step towards the proof of Theorem 6.9, we illustrate a general technique for generating points in
![]() $\mathcal {R}^{n,k}_Q(D)$
from a given point in
$\mathcal {R}^{n,k}_Q(D)$
from a given point in
![]() $\mathcal {R}^{n,k}_Q(D)$
. This kind of idea appears in many recent or less recent articles in the literature (see, for example, [Reference Platonov and RapinchukPR94, Theorem 8.2], [Reference Ellenberg and VenkateshEV08], [Reference Aka, Einsiedler and ShapiraAES16b], [Reference Aka, Einsiedler and ShapiraAES16a] and [Reference Aka, Einsiedler and WieserAEW22]).
$\mathcal {R}^{n,k}_Q(D)$
. This kind of idea appears in many recent or less recent articles in the literature (see, for example, [Reference Platonov and RapinchukPR94, Theorem 8.2], [Reference Ellenberg and VenkateshEV08], [Reference Aka, Einsiedler and ShapiraAES16b], [Reference Aka, Einsiedler and ShapiraAES16a] and [Reference Aka, Einsiedler and WieserAEW22]).
For
![]() $g \in \mathbf {G} = \mathrm {Spin}_Q \times \mathbf {P}_{n,k}$
we write
$g \in \mathbf {G} = \mathrm {Spin}_Q \times \mathbf {P}_{n,k}$
we write
![]() $g=(g_1,g_2)$
, where
$g=(g_1,g_2)$
, where
![]() $g_1$
is the first (respectively,
$g_1$
is the first (respectively,
![]() $g_2$
is the second) coordinate of g. Consider the open subset (principal genus)
$g_2$
is the second) coordinate of g. Consider the open subset (principal genus)
On
![]() $\mathcal {U}$
, there is a projection map
$\mathcal {U}$
, there is a projection map
where the first map takes, for any point
![]() $x \in \mathcal {U}$
, a representative in
$x \in \mathcal {U}$
, a representative in
![]() $\mathbf {G}(\mathbb {R}\times \widehat {\mathbb {Z}})$
and projects onto the real component. Note that the first map is clearly
$\mathbf {G}(\mathbb {R}\times \widehat {\mathbb {Z}})$
and projects onto the real component. Note that the first map is clearly
![]() $\mathbf {G}(\mathbb {R})$
-equivariant. For
$\mathbf {G}(\mathbb {R})$
-equivariant. For
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
, we define
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
, we define
Proposition 7.1. For any oriented k-dimensional subspace
![]() $L\subset \mathbb {Q}^n$
of discriminant D,
$L\subset \mathbb {Q}^n$
of discriminant D,
Proof. Fix a coset
![]() $b\mathbf {G}(\mathbb {Q}) \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q}) \cap \mathcal {U}$
and a representative
$b\mathbf {G}(\mathbb {Q}) \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q}) \cap \mathcal {U}$
and a representative
![]() $b = (b_1, b_2) \in \mathbf {G}(\mathbb {R} \times \widehat {\mathbb {Z}})$
. By definition of
$b = (b_1, b_2) \in \mathbf {G}(\mathbb {R} \times \widehat {\mathbb {Z}})$
. By definition of
![]() $\Phi $
,
$\Phi $
,
Note that, since
![]() $b\mathbf {G}(\mathbb {Q}) \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})$
, there exists
$b\mathbf {G}(\mathbb {Q}) \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})$
, there exists
![]() $h \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})$
and
$h \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})$
and
![]() $\gamma \in \mathbf {G}(\mathbb {Q})$
such that
$\gamma \in \mathbf {G}(\mathbb {Q})$
such that
![]() $b= h \gamma $
. By definition of
$b= h \gamma $
. By definition of
![]() $\boldsymbol {\Delta}{\mathbf H}_L$
, we have
$\boldsymbol {\Delta}{\mathbf H}_L$
, we have
![]() $h_2 = g_L^{-1}\rho _Q(h_1)g_L$
. We first show that the point in
$h_2 = g_L^{-1}\rho _Q(h_1)g_L$
. We first show that the point in
![]() corresponding to
corresponding to
![]() $\Phi (\mathsf {s}_L b \mathbf {G}(\mathbb {Q}))$
lies above a rational subspace under the natural map
$\Phi (\mathsf {s}_L b \mathbf {G}(\mathbb {Q}))$
lies above a rational subspace under the natural map
![]() $\mathcal {Y} \to \mathrm {Gr}^+_{n,k}(\mathbb {R})$
. Note that, by definition of the maps in (7.1), the subspace attached to
$\mathcal {Y} \to \mathrm {Gr}^+_{n,k}(\mathbb {R})$
. Note that, by definition of the maps in (7.1), the subspace attached to
![]() $\Phi (\mathsf {s}_L b \mathbf {G}(\mathbb {Q}))$
is
$\Phi (\mathsf {s}_L b \mathbf {G}(\mathbb {Q}))$
is
![]() $\rho _Q(b_{1,\infty }^{-1})\rho _L^{-1}L_0 = b_{1,\infty }^{-1}.L$
. But
$\rho _Q(b_{1,\infty }^{-1})\rho _L^{-1}L_0 = b_{1,\infty }^{-1}.L$
. But
Next, we show that
![]() $\gamma _1^{-1}.L$
has discriminant D. To this end, note that, by an analogous argument to that in (7.6), for a prime p, we have
$\gamma _1^{-1}.L$
has discriminant D. To this end, note that, by an analogous argument to that in (7.6), for a prime p, we have
![]() $b_{1,p}^{-1}.L = \gamma _1^{-1}.L$
so that
$b_{1,p}^{-1}.L = \gamma _1^{-1}.L$
so that
where we used that
![]() $b_{1,p} \in \mathrm {Spin}_Q(\mathbb {Z}_p)$
preserves the local discriminant at p. Thus,
$b_{1,p} \in \mathrm {Spin}_Q(\mathbb {Z}_p)$
preserves the local discriminant at p. Thus,
![]() $\mathrm {disc}_Q(\gamma _1^{-1}.L) = D$
by (1.5).
$\mathrm {disc}_Q(\gamma _1^{-1}.L) = D$
by (1.5).
It remains to show that
![]() $\Phi (\mathsf {s}_L b \mathbf {G}(\mathbb {Q}))$
corresponds to
$\Phi (\mathsf {s}_L b \mathbf {G}(\mathbb {Q}))$
corresponds to
![]() $[\gamma _1^{-1}.L,\Lambda _{\gamma _1^{-1}.L}]_{\star }$
. For this, notice that, under (7.1),
$[\gamma _1^{-1}.L,\Lambda _{\gamma _1^{-1}.L}]_{\star }$
. For this, notice that, under (7.1),
by definition of the equivalence relation. Now,
Quite analogously, we have
![]() $\rho _Q(\gamma _1^{-1})g_L \gamma _2 = \rho _Q(b_{1,p}^{-1})g_L b_{2,p}$
so that
$\rho _Q(\gamma _1^{-1})g_L \gamma _2 = \rho _Q(b_{1,p}^{-1})g_L b_{2,p}$
so that
This shows that
by the third property of
![]() $\Lambda _L$
in Proposition 6.6. This shows that
$\Lambda _L$
in Proposition 6.6. This shows that
and hence the proposition follows.
Remark 7.2. (Equivalence class induced by packets)
Note that, for any two
![]() $L,L'$
of discriminant D, the sets
$L,L'$
of discriminant D, the sets
![]() $\mathrm {P}(L),\mathrm {P}(L')$
are either equal or disjoint. Indeed, these sets are equivalence classes for an equivalence relation that is implicitly stated in the proof of Proposition 7.1 (see also Remark 6.7).
$\mathrm {P}(L),\mathrm {P}(L')$
are either equal or disjoint. Indeed, these sets are equivalence classes for an equivalence relation that is implicitly stated in the proof of Proposition 7.1 (see also Remark 6.7).
We analyze the fibers of the map
![]() $\Phi $
when restricted to the piece of the homogeneous set
$\Phi $
when restricted to the piece of the homogeneous set
![]() $\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})$
in the open set
$\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q})$
in the open set
![]() $\mathcal {U}$
. For any
$\mathcal {U}$
. For any
![]() $L\in \mathrm {Gr}_{n,k}(\mathbb {Q})$
, we set
$L\in \mathrm {Gr}_{n,k}(\mathbb {Q})$
, we set
We remark that
![]() $\Delta H^{\mathrm {cpt}}_L$
is not equal to
$\Delta H^{\mathrm {cpt}}_L$
is not equal to
![]() $\boldsymbol {\Delta}{\mathbf H}_L(\mathbb {R} \times \widehat {\mathbb {Z}})$
as
$\boldsymbol {\Delta}{\mathbf H}_L(\mathbb {R} \times \widehat {\mathbb {Z}})$
as
![]() $g_L$
can have denominators (cf. (2.2)).
$g_L$
can have denominators (cf. (2.2)).
Lemma 7.3. Let
![]() $x,y \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q}) \cap \mathcal {U}$
. Then
$x,y \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})\mathbf {G}(\mathbb {Q}) \cap \mathcal {U}$
. Then
Proof. We fix representatives
![]() $b^x \in \mathbf {G}(\mathbb {R} \times \widehat {\mathbb {Z}})$
of x and
$b^x \in \mathbf {G}(\mathbb {R} \times \widehat {\mathbb {Z}})$
of x and
![]() $b^y \in \mathbf {G}(\mathbb {R} \times \widehat {\mathbb {Z}})$
of y. Moreover, we write
$b^y \in \mathbf {G}(\mathbb {R} \times \widehat {\mathbb {Z}})$
of y. Moreover, we write
![]() $b^x = h^x\gamma ^x$
and
$b^x = h^x\gamma ^x$
and
![]() $b^y = h^y \gamma ^y$
with
$b^y = h^y \gamma ^y$
with
![]() $h^x,h^y \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})$
and
$h^x,h^y \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})$
and
![]() $\gamma ^x,\gamma ^y \in \mathbf {G}(\mathbb {Q})$
. The direction ‘
$\gamma ^x,\gamma ^y \in \mathbf {G}(\mathbb {Q})$
. The direction ‘
![]() $\Leftarrow $
’ is straightforward to verify; we leave it to the reader.
$\Leftarrow $
’ is straightforward to verify; we leave it to the reader.
Assume that
![]() $\Phi (\mathsf {s}_L x) = \Phi (\mathsf {s}_L y)$
. We recall from Proposition 7.1 and its proof that
$\Phi (\mathsf {s}_L x) = \Phi (\mathsf {s}_L y)$
. We recall from Proposition 7.1 and its proof that
and similarly for
![]() $\Phi (\mathsf {s}_L y)$
. By assumption, we have that there exists
$\Phi (\mathsf {s}_L y)$
. By assumption, we have that there exists
![]() $\eta \in \mathrm {Spin}_Q(\mathbb {Z})$
such that
$\eta \in \mathrm {Spin}_Q(\mathbb {Z})$
such that
![]() $\eta (\gamma _1^x)^{-1}.L = (\gamma _1^y)^{-1}.L$
. Therefore,
$\eta (\gamma _1^x)^{-1}.L = (\gamma _1^y)^{-1}.L$
. Therefore,
![]() $ \gamma _1^y \eta (\gamma _1^x)^{-1} \in \mathbf {H}_L(\mathbb {Q})$
and we obtain that
$ \gamma _1^y \eta (\gamma _1^x)^{-1} \in \mathbf {H}_L(\mathbb {Q})$
and we obtain that
The element
![]() $h = (h_1, g_L^{-1}\rho _Q(h_1)g_L) \in \Delta H^{\mathrm {cpt}}_L$
corresponding to
$h = (h_1, g_L^{-1}\rho _Q(h_1)g_L) \in \Delta H^{\mathrm {cpt}}_L$
corresponding to
![]() $h_1 = b_1^x \eta (b_1^y)^{-1} \in \mathbf {H}_L(\mathbb {R} \times \widehat {\mathbb {Z}})$
satisfies
$h_1 = b_1^x \eta (b_1^y)^{-1} \in \mathbf {H}_L(\mathbb {R} \times \widehat {\mathbb {Z}})$
satisfies
![]() $hy = x$
. To see this, note that
$hy = x$
. To see this, note that
For the first component, we have
![]() $b_1^x \eta (b_1^y)^{-1}b_1^y\mathrm {Spin}_Q(\mathbb {Q}) = b_1^x \mathrm {Spin}_Q(\mathbb {Q})$
because
$b_1^x \eta (b_1^y)^{-1}b_1^y\mathrm {Spin}_Q(\mathbb {Q}) = b_1^x \mathrm {Spin}_Q(\mathbb {Q})$
because
![]() $\eta \in \mathrm {Spin}_Q(\mathbb {Z})$
. For the second component, we first recall that
$\eta \in \mathrm {Spin}_Q(\mathbb {Z})$
. For the second component, we first recall that
Therefore, we may rewrite
Using that
![]() $\gamma _2^y \in \mathbf {P}_{n,k}(\mathbb {Q})$
and
$\gamma _2^y \in \mathbf {P}_{n,k}(\mathbb {Q})$
and
![]() $h_2^x = g_L^{-1}\rho _Q(h_1^x)g_L$
, we obtain
$h_2^x = g_L^{-1}\rho _Q(h_1^x)g_L$
, we obtain
Finally,
![]() $g_L^{-1}\rho _Q(\gamma _1^x\eta (\gamma _1^y)^{-1})g_L \in \mathbf {P}_{n,k}(\mathbb {Q})$
because
$g_L^{-1}\rho _Q(\gamma _1^x\eta (\gamma _1^y)^{-1})g_L \in \mathbf {P}_{n,k}(\mathbb {Q})$
because
![]() $\gamma _1^x\eta (\gamma _1^y)^{-1}$
stabilizes L, and thus,
$\gamma _1^x\eta (\gamma _1^y)^{-1}$
stabilizes L, and thus,
It follows that
![]() $hx =y$
and the proof is complete.
$hx =y$
and the proof is complete.
7.4 The correct weights
Let
![]() $\mu _L$
be the Haar probability measure on the orbit
$\mu _L$
be the Haar probability measure on the orbit
![]() $\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q})\subset \mathbf {G}(\mathbb {A})/\mathbf {G}(\mathbb {Q})$
and let
$\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q})\subset \mathbf {G}(\mathbb {A})/\mathbf {G}(\mathbb {Q})$
and let
![]() $\mu _L|_{\mathcal {U}}$
be the normalized restriction to
$\mu _L|_{\mathcal {U}}$
be the normalized restriction to
![]() $\mathcal {U}$
. (Note that the normalized restriction is well defined (i.e.
$\mathcal {U}$
. (Note that the normalized restriction is well defined (i.e.
![]() $\mu _L(\mathcal {U})\neq 0$
) as the intersection
$\mu _L(\mathcal {U})\neq 0$
) as the intersection
![]() $\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q})\cap \mathcal {U}$
contains
$\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q})\cap \mathcal {U}$
contains
![]() $\mathsf {s}_L (\boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \cap \mathbf {G}(\mathbb {R}\times \widehat {\mathbb {Z}}))\mathbf {G}(\mathbb {Q})$
, which is open in
$\mathsf {s}_L (\boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \cap \mathbf {G}(\mathbb {R}\times \widehat {\mathbb {Z}}))\mathbf {G}(\mathbb {Q})$
, which is open in
![]() $\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q})$
.)
$\mathsf {s}_L \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q})$
.)
We compute the measure of a fiber through any point
![]() $x\in \mathcal {U}$
in the packet.
$x\in \mathcal {U}$
in the packet.
Lemma 7.4. Let
![]() $x \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q}) \cap \mathcal {U}$
and write
$x \in \boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q}) \cap \mathcal {U}$
and write
![]() $\Phi (\mathsf {s}_L x) = [\hat {L},\Lambda _{\hat {L}}]_{\star }$
. Then
$\Phi (\mathsf {s}_L x) = [\hat {L},\Lambda _{\hat {L}}]_{\star }$
. Then
 $$ \begin{align} \mu_L|_{\mathcal{U}}(\mathsf{s}_L\Delta H^{\mathrm{cpt}}_L x) = \bigg(\sum_{[L',\Lambda_{L'}]_{\star} \in \mathrm{P}(L)} \frac{|\mathbf{H}_{\hat{L}}(\mathbb{Z})|}{|\mathbf{H}_{L'}(\mathbb{Z})|}\bigg)^{-1}. \end{align} $$
$$ \begin{align} \mu_L|_{\mathcal{U}}(\mathsf{s}_L\Delta H^{\mathrm{cpt}}_L x) = \bigg(\sum_{[L',\Lambda_{L'}]_{\star} \in \mathrm{P}(L)} \frac{|\mathbf{H}_{\hat{L}}(\mathbb{Z})|}{|\mathbf{H}_{L'}(\mathbb{Z})|}\bigg)^{-1}. \end{align} $$
Proof. We must trace through a normalization: let m be the Haar measure on
![]() $\boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})$
induced by requiring that
$\boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A})$
induced by requiring that
![]() $\mu _L$
is a probability measure and let
$\mu _L$
is a probability measure and let
![]() $C_1 = m(\Delta H^{\mathrm {cpt}}_L)$
. Then
$C_1 = m(\Delta H^{\mathrm {cpt}}_L)$
. Then
 $$ \begin{align} \mu_L(\mathsf{s}_L\Delta H^{\mathrm{cpt}}_L x) = \frac{C_1}{|\mathrm{Stab}_{\Delta H^{\mathrm{cpt}}_L}(x)|}. \end{align} $$
$$ \begin{align} \mu_L(\mathsf{s}_L\Delta H^{\mathrm{cpt}}_L x) = \frac{C_1}{|\mathrm{Stab}_{\Delta H^{\mathrm{cpt}}_L}(x)|}. \end{align} $$
We compute the stabilizer. Write
![]() $x = b \mathbf {G}(\mathbb {Q})$
for some
$x = b \mathbf {G}(\mathbb {Q})$
for some
![]() $b \in \mathbf {G}(\mathbb {R} \times \widehat {\mathbb {Z}})$
and observe that
$b \in \mathbf {G}(\mathbb {R} \times \widehat {\mathbb {Z}})$
and observe that
as
![]() $\hat {L} = b^{-1}_{1,\infty }.L$
. The intersection
$\hat {L} = b^{-1}_{1,\infty }.L$
. The intersection
![]() $\Delta H^{\mathrm {cpt}}_{\hat {L}}\cap \mathbf {G}(\mathbb {Q})$
consists of rational elements g of
$\Delta H^{\mathrm {cpt}}_{\hat {L}}\cap \mathbf {G}(\mathbb {Q})$
consists of rational elements g of
![]() $\boldsymbol {\Delta}{\mathbf H}_{\hat {L}}(\mathbb {Q})$
whose first component
$\boldsymbol {\Delta}{\mathbf H}_{\hat {L}}(\mathbb {Q})$
whose first component
![]() $g_1$
is in
$g_1$
is in
![]() $\mathrm {Spin}_Q(\mathbb {R} \times \widehat {\mathbb {Z}})$
. Equivalently, it is the subgroup of
$\mathrm {Spin}_Q(\mathbb {R} \times \widehat {\mathbb {Z}})$
. Equivalently, it is the subgroup of
![]() $\boldsymbol {\Delta}{\mathbf H}_{\hat {L}}(\mathbb {Q})$
of elements g with
$\boldsymbol {\Delta}{\mathbf H}_{\hat {L}}(\mathbb {Q})$
of elements g with
![]() $g_1 \in \mathrm {Spin}_Q(\mathbb {Z})$
, which is clearly isomorphic to
$g_1 \in \mathrm {Spin}_Q(\mathbb {Z})$
, which is clearly isomorphic to
![]() $\mathbf {H}_{\hat {L}}(\mathbb {Z})$
. In particular,
$\mathbf {H}_{\hat {L}}(\mathbb {Z})$
. In particular,
We now use the one-to-one correspondence between
![]() $\mathrm {P}(L)$
and
$\mathrm {P}(L)$
and
![]() $\Delta H^{\mathrm {cpt}}_L$
-orbits in
$\Delta H^{\mathrm {cpt}}_L$
-orbits in
![]() $\boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q}) \cap \mathcal {U}$
(Lemma 7.3). By summing (7.7) over all such orbits, we obtain
$\boldsymbol {\Delta}{\mathbf H}_L(\mathbb {A}) \mathbf {G}(\mathbb {Q}) \cap \mathcal {U}$
(Lemma 7.3). By summing (7.7) over all such orbits, we obtain
 $$ \begin{align*} \mu_L(\mathcal{U}) = \sum_{[L',\Lambda_{L'}]_{\star} \in \mathrm{P}(L)} \frac{C_1}{|\mathbf{H}_{L'}(\mathbb{Z})|} \end{align*} $$
$$ \begin{align*} \mu_L(\mathcal{U}) = \sum_{[L',\Lambda_{L'}]_{\star} \in \mathrm{P}(L)} \frac{C_1}{|\mathbf{H}_{L'}(\mathbb{Z})|} \end{align*} $$
which determines
![]() $C_1$
. This concludes the lemma as, by (7.8) and (7.9),
$C_1$
. This concludes the lemma as, by (7.8) and (7.9),
7.4.1 Measures on

We have different measures on the set of cosets
![]() .
.
-
•
 $\nu _D$
is the pushforward of the normalized sum of Dirac measures on
$\nu _D$
is the pushforward of the normalized sum of Dirac measures on
 $\mathcal {R}^{n,k}_Q(D)$
.
$\mathcal {R}^{n,k}_Q(D)$
. -
• For any
 $L\subset \mathbb {Q}^n$
oriented k-dimensional with
$L\subset \mathbb {Q}^n$
oriented k-dimensional with
 $\mathrm {disc}_Q(L) = D$
, the measure
$\mathrm {disc}_Q(L) = D$
, the measure
 $\nu _{\mathrm {P}(L)}$
is the pushforward of
$\nu _{\mathrm {P}(L)}$
is the pushforward of
 $\mu _L|_{\mathcal {U}}$
under the map
$\mu _L|_{\mathcal {U}}$
under the map
 $\Phi $
defined in (7.4). Here, the collection
$\Phi $
defined in (7.4). Here, the collection
 $\mathrm {P}(L)$
is defined in (7.5).
$\mathrm {P}(L)$
is defined in (7.5).
We claim that
![]() $\nu _D$
is a convex combination of the measures
$\nu _D$
is a convex combination of the measures
![]() $\nu _{\mathrm {P}(L)}$
for L, varying with discriminant D. The weights of the above measures may be computed explicitly. Beginning with the former, note that the mass that
$\nu _{\mathrm {P}(L)}$
for L, varying with discriminant D. The weights of the above measures may be computed explicitly. Beginning with the former, note that the mass that
![]() $\nu _D$
gives to a point
$\nu _D$
gives to a point
![]() is, up to a fixed scalar multiple, the number of preimages of
is, up to a fixed scalar multiple, the number of preimages of
![]() $[\hat {L},\Lambda _{\hat {L}}]_{\star }$
under the quotient map
$[\hat {L},\Lambda _{\hat {L}}]_{\star }$
under the quotient map
![]() . In other words, it is a constant times
. In other words, it is a constant times
 $$ \begin{align*} \#\{[g.\hat{L},\Lambda_{g.\hat{L}}]: g \in \mathrm{Spin}_Q(\mathbb{Z})\} = \#\{g.\hat{L} : g \in \mathrm{Spin}_Q(\mathbb{Z})\} = \frac{|\mathrm{Spin}_Q(\mathbb{Z})|}{|\mathbf{H}_{\hat{L}}(\mathbb{Z})|}. \end{align*} $$
$$ \begin{align*} \#\{[g.\hat{L},\Lambda_{g.\hat{L}}]: g \in \mathrm{Spin}_Q(\mathbb{Z})\} = \#\{g.\hat{L} : g \in \mathrm{Spin}_Q(\mathbb{Z})\} = \frac{|\mathrm{Spin}_Q(\mathbb{Z})|}{|\mathbf{H}_{\hat{L}}(\mathbb{Z})|}. \end{align*} $$
By the same argument as in Lemma 7.4, we have (as
![]() $|\mathrm {Spin}_Q(\mathbb {Z})|$
cancels out)
$|\mathrm {Spin}_Q(\mathbb {Z})|$
cancels out)

On the other hand, the measure
![]() $\nu _{\mathrm {P}(L)}$
satisfies, for any
$\nu _{\mathrm {P}(L)}$
satisfies, for any
![]() $[\hat {L},\Lambda _{\hat {L}}]_{\star } \in \mathrm {P}(L)$
,
$[\hat {L},\Lambda _{\hat {L}}]_{\star } \in \mathrm {P}(L)$
,
 $$ \begin{align} \nu_{\mathrm{P}(L)}([\hat{L},\Lambda_{\hat{L}}]_{\star}) = \bigg(\sum_{[L',\Lambda_{L'}]_{\star} \in \mathrm{P}(L)} \frac{1}{|\mathbf{H}_{L'}(\mathbb{Z})|}\bigg)^{-1}\frac{1}{|\mathbf{H}_{\hat{L}}(\mathbb{Z})|}, \end{align} $$
$$ \begin{align} \nu_{\mathrm{P}(L)}([\hat{L},\Lambda_{\hat{L}}]_{\star}) = \bigg(\sum_{[L',\Lambda_{L'}]_{\star} \in \mathrm{P}(L)} \frac{1}{|\mathbf{H}_{L'}(\mathbb{Z})|}\bigg)^{-1}\frac{1}{|\mathbf{H}_{\hat{L}}(\mathbb{Z})|}, \end{align} $$
by Lemma 7.4.
Thus, the relative weights that the measures
![]() $\nu _D$
and
$\nu _D$
and
![]() $\nu _{\mathrm {P}(L)}$
assign agree. It follows from Remark 7.2 and from (7.11) and (7.10) that
$\nu _{\mathrm {P}(L)}$
assign agree. It follows from Remark 7.2 and from (7.11) and (7.10) that
![]() $\nu _D$
is a convex combination of the measures
$\nu _D$
is a convex combination of the measures
![]() $\nu _{\mathrm {P}(L)}$
, as claimed.
$\nu _{\mathrm {P}(L)}$
, as claimed.
7.5 Conclusion
We now prove the remaining theorems. We proved in §6.4 that Theorem 6.9 implies Theorem 1.4 when
![]() $k>2$
and Theorem 1.11. So it is left to prove Theorems 6.9 and 1.4 when
$k>2$
and Theorem 1.11. So it is left to prove Theorems 6.9 and 1.4 when
![]() $k=2$
.
$k=2$
.
Proof of Theorem 6.9
The key insight is that
![]() $\nu _{D_i}$
is a convex combination of measures that are equidistributed along any sequence of admissible subspaces. The assumption of
$\nu _{D_i}$
is a convex combination of measures that are equidistributed along any sequence of admissible subspaces. The assumption of
![]() $D_i$
to be k-power free implies admissibility.
$D_i$
to be k-power free implies admissibility.
Let p be an odd prime not dividing
![]() $\mathrm {disc}(Q)$
and let
$\mathrm {disc}(Q)$
and let
![]() $D_i \to \infty $
be a sequence of integers as in the assumptions of the theorem for the prime p. We first claim that any sequence
$D_i \to \infty $
be a sequence of integers as in the assumptions of the theorem for the prime p. We first claim that any sequence
![]() $L_i \in \mathcal {H}_{Q}^{n,k}(D_i)$
is admissible (cf. §3). Observe that Condition (1) is automatic. Also, the assumption
$L_i \in \mathcal {H}_{Q}^{n,k}(D_i)$
is admissible (cf. §3). Observe that Condition (1) is automatic. Also, the assumption
![]() $D_i^{[k]}\to \infty $
implies Condition (2). By Proposition 5.1 and
$D_i^{[k]}\to \infty $
implies Condition (2). By Proposition 5.1 and
![]() $n-k \geq k$
,
$n-k \geq k$
,
which proves Condition (3). Then, Condition (4) follows from Propositions 5.1 and 2.9 (where the former implies that
![]() $p \nmid \mathrm {disc}_Q(L^\perp )$
).
$p \nmid \mathrm {disc}_Q(L^\perp )$
).
For any sequence
![]() $L_i$
, as above, together with an additional given orientation, the measures
$L_i$
, as above, together with an additional given orientation, the measures
![]() $\nu _{\mathrm {P}(L_i)}$
equidistribute to the Haar measure on
$\nu _{\mathrm {P}(L_i)}$
equidistribute to the Haar measure on
![]() . Indeed, by admissibility, the measures
. Indeed, by admissibility, the measures
![]() $\mu _{L_i}$
converge to the Haar measure
$\mu _{L_i}$
converge to the Haar measure
![]() $\mu $
on
$\mu $
on
![]() by Theorem 3.1. In particular, as
by Theorem 3.1. In particular, as
![]() $\mathcal {U}$
is compact open, we have
$\mathcal {U}$
is compact open, we have
![]() $\mu _{L_i}|_{\mathcal {U}} \to \mu |_{\mathcal {U}}$
. Taking the pushforward under
$\mu _{L_i}|_{\mathcal {U}} \to \mu |_{\mathcal {U}}$
. Taking the pushforward under
![]() $\Phi $
yields
$\Phi $
yields
![]() $\nu _{\mathrm {P}(L_i)} \to \nu $
, where
$\nu _{\mathrm {P}(L_i)} \to \nu $
, where
![]() $\nu $
is the Haar measure on
$\nu $
is the Haar measure on
![]() .
.
The fact that
![]() $\nu _{D_i}$
is a convex combination of the measures
$\nu _{D_i}$
is a convex combination of the measures
![]() $\nu _{\mathrm {P}(L_i)}$
finally implies Theorem 6.9.
$\nu _{\mathrm {P}(L_i)}$
finally implies Theorem 6.9.
Proof of Theorem 1.4 for
 $k=2$
$k=2$
Let
![]() $\bar {\mathcal {U}}$
be the principal genus of
$\bar {\mathcal {U}}$
be the principal genus of
. The following diagram commutes by construction.

By Theorem 4.1, the images of
![]() $\mathsf {s}_{L_i} \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})\mathbf {G}(\mathbb {Q})\cap \mathcal {U}$
in
$\mathsf {s}_{L_i} \boldsymbol {\Delta}{\mathbf H}_{L_i}(\mathbb {A})\mathbf {G}(\mathbb {Q})\cap \mathcal {U}$
in
![]() $\bar {\mathcal {U}}$
along any admissible sequence of subspaces
$\bar {\mathcal {U}}$
along any admissible sequence of subspaces
![]() $L_i$
are equidistributed. On the other hand, by the above commutative diagram, these images are given by the images of
$L_i$
are equidistributed. On the other hand, by the above commutative diagram, these images are given by the images of
![]() $\mathrm {P}(L_i)$
under the bottom map. The rest of the argument is analogous to the case
$\mathrm {P}(L_i)$
under the bottom map. The rest of the argument is analogous to the case
![]() $k>2$
.
$k>2$
.
Acknowledgments
The authors would like to thank Michael Bersudsky, Manfred Einsiedler and Manuel Luethi for useful discussions. We also thank the anonymous referee who made various valuable suggestions towards improving the exposition. A.W. was supported by ERC grant HomDyn, ID 833423, SNF grant 178958 and the SNF Doc. Mobility grant 195737.
A Appendix. Non-emptiness for the sum of squares
In this section, we discuss non-emptiness conditions for the set
![]() $\mathcal {H}^{n,k}_Q(D)$
when Q is the sum of squares. To simplify notation, we write
$\mathcal {H}^{n,k}_Q(D)$
when Q is the sum of squares. To simplify notation, we write
![]() $\mathcal {H}^{n,k}(D)$
. Note that we have a bijection
$\mathcal {H}^{n,k}(D)$
. Note that we have a bijection
as Q is unimodular (see Proposition 5.4 and its corollary). In view of our goal, we will thus assume that
![]() $k \leq n-k$
throughout. We will also suppose that
$k \leq n-k$
throughout. We will also suppose that
![]() $n-k \geq 2$
.
$n-k \geq 2$
.
The question of when
![]() $\mathcal {H}^{n,k}(D)$
is non-empty is a classical problem in number theory, in particular, if
$\mathcal {H}^{n,k}(D)$
is non-empty is a classical problem in number theory, in particular, if
![]() $k=1$
. Here, note that
$k=1$
. Here, note that
![]() $\mathcal {H}^{n,1}(D)$
is non-empty if and only if there exists a primitive vector
$\mathcal {H}^{n,1}(D)$
is non-empty if and only if there exists a primitive vector
![]() $v \in \mathbb {Z}^n$
with
$v \in \mathbb {Z}^n$
with
![]() $Q(v) =D$
(i.e. D is primitively represented as a sum of n squares).
$Q(v) =D$
(i.e. D is primitively represented as a sum of n squares).
-
• For
 $n=3$
, Legendre proved, assuming the existence of infinitely many primes in arithmetic progression, that
$n=3$
, Legendre proved, assuming the existence of infinitely many primes in arithmetic progression, that
 $\mathcal {H}^{3,1}(D)$
is non-empty if and only if
$\mathcal {H}^{3,1}(D)$
is non-empty if and only if
 $D \not \equiv 0,4,7 \,\mod 8$
. A complete proof was later given by Gauss [Reference GaussGau86]; we shall nevertheless refer to this result as Legendre’s three squares theorem.
$D \not \equiv 0,4,7 \,\mod 8$
. A complete proof was later given by Gauss [Reference GaussGau86]; we shall nevertheless refer to this result as Legendre’s three squares theorem. -
• For
 $n=4$
, Lagrange’s four squares theorem states that
$n=4$
, Lagrange’s four squares theorem states that
 $\mathcal {H}^{4,1}(D)$
is non-empty if and only if
$\mathcal {H}^{4,1}(D)$
is non-empty if and only if
 $D \not \equiv 0 \,\mod 8$
.
$D \not \equiv 0 \,\mod 8$
. -
• For
 $n\geq 5$
, we have
$n\geq 5$
, we have
 $\mathcal {H}^{5,1}(D) \neq \emptyset $
for all
$\mathcal {H}^{5,1}(D) \neq \emptyset $
for all
 $D \in \mathbb {N}$
, as one can see from Lagrange’s four square theorem. Indeed, if
$D \in \mathbb {N}$
, as one can see from Lagrange’s four square theorem. Indeed, if
 $D \not \equiv 0 \,\mod 8$
, the integer D is primitively represented as a sum of four squares and hence also of n squares (by adding zeros). If
$D \not \equiv 0 \,\mod 8$
, the integer D is primitively represented as a sum of four squares and hence also of n squares (by adding zeros). If
 $D \equiv 0 \,\mod 8$
, one can primitively represent
$D \equiv 0 \,\mod 8$
, one can primitively represent
 $D-1$
as a sum of four squares, which yields a primitive representation of D as a sum of five squares.
$D-1$
as a sum of four squares, which yields a primitive representation of D as a sum of five squares.
When
![]() $k=2$
, this question has been studied by Mordell [Reference MordellMor32, Reference MordellMor37] and Ko [Reference KoKo37]. In [Reference Aka, Einsiedler and WieserAEW22], the first and last named authors, together with Einsiedler, showed that
$k=2$
, this question has been studied by Mordell [Reference MordellMor32, Reference MordellMor37] and Ko [Reference KoKo37]. In [Reference Aka, Einsiedler and WieserAEW22], the first and last named authors, together with Einsiedler, showed that
This concludes all cases with
![]() $n \in \{3,4\}$
. In this appendix, we show the following by completely elementary methods.
$n \in \{3,4\}$
. In this appendix, we show the following by completely elementary methods.
Proposition A.1. Suppose that
![]() $n \geq 5$
. Then
$n \geq 5$
. Then
![]() $\mathcal {H}^{n,k}(D)$
is non-empty.
$\mathcal {H}^{n,k}(D)$
is non-empty.
First, we claim that it suffices to show that
![]() $\mathcal {H}^{5,2}(D)$
is non-empty. For this, observe that there exist, for any
$\mathcal {H}^{5,2}(D)$
is non-empty. For this, observe that there exist, for any
![]() $(n,k)$
, injective maps
$(n,k)$
, injective maps
The first map is given by viewing
![]() $L \in \mathcal {H}^{n,k}(D)$
as a subspace of
$L \in \mathcal {H}^{n,k}(D)$
as a subspace of
![]() $\mathbb {Q}^{n+1}$
via
$\mathbb {Q}^{n+1}$
via
![]() $\mathbb {Q}^n \to \mathbb {Q}^{n}\times \{0\} \subset \mathbb {Q}^{n+1}$
. The second map associates to
$\mathbb {Q}^n \to \mathbb {Q}^{n}\times \{0\} \subset \mathbb {Q}^{n+1}$
. The second map associates to
![]() $L = \mathbb {Q} v_1 \oplus \cdots \mathbb {Q} v_k \in \mathcal {H}^{n,k}(D)$
the subspace
$L = \mathbb {Q} v_1 \oplus \cdots \mathbb {Q} v_k \in \mathcal {H}^{n,k}(D)$
the subspace
![]() $\mathbb {Q} (v_1,0) \oplus \cdots \oplus \mathbb {Q} (v_k,0) \oplus \mathbb {Q} e_{n+1} \in \mathcal {H}^{n+1,k+1}(D)$
. In particular, Proposition A.1 for
$\mathbb {Q} (v_1,0) \oplus \cdots \oplus \mathbb {Q} (v_k,0) \oplus \mathbb {Q} e_{n+1} \in \mathcal {H}^{n+1,k+1}(D)$
. In particular, Proposition A.1 for
![]() $(n,k) = (5,2)$
implies Proposition A.1 for
$(n,k) = (5,2)$
implies Proposition A.1 for
![]() $(n,k) = (6,2),(6,3)$
. One then proceeds inductively to verify the claim.
$(n,k) = (6,2),(6,3)$
. One then proceeds inductively to verify the claim.
A.1 A construction of Schmidt
Though it is not, strictly speaking, necessary, we introduce here a conceptual construction of Schmidt [Reference SchmidtSch68] that captures what can be done with inductive arguments as in (A.2). As before, we identify
![]() $\mathbb {Q}^n$
with a subspace of
$\mathbb {Q}^n$
with a subspace of
![]() $\mathbb {Q}^{n+1}$
via
$\mathbb {Q}^{n+1}$
via
![]() $\mathbb {Q}^n \simeq \mathbb {Q}^{n}\times \{0\}$
. Given any
$\mathbb {Q}^n \simeq \mathbb {Q}^{n}\times \{0\}$
. Given any
![]() $L \in \mathrm {Gr}_{n+1,k}(\mathbb {Q})$
, we have that either the intersection
$L \in \mathrm {Gr}_{n+1,k}(\mathbb {Q})$
, we have that either the intersection
![]() $L \cap \mathbb {Q}^{n}$
is
$L \cap \mathbb {Q}^{n}$
is
![]() $(k-1)$
-dimensional or L is contained in
$(k-1)$
-dimensional or L is contained in
![]() $\mathbb {Q}^n$
. In particular, we can write
$\mathbb {Q}^n$
. In particular, we can write
where
![]() $\mathcal {H}_{\mathrm {nd}}^{n+1,k}(D)$
denotes the subspaces
$\mathcal {H}_{\mathrm {nd}}^{n+1,k}(D)$
denotes the subspaces
![]() $L\in \mathcal {H}^{n+1,k}(D)$
for which
$L\in \mathcal {H}^{n+1,k}(D)$
for which
![]() $L \not \subset \mathbb {Q}^n$
. We also let
$L \not \subset \mathbb {Q}^n$
. We also let
![]() $\mathrm {Gr}_{n+1,k}^{\mathrm {nd}}(\mathbb {Q})$
be the subspaces
$\mathrm {Gr}_{n+1,k}^{\mathrm {nd}}(\mathbb {Q})$
be the subspaces
![]() $L\in \mathrm {Gr}_{n+1,k}(\mathbb {Q})$
for which
$L\in \mathrm {Gr}_{n+1,k}(\mathbb {Q})$
for which
![]() $L \not \subset \mathbb {Q}^n$
. Here, ‘
$L \not \subset \mathbb {Q}^n$
. Here, ‘
![]() $\mathrm {nd}$
’ stands for ‘non-degenerate’.
$\mathrm {nd}$
’ stands for ‘non-degenerate’.
We now associate to
![]() $L \in \mathrm {Gr}_{n+1,k}^{\mathrm {nd}}(\mathbb {Q})$
three quantities. Let
$L \in \mathrm {Gr}_{n+1,k}^{\mathrm {nd}}(\mathbb {Q})$
three quantities. Let
![]() $L' = L \cap \mathbb {Q}^n$
. Furthermore, note that the projection of
$L' = L \cap \mathbb {Q}^n$
. Furthermore, note that the projection of
![]() $L(\mathbb {Z})$
onto the
$L(\mathbb {Z})$
onto the
![]() $x_{n+1}$
-axis consists of multiples of some vector
$x_{n+1}$
-axis consists of multiples of some vector
![]() $(0,\ldots ,0,h_L)$
, where
$(0,\ldots ,0,h_L)$
, where
![]() $h_L \in \mathbb {N}$
. Because
$h_L \in \mathbb {N}$
. Because
![]() $(0,\ldots ,0,h_L)$
comes from projection of
$(0,\ldots ,0,h_L)$
comes from projection of
![]() $L(\mathbb {Z})$
, there exists some vector
$L(\mathbb {Z})$
, there exists some vector
![]() $(u_L,h_L) \in L(\mathbb {Z})$
. We define
$(u_L,h_L) \in L(\mathbb {Z})$
. We define
![]() $v_L$
to be the projection of
$v_L$
to be the projection of
![]() $u_L$
onto the orthogonal complement of
$u_L$
onto the orthogonal complement of
![]() $L'$
inside
$L'$
inside
![]() $\mathbb {Q}^n$
.
$\mathbb {Q}^n$
.
Proposition A.2. [Reference SchmidtSch68, §5]
The following properties hold.
-
(i) For any
 $L \in \mathrm {Gr}_{n+1,k}^{\mathrm {nd}}(\mathbb {Q})$
, the pair
$L \in \mathrm {Gr}_{n+1,k}^{\mathrm {nd}}(\mathbb {Q})$
, the pair
 $(h_L,v_L)$
is relatively prime in the following sense: there is no integer
$(h_L,v_L)$
is relatively prime in the following sense: there is no integer
 $d>1$
such that
$d>1$
such that
 $d^{-1}h_L \in \mathbb {N}$
and
$d^{-1}h_L \in \mathbb {N}$
and
 $d^{-1}v_L \in \pi _{L^{\prime \perp }}(\mathbb {Z}^{n-1})$
.
$d^{-1}v_L \in \pi _{L^{\prime \perp }}(\mathbb {Z}^{n-1})$
. -
(ii) Let
 $(h,\bar {L},v)$
be any triplet with
$(h,\bar {L},v)$
be any triplet with
 $h \in \mathbb {N}$
,
$h \in \mathbb {N}$
,
 $\bar {L} \in \mathrm {Gr}_{n,k-1}(\mathbb {Q})$
and
$\bar {L} \in \mathrm {Gr}_{n,k-1}(\mathbb {Q})$
and
 $v \in \pi _{\bar {L}}(\mathbb {Z}^{n-1})$
such that
$v \in \pi _{\bar {L}}(\mathbb {Z}^{n-1})$
such that
 $(h_L,v_L)$
is relatively prime. Then there exists a unique
$(h_L,v_L)$
is relatively prime. Then there exists a unique
 $L \in \mathrm {Gr}_{n+1,k}^{\mathrm {nd}}(\mathbb {Q})$
with
$L \in \mathrm {Gr}_{n+1,k}^{\mathrm {nd}}(\mathbb {Q})$
with
 $(h,\bar {L},v) = (h_L,L',v_L)$
.
$(h,\bar {L},v) = (h_L,L',v_L)$
. -
(iii) We have
 $$ \begin{align*} \mathrm{disc}(L) = \mathrm{disc}(L')(h_L^2 + Q(v_L)). \end{align*} $$
$$ \begin{align*} \mathrm{disc}(L) = \mathrm{disc}(L')(h_L^2 + Q(v_L)). \end{align*} $$
We remark that the construction in (ii) is quite explicit: if
![]() $u \in \mathbb {Z}^{n-1}$
satisfies
$u \in \mathbb {Z}^{n-1}$
satisfies
![]() $\pi _{\bar {L}}(u) = v$
, one defines L to be the span of
$\pi _{\bar {L}}(u) = v$
, one defines L to be the span of
![]() $\bar {L}$
and the vector
$\bar {L}$
and the vector
![]() $(u,h)$
.
$(u,h)$
.
To illustrate this construction, we show the direction in (A.1) that we need for Proposition A.1.
Lemma A.3. If
![]() $D \in \mathbb {N}$
satisfies
$D \in \mathbb {N}$
satisfies
![]() $D \not \equiv 0,7,12,15 \,\mod 16$
, then
$D \not \equiv 0,7,12,15 \,\mod 16$
, then
![]() $\mathcal {H}^{4,2}(D)$
is non-empty.
$\mathcal {H}^{4,2}(D)$
is non-empty.
Proof. By Legendre’s three squares theorem and (A.2),
Suppose that D is congruent to
![]() $4,8$
modulo
$4,8$
modulo
![]() $16$
. In view of Proposition A.2, we let
$16$
. In view of Proposition A.2, we let
![]() $L'$
be the line through
$L'$
be the line through
![]() $(1,-1,0)$
so that
$(1,-1,0)$
so that
![]() $\mathrm {disc}(L') = 2$
. Thus, it remains to find relatively prime
$\mathrm {disc}(L') = 2$
. Thus, it remains to find relatively prime
![]() $h \in \mathbb {N}$
and
$h \in \mathbb {N}$
and
![]() $v \in \pi _{L'}(\mathbb {Z}^3)$
with
$v \in \pi _{L'}(\mathbb {Z}^3)$
with
![]() ${D}/{2} = h^2 + Q(v)$
. Note that
${D}/{2} = h^2 + Q(v)$
. Note that
so that we may choose
![]() $v= a ({e_1+e_2})/{2} + be_3$
for
$v= a ({e_1+e_2})/{2} + be_3$
for
![]() $a,b \in \mathbb {Z}$
. Hence, we need to find a solution to
$a,b \in \mathbb {Z}$
. Hence, we need to find a solution to
such that
![]() $(h,a,b)$
is primitive.
$(h,a,b)$
is primitive.
Equivalently, this corresponds to finding a primitive representation of D by the ternary form
![]() $x_1^2 + 2x_2^2 + 2x_3^2$
. This is again a classical problem and has been settled by Dickson [Reference DicksonDic27]; as the argument is very short and elementary, we give it here. Note that
$x_1^2 + 2x_2^2 + 2x_3^2$
. This is again a classical problem and has been settled by Dickson [Reference DicksonDic27]; as the argument is very short and elementary, we give it here. Note that
![]() ${D}/{4}$
is congruent to
${D}/{4}$
is congruent to
![]() $1$
or
$1$
or
![]() $2$
modulo
$2$
modulo
![]() $4$
and hence there is
$4$
and hence there is
![]() $(x,y,z) \in \mathbb {Z}^3$
primitive with
$(x,y,z) \in \mathbb {Z}^3$
primitive with
![]() $x^2+y^2+z^2 = {D}/{4}$
. As
$x^2+y^2+z^2 = {D}/{4}$
. As
![]() ${D}/{4}\equiv 1,2 \,\mod 4$
, at least one and at most two of the integers
${D}/{4}\equiv 1,2 \,\mod 4$
, at least one and at most two of the integers
![]() $x,y,z$
must be even. Suppose, without loss of generality, that x is even and y is odd. One checks that
$x,y,z$
must be even. Suppose, without loss of generality, that x is even and y is odd. One checks that
and, observing that
![]() $(x+y,x-y,2z)$
is primitive as
$(x+y,x-y,2z)$
is primitive as
![]() $x+y$
is odd, the claim follows in this case.
$x+y$
is odd, the claim follows in this case.
Proof of Proposition A.1
As explained, it suffices to consider the case
![]() $(n,k) = (5,2)$
. In view of Lagrange’s four squares theorem and (A.2), we may suppose that
$(n,k) = (5,2)$
. In view of Lagrange’s four squares theorem and (A.2), we may suppose that
![]() $D \equiv 0 \,\mod 8$
. Moreover, we can assume that
$D \equiv 0 \,\mod 8$
. Moreover, we can assume that
![]() $D \equiv 0,7,12,15 \,\mod 16$
by (A.2) and Lemma A.3. To summarize, we only need to consider the case
$D \equiv 0,7,12,15 \,\mod 16$
by (A.2) and Lemma A.3. To summarize, we only need to consider the case
![]() $D \equiv 0 \,\mod 16$
.
$D \equiv 0 \,\mod 16$
.
Again, we employ the technique in Proposition A.2. Consider the subspace
![]() $L' \subset \mathbb {Q}^4$
spanned by the vector
$L' \subset \mathbb {Q}^4$
spanned by the vector
![]() $(1,-1,0,0)$
, which has discriminant
$(1,-1,0,0)$
, which has discriminant
![]() $2$
. Then
$2$
. Then
and, as in the proof of Lemma A.3, we need to find a primitive representation
![]() $(h,a,b,c)$
of
$(h,a,b,c)$
of
![]() ${D}/{2}$
as
${D}/{2}$
as
Setting
![]() $a=2$
and observing that
$a=2$
and observing that
![]() ${D}/{2}-2 \equiv 6 \,\mod 8$
, the claim follows from Legendre’s three squares theorem.
${D}/{2}-2 \equiv 6 \,\mod 8$
, the claim follows from Legendre’s three squares theorem.
B Appendix. More results around discriminants and induced forms
The contents of this section of the appendix are of elementary nature and complement the results in §5.1.
B.1 Local glue groups
In this section, we briefly explain how to compute the glue group in terms of local data. This is largely analogous to the local formula for the discriminant (1.5). For any prime p, define
where we recall that
![]() $L(\mathbb {Z}_p) = L(\mathbb {Q}_p) \cap \mathbb {Z}_p^n$
and
$L(\mathbb {Z}_p) = L(\mathbb {Q}_p) \cap \mathbb {Z}_p^n$
and
Observe that
![]() $\mathcal {G}_p(L)$
is trivial for all but finitely many p. Indeed,
$\mathcal {G}_p(L)$
is trivial for all but finitely many p. Indeed,
![]() $\mathcal {G}_p(L)$
is trivial if L is p-unimodular for an odd prime p, that is,
$\mathcal {G}_p(L)$
is trivial if L is p-unimodular for an odd prime p, that is,
![]() $p\nmid \mathrm {disc}_Q(L)$
(see also Remark B.2 for a much finer statement). Also, it is easy to adapt Lemma 5.3 and Proposition 5.4 to their local analogues. Here, we prove the following lemma.
$p\nmid \mathrm {disc}_Q(L)$
(see also Remark B.2 for a much finer statement). Also, it is easy to adapt Lemma 5.3 and Proposition 5.4 to their local analogues. Here, we prove the following lemma.
Lemma B.1. We have
Taking cardinalities, (B.1) encodes the (obvious) local product formula for discriminants (1.5).
Proof. The image of the natural inclusion
![]() $L(\mathbb {Z}) \hookrightarrow L(\mathbb {Z}_p)$
is dense for every p. In particular, the image of
$L(\mathbb {Z}) \hookrightarrow L(\mathbb {Z}_p)$
is dense for every p. In particular, the image of
![]() $L(\mathbb {Z})^\#$
under
$L(\mathbb {Z})^\#$
under
![]() $L(\mathbb {Q}) \hookrightarrow L(\mathbb {Q}_p)$
lies in
$L(\mathbb {Q}) \hookrightarrow L(\mathbb {Q}_p)$
lies in
![]() $L(\mathbb {Z}_p)^\#$
and is dense therein. We obtain a homomorphism
$L(\mathbb {Z}_p)^\#$
and is dense therein. We obtain a homomorphism
![]() $\iota :\mathcal {G}(L) \to \prod _p \mathcal {G}_p(L)$
. We prove that
$\iota :\mathcal {G}(L) \to \prod _p \mathcal {G}_p(L)$
. We prove that
![]() $\iota $
is the desired isomorphism. Let
$\iota $
is the desired isomorphism. Let
![]() $(v_i)_i$
be an integral basis of
$(v_i)_i$
be an integral basis of
![]() $L(\mathbb {Z})$
.
$L(\mathbb {Z})$
.
Let
![]() $v+L(\mathbb {Z})$
be in the kernel of
$v+L(\mathbb {Z})$
be in the kernel of
![]() $\iota $
. Then
$\iota $
. Then
![]() $v \in L(\mathbb {Z}_p)$
for every p or, equivalently, the coordinates of v in the
$v \in L(\mathbb {Z}_p)$
for every p or, equivalently, the coordinates of v in the
![]() $\mathbb {Z}$
-basis
$\mathbb {Z}$
-basis
![]() $(v_i)_i$
of
$(v_i)_i$
of
![]() $L(\mathbb {Z})$
have no denominators in p for every p. Hence,
$L(\mathbb {Z})$
have no denominators in p for every p. Hence,
![]() $v \in L(\mathbb {Z})$
and
$v \in L(\mathbb {Z})$
and
![]() $\iota $
is injective.
$\iota $
is injective.
As
![]() $\mathcal {G}_p(L)$
is trivial for all but finitely many p, it suffices to find, for any
$\mathcal {G}_p(L)$
is trivial for all but finitely many p, it suffices to find, for any
![]() $v \in L(\mathbb {Z}_p)^\#$
, an element
$v \in L(\mathbb {Z}_p)^\#$
, an element
![]() $w \in L(\mathbb {Z})^\#$
with
$w \in L(\mathbb {Z})^\#$
with
![]() $w+L(\mathbb {Z}_p) = v+L(\mathbb {Z}_p)$
and
$w+L(\mathbb {Z}_p) = v+L(\mathbb {Z}_p)$
and
![]() $w \in L(\mathbb {Z}_q)$
for any
$w \in L(\mathbb {Z}_q)$
for any
![]() $q \neq p$
. Let
$q \neq p$
. Let
![]() $v \in L(\mathbb {Z}_p)^\#$
and write
$v \in L(\mathbb {Z}_p)^\#$
and write
![]() $v = \sum _{i}\alpha _i v_i$
, where
$v = \sum _{i}\alpha _i v_i$
, where
![]() $\alpha _i \in \mathbb {Q}_p$
. For every i, let
$\alpha _i \in \mathbb {Q}_p$
. For every i, let
![]() $\beta _i \in \mathbb {Z}[{1}/{p}]$
be such that
$\beta _i \in \mathbb {Z}[{1}/{p}]$
be such that
![]() $\alpha _i \in \beta _i + \mathbb {Z}_p$
and set
$\alpha _i \in \beta _i + \mathbb {Z}_p$
and set
![]() $w = \sum _i \beta _i v_i\in L(\mathbb {Q})$
as well as
$w = \sum _i \beta _i v_i\in L(\mathbb {Q})$
as well as
![]() $u = w-v\in L(\mathbb {Z}_p)$
. Then, clearly, for every i,
$u = w-v\in L(\mathbb {Z}_p)$
. Then, clearly, for every i,
that is,
![]() $w \in L(\mathbb {Z}_p)^\#$
and
$w \in L(\mathbb {Z}_p)^\#$
and
![]() $\langle w,v_i\rangle \in \mathbb {Z}[{1}/{p}]$
. But
$\langle w,v_i\rangle \in \mathbb {Z}[{1}/{p}]$
. But
![]() $\mathbb {Z}_p \cap \mathbb {Z}[{1}/{p}] = \mathbb {Z}$
and hence
$\mathbb {Z}_p \cap \mathbb {Z}[{1}/{p}] = \mathbb {Z}$
and hence
![]() $w \in L(\mathbb {Z})^\#$
. Observe also that, by construction,
$w \in L(\mathbb {Z})^\#$
. Observe also that, by construction,
![]() $w \in L(\mathbb {Z}_q)$
for every prime
$w \in L(\mathbb {Z}_q)$
for every prime
![]() $q \neq p$
. Hence,
$q \neq p$
. Hence,
![]() $\iota $
is surjective.
$\iota $
is surjective.
Remark B.2. The isomorphism in (B.1) is particularly useful when one tries to explicitly compute glue groups. Indeed, recall that, for any odd prime, p an integral quadratic form q over
![]() $\mathbb {Z}_p$
is diagonalizable [Reference CasselsCas78, Ch. 8]. For
$\mathbb {Z}_p$
is diagonalizable [Reference CasselsCas78, Ch. 8]. For
with units
![]() $\alpha _i \in \mathbb {Z}_p^\times $
and
$\alpha _i \in \mathbb {Z}_p^\times $
and
![]() $\ell _i \geq 0$
, the glue group is
$\ell _i \geq 0$
, the glue group is
For
![]() $p=2$
, an integral quadratic form q need not be diagonalizable over
$p=2$
, an integral quadratic form q need not be diagonalizable over
![]() $\mathbb {Z}_2$
. However, by [Reference CasselsCas78, Lemma 4.1], we may write q as a (direct) sum of forms of the following types in distinct variables: that is,
$\mathbb {Z}_2$
. However, by [Reference CasselsCas78, Lemma 4.1], we may write q as a (direct) sum of forms of the following types in distinct variables: that is,
with
![]() $\ell \geq 0$
and
$\ell \geq 0$
and
![]() $\alpha \in \mathbb {Z}_2^{\times }$
. An elementary computation leads to observing that the glue groups of the quadratic forms in (B.2) are, respectively,
$\alpha \in \mathbb {Z}_2^{\times }$
. An elementary computation leads to observing that the glue groups of the quadratic forms in (B.2) are, respectively,
It follows that the glue group has essentially the same structure as in the case of p odd. More precisely, assume that
where the
![]() $q_{i}$
are forms as in (B.2) with exponents
$q_{i}$
are forms as in (B.2) with exponents
![]() $\ell = \ell _i$
satisfying
$\ell = \ell _i$
satisfying
![]() $\ell _1 \leq \cdots \leq \ell _m$
. Then the glue group is a product of groups as in (B.3) with exponents
$\ell _1 \leq \cdots \leq \ell _m$
. Then the glue group is a product of groups as in (B.3) with exponents
![]() $\ell _1 \leq \cdots \leq \ell _m$
.
$\ell _1 \leq \cdots \leq \ell _m$
.
B.2 Indices of projected lattices
For any subspace
![]() $L\subset \mathbb {Q}^n$
, we denote the index of
$L\subset \mathbb {Q}^n$
, we denote the index of
![]() $L(\mathbb {Z})$
in
$L(\mathbb {Z})$
in
![]() $L \cap (\mathbb {Z}^n)^\#$
by
$L \cap (\mathbb {Z}^n)^\#$
by
![]() $i(L)$
. Then the proof of Proposition 5.1 and Lemma 5.3 shows that
$i(L)$
. Then the proof of Proposition 5.1 and Lemma 5.3 shows that
 $$ \begin{align*} \mathrm{disc}_Q(L^\perp) = \frac{i(L^\perp)}{i(L)} \mathrm{disc}_Q(L). \end{align*} $$
$$ \begin{align*} \mathrm{disc}_Q(L^\perp) = \frac{i(L^\perp)}{i(L)} \mathrm{disc}_Q(L). \end{align*} $$
The following proposition establishes a fundamental relation between the indices for L and
![]() $L^\perp $
.
$L^\perp $
.
Proposition B.3. Let
![]() $L\subset \mathbb {Q}^n$
be a subspace. The sequence
$L\subset \mathbb {Q}^n$
be a subspace. The sequence
obtained by inclusion and projection, is exact. In particular,
Similarly, for any prime p,
Proof. By Lemma 5.3, the orthogonal projection
![]() $\pi _L$
defines a surjective morphism
$\pi _L$
defines a surjective morphism
The kernel of this morphism can be described by
Clearly,
![]() $L^{\perp } \cap (\mathbb {Z}^n)^{\#} \subset \ker (f)$
. We claim that the inclusion of
$L^{\perp } \cap (\mathbb {Z}^n)^{\#} \subset \ker (f)$
. We claim that the inclusion of
![]() $L^{\perp } \cap (\mathbb {Z}^n)^{\#}$
into
$L^{\perp } \cap (\mathbb {Z}^n)^{\#}$
into
![]() $\ker (f)$
induces an isomorphism
$\ker (f)$
induces an isomorphism
The fact that the map
![]() $L^{\perp } \cap (\mathbb {Z}^n)^{\#} \rightarrow \ker (f)/\mathbb {Z}^n$
induced by the inclusion is surjective follows immediately from the characterization of
$L^{\perp } \cap (\mathbb {Z}^n)^{\#} \rightarrow \ker (f)/\mathbb {Z}^n$
induced by the inclusion is surjective follows immediately from the characterization of
![]() $\ker (f)$
in (B.4). Since the kernel of this map is clearly
$\ker (f)$
in (B.4). Since the kernel of this map is clearly
![]() $L^{\perp }(\mathbb {Z})$
, the claim is proved. It follows that
$L^{\perp }(\mathbb {Z})$
, the claim is proved. It follows that
is a short exact sequence. The local analogue follows similarly.
Remark B.4. It would be interesting to see statistical results regarding these indices. To give a concrete example, suppose that
![]() $\mathrm {disc}(Q) =2$
. Then, clearly,
$\mathrm {disc}(Q) =2$
. Then, clearly,
![]() $i(L) \in \{1,2\}$
for any subspace L and one can ask what is the proportion of subspaces L with
$i(L) \in \{1,2\}$
for any subspace L and one can ask what is the proportion of subspaces L with
![]() $i(L) =1$
(or
$i(L) =1$
(or
![]() $i(L^\perp ) =2$
). If
$i(L^\perp ) =2$
). If
![]() $k=n-k$
, Proposition B.3 shows that the number of subspaces with
$k=n-k$
, Proposition B.3 shows that the number of subspaces with
![]() $i(L) = 1$
and
$i(L) = 1$
and
![]() $i(L) =2$
is the same.
$i(L) =2$
is the same.
B.3 Primitive forms
Here, we study to what extent the induced forms
![]() $q_L,q_{L^\perp }$
(defined in §1.4.2 up to equivalence) for a given subspace
$q_L,q_{L^\perp }$
(defined in §1.4.2 up to equivalence) for a given subspace
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
need to be primitive. For example, we establish that, for
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
need to be primitive. For example, we establish that, for
![]() $k<n-k$
, the form
$k<n-k$
, the form
![]() $q_{L^\perp }$
needs to be essentially primitive (while
$q_{L^\perp }$
needs to be essentially primitive (while
![]() $q_{L}$
does not). First, observe that, indeed, the form
$q_{L}$
does not). First, observe that, indeed, the form
![]() $q_L$
need not be primitive.
$q_L$
need not be primitive.
Example B.5. Let
![]() $n \geq 6$
, let
$n \geq 6$
, let
![]() $(e_i)_{i=1}^n$
denote the standard basis vectors of
$(e_i)_{i=1}^n$
denote the standard basis vectors of
![]() $\mathbb {Q}^n$
and suppose that
$\mathbb {Q}^n$
and suppose that
![]() $Q = Q_0$
is the standard positive definite form. Let
$Q = Q_0$
is the standard positive definite form. Let
![]() $(v_1,v_2) \in \mathbb {Z}^2$
be a primitive vector. Then the integer lattice in the subspace
$(v_1,v_2) \in \mathbb {Z}^2$
be a primitive vector. Then the integer lattice in the subspace
is spanned by
![]() $v_1e_1+v_2e_2, v_1e_3+v_2e_4, v_1e_5+v_2e_6$
, which are orthogonal vectors. In this basis,
$v_1e_1+v_2e_2, v_1e_3+v_2e_4, v_1e_5+v_2e_6$
, which are orthogonal vectors. In this basis,
which is a highly non-primitive form. Similarly,
![]() $L^\perp (\mathbb {Z})$
is spanned by the integer vectors
$L^\perp (\mathbb {Z})$
is spanned by the integer vectors
![]() $v_2e_1-1v_1e_2, v_2e_3-v_1e_4, v_2e_5-v_1e_6,e_{7},\ldots ,e_n$
and hence, in this basis,
$v_2e_1-1v_1e_2, v_2e_3-v_1e_4, v_2e_5-v_1e_6,e_{7},\ldots ,e_n$
and hence, in this basis,
In particular,
![]() $q_{L^\perp }$
is primitive if
$q_{L^\perp }$
is primitive if
![]() $n>3$
; otherwise,
$n>3$
; otherwise,
![]() $\gcd (q_{L^\perp })= \gcd (q_{L})$
(as
$\gcd (q_{L^\perp })= \gcd (q_{L})$
(as
![]() $q_{L^\perp }=q_L$
in this specific example). This type of behavior is generally true, as established below. For more examples, we refer to [Reference Aka, Einsiedler and WieserAEW22, Example 2.4].
$q_{L^\perp }=q_L$
in this specific example). This type of behavior is generally true, as established below. For more examples, we refer to [Reference Aka, Einsiedler and WieserAEW22, Example 2.4].
Proposition B.6. Let
![]() $L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
. If
$L \in \mathrm {Gr}_{n,k}(\mathbb {Q})$
. If
![]() $k> n-k$
,
$k> n-k$
,
![]() $\gcd (q_L)$
divides
$\gcd (q_L)$
divides
![]() $\mathrm {disc}(Q)$
and
$\mathrm {disc}(Q)$
and
Conversely, if
![]() $k < n-k$
,
$k < n-k$
,
![]() $\gcd (q_{L^\perp })$
divides
$\gcd (q_{L^\perp })$
divides
![]() $\mathrm {disc}(Q)$
and
$\mathrm {disc}(Q)$
and
![]() $\mathrm {disc}(\tilde {q}_{L^\perp }) \asymp _Q \mathrm {disc}_Q(L)$
.
$\mathrm {disc}(\tilde {q}_{L^\perp }) \asymp _Q \mathrm {disc}_Q(L)$
.
Moreover, if
![]() $k=n-k$
, we have
$k=n-k$
, we have
![]() $\gcd (q_L) \asymp _Q \gcd (q_{L^\perp })$
and
$\gcd (q_L) \asymp _Q \gcd (q_{L^\perp })$
and
For the convenience of the reader, we provide two proofs of the first claim in the proposition; the second uses glue groups and generalizes to
![]() $k=n-k$
.
$k=n-k$
.
Proof. First proof for
![]() $k \neq n-k$
.Fix a basis
$k \neq n-k$
.Fix a basis
![]() $v_1, \ldots , v_k$
of
$v_1, \ldots , v_k$
of
![]() $L(\mathbb {Z})$
and complete it into a basis
$L(\mathbb {Z})$
and complete it into a basis
![]() $v_1, \ldots ,v_n$
of
$v_1, \ldots ,v_n$
of
![]() $\mathbb {Z}^n$
. Let
$\mathbb {Z}^n$
. Let
![]() $v_1^{*}, \ldots , v_n^{*}$
be its dual basis. Since
$v_1^{*}, \ldots , v_n^{*}$
be its dual basis. Since
![]() $k> n-k$
, without loss of generality, we may assume that
$k> n-k$
, without loss of generality, we may assume that
![]() $v_1 \in \mathrm {span}_{\mathbb {R}}(v_{k+1}, \ldots ,v_n)^{\perp }$
. Note that
$v_1 \in \mathrm {span}_{\mathbb {R}}(v_{k+1}, \ldots ,v_n)^{\perp }$
. Note that
![]() $v_1^{*} \in (\mathbb {Z}^n)^{\#}$
and so
$v_1^{*} \in (\mathbb {Z}^n)^{\#}$
and so
![]() $\mathrm {disc}(Q)v_1^{*} \in \mathbb {Z}^n$
. In particular, we may write
$\mathrm {disc}(Q)v_1^{*} \in \mathbb {Z}^n$
. In particular, we may write
By our choice of
![]() $v_1$
,
$v_1$
,
and the first claim follows as
![]() $\gcd (q_L)$
divides the right-hand side.
$\gcd (q_L)$
divides the right-hand side.
Proof. Given a prime p, we write
![]() $\mathrm {ord}_p(q_L)$
for the largest integer m with
$\mathrm {ord}_p(q_L)$
for the largest integer m with
![]() $p^m\mid \gcd (q_L)$
. Note that
$p^m\mid \gcd (q_L)$
. Note that
![]() $\mathrm {ord}_p(q_L)$
can be extracted from the glue group of L whenever
$\mathrm {ord}_p(q_L)$
can be extracted from the glue group of L whenever
![]() $p \mid \gcd (q_L)$
(see Remark B.2).
$p \mid \gcd (q_L)$
(see Remark B.2).
To begin the proof, fix p and note that
![]() $a_L := \mathrm {ord}_p(q_L)$
can be characterized as follows: it is the smallest integer m so that there exists a primitive vector
$a_L := \mathrm {ord}_p(q_L)$
can be characterized as follows: it is the smallest integer m so that there exists a primitive vector
![]() $v \in L(\mathbb {Z}_p)^\#$
with
$v \in L(\mathbb {Z}_p)^\#$
with
![]() $p^m v \in L(\mathbb {Z}_p)$
. To see this, first assume that p is an odd prime. Then, as in Remark B.2 (after possibly changing the basis), we may write
$p^m v \in L(\mathbb {Z}_p)$
. To see this, first assume that p is an odd prime. Then, as in Remark B.2 (after possibly changing the basis), we may write
with
![]() $\ell _1 \leq \ell _2 \leq \cdots \leq \ell _k$
. If v is a vector as above, the expression for the glue group in Remark B.2 as well as primitivity imply that
$\ell _1 \leq \ell _2 \leq \cdots \leq \ell _k$
. If v is a vector as above, the expression for the glue group in Remark B.2 as well as primitivity imply that
![]() $m \geq \ell _1$
. Conversely, it is easy to see that the first vector v in the above (implicit) choice of basis of
$m \geq \ell _1$
. Conversely, it is easy to see that the first vector v in the above (implicit) choice of basis of
![]() $L(\mathbb {Z}_p)$
satisfies
$L(\mathbb {Z}_p)$
satisfies
![]() $p^{-\ell _1}v \in L(\mathbb {Z}_p)^{\#}$
and is primitive. For
$p^{-\ell _1}v \in L(\mathbb {Z}_p)^{\#}$
and is primitive. For
![]() $p=2$
, the proof above can be adapted using Remark B.2.
$p=2$
, the proof above can be adapted using Remark B.2.
Define
![]() $a_{L}'$
as the smallest integer m so that there exists a primitive vector
$a_{L}'$
as the smallest integer m so that there exists a primitive vector
![]() $v' \in \pi _L(\mathbb {Z}_p^n)$
with
$v' \in \pi _L(\mathbb {Z}_p^n)$
with
![]() $p^m v' \in L(\mathbb {Z}_p)$
. We argue that
$p^m v' \in L(\mathbb {Z}_p)$
. We argue that
![]() $a^{\prime }_L \leq a_L$
. Let v be as in the above definition of
$a^{\prime }_L \leq a_L$
. Let v be as in the above definition of
![]() $a_L$
. Then, there exists an integer
$a_L$
. Then, there exists an integer
![]() $i \leq a_L$
such that
$i \leq a_L$
such that
![]() $p^iv \in \pi _L(\mathbb {Z}_p^n)$
and
$p^iv \in \pi _L(\mathbb {Z}_p^n)$
and
![]() $p^iv$
is primitive in
$p^iv$
is primitive in
![]() $\pi _L(\mathbb {Z}_p^n)$
. For this integer i, set
$\pi _L(\mathbb {Z}_p^n)$
. For this integer i, set
![]() $v':=p^iv$
and observe that
$v':=p^iv$
and observe that
![]() $p^{a_L-i}v' = p^{a_L}v \in L(\mathbb {Z}_p)$
. Therefore,
$p^{a_L-i}v' = p^{a_L}v \in L(\mathbb {Z}_p)$
. Therefore,
![]() $a_L' \leq a_L-i \leq a_L$
, as claimed. In analogous fashion, one argues that
$a_L' \leq a_L-i \leq a_L$
, as claimed. In analogous fashion, one argues that
![]() $a_L \leq a_L' + \mathrm {ord}_p(i_p(L))$
, so that
$a_L \leq a_L' + \mathrm {ord}_p(i_p(L))$
, so that
Suppose that
![]() $k>n-k$
. Applying Proposition 5.4, we see that there exists
$k>n-k$
. Applying Proposition 5.4, we see that there exists
![]() $v' \in \pi _L(\mathbb {Z}_p^n)$
primitive with
$v' \in \pi _L(\mathbb {Z}_p^n)$
primitive with
![]() $v'\in L(\mathbb {Z}_p)$
. Indeed, as
$v'\in L(\mathbb {Z}_p)$
. Indeed, as
![]() $\pi _{L^\perp }(\mathbb {Z}_p^n)/L^\perp (\mathbb {Z}_p)$
is a product of at most k non-trivial cyclic groups, the same is true for
$\pi _{L^\perp }(\mathbb {Z}_p^n)/L^\perp (\mathbb {Z}_p)$
is a product of at most k non-trivial cyclic groups, the same is true for
![]() $\pi _{L}(\mathbb {Z}_p^n)/L(\mathbb {Z}_p)$
, which implies the claim. Therefore,
$\pi _{L}(\mathbb {Z}_p^n)/L(\mathbb {Z}_p)$
, which implies the claim. Therefore,
![]() $a_L' = 0$
and hence
$a_L' = 0$
and hence
![]() $a_L \leq \mathrm {ord}_p(i_p(L))$
. This shows that
$a_L \leq \mathrm {ord}_p(i_p(L))$
. This shows that
![]() $\gcd (q_L) \mid i(L)$
, which proves a sharpened version of the first part of the proposition (cf. Proposition B.3).
$\gcd (q_L) \mid i(L)$
, which proves a sharpened version of the first part of the proposition (cf. Proposition B.3).
Now, suppose that
![]() $k=n-k$
. We show first that
$k=n-k$
. We show first that
![]() $a_L'=a_{L^\perp }'$
. If
$a_L'=a_{L^\perp }'$
. If
![]() $a_L'=0$
,
$a_L'=0$
,
![]() $\pi _{L}(\mathbb {Z}_p^n)/L(\mathbb {Z}_p)$
is a product of at most
$\pi _{L}(\mathbb {Z}_p^n)/L(\mathbb {Z}_p)$
is a product of at most
![]() $k-1$
cyclic groups and hence the same is true for
$k-1$
cyclic groups and hence the same is true for
![]() $\pi _{L^\perp }(\mathbb {Z}_p^n)/L^\perp (\mathbb {Z}_p)$
, by Proposition 5.4. This implies that
$\pi _{L^\perp }(\mathbb {Z}_p^n)/L^\perp (\mathbb {Z}_p)$
, by Proposition 5.4. This implies that
![]() $a_{L^\perp }'=0$
. If
$a_{L^\perp }'=0$
. If
![]() $a_L'\neq 0$
, the number
$a_L'\neq 0$
, the number
![]() $a_L'$
is exactly the smallest order of a non-trivial element in
$a_L'$
is exactly the smallest order of a non-trivial element in
![]() $\pi _{L}(\mathbb {Z}_p^n)/L(\mathbb {Z}_p)$
. Applying the same for
$\pi _{L}(\mathbb {Z}_p^n)/L(\mathbb {Z}_p)$
. Applying the same for
![]() $L^\perp $
, yields
$L^\perp $
, yields
![]() $a_L'=a_{L^\perp }'$
in all cases. In particular,
$a_L'=a_{L^\perp }'$
in all cases. In particular,
Varying the prime p, we obtain that
and conversely. This finishes the proof of the proposition.