Insights in Hierarchical Clustering of Variables for Compositional Data

Abstract

R-mode hierarchical clustering is a method for forming hierarchical groups of mutually exclusive subsets of variables. This R-mode cluster method identifies interrelationships between variables which are useful for variable selection and dimension reduction. Importantly, the method is based on metric elements defined on the sample space of variables. Consequently, hierarchical clustering of compositional parts should respect the particular geometry of the simplex. In this work, the connections between concepts such as distance, cluster representative, compositional biplot, and log-ratio basis are explored within the framework of the most popular R-mode agglomerative hierarchical clustering methods. The approach is illustrated in a paleoecological study to identify groups of species sharing similar behavior.

1 Introduction

Hierarchical clustering (HC) is a method for forming hierarchical groups of mutually exclusive subsets (Hennig et al. 2015). In agglomerative HC techniques, initially, each object is assigned to a single cluster. Afterward, the union of two clusters is selected which provides an optimal value for an objective function reflecting some criterion chosen by the investigator. That is, given a data set formed by n objects, the procedure works by reducing in the first step the number of groups from n to $n - 1$, and then, without modifying the groups formed, repeating the process until the number of groups is reduced to 1. On the other hand, the divisive HC techniques, which are less popular than the agglomerative methods, construct the hierarchy in the opposite manner. Although an objective function may be any functional relation selected by the investigator, the objective function adopted is commonly based on a metric concept defined on the sample space of objects (e.g., a distance).

In general, HC methods are designed to group objects in a space defined by the variables, and as such they can be considered Q-mode methods. However, there are several application examples in which HC is computed in R-mode to identify interrelationships between variables, useful for variable selection and dimension reduction. In these cases, Pearson’s r correlation coefficient is sometimes adopted as a measure of distance (i.e., R-analysis) (Legendre and Legendre 2012). However, the application of HC in R-mode obviously raises questions regarding the efficiency of algorithms designed primarily to group objects. The investigation of the interrelationships between the variables is of particular interest in those studies, including, for example, those in the paleoecological field, in which the composition of the assemblages is expressed in terms of relative abundances. The application of R-mode HC can help in studies aimed at identifying groups of species (parts in a composition) sharing a similar behavior. Importantly, the application of HC in R-mode must be consistent with the fundamental properties of the analysis of compositional data (CoDa) (Aitchison 1986), in particular when the compositional variables (parts) are analyzed (Pawlowsky-Glahn and Egozcue 2022).

To the best of our knowledge, only van den Boogaart and Tolosana-Delgado (2013, section 6.2.3), Facevicova et al. (2016), and Filzmoser et al. (2018, section 6.6) present a short preliminary study of an R-mode HC for CoDa, while it was used in Boyraz et al. (2022) to define principal microbial groups (PMGs). These previous works, following Pawlowsky-Glahn et al. (2011), merely describe the R-mode HC using Ward’s method (Ward 1963). Martín-Fernández et al. (2018) further develop this idea for Ward’s method by describing its link with the Aitchison distance (Aitchison et al. 2000) between two parts, whereas Di Donato et al. (2022) present a preliminary exploration of the relationship between the Ward R-mode HC for CoDa and the compositional biplot (Aitchison and Greenacre 2002). This data visualization technique consists of a principal component analysis based on a singular value decomposition of the centered log-ratio (clr) data set (Aitchison 1986) (i.e., clr-biplots). Obviously, any other HC method could be used, such as single, complete, and average linkage methods. The performance of these other methods in terms of Aitchison distance, of the clr-biplot, and for creating an orthonormal log-ratio (olr) basis using a sequential binary partition (SBP) of the parts of a composition (Egozcue and Pawlowsky-Glahn 2005) remains unexplored. The literature on cluster analysis is very extensive and continually comes up with new methods or improvements of old ones (Hennig et al. 2015). It is not our aim to present an exhaustive description of R-mode cluster methods for CoDa. Our purpose is to explore the connections between concepts such as distance, cluster representative, clr-biplot, and olr-basis. That is why we focus only on the most popular agglomerative HC methods.

Section 2 presents some basic CoDa concepts, where the focus is on the elements for the analysis of the parts of a composition. In Sect. 3, the performance and properties of some R-mode HC methods are described. The relationship with the SBP and the clr-biplots is provided. Section 4 illustrates this approach in a paleoecological study to identify groups of species sharing similar behavior. Finally, we present the concluding remarks in Sect. 5.

2 Basic Elements in a Compositional Analysis

CoDa (Aitchison 1986) are quantitative descriptions of the parts or components of a whole conveying relative information. In this sense, the relative information collected in any observation ${\textbf {x}}$ is the same as in $\alpha \cdot {\textbf {x}}$ for any real scalar $\alpha >0$, the property known as scale invariance (Aitchison 1986). Historically, the sample space of CoDa is designed as the D-part unit simplex ${\mathscr {S}}^D = \{{\textbf {x}}\in {\mathscr {R}}^D: x_j>0; \sum x_j =1; j=1,\dots , D \}$. According to the ratio scale nature of CoDa, any function of a composition ${\textbf {x}}$ should be expressed in terms of ratios between variables (Aitchison 1986). Note that any ratio ${x_{j}}/{x_{k}}$ takes values in $(0, +\infty )$, whereas a log-ratio $\ln ({x_{j}}/{x_{k}})$ takes values in the full real space. Following Aitchison (1986), the general expression of a log-ratio is a log-contrast

$$\begin{aligned} a_1\cdot \ln (x_{1}) +\cdots +a_D\cdot \ln (x_{D})&= \ln \left( \prod _{j=1}^{D} x_{j}^{a_j}\right) =\ln \frac{\prod _{a_j>0} x_{j}^{a_j}}{\prod _{a_j<0} x_{j}^{|a_j|}}, \end{aligned}$$

(1)

where $\sum a_j=0$, so as to verify the scale invariance property. One example of the very useful log-ratios are the centered log-ratio (clr) variables defined in Aitchison (1986) by $\textrm{clr}({\textbf {x}})_j = \ln \frac{x_{j}}{\left( \prod x_{k} \right) ^{1/D}}= \ln x_{j}- \overline{\ln {\textbf {x}}},\quad j=1,\ldots ,D$, where $\overline{\ln {\textbf {x}}}$ stands for the arithmetic mean of the elements in $\ln {\textbf {x}}$. The log-contrast expression (Eq. 1) of a clr-variable satisfies that $a_{jk}=-1/D$ for $k \ne j$ and $a_{jj}=1-1/D$.

The formal geometric framework for the analysis of CoDa first appeared independently in Pawlowsky-Glahn and Egozcue (2001) and in Billheimer et al. (2001). This geometry was coined the Aitchison geometry in Pawlowsky-Glahn and Egozcue (2001), later formally established in Barceló-Vidal and Martín-Fernández (2016). The critical element of the Aitchison geometry is the inner product defined via the log-ratio coordinates. Indeed, let ${\textbf {x}}_1$ and ${\textbf {x}}_2$ be two compositions, then $\langle {\textbf {x}}_1,{\textbf {x}}_2\rangle _a=\langle \textrm{clr}({\textbf {x}}_1),\textrm{clr}({\textbf {x}}_2)\rangle _e$. Here, the subscripts a and e represent, respectively, Aitchison and Euclidean metric elements. As usual, a distance and a norm can be derived from the inner product, resulting in $\textrm{d}_a({\textbf {x}}_1,{\textbf {x}}_2)= \textrm{d}_e(\textrm{clr}({\textbf {x}}_1),\textrm{clr}({\textbf {x}}_2))$ and $||{\textbf {x}}_1||_a=||\textrm{clr}({\textbf {x}}_1)||_e$. Remarkably, the Aitchison distance (Aitchison et al. 2000) verifies that $\textrm{d}_a({\textbf {x}}_1,{\textbf {x}}_2)=||(\frac{x_{11}}{x_{21}},\ldots ,\frac{x_{1D}}{x_{2D}})||_a$, providing information about the relative difference between two compositions.

The Aitchison geometry allows compositions to be expressed as coordinates in an orthonormal basis, formed by log-ratios and called olr-coordinates (Egozcue et al. 2003; Martín-Fernández 2019). Following Egozcue and Pawlowsky-Glahn (2005), one can use an SBP to create a particular set of olr-coordinates, originally named isometric log-ratio (ilr) coordinates. According to Eq. (1), any log-ratio consists of selecting which parts contribute to the log-ratio and deciding if they will appear in the numerator or in the denominator. In the first step of an SBP, when the first olr-coordinate is created, the complete composition ${\textbf {x}}=(x_1,\ldots ,x_D)$ is split into two groups of parts: one for the numerator and the other for the denominator. In the following steps, each group is in turn split into two groups. That is, in step j, when the $\textrm{olr}({\textbf {x}})_j$ coordinate is created, the $r_j$ parts $(x_{n_1},\ldots ,x_{n_{r_j}})$ in the first group are placed in the numerator, and the $s_j$ parts $(x_{d_1},\ldots ,x_{d_{s_j}})$ in the second group will appear in the denominator. As a result, the $\textrm{olr}({\textbf {x}})_j$ coordinate, in this case called jth balance, is

$$\begin{aligned} \textrm{olr}({\textbf {x}})_j = \sqrt{\frac{r_j\cdot s_j}{r_j+s_j}}\ln \frac{(x_{n_1}\ldots x_{n_{r_j}})^{1/r_j}}{(x_{d_1}\ldots x_{d_{s_j}})^{1/s_j}},\; j=1,\ldots ,D-1, \end{aligned}$$

(2)

where $\sqrt{\frac{r_j\cdot s_j}{r_j+s_j}}$ is the factor for normalizing the balance to unit length.

In CoDa analysis, given a data set ${\textbf {X}}$ ($n\times D$) with sample size n and D parts, the variability can be expressed by the variation matrix (Aitchison 1986). The (r, s) entry of the variation matrix is $\textrm{var}(\ln ({\textbf {X}}_r/{\textbf {X}}_s))$, which is the log-ratio variance of parts $({\textbf {X}}_r,{\textbf {X}}_s)$, two columns of a data set ${\textbf {X}}$. For example, when $\textrm{var}(\ln ({\textbf {X}}_r/{\textbf {X}}_s))$ is exactly zero, the ratio ${\textbf {X}}_r/{\textbf {X}}_s$ is constant, the two parts involved being proportional. Martín-Fernández et al. (2018) stated that the entries of the variation matrix can also be expressed in terms of the Aitchison distance between parts. Indeed, the columns of ${\textbf {X}}$ can be considered as compositions in an n-part simplex (Pawlowsky-Glahn and Egozcue 2022). The ith component of the vector $\textrm{clr}({\textbf {X}}_r)$ is $\ln x_{ir} - \overline{\ln {\textbf {X}}_r}$, where $\overline{\ln {\textbf {X}}_r}$ is the average of the logarithms $\ln x_{ir}$ along the column ${\textbf {X}}_r$. It is equivalent to considering ${\textbf {X}}^\top$ as a CoDa set and then taking $\textrm{clr}$-scores. This leads to

$$\begin{aligned} \textrm{var}\left( \ln \left( \frac{{\textbf {X}}_r}{{\textbf {X}}_s}\right) \right) =\frac{1}{n}\ \textrm{d}_a^2\left( {\textbf {X}}^\top _r,{\textbf {X}}^\top _s\right) =\frac{1}{n}\ \left\| \left( \frac{x_{1r}}{x_{1s}},\ldots ,\frac{x_{nr}}{x_{ns}}\right) \right\| ^2_a\, \end{aligned}$$

(3)

where the last term is an Aitchison norm in the n-part simplex, that is, an Aitchison norm in the space of parts (Pawlowsky-Glahn and Egozcue 2022), providing information about the relative difference between two parts. The factor 1/n can be $1/(n-1)$, depending on the definition of variance used. In any case, because HC methods are invariant under a scaling factor applied to the distance matrix, one can use the variation matrix as input data in the HC algorithm.

A graphical display of the information provided by the variation matrix can be obtained using the clr-biplot (Aitchison and Greenacre 2002), where the clr-variables are represented by rays. In addition, the clr-biplot can suggest clusters of rays, that is, groups formed by parts. Although the quality of the display depends on the variance accounted for by the two selected principal axes, the position of rays in the clr-biplot usually suggests which parts are approximately proportional and which are not, because the squared length of a link between two rays approximates $\textrm{var}[\ln (X_i/ X_j)]$, the latter being proportional to the Aitchison distance between the two involved parts. Indeed, let $\textrm{clr}({\textbf {X}})$ be the clr data matrix (clr scores by rows) of the data matrix ${\textbf {X}}$; and let ${\textbf{Y}}$ be the column centered matrix of $\textrm{clr}({\textbf {X}})$ (i.e., the log-data matrix double centered). The covariance clr-biplot is based on the singular value decomposition ${\textbf {Y}}={\textbf {U}}\cdot {\textbf {D}}\cdot {\textbf {V}}^\top$, with factor scores ${\textbf {F}}={\textbf {U}}$ and loadings ${\textbf {L}}={\textbf {V}}\cdot {\textbf {D}}$. Matrices ${\textbf {U}}$ and ${\textbf {V}}$ are, respectively, the left and right eigenvectors, and ${\textbf {D}}$ is the diagonal matrix with singular values. According to Eq. (3), the Aitchison distance matrix between parts can be calculated by $(\textrm{clr}({\textbf {X}}))^\top \cdot \textrm{clr}({\textbf {X}})$, which is equal to ${\textbf {Y}}^\top \cdot {\textbf {Y}}={\textbf {V}}\cdot {\textbf {D}}^2 \cdot {\textbf {V}}^\top =({\textbf {V}}\cdot {\textbf {D}})\cdot ({\textbf {V}}\cdot {\textbf {D}})^\top$, with ${\textbf {V}}\cdot {\textbf {D}}$ being the vector of coordinates of the rays. Consequently, when one selects two particular coordinates (usually the first and second) for representing the clr-biplot, then the distances between the rays on the display are an approximation of the Aitchison distance between the parts.

The expression in Eq. (3) can be extended to the variance of the jth balance (Martín-Fernández et al. 2018)

$$\begin{aligned} \textrm{var}(\textrm{olr}({\textbf {X}})_j)=\textrm{var}\left( \sqrt{\frac{r_j\cdot s_j}{r_j+s_j}}\ln \left( \frac{{\textbf {G}}_{n}}{{\textbf {G}}_{d}}\right) \right) =\frac{r_j\cdot s_j}{r_j+s_j}\cdot \frac{1}{n}\textrm{d}_a^2({\textbf {G}}_{n},{\textbf {G}}_{d}), \end{aligned}$$

(4)

where the geometric means ${\textbf {G}}_{n}=({\textbf {X}}_{n_1}\cdots {\textbf {X}}_{n_{r_j}})^{1/r_j}$ and ${\textbf {G}}_{d}=({\textbf {X}}_{d_1}\cdots {\textbf {X}}_{d_{s_j}})^{1/s_j}$ are, respectively, the center of a cluster formed by $r_j$ and $s_j$ parts. Both expressions (Eqs. 3 and 4) provide the required elements for defining an adequate distance between objects and/or clusters in R-mode HC for CoDa.

3 Compositional R-mode Hierarchical Clustering

Cluster analysis tries to form groups in such a way that parts in the same group are similar to each other, whereas parts in different groups are as dissimilar as possible. Among the many possible dissimilarities and distances ($\textrm{d}$) for data analysis, almost all of them share one feature: given two objects ${\textbf {x}}_a$ and ${\textbf {x}}_b$, the value of $\textrm{d}({\textbf {x}}_a,{\textbf {x}}_b)$ does not depend on other objects different from ${\textbf {x}}_a$ and ${\textbf {x}}_b$ (Deza and Deza 2009). In an R-mode HC for CoDa, this feature is associated with the property of subcompositional coherence (Aitchison 1986; Pawlowsky-Glahn and Egozcue 2022). That is, given two compositional parts ${\textbf {X}}_r$ and ${\textbf {X}}_s$ of a data set ${\textbf {X}}$, the value of $\textrm{d}({\textbf {X}}_r,{\textbf {X}}_s)$ should be the same regardless if other columns are added to or removed from ${\textbf {X}}$. In addition, due to the scale invariance property, it should hold that $\textrm{d}({\textbf {X}}_r,{\textbf {X}}_s)=\textrm{d}(\alpha \cdot {\textbf {X}}_r,\beta \cdot {\textbf {X}}_s)$ for $\alpha , \beta >0$. To the best of our knowledge, only the distance $\textrm{d}_a$ (Eq. 3) has been explored as a distance for compositional variables (Martín-Fernández et al. 2018; Pawlowsky-Glahn and Egozcue 2022). Other potential measures of difference, such as the CoDa dissimilarity based on the Kullback–Leibler divergence described in Palarea-Albaladejo et al. (2012), remain unexplored.

According to the usual procedure for the most popular HC methods (Hennig et al. 2015), the following steps perform an R-mode HC for an $n\times D$ CoDa set ${\textbf {X}}$:

Step 1: :

Consider D clusters: ${\textbf {C}}_j=\{{\textbf {X}}_j\}$, for $j=1,\ldots ,D$. Compute the $D\times D$ Aitchison distance matrix between all the parts $\{{\textbf {X}}_1,\ldots ,{\textbf {X}}_D\}$.

Step 2: :

Merge clusters as ${\textbf {C}}_{a\cup b} = {\textbf {C}}_a \cup {\textbf {C}}_b$, where $\textrm{d}_a({\textbf {C}}_a,{\textbf {C}}_b)$ is the smallest value in the distance matrix.

Step 3: :

Delete the row and the column of ${\textbf {C}}_a$ and of ${\textbf {C}}_b$ in the distance matrix. Insert a new row and column containing the distances between the new cluster ${\textbf {C}}_{a\cup b}$ and the remaining clusters.

Step 4: :

Repeat steps 2 and 3 until only one maximal cluster remains ($\{{\textbf {X}}\}$).

The crucial step in the procedure is the updating of the distance matrix when a new cluster is created. That is, when clusters ${\textbf {C}}_a$ and ${\textbf {C}}_b$ are merged into cluster ${\textbf {C}}_{a\cup b}$, one must specify the new dissimilarity between the cluster and all other objects (parts or clusters). The Lance–Williams dissimilarity update formula, which embraces the most common HC methods, solves the issue of updating the distance matrix (Hennig et al. 2015, page 109). Using this formula, one can easily apply HC methods such as, among others, single, complete, and average linkage, and Ward’s (i.e., minimum variance) method. The difference among the HC methods lies in the definition of distance between two clusters (Table 1).

Table 1 R-mode HC methods for CoDa. The geometric means ${\textbf {G}}_{k}$, $k=a,b$ are, respectively, the center of the cluster

In the single linkage method, the distance between two clusters ${\textbf {C}}_a$ and ${\textbf {C}}_b$ is the distance between the nearest parts, that is, the parts one in each cluster that are more proportional. In this sense, clusters merged at the initial iterations of the algorithm are clusters with parts providing more redundant information. However, the single linkage method can exhibit a notable disadvantage in summarizing interrelationships: the chaining effect (Hennig et al. 2015). This effect is illustrated by means of a paleoecological study in Sect. 4. On the other hand, the complete linkage method emphasizes the homogeneity of clusters over their separation because its criterion for merging two clusters is based on the pairwise maximum distance. In this method, the distance between two clusters ${\textbf {C}}_a$ and ${\textbf {C}}_b$ is the distance between the parts in each cluster that are most separated, that is, the two columns that are least proportional. Consequently, single and complete linkage methods share the difficulty in defining a unique representative of each cluster because one has to adapt the representative as regards the other cluster in measuring the distance. This may be a serious handicap if the study aims to reduce the spatial dimension of the parts. On the other hand, for the average linkage and Ward’s method, the representative of the cluster is the geometric center

$$\begin{aligned} {\textbf {G}}_k= \left( \prod _{{\textbf {X}}_j\in {\textbf {C}}_k} {\textbf {X}}_j \right) ^{1/|{\textbf {C}}_k|}, \end{aligned}$$

(5)

where $|{\textbf {C}}_k|$ is the number of parts in the cluster $k=a,b$ (Table 1). Historically, the average linkage method is defined as a compromise between single and complete linkage methods (Hennig et al. 2015). In addition, this method is described as computationally expensive, especially when the number of parts becomes large, because the distance between two clusters is the average of all the pairwise distances between the parts in these two clusters. From our experience, no relevant differences are detected in the execution time of the three algorithms, whereas clusters detected by the average linkage method are more similar to the groups created by the complete than the single linkage method, which is mainly attributable to the chaining effect.

Ward’s minimum variance method (Ward 1963) is a special case of the HC because it establishes a direct link between the concepts of variance and distance between clusters (Hennig et al. 2015). Indeed, in the presence of groups in a data set, the total variance can be decomposed into the sum of two components: variability between groups and within-group variation, where all these concepts are computed using the corresponding error sum of squares. Importantly, the distance between two cluster candidates for merging in Ward’s method (Table 1) is equal to the increase in the within-group variation with the fusion of the two clusters. Consequently, Ward’s method pursues the cluster configuration with the minimum within-group variation (i.e., the maximum between-group variation). Importantly, the distance between two clusters (Table 1) is proportional to the variance of a balance (Eq. 4), indicating a direct link between the SBP and the HC configuration of a set of compositional parts. In other words, it is the link between the dendrogram, a popular graphical display for an HC, and the CoDa dendrogram, a representation of an SBP (Egozcue and Pawlowsky-Glahn 2005; Pawlowsky-Glahn and Egozcue 2011). By definition, Ward’s method typically creates a dendrogram with low fusion levels at the bottom and the largest merger level at the top. Ward’s algorithm starts detecting the smallest entry in the variation matrix (proportional parts), and the corresponding parts are merged to form a group. The method iteratively continues merging groups of parts according to the smallest variance of the corresponding balance. The final stage consists of the fusion of the last two remaining groups into one, which gives the balance with the largest variance. Consequently, it is expected that an $\textrm{olr}$ basis created by Ward’s method is formed by balances as constant as possible, with the first balances created (at the bottom of the dendrogram) being mostly pairwise log-ratios of proportional parts, and the last balance created (at the top of the dendrogram) being the balance involving the full composition which retains the largest percentage of the total variance.

In the literature, other agglomerative HC methods are provided, such as McQuitty’s, median, and centroid (Hennig et al. 2015). Although they are less popular, they have their advantages and their difficulties over the rest of the methods. In an R-mode analysis for CoDa, the particularities of each method concerning compositional parts might be interpreted in similar terms as for the methods described above. In addition, one could consider a divisive HC method or even other methods from a family different from the hierarchical one (e.g., K-means, model-based clustering, fuzzy clustering). In terms of creating an $\textrm{olr}$ basis, one advantage of an R-mode HC is its link with the SBP of a composition. Whereas, as regards the dimension reduction, HC methods have the particularity of deciding the number of clusters once the hierarchical configuration has been created.

Determining the optimal number of clusters, $K_{opt}$, is crucial for cluster validation (Hennig et al. 2015). Most indices used for this task (e.g., Dunn, Calinski–Harabasz, average silhouette width) are designed in such a way that their maximum or minimum value indicates an “optimal” clustering. Clustering is computed for various values of K (often in an interval between 1 and 2 and a maximum value $K_{max}$), and then the best one is selected (Karacan et al. 2021). However, there are also other indices that increase (or decrease) with increasing K, in which case, researchers look for a change of curvature, known as elbow, as in the scree plot for the eigenvalues in principal component analysis (Jolliffe 2002). That is, a value K where a strong increase (respectively decrease) is followed by a weak one. Typically, in cluster analysis, the index represented is the ratio of the between-group sum of squares to the total sum of squares. In this case, the first clusters typically add much information (explain a lot of variance). But at some point, the marginal gain will drop, giving an elbow in the graph.

The above methods proposed for Q-mode clustering are easily adapted for R-mode. In addition, in our context, one can take advantage of the relationship between the variance of a balance and the distance between centers of clusters (Eq. 4) for introducing a novel graphical display which shows the structure of variance accounted for by the balances. Let $\textrm{olr}({\textbf {X}})$ be the $n \times (D-1)$ matrix of $\textrm{olr}$ coordinates (Eq. 2) calculated using the $\textrm{olr}$ basis resulting from an SBP according to the results of an R-mode HC. The variance of columns in matrix $\textrm{olr}({\textbf {X}})$ can be calculated as a distance between the centers of two groups of parts (Eq. 4) and added to the total variance (Aitchison 1997)

$$\begin{aligned} \textrm{totvar}({\textbf {X}})=\frac{1}{2D}\cdot \sum _{j=1}^{D} \sum _{k=1}^{D} \textrm{var}\left( \ln \frac{{\textbf {X}}_j}{{\textbf {X}}_k}\right) = \sum _{j=1}^{D-1} \textrm{var}\left( \textrm{olr}({\textbf {X}})_j\right) , \end{aligned}$$

(6)

where $\textrm{olr}({\textbf {X}})_1$ is the first cluster created at the bottom of the dendrogram (i.e., pairwise minimum variance), and $\textrm{olr}({\textbf {X}})_{D-1}$ corresponds to the last cluster fusion (i.e., involving the full composition). In the hypothetical case when the result of the HC is only one cluster, one can imagine a $\textrm{clr}$-biplot where all the rays overlap, with a total variance of approximately zero, resulting in a flat dendrogram. On the other hand, in the scenario of no clusters (i.e., D single clusters), each balance should have a variance approximating $\frac{1}{D-1}\cdot \textrm{totvar}({\textbf {X}})$, while the rays of the parts are uniformly distributed in a $(D-1)$-multivariate sphere. In the other scenarios of $1<K<D$, with K the number of clusters, at least one balance should have a variance above $\frac{1}{D-1}\cdot \textrm{totvar}({\textbf {X}})$ and at least another balance below.

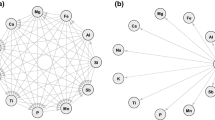
Figure 1a shows the clr-biplot for an R-mode HC with $K=2$ clusters in a data set ${\textbf {X}}$ ($107 \times 13$). The CoDa set is actually a subcomposition of a 22-part composition described in the following section. Note that the quality of the representation is reasonable ($65.81\%$ of variance retained) where the first axis retains up to $55.06\%$ of the total variance. The clr-biplot suggests $K=2$ clusters for the 13 compositional parts due to the loadings in the first axis (i.e., positive loadings versus negative). The R-mode Ward’s method creates the dendrogram in Fig. 1b, which confirms that two clusters is a reasonable option. However, options such as $K=3$ or $K=4$ clusters may be considered adequate as well. When the hierarchical structure from Ward’s method (Fig. 1b) is transformed in an SBP, then the corresponding $\textrm{olr}$ basis is created. Figure 2a shows the CoDa dendrogram of balances where the first balance

$$\begin{aligned} \textrm{olr}({\textbf {X}})_1=\sqrt{\frac{42}{13}} \cdot \ln \frac{({\textbf {X}}_8\cdot {\textbf {X}}_9\cdot {\textbf {X}}_{10}\cdot {\textbf {X}}_3\cdot {\textbf {X}}_6\cdot {\textbf {X}}_7\cdot {\textbf {X}}_{12})^{1/7}}{({\textbf {X}}_1\cdot {\textbf {X}}_{13}\cdot {\textbf {X}}_{2}\cdot {\textbf {X}}_{11}\cdot {\textbf {X}}_4\cdot {\textbf {X}}_5)^{1/6}}, \end{aligned}$$

has the largest variance ($\textrm{var}(\textrm{olr}({\textbf {X}})_1=6.102$), as suggested by the largest vertical line, representing $48.39\%$ of the total variance ($\textrm{totvar}({\textbf {X}})=12.609$). This value suggests a large distance between the centers of the two clusters. Each vertical line of the branches in the CoDa dendrogram represents the variance of the corresponding balance. Figure 2b shows the value of the variance of balances as a bar plot, where one can see how the rest of the total variance is decomposed among the 12 balances. In the extreme scenario of $K=13$ clusters, one would expect that the variance of each balance is approximately 1.05 ($=\textrm{totvar}({\textbf {X}})/12$, red horizontal line), that is, the equal variance level. The bar plot suggests an elbow for the second balance, with a variance slightly larger than this level. The other 10 balances have a variance smaller than the second one. One can conclude that the structure of the decomposition of the total variance (Fig. 2b) reinforces the decision of taking $K=2$ clusters for the parts in the composition. The other typical indices explored (Dunn, Calinski–Harabasz, and average silhouette width) agree, in that two groups are a reasonable option.

Once the R-mode HC is finished, any Q-mode analysis can be done using the $\textrm{olr}$ coordinates created from the SBP (Fig. 2a). Importantly, the coordinate $\textrm{olr}({\textbf {X}})_1$ plays a relevant role because it can discriminate between samples. Indeed, samples associated with parts belonging to the first cluster of parts (the numerator in the balance) take positive values Conversely, the first coordinate takes negative values for samples associated with the parts in the second cluster (the denominator in the balance). On the other hand, if the analyst aims to reduce the dimension of the space of parts, then one representative for each cluster of parts should be selected or created. In this case, the number of parts will be reduced from $D=13$ to 2, that is, the dimension 12 becomes 1 (univariate case). By definition, the representative of clusters in Ward’s method is the center of the group (Eq. 5); that is, for each sample, the average values over the parts of each cluster.

Fig. 1

R-mode HC for a CoDa set ${\textbf {X}}$ ($107 \times 13$): a covariance clr-biplot ($65.81\%$ variance retained); b Ward’s method dendrogram. The red horizontal line indicates the cutting level for $K=2$ clusters

Fig. 2

R-mode HC for a CoDa set ${\textbf {X}}$ ($107 \times 13$): a CoDa dendrogram for the $\textrm{olr}$ basis created from Ward’s method; b bar plot for the variances of the balances in the $\textrm{olr}$ basis created from Ward’s method. The horizontal red line is the level for the equal variance case (1.05)

The example in Fig. 2b supports the idea that analyzing the variance decomposition in terms of balances can be helpful for deciding the number of clusters in R-mode HC. In the above example, for Ward’s method, the height of bars decreases as the number of clusters increases. This is not necessarily so for the other HC methods because only Ward’s method links the concepts of balance variance and distance between clusters (Hennig et al. 2015). In any case, the valuable information of the display is the position of the elbow, if it exists, because it suggests a potential number of clusters in the compositional parts. That is, the analyst should look for the tail in the bar plot, detecting the balances with a negligible variance because these balances suggest clusters with near centers that might be merged.

4 Example: A Paleoecological Study

R-Mode HC is commonly adopted in paleoecological studies to identify groups of species sharing similar behavior. The benthic foraminiferal data of the example (Fig.  3) are taken from a study carried out on the core TEA-C6 (39$^{\circ }$46.45’ N, 17$^{\circ }$02.96’ E, 907.5-m water depth) recovered in the Ionian Sea (Mediterranean Sea) (Di Donato et al. 2019). The data set consists of 107 samples with 22 parts (Table 4). The age model of this core TEA-C6 is based on tephrostratigraphical analysis and AMS-14C dating. The stratigraphic record of the core covers the last 15,000 years and includes the so-called Sapropel S1, the latest of a series of organic carbon-enriched layers which were deposited in the eastern Mediterranean in connection with precession-driven periodic events characterized by enhanced organic flux at the sea floor and deep-water anoxia (see Rohling et al. (2015), among many others, for a review). The distribution of benthic foraminiferal taxa within the core TEA-C6 is summarized in Fig. 3. White bands indicate intervals devoid of benthic foraminifera, as a consequence of anoxic conditions established during the Sapropel S1 stagnation phase at the bottom of the Gulf of Taranto. Using CONISS (Grimm 1987) (basically a constrained Q-mode Ward’s algorithm), computed on log-ratio coordinates (Di Donato et al. 2009), four benthic foraminiferal compositional zones (BFCZ) were determined. BFCZ4 includes late glacial to early Holocene assemblages. BFCZ3 and BFCZ2 surround Sapropel S1, and BFCZ1 includes post-Sapropel S1 to recent assemblages. Notes on the ecology of the benthic foraminiferal taxa included in the case study can be found in Di Donato et al. (2019); Di Donato et al. (2022).

Table 2 Compositional parts of the benthic foraminiferal data: the core TEA-C6 ($107 \times 22$)

Fig. 3

Location, stratigraphical log, and benthic foraminiferal assemblages of the core TEA-C6

R-mode HC can be useful for investigating potential groups of species in the core C6 data set. The covariance $\textrm{clr}$-biplot (Fig. 4) is not very representative of high quality because the first two axes retain up to $58.89\%$ of the total variance. The position of rays suggests that some parts may be considered redundant and other parts may be clustered. The smallest value in the variation matrix is $\textrm{var}(\ln \frac{{\textbf {X}}_{21}}{{\textbf {X}}_{22}}) = 0.49$; the second is $\textrm{var}(\ln \frac{{\textbf {X}}_{5}}{{\textbf {X}}_{6}}) = 0.51$ (see Appendix). They can be considered as small values because the expected log-ratio variance in case of equal pairwise variance is 2.43 for any of pairwise log-ratio ($2.43 = \textrm{totvar}({\textbf {X}})/(D\cdot (D-1)/2)$ (Egozcue et al. 2018). Consequently, one expects that the first cluster formed by any R-mode HC is $\{{\textbf {X}}_{21}, {\textbf {X}}_{22}\}$= $\{Chilostomella, C.~bradyi\}$. On the other hand, the largest value in the variation matrix is $\textrm{var}(\ln \frac{{\textbf {X}}_{1}}{{\textbf {X}}_{7}}) = 8.20$. That is, the parts ${\textbf {X}}_1= \{B.~spathulata\}$ and ${\textbf {X}}_7= \{M.~barleeanum \}$ should be assigned to different clusters for all the methods.

Fig. 4

Covariance clr-biplot ($58.89\%$ total variance retained) of the core C6 data set ($107 \times 22$)

Figure 5 shows the dendrograms for the four methods: single, complete, and average linkage, and Ward’s method. Clearly, there are differences among the clusters of parts formed, but one can recognize some typical features of the HC methods. The chaining effect is present in the clustering structure created by the single linkage method (Fig. 5a) because almost half of the fusions consists in merging a unique part to a previously formed cluster. The complete linkage dendrogram (Fig. 5b) suggests more compact clusters than the single linkage dendrogram because the leaves of the tree merge at levels substantially lower than the clusters on the root at the top of the dendrogram. One can consider that the average linkage method (Fig. 5c) is an option in the middle of single and complete linkage methods because there are many fusions between a cluster and a unique part, as in the single linkage, but the difference between the level of fusion of clusters at the root and at leaves is more similar to the complete linkage dendrogram. At first glance, the structures of dendrograms created by complete linkage and Ward’s methods (Fig. 5d) are similar. However, because the structure of the dendrograms is important, a comparison between two types of clustering should be based on the number of clusters and the objects forming the groups.

Fig. 5

Dendrogram for R-mode HC of parts in the core C6 data set: a single linkage; b complete linkage; c average linkage; and d Ward’s method (squared distance). The horizontal red line is the cutting level (see text for more details)

As regards the number of clusters, the horizontal red line in Fig. 5 is the cutting level for creating a number of clusters suggested by the variance retained in the balances shown in Fig. 6. The horizontal red line in the bar plots is the value $\textrm{totvar}({\textbf {X}})/(D-1)=\frac{25.53}{21}=1.22$ representing the case of equal variance retained by each variance, that is, equal distance between all the clusters merged along the clustering process (i.e., D clusters case). As explained in Sect. 3, there is a link between balances and clusters created. For example, the balance $B_{21}$ (first bar in Fig. 6) corresponds to a clustering formed by two groups. Note that single, complete, and average linkage methods create the balance $B_{21}$ in terms of the log-ratio between part ${\textbf {X}}_1$ (B.spathulata) against the rest of the taxa. On the other hand, the balance $B_{21}$ created with the Ward’s method is associated with the two groups $\{{\textbf {X}}_1, {\textbf {X}}_2, {\textbf {X}}_3, {\textbf {X}}_5, {\textbf {X}}_6, {\textbf {X}}_{11}, {\textbf {X}}_{14},$ ${\textbf {X}}_{17}, {\textbf {X}}_{18}, {\textbf {X}}_{20}, {\textbf {X}}_{21}, {\textbf {X}}_{22} \}$ and $\{{\textbf {X}}_{4}, {\textbf {X}}_{7}, {\textbf {X}}_{8}, {\textbf {X}}_{9}, {\textbf {X}}_{10}, {\textbf {X}}_{12}, {\textbf {X}}_{13}, {\textbf {X}}_{15}, {\textbf {X}}_{16}, {\textbf {X}}_{19} \}$. According to the elbow of the bar series, the four HC methods suggest forming four, five, or six groups of parts. The options four and five groups are also suggested by other popular indices (Dunn, Calinski–Harabasz, and average silhouette width). In particular, the single linkage method suggests five clusters for the 22 parts, whereas the other three methods suggest creating four groups.

Fig. 6

Balance-variance bar plot for R-mode HC of the core C6 data set: a single linkage; b complete linkage; c average linkage; and d Ward. The horizontal red line is the level for the equal variance case (1.22)

Table 3 shows two measures of agreement between the four HC methods when four groups are created in the parts of the core C6 data set. To measure the agreement of the results of the four HC methods, two popular indices, out of 25 listed in the R package mclustcomp (You 2021), were used: adjusted Rand index (ARI) and normalized mutual information (NMI). The ARI, based on the confusion matrix, ranges in $[-1, 1]$, where 1 means identical cluster sets, while values in the range $[-1, 0]$ suggest independent groups. On the other hand, NMI, based on the mutual information metric (MI), is calculated by dividing MI with the geometric mean of the entropies of the individual cluster sets. It ranges in [0, 1], with 1 for total agreement and 0 for independent groups. Meilă (2007) presents a more detailed description of the type and properties of indices for measuring clustering agreement. According to the ARI (upper diagonal in Table 3), the single linkage method creates groups less coincident with the clusters created by the other methods, where complete linkage reflects a similar behavior. On the other hand, the average linkage and Ward’s method are highly coincident (ARI= 0.876). These two methods assign to a different group only the parts ${\textbf {X}}_{11}$ and ${\textbf {X}}_{20}$, with the remaining up to $D=22$ parts assigned to the same clusters. This fact is also detected by the NMI index (lower diagonal in Table 3) with NMI = 0.843. In this case, the worst behavior is for the complete linkage method, which is very similar to the values for the single linkage.

R-mode HC is a data-driven procedure where the analyst can select the clustering technique and the measure of dissimilarity between variables to finally decide the number of groups and validate the groups. However, the final decision on the quality of the groups created should be agreed upon using the expert knowledge of the data set. Regarding the dendrogram derived by Ward’s method (Fig. 5d), the results seem consistent with the ecology of the taxa and their distribution within the core. In particular, the taxa included in the left-hand group have in common that they are relatively more abundant in the Holocene range of the core and are mostly related to conditions of good oxygenation or not high organic matter fluxes at the bottom (Di Donato et al. 2019). In contrast, the taxa included in the middle group share the highest relative abundance in the late-glacial interval of the core. The cluster on the right includes low-oxygen-resistant and/or opportunistic species related to higher flux of organic matter at the bottom, such as Bolivina. These taxa are associated, in the considered core, with Sapropel S1. The clustering in the dendrogram derived by the single linkage appears less straightforward. On the right, there are low-oxygen-resistant species. In this dendrogram B. spathulata is the last added element. In the clr-biplot, the column point of this species is located on the positive side of the first axis, with the B. costata-inflata column point as the closest one (to which, in Ward’s method, this species is linked). From a certain point of view, the position of B. spathulata in the dendrogram has its own logic, as this species shows within this core a distinctive behavior by contours with high abundance in the interval immediately preceding and following the Sapropel S1. However, maybe the group of Sapropel S1-related species with oxygen-resistant taxa and B. spathulata defined by Ward’s method seems even more coherent. What does not seem satisfactory in the single linkage dendrogram is a quite clear chaining effect, with a cluster in which taxa are included (from Miliolidae to Bolivina albatrossi in Fig. 5a) with different distribution and ecology. In the complete linkage, B. spathulata is the last added element, as in the case of the single linkage. A group of Sapropel S1 taxa is also defined. The main difference from Ward’s method lies in the fact that a group of taxa (Bulimina marginata, Gyroidina altiformis, Miliolidae, Uvigerina mediterranea) that in the clr-biplot are found in an intermediate position between the group of taxa typical of the Holocene post-Sapropel S1 and those more abundant in the Late Glacial are in this case linked with the latter. With regard to average linkage, the relationships seem in general similar to those obtained with Ward’s method, with two differences: the first concerns B. spathulata, which, as in the case of single and complete linkage, is linked as the last element; the second concerns B. costata-inflata, which with Ward’s method is associated with Globobulimina spp., while with average linkage, it is linked to an already formed cluster, which includes taxa more abundant in the Late Glacial. In summary, single linkage appears to suffer from the chain effect whereby taxa that are placed on opposite sides of the first $\textrm{clr}$-biplot axis are grouped together. The other methods provide slightly different results, which nevertheless seem justifiable. In general, in the present case, Ward’s method provides results that are fully consistent with the distribution and ecology of the benthic foraminiferal taxa.

Table 3 Measures of agreement between the four HC methods when four groups are created (ARI, upper diagonal; NMI, lower diagonal)

5 Concluding Remarks

We have stated that R-mode HC can be useful for investigating potential groups of compositional parts. The connections between Aitchison distance, cluster representative, $\textrm{clr}$-biplot, and SBP for creating an $\textrm{olr}$ basis have been analyzed in the context of the most popular HC methods, such as single, complete, and average linkage, and Ward’s method. As a result of this study, a new data visualization technique has been introduced. The balance–variance bar plot, based on the total variance decomposition, is useful when deciding the number of clusters of compositional parts, becoming a tool to be integrated with the set of usual cluster validation techniques. Still pending is the analysis of other popular non-agglomerative HC methods, such as, among others, hierarchical divisive methods and K-means clustering. In any case, for all R-mode clustering methods, when detecting redundant parts, a variable selection can be done, whereas a dimension reduction of the space of parts can be obtained when selecting a representative of clusters created.

Appendix

See Table 4.

Table 4 Variation matrix of the benthic foraminiferal data: the core TEA-C6 ($107 \times 22$)

Table 5 continued