A Time Series Decomposition and Reinforcement Learning Ensemble Method for Short-Term Passenger Flow Prediction in Urban Rail Transit

Abstract

Short-term passenger flow prediction (STPFP) helps ease traffic congestion and optimize the allocation of rail transit resources. However, the nonlinear and nonstationary nature of passenger flow time series challenges STPFP. To address this issue, a hybrid model based on time series decomposition and reinforcement learning ensemble strategies is proposed. Firstly, the improved arithmetic optimization algorithm is constructed by adding sine chaotic mapping, a new dynamic boundary strategy, and adaptive T distribution mutations for optimizing variational mode decomposition (VMD) parameters. Then, the original passenger flow data containing nonlinear and nonstationary irregular changes of noise is decomposed into several intrinsic mode functions (IMFs) by using the optimized VMD technology, which reduces the time-varying complexity of passenger flow time series and improves predictability. Meanwhile, the IMFs are divided into different frequency series by fluctuation-based dispersion entropy, and diverse models are utilized to predict different frequency series. Finally, to avoid the cumulative error caused by the direct superposition of each IMF’s prediction result, reinforcement learning is adopted to ensemble the multiple models to acquire the multistep passenger flow prediction result. Experiments on four subway station passenger flow datasets proved that the prediction performance of the proposed method was better than all benchmark models. The excellent prediction effect of the proposed model has important guiding significance for evaluating the operation status of urban rail transit systems and improving the level of passenger service.

1 Introduction

Urban rail transit (URT) has developed rapidly in recent years and gradually occupied a crucial position in urban public transport. However, with the increasing passenger flow, problems such as passenger congestion and mismatches between supply and demand have attracted increasing attention. Thus, to ensure the stable operation of the URT systems, accurate short-term passenger flow prediction (STPFP) is of great importance in traffic planning [1]. Accurate STPFP results can help URT station managers organize and guide passengers inside the station, ease passenger congestion, and avoid some accidents. For operators, the STPFP results can be used to allocate resources to improve service levels rationally and meet demand for passenger flow. Passengers can also fully grasp the carrying situation of rail transit to improve their travel experience.

The ridership of URT is time-series data continuously recorded and counted by the station card-swiping equipment. Therefore, in earlier studies, time series models were often utilized for STPFP. These models include linear models [2, 3], gray prediction [4], history average [5], and Kalman filter [6]. The premise of these methods is that the time series remains stationary. Still, the traffic situation is changeable in practice, and the passenger flow time-series data are typically complex and nonstationary. As a result, in practical application, these preconditions are challenging to achieve, and the performance of these methods is poor. Thus, some machine learning methods with shallow architecture have been applied to STPFP, such as gradient boosting decision trees (GBDT) [7], support vector machines [8], extreme learning machines [9], and shallow back-propagation neural networks (BPNN) [10]. Although these models can effectively map nonlinear relationships, their performance depends on feature engineering. The production of feature engineering is undoubtedly complex and time-consuming. Therefore, machine learning methods cannot entirely extract the nonlinear characteristics of ridership data. Deep learning based on deep architecture has gained attention in the past few years. It can automatically extract features and has good nonlinear learning abilities. Huang et al. [11] applied deep belief networks to STPFP for different modes of passenger flow. Lv et al. [12] first applied stacked auto-encoders for STPFP. Liu et al. [13] introduced the deep learning theoretical model of recurrent neural networks into transportation. Subsequently, Liu et al. [14] utilized the variant long short-term memory (LSTM) of recurrent neural networks for STPFP. Ma et al. [15] adopted convolutional neural networks to predict large-scale passenger flows. Wu et al. [16] also used graph convolutional neural networks for large-scale STPFP.

However, these single prediction models can only partially cover some influencing factors. The STPFP of the URT stations needs to fully understand the seasonality and trend of passenger flow series and be able to effectively identify impulse noise in the data. URT is a complex system susceptible to heterogeneous interference. The statistical ridership data presents high-level nonlinearity, which makes it challenging for the model to obtain the features of passenger flow [17]. Therefore, some scholars have decomposed the ridership data into several interdependent sub-series using decomposition methods. The sub-series have pronounced apparent trend and fluctuation characteristics, which helps reduce the burden of prediction models [18]. Wei and Chen [19] proposed an empirical mode decomposition (EMD) hybrid model for STPFP, including the transportation time series decomposed by EMD, and formed a hybrid prediction method with a neural network for STPFP. Subsequently, Yang et al. [20] combined EMD and an SAE model for STPFP. Based on EMD, Li and Ma [21] used sample entropy (SE) and EMD to better decrease the sophistication of the time series. Zhang et al. [22] and Liu et al. [23] applied ensemble EMD (EEMD) to decompose ridership data in their research and combined different deep learning models for STPFP. Jia et al. [24] adopted the improved EMD algorithm, CEEMDAN (complete ensemble empirical mode decomposition with adaptive noise), to decompose travel time data. Huang et al. [25] put forward a decomposition and ensemble strategy consisting of CEEMDAN decomposition of original passenger flow data, recurrence quantification analysis reconstruction, and attention mechanism multistep prediction. In addition to EMD and its improved algorithm for decomposing passenger flow time series, wavelet decomposition (WD) is also used for STPFP. Diao et al. [26] proposed a novel Gaussian process model to forecast the detailed components. Liu et al. [27] applied WD to decompose ridership into components of different frequencies, denoise and reconstruct the decomposed data, and finally use a convolutional neural network for STPFP. Yang et al. [28] used WD and deep learning for station passenger flow prediction. However, WD and EMD each have their drawbacks. WD is less adaptive than other modal decomposition methods and must select the parent wavelet to be used in advance. EMD has the disadvantages of mode mixing, endpoint effects, and a lack of a complete theoretical basis. These defects will affect the prediction accuracy of STPFP. Dragomiretskiy and Zosso [29] proposed variational mode decomposition (VMD), which solves the problem of mode mixing and endpoint effect in EMD. Afterward, Li et al. [30] developed a metro passenger flow prediction framework with VMD. Li et al. [31] applied VMD to effectively suppress the influence of randomness and volatility on passenger flow, and the STPFP was carried out accurately. Yang et al. [32] utilized VMD to decompose nonlinear and nonstationary ridership data. They used an extreme learning machine model to correct the prediction errors of each intrinsic mode function (IMF) to complete the prediction. Their experimental results also showed that VMD has a practical application value in STPFP prediction.

The performance of VMD is affected by its parameters. Therefore, the selection of VMD parameters is essential to ensure the result of the hybrid model. Zhang et al. [33] and Fu et al. [34] selected VMD parameters using the center frequency observation method. Their experiments confirmed that this model could enhance the capabilities of hybrid models. But its effect needs to be apparent. With the development of heuristic optimization algorithms, many scholars have applied them to select VMD parameters. For example, genetic algorithms [35], particle swarm optimization (PSO) [36], seagull optimization algorithms [37], and gray wolf optimizers (GWO) [38] have been used. These optimization algorithms generally have the weaknesses of slow convergence speeds, poor stability, and quickly falling into the local optimum, which will affect the VMD parameter optimization. Abualigah et al. [39] put forward a novel arithmetic optimization algorithm (AOA) in 2021, and their experimental results showed that the AOA had surprising advantages in solving challenging optimization problems. Unfortunately, in the optimization process of the AOA, its population diversity will decrease, and it is easiest to fall into a local optimum. An improved AOA (IAOA) is proposed to solve these problems. Sine chaotic mapping, a nonlinear dynamic boundary strategy, and adaptive T distribution mutations are added to enhance the AOA. Afterward, the VMD parameters are optimized by the IAOA.

Many scholars use a fixed machine learning or deep learning model to predict all the decomposed components. Generally, deep learning models are more appropriate for learning high-complexity data, while shallow learning models are more appropriate for stationary series. Although Goh et al. [40] proposed a multimodal approach to predict IMFs, they could have explained more about the complexity criterion of IMFs. Sun and Duan [41] applied sample entropy (SE) to calculate the intricacy of each IMF after decomposition. Similarly, Li et al. [42] adopted SE to analyze the decomposed sub-series. However, SE makes it easy to overlook components that contain helpful information. Azami and Escudero [43] proposed fluctuation-based dispersion entropy (FDE) to process time series. Compared with SE, FDE is more sensitive to time series changes, and the algorithm is more efficient. Thus, the FDE is used in this paper to analyze each IMF’s intricacy. According to the FDE results of the sub-series, they are divided into high-frequency and low-frequency series. The models suitable for their respective complexity are used to predict each sub-series.

In addition, most studies usually use direct superposition to reconstruct the prediction results of each IMF. However, they did not consider the cumulative error caused by sub-series superposition. In some other prediction fields, some scholars use ensemble learning methods to integrate multiple different models’ prediction results. In applying stacking-based methods [44], Dong et al. [45] applied the stacking-based strategy to integrate the prediction results of five models by taking five prediction models as the base learners. Liu et al. [46] utilized a GBDT to integrate the predictions of the three models. For weight-based ensemble learning methods, some scholars apply heuristic optimization algorithms to obtain the optimal weight of the model. Tian [47] proposed an improved PSO to integrate the predicted values of each prediction mode. Song et al. [48] applied GWO to overcome the limitations of a single prediction model. Moreover, single-objective optimization algorithms can only achieve one criterion. Cheng et al. [49] used a multi-objective salp swarm optimization algorithm to integrate the prediction results of the four basic models. Their optimization objectives include prediction error and model stability. Chen et al. [50] exploited a multi-objective hybrid optimization algorithm with six basic models. The method effectively improved the prediction result. The above studies have shown that stacking-based and weight-based ensemble learning methods perform well. However, the stack-based method belongs to the black box system, and its integration method is incomprehensible. The weight-based ensemble learning method directly assigns weights to each basic model for integration, which is easier to understand than the stacking-based method. Although heuristic algorithms are essential in ensemble learning, making breakthroughs has not been easy. Compared with standard heuristic optimization algorithms, reinforcement learning has a more vital learning ability and has shown strong performance in many fields [51]. Therefore, reinforcement learning is applied to integrate the prediction results of the sub-series prediction model.

In summary, ridership data often exhibit high complexity, making it challenging to improve prediction accuracy. A model called optimized variational mode decomposition-fluctuation-based dispersion entropy-Q-Learning (OVMD-FDE-QL) based on optimized VMD (OVMD), FDE, and ensemble Q-Learning (QL) is proposed for STPFP. Firstly, sine chaotic mapping, a nonlinear dynamic boundary strategy, and adaptive T distribution mutations are added to improve the AOA. The search speed of the AOA is improved by initializing sine chaotic mapping. The nonlinear dynamic boundary strategy is used to improve the local development ability of the AOA in the later stages to balance the global and local search abilities of the algorithm. The adaptive T distribution mutation is applied to prevent the AOA from falling into a local optimal value. Meanwhile, the IAOA is used to find the best parameters of VMD to avoid the shortcomings of VMD selection parameters relying on experience, improving the algorithm’s adaptability. Then, the original passenger flow data containing nonlinear and nonstationary irregular noise changes is decomposed into different fluctuation components using OVMD technology, which reduces the time-varying complexity of passenger flow time series and improves predictability. OVMD decomposes the original passenger flow time series to obtain several IMFs, and the FDE is applied to calculate the entropy of each IMF to divide each IMF series into high-frequency and low-frequency series. Higher than a certain threshold are the high-frequency components, and lower than a certain threshold are the stationary low-frequency components. High-frequency IMFs are predicted using LSTMs that are good at processing high-frequency series, and low-frequency IMFs are predicted using back-propagation (BP) neural networks that are good at processing stationary series. Finally, the QL algorithm integrates BP and LSTM to obtain prediction results. The main contributions are as follows:

• 1. An IAOA algorithm based on sine chaotic mapping, a nonlinear dynamic boundary strategy, and adaptive T distribution mutations is proposed to search the optimal parameters of VMD. The adaptability of the VMD algorithm is enhanced. The experimental results show that the IAOA has better optimization ability and faster convergence speed.

• 2. The FDE is applied to divide the IMFs into high-frequency and low-frequency series, and the models suitable for their respective complexity are used to predict each sub-series. The experimental results show that FDE can well reflect the complexity of the signal and reasonably divide different frequency components.

• 3. An ensemble learning method based on reinforcement learning is proposed. The QL method integrates each IMF’s results, which avoids the error superposition and blindness of the direct addition of IMFs. The experimental results show that the QL algorithm can effectively integrate the prediction results of each IMF and further improve the prediction results of the model.

• 4. The ridership of four Nanning Metro stations is applied to certify the performance of OVMD-FDE-QL. Four evaluation indices and four experiments were used for comparison. The experimental results show that OVMD-FDE-QL has strong prediction performance and good versatility.

2 Methodology

2.1 The Passenger Flow Process of OVMD-FDE-QL Model

The framework of the OVMD-FDE-QL STPFP model is shown in Fig. 1. The model includes three modules, and the specific three modules are as follows:

Fig. 1

The flowchart of OVMD-FDE-QL

Module 1: Data preprocessing. The IAOA is utilized to optimize the VMD parameters. After obtaining the optimal parameters, the passenger flow data is decomposed into k IMFs by OVMD.

Module 2: Calculate the results of each IMF’s FDE and make predictions. Calculate the FDE for each IMF. According to different FDE values, each IMF is split into high-frequency and low-frequency series. The shallow learning BP model is applied to predict the low-frequency component. The deep learning LSTM is utilized to predict high-frequency components.

Module 3: Integrate component prediction results based on the QL. The QL is utilized to integrate predicted values of BP and LSTM. The weighted coefficient w_i is introduced, which is the weighted coefficient of the ith IMF component prediction result. The QL is utilized to optimize the weight coefficients of k IMF components, and a satisfactory result is obtained. Therefore, the output of the ensemble model can be expressed as follows:

$$\hat{O}(t) = w_{1} \hat{O}_{1} (t) + w_{2} \hat{O}_{2} (t) + \cdots + w_{k} \hat{O}_{k} (t),$$

(1)

where w₁, w₂, and w_k are the weight coefficients of the first, second, and k IMF components, respectively.$\hat{O}_{1} (t)$,$\hat{O}_{2} (t)$, and $\hat{O}_{k} (t)$ are the prediction results of the first, second, and k IMF components, respectively. In addition, the validation dataset is used to train the QL algorithm. The test dataset is used to evaluate the predictive ability of the OVMD-FDE-QL model.

2.2 VMD

VMD is an adaptive, completely non-recursive modal variational and signal processing method. VMD can decompose the signal into k IMFs. Each IMF represents the components of different frequencies and amplitudes, which can better adapt to the characteristics and changes of time series signals. Compared with other traditional decomposition methods, such as WD and EMD, VMD can accurately capture the local characteristics and non-stationarity of signals. In addition, the low coupling of VMD makes it better able to deal with complex time series signals, avoiding the problem of modal aliasing or information loss that may occur in traditional decomposition methods. Therefore, VMD is very suitable for decomposing time-series signals. However, VMD must artificially set the number of modal components k and the penalty factor α [52]. Setting a k value that is too small will make the time series under-decomposed, and a k value that is too large will produce irrelevant modal components. The smaller the α, the greater the noise contained in the decomposed components. The arbitrary setting of these two parameters will affect the effectiveness of VMD decomposition, so selecting the best parameters through an optimization algorithm is necessary.

2.3 Improved AOA Optimized VMD

2.3.1 AOA Algorithm

Abualigah et al. [44] proposed the AOA. They evaluated the AOA’s performance, convergence behavior, and computational complexity through different scenarios. Their experimental results showed that the AOA has surprising advantages in solving challenging optimization problems compared to 11 well-known optimization algorithms. Therefore, the AOA is used to select the parameters of VMD in this paper adaptively. The AOA uses a simple arithmetic operator to calculate the best component in the candidate scheme group, and it generates random numbers through Eq. (2) to initialize the population.

$$X = \left[ {\begin{array}{*{20}c} {x_{1,1} } & \cdots & {x_{1,j} } & \cdots & {x_{1,d} } \\ {x_{2,1} } & \cdots & {x_{2,j} } & \cdots & {x_{2,d} } \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {x_{N,1} } & \cdots & {x_{N,j} } & \cdots & {x_{N,d} } \\ \end{array} } \right],$$

(2)

where N and d denote the number and dimension of solutions, respectively. x_i,j is the position of the ith solution in the j-dimensional space. Before the AOA starts optimization, the specific function values of the math optimizer accelerated (MOA) are calculated by Eq. (3) to control the switching between exploration and development of the algorithm.

$$\text{MOA}(t) = \text{Min} + t \times \left(\frac{\text{Max} - \text{Min}}{{t_{\text{max}} }}\right),$$

(3)

where MOA(t) is the specific value of the mathematical optimization coefficient calculated by the current iteration, t is the current number of iterations, and t_max is the maximum number of iterations. The minimum and maximum values of MOA are represented by Min and Max, which are 0.2 and 1, respectively. The random number r₁ with a uniform distribution subject to [0, 1] is selected. The exploration phase is carried out when r₁ is more than MOA. The development phase is performed when r₁ is less than or equal to MOA. The updated expression of the AOA solution in the exploration phase is as follows:

$$x_{i,j}^{t + 1} = \left\{ \begin{gathered} x_{\text{best},j}^{t} \div (\text{MOP}(t) + \varepsilon ) \times ((x_{\text{ub},j} - x_{\text{lb},j} ) \times \mu + x_{\text{lb},j} ),\quad r_{2}<{0}{.5} \hfill \\ x_{\text{best},j}^{t} \times \text{MOP}(t) \times ((x_{\text{ub},j} - x_{\text{lb},j} ) \times \mu + x_{\text{lb},j} ),\quad \quad \text{otherwise} \hfill \\ \end{gathered} \right.,$$

(4)

$$\text{MOP}(t) = 1 - \frac{{t^{1/\alpha } }}{{t_{\max }^{1/\alpha } }},$$

(5)

where $x_{i,j}^{t + 1}$ represents the position of the ith solution in the jth dimension at the t + 1 iteration; $x_{\text{best},j}^{t}$ represents the position of the tth-iteration optimal solution in the jth dimension; ε is a small integer, x_ub,j and x_lb,j represent the upper and lower bounds of the search space on the jth dimension, respectively; u is an adjustable parameter that can reduce the influence of local extremum points on the algorithm optimization, and its value is 0.5; and r₂ is a random number subject to a uniform distribution [0, 1]. When r₂ < 0.5, the division operator is used for updating; otherwise, the multiplication operator is used. Math optimizer probability (MOP) is a probability function; α is a sensitivity coefficient, which is used to define the exploration accuracy, and α = 5 in the AOA. In the development phase of the AOA, the subtraction search strategy and the addition search strategy are mainly used for development and calculation. The random number r₃ subject to a uniform distribution [0, 1] is selected. If r₃ < 0.5, we use the subtraction for optimizing; otherwise, we use the addition for optimizing, which can be expressed as follows:

$$x_{i,j}^{t + 1} = \left\{ \begin{gathered} x_{\text{best},j}^{t} - MOP(t) \times ((x_{{\text{ub}},j} - x_{{\text{lb}},j} ) \times \mu + x_{{\text{lb}},j} ),\quad r_{3} < 0.5 \hfill \\ x_{\text{best},j}^{t} + \text{MOP}(t) \times ((x_{{\text{ub}},j} - x_{{\text{lb}},j} ) \times \mu + x_{{\text{lb}},j} ),\quad \text{otherwise} \hfill \\ \end{gathered} \right.$$

(6)

2.3.2 Improved AOA

However, in the optimization process for the AOA, its population diversity will decrease, and it is easy to fall into the local optimum. To solve these problems, an improved AOA (IAOA) is proposed in this paper. Firstly, to improve the diversity of the initial population, sine chaotic mapping [53] is used for population initialization. The formula is as follows:

$$x_{k + 1} = \frac{\alpha }{4}\sin (\pi x_{k} ),\,\alpha \in (0,4].$$

(7)

Then, the coefficient MOA in the AOA is a vital parameter to coordinate the exploration and development phases. However, the linear MOA in Eq. (3) will cause the probability of local development of the algorithm in the later stage of the search to be smaller than that of global exploration. This undoubtedly weakens the local development ability of the AOA in the later stages, which could be more conducive to the optimization speed and accuracy of the algorithm. To improve the AOA’s convergence speed and optimization accuracy, a new nonlinear MOA is designed to balance the algorithm's global and local search abilities.

$$\text{MOA}(t) = \text{Min} + (1 - {\text{exp}}( - (t_{\max } - t)/t_{\max } )) \times (\text{Max} - \text{Min})$$

(8)

The new MOA(t) is a nonlinear monotonically decreasing function of t. This enables the algorithm to invest more individuals in global exploration in the early stages of the search. More individuals are invested in local development in the later stages of the algorithmic search. By dynamically adjusting the balance between global search and local search, the precision and stability of the algorithm are improved. Finally, adaptive T distribution [54] mutation ensures the algorithm does not fall into a local optimum in the later iteration stage. The specific mutations are as follows:

$$x_{i}^{t} = x_{i} + x_{i} \times T(t),$$

(9)

where $x_{i}^{t}$ is the position of the optimal solution after mutation, x_i is the position of the optimal solution before mutation, and T(t) is the T distribution with the number of iterations of the algorithm as the parameter freedom.

2.3.3 IAOA-VMD

Entropy can be used to evaluate the complexity and sparsity of time series [55]. The smaller the entropy, the better the complexity and sparsity of the time series. This paper uses the envelope entropy as the objective function to optimize VMD. The IAOA is used to obtain the best parameters.

Step 1 Initialization of the IAOA population size, iteration number, dimensions, and the optimal boundary of k and α. In addition, the minimum envelope entropy is used as the fitness function.

Step 2 The population is initialized by sine chaotic mapping, and the fitness value is calculated.

Step 3 Equation (8) is used to calculate the MOA(t), and Eq. (5) is used to calculate the MOP(t). Generate a random number r₁, and find the current optimal individual.

Step 4 If r₁ < MOA(t), Eq. (4) is used to update the position; otherwise, use Eq. (6) to update the position.

Step 5 Equation (9) is used to carry out adaptive T distribution mutation and retain excellent mutation individuals.

Step 6 Determine whether the algorithm has reached the maximum number of iterations. If the algorithm ends, the best VMD parameters are obtained, or step 2 is returned for re-optimization.

2.4 Sub-series Prediction Models

2.4.1 Long Short-Term Memory Neural Network

LSTM is a temporal recurrent neural network suitable for processing and predicting important events with relatively long intervals and delays in time series [56]. The main difference between LSTM and recurrent neural networks is that LSTM adds a memory cell to judge whether the information is valuable. Three gates are placed in a cell: the forgetting gate (f_t), the input gate (i_t), and the output gate (o_t). The basic structure of LSTM is shown in Fig. 2.

Fig. 2

The basic structure of LSTM

The state of memory cells is controlled by three gates, which can record the history and current system state. The role of the forgetting gate is to control which data in C_t−1 should be forgotten, which can be expressed as follows:

$$f_{t} = \sigma (W_{f} \cdot [h_{t - 1} ,x_{t} ] + b_{f} ),$$

(10)

where h_t−1 represents the cell’s output at the previous moment, x_t represents the input at the current moment, σ is the sigmoid function, and C_t−1 represents the state of the cell at the previous moment. t represents the time step. W is the weight matrix. b is the bias vector parameter of the neural network. [h_t−1, x_t] indicates that the two vectors are connected into a more extended vector.

The role of the input gate is to control which data in $\tilde{C}_{t}$ can be added to the cell state. Specifically, the sigmoid layer determines the information to be updated, while the tanh layer generates a vector added to the state. The formula for the input layer is as follows:

$$i_{t} = \sigma (W_{i} \cdot [h_{t - 1} ,x_{t} ] + b_{i} )$$

(11)

$$\tilde{C}_{t} = \tanh (W_{C} \cdot [h_{t - 1} ,x_{t} ] + b_{C} ).$$

(12)

The update of the cell state requires simultaneous action of the forgetting and input gates. The forgetting gate acts on the previous state C_t−1, and the input gate acts on the current input $\tilde{C}_{t}$. In this way, when a new input a is added to the C_t−1 after the forgotten gate processing, a new C_t is formed, and an update of the cell state is completed, which can be expressed as follows:

$$C_{t} = f_{t} \otimes C_{t - 1} + i_{t} \otimes \tilde{C}_{t},$$

(13)

where $\otimes$ represents the Hadamard product. The role of the output gate is to determine what value to output. Specifically, the state of the cell is processed by the tanh layer, and the result is multiplied by the sigmoid layer. Finally, the required information is outputted, and the formula of the output gate is as follows:

$$O_{t} = \sigma (W_{O} \cdot [h_{t - 1} ,x_{t} ] + b_{O} )$$

(14)

$$h_{t} = O_{t} \otimes \tanh (C_{t} ).$$

(15)

In addition, the output at the top is the prediction for the next step’s state, achieved through a linear layer, which can be expressed as

$$y_{t} = W_{y} h_{t} + b_{y}.$$

(16)

2.4.2 BP Neural Network

The BPNN is a shallow architecture model composed of an input, hidden, and output layer [57]. Its principle is to adjust the weights and thresholds between the network layers in the form of error reverse propagation to minimize the sum of squared errors. The gradient descent method is usually used as the learning strategy of the BP neural network, and it is very suitable for predicting stationary time series. The modeling process can be expressed as follows:

$$Y = b_{1} + \varpi_{1} (f(b_{2} + \varpi_{2} \cdot X)),$$

(17)

where ω₁ and ω₂ are weights, b₂ and b₁ are biases, and f is the activation function.

2.5 Fluctuation-Based Dispersion Entropy

FDE is a method to measure the complexity and irregularity of time series. FDE is an improved algorithm based on discrete entropy theory. In the calculation process, FDE considers the amplitude difference of adjacent data in the embedded vector and replaces the original data with the difference so that the m-dimensional vector group is compressed into the m − 1 dimension. After replacement and reduction, the vector model constructed by the original time series can contain local floating changes. Its calculation speed is faster than sample entropy and avoids the problem that permutation entropy ignores signal amplitude. Therefore, FDE is used to evaluate the complexity of the time series in this paper. The calculation steps of FDE are summarized as follows [43]:

• (1) Define time series as x = {x_j, j = 1, 2, …, N} with length N, and y is mapped to y = {y_j, j = 1, 2, …, N}. According to the normal distribution function, where $y_{j} \in (0,\;1)$ and normal distribution function, y_j is defined as

  $$y_{j} = \frac{1}{{\sigma \sqrt {2\pi } }}\int_{ - \infty }^{{x_{j} }} {e\frac{{ - (t - u)^{2} }}{{2\sigma^{2} }}dt},$$

  (18)

  where µ and σ represent the expectation and standard deviation of the time series, respectively.

• (2) The y is linearly mapped to an integer from 1 to c.

  $$z_{j}^{c} = \text{round}(c \cdot y_{j} + \frac{1}{2}),$$

  (19)

  where $z_{j}^{c}$ shows the jth member of the classified time series, and rounding involves either increasing or decreasing a number to the next digit. c is the classification number.

• (3) Calculate the embedded vector $z_{i}^{m,c}$:

  $$z_{i}^{m,c} = \{ z_{i}^{c} ,z_{i + d}^{c} ,\ldots,\,z_{i + (m - 1)d}^{c} \} ,\;i = 1,\,2,\,\ldots,\,N - (m - 1)d,$$

  (20)

  where m is the embedding dimension, and d is the delay.

• (4) The dispersion entropy pattern is defined as π_{v0, v1,} …_{, vm − 1} (v = 1, 2, …, c). Each $z_{i}^{m,c}$ is mapped to a dispersion pattern π_{v0, v1,} …_{, vm−1} (v = 1, 2, …, c), where $z_{i}^{c} = v_{0} ,\;z_{i + d}^{c} = v_{1} ,\ldots,\,z_{i + (m - 1)d}^{c} = v_{m - 1}.$ The number of possible dispersion patterns assigned to each vector $z_{i}^{m,c}$ is equal to (2c − 1)^m−1, since $z_{i}^{m,c}$ has m elements, and each can be one of the integers from −c + 1 to c + 1.

• (5) For each dispersion pattern π_{v0, v1,} …_{, vm−1}, relative frequency p(π_{v0, v1,} …_{, vm−1}) is defined as follows:

  $$p(\pi_{v0,v1,\ldots,vm - 1} ) = \frac{{N_{b} (\pi_{v0,v1,\ldots,vm - 1} )}}{N - (m - 1)d},$$

  (21)

  where N_b(π_{v0, v1,} …_{, vm−1}) represents the number of $z_{i}^{m,c}$ mapped to π_{v0, v1,} …_{, vm−1}. Actually, p(π_{v0, v1,} …_{, vm−1}) shows the ratio of N_b(π_{v0, v1,} …_{, vm−1}) to $z_{i}^{m,c}$.

• (6) According to the Shannon entropy definition, the FDE of original time series x is defined as

  $${\text{FDE}}(x,m,c,d) = - \sum\limits_{\pi = 1}^{{(2c - 1)^{m - 1} }} {p(\pi_{v0,v1,\ldots,\,vm - 1} ){\text{ln}}(p(\pi_{v0,v1,\ldots,\,vm - 1} ))},$$

  (22)

  where x is a time series, m is the embedding dimension, c is the classification number, and d is the delay. This paper sets m, d, and c as 3, 1, and 6, respectively.

As an example, let us have a signal x = {2, 3.5, 5.2, 4.1, 2.2, 2.1, 2.5, 4.6, 3.9, 7.4}, where we set d = 1, m = 3, c = 2, leading to a 3² = 9 potential dispersion pattern, ({(− 1, − 1), (− 1, 0), (− 1, 1), (0, − 1), (0, 0), (0, 1), (1,− 1), (1, 0), (1, 1)}). Then, x_j(j = 1, 2, …, 10) are linearly mapped into two classes with integer indices from 1 to 2 ({1, 1, 2, 1, 1, 1, 1, 1, 1, 2}). Afterward, a window with length of 3 moves along the time series, and the differences between adjacent elements are calculated as x = {(0, 1), (1, − 1), (− 1, 0), (0, 0), (0, 0), (0, 0), (0, 0), (0, 1)}. Afterward, the number of each dispersion pattern is counted. Finally, using Eq. (22), the FDE value of x is equal to $- \left( {\frac{1}{8}\ln \left( \frac{1}{8} \right) + \frac{4}{8}\ln \left( \frac{4}{8} \right) + \frac{2}{8}\ln \left( \frac{2}{8} \right) + \frac{1}{8}\ln \left( \frac{1}{8} \right)} \right) = 1.2130$.

2.6 Ensemble Reinforcement Learning Method

Reinforcement learning is different from supervised and unsupervised learning. It learns through agents in a trial-and-error way. Compared with the stacking-based and optimization-based ensemble methods, reinforcement learning has a more vital ensemble learning ability. Learning information is obtained by receiving environment rewards for actions, and model parameters are updated [58]. Q-learning (QL) is a value-based learning algorithm in reinforcement learning [59]. QL creates a Q table for the relationship between state and action, and the value of the Q table is the reward for each action taken in each state. The algorithm is used to combine the prediction results of the k-modal components. The QL algorithm obtains the optimal ensemble weights of each modal component to minimize the reconstruction error of the modal component. The specific steps are as follows:

Step 1 Initialize QL’s state S and various parameters, including the reward discount factor γ, learning rate α, greedy parameter ε, and Q table Q(S, a). The state matrix S = [w₁, w₂, …, w_k], and action matrix a = [Δw₁, Δw₂, …, Δw_k]. w represents the weight of each sub-series, and Δw is the weight change.

Step 2 Choose a according to the ε-greedy strategy. Its mathematical expression is as follows:

$$a_{n} = \left\{ \begin{gathered} randomly\;action,probability\;\varepsilon \hfill \\ based\;on\;Q_{\max } ,probability\;1 - \varepsilon \hfill \\ \end{gathered} \right.$$

(23)

Step 3 Establish a loss function L and a reward mechanism R. The role of the reward is to allow the agent to minimize the prediction error, and the mean squared error (MSE) is used as the loss function:

$$L = \frac{1}{N}\sum\limits_{t = 1}^{N} {[\hat{O}(t) - O(t)]^{2} },$$

(24)

where $\hat{O}(t)$ is the predicted passenger flow data, O(t) is the actual passenger flow data, and N is the sample number of the actual value. The agent’s reward is determined by the MSE obtained by the model taking action. The rewards can be expressed as

$$R = \left\{ \begin{gathered} - 1 + L_{n} - L_{n + 1} (L_{n + 1} > L_{n} ) \hfill \\ + 1 + L_{n} - L_{n + 1} (L_{n + 1} < L_{n} ) \hfill \\ \end{gathered} \right.$$

(25)

Step 4 Calculate L and R and update the Q table. The updated mathematical formula is (26):

$$Q_{n + 1} (S_{n} ,a_{n} ) = Q_{n} (S_{n} ,a_{n} ) + \alpha [R(S_{n} ,a_{n} ) + \gamma \max_{a} Q_{n} (S_{n + 1} ,a_{n + 1} ) - Q_{n} (S_{n} ,a_{n} )].$$

(26)

Step 5 Repeat steps 2–4 until the iteration termination condition is met. Finally, the optimal weight of each sub-series is obtained, and the final output of the integrated model is obtained according to Eq. (1). The right half of Fig. 1 shows the reinforcement learning ensemble strategy process. The specific steps of the ensemble prediction method based on the QL algorithm are shown in Algorithm 1.

Algorithm 1. Ensemble strategy method based on QL algorithm

3 Experiments and Discussion

Four different types of URT station passenger flow data are tested and analyzed to certify the predictive ability and versatility of the proposed model. In addition, the ablation experiments are also carried out to certify OVMD-FDE-QL.

3.1 Dataset Description

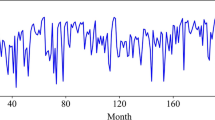
The datasets were collected from the inbound ridership data of four URT stations in Nanning, including Chaoyang Square Station (CYSS), Nanning East Railway Station (NNERS), Nanning Railway Station (NNRS), and Jinhu Square Station (JHSS). CYSS is the hub station with enormous passenger flow. NNRS and JJHSS are transfer stations. NNERS is a high-speed railway station with greater passenger flow. The automatic fare collection (AFC) data from July 26 to August 29, 2021, was used for experiments in the study. Since the operation time of Nanning Metro Line 1 is 6:30–23:00, the ridership data from 6:30–23:30 is filtered and retained. The datasets were aggregated for 15 minutes, and each dataset time series has 2415 continuous data points. Table 1 shows various statistical features of the datasets. Figure 3 shows the original ridership time series required for the experiment. Table 1 and Fig. 3 indicate that the original passenger flow datasets have nonlinear and nonstationary characteristics. Among them, 1449 data points in the first 3 weeks were utilized to train the two benchmark models of BP and LSTM, 483 data points in the fourth week were used to train the QL algorithm, and the remaining data were used to test the prediction capability of OVMD-FDE-QL.

Table 1 The features of the original passenger flow data

Fig. 3

Passenger flow data for four Nanning Metro stations

3.2 Baseline Models

To verify the effectiveness of the proposed model, OVMD-FDE-QL was compared with some traditional and hybrid methods in experiments as follows:

BP: As mentioned above, this is a traditional machine-learning model. The experiment uses BP with a three-layer architecture of an input layer, a hidden layer, and an output layer. The learning rate is set to 0.001, and the hidden layer size is 64.

Temporal convolutional network (TCN): The TCN increases the layer depth by dilated convolution, thus allowing an exponentially large receiving domain. Dilated convolution can correctly handle longer sequences in a non-recursive manner, which is conducive to parallel computing and alleviates the gradient explosion problem. The exponential strategy is used to increase the dilated factor in the experiment.

LSTM: As described above, the model is good at dealing with time series. LSTM contains two hidden layers, one of which has 128 neurons, and the other has 64 neurons. The batch size is set to 16, the time step is set to 5, the optimizer uses Adam, the number of iterations is set to 250, and the learning rate is set to 0.001.

BP-LSTM-QL: This model is established by integrating the BP and LSTM prediction results through QL.

LSTM-TCN-QL: This model is built by integrating the prediction results of the TCN and LSTM through QL.

OVMD-BP: The model decomposes the original passenger flow time series through OVMD and then directly uses BP to predict all sub-series. Instead of integrating all the predicted results through QL, the model uses direct superposition.

OVMD-LSTM: Like OVMD-BP, this model directly uses LSTM to predict all sub-series and also does not use QL to integrate the prediction results of all sub-series.

OVMD-FDE: After OVMD decomposition, this model uses FDE to divide the high-frequency and low-frequency components. LSTM predicts the high-frequency components, and BP predicts the low-frequency components. Finally, the model does not use QL to integrate the prediction results of all sub-series.

EMD-FDE-QL: This model uses EMD to decompose the original passenger flow time series, and the rest is consistent with OVMD-FDE-QL.

EEMD-FDE-QL: This model uses EEMD to decompose the original passenger flow time series, and the rest is consistent with OVMD-FDE-QL.

CEEMDAN-FDE-QL: This model uses CEEMDAN to decompose the original passenger flow time series, and the rest is consistent with OVMD-FDE-QL.

WD-FDE-QL: This model uses WD to decompose the original passenger flow time series, and the rest is consistent with OVMD-FDE-QL.

OVMD-FDE-GBDT: After using OVMD decomposition and FDE to divide the sub-series, this model uses the GBDT ensemble method to obtain the final prediction results.

OVMD-FDE-NSGA-II: This model uses the NSGA-II ensemble method to obtain the final prediction results.

OVMD-FDE-IAOA: The IAOA is used in the ensemble method to obtain the final prediction results.

OVMD-FDE-GWO: The GWO is used in the ensemble method to obtain the final prediction results.

3.3 Experimental Configuration

All the experiments in the study were carried out on a Linux server (CPU: i9-10900X, GPU: RTX 3090). TensorFlow and Keras developed the proposed model. In the process of the IAOA optimizing VMD, the search population is 30 in two-dimensional space, the search range of k is set to be between 1 and 20, and the search range of α is set to be between 1 and 5000. The maximum number of iterations is 20. In the OVMD-FDE-QL model, LSTM contains two hidden layers, one with 128 neurons and the other with 64 neurons. The batch size is 16, the time step is 5, and the prediction step is 3. The optimizer uses Adam, the number of iterations is 250, and the learning rate is 0.001. The reward discount coefficient γ of the QL algorithm is 0.99, the learning rate α is 0.01, the initial greedy parameter ε is 1, the final greedy parameter is 0.1, and the maximum episode is 100. For the passenger flow prediction results, mean absolute error (MAE), mean absolute percentage error (MAPE), root mean square error (RMSE), and standard deviation of the error (SDE) [60] were used to verify the accuracy of the prediction and estimate the prediction ability of the proposed hybrid model. The mathematical expression of these indicators can be written as follows:

$$\text{MAE} = \frac{1}{N}\sum\limits_{t = 1}^{N} {\left| {\hat{y}_{t} - y_{t} } \right|}$$

(27)

$$\text{MAPE} = \frac{1}{N}\sum\limits_{t = 1}^{N} {\left| {\frac{{\hat{y}_{t} - y_{t} }}{{y_{t} }}} \right|}$$

(28)

$$\text{RMSE} = \sqrt {\frac{1}{N}\sum\limits_{t = 1}^{N} {(\hat{y}_{t} - y_{t} )^{2} } }$$

(29)

$$\text{SDE} = \sqrt {\frac{1}{N}\sum\limits_{t = 1}^{N} {\left[ {y_{t} - \hat{y}_{t} - \frac{1}{N}\sum\limits_{t = 1}^{N} {(y_{t} - \hat{y}_{t} )} } \right]^{2} } }$$

(30)

3.4 Hyperparameter Analysis

3.4.1 VMD Parameter Optimization Results

To obtain the best modal component k and penalty factor α of VMD, the IAOA is used to optimize VMD with the minimum envelope entropy of the modal component as the fitness function. In addition, to prove the optimization ability of the IAOA, AOA, GWO, PSO, and BA [61] selected for optimization comparison, their optimization processes are shown in Fig. 4. It can be seen from Fig. 4 that the IAOA has achieved the smallest minimum value compared to other optimization algorithms, and the IAOA has the fastest convergence speed. This proves that the proposed IAOA has excellent performance in optimizing VMD. According to the optimization results of the IAOA, the optimal k and α are [15, 244] in CYSS, [19, 206] in NNERS, [19] in NNRS, and [3, 18] in JHSS.

Fig. 4

Comparison of algorithm results

3.4.2 OVMD Decomposition Results and FDE Calculation Results

After obtaining the best VMD parameters, the OVMD is applied to decompose the passenger flow data. Figure 5 shows the decomposition results of four ridership time series. The sub-series are more stable and regular than the original ridership data, which undoubtedly reduces the prediction pressure of the model.

Fig. 5

Decomposition results of OVMD on four station datasets

OVMD obtains a finite number of IMF components of different complexity by decomposition. The calculation error will increase if a single prediction model is used to predict each sub-component directly. To reduce the calculation error, the complexity of each IMF sub-series is calculated by FDE and divided into high-frequency IMF and low-frequency IMF. Furthermore, the FDE threshold is set to 0.8, the IMF components below 0.8 are the low-frequency series, and the high-frequency series is higher than 0.8 [37]. The FDE calculation results of IMF components in the four datasets are shown in Fig. 6, which reveals that the first component in the four datasets is the low-frequency component, and the rest are the high-frequency components. Therefore, BP is used to predict IMF1, and LSTM is used to predict the remaining IMFs.

Fig. 6

The FDE values of each sub-series after OVMD decomposition of four passenger flow datasets

3.4.3 FDE Threshold Selection

When FDE is used as a criterion for the complexity of each IMF, selecting the FDE threshold is the key to determine the combined forecasting model. If the FDE threshold is too high, BP will predict some high-frequency IMFs. On the contrary, if the FDE threshold is too low, LSTM will predict some low-frequency IMFs. The combined prediction model can obtain higher accuracy by selecting the appropriate FDE threshold. Therefore, different values were selected in [0.1, 0.2, 0.5, 0.8, 1, 2, 3, 4, 4.5] to analyze the sensitivity of the FDE threshold. When the FDE of IMF is less than the threshold, BP is used to predict the components; otherwise, LSTM is used to predict the components. Finally, the QL algorithm is used to integrate the prediction results of each component. The calculation results are shown in Fig. 7.

Fig. 7

The relationship between the FDE threshold and the prediction error

Theoretically, when the threshold for FDE is 0.1, all IMFs use LSTM for prediction. When the threshold for FDE is 4.5, all IMFs use BP for prediction. As the threshold of FDE increases from 0.1, more and more low-frequency components begin to choose BP for prediction, so the prediction error of the reconstructed signal begins to decrease. When the threshold of FDE exceeds a specific value, high-frequency IMFs increasingly begin to choose BP for prediction, and the prediction error will increase. It can be seen from Fig. 7 that as the FDE threshold increases, the error of the reconstructed signal decreases first and then increases, which is in line with expectations. Combining the thresholds of the four cases in Fig. 7, the prediction error is the smallest when the threshold of FDE is 0.8. Therefore, the threshold of FDE is set to 0.8 in this paper. In general, when the threshold of FDE is selected appropriately, all low-frequency IMFs are predicted by BP, and LSTM predicts high-frequency IMFs. The prediction error of the hybrid prediction model for the reconstructed signal is smaller than that of the single model. This reflects the advantages of the hybrid model over the single model and proves that FDE can well reflect the complexity of the time series signal. Using FDE to divide IMF into high-frequency and low-frequency components is reasonable.

3.5 Comparative Experiments

3.5.1 Comparison of Single and Integrated Models Without Decomposition

This section compares the proposed OVMD-FDE-QL model with several single and integrated models’ prediction results. The single models include BP, LSTM, and the temporal convolutional network (TCN). The integrated models include a hybrid model of BP and LSTM integrated by QL and a hybrid model of LSTM and TCN integrated by QL. The results on the four datasets are shown in Table 2, where the best prediction results are bolded in the table, and the suboptimal results are shown next to *.

Table 2 Results of OVMD-FDE-QL and baseline models

The prediction results in Table 2 show that the prediction ability of OVMD-FDE-QL is more evident than that of other prediction models. OVMD data do not preprocess these models but are directly predicted. Single and integrated models cannot predict the nonlinear passenger flow time series well. Therefore, it is wise to process ridership using the decomposition method for URT station passenger flow prediction. In a one-step prediction in CYSS, the MAE of OVMD-FDE-QL is 2.695. Compared with LSTM-TCN-QL, BP-LSTM-QL, LSTM, TCN, and BP, the prediction accuracy of OVMD-FDE-QL is improved by 85.21%, 85.54%, 86.36%, 89.42%, and 89.95%, respectively. In a one-step prediction in NNERS, the MAPE of OVMD-FDE-QL is 0.198. Compared with LSTM-TCN-QL, BP-LSTM-QL, LSTM, TCN, and BP, the prediction accuracy of OVMD-FDE-QL is improved by 82.37%, 82.26%, 85.41%, 82.71%, and 82.89%, respectively. In a one-step prediction in NNRS, the RMSE of OVMD-FDE-QL is 2.673. Compared with LSTM-TCN-QL, BP-LSTM-QL, LSTM, TCN, and BP, the prediction accuracy of OVMD-FDE-QL is improved by 91.25%, 90.94%, 91.62%, 92.64%, and 92.3%, respectively. In a one-step prediction in JHSS, the SDE of OVMD-FDE-QL is 2.985. Compared with LSTM-TCN-QL, BP-LSTM-QL, LSTM, TCN, and BP, the prediction accuracy of OVMD-FDE-QL is improved by 80.15%, 78.99%, 81.09%, 84.24%, and 81.06%, respectively.

As a shallow neural network, the nonlinear prediction ability of BP is weaker than that of TCN and LSTM deep learning models. The TCN utilizes dilated causal convolutions to provide the model with sequential logic without increasing the parameter size, and it achieves associations between any two temporal nodes through stacking. TCN may need to be improved when dealing with particular sequence data, such as data with nonstationary, nonlinear relationships or very long sequences. In these cases, LSTM can better adapt to the characteristics of the data and provide better prediction performance than TCN. For example, in a two-step prediction in NNERS, the MAE of LSTM is 68.92, and TCN and BP correspond to 75.317 and 76.776, respectively. LSTM’s MAE decreased by 8.49% and 10.23%, respectively.

In addition, the results of LSTM-TCN-QL and BP-LSTM-QL are better than those of BP, LSTM, and TCN. This shows that the QL algorithm can integrate the two benchmark models well and obtain better prediction performance than the benchmark models. For example, in a three-step prediction in NNRS, the MAE of LSTM-TCN-QL is 74.513. Compared with LSTM, TCN, and BP, the predictive performance of the LSTM-TCN-QL model improved by 0.74%, 7.33%, and 11.62%, respectively. Although LSTM-TCN-QL and BP-LSTM-QL improve prediction accuracy to a certain extent, they still need to be preprocessed and have a large gap compared to OVMD-FDE-QL, which OVMD decomposes. The hybrid model of data preprocessing technology based on OVMD has better predictive ability than the single models. Data preprocessing techniques can help reduce the impact of noise in the data, thereby significantly improving prediction performance. Figure 8 shows the predicted value, error value, scatter plot, and evaluation index comparison of each model on CYSS.

Fig. 8

Results for each model in CYSS

3.5.2 Comparison with Other OVMD-Based Models

This section combines OVMD with different prediction models to compare the prediction performance with OVMD-FDE-QL. In the experiment, OVMD-BP and OVMD-LSTM models are designed. These two models do not calculate the complexity of IMFs but directly use BP and LSTM for prediction. Moreover, the OVMD-FDE model is constructed, which obtains the final prediction result by superimposing all the results of the sub-series and is shown in Table 3.

Table 3 Results based on OVMD combination models

The results of OVMD-BP are better than those of OVMD-LSTM in the four datasets, while BP predicted worse than LSTM in experiment 3.5.1. This is because OVMD-BP and OVMD-LSTM do not distinguish between high-frequency and low-frequency series by FDE but directly use a model to make predictions. The low-frequency components contain more inherent nature and information about passenger flow. Accurately grasping the inherent nature of short-term passenger flow is the key to improving prediction performance. However, LSTM produces an overfitting phenomenon when predicting stationary low-frequency series, which influences the final prediction results. For example, in a one-step prediction in CYSS, the MAPE of OVMD-BP is 0.124, and OVMD-LSTM corresponds to 0.16. The prediction accuracy of OVMD-BP has improved by 22.5%. OVMD-FDE uses FDE to divide sub-series, maximizing the strengths of each model and improving prediction accuracy. In a two-step prediction in NNERS, the MAPE of OVMD-FDE is 0.268. OVMD-BP and OVMD-LSTM correspond to 0.392 and 0.479, respectively. The predictive performance of the OVMD-FDE model improved by 31.75% and 44.15% through FDE. All of these demonstrate the importance of dividing sub-series.

Moreover, by comparing OVMD-FDE-QL and OVMD-FDE, it can be found that the QL algorithm can effectively integrate BP and LSTM models, further improving the prediction accuracy. In a three-step prediction in NNRS, compared with the OVMD-FDE, the prediction accuracy of the OVMD-FDE-QL has improved by 7.69%. In a three-step prediction in JHSS, compared with the OVMD-FDE, the prediction accuracy of the OVMD-FDE-QL has improved by 21.25%. Figure 9 compares each model's predicted value, error, scatter plot, and evaluation index on NNERS. The experiment in this part shows that analyzing the complexity of sub-series is very important when using data decomposition technology for prediction. In addition, the QL ensemble method can effectively improve prediction accuracy.

Fig. 9

Results of each model in NNERS

3.5.3 Comparison of Integrated Prediction Models Constructed Using Various Decomposition Algorithms

This section compares the proposed model to EMD-based, EEMD-based, CEEMDAN-based, and WD-based models. The experimental results are shown in Table 4. The results of Table 4 show that EMD has a good processing effect on nonlinear and nonstationary signals, but the inherent defects of mode mixing limit its wide application. EEMD solves mode mixing by adding white noise. Based on this, CEEMDAN adds adaptive white noise to each decomposition to improve the integrity of EEMD and reduce the reconstruction error. The basic principles of these three algorithms are the same, but the noise is different. Thus, their prediction performance is different. For example, in a one-step prediction in CYSS, the RMSE values of EMD-FDE-QL, EEMD-FDE-QL, and CEEMDAN-FDE-QL are 12.826, 11.029, and 12.464, respectively. The predictive abilities of CEEMDAN-FDE-QL and EMD-FDE-QL are comparable. The capability of EEMD-FDE-QL is better than that of CEEMDAN-FDE-QL and EMD-FDE-QL. The decomposition stability of WD is better than that of EMD, so the capability of WD-FDE-QL is better than that of all EMD-based hybrid models. For example, in a two-step prediction in NNERS, compared to EEMD-FDE-QL, the prediction accuracy of WD-FDE-QL has improved by 2.81%.

Table 4 Comparison of prediction performance of models based on different decomposition techniques

In contrast, this paper uses OVMD for data preprocessing, which gives the proposed OVMD-FDE-QL model the best prediction accuracy. In a three-step prediction in CYSS, compared with the WD-FDE-QL, the prediction accuracy of the OVMD-FDE-QL has improved by 75.35%. In a three-step prediction in NNERS, compared with the WD-FDE-QL, the prediction accuracy of the OVMD-FDE-QL has improved by 47.78%. In a three-step prediction in NNRS, compared with the WD-FDE-QL, the prediction accuracy of the OVMD-FDE-QL has improved by 63.64%. In a three-step prediction in JHSS, compared with the WD-FDE-QL, the prediction accuracy of the OVMD-FDE-QL has improved by 47.5%. Figure 10 compares the predicted value, error, scatter plot, and evaluation index for each model on the NNRS. It can also be seen from Fig. 10 that the hybrid strategy based on OVMD is consistently ranked higher than the hybrid strategy based on other decomposition algorithms and has a very stable prediction ability.

Fig. 10

Results of different data preprocessing techniques in NNRS

3.5.4 Comparison with Different Ensemble Learning Strategy Models

This section aims to use different ensemble strategies to compare the capabilities of each model. In the experiment, the gradient boosting decision tree (GBDT), the non-dominated sorting genetic algorithm II (NAGA-II) [62], the IAOA, and the GWO algorithm are selected for comparison. The experimental results are shown in Table 5.

Table 5 Comparison of predictive capability of hybrid models with different ensemble strategies

It can be seen from Table 5 that the QL ensemble demonstrates the best capability, followed by the ensemble strategy based on GBDT. GBDT is a stacking-based ensemble strategy. Although the GBDT ensemble strategy is second only to the QL algorithm, it is not easier to understand than the weighted ensemble. NSGA-II is a multi-objective optimization algorithm, while IAOA and GWO are single-objective optimization algorithms. There is no doubt that the capability of a multi-objective optimization algorithm is better than that of a single-objective optimization algorithm. Thus, NSGA-II is superior to IAOA and GWO in performance. Since the optimization performance of GWO is not as good as that of IAOA, the ensemble strategy based on GWO is better than that based on IAOA. Unlike the meta-heuristic optimization algorithm, the QL algorithm has achieved excellent results in weight optimization through reward and punishment mechanisms. In the three-step prediction of the four datasets, compared with the GBDT-based ensemble strategy, the QL-based ensemble improves the prediction results of the model by 42.82%, 19.82%, 2.93%, and 6.21%, respectively. Compared with the multi-objective optimization algorithm, the QL improves the model’s prediction performance by 45.14%, 23.6%, 11.44%, and 13.74%, respectively, and compared with the single-objective optimization algorithm, the QL improves the model’s prediction performance by 72.49%, 25.44%, 13.74%, and 19.03%, respectively. Figure 11 compares the predicted value, error, scatter plot, and evaluation index of each model for experiment 4 on the NNRS. All in all, the ensemble strategy based on QL is very effective.

Fig. 11

Results of each models in JHSS in experiment 4

3.6 Ablation Experiments

To explore the influence of different components on the performance of OVMD-FDE-QL, ablation experiments were carried out in this part, and the experimental results were analyzed. The designed variant models are as follows:

OVMD-BP-QL: This model removes the FDE algorithm, directly uses BP to predict all components after OVMD decomposition, and uses QL to ensemble the prediction results of all components.

OVMD-LSTM-Q: This model also removes the FDE algorithm, directly uses LSTM to predict all components after OVMD decomposition, and uses QL to ensemble the prediction results of all components.

VMD-FDE-Q: This model does not use IAOA to find the best parameters of VMD but directly selects the parameters of VMD through experience, and the remaining components are consistent with OVMD-FDE-QL. In addition, the number of modal components decomposed by VMD is consistent with EMD.

OVMD-FD: This model is the comparative baseline model in the above experiment, which has been described in detail above.

All the parameters of these variant models in the experiment are the same as those of OVMD-FDE-QL. The passenger flow prediction results at the four subway stations are shown in Table 6. By comparing OVMD-FDE-QL, OVMD-BP-QL, and OVMD-LSTM-QL, it can be seen that FDE is an essential part of the hybrid model. Through FDE, the most suitable prediction model for sub-series can be selected to improve the prediction accuracy of the hybrid model. The prediction accuracy of OVMD-BP-QL is better than that of OVMD-LSTM-QL, which is consistent with the conclusion in part 3.5.1. The prediction performance of VMD-FDE-QL is worse than that of OVMD-FDE-QL, which shows that it is not appropriate to select the parameters of VMD only by experience. The randomness of the parameters selected by experience will weaken the final prediction ability of the model. The proposed IAOA-VMD algorithm selects the parameters of VMD well and helps OVMD-FDE-QL obtain the best prediction performance. OVMD-FDE does not select the QL algorithm to ensemble the prediction results of each sub-series, which makes its prediction performance worse than OVMD-FDE-QL. OVMD-FDE-QL effectively ensembles the prediction results of high-frequency and low-frequency components through the QL algorithm, which further improves the prediction results of the model.

Table 6 Comparison of passenger flow prediction performance of different variant models

3.7 Statistical Test

To further evaluate the effectiveness of the OVMD-FDE-QL, the Diebold–Mariano test [48] is utilized in this section to test whether there are significant differences between the OVMD-FDE-QL and the comparison models used in the experiment in Sect. 3.4 under a certain confidence level. The DM values predicted in three steps are shown in Table 7, which indicates that except for the ensemble model based on GBDT and NSGA-II, the DM test values of OVMD-FDE-QL and other comparison models are within the rejection range of 1%. Therefore, OVMD-FDE-QL has significant predictive performance at the 1% significance level compared with the standard single models and other hybrid models. Compared with OVMD-FDE-GBDT and OVMD-FDE-NSGA-II, OVMD-FDE-QL can still expressively enhance prediction accuracy at a 5% or 10% significance level. In conclusion, the established OVMD-FDE-QL model has better prediction accuracy, which other models still need to achieve.

Table 7 Diebold–Mariano test results

3.8 Prediction Performance in Different Time Granularities

The time granularity used in existing studies for STPFP varies in length, and most studies do not consider whether the time granularity used is reasonable. Moreover, for the STPFP at the station level, more emphasis is placed on exemplary management. To ensure prediction accuracy, the appropriate time granularity should be selected as far as possible for STPFP. To compare the prediction performance of the proposed model under different time granularities, the AFC swiping card data were aggregated to 5 minutes and 10 minutes for experiments and compared with the experiment with a 15-minute time granularity. Due to different time granularities, the observed values of the data could be more consistent. Therefore, the correlation coefficient is used as the evaluation index of the model in this section, as shown in Eq. 31:

$$R^{2} = 1 - \frac{{\sum\nolimits_{t = 1}^{N} {(y_{t} - \hat{y}_{t} )^{2} } }}{{\sum\nolimits_{t = 1}^{N} {(y_{t} - \overline{y}_{t} )^{2} } }},$$

(31)

where $\hat{y}_{t}$ is the predicted value, y_t is the true value, $\overline{y}_{t}$ is the average value of all true values, and N is the number of samples. Some models in the comparison model are used to compare with OVMD-FDE-QL. The experimental results are shown in Table 8, in which OVMD-FDE-QL has better prediction performance under three different time granularities in four datasets. In addition, with the increase in time granularity, the R² value of each model is also increasing, indicating that the prediction accuracy is also increasing with the increase in time granularity. From a statistical point of view, although the passenger flow series extracted at a shorter time granularity can describe the refined information of passenger flow, the regularity is poor, and the prediction accuracy is low. Although the passenger flow series extracted at a more significant time granularity will lose the detailed information on passenger flow. It has strong regularity and high prediction accuracy. Therefore, the selection of time granularity is not smaller, better, or larger. It is necessary to balance the details of passenger flow, regularity, and prediction accuracy. A reasonable time granularity is conducive to capturing more detailed passenger flow information and obtaining acceptable prediction accuracy. According to the experimental results in Table 8, the 15-minute time granularity used in this paper is reasonable given the research background.

Table 8 Comparison of prediction precision obtained using different time granularities

4 Conclusions

With the continuous growth of passenger demand, ultra-large-scale passenger flow is becoming more and more normalized. Accurate STPFP can effectively alleviate the operational pressure of the URT. Aiming at the difficulty of STPFP caused by nonlinear and nonstationary passenger flow time series at URT stations, a model called OVMD-FDE-QL based on optimized VMD hybrid ensemble reinforcement learning is proposed. Specifically, the improved IAOA is used for VMD parameter optimization with envelope entropy as the fitness function. The results show that the IAOA has the best convergence speed and optimization ability compared with other optimization algorithms. Then, the original passenger flow sequence is decomposed by OVMD technology, and the complexity of the sub-series is divided by FDE. BP and LSTM are utilized to predict sub-series. The results of OVMD decomposition show that OVMD can decompose complex time series into a series of stable and regular sub-series. In addition, the threshold sensitivity analysis of FDE shows that FDE can not only reflect the complexity of the signal well but also that it is reasonable to divide the high-frequency and low-frequency signals by FDE. Finally, the QL algorithm is used to integrate the prediction results of each sub-series to obtain the final prediction result. The experimental results show that the QL algorithm has better ensemble learning abilities than several classical ensemble methods. The prediction performance and effectiveness of OVMD-FDE-QL are verified by passenger flow time series data and statistical tests at four stations. The main conclusions are as follows:

• 1. The proposed IAOA optimization algorithm has better optimization abilities than others. In addition, the excellent performance of the IAOA can be used not only for VMD parameter optimization in this paper but also for other optimization scenarios. VMD optimized by the IAOA has better decomposition abilities than other decomposition algorithms, so the time series can be better predicted. In addition, OVMD can be used not only for time series decomposition but also for signal denoising.

• 2. Through FDE sub-series partitioning, the model can maximize its ability in the appropriate sub-series. The experimental results not only prove the rationality of FDE as a method to judge the complexity of IMF but also help select subsequent combined prediction models.

• 3. To better integrate the prediction results of the sub-series, a reinforcement learning ensemble strategy is developed in short-term passenger flow prediction. The experimental results show that the reinforcement learning strategy has better ensemble learning ability than other ensemble methods and can effectively improve the overall prediction performance of the proposed model.

• 4. Experiments are conducted on four station ridership datasets. The experimental results show that OVMD-FDE-QL has good prediction accuracy and significant advantages. In addition, the excellent universality of the model for different subway stations indicates that OVMD-FDE-QL can be used not only for short-term passenger flow prediction but also for other time series prediction fields, such as wind speed prediction and PM2.5 prediction.

However, this study also has limitations. The correlation between URT stations is not considered in the study. Future research will attempt to address these limitations.