Methods for determining cycles of a specific length in undirected graphs with edge weights

Abstract

In this paper, we consider the ${{\mathcal{N}\mathcal{P}}}$-hard problem of determining fixed-length cycles in undirected edge-weighted graphs. Two solution methods are proposed, one based on integer programming (IP) and one that uses bespoke local search operators. These methods are executed under a common algorithmic framework that seeks to partition problem instances into a series of smaller sub-problems. Large-scale empirical tests indicate that the local search algorithm is generally preferable to IP, even with short run times. However, it can still produce suboptimal solutions, even with relatively small graphs.

1 Introduction

In this paper, we consider the combinatorial optimisation problem of finding cycles of a specific length in undirected edge-weighted graphs. This problem is relevant in the design of exercise routes and cycling tours (Lewis and Corcoran 2022; Willems et al. 2018). Applications also arise in network visualisation (Tamassia 2016), protein analysis (Salwinski et al. 2004), statistical mechanics (Marinari et al. 2007), and drawing metabolic pathways (Becker and Rojas 2001).

We use the following terminology.

Definition 1

A walk is a series of pairwise incident edges in a graph; a trail is a walk with no repeated edges; a path is a trail with no repeated edges or vertices.

We can also add the prefix $u-v$ to these terms to signify a walk/trail/path that starts at vertex u and terminates at vertex v. The following definitions can also be applied in cases where $u=v$.

Definition 2

A $u-v$-walk/trail/path is considered closed whenever $u=v$. Closed trails are known as circuits; closed paths are known as cycles.

Similarly to the above, the term u-circuit (u-cycle) can be used to denote a circuit (cycle) that starts and ends at a vertex u.

For this paper, two problem variants are considered.

Definition 3

Let $G=(V,E)$ be an undirected edge-weighted graph with n vertices and m edges, let $k\ge 0$ define a desired cycle length, and let w(u, v) denote a nonnegative weight (length) for each edge $\{u,v\}\in E$. The k-length cycle problem (KCP) involves identifying a cycle $C=(u_1,u_2,\ldots ,u_l=u_1)$ whose length $L(C)=\sum _{i=1}^{l-1}w(u_i,u_{i+1})$ minimises the objective function $|k-L(C)|$.

Definition 4

Given the same input as Definition 3 together with a source vertex $s\in V$, the k-length s-cycle problem (KSCP) involves identifying an s-cycle $C=(s=u_1,u_2,\ldots ,u_l=s)$ whose length L(C) minimises $|k-L(C)|$.

Note that a cycle in a graph G is a connected subgraph in which all vertices have a degree of exactly two. As such, any cycles in a graph must occur within a single biconnected component (that is, they cannot contain pairs of vertices separated by an articulation point in G). The problems of determining the shortest and longest cycles and s-cycles in a graph are also included in our problem definitions by setting $k=0$ and $k=\sum _{\forall \{u,v\}\in E}w(u,v)$ respectively.

At present, the problem of finding fixed-length cycles in edge-weighted graphs is largely unstudied in the literature; however, several related complexity results are known. For unweighted graphs¹ the number of walks of length k between pairs of vertices can be calculated by taking the binary adjacency matrix and raising it to the kth power (Kocay and Kreher 2023). Basagni et al. (1997) have also shown that, in unweighted graphs, a $u-v$-walk of length k can be determined in polynomial time providing that $k=n^{{\mathcal {O}}(1)}$. They also show that this problem is ${{\mathcal {N}}}{{\mathcal {P}}}$-hard for edge-weighted graphs.

The task of calculating $u-v$-paths of length k in a graph is also known to be ${{\mathcal {N}}}{{\mathcal {P}}}$-hard for both weighted and unweighted graphs, though certain topologies such as trees and directed acyclic graphs can be solved in polynomial time (Hetland 2011). Finding the longest $u-v$-path in an unweighted graph is also known to be fixed-parameter tractable when parametrized by the length of the path or by the treewidth of the graph (Bodlaender 1993). On the other hand, the problem of calculating the shortest $u-v$-path in an edge-weighted graph can be solved in polynomial time using, among others, the well-known Dijkstra, Bellman–Ford and Floyd–Warshall algorithms (Sedgewick and Wayne 2011).

For circuits and cycles, similar complexity results are known. The task of identifying a circuit in a graph G is equivalent to the problem of identifying an Eulerian subgraph of G; however, identifying the longest Eulerian subgraph is known to be ${{\mathcal {N}}}{{\mathcal {P}}}$-hard, both for weighted and unweighted graphs (Skiena 1990). Similar reasoning can also be used to show that the KCP and KSCP are ${{\mathcal {N}}}{{\mathcal {P}}}$-hard since they generalise the classical ${{\mathcal {N}}}{{\mathcal {P}}}$-hard problem of determining the circumference (length of the longest cycle) of a graph (Garey and Johnson 1979). In more recent work, Fomin et al. (2021) have shown that the problem of deciding whether an unweighted graph G has a cycle of at least $\gamma (G)+k$ edges is fixed parameter tractable. (Here, $\gamma (G)$ denotes the minimum length of a cycle in G, usually known as the girth of G—see also Sect. 2.) The problem of counting the number of $u-v$-paths and s-cycles in a graph is also known to be $\mathcal {\#P}$-complete (Roberts and Kroese 2007).

Several results on the lengths of cycles in unweighted undirected graphs are also known. The well-known theorem of Dirac (1952) tells us that, if $\forall v\in V, \deg (v) \ge \frac{n}{2}$, then G must contain a Hamiltonian cycle (that is, a cycle comprising exactly n vertices and n edges). Stated another way, this tells us that, given a biconnected graph G with minimum degree $\delta (G)$, then either G contains a cycle of at least $2\delta (G)$ edges, or G contains a Hamiltonian cycle. Pósa (1963) has also shown that if $\deg (u)+\deg (v)\ge 2d$ for all pairs of non-adjacent vertices in an undirected biconnected graph G, then either G contains a cycle of at least 2d edges, or G has a Hamiltonian cycle. Note, that the problem of identifying a Hamiltonian cycle in a graph is ${{\mathcal {N}}}{{\mathcal {P}}}$-hard, fixed parameter tractable under treewidths, and W[1]-hard under clique-widths (Fomin et al. 2009).

Variants of these theorems are also available for undirected edge-weighted graphs, many of which are summarised by Fujisawa (2009) who make use of the weighted degrees of vertices: $\deg ^w(u)=\sum _{v\in \Gamma (u)}w(u,v)$, where $\Gamma (u)$ denotes the open neighbourhood of a vertex u. Bondy and Fan (1989), for example, have extended Dirac’s theorem to the following.

Theorem 1

Let G be a biconnected undirected edge-weighted graph and $d\ge 0$. Then, if $\deg ^w(v)\ge d$ for all $v\in V$, then either G contains a cycle of length at least 2d, or all of the longest cycles in G are Hamiltonian.

Bondy et al. (2002) have also provided a variant of Pósa’s theorem for edge-weighted graphs:

Theorem 2

Let G be a biconnected undirected edge-weighted graph and $d\ge 0$. Then, if $\deg ^w(u) + \deg ^w(v)\ge 2d$ for all $\{u,v\}\notin E$, then either G contains a cycle of length at least 2d, or G contains a Hamiltonian cycle.

A further theorem due to Bondy and Fan (1991) provides a lower bound on the length of the longest cycle:

Theorem 3

Let G be an undirected biconnected edge-weighted graph. Then G contains a cycle of length at least:

$$\begin{aligned} \frac{2 \sum _{\{u,v\}\in E}w(u,v)}{n-1}. \end{aligned}$$

(1)

Upper bounds on the length of the longest cycle in an undirected edge-weighted graph G can also be stated, for example,

$$\begin{aligned} UB _1(G)= \sum _{i=1}^n w(e_i), \end{aligned}$$

(2)

where $e_1,\ldots ,e_n$ are the n edges in G with the largest weights. If G is biconnected, we can also calculate a second upper bound,

$$\begin{aligned} UB _2(G) = \left\lfloor \frac{\sum _{v\in V} \tau (v)}{2}\right\rfloor , \end{aligned}$$

(3)

where $\tau (v)$ gives the sum of the weights of the two heaviest edges incident to a vertex v. A summary of these bounds is illustrated in Fig. 1.

Fig. 1

Summary of upper and lower bounds on cycle length in undirected edge-weighted graphs. Point (A) corresponds to Eq. (1)

In the next section, we will survey some relevant algorithms for constructing and enumerating cycles in graphs. In Sect. 3 we then describe several new algorithms for the KCP and KSCP. Section 4 analyses the performance of these algorithms across a variety of different graph types. It also identifies a case in which the KCP and KSCP are solvable in polynomial time. Finally, Sect. 5 concludes the paper.

2 Existing algorithmic strategies

Johnson (1975) has previously proposed a method for generating the set ${\mathbb {C}}$ of all cycles in a directed graph. In this approach, each cycle is determined by an ${\mathcal {O}}(n+m)$ process, leading to an overall run time of ${\mathcal {O}}(|{\mathbb {C}}|(n + m))$. Johnson’s method can also be used to generate the set of all cycles in undirected graphs. This is achieved by replacing each edge $\{u,v\}$ in the undirected graph with the directed arcs (u, v) and (v, u). Following the execution of the algorithm, cycles containing just two arcs must then be removed from ${\mathbb {C}}$. The cardinality of ${\mathbb {C}}$ should then also be halved by removing the “reverse” of each cycle (that is, if the cycle $(u_1,u_2,\ldots ,u_l=u_1)$ is present in ${\mathbb {C}}$, then the reverse cycle $(u_1=u_l,u_{l-1},\ldots ,u_1)$ should be removed from ${\mathbb {C}}$). This method, therefore, provides the basis of an exact algorithm for the KCP and KSCP; however, as Johnson notes, the growth rate of $|{\mathbb {C}}|$ can exceed the exponential $2^n$, leading to infeasible run times for non-trivial cases.² Alon et al. (1995) have also proposed an exact method for determining length-k cycles in directed unweighted graphs, though this also has a high growth rate of ${\mathcal {O}}(2^kn^{2.37}\log n)$.

Algorithm 1

Make-Cycle

An arbitrary cycle in a biconnected graph G can be formed using the simple procedure Make-Cycle given in Algorithm 1. As shown, this operates by removing an edge $\{u,v\}$ and then determining a $v-u$-path P in the resultant graph. The final cycle C is made by concatenating P and $\{u,v\}$. Note that different cycles will be produced by this process depending on the algorithm chosen for constructing P. If breadth-first search (BFS) is used, the $v-u$-path with the minimal number of edges will be returned; if depth-first search (DFS) is used, paths with higher numbers of edges are likely.

Make-Cycle can also be used as the basis of an exact polynomial-time algorithm for determining the shortest cycle in an edge-weighted graph. For s-cycles, this involves executing Make-Cycle with each edge $\{s,v\}$ incident to s as input, and then determining the shortest $v-s$-path in each case. If Dijkstra’s ${\mathcal {O}}(m+n\lg n)$ algorithm is used for the latter, this gives an overall run time of ${\mathcal {O}}(\deg (s)(m+n\lg n))$. To calculate the shortest cycle across the whole graph (sometimes known as the weighted girth of a graph), the same process should be followed using all edges $\{u,v\}\in E$. This gives a run time of ${\mathcal {O}}(m(m+n\lg n))$. Orlin and Sedeno-Noda (2017) have also outlined a more efficient ${\mathcal {O}}(mn)$ method for this problem, while Ducoffe (2021) has proposed a $(2+\epsilon )$-approximation scheme running in ${\mathcal {O}}(n^{5/3}polylog (1/\epsilon )+m)$ time.

An exact algorithm for the KSCP was recently suggested by Willems et al. (2018). This operates by first creating an additional vertex $s'$ whose neighbourhood $\Gamma (s')=\Gamma (s)$. Cycles in G therefore correspond to an $s-s'$-path. To find an $s-s'$-path of the correct length, the well-known algorithm of Yen (1971) is then used. This operates by determining a ranking of the shortest $s-s'$ paths in G; hence Yen’s algorithm must continue to execute until a path is observed that has at least three edges and a length of at least k. A drawback of this approach is that the number of paths to be considered in this ranking can grow exponentially with regard to k. The use of Yen’s algorithm also means that each successive cycle takes up to ${\mathcal {O}}(n(m+n\lg n))$ time to generate. This leads to serious scaling-up issues, particularly with large graphs and high values of k (Lewis and Carroll 2022).

An ${\mathcal {O}}(mn^2)$ heuristic for the KSCP has also previously been suggested by Lewis and Corcoran (2022). This operates by considering vertices $v\in (V-\{s\})$ one at a time and generating pairs of short vertex-disjoint $s-v$-paths. When merged, these $s-v$-path pairs form an s-cycle. This particular algorithm is concerned with finding attractive-looking round trips in road networks; consequently, several accommodations are made that (a) stop solutions from looking too complicated to the user, and (b) allow the round trips to cross articulation points and bridges in the underlying graph more than once when necessary.

Relevant work in this area has also been carried out by Chalupa et al. (2017), who have investigated several integer programming (IP) formulations for finding the longest cycles in unweighted graphs. These formulations are the basis of the IP models for the KCP and KSCP, shown in the next section. Further work on the longest cycle problem is also due to Chalupa et al. (2018), who suggest using a probabilistic variant of BFS for producing long cycles. Simple operators are also used that can lengthen a cycle by up to two edges at a time.

Finally, there are also similarities to note between the KCP and the well-known maximum travelling salesman problem. In the latter, we are interested in finding a maximum-length cycle in an edge-weighted graph. Unlike the KCP, however, these cycles must also be Hamiltonian. Consequently, problem instances considered in the maximum travelling salesman problem usually correspond to complete edge-weighted graphs (Dudycz et al. 2017; Guo et al. 2013).

3 Algorithmic framework

Our approach in this paper will be to try and find high-quality solutions for the KCP and KSCP using a process that operates under a fixed time limit. Since, as noted, cycles cannot span parts of graphs that are separated by an articulation point, we choose to first partition the input graph G into a set of biconnected components. Each of these subgraphs can then be tackled separately, with the best solution among these then being returned as the final solution. Two bespoke methods are considered for tackling each biconnected subgraph: one based on integer programming (IP) and one based on local search using specialised neighbourhood operators. These two methods are considered in Sects. 3.1 and 3.2 respectively.

Algorithm 2

Random-First-Search

As we will see, an important part of our algorithms will be the ability to produce random paths between vertex pairs. For these purposes, Algorithm 2 shows a generalised version of BFS and DFS that we call random-first search (RFS). Like DFS and BFS, this procedure operates in ${\mathcal {O}}(n+m)$ time and calculates a directed tree T that specifies paths from a given root vertex $r\in V$ to all reachable vertices (that is, a spanning tree of the connected component containing r). The main stochastic element of this procedure is achieved in Step 3, where the next vertex to be explored is always chosen randomly from the list L. In contrast, BFS always selects and removes the first item in L (making L a queue), while DFS always selects and removes the last item (making L a stack). Note that while RFS produces a greater variety of spanning trees than BFS and DFS, it does not produce a uniform spanning tree (that is, a spanning tree that can be said to have been drawn randomly from the set of all spanning trees). Uniform spanning trees can be produced using the methods of Aldous (1990) or Wilson (1996), though these are based on performing random walks in the graph and are subject to more unpredictable run times.

Algorithm 3 shows our overall framework for the KCP. An example of this process is also shown in Fig. 2. In Step 1 of this pseudocode, we first determine whether adjustments can be made to the target cycle length k. Specifically, if the given value for k is seen to exceed the upper bound $UB _1(G)$, then k can be reduced to this value. This adjustment allows the algorithm to halt early if a cycle of length $UB _1(G)$ is determined (which would not be the case otherwise).

Algorithm 3

Algorithm Framework for the KCP

Fig. 2

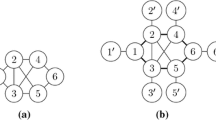
An illustration of Algorithm 3. Part (a) shows an example instance of the KCP using $k=20$ and a graph G with $n=9$ vertices, $m=12$ weighted edges, and $UB _1(G)=36$. Part (b) shows how this instance is partitioned into $l=2$ (non-dyad) biconnected components, $G_1$ and $G_2$. Also shown are the associated $k_i$ values, and the initial cycles $C_i$ (in bold). Part (c) shows the solutions produced by the chosen optimiser, executed at Step 10 of Algorithm 3. In this case, the returned solution $C_{best }=C_2$, with cost of $|k-L(C_2)|=1$

In Step 2, G is broken up into its (non-dyad) biconnected components $G_1,\ldots ,G_l$. This can be achieved using the ${\mathcal {O}}(n+m)$ algorithm of Hopcroft and Tarjan (1973), based on depth-first search. In our case, we also choose to label these subgraphs such that $|V_1|+|E_1| \ge |V_2|+|E_2| \ge \ldots \ge |V_l|+|E_l|$. The rationale for this labelling is that a solution of length k is more likely to be found in larger graphs (which will tend to feature larger solution spaces), hopefully allowing the algorithm to halt sooner.

In Steps 3 to 7 of Algorithm 3, each subgraph $G_i$ is first considered in turn and an associated k-value, $k_i$, is calculated, as with Step 1. Since each subgraph is now a biconnected component, the upper bound from Eq. (3) is also used here. An initial solution is then formed using the Make-Cycle procedure. In our case, this is done by executing Make-Cycle four times, using BFS, DFS, RFS and Dijkstra’s algorithm (respectively) for the determination of the paths P. The cycle $C_i$ is then set to the best among these four options. The variable $C_best$ is also used to store the best cycle observed across the whole run.

The main actions of Algorithm 3 occur in Steps 8 to 12. Note that optimisation only takes place when both conditions on Line 9 are satisfied. The first condition ensures that $C_i$ is not yet optimal with respect to $k_i$; the second prevents optimisation in cases where $L(C_{best })$ is guaranteed not to be improved upon by the cycles of $G_i$.

In cases where optimisation is carried out at Line 10, we choose to set the time limit to:

$$\begin{aligned} t \cdot \frac{|V_i|+|E_i|}{\sum _{j=i}^{l}|V_j|+|E_j|} \end{aligned}$$

(4)

where t is the amount of remaining run time. This means that each subgraph $G_i$ is allocated a run time in (linear) proportion to its size. Other options are also possible, however. Once all graphs $G_i$ have been considered, the algorithm ends by returning the best-observed solution $C_{best }$.

Fig. 3

Size of the ten largest biconnected components for graphs with $n=1000$ vertices and varying densities. The first chart shows results for planar graphs with varying numbers of edges; the second shows the same for various random graphs G(1000, p). All figures are means taken across 100 graphs

Figure 3 illustrates the sizes of the biconnected components that can be expected as a result of the partitioning process. As shown, when a graph is very sparse, many small subgraphs are formed. This will allow our algorithm to consider a series of small sub-problems as opposed to one large one; however, for denser graphs, the partitioning process has little or no effect because the original graph G is likely to already be biconnected.

For the KSCP three small modifications to Algorithm 3 are also required. First, in Step 2, only non-dyad biconnected components containing the source vertex s need to be considered. Second, when generating an initial solution in Step 5, the randomly selected edge must always be incident to s. Third, the optimisation stage at Step 10 requires modification to ensure that s is always present in a solution. The latter modification is considered in the following two subsections.

3.1 Integer programming (IP) formulations

In this section, we specify the IP formulations that can be used for Step 10 of Algorithm 3. We first give a formulation for the KSCP. This is then extended for the KCP. Our IP formulation for the KSCP is adapted from a recent model for finding the longest s-cycles in unweighted graphs (Chalupa et al. 2017). It is also purported to outperform an earlier formulation for the same problem due to Dixon and Goodman (1976). In both cases, runs of the IP solver can also be warm-started using the initial solutions produced by Step 5 of Algorithm 3.

Given $G=(V,E)$, let $V=\{v_1,v_2,\ldots ,v_n\}$, and assume (without loss of generality) that $s=v_1$. For this IP model the adjacencies and weights of G are stored in the matrices ${\textbf{A}}_{n\times n}$ and ${\textbf{W}}_{n\times n}$ such that $A_{ij}=1$ if $\{v_i,v_j\}\in E$ (and $A_{ij}=0$ otherwise); and $W_{ij}=w(v_i,v_j)$ if $\{v_i,v_j\}\in E$ (and $W_{ij}=\infty$ otherwise). An s-cycle is then stored using the binary variables $X_{ij}$, where $X_{ij}=1$ signifies that a transition is made from $v_i$ to $v_j$ in the cycle, and $X_{ij}=0$ otherwise. The objective is to now

$$\begin{aligned} minimize: \;\; |k - \sum _{i=1}^{n} \sum _{j=1}^{n} A_{ij} W_{ij} X_{ij}| \end{aligned}$$

(5)

subject to:

$$\begin{aligned} X_{ij}&\le A_{ij}{} & {} \forall i\in \{1,\ldots ,n\},\; \forall j \in \{1,\ldots ,n\} \end{aligned}$$

(6)

$$\begin{aligned} \sum _{i=1}^nX_{ij} - \sum _{i=1}^nX_{ji}&= 0{} & {} \forall j\in \{1,\ldots ,n\} \end{aligned}$$

(7)

$$\begin{aligned} \sum _{i=1}^nX_{ij} + \sum _{i=1}^nX_{ji}&\le 2{} & {} \forall j\in \{1,\ldots ,n\} \end{aligned}$$

(8)

$$\begin{aligned} \sum _{i=1}^n \sum _{j=1}^n A_{ij}X_{ij}&\ge 3{} & {} \end{aligned}$$

(9)

$$\begin{aligned} 0 \le Y_{ij}&\le (n-1)X_{ij}{} & {} \forall i\in \{2,\ldots ,n\},\; \forall j\in \{1,\ldots ,n\}\nonumber \\ \end{aligned}$$

(10)

$$\begin{aligned} 2\sum _{\begin{array}{c} j=1:\\ j\ne i \end{array}}^{n}Y_{ij} - 2\sum _{\begin{array}{c} j=2:\\ j\ne i \end{array}}^{n}Y_{ji} - \sum _{\begin{array}{c} j=1:\\ j\ne i \end{array}}^{n}X_{ij} - \sum _{\begin{array}{c} j=2:\\ j\ne i \end{array}}^{n}X_{ji}&= 0{} & {} \forall i\in \{2,\ldots ,n\} \end{aligned}$$

(11)

$$\begin{aligned} X_{ij}&\in \{0,1\}{} & {} \forall i\in \{1,\ldots ,n\},\; \forall j\in \{1,\ldots ,n\}\nonumber \\ \end{aligned}$$

(12)

$$\begin{aligned} Y_{ij}&\in {\mathbb {R}}{} & {} \forall i\in \{1,\ldots ,n\},\; \forall j\in \{1,\ldots ,n\}. \end{aligned}$$

(13)

Here, (5) corresponds to the objective function given in Definition 4, while (6) ensures that $X_{ij}=1$ only if $\{v_i,v_j\}\in E$. Constraints (7) and (8) ensure that a vertex is present in the cycle only when it has exactly one edge entering and one edge leaving, else it has no such edges. Constraint (9) also ensures that cycles contain at least three edges. Finally, (10) and (11) make use of the auxiliary variables $Y_{ij}$. These represent flows on the edges and are used to ensure that solutions comprise exactly one s-cycle. (Specifically, a solution with more than one cycle would imply the existence of cycles not containing the source vertex $s=v_1$; however, cycles not containing $v_1$ are disallowed by the above constraints. Further explanations and proofs of this concept are given by Bezalel and Graves (1978) and Chalupa et al. (2017).)

To tackle the KCP, we could choose to execute the above model n times, using each $v_i\in V$ in turn as the source vertex. However, for large graphs this could lead to very long run times. Here, we use an alternative approach that involves taking an edge-weighted graph $G=(V,E)$ with $V=\{v_1,v_2,\ldots ,v_n\}$ as before, but then also adding a dummy vertex $v_0$ together with zero-weighted edges $\{v_0,v_i\}$ for each $i\in \{1,\ldots ,n\}$. Our task is to now find a $v_0$-cycle in this extended graph such that, if the edges $\{v_0,u\}$ and $\{v_0,v\}$ are being used in the cycle, then the edge $\{u,v\}$ also exists. This latter constraint involves introducing the additional binary variables $Z_{ij}$. The full model is now:

$$\begin{aligned} minimize: \;\; |k - \left( \sum _{i=0}^{n} \sum _{j=0}^{n} A_{ij} W_{ij} X_{ij} + \sum _{i=0}^{n} \sum _{j=0}^{n} A_{ij} W_{ij} Z_{ij} \right) | \end{aligned}$$

(14)

subject to:

$$\begin{aligned} X_{ij}&\le A_{ij}{} & {} \forall i\in \{0,\ldots ,n\},\; \forall j\in \{0,\ldots ,n\} \end{aligned}$$

(15)

$$\begin{aligned} \sum _{i=0}^nX_{ij} - \sum _{i=0}^nX_{ji}&= 0{} & {} \forall j\in \{0,\ldots ,n\} \end{aligned}$$

(16)

$$\begin{aligned} \sum _{i=0}^nX_{ij} + \sum _{i=0}^nX_{ji}&\le 2{} & {} \forall j\in \{0,\ldots ,n\} \end{aligned}$$

(17)

$$\begin{aligned} \sum _{i=0}^n \sum _{j=0}^n A_{ij}X_{ij}&\ge 4{} & {} \end{aligned}$$

(18)

$$\begin{aligned} 0 \le Y_{ij}&\le nX_{ij}{} & {} \forall i\in \{1,\ldots ,n\},\; \forall j\in \{0,\ldots ,n\} \end{aligned}$$

(19)

$$\begin{aligned} 2\sum _{\begin{array}{c} j=0:\\ j\ne i \end{array}}^{n}Y_{ij} - 2\sum _{\begin{array}{c} j=1:\\ j\ne i \end{array}}^{n}Y_{ji} - \sum _{\begin{array}{c} j=0:\\ j\ne i \end{array}}^{n}X_{ij} - \sum _{\begin{array}{c} j=1:\\ j\ne i \end{array}}^{n}X_{ji}&= 0{} & {} \forall i\in \{1,\ldots ,n\} \end{aligned}$$

(20)

$$\begin{aligned} Z_{ij}&\le A_{ij}{} & {} \forall i\in \{0,\ldots ,n\},\; \forall j \in \{0,\ldots ,n\} \end{aligned}$$

(21)

$$\begin{aligned} \sum _{i=1}^n \sum _{j=1}^n Z_{ij}&= 1{} & {} \end{aligned}$$

(22)

$$\begin{aligned} X_{0j} + X_{i0} - 2Z_{ij}&\ge 0{} & {} \forall i\in \{1,\ldots ,n\},\; \forall j \in \{1,\ldots ,n\} \end{aligned}$$

(23)

$$\begin{aligned} X_{ij}&\in \{0,1\}{} & {} \forall i\in \{1,\ldots ,n\},\; \forall j\in \{1,\ldots ,n\} \end{aligned}$$

(24)

$$\begin{aligned} Y_{ij}&\in {\mathbb {R}}{} & {} \forall i\in \{1,\ldots ,n\},\; \forall j\in \{1,\ldots ,n\} \end{aligned}$$

(25)

$$\begin{aligned} Z_{ij}&\in \{0,1\}{} & {} \forall i\in \{1,\ldots ,n\},\; \forall j\in \{1,\ldots ,n\}. \end{aligned}$$

(26)

In this case, the additional term in (14) ensures that the cost of a solution corresponds to the objective function given in Definition 3. Constraints (15) to (20) also match (6) to (11) in the previous model, albeit with modified ranges. Finally, (21) to (23) concern the variables $Z_{ij}$. These are used to ensure that the two edges $\{v_0,u\}$ and $\{v_0,v\}$ can be replaced by the edge $\{u,v\}$ in the evaluated cycle. This also means that solutions must contain at least four edges instead of three, as stipulated by (18).

3.2 Local search algorithm

An alternative to using integer programming in Step 10 of Algorithm 3 is to employ a bespoke local search method. Local search is a heuristic framework that seeks to identify high-quality solutions within a space of candidate solutions. It does this by moving among solutions within this space using neighbourhood operators that make alterations to previously observed solutions. Typically, this continues until a solution of sufficient quality is discovered or until some computation limit is exceeded. Our local search algorithm for the KCP is described in the following two subsections. Section 3.2.3 then details the modifications needed for the KSCP.

3.2.1 Neighbourhood operators

The solution space for the KCP is defined by the set of all cycles in the input graph. Neighbourhood operators should therefore be able to take an existing cycle and make alterations that result in new, different cycles. Let $C=(u_1, u_2,\ldots ,u_l=u_1)$ be an arbitrary cycle, written as a sequence of vertices. The edges of C are therefore given by the set $\{\{u_i, u_{i+1}\}: i \in \{1, 2,\ldots ,l-1\}\}$. An intuitive neighbourhood operator is to now select two vertices $u_i,u_j\in C$, remove the current $u_i-u_j$-path in C, and replace it with a new $u_i-u_j$-path. This new path might be generated using path-finding algorithms such as BFS, DFS, RFS, Wilson’s and Dijkstra’s, as discussed earlier.

Our main neighbourhood operator for the KCP extends these ideas by allowing several new solutions to be evaluated following just one application of a path-finding algorithm. The idea is to select a vertex $u_i\in C$ and then try to produce paths from this to all other vertices $v_j\in C$ but without using any of the edges currently in C. The operator proceeds as follows. Given the graph G, the current cycle C and a vertex $u_i\in C$, we first form a new graph $G'$. This is simply a copy of G with all edges of C removed. A further vertex, $u_i'$, is then also added to $G'$, with the neighbours of $u_i'$ being set to those of $u_i$ in $G'$. In the next step, RFS (Algorithm 2) is used to form a tree T in $G'$ that is rooted at $u_i$ and that defines paths to all reachable vertices $u_j\in C\cup \{u_i'\}$. A new candidate solution $C'$ can then be produced with respect to $u_i$ and each $u_j$ in three different ways.

• (i) By setting $C'$ to be a copy of C with its $u_i-u_j$-path replaced by the $u_i-u_j$-path in T;

• (ii) Forming $C'$ by joining the $u_i-u_j$-path in C to the $u_i-u_j$-path in T;

• (iii) If $u_j=u_i'$, by setting $C'$ to be the $u_i-u_i'$-path in T.

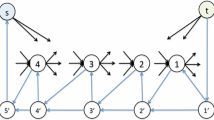
Examples of these three actions are shown in Fig. 4. Note also that the actions of (i) and (ii) may result in solutions containing duplicate vertices. Such solutions will constitute circuits as opposed to cycles and are therefore rejected by the algorithm. An example is shown in Fig. 5a.

Fig. 4

Demonstration of our main neighbourhood operator. Part (a) shows an example graph G, a cycle C and a selected vertex $u_i\in C$. Part (b) shows the graph $G'$ formed from Part (a), together with a tree T rooted at $u_i$. Parts (c), (d) and (e) demonstrate the various ways that new cycles $C'$ can be formed using this information. These correspond to points (i), (ii), and (iii) in the text, respectively

Although the above neighbourhood operator can produce cycles in a variety of ways, observe that the new cycle $C'$ will always share at least one common vertex with its predecessor C. In some cases, this limitation can cause difficulties. Figure 5b gives an example of this, illustrating a current cycle C and the optimal cycle $C^*$. To move from C to $C^*$ using our current neighbourhood operator, C must first be transformed into one of its surrounding cycles. However, the options available in this case are much longer and will therefore feature a much higher cost than C. The cycle C can therefore be seen as representing a prominent local optimum from which it is difficult to escape using our current neighbourhood operator. For these reasons, we therefore also choose to include a second neighbourhood operator that allows the production of new cycles that share no vertices with their predecessor. In our case, this operator simply generates a new cycle using the same process as described in Step 5 of Algorithm 3.

Fig. 5

Part (a) shows how some applications of our main neighbourhood operator can result in an infeasible solution. Here, replacing the $u_i-u_j$-path in C with the only available alternative results in a vertex appearing twice in the solution. This is illegal. Part (b) demonstrates the limitations of the main neighbourhood operator. For illustrative purposes, edge weights correspond to the lengths of the lines in this example

3.2.2 Local search

A full description of how our neighbourhood operators are applied to the KCP is given in Algorithm 4. As shown, we choose to use the great deluge metaheuristic here. This operates by maintaining a boundary value B. During execution, a newly generated solution $C'$ is then accepted if its cost is seen to be less than or equal to B, or less than or equal to the cost of the current solution C. At the start of execution, B is typically set to a high value, allowing many worsening moves to take place. During a run, B is then gradually reduced, thereby discouraging worsening moves from being accepted.

Algorithm 4

Local Search Algorithm for the KCP

As shown in Algorithm 4, our local search method starts by setting B to the cost of the initial solution. During execution, the variable $C_best$ is then used to store the best-observed solution. This is returned by the algorithm once the time limit is exceeded, or when $L(C_best )=k$. Each iteration of the algorithm takes place between Lines 2 and 25. First, a vertex $v_i\in C$ is randomly selected, and $G'$ and T are formed as previously described. In Line 6, the set S is constructed. The use of this set allows the various modifications available from our neighbourhood operators to be considered in a randomised order, as shown in Lines 8 to 22. At the end of each iteration, a new solution will have been generated, or all neighbourhood moves currently under consideration will have been rejected. In either case, at Line 25 an adjustment to B is required. Due to the time-dependent nature of this algorithm, we do this by setting $B=(1-p)\cdot B_{init }$, where p is the proportion of the allocated time limit consumed by the local search algorithm so far. This ensures that B is reduced linearly so that it hits zero at the time limit.

Similarities clearly exist between great deluge and the more well-known simulated annealing metaheuristic. However, in initial experiments with the KCP, we found that simulated annealing was very sensitive to the imposed cooling schedule and value on the initial temperature. This made its behaviour hard to control. Another alternative would have been to use the tabu search metaheuristic. However, tabu search usually operates by, at each iteration, evaluating the set of all solutions that neighbour the current solution. Given the exponential number of different paths that can exist between vertex pairs, for this problem this set is likely to be too large in most cases.

3.2.3 Adjustments for the KSCP

As with previous sections, a small number of adjustments are also required to make the local search algorithm suitable for the KSCP. To do this, Algorithm 4 is modified in the following way.

• Step 6 is adjusted so that v is not added to the set S. This ensures that Steps 8–11 are never executed;

• Steps 12–15 are only executed if $u_j=s$;

• Steps 20–22 are not executed.

These modifications ensure that the source vertex s is always present in any new cycle $C'$.

For the KSCP it is also possible to reduce the size of the considered graph G during execution. To do this, an additional variable ${\bar{C}}$ needs to be maintained that contains the shortest observed cycle whose length exceeds k. Whenever ${\bar{C}}$ is updated, we can then remove all vertices v from G for which the shortest $s-v$-path is greater than $L({\bar{C}})/2$. This is because the length of any s-cycle containing v will have a cost exceeding that of ${\bar{C}}$ and cannot, therefore, improve on $C_{best }$. Such vertices can be identified by using Dijkstra’s algorithm to produce a shortest-path tree rooted at s. Reducing the size of G in this way has the potential to improve algorithm efficiency and lessen memory requirements.

4 Experimental analysis

In this section, we compare the performance of the IP and local search algorithms using the overall framework given by Algorithm 3. Our aim is to gauge the accuracy and scaling-up characteristics of these methods for differing graph sizes, topologies, and values of k. In our trials, all heuristics were implemented in C++ while the IP models were executed using FICO Xpress, version 8. For our heuristics, graphs were stored using adjacency lists. On the other hand, the IP models required adjacency matrices. Both algorithms were executed using a time limit of 300 s per instance. For comparison’s sake, a second time limit of ten seconds was also used with the local search algorithm. All trials were executed on Windows 7 machines with 3.2 GHz quad-core CPUs and 8 GB RAM. Source code and a full listing of these results are available at http://www.rhydlewis.eu/resources/kcycle.zip.

Three graph topologies are considered here.

Planar graphs:

are graphs that can be drawn in two-dimensional space so that no edges cross. In this sense, they are similar in structure to real-world transportation networks because, at the points where streets intersect on a map, there is usually a vertex present that allows the user to switch between them. In our case, planar graphs were formed by randomly placing n vertices into a 10,000 $\times$ 10,000 unit square. A random Delaunay triangulation was then generated on these vertices to give a set of edges. Edge weights were set to the Euclidean distances between their endpoints, rounded to the nearest integer.

d-Regular graphs:

are graphs for which $\deg (v)=d$ for all $v\in V$, where $d\in \{1,2,\ldots ,n-1\}$. In our case, these graphs were generated at random using the Python library NetworkX. Edge weights were then set to values chosen at random from the set $\{1,2,\ldots ,10{,}000\}$. Note that, according to Robinson and Wormald (1994), d-regular graphs almost certainly contain Hamiltonian cycles whenever $d\ge 3$. The KCP and KSCP are also solvable in polynomial time in cases where $d=2$, since such graphs are composed of cycles only.

Rectangular grid graphs:

are graphs in which both the vertices are arranged in an $x\times y$ lattice. The neighbours of a vertex then correspond to the vertices above, below, to the left, and to the right (where present). Such graphs can also be defined as the Cartesian product of the path graph on x vertices and the path graph on y vertices. Rectangular grid graphs therefore have $n=xy$ vertices and $m=(x-1)y+(y-1)x=2xy-x-y$ edges. This particular topology helps to model street maps of cities that follow a grid plan, such as Chicago, Calgary and Adelaide. In our case, all edges in these graphs were allocated a weight of one and can therefore be considered unweighted. As we will see in Sect. 4.3, the KCP and KSCP are both polynomially solvable for such cases.

Fig. 6

Distribution of cycle lengths with our three considered graph topologies. The first chart considers a planar graph on 15 vertices; the second, a 4-regular graph on 20 vertices; the third, a $5\times 5$ grid graph. These results were determined using the NetworkX implementation of Johnson’s algorithm as detailed in Sect. 2. The maximum length cycles seen in these graphs were, respectively, 77,303, 139,943, and 24

Figure 6 illustrates the distribution of cycle lengths for small instances of these three topologies. As shown, each distribution is roughly normal in shape, with a slight negative skew. This suggests that cycles of length k are more common when k is roughly halfway between the upper and lower bounds. Similarly, long cycles are less common in the solution space and, therefore, could be more difficult to identify. The results in the following subsections seem to confirm this.

4.1 Planar graphs

Figure 7 summarises the performance of our algorithms with planar graphs using $n\in \{100,500,1000\}$ and a wide range of values for k. In all cases, we see that there is little difference in the costs returned for the KCP and KSCP, despite the latter being a more restricted problem. We also see that the cost of the returned solutions tends to increase when k is raised. This is because, as we saw in Fig. 6, long cycles tend to be less frequent within the search space, making them more difficult to identify. With the local search algorithm, this is also exacerbated by the fact that movements in the solution space are more difficult to achieve when considering long cycles. This is because, when the incumbent solution C contains many vertices, the proposed new solution $C'$ is more likely to contain duplicates of vertices and therefore be rejected by the operator. Despite these difficulties with the neighbourhood operator, however, it is clear that the local search algorithm, even with the shorter time limit, consistently outperforms the IP method, particularly with larger graphs.

Fig. 7

The top row shows the costs achieved using the IP and local search algorithms with the KCP using planar graphs with $n=100$, 500 and 1000 vertices (respectively) and various values of k. Each point is the mean across 20 graphs. The bottom row shows the same information for the KSCP using randomly selected source vertices

An oft-cited advantage of using IP methods is that, given enough time, they can provide the user with a certificate of optimality. In contrast, our local search algorithm can only return such a certificate if a zero-cost solution (i.e., a solution that is exactly k units in length) is found. Despite this, our trials found that the local search method was still seen to return certificates of optimality more frequently across nearly all values of n and k with these graphs. The exception to this pattern was with the KSCP using $n=100$ and the highest values of k. In these cases, the small graphs allowed the IP method to often produce a certificate of optimality and conclude that no cycles of length k existed in the graph. The effects of this characteristic can be seen in Fig. 7 where, for a small number of high values of k, slightly superior results are returned by the IP method.

4.2 d-regular graphs

Figure 8 summarises the performance of our algorithms with d-regular graphs using $d\in \{3,4,5\}$ and $n=1000$. Similar patterns to the planar graphs are shown here, with the local search algorithm consistently identifying better solutions than the IP method, even when using the shorter ten-second time limit. Indeed, for the larger values of k, we found that the IP solver was often unable to make any improvements on the initial solutions supplied by Algorithm 3. For the highest values of k in these figures, we also see that lower-cost solutions are achieved by the local search algorithm when d is at a higher value. This is because the larger number of edges in these graphs contributes to a wider variety of cycles available in the solution space. Hence solutions with lower costs can usually be identified.

Fig. 8

The top row shows the costs achieved using the IP and local search algorithms with the KCP using 1000-vertex 3- 4- and 5-regular graphs (respectively) over various values of k. Each point is the mean across 20 graphs. The bottom row shows the same information for the KSCP using randomly selected source vertices

4.3 Rectangular grid graphs

Our final set of results concerns unweighted $x\times y$ rectangular grid graphs. It is trivial to show that cycles are present in any rectangular grid graphs for which both $x\ge 2$ and $y\ge 2$. Because of their bipartite nature, cycles in these graphs must also contain an even number of vertices and edges. For the KCP, the solution space of these graphs is known to expand quickly with respect to increases in x and y.³ For example, the number of different cycles in a $3\times 3$ grid is 13, while the number in a $10\times 10$ graph is approximately $2.74\times 10^{19}$.

In Theorem 4 below, we show that the KCP and KSCP are polynomially solvable for unweighted rectangular grid graphs. As a corollary, this also proves that cycles and s-cycles exist for all even values of k between 4 and n. That said, it is still interesting to gauge the performance of our algorithms on these graphs. We should also note that KCP and KSCP remain ${{\mathcal {N}}}{{\mathcal {P}}}$-hard for non-rectangular grid graphs since they generalise the problem of finding Hamiltonian paths in these graphs. The latter problem was proved to be ${{\mathcal {N}}}{{\mathcal {P}}}$-hard by Itai et al. (1982).

Fig. 9

Part (a) illustrates how a Hamiltonian cycle can be formed in an $x\times y=n$-vertex rectangular grid graph in cases where n is even. To do this, we simply follow the outline of the grey “snake” depicted. Part (b) illustrates the shape of the snake in cases where n is odd. In these cases, the maximum cycle length is $n-1$ vertices/edges. Part (c) shows a $10\times 10$ rectangular grid graph with a cycle of length 98; hence two of the 100 vertices are not included in the cycle

Theorem 4

The KCP and KSCP are polynomially solvable with unweighted rectangular grid graphs.

Proof

Let G be a rectangular grid graph with $x\ge 2$ rows, $y\ge 2$ columns and therefore $n=xy$ vertices. Without loss of generality, if x is even and y is odd, rotate the graph by 90 degrees to make x odd and y even. Also, assume that the desired length k is an even number between 4 and n (cycles with k edges do not exist for any other values).

In cases where y is even, a snake-like pattern can be drawn on G in the manner depicted in Fig. 9a. A Hamiltonian cycle can then be found by following the edges on the outline of this “snake”. In cases where y is odd (implying that x and n are also odd), a cycle with $n-1$ edges can be determined by following the outline of the snake shown in Fig. 9b. Given these cycles, in both cases cycles with two fewer edges can be formed by removing the head (or a tail) from the snake and using the resultant outline as before. This action can be repeated until the snake defines a cycle of k edges. Hence the KCP is polynomially solvable.

For the KSCP, the same process is followed except that, if the source vertex s is on the outline of the snake’s head, then only tails should be removed. Similarly, if s is touching a tail, then only the head (or any other tails) should be removed. Hence the KSCP is also polynomially solvable. $\square$

Fig. 10

The top row shows the costs achieved using the IP and local search algorithms with the KCP using $50\times 50$ and $100\times 100$ rectangular grid graphs (respectively) for various values of k. Each point is the mean across 20 runs. The bottom row shows the same information for the KSCP (each point is the mean across 20 runs using randomly selected source vertices)

Figure 10 shows the performance of our algorithms with $50\times 50$ and $100\times 100$ rectangular grid graphs. Here we find the IP to be particularly poor; indeed, in our trials with the $100\times 100$ graphs, it was never able to improve on the initial solutions provided by the warm start. In contrast, the local search algorithm is much more effective, even with the restricted time limit.

Despite the general superiority of the local search algorithm with these graphs, Fig. 10 still indicates that it experiences difficulties when seeking solutions of lengths close to the maximum of n (where, we recall, zero-cost solutions must exist for even values of k between 4 and n.) The reasons for this are illustrated in the example 100-vertex graph shown in Fig. 9c. The solution, in this case, comprises 98 of the maximum 100 edges possible; however, there is no way of applying our neighbourhood operators to this current solution that will lengthen the cycle further. This solution can therefore be seen as representing a conspicuous local optimum from which it is difficult for the algorithm to escape under our current operators.

5 Conclusions and discussion

This paper has proposed two different approaches for tackling the ${{\mathcal {N}}}{{\mathcal {P}}}$-hard k-length cycle and k-length s-cycle problems. Both of these methods operate under a common framework whereby the input graph is first partitioned into biconnected components. We have also shown that the KSCP and KCP are polynomially solvable for unweighted rectangular grid graphs.

Our IP-based approach has been shown to perform well with very small instances; however, under our imposed time limits it struggles on larger instances and higher values of k. In contrast, our local search method has produced superior results in most cases, even under very restricted time limits. The latter also operates using a ${\mathcal {O}}(n+m)$ adjacency list representation of a graph, which is more memory efficient than the ${\mathcal {O}}(n^2)$-sized adjacency matrices required by the IP. Note, however, that the local search method is not exact and can produce sub-optimal solutions even with relatively small graphs, as illustrated in Fig. 9c.

As part of our local search algorithm, we have proposed using the random-first search (RFS) method for determining paths in graphs. This occurs in Step 5 of Algorithm 4. We also tried replacing RFS with the alternative path-finding algorithms listed in Sect. 3. In general, the use of Dijkstra’s algorithm or DFS here produced poor results because these methods are biased towards short and long paths (respectively) and lack sufficient randomisation. BFS and Wilson’s algorithm showed better prospects, though we still found their results to be marginally worse than RFS for high values of k. For BFS, this also seems to be due to the lack of randomisation; on the other hand, Wilson’s algorithm was found to be more costly than RFS, resulting in fewer iterations of the local search algorithm within the imposed time limit.

A direction of future research would be to seek improvements to our proposed methods. This could include using different IP formulations, further (or improved) neighbourhood operators, and/or different metaheuristic frameworks. It would also be interesting to consider extending the KSCP so that more than one vertex is considered compulsory in a cycle. In road networks, this would allow the user to create a route that includes several locations, such as a school, shop, and cafe.

Another avenue of research is to consider the KCP and KSCP when applied to directed graphs. Such problems will require different schemes for graph partitioning. Our current algorithms would also require modified IP formulations and neighbourhood operators in these cases.