Abstract
The recently derived Hybrid-Incidence Susceptible-Transmissible-Removed (HI-STR) prototype is a deterministic compartment model for epidemics and an alternative to the Susceptible-Infected-Removed (SIR) model. The HI-STR predicts that pathogen transmission depends on host population characteristics including population size, population density and social behaviour common within that population.
The HI-STR prototype is applied to the ancestral Severe Acute Respiratory Syndrome Coronavirus 2 (SARS-CoV2) to show that the original estimates of the Coronavirus Disease 2019 (COVID-19) basic reproduction number \(\mathcal{R}_{0}\) for the United Kingdom (UK) could have been projected onto the individual states of the United States of America (USA) prior to being detected in the USA.
The Imperial College London (ICL) group’s estimate of \(\mathcal{R}_{0}\) for the UK is projected onto each USA state. The difference between these projections and the ICL’s estimates for USA states is either not statistically significant on the paired Student t-test or not epidemiologically significant.
The SARS-CoV2 Delta variant’s \(\mathcal{R}_{0}\) is also projected from the UK to the USA to prove that projection can be applied to a Variant of Concern (VOC). Projection provides both a localised baseline for evaluating the implementation of an intervention policy and a mechanism for anticipating the impact of a VOC before local manifestation.
Similar content being viewed by others
1 Introduction
Motivation
The COVID-19 pandemic highlighted the need to anticipate the impact of a novel pathogen on healthcare [1–4] or the economy [5, 6]. One of the impact factors is the basic reproduction number \(\mathcal{R}_{0}\) [7], a demographic concept that has been repurposed for infectious disease epidemiology [8–12]. \(\mathcal{R}_{0}\) represents the average number of susceptible people a host infects in a completely susceptible population whilst that host is in its infected state [13, 14]. Based on estimates of \(\mathcal{R}_{0}\) for COVID-19’s causative agent SARS-CoV2, various categories of predictive [1, 15–18], forecast [19–21] and regression [22–25] models have been constructed to anticipate healthcare system demand.
The COVID-19 pandemic’s infections have been periodic [24–28]. Continuous feedback control loops like prevalence-dependent contact rates [29] and intervention fatigue [30] may contribute. Equally, irregular events like relaxation of previous restrictions, superspreader events and migration [30] result in perturbations in the rate of new infections or the active infections [26]. Cyclical events like seasonal host behaviour, pathogen biology, migration or waning immunity [28, 30] result in periodic infection perturbations [25]. The superposition of these perturbations manifest as pandemic waves [31].
For the COVID-19 pandemic, some subsequent waves of infection have been associated with mutations to the ancestral (wild-type) SARS-CoV2 in some countries [30, 32–36]. Paradoxically, these distinct variant waves may be a consequence of SARS-CoV2’s slow virion mutation rate [35, 37–39]. Even if the virion mutation rate is constant, the time to accumulate the appropriate number of mutations at the appropriate loci of a virion’s genome in a sufficiently gregarious individual and sufficiently connected geographical location to collectively constitute a VOC may vary [35, 37, 38]. Thus the timing and the impact of these events will be treated as random [35], and prediction requires manifestation in at least one region. This paper projects the impact of a random event like a novel VOC from a region in which it has manifested to one in which it has not [32]. We propose that the distinct collection and distribution of clinical manifestations, pathologies and mortality of each of the SARS-CoV2 VOCs [40–42] can be treated as a novel pandemic and that COVID-19 is the collective manifestation of this family of overlapping pandemics [43]. These VOCs’ distinct transmission dynamics [32, 44–47] provide additional justification for this approach.
Implicitly, each VOC contender is a potential new pandemic [30, 39, 48–50]. For the particular case where the contender and incumbent VOC do not form a mixture and, instead, the contender rapidly replaces the incumbent, the reproduction number \(\mathcal{R}(t)\) for the SARS-CoV2 variant family at the time of transition \(t_{0}\) represents the challenger VOC’s \(\mathcal{R}_{0}\). This \(\mathcal{R}_{0}\) represents an upperbound of the challenger VOC’s impact in anticipation of it outcompeting and supplanting the incumbent [51]. It is an upperbound because by definition the \(\mathcal{R}_{0}\) assumes complete susceptibility to the new variant.
The HI-STR[52] model is a deterministic, compartment model prototype constructed to replace two assumptions of Kermack–McKendrick’s SIR prototype [53–55]. It replaces the assumption that the removal rate from a compartment is proportional to the size of that compartment with the more biologically appropriate assumption that the transmissible period is fixed and, consequently, the removal rate is the same as the entrance rate one transmissible period ago [52]. It also replaces Hamer’s mass action law with its chemistry precursor – the law of mass action [56]. The latter allows the derivation of a population density-dependent \(\mathcal{R}_{0}\) [22, 23, 52].
The HI-STR model differs from existing compartment models by predicting that \(\mathcal{R}_{0}\) is not only a pathogen property but also depends on the host population’s characteristics, including population size N, density \(\rho _{n}\) [23] and social behaviour [30, 57–59] common to that population. This paper describes a novel method of foretelling local \(\mathcal{R}_{0}\) in isolated populations with similar social behaviour. The method is designated projection. It proposes that if an estimate of \(\mathcal{R}_{0}\) exists for an isolated population \(y \; ({}^{y}\widehat{\mathcal{R}}_{0} )\), then the projection of \({}^{y}\widehat{\mathcal{R}}_{0}\) onto an isolated population z \(({}^{z}\widetilde{\mathcal{R}}_{0} )\) with similar social behaviour is
where \(\mathfrak{B}\) is specific for that pathogen variant’s transmission dynamics in those populations with similar social behaviour. The symbol ˆ represents an estimate.
Background
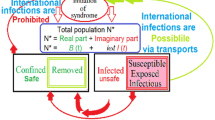
The omnipresent SIR compartment model for the temporal evolution of an infectious disease proposes that the individuals of an homogenous population can be grouped into three compartments: susceptible, infected and removed [53–55]. Susceptible implies capable of contracting a pathogen, infected implies capable of replicating and spreading the pathogen, and removed refers to either recovery (expulsion of the pathogen and immunity) or death. Additional compartments [1, 60] and stratified or heterogenous populations [61–64] result in sophisticated deterministic, compartment models.
An infectious epidemiology modelling taxonomy is proposed (Fig. 1) to distinguish between foretell’s common synonyms [65] in mathematical epidemiology. This taxonomy proposes that deterministic, compartment models are a subcategory of Differential Equation (DE), orthodox, predictive models. Predictive (mechanistic [66]) models presuppose that phenomena can be explained and that these explanations can be simulated. The orthodox predictive models consist of a three- or four-step process of explanation, abstraction into mathematics, the application of a numerical method and in silico simulation of the abstraction. The pioneering categories of orthodox models are stochastic and deterministic.
The deterministic compartment models are DE models. The DEs assume a homogenous population and simulate averaged phenomena. The Ordinary Differential Equation (ODE) models only simulate the rate of change of the compartment sizes. Historically, the Delay Differential Equation (DDE) compartment models [67, 68] are an alternative to the Exposed (E) compartment of the Susceptible-Exposed-Infectious-Removed (SEIR) ODE model [69–71]. Both the traditional delay term and the E compartment incorporate an incubation period into the SIR prototype. The HI-STR is a DDE model that reduces to an ODE for periodic phenomena [52]. The HI-STR’s delay is not due to incubation; it is intended to simulate a constant transmissible period. The transmissible period is another subtle difference from traditional ODE models. Similar to the infectious period, it is the period of time that a host can transmit the disease but can be limited biologically (e.g. the incubation period), behaviourally (e.g. isolation, quarantine [72] or hospitalisation) or technologically (e.g. face mask or pharmacy). An example of pharmacological restriction to a transmissible period is Human Immunodeficiency Virus (HIV) control where anti-retrovirals (ARVs) substantially reduce viral load and therefore transmissibility. Thus transmissibility may be idealised as a step function under appropriate circumstances [73]. Implicitly, transmissibility is a population characteristic, whereas infectivity is an individual characteristic. Partial Differential Equation (PDE) models typically model spatial spread as diffusion [74–76]. Algebraic formulae for thresholds like \(\mathcal{R}_{0}\) and proportion to vaccinate are a consequence of deterministic models.
Stochastic, orthodox models translate to Binomial Chain Models (BCMs) [77–79] or Stochastic Differential Equation (SDE) models that superimpose uncertainty on ODE models [80–82]. They complement deterministic models with their ability to assign probabilities to outlier events [83] like pathogen extinction, provide confidence intervals to their predictions, incorporate noise and their applicability and utility in small samples. The distribution of the uncertainty is an assumption [84]. Note that the forecasting models (to be described) are also statistical. The distinction is that like the deterministic models, the stochastic models simulate a theory to prophesize the future, whereas the forecasting models extrapolate the past into the future.
Graph based epidemiological models can be interpreted as an abstraction of an explanation (or a translation) to a branch of mathematics, graph theory [85, 86], before in silico simulation [87–90]. The latter interpretation provides the flexibility of graph theory or the heritage of an established application like social network theory [91–94]. Here graph- or network-based methods are therefore classified as orthodox predictive methods and ODE alternatives.
The unorthodox predictive methods also presume that phenomena can be explained but the explanation is not translated into mathematics before simulation. Rather, direct in silico simulation of the explanation is performed. Thus some graph-based implementations can be interpreted as unorthodox [18, 95–98]. Graphs consist of vertices and edges, where (for infectious diseases and social networks) the vertices represent individuals, and the edges represent relationships or interactions. Traditionally, the vertices have no geometric interpretation and do not simulate spatial spread [99], but the vertices can be mapped to location [97].
Agent Based Models (ABMs) [6, 17, 100, 101] and Cellular Automata (CA) [102–104] are spatial, unorthodox, predictive models and PDE alternatives. CA are constructed on a regular lattice, and this restriction is removed for ABMs [105]. As examples of Artificial Life [106], an agent (or node) acts independently subject to simple rules on the local environment. The collective can prophesize complex phenomena that other predictive methods cannot [107]. These models simulate heterogeneity and mixing [108], but the PDEs that they represent are not apparent [52, 109]. CA can reduce to ODEs [110], and for at least one application (computational fluid dynamics), the PDEs that they represent have been derived [111]. Lattice Gas Cellular Automata (LGCA) [110] and Probabilistic Cellular Automata (PCA) or Stochastic Cellular Automata (SCA) [103, 104] are subclassifications of CA [52, 109].
The author considers Monte Carlo simulations of COVID-19 to be an unorthodox predictive method [112–115]. Note that here the BCMs have been classified as stochastic orthodox predictive. One may require reclassification [116]. Other less traditional, in the infectious epidemiology context, stochastic models [113] include multivariate stochastic processes [117] and Brownian motion [118].
Forecasting presumes that phenomena have a recognisable and reproducible pattern. Forecasting fits a curve to a historical pattern and extrapolates the pattern into the foreseeable future [66, 119–124]. The Fourier theorem states that any curve can be reproduced by an infinite series of superimposed sinusoidal waves [24, 125–129]. Filtering refers to the attenuation (or omission) of frequencies that do not substantively contribute to the signal [24, 125, 130], resulting in a finite series. In electrical engineering, signal noise is presumed to have high frequency. A low-pass filter (allowing low frequencies to pass) attenuates the noise and smooths the resultant signal [125]. Generally, smoothing is a subset of filtering [125] that attenuates high-frequency signals.
The Box–Jenkins forecasting models [121, 122, 131–133] also fit curves. The prototype is the Autoregressive Moving Average (ARMA) model that forecasts weakly stationary behaviour. The Autoregressive Integrated Moving Average (ARIMA) includes trend by differencing to transform the ARIMA model into a stationary model [121, 131–136]. Seasonality (periodicity) can be incorporated into these time series models [132, 137]. The term autoregression refers to historical data points of a curve being used to estimate the model parameters that predict future values of that same curve [138]. Autocorrelation is a metric of how well past results may foretell future results.
ARIMA models fit a linear combination of a finite number of earlier observations and their differences – parsimonious models [131, 133, 137, 139–142]. See Mills [138, Chaps. 6 and 11] for an introduction to nonlinear functions. The curve fitting distinguishes the traditional time-series models [19, 122, 133, 135, 137, 140–145] from the Artificial Intelligence (AI) time-series models [143, 146–148]. Traditional, statistical estimation methods include the maximum likelihood method, the conditional sum of least squares and the ordinary sum of least squares [131–133, 135, 145, 149, 150]. AI is an expanding topic with an evolving definition [151–156]. For the examples in this paper, AI is defined mechanistically as a collection of methods (techniques) that searches a space for an adequate solution [152, 153, 155]. For COVID-19 forecasting, the AI methods search for a set of parameters that fits a curve adequately [20, 21, 146, 147, 157]. Although the parameters are not necessarily optimal, AI excels at nonlinear models with or without a priori knowledge or understanding of the system’s behaviour [158]. The search techniques used in COVID-19 are biologically inspired, modern AI methods [153, 155, 156]. These include swarming-inspired Particle Swarm Optimisation (PSO)[159], evolution-inspired Genetic Algorithms (GA)[160], neurologically inspired Artificial Neural Network (ANN) [161] and deep learning methods like Long Short-term Memory (LSTM) [161].
Orthodox, predictive models also generate time-series that can be compared to field epidemiology time-series [162, 163]. Machine Learning (ML) [143, 164–166], ANN [167–169] and GA [168, 169] have found orthodox, predictive model parameters that adequately replicate COVID-19 field time-series. Deep learning is a neurologically inspired ML technique [146, 154, 156, 164] that has also been used in orthodox, predictive model parameter estimation [170, 171]. Forecasting provides a framework (e.g. ARIMA) and the orthodox, predictive models provide context (e.g. SIR) that constrain the AI search. AI also finds “black-box” associations [147, 161, 172] – associations found without a priori knowledge of mechanism (transmission dynamics in the infectious epidemiology context) and not providing a posteriori understanding of causation (pathophysiology here). ANN [173–175] and ML techniques like Random-Forest [176–179], decision tree [178, 180, 181], support vector machine [136, 178, 179, 182–184] and LSTM [136, 185, 186] have found such unbiased COVID-19 associations [147, 156]. A time series can also be an association [136, 186–189]. Unorthodox, predictive models like CA and ABMs are swarming-inspired AI [153, 155], which are not search methods. Figure 2 classifies the AI methods discussed in citations of this paper.
State-space models are a subset of signal-plus-noise problems [130] and are introduced as a form of forecasting [132, 138]. Briefly, an observation (space) equation and a state equation are coupled. Each of these equations has a superimposed uncertainty that is assumed Gaussian [190]. The observation (measurement) equation’s independent variable is the signal. In infectious epidemiology, reported new cases, disease mortality [191], waste water serology [192] and combinations thereof are examples of signals. The signal can be a proxy [193, 194] that can be affected by both testing strategy and implementation [36, 47, 191]. For example, South Korea’s strategy of significantly increasing access to testing [195] in COVID-19 may have affected the signal quality. Conceivably, universal testing is more effective [196, 197] but less efficient [198] than opportunistic, symptomatic testing [199–202]. Nevertheless, the effectiveness of these strategies should converge when asymptomatic infection is rare. Conceivably, a well-implemented track-and-trace policy can outperform a poorly promoted/implemented universal testing policy [198, 203, 204].
The unobserved state function is based on a priori knowledge of a system’s behaviour and can be deterministic [205, 206] or empiric [207, 208]. The measured observation/signal is coupled to an unknown state. Backward and forward recursion approximates a state that corresponds to the signal [130]. The Kalman filter is a popular recursion method for implementing state-space models [192, 205–210].
The above models require local, disease-specific data for prophesy. The local estimate requirement causes delay. Cardoso and Gonçalves [22] propose a form for a universal population size- or density-dependent scaling law and use regression [119] to determine the parameters for COVID-19. Their approach potentially circumvents the need to estimate local modelling parameters locally. Rather, parameters from other centres can be projected – adjusted for local conditions. Figure 3 illustrates the one week delay [211] in the stage of spread of the ancestral SARS-CoV2 between the UK and the USA [212, 213]. Given the time dependence of intervention, the universal scaling law may prove more beneficial to regions less connected to the epicentre like India in Fig. 3’s COVID-19 example.
Hu et al. [214] potentially circumvent Cardoso and Gonçalves’ [22] regression’s requirement for multiple pre-existing disease centres by repurposing formulae from the kinetic theory of ideal gases to derive population density-dependent contact rates. Hu et al.’s contact rates are an alternative to the HI-STR model’s law of mass action. The HI-STR prototypes’s contact rate is population-size and density dependent [52].
The orthodox, predictive models generally assume that the rate of change of the infectious compartment is directly proportional to the size of the infectious and susceptible compartments:
where \(S\ast I\) is a state where members of the two compartments are sufficiently close to transmit the pathogen (or react in the chemistry analogue to follow). This assumption is Hamer’s mass action law. As its name suggests, it is modified from chemistry’s (empiric) law of mass action, which states that the reaction rate is proportional to the concentration of the reagents:
where s and i are the concentration in the chemistry analogue and the density (per unit surface area) in the epidemiology analogue. Superficially, if the volumes (or surfaces) remain constant, then these equations are the same. Intuitively, S and I molecules occupying 1 m3 are more likely to interact than the same number of molecules occupying 1000 m3 because of their proximity to each other.
The HI-STR [52] proposes that a probability density function exists for the likelihood that an infected (or transmission-cable) individual in compartment I can be sufficiently physically close to an individual in compartment S to transmit enough pathogen for the individual in S to become infected and a member of I – transmission. It further proposes that this probability density function is proportional to the population densities in the two compartments:
For population \(N \gg 1\), the possible interactions are \(\approxeq \frac{N^{2}}{2}\) [52], and the transmission rate Ṫ is
which resembles the law of mass action – the rate of the reaction is proportional to the concentration of the reactants.
The HI-STR further proposes that there are location-specific behavioural differences that either retard or promote the transmission of the pathogen [59] such that the rate at which individuals enter the transmissible compartment is
where \(\kappa (\mathbf{x})\) is a metric reflecting behavioural difference with respect to the transmission of disease.
Given that experimentally determined \(\kappa (\mathbf{x})\) are unavailable, HI-STR projection can only be applied across populations with the same behaviour. This paper creates the intuitive concept of Sufficiently Similar Social Bahaviour (SSSB) with respect to pathogen transmission. Two populations have SSSB with respect to a disease’s transmission if transposing the behaviour of group A to group B does not result in an appreciable change in the transmission dynamics for that disease in group B. A possible formalism could be let \(\varepsilon (x)\) represent uncertainty in x. Then the uncertainty in the measurement of disease transmission metric ζ for behaviour A is \(\varepsilon (\widehat{\zeta}(A))\). After fitting a prediction curve, let the predicted \(\zeta (A)\) be \(\breve{\zeta}(A)\). The prediction uncertainty is
Let SSSB exist if
The rate at which individuals leave the transmissible compartment is not proportional to the size of the compartment but to the rate at which they leave the susceptible compartment one transmissible period (Δτ̅) ago. Thus
The resultant rate of change in the T compartment (\(\dot{T}_{\mathrm{in}} + \dot{T}_{\mathrm{out}}\)) is a DDE,
The population densities \(s(t)\) and \(i(t)\) emphasize that (2) has been constructed for an homogenous population on a surface. However, (2) is not a PDE and can predict neither spatial spread nor a spatial gradient.
The HI-STR creates another intuitive concept – the Sufficiently Isolated Population (SIP) – to circumvent the problem that (2) is not a PDE. The SIP is related to the flow of information – in this instance, SARS-CoV2 Ribonucleic Acid (RNA) – onto and over a surface [215]. There are two requirements for a SIP to exist. For a completely isolated population, information never flows across the boundary of the SIP’s surface. For a completely connected region, information flows instantaneously across the boundary between regions A and B as soon as it appears in one. Clearly, each of these extremes is an idealisation. Incompletely isolated (or connected) regions are characterised by a delay in the transmission of information. This first SIP criterion can be identified retrospectively and phenomenologically as illustrated in Fig. 3, where the daily per capita cases for six countries follow the same trajectory, but there is s delay. In Fig. 3 the UK is well connected to Germany, and the USA is well connected to Canada. In Fig. 3, it is also evident that India is more isolated from Italy than the UK is isolated from Italy. In the opposite direction, it is not obvious that the UK is more isolated from India than the USA is isolated from India. Restated, isolation may be directional. The sufficiency in SIP depends on objective. For example, India may take longer to convert 10% of ward beds to intensive care unit (ICU) beds than Germany. In this context the time to readiness may define the delay that equates to sufficient isolation. The second SIP criterion avoids a spatial gradient on the surface on which a SIP exists by requiring information to flow instantly over the surface. Effectively, this criterion is recursive – SIPs cannot exist within a SIP – and the probability of transmission is the same for all points on the surface. For HI-STR projection, the delay is of less significance. Potential SIPs are recognised by demonstrable distinct regional pandemic characteristics [23, 216–219] instead.
The much broader topic of \(\mathcal{R}_{0}\) estimation is beyond the scope of this paper [7, 59, 220]. Let it suffice that Böckh’s original concept of \(\mathcal{R}_{0}\) – the average number of girls produced by a female during her reproductive years – was calculated by counting births in the public record [8, 12, 220, 221]. This statistical approach to the estimation of \(\mathcal{R}_{0}\) is distinct from the stochastic models presented above, in part, because they make no a priori assumptions about the mechanism by which pathogens propagate and spread – in the epidemiology analogue. Here the (noun) estimate of a parameter refers to the metrics that quantify that parameter (e.g. \(\mathcal{R}_{0}\)) and the uncertainty in the quantification of that parameter. The verb estimate refers to the experimental or field epidemiology techniques used to generate an estimate. Implicitly, estimating does not prophesize. The latter also distinguishes estimating from stochastic modelling and forecasting. This paper reviews models that prophesize the proliferation of diseased individuals, contextualises the recently derived HI-STR model within a classification of these models, uses \(\mathcal{R}_{0}\) estimates \(\widehat{\mathcal{R}}_{0}\) to validate the HI-STR’s prediction of population size- and density-dependent \(\mathcal{R}_{0}\) and demonstrates the HI-STR’s ability to project \(\mathcal{R}_{0}\) (\(\widetilde{\mathcal{R}}_{0}\)).
Restated, a spectrum of methods exist for estimating \(\mathcal{R}_{0}\). Direct counting makes no a priori assumptions about the mechanism of disease propagation nor does it prophesize disease proliferation [222]. The most obvious and direct counting method would involve frequently, regularly, efficiently and effectively recording the state of every individual in a population with a perfect test of state (infection) [223]. At the other extreme, \(\mathcal{R}_{0}\) estimation assumes a model of disease proliferation and then uses curve-fitting to estimate parameters [215, 224–227]. In principle, the predictive models reviewed in this paper (and summarised in Fig. 1) constitute the a priori assumptions of the curve-fitting extreme. The forecasting models described above can appear as methods at either extreme depending upon whether they make a priori assumptions about the mechanism of propagation. The method of curve-fitting can either be traditional (a collection of statistical methods) or AI as described above.
Between the above estimation extremes are at least two types of indirect counting methods. The first counts the relevant parameter (e.g. \(\mathcal{R}_{0}\)) more efficiently than direct counting by assuming a recognised statistical distribution for a sample of that parameter (\(\mathcal{R}_{0}\)) [223, 228]. It assumes neither a mechanism of propagation nor a form of proliferation. The second indirect method assumes a model of propagation to relate the parameter being estimated to a proxy and then indirectly counts the proxy [211, 216, 219, 223, 226, 228–231]. For example, \(\mathcal{R}(t)\), the number of secondary cases directly generated by a primary case, is mathematically related to the generation interval \(T_{c}\) by assuming a form to the proliferation. \(T_{c}\) is counted indirectly and efficiently by assuming a statistical distribution for the \(T_{c}\) sample [229, 232]. Finally, \(\mathcal{R}\) is inferred from the mathematical relationship between \(T_{c}\) and \(\mathcal{R}\). Several relationships \(T_{c} \sim \mathcal{R}\) exist [9, 225, 233, 234]. Two such relationships are [229]
where r is the rate of exponential growth, a consequence of the Lotka–Euler equation [9, 229]). Other proxies include final epidemic size, equilibrium conditions like age-independent prevalence data and age-specific prevalence data [8].
Superimposed on biases introduced by different estimation methods, differences in the definition of \(\mathcal{R}_{0}\) and their formalisation can exist. The Sharpe and Lotka [235] formalisation of Böckh’s demographic calculation [8, 12, 229] is
In the demographic analogy, \(p(a)\) is the probability of a woman surviving to age a, and \(\beta (a)\) is the rate at a which women of age a give birth to girls. In the epidemic analogue, a is the time from becoming infected and is designated the age of infection [222], \(p(a)\) is the probability that a host remains a host at time a, and \(\beta (a)\) is the rate at which new hosts are generated at time a. The formalism can, in principle, be applied directly early in the epidemic when contact tracing is practical. In this context, (3) is the average number of secondary cases that a host would infect in a completely susceptible population – MacDonald’s epidemiological definition of \(\mathcal{R}_{0}\) [8, 12, 236]. The author has not seen McDonald’s original paper [236], only quotations [8, 12].
For ODE compartment models, several formalisations of \(\mathcal{R}_{0}\) exist. For the SIR model [13, 237],
where \(\xi (t)\) is the contact rate [13] (the average number of adequate contacts that an infective makes per day [237]) or the horizontal transmission incidence [238] (infection rate of susceptible individuals through their contacts with infectives), α is the removal rate [13, 237], and \(1/{\alpha}\) is the duration of infection. This formalism and similar (e.g. the equivalent for the SEIR model) are sufficiently intuitive that the parameters can be estimated and, in turn, be used to calculate \(\widehat{\mathcal{R}}_{0}\) [8, 230, 237, 238].
In an homogenous population, one may anticipate a unimodal (and possibly symmetric) distribution of secondary infections from a sample of hosts. In such a population, a direct application of formalism (3) may calculate \(\widehat{\mathcal{R}}_{0}\). In a heterogenous population, host samples with such unimodal distributions may be anticipated in carefully selected subpopulations, but this assumption may be implausible for the whole population [239]. To apply (3) directly would require both appropriately defined subpopulations and the appropriate formula for averaging over the subpopulations [7, 59]. Diekmann et al. [240] define \(\mathcal{R}_{0}\) as the average number of new cases of an infection caused by one typical infected individual in a population consisting of susceptibles only [241]. A typical host is a distributed individual – a composite of the homogenous subpopulations that form the heterogenous population [240]. This \(\mathcal{R}_{0}\) is formalised as the spectral radius (dominant eigenvalue) of the Next Generation Matrix (NGM) [240]. Neither the definition nor the formalism is intuitive and does not necessarily produce the same value as MacDonald’s definition and corresponding formalisms [8, 240]. However, it identifies the average \(\mathcal{R}_{0}\) as the geometric mean of the subpopulations’ \(\mathcal{R}_{0}\)s [8, 239, 240]; it provides the formula for relating the fitted parameters to \(\widehat{\mathcal{R}}_{0}\) in curve-fitting estimates [163, 227, 241] and retains the threshold (\(\mathcal{R}_{0} =1\)) between self-limitation and endemicity. Although Diekmann et al.’s definition is interpreted as applying to heterogenous populations occupying the same geographic space [242] (like the 8 population gonorrhea model [239]), it can also be interpreted as applying to composite generations – super-generations consisting of sub-generations containing unique hosts in the same spatial region. Examples include the two-gender gonorrhea model [239] and host-vector models [240].
For the HI-STR[52], two timescales are constructed. The transmissible timescale is constructed to reduce the DDE model to a more familiar ODE model. A rhythmic timescale is constructed to obviate the periodicity of the contact rate (e.g. diurnal variation). \(\mathcal{R}_{0}\) is defined as the average number of secondary cases that a host produces in a completely susceptible population while that primary host is in a transmissible state. It differs from MacDonald’s definition because the primary host does not necessarily directly infect secondary hosts. Restated, Benjamin [52]’s definition of \(\mathcal{R}_{0}\) allows (incomplete) tertiary and quarternary generations of hosts to be included in the sum, provided that the infections occur whilst the primary host is still in the transmissible state. This definition was selected to be consistent with the \(\mathcal{R}_{0}\) formalism derived from the HI-STR’s system of ODEs in the transmissible timescale. Like MacDonald’s definition, it is for a homogenous population. Nevertheless, given that the spectral radius of the NGM reduces to ODE compartment models’ formulae for \(\mathcal{R}_{0}\) in homogenous populations, the NGM represents an alternative formalism for the HI-STR’s \(\mathcal{R}_{0}\) in the transmissible times scale. A generation in the transmissible timescale is a compound generation consisting of \(\mathfrak{B}\) generations in the rhythmic timescale. A compound generation is a super-generation consisting of sub-generations having the same characteristics. The \(\mathcal{R}_{0}\) in the rhythmic time scale is the geometric mean of the \(\mathcal{R}_{0}\) in the transmissible timescale [52] – similar to the NGM’s \(\mathcal{R}_{0}\) for composite generations.
This paper neither endeavours to compare \(\mathcal{R}_{0}\) definitions and formalisms nor the most efficient and effective \(\mathcal{R}_{0}\) estimation methods. It accepts that every combination of definition, formalism and method is biased. Of relevance is that the same definition-formalism-method combination is used across regions to validate HI-STR projection for COVID-19.
2 Methods
The HI-STR prototype is based on the SIR model but replaces two assumptions and is formulated for an isolated population on a surface [52]. Thus
-
1.
it is explicit that the model only applies to SIPs,
-
2.
results in a population-density-dependent contact rate, and
-
3.
the PDE problem is replaced by SIPs and SSSB recognition problems.
Hamer’s mass action law [243] assumption is replaced with the law of mass action [52], its chemistry precursor [244, 245]. A probability density function for a single successful transmission is constructed, which reflects the proximity of transmission capable and susceptible:
where η is an infectious disease-specific variable that reflects avidity, μ is a function of mode of transmission, \(\kappa (\mathbf{x})\) is a function of social behaviour, \(s(t)\) is the density of susceptible individuals, and \(\tau (t)\) is the density of hosts capable of transmitting the pathogen [52]. The total transmission (including those of secondary hosts) in a population of size \(N \gg 1\) and population density \(\rho _{n}\) over the period that the primary host is transmission capable (Δτ̅) is shown to be
where \(S(t)\) is the size of the susceptible population, \(T(t)\) is the size of the transmission-capable population, and \(\beta _{A} =\frac{\eta \mu \kappa}{2}\) [52].
The SIR model’s exponential infectious period assumption is replaced with the HI-STR prototype’s more biologically appropriate constant transmission period. This results in the SIR-like DDE system of equations [52]
The delay term reflects that the rate at which individuals leave a compartment is the same as that at which they entered one transmissible period (Δτ̅) ago.
Selecting a timescale (the transmissible timescale) in which a unit of time Δt equates to Δτ̅ (\(1:\Delta t = 1: \Delta \overline{\tau}\)) renders the delay negligible, reducing the above DDE model to an ODE model [52]:
where the τ identifies the timescale being used. The transmissible timescale is a short timescale with less temporal detail – remaining consistent with the spatial scaling analogy’s terminology.
The short-term periodicity of infection opportunity in (4) – e.g. diurnal variation in contact rate in (5) – is obviated by constructing a second timescale (the rhythmic timescale) in which the infection opportunity can be treated as constant. The rhythmic timescale is \(1:\Delta t = 1: \delta t\), where δt is the period of the infection opportunity cycle for Equation (4). For respiratory infectious diseases, δt is the host’s sleep-wake cycle (i.e. 1 day). A unit of time in the rhythmic timescale is necessarily shorter than the equivalent in the transmissible timescale because at least one cycle of infection opportunity must exist within the period that the host is infectious for an infectious disease to spread. The rhythmic timescale is a long timescale with greater temporal detail to remain consistent with the spatial scaling analogy’s terminology.
Let there be \(\mathfrak{B}\in \mathbb{N}\) units of δt in Δτ̅. For temporal continuity between the timescales, the number of new transmission after one compound generation in the transmissible timescale must equal the new transmissions after \(\mathfrak{B}\) generations in the rhythmic timescale. Alternatively, the new infections after \(\mathfrak{B}\delta t\) in the rhythmic timescale are the same as after Δτ̅ in the transmissible timescale [52]. The temporal continuity condition can be formalised as
where ρ identifies the rhythmic timescale. Using a binomial expansion to enforce continuity, the transmissible timescale ODE system (5) reduces to
in the rhythmic timescale [52], where τα is the infection frequency in the transmissible timescale. The HI-STR model’s rhythmic timescale basic reproduction number for SIP z is then [52, 246]
Both \(\beta _{A}\) and τα are dependent on social behaviour, which may be cultural [47, 57, 247]. These are assumed constant for populations with SSSB. There is a subtle difference between Böckh’s \(\mathcal{R}_{0}\) and its rhythmic timescale equivalent \({}_{\rho}\mathcal{R}_{0}\). The former only counts new infections in the second generation, whereas the latter also counts new infections in subsequent generations, provided that they are infected in the primary host’s transmissible period. Nevertheless, these are used interchangeably here [52]. Equation (6) is recognised as the geometric mean of the \(\mathcal{R}_{0}\)s for the \(\mathfrak{B}\) generations in the rhythmic timescale that constitute a compound generation in the transmissible timescale.
Dividing Equation (6) for SIP z by the same for SIP y with SSSB derives
– the origin of Equation (1). It is assumed that the anglophone UK and USA have similar concepts of personal space and familiarity with an associated hierarchy of physical interaction rituals [248] such that Equation (1) applies. A metric for SSSB was not identified. Conceivably, host social behaviour could be sufficiently similar across all SIPs. In this case, Equation (1) is a universal scaling law (independent of social behaviour) and should be compared with Cardoso and Gonçalves’ universal scaling law [22] obtained by regression. The UK and USA were selected to increase the likelihood of a successful validation. From Fig. 3, projection should provide the states most connected to the UK an additional week to prepare based on \(\widetilde{\mathcal{R}}_{0}\). The ancestral SARS-CoV2 pathogen was selected because transmission dynamics data were available; there was no interference from VOCs, and the ICL group used the same \(\mathcal{R}_{0}\) estimation method for the ancestral SARS-CoV2 in both the USA and the UK.
The ICL group’s statistical estimates of \(\mathcal{R}_{0}\) for the wild-type SARS-CoV2 in the UK and the states of the USA are used to validate the HI-STR’s projection from the UK to these USA states. The ICL group estimated the ancestral SARS-CoV2’s \(\widehat{\mathcal{R}}_{0}\) for the UK [211] and the individual states of the USA [219] by counting a proxy – reported mortality. For the UK, estimates counted reported COVID-19 deaths from February 2020 to 4 May 2020 [211]. The USA estimates extend the UK method by counting \(100{,}506\) deaths and \(479{,}422\) cases due to COVID-19 from 11 May 2020 to 1 June 2020 for each state [219]. Their semi-mechanistic Bayesian hierarchical model is sensitive to the generation interval [211], but a gamma distribution with mode 6.5 days was used in their \(\widehat{\mathcal{R}}_{0}\) for both the UK and the USA’s states. Consequently, biases introduced by different field and estimation methods are avoided.
From Equation (1),
The paired Student t-test is used to compare the USA basic reproduction number estimate for state z \(( {}^{z}\widehat{\mathcal{R}}_{0} )\) [219] to the UK’s projection on z \(( {}^{z}\widetilde{\mathcal{R}}_{0} )\).
Fortuitously, the UK and USA subsequently embarked on similar COVID-19 interventions [247]. Thus, having demonstrated that projection can be performed between the UK and the USA’s states, a contender VOC – common to the UK and USA – that rapidly replaced an incumbent was selected to demonstrate that projection could be applied to a VOC. For this implementation of projection, rapid replacement (minimal mixing) is required to ensure that the SARS-CoV2 family’s reproduction number \(\widehat{\mathcal{R}}(t)\) estimated when the VOC contender emerges at \(t = t_{0}\) represents that VOC’s \(\widehat{\mathcal{R}}_{0}\). The Delta (B.1.617.2) variant was selected because it replaced the incumbent Alpha (B.1.1.7) variant in both the UK [32, 249] and the USA [35, 47, 250] within a month as described in Appendix D.
Vaccination protects against symptomatic SARS-CoV2 Delta infection [251] but is not as effective against Delta infection [252–255] depending on the time from vaccination [256, 257]. This finding supports the argument that \(\mathcal{R}(t_{0})\) is equivalent to \(\mathcal{R}_{0}\) for the SARS-CoV2 Delta variant when it emerged.
A private organisation’s variant sequencing data [250] was used to establish \(t_{0}\) – the date of the transition to Delta – for each state of the USA. They were selected because they provided state level variant sequencing data for the USA. Variant prevalence data can be found at https://public.tableau.com/ [258]. The threshold prevalence for \(t_{0}\) was arbitrarily set as the Delta variant representing 20% of the sequenced SARS-CoV2 genomes. 20% was considered small enough to satisfy the condition that the population is completely susceptible to the Delta variant. Conversely, given that most time series treat COVID-19 as one disease with one time series for all SARS-CoV2 variants, 20% was considered large enough for a substantial portion of a combined \(\widehat{\mathcal{R}}(t)\) to be due to the Delta variant. It is recognised that these criteria introduce bias.
Counting a proxy estimates \(\mathcal{R}_{0}\) for the Delta variant. These estimates validated the HI-STR’s VOC \(\widehat{\mathcal{R}}_{0}\) projection from the UK to the USA. Yap and Yong [216] smooth reported case time series with a moving average. A Poisson distribution then constructs a symptom onset time series based on the reported case time series. A second Poisson distribution constructs a date infected time series (\(k_{t}\)). A third Poisson distribution is fitted to the date infected time series to estimate \(\lambda _{t}\) – the expected infections for the day. For the previous day’s estimated new infections (\(k_{t-1}\)), the formula relating \(\mathcal{R} \sim \lambda _{t}, k_{t-1}\) is
where \(\alpha ^{-1}\) is the infectious period. The https://cv19.one [216, 259] data repository was selected to provide \(\widehat{\mathcal{R}}_{0}(\Delta )\) – the Delta variant’s \(\widehat{\mathcal{R}}_{0}\). This selection ensures that the same method can be used to estimate the UK’s \(\widehat{\mathcal{R}}(t,\Delta )\) and state level USA \(\widehat{\mathcal{R}}(t,\Delta ) \) [216, 259]; \(\widehat{\mathcal{R}}(t_{0},\Delta ) \approx \widehat{\mathcal{R}}_{0}( \Delta )\).
Independent \({}^{UK}\widehat{\mathcal{R}}_{0}(\Delta ) = 1.44-1.5\) [249, 260] with 95% CI [1.2-1.75] [260] is provided for comparison. The statistical analysis was conducted in the open-source R Project for statistical computing (https://www.r-project.org).
The \(\mathfrak{B}\) for the ancestral SARS-CoV2 and the Delta variant are estimated in Appendices A and D, respectively. The transmissible periods are estimated as the median of other estimates with neither weighting nor confidence intervals.
3 Results
This parameter estimations performed for both the wild-type SARS-CoV2 and for the SARS-CoV2 Delta variant assume no inherent immunity to COVID-19. In immunology, innate immunity refers to a static, generic immune system that non-specifically targets any pathogen invasion. The adaptive immune system generates variations that specifically target a particular invasive pathogen. Natural immunity to a pathogen is due to either previous exposure to that pathogen or cross-reactivity from exposure to another pathogen – heterologous immunity [261]. To avoid confusion with these terms, inherent immunity refers to a genetic (inborn) resistance to or attenuation of certain diseases. Examples of inherent immunity are mutations to the CCR5 receptor on cells that renders some individuals immune to infection by HIV [262], the haemoglobinopathy-malaria hypothesis that proposes that the high haemoglobinopathy carrier prevalence in some population may exist because this carrier state protects against malaria [263] and cystic fibrosis that may offer carriers protection against cholera [264]. Immunity can be natural, inherent or due to vaccination. Vaccination can be heterologous immunity.
3.1 The ancestral SARS-CoV2
The transmission dynamics, distribution of pathology, case fatality rate and other clinical, pathological and epidemiological characteristics associated with the ancestral (wild-type) SARS-CoV2 variant are collectively designated COVID-19(wt). Appendix A demonstrates that the transmissible timescale for COVID-19(wt) is \(1:9\) days, and the rhythmic timescale is \(1:1\) day. The scaling factor between these timescales (\(\mathfrak{B}(wt)\)) is 9.
The \({}^{UK}\widehat{\mathcal{R}}_{0}(wt) = 3.8 \) [3.0–4.5] [211], the \({}^{UK}\widehat{N} = 67{,}886{,}011\) and the \({}^{UK}\hat{\rho}_{n} = 280.6~\mathrm{km^{-2}}\) in 2020 [265]. Equation (7) projects this \({}^{UK}\widehat{\mathcal{R}}_{0}(wt)\) onto the states of the USA. Appendix B removes any outliers among these projections – reducing the sample size to 40 states.
Figure 4 compares the estimated basic reproduction number \(\widehat{\mathcal{R}}_{0}(wt)\) density distribution [219] of the remaining 40 states to those projected from the UK’s wild type SARS-CoV2 estimate \({}^{UK}\widehat{\mathcal{R}}_{0}(wt)\) [211]. Figure 4(a) projects the median UK estimate \(({}^{UK}\widehat{\mathcal{R}}_{0}(wt) = 3.8 )\) for the wild-type SARS-CoV2, whereas Fig. 4(b) projects \({}^{UK}\widehat{\mathcal{R}}_{0}(wt) = 4.2\). The latter remains within the uncertainty of the UK’s \(\widehat{\mathcal{R}}_{0}(wt)\) estimate [211].
(a) Density distribution comparison between estimated wild-type SARS-CoV2 \(\mathcal{R}_{0}\) and the median estimated wild-type SARS-CoV2 \(\mathcal{R}_{0}\) for the UK projected on to the USA’s states. (b) Box-and-whisker plot comparison between estimated wild-type SARS-CoV2 \(\mathcal{R}_{0}\) and a wild-type SARS-CoV2 \(\widehat{\mathcal{R}}_{0} = 4.2\) for the UK projected on to the USA’s states
Table 1 summarises the results of the paired Student t-test comparing the \(\widehat{\mathcal{R}}_{0}(wt)\)s [219] of the 40 USA states \(({}^{z}\widehat{\mathcal{R}}_{0}(wt):1\leq z\leq 40, z \in \mathbb{N} )\) to the UK’s projections \((\widetilde{\mathcal{R}}_{0}(wt) )\) for \(3.0 \leq {}^{UK}\widehat{\mathcal{R}}_{0}(wt) \leq 4.5 \) [211] onto those 40 states. For \(4.2 \leq {}^{UK}\widehat{\mathcal{R}}_{0}(wt) \leq 4.5\), a statistically significant difference between the \({}^{z}\widehat{\mathcal{R}}_{0}(wt)\) and \({}^{z}\widetilde{\mathcal{R}}_{0}(wt)\) samples does not exist for those 40 states. For \(3.0 \leq {}^{UK}\widehat{\mathcal{R}}_{0}(wt) \leq 4.1\), although there is a statistically significant difference between the \(\widehat{\mathcal{R}}_{0}(wt)\) and \(\widetilde{\mathcal{R}}_{0}(wt)\) samples, this difference is not epidemiologically significant when compared to the uncertainty in \({}^{z}\widehat{\mathcal{R}}_{0}(wt) \) [219]. An epidemiologically significant change is one greater than the uncertainty in the estimate.
The parameter estimates for \(\mathfrak{B}(wt)\) have considerable variation (Tables 2 and 3). Appendix C is a sensitivity analysis demonstrating that, up to an inherently immune fraction of 50%, the change in the \({}^{z}\mathcal{R}_{0}(wt)\) projections are not epidemiologically significant – Fig. 5(b). Similarly, changing the symptomatic fraction causes no significant change in \(\mathcal{R}_{0}(wt)\) relative to the uncertainty in the estimate – Fig. 5(a). The infectious and transmissible periods are varied in Figs. 5(c) and (d), respectively.
Despite symptomatic fraction and inherent immune fraction not having significant effects on \(\widetilde{\mathcal{R}}_{0}(wt)\) relative to the uncertainty in the ICL’s \(\widehat{\mathcal{R}}_{0}(wt)\) for the UK and the states of the USA, the HI-STR predicts that increasing the symptomatic fraction decreases \(\mathfrak{B}(wt)\) and, consequently, \(\mathcal{R}_{0}(wt)\) by increasing the contribution of those with a shorter transmissible period (Fig. 5(a)). It confirms that increasing the inherently immune fraction reduces \(\mathcal{R}_{0}(wt)\) (Fig. 5(b)). As expected, increasing the infectious or transmissible periods increase \(\mathfrak{B}(wt)\) and therefore \(\mathcal{R}_{0}(wt)\) (Figs. 5(c) and (d)).
3.2 The SARS-CoV2 Delta variant
Appendix D calculates that \(\mathfrak{B}(\Delta )=6\) when 40% of the UK and USA populations were fully vaccinated against COVID-19.
The ‘COVID-19 HeatMap’ dashboard [216, 259] was used to lookup \(\widehat{\mathcal{R}}_{0}(\Delta )\). This database relates reported cases to infection dates via Poisson distributions. The infection date time series is related to \(\mathcal{R}(t,\Delta )\). This database was selected because it provides both state and country level \(\widehat{\mathcal{R}}(t,\Delta )\) using the same method – avoiding method biases in \(\mathcal{R}(t,\Delta )\) estimation.
The Delta variant transition date for a SIP was arbitrarily set as the date when the Delta variant represents 20% of the SARS-CoV2 Reverse Transcriptase Polymerase Chain Reaction (RT-PCR) sequences for that SIP on that date. From Fig. 10(a) in Sect. D, the UK’s transition date (\(t_{0}\)) is May 15, 2021 [249, 260]. On May 15, 2021, the ‘COVID-19 HeatMap’ dashboard [216, 259] finds that UK’s \(\widehat{\mathcal{R}}(t_{0}) = 1.5 \approx {}^{UK} \widehat{\mathcal{R}}_{0}(\Delta )\). The ‘our world in data’ dashboard [212] and the ‘COVID-19 HeatMap’ dashboard [216, 259] estimates in May 2021 are within the \({}^{UK}\widehat{\mathcal{R}}_{0}(\Delta )\)’s 95% confidence interval [249, 260]. The population size and density estimates for the UK and the USA states used for the ancestral SARS-CoV2 were reused for the SARS-CoV2 Delta variant’s projection.
The date of the transition to the Delta variant could be established for 11 states of the USA. This small sample is because the private organisation’s [250] variant sequencing is opportunistic (not from a screening program) and several states had no data for periods that included the transition prevalence of 20%. \({}^{UK}\widehat{\mathcal{R}}_{0}(\Delta )\) was projected onto these states using (7) with \({}^{UK}\widehat{\mathcal{R}}_{0}(\Delta )\) as the independent variable. These projections are compared to the ‘COVID-19 HeatMap’ estimates [216, 259] in Fig. 6.
4 Discussion
COVID-19 is the collective pathological manifestation of the ancestral SARS-CoV2 and its variants. New variants have the potential to supplant pre-existing variants. Projection provides an efficient method to prophesize location- and variant-specific resource requirements. The HI-STR has demonstrated that projection can foretell the impact of a pathogen variant (the ancestral SARS-CoV2) on the individual states of the USA, provided that an estimate exists for the UK. This was possible because the HI-STR accounts for the effect of population characteristics on the basic reproduction number \(\mathcal{R}_{0}\). These regions were selected because it is assumed that the individual states of the USA can be approximated as SIPs and because it is assumed that these anglophone regions possess SSSB.
It is noted that the HI-STR prototype does not include the effect of demography [266] on \(\mathcal{R}_{0}\) estimation and projection but age-stratified SIR models can be adapted for the HI-STR. Genetically or behaviourally predisposed individuals also represent subpopulations that affect the average transmission period. For COVID-19, diabetics are a subpopulation that are at increased risk of severe disease and death [267, 268]. The opportunity exists to extend the HI-STR to heterogenous populations. Clearly, neither the UK nor the individual states of the USA are homogenous, but an accepted collection of public social behaviourial norms must exist in each instance.
Hawaii, Montana, Alaska and Wyoming are among the outliers. The HI-STR model’s \(\widetilde{\mathcal{R}}_{0}\) is an overestimate for these states. For Hawaii, the sea acts as a natural barrier between SIPs. Because the HI-STR is nonlinear, these regions cannot be combined. Combining SIPs results in \(\widetilde{\mathcal{R}}_{0}\) overestimates. Communities within Alaska, Montana and Wyoming may be sufficiently isolated for them to be treated as SIPs. Conversely, states like New York and Washington, DC, may be insufficiently isolated. Neither the method for averaging \(\widehat{\mathcal{R}}_{0}\) across SIPs nor the determination of \(\widehat{\mathcal{R}}_{0}\) across SIPs is obvious.
The transition to the SARS-CoV2 Delta variant could only be identified for 11 States of the USA. The significance of the comparison between the estimated and projected basic reproduction numbers for the 11 states of the USA could not be determined. Nevertheless, it has been demonstrated that for the minimal-mixing VOC projection, the SARS-CoV2 Delta variant’s \(\widehat{\mathcal{R}}_{0}\) for the UK could have been projected onto at least 11 states in the USA.
This paper’s motivation is the anticipation and preparation for the local impact of novel pathogen or new VOC. Implicitly, each variant is being treated as a new pathogen to which the local population is completely susceptible. The SARS-CoV2 variants are sufficiently closely related that both vaccination and previous infection by the incumbent may confer immunity to the new variant in some individuals. Thus the projection represents an upperbound in which the challenger VOC replaces the incumbent [51]. This model does not address equilibrium states where VOCs form a mixture [39]. Intuitively and theoretically, the inherently and naturally immune individuals should affect the transmission dynamics of the variant and the transmissible period. Given the uncertainty in the wild-type SARS-CoV2 \(\widehat{\mathcal{R}}_{0}\), an epidemiologically significant impact could not be demonstrated here.
Intuitively, asymptomatic carriers increase the reproduction number [269]. Uniquely, the HI-STR predicts this phenomenon (see Appendix C and Fig. 5(a)) but, given the uncertainty in the ancestral SARS-CoV2’s \(\mathcal{R}_{0}\) estimates, epidemiological significance could not be demonstrated. For diseases where a correlation exists between symptoms and mortality, an intervention that only converts symptomatic individuals into asymptomatic individuals may reduce mortality. Ironically, the theory predicts that such an intervention will increase \(\mathcal{R}_{0}\) [270]. Conversely, the HI-STR model explains why the SARS-CoV2 Delta’s higher symptomatic ratio [270] is associated with lower reproductive numbers.
5 Conclusion
When confronting a novel pathogen, the impact of the disease has to be foretold to prepare accordingly. Some of these impacts are the basic reproduction numbers (a proxy for how fast the disease will spread), mortality and morbidity. Some of the impacts that are beyond the scope of this document are the economic and socio-political instabilities caused by the disease and interventions, as well as pathogen evolution.
The HI-STR prototype is a deterministic alternative to the SIR prototype. In principle, it has two advantages over the more mature deterministic compartment models – it incorporates the population size and density in the model, and it acknowledges and includes the impact of social behaviour. The latter is controversial, but it should be noted that the HI-STR has the flexibility to include social behaviour. It may be that physical interaction across regions and cultures is sufficiently similar (from an infectious disease perspective), so that this variable can be treated as a constant. In the latter case, the HI-STR derives a population size- and density-dependent universal scaling law for \(\mathcal{R}_{0}\).
Projection allows region-specific planning and pre-emptive resource allocation. This region-specific \(\mathcal{R}_{0}\) provides a baseline to compare interventions. This paper demonstrates that the HI-STR model can project the UK’s ancestral SARS-CoV2’s \(\widehat{\mathcal{R}}_{0}\) and the SARS-CoV2 Delta variant’s \(\widehat{\mathcal{R}}_{0}\) onto the states of the USA. Applicability in other anglophone and non-anglophone regions remains to be demonstrated.
The long-term success of an intervention depends both on the policy [271, 272] and implementation [273, 274]. Policies and strategies can only be evaluated retrospectively [275–278] because of unforeseen long-term risks [279–283], low-probability high-impact events [284–287] and unintended consequences [288–294]. Nevertheless, projection provides timeous local baselines for the comparison of the implementation of similar policies across SIPs with SSSB.
The HI-STR model, like other ODE compartment models, does not predict COVID-19’s waves. COVID-19 has demonstrated that some of these waves may be due to new variants outcompeting incumbents [30]. Although the HI-STR model does not incorporate pathogen evolution and random events like VOCs, here (for the SARS-CoV2 Delta variant) it has been demonstrated that an impact of such a random event can still be projected timeously.
Availability of data and materials
The data used in this paper is publicly available. The basic reproduction number estimates for the projection of the wild-type SARS-CoV2 is available at ICL (https://www.imperial.ac.uk/mrc-global-infectious-disease-analysis/covid-19/). The Delta variant data is available at https://public.tableau.com and https://cv19.one. Population sizes and densities are available at https://worldpopulationreview.com.
Abbreviations
- HI-STR:
-
Hybrid-Incidence Susceptible-Transmissible-Removed
- SIR:
-
Susceptible-Infected-Removed
- SARS-CoV2:
-
Severe Acute Respiratory Syndrome Coronavirus 2
- COVID-19:
-
Coronavirus Disease 2019
- UK:
-
United Kingdom
- USA:
-
United States of America
- ICL:
-
Imperial College London
- VOC:
-
Variant of Concern
- DE:
-
Differential Equation
- ODE:
-
Ordinary Differential Equation
- DDE:
-
Delay Differential Equation
- E:
-
Exposed
- SEIR:
-
Susceptible-Exposed-Infectious-Removed
- HIV:
-
Human Immunodeficiency Virus
- ARVs:
-
Anti-retrovirals
- PDE:
-
Partial Differential Equation
- BCMs:
-
Binomial Chain Models
- SDE:
-
Stochastic Differential Equation
- ABMs:
-
Agent Based Models
- CA:
-
Cellular Automata
- LGCA:
-
Lattice Gas Cellular Automata
- PCA:
-
Probabilistic Cellular Automata
- SCA:
-
Stochastic Cellular Automata
- ARMA:
-
Autoregressive Moving Average
- ARIMA:
-
Autoregressive Integrated Moving Average
- AI:
-
Artificial Intelligence
- ML:
-
Machine Learning
- PSO:
-
Particle Swarm Optimisation
- GA:
-
Genetic Algorithms
- ANN:
-
Artificial Neural Network
- LSTM:
-
Long Short-term Memory
- SIP:
-
Sufficiently Isolated Population
- SSSB:
-
Sufficiently Similar Social Bahaviour
- NGM:
-
Next Generation Matrix
- RNA:
-
Ribonucleic Acid
- RT-PCR:
-
Reverse Transcriptase Polymerase Chain Reaction
- Ct:
-
Cycle Count Threshold
- \(\mathcal{R}_{0}\) :
-
the theoretical basic reproduction number – only primary infections
- \(\widehat{\mathcal{R}}_{0}\) :
-
the experimentally estimated basic reproduction number
- \(\widetilde{\mathcal{R}}_{0}\) :
-
the basic reproduction number projected from an estimate
- \(\bar{\bar{\mathcal{R}}}_{0}\) :
-
basic reproduction number obtained by applying regression to the theory
- \(\mathcal{R}_{e}\) :
-
the effective reproduction number – partial susceptibility
- \({}_{\rho}\mathcal{R}_{0}\) :
-
number of primary and secondary infections due to a host over its transmissible period
- N :
-
theoretical population size
- N̂ :
-
experimentally determined estimate of population size
- \(\rho _{n}\) :
-
theoretical population density
- \(\hat{\rho}_{n}\) :
-
experimentally determined estimate population density
- \(\mathfrak{B}\) :
-
temporal scaling factor between transmissible and rhythmic timescales
- \(P(t)\) :
-
probability density function for the infection of a potential host
- η :
-
pathogen antigen host receptor avidity
- μ :
-
variable associated with the pathogen’s mode of transmission
- \(\kappa (\mathbf{x})\) :
-
variable associated with host social behaviour
- \(s(t)\) :
-
density of susceptible individuals – potential hosts
- \(S(t)\) :
-
number of susceptible individuals – potential hosts
- \(\tau (t)\) :
-
density of transmission cable individuals or hosts
- \(T(t)\) :
-
number of transmission cable individuals or hosts
- \(R(t)\) :
-
number of individuals removed due to immunity or death
- τ α :
-
transmission frequency in the transmissible timescale
- ΔI :
-
the period of time that a host is infectious
- Δτ :
-
the period of time a host is both infectious and interacting socially (with close physical proximity) with potential hosts
- Δτ̅ :
-
the average time that a group of hosts is both infectious and interacting socially (with close physical) contact with potential hosts
- δt :
-
the period of the infection opportunity cycle
- σ :
-
inherently susceptible proportion of the population
- \(1-\sigma \) :
-
inherently immune proportion of the population
- ψ :
-
symptomatic proportion of those infected
- \(1-\psi \) :
-
asymptomatic proportion of those infected
- M :
-
predicted proportionality constant relating \(\mathcal{R}_{0}\) to N and \(\rho _{n}\)
- E :
-
the relative difference between the experimental \(\mathcal{R}_{0}\) and the equivalent obtained by regression based on the theory
- p :
-
statistical significance level
- \(\mu _{d}\) :
-
mean of the differences
- \(CI_{d}\) :
-
95% confidence interval of the difference
- IQR :
-
interquartile range
References
Giordano, G., Blanchini, F., Bruno, R., Colaneri, P., Di Filippo, A., Di Matteo, A., Colaneri, M.: Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 26(6), 855–860 (2020). https://doi.org/10.1038/s41591-020-0883-7
Nikolopoulos, K., Punia, S., Schäfers, A., Tsinopoulos, C., Vasilakis, C.: Forecasting and planning during a pandemic: COVID-19 growth rates, supply chain disruptions, and governmental decisions. Eur. J. Oper. Res. 290(1), 99–115 (2021). https://doi.org/10.1016/j.ejor.2020.08.001
Campillo-Funollet, E., Van Yperen, J., Allman, P., Bell, M., Beresford, W., Clay, J., Dorey, M., Evans, G., Gilchrist, K., Memon, A., Pannu, G., Walkley, R., Watson, M., Madzvamuse, A.: Predicting and forecasting the impact of local outbreaks of COVID-19: use of SEIR-D quantitative epidemiological modelling for healthcare demand and capacity. Int. J. Epidemiol. 50(4), 1103–1113 (2021). https://doi.org/10.1093/ije/dyab106
Ioannidis, J.P.A., Cripps, S., Tanner, M.A.: Forecasting for COVID-19 has failed. Int. J. Forecast. (2020). https://doi.org/10.1016/j.ijforecast.2020.08.004
Lazebnik, T., Shami, L., Bunimovich-Mendrazitsky, S.: Spatio-temporal influence of non-pharmaceutical interventions policies on pandemic dynamics and the economy: the case of COVID-19. Ekon. Istraž. 0(0), 1–29 (2021). https://doi.org/10.1080/1331677X.2021.1925573
Silva, P.C.L., Batista, P.V.C., Lima, H.S., Alves, M.A., Guimarães, F.G., Silva, R.C.P.: COVID-ABS: an agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos Solitons Fractals 139, 110088 (2020). https://doi.org/10.1016/j.chaos.2020.110088
Ahammed, T., Anjum, A., Rahman, M.M., Haider, N., Kock, R., Uddin, M.J.: Estimation of novel coronavirus (COVID-19) reproduction number and case fatality rate: a systematic review and meta-analysis. Health Sci. Rep. 4(2), 274 (2021). https://doi.org/10.1002/hsr2.274
Dietz, K.: The estimation of the basic reproduction number for infectious diseases. Stat. Methods Med. Res. 2(1), 23–41 (1993). https://doi.org/10.1177/096228029300200103
Dublin, L.I., Lotka, A.J.: On the true rate of natural increase. J. Am. Stat. Assoc. 20(151), 305–339 (1925). https://doi.org/10.2307/2965517. Full publication date: Sep., 1925
Lotka, A.J.: The measure of net fertility. J. Wash. Acad. Sci. 15(21), 469–472 (1925)
Heesterbeek, J.A.P., Dietz, K.: The concept of \(\mathcal{R}_{0}\) in epidemic theory. Stat. Neerl. 50, 89–110 (1993)
Heesterbeek, J.A.P.: A brief history of \(\mathcal{R}_{0}\) and a recipe for its calculation. Acta Biotheor. 50, 189–204 (2002). https://doi.org/10.1023/A:1016599411804
Dietz, K.: Transmission and control of arbovirus diseases. In: In Proceedings of the Society for Industrial and Applied Mathematics, pp. 104–121. Philadelphia, Epidemiology (1975)
Delamater, P.L., Street, E.J., Leslie, T.F., Yang, Y.T., Jacobsen, K.H.: Complexity of the basic reproduction number (\(\mathcal{R}_{0}\)). Emerg. Infect. Dis. 25(1), 1–4 (2019). https://doi.org/10.3201/eid2501.171901
Zhang, Y., You, C., Cai, Z., Sun, J., Hu, W., Zhou, X.-H.: Prediction of the COVID-19 outbreak in China based on a new stochastic dynamic model. Sci. Rep. 10(1), 21522 (2020). https://doi.org/10.1038/s41598-020-76630-0
Podolski, P., Nguyen, H.S.: Cellular automata in COVID-19 prediction. Proc. Comput. Sci. 192, 3370–3379 (2021). https://doi.org/10.1016/j.procs.2021.09.110
Hoertel, N., Blachier, M., Blanco, C., Olfson, M., Massetti, M., Rico, M.S., Limosin, F., Leleu, H.: A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nat. Med. 26(9), 1417–1421 (2020). https://doi.org/10.1038/s41591-020-1001-6
Firth, J.A., Hellewell, J., Klepac, P., Kissler, S., Jit, M., Atkins, K.E., Clifford, S., Villabona-Arenas, C.J., Meakin, S.R., Diamond, C., Bosse, N.I., Munday, J.D., Prem, K., Foss, A.M., Nightingale, E.S., van Zandvoort, K., Davies, N.G., Gibbs, H.P., Medley, G., Gimma, A., Flasche, S., Simons, D., Auzenbergs, M., Russell, T.W., Quilty, B.J., Rees, E.M., Leclerc, Q.J., Edmunds, W.J., Funk, S., Houben, R.M.G.J., Knight, G.M., Abbott, S., Sun, F.Y., Lowe, R., Tully, D.C., Procter, S.R., Jarvis, C.I., Endo, A., O’Reilly, K., Emery, J.C., Jombart, T., Rosello, A., Deol, A.K., Quaife, M., Hué, S., Liu, Y., Eggo, R.M., Pearson, C.A.B., Kucharski, A.J., Spurgin, L.G., Group, C.C.-.W.: Using a real-world network to model localized COVID-19 control strategies. Nat. Med. 26(10), 1616–1622 (2020). https://doi.org/10.1038/s41591-020-1036-8
Maurya, S., Singh, S.: Time series analysis of the COVID-19 datasets. In: 2020 IEEE International Conference for Innovation in Technology (INOCON), pp. 1–6 (2020). https://doi.org/10.1109/INOCON50539.2020.9298390
Shaikh, S., Gala, J., Jain, A., Advani, S., Jaidhara, S., Roja Edinburgh, M.: Analysis and prediction of COVID-19 using regression models and time series forecasting. In: 2021 11th International Conference on Cloud Computing, Data Science Engineering (Confluence), pp. 989–995 (2021). https://doi.org/10.1109/Confluence51648.2021.9377137
Zeroual, A., Harrou, F., Dairi, A., Sun, Y.: Deep learning methods for forecasting COVID-19 time-series data: a comparative study. Chaos Solitons Fractals 140, 110121 (2020). https://doi.org/10.1016/j.chaos.2020.110121
Cardoso, B.-H.F., Gonçalves, S.: Universal scaling law for human-to-human transmission diseases. Europhys. Lett. 133(5), 58001 (2021). https://doi.org/10.1209/0295-5075/133/58001
Sy, K.T.L., White, L.F., Nichols, B.E.: Population density and basic reproductive number of COVID-19 across United States counties. PLoS ONE 16(4), 1–11 (2021). https://doi.org/10.1371/journal.pone.0249271
Derakhshan, M., Ansarian, H.R., Ghomshei, M.: Temporal variations in COVID-19: an epidemiological discussion with a practical application. J. Int. Med. Res. 49(8), 3000605211033208 (2021). https://doi.org/10.1177/03000605211033208
Cherednik, I.: Modeling the waves of Covid-19. Acta Biotheor. 70(1), 8 (2021). https://doi.org/10.1007/s10441-021-09428-w
Cacciapaglia, G., Cot, C., Sannino, F.: Multiwave pandemic dynamics explained: how to tame the next wave of infectious diseases. Sci. Rep. 11(1), 6638 (2021). https://doi.org/10.1038/s41598-021-85875-2
Hethcote, H.W., Levin, S.A.: Periodicity in epidemiological models. In: Levin, S.A., Hallam, T.G., Gross, L.J. (eds.) Applied Mathematical Ecology. Biomathematics, vol. 18, pp. 193–211. Springer, Berlin Heidelberg (1989)
Buonomo, B., Chitnis, N., d’Onofrio, A.: Seasonality in epidemic models: a literature review. Ric. Mat. 67(1), 7–25 (2018). https://doi.org/10.1007/s11587-017-0348-6
Ochab, M., Manfredi, P., Puszynski, K., d’Onofrio, A.: Multiple epidemic waves as the outcome of stochastic SIR epidemics with behavioral responses: a hybrid modeling approach. Nonlinear Dyn. (2022). https://doi.org/10.1007/s11071-022-07317-6
Brand, S.P.C., Ojal, J., Aziza, R., Were, V., Okiro, E.A., Kombe, I.K., Mburu, C., Ogero, M., Agweyu, A., Warimwe, G.M., Nyagwange, J., Karanja, H., Gitonga, J.N., Mugo, D., Uyoga, S., Adetifa, I.M.O., Scott, J.A.G., Otieno, E., Murunga, N., Otiende, M., Ochola-Oyier, L.I., Agoti, C.N., Githinji, G., Kasera, K., Amoth, P., Mwangangi, M., Aman, R., Ng’ang’a, W., Tsofa, B., Bejon, P., Keeling, M.J., Nokes, D.J., Barasa, E.: COVID-19 transmission dynamics underlying epidemic waves in Kenya. Science 374(6570), 989–994 (2021). https://doi.org/10.1126/science.abk0414
Tkachenko, A.V., Maslov, S., Elbanna, A., Wong, G.N., Weiner, Z.J., Goldenfeld, N.: Time-dependent heterogeneity leads to transient suppression of the COVID-19 epidemic, not herd immunity. Proc. Natl. Acad. Sci. USA 118(17) (2021). https://doi.org/10.1073/pnas.2015972118
Campbell, F., Archer, B., Laurenson-Schafer, H., Jinnai, Y., Konings, F., Batra, N., Pavlin, B., Vandemaele, K., Van Kerkhove, M.D., Jombart, T., Morgan, O.: le Polain de Waroux, O.: Increased transmissibility and global spread of SARS-CoV-2 variants of concern as at June 2021. Euro Surveill. 26(24) (2021). https://doi.org/10.2807/1560-7917.ES.2021.26.24.2100509
Lauring, A.S., Tenforde, M.W., Chappell, J.D., Gaglani, M., Ginde, A.A., McNeal, T., Ghamande, S., Douin, D.J., Talbot, H.K., Casey, J.D., Mohr, N.M., Zepeski, A., Shapiro, N.I., Gibbs, K.W., Files, D.C., Hager, D.N., Shehu, A., Prekker, M.E., Erickson, H.L., Exline, M.C., Gong, M.N., Mohamed, A., Johnson, N.J., Srinivasan, V., Steingrub, J.S., Peltan, I.D., Brown, S.M., Martin, E.T., Monto, A.S., Khan, A., Hough, C.L., Busse, L.W., ten Lohuis, C.C., Duggal, A., Wilson, J.G., Gordon, A.J., Qadir, N., Chang, S.Y., Mallow, C., Rivas, C., Babcock, H.M., Kwon, J.H., Halasa, N., Grijalva, C.G., Rice, T.W., Stubblefield, W.B., Baughman, A., Womack, K.N., Rhoads, J.P., Lindsell, C.J., Hart, K.W., Zhu, Y., Adams, K., Schrag, S.J., Olson, S.M., Kobayashi, M., Verani, J.R., Patel, M.M., Self, W.H.: Clinical severity of, and effectiveness of mRNA vaccines against, Covid-19 from omicron, delta, and alpha SARS-CoV-2 variants in the United States: prospective observational study. BMJ 376 (2022). https://doi.org/10.1136/bmj-2021-069761. https://www.bmj.com/content/376/bmj-2021-069761.full.pdf
Saha, S., Tanmoy, A.M., Tanni, A.A., Goswami, S., Sium, S.M.A., Saha, S., Islam, S., Hooda, Y., Malaker, A.R., Anik, A.M., Haq, M.S., Jabin, T., Hossain, M.M., Tabassum, N., Rahman, H., Hossain, M.J., Islam, M.S., Saha, S.K.: New waves, new variants, old inequity: a continuing COVID-19 crisis. BMJ Glob. Health 6(8) (2021). https://doi.org/10.1136/bmjgh-2021-007031. https://gh.bmj.com/content/6/8/e007031.full.pdf
Callaway, E.: Beyond Omicron: what’s next for COVID’s viral evolution. Nature 600(7888), 204–207 (2021). https://doi.org/10.1038/d41586-021-03619-8
Yang, W., Shaman, J.L.: COVID-19 pandemic dynamics in South Africa and epidemiological characteristics of three variants of concern (beta, delta, and omicron). eLife 11, 78933 (2022). https://doi.org/10.7554/eLife.78933
Callaway, E.: The coronavirus is mutating - does it matter? Nature 585(7824), 174–177 (2020). https://doi.org/10.1038/d41586-020-02544-6
Kupferschmidt, K.: The pandemic virus is slowly mutating. But does it matter? Science 369(6501), 238–239 (2020). https://doi.org/10.1126/science.369.6501.238
Arribas, M., Aguirre, J., Manrubia, S., Lázaro, E.: Differences in adaptive dynamics determine the success of virus variants that propagate together. Virus Evol. 4(1), 043 (2018). https://doi.org/10.1093/ve/vex043
Luna-Muschi, A., Borges, I.C., de Faria, E., Barboza, A.S., Maia, F.L., Leme, M.D., Guedes, A.R., Mendes-Correa, M.C., Kallas, E.G., Segurado, A.C., Duarte, A.J.S., Lazari, C.S., Andrade, P.S., Sales, F.C.S., Claro, I.M., Sabino, E.C., Levin, A.S., Costa, S.F.: Clinical features of COVID-19 by SARS-CoV-2 Gamma variant: a prospective cohort study of vaccinated and unvaccinated healthcare workers. J. Infect. 84(2), 248–288 (2022). https://doi.org/10.1016/j.jinf.2021.09.005
Nyberg, T., Ferguson, N.M., Nash, S.G., Webster, H.H., Flaxman, S., Andrews, N., Hinsley, W., Bernal, J.L., Kall, M., Bhatt, S., Blomquist, P., Zaidi, A., Volz, E., Aziz, N.A., Harman, K., Funk, S., Abbott, S., Nyberg, T., Ferguson, N.M., Nash, S.G., Webster, H.H., Flaxman, S., Andrews, N., Hinsley, W., Lopez Bernal, J., Kall, M., Bhatt, S., Blomquist, P., Zaidi, A., Volz, E., Abdul Aziz, N., Harman, K., Funk, S., Abbott, S., Hope, R., Charlett, A., Chand, M., Ghani, A.C., Seaman, S.R., Dabrera, G., De Angelis, D., Presanis, A.M., Thelwall, S., Hope, R., Charlett, A., Chand, M., Ghani, A.C., Seaman, S.R., Dabrera, G., De Angelis, D., Presanis, A.M., Thelwall, S.: Comparative analysis of the risks of hospitalisation and death associated with SARS-CoV-2 omicron (B.1.1.529) and delta (B.1.617.2) variants in England: a cohort study. Lancet 399(10332), 1303–1312 (2022). https://doi.org/10.1016/S0140-6736(22)00462-7
Hu, Z., Huang, X., Zhang, J., Fu, S., Ding, D., Tao, Z.: Differences in clinical characteristics between Delta variant and wild-type SARS-CoV-2 infected patients. Front. Med. 8 (2022). https://doi.org/10.3389/fmed.2021.792135
Boehm, E., Kronig, I., Neher, R.A., Eckerle, I., Vetter, P., Kaiser, L.: Novel SARS-CoV-2 variants: the pandemics within the pandemic. Clin. Microbiol. Infect. 27(8), 1109–1117 (2021). https://doi.org/10.1016/j.cmi.2021.05.022
Hart, W.S., Miller, E., Andrews, N.J., Waight, P., Maini, P.K., Funk, S., Thompson, R.N.: Generation time of the alpha and delta SARS-CoV-2 variants: an epidemiological analysis. Lancet Infect. Dis. 22(5), 603–610 (2022). https://doi.org/10.1016/S1473-3099(22)00001-9
Davies, N.G., Abbott, S., Barnard, R.C., Jarvis, C.I., Kucharski, A.J., Munday, J.D., Pearson, C.A.B., Russell, T.W., Tully, D.C., Washburne, A.D., Wenseleers, T., Gimma, A., Waites, W., Wong, K.L.M., van Zandvoort, K., Silverman, J.D., Diaz-Ordaz, K., Keogh, R., Eggo, R.M., Funk, S., Jit, M., Atkins, K.E., Edmunds, W.J.: Estimated transmissibility and impact of SARS-CoV-2 lineage B.1.1.7 in England. Science 372(6538), 3055 (2021). https://doi.org/10.1126/science.abg3055
Gräf, T., Bello, G., Naveca, F.G., Gomes, M., Cardoso, V.L.O., da Silva, A.F., Dezordi, F.Z., dos Santos, M.C., dos Santos, K.C., Batista, É.L.R., Magalhães, A.L.Á., Vinhal, F., Miyajima, F., Faoro, H., Khouri, R., Wallau, G.L., Delatorre, E., Siqueira, M.M., Resende, P.C., Mattos, T.P., Nascimento, V.A., Souza, V., Corado, A.L.G., Nascimento, F., Silva, G., Mejía, M., Brandão, M.J., Costa, Á., Pessoa, K., Jesus, M., Gonçalves, L.F., Fernandes, C., Andrade, V., Barbagelata, L., Cruz, A.C.R., Costa, A., Silva, L.d.A., Galvão, J.D., Leite, A.B., Pereira, F.M., Costa, T.O., Sousa Jr., J.C., Neto, L.G.L., Barroso, H., Teixeira, D.L.F., Bezerra, J.F., Docena, C., de Lima, R.E., Silva, L.C.A., de Lima, G.B., Machado, L.C., Bezerra, M.F., Paiva, M.H.S., Dantas, M.E.P.L., Pereira, R.L.D.N., Araújo, J., Santos, C.A., Ribeiro-Rodrigues, R., Bernardes, A.L., Iani, F.C.d.M., Grinsztejn, B., Veloso, V.G., Brasil, P., da Paixão, A.C.D., Appolinario, L.R., Lopes, R.S., Motta, F.d.C., Rocha, A.S., Venas, T.M.M., Pereira, E.C., Cavalcanti, A.C., Bastos, L.S., Brigido, L.F.d.M., Oliveira, M.d.M., Schemberger, M.O., Suzukawa, A.A., Riediger, I., Debur, M.d.C., Salvato, R.S., Gregianini, T.S., Rovaris, D.B., Fernandes, S.B.: Phylogenetic-based inference reveals distinct transmission dynamics of SARS-CoV-2 lineages Gamma and P.2 in Brazil. iScience 25(4) (2022). https://doi.org/10.1016/j.isci.2022.104156
Earnest, R., Uddin, R., Matluk, N., Renzette, N., Turbett, S.E., Siddle, K.J., Loreth, C., Adams, G., Tomkins-Tinch, C.H., Petrone, M.E., Rothman, J.E., Breban, M.I., Koch, R.T., Billig, K., Fauver, J.R., Vogels, C.B.F., Bilguvar, K., De Kumar, B., Landry, M.L., Peaper, D.R., Kelly, K., Omerza, G., Grieser, H., Meak, S., Martha, J., Dewey, H.B., Kales, S., Berenzy, D., Carpenter-Azevedo, K., King, E., Huard, R.C., Novitsky, V., Howison, M., Darpolor, J., Manne, A., Kantor, R., Smole, S.C., Brown, C.M., Fink, T., Lang, A.S., Gallagher, G.R., Pitzer, V.E., Sabeti, P.C., Gabriel, S., MacInnis, B.L., Altajar, A., DeJesus, A., Brito, A., Watkins, A.E., Muyombwe, A., Blumenstiel, B.S., Neal, C., Kalinich, C.C., Liu, C., Loreth, C., Castaldi, C., Pearson, C., Bernard, C., Nolet, C.M., Ferguson, D., Buzby, E., Laszlo, E., Reagan, F.L., Vicente, G., Rooke, H.M., Munger, H., Johnson, H., Tikhonova, I.R., Ott, I.M., Razeq, J., Meldrim, J.C., Brown, J., Wang, J., Vostok, J., Beauchamp, J.P., Grimsby, J.L., Hall, J., Messer, K.S., Larkin, K.L., Vernest, K., Madoff, L.C., Green, L.M., Webber, L., Gagne, L., Ulcena, M.A., Ray, M.C., Fisher, M.E., Barter, M., Lee, M.D., DeFelice, M.T., Cipicchio, M.C., Smith, N.L., Lennon, N.J., Fitzgerald, N.A., Kerantzas, N., Hui, P., Harrington, R., Downing, R., Haye, R., Lynch, R., Anderson, S.E., Hennigan, S., English, S., Cofsky, S., Clancy, S., Mane, S., Ash, S., Baez, S., Fleming, S., Murphy, S., Chaluvadi, S., Alpert, T., Rivard, T., Schulz, W., Mandese, Z.M., Tewhey, R., Adams, M.D., Park, D.J., Lemieux, J.E., Grubaugh, N.D.: Comparative transmissibility of SARS-CoV-2 variants Delta and Alpha in new. Cell Rep. Med. 3(4), 100583 (2022). https://doi.org/10.1016/j.xcrm.2022.100583
Vargas-Herrera, N., Araujo-Castillo, R.V., Mestanza, O., Galarza, M., Rojas-Serrano, N., Solari-Zerpa, L.: SARS-CoV-2 Lambda and Gamma variants competition in Peru, a country with high seroprevalence. Lancet Regional Health. Americas 6, 100112 (2022). https://doi.org/10.1016/j.lana.2021.100112
Roberts, M., Andreasen, V., Lloyd, A., Pellis, L.: Nine challenges for deterministic epidemic models. Epidemics 10, 49–53 (2015). https://doi.org/10.1016/j.epidem.2014.09.006
Bessière, P., Volmer, R.: From one to many: the within-host rise of viral variants. PLoS Pathog. 17(9), 1–5 (2021). https://doi.org/10.1371/journal.ppat.1009811
Korber, B., Fischer, W.M., Gnanakaran, S., Yoon, H., Theiler, J., Abfalterer, W., Hengartner, N., Giorgi, E.E., Bhattacharya, T., Foley, B., Hastie, K.M., Parker, M.D., Partridge, D.G., Evans, C.M., Freeman, T.M., de Silva, T.I., Angyal, A., Brown, R.L., Carrilero, L., Green, L.R., Groves, D.C., Johnson, K.J., Keeley, A.J., Lindsey, B.B., Parsons, P.J., Raza, M., Rowland-Jones, S., Smith, N., Tucker, R.M., Wang, D., Wyles, M.D., McDanal, C., Perez, L.G., Tang, H., Moon-Walker, A., Whelan, S.P., LaBranche, C.C., Saphire, E.O., Montefiori, D.C.: Tracking changes in SARS-CoV-2 spike: evidence that D614G increases infectivity of the COVID-19 virus. Cell 182(4), 812–82719 (2020). https://doi.org/10.1016/j.cell.2020.06.043
Benjamin, R.L.: The hybrid incidence susceptible-transmissible-removed model for pandemics. Acta Biotheor. 70(1), 10 (2022). https://doi.org/10.1007/s10441-021-09431-1
Kermack, W.O., McKendrick, A.G.: Contributions to the mathematical theory of epidemics – I. 1927. Bull. Math. Biol. 53(1–2), 33–55 (1991)
Kermack, W.O., McKendrick, A.G.: Contributions to the mathematical theory of epidemics – II. The problem of endemicity. 1932. Bull. Math. Biol. 53(1–2), 57–87 (1991)
Kermack, W.O., McKendrick, A.G.: Contributions to the mathematical theory of epidemics – III. Further studies of the problem of endemicity. 1933. Bull. Math. Biol. 53(1–2), 89–118 (1991)
Hamer, W.H.: The Milroy lectures on epidemic disease in England—the evidence of variability and of persistency of type. Lancet 167(4305), 569–574 (1906). https://doi.org/10.1016/S0140-6736(01)80187-2. Originally published as Volume 1, Issue 4305
Moore, C.A., Ruisch, B.C., Granados Samayoa, J.A., Boggs, S.T., Ladanyi, J.T., Fazio, R.H.: Contracting COVID-19: a longitudinal investigation of the impact of beliefs and knowledge. Sci. Rep. 11(1), 20460 (2021). https://doi.org/10.1038/s41598-021-99981-8
Albrecht, D.: Vaccination, politics and COVID-19 impacts. BMC Public Health 22(1), 96 (2022). https://doi.org/10.1186/s12889-021-12432-x
Vegvari, C., Abbott, S., Ball, F., Brooks-Pollock, E., Challen, R., Collyer, B.S., Dangerfield, C., Gog, J.R., Gostic, K.M., Heffernan, J.M., Hollingsworth, T.D., Isham, V., Kenah, E., Mollison, D., Panovska-Griffiths, J., Pellis, L., Roberts, M.G., Tomba, G.S., Thompson, R.N., Trapman, P.: Commentary on the use of the reproduction number \(\mathcal{R}\) during the COVID-19 pandemic. Stat. Methods Med. Res. 31(9), 1675–1685 (2022). https://doi.org/10.1177/09622802211037079
Varghese, A., Kolamban, S., Sherimon, V., Lacap, E.M., Ahmed, S.S., Sreedhar, J.P., Al Harthi, H., Al Shuaily, H.S.: SEAMHCRD deterministic compartmental model based on clinical stages of infection for COVID-19 pandemic in Sultanate of Oman. Sci. Rep. 11(1), 11984 (2021). https://doi.org/10.1038/s41598-021-91114-5
Lyra, W., do Nascimento, J.-D. Jr., Belkhiria, J., de Almeida, L., Chrispim, P.P.M., de Andrade, I.: COVID-19 pandemics modeling with modified determinist SEIR, social distancing, and age stratification. The effect of vertical confinement and release in Brazil. PLoS ONE 15(9), 1–17 (2020). https://doi.org/10.1371/journal.pone.0237627
Rǎdulescu, A., Williams, C., Cavanagh, K.: Management strategies in a SEIR-type model of COVID 19 community spread. Sci. Rep. 10(1), 21256 (2020). https://doi.org/10.1038/s41598-020-77628-4
Ram, V., Schaposnik, L.P.: A modified age-structured SIR model for COVID-19 type viruses. Sci. Rep. 11(1), 15194 (2021). https://doi.org/10.1038/s41598-021-94609-3
Balabdaoui, F., Mohr, D.: Age-stratified discrete compartment model of the COVID-19 epidemic with application to Switzerland. Sci. Rep. 10(1), 21306 (2020). https://doi.org/10.1038/s41598-020-77420-4
Jewell, N.P., Lewnard, J.A., Jewell, B.L.: Predictive mathematical models of the COVID-19 pandemic: underlying principles and value of projections. JAMA 323(19), 1893–1894 (2020). https://doi.org/10.1001/jama.2020.6585
Holmdahl, I., Buckee, C.: Wrong but useful – what COVID-19 epidemiologic models can and cannot tell us. N. Engl. J. Med. 383(4), 303–305 (2020). https://doi.org/10.1056/NEJMp2016822
Dell’Anna, L.: Solvable delay model for epidemic spreading: the case of COVID-19 in Italy. Sci. Rep. 10(1), 15763 (2020). https://doi.org/10.1038/s41598-020-72529-y
Devipriya, R., Dhamodharavadhani, s., Selvi, S.: SEIR model for COVID-19 epidemic using delay differential equation. J. Phys. Conf. Ser. 1767, 012005 (2021). https://doi.org/10.1088/1742-6596/1767/1/012005
Feng, S., Feng, Z., Ling, C., Chang, C., Feng, Z.: Prediction of the COVID-19 epidemic trends based on SEIR and AI models. PLoS ONE 16(1), 1–15 (2021). https://doi.org/10.1371/journal.pone.0245101
Carcione, J.M., Santos, J.E., Bagaini, C., Ba, J.: A simulation of a COVID-19 epidemic based on a deterministic SEIR model. Front. Public Health 8, 230 (2020). https://doi.org/10.3389/fpubh.2020.00230
Khedher, N.b., Kolsi, L., Alsaif, H.: A multi-stage SEIR model to predict the potential of a new COVID-19 wave in KSA after lifting all travel restrictions. Alex. Eng. J. 60(4), 3965–3974 (2021). https://doi.org/10.1016/j.aej.2021.02.058
Walsh, K.A., Spillane, S., Comber, L., Cardwell, K., Harrington, P., Connell, J., Teljeur, C., Broderick, N., de Gascun, C.F., Smith, S.M., Ryan, M., O’Neill, M.: The duration of infectiousness of individuals infected with SARS-CoV-2. J. Infect. 81(6), 847–856 (2020). https://doi.org/10.1016/j.jinf.2020.10.009
Lythgoe, K.A., Fraser, C.: New insights into the evolutionary rate of HIV-1 at the within-host and epidemiological levels. Proc. R. Soc. Lond. B, Biol. Sci. 279(1741), 3367–3375 (2012). https://doi.org/10.1098/rspb.2012.0595
Wang, H.Y., Yamamoto, N.: Using a partial differential equation with Google Mobility data to predict COVID-19 in arizona. Math. Biosci. Eng. 17(5), 4891–4904 (2020). https://doi.org/10.3934/mbe.2020266
Viguerie, A., Lorenzo, G., Auricchio, F., Baroli, D., Hughes, T.J.R., Patton, A., Reali, A., Yankeelov, T.E., Veneziani, A.: Simulating the spread of COVID-19 via a spatially-resolved susceptible-exposed-infected-recovered-deceased (SEIRD) model with heterogeneous diffusion. Appl. Math. Lett. 111, 106617 (2021). https://doi.org/10.1016/j.aml.2020.106617
Chalub, F.A.C.C., Souza, M.O.: The SIR epidemic model from a PDE point of view. Math. Comput. Model. 53(7), 1568–1574 (2011). https://doi.org/10.1016/j.mcm.2010.05.036. Mathematical Methods and Modelling of Biophysical Phenomena
Lefèvre, C., Picard, P., Simon, M., Utev, S.: A chain binomial epidemic with asymptomatics motivated by COVID-19 modelling. J. Math. Biol. 83(5), 54 (2021). https://doi.org/10.1007/s00285-021-01680-5
Hellewell, J., Abbott, S., Gimma, A., Bosse, N.I., Jarvis, C.I., Russell, T.W., Munday, J.D., Kucharski, A.J., Edmunds, W.J.: The lancet. Glob. Health 8(4), 488–496 (2020). https://doi.org/10.1016/S2214-109X(20)30074-7
Levesque, J., Maybury, D.W., Shaw, R.H.A.D.: A model of COVID-19 propagation based on a gamma subordinated negative binomial branching process. J. Theor. Biol. 512, 110536 (2021). https://doi.org/10.1016/j.jtbi.2020.110536
Niu, R., Chan, Y.-C., Wong, E.W.M., van Wyk, M.A., Chen, G.: A stochastic SEIHR model for COVID-19 data fluctuations. Nonlinear Dyn. 1(13) (2021). https://doi.org/10.1007/s11071-021-06631-9
Zhang, Z., Zeb, A., Hussain, S., Alzahrani, E.: Dynamics of COVID-19 mathematical model with stochastic perturbation. Adv. Differ. Equ. 2020(1), 451 (2020). https://doi.org/10.1186/s13662-020-02909-1
Dordevic, J., Papic, I., Suvak, N.: A two diffusion stochastic model for the spread of the new corona virus SARS-CoV-2. Chaos Solitons Fractals 148, 110991 (2021). https://doi.org/10.1016/j.chaos.2021.110991
Allen, L.J.S., Burgin, A.M.: Comparison of deterministic and stochastic SIS and SIR models in discrete time. Math. Biosci. 163(1), 1–33 (2000). https://doi.org/10.1016/S0025-5564(99)00047-4
Osthus, D., Hickmann, K.S., Caragea, P.C., Higdon, D., Del Valle, S.Y.: Forecasting seasonal influenza with a state-space SIR model. Ann. Appl. Stat. 11(1), 202–224 (2017). https://doi.org/10.1214/16-AOAS1000
Newman, M.E.J.: Spread of epidemic disease on networks. Phys. Rev. E 66, 016128 (2002). https://doi.org/10.1103/PhysRevE.66.016128
Moreno, Y., Pastor-Satorras, R., Vespignani, A.: Epidemic outbreaks in complex heterogeneous networks. Eur. Phys. J. B, Condens. Matter Complex Syst. 26(4), 521–529 (2002). https://doi.org/10.1140/epjb/e20020122
Schimit, P.H.T., Pereira, F.H.: Disease spreading in complex networks: a numerical study with principal component analysis. Expert Syst. Appl. 97, 41–50 (2018). https://doi.org/10.1016/j.eswa.2017.12.021
Pastor-Satorras, R., Castellano, C., Van Mieghem, P., Vespignani, A.: Epidemic processes in complex networks. Rev. Mod. Phys. 87, 925–979 (2015). https://doi.org/10.1103/RevModPhys.87.925
Rorres, C., Romano, M., Miller, J.A., Mossey, J.M., Grubesic, T.H., Zellner, D.E., Smith, G.: Contact tracing for the control of infectious disease epidemics: Chronic wasting disease in deer farms. Epidemics 23, 71–75 (2018). https://doi.org/10.1016/j.epidem.2017.12.006
Pavlopoulos, G.A., Secrier, M., Moschopoulos, C.N., Soldatos, T.G., Kossida, S., Aerts, J., Schneider, R., Bagos, P.G.: Using graph theory to analyze biological networks. BioData Min. 4, 10 (2011). https://doi.org/10.1186/1756-0381-4-10
Read, J.M., Eames, K.T.D., Edmunds, W.J.: Dynamic social networks and the implications for the spread of infectious disease. J. R. Soc. Interface 5(26), 1001–1007 (2008). https://doi.org/10.1098/rsif.2008.0013
Jo, W., Chang, D., You, M., Ghim, G.-H.: A social network analysis of the spread of COVID-19 in South Korea and policy implications. Sci. Rep. 11(1), 8581 (2021). https://doi.org/10.1038/s41598-021-87837-0
Block, P., Hoffman, M., Raabe, I.J., Dowd, J.B., Rahal, C., Kashyap, R., Mills, M.C.: Social network-based distancing strategies to flatten the COVID-19 curve in a post-lockdown world. Nat. Hum. Behav. 4(6), 588–596 (2020). https://doi.org/10.1038/s41562-020-0898-6
Del Valle, S.Y., Hyman, J.M., Hethcote, H.W., Eubank, S.G.: Mixing patterns between age groups in social networks. Soc. Netw. 29(4), 539–554 (2007). https://doi.org/10.1016/j.socnet.2007.04.005
Silva, C.J., Cantin, G., Cruz, C., Fonseca-Pinto, R., Passadouro, R., Soares Dos Santos, E., Torres, D.F.M.: Complex network model for COVID-19: Human behavior, pseudo-periodic solutions and multiple epidemic waves. J. Math. Anal. Appl. 514, 125171 (2021). https://doi.org/10.1016/j.jmaa.2021.125171
Kucharski, R., Cats, O., Sienkiewicz, J.: Modelling virus spreading in ride-pooling networks. Sci. Rep. 11(1), 7201 (2021). https://doi.org/10.1038/s41598-021-86704-2
Lazebnik, T., Bunimovich-Mendrazitsky, S., Shami, L.: Pandemic management by a spatio-temporal mathematical model. Int. J. Nonlinear Sci. Numer. Simul. 000010151520210063 (2021). https://doi.org/10.1515/ijnsns-2021-0063
Thurner, S., Klimek, P., Hanel, R.: A network-based explanation of why most COVID-19 infection curves are linear. Proc. Natl. Acad. Sci. 117(37), 22684–22689 (2020). https://doi.org/10.1073/pnas.2010398117. https://www.pnas.org/content/117/37/22684.full.pdf
Fall, A., Fortin, M.-J., Manseau, M., O’Brien, D.: Spatial graphs: principles and applications for habitat connectivity. Ecosystems 10(3), 448–461 (2007). https://doi.org/10.1007/s10021-007-9038-7
Kerr, C.C., Stuart, R.M., Mistry, D., Abeysuriya, R.G., Rosenfeld, K., Hart, G.R., Núñez, R.C., Cohen, J.A., Selvaraj, P., Hagedorn, B., George, L., Jastrzebski, M., Izzo, A.S., Fowler, G., Palmer, A., Delport, D., Scott, N., Kelly, S.L., Bennette, C.S., Wagner, B.G., Chang, S.T., Oron, A.P., Wenger, E.A., Panovska-Griffiths, J., Famulare, M., Klein, D.J.: Covasim: an agent-based model of COVID-19 dynamics and interventions. PLoS Comput. Biol. 17(7), 1009149 (2021). https://doi.org/10.1371/journal.pcbi.1009149
Najmi, A., Nazari, S., Safarighouzhdi, F., Miller, E.J., MacIntyre, R., Rashidi, T.H.: Easing or tightening control strategies: determination of COVID-19 parameters for an agent-based model. Transportation (2021). https://doi.org/10.1007/s11116-021-10210-7
Medrek, M., Pastuszak, Z.: Numerical simulation of the novel coronavirus spreading. Expert Syst. Appl. 166, 114109 (2021). https://doi.org/10.1016/j.eswa.2020.114109
Zhou, Y., Wang, L., Zhang, L., Shi, L., Yang, K., He, J., Zhao, B., Overton, W., Purkayastha, S., Song, P.: A spatiotemporal epidemiological prediction model to inform county-level COVID-19 risk in the United States. Harv. Data Sci. Rev. (2020). https://doi.org/10.1162/99608f92.79e1f45e. https://hdsr.mitpress.mit.edu/pub/qqg19a0r
Schimit, P.H.T.: A model based on cellular automata to estimate the social isolation impact on COVID-19 spreading in Brazil. Comput. Methods Programs Biomed. 200, 105832 (2021). https://doi.org/10.1016/j.cmpb.2020.105832
Almeida Simoes, J.: An agent-based approach to spatial epidemics through GIS. PhD thesis, University of London (2007) http://ethos.bl.uk/ProcessSearch.do?query=444185
Aguilar, W., Santamaría-Bonfil, G., Froese, T., Gershenson, C.: The past, present, and future of artificial life. Front. Neurorobot. 1, 8 (2014). https://doi.org/10.3389/frobt.2014.00008
Bonabeau, E.: Agent-based modeling: methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. 99(suppl 3), 7280–7287 (2002). https://doi.org/10.1073/pnas.082080899. https://www.pnas.org/content/99/suppl_3/7280.full.pdf
Jin, Z., Liu, Q.-X.: A cellular automata model of epidemics of a heterogeneous susceptibility. Chin. Phys. 15, 1248 (2006). https://doi.org/10.1088/1009-1963/15/6/019
Schneckenreither, G., Popper, N., Zauner, G., Breitenecker, F.: Modelling SIR-type epidemics by ODEs, PDEs, difference equations and cellular automata – a comparative study. Simul. Model. Pract. Theory 16(8), 1014–1023 (2008). https://doi.org/10.1016/j.simpat.2008.05.015
Boccara, N., Cheong, K.: Automata network SIR models for the spread of infectious diseases in populations of moving individuals. J. Phys. A, Math. Gen. 25(9), 2447–2461 (1992). https://doi.org/10.1088/0305-4470/25/9/018
Guo, Z., Shi, B., Wang, N.: Lattice bgk model for incompressible Navier–Stokes equation. J. Comput. Phys. 165(1), 288–306 (2000). https://doi.org/10.1006/jcph.2000.6616
Ciufolini, I., Paolozzi, A.: Mathematical prediction of the time evolution of the COVID-19 pandemic in Italy by a Gauss error function and Monte Carlo simulations. Eur. Phys. J. Plus 135(4), 355 (2020). https://doi.org/10.1140/epjp/s13360-020-00383-y
Amaro, J., Orce, J.: Monte Carlo simulation of COVID-19 pandemic using Planck’s probability distribution. Biosystems 218, 104708 (2022). https://doi.org/10.1016/j.biosystems.2022.104708
Triambak, S., Mahapatra, D.P.: A random walk Monte Carlo simulation study of COVID-19-like infection spread. Phys. A, Stat. Mech. Appl. 574, 126014 (2021). https://doi.org/10.1016/j.physa.2021.126014
Xie, G.: A novel Monte Carlo simulation procedure for modelling COVID-19 spread over time. Sci. Rep. 10(1), 13120 (2020). https://doi.org/10.1038/s41598-020-70091-1
Olabode, D., Culp, J., Fisher, A., Tower, A., Hull-Nye, D., Wang, X.: Deterministic and stochastic models for the epidemic dynamics of COVID-19 in Wuhan, China. Math. Biosci. Eng. 18(1), 950–967 (2021). https://doi.org/10.3934/mbe.2021050
Kim, M., Paini, D., Jurdak, R.: Modeling stochastic processes in disease spread across a heterogeneous social system. Proc. Natl. Acad. Sci. USA 116(2), 401–406 (2019). https://doi.org/10.1073/pnas.1801429116
Ming, R.-X., Liu, J.-M., Cheung, W.K.W., Wan, X.: Stochastic modelling of infectious diseases for heterogeneous populations. Infect. Dis. Poverty 5(1), 107 (2016). https://doi.org/10.1186/s40249-016-0199-5
Montgomery, D., Jennings, C., Kulahci, M.: Introduction to Time Series Analysis and Forecasting, 2nd edn. Wiley, Hoboken, New Jersey (2015)
Papastefanopoulos, V., Linardatos, P., Kotsiantis, S.: COVID-19: a comparison of time series methods to forecast percentage of active cases per population. Appl. Sci. 10(11) (2020). https://doi.org/10.3390/app10113880
Wang, Y., Yan, Z., Wang, D., Yang, M., Li, Z., Gong, X., Wu, D., Zhai, L., Zhang, W., Wang, Y.: Prediction and analysis of COVID-19 daily new cases and cumulative cases: times series forecasting and machine learning models. BMC Infect. Dis. 22(1), 495 (2022). https://doi.org/10.1186/s12879-022-07472-6
Gecili, E., Ziady, A., Szczesniak, R.D.: Forecasting COVID-19 confirmed cases, deaths and recoveries: revisiting established time series modeling through novel applications for the USA and Italy. PLoS ONE 16(1), 1–11 (2021). https://doi.org/10.1371/journal.pone.0244173
Roosa, K., Lee, Y., Luo, R., Kirpich, A., Rothenberg, R., Hyman, J.M., Yan, P., Chowell, G.: Real-time forecasts of the COVID-19 epidemic in China from February 5th to February 24th, 2020. Infect. Dis. Model. 5, 256–263 (2020). https://doi.org/10.1016/j.idm.2020.02.002
Koczkodaj, W.W., Mansournia, M.A., Pedrycz, W., Wolny-Dominiak, A., Zabrodskii, P.F., Strzalka, D., Armstrong, T., Zolfaghari, A.H., Debski, M., Mazurek, J.: 1,000,000 cases of COVID-19 outside of China: the date predicted by a simple heuristic. Glob. Epidemiol. 2, 100023 (2020). https://doi.org/10.1016/j.gloepi.2020.100023
Holloway, J.L.: Smoothing and filtering of time series and space fields. In: Landsberg, H.E., Van Mieghem, J. (eds.) Advances in Geophysics, vol. 4, pp. 351–389. Academic Press, New York (1958). https://doi.org/10.1016/S0065-2687(08)60487-2. https://www.sciencedirect.com/science/article/pii/S0065268708604872
Takefuji, Y.: Fourier analysis using the number of COVID-19 daily deaths in the US. Epidemiol. Infect. 149, 64 (2021). https://doi.org/10.1017/S0950268821000522
Kuzmenko, O.V., Smiianov, V.A., Rudenko, L.A., Kashcha, M.O., Vasilyeva, T.A., Kolomiiets, S.V., Antoniuk, N.A.: Impact of vaccination on the COVID-19 pandemic: bibliometric analysis and cross country forecasting by Fourier series. Wiad. Lek. 74(10 pt 1), 2359–2367 (2021)
Kashcha, M., Palienko, M., Marchenko, R.: Forecast of COVID-19 progress considering the seasonal fluctuations. Health Econ. Manag. Rev. 2, 71–82 (2021)
Wang, X., Washington, D., Weber, G.F.: Complex systems analysis informs on the spread of COVID-19. Epidemiol. Methods 10(s1), 20210019 (2021). https://doi.org/10.1515/em-2021-0019
Eubank, R.L.: A Kalman Filter Primer. Chapman & Hall/CRC, Boca Raton (2006)
Bisgaard, S., Kulahci, M.: Time Series Analysis and Forecasting by Example, 1st edn. Wiley, Hoboken (2011)
Box, G.E.P., Jenkins, G.M., Reinsel, G.C., Ljung, G.M.: TIME SERIES ANALYSIS Forecasting and Control, 5th edn. Wiley, Hoboken, New Jersey (2016)
Alzahrani, S.I., Aljamaan, I.A., Al-Fakih, E.A.: Forecasting the spread of the COVID-19 pandemic in Saudi Arabia using ARIMA prediction model under current public health interventions. J. Infect. Publ. Health 13(7), 914–919 (2020). https://doi.org/10.1016/j.jiph.2020.06.001
Papastefanopoulos, V., Linardatos, P., Kotsiantis, S.: COVID-19: a comparison of time series methods to forecast percentage of active cases per population. Appl. Sci. 10(11) (2020). https://doi.org/10.3390/app10113880
Claris, S., Peter, N.: ARIMA model in predicting of COVID-19 epidemic for the southern Africa region. Afr. J. Infect. Dis. 17(1), 1–9 (2023). https://doi.org/10.21010/Ajidv17i1.1
Shahid, F., Zameer, A., Muneeb, M.: Predictions for Covid-19 with deep learning models of LSTM, GRU and Bi-LSTM. Chaos Solitons Fractals 140, 110212 (2020). https://doi.org/10.1016/j.chaos.2020.110212
Chaurasia, V., Pal, S.: COVID-19 pandemic: ARIMA and regression model-based worldwide death cases predictions. SN Comput. Sci. 1(5), 288 (2020). https://doi.org/10.1007/s42979-020-00298-6
Mills, T.C.: Applied Time Series Analysis, 1st edn. Academic Press, New York (2019)
Ahmar, A.S., del Val, E.B.: SutteARIMA: short-term forecasting method, a case: COVID-19 and stock market in Spain. Sci. Total Environ. 729, 138883 (2020). https://doi.org/10.1016/j.scitotenv.2020.138883
Malki, Z., Atlam, E.-S., Ewis, A., Dagnew, G., Alzighaibi, A.R., ELmarhomy, G., Elhosseini, M.A., Hassanien, A.E., Gad, I.: ARIMA models for predicting the end of COVID-19 pandemic and the risk of second rebound. Neural Comput. Appl. 33(7), 2929–2948 (2021). https://doi.org/10.1007/s00521-020-05434-0
Chakraborty, T., Ghosh, I.: Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: a data-driven analysis. Chaos Solitons Fractals 135, 109850 (2020). https://doi.org/10.1016/j.chaos.2020.109850
Chintalapudi, N., Battineni, G., Amenta, F.: COVID-19 virus outbreak forecasting of registered and recovered cases after sixty day lockdown in Italy: a data driven model approach. J. Microbiol. Immunol. Infect. 53(3), 396–403 (2020). https://doi.org/10.1016/j.jmii.2020.04.004
Liao, Z., Lan, P., Liao, Z., Zhang, Y., Liu, S.: TW-SIR: time-window based sir for COVID-19 forecasts. Sci. Rep. 10(1), 22454 (2020). https://doi.org/10.1038/s41598-020-80007-8
Maleki, M., Mahmoudi, M.R., Heydari, M.H., Pho, K.-H.: Modeling and forecasting the spread and death rate of coronavirus (COVID-19) in the world using time series models. Chaos Solitons Fractals 140, 110151 (2020). https://doi.org/10.1016/j.chaos.2020.110151
Cheng, C., Jiang, W.-M., Fan, B., Cheng, Y.-C., Hsu, Y.-T., Wu, H.-Y., Chang, H.-H., Tsou, H.-H.: Real-time forecasting of COVID-19 spread according to protective behavior and vaccination: autoregressive integrated moving average models. BMC Public Health 23(1), 1500 (2023). https://doi.org/10.1186/s12889-023-16419-8
Rahimi, I., Chen, F., Gandomi, A.H.: A review on COVID-19 forecasting models. Neural Comput. Appl. (2021). https://doi.org/10.1007/s00521-020-05626-8
Wang, L., Zhang, Y., Wang, D., Tong, X., Liu, T., Zhang, S., Huang, J., Zhang, L., Chen, L., Fan, H., Clarke, M.: Artificial Intelligence for COVID-19: A Systematic Review. Frontiers in Medicine, vol. 8 (2021). https://doi.org/10.3389/fmed.2021.704256
Benvenuto, D., Giovanetti, M., Vassallo, L., Angeletti, S., Ciccozzi, M.: Application of the ARIMA model on the COVID-2019 epidemic dataset. Data Brief 29, 105340 (2020). https://doi.org/10.1016/j.dib.2020.105340
Rath, S., Tripathy, A., Tripathy, A.R.: Prediction of new active cases of coronavirus disease (COVID-19) pandemic using multiple linear regression model. Diabetes Metab. Syndr. Clin. Res. Rev. 14(5), 1467–1474 (2020). https://doi.org/10.1016/j.dsx.2020.07.045
Tan, C.V., Singh, S., Lai, C.H., Zamri, A.S.S.M., Dass, S.C., Aris, T.B., Ibrahim, H.M., Gill, B.S.: Forecasting COVID-19 case trends using SARIMA models during the third wave of COVID-19 in Malaysia. Int. J. Environ. Res. Public Health 19(3) (2022). https://doi.org/10.3390/ijerph19031504
Amisha, M.P., Pathania, M., Rathaur, V.K.: Overview of artificial intelligence in medicine. J. Family Med. Prim. Care 8(7), 2328–2331 (2019). https://doi.org/10.4103/jfmpc.jfmpc_440
Khemani, D.: A First Course in Artificial Intelligence, 1st edn. McGraw Hill, New Delhi (2013). http://repo.darmajaya.ac.id/3793/1/A
Warwick, K.: Artificial Intelligence: The Basics. Routledge, New York (2011)
Markiewicz, T., Zheng, J.: Getting Started with Artificial Intelligence, 2nd edn. O’Reilly, Sebastopol, California (2020)
Flasiński, M.: Introduction to Artificial Intelligence, 1st edn. Springer, Cham, Switzerland (2016). https://doi.org/10.1007/978-3-319-40022-8
Khan, M., Mehran, M.T., Haq, Z.U., Ullah, Z., Naqvi, S.R., Ihsan, M., Abbass, H.: Applications of artificial intelligence in COVID-19 pandemic: a comprehensive review. Expert Syst. Appl. 185, 115695 (2021). https://doi.org/10.1016/j.eswa.2021.115695
Wieczorek, M., Siłka, J., Woźniak, M.: Neural network powered COVID-19 spread forecasting model. Chaos Solitons Fractals 140, 110203 (2020). https://doi.org/10.1016/j.chaos.2020.110203
Hssayeni, M.D., Chala, A., Dev, R., Xu, L., Shaw, J., Furht, B., Ghoraani, B.: The forecast of COVID-19 spread risk at the county level. J. Big Data 8(1), 99 (2021). https://doi.org/10.1186/s40537-021-00491-1
Haouari, M., Mhiri, M.: A particle swarm optimization approach for predicting the number of COVID-19 deaths. Sci. Rep. 11(1), 16587 (2021). https://doi.org/10.1038/s41598-021-96057-5
Salgotra, R., Gandomi, M., Gandomi, A.H.: Time series analysis and forecast of the COVID-19 pandemic in India using genetic programming. Chaos Solitons Fractals 138, 109945 (2020). https://doi.org/10.1016/j.chaos.2020.109945
Chimmula, V.K.R., Zhang, L.: Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 135, 109864 (2020). https://doi.org/10.1016/j.chaos.2020.109864
Zhao, C., Tepekule, B., Criscuolo, N.G., Wendel Garcia, P.D., Hilty, M.P., RISC-19-ICU Investigators for Switzerland, Fumeaux, T., Van Boeckel, T.: icumonitoring.ch: a platform for short-term forecasting of intensive care unit occupancy during the COVID-19 epidemic in Switzerland. Swiss Med. Wkly. 150, 20277 (2020). https://doi.org/10.4414/smw.2020.20277
Stanke, Z., Spouge, J.L.: Estimating age-stratified transmission and reproduction numbers during the early exponential phase of an epidemic: a case study with COVID-19 data. Epidemics 44, 100714 (2023). https://doi.org/10.1016/j.epidem.2023.100714
Sarker, I.H.: Machine learning: algorithms, real-world applications and research directions. SN Comput. Sci. 2(3), 160 (2021). https://doi.org/10.1007/s42979-021-00592-x
Vega, R., Flores, L., Greiner, R.: SIMLR: machine learning inside the SIR model for COVID-19 forecasting. Forecasting 4(1), 72–94 (2022). https://doi.org/10.3390/forecast4010005
Watson, G.L., Xiong, D., Zhang, L., Zoller, J.A., Shamshoian, J., Sundin, P., Bufford, T., Rimoin, A.W., Suchard, M.A., Ramirez, C.M.: Pandemic velocity: forecasting COVID-19 in the US with a machine learning & Bayesian time series compartmental model. PLoS Comput. Biol. 17(3), 1–20 (2021). https://doi.org/10.1371/journal.pcbi.1008837
Delli Compagni, R., Cheng, Z., Russo, S., Van Boeckel, T.P.: A hybrid neural network-SEIR model for forecasting intensive care occupancy in Switzerland during COVID-19 epidemics. PLoS ONE 17(3), 1–15 (2022). https://doi.org/10.1371/journal.pone.0263789
Botmart, T., Sabir, Z., Javeed, S., Sandoval Núñez, R.A., Wajaree weera, Ali, M.R., Sadat, R.: Artificial neural network-based heuristic to solve COVID-19 model including government strategies and individual responses. Inform. Med. Unlocked 32, 101028 (2022). https://doi.org/10.1016/j.imu.2022.101028
Alsayed, A., Sadir, H., Kamil, R., Sari, H.: Prediction of epidemic peak and infected cases for COVID-19 disease in Malaysia. Int. J. Environ. Res. Public Health 17(11) (2020). https://doi.org/10.3390/ijerph17114076. 2020
Liao, Z., Lan, P., Fan, X., Kelly, B., Innes, A., Liao, Z.: SIRVD-DL: a COVID-19 deep learning prediction model based on time-dependent SIRVD. Comput. Biol. Med. 138, 104868 (2021). https://doi.org/10.1016/j.compbiomed.2021.104868
Zheng, N., Du, S., Wang, J., Zhang, H., Cui, W., Kang, Z., Yang, T., Lou, B., Chi, Y., Long, H., Ma, M., Yuan, Q., Zhang, S., Zhang, D., Ye, F., Xin, J.: Predicting COVID-19 in China using hybrid AI model. IEEE Trans. Cybern. 50(7), 2891–2904 (2020). https://doi.org/10.1109/TCYB.2020.2990162
Ghafouri-Fard, S., Mohammad-Rahimi, H., Motie, P., Minabi, M.A.S., Taheri, M., Nateghinia, S.: Application of machine learning in the prediction of COVID-19 daily new cases: a scoping review. Heliyon 7(10), 08143 (2021). https://doi.org/10.1016/j.heliyon.2021.e08143
Adebayo Ifeoluwapo, R., Supriyanto, E., Taheri, S.: COVID-19 death risk assessment in Iran using Artificial Neural Network. J. Phys. Conf. Ser. 1964(6), 062117 (2021). https://doi.org/10.1088/1742-6596/1964/6/062117
Shanbehzadeh, M., Nopour, R., Kazemi-Arpanahi, H.: Developing an artificial neural network for detecting COVID-19 disease. Int. J. Health Promot. Educ. 11(2), 387 (2022). https://doi.org/10.4103/jehp.jehp_387
Abdulaal, A., Patel, A., Charani, E., Denny, S., Mughal, N., Moore, L.: Prognostic modeling of COVID-19 using Artificial Intelligence in the United Kingdom: model development and validation. J. Med. Internet Res. 22(8), 20259 (2020). https://doi.org/10.2196/20259
Yesilkanat, C.M.: Spatio-temporal estimation of the daily cases of COVID-19 in worldwide using random forest machine learning algorithm. Chaos Solitons Fractals 140, 110210 (2020). https://doi.org/10.1016/j.chaos.2020.110210
Moulaei, K., Shanbehzadeh, M., Mohammadi-Taghiabad, Z., Kazemi-Arpanahi, H.: Comparing machine learning algorithms for predicting COVID-19 mortality. BMC Med. Inform. Decis. Mak. 22(1), 2 (2022). https://doi.org/10.1186/s12911-021-01742-0
Assaf, D., Gutman, Y., Neuman, Y., Segal, G., Amit, S., Gefen-Halevi, S., Shilo, N., Epstein, A., Mor-Cohen, R., Biber, A., Rahav, G., Levy, I., Tirosh, A.: Utilization of machine-learning models to accurately predict the risk for critical COVID-19. Intern. Emerg. Medicine 15(8), 1435–1443 (2020). https://doi.org/10.1007/s11739-020-02475-0
da Silva, R.G., Ribeiro, M.H.D.M., Mariani, V.C., dos Santos Coelho, L.: Forecasting Brazilian and American COVID-19 cases based on artificial intelligence coupled with climatic exogenous variables. Chaos Solitons Fractals 139, 110027 (2020). https://doi.org/10.1016/j.chaos.2020.110027
Moslehi, S., Rabiei, N., Soltanian, A.R., Mamani, M.: Application of machine learning models based on decision trees in classifying the factors affecting mortality of COVID-19 patients in Hamadan, Iran. BMC Med. Inform. Decis. Mak. 22(1), 192 (2022). https://doi.org/10.1186/s12911-022-01939-x
Giotta, M., Trerotoli, P., Palmieri, V.O., Passerini, F., Portincasa, P., Dargenio, I., Mokhtari, J., Montagna, M.T., De Vito, D.: Application of a Decision Tree model to predict the outcome of non-intensive inpatients hospitalized for COVID-19. Int. J. Environ. Res. Public Health 19(20) (2022). https://doi.org/10.3390/ijerph192013016
Yao, H., Zhang, N., Zhang, R., Duan, M., Xie, T., Pan, J., Peng, E., Huang, J., Zhang, Y., Xu, X., Xu, H., Zhou, F., Wang, G.: Severity detection for the Coronavirus Disease 2019 (COVID-19) patients using a Machine Learning model based on the blood and urine tests. Front. Cell Dev. Biol. 8, 683 (2020). https://doi.org/10.3389/fcell.2020.00683
Fu, L., Li, Y., Cheng, A., Pang, P., Shu, Z.: A novel Machine Learning-derived Radiomic Signature of the whole lung differentiates stable from progressive COVID-19 infection: a retrospective cohort study. J. Thorac. Imaging 35(6) (2020)
Sun, L., Song, F., Shi, N., Liu, F., Li, S., Li, P., Zhang, W., Jiang, X., Zhang, Y., Sun, L., Chen, X., Shi, Y.: Combination of four clinical indicators predicts the severe/critical symptom of patients infected Covid-19. J. Clin. Virol. 128, 104431 (2020). https://doi.org/10.1016/j.jcv.2020.104431
Islam, M.Z., Islam, M.M., Asraf, A.: A combined deep CNN-LSTM network for the detection of novel coronavirus (COVID-19) using X-ray images. Inform. Med. Unlocked 20, 100412 (2020). https://doi.org/10.1016/j.imu.2020.100412
Arora, P., Kumar, H., Panigrahi, B.K.: Prediction and analysis of COVID-19 positive cases using deep learning models: a descriptive case study of India. Chaos Solitons Fractals 139, 110017 (2020). https://doi.org/10.1016/j.chaos.2020.110017
Niazkar, H.R., Niazkar, M.: Application of artificial neural networks to predict the COVID-19 outbreak. Glob. Health Res. Policy 5(1), 50 (2020). https://doi.org/10.1186/s41256-020-00175-y
Mollalo, A., Rivera, K.M., Vahedi, B.: Artificial neural network modeling of novel coronavirus (COVID-19) incidence rates across the continental United States. Int. J. Environ. Res. Public Health 17(12) (2020). https://doi.org/10.3390/ijerph17124204
Ribeiro, M.H.D.M., da Silva, R.G., Mariani, V.C., dos Santos Coelho, L.: Short-term forecasting COVID-19 cumulative confirmed cases: perspectives for Brazil. Chaos Solitons Fractals 135, 109853 (2020). https://doi.org/10.1016/j.chaos.2020.109853
Commandeur, J.F.F., Koopman, S.J.: An Introduction to State-Space Time Series Analysis, Practical Econometrics, 1st edn. Oxford University Press, Oxford, UK (2007)
Watson, O., Alhaffer, M., Mehchy, Z., Whittaker, C., et al.: Report 31: estimating the burden of COVID-19 in Damascus, Syria: an analysis of novel data sources to infer mortality under-ascertainment (2020). https://doi.org/10.25561/82443
Proverbio, D., Kemp, F., Magni, S., Ogorzaly, L., Cauchie, H.-M., Gonçalves, J., Skupind, A., Aalto, A.: Model-based assessment of COVID-19 epidemic dynamics by wastewater analysis. Sci. Total Environ. 827, 154235 (2022). https://doi.org/10.1016/j.scitotenv.2022.154235
Woolf, S.H., Chapman, D.A., Sabo, R.T., Weinberger, D.M., Hill, L., Taylor, D.D.H.: Excess deaths from COVID-19 and other causes, March–July 2020. JAMA 324(15), 1562–1564 (2020). https://doi.org/10.1001/jama.2020.19545
Achilleos, S., Quattrocchi, A., Gabel, J., Heraclides, A., Kolokotroni, O., Constantinou, C., Pagola Ugarte, M., Nicolaou, N., Rodriguez-Llanes, J.M., Bennett, C.M., Bogatyreva, E., Schernhammer, E., Zimmermann, C., Costa, A.J.L., Lobato, J.C.P., Fernandes, N.M., Semedo-Aguiar, A.P., Jaramillo Ramirez, G.I., Martin Garzon, O.D., Mortensen, L.H., Critchley, J.A., Goldsmith, L.P., Denissov, G., Rüütel, K., Le Meur, N., Kandelaki, L., Tsiklauri, S., O’Donnell, J., Oza, A., Kaufman, Z., Zucker, I., Ambrosio, G., Stracci, F., Hagen, T.P., Erzen, I., Klepac, P., Arcos González, P., Camporro, Á.F., Burström, B., Pidmurniak, N., Verstiuk, O., Huang, Q., Mehta, N.K., Polemitis, A., Charalambous, A., Demetriou, C.A.: Excess all-cause mortality and COVID-19-related mortality: a temporal analysis in 22 countries, from January until August 2020. Int. J. Epidemiol. 51(1), 35–53 (2020). https://doi.org/10.1093/ije/dyab123
Lee, D., Heo, K., Seo, Y.: COVID-19 in South Korea: lessons for developing countries. World Dev. 135, 105057 (2020). https://doi.org/10.1016/j.worlddev.2020.105057
Lindner, A.K., Sarma, N., Rust, L.M., Hellmund, T., Krasovski-Nikiforovs, S., Wintel, M., Klaes, S.M., Hoerig, M., Monert, S., Schwarzer, R., Edelmann, A., Martinez, G.E., Mockenhaupt, F.P., Kurth, T., Seybold, J.: Monitoring for COVID-19 by universal testing in a homeless shelter in Germany: a prospective feasibility cohort study. BMC Infect. Dis. 21(1), 1241 (2021). https://doi.org/10.1186/s12879-021-06945-4
O’Shea, T., Mbuagbaw, L., Mokashi, V., Bulir, D., Gilchrist, J., Smieja, N., Chong, S., Marttala, S., Vera, V., Cvetkovic, A., Smieja, M.: Comparison of four COVID-19 screening strategies to facilitate early case identification within the homeless shelter population: a structured summary of a study protocol for a randomised controlled trial. Trials 21(1), 941 (2020). https://doi.org/10.1186/s13063-020-04890-2
Silva, P.J.S., Pereira, T., Sagastizábal, C., Nonato, L., Cordova, M.M., Struchiner, C.J.: Smart testing and critical care bed sharing for COVID-19 control. PLoS ONE 16(10), 1–17 (2021). https://doi.org/10.1371/journal.pone.0257235
Arons, M.M., Hatfield, K.M., Reddy, S.C., Kimball, A., James, A., Jacobs, J.R., Taylor, J., Spicer, K., Bardossy, A.C., Oakley, L.P., Tanwar, S., Dyal, J.W., Harney, J., Chisty, Z., Bell, J.M., Methner, M., Paul, P., Carlson, C.M., McLaughlin, H.P., Thornburg, N., Tong, S., Tamin, A., Tao, Y., Uehara, A., Harcourt, J., Clark, S., Brostrom-Smith, C., Page, L.C., Kay, M., Lewis, J., Montgomery, P., Stone, N.D., Clark, T.A., Honein, M.A., Duchin, J.S., Jernigan, J.A.: Presymptomatic SARS-CoV-2 infections and transmission in a skilled nursing facility. N. Engl. J. Med. 382(22), 2081–2090 (2020). https://doi.org/10.1056/NEJMoa2008457
Nishiura, H., Kobayashi, T., Yang, Y., Hayashi, K., Miyama, T., Kinoshita, R., Linton, N.M., Jung, S.-m., Yuan, B., Suzuki, A., Akhmetzhanov, A.R.: The rate of underascertainment of Novel Coronavirus (2019-nCoV) infection: estimation using Japanese passengers data on evacuation flights. J. Clin. Med. 9(2) (2020). https://doi.org/10.3390/jcm9020419
Mizumoto, K., Kagaya, K., Zarebski, A., Chowell, G.: Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the diamond princess cruise ship. Euro Surveill. 25(10) (2020). https://doi.org/10.2807/1560-7917.ES.2020.25.10.2000180. 2020
Ing, A.J., Cocks, C., Green, J.P.: COVID-19: in the footsteps of Ernest Shackleton. Thorax 75(8), 693–694 (2020). https://doi.org/10.1136/thoraxjnl-2020-215091
Yoo, K.J., Kwon, S., Choi, Y., Bishai, D.M.: Systematic assessment of South Korea’s capabilities to control COVID-19. Health Policy 125(5), 568–576 (2021). https://doi.org/10.1016/j.healthpol.2021.02.011
Majeed, A., Seo, Y., Heo, K., Lee, D.: Can the UK emulate the South Korean approach to COVID-19? BMJ 369 (2020). https://doi.org/10.1136/bmj.m2084. https://www.bmj.com/content/369/bmj.m2084.full.pdf
Arroyo-Marioli, F., Bullano, F., Kucinskas, S., Rondón-Moreno, C.: Tracking R of COVID-19: a new real-time estimation using the Kalman filter. PLoS ONE 16(1), 1–16 (2021). https://doi.org/10.1371/journal.pone.0244474
Song, J., Xie, H., Gao, B., Zhong, Y., Gu, C., Choi, K.-S.: Maximum likelihood-based extended Kalman filter for COVID-19 prediction. Chaos Solitons Fractals 146, 110922 (2021). https://doi.org/10.1016/j.chaos.2021.110922
Koyama, S., Horie, T., Shinomoto, S.: Estimating the time-varying reproduction number of COVID-19 with a state-space method. PLoS Comput. Biol. 17(1), 1–18 (2021). https://doi.org/10.1371/journal.pcbi.1008679
Aslam, M.: Using the Kalman filter with ARIMA for the COVID-19 pandemic dataset of Pakistan. Data Brief 31, 105854 (2020). https://doi.org/10.1016/j.dib.2020.105854
Assimakis, N., Ktena, A., Manasis, C., Mele, E., Kunicina, N., Zabasta, A., Juhna, T.: Using the time varying Kalman filter for prediction of COVID-19 cases in Latvia and Greece. In: 2020 IEEE 61th International Scientific Conference on Power and Electrical Engineering of Riga Technical University (RTUCON), pp. 1–7 (2020). https://doi.org/10.1109/RTUCON51174.2020.9316598
Singh, K.K., Kumar, S., Dixit, P., Bajpai, M.K.: Kalman filter based short term prediction model for COVID-19 spread. Appl. Intell. 51(5), 2714–2726 (2021). https://doi.org/10.1007/s10489-020-01948-1
Flaxman, S., Mishra, S., Gandy, A., Unwin, H.J.T., Mellan, T.A., Coupland, H., Whittaker, C., Zhu, H., Berah, T., Eaton, J.W., Monod, M., Perez-Guzman, P.N., Schmit, N., Cilloni, L., Ainslie, K.E.C., Baguelin, M., Boonyasiri, A., Boyd, O., Cattarino, L., Cooper, L.V., Cucunubá, Z., Cuomo-Dannenburg, G., Dighe, A., Djaafara, B., Dorigatti, I., van Elsland, S.L., FitzJohn, R.G., Gaythorpe, K.A.M., Geidelberg, L., Grassly, N.C., Green, W.D., Hallett, T., Hamlet, A., Hinsley, W., Jeffrey, B., Knock, E., Laydon, D.J., Nedjati-Gilani, G., Nouvellet, P., Parag, K.V., Siveroni, I., Thompson, H.A., Verity, R., Volz, E., Walters, C.E., Wang, H., Wang, Y., Watson, O.J., Winskill, P., Xi, X., Walker, P.G.T., Ghani, A.C., Donnelly, C.A., Riley, S., Vollmer, M.A.C., Ferguson, N.M., Okell, L.C., Bhatt, S., Team, I.C.C.-.R.: Estimating the effects of non-pharmaceutical interventions on COVID-19 in Europe. Nature 584(7820), 257–261 (2020). https://doi.org/10.1038/s41586-020-2405-7
Ritchie, H., Mathieu, E., Rodés-Guirao, L., Appel, C., Giattino, C., Ortiz-Ospina, E., Hasell, J., Macdonald, B., Beltekian, D., Roser, M.: Coronavirus Pandemic (COVID-19). https://ourworldindata.org/coronavirus
Mathieu, E., Ritchie, H., Ortiz-Ospina, E., Roser, M., Hasell, J., Appel, C., Giattino, C., Rodés-Guirao, L.: A global database of COVID-19 vaccinations. Nat. Hum. Behav. 5(7), 947–953 (2021). https://doi.org/10.1038/s41562-021-01122-8
Hu, H., Nigmatulina, K., Eckhoff, P.: The scaling of contact rates with population density for the infectious disease models. Math. Biosci. 244(2), 125–134 (2013). https://doi.org/10.1016/j.mbs.2013.04.013
Read, J.M., Bridgen, J.R.E., Cummings, D.A.T., Ho, A., Jewell, C.P.: Novel coronavirus 2019-nCoV (COVID-19): early estimation of epidemiological parameters and epidemic size estimates. Philos. Trans. R. Soc. Lond. B, Biol. Sci. 376(1829), 20200265 (2021). https://doi.org/10.1098/rstb.2020.0265
Yap, F.F., Yong, M.: Implementation of a real-time, data-driven online epidemic calculator for tracking the spread of COVID-19 in Singapore and other countries. Infect. Dis. Model. 6, 1159–1172 (2021). https://doi.org/10.1016/j.idm.2021.10.002
Rawat, S., Deb, S.: A spatio-temporal statistical model to analyze COVID-19 spread in the USA. J. Appl. Stat. 50(11–12), 2310–2329 (2023). https://doi.org/10.1080/02664763.2021.1970122
Bergquist, S., Otten, T., Sarich, N.: COVID-19 pandemic in the United States. Health Policy Technol. 9(4), 623–638 (2020). https://doi.org/10.1016/j.hlpt.2020.08.007
Unwin, H.J.T., Mishra, S., Bradley, V.C., Gandy, A., Mellan, T.A., Coupland, H., Ish-Horowicz, J., Vollmer, M.A.C., Whittaker, C., Filippi, S.L., Xi, X., Monod, M., Ratmann, O., Hutchinson, M., Valka, F., Zhu, H., Hawryluk, I., Milton, P., Ainslie, K.E.C., Baguelin, M., Boonyasiri, A., Brazeau, N.F., Cattarino, L., Cucunuba, Z., Cuomo-Dannenburg, G., Dorigatti, I., Eales, O.D., Eaton, J.W., van Elsland, S.L., FitzJohn, R.G., Gaythorpe, K.A.M., Green, W., Hinsley, W., Jeffrey, B., Knock, E., Laydon, D.J., Lees, J., Nedjati-Gilani, G., Nouvellet, P., Okell, L., Parag, K.V., Siveroni, I., Thompson, H.A., Walker, P., Walters, C.E., Watson, O.J., Whittles, L.K., Ghani, A.C., Ferguson, N.M., Riley, S., Donnelly, C.A., Bhatt, S., Flaxman, S.: State-level tracking of COVID-19 in the United States. Nat. Commun. 11(1), 6189 (2020). https://doi.org/10.1038/s41467-020-19652-6
Billah, M.A., Miah, M.M., Khan, M.N.: Reproductive number of coronavirus: a systematic review and meta-analysis based on global level evidence. PLoS ONE 15(11), 1–17 (2020). https://doi.org/10.1371/journal.pone.0242128
Lewes, F.M.M.: A note on the origin of the net reproduction ratio. Popul. Stud. 38(2), 321–324 (1984). Accessed 2023-08-13
Levin, B.R., Bull, J.J., Stewart, F.M.: The intrinsic rate of increase of HIV/AIDS: epidemiological and evolutionary implications. Math. Biosci. 132(1), 69–96 (1996). https://doi.org/10.1016/0025-5564(95)00053-4
Li, Q., Guan, X., Wu, P., Wang, X., Zhou, L., Tong, Y., Ren, R., Leung, K.S.M., Lau, E.H.Y., Wong, J.Y., Xing, X., Xiang, N., Wu, Y., Li, C., Chen, Q., Li, D., Liu, T., Zhao, J., Liu, M., Tu, W., Chen, C., Jin, L., Yang, R., Wang, Q., Zhou, S., Wang, R., Liu, H., Luo, Y., Liu, Y., Shao, G., Li, H., Tao, Z., Yang, Y., Deng, Z., Liu, B., Ma, Z., Zhang, Y., Shi, G., Lam, T.T.Y., Wu, J.T., Gao, G.F., Cowling, B.J., Yang, B., Leung, G.M., Feng, Z.: Early transmission dynamics in Wuhan, China, of novel coronavirus–infected pneumonia. N. Engl. J. Med. 382(13), 1199–1207 (2020). https://doi.org/10.1056/NEJMoa2001316
Lloyd, A.L.: The dependence of viral parameter estimates on the assumed viral life cycle: limitations of studies of viral load data. Proc. R. Soc. Lond. B, Biol. Sci. 268(1469), 847–854 (2001). https://doi.org/10.1098/rspb.2000.1572
Wearing, H.J., Rohani, P., Keeling, M.J.: Appropriate models for the management of infectious diseases. PLoS Med. 2(7) (2005). https://doi.org/10.1371/journal.pmed.0020174
Lai, A., Bergna, A., Acciarri, C., Galli, M., Zehender, G.: Early phylogenetic estimate of the effective reproduction number of SARS-CoV-2. J. Med. Virol. 92(6), 675–679 (2020). https://doi.org/10.1002/jmv.25723
Kuniya, T.: Prediction of the epidemic peak of coronavirus disease in Japan, 2020. J. Clin. Med. 9(3) (2020). https://doi.org/10.3390/jcm9030789
Zhang, S., Diao, M., Yu, W., Pei, L., Lin, Z., Chen, D.: Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: a data-driven analysis. Int. J. Infect. Dis. 93, 201–204 (2020). https://doi.org/10.1016/j.ijid.2020.02.033
Wallinga, J., Lipsitch, M.: How generation intervals shape the relationship between growth rates and reproductive numbers. Proc. Biol. Sci. 274(1609), 599–604 (2007). https://doi.org/10.1098/rspb.2006.3754
Hong, H.G., Li, Y.: Estimation of time-varying reproduction numbers underlying epidemiological processes: a new statistical tool for the COVID-19 pandemic. PLoS ONE 15(7), 0236464 (2020). https://doi.org/10.1371/journal.pone.0236464
Ferretti, L., Wymant, C., Kendall, M., Zhao, L., Nurtay, A., Abeler-Dörner, L., Parker, M., Bonsall, D., Fraser, C.: Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 368(6491), 6936 (2020). https://doi.org/10.1126/science.abb6936
Wallinga, J., Teunis, P.: Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am. J. Epidemiol. 160(6), 509–516 (2004). https://doi.org/10.1093/aje/kwh255. https://academic.oup.com/aje/article-pdf/160/6/509/179728/kwh255.pdf
Lipsitch, M., Cohen, T., Cooper, B., Robins, J.M., Ma, S., James, L., Gopalakrishna, G., Chew, S.K., Tan, C.C., Samore, M.H., Fisman, D., Murray, M.: Transmission dynamics and control of severe acute respiratory syndrome. Science 300(5627), 1966–1970 (2003). https://doi.org/10.1126/science.1086616
Anderson, R.M., Medley, G.F., May, R.M., Johnson, A.M.: A preliminary study of the transmission dynamics of the human immunodeficiency virus (HIV), the causative agent of AIDS. IMA J. Math. Appl. Med. Biol. 3(4), 229–263 (1986). https://doi.org/10.1093/imammb/3.4.229
Sharpe, F.R., Lotka, A.J.: L. a problem in age-distribution. Lond. Edinb. Dublin Philos. Mag. J. Sci. 21(124), 435–438 (1911). https://doi.org/10.1080/14786440408637050
MacDonald, G.: The analysis of equilibrium in malaria. Trop. Dis. Bull. 49(9), 813–829 (1952)
Hethcote, H.W., Van Ark, J.W.: Epidemiological models for heterogeneous populations: proportionate mixing, parameter estimation, and immunization programs. Math. Biosci. 84(1), 85–118 (1987). https://doi.org/10.1016/0025-5564(87)90044-7
Hethcote, H.W.: The basic epidemiology models: models, expressions for \(\mathcal{R}_{0}\), parameter estimation, and application, pp. 1–61. https://doi.org/10.1142/9789812834836_0001
Hethcote, H.W., Yorke, J.A.: Gonorrhea transmission dynamics and control. In: Levin, S.A. (ed.) Lecture Notes in Biomathematics, vol. 56. Springer, Berlin (1984). https://api.semanticscholar.org/CorpusID:70938668
Diekmann, O., Heesterbeek, J.A.P., Metz, J.A.J.: On the definition and the computation of the basic reproduction ratio \(\mathcal{R}_{0}\) in models for infectious diseases in heterogeneous populations. J. Math. Biol. 28(4), 365–382 (1990). https://doi.org/10.1007/BF00178324
Diekmann, O., Heesterbeek, J.A.P., Roberts, M.G.: The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 7(47), 873–885 (2010). https://doi.org/10.1098/rsif.2009.0386
van den Driessche, P., Watmough, J.: Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 180(1), 29–48 (2002). https://doi.org/10.1016/S0025-5564(02)00108-6
Heesterbeek, H.: 5 - the law of mass-action in epidemiology: a historical perspective. In: Cuddington, K., Beisner, B.E. (eds.) Ecological Paradigms Lost, pp. 81–105. Academic Press, Burlington (2005). https://doi.org/10.1016/B978-012088459-9/50007-8
Ferner, R.E., Aronson, J.K.: Cato Guldberg and Peter Waage, the history of the Law of Mass Action, and its relevance to clinical pharmacology. Br. J. Clin. Pharmacol. 81(1), 52–55 (2016). https://doi.org/10.1111/bcp.12721
Adleman, L., Gopalkrishnan, M., Huang, M.-d., Moisset, P., Reishus, D.: 1. On the Mathematics of the Law of Mass Action pp. 3–46. Springer, Dordrecht (2008). https://doi.org/10.1007/978-94-017-9041-3_1
Brauer, F., Castillo-Chávez, C., Feng, Z.: Mathematical Models in Epidemiology. Springer, Netherlands (2019). https://doi.org/10.1007/978-1-4939-9828-9
Tang, J.W., Caniza, M.A., Dinn, M., Dwyer, D.E., Heraud, J.-M., Jennings, L.C., Kok, J., Kwok, K.O., Li, Y., Loh, T.P., Marr, L.C., Nara, E.M., Perera, N., Saito, R., Santillan-Salas, C., Sullivan, S., Warner, M., Watanabe, A., Zaidi, S.K.: An exploration of the political, social, economic and cultural factors affecting how different global regions initially reacted to the COVID-19 pandemic. Interface Focus 12(2), 20210079 (2022). https://doi.org/10.1098/rsfs.2021.0079
Suvilehto, J.T., Nummenmaa, L., Harada, T., Dunbar, R.I.M., Hari, R., Turner, R., Sadato, N., Kitada, R.: Cross-cultural similarity in relationship-specific social touching. Proc. Biol. Sci. 286(1901), 20190467 (2019). https://doi.org/10.1098/rspb.2019.0467
Elliott, P., Haw, D., Wang, H., Eales, O., Walters, C.E., Ainslie, K.E.C., Atchison, C., Fronterre, C., Diggle, P.J., Page, A.J., Trotter, A.J., Prosolek, S.J., Ashby, D., Donnelly, C.A., Barclay, W., Taylor, G., Cooke, G., Ward, H., Darzi, A., Riley, S.: Exponential growth, high prevalence of SARS-CoV-2, and vaccine effectiveness associated with the Delta variant. Science 374(6574), 9551 (2021). https://doi.org/10.1126/science.abl9551
Bolze, A., Luo, S., White, S., Cirulli, E.T., Wyman, D., Dei Rossi, A., Machado, H., Cassens, T., Jacobs, S., Schiabor Barrett, K.M., Tanudjaja, F., Tsan, K., Nguyen, J., Ramirez, I.J.M., Sandoval, E., Wang, X., Wong, D., Becker, D., Laurent, M., Lu, J.T., Isaksson, M., Washington, N.L., Lee, W.: SARS-CoV-2 variant Delta rapidly displaced variant Alpha in the United States and led to higher viral loads. Cell Rep. Med. 3(3) (2022). https://doi.org/10.1016/j.xcrm.2022.100564
Lopez Bernal, J., Andrews, N., Gower, C., Gallagher, E., Simmons, R., Thelwall, S., Stowe, J., Tessier, E., Groves, N., Dabrera, G., Myers, R., Campbell, C.N.J., Amirthalingam, G., Edmunds, M., Zambon, M., Brown, K.E., Hopkins, S., Chand, M., Ramsay, M.: Effectiveness of COVID-19 vaccines against the B.1.617.2 (Delta) Variant. N. Engl. J. Med. 385(7), 585–594 (2021). https://doi.org/10.1056/NEJMoa2108891
Boschi, C., Aherfi, S., Houhamdi, L., Colson, P., Raoult, D., Scola, B.L.: Isolation of 4000 SARS-CoV-2 shows that contagiousness is associated with viral load, not vaccine or symptomatic status. Emerg. Microbes Infect. 10(1), 2276–2278 (2021). https://doi.org/10.1080/22221751.2021.2008776
Chau, N.V.V., Ngoc, N.M., Nguyet, L.A., Quang, V.M., Ny, N.T.H., Khoa, D.B., Phong, N.T., Toan, L.M., Hong, N.T.T., Tuyen, N.T.K., Phat, V.V., Nhu, L.N.T., Truc, N.H.T., That, B.T.T., Thao, H.P., Thao, T.N.P., Vuong, V.T., Tam, T.T.T., Tai, N.T., Bao, H.T., Nhung, H.T.K., Minh, N.T.N., Tien, N.T.M., Huy, N.C., Choisy, M., Man, D.N.H., Ty, D.T.B., Anh, N.T., Uyen, L.T.T., Tu, T.N.H., Yen, L.M., Dung, N.T., Hung, L.M., Truong, N.T., Thanh, T.T., Thwaites, G., Tan, L.V.: An observational study of breakthrough SARS-CoV-2 Delta variant infections among vaccinated healthcare workers in Vietnam. eClinicalMedicine 41 (2021). https://doi.org/10.1016/j.eclinm.2021.101143
Brown, C.M., Vostok, J., Johnson, H., Burns, M., Gharpure, R., Sami, S., Sabo, R.T., Hall, N., Foreman, A., Schubert, P.L., Gallagher, G.R., Fink, T., Madoff, L.C., Gabriel, S.B., MacInnis, B., Park, D.J., Siddle, K.J., Harik, V., Arvidson, D., Brock-Fisher, T., Dunn, M., Kearns, A., Laney, A.S.: Outbreak of SARS-CoV-2 infections, including COVID-19 vaccine breakthrough infections, associated with large public gatherings – Barnstable County. Morb. Mort. Wkly. Rep. 70(31), 1059–1062 (2021). https://doi.org/10.15585/mmwr.mm7031e2
Gharpure, R., Sami, S., Vostok, J., Johnson, H., Hall, N., Foreman, A., Sabo, R.T., Schubert, P.L., Shephard, H., Brown, V.R., Brumfield, B., Ricaldi, J.N., Conley, A.B., Zielinski, L., Malec, L., Newman, A.P., Chang, M., Finn, L.E., Stainken, C., Mangla, A.T., Eteme, P., Wieck, M., Green, A., Edmundson, A., Reichbind, D., Brown, V.J., Quiñones, L., Longenberger, A., Hess, E., Gumke, M., Manion, A., Thomas, H., Barrios, C.A., Koczwara, A., Williams, T.W., Pearlowitz, M., Assoumou, M., Senisse Pajares, A.F., Dishman, H., Schardin, C., Wang, X., Stephens, K., Moss, N.S., Singh, G., Feaster, C., Webb, L.M., Krueger, A., Dickerson, K., Dewart, C., Barbeau, B., Salmanson, A., Madoff, L.C., Villanueva, J.M., Brown, C.M., Laney, A.S.: Multistate outbreak of SARS-CoV-2 infections, including vaccine breakthrough infections, associated with large public gatherings, United States. Emerg. Infect. Dis. 28(1), 35–43 (2022). https://doi.org/10.3201/eid2801.212220
Bruxvoort, K.J., Sy, L.S., Qian, L., Ackerson, B.K., Luo, Y., Lee, G.S., Tian, Y., Florea, A., Aragones, M., Tubert, J.E., Takhar, H.S., Ku, J.H., Paila, Y.D., Talarico, C.A., Tseng, H.F.: Effectiveness of mRNA-1273 against delta, mu, and other emerging variants of SARS-CoV-2: test negative case-control study. BMJ 375 (2021). https://doi.org/10.1136/bmj-2021-068848. https://www.bmj.com/content/375/bmj-2021-068848.full.pdf
Pouwels, K.B., Pritchard, E., Matthews, P.C., Stoesser, N., Eyre, D.W., Vihta, K.-D., House, T., Hay, J., Bell, J.I., Newton, J.N., Farrar, J., Crook, D., Cook, D., Rourke, E., Studley, R., Peto, T.E.A., Diamond, I., Walker, A.S.: Effect of Delta variant on viral burden and vaccine effectiveness against new SARS-CoV-2 infections in the UK. Nat. Med. 27(12), 2127–2135 (2021). https://doi.org/10.1038/s41591-021-01548-7
Bolze, A., Luo, S., White, S., Cirulli, E.T., Wyman, D., Dei Rossi, A., Machado, H., Cassens, T., Jacobs, S., Schiabor Barrett, K.M., Tanudjaja, F., Tsan, K., Nguyen, J., Ramirez, I.J.M., Sandoval, E., Wang, X., Wong, D., Becker, D., Laurent, M., Lu, J.T., Isaksson, M., Washington, N.L., Lee, W.: SARS-CoV-2 variant delta rapidly displaced variant Alpha in the United States and Led to Higher Viral Loads: supplemental data. https://public.tableau.com/app/profile/helix6052/viz/HelixSARS-CoV-2LineagesofInterest/Lineages
Yap, F.F., Yong, M.:. COVID-19 Heat Map. https://cv19.one/us-map/
Kläser, K., Molteni, E., Graham, M., Canas, L.S., Österdahl, M.F., Antonelli, M., Chen, L., Deng, J., Murray, B., Kerfoot, E., Wolf, J., May, A., Fox, B., Capdevila, J., The COVID-19 Genomics U. K. (COG-UK) Consortium, Aanensen, D.M., Abudahab, K., Adams, H., Adams, A., Afifi, S., Aggarwal, D., Ahmad, S.S.Y., Aigrain, L., Alcolea-Medina, A., Alikhan, N.-F., Allara, E., Amato, R., Angyal, A., Annett, T., Aplin, S., Ariani, C.V., Asad, H., Ash, A., Ashfield, P., Ashford, F., Atkinson, L., Attwood, S.W., Auckland, C., Aydin, A., Baker, D.J., Baker, P., Balcazar, C.E., Ball, J., Barrett, J.C., Barrow, M., Barton, E., Bashton, M., Bassett, A.R., Batra, R., Baxter, C., Bayzid, N., Beaver, C., Beckett, A.H., Beckwith, S.M., Bedford, L., Beer, R., Beggs, A., Bellis, K.L., Berry, L., Bertolusso, B., Best, A., Betteridge, E., Bibby, D., Bicknell, K., Binns, D., Birchley, A., Bird, P.W., Bishop, C., Blacow, R., Blakey, V., Blane, B., Bolt, F., Bonfield, J., Bonner, S., Bonsall, D., Boswell, T., Bosworth, A., Bourgeois, Y., Boyd, O., Bradley, D.T., Breen, C., Bresner, C., Breuer, J., Bridgett, S., Bronner, I.F., Brooks, E., Broos, A., Brown, J.R., Bucca, G., Buchan, S.L., Buck, D., Bull, M., Burns, P.J., Burton-Fanning, S., Byaruhanga, T., Byott, M., Campbell, S., Carabelli, A.M., Cargill, J.S., Carlile, M., Carvalho, S.F., Casey, A., Castigador, A., Catalan, J., Chalker, V., Chaloner, N.J., Chand, M., Chappell, J.G., Charalampous, T., Chatterton, W., Chaudhry, Y., Churcher, C.M., Clark, G., Clarke, P., Cogger, B.J., Cole, K., Collins, J., Colquhoun, R., Connor, T.R., Cook, K.F., Coombes, J., Corden, S., Cormie, C., Cortes, N., Cotic, M., Cotton, S., Cottrell, S., Coupland, L., Cox, M., Cox, A., Craine, N., Crawford, L., Cross, A., Crown, M.R., Crudgington, D., Cumley, N., Curran, T., Curran, M.D., da Silva Filipe, A., Dabrera, G., Darby, A.C., Davidson, R.K., Davies, A., Davies, R.M., Davis, T., de Angelis, D., De Lacy, E., de Oliveira Martins, L., de Silva, T.I., Debebe, J., Denton-Smith, R., Dervisevic, S., Dewar, R., Dey, J., Dias, J., Dobie, D., Dorman, M.J., Downing, F., Driscoll, M., du Plessis, L., Duckworth, N., Durham, J., Eastick, K., Easton, L.J., Eccles, R., Edgeworth, J., Edwards, S., Bouzidi, K.E., Eldirdiri, S., Ellaby, N., Elliott, S., Eltringham, G., Ensell, L., Erkiert, M.J., Zamudio, M.E., Essex, S., Evans, J.M., Evans, C., Everson, W., Fairley, D.J., Fallon, K., Fanaie, A., Farr, B.W., Fearn, C., Feltwell, T., Ferguson, L., Fina, L., Flaviani, F., Fleming, V.M., Forrest, S., Foster-Nyarko, E., Foulkes, B.H., Foulser, L., Fragakis, M., Frampton, D., Francois, S., Fraser, C., Freeman, T.M., Fryer, H., Fuchs, M., Fuller, W., Gajee, K., Galai, K., Gallagher, A., Gallagher, E., Gallagher, M.D., Gallis, M., Gaskin, A., Gatica-Wilcox, B., Geidelberg, L., Gemmell, M., Georgana, I., George, R.P., Gifford, L., Gilbert, L., Girgis, S.T., Glaysher, S., Goldstein, E.J., Golubchik, T., Gomes, A.N., Gonçalves, S., Goodfellow, I.G., Goodwin, S., Goudarzi, S., Gourtovaia, M., Graham, C., Graham, L., Grant, P.R., Green, L.R., Green, A., Greenaway, J., Gregory, R., Guest, M., Gunson, R.N., Gupta, R.K., Gutierrez, B., Haldenby, S.T., Hamilton, W.L., Hansford, S.E., Haque, T., Harris, K.A., Harrison, I., Harrison, E.M., Hart, J., Hartley, J.A., Harvey, W.T., Harvey, M., Hassan-Ibrahim, M.O., Heaney, J., Helmer, T., Henderson, J.H., Hesketh, A.R., Hey, J., Heyburn, D., Higginson, E.E., Hill, V., Hill, J.D., Hilson, R.A., Hilvers, E., Holden, M.T.G., Hollis, A., Holmes, C.W., Holmes, N., Holmes, A.H., Hopes, R., Hornsby, H.R., Hosmillo, M., Houlihan, C., Howson-Wells, H.C., Hsu, S.N., Hubb, J., Huckson, H., Hughes, W., Hughes, J., Hughes, M., Hutchings, S., Idle, G., Illingworth, C.J., Impey, R., Irish-Tavares, D., Iturriza-Gomara, M., Izuagbe, R., Jackson, C., Jackson, B., Jackson, L.M., Jackson, K.A., Jackson, D.K., Jahun, A.S., James, V., James, K., Jeanes, C., Jeffries, A.R., Jeremiah, S., Jermy, A., John, M., Johnson, R., Johnson, K., Johnston, I., Jones, O., Jones, S.: COVID-19 due to the B.1.617.2 (Delta) variant compared to B.1.1.7 (Alpha) variant of SARS-CoV-2: a prospective observational cohort study Sci. Rep. 12(1), 10904 (2022). https://doi.org/10.1038/s41598-022-14016-0
Agrawal, B.: Heterologous immunity: role in natural and vaccine-induced resistance to infections. Front. Immunol. 10, 2631 (2019). https://doi.org/10.3389/fimmu.2019.02631
de Silva, E., Stumpf, M.P.H.: HIV and the CCR5-δ32 resistance allele. FEMS Microbiol. Lett. 241(1), 1–12 (2004)
Piel, F.B., Patil, A.P., Howes, R.E., Nyangiri, O.A., Gething, P.W., Williams, T.N., Weatherall, D.J., Hay, S.I.: Global distribution of the sickle cell gene and geographical confirmation of the malaria hypothesis. Nat. Commun. 1(1), 104 (2010). https://doi.org/10.1038/ncomms1104
Gabriel, S.E., Brigman, K.N., Koller, B.H., Boucher, R.C., Stutts, M.J.: Cystic Fibrosis heterozygote resistance to Cholera toxin in the Cystic Fibrosis mouse model. Science 266(5182), 107–109 (1994). https://doi.org/10.1126/science.7524148
Population sizes and densities for countries and states. https://worldpopulationreview.com
Davies, N.G., Klepac, P., Liu, Y., Prem, K., Jit, M., Pearson, C.A.B., Quilty, B.J., Kucharski, A.J., Gibbs, H., Clifford, S., Gimma, A., van Zandvoort, K., Munday, J.D., Diamond, C., Edmunds, W.J., Houben, R.M.G.J., Hellewell, J., Russell, T.W., Abbott, S., Funk, S., Bosse, N.I., Sun, Y.F., Flasche, S., Rosello, A., Jarvis, C.I., Eggo, R.M.: Working group, C.C.-.: Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat. Med. 26(8), 1205–1211 (2020). https://doi.org/10.1038/s41591-020-0962-9
Guo, W., Li, M., Dong, Y., Zhou, H., Zhang, Z., Tian, C., Qin, R., Wang, H., Shen, Y., Du, K., Zhao, L., Fan, H., Luo, S., Hu, D.: Diabetes is a risk factor for the progression and prognosis of COVID-19. Diabetes/Metab. Res. Rev. 36, 3319 (2020). https://doi.org/10.1002/dmrr.3319
Singh, A.K., Gupta, R., Ghosh, A., Misra, A.: Diabetes in COVID-19: prevalence, pathophysiology, prognosis and practical considerations. Diabetes Metab. Syndr. 14(4), 303–310 (2020). https://doi.org/10.1016/j.dsx.2020.04.004
Brooks, J.: The sad and tragic life of Typhoid Mary. CMAJ, Can. Med. Assoc. J. 154(6), 915–916 (1996)
Ogata, T., Tanaka, H., Irie, F., Nozawa, Y., Noguchi, E., Seo, K., Tanaka, E.: A low proportion of asymptomatic COVID-19 patients with the Delta variant infection by viral transmission through household contact at the time of confirmation in Ibaraki, Japan. Glob. Health Med. 4(3), 192–196 (2022). https://doi.org/10.35772/ghm.2021.01116
Jain, N., Hung, I.-C., Kimura, H., Goh, Y.L., Jau, W., Huynh, K.L.A., Panag, D.S., Tiwari, R., Prasad, S., Manirambona, E., Vasanthakumaran, T., Amanda, T.W., Lin, H.-W., Vig, N., An, N.T., Uwiringiyimana, E., Popkova, D., Lin, T.-H., Nguyen, M.A., Jain, S., Umar, T.P., Suleman, M.H., Efendi, E., Kuo, C.-Y., Bansal, S.P.S., Kauškale, S., Peng, H.-H., Bains, M., Rozevska, M., Tran, T.H., Tsai, M.-S., Pahulpreet, J.S., Tai, R.-Z., Khan, Z.A., Huy, D.T., Kositbovornchai, S., Chiu, C.-W., Nguyen, T.H.H., Chen, H.-Y., Khongyot, T., Chen, K.-Y., Quyen, D.T.K., Lam, J., Dila, K.A.S., Cu, N.T., Thi, M.T.H., Dung, L.A., Thi, K.O.N., Thi, H.A.N., Trieu, M.D.T., Thi, Y.C., Pham, T.T., Ariyoshi, K., Smith, C., Huy, N.T.: The global response: how cities and provinces around the globe tackled COVID-19 outbreaks in 2021. The Lancet Regional Health – Southeast Asia 4 (2022). https://doi.org/10.1016/j.lansea.2022.100031
Nilsen, P., Seing, I., Ericsson, C., Andersen, O., Stefánsdóttir, N.T., Tjørnhøj-Thomsen, T., Kallemose, T., Kirk, J.W.: Implementing social distancing policy measures in the battle against the coronavirus: protocol of a comparative study of Denmark and Sweden. Implement. Sci. Commun. 1(1), 77 (2020). https://doi.org/10.1186/s43058-020-00065-x
Sitti, A., Hotnier, S., Tomo, H., Tini, A., Siti, M., Agustinus, H., Muhamad, I.: The barriers of policy implementation of handling Covid-19 pandemic in Indonesia. Eur. J. Mol. Clin. Med. 8(1), 1222–1241 (2021). https://ejmcm.com/article__1b62967de65b0c73a21d0ddeea9002bf6798.pdf
Stockenhuber, R.: Did we respond quickly enough? How policy-implementation speed in response to COVID-19 affects the number of fatal cases in Europe. World Med. Health Policy 12(4), 413–429 (2020). https://doi.org/10.1002/wmh3.374
Chen, H., Shi, L., Zhang, Y., Wang, X., Jiao, J., Yang, M., Sun, G.: Response to the COVID-19 pandemic: comparison of strategies in six countries. Front. Public Health 9, 708496 (2021). https://doi.org/10.3389/fpubh.2021.708496
Walker, P.G.T., Whittaker, C., Watson, O.J., Baguelin, M., Winskill, P., Hamlet, A., Djafaara, B.A., Cucunubá, Z., Mesa, D.O., Green, W., Thompson, H., Nayagam, S., Ainslie, K.E.C., Bhatia, S., Bhatt, S., Boonyasiri, A., Boyd, O., Brazeau, N.F., Cattarino, L., Cuomo-Dannenburg, G., Dighe, A., Donnelly, C.A., Dorigatti, I., van Elsland, S.L., FitzJohn, R., Fu, H., Gaythorpe, K.A.M., Geidelberg, L., Grassly, N., Haw, D., Hayes, S., Hinsley, W., Imai, N., Jorgensen, D., Knock, E., Laydon, D., Mishra, S., Nedjati-Gilani, G., Okell, L.C., Unwin, H.J., Verity, R., Vollmer, M., Walters, C.E., Wang, H., Wang, Y., Xi, X., Lalloo, D.G., Ferguson, N.M., Ghani, A.C.: The impact of COVID-19 and strategies for mitigation and suppression in low- and middle-income countries. Science 369(6502), 413–422 (2020). https://doi.org/10.1126/science.abc0035
Ludvigsson, J.F.: The first eight months of Sweden’s COVID-19 strategy and the key actions and actors that were involved. Acta Pædiatr. 109(12), 2459–2471 (2020). https://doi.org/10.1111/apa.15582
Paterlini, M.: What now for Sweden and COVID-19? BMJ 375 (2021). https://doi.org/10.1136/bmj.n3081. https://www.bmj.com/content/375/bmj.n3081.full.pdf
Van Egeren, D., Novokhodko, A., Stoddard, M., Tran, U., Zetter, B., Rogers, M., Pentelute, B.L., Carlson, J.M., Hixon, M., Joseph-McCarthy, D., Chakravarty, A.: Risk of rapid evolutionary escape from biomedical interventions targeting SARS-CoV-2 spike protein. PLoS ONE 16(4), 1–17 (2021). https://doi.org/10.1371/journal.pone.0250780
Barrett, C., Koyama, A., Alvarez, P., et al.: Risk for newly diagnosed diabetes >30 days after SARS-CoV MMWR Morb Mortal Wkly Rep-2 Infection among persons aged <18 years — United States, March 1, 2020–June 28, 2021. Morb. Mort. Wkly. Rep. 71, 59–65 (2022)
Dar-Odeh, N., Abu-Hammad, O., Qasem, F., Jambi, S., Alhodhodi, A., Othman, A., Abu-Hammad, A., Al-Shorman, H., Ryalat, S., Abu-Hammad, S.: Long-term adverse events of three COVID-19 vaccines as reported by vaccinated physicians and dentists, a study from Jordan and Saudi Arabia. Hum. Vaccin. Immunother. 18(1), 2039017 (2022). https://doi.org/10.1080/21645515.2022.2039017
Majeed, A., Papaluca, M., Molokhia, M.: Assessing the long-term safety and efficacy of COVID-19 vaccines. J. R. Soc. Med. 114(7), 337–340 (2021). https://doi.org/10.1177/01410768211013437
Lopez-Leon, S., Wegman-Ostrosky, T., Perelman, C., Sepulveda, R., Rebolledo, P.A., Cuapio, A., Villapol, S.: More than 50 long-term effects of COVID-19: a systematic review and meta-analysis. Sci. Rep. 11(1), 16144 (2021). https://doi.org/10.1038/s41598-021-95565-8
Buchan, S.A., Seo, C.Y., Johnson, C., Alley, S., Kwong, J.C., Nasreen, S., Calzavara, A., Lu, D., Harris, T.M., Yu, K., Wilson, S.E.: Epidemiology of Myocarditis and Pericarditis following mRNA vaccination by vaccine product, schedule, and interdose interval among adolescents and adults in Ontario Canada. JAMA Netw. Open 5(6), 2218505 (2022). https://doi.org/10.1001/jamanetworkopen.2022.18505. https://jamanetwork.com/journals/jamanetworkopen/articlepdf/2793551/buchan_2022_oi_220537_1655221490.69116.pdf
Weintraub, E.S., Oster, M.E., Klein, N.P.: Myocarditis or pericarditis following mRNA COVID-19 vaccination. JAMA Netw. Open 5(6), 2218512 (2022). https://doi.org/10.1001/jamanetworkopen.2022.18512. https://jamanetwork.com/journals/jamanetworkopen/articlepdf/2793555/weintraub_2022_ic_220111_1655221508.87623.pdf
Karlstad, Ø., Hovi, P., Husby, A., Härkänen, T., Selmer, R.M., Pihlström, N., Hansen, J.V., Nohynek, H., Gunnes, N., Sundström, A., Wohlfahrt, J., Nieminen, T.A., Grünewald, M., Gulseth, H.L., Hviid, A., Ljung, R.: SARS-CoV-2 vaccination and myocarditis in a nordic cohort study of 23 million residents. JAMA Cardiol. 7(6), 600–612 (2022). https://doi.org/10.1001/jamacardio.2022.0583. https://jamanetwork.com/journals/jamacardiology/articlepdf/2791253/jamacardiology_karlstad_2022_oi_220012_1654532426.73967.pdf
Hanson, K.E., Goddard, K., Lewis, N., Fireman, B., Myers, T.R., Bakshi, N., Weintraub, E., Donahue, J.G., Nelson, J.C., Xu, S., Glanz, J.M., Williams, J.T.B., Alpern, J.D., Klein, N.P.: Incidence of Guillain-Barré syndrome after COVID-19 vaccination in the vaccine safety datalink. JAMA Netw. Open 5(4), 228879 (2022). https://doi.org/10.1001/jamanetworkopen.2022.8879. https://jamanetwork.com/journals/jamanetworkopen/articlepdf/2791533/hanson_2022_oi_220270_1650297826.97397.pdf
Groves, H.E., Papenburg, J., Mehta, K., Bettinger, J.A., Sadarangani, M., Halperin, S.A., Morris, S.K., Bancej, C., Burton, C., Embree, J., Foo, C., Bridger, N., Morris, R., Jadavji, T., Lebel, M., Le Saux, N., Top, K.A., Tan, B., McConnell, A., Purewal, R., Déry, P., Thibeault, R., Vaudry, W., Tran, D., Sauvé, L., Moore, D.L., Lefebvre, M.-A.: The effect of the COVID-19 pandemic on influenza-related hospitalization, intensive care admission and mortality in children in Canada: a population-based study. The Lancet Regional Health – Americas 7 (2022). https://doi.org/10.1016/j.lana.2021.100132
Feng, L., Zhang, T., Wang, Q., Xie, Y., Peng, Z., Zheng, J., Qin, Y., Zhang, M., Lai, S., Wang, D., Feng, Z., Li, Z., Gao, G.F.: Impact of COVID-19 outbreaks and interventions on influenza in China and the United States. Nat. Commun. 12(1), 3249 (2021). https://doi.org/10.1038/s41467-021-23440-1
Roy, C.M., Bukuluki, P., Casey, S.E., Jagun, M.O., John, N.A., Mabhena, N., Mwangi, M., McGovern, T.: Impact of COVID-19 on gender-based violence prevention and response services in Kenya, Uganda, Nigeria, and South Africa: a cross-sectional survey. Frontiers in Global Women’s Health 2, 780771 (2022). https://doi.org/10.3389/fgwh.2021.780771
Jalongo, M.R.: The effects of COVID-19 on early childhood education and care: research and resources for children, families, teachers, and teacher educators. Early Child. Educ. J. 1–12 (2021). https://doi.org/10.1007/s10643-021-01208-y
Bardosh, K., de Figueiredo, A., Gur-Arie, R., Jamrozik, E., Doidge, J., Lemmens, T., Keshavjee, S., Graham, J.E., Baral, S.: The unintended consequences of COVID-19 vaccine policy: why mandates, passports and restrictions may cause more harm than good. BMJ Glob. Health 7(5) (2022). https://doi.org/10.1136/bmjgh-2022-008684. https://gh.bmj.com/content/7/5/e008684.full.pdf
Aviña, M.M., Sevi, S.: Did exposure to COVID-19 affect vote choice in the 2020 presidential election? Res. Polit. 8(3), 20531680211041505 (2021). https://doi.org/10.1177/20531680211041505
Clarke, H., Stewart, M.C., Ho, K.: Did Covid-19 kill Trump politically? The pandemic and voting in the 2020 presidential election. Soc. Sci. Q. 102(5), 2194–2209 (2021). https://doi.org/10.1111/ssqu.12992
Rodriguez-Morales, A.J., Cardona-Ospina, J.A., Gutiérrez-Ocampo, E., Villamizar-Peña, R., Holguin-Rivera, Y., Escalera-Antezana, J.P., Alvarado-Arnez, L.E., Bonilla-Aldana, D.K., Franco-Paredes, C., Henao-Martinez, A.F., Paniz-Mondolfi, A., Lagos-Grisales, G.J., Ramírez-Vallejo, E., Suárez, J.A., Zambrano, L.I., Villamil-Gómez, W.E., Balbin-Ramon, G.J., Rabaan, A.A., Harapan, H., Dhama, K., Nishiura, H., Kataoka, H., Ahmad, T., Sah, R.: Clinical, laboratory and imaging features of COVID-19: a systematic review and meta-analysis. Trav. Med. Infect. Dis. 34, 101623 (2020). https://doi.org/10.1016/j.tmaid.2020.101623
Pormohammad, A., Ghorbani, S., Baradaran, B., Khatami, A., Turner, R.J., Mansournia, M.A., Kyriacou, D.N., Idrovo, J.-P., Bahr, N.C.: Clinical characteristics, laboratory findings, radiographic signs and outcomes of 61,742 patients with confirmed COVID-19 infection: a systematic review and meta-analysis. Microb. Pathog. 147, 104390 (2020). https://doi.org/10.1016/j.micpath.2020.104390
Ghosh, N., Nandi, S., Saha, I.: A review on evolution of emerging SARS-CoV-2 variants based on spike glycoprotein. Int. Immunopharmacol. 105, 108565 (2022). https://doi.org/10.1016/j.intimp.2022.108565
Cosar, B., Karagulleoglu, Z.Y., Unal, S., Ince, A.T., Uncuoglu, D.B., Tuncer, G., Kilinc, B.R., Ozkan, Y.E., Ozkoc, H.C., Demir, I.N., Eker, A., Karagoz, F., Simsek, S.Y., Yasar, B., Pala, M., Demir, A., Atak, I.N., Mendi, A.H., Bengi, V.U., Cengiz Seval, G., Gunes Altuntas, E., Kilic, P., Demir-Dora, D.: SARS-CoV-2 mutations and their viral variants. Cytokine Growth Factor Rev. 63, 10–22 (2022). https://doi.org/10.1016/j.cytogfr.2021.06.001
Harvey, W.T., Carabelli, A.M., Jackson, B., Gupta, R.K., Thomson, E.C., Harrison, E.M., Ludden, C., Reeve, R., Rambaut, A., Peacock, S.J., Robertson, D.L., Consortium C.-.G.U.C.-U.: SARS-CoV-2 variants, spike mutations and immune escape. Nat. Rev. Microbiol. 19(7), 409–424 (2021). https://doi.org/10.1038/s41579-021-00573-0
Yuki, K., Fujiogi, M., Koutsogiannaki, S.: COVID-19 pathophysiology: a review. Clin. Immunol. 215, 108427 (2020). https://doi.org/10.1016/j.clim.2020.108427
Galanopoulos, M., Gkeros, F., Doukatas, A., Karianakis, G., Pontas, C., Tsoukalas, N., Viazis, N., Liatsos, C., Mantzaris, G.J.: COVID-19 pandemic: pathophysiology and manifestations from the gastrointestinal tract. World J. Gastroenterol. 26(31), 4579–4588 (2020). https://doi.org/10.3748/wjg.v26.i31.4579
Wang, D., Hu, B., Hu, C., Zhu, F., Liu, X., Zhang, J., Wang, B., Xiang, H., Cheng, Z., Xiong, Y., Zhao, Y., Li, Y., Wang, X., Peng, Z.: Clinical characteristics of 138 hospitalized patients with 2019 novel coronavirus-infected pneumonia in Wuhan China. JAMA 323(11), 1061–1069 (2020). https://doi.org/10.1001/jama.2020.1585
Girona-Alarcon, M., Bobillo-Perez, S., Sole-Ribalta, A., Hernandez, L., Guitart, C., Suarez, R., Balaguer, M., Cambra, F.-J., Jordan, I., on behalf of the KIDS-Corona study group, Kids Corona Platform: The different manifestations of COVID-19 in adults and children: a cohort study in an intensive care unit. BMC Infect. Dis. 21(1), 87 (2021). https://doi.org/10.1186/s12879-021-05786-5
Wiersinga, W.J., Rhodes, A., Cheng, A.C., Peacock, S.J., Prescott, H.C.: Pathophysiology, transmission, diagnosis, and treatment of Coronavirus disease 2019 (COVID-19): A review. JAMA 324(8), 782–793 (2020). https://doi.org/10.1001/jama.2020.12839. https://jamanetwork.com/journals/jama/articlepdf/2768391/jama_wiersinga_2020_rv_200009_1597950376.62291.pdf
Bienvenu, L.A., Noonan, J., Wang, X., Peter, K.: Higher mortality of COVID-19 in males: sex differences in immune response and cardiovascular comorbidities. Cardiovasc. Res. 116(14), 2197–2206 (2020). https://doi.org/10.1093/cvr/cvaa284
Ramesh, S., Govindarajulu, M., Parise, R.S., Neel, L., Shankar, T., Patel, S., Lowery, P., Smith, F., Dhanasekaran, M., Moore, T.: Emerging SARS-CoV-2 variants: a review of its mutations, its implications and vaccine efficacy. Vaccines 9(10), 1195 (2021). https://doi.org/10.3390/vaccines9101195
Awadasseid, A., Wu, Y., Tanaka, Y., Zhang, W.: SARS-CoV-2 variants evolved during the early stage of the pandemic and effects of mutations on adaptation in Wuhan populations. Int. J. Biol. Sci. 17, 97–106 (2021). https://doi.org/10.7150/ijbs.47827
SeyedAlinaghi, S., Mirzapour, P., Dadras, O., Pashaei, Z., Karimi, A., MohsseniPour, M., Soleymanzadeh, M., Barzegary, A., Afsahi, A.M., Vahedi, F., Shamsabadi, A., Behnezhad, F., Saeidi, S., Mehraeen, E., Jahanfar, S.: Characterization of SARS-CoV-2 different variants and related morbidity and mortality: a systematic review. Eur. J. Med. Res. 26(1), 51 (2021). https://doi.org/10.1186/s40001-021-00524-8
Ingraham, N.E., Ingbar, D.H.: The omicron variant of SARS-CoV-2: understanding the known and living with unknowns. Clin. Transl. Med. 11(12), 685 (2021). https://doi.org/10.1002/ctm2.685
Lou, F., Li, M., Pang, Z., Jiang, L., Guan, L., Tian, L., Hu, J., Fan, J., Fan, H.: Understanding the secret of SARS-CoV-2 variants of concern/interest and immune escape. Front. Immunol. 12, 744242 (2021). https://doi.org/10.3389/fimmu.2021.744242
Bhattacharya, M., Sharma, A.R., Dhama, K., Agoramoorthy, G., Chakraborty, C.: Omicron variant (B.1.1.529) of SARS-CoV-2: understanding mutations in the genome, S-glycoprotein, and antibody-binding regions. GeroScience (2022). https://doi.org/10.1007/s11357-022-00532-4
Kissler, S.M., Fauver, J.R., Mack, C., Tai, C.G., Breban, M.I., Watkins, A.E., Samant, R.M., Anderson, D.J., Metti, J., Khullar, G., Baits, R., MacKay, M., Salgado, D., Baker, T., Dudley, J.T., Mason, C.E., Ho, D.D., Grubaugh, N.D., Grad, Y.H.: Viral dynamics of SARS-CoV-2 variants in vaccinated and unvaccinated persons. N. Engl. J. Med. 385(26), 2489–2491 (2021). https://doi.org/10.1056/NEJMc2102507
Andreakos, E., Abel, L., Vinh, D.C., Kaja, E., Drolet, B.A., Zhang, Q., O’Farrelly, C., Novelli, G., Rodríguez-Gallego, C., Haerynck, F., Prando, C., Pujol, A., Bastard, P., Biggs, C.M., Bigio, B., Boisson, B., Bolze, A., Bondarenko, A., Brodin, P., Chakravorty, S., Christodoulou, J., Cobat, A., Condino-Neto, A., Constantinescu, S.N., Feldman, H.B., Fellay, J., Flores, C., Halwani, R., Jouanguy, E., Lau, Y.-L., Meyts, I., Mogensen, T.H., Okada, S., Okamoto, K., Ozcelik, T., Pan-Hammarström, Q., de Diego, R.P., Planas, A.M., Puel, A., Quintana-Murci, L., Renia, L., Resnick, I., Sediva, A., Shcherbina, A., Slaby, O., Tancevski, I., Turvey, S.E., Uddin, K.M.F., van de Beek, D., Zatz, M., Zawadzki, P., Zhang, S.-Y., Su, H.C., Casanova, J.-L., Spaan, A.N., Effort, C.H.G.: A global effort to dissect the human genetic basis of resistance to SARS-CoV-2 infection. Nat. Immunol. 23(2), 159–164 (2022). https://doi.org/10.1038/s41590-021-01030-z
Doshi, P.: COVID-19: do many people have pre-existing immunity? BMJ 370 (2020). https://doi.org/10.1136/bmj.m3563. https://www.bmj.com/content/370/bmj.m3563.full.pdf
Castelli, E.C., de Castro, M.V., Naslavsky, M.S., Scliar, M.O., Silva, N.S.B., Andrade, H.S., Souza, A.S., Pereira, R.N., Castro, C.F.B., Mendes-Junior, C.T., Meyer, D., Nunes, K., Matos, L.R.B., Silva, M.V.R., Wang, J.T.W., Esposito, J., Coria, V.R., Bortolin, R.H., Hirata, M.H., Magawa, J.Y., Cunha-Neto, E., Coelho, V., Santos, K.S., Marin, M.L.C., Kalil, J., Neto, M.M., Maciel, R.M.B., Passos-Bueno, M.R., Zatz, M.: Immunogenetics of resistance to SARS-CoV-2 infection in discordant couples. medRxiv (2021) https://doi.org/10.1101/2021.04.21.21255872. https://www.medrxiv.org/content/early/2021/04/25/2021.04.21.21255872.full.pdf
Nishiura, H., Kobayashi, T., Miyama, T., Suzuki, A., Jung, S.-M., Hayashi, K., Kinoshita, R., Yang, Y., Yuan, B., Akhmetzhanov, A.R., Linton, N.M.: Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19). Int. J. Infect. Dis. 94, 154–155 (2020). https://doi.org/10.1016/j.ijid.2020.03.020
Van Vinh Chau, N., Lam, V.T., Dung, N.T., Yen, L.M., Minh, N.N.Q., Hung, L.M., Ngoc, N.M., Dung, N.T., Man, D.N.H., Nguyet, L.A., Nhat, L.T.H., Nhu, L.N.T., Ny, N.T.H., Hong, N.T.T., Kestelyn, E., Dung, N.T.P., Xuan, T.C., Hien, T.T., Phong, N.T., Tu, T.N.H., Geskus, R.B., Thanh, T.T., Truong, N.T., Binh, N.T., Thuong, T.C., Thwaites, G., Van Tan, L.: The natural history and transmission potential of asymptomatic severe acute respiratory syndrome coronavirus 2 infection. Clin. Infect. Dis. 71(10), 2679–2687 (2020). https://doi.org/10.1093/cid/ciaa711
Oran, D.P., Topol, E.J.: Prevalence of asymptomatic SARS-CoV-2 infection. Ann. Intern. Med. 173(5), 362–367 (2020). https://doi.org/10.7326/M20-3012
Johansson, M.A., Quandelacy, T.M., Kada, S., Prasad, P.V., Steele, M., Brooks, J.T., Slayton, R.B., Biggerstaff, M., Butler, J.C.: SARS-CoV-2 transmission from people without COVID-19 symptoms. JAMA Netw. Open 4(1), 2035057 (2021). https://doi.org/10.1001/jamanetworkopen.2020.35057
Ellinghaus, D., Degenhardt, F., Bujanda, L., Buti, M., Albillos, A., Invernizzi, P., Fernández, J., Prati, D., Baselli, G., Asselta, R., Grimsrud, M.M., Milani, C., Aziz, F., Kässens, J., May, S., Wendorff, M., Wienbrandt, L., Uellendahl-Werth, F., Zheng, T., Yi, X., de Pablo, R., Chercoles, A.G., Palom, A., Garcia-Fernandez, A.-E., Rodriguez-Frias, F., Zanella, A., Bandera, A., Protti, A., Aghemo, A., Lleo, A., Biondi, A., Caballero-Garralda, A., Gori, A., Tanck, A., Carreras Nolla, A., Latiano, A., Fracanzani, A.L., Peschuck, A., Julià, A., Pesenti, A., Voza, A., Jiménez, D., Mateos, B., Nafria Jimenez, B., Quereda, C., Paccapelo, C., Gassner, C., Angelini, C., Cea, C., Solier, A., Pestaña, D., Muñiz-Diaz, E., Sandoval, E., Paraboschi, E.M., Navas, E., García Sánchez, F., Ceriotti, F., Martinelli-Boneschi, F., Peyvandi, F., Blasi, F., Téllez, L., Blanco-Grau, A., Hemmrich-Stanisak, G., Grasselli, G., Costantino, G., Cardamone, G., Foti, G., Aneli, S., Kurihara, H., ElAbd, H., My, I., Galván-Femenia, I., Martín, J., Erdmann, J., Ferrusquía-Acosta, J., Garcia-Etxebarria, K., Izquierdo-Sanchez, L., Bettini, L.R., Sumoy, L., Terranova, L., Moreira, L., Santoro, L., Scudeller, L., Mesonero, F., Roade, L., Rühlemann, M.C., Schaefer, M., Carrabba, M., Riveiro-Barciela, M., Figuera Basso, M.E., Valsecchi, M.G., Hernandez-Tejero, M., Acosta-Herrera, M., D’Angiò, M., Baldini, M., Cazzaniga, M., Schulzky, M., Cecconi, M., Wittig, M., Ciccarelli, M., Rodríguez-Gandía, M., Bocciolone, M., Miozzo, M., Montano, N., Braun, N., Sacchi, N., Martínez, N., Özer, O., Palmieri, O., Faverio, P., Preatoni, P., Bonfanti, P., Omodei, P., Tentorio, P., Castro, P., Rodrigues, P.M., Blandino Ortiz, A., de Cid, R., Ferrer, R., Gualtierotti, R., Nieto, R., Goerg, S., Badalamenti, S., Marsal, S., Matullo, G., Pelusi, S., Juzenas, S., Aliberti, S., Monzani, V., Moreno, V., Wesse, T., Lenz, T.L., Pumarola, T., Rimoldi, V., Bosari, S., Albrecht, W., Peter, W., Romero-Gómez, M., D’Amato, M., Duga, S., Banales, J.M., Hov, J.R., Folseraas, T., Valenti, L., Franke, A., Karlsen, T.H.: Genomewide association study of severe COVID-19 with respiratory failure. N. Engl. J. Med. 383(16), 1522–1534 (2020). https://doi.org/10.1056/NEJMoa2020283
Buitrago-Garcia, D., Egli-Gany, D., Counotte, M.J., Hossmann, S., Imeri, H., Ipekci, A.M., Salanti, G., Low, N.: Occurrence and transmission potential of asymptomatic and presymptomatic SARS-CoV-2 infections: a living systematic review and meta-analysis. PLoS Med. 17(9), 1–25 (2020). https://doi.org/10.1371/journal.pmed.1003346
Killingley, B., Mann, A.J., Kalinova, M., Boyers, A., Goonawardane, N., Zhou, J., Lindsell, K., Hare, S.S., Brown, J., Frise, R., Smith, E., Hopkins, C., Noulin, N., Löndt, B., Wilkinson, T., Harden, S., McShane, H., Baillet, M., Gilbert, A., Jacobs, M., Charman, C., Mande, P., Nguyen-Van-Tam, J.S., Semple, M.G., Read, R.C., Ferguson, N.M., Openshaw, P.J., Rapeport, G., Barclay, W.S., Catchpole, A.P., Chiu, C.: Safety, tolerability and viral kinetics during SARS-CoV-2 human challenge in young adults. Nat. Med. (2022). https://doi.org/10.1038/s41591-022-01780-9
Lavezzo, E., Franchin, E., Ciavarella, C., Cuomo-Dannenburg, G., Barzon, L., Del Vecchio, C., Rossi, L., Manganelli, R., Loregian, A., Navarin, N., Abate, D., Sciro, M., Merigliano, S., De Canale, E., Vanuzzo, M.C., Besutti, V., Saluzzo, F., Onelia, F., Pacenti, M., Parisi, S.G., Carretta, G., Donato, D., Flor, L., Cocchio, S., Masi, G., Sperduti, A., Cattarino, L., Salvador, R., Nicoletti, M., Caldart, F., Castelli, G., Nieddu, E., Labella, B., Fava, L., Drigo, M., Gaythorpe, K.A.M., Brazzale, A.R., Toppo, S., Trevisan, M., Baldo, V., Donnelly, C.A., Ferguson, N.M., Dorigatti, I., Crisanti, A.: Suppression of a SARS-CoV-2 outbreak in the Italian municipality of Vo’. Nature 584(7821), 425–429 (2020). https://doi.org/10.1038/s41586-020-2488-1
Walsh, K.A., Jordan, K., Clyne, B., Rohde, D., Drummond, L., Byrne, P., Ahern, S., Carty, P.G., O’Brien, K.K., O’Murchu, E., O’Neill, M., Smith, S.M., Ryan, M., Harrington, P.: SARS-CoV-2 detection, viral load and infectivity over the course of an infection. J. Infect. 81(3), 357–371 (2020). https://doi.org/10.1016/j.jinf.2020.06.067
McEvoy, D., McAloon, C., Collins, A., Hunt, K., Butler, F., Byrne, A., Casey-Bryars, M., Barber, A., Griffin, J., Lane, E.A., Wall, P., More, S.J.: Relative infectiousness of asymptomatic SARS-CoV-2 infected persons compared with symptomatic individuals: a rapid scoping review. BMJ Open 11(5) (2021). https://doi.org/10.1136/bmjopen-2020-042354. https://bmjopen.bmj.com/content/11/5/e042354.full.pdf
Atkinson, B., Petersen, E.: SARS-CoV-2 shedding and infectivity. Lancet 395(10233), 1339–1340 (2020). https://doi.org/10.1016/S0140-6736(20)30868-0
Singanayagam, A., Patel, M., Charlett, A., Lopez Bernal, J., Saliba, V., Ellis, J., Ladhani, S., Zambon, M., Gopal, R.: Duration of infectiousness and correlation with RT-PCR cycle threshold values in cases of COVID-19, England, January to May 2020. Euro Surveill. 25(32) (2020). https://doi.org/10.2807/1560-7917.ES.2020.25.32.2001483
Lee, S., Kim, T., Lee, E., Lee, C., Kim, H., Rhee, H., Park, S.Y., Son, H.-J., Yu, S., Park, J.W., Choo, E.J., Park, S., Loeb, M., Kim, T.H.: Clinical course and molecular viral shedding among asymptomatic and symptomatic patients with SARS-CoV-2 infection in a community treatment center in the Republic of Korea. JAMA Intern. Med. 180(11), 1447–1452 (2020). https://doi.org/10.1001/jamainternmed.2020.3862. https://jamanetwork.com/journals/jamainternalmedicine/articlepdf/2769235/jamainternal_lee_2020_oi_200057_1603479600.04745.pdf
Uhm, J.-S., Ahn, J.Y., Hyun, J., Sohn, Y., Kim, J.H., Jeong, S.J., Ku, N.S., Choi, J.Y., Park, Y.-K., Yi, H.-S., Park, S.K., Kim, B.-O., Kim, H., Choi, J., Kang, S.-M., Choi, Y.H., Yoon, H.K., Jung, S., Kim, H.N., Yeom, J.-S., Park, Y.S.: Patterns of viral clearance in the natural course of asymptomatic COVID-19: comparison with symptomatic non-severe COVID-19. Int. J. Infect. Dis. 99, 279–285 (2020). https://doi.org/10.1016/j.ijid.2020.07.070
He, X., Lau, E.H.Y., Wu, P., Deng, X., Wang, J., Hao, X., Lau, Y.C., Wong, J.Y., Guan, Y., Tan, X., Mo, X., Chen, Y., Liao, B., Chen, W., Hu, F., Zhang, Q., Zhong, M., Wu, Y., Zhao, L., Zhang, F., Cowling, B.J., Li, F., Leung, G.M.: Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 26(5), 672–675 (2020). https://doi.org/10.1038/s41591-020-0869-5
Long, Q.-X., Tang, X.-J., Shi, Q.-L., Li, Q., Deng, H.-J., Yuan, J., Hu, J.-L., Xu, W., Zhang, Y., Lv, F.-J., Su, K., Zhang, F., Gong, J., Wu, B., Liu, X.-M., Li, J.-J., Qiu, J.-F., Chen, J., Huang, A.-L.: Clinical and immunological assessment of asymptomatic SARS-CoV-2 infections. Nat. Med. 26(8), 1200–1204 (2020). https://doi.org/10.1038/s41591-020-0965-6
Tiwari, L., Gupta, P., Singh, C.M., Singh, P.K.: Persistent positivity of SARS-CoV-2 nucleic acid in asymptomatic healthcare worker: infective virion or inactive nucleic acid? BMJ Case Reports CP 14(3) (2021). https://doi.org/10.1136/bcr-2020-241087. https://casereports.bmj.com/content/14/3/e241087.full.pdf
Siedner, M.J., Boucau, J., Gilbert, R.F., Uddin, R., Luu, J., Haneuse, S., Vyas, T., Reynolds, Z., Iyer, S., Chamberlin, G.C., Goldstein, R.H., North, C.M., Sacks, C.A., Regan, J., Flynn, J.P., Choudhary, M.C., Vyas, J.M., Barczak, A.K., Lemieux, J.E., Li, J.Z.: Duration of viral shedding and culture positivity with postvaccination SARS-CoV-2 delta variant infections. JCI Insight 7(2) (2022). https://doi.org/10.1172/jci.insight.155483
Li, B., Deng, A., Li, K., Hu, Y., Li, Z., Shi, Y., Xiong, Q., Liu, Z., Guo, Q., Zou, L., Zhang, H., Zhang, M., Ouyang, F., Su, J., Su, W., Xu, J., Lin, H., Sun, J., Peng, J., Jiang, H., Zhou, P., Hu, T., Luo, M., Zhang, Y., Zheng, H., Xiao, J., Liu, T., Tan, M., Che, R., Zeng, H., Zheng, Z., Huang, Y., Yu, J., Yi, L., Wu, J., Chen, J., Zhong, H., Deng, X., Kang, M., Pybus, O.G., Hall, M., Lythgoe, K.A., Li, Y., Yuan, J., He, J., Lu, J.: Viral infection and transmission in a large, well-traced outbreak caused by the SARS-CoV-2 Delta variant. Nat. Commun. 13(1), 460 (2022). https://doi.org/10.1038/s41467-022-28089-y
Kang, M., Xin, H., Yuan, J., Ali, S.T., Liang, Z., Zhang, J., Hu, T., Lau, E.H., Zhang, Y., Zhang, M., Cowling, B.J., Li, Y., Wu, P.: Transmission dynamics and epidemiological characteristics of SARS-CoV-2 Delta variant infections in Guangdong, China, May to June 2021. Euro Surveill. 27(10) (2022). https://doi.org/10.2807/1560-7917.ES.2022.27.10.2100815
Boucau, J., Marino, C., Regan, J., Uddin, R., Choudhary, M.C., Flynn, J.P., Chen, G., Stuckwisch, A.M., Mathews, J., Liew, M.Y., Singh, A., Lipiner, T., Kittilson, A., Melberg, M., Li, Y., Gilbert, R.F., Reynolds, Z., Iyer, S.L., Chamberlin, G.C., Vyas, T.D., Goldberg, M.B., Vyas, J.M., Li, J.Z., Lemieux, J.E., Siedner, M.J., Barczak, A.K.: Duration of shedding of culturable virus in SARS-CoV-2 Omicron (BA.1) infection. N. Engl. J. Med. 387(3), 275–277 (2022). https://doi.org/10.1056/NEJMc2202092
Eyre, D.W., Taylor, D., Purver, M., Chapman, D., Fowler, T., Pouwels, K.B., Walker, A.S., Peto, T.E.A.: Effect of Covid-19 vaccination on transmission of Alpha and Delta variants. N. Engl. J. Med. 386(8), 744–756 (2022). https://doi.org/10.1056/NEJMoa2116597
Acharya, C.B., Schrom, J., Mitchell, A.M., Coil, D.A., Marquez, C., Rojas, S., Wang, C.Y., Liu, J., Pilarowski, G., Solis, L., Georgian, E., Belafsky, S., Petersen, M., DeRisi, J., Michelmore, R., Havlir, D.: Viral load among vaccinated and unvaccinated, asymptomatic and symptomatic persons infected with the SARS-CoV-2 Delta variant. Open Forum Infect. Dis. 9(5) (2022). https://doi.org/10.1093/ofid/ofac135.ofac135. https://academic.oup.com/ofid/article-pdf/9/5/ofac135/43469828/ofac135.pdf
Ssentongo, P., Ssentongo, A.E., Voleti, N., Groff, D., Sun, A., Ba, D.M., Nunez, J., Parent, L.J., Chinchilli, V.M., Paules, C.I.: SARS-CoV-2 vaccine effectiveness against infection, symptomatic and severe COVID-19: a systematic review and meta-analysis. BMC Infect. Dis. 22(1), 439 (2022). https://doi.org/10.1186/s12879-022-07418-y
Stein, C., Nassereldine, H., Sorensen, R.J.D., Amlag, J.O., Bisignano, C., Byrne, S., Castro, E., Coberly, K., Collins, J.K., Dalos, J., Daoud, F., Deen, A., Gakidou, E., Giles, J.R., Hulland, E.N., Huntley, B.M., Kinzel, K.E., Lozano, R., Mokdad, A.H., Pham, T., Pigott, D.M., Reiner, R.C. Jr., Vos, T., Hay, S.I., Murray, C.J.L., Lim, S.S.: Past SARS-CoV-2 infection protection against re-infection: a systematic review and meta-analysis. Lancet 401(10379), 833–842 (2023). https://doi.org/10.1016/S0140-6736(22)02465-5
Acknowledgements
R (https://www.r-project.org) was used for statistical analysis, and images were transformed in GIMP (https://www.gimp.org). Composite images were created in Scribus (https://www.scribus.net). Source images for the graphical abstract are from Wikimedia commons (https://commons.wikimedia.org/). The flagged UK map is accredited to Stasyan117 – Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=37821767. The flagged USA map is by SiBr4 and respective authors of base files – Own work based on: Blank US Map.svg and SVG flags of states of the United States, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=43299314. The Wikimedia RNA image is by DataBase Center for Life Science (DBCLS) – https://doi.org/10.7875/togopic.2019.08, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=77793593. Alissa Eckert, MS; Dan Higgins, MAM of the Center for Disease Control provided the coronavirus image available on Wikimedia commons.
Authors’ information
The author is a chemical pathologist at Lancet Laboratories in the Republic of South Africa.
Funding
This work is unfunded, I am not employed or associated with a tertiary institution, and I have received no material benefit.
Author information
Authors and Affiliations
Contributions
The author is responsible for conceptualisation, formulation, analysis, writing and composition of images. The author read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Neither ethical approval nor consent to participate are applicable.
Consent for publication
Not applicable
Consent to participate
Not applicable
Competing interests
The author declares no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: The HI-STR parameters for the ancestral SARS-CoV2
COVID-19 is a collection of clinical symptoms and pathologies [295, 296] assigned to several variants of SARS-CoV2[297–299]. The heterogeneity of pathology [300, 301] is due to variable host responses to both a variant [302–305] and multiple viral lineages [306, 307], their variants [308, 309] and their mutations [310, 311]. Here COVID-19(wt) will refer to the distribution of pathology, case fatality rate, severity and transmission dynamics of the subset of COVID-19 due to L lineage of the ancestral (wild-type) SARS-CoV2 [304] to distinguish it from the corresponding findings of the Alpha (B.1.1.7) [312], Beta (B.1.351), Delta (B.1.617.2) [43, 306] and Omicron (B.1.1.529) [309] variants.
Benjamin [52] defines a time unit in the transmissible timescale as the weighted average of the time a host can transmit a pathogen. The transmission period is limited by viral load in a latent period, recovery, death, pharmacological intervention and behavioural adaptation like quarantine. The weighting is based on the relative proportions of inherently immune (\(1-\sigma \)), symptomatic (ψ), asymptomatic (\(1-\psi \)) and other subpopulations with distinct transmission periods.
The assumption is that for a novel pathogen, when sufficient contact is made between a host and a potential host (in a completely susceptible population), there are three possible outcomes. There are inherently immune/resistant individuals (not previously exposed) that will not become infected and therefore have a transmission period of zero [313–315], asymptomatic individuals [200, 316] that may have the transmission period shortened by clearing the virus [312, 317] or prolonged by not isolating [64, 318] and the symptomatically infected who will have the transmission shortened by either self-isolation, hospitalisation or death. Each group’s transmission periods and transmissibility [317, 319] are dependent on the demography [266, 318], co-morbidities [267, 268] and genetic predispositions [320] within that group.
The prevalence of asymptomatic infection has been reviewed [318, 321]. Whole population survey’s from 2020 of presumed COVID-19(wt) and a young adult challenge trial [322] are presented in Table 2. The prevalences may reflect demography. The median asymptomatic prevalence is 42.2%.
The infectious period and infectiousness of these groups have been reviewed [72, 319, 324, 325]. Each study uses viral load as an imperfect proxy for infectiousness [199, 325–327]. Lavezzo et al. [323] determine the infectious period by shortening the viral particle shedding period by 4 days [199, 327] because of the later shedding of detectable, inactive viral RNA fragments. Table 3 presents the latent, incubation, transmission and infectious periods for the symptomatic and asymptomatic.
The latent period is from infection to sufficient viral shedding for successful transmission. Incubation is from infection to symptom onset. The period of time that a virus is detectable has been shortened by 4 days to obtain the infectious period [323]. It is assumed that (for COVID-19) symptomatic patients self-isolate and are hospitalised or ostracised at symptom onset or within a day thereof. Therefore the transmission period is the difference between the incubation and latent periods.
In each of these studies, there is no demonstrable difference in infectivity between these groups [324, 325, 327, 329]. Table 3 mitigates the bias of retrospective studies [317] by only including whole population studies. Nevertheless, each population is unique and not necessarily representative. Of note: there may be small differences in the definition of symptomatic and asymptomatic individuals and different real-time RT-PCR platforms with different cycle count thresholds used. RT-PCR does not distinguish active virions from inactive nucleic acid [332].
The proportion of inherently immune or resistant (\(1-\sigma \)) is unknown. Although the UK challenge trial [322] is prospective, neither the sample nor the inoculum is necessarily representative. It is assumed that the inherently immune and resistant are negligible (\(\sigma =1\)). In summary, 42.2% are asymptomatic carriers with a 15-day transmission period Δτ, and the symptomatic 57.8% have \(\Delta \tau =5\) days. Consequently, the weighted average transmission period is \(\Delta \overline{\tau} = 9\) days, and the transmissible times scale is \(1:9\) days.
Periodic human behaviour is the result of superimposed daily, weekly, monthly and annual cycles. For infectious diseases, the rhythmic timescale is determined by the periodicity of transmission opportunity. For airborne diseases, like COVID-19, the relevant cycle is diurnal with maximum transmission opportunity during day time social interactions and a trough while sleeping. The rhythmic timescale (\(1:\delta t\)) for COVID-19 is thus \(1:1\) day.
The wild-type SARS-CoV2 temporal scaling factor (\(\mathfrak{B}(wt)\)) in Equations (1) and (6) is the ratio of a unit of time in transmissible times scale (Δτ̅) to that in the rhythmic timescale (δt). For COVID-19(wt), \(\mathfrak{B}(wt)=9\).
Appendix B: USA states’ basic reproduction number outliers
Re-arranging Equation (6), substituting the median reproduction numbers estimates \(({}^{z}\widehat{\mathcal{R}}_{0} )\) for the \(1\leq z \leq 51\) states of the USA [219] and the population sizes (zN̂) and densities (\({}^{z} \hat{\rho}_{n}\)) for these states [265] allows us to determine the proportionality constant \((M =\frac{\beta _{A}}{{}_{\tau}\alpha} )\) in
Figure 7 (the density distribution for M̂) identifies six outliers. M̂’s median [IQR] is \(1.1\times 10^{-7}[3.4\times 10^{-8},6.2\times 10^{-7}]\). New Mexico, Alaska, Oklahoma, New York, South Dakota and Louisiana are removed from further analysis.
The relative error between the regression basic reproductive \(({}^{z}\bar{\bar{\mathcal{R}}}_{0}(wt) )\) and \({}^{z}\widehat{\mathcal{R}}_{0}(wt)\):
is assumed to have a Gaussian distribution with zero mean. The Median [IQR] of E is \(-0.02[-0.17,0.05]\). Figure 8 is the density distribution of the relative error between the regressed and estimated \(\mathcal{R}_{0}(wt)\)s. Hawaii, Montana, Minnesota, Wyoming and Washington DC are removed as outliers.
Figure 9 compares the density distributions of \(\widehat{\mathcal{R}}_{0}(wt)\) and \(\bar{\bar{\mathcal{R}}}_{0}(wt)\) for the remaining 40 states and demonstrates that the relative error E is normally distributed. The Shapiro–Wilk test on E does not exclude normality (\(p=0.31\)).
Appendix C: Sensitivity analysis – impact of asymptomatic ratio
The ratio of the time units in the transmissible timescale to the time units in the rhythmic timescale (\(\mathfrak{B}\)) translates to the average transmissible period (Δτ̅) for the particular case where the time units in the rhythmic timescale (δt) = 1. For this particular case, \(\mathfrak{B}\) is dependent on four variables:
σ is the non-immune or susceptible portion of the population, \(1-\sigma \) is the immune portion that cannot be infected, ψ is the portion of σ that will be symptomatic if infected, \(1-\psi \) is the proportion that will be asymptomatic if infected, ΔI is the infectious period, and Δτ is the transmissible period.
For wild-type SARS-CoV2 early in the epidemic, when \(\mathcal{R}_{0}\) is relevant, there is no natural immunity, and \(1-\sigma \) represents inherent immunity. Thus far, it has been assumed that \(\sigma =1\), whereas Tables 2 and 3 demonstrate the variance in the estimates of ψ and ΔI and Δτ, respectively. Figure 5 is a sensitivity analysis depicting the effect of changes in:
-
1.
the symptomatic fraction (ψ) when the inherently immune fraction (\(1-\sigma \)), infectious period (ΔI) and transmissible period (Δτ) are held constant at 0; 15 days and 5 days, respectively;
-
2.
the inherently immune fraction (\(1-\sigma \)) is varied from 0 to 0.5 with \(\psi = 0.6\), \(\Delta I = 15\) days and \(\Delta \tau = 5\) days. The distribution of the constants M and E deviate from normality for \(\psi > 0.5\);
-
3.
infectious period (ΔI) with \(1 - \sigma = 0\), \(\psi = 0.6\) and \(\Delta \tau = 5\) days and
-
4.
transmissible period (Δτ) with \(1- \sigma = 0\), \(\psi = 0.6\) and \(\Delta I = 15\) days
on the difference between UK’s projection of \({}^{UK}\widehat{\mathcal{R}}_{0}(wt) = 4.2\) onto the USA states and their \(\widehat{\mathcal{R}}_{0}(wt)\)s – projection \(({}^{z}\widetilde{\mathcal{R}}_{0}(wt) )\) – estimate \(({}^{z}\widehat{\mathcal{R}}_{0}(wt) )\).
As expected, increasing the symptomatic fraction ψ or the inherently immune fraction (\(1-\sigma \)) reduced \(\mathcal{R}_{0}\). Of note: relative to the estimates and the uncertainties in these estimates [219], the reduction in \(\mathcal{R}_{0}\) is not epidemiologically significant over the domains investigated. The E distribution deviates from normality on the Shapiro–Wilk test for inherently immune ratios greater than 40% and visibly for ratios greater than 50%.
Increasing either the infectious period ΔI or the transmissible period Δτ increased \(\mathcal{R}_{0}\). Again, relative to the estimates and the uncertainties in these estimates [219], the increase in \(\mathcal{R}_{0}\) is not epidemiologically significant.
Appendix D: The UK and USA’s HI-STR model \(\mathfrak{B}\) for SARS-CoV2(Δ)
Figure 10 [212, 213] demonstrates that the criteria for this implementation of VOC projection is satisfied by the Delta variant in the USA and UK. In particular, projection has greatest utility when there is delay in the VOC manifesting in a region. Figure 10(a) demonstrates that the Δ variant becomes prominent in the the most connected of the USA states at least 1 month after the UK. Figure 10(b) shows that the UK’s fully vaccinated proportion was 25–45% during the transition to Δ variant, whereas the USA’s was 30–55% during this transition. The USA is complicated by both state-level vaccination proportion differences and differences in epidemic development stage. Figure 10(c) demonstrates the rapid and complete transition to Δ in the UK – satisfying this projection implementation’s requirement for negligible mixing. Figure 10(d) demonstrates the same (negligible mixing) for the USA. It also contrasts this by displaying co-existent wt, α and γ variants. The co-existent variants are not necessarily a consequence of mixing – the states of the USA may be at different epidemic stages. Both the resultant staggered transition and mixing will manifest with co-existent variants.
A cohort (\(n=24\)) of post-vaccination breakthrough infection had a 100% symptomatic fraction [333]. Retrospective surveys indicate that 85–90% of the vaccinated are symptomatic vs 70–80% of the unvaccinated [252, 253, 270].
The host becomes infectious 4 days after exposure [334] and is symptomatic 4 days after becoming infectious [335]. The median time from symptom onset to undetectable viral load was 13.5 days, whereas the median time from symptom onset to negative viral culture was 7 days [333, 336].
The viral loads (based on RT-PCR Cycle Count Threshold (Ct) values) were higher in the unvaccinated [249, 257, 337], but a statistically significant difference in Ct was not evident among the 4 group combinations of vaccination and symptom status [252, 337, 338]. Note that the Ct scale represents a viral load logarithmic scale.
As for SARS-CoV2(wt), the inherently immune fraction is unknown and assumed negligible. The naturally immune fraction is not known. The vaccinated portion is approximately 40% in the UK and USA (Fig. 10(b)) during the period of transition to the Delta variant (Fig. 10(a)). Vaccination does not prevent SARS-CoV2(Δ) infection [252–255], but this depends on time from vaccination [256, 257, 339].
These findings are summarised in Table 4, where the naturally immune fraction is unknown and treated as negligible. The resultant transmissible period is 6 days, and thus \(\mathfrak{B}(\Delta ) = 6\) for the SARS-CoV2 Delta variant. For the asymptomatic, there are no symptoms, the patient is infectious, and the transmissible period is from detectable virus to recovery.
Assuming 100% natural immunity, we can assume that the symptomatic and asymptomatic fraction will be similar to the vaccinated [340]. The vaccinated and naturally immune fraction will be 100% with weightings 10% and 90% for asymptomatic and symptomatic, respectively; \(\mathfrak{B}(\Delta ) = 5.6 \approx 6\).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Benjamin, R. Reproduction number projection for the COVID-19 pandemic. Adv Cont Discr Mod 2023, 46 (2023). https://doi.org/10.1186/s13662-023-03792-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-023-03792-2