INS-aiding information error modeling in GNSS/INS ultra-tight integration

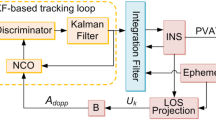
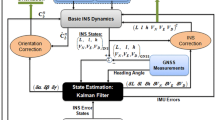
Abstract

In the ultra-tight integration system of the global navigation satellite system/ inertial navigation system (GNSS/INS), the error models of INS aiding information are significant to analyze the performance of system. However, it is difficult to comprehensively describe the error propagation process between INS and GNSS when using the traditional transfer functions and inertial computation formulas. To overcome the issues, a comprehensive error modeling scheme of INS aiding information for GNSS tracking loops is proposed from the state space design perspective. Using the proper integrated navigation filter derived in Earth-centered, Earth-fixed frame, the error propagation process from integrated navigation filter to INS-aiding information can be constructed, by taking the overall error sources into consideration. In addition, the error item of acceleration caused by rotations of the line-of-sight direction is analyzed, which is especially important for high-dynamic receivers or middle-orbit satellites positioning. Simulation and experiment results verify the effectiveness of the proposed error modeling method. This method has significant application potential for the performance analysis of tracking loops in GNSS/INS ultra-tight integration system.

Appendices

Appendix 1: Derivations of some important formulas in detail

The detailed derivation of (6) is organized as follows. Using assumptions ${\tilde{\mathbf{v}}}_{S} \approx {\mathbf{v}}_{S}$, ${\tilde{\mathbf{r}}}_{S} \approx {\mathbf{r}}_{S}$, and ${\tilde{\mathbf{r}}}_{R} = {\mathbf{r}}_{R} + \delta {\mathbf{r}}_{R}$, then ${\tilde{\mathbf{e}}}$ is expanded as,

$$ {\tilde{\mathbf{e}}} = \frac{{{\tilde{\mathbf{r}}}_{R} - {\tilde{\mathbf{r}}}_{S} }}{{\left\| {{\tilde{\mathbf{r}}}_{R} - {\tilde{\mathbf{r}}}_{S} } \right\|}} \approx \frac{{{\tilde{\mathbf{r}}}_{R} - {\mathbf{r}}_{S} }}{{\left\| {{\tilde{\mathbf{r}}}_{R} - {\mathbf{r}}_{S} } \right\|}} = \frac{{{\mathbf{r}}_{R} - {\mathbf{r}}_{S} + \delta {\mathbf{r}}_{R} }}{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} + \delta {\mathbf{r}}_{R} } \right\|}} $$

(36)

Noticing the fact ${\mathbf{r}}_{R} - {\mathbf{r}}_{S} \gg \delta {\mathbf{r}}_{R}$, and expand the denominator of (36) around point $\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|$,

$$ {\tilde{\mathbf{e}}} \approx \frac{{{\mathbf{r}}_{R} - {\mathbf{r}}_{S} + \delta {\mathbf{r}}_{R} }}{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\| + {\mathbf{e}}^{T} \delta {\mathbf{r}}_{R} }} \approx \frac{{{\mathbf{r}}_{R} - {\mathbf{r}}_{S} }}{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|}} = {\mathbf{e}} $$

(37)

The detailed derivation of (9) is organized as follows. The derivative of $\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|$ can be obtained using the derivative expression of L2-norm,

$$ \frac{{{\text{d}}\left( {\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|} \right)}}{{{\text{d}}t}} = \frac{{{\text{d}}\left( {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right)}}{{{\text{d}}t}} \cdot \frac{{\left( {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right)}}{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|}} = {\mathbf{e}}^{T} \left( {{\mathbf{v}}_{R} - {\mathbf{v}}_{S} } \right) $$

(38)

Then the derivative of unit direction vector ${\mathbf{e}}$ is expressed as,

$$ \begin{aligned} \frac{{{\text{d}}\left( {\mathbf{e}} \right)}}{{{\text{d}}t}} = & \frac{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|}}{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|^{2} }} \cdot \frac{{{\text{d}}\left( {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right)}}{{{\text{d}}t}} - \frac{{\left( {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right)}}{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|^{2} }} \cdot \frac{{{\text{d}}\left( {\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|} \right)}}{{{\text{d}}t}} \\ = & \frac{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\| \cdot \left( {{\mathbf{v}}_{R} - {\mathbf{v}}_{S} } \right) - \left[ {{\mathbf{e}}^{T} \left( {{\mathbf{v}}_{R} - {\mathbf{v}}_{S} } \right)} \right] \cdot \left( {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right)}}{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|^{2} }} \\ = & \frac{{\left( {{\mathbf{I}} - {\mathbf{ee}}^{T} } \right)\left( {{\mathbf{v}}_{R} - {\mathbf{v}}_{S} } \right)}}{{\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|}} \\ \end{aligned} $$

(39)

The detailed derivation of (12) is organized as follows. Let ${\tilde{\mathbf{F}}} = - \frac{{2\pi f_{L} }}{c}\frac{{\left( {{\mathbf{I}} - {\mathbf{\tilde{e}\tilde{e}}}^{T} } \right)}}{{\left\| {{\tilde{\mathbf{r}}}_{R} - {\mathbf{r}}_{S} } \right\|}}$, ${\tilde{\mathbf{x}}} = {\tilde{\mathbf{v}}}_{R} - {\mathbf{v}}_{S}$, then the estimation of $\delta \dot{\omega }_{IA}$ is expressed as,

$$ \delta \dot{\omega }_{IA} = \tilde{\dot{\omega }}_{IA} - \dot{\omega }_{IA} = {\tilde{\mathbf{x}}}^{T} {\mathbf{\tilde{F}\tilde{x}}} - {\mathbf{x}}^{T} {\mathbf{Fx}} $$

(40)

Notice the fact ${\tilde{\mathbf{e}}} \approx {\mathbf{e}}$, therefore we can obtain ${\tilde{\mathbf{F}}} = {\mathbf{F}}$. Using the derivative expression of the quadratic form, equation (40) can be further expressed as,

$$ \delta \dot{\omega }_{IA} = \delta \left( {{\mathbf{x}}^{T} {\tilde{\mathbf{F}}\mathbf{x}}} \right) \approx 2{\tilde{\mathbf{F}}}\delta {\mathbf{x}} = - \frac{{4\pi f_{L} }}{c}\frac{{\left( {{\tilde{\mathbf{v}}}_{R} - {\mathbf{v}}_{S} } \right)^{T} \left( {{\mathbf{I}} - {\mathbf{\tilde{e}\tilde{e}}}^{T} } \right)}}{{\left\| {{\tilde{\mathbf{r}}}_{R} - {\mathbf{r}}_{S} } \right\|}}\delta {\mathbf{v}}_{R} $$

(41)

The detailed derivation of (32)–(34) is organized as follows. Substitute $\delta {\mathbf{f}}^{b} = {\mathbf{b}}_{a} + {\mathbf{n}}_{ra}$ and (25) in (30), it can be obtained that,

$$ \delta a^{e} \approx {\tilde{\mathbf{D}}}^{e} \delta {\mathbf{q}}_{b}^{e} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{b}}_{a} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{n}}_{ra} - 2{{\varvec{\upomega}}}_{ie}^{e} \times \delta {\mathbf{v}}^{e} + \delta {\mathbf{g}}^{e} $$

(42)

Hence, the items $E\left( {\delta {\mathbf{v}}_{R} \delta {\varvec{a}}_{R}^{T} } \right)$, $E\left( {\delta {\varvec{a}}_{R} \delta {\mathbf{v}}_{R}^{T} } \right)$ and $E\left( {\delta {\varvec{a}}_{R} \delta {\varvec{a}}_{R}^{T} } \right)$ are expanded as,

$$ E\left( {\delta {\mathbf{v}}_{R} \delta {\varvec{a}}_{R}^{T} } \right) \approx E\left[ {\delta {\mathbf{v}}^{e} \left( {{\tilde{\mathbf{D}}}^{e} \delta {\mathbf{q}}_{b}^{e} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{b}}_{a} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{n}}_{ra} - 2{{\varvec{\upomega}}}_{ie}^{e} \times \delta {\mathbf{v}}^{e} + \delta {\mathbf{g}}^{e} } \right)^{T} } \right] $$

(43)

$$ E\left( {\delta {\varvec{a}}_{R} \delta {\mathbf{v}}_{R}^{T} } \right) \approx E\left[ {\left( {{\tilde{\mathbf{D}}}^{e} \delta {\mathbf{q}}_{b}^{e} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{b}}_{a} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{n}}_{ra} - 2{{\varvec{\upomega}}}_{ie}^{e} \times \delta {\mathbf{v}}^{e} + \delta {\mathbf{g}}^{e} } \right)\left( {\delta {\mathbf{v}}^{e} } \right)^{T} } \right] $$

(44)

$$ E\left( {\delta {\varvec{a}}_{R} \delta {\varvec{a}}_{R}^{T} } \right) \approx E\left[ {\left( {{\tilde{\mathbf{D}}}^{e} \delta {\mathbf{q}}_{b}^{e} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{b}}_{a} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{n}}_{ra} - 2{{\varvec{\upomega}}}_{ie}^{e} \times \delta {\mathbf{v}}^{e} + \delta {\mathbf{g}}^{e} } \right)\left( {{\tilde{\mathbf{D}}}^{e} \delta {\mathbf{q}}_{b}^{e} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{b}}_{a} + {\tilde{\mathbf{C}}}_{b}^{e} {\mathbf{n}}_{ra} - 2{{\varvec{\upomega}}}_{ie}^{e} \times \delta {\mathbf{v}}^{e} + \delta {\mathbf{g}}^{e} } \right)^{T} } \right] $$

(45)

Expand the polynomials in (43)–(45), and we can substitute the state covariance items using the corresponding elements of the partitioned matrix ${\mathbf{P}}_{k}$ in (29), e.g. $E\left( {\delta {\mathbf{v}}^{e} \delta {\mathbf{q}}_{b}^{e} } \right) = {\mathbf{P}}_{vq}$. It needs to be noted that ${\mathbf{n}}_{ra}$ and $\delta {\mathbf{g}}^{e}$ are white noises. Thus, the covariance items associated with them are all equal to zero. Finally, we can obtain (32)–(34) by expanding (43)–(45).

Appendix 2: Qualitative evaluation on the proportions of part A in INS-acceleration aiding

For convenience, the following descriptions are specific to INS acceleration aiding (INS velocity aiding includes only part B). The expressions of part A and part B for INS aiding error are given as (12) and (13). Part A for INS aiding information is defined as (11), and part B for INS aiding information is given as,

$$ \tilde{\dot{\omega }}_{IB} = - \frac{{2\pi f_{L} }}{c}{\tilde{\mathbf{e}}}^{T} \left( {\tilde{\user2{a}}_{R} - {\varvec{a}}_{S} } \right) $$

(46)

In the following rough estimation, we will not consider the influence of the term ${\tilde{\mathbf{e}}}$ and ${\mathbf{I}} - {\mathbf{\tilde{e}\tilde{e}}}^{T}$ because it can hardly affect the magnitudes of expressions (11)–(13), and (46). Additionally, it is assumed that the magnitudes of terms $\delta {\mathbf{v}}_{R}$ and $\delta {\varvec{a}}_{R}$ are consistent. Here are three typical cases for evaluation.

• (1) GEO satellite, low-dynamic receiver

  $$ \left\| {{\tilde{\mathbf{v}}}_{R} } \right\| = 10\;{\text{m}}/{\text{s}},\;\left\| {{\mathbf{v}}_{S} } \right\| = 0\;{\text{m}}/{\text{s}},\;\left\| {{\tilde{\mathbf{r}}}_{R} } \right\| = 6400\;{\text{km}},\;\left\| {{\mathbf{r}}_{S} } \right\| = 42400\;{\text{km}},\;\left\| {\tilde{\user2{a}}_{R} } \right\| = 1\;{\text{m}}/{\text{s}}^{2} ,\;\left\| {{\varvec{a}}_{S} } \right\| = 0\;{\text{m}}/{\text{s}}^{2} $$

• (2) IGSO satellite, high-dynamic receiver

  $$ \left\| {{\tilde{\mathbf{v}}}_{R} } \right\| = 1000\;{\text{m}}/{\text{s}},\;\left\| {{\mathbf{v}}_{S} } \right\| = 2500\;{\text{m}}/{\text{s}},\;\left\| {{\tilde{\mathbf{r}}}_{R} } \right\| = 6400\;{\text{km}},\;\left\| {{\mathbf{r}}_{S} } \right\| = 42400\;{\text{km}},\;\left\| {\tilde{\user2{a}}_{R} } \right\| = 1\;{\text{m}}/{\text{s}}^{2} ,\;\left\| {{\varvec{a}}_{S} } \right\| = 0.1\;{\text{m}}/{\text{s}}^{2} $$

• (3) MEO satellite, middle-orbit satellite receiver

  $$ \left\| {{\tilde{\mathbf{v}}}_{R} } \right\| = 3000\;{\text{m}}/{\text{s}},\;\left\| {{\mathbf{v}}_{S} } \right\| = 3000\;{\text{m}}/{\text{s}},\;\left\| {{\tilde{\mathbf{r}}}_{R} } \right\| = 27900\;{\text{km}},\;\left\| {{\mathbf{r}}_{S} } \right\| = 28000\;{\text{km}},\;\left\| {\tilde{\user2{a}}_{R} } \right\| = 0.5\;{\text{m}}/{\text{s}}^{2} ,\;\left\| {{\varvec{a}}_{S} } \right\| = 0.5\;{\text{m}}/{\text{s}}^{2} $$

If we use $\eta_{1}$ and $\eta_{2}$ to represent the proportions of part A in INS aiding information and INS aiding error, then rough estimations of them can be expressed as,

$$ \eta_{1} = \frac{{\tilde{\dot{\omega }}_{IA} }}{{\tilde{\dot{\omega }}_{IA} + \tilde{\dot{\omega }}_{IB} }} \approx \frac{{{{\left( {\left\| {{\tilde{\mathbf{v}}}_{R} } \right\| + \left\| {{\mathbf{v}}_{S} } \right\|} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\left\| {{\tilde{\mathbf{v}}}_{R} } \right\| + \left\| {{\mathbf{v}}_{S} } \right\|} \right)^{2} } {\left( {\left\| {{\mathbf{r}}_{S} } \right\| - \left\| {{\tilde{\mathbf{r}}}_{R} } \right\|} \right)}}} \right. \kern-0pt} {\left( {\left\| {{\mathbf{r}}_{S} } \right\| - \left\| {{\tilde{\mathbf{r}}}_{R} } \right\|} \right)}}}}{{{{\left( {\left\| {{\tilde{\mathbf{v}}}_{R} } \right\| + \left\| {{\mathbf{v}}_{S} } \right\|} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\left\| {{\tilde{\mathbf{v}}}_{R} } \right\| + \left\| {{\mathbf{v}}_{S} } \right\|} \right)^{2} } {\left( {\left\| {{\mathbf{r}}_{S} } \right\| - \left\| {{\tilde{\mathbf{r}}}_{R} } \right\|} \right)}}} \right. \kern-0pt} {\left( {\left\| {{\mathbf{r}}_{S} } \right\| - \left\| {{\tilde{\mathbf{r}}}_{R} } \right\|} \right)}} + \left( {\left\| {\tilde{\user2{a}}_{R} } \right\| + \left\| {{\varvec{a}}_{S} } \right\|} \right)}} \times 100\% $$

(47)

$$ \eta_{2} = \frac{{\delta \dot{\omega }_{IA} }}{{\delta \dot{\omega }_{IA} + \delta \dot{\omega }_{IB} }} \approx \frac{{{{2\left( {\left\| {{\tilde{\mathbf{v}}}_{R} } \right\| + \left\| {{\mathbf{v}}_{S} } \right\|} \right)} \mathord{\left/ {\vphantom {{2\left( {\left\| {{\tilde{\mathbf{v}}}_{R} } \right\| + \left\| {{\mathbf{v}}_{S} } \right\|} \right)} {\left( {\left\| {{\mathbf{r}}_{S} } \right\| - \left\| {{\tilde{\mathbf{r}}}_{R} } \right\|} \right)}}} \right. \kern-0pt} {\left( {\left\| {{\mathbf{r}}_{S} } \right\| - \left\| {{\tilde{\mathbf{r}}}_{R} } \right\|} \right)}}}}{{{{2\left( {\left\| {{\tilde{\mathbf{v}}}_{R} } \right\| + \left\| {{\mathbf{v}}_{S} } \right\|} \right)} \mathord{\left/ {\vphantom {{2\left( {\left\| {{\tilde{\mathbf{v}}}_{R} } \right\| + \left\| {{\mathbf{v}}_{S} } \right\|} \right)} {\left( {\left\| {{\mathbf{r}}_{S} } \right\| - \left\| {{\tilde{\mathbf{r}}}_{R} } \right\|} \right)}}} \right. \kern-0pt} {\left( {\left\| {{\mathbf{r}}_{S} } \right\| - \left\| {{\tilde{\mathbf{r}}}_{R} } \right\|} \right)}} + 1}} \times 100\% $$

(48)

The rough estimation results for three typical cases are shown in Table

Table 5 Rough estimations on proportions of part A for three typical cases

5.

For INS aiding error, part A accounts for a very small proportion in majority of cases, which can usually be ignored. The reason is that the magnitude of the relative velocity ${\tilde{\mathbf{v}}}_{R} - {\mathbf{v}}_{S}$ between the satellite and the receiver is typically much smaller than that of their relative distance $\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|$. Only in the case of middle-orbit satellite receivers when the LOS distance $\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|$ is significantly shorter, then part A reaches a level that cannot be ignored.

However, for INS aiding information, part A is usually unignorable. This is because the impact of relative velocity ${\tilde{\mathbf{v}}}_{R} - {\mathbf{v}}_{S}$ becomes a squared term, amplifying its influence to the point where it becomes comparable to the LOS distance $\left\| {{\mathbf{r}}_{R} - {\mathbf{r}}_{S} } \right\|$. In practical applications, we can choose to ignore or consider the impact of part A based on real-world circumstances as well as the qualitative analysis provided above.