Capacity decisions and revenue sharing in a telemedicine healthcare system

Abstract

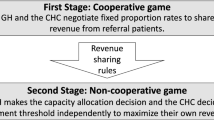
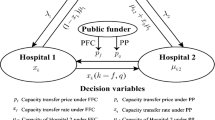
This paper studies the operations of a telemedicine service system consisting of independent hospitals [general hospital (GH) and telemedicine firm (TF)]. Through the healthcare alliance, the GH and the TF collaborate in capacity decisions and revenue sharing, and establish a green channel to refer patients. We adopt a two-stage game model to study a revenue sharing scheme of the telemedicine healthcare alliance. In the first-stage the game, the GH and the TF negotiate a revenue-sharing ratio to distribute the revenue of the referred patients. In the second stage game, given the profit-sharing ratio, GH makes capacity allocation decisions, and TF determines its own price to maximize its own revenue. Results show that the revenue sharing scheme can increase profits and promote collaboration between GH and TF. When a large number of mild patients arrive at the GH, the GH tends to participate in the alliance. For the TF, high prices do not always yield high profit under the comprehensive influence of the alliance.

Appendix

Proof of Proposition 1

When the green channel capacity can accommodate all referral patients, i.e.,$\frac{{{k^2}}}{2}\left( {{\lambda _1} + {\lambda _2}t} \right) < t$, by Eq. (4), we can obtain,

${\pi _{GH}} = \left[ {\frac{{{\lambda _3}\left( {1 + k} \right) }}{2} + \frac{{k\left( {{\lambda _2} - {\lambda _2}t} \right) }}{2}} \right] \frac{{1 - t}}{{{\lambda _3} + \left( {{\lambda _2} - {\lambda _2}t} \right) }}\eta + \beta \eta \frac{{{k^2}\left( {k + 1} \right) }}{4}\left( {{\lambda _1} + {\lambda _2}t} \right) .$

$2{\pi _{GH}} = \left[ {\frac{{{\lambda _3}\left( {1 - t} \right) }}{{{\lambda _3} + \left( {{\lambda _2} - {\lambda _2}t} \right) }} + k\left( {1 - t} \right) + \beta \frac{{{k^2}\left( {k + 1} \right) }}{2}\left( {{\lambda _1} + {\lambda _2}t} \right) } \right] \eta .$

In order to simplify the calculation, we take the derivative of $2{\pi _{GH}}$ with respect to t.

$$\begin{aligned} \begin{array}{c} \frac{{\partial 2{\pi _{GH}}}}{{\partial t}} = \left[ {\frac{{{\lambda _2}{k^2}\left( {k + 1} \right) }}{2}\beta - k - \frac{{{\lambda _3}^2}}{{{{\left[ {{\lambda _3} + {\lambda _2}\left( {1 - t} \right) } \right] }^2}}}} \right] \eta \\ \quad \quad \quad \qquad = \left[ {\frac{{{k^2}\left( {k + 1} \right) {\lambda _2}}}{2}\beta - k - \frac{{{\lambda _3}^2}}{{{\lambda _2}^2}}\frac{1}{{{{\left[ {\frac{{{\lambda _3}}}{{{\lambda _2}}} + \left( {1 - t} \right) } \right] }^2}}}} \right] . \end{array} \end{aligned}$$

Taking the first-order condition $\frac{{\partial 2{\pi _{GH}}}}{{\partial t}} = 0$, we can obtain

$$\begin{aligned} \beta = \left[ {\frac{{{\lambda _3}^2}}{{{\lambda _2}^2}}\frac{1}{{\left[ {\frac{{{\lambda _3}}}{{{\lambda _2}}} + \left( {1 - t} \right) } \right] }} + k} \right] \frac{2}{{{\lambda _2}{k^2}\left( {k + 1} \right) }}, \end{aligned}$$

and then we can get

$$\begin{aligned} \beta > \left[ {{{\left( {\frac{{{\lambda _3}}}{{{\lambda _2} + {\lambda _3}}}} \right) }^2} + k} \right] \frac{2}{{{\lambda _2}{k^2}\left( {k{{ + 1}}} \right) }}. \end{aligned}$$

by scaling.

When $\beta \le \left[ {{{\left( {\frac{{{\lambda _3}}}{{{\lambda _2} + {\lambda _3}}}} \right) }^2} + k} \right] \frac{2}{{{\lambda _2}{k^2}\left( {k{{ + 1}}} \right) }}$, GH’s profit decreases with the increase of t, so GH will not allocate capacity to the green channel.

When the number of patients referred is greater than the green channel capacity, i.e., $\frac{{{k^2}}}{2}({\lambda _1} + {\lambda _2}t) > t$. By Eq. (4), we can obtain,

$$\begin{aligned} 2{\pi _{GH}} = \left[ {\frac{{{\lambda _3}\left( {1 - t} \right) }}{{\left[ {{\lambda _3} + \left( {{\lambda _2} - {\lambda _2}t} \right) } \right] }} + k\left( {1 - t} \right) + \beta \left( {{{k + 1}}} \right) t} \right] \eta . \end{aligned}$$

and then

$$\begin{aligned} \begin{array}{c} \frac{{\partial {{2}}{\pi _{GH}}}}{{\partial t}} = \left[ {\beta \left( {k + 1} \right) - k - \frac{{{\lambda _3}^2}}{{{{\left[ {{\lambda _3} + {\lambda _2}\left( {1 - t} \right) } \right] }^2}}}} \right] \eta \\ = \left[ {\beta \left( {k + 1} \right) - k - \frac{{{\lambda _3}^2}}{{{\lambda _2}^2}}\frac{1}{{{{\left[ {\frac{{{\lambda _3}}}{{{\lambda _2}}} + \left( {1 - t} \right) } \right] }^2}}}} \right] \end{array}. \end{aligned}$$

If $\frac{{\partial {{2}}{\pi _{GH}}}}{{\partial t}} = 0$, then $\beta = \left[ {\frac{{{\lambda _3}^2}}{{{\lambda _2}^2}}\frac{1}{{\left[ {\frac{{{\lambda _3}}}{{{\lambda _2}}} + \left( {1 + t} \right) } \right] }} + k} \right] \frac{1}{{\left( {k + 1} \right) }} > \left[ {{{\left( {\frac{{{\lambda _3}}}{{{\lambda _2} + {\lambda _3}}}} \right) }^2} + k} \right] \frac{1}{{\left( {k + 1} \right) }}$.

When $\beta \le \left[ {{{\left( {\frac{{{\lambda _{{3}}}}}{{{\lambda _{{2}}}{{ + }}{\lambda _{{3}}}}}} \right) }^{{2}}} + k} \right] \frac{1}{{\left( {k + 1} \right) }}$, GH’s profit decreases with the increase of t. At this time, GH will not allocate capacity for TF referral patients.

Let $\widehat{\lambda }{{ = }}{\left( {\frac{{{\lambda _{{3}}}}}{{{\lambda _{{2}}}{{ + }}{\lambda _{{3}}}}}} \right) ^{{2}}}$ and then $\beta \ge \frac{{2\left( {\widehat{\lambda }+ k} \right) }}{{{\lambda _2}{k^2}\left( {k{{ + 1}}} \right) }}$, then GH would allocate capacity for TF referral patients to join the alliance. $\square$

Proof of Proposition 2

If $\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}}{{ + }}{\lambda _{{2}}}t} \right) \ge t$,then $t \le \frac{{{k^2}{\lambda _1}/2}}{{1 - {k^2}{\lambda _2}/2}}$.

By Eq. (4), we can obtain

$2{\pi _{GH}} = \left[ {\frac{{{\lambda _3}\left( {1 - t} \right) }}{{\left[ {{\lambda _3} + \left( {{\lambda _2} - {\lambda _2}t} \right) } \right] }} + k\left( {1 - t} \right) + \beta \left( {{{k + 1}}} \right) t} \right] \eta$

$\frac{{\partial 2{\pi _{GH}}}}{{\partial t}} = \frac{{ - {\lambda ^2}_3}}{{{{\left[ {{\lambda _3} + ({\lambda _2} - {\lambda _2}t)} \right] }^2}}} - k + \beta \left( {k + 1} \right)$

By solving the first derivative with zero point, we can obtain ${t_1} = 1{{ + }}\frac{{{\lambda _{{3}}}}}{{{\lambda _{{2}}}}} - \frac{{{\lambda _3}}}{{{\lambda _2}\sqrt{\beta \left( {k + 1} \right) - k} }}$.

According to the derivative property, if $t < {t_1}$, then ${\pi _{GH}}$ is monotonically decreasing, and if $t>{t_1}$, then ${\pi _{GH}}$ is monotonically increasing.So the optimal solution is ${t^*} = \min \left\{ {1{{ + }}\frac{{{\lambda _{{3}}}}}{{{\lambda _{{2}}}}} - \frac{{{\lambda _3}}}{{{\lambda _2}\sqrt{\beta \left( {k + 1} \right) - k} }},\frac{{{k^2}{\lambda _1}/2}}{{1 - {k^2}{\lambda _2}/2}}} \right\}$.

When ${k^2} > \frac{{2({\lambda _3} + {\lambda _2})}}{{{\lambda _2}({\lambda _1} + {\lambda _2} + {\lambda _3})}}$, the optimal solution of is ${t^*} = {t_1}$.

When ${k^2} < \frac{{2({\lambda _3} + {\lambda _2})}}{{{\lambda _2}({\lambda _1} + {\lambda _2} + {\lambda _3})}}$, the optimal solution of t is ${t^*} = \frac{{{k^2}{\lambda _1}/2}}{{1 - {k^2}{\lambda _2}/2}}$, i.e.,

$$\begin{aligned} {t^*} = \frac{{{k^2}}}{2}\left( {{\lambda _{{1}}} + {\lambda _2}t} \right) . \end{aligned}$$

If $\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}}{{ + }}{\lambda _{{2}}}t} \right) \le t$, then $t \ge \frac{{{k^2}{\lambda _1}/2}}{{1 - {k^2}{\lambda _2}/2}}$.

By Equation (4), we can obtain

$$\begin{aligned}2{\pi _{GH}} = \left[ {\frac{{{\lambda _3}\left( {1 - t} \right) }}{{\left[ {{\lambda _3} + \left( {{\lambda _2} - {\lambda _2}t} \right) } \right] }} + k\left( {1 - t} \right) + \beta \frac{{{k^2}\left( {k + 1} \right) }}{2}\left( {{\lambda _1}{{ + }}{\lambda _2}t} \right) } \right] \eta , \end{aligned}$$

and $\frac{{\partial 2{\pi _{GH}}}}{{\partial t}} = \frac{{ - {\lambda ^2}_3}}{{{{[{\lambda _3} + ({\lambda _2} - {\lambda _2}t)]}^2}}} - k + \frac{{{k^2}\left( {k + 1} \right) }}{2}\beta {\lambda _2}.$

Let $\frac{{\partial {{2}}{\pi _{GH}}}}{{\partial t}} = 0$,we can obtain ${t_2} = 1{{ + }}\frac{{{\lambda _{{3}}}}}{{{\lambda _{{2}}}}} - f(\beta ,k,{\lambda _3},{\lambda _2})$.

According to the derivative property, if $t < {t_2}$, then ${\pi _{GH}}$is monotonically increasing, and if $t > {t_2}$, then ${\pi _{GH}}$ is monotonically decreasing.

So the optimal solution is ${t^*} = \max \left\{ {{t_2} = 1{{ + }}\frac{{{\lambda _{{3}}}}}{{{\lambda _{{2}}}}} - f(\beta ,k,{\lambda _3},{\lambda _2}),\frac{{{k^2}{\lambda _1}/2}}{{1 - {k^2}{\lambda _2}/2}}} \right\}$.

When ${k^2} > \frac{{2({\lambda _3} + {\lambda _2})}}{{{\lambda _2}({\lambda _1} + {\lambda _2} + {\lambda _3})}}$, we can obtain ${t_2}<\frac{{{k^2}{\lambda _1}/2}}{{1 - {k^2}{\lambda _2}/2}}$. The optimal solution of t is ${t^*} = \frac{{{k^2}{\lambda _1}/2}}{{1 - {k^2}{\lambda _2}/2}}$, i.e.,

$$\begin{aligned} {t^*} = \frac{{{k^2}}}{2}\left( {{\lambda _{{1}}} + {\lambda _2}t} \right) .. \end{aligned}$$

$\square$

Proof of Proposition 3

Without alliance, we can get by Eq. (2), ${\pi _{TF}} = {\lambda _1}\left( {p - \frac{k}{2} - \frac{{{k^3}}}{3}} \right)$

$\frac{{\partial {\pi _{TF}}}}{{\partial p}} = k{\lambda _L} - {\alpha _L}pk{\lambda _L} + k{\lambda _H} - {\alpha _H}pk{\lambda _H} - k\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {p - \frac{k}{2} - \frac{{{k^3}}}{2}} \right)$

From the derivative property, if $\frac{{\partial {\pi _{TF}}}}{{\partial p}} = 0$, the optimal price of TF is $p_0^* = \frac{\lambda }{{2\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) }} + \frac{k}{4} + \frac{{{k^3}}}{4}$ by solving Eq. (2).

Next, we will analyze the case that GH participates in the alliance. When $\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}}{{ + }}{\lambda _{{2}}}t} \right) < t$, the price of TF is $p < \frac{{{{2t} / {{k^3}}} - \lambda }}{{\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {t - 1} \right) }}$.The derivation of Eq. (5) is

$\begin{array}{l} \frac{{\partial {\pi _{TF}}}}{{\partial p}} = \left[ {{\alpha _L}k{\lambda _L}\left( {t - 1} \right) + {\alpha _H}k{\lambda _H}\left( {t - 1} \right) } \right] \left( {p - \frac{k}{2}} \right) \left( {1 - \frac{{{k^2}}}{2}} \right) \\ \qquad \qquad + k{\lambda _L}\left( {1 - {\alpha _L}p - {\alpha _L}pt} \right) \left( {1 - \frac{{{k^2}}}{2}} \right) \\ \qquad \qquad + k{\lambda _H}\left( {1 - {\alpha _H}p - {\alpha _H}pt} \right) \left( {1 - \frac{{{k^2}}}{2}} \right) \\ \qquad \qquad + \eta \left( {1 - \beta } \right) \frac{{{k^2}\left( {k + 1} \right) }}{4}\left[ {{\alpha _L}k{\lambda _L}\left( {t - 1} \right) + {\alpha _H}k{\lambda _H}\left( {t - 1} \right) } \right] \end{array}$

By solving the first derivative with zero point $\frac{{\partial {\pi _{TF}}}}{{\partial p}} = 0$, we can obtain a solution for the price of TF and denote it as ${p_2}$

$$\begin{aligned} {p_2} = \frac{{{\lambda _L} + {\lambda _H}}}{{2\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {1 - t} \right) }} + \frac{k}{4} - \frac{{\eta {k^2}\left( {k + 1} \right) \left( {1 - \beta } \right) }}{{4\left( {2 - {k^2}} \right) }}. \end{aligned}$$

According to the derivative property, if $p < {p_2}$, then ${\pi _{TF}}$ is monotonically increasing, and if $p > {p_2}$, then ${\pi _{TF}}$ is monotonically decreasing. Therefore, the optimal price of TF is ${p^*} = \min \left\{ {\frac{\lambda }{{2\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {1 - t} \right) }} + \frac{k}{4} - \frac{{\eta {k^2}\left( {k + 1} \right) \left( {1 - \beta } \right) }}{{4\left( {2 - {k^2}} \right) }},\frac{{{{2t} / {{k^3}}} - \lambda }}{{\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {t - 1} \right) }}} \right\}$

When $\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}}{{ + }}{\lambda _{{2}}}t} \right) > t$, the price of TF is $p > \frac{{{{2t} / {{k^3}}} - \lambda }}{{\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {t - 1} \right) }}$. By solving the first derivative with zero point $\frac{{\partial {\pi _{TF}}}}{{\partial p}} = 0$, we can obtain a solution for the price of TF and denote it as ${p_3}$

$$\begin{aligned} {p_3} = \frac{\lambda }{{2\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {1 - t} \right) }} + \frac{k}{4}. \end{aligned}$$

According to the derivative property, if $p<p_3$, then $\pi _{TF}$ is monotonically increasing, and if $p>p_3$, then $\pi _{TF}$ is monotonically decreasing. Therefore, the optimal price of TF is ${p^*} = \max \left\{ {\frac{\lambda }{{2\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {1 - t} \right) }} + \frac{k}{4},\frac{{{{2t} / {{k^3}}} - \lambda }}{{\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {t - 1} \right) }}} \right\}$.

It is obviously ${p_2} < {p_3}$, if $t < \frac{{{k^3}\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) }}{{{k^3}\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) {{ + }}2\lambda }}$, then ${p_2}< {p_3} < p_0^*$.

If $p_0^* > \frac{{{{2t} / {{k^3}}} - \lambda }}{{\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {t - 1} \right) }}$, because of $p_0^* = \frac{\lambda }{{2\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) }} + \frac{k}{4} + \frac{{{k^3}}}{4}$, then we can get $\frac{{{{2t} / {{k^3}}} - \lambda }}{{\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {t - 1} \right) }} < \frac{\lambda }{{2\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) }} + \frac{k}{4} + \frac{{{k^3}}}{4}$.

Then, $t < \frac{{{k^3}\lambda }}{4}$ can be obtained by simplifying$\frac{{{{2t} / {{k^3}}} - \lambda }}{{\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) \left( {t - 1} \right) }} < \frac{\lambda }{{2\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) }} + \frac{k}{4} + \frac{{{k^3}}}{4}$.

Based on the above derivation, when $t \le \min \left\{ {\frac{{{k^3}\lambda }}{4},\frac{{{k^3}\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) }}{{{k^3}\left( {{\alpha _L}{\lambda _L} + {\alpha _H}{\lambda _H}} \right) {{ + }}2\lambda }},\frac{{{\lambda _{{1}}}{k^2}}}{{2 - {\lambda _2}{k^2}}}} \right\}$, the optimal price of TF is ${p^{{*}}} < p_0^*$ and the strategy of TF is $P_2$, that is, the low price strategy. $\square$

Proof of Proposition 4

Define total profit of the alliance as ${\pi _t}$, and ${\pi _t} = {\pi _{GH}} + {\pi _{TF}}$,

$\begin{array}{c} {\pi _t} = \left( {{\lambda _1} + {\lambda _2}t} \right) \left( {1 - \frac{{{k^2}}}{2}} \right) \left( {p - \frac{k}{2}} \right) + \frac{\eta }{{{2}}}\left[ {{\lambda _3}\left( {1 + k} \right) + \left( {{\lambda _2} - {\lambda _2}t} \right) k} \right] \frac{{1 - t}}{{{\lambda _3} + \left( {{\lambda _2} - {\lambda _2}t} \right) }}\\ + \frac{\eta }{{{2}}}\left( {k + 1} \right) \min \left\{ {\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}} + {\lambda _2}t} \right) ,t} \right\} . \end{array}$

When $\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}}{{ + }}{\lambda _{{2}}}t} \right) > t$, in order to simplify the calculation, we choose to solve the derivative of ${{2}}{\pi _t}$.

$\frac{{\partial 2{\pi _t}}}{{\partial t}} = 2{\lambda _2}\left( {1 - \frac{{{k^2}}}{2}} \right) \left( {p - \frac{k}{2}} \right) + \eta - \frac{{{\lambda _3}^2\eta }}{{{{\left[ {{\lambda _3} + {\lambda _2}\left( {1 - t} \right) } \right] }^2}}}.$

When $\sqrt{\frac{{2{\lambda _2}p}}{\eta }} = \sigma$, ${\lambda _3} > \frac{{{\lambda _2}\sigma }}{{1 - \sigma }}$, according to the derivative property,${\pi _t}$ decreases with the increase of t. At this time, GH’s capacity allocation to the green channel will damage the total profit of the alliance. Therefore, if a large number of severe patients go to GH for treatment, GH would not allocate capacity for TF referral patients, that is $t=0$.

Similarly, it can be obtained, when $\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}}{{ + }}{\lambda _{{2}}}t} \right) < t$, ${\lambda _3} > \frac{{{\lambda _2}\sigma }}{{1 - \sigma }}$, $\pi _t$ decreases with the increase of t. $\square$

Proof of Proposition 5

Assume that the difference between TF without alliance profit and alliance profit is $\pi$, we can get from Eqs. (2)–(5):

$\begin{array}{c} \pi = {\lambda _1}\left( {p - \frac{{k + {k^3}}}{2}} \right) - \left( {{\lambda _1} + {\lambda _2}t} \right) \left( {1 - \frac{{{k^2}}}{2}} \right) \left( {p - \int _0^k {\frac{1}{k}KdK} } \right) \\ - \left( {1 - \beta } \right) \eta \int _k^1 {\frac{1}{{1 - k}}KdK\min \left\{ {\frac{{{k^2}}}{2}({\lambda _1} + {\lambda _2}t),t} \right\} } \end{array}$

Then, simplify the equation of $\pi$ to get

$$\begin{aligned} \pi{} & {} = {\lambda _1}\left( {p - \frac{{k + {k^3}}}{2}} \right) - \left( {{\lambda _1} + {\lambda _2}t} \right) \left( {1 - \frac{{{k^2}}}{2}} \right) \left( {p - \int _0^k {\frac{1}{k}KdK} } \right) \nonumber \\{} & {} \quad - t\left( {1 - \beta } \right) \eta \int _k^1 {\frac{1}{{1 - k}}KdK} \end{aligned}$$

(A.1)

The threshold of patient price sensitivity is denoted as $\alpha _1$ when $\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}}{{ + }}{\lambda _{{2}}}t} \right) > t$, $\alpha < {\alpha _1} = \frac{{\left( {{\lambda _L} + {\lambda _H}} \right) \left( {2{k^3}p - 3{k^4}} \right) - 2\eta t\left( {1 - \beta } \right) \left( {1 + k} \right) }}{{pk\left( {{c_3}{\lambda _L} + {\lambda _H}} \right) \left[ {3{k^3} + pt\left( {2{k^2} - 4} \right) - 2{k^2}p + kt\left( {2 - {k^2}} \right) } \right] }}$ can be obtained by taking ${\alpha _L} = {c_3}{\alpha _H} = {c_3}\alpha$, ${\lambda _1} = \left( {{{1 - }}{\alpha _L}p} \right) k{\lambda _L} + \left( {{{1 - }}{\alpha _H}p} \right) k{\lambda _H}$, ${\lambda _2} = {\alpha _L}pk{\lambda _L} + {\alpha _H}pk{\lambda _H}$, ${\lambda _3} = \left( {1 - k} \right) \lambda$ into Eq. A.1.

Also, the threshold of patient price sensitivity is denoted as $\alpha _2$ when $\frac{{{k^2}}}{2}\left( {{\lambda _{{1}}}{{ + }}{\lambda _{{2}}}t} \right) < t$, $\alpha < {\alpha _2} = \frac{{\left( {{\lambda _L} + {\lambda _H}} \right) \left[ {2p{k^3} - 3{k^4} - \eta {k^3}\left( {1 + k} \right) \left( {1 - \beta } \right) } \right] }}{{pk\left( {{c_3}{\lambda _L} + {\lambda _H}} \right) \left[ {3{k^2} - 2{k^2} - t\left( {4p - 2k - 2p{k^2} + {k^3}} \right) + \left( {1 - t} \right) \left( {1 + k} \right) \left( {1 - \beta } \right) {k^2}} \right] }}$can be obtained by taking ${\alpha _L} = {c_3}{\alpha _H} = {c_3}\alpha$, ${\lambda _1} = \left( {{{1 - }}{\alpha _L}p} \right) k{\lambda _L} + \left( {{{1 - }}{\alpha _H}p} \right) k{\lambda _H}$, ${\lambda _2} = {\alpha _L}pk{\lambda _L} + {\alpha _H}pk{\lambda _H}$, ${\lambda _3} = \left( {1 - k} \right) \lambda$ into Eq. A.1.

Based on the above calculation, when $\alpha < \min \left\{ {{\alpha _1},{\alpha _2}} \right\}$, the profit of TF without alliance is higher than that of alliance, that is $\pi >0$. Therefore, TF will refuse to participate in the alliance. $\square$