Abstract
Problems related to projections on closed convex cones are frequently encountered in optimization theory and related fields. To study these problems, various unifying ideas have been introduced, including asymmetric vector-valued norms and certain generalized lattice-like operations. We propose a new perspective on these studies by describing how the problem of cone projection can be formulated using an order-theoretic formalism developed in this paper. The underlying mathematical structure is a partially ordered vector space that generalizes the notion of a vector lattice by using two partial orderings and having certain lattice-type properties with respect to these orderings. In this note we introduce a generalization of these so-called mixed lattice spaces, and we show how such structures arise quite naturally in some of the applications mentioned above.
Similar content being viewed by others
1 Introduction
The problem of cone projection and the related decomposition method with respect to dual cones is of significant importance in convex analysis, and it has been studied extensively since the pioneering work of Moreau [11]. In this paper we present an order-theoretic setting in which the basic projection problem can be stated and studied. The theoretical framework on which this note is based is called a mixed lattice space which is a partially ordered vector space (or more generally, a group) with two partial orderings and certain “mixed” lattice-type properties with respect to these two orders. In a mixed lattice space, the vector lattice operations of supremum and infimum are replaced by asymmetric mixed upper and lower envelopes, which are formed with respect to the two partial orders. A mixed lattice space is a generalization of a vector lattice in the sense that if the two partial orders are identical, then the mixed lattice space reduces to a vector lattice. However, the two partial orders of a mixed lattice space do not need to be lattice orderings. A systematic development of this theory is quite recent [4, 9, 10], although some earlier studies on mixed lattice groups date back to 1990s [5, 6]. The theory of mixed lattice spaces and groups is heavily based on an earlier theory of mixed lattice semigroups, which was developed by M. Arsove and H. Leutwiler in the 1970s for the purposes of axiomatic potential theory (see [2] and references therein).
In Sect. 2 we give a brief overview of the terminology and the elementary properties of mixed lattice spaces. In Sect. 3 we present a generalization of mixed lattice structures by relaxing some of the assumptions in the definitions, resulting in a significant gain in generality. This modification gives the structure more flexibility in terms of applications to cone projections, and this is what our main results are concerned with. In Sect. 4 we formulate certain problems in convex optimization using this generalized order-theoretic framework. Here we observe a close connection between the mixed lattice theory and the theory of cone projections.
In metric cone projections there are two cones involved (a cone and its dual), and we show that this setting has a generalized mixed lattice structure. We then look at some other fundamental facts and results concerning cone projections, and formulate them in the language of mixed lattice theory. We also observe that the so-called lattice like operations introduced in [12] can be viewed as the generalized mixed lattice operations.
We should also mention the more general concept of isotone cone retraction, introduced by Németh [14], and the related notion of an asymmetric cone norm, recently studied in [13]. Some of the connections between these and the mixed lattice theory is investigated in [10].
2 Mixed lattice spaces
In this section we collect the essential terminology, definitions and basic results. For a more detailed presentation with proofs, we refer to [4, 6, 9].
Let V be a partially ordered real vector space with two partial orderings \(\le \) and \(\preccurlyeq \) (i.e. we assume that both orderings are compatible with the linear structure of V). The partial order \(\le \) is called the initial order and \(\preccurlyeq \) is called the specific order. With these two partial orders \(\le \) and \(\preccurlyeq \) we define the mixed upper and lower envelopes

and

respectively, where the minimum and maximum (whenever they exist) are taken with respect to the initial order \(\le \). These definitions were introduced by Arsove and Leutwiler in [1]. We observe that these operations are not commutative, i.e.  and
and  are not necessarily equal. We recall that a subset K of a vector space is called a cone if (i) \(t K \subseteq K\) for all \(t \ge 0\), (ii) \(K+K \subseteq K\) and (iii) \(K\cap (-K)=\{0\}\). Although the above definition of a cone is rather standard in the theory of partially ordered spaces, we should point out that there are also different definitions in use, and sometimes a subset satisfying the above conditions is called a full-dimensional convex pointed cone.
are not necessarily equal. We recall that a subset K of a vector space is called a cone if (i) \(t K \subseteq K\) for all \(t \ge 0\), (ii) \(K+K \subseteq K\) and (iii) \(K\cap (-K)=\{0\}\). Although the above definition of a cone is rather standard in the theory of partially ordered spaces, we should point out that there are also different definitions in use, and sometimes a subset satisfying the above conditions is called a full-dimensional convex pointed cone.
Definition 2.1
Let V be a partially ordered real vector space with respect to two partial orders \(\le \) and \(\preccurlyeq \), and let \(V_p\) and \(V_{sp}\) be the corresponding positive cones, respectively. Then \(V=(V,\le ,\preccurlyeq )\) is called a mixed lattice vector space if the following conditions hold:
-
(1)
The elements
 and
and  exist in V for all \(x,y\in V\),
exist in V for all \(x,y\in V\), -
(2)
The elements
 and
and  are in \(V_{sp}\) whenever \(x,y\in V_{sp}\).
are in \(V_{sp}\) whenever \(x,y\in V_{sp}\).
Remark 2.2
A more general definition of a mixed lattice structure does not require the condition (2) in the above definition. It is included here for convenience, as many important properties depend on it. For more details on these technicalities, as well as many examples of mixed lattice spaces, we refer to [4]. If the condition (2) holds, then \(V_{sp}\) is a called a mixed lattice cone. A mixed lattice space satisfying (2) is called quasi-regular, and if in addition the cone \(V_{sp}\) is generating then V is called regular. It follows from the condition (2) that \(V_{sp}\subseteq V_p\) ([4, Theorem 2.10]). We also note that the cone \(V_p\) is always generating, that is \(V=V_p - V_p\). This is a consequence of Theorem 2.5(b) given below.
The definition of the mixed envelopes implies that in a mixed lattice space V the inequalities  and
and  hold for all \(x,y\in V\). For proofs and further discussion on the properties given in the next theorem, see [4, 6, 9].
hold for all \(x,y\in V\). For proofs and further discussion on the properties given in the next theorem, see [4, 6, 9].
Theorem 2.3
Let V be a mixed lattice space. The mixed envelopes have the following properties for all \(x,y,z,u,v\in V\) and \(a\in \mathbb {R}\).
-
(a)

-
(b)
 and
and 
-
(c)

-
(d)

-
(e)

-
(f)

-
(g)

-
(h)

-
(i)

-
(j)

The upper and lower parts of an element were introduced in [4, Definition 3.1]. Their roles are similar to those of the positive and negative parts of an element in a vector lattice.
Definition 2.4
Let V be a mixed lattice space and \(x\in V\). The elements  and
and  are called the upper part and lower part of x, respectively. Similarly, the elements
are called the upper part and lower part of x, respectively. Similarly, the elements  and
and  are called specific upper part and specific lower part of x, respectively.
are called specific upper part and specific lower part of x, respectively.
From the above definitions we observe that for the specific upper and lower parts we have  and
and  , and for the upper and lower parts
, and for the upper and lower parts  and
and  . The upper and lower parts have several important basic properties, which were proved in [4, Section 3]. Some of these properties are given in the next theorem.
. The upper and lower parts have several important basic properties, which were proved in [4, Section 3]. Some of these properties are given in the next theorem.
Theorem 2.5
Let V be a mixed lattice space and \(x\in V\). Then we have
-
(a)
 and
and  .
. -
(b)
 .
. -
(c)
 and
and  .
. -
(d)
 and
and  .
. -
(e)
 .
. -
(f)
 if and only if
if and only if  and
and  .
. -
(g)
\(x\ge 0\) if and only if
 and
and  .
.
3 The generalized mixed lattice structure
In a mixed lattice space V the existence of the mixed envelopes places rather strict restrictions on the cones \(V_p\) and \(V_{sp}\) which limits the range of possible applications. In this section we present a generalization of a mixed lattice space to overcome this limitation. Our main motivation for the generalization is that when studying cone projections in optimization problems, the upper and lower parts of elements do not typically exist.
Let \((V,\le ,\preccurlyeq )\) be a partially ordered vector space with two partial orderings, as in the preceding section. We introduce the following set notation.

Let \(E\subset V\). An element \(x\in E\) is called a minimal element of E if \(y\in E\) and \(y\le x\) implies \(y=x\). A dual notion of a maximal element is defined similarly. The set of minimal elements of the set  will be denoted by
will be denoted by  , and the set of maximal elements of the set
, and the set of maximal elements of the set  will be denoted by
will be denoted by  .
.
We now define a generalization of the mixed lattice structure in which the elements  and
and  are replaced by set-valued mappings
are replaced by set-valued mappings  and
and  . This provides a considerable increase in generality, at the expense of losing some good properties of mixed lattice spaces and becoming somewhat more difficult to work with.
. This provides a considerable increase in generality, at the expense of losing some good properties of mixed lattice spaces and becoming somewhat more difficult to work with.
Definition 3.1
Let V be a partially ordered vector space with respect to two partial orders \(\le \) and \(\preccurlyeq \), and let \(V_p\) and \(V_{sp}\) be the corresponding positive cones, respectively. Then \(V=(V,\le ,\preccurlyeq )\) is called a generalized mixed lattice structure if the sets  and
and  are non-empty for all \(x,y\in V\).
are non-empty for all \(x,y\in V\).
Clearly, if the sets  and
and  contain only one element for every \(x,y\in V\) then these elements are equal to
contain only one element for every \(x,y\in V\) then these elements are equal to  and
and  , respectively, and the generalized mixed lattice structure then reduces to an ordinary mixed lattice space.
, respectively, and the generalized mixed lattice structure then reduces to an ordinary mixed lattice space.
In the following we introduce selected fundamental properties of generalized mixed lattice structures to facilitate the study of cone projections in Sect. 4. The next theorem gives some of the basic properties of generalized mixed lattice structures corresponding to the properties of the mixed envelopes listed in Theorem 2.3.
Theorem 3.2
Let V be a generalized mixed lattice structure. The following hold for all \(x,y\in V\).
-
(a)

-
(b)
If
 then there exists an element
then there exists an element  such that \(x+y=u+w\). Similarly, for any
such that \(x+y=u+w\). Similarly, for any  there exists an element
there exists an element  such that \(x+y=u+w\). Hence, we have
such that \(x+y=u+w\). Hence, we have  .
. -
(c)
 for all \(z\in V\).
for all \(z\in V\). -
(d)
 for all \(z\in V\).
for all \(z\in V\). -
(e)

 .
. -
(f)
For all \(a\in \mathbb {R}\), \(a\ge 0\) we have
 and
and  .
. -
(g)
For all \(a\in \mathbb {R}\), \(a< 0\) we have
 and
and  .
.
Proof
(a) If  then \(u\succcurlyeq x\) and \(u\ge y\), so \(-u\preccurlyeq -x\) and \(-u\le -y\), and thus
then \(u\succcurlyeq x\) and \(u\ge y\), so \(-u\preccurlyeq -x\) and \(-u\le -y\), and thus  . If
. If  and \(w\ge -u\) then by a similar argument
and \(w\ge -u\) then by a similar argument  . But \(-w\le u\) and u is a minimal element of
. But \(-w\le u\) and u is a minimal element of  , so we must have \(-w=u\). Hence,
, so we must have \(-w=u\). Hence,  . The reverse inclusion is proved similarly, so
. The reverse inclusion is proved similarly, so  .
.
(b) If  then \(u\succcurlyeq x\) and \(u\ge y\). This implies that \(x+y\preccurlyeq u+y\) and \(x+y\le x+u\), and so
then \(u\succcurlyeq x\) and \(u\ge y\). This implies that \(x+y\preccurlyeq u+y\) and \(x+y\le x+u\), and so  . We want to show that \(x+y-u\) is a maximal element of the set
. We want to show that \(x+y-u\) is a maximal element of the set  . For this, suppose that
. For this, suppose that  and \(w\ge x+y-u\). Then \(w\preccurlyeq y\) and \(w\le x\), and it follows that \(u\ge x+y-w\succcurlyeq x\) and \(u\ge x+y-w\ge y\). Hence
and \(w\ge x+y-u\). Then \(w\preccurlyeq y\) and \(w\le x\), and it follows that \(u\ge x+y-w\succcurlyeq x\) and \(u\ge x+y-w\ge y\). Hence  . But u is a minimal element of the set
. But u is a minimal element of the set  , so we must have \(u=x+y-w\) and thus
, so we must have \(u=x+y-w\) and thus  and \(u+w=x+y\). The dual statement is proved similarly.
and \(u+w=x+y\). The dual statement is proved similarly.
(c) If  then \(v \succcurlyeq x\) and \(v \ge y\). Consequently, \(v+z \succcurlyeq x+z\) and \(v+z \ge y+z\) for all \(z\in V\), and so
then \(v \succcurlyeq x\) and \(v \ge y\). Consequently, \(v+z \succcurlyeq x+z\) and \(v+z \ge y+z\) for all \(z\in V\), and so  . If
. If  and \(w\le v+z\) then \(v\ge w-z\succcurlyeq x+z-z=x\) and \(v\ge w-z\ge y+z-z=y\). But then
and \(w\le v+z\) then \(v\ge w-z\succcurlyeq x+z-z=x\) and \(v\ge w-z\ge y+z-z=y\). But then  , and since v is a minimal element, it follows that \(v=w-z\), or \(w=v+z\). Hence,
, and since v is a minimal element, it follows that \(v=w-z\), or \(w=v+z\). Hence,  for all \(z\in V\).
for all \(z\in V\).
For the converse, if  then \(w\succcurlyeq z+x\) and \(w\ge z+y\). Thus \(w-z\succcurlyeq x\) and \(w-z\ge y\), so
then \(w\succcurlyeq z+x\) and \(w\ge z+y\). Thus \(w-z\succcurlyeq x\) and \(w-z\ge y\), so  . Again, if
. Again, if  and \(v\le w-z\) then \(w\ge v+z\succcurlyeq x+z\) and \(w\ge v+z\ge y+z\), and it follows that
and \(v\le w-z\) then \(w\ge v+z\succcurlyeq x+z\) and \(w\ge v+z\ge y+z\), and it follows that  . Since w is minimal, we have \(w=v+z\), or \(v=w-z\). Hence,
. Since w is minimal, we have \(w=v+z\), or \(v=w-z\). Hence,  . This shows that
. This shows that  , proving the equality of the two sets.
, proving the equality of the two sets.
(d) is similar to (c).
(e) Let \(x\succcurlyeq y\). Since \(x\ge x\) we have  . If
. If  is an element such that \(u\le x\) then \(x\le u\le x\), and hence \(x=u\) because \(V_p \cap (-V_p)=\{0\}\) holds by assumption. This shows that
is an element such that \(u\le x\) then \(x\le u\le x\), and hence \(x=u\) because \(V_p \cap (-V_p)=\{0\}\) holds by assumption. This shows that  . Next, if
. Next, if  and
and  then \(w\ge x\). But then w and x are both minimal elements, so they are comparable only if \(w=x\). Hence
then \(w\ge x\). But then w and x are both minimal elements, so they are comparable only if \(w=x\). Hence  .
.
If  then it follows by part (b) that
then it follows by part (b) that  . If there is some other element
. If there is some other element  then \(y\le w\). But y and w are both maximal elements of the set
then \(y\le w\). But y and w are both maximal elements of the set  , and so \(w=y\). This shows that
, and so \(w=y\). This shows that  . Finally, if
. Finally, if  then of course \(y\preccurlyeq x\), finishing the proof.
then of course \(y\preccurlyeq x\), finishing the proof.
(f) The case \(a=0\) is trivial. If \(a> 0\) and  then \(z\preccurlyeq ax\) and \(z\le ay\). Hence \(\frac{z}{a}\preccurlyeq x\) and \(\frac{z}{a}\le y\), and so
then \(z\preccurlyeq ax\) and \(z\le ay\). Hence \(\frac{z}{a}\preccurlyeq x\) and \(\frac{z}{a}\le y\), and so  . The reverse inclusion is straightforward, and the other equality is similar.
. The reverse inclusion is straightforward, and the other equality is similar.
(g) follows from (a) and (f). \(\square \)
The preceding theorem suggests a useful characterization for general mixed lattice structures.
Theorem 3.3
Let V be a partially ordered vector space with two partial orders \(\le \) and \(\preccurlyeq \), and let \(V_p\) and \(V_{sp}\) be the corresponding positive cones, respectively. Then \(V=(V,\le ,\preccurlyeq )\) is a generalized mixed lattice structure if and only if the set  is non-empty for all \(x\in V\).
is non-empty for all \(x\in V\).
Proof
The given condition is obviously necessary. To prove that it is sufficient, let \(x,y\in V\). By assumption, the set  is non-empty, and the same arguments as in the proof of Theorem 3.2(c) show that
is non-empty, and the same arguments as in the proof of Theorem 3.2(c) show that  , and so the set
, and so the set  is also non-empty. Since x and y were arbitrary, we can apply the arguments from the proof of Theorem 3.2(a) to see that the set
is also non-empty. Since x and y were arbitrary, we can apply the arguments from the proof of Theorem 3.2(a) to see that the set  is non-empty too. Hence V is a mixed lattice structure. \(\square \)
is non-empty too. Hence V is a mixed lattice structure. \(\square \)
The next result shows that in a generalized mixed lattice structure every element can be written as a difference of a positive part and a negative part, but the representation is not unique. The following is thus a generalized version of [4, Theorem 3.6] and parts (b) and (e) of Theorem 2.5.
Theorem 3.4
Let V be a generalized mixed lattice structure and \(x\in V\).
-
(a)
For any
 there exist an element
there exist an element  such that \(x=u-w\). Moreover, if
such that \(x=u-w\). Moreover, if  and
and  are any such elements that \(x=u-w\) then
are any such elements that \(x=u-w\) then  and
and  . On the other hand, if \(x=u-w\) and
. On the other hand, if \(x=u-w\) and  then
then  and
and  .
. -
(b)
For any
 there exist an element
there exist an element  such that \(x=u-w\). Moreover, if
such that \(x=u-w\). Moreover, if  and
and  are any such elements that \(x=u-w\) then
are any such elements that \(x=u-w\) then  and
and  . On the other hand, if \(x=u-w\) and
. On the other hand, if \(x=u-w\) and  then
then  and
and  .
.
Proof
-
(a)
The first part follows immediately from Theorem 3.2(b). Indeed, if \(x\in V\) and
 then there exists
then there exists  such that \(x=u+v\). If we put \(w=-v\) then
such that \(x=u+v\). If we put \(w=-v\) then  and \(x=u-w\). Next, let
and \(x=u-w\). Next, let  and
and  be such that \(x=u-w\). Since \(0\preccurlyeq w\) and \(0\le u\), it follows that
be such that \(x=u-w\). Since \(0\preccurlyeq w\) and \(0\le u\), it follows that  . Suppose there exists some
. Suppose there exists some  such that \(y\ge 0\). Now
such that \(y\ge 0\). Now  (by Theorem 3.2(d)), so there exists
(by Theorem 3.2(d)), so there exists  such that \(y=w+z\). But then \(z=y-w\ge -w\), and since \(-w\) is a maximal element of the set
such that \(y=w+z\). But then \(z=y-w\ge -w\), and since \(-w\) is a maximal element of the set  , it follows that \(z=-w\), and so \(y=0\). This shows that
, it follows that \(z=-w\), and so \(y=0\). This shows that  , and by Theorem 3.2(b) there exists an element
, and by Theorem 3.2(b) there exists an element  such that \(u+w=0+r=r\). Therefore,
such that \(u+w=0+r=r\). Therefore,  . On the other hand, if \(x=u-w\) and
. On the other hand, if \(x=u-w\) and  then by Theorem 3.2(c) and (b) we have
then by Theorem 3.2(c) and (b) we have  . Hence,
. Hence,  . But then
. But then 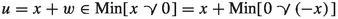 and this shows that
and this shows that  .
. -
(b)
This is similar to the proof of part of (a), but we will prove the second statement just to indicate how to prove dual statements such as this. Let
 and
and  be such that \(x=u-w\). Since \(0\le w\) and \(0\preccurlyeq u\), it follows that
be such that \(x=u-w\). Since \(0\le w\) and \(0\preccurlyeq u\), it follows that  . Assume that
. Assume that  and \(y\ge 0\). Then
and \(y\ge 0\). Then  , so there exists
, so there exists  such that \(y=w+z\). But then \(z=y-w\ge -w\), and since \(-w\) is a maximal element of the set
such that \(y=w+z\). But then \(z=y-w\ge -w\), and since \(-w\) is a maximal element of the set  (by Theorem 3.2(a)), it follows that \(z=-w\), and so \(y=0\). This shows that
(by Theorem 3.2(a)), it follows that \(z=-w\), and so \(y=0\). This shows that  , and by Theorem 3.2(b) there exists an element
, and by Theorem 3.2(b) there exists an element  such that \(u+w=0+r=r\). Therefore,
such that \(u+w=0+r=r\). Therefore,  . The last statement is again proved as in part (a). \(\square \)
. The last statement is again proved as in part (a). \(\square \)
By the preceding theorem, the set  can be called the set of specific upper parts of x, and
can be called the set of specific upper parts of x, and  the set of lower parts of x. For any \(x\in V\) we can choose an upper part
the set of lower parts of x. For any \(x\in V\) we can choose an upper part  , and there always exists a corresponding lower part
, and there always exists a corresponding lower part  such that \(x=u-v\). Similar remarks apply to the sets
such that \(x=u-v\). Similar remarks apply to the sets  and
and  , called the set of upper parts of x and the set of specific lower parts of x, respectively.
, called the set of upper parts of x and the set of specific lower parts of x, respectively.
Under an additional assumption we can add the following properties to the list of Theorem 3.2.
Proposition 3.5
Let V be a generalized mixed lattice structure such that \(V_{sp}\cap -V_p = \{0\}\). Then the following equivalences hold:

Proof
Let \(x\ge y\). Since \(x\succcurlyeq x\) we have  . Let
. Let  and \(u\le x\). Then \(x\preccurlyeq u\) and \(u\le x\), or \(0\preccurlyeq u-x\) and \(u-x\le 0\). By assumption this implies that \(u-x=0\), or \(u=x\). This shows that
and \(u\le x\). Then \(x\preccurlyeq u\) and \(u\le x\), or \(0\preccurlyeq u-x\) and \(u-x\le 0\). By assumption this implies that \(u-x=0\), or \(u=x\). This shows that  . Conversely, if
. Conversely, if  then \(x\ge y\). The equivalence \(x\ge y\) \(\iff \)
then \(x\ge y\). The equivalence \(x\ge y\) \(\iff \)  can be proved by a similar argument. \(\square \)
can be proved by a similar argument. \(\square \)
We introduce some additional terminology for the next section. The set

is called the right dual of \(V_{sp}\), and the set

is called the left dual of \(V_{p}\).
Proposition 3.6
\(V_{sp}^*\subseteq V_p\) and \(^*V_p\subseteq V_{sp}\). Moreover, \(V_{sp}\subseteq \, ^{*}\!(V_{sp}^*)\) and \(V_{p}\subseteq (^*V_p)^*\).
Proof
Let \(y\in V_{sp}^*\). Then for any \(x\in V_{sp}\) there exist  and \(0\le w\le y\). Thus \(y\in V_p\), proving that \(V_{sp}^*\subseteq V_p\). Next, if \(x\in ^{*}\!\!V_p\) then for any \(y\in V_{p}\) there exist
and \(0\le w\le y\). Thus \(y\in V_p\), proving that \(V_{sp}^*\subseteq V_p\). Next, if \(x\in ^{*}\!\!V_p\) then for any \(y\in V_{p}\) there exist  such that \(w\ge 0\). In particular, if \(y=0\) then there exist
such that \(w\ge 0\). In particular, if \(y=0\) then there exist  such that \(v\ge 0\). But then \(0\le v\le 0\), so \(v=0\) and \(v\preccurlyeq x\) implies that \(x\in V_{sp}\). This shows that \(^*V_p\subseteq V_{sp}\).
such that \(v\ge 0\). But then \(0\le v\le 0\), so \(v=0\) and \(v\preccurlyeq x\) implies that \(x\in V_{sp}\). This shows that \(^*V_p\subseteq V_{sp}\).
Since \(V_{sp}^*\subseteq V_p\) and \(^*V_p\subseteq V_{sp}\), it makes sense to consider the sets

and

If \(x\in V_{sp}\) then by the definition of \(V_{sp}^*\) we have  for all \(y\in V_{sp}^*\), and so \(x\in ^{*}\!\!(V_{sp}^*)\). Hence \(V_{sp}\subseteq ^{*}\!\!(V_{sp}^*)\), and by a similar argument, \(V_{p}\subseteq (^*V_p)^*\). \(\square \)
for all \(y\in V_{sp}^*\), and so \(x\in ^{*}\!\!(V_{sp}^*)\). Hence \(V_{sp}\subseteq ^{*}\!\!(V_{sp}^*)\), and by a similar argument, \(V_{p}\subseteq (^*V_p)^*\). \(\square \)
4 Mixed lattice structure in the problem of cone projection
The main application of the results of this paper are given in this section. The aim is to show how the problem of cone projection can be stated in a purely order-theoretic form in the framework of generalized mixed lattice structure, thus providing a new perspective on such problems. We assume the knowledge of basic notions and terminology of convex optimization. For these we refer to [3, 8].
Let K be a closed and convex pointed cone in \(\mathbb {R}^n\) with the dual cone \(K^*=\{y:\langle x, y \rangle \ge 0 \text { for all } x\in K\}\). Let \(\preccurlyeq _{\scriptscriptstyle K}\) be the partial ordering induced by the cone K and let \(\le _{\scriptstyle *}\) be the partial ordering given by the dual cone \(K^*\).
Let \(P_{\scriptscriptstyle K}:\mathbb {R}^n \rightarrow K\) be the projection mapping that gives the unique point \(P_{\scriptscriptstyle K}x\) on K nearest to x. That is,
This nearest point \(P_{\scriptscriptstyle K}x\) has the characterization ([8, Theorem 3.1.1])
The projection mapping also has the translation property
The mapping \(P_{\scriptscriptstyle K}\) is called K-isotone if \(x\preccurlyeq _{\scriptscriptstyle K}y\) implies \(P_{\scriptscriptstyle K}x\preccurlyeq _{\scriptscriptstyle K}P_{\scriptscriptstyle K}y\).
A fundamental tool in the study of cone projections is the following classical theorem of Moreau [11].
Theorem 4.1
(Moreau) Let K be a closed convex cone in \(\mathbb {R}^n\) and \(K^*\) its dual cone. Every \(x\in \mathbb {R}^n\) can be written as \(x=P_{\scriptscriptstyle K}x- P_{\scriptscriptstyle K^*}(-x)\) where \(\langle P_{\scriptscriptstyle K}x, P_{\scriptscriptstyle K^*}(-x) \rangle =0\). Moreover, \(P_{\scriptscriptstyle K}x=0\) holds if and only if \(x\in -K^*\).
With the notation introduced above, the projection \(P_{\scriptscriptstyle K}x\) clearly satifies \(P_{\scriptscriptstyle K}x\succcurlyeq _{\scriptscriptstyle K}0\) and \(P_{\scriptscriptstyle K}x\ge _{\scriptstyle *}x\). Now we can show that \(V=(\mathbb {R}^n, \le _{\scriptstyle *}, \preccurlyeq _{\scriptscriptstyle K})\) is a generalized mixed lattice structure in the sense of Definition 3.1, and the orthogonal projection \(P_{\scriptscriptstyle K}x\) is in fact a minimal element satisfying the inequalities \(P_{\scriptscriptstyle K}x\succcurlyeq _{\scriptscriptstyle K}0\) and \(P_{\scriptscriptstyle K}x\ge _{\scriptstyle *}x\).
Theorem 4.2
Let K be a closed and convex cone in \(\mathbb {R}^n\) and \(K^*\) its dual cone, and let \(\preccurlyeq _{\scriptscriptstyle K}\) and \(\le _{\scriptstyle *}\) be the partial orderings determined by the cones K and \(K^*\), respectively. Then \(V=(\mathbb {R}^n, \le _{\scriptstyle *},\preccurlyeq _{\scriptscriptstyle K})\) is a generalized mixed lattice structure and for every \(x\in \mathbb {R}^n\) the projection element \(P_{\scriptscriptstyle K}x\) satisfies  .
.
Proof
Let \(x\in \mathbb {R}^n\). By Theorem 4.1 we have \(\langle P_{\scriptscriptstyle K}x -x, P_{\scriptscriptstyle K}x \rangle = 0\), and from this we get \(\langle P_{\scriptscriptstyle K}x, P_{\scriptscriptstyle K}x \rangle = \langle x, P_{\scriptscriptstyle K}x \rangle \). As noted above, the element \(P_{\scriptscriptstyle K}x\) satifies \(P_{\scriptscriptstyle K}x\succcurlyeq _{\scriptscriptstyle K}0\) and \(P_{\scriptscriptstyle K}x\ge _{\scriptstyle *}x\). Suppose there is some other element w such that \(w\succcurlyeq _{\scriptscriptstyle K}0\), \(w\ge _{\scriptstyle *}x\) and \(w\le _{\scriptstyle *}P_{\scriptscriptstyle K}x\). Then \(P_{\scriptscriptstyle K}x\in K\) and \(P_{\scriptscriptstyle K}x -w\ge _{\scriptstyle *}0\), or \(P_{\scriptscriptstyle K}x -w\in K^*\), so by the definition of \(K^*\) we have \(\langle P_{\scriptscriptstyle K}x -w, P_{\scriptscriptstyle K}x \rangle \ge 0\), so \(\langle P_{\scriptscriptstyle K}x, P_{\scriptscriptstyle K}x \rangle \ge \langle w, P_{\scriptscriptstyle K}x \rangle \). On the other hand, \(w-x\in K^*\), and so \(\langle w- x, P_{\scriptscriptstyle K}x \rangle \ge 0\), which gives \(\langle w, P_{\scriptscriptstyle K}x \rangle \ge \langle x, P_{\scriptscriptstyle K}x \rangle \). Hence, we have
Thus, \(\langle P_{\scriptscriptstyle K}x, P_{\scriptscriptstyle K}x \rangle = \langle x, P_{\scriptscriptstyle K}x \rangle = \langle w, P_{\scriptscriptstyle K}x \rangle \), and it follows that
Now, for every \(y\in K\) we have
where the first term on the right hand side is zero, as we have shown, and for the second term we have \(\langle P_{\scriptscriptstyle K}x -w, y \rangle \ge 0\) by the definition of the dual cone. Hence, we have \(\langle P_{\scriptscriptstyle K}x -w, P_{\scriptscriptstyle K}x - y \rangle \le 0\) for all \(y\in K\). By characterization (4.1) this means that \(P_{\scriptscriptstyle K}x\) is the unique point on K nearest to w. But \(w\in K\), so we must have \(P_{\scriptscriptstyle K}x=P_{\scriptscriptstyle K}w =w\). This shows that  , and since this holds for any \(x\in V\) it follows by Theorem 3.3 that V is a generalized mixed lattice structure. \(\square \)
, and since this holds for any \(x\in V\) it follows by Theorem 3.3 that V is a generalized mixed lattice structure. \(\square \)
Now Theorem 4.2 allows us to translate the projection problem to the mixed lattice setting. Let us choose an element  by the criterion of shortest distance, that is,
by the criterion of shortest distance, that is,  . Then, if we denote by
. Then, if we denote by  the corresponding element in
the corresponding element in  (see Theorem 3.4), we have the unique representation
(see Theorem 3.4), we have the unique representation  for every \(x\in V\), and this is the most natural representation in the present setting.
for every \(x\in V\), and this is the most natural representation in the present setting.
After fixing the ”representatives”  and
and  of each x in this way, we can now simplify (or rather abuse) the notation and write
of each x in this way, we can now simplify (or rather abuse) the notation and write  and
and  (we observe here that the element
(we observe here that the element  gives the projection of \(-x\) on \(K^*\)). It now follows from the results of Sect. 3 that, in essence, our generalized mixed lattice structure behaves much like an ordinary mixed lattice space, and (with some care) we can apply the rules \((a)-(h)\) of Theorem 2.3. Hence, by Theorem 3.2(c) equation (4.2) becomes
gives the projection of \(-x\) on \(K^*\)). It now follows from the results of Sect. 3 that, in essence, our generalized mixed lattice structure behaves much like an ordinary mixed lattice space, and (with some care) we can apply the rules \((a)-(h)\) of Theorem 2.3. Hence, by Theorem 3.2(c) equation (4.2) becomes

In other words,  is the point on the cone \(x+K\) that is nearest to the point y, or equivalently, the point on the cone \(y+K^*\) that is nearest to the point x. In a similar manner, the lower envelope
is the point on the cone \(x+K\) that is nearest to the point y, or equivalently, the point on the cone \(y+K^*\) that is nearest to the point x. In a similar manner, the lower envelope  is associated with the projections on the cones \(x-K\) and \(y-K^*\), i.e.
is associated with the projections on the cones \(x-K\) and \(y-K^*\), i.e.  .
.
Moreover, we observe that the duality between the cones K and \(K^*\) is a special case of the order-theoretic notion of duality, which was discussed in Proposition 3.6. We next show that orthogonality in the usual sense implies the order-theoretic version of the orthogonality condition.
Proposition 4.3
If \(x\in K\) and \(y\in K^*\) are elements such that \(\langle x,y\rangle =0\) then  .
.
Proof
Let \(z\in K\). Then by the definition of \(K^*\) we have \(\langle z,y\rangle \ge 0\), and since \(\langle x,y\rangle =0\) we obtain \(\langle x-z,y\rangle =\langle x,y\rangle - \langle z,y\rangle =- \langle z,y\rangle \le 0\). This holds for all \(z\in K\), so if we define \(u=x-y\) then \(y=x-u\) and the above inequality becomes \(\langle x-u,x-z\rangle \le 0\) for all \(z\in K\). By the characterization (4.1) this means that \(x=P_{\scriptscriptstyle K}u\). Then by Theorem 4.2 we have  , so by Theorem 3.2(c) we get
, so by Theorem 3.2(c) we get  . We have now shown that \(u=x-y\) where
. We have now shown that \(u=x-y\) where  and
and  . Hence,
. Hence,  , by Theorem 3.4. \(\square \)
, by Theorem 3.4. \(\square \)
Using the notation introduced above, we get the following special case of Theorem 3.4, which can be viewed as the order-theoretic version of Moreau’s theorem.
Theorem 4.4
Let \(V=(\mathbb {R}^n, \le _{\scriptstyle *},\preccurlyeq _{\scriptscriptstyle K})\) be the generalized mixed lattice structure on \(\mathbb {R}^n\), where \(\preccurlyeq _{\scriptscriptstyle K}\) is the partial order defined by a closed convex cone K and \(\le _{\scriptstyle *}\) is the partial order defined by the dual cone \(K^*\). Then every \(x\in V\) can be written as  where
where  ,
,  and
and  . Moreover,
. Moreover,  if and only if \(x\le _{\scriptstyle *}0\).
if and only if \(x\le _{\scriptstyle *}0\).
Proof
By Theorem 4.2, for any \(x\in V\) we have  , and as noted above, if we put
, and as noted above, if we put  then
then  and by Theorem 3.4, if
and by Theorem 3.4, if  is the corresponding element in
is the corresponding element in  , then
, then  and we have the unique representation
and we have the unique representation  . Since
. Since  , it follows by Proposition 4.3 that
, it follows by Proposition 4.3 that  . Also, by Theorem 3.2 we have
. Also, by Theorem 3.2 we have  , so from Eq. (4.3) we get
, so from Eq. (4.3) we get  . On the other hand, by (4.2) we obtain
. On the other hand, by (4.2) we obtain

and this gives justification for writing  . (Again, this just amounts to the fact that we have chosen the ”representative” from the set
. (Again, this just amounts to the fact that we have chosen the ”representative” from the set  by the criterion of shortest distance, which is consistent with our earlier choice of
by the criterion of shortest distance, which is consistent with our earlier choice of  , that is, if
, that is, if  and
and  are chosen as above then the element in the set
are chosen as above then the element in the set  corresponding to this choice is 0.)
corresponding to this choice is 0.)
For the last statement, we first note that if \(z\in (-K)\cap K^*\) then by the definition of \(K^*\) we have \(\langle z,z \rangle = \Vert z\Vert ^2\le 0\), which implies that \(z=0\), or \((-K)\cap K^* = \{0\}\). Thus, using Theorem 4.2 and Proposition 3.5, we have \(x\le _{\scriptstyle *}0\) if and only if  . \(\square \)
. \(\square \)
It should be stressed again that the notation we use here is not entirely correct because our structure is not a mixed lattice space in the sense of Definition 2.1, but rather a generalized structure as described in the preceding section. Although the element \(P_{\scriptscriptstyle K}x\) is the minimum in terms of distance to the cone K, it is not necessarily the order-theoretic minimum in the sense of (2.1). Because of this, some properties of mixed lattice space do not hold in the present situation, and some care should be taken when manipulating expressions that contain the mixed envelopes. For instance, the inequalities in Theorem 2.3(i) do not necessarily hold, which means that the projection mapping is not isotone, in general. The conditions for the isotonicity of the cone projection have been extensively studied (see [12] and the references therein). However, the following discussion gives further justification for the use of this notation.
The authors in [12] introduced what they called the lattice-like operations for studying questions related to cone projections. These operations are a generalization of similar operations that were introduced in [7] for the special case of self-dual cones (i.e. \(K=K^*\)). The lattice-like operations are defined by
There is an interesting connection between the lattice-like operations and the generalized mixed lattice operations. As we have shown, the projection element \(P_{x+ \scriptscriptstyle K}y\) is a minimal element of the set  , and in the notation of (4.3) we denote this element by
, and in the notation of (4.3) we denote this element by  . We can now observe that in the case of the projection elements, the generalized mixed lattice operations reduce to the lattice-like operations as follows:
. We can now observe that in the case of the projection elements, the generalized mixed lattice operations reduce to the lattice-like operations as follows:

In fact, most of the properties of the lattice-like operations ( [12, Lemma 2 and Lemma 3]) are identical to the properties of the mixed envelopes listed in Theorem 2.3\((a)-(h)\). The above discussion places the lattice-like operations in the present order-theoretic context.
5 Conclusions
In this paper we presented a new approach to the problem of cone projection based on an ordered algebraic structure called a mixed lattice space. We first introduced a generalization of the notion of mixed lattice space, and we showed that many of the basic properties of mixed lattice spaces can be extended to the generalized mixed lattice structure. The motivation for this generalization is that it can be applied in a broader range of situations. As our main application, we showed how the mixed lattice structure arises quite naturally in the study of cone projections. We demonstrated how the problem of cone projection can be formulated in the mixed lattice setting, and we also observed that the related notion of lattice-like operations can be interpreted as the generalized mixed lattice operations.
Data Availibility Statement
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Arsove, M., Leutwiler, H.: Infinitesimal generators and quasi-units in potential theory. Proc. Nat. Acad. Sci. U.S.A. 72, 2498–2500 (1975)
Arsove, M., Leutwiler, H.: Algebraic Potential Theory. Memoirs of the American Mathematical Society, No. 226 (1980)
Boyd, S., Vandenberghe, L.: Convex optimization. Cambridge University Press, Cambridge (2004)
Eriksson, S.-L., Jokela, J., Paunonen, L.: Generalized absolute values, ideals and homomorphisms in mixed lattice groups. Positivity 25(3), 939–972 (2021). https://doi.org/10.1007/s11117-020-00794-2
Eriksson-Bique, S.-L.: Generalized Riesz spaces. Rev. Roumaine Math. Pures Appl. 36(1–2), 47–69 (1991)
Eriksson-Bique, S.-L.: Mixed lattice groups. Rev. Roumaine Math. Pures Appl. 44(2), 171–180 (1999)
Gowda, M.S., Sznajder, R., Tao, J.: Some p-properties for linear transformations on Euclidean Jordan algebras. Linear Algebra Appl. 393, 203–232 (2004)
Hiriart-Urruty, J.-B., Lemaréchal, C.: Fundamentals of Convex Analysis. Springer, Berlin (2001)
Jokela, J.: Ideals, bands and direct sum decompositions in mixed lattice vector spaces. Positivity (2023). https://doi.org/10.1007/s11117-023-00985-7
Jokela, J.: Compatible topologies on mixed lattice vector spaces. Topol. Appl. (2022). https://doi.org/10.1016/j.topol.2022.108241
Moreau, J.: Décomposition orthogonale d’un espace hilbertien selon deux cônes mutuellement polaires. C. R. Acad. Sci. Paris 255, 238–240 (1962)
Németh, A.B., Németh, S.Z.: Lattice-like operations and isotone projection sets. Linear Algebra Appl. 439, 2815–2828 (2013). https://doi.org/10.1016/j.laa.2013.08.032
Németh, A.B., Németh, S.Z.: Subadditive retractions on cones and asymmetric vector norms (2020). arXiv:2005.10508
Németh, S.Z.: Isotone retraction cones in Hilbert spaces. Nonlinear Anal. 73, 495–499 (2010)
Acknowledgements
The author would like to thank the referees whose comments and suggestions helped to improve the manuscript. The author would also like to thank Dr. Lassi Paunonen for useful comments and discussions.
Funding
Open access funding provided by Tampere University (including Tampere University Hospital).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interests
The author declared that he has no conflict of interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jokela, J. Mixed lattice structures and cone projections. Optim Lett (2023). https://doi.org/10.1007/s11590-023-02075-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11590-023-02075-9





 and
and  exist in V for all
exist in V for all  and
and  are in
are in 
 and
and 








 and
and  .
. .
. and
and  .
. and
and  .
. .
. if and only if
if and only if  and
and  .
. and
and  .
.
 then there exists an element
then there exists an element  such that
such that  there exists an element
there exists an element  such that
such that  .
. for all
for all  for all
for all 
 .
. and
and  .
. and
and  .
. there exist an element
there exist an element  such that
such that  and
and  are any such elements that
are any such elements that  and
and  . On the other hand, if
. On the other hand, if  then
then  and
and  .
. there exist an element
there exist an element  such that
such that  and
and  are any such elements that
are any such elements that  and
and  . On the other hand, if
. On the other hand, if  then
then  and
and  .
. then there exists
then there exists  such that
such that  and
and  and
and  be such that
be such that  . Suppose there exists some
. Suppose there exists some  such that
such that  (by Theorem
(by Theorem  such that
such that  , it follows that
, it follows that  , and by Theorem
, and by Theorem  such that
such that  . On the other hand, if
. On the other hand, if  then by Theorem
then by Theorem  . Hence,
. Hence,  . But then
. But then 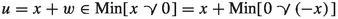 and this shows that
and this shows that  .
. and
and  be such that
be such that  . Assume that
. Assume that  and
and  , so there exists
, so there exists  such that
such that  (by Theorem
(by Theorem  , and by Theorem
, and by Theorem  such that
such that  . The last statement is again proved as in part (a).
. The last statement is again proved as in part (a).