Abstract
In a homogeneous good industry composed of a dominant firm and a fringe of followers that can choose non-linear pricing contracts to sell the good, we demonstrate that only the dominant firm uses them. Compared with the standard dominant firm model in which only linear pricing contracts are feasible, the dominant firm supplies an inefficiently low number of customers as a way to extract more surplus, since the alternative for customers is a fringe cluttered by excess demand. Thus, allowing market-power firms to deploy non-linear pricing contracts leads to market segmentation, and customers end up worse off than under linear pricing contracts. Fringe firms, in contrast, are better off since they end up charging a higher price for the good. Finally, aggregate welfare under non-linear pricing increases (decreases) as compared to linear pricing if the dominant firm’s share of production capacity is (is not) large enough.




Similar content being viewed by others
Notes
Personalized pricing is considered easier to execute nowadays, since the availability of big data technologies allows firms to extract more information about customers (in this respect, see, for instance, “Big data and differential pricing”, released by the Council of Economic Advisers of the Obama Administration on February 2015 and available at https://obamawhitehouse.archives.gov/sites/default/files/whitehouse_files/docs/Big_Data_Report_Nonembargo_v2.pdf.).
We, however, maintain that the DF is the first that sets the price (more generally, the first that sets the selling contract with buyers) for the good and that the fringe firms therefore take this price (more generally, this selling contract) as given. In Tasnádi (2010), the DF is also the first mover, but firms (both the leader firm and fringe followers) strategically choose production quantities instead of prices, and it is shown under which conditions the equilibrium market price converges to the price obtained in the price leadership model.
For product-differentiation models with free entry, Bhaskar and To (2004) point out another inefficiency, namely, the entry of too many firms in the market.
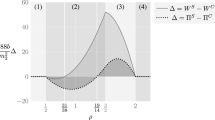
Condition \(\rho <2\) on the convexity of the demand function ensures that the second-order condition of the monopolist’s problem is satisfied, and also ensures satisfaction of the second-order condition of the DF’s problem under both linear and non-linear pricing.
Gowrisankaran and Holmes (2004) also assume that the DF and the fringe share identical constant returns to scale technology.
When we solve for the equilibrium, we assume that any customer approached by a fringe firm, and who is indifferent between accepting the DF or fringe firm offer, decides to purchase from the fringe.
From here, it must not be inferred that fringe firms have some market power, because, as shown below, in equilibrium, \({F}_{f}=0\) will hold.
This is in accordance with the standard result that a monopoly extracting consumer surplus through the fixed part of a 2PT contract sets the quantity that maximizes joint welfare (see, e.g., Tirole 1988, p. 136).
With constant marginal costs of production \(c\), the quantity shipped to each customer would satisfy \({U}^{\prime}\left(q\right)=c\) and would be independent of the total number of customers served.
This way of stating DF’s behavior will be useful later on when comparing equilibrium outcomes under linear versus non-linear prices.
We take for granted that the problem is concave in \(a\). See the Appendix for conditions that guarantee this.
Moreover, customers supplied by fringe firms consume smaller quantities of the good than in a competitive market, whereas customers supplied by the DF consume larger quantities than in a competitive market.
Hence, \({p}^{l}\left({a}^{l}\left(k\right),k\right)=\frac{2}{4-{k}^{2}}\) is the market price and \({q}_{f}\left({a}^{l}\left(k\right),k\right)=\frac{2-{k}^{2}}{4-{k}^{2}}\) is the consumption level of each customer in terms of the DF’s size.
References
Armstrong M (2006) Recent developments in the economics of price discrimination. In: Blundell R, Newey WK, Persson T (eds) Advances in economics and econometrics: theory and applications. Ninth World Congress, vol II. Cambridge University Press, Cambridge, pp 97–141
Armstrong M, Vickers J (2001) Competitive price discrimination. RAND J Econ 32:579–605
Bhaskar V, To T (2004) Is perfect price discrimination really efficient? Anal Free Entry Rand J Econ 35:762–776
Bonacina M, Gulli F (2007) Electricity pricing under ‘‘carbon emissions trading: a dominant firm. Energy Policy 35:4200–4220
Brown DP, Eckert A (2021) Analyzing firm behavior in restructured electricity markets: empirical challenges with a residual demand analysis. Int J Ind Organ 74:102676
Calzolari G, Denicolò V (2020) Loyalty discounts and price-cost tests. Int J Ind Organ 73:102589
Carlton DW, Perloff JM (2000) Modern industrial organization, 3rd edn. Addison-Wesley, Reading MA
Chao Y, Tan G, Wong ACL (2018) All-units discounts as a partial foreclosure device. Rand J Econ 49:155–180
Chao Y, Tan G, Wong ACL (2019) Asymmetry in capacity and the adoption of all-units discounts. Int J Ind Organ 65:152–172
Colucci D, Doni N, Ricchiuti G, Valori V (2022) Market dynamics with a state-owned dominant firm and a competitive fringe. Chaos Solitons Fract 161:112365
Golombek R, Irarrazabal AA, Ma L (2018) OPEC’s market power: an empirical dominant firm model for the oil market. Energy Econ 70:98–115
Gowrisankaran G, Holmes TJ (2004) Mergers and the evolution of industry concentration: results from DF model. RAND J Econ 35:561–582
Kahai SK, Kaserman DL, Mayo JW (1996) Is the “dominant firm” dominant? Empirical Anal AT&T’s Market Power J Law Econ 39:499–517
Rassenti SJ, Wilson BJ (2004) How applicable is the dominant firm model of price leadership? Exp Econ 7:271–288
Schenzler C, Siegfried JJ, Thweatt WO (1992) The history of the static equilibrium dominant firm price leadership model. East Econ J 18:171–186
Stole LA (2007) Price discrimination and competition. In: Armstrong M, Porter R (eds) Handbook of Industrial Organization, vol 3. Elsevier, Amsterdam, pp 2221–2299
Tasnádi A (2010) Quantity-setting games with a dominant firm. J Econ 99:251–266
Tirole J (1988) The theory of industrial organization. The MIT Press, Cambridge, MA
Von der Fher NHM (2010) Leader, or just dominant? The dominant-firm model revisited, Memorandum 15/2010. Oslo University, Department of Economics
Acknowledgements
The authors are grateful to Giacomo Corneo (Managing Editor) and two anonymous reviewers for their insightful comments and constructive suggestions. The paper has also benefited from comments by R. Caminal, D. Cardona-Coll, M. González-Maestre, and J.M. Ordóñez de Haro. We naturally assume responsibility for any remaining errors or omissions.
Funding
Manel Antelo acknowledges financial aid from Consellería de Cultura, Educación, Formación Profesional e Universidades (Xunta de Galicia) through Grant Consolidación e estruturación – 2023 GRC GI-2016 Análise económica dos mercados e institucións (AEMI). Lluís Bru acknowledges financial aid from the Spanish Ministry of Economy and Innovation through Grant PID 2020-115018RB-C33. The authors declare that none of these institutions may gain or lose financially through publication of this paper.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no affiliations with or involvement in any organization or entity with any financial or non-financial interest in the subject matter or materials discussed in this research.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Proof of Lemma 1
(i) When \(0\le CS\left(F,q\right)\le \underline{CS}\), it follows that \(\frac{{\partial \pi }_{f}\left({q}_{f},{a}_{f}|CS(F,q)\right)}{\partial {a}_{f}}>0\) when evaluated at \({a}_{f}=\frac{1}{1-k}\). Thus, fringe firms compete among them to offer customers the competitive quantity \({q}_{min}\) and a strictly better deal than that offered by the DF and leading to consumer surplus CS. (If there were only one firm in the fringe with \(1-k\) productive plants, then it would sell to all customers, and would offer the quantity \({q}_{min}\) in Eq. (10) in exchange for a payment that leads to a consumer surplus slightly above \(CS\left(F,q\right)\).)
(ii) When \(CS\left(F,q\right)>\underline{CS}\), it follows that \(\frac{{\partial \pi }_{f}\left({q}_{f},{a}_{f}|CS(F,q)\right)}{\partial {a}_{f}}=0\) in Eq. (8) for a quantity \({q}_{f}\) above \({q}_{min}\) and \({a}_{f}<\frac{1}{1-k}\). Therefore, \(CS\left(F,q\right)>\underline{CS}\) guarantees that the fringe does not hoard all customers and DF has strictly positive sales. Moreover, the fact that \(\frac{{\partial \pi }_{f}\left({q}_{f},{a}_{f}|CS(F,q)\right)}{\partial {a}_{f}}=0\) in Eq. (8) shows that fringe firms optimally choose linear prices.
Proof of Lemma 2
(i) From Eq. (11) we know that, in equilibrium, the number of customers the DF chooses to serve, \({a}^{l}\), leads to \({U}^{\prime}\left({q}_{f}\right)>{c}^{\prime}\left(\frac{{a}^{l}}{k}{q}_{f}\right)\). Both the condition given in Eq. (10) and the strict convexity of the firms’ cost functions imply that \(\frac{{a}^{l}}{k}{q}_{f}<\frac{1-{a}^{l}}{1-k}{q}_{f}\), so this part of the lemma is straightforwardly proved.
(ii) In the first-best scenario, fringe firms supply the good to 1 − k customers, whereas part (i) of this lemma shows that they supply, in equilibrium, more than 1 − k customers. Hence, from Eq. (11) it follows that \({q}_{f}<{q}^{fb}\), since the larger the customer base, the lower the quantity offered to each customer.
(iii) Immediate from (ii).
Proof of Lemma 3.
(i) From the FOC given in Eq. (14), the DF chooses the pair \((a,q)\) satisfying
and from the inequality stated in Eq. (23), the fact that \(\frac{\partial \left(U\left(x\right)-{U}^{\prime}\left(x\right) x\right)}{\partial x}=-{U}^{{\prime}{\prime}}\left(x\right) x>0\) holds, for \(x\in \left\{q,{q}_{f}\right\}\), leads to \(q>{q}_{f}\).
(ii) and (iii) From \({U}^{{\prime}{\prime}}<0\), the inequality \(q>{q}_{f}\) implies that \({U}^{\prime}\left(q\right)<{U}^{\prime}\left({q}_{f}\right)\). From Eqs. (6) and (12), this requires that \({c}^{\prime}\left(\frac{a q}{k}\right)<{c}^{\prime}\left(\frac{(1-a){q}_{f}}{1-k}\right)\) holds, which implies that \(\frac{a q}{k}<\frac{(1-a){q}_{f}}{1-k}\) by the fact that \({c}^{{\prime}{\prime}}\left(\cdot \right)>0\). In turn, the inequality \(\frac{a q}{k}<\frac{(1-a){q}_{f}}{1-k}\) and the fact that \(q>q(a)\) together imply that \(a<{a}^{fb}=k\). Since fringe firms supply more customers and the DF supplies fewer customers than in the first-best scenario and, since all customers receive the efficient quantity of the good (given the number of customers supplied), it immediately follows that \({q}_{f}^{nl}<{q}^{fb}<{q}^{nl}\).
(iv) The inequality \({q}_{f}^{nl}<{q}^{fb}\) implies that customers supplied by fringe firms are worse off than if they were supplied in a competitive environment. On the other hand, customers supplied by the DF consume a larger quantity of the good than customers supplied by fringe firms, but are charged a positive fixed fee that yields the same consumer surplus as if they were supplied by fringe firms.
Proof of Proposition 1.
To prove this proposition, we first need to state two preliminary lemmas denoted by Lemmas A1 and A2.
Lemma A1
Proof
That customers supplied by the DF receive a smaller quantity of good if linear pricing rather than non-linear is allowed is proved as follows. From Lemmas 2 and 3 we know that \(\mathrm{max }\left\{{a}^{l},{a}^{nl}\right\}<k\). Assume that \({a}^{l}>{a}^{nl}\). In this case, \({q}_{f}\left({a}^{l}\right)<q\left({a}^{nl}\right)<q\left({a}^{l}\right)\), where the first inequality, \({q}_{f}\left({a}^{l}\right)<q\left({a}^{nl}\right),\) holds from Eqs. (7) and (13) and the fact that \({a}^{l}<k\), whereas the second inequality, \(q\left({a}^{nl}\right)<q\left({a}^{l}\right)\), holds from assuming \({a}^{nl}<{a}^{l}\).
Assume now that \({a}^{l}<{a}^{nl}\). In this case, \({q}_{f}\left({a}^{l}\right)<{q}_{f}\left({a}^{nl}\right)<q\left({a}^{nl}\right),\) where the first inequality, \({q}_{f}\left({a}^{l}\right)<{q}_{f}\left({a}^{nl}\right),\) follows from the factsa that fringe firms supply fewer customers when \({a}^{l}<{a}^{c}\), and the second inequality, \({q}_{f}\left({a}^{nl}\right)<q\left({a}^{nl}\right),\) holds from Eqs. (10) and (16) and the fact that \({a}^{nl}<k\)
Now, with Lemma A1 in mind, let \(H\left(a,q\right)\) be the function defined as:
Note that \(H\left({a}^{l},{q}_{f}({a}^{l})\right)\) is equivalent to the FOC of the DF’s maximization problem when only linear pricing contracts are feasible; therefore, it follows that \(H\left({a}^{l},{q}_{f}({a}^{l})\right)=0\). In turn, since \(H\left({a}^{nl},q({a}^{nl})\right)\) is equivalent to the FOC of the DF’s maximization problem when non-linear pricing contracts are allowed, it also follows that \(H\left({a}^{nl},q({a}^{nl})\right)=0\).
Since \({q}_{f}\left({a}^{nl}\right)<q\left({a}^{nl}\right)\) from Lemma A1, we can analyze how the number of customers, \(a\), evolves when \(q\) increases in the interval \(\left[{q}_{f}\left({a}^{l}\right), q\left({a}^{nl}\right)\right]\) to satisfy \(H\left(a(q),q\right)=0\) in Eq. (24). We can therefore state the following lemma.
Lemma A2.
\(\frac{\partial a}{\partial q}<0\) along \(H\left(a(q),q\right)=0\).
Proof.
The part in brackets of function \(H\left(a,q\right)\) defined in Eq. (24) is always positive in the interval \(q\in \left[{q}_{f}\left({a}^{l}\right),q\left({a}^{nl}\right)\right]\), since
where the first inequality, \(U\left(q\right)-{c}^{\prime}\left(\frac{aq}{k}\right)q>U\left(q\right)-{U}^{\prime}\left(q\right)q,\) holds from Eq. (12), and where \(q\le q\left({a}^{nl}\right) \text{ and } {c}^{{\prime}{\prime}}\left(\cdot \right)>0,\) whereas the second inequality, \(U\left(q\right)-{U}^{\prime}\left(q\right)q>CS\left({q}_{f}\left(a\right)\right),\) derives from the fact that \({{CS}^{{\prime}{\prime}}\left(q\right)=-U}^{{\prime}{\prime}}\left(q\right)q>0\) and \({q>q}_{f}\left({a}^{l}\right).\)
From the implicit function theorem, it holds that \(\frac{\partial a}{\partial q}=-\frac{\frac{\partial H\left(a,q\right)}{\partial q}}{\frac{\partial H\left(a,q\right)}{\partial a}},\) whereby it follows that \(\mathrm{sign} \frac{\partial a}{\partial q}=\mathrm{sign}\frac{\partial H\left(a,q\right)}{\partial q}\). Thus, taking into account that
we can conclude from Eq. (24) that
On the other hand
where the first inequality,
holds from the assumption
and the second inequality, \(\frac{\left({U}^{{\prime}{\prime}}\left(q\right)-{c}^{{\prime}{\prime}}\left(\frac{aq}{k}\right)\frac{a}{k}\right)\left({U}^{{\prime}{\prime}}\left(q\right)q+{U}^{\prime}\left(q\right)-{c}^{\prime}\left(\frac{aq}{k}\right)\right)}{{\left[{U}^{{\prime}{\prime}}\left(q\right)q\right]}^{2}}>\frac{{U}^{{\prime}{\prime}}\left(q\right)q+{U}^{\prime}\left(q\right)-{c}^{\prime}\left(\frac{aq}{k}\right)}{{\left[{U}^{{\prime}{\prime}}\left(q\right)q\right]}^{2}}\), holds from the fact that
Finally, the last expression in Eq. (28), \(\frac{{U}^{{\prime}{\prime}}\left(q\right)q+{U}^{\prime}\left(q\right)-{c}^{\prime}\left(\frac{aq}{k}\right)}{{\left[{U}^{{\prime}{\prime}}\left(q\right)q\right]}^{2}}\), is positive since the pair \((a,q)\) satisfies \({U}^{{\prime}{\prime}}\left(q\right) q+{U}^{\prime}\left(q\right)-{c}^{\prime}\left(\frac{aq}{k}\right)<0\) (see above). Thus, Eqs. (27) and (28) together imply that
and the last expression in Eq. (31), \(-\frac{CS\left(q\right)-CS\left({q}^{l}\right)}{q}-{c}^{{\prime}{\prime}}\left(\frac{a q}{k}\right)\frac{a q}{k}\), is negative from the fact that consumer surplus is increasing in \(q\), \(q>{q}^{l}\) and \({c}^{{\prime}{\prime}}\left(\cdot \right)>0\). In sum, both \(\mathrm{sign}\frac{\partial H\left(a,q\right)}{\partial q}<0\) and \({q}_{f}\left({a}^{l}\right)<q\left({a}^{nl}\right)\) imply that \({a}^{nl}<{a}^{l}\). Hence, Proposition 1 straightforwardly holds from Lemmas A1 and A2.
Proof of Proposition 2.
If the DF uses linear pricing contracts and decides to supply \(a\) customers, customers that purchase from fringe firms pay the unit price \(p\left(a,k\right)=\frac{1-a}{2-a-k}\) and consume the quantity \({q}_{f}\left(a,k\right)=\frac{1-k}{2-a-k}\). Therefore, the DF obtains profits \({\pi }^{l}\left(a,k\right)=\frac{a\left(2k+a\left(1+k\right)\right)(1-k)}{2k{\left(2-k-a\right)}^{2}}\), and decides to supply \({a}^{l}\left(k\right)=\frac{k\left(2-k\right)}{2-{k}^{2}}\) customers. These customers consume the quantity \({q}^{l}\left(k\right)=\frac{2-{k}^{2}}{2-{k}^{2}}\) and obtain the consumer surplus \({CS}^{l}\left(k\right)=\frac{1}{2}{\left(\frac{2-{k}^{2}}{2-{k}^{2}}\right)}^{2}\). Thus, aggregate welfare in equilibrium amounts to \({W}^{l}\left(k\right)=\frac{4+2k-{k}^{2}-{k}^{3}}{2\left(2-k\right)(2+{k)}^{2}}\). Contrariwise, if the DF uses non-linear pricing contracts with its customers, then it offers the marginal price \({p}^{nl}\left(a,k\right)=\frac{a}{k+a}\) in the 2PT contract, which leads to the consumption level \({q}^{nl}\left(a,k\right)=\frac{k}{k+a}\). As a result, the DF obtains profits \({\pi }^{nl}(a,k)=\frac{a\left(3-2k-\left(1+2k-{k}^{2}\right)a+k{a}^{2}\right)}{2\left(k+a\right){(2-k-a)}^{2}}\) and chooses the market share \({a}^{nl}(k)\) that satisfies the FOC
Figure 1 in the main text shows that \({a}^{nl}\left(k\right)<{a}^{l}\left(k\right)<k\). As a consequence, customers supplied by fringe firms consume lower quantities, \({q(a}^{nl},k)<{q(a}^{l},k)\), and pay higher prices, \({p(a}^{nl},k)>{p(a}^{l},k)\), when the DF sets non-linear pricing contracts than when it sets linear pricing contracts. This means that \({CS}^{nl}\left(k\right)<{CS}^{l}\left(k\right)\), i.e., the consumer surplus is lower when non-linear pricing is allowed, whereas the fringe firms’ profits are higher. Moreover, under both pricing strategies, as the DF’s size \(k\) increases the consumer surplus decreases to converge to the consumer surplus achieved under monopoly, \({CS}^{nl}\left(1\right)=0<{CS}^{l}\left(1\right)\). Finally, the aggregate welfare obtained under non-linear pricing contracts, amounting to \({W(a}^{nl},k)=\frac{\left(1-k\right)k+\left(1-a\right)a}{2\left(2-k-a\right)(k+a)}\), is higher than that achieved under linear pricing contracts whenever the DF’s size is \(k\in \left(0.7190, 1\right]\) and otherwise is lower. This completes the proof of Proposition 2.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Antelo, M., Bru, L. Intrapersonal price discrimination and welfare in a dominant firm model. J Econ 141, 163–188 (2024). https://doi.org/10.1007/s00712-023-00847-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-023-00847-6