1 Introduction

Change of scales for measurable observables is profitably employed for those sets of problems that require the dealing of properties involving large ranges of variation of quantities: they are often encountered for phenomena in nature and studied in laboratories, engineering, and materials science. In modern approaches, on the footsteps of the classical kinetic theory of gases, the systematic development of scaling and renormalization techniques permitted formulations of models at the foundation of theories, in order to transfer them up and down across micro-, meso-, macro-levels. As lucidly presented in (Weinberg 1995) (especially in Chapter 18), the procedures involve inevitably the costs and the benefits of the progressive reduction in the number of variables and effective degrees of freedom in descriptions preserving the essential features of the processes.

In the last decades, treatments of phase transitions lead to the discovery of classes of universalities beyond those well consolidated previously (Honig and Spalek 2018). Reference models set the gauge to calibrate renormalization by scaling, essentially providing a “theory of the theories”—with no claim of uniqueness but rather with perspective gain in insight and predictivity. The efficacy of parametrizations has to be assessed a posteriori.

In pure and applied chemistry, logarithmic scaling is familiar: the definitions of pH and pK for hydrogen ion concentrations and equilibrium constants involve reciprocals and logarithms of quantities. The development of chemical thermodynamics mapped reductions of the statistical–mechanical properties of the components of a system, for example the chemical potentials and the partition functions, unto those of a simpler one: the condition is that sacrifice of details involves minimal loss of generality and accuracy. These ideas were applied with spectacular success in the high-energy context of elementary particle physics, beyond that of gaseous and condensed matter (Wilson 1971a, 1990; Kadanoff 2013); they did not circulate systematically for molecular processes in the so-called thermal energy range, and specifically in the field of chemical reaction kinetics: yet in perspective, applications look promising regarding in particular biochemical reactions and biophysical processes.

Along the lines of the earliest applications of the renormalization methods to several basic statistical–mechanical problems [see seminal papers (Di Castro and Jona-Lasinio 1969; Wilson 1971a, b)], it is important to extend concepts related to scale invariance and universality classes to the modern phenomenology of the kinetics of chemical reactions, with perspectives of usefulness under extreme conditions, where the reference standard, the Arrhenius formula for the temperature dependence of rates, is violated. The enormously diversified quantitative and qualitative experimental information on the kinetics of chemical reactions has been considered since the middle of the nineteenth century as a fundamental yet challenging branch of modern science (Laidler 1985; Stiller 1989; Gorban 2021). The developments, specifically awkward when quantum effects are under focus, in principle require the numerically demanding solutions of a large set of coupled-channel Schrödinger equation, or explicitly dedicated semi-classical techniques (De Fazio et al. 2006, 2011; Aquilanti et al. 2010).

Benchmark results for quantum mechanical converged rate constants as a function of temperature that we have been progressively made available (Aquilanti et al. 2012; Cavalli et al. 2014; De Fazio et al. 2016, 2019, 2020) provide the basis for formulation and implementation of the theoretical construction for a prototypical three-atom reaction. The effort in the present paper is to explore the arguable power of a heuristic approach: indeed, as soon as the number of atoms in a reactive process increases even from small to moderate, accurate numerical solutions in general become intractable, approximations must be introduced, and their reliability checked. Accordingly, in this work, we focus on scaling and renormalization formulations to assist in the identification of universalities in the kinetics of chemical reactions and to enforce the theoretical modelling by effective, physically motivated parametrizations.

Ample phenomenological evidence suggests that the rates of a variety of processes near “room” temperature slow down by cooling according to the Arrhenius prediction, but then decline faster until practically stopping. This classical behaviour, referred to as super-Arrhenius, involves acceleration of rates by heating higher than anticipated by Arrhenius formula. The opposite viewpoint is needed in a predicting the sub-Arrhenius cases when quantum mechanics is operative, attenuating the decline by cooling and describing rather the approach to zero absolute temperature at a finite value, referred to as Wigner’s limit (Wigner 1932; Takayanagi et al. 1987).

This especially challenging case has been tackled by a sequence of recent converged quantum–mechanical three-body scattering calculations (De Fazio et al. 2006, 2011, 2016, 2019, 2020; Aquilanti et al. 2012; Cavalli et al. 2014): they involve the elementary reactions of F atoms with H2 and HD, and benchmark rate constants were obtained in a full temperature range, from ultracold to higher than thermal. The region of validity of the Arrhenius formula and the observed experimental deviations (Tizniti et al. 2014) were quantitatively accounted for theoretically. The search of parametrized equations that permit scaling and formulation of uniform analytic models for the kinetics of chemical change, involves rescaling of the transitivity function, first introduced in (Aquilanti et al. 2017; Carvalho-Silva et al. 2017), which provide a comprehensive framework to disentangle universal features and a smooth description of the transition between the Arrhenius and the quantum tunnelling regimes.

For the corresponding set of essentially two reactions, the second one evolving in two channels, apparent activation energies and transitivities are considered for temperatures higher than 10 K, below which resonances and other quantum mechanical effects emerge (De Fazio et al. 2019, 2020): these features are studied in the given references, and only alluded to in the present work. The range, where reactivity is dominated by moderate quantum–mechanical tunnelling, is of relevance in cold environments and particularly in astrochemistry. Interest in these reactions continues regarding experiments. New kinetic measurements (Bedjanian 2021) although not covering the tunnelling regime, confirm our previous theoretical validation of experimentally available data.

A scheme of the paper follows: in the next section, we tackle the ever-increasing observational evidence of a variety of cases that deviate substantially from the Arrhenius behaviour, applying scaling and renormalization ideas to basic aspects of chemical kinetics. As suggested previously (Carvalho-Silva et al. 2020), theoretical treatments permit us to generate analytic models starting from formulations of the apparent activation energy, or its reciprocal, the transitivity function, transparently allowing identification and cataloguing classes of universal behaviour. A coupled set of two first-order equations defines renormalized functions and connects information between the temporal evolution and the temperature dependence of the composition of the molecular constituents that participate in a reactive process.

The transitivity analysis relevant to the sub-Arrhenius case is applied in the third section for the prototypical three-atom reactions of fluorine atoms with both H2 and HD covering rate constants in the range from 10 to 350 K. Universal behaviour of the transitivity functions renormalized and dimensionless is unveiled as asymptotically tending to the Wigner limit. The physical meaning of parameters is assessed and their relationship with features of the potential surface exhibited. Final remarks and a summary conclude the paper. An Appendix reports notions and notations.

2 Rise and fall of rate processes at low and high temperatures

2.1 Scaling and renormalization

The extraordinary heuristic success of the 150-year-old Arrhenius formula in describing the temperature dependence of rate processes was consolidated by the accompanying modern theoretical interpretation and molecular dynamics simulation of microscopic processes as manifestation of collisional activation of molecules, macroscopically observed as a statistically averaged distribution of myriads of events (Laidler 1985; Stiller 1989). This concept continues to provide the cornerstone of present chemical kinetics: in this research area, the current practice involves the graphical representation of the scaled semi-logarithmic plot of either experimentally measured, else calculated, or variously estimated rate constants \(k\) against reciprocal absolute temperature, the Arrhenius plane:

$$\mathrm{ln}\;k(\beta )\; \mathrm{vs}.\; \beta ,$$
(1)

where the identification

$$\beta =1/{k}_{B}T.$$
(2)

establishes the relationship of the variable \(\beta\) with the reciprocal absolute temperature \(T\), scaled by Boltzmann constant \({k}_{B}\) in consistent units of measurement. As exemplarily plotted in Fig. 1, the graph represents from left to right the cooling of the system, and from right to left the performance of the process upon heating.

Fig. 1
figure 1

Ascent and decline of the rate constant \(k\left(\beta \right)\) by cooling or heating. The graphs in the \(k\left(\beta \right)\) vs \(\beta\) plane are here coloured to emphasise ubiquitous marginalisation of behaviour at extreme cold (blue) and hot (red) regions, the standard model is the deformed transition state theory, \({k}_{{d}TST}\). Illustrated are the deviations from linearity of the logarithmically scaled rate constant that occur in general and particularly for physicochemical processes: (i) in the low-temperature regime, where bifurcation occurs between quantum and classical (or respectively sub- and super-)Arrhenius regimes. (ii) At high temperatures, deviations are observed and the fall off is modelled by a power-like asymptotic parametrization by the exponent \(\nu\) (this embodies the so-called anti-Arrhenius behaviour). The case \(\nu =0\) is considered in this work and denoted \({k}_{AM}\), see Appendix

Full size image

The important property of a graph of \(k\left(\beta \right)\) in the plane (1) is that a decaying linear behaviour of the logarithmically scaled rate as a function of \(\beta\) is taken as abiding the Arrhenius law

$$k\left( \beta \right) = A\;{\text{exp}}\left( { - \varepsilon ^{\ddag } /k_{B} T} \right).$$
(3)

The temperature-independent parameter, here designated \({\varepsilon }^{\ddagger }\), is conveniently individuated as the activation energy taken as constant by Arrhenius and Eyring: the temperature-dependent generalisation is the apparent “activation energy “ \({E}_{a}\), operationally obtained by logarithmic differentiation of \(k\left(\beta \right)\) with respect to \(\beta\):

$${E}_{a}\left(\beta \right)\equiv -\frac{\mathrm{d}}{\mathrm{d}\beta }\mathrm{ln}\,k\left(\beta \right)=-\frac{1}{k\left(\beta \right)}\frac{\mathrm{d }\,k\left(\beta \right)}{\mathrm{d}\beta }.$$
(4)

This agrees with the definition recommended by the International Union for Pure and Applied Chemistry (IUPAC) (Laidler 1996). For any formula where \(k\left(\beta \right)\) is written in factored form like Eq. (3) or in Fig. 1, the pre-exponential factor or better the ‘prefactor’ A that carries the units of measurement is independent of \(\beta\) and disappears by logarithmic differentiation.

This property of the logarithmic differentiation scaling (common in renormalization approach) compensates for any temperature-independent contribution embodied in \(A\). According to the intuitive interpretation by Arrhenius, the macroscopic observable \({\varepsilon }^{\ddagger }\) is an energetic barrier, namely an obstacle to reaction: the kinetic theory of gases microscopically correlated this potential energy to the kinetic energy that the reactant molecules must acquire for the reaction to start or to proceed to yield the products. The double dagger superscript (\(\ddagger\)) is due to Eyring with reference to an assumed transition state of the reaction (Glasstone et al. 1941).

Deviations from linearities of the \(k\left(\beta \right)\) vs \(\beta\) plot manifest as a rule rather than exceptions at extreme either low or high temperatures that confine the range of performance of the processes. At low temperature, convex or concave cases of curvature are designated as belonging to the sub-Arrhenius or super-Arrhenius behaviour, respectively corresponding to a temperature dependence that involves either higher or lower reactivity upon cooling (Aquilanti et al. 2017; Carvalho-Silva et al. 2017; Coutinho et al. 2018): reference to this behaviour expected from the Arrhenius formula. Decline in reactivity (the anti-Arrhenius behaviour) occurs eventually at temperatures higher than thermal, widely documented in radical–radical or ion–molecule reactions. This case is only briefly mentioned here but is extensively alluded to elsewhere (Coutinho et al. 2015, 2016; Sanches-Neto et al. 2021), it occurs as universal behaviour in biophysical processes and biochemical reactions (Arroyo et al. 2022; Guberman-Pfeffer 2022) as temperature increases.

The reaction rate constant expression of the variant of Transition State theory (\({d}\) TST) (Fig. 1) is compacted introducing both the parameters \(\nu\) and \({d}\) that encode the deviations at high and low temperatures (Carvalho-Silva et al. 2017), respectively. See Sect. 2.4 and in particular the Appendix for the notations.

A classical derivation due to Tolman (Tolman 1920, 1927) and generalised to quantum mechanics by Fowler and Guggenheim in their treatise on Statistical Thermodynamics (Fowler and Guggenheim 1939) provides an interpretation for the function \({E}_{a}\) [Eq. (4)] as the difference between the average over the kinetic energy of all reacting particles in the system and that of all particles, both reactive and nonreactive. Therefore, Eq. (4) establishes the key role of \({E}_{a}\) as a coupling function in the presently enforced renormalization procedure of the rate constant and propitiates a connexion between canonical quantities with microcanonical features. The association of parameters from a renormalization procedure to those of the potential energy surface upon which the process is supposed to adiabatically evolve, is resumed in (Aquilanti et al. 2018) and amplified here with respect to the presentation of the alpha–zeta totem in (Carvalho-Silva et al. 2020).

It has been recently demonstrated as crucial to the theory to introduce the reciprocal of the apparent activation energy (Carvalho-Silva et al. 2019, 2020)

$$\gamma \left(\beta \right)\equiv \frac{1}{{E}_{a}\left(\beta \right)}=-k\left(\beta \right)\frac{\mathrm{d}\beta }{k\left(\beta \right)}.$$
(5)

This differential equation defines the transitivity function \(\gamma \left(\beta \right)\) (Carvalho-Silva et al. 2019, 2020; Machado et al. 2019). Remarkable is a formal similarity between the functional form of this definition involving the reciprocal of a logarithmic differentiation and the Callan–Symanzik (Callan 1970; Symanzik 1971) function occurring as the renormalization group order parameter, which encodes the mathematical apparatus of statistical field theories (Parisi 1998), and permits handling of singularities in the treatment of critical phenomena.

In a chemical kinetics scenario, the temperature \(T\) or its scaled reciprocal \(\beta\) play the part of the control parameter, whilst the role of the coupling is provided by the rate constant \(k\left(\beta \right)\). Conversely, let us consider as usual its reciprocal \(\tau (\beta )\) defined as follows and designated as the generalised lifetime of the process

$$\tau \left(\beta \right)\equiv \frac{1}{k\left(\beta \right)} .$$
(6)

It is the renormalization though Eq. (5) that permits a substantial advance for the interpretation of the dynamics of chemical reactions and motivates the construction of an appropriate scaling transitivity plane,

$$\gamma \left(\beta \right) \; \mathrm{vs}.\; \beta$$
(7a)

The deviation from constancy of the transitivity as a function of temperature is graphically emphasised: according to Eq. (5). \(\gamma \left(\beta \right)\) can be interpreted as the function that measures the propensity for the reaction to proceed. It permits us to uniformly account for experimental and theoretical important features in rate processes, intrinsic of the reacting system. They include quantum mechanical tunnelling and the effects on transport properties in neighbourhoods of changes in chemical kinetics mechanisms: these enforce continuities excluding apparent breaks occurring at sudden regime changes (Carvalho-Silva et al. 2020).

As already remarked (Carvalho-Silva et al. 2019, 2020), the plot in the transitivity plane, Eq. (7a), enjoys the features that deviations from Arrhenius behaviour can be given a geometrical representation by the deformation parameter \({d}\) as the arc measuring the angular slope \(\delta\) of \(k(\beta )\) as \(\beta\) varies as [see Fig. 1 in (Carvalho-Silva et al. 2019) and Eq. (18b) in SubSect. 2.3]

$$d = - \tan \delta$$
(7b)

This parametrization is important for transition from the Arrhenius to quantum tunnelling regime: it makes explicit the bifurcation to the super- and sub-Arrhenius propensities according to whether \({d}\) is respectively positive or negative. In the latter case, of particular relevance in this paper, it is directly correlated with quantum mechanical tunnelling, and explicit formulas involving the curvature transversal to the reaction profile were derived, implemented and tested in (Aquilanti et al. 2012).

2.2 Time dependence of rate processes: the mechanism

For handling expressions for rates describing dependences of compositions of systems occurring either in experiments or in modelling, we consider effective reformulations from the mass action law as initially systematised according to the famous van’t Hoff book in 1884 (van’t Hoff 1884): see recent developments (Laidler 1985; Gorban 2021).

This is also expedient to consider the concept of rate constant and activation energy as function not only of temperature but also of time, as discussed in various contexts (Vyazovkin 2016; Piskulich et al. 2019; Rufino and Guedes 2022).

Formally, let’s write as usual a general chemical reaction as a transformation between left- and right-hand sides of the formally balanced “equation”:

$$a\mathrm{A}+b\mathrm{B }\cdots \to c\mathrm{C }\cdots$$
(8)

where \([\mathrm{A}]\), \([\mathrm{B}]\), \(\cdots\) are a measure of compositions of reacting species with stoichiometric coefficients \(a, b, \cdots\) (counterparts for one of products are [C] and c). An inherent ambiguity of balancing chemical equations is that for example (8) can be multiplied or divided by any number, so that the set of stoichiometric coefficients is defined modulo this number. An ad hoc, admittedly partial, disambiguation is here attempted by a renormalizing standardisation.

As time evolves, the progressive conversion of chemical species \(\mathrm{A}\), \(\mathrm{B}\), \(\cdots\) (the “reactants”) into \(\mathrm{C}\), \(\cdots\) (the “products”) under idealised conditions occurs with the rate,

$$-\frac{1}{a}\frac{\mathrm{d}}{\mathrm{dt}}[\mathrm{A}]=-\frac{1}{b}\frac{\mathrm{d}}{\mathrm{dt}}[\mathrm{B}]=\frac{1}{c}\frac{\mathrm{d}}{\mathrm{dt}}[\mathrm{C}]=\cdots$$
(9)

The practice of chemistry, as evolved after the statement of the “law of mass action” (Laidler 1985; Gorban 2021) thus involves the description of a system as a field of the system containing the \(\mathrm{A}\), \(\mathrm{B}\), \(\mathrm{C}\), species as a function of time and temperature.

It is often operationally attempted, especially in chemical engineering or in industrial chemistry, to focus on compactly one reagent only, say \(\mathrm{R}\), that is generally decreasing. If this is possible, we denote the corresponding renormalized stoichiometric coefficient by \(\rho\), to be interpreted as the generalised reaction order, also designated as the pseudomolecularity. If one instead of following the reagent R, finds it practical to monitor experimentally or to simulate in molecular dynamics a representative product increasing progressively in time, formally the stoichiometry should provide a connexion. This procedure requires the knowledge of independent information, or as stated commonly, some knowledge of the reaction “mechanism”.

The effective compositions for the system under study should be ideally followed for each species, as a measure of either experimentally the involved macroscopic mass, or else in simulations the microscopic number of particles in a given volume. The units of measurements can be those of partial pressures, concentrations in solution, fugacities, activities: these alternatives and the connexions between them were canonised principally according to the 1922 treatise Lewis–Randall (Lewis and Randall 1922).

In this view, a heterogenous process is considered as a homogeneous system, where activities of components of different phases do not appear explicitly, because they are assumed in equilibrium and therefore with the activity value 1 of the standard state at that temperature. In practice, let’s assume as operationally in a reaction kinetics experiment, the instantaneous measurements of \(\mathrm{R}\) in progressive intervals of times as performed on a temporal grid spacing much greater than the estimated “time scale” \(\tau\) of the process: then, one may implicitly enforce a thermodynamic macrocanonical description of the time dependence of the mixture as it nearly equilibrated at key intermediated steps, in particular at the transition state.

By focussing on a reactant \(\mathrm{R}\), one enunciates that it exists a function of \(\beta\), the rate coefficient \(\widehat{k}\left(\beta ,t\right)\) of the reaction (and its reciprocal \(\widehat{\tau }\)) that is defined from the time change of \(\widehat{\mathrm{R}}\), the cap making explicit the time-dependence functionality:

$$-\frac{\partial }{\partial t}\widehat{[\mathrm{R}}\left(t,\beta \right)]=\widehat{k}\left(t,\beta \right)[{\widehat{\mathrm{R}}}^{\rho }\left(t,\beta \right)]$$
(10)

This operational enunciation of the existence of \(\widehat{k}\) is not free from ambiguities: to be implemented, it must be flexibly adapted with respect to the external conditions into which the process is embedded, in general the reaction “mechanism”.

The interpretation and the use of this and following equations need also explicit operational definitions, and specification of the experimental configuration, for example whether the reaction takes place in a closed system [the “reactor” Astarita and Ocone 1988, 1990; Astarita 1989)] or in an open environment, such as in atmospheric or combustion processes (Adam et al. 2012). Equation (10) embodies the role of the ambient on the system and permits us to establish an extrinsic renormalized rate constant \(\widehat{k}\), which according to the chosen presentation can be compacted by the observation of only the single reactant R as a monitor.

In general, the above references show that a variety of different situations may occur, specifically in a chemical industrial or pharmaceutical plant, in geochemistry, in flames or in atmospheric chemistry implementations, or even in a biological cell: see (Kummer and Ocone 2005) and references therein. Often, the terminology of chemical kinetics is employed, compacting (lumping) a complicate process as described by the representative reagent R; then \(\rho\) as in Eq. (10) is a heuristic reaction order parameter that we allow to be possibly non-integer and even continuous but typically a small number.

In favourable cases, when sets of data on time evolution are available on more than one reagent or more than one product, the practice of chemical reaction mechanisms suggests to profitably exploit the augmented information to increase the accuracy of parametrizations. An example is given in (Nishiyama et al. 2009a, b), where in a study on respiration kinetics of leaves, the configuration of the reactor is a closed volume vessel, and both decrease in reactant O2 and simultaneous increase in product CO2 were accurately monitored. The observed super-Arrhenius process was constrained as pseudo-unimolecular, namely in the present context assigning the value \(\rho =1\).

2.3 A set of coupled renormalization equations and their decoupling

In order to encode information both on the temporal evolution and on the temperature dependence of the composition of the molecular constituents participating in a reactive process, here we formulate a system of coupled set of differential equations that provide an explicit reference framework for renormalization in chemical kinetics.

Considering time t as a running variable, and assigning the role of the order variable to the properly rescaled absolute temperature T or its reciprocal \(\beta\), the field of matter transformations (Weinberg 1995) of interest in chemical reaction kinetics can be written as the function designated by \(\widehat{\mathrm{R}}\left(t,\beta ,k\right)\), that obeys Eq. (10). This equation compacts the experimental and the empirical available data on the compositions. Then, let’s formulate that the following coupled set of two partial differential equations represents a concrete coupling scheme, transcribed by rearranging Eqs. (5) and (10) (the dependence on the \(\rho\) order parameter is omitted from the notation for \(\widehat{\mathrm{R}}\) and \(\widehat{k}\)),

$$-\frac{\partial }{\partial t}\mathrm{ln}[\widehat{\mathrm{R}}\left(\mathrm{t},\beta \right)]=\widehat{k}\left(t,\beta \right){\left[\widehat{\mathrm{R}}\left(\mathrm{t},\beta \right)\right]}^{\rho -1},$$
(11)
$$-\frac{\partial }{\partial \beta }\mathrm{ln}\widehat{k}\left(t,\beta \right)=\frac{1}{ \widehat{\gamma }\left(t,\beta \right)}.$$
(12)

The first Eq. (11) is a generalisation of the mass action law introduced by van’t Hoff in chemical kinetics: it is twinned to the second one (12) that generalises the validity range of Arrhenius law through the transitivity function \(\widehat{\gamma }\), that we momentarily consider as time-dependent.

Exploiting transformations of variables, we may have formulated equivalent coupled systems writing the first equation as a function of temperature T instead of \(\beta\) [Eq. (2)], and the time dependence of rate constant \(\widehat{k}\left(\beta ,t\right)\), namely the parameter controlling the coupling, introducing its reciprocal

$$\widehat{\tau }\left(\beta ,t\right)=\frac{1}{ \widehat{k}\left(\beta ,t\right)},$$
(13)

the generalised lifetime of the process or its time constant.

As a practical scheme, Eqs. (11) and (12) are operationally applied “instantaneously”, from the neighbourhood of an initial time, \(t\approx 0\), when the “clock” is started experimentally, or simulations are initiated computationally. Then, when \(t\to 0\), the caps are eliminated from the notation and one can turn the coupled set to look like a renormalization set of two uncoupled ordinary differential equations, explicitly

$$-\left[\mathrm{R}\left(\mathrm{t}\right)\right]\frac{\mathrm{dt}}{\mathrm{dR}\left(t\right)}=\frac{1}{k\left(\beta \right)}{\left[\mathrm{R}\left(\mathrm{t}\right)\right]}^{1-\rho } ,$$
(14)
$$- k\left( \beta \right)\frac{{{\text{d}} \beta }}{{{\text{d}} k\left( \beta \right)}} = \gamma \left( \beta \right) ,$$
(15)

This set involving reciprocals of logarithmic differentiation has to be regarded as similar to (and playing an analogous fundamental role of) the reciprocal of logarithmic differentiation in Sec. 12.4 of (Weinberg 1995) and in Eq. (9) of (Wilson 1971a).

Useful is the property that these equations can be written in alternative equivalent coupling schemes by convenient change of notations for key quantities explicitly defined, for example in terms of their reciprocals and/or opposites. The procedure permits a variety of applications. One can enforce robust models, either for the dependence only on the temperature of \(\tau\) or \(k\), and also of \(E_{a}\) or \(\gamma\), but not from time. This gives to the apparent activation energy and the transitivity function in Eq. (15) the feature of an intrinsic characterisation of the reacting system.

Important is to exploit the extrapolation of \(\hat{k}\) in the limit of \(t\) → 0, that enables a general solution to Eq. (14) as a one-dimensional integral: when complemented by boundary conditions dictated by features of the “reactor”. Typically, at a given initial time t = 0 in a closed volume, let [R] be [\({\text{R}}]_{0}\). Then, the solution of (14) is

$$\left[ {{\text{R}}\left( t \right)} \right] = \left[ {\text{R}} \right]_{0} \left[ {1 - \left( {1 - \rho } \right)k\left( \beta \right)\left[ {\text{R}} \right]_{0}^{\rho - 1} t} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {1 - \rho }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${1 - \rho }$}}}} ;\;\;\;\forall \rho \ne 1$$
(16a)

when \(\rho = 1\), the apparent singularity disappears through the Euler’s limit, and the common case occurs of the typical exponential decay of first-order or pseudounimolecular kinetics

$$\left[ {{\text{R}}\left( t \right)} \right] = \left[ {\text{R}} \right]_{0} e^{ - kt} ,$$
(16b)

in this case, \(\tau = 1/k\left( \beta \right)\) is considered as the time constant of the system in consistent units of time−1.

The freedom of choosing alternative representations in some quantities like their reciprocals, can be syncretically exploited as alternative coupling schemes, up advantage specifically in perturbation formulations or as more convergent basis set in computational approaches. A cautionary remark is in order. In practice, the equations in this section have much more than only a formal character and are ubiquitously used, although not in this form in chemical kinetics: however, one-to-one correspondence with observables needs consideration, such as dependence on scaling to express the field function [R] in alternative composition units. Note that the treatment and the parametrization of the coupled set may serve both to provide models from measured quantities, and also conversely to physically substantiate theoretical parameters in order to predict time and temperature dependence of the observables of rate processes.

2.4 General models for transitivities and the transition between thermal and sub-Arrhenius regimes

To be considered next are recent systematic investigations leading to formulations of models to be inserted in Eq. (15) involving transitivities, and the temperature dependence of apparent activation energies. We argue that it is expedient to use the already encountered dimensionless deformation parameter \(d\) to describe low-temperature deviation from Arrhenius behaviour. The \(d\)-Arrhenius, also known as the Aquilanti–Mundim formula, was obtained (Aquilanti et al. 2010) by extending the Tsallis non-extensive statistical–mechanics (Tsallis 2009) to the quantum tunnelling case. One exploits Euler’s expression of the exponential function as the limit of a succession. This in previous work was documented as crucial for monitoring how close a system to reach the thermodynamic limit, see Appendix and Refs. (Carvalho-Silva et al. 2019, 2020). In Fig. 1, the general \({d}\) TST formula is written

$$k_{{d}TST} \left( \beta \right) \equiv A\beta^{\nu } \left( {1 {-} {d}\varepsilon^{\ddag } \beta } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 d}}\right.\kern-0pt} \!\lower0.7ex\hbox{${d}$}}}}$$
(17a)

and the quantum tunnelling case corresponding to \(d < 0\). Equation (17a) implies for \(\nu = 0\) the Aquilanti–Mundim formula

$$k_{AM} \left( \beta \right) \equiv A\left( {1 {-} {d}\varepsilon^{\ddag } \beta } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \mathcalligra{d}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${d}$}}}}$$
(17b)

The expression for the rate formula Eq. (17a) was derived in (Carvalho-Silva et al. 2017). It is here compacted introducing the parameter \(\nu\) additionally to \({d}\): they encode the deviations from Arrhenius law at high and low temperatures, respectively. In the following, since for this system there is no evidence of high temperature deviation from Arrhenius in the studied range, we take \(\nu = 0\), pertinent to the range of thermal and low temperatures here investigated.

In (Carvalho-Silva et al. 2019, 2020; Machado et al. 2019), an analytical form was proposed and implemented for the transitivity beyond the Aquilanti–Mundim (AM) formula

$$\gamma \left( {\beta ;\zeta } \right) = \frac{1}{{\varepsilon^{\ddag } }}\left( {1 - \varepsilon^{\dag } \beta } \right)^{\zeta }$$
(18a)

where for the AM case (\(\zeta = 1)\), the identification holds

$$\varepsilon^{\dag } = {d}\varepsilon^{\ddag } = k_{B} T^{\dag } .$$
(18b)

Equation (18a) condenses the generic temperature dependence at low temperatures, as extensively exemplified in the above references. In the classical propensity case, the parameter \(\varepsilon^{\dag }\) is the energy that upon cooling marks the minimal energy for survival, whilst upon heating, it marks the onset energy for the process to start performing (this concept is arguably of interest in biological systems, see for example (Consolini et al. 1992; Carrà 2021). Therefore, in the classical case, it may serve to elucidate the meaning of the energy term \(\varepsilon^{\dag }\) and temperature \(T^{\dag }\), which for the quantum case needs particular scrutiny: it can be shown at face value that both should be negative, according to the negative sign of \(d\) for the quantum mechanical tunnelling regime. Then, the \(\varepsilon^{\dag }\) energy parameter (and \(T^{\dag }\) through 18b) can be interestingly connected to the imaginary frequency mode of the transition state: this has been previously investigated explicitly in (Silva et al. 2013; Cavalli et al. 2014; Carvalho-Silva et al. 2017), where robust models of quantum mechanical tunnelling were implemented and tested for the processes considered in the next section.

The general model for transitivity Eq. (18a) permits by direct rearrangement to propose a dimensionless renormalization plane

$$\left( {\varepsilon^{\ddag } \gamma } \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \zeta }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\zeta $}}}} \qquad\textit{vs}\qquad 1 - \varepsilon^{\dag } \beta .$$
(18c)

to be tested in the next section for the sub-Arrhenius case, and to be compared with the two cases \(\gamma\) vs \(\beta\) presented in (Carvalho-Silva et al. 2019) (Fig. 2) and distinguishing the behaviour for \({d} > 0\) and \({d} < 0\).

Fig. 2
figure 2

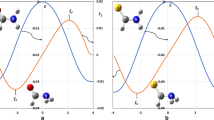
Arrhenius plots and Activation energies for the F + H2 reaction and its isotopic variant producing HF + D and DF + H. \(E_{a} \left( \beta \right)\) is calculated as the negative of the numerical logarithmic derivatives of rate constants with respect to the reciprocal of absolute temperature T. Continuous lines in the upper panel are result of the final fit (parameters in bold in Table 1). In the lower panel, as well as in Fig. 3, broken lines are aid to the view. Trends of converging behaviour is qualitatively shown and quantitatively assessed numerically, confirming the results for \(\varepsilon^{\ddag }\) in Table 1

Full size image

Then, the expression for \(\gamma\) on Eq. (18a) can be obtained as a general formula for the temperature dependence of the reaction rate constant. Inserting Eq. (18a) in Eq. (5) and considering the integral

$$\ln k\left( {\beta ;\zeta } \right) = - \int \frac{d\beta }{{\gamma \left( {\beta ;\zeta } \right)}} + const$$
(19a)

the identification of the constant with the logarithm of the prefactor gives the Carvalho–Coutinho–Aquilanti (CCA) formula

$$k_{CCA} \left( {\beta ;\zeta } \right) = A \exp \left[ { - \frac{1}{{\left( {\zeta - 1} \right)}}\frac{{\varepsilon^{\ddag } }}{{\varepsilon^{\dag } }}\left( {1 - \varepsilon^{\dag } \beta } \right)^{1 - \zeta } } \right],$$
(19b)

that when the exponent \(\zeta\) tends to 0, 1, and 2 generates the Arrhenius, Aquilanti–Mundim (AM), and Vogel–Fulcher–Tammann (VFT) laws, respectively, see also (Carvalho-Silva et al. 2019, 2020).

Detailed derivation of (19b) involves Eulerian integrals and hypergeometric functions. For the uniform covering of the high-energy behaviour, the treatment for the passage between the anti-Arrhenius case and the thermal regime (Carvalho-Silva et al. 2020) involves a Confluent Hypergeometric Function, explicitly an Incomplete Gamma Function (Abramowitz and Stegun 1965). Further, using a Gaussian Hypergeometric Function, explicitly an Incomplete Beta Function (Abramowitz and Stegun 1965), the formulation is possible to cover both high- and low-regime changes illustrated in Fig. 1. This will be documented elsewhere.

3 An elementary chemical reaction as a complex system

3.1 Converged results for the kinetics of the F + H2 (HD) reactions

As prototypical of the Arrhenius vs sub case transition, explicit focus will be devoted next to applying the transitivity-based approach of the previous sections to two reactions of fluorine atoms, one with hydrogen molecules leading to hydrogen fluoride,

figure a

and the other with HD leading to both HF + D and DF + H.

figure b

The search of universality of behaviour is illustrated for the moderate tunnelling range including that of validity of the Arrhenius law and excluding that of quantum mechanical resonances towards the Wigner limit at zero Kelvin.

The rate constants for the F + H2 reaction and its isotopic variants have aroused great attention from experimental and theoretical chemical kinetics studies (Aquilanti et al. 2005b; Cavalli et al. 2014; Tizniti et al. 2014; De Fazio et al. 2019). These processes are prototypical of exothermic elementary reactions driven by the quantum tunnelling effect even at room temperature, becoming dominant in the colder environments. In the present demonstrative simulations of the renormalization approach, we take at face value selected data from calculations from (Aquilanti et al. 2012) for R1 and from (De Fazio et al. 2016) for R2 and R3. The numerically converged results included all open roto-vibrational levels of products. R1 is studied on PES I, a variant of the early Stark–Werner potential energy surface (Stark and Werner 1996; Aquilanti et al. 2012), extensively modified afterwards. The much harder case of HD, carried out later (Cavalli et al. 2014) employed a more recent surface denoted FXZ (Fu et al. 2008).

These reactions are written as elementary chemical reactions, but are actually case studies of complex systems. (Cavalli et al. 2014) and (De Fazio et al. 2019) provide additional detailed insights coming from rigorous quantum scattering calculations carried out for rate constants \(k\left( T \right)\) and including the temperature dependence on alternative potential energy surfaces. All results confirm a linear asymptotic behaviour in Arrhenius plots at high temperature, whilst ubiquitous concave curvature was observed at low temperature. This is a manifestation of the insurgence of sub-Arrhenius behaviour, as macroscopic evidence of quantum mechanical tunnel of H atoms in R1 and R2 or D atoms in R3, to be looked at next from the viewpoint of this paper.

3.2 Renormalization across the thermal and the sub-Arrhenius regimes

The data selected from 10 to 350 K for the reaction constants and those calculated for the temperature dependence of activation energies and transitivities are presented in the next figures. Available data at lower energies fall in the quantum mechanical resonance region extensively investigated elsewhere (Aquilanti et al. 2004, 2005a; Sokolovski et al. 2007). Activation energies and Transitivities defined in Eq. (5) are obtained numerically by logarithmic differentiation of the reaction rate constants with respect to \(\beta\), Eq. (2). Having to deal with experimental or theoretically concrete systems, notations will be specialised somewhat in this section with respect to previous ones. Specifically, \(\beta\) will be given in 1000/T units for Arrhenius and Activation Energy plots and consequently inverse units for the plots of Transitivities. This was the initial step of the approach was to assign the energy parameter \(\varepsilon^{\ddag }\) (see Refs. Aquilanti et al. 2012; De Fazio et al. 2016)) to be intended as the Arrhenius–Eyring barrier to reaction, arguably similar for the three cases. For these systems, \(\varepsilon^{\ddag }\) and \(\zeta\) are fitted from Eq. (18a) on the transitivity data, to be discussed below, but the temperature dependence was poor.

Figure 2 shows Arrhenius (top) and Activation energies (bottom) plots for the F + H2 reaction and its isotopic variant with HD producing HF + D and DF + H. In all cases, a decrease of activation energies was observed as temperature decreases. This behaviour of the apparent activation energy had been already reported in the previous paper (Aquilanti et al. 2012) for the first reaction only. Their scrutiny makes the search of universalities of behaviour easier to be captured visually: convergence to similar trend for \(\beta = 0\) is observed (Fig. 2) as for the reasonably common initial guess. Indeed, numerical search involving extrapolation of \(E_{a} \left( \beta \right)\) towards \(\beta = 0\) confirms the results for \(\varepsilon^{\ddag }\) in the three cases and listed in Table 1 in units of kcal.mol−1. On taking into account that in theoretical chemistry conventionally “chemical accuracy” is considered tolerable within 1 kcal.mol−1 and “spectroscopical” data are accepted as reliable within a 0.10 kcal.mol−1 accuracy, we can affirm that the four values (Table 1) indicate essentially the same height of the derived effective barrier energy \(\varepsilon^{\ddag }\) for the reactions to proceed.

Table 1 Kinetic parameters obtained fitting  data for F + H2 and HD reactionsa
Full size table

Figure 3 presents the plots of the Transitivity function for the three cases. Upon cooling, i.e. when \(\beta\) increases, transitivities grow indefinitely according to a trend to be expected from exothermic tunnelling (Takayanagi et al. 1987; Carvalho-Silva et al. 2019) and to be compared to that of the proposed model relationship in the Eq. (18a). Remarkably, Refs. (Silva et al. 2013; Carvalho-Silva et al. 2017, 2019) advocate the relevant property of the transitivity function to behave linearly in the small \(\beta\) limit for processes that deviate from the Arrhenius formula according to the Aquilanti–Mundim (Aquilanti et al. 2010) formula, and implemented in the deformed Transition State Theory (\({d}\) TST) (Carvalho-Silva et al. 2017). Calculations applying the \({d}\) TST for chemical reactions upon the potential energy quantum chemical calculated surface profile have been reported for a variety of processes, such as the CH4 + OH (Carvalho-Silva et al. 2017), CH3OH + H (Sanches-Neto et al. 2017), OH + HCl (Coutinho et al. 2018) reactions, the proton rearrangement of enol forms of curcumin (Santin et al. 2016), the degradation of a pesticide (Sanches-Neto et al. 2021), and the Claisen–Schmidt condensation (Coutinho et al. 2021), all involving deviations from Arrhenius because of quantum mechanical tunnel.

Fig. 3
figure 3

Transitivities function \(\gamma\) as a function of reciprocal of temperature for the studied reactions, symbols as in Fig. 2, obtained from quantum scattering reaction rate constants of Refs. (Aquilanti et al. 2012; De Fazio et al. 2016). The inset shows the general trend. Blown up is the transition temperature range across the thermal and moderate tunnelling regimes where broken lines indicate the trends to linearization leading to parametrization through the Aquilanti-Mundim formula

Full size image

The scaling plane exhibits the transitivity function, which allows the estimation of potential energy surface parameters whilst avoiding the kinetic compensation effect (Garn 1975; Zuniga-Hansen et al. 2018). For systems that exhibit a well-behaved trend, such as the one shown for reaction R1 in Fig. 3, the model given by Eq. (18a) fits perfectly. Table 1 presents a comparison of fits made on Arrhenius (Fig. 1) and transitivity planes (Fig. 3). In Table 1, the first three lines list parameters in this work whereby fit improved by letting \(\zeta\) varying additional to \(\varepsilon^{\dag }\). In the fourth line of each system, the parameters from previous fit using the \(k_{AM}\) formula corresponding to \(\zeta =\) 1. For each reaction, an initial fit of the temperature dependence of transitivity was performed using Eq. (18a) in the range of 10–350 K. As a first step, \(\varepsilon^{\ddag }\) was kept constant and equal to the energetic barrier obtained by electronic structure calculations in the references cited in the table; in a second step, the fit is performed without restrictions. In the third case for each reaction, from the temperature dependence for the reaction rate constant, a fit was also performed using the general model proposed in Eq. (19a, 19b), inserting the pre-factor as an additional variable to be obtained.

The third case is compared with fits made previously in a temperature range where the linear model of transitivity is appropriated and described by the Aquilanti–Mundim formula. In both cases, the energetic barriers present values consistent with calculations obtained through electronic structure methods, considering that differences do not exceed error limits of 1 kcal.mol−1. Additionally, energetic barriers obtained by electronic structure calculations ignore dynamic effects embedded in reaction rate constant calculations and emphasised here by scaling and renormalization methods.

The transitivity at cold and ultracold temperature sharply increases according to the universality class measured by the \(\zeta\) parameter, and balances the loss of active number of particles with decreasing temperature. This results in the finite Wigner limit at zero kelvin.

Rearrangement of Eq. (18a) (Eq. 18c and Fig. 4) in terms of rescaled dimensionless variables \(\varepsilon^{\ddag } \gamma\) and \(\varepsilon^{\dag } \beta\) collapses in a universal behaviour (see fitting data in Table 1). A linear relationship is found for the three reactions in the limit of low temperatures where the passage from the room temperature regime to that of quantum mechanical tunnelling occurs. Remarkable is the diagnostic that indicates as anomalous the deviation from linearity observed for F + HD → HF + D at intermediate temperatures, although at low temperatures, linearity is recovered. This anomaly may be ascribed to previously observed insurgent quantum resonances (De Fazio et al. 2020) at low temperatures. Open is the interesting perspective of further investigation along this direction for these systems at higher energies to study the transition across the Arrhenius vs anti-case regimes. This is in a region of temperature very demanding for exact converged calculations, especially for the R3 channel that requires including a very high roto-vibrational density of states of the product.

Fig. 4
figure 4

Universal behaviour of the transitivity functions \(\gamma (\beta\)) renormalized according to Eq. (18a) for the reactions R1, R2 and R3, symbols as Figs. 2 and 3. Parameters are listed in Table 1

Full size image

4 Conclusions and perspective remarks

In retrospect, renormalized formulations widely used in the physics of critical phenomena and of elementary particles, have been here exemplarily applied to the kinetics of elementary chemical reactions. In the thermal and low-temperature regimes, this study of the F + H2 (HD) reaction provides accurate information on the temperature dependence of the quantum mechanical benchmark rate constants, permitting a reliable opportunity to applying the renormalization approach at the transition across the Arrhenius and the sub-Arrhenius cases. The notations for atoms and molecules in the previous sections and specifically in R1, R2 and R3 above hide the complexity of many-electron atoms and molecules limiting to their bound states, and deal basically on average properties, in the case of F by treating adiabatically the fine structure due to the spin–orbit interaction (Aquilanti et al. 1990, 2001b), in the case of H2 by averaging through nuclear isotopic statistics. The kinetic energy and the roto-vibrational manifold were Boltzmann-convoluted at the given temperature. For computational overcoming of convergence problems, see (Aquilanti et al. 1998, 2001a), and for complexities from steric, isotopic and state-to-state dynamics, see (De Fazio et al. 2006, 2008; Skouteris et al. 2009). Renormalization by the transitivity function is enforced by Eqs. (18a) and (18c), which compact by a uniform description, the behaviour of processes at low temperatures.

The plot in Fig. 1 illustrates the chemical kinetics and expands the previous ones in (Fig. 2) of (Carvalho-Silva et al. 2019, 2020) to cover both rise and fall as a function of temperature of the performances of processes for diverse models that operate at widely differing scale ranges. Prime interest is for chemical and biophysical processes upon cooling or heating. Enormous changes in the orders of magnitudes are involved in materials sciences, and in geochemistry at the largest of scales. It is even tempting to conceive a cosmochemical toy model for the molecular evolution of the universe, as it had been cooling down from formation of atoms and molecules after the big-bang to the present biosphere, eventually marginalised by the final death by freezing.

Since chemical kinetics advocates a syncretical grafting of time in a thermodynamic framework at the level of biophysical and biochemical processes that involve a restricted temperature range. As the margins of this range are approaching, the thermodynamical-like formulations inevitably need modification.

The theoretical framework elaborated in this and previous papers (Carvalho-Silva et al. 2019, 2020) becomes relevant because the scaling of the reaction rate constant as a function of the control variable β allows a simple renormalization scheme regarding the canonical definition of the activation energy \(E_{a}\), the quantity which controls the coupling in a reactive process. Singularities at low temperatures are uniformly removed by the reciprocal of the activation energy \(E_{a}\), the transitivity γ, and an effective coupling parameter \({d}\) serves to cover the initially linear deviations from Arrhenius law that develop in the moderately low-temperature range.

Figure 1 points out at the insurgence of “unrenormalizable” ranges of temperature on the cold and hot sides: these general phenomena occur due to a variety of specific origins, hard to be treated by chemical kinetics. In a very different context, elementary particle investigations on a much higher-energy scale employ the so-called “ultraviolet cut off”: such marginalisation is actively investigated in high-energy physics (Weinberg 1995). In the view of Fig. 1, the “hot” marginalisation makes explicit the tendency to anti-behaviour: there is an increase of density of states emphasises the specificity of openings of additional channels. They may correspond to (molecular electronic, roto-vibrational and translational) degrees of freedom, as well as to more drastic events, such as molecular fragmentations and ionizations (Leenson and Sergeev 1984). Aspects of this behaviour have been recently elucidated for tetratomic reactions (Coutinho et al. 2015, 2016, 2018) and for the conductivity of nanowires in proteins (Dahl et al. 2022; Guberman-Pfeffer 2022).

The present work has been focussed on the “cold” marginalisation, where the description of the reaction progress bifurcates into sub- and super-behaviour upon cooling (Fig. 1): only aspects are considered of the quantum mechanical phenomena regarding the approach to the Wigner’s limit as the temperature decreases. A variety of processes exhibiting sub and super-Arrhenius behaviour have been found and implementation of the present renormalization approach appears of interest.

The heuristic nature of the set of two coupled equations presented in this study enables access to classes of universality occurring for the tendency of tunnel dominated chemical reactions much before the Wigner’s limit. The fundamental significance of the microscopic origin of the curvatures depicted in Fig. 1 will be further evaluated in the future research through the incorporation of the definition of activation heat capacity (La Mer 1933; Hobbs et al. 2013), providing progress from a complementary predictive approach formulated in an extended thermodynamic language.