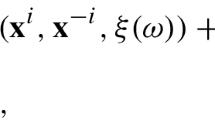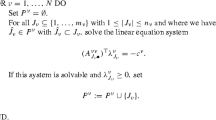Abstract
In this paper, we consider stochastic monotone Nash games where each player’s strategy set is characterized by possibly a large number of explicit convex constraint inequalities. Notably, the functional constraints of each player may depend on the strategies of other players, allowing for capturing a subclass of generalized Nash equilibrium problems (GNEP). While there is limited work that provide guarantees for this class of stochastic GNEPs, even when the functional constraints of the players are independent of each other, the majority of the existing methods rely on employing projected stochastic approximation (SA) methods. However, the projected SA methods perform poorly when the constraint set is afflicted by the presence of a large number of possibly nonlinear functional inequalities. Motivated by the absence of performance guarantees for computing the Nash equilibrium in constrained stochastic monotone Nash games, we develop a single timescale randomized Lagrangian multiplier stochastic approximation method where in the primal space, we employ an SA scheme, and in the dual space, we employ a randomized block-coordinate scheme where only a randomly selected Lagrangian multiplier is updated. We show that our method achieves a convergence rate of \(\mathcal {O}\left( \frac{\log (k)}{\sqrt{k}}\right)\) for suitably defined suboptimality and infeasibility metrics in a mean sense.

Similar content being viewed by others
References
Hu, X., Ralph, D.: Using EPECs to model bilevel games in restructured electricity markets with locational prices. Oper. Res. 55(5), 809–827 (2007)
Ferris, M.C., Pang, J.-S.: Engineering and economic applications of complementarity problems. SIAM Rev. 39(4), 669–713 (1997)
Deligiannis, A., Panoui, A., Lambotharan, S., Chambers, J.A.: Game-theoretic power allocation and the Nash equilibrium analysis for a multistatic MIMO radar network. IEEE Trans. Signal Process. 65(24), 6397–6408 (2017)
Von Neumann, J., Morgenstern, O.: Theory of games and economic behavior, 2nd rev (1947)
Nash, J.: Non-cooperative games. Ann. Math. 286–295 (1951)
Facchinei, F., Kanzow, C.: Generalized Nash equilibrium problems. Ann. Oper. Res. 175(1), 177–211 (2010)
Krilašević, S., Grammatico, S.: Learning generalized Nash equilibria in monotone games: a hybrid adaptive extremum seeking control approach. Automatica 151, 110931 (2023). https://doi.org/10.1016/j.automatica.2023.110931
Neumann: Zur theorie der gesellschaftsspiele. Mathematische Annalens 19(2), 295–320 (1928)
Korpelevich, G.M.: An extragradient method for finding saddle points and for other problems. Eknomika i Matematicheskie Metody 12(4), 747–756 (1976)
Golshtein, E.: Generalized gradient method for finding saddlepoints. Matekon 10(3), 36–52 (1974)
Chen, G.H.-G., Rockafellar, R.T.: Convergence rates in forward–backward splitting. SIAM J. Optim. 7(2), 421–444 (1997). https://doi.org/10.1137/S1052623495290179
Nemirovski, A.: Prox-method with rate of convergence O(1/t) for variational inequalities with Lipschitz continuous monotone operators and smooth convex–concave saddle point problems. SIAM J. Optim. 15(1), 229–251 (2004). https://doi.org/10.1137/S1052623403425629
Nedić, A., Ozdaglar, A.: Subgradient methods for saddle-point problems. J. Optim. Theory Appl. 142, 205–228 (2009)
Zhao, R.: Accelerated stochastic algorithms for convex–concave saddle-point problems. Math. Oper. Res. 47(2), 1443–1473 (2022)
Hamedani, E.Y., Aybat, N.S.: A primal-dual algorithm with line search for general convex–concave saddle point problems. SIAM J. Optim. 31(2), 1299–1329 (2021)
Facchinei, F., Pang, J.-S.: Finite-Dimensional Variational Inequalities and Complementarity Problems. Springer Series in Operations Research, vol. I, II. Springer, New York (2003)
Sanjabi, M., Ba, J., Razaviyayn, M., Lee, J.D.: On the convergence and robustness of training GANs with regularized optimal transport. Adv. Neural Inf. Process. Syst. 31 (2018)
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., Bengio, Y.: Generative adversarial nets. Adv. Neural Inf. Process. Syst. 27 (2014)
Sinha, A., Namkoong, H., Duchi, J.: Certifiable distributional robustness with principled adversarial training. In: International Conference on Learning Representations (2018). https://openreview.net/forum?id=Hk6kPgZA-
Zhang, L., Xu, D., Yuan, S., Wu, X.: FairGAN: Fairness-aware generative adversarial networks. CoRR. arXiv:1805.11202 (2018)
Jin, Y., Sidford, A., Tian, K.: Sharper rates for separable minimax and finite sum optimization via primal-dual extragradient methods. In: Conference on Learning Theory, pp. 4362–4415. PMLR (2022)
Deng, Y., Kamani, M.M., Mahdavi, M.: Distributionally robust federated averaging. Adv. Neural Inf. Process. Syst. 33 (2020)
Scarf, H.: The approximation of fixed points of a continuous mapping. SIAM J. Appl. Math. 15(5), 1328–1343 (1967)
Jiang, H., Xu, H.: Stochastic approximation approaches to the stochastic variational inequality problem. IEEE Trans. Autom. Control 53(6), 1462–1475 (2008)
Kannan, A., Shanbhag, U.V.: Distributed computation of equilibria in monotone Nash games via iterative regularization techniques. SIAM J. Optim. 22(4), 1177–1205 (2012)
Koshal, J., Nedić, A., Shanbhag, U.V.: Regularized iterative stochastic approximation methods for stochastic variational inequality problems. IEEE Trans. Autom. Control 58(3), 594–609 (2013)
Yousefian, F., Nedić, A., Shanbhag, U.V.: On smoothing, regularization, and averaging in stochastic approximation methods for stochastic variational inequality problems. Math. Program. 165(1), 391–431 (2017). https://doi.org/10.1007/s10107-017-1175-y
Yousefian, F., Nedić, A., Shanbhag, U.V.: On stochastic mirror-prox algorithms for stochastic Cartesian variational inequalities: randomized block coordinate and optimal averaging schemes. Set Valued Var. Anal. 26(4), 789–819 (2018). https://doi.org/10.1007/s11228-018-0472-9
Long, X.-J., He, Y.-H.: A fast stochastic approximation-based subgradient extragradient algorithm with variance reduction for solving stochastic variational inequality problems. J. Comput. Appl. Math. 420, 114786 (2023)
Iusem, A.N., Jofré, A., Oliveira, R.I., Thompson, P.: Extragradient method with variance reduction for stochastic variational inequalities. SIAM J. Optim. 27(2), 686–724 (2017)
Malitsky, Y.: Proximal extrapolated gradient methods for variational inequalities. Optim. Methods Softw. 33(1), 140–164 (2018). https://doi.org/10.1080/10556788.2017.1300899. (PMID: 29348705)
Juditsky, A., Nemirovski, A., Tauvel, C.: Solving variational inequalities with stochastic mirror-prox algorithm. Stoch. Syst. 1(1), 17–58 (2011)
Iusem, A.N., Jofré, A., Oliveira, R.I., Thompson, P.: Variance-based extragradient methods with line search for stochastic variational inequalities. SIAM J. Optim. 29(1), 175–206 (2019)
Chambolle, A., Pock, T.: On the ergodic convergence rates of a first-order primal-dual algorithm. Math. Program. 159(1–2), 253–287 (2016)
He, Y., Monteiro, R.D.: An accelerated HPE-type algorithm for a class of composite convex–concave saddle-point problems. SIAM J. Optim. 26(1), 29–56 (2016)
Kolossoski, O., Monteiro, R.D.: An accelerated non-Euclidean hybrid proximal extragradient-type algorithm for convex–concave saddle-point problems. Optim. Methods Softw. 32(6), 1244–1272 (2017)
He, Y., Monteiro, R.D.: Accelerating block-decomposition first-order methods for solving composite saddle-point and two-player Nash equilibrium problems. SIAM J. Optim. 25(4), 2182–2211 (2015)
Nemirovski, A., Juditsky, A., Lan, G., Shapiro, A.: Robust stochastic approximation approach to stochastic programming. SIAM J. Optim. 19(4), 1574–1609 (2009)
Zhao, R., Haskell, W.B., Tan, V.Y.: An optimal algorithm for stochastic three-composite optimization. In: The 22nd International Conference on Artificial Intelligence and Statistics, pp. 428–437. PMLR (2019)
Mosco, U.: Dual variational inequalities. J. Math. Anal. Appl. 40(1), 202–206 (1972)
Gabay, D.: Applications of the method of multipliers to variational inequalities. vol. 15, pp. 299–331. Elsevier (1983). Chap. ix. In: Studies in mathematics and its applications
Eckstein, J., Ferris, M.C.: Smooth methods of multipliers for complementarity problems. Math. Program. 86(1), 65–90 (1999)
Auslender, A.: Optimisation. Méthodes numériques (1976)
Auslender, A., Teboulle, M.: Lagrangian duality and related multiplier methods for variational inequality problems. SIAM J. Optim. 10(4), 1097–1115 (2000). https://doi.org/10.1137/S1052623499352656
Auslender, A., Haddou, M.: An interior-proximal method for convex linearly constrained problems and its extension to variational inequalities. Math. Program. 71(1), 77–100 (1995)
Burachik, R.S., Iusem, A.N.: A generalized proximal point algorithm for the variational inequality problem in a Hilbert space. SIAM J. Optim. 8(1), 197–216 (1998)
Xu, Y.: Primal-dual stochastic gradient method for convex programs with many functional constraints. SIAM J. Optim. 30(2), 1664–1692 (2020). https://doi.org/10.1137/18M1229869
Kaushik, H.D., Yousefian, F.: A method with convergence rates for optimization problems with variational inequality constraints. SIAM J. Optim. 31(3), 2171–2198 (2021). https://doi.org/10.1137/20M1357378
Karamardian, S.: An existence theorem for the complementarity problem. J. Optim. Theory Appl. 19(2), 227–232 (1976)
Minty, G.J., et al.: Monotone (nonlinear) operators in Hilbert space. Duke Math. J. 29(3), 341–346 (1962)
Acknowledgements
This work is supported in part by the National Science Foundation under CAREER Grant ECCS-1944500 and Grant ECCS-2231863, the Office of Naval Research under Grant N00014-22-1-2757, the University of Arizona Research, Innovation & Impact (RII) Funding, and the Arizona Technology and Research Initiative Fund (TRIF) for Innovative Technologies for the Fourth Industrial Revolution initiatives.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
1.1 Proof of Lemma 1
Proof
Invoking Proposition 1 and taking into account that \(\mathcal {N}_X(x^*) = \partial \mathcal {I}_X(x^*)\), we have that \(x^* \in X\) solves the following augmented variational inequality problem \(\text{ VI }\left( X,F+J^{-1}\nabla f^T\lambda ^*\right) ,\) that is parameterized by J and \(\lambda ^*\). This implies that
From the convexity of function \(f_j\) for all \(j \in [J]\) and that \(\lambda _j \ge 0\), we have
Summing the preceding relation over \(j \in [J]\) and recalling the definition of the mapping f(x), we obtain
Invoking Proposition 1(ii) we obtain \(f(x)^T\lambda ^* \ge \left( \nabla f(x^*)^T\lambda ^*\right) ^T(x-x^*)\). From the preceding relation and (18) we obtain \(F(x^*) ^T(x-x^*) +J^{-1}f(x)^T\lambda ^* \ge 0\) for all \(x \in X\). \(\square\)
1.2 Proof of Lemma 2
Proof
(i) Note that \(x^*\) is a feasible point to problem (cSVI) with respect to the set \(\mathcal {X}\), i.e., \(x^* \in \mathcal {X}\). Also, note that \({{\hat{\lambda }} \ge 0}\). From the definition of \(\Phi _\rho\), we have that \(\Phi _\rho (x^*,{\hat{\lambda }})\le 0\). Let \(x:=x^*\) in (4). Then we have
Also, from Lemma 1 and that \({\hat{x}} \in X\) we have
The preceding relation and that \(\lambda ^* \ge 0\) imply that
Summing the preceding relation and (19) and rearranging the terms, we obtain
Let us choose \(\lambda _j:=1+\lambda ^*_j\) if \(f_j({\hat{x}})>0\), and \(\lambda _j:=0\) otherwise for all \(j \in [J]\). Then, we obtain the desired relation in (i).
(ii) Let \(\lambda =0\) in (4) and note that \(\Phi _\rho (x,{\hat{\lambda }})\le 0\) for all \(x\in \mathcal X\). We have \(F(x)^T({\hat{x}}-x)\le C(x,0)\) for all \(x\in \mathcal X\). Taking supremum from the both sides, we obtain desired results in (ii). \(\square\)
1.3 Proof of Lemma 3
Proof
The relations in part (i) hold as a consequence of Assumption 2. To show \(\mathbb {E}[\delta _k \mid \mathcal {F}_k]=0\), we can write
where the last inequality is implied from the assumption that \(j_k\) is uniformly drawn from the set [J]. Next, we derive the bound on \(\mathbb {E}[\Vert \delta _k\Vert ^2\mid \mathcal {F}_k]\). We have
Dropping the non-negative term in the preceding relation and invoking Remark 5, we obtain
\(\square\)
1.4 Proof of Lemma 4
Proof
From the update rule of \(v_{k+1}\), we know \(\sigma _k={1\over \tau _k}(v_{k+1}-v_k)\), hence we have that
where the first equality is obtained from three points equality in the Euclidean space and in the last inequality we used Young’s inequality. \(\square\)
1.5 Proof of Lemma 5
Proof
From the fact that \(\lambda _{k+1}-\lambda _k=J\rho _k e_{j_k}\odot \nabla _{\lambda } \Phi _{\rho _k}(x_k,\lambda _k)\), one can get the following:
Moreover, using the fact that \(\tfrac{1}{\rho _k}{ (\lambda _k-\lambda )^T (\lambda _{k+1}-\lambda _k)} =\tfrac{1}{2\rho _k}\left( \Vert \lambda _{k+1}-\lambda \Vert ^2-\Vert \lambda _{k}-\lambda \Vert ^2-\Vert \lambda _{k+1}-\lambda _k\Vert ^2\right)\) and using previous equality one can obtain:
Using (21), one can easily show that:
From definition of \(\Phi _{\rho _k}(x_k,\lambda _k)\), \(J^+_k\) and \(J_k^-\) we have:
Using (22), (23) and the fact that \(\nabla _{\lambda } \Phi _\rho (x,\lambda )=\tfrac{1}{J}\Big [\max (\tfrac{-\lambda ^{(j)}}{\rho },f_j(x))\Big ]_{j=1}^{J}\), the following holds:
Note that \(\lambda \ge 0\) and by definition \(J_k^-\) it holds that \(\lambda ^{(j)}(f_j(x_k)+\tfrac{\lambda _k^{(j)}}{\rho _k})\le 0\), so we conclude that
Hence we have the desired result by putting (25) in (24). \(\square\)
1.6 Proof of Lemma 6
Proof
(a) From definition of \(\nabla _\lambda \Phi _{\rho _k}\), using Assumption 1(ii) and the fact that \(\lambda _k^{(j_k)}\ge 0\) for all k and j, we have that \(\Vert Je_{j_k}\odot \nabla _{\lambda } \Phi _{\rho _k}(x_k,\lambda _k)\Vert ^2=\left| \max \left( \tfrac{-\lambda _k^{(j_k)}}{{\rho _k}},f_{j_k}(x_k)\right) \right| ^2\le D_f^2.\)
(b) By definition of \(\bar{\sigma }_k\) and \(\bar{v}_k\) and using Lemma 4, one can obtain the following.
\(\square\)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Alizadeh, Z., Jalilzadeh, A. & Yousefian, F. Randomized Lagrangian stochastic approximation for large-scale constrained stochastic Nash games. Optim Lett 18, 377–401 (2024). https://doi.org/10.1007/s11590-023-02079-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11590-023-02079-5