Byzantine consensus is $\Theta (n^2)$: the Dolev-Reischuk bound is tight even in partial synchrony!

Abstract

The Dolev-Reischuk bound says that any deterministic Byzantine consensus protocol has (at least) quadratic (in the number of processes) communication complexity in the worst case: given a system with n processes and at most $f < n / 3$ failures, any solution to Byzantine consensus exchanges $\Omega \big (n^2\big )$ words, where a word contains a constant number of values and signatures. While it has been shown that the bound is tight in synchronous environments, it is still unknown whether a consensus protocol with quadratic communication complexity can be obtained in partial synchrony where the network alternates between (1) asynchronous periods, with unbounded message delays, and (2) synchronous periods, with $\delta$-bounded message delays. Until now, the most efficient known solutions for Byzantine consensus in partially synchronous settings had cubic communication complexity (e.g., HotStuff, binary DBFT). This paper closes the existing gap by introducing SQuad, a partially synchronous Byzantine consensus protocol with $O\big (n^2\big )$ worst-case communication complexity. In addition, SQuad is optimally-resilient (tolerating up to $f < n / 3$ failures) and achieves $O(f \cdot \delta )$ worst-case latency complexity. The key technical contribution underlying SQuad lies in the way we solve view synchronization, the problem of bringing all correct processes to the same view with a correct leader for sufficiently long. Concretely, we present RareSync, a view synchronization protocol with $O\big (n^2\big )$ communication complexity and $O(f \cdot \delta )$ latency complexity, which we utilize in order to obtain SQuad.

1 Introduction

Byzantine consensus [1] is a fundamental distributed computing problem. In recent years, it has become the target of widespread attention due to the advent of blockchain [2,3,4] and decentralized cloud computing [5], where it acts as a key primitive. The demand of these contexts for high performance has given a new impetus to research towards Byzantine consensus with optimal communication guarantees.

Intuitively, Byzantine consensus enables processes to agree on a common value despite Byzantine failures. Formally, each process is either correct or faulty; correct processes follow a prescribed protocol, whereas faulty processes (up to $0< f < n / 3$) can arbitrarily deviate from it. Each correct process proposes a value, and should eventually decide a value (no more than once). The following properties are guaranteed:

• Validity: If all correct processes propose the same value, then only that value can be decided by a correct process.

• Agreement: No two correct processes decide different values.

• Termination: All correct processes eventually decide.

The celebrated Dolev-Reischuk bound [6] on message complexity implies that any deterministic solution of the Byzantine consensus problem incurs $\Omega (n^2)$ communication complexity: correct processes must send $\Omega (n^2)$ words in the worst case, where a word contains a constant number of values and signatures. It has been shown that the bound is tight in synchronous environments [7, 8]. However, for the partially synchronous environments [9] in which the network initially behaves asynchronously and starts being synchronous with $\delta$-bounded message delays only after some unknown Global Stabilization Time ($GST$), no Byzantine consensus protocol achieving quadratic communication complexity is known.¹ (Importantly, the communication complexity of partially synchronous Byzantine consensus protocols only counts words sent after $GST$ as the number of words sent before $GST$ is unbounded [11]). Therefore, the question remains whether a partially synchronous Byzantine consensus with quadratic communication complexity exists [12]. Until now, the most efficient known solutions in partially synchronous environments had $O(n^3)$ communication complexity (e.g., HotStuff [13], binary DBFT [2]).

We close the gap by introducing SQuad, a partially synchronous Byzantine consensus protocol with $O(n^2)$ worst-case communication complexity, matching the Dolev-Reischuk [6] bound. In addition, SQuad is optimally-resilient (tolerating up to $f < n / 3$ failures) and achieves $O(f \cdot \delta )$ worst-case latency (measured from $GST$ onwards).

1.1 Partially synchronous “leader-based” Byzantine consensus

Partially synchronous “leader-based” consensus protocols [13,14,15,16] operate in views, each with a designated leader whose responsibility is to drive the system towards a decision. If a process does not decide in a view, the process moves to the next view with a different leader and tries again. Once all correct processes overlap in the same view with a correct leader for sufficiently long, a decision is reached. Sadly, ensuring such an overlap is non-trivial; for example, processes can start executing the protocol at different times or their local clocks may drift before $GST$, thus placing them in views which are arbitrarily far apart.

Typically, these protocols contain two independent modules:

• 1. View core: The core of the protocol, responsible for executing the protocol logic of each view.

• 2. View synchronizer: Auxiliary to the view core, responsible for “moving” processes to new views with the goal of ensuring a sufficiently long overlap to allow the view core to decide.

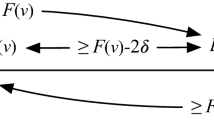
Immediately after $GST$, the view synchronizer brings all correct processes together to the view of the most advanced correct process and keeps them in that view for sufficiently long. At this point, if the leader of the view is correct, the processes decide. Otherwise, they “synchronously” transit to the next view with a different leader and try again. Figure 1 illustrates this mechanism in HotStuff [13]. In summary, the communication complexity of such consensus protocols can be approximated by $n \cdot C + S$, where:

• C denotes the maximum number of words a correct process sends while executing its view core during $[ GST , t_d]$, where $t_d$ is the first time by which all correct processes have decided,² and

• S denotes the communication complexity of the view synchronizer during $[ GST , t_d]$.

Fig. 1

Overview of HotStuff [13]: Processes change views via the view synchronizer. After $GST$, once a correct leader is reached all correct processes are guaranteed to decide (by time $t_d$). In the worst case, the first $f \in O(n)$ leaders after $GST$ are faulty and O(n) view synchronizations are executed, resulting in $O(n^3)$ communication complexity

Since the adversary can corrupt up to f processes, correct processes must transit through at least $f + 1$ views after $GST$, in the worst case, before reaching a correct leader. In fact, PBFT [15] and HotStuff [13] show that passing through $f + 1$ views is sufficient to reach a correct leader. Furthermore, HotStuff employs the “leader-to-all, all-to-leader” communication pattern in each view. As (1) each process is the leader of at most one view during $[ GST , t_d]$, and (2) a process sends O(n) words in a view if it is the leader of the view, and O(1) words otherwise, HotStuff achieves $C = 1 \cdot O(n) + f \cdot O(1) = O(n)$. Unfortunately, $S = (f + 1) \cdot O(n^2) = O(n^3)$ in HotStuff due to “all-to-all” communication exploited by its view synchronizer in every view.³ Thus, $S = O(n^3)$ dominates the communication complexity of HotStuff, preventing it from matching the Dolev-Reischuk bound. If we could design a consensus algorithm for which $S = O(n^2)$ while preserving $C = O(n)$, we would obtain a Byzantine consensus protocol with optimal communication complexity. The question is if a view synchronizer achieving $S = O(n^2)$ in partial synchrony exists.

1.2 Warm-up: View synchronization in complete synchrony

Solving the synchronization problem in a completely synchronous environment is not hard. As all processes start executing the protocol at the same time and their local clocks do not drift, the desired overlap can be achieved without any communication: processes stay in each view for the fixed, overlap-required time. However, this simple method cannot be used in a partially synchronous setting as it is neither guaranteed that all processes start at the same time nor that their local clocks do not drift (before $GST$). Still, the observation that, if the system is completely synchronous, processes are not required to communicate in order to synchronize plays a crucial role in developing our view synchronizer which achieves $O(n^2)$ communication complexity in partially synchronous environments.

1.3 RareSync

The main technical contribution of this work is RareSync, a partially synchronous view synchronizer that achieves synchronization within $O(f \cdot \delta )$ time after $GST$, and has $O(n^2)$ worst-case communication complexity. In a nutshell, RareSync adapts the “no-communication” technique of synchronous view synchronizers to partially synchronous environments.

Namely, RareSync groups views into epochs; each epoch contains $f + 1$ sequential views. Instead of performing “all-to-all” communication in each view (like the “traditional” view synchronizers [14]), RareSync performs a single “all-to-all” communication step per epoch. Specifically, only at the end of each epoch do all correct processes communicate to enable further progress. Once a process has entered an epoch, the process relies solely on its local clock (without any communication) to move forward to the next view within the epoch.

Let us give a (rough) explanation of how RareSync ensures synchronization. Let E be the smallest epoch entered by all correct processes at or after $GST$; let the first correct process enter E at time $t_E \ge GST$. Due to (1) the “all-to-all” communication step performed at the end of the previous epoch $E - 1$, and (2) the fact that message delays are bounded by a known constant $\delta$ after $GST$, all correct processes enter E by time $t_E + \delta$. Hence, from the epoch E onward, processes do not need to communicate in order to synchronize: it is sufficient for processes to stay in each view for $\delta + \Delta$ time to achieve $\Delta$-time overlap. In brief, RareSync uses communication to synchronize processes, while relying on local timeouts (and not communication!) to keep them synchronized.

1.4 SQuad

The second contribution of our work is SQuad, an optimally-resilient partially synchronous Byzantine consensus protocol with (1) $O(n^2)$ worst-case communication complexity, and (2) $O(f \cdot \delta )$ worst-case latency complexity. The view core module of SQuad is the same as that of HotStuff; as its view synchronizer, SQuad uses RareSync. The combination of HotStuff’s view core and RareSync ensures that $C = O(n)$ and $S = O(n^2)$. By the aforementioned complexity formula, SQuad achieves $n \cdot O(n) + O(n^2) = O(n^2)$ communication complexity. SQuad ’s linear latency is a direct consequence of RareSync ’s ability to synchronize processes within $O(f \cdot \delta )$ time after $GST$.

1.5 Roadmap

We discuss related work in Sect. 2. In Sect. 3, we define the system model. We introduce RareSync in Sect. 4. In Sect. 5, we present SQuad. We conclude the paper in Sect. 6. Detailed proofs of the most basic properties of RareSync are delegated to Appendix B.

2 Related work

In this section, we discuss existing results in two related contexts: synchronous networks and randomized algorithms. In addition, we discuss some precursor (and concurrent) results to our own.

2.1 Synchronous networks

The first natural question is whether we can achieve synchronous Byzantine agreement with optimal latency and optimal communication complexity. Momose and Ren answer that question in the affirmative, giving a synchronous Byzantine agreement protocol with optimal n/2 resiliency, optimal $O(n^2)$ worst-case communication complexity and optimal O(f) worst-case latency [8]. Optimality follows from two lower bounds: Dolev and Reischuk show that any Byzantine consensus protocol has an execution with quadratic communication complexity [6]; Dolev and Strong show that any synchronous Byzantine consensus protocol has an execution with $f+1$ rounds [17]. Various other works have tackled the problem of minimizing the latency of Byzantine consensus [18,19,20].

2.2 Randomization

A classical approach to circumvent the FLP impossibility [10] is using randomization [21], where termination is not ensured deterministically. Exciting recent results by Abraham et al. [22] and Lu et al. [23] give fully asynchronous randomized Byzantine consensus with optimal n/3 resiliency, optimal $O(n^2)$ expected communication complexity and optimal O(1) expected latency complexity. Spiegelman [11] took a neat hybrid approach that achieved optimal results for both synchrony and randomized asynchrony simultaneously: if the network is synchronous, his algorithm yields optimal (deterministic) synchronous complexity; if the network is asynchronous, it falls back on a randomized algorithm and achieves optimal expected complexity.

Recently, it has been shown that even randomized Byzantine agreement requires $\Omega (n^2)$ expected communication complexity, at least for achieving guaranteed safety against an adaptive adversary in an asynchronous setting or against a strongly rushing adaptive adversary in a synchronous setting [22, 24]. (See the papers for details). Amazingly, it is possible to break the $O(n^2)$ barrier by accepting a non-zero (but o(1)) probability of disagreement [25,26,27].

2.3 Authentication

Most of the results above are authenticated: they assume a trusted setup phase⁴ wherein devices establish and exchange cryptographic keys; this allows for messages to be signed in a way that proves who sent them. Recently, many of the communication-efficient agreement protocols (such as [22, 23]) rely on threshold signatures (such as [28]). The Dolev-Reischuk [6] lower bound shows that quadratic communication is needed even in such a case (as it looks at the message complexity of authenticated agreement).

Among deterministic, non-authenticated Byzantine agreement protocols, DBFT [2] achieves $O(n^3)$ communication complexity. For randomized non-authenticated Byzantine agreement protocols, Abraham et al. [29] generalize and refine the findings of Mostefaoui et al. [30] to achieve $O(n^2)$ communication complexity; however they assume a weak common coin, for which an implementation with $O(n^2)$ communication complexity may also require signatures (as far as we are aware, known implementations without signatures, such as [31, 32], have higher than $O(n^2)$ communication complexity).

We note that it is possible to (1) work towards an authenticated setting from a non-authenticated one by rolling out a public key infrastructure (PKI) [33,34,35], (2) setting up a threshold scheme [36] without a trusted dealer, and (3) asynchronously emulating a perfect common coin [37] used by randomized Byzantine consensus protocols [22, 23, 30, 38], or implementing it without signatures [32, 32].

2.4 Other related work

In this paper, we focus on the partially synchronous setting [9], where the question of optimal communication complexity of Byzantine agreement has remained open. The question can be addressed precisely with the help of rigorous frameworks [39,40,41] that were developed to express partially synchronous protocols using a round-based paradigm. More specifically, state-of-the-art partially synchronous BFT protocols  [13, 14, 16, 42] have been developed within a view-based paradigm with a rotating leader, e.g., the seminal PBFT protocol [15]. While many approaches improve the complexity for some optimistic scenarios [43,44,45,46,47], none of them were able to reach the quadratic worst-case Dolev-Reischuk bound.

The problem of view synchronization was defined in [48]. An existing implementation of this abstraction [42] was based on Bracha’s double-echo reliable broadcast at each view, inducing a cubic communication complexity in total. This communication complexity has been reduced for some optimistic scenarios [48] and in terms of expected complexity [49]. The problem has been formalized more precisely in [50] to facilitate formal verification of PBFT-like protocols.

It might be worthwhile highlighting some connections between the view synchronization abstraction and the leader election abstraction $\Omega$ [51, 52], capturing the weakest failure detection information needed to solve consensus (and extended to the Byzantine context in [53]). Leaderless partially synchronous Byzantine consensus protocols have also been proposed [54], somehow indicating that the notion of a leader is not necessary in the mechanisms of a consensus protocol, even if $\Omega$ is the weakest failure detector needed to solve the problem. Clock synchronization [55, 56] and view synchronization are orthogonal problems.

2.5 Concurrent research

We have recently discovered concurrent and independent research by Lewis-Pye [57]. Lewis-Pye appears to have discovered a similar approach to the one that we present in this paper, giving an algorithm for state machine replication in a partially synchronous model with quadratic message complexity. As in this paper, Lewis-Pye makes the key observation that we do not need to synchronize in every view; views can be grouped together, with synchronization occurring only once every fixed number of views. This yields essentially the same algorithmic approach. Lewis-Pye focuses on state machine replication, instead of Byzantine agreement (though state machine replication is implemented via repeated Byzantine agreement). The other useful property of his algorithm is optimistic responsiveness, which applies to the multi-shot case and ensures that, in good portions of the executions, decisions happen as quickly as possible. We encourage the reader to look at [57] for a different presentation of a similar approach.

Moreover, the similar approach to ours and Lewis-Pye’s has been proposed in the first version of HotStuff [58]: processes synchronize once per level, where each level consists of n views. The authors mention that this approach guarantees the quadratic communication complexity; however, this claim was not formally proven in their work. The claim was dropped in later versions of HotStuff (including the published version). We hope readers of our paper will find an increased appreciation of the ideas introduced by HotStuff.

3 System model

3.1 Processes

We consider a static set $\{P_1, P_2,\ldots , P_n\}$ of $n = 3f + 1$ processes out of which at most f can be Byzantine, i.e., can behave arbitrarily. If a process is Byzantine, the process is faulty; otherwise, the process is correct. Processes communicate by exchanging messages over an authenticated point-to-point network. The communication network is reliable: if a correct process sends a message to a correct process, the message is eventually received. We assume that processes have local hardware clocks. Furthermore, we assume that local steps of processes take zero time, as the time needed for local computation is negligible compared to message delays. Finally, we assume that no process can take infinitely many steps in finite time.

3.2 Partial synchrony

We consider the partially synchronous model introduced in [9]. For every execution, there exists a Global Stabilization Time ($GST$) and a positive duration $\delta$ such that message delays are bounded by $\delta$ after $GST$. Furthermore, $GST$ is not known to processes, whereas $\delta$ is known to processes. We assume that all correct processes start executing their protocol by $GST$. The hardware clocks of processes may drift arbitrarily before $GST$, but do not drift thereafter.

3.3 Cryptographic primitives

We assume a (k, n)-threshold signature scheme [28], where $k = 2f + 1 = n - f$. In this scheme, each process holds a distinct private key and there is a single public key. Each process $P_i$ can use its private key to produce an unforgeable partial signature of a message m by invoking $ShareSign _i(m)$. A partial signature $tsignature$ of a message m produced by a process $P_i$ can be verified by $ShareVerify _i(m, tsignature )$. Finally, set $S = \{ tsignature _i\}$ of partial signatures, where $|S| = k$ and, for each $tsignature _i \in S$, $tsignature _i = ShareSign _i(m)$, can be combined into a single (threshold) signature by invoking $Combine (S)$; a combined signature $tcombined$ of message m can be verified by $CombinedVerify (m, tcombined )$. Where appropriate, invocations of $ShareVerify (\cdot )$ and $CombinedVerify (\cdot )$ are implicit in our descriptions of protocols. $\mathsf {P\_Signature}$ and $\mathsf {T\_Signature}$ denote a partial signature and a (combined) threshold signature, respectively. A formal treatment of the aforementioned threshold signature scheme is relegated to Appendix A.

3.4 Complexity of Byzantine consensus

Let $\textsf{Consensus}$ be a partially synchronous Byzantine consensus protocol and let ${\mathcal {E}}(\textsf{Consensus})$ denote the set of all possible executions. Let $\alpha \in {\mathcal {E}}(\textsf{Consensus})$ be an execution and $t_d(\alpha )$ be the first time by which all correct processes have decided in $\alpha$.

A word contains a constant number of signatures and values. Each message contains at least a single word. We define the communication complexity of $\alpha$ as the number of words sent in messages by all correct processes during the time period $[ GST , t_d(\alpha )]$; if $GST > t_d(\alpha )$, the communication complexity of $\alpha$ is 0. The latency complexity of $\alpha$ is $\max (0, t_d(\alpha ) - GST )$.

The communication complexity of $\textsf{Consensus}$ is defined as

$$\begin{aligned} \max _{\alpha \in {\mathcal {E}}(\textsf{Consensus})}\bigg \{\text {communication complexity of } \alpha \bigg \}. \end{aligned}$$

Similarly, the latency complexity of $\textsf{Consensus}$ is defined as

$$\begin{aligned} \max _{\alpha \in {\mathcal {E}}(\textsf{Consensus})}\bigg \{\text {latency complexity of } \alpha \bigg \}. \end{aligned}$$

We underline that the number of words sent by correct processes before $GST$ is unbounded in any partially synchronous Byzantine consensus protocol [11]. Moreover, not a single correct process is guaranteed to decide before $GST$ in any partially synchronous Byzantine consensus protocol [10]; that is why the latency complexity of such protocols is measured from $GST$.

Note on communication complexity. The communication complexity metric as defined above is sometimes referred to as word complexity [59, 60]. Another traditional communication complexity metric is bit complexity [7, 61], which counts bits (and not words) sent by correct processes. Note that the Dolev-Reischuk lower bound on exchanged messages implies $\Omega (n^2)$ (with $f \in \Omega (n)$) lower bound on both word (a message contains at least one word) and bit complexity (a message contains at least one bit). We underline that Quad is not optimal with respect to the bit complexity as it achieves $O(n^2L + n^2\kappa )$ bit complexity, where L is the size of the values and $\kappa$ is the security parameter (e.g., size of a signature).

4 RareSync

This section presents RareSync, a partially synchronous view synchronizer that achieves synchronization within $O(f \cdot \delta )$ time after $GST$, and has $O(n^2)$ worst-case communication complexity. First, we define the problem of view synchronization (Sect. 4.1). Then, we describe RareSync, and present its pseudocode (Sect. 4.2). Finally, we reason about RareSync ’s correctness and complexity (Sect. 4.3) before presenting a formal proof (Sect. 4.4).

4.1 Problem definition

View synchronization is defined as the problem of bringing all correct processes to the same view with a correct leader for sufficiently long [48,49,50]. More precisely, let $\textsf{View} = \{1, 2,\ldots \}$ denote the set of views. For each view $v \in \textsf{View}$, we define $\textsf{leader}(v)$ to be a process that is the leader of view v. The view synchronization problem is associated with a predefined time $\Delta > 0$, which denotes the desired duration during which processes must be in the same view with a correct leader in order to synchronize. View synchronization provides the following interface:

• Indication $\textsf{advance}(\textsf{View} \text { } v)$: The process advances to a view v.

We say that a correct process enters a view v at time t if and only if the $\textsf{advance}(v)$ indication occurs at time t. Moreover, a correct process is in view v between the time t (including t) at which the $\textsf{advance}(v)$ indication occurs and the time $t'$ (excluding $t'$) at which the next $\textsf{advance}(v' \ne v)$ indication occurs. If an $\textsf{advance}(v' \ne v)$ indication never occurs, the process remains in the view v from time t onward.

Next, we define a synchronization time as a time at which all correct processes are in the same view with a correct leader for (at least) $\Delta$ time.

Definition 1

(Synchronization time) Time $t_s$ is a synchronization time if (1) all correct processes are in the same view v from time $t_s$ to (at least) time $t_s + \Delta$, and (2) $\textsf{leader}(v)$ is correct.

View synchronization ensures the eventual synchronization property which states that there exists a synchronization time at or after $GST$.

4.1.1 Complexity of view synchronization

Let $\textsf{Synchronizer}$ be a partially synchronous view synchronizer and let ${\mathcal {E}}(\textsf{Synchronizer})$ denote the set of all possible executions. Let $\alpha \in {\mathcal {E}}(\textsf{Synchronizer})$ be an execution and $t_s(\alpha )$ be the first synchronization time at or after $GST$ in $\alpha$ ($t_s(\alpha ) \ge GST$). We define the communication complexity of $\alpha$ as the number of words sent in messages by all correct processes during the time period $[ GST , t_s(\alpha ) + \Delta ]$. The latency complexity of $\alpha$ is $t_s(\alpha ) + \Delta - GST$.

The communication complexity of $\textsf{Synchronizer}$ is defined as

$$\begin{aligned} \max _{\alpha \in {\mathcal {E}}(\textsf{Synchronizer})}\bigg \{\text {communication complexity of } \alpha \bigg \}. \end{aligned}$$

Similarly, the latency complexity of $\textsf{Synchronizer}$ is defined as

$$\begin{aligned} \max _{\alpha \in {\mathcal {E}}(\textsf{Synchronizer})}\bigg \{\text {latency complexity of } \alpha \bigg \}. \end{aligned}$$

4.2 Protocol

This subsection details RareSync (Algorithm 2). In essence, RareSync achieves $O(n^2)$ communication complexity and $O(f \cdot \delta )$ latency complexity by exploiting “all-to-all” communication only once per $f + 1$ views instead of once per view.

4.2.1 Intuition

We group views into epochs, where each epoch contains $f + 1$ sequential views; $\textsf{Epoch} = \{1, 2,\ldots \}$ denotes the set of epochs. Processes move through an epoch solely by means of local timeouts (without any communication). However, at the end of each epoch, processes engage in an “all-to-all” communication step to obtain permission to move onto the next epoch: (1) Once a correct process has completed an epoch, it broadcasts a message informing other processes of its completion; (2) Upon receiving $2f + 1$ of such messages, a correct process enters the future epoch. Note that (2) applies to all processes, including those in arbitrarily “old” epochs. Overall, this “all-to-all” communication step is the only communication processes perform within a single epoch, implying that per-process communication complexity in each epoch is O(n). Figure 2 illustrates the main idea behind RareSync.

Fig. 2

Intuition behind RareSync: Processes communicate only in the last view of an epoch; before the last view, they rely solely on local timeouts

Roughly speaking, after $GST$, all correct processes simultaneously enter the same epoch within $O(f \cdot \delta )$ time. After entering the same epoch, processes are guaranteed to synchronize in that epoch, which takes (at most) an additional $O(f \cdot \delta )$ time. Thus, the latency complexity of RareSync is $O(f \cdot \delta )$. The communication complexity of RareSync is $O(n^2)$ as every correct process executes at most a constant number of epochs, each with O(n) per-process communication, after $GST$.

4.2.2 Protocol description

We now explain how RareSync works. The pseudocode of RareSync is given in Algorithm 2, whereas all variables, constants, and functions are presented in Algorithm 1.

Algorithm 1

RareSync: Variables (for process $P_i$), constants, and functions

Algorithm 2

RareSync: Pseudocode (for process $P_i$)

We explain RareSync ’s pseudocode (Algorithm 2) from the perspective of a correct process $P_i$. Process $P_i$ utilizes two timers: $view\_timer _i$ and $dissemination\_timer _i$. A timer has two methods:

• 1. $\textsf{measure}(\textsf{Time} \text { } x)$: After exactly x time as measured by the local clock, an expiration event is received by the host. Note that, as local clocks can drift before $GST$, x time as measured by the local clock may not amount to x real time (before $GST$).

• 2. $\mathsf {cancel()}$: This method cancels all previously invoked $\textsf{measure}(\cdot )$ methods on that timer, i.e., all pending expiration events (pertaining to that timer) are removed from the event queue.

In RareSync, $\textsf{leader}(\cdot )$ is a round-robin function (line 10 of Algorithm 1).

Once $P_i$ starts executing $\textsc {RareSync}$ (line 1), it instructs $view\_timer _i$ to measure the duration of the first view (line 2) and it enters the first view (line 3).

Once $view\_timer _i$ expires (line 4), $P_i$ checks whether the current view is the last view of the current epoch, $epoch _i$ (line 5). If that is not the case, the process advances to the next view of $epoch _i$ (line 9). Otherwise, the process broadcasts an $\textsc {epoch-completed}$ message (line 12) signaling that it has completed $epoch _i$. At this point in time, the process does not enter any view.

If, at any point in time, $P_i$ receives either (1) $2f + 1$ $\textsc {epoch-completed}$ messages for some epoch $e \ge epoch _i$ (line 13), or (2) an enter-epoch message for some epoch $e' > epoch _i$ (line 19), the process obtains a proof that a new epoch $E > epoch _i$ can be entered. However, before entering E and propagating the information that E can be entered, $P_i$ waits $\delta$ time (either line 18 or line 24). This $\delta$-waiting step is introduced to limit the number of epochs $P_i$ can enter within any $\delta$ time period after $GST$ and is crucial for keeping the communication complexity of RareSync quadratic. For example, suppose that processes are allowed to enter epochs and propagate enter-epoch messages without waiting. Due to an accumulation (from before $GST$) of enter-epoch messages for different epochs, a process might end up disseminating an arbitrary number of these messages by receiving them all at (roughly) the same time. To curb this behavior, given that message delays are bounded by $\delta$ after $GST$, we force a process to wait $\delta$ time, during which it receives all accumulated messages, before entering the largest known epoch.

Finally, after $\delta$ time has elapsed (line 25), $P_i$ disseminates the information that the epoch E can be entered (line 26) and it enters the first view of E (line 30).

4.3 Proof overview

This subsection presents an overview of the proof of the correctness, latency complexity, and communication complexity of RareSync.

In order to prove the correctness of RareSync, we must show that the eventual synchronization property is ensured, i.e., there is a synchronization time $t_s \ge GST$. For the latency complexity, it suffices to bound $t_s + \Delta - GST$ by $O(f \cdot \delta )$. This is done by proving that synchronization happens within (at most) 2 epochs after $GST$. As for the communication complexity, we prove that any correct process enters a constant number of epochs during the time period $[ GST , t_s + \Delta ]$. Since every correct process sends O(n) words per epoch, the communication complexity of RareSync is $O(1) \cdot O(n) \cdot n = O(n^2)$. We work towards these conclusions by introducing some key concepts and presenting a series of intermediate results.

A correct process enters an epoch e at time t if and only if the process enters the first view of e at time t (either line 3 or line 30). We denote by $t_e$ the first time a correct process enters epoch e.

Result 1: If a correct process enters an epoch $e > 1$, then (at least) $f + 1$ correct processes have previously entered epoch $e - 1$.

The goal of the communication step at the end of each epoch is to prevent correct processes from arbitrarily entering future epochs. In order for a new epoch $e > 1$ to be entered, at least $f + 1$ correct processes must have entered and “gone through” each view of the previous epoch, $e - 1$. This is indeed the case: in order for a correct process to enter e, the process must either (1) collect $2f + 1$ $\textsc {epoch-completed}$ messages for $e - 1$ (line 13), or (2) receive an enter-epoch message for e, which contains a threshold signature of $e - 1$ (line 19). In either case, at least $f + 1$ correct processes must have broadcast $\textsc {epoch-completed}$ messages for epoch $e - 1$ (line 12), which requires them to go through epoch $e - 1$. Furthermore, $t_{e - 1} \le t_{e}$; recall that local clocks can drift before $GST$.

Result 2: Every epoch is eventually entered by a correct process.

By contradiction, consider the greatest epoch ever entered by a correct process, $e^*$. In brief, every correct process will eventually (1) receive the enter-epoch message for $e^*$ (line 19), (2) enter $e^*$ after its $dissemination\_timer$ expires (lines 25 and 30), (3) send an $\textsc {epoch-completed}$ message for $e^*$ (line 12), (4) collect $2f+1$ $\textsc {epoch-completed}$ messages for $e^*$ (line 13), and, finally, (5) enter $e^* + 1$ (lines 15, 18, 25 and 30), resulting in a contradiction. Note that, if $e^* = 1$, no enter-epoch message is sent: all correct processes enter $e^* = 1$ once they start executing RareSync (line 3).

We now define two epochs: $e_{ max }$ and $e_{ final } = e_{ max } + 1$. These two epochs are the main protagonists in the proof of correctness and complexity of RareSync.

Definition of $\varvec{e_{ max }}$: Epoch $e_{ max }$ is the greatest epoch entered by a correct process before $GST$; if no such epoch exists, $e_{ max } = 0$.⁵

Definition of $\varvec{e_{ final }}$: Epoch $e_{ final }$ is the smallest epoch first entered by a correct process at or after $GST$. Note that $GST \le t_{e_{ final }}$. Moreover, $e_{ final } = e_{ max } + 1$ (by Result 1).

Result 3: For any epoch $e \ge e_{ final }$, no correct process broadcasts an epoch-completed message for e (line 12) before time $t_e + epoch\_duration$, where $epoch\_duration = (f + 1) \cdot view\_duration$.

This statement is a direct consequence of the fact that, after $GST$, it takes exactly $epoch\_duration$ time for a process to go through $f+1$ views of an epoch; local clocks do not drift after $GST$. Specifically, the earliest a correct process can broadcast an epoch-completed message for e (line 12) is at time $t_e + epoch\_duration$, where $t_e$ denotes the first time a correct process enters epoch e.

Result 4: Every correct process enters epoch $e_{ final }$ by time $t_{e_{ final }} + 2\delta$.

Recall that the first correct process enters $e_{ final }$ at time $t_{e_{ final }}$. If $e_{ final } = 1$, all correct processes enter $e_{ final }$ at $t_{e_{ final }}$. Otherwise, by time $t_{e_{ final }} + \delta$, all correct processes will have received an enter-epoch message for $e_{ final }$ and started the $dissemination\_timer _i$ with $epoch_i = e_{ final }$ (either lines 15, 18 or 21, 24). By results 1 and 3, no correct process sends an epoch-completed message for an epoch $\ge e_{ final }$ (line 12) before time $t_{e_{ final }} + epoch\_duration$, which implies that the $dissemination\_timer$ will not be cancelled. Hence, the $dissemination\_timer$ will expire by time $t_{e_{ final }} + 2\delta$, causing all correct processes to enter $e_{ final }$ by time $t_{e_{ final }} + 2\delta$.

Result 5: In every view of $e_{ final }$, processes overlap for (at least) $\Delta$ time. In other words, there exists a synchronization time $t_s \le t_{e_{ final }} + epoch\_duration - \Delta$.

By Result 3, no future epoch can be entered before time $t_{e_{ final }} + epoch\_duration$. This is precisely enough time for the first correct process (the one to enter $e_{ final }$ at $t_{e_{ final }}$) to go through all $f+1$ views of $e_{ final }$, spending $view\_duration$ time in each view. Since clocks do not drift after $GST$ and processes spend the same amount of time in each view, the maximum delay of $2\delta$ between processes (Result 4) applies to every view in $e_{ final }$. Thus, all correct processes overlap with each other for (at least) $view\_duration - 2\delta = \Delta$ time in every view of $e_{ final }$. As the $\textsf{leader}(\cdot )$ function is round-robin, at least one of the $f+1$ views must have a correct leader. Therefore, synchronization must happen within epoch $e_{ final }$, i.e., there is a synchronization time $t_s$ such that $t_{e_{ final }} + \Delta \le t_s + \Delta \le t_{e_{ final }} + epoch\_duration$.

Result 6: $t_{e_ final } \le GST + epoch\_duration + 4\delta$.

If $e_{ final } = 1$, all correct processes started executing RareSync at time $GST$. Hence, $t_{e_{ final }} = GST$. Therefore, the result trivially holds in this case.

Let $e_{ final } > 1$; recall that $e_{ final } = e_{ max } + 1$. (1) By time $GST + \delta$, every correct process receives an enter-epoch message for $e_{ max }$ (line 19) as the first correct process to enter $e_{ max }$ has broadcast this message before $GST$ (line 26). Hence, (2) by time $GST + 2\delta$, every correct process enters $e_{ max }$.⁶ Then, (3) every correct process broadcasts an epoch-completed message for $e_{ max }$ at time $GST + epoch\_duration + 2\delta$ (line 12), at latest. (4) By time $GST + epoch\_duration + 3\delta$, every correct process receives $2f + 1$ epoch-completed messages for $e_{ max }$ (line 13), and triggers the $\textsf{measure}(\delta )$ method of $dissemination\_timer$ (line 18). Therefore, (5) by time $GST + epoch\_duration + 4\delta$, every correct process enters $e_{ max } + 1 = e_{ final }$. Figure 3 depicts this scenario.

Note that for the previous sequence of events not to unfold would imply an even lower bound on $t_{e_{ final }}$: a correct process would have to receive $2f+1$ epoch-completed messages for $e_{ max }$ or an enter-epoch message for $e_{ max } + 1 = e_{ final }$ before step (4) (i.e., before time $GST + epoch\_duration + 3\delta$), thus showing that $t_{e_{ final }} < GST + epoch\_duration + 4\delta$.

Latency: Latency complexity of RareSync is $O(f \cdot \delta )$.

By Result 5, $t_s \le t_{e_{ final }} + epoch\_duration - \Delta$. By Result 6, $t_{e_{ final }} \le GST + epoch\_duration + 4\delta$. Therefore, $t_s \le GST + epoch\_duration + 4\delta + epoch\_duration - \Delta = GST + 2 epoch\_duration + 4\delta - \Delta$. Hence, $t_s + \Delta - GST \le 2 epoch\_duration + 4\delta = O(f \cdot \delta )$.

Communication: Communication complexity of RareSync is $O(n^2)$.

Roughly speaking, every correct process will have entered $e_{ max }$ (or potentially $e_{ final } = e_{ max } + 1$) by time $GST + 2\delta$ (as seen in the proof of Result 6). From then on, it will enter at most one other epoch ($e_{ final }$) before synchronizing (which is completed by time $t_s + \Delta$). As for the time interval $[ GST , GST +2\delta )$, due to $dissemination\_timer$’s interval of $\delta$, a correct process can enter (at most) two other epochs during this period. Therefore, a correct process can enter (and send messages for) at most O(1) epochs between $GST$ and $t_s + \Delta$. The individual communication cost of a correct process is bounded by O(n) words per epoch: O(n) epoch-completed messages (each with a single word), and O(n) enter-epoch messages (each with a single word, as a threshold signature counts as a single word). Thus, the communication complexity of RareSync is $O(1) \cdot O(n) \cdot n = O(n^2)$.

Fig. 3

Worst-case latency of RareSync: $t_s + \Delta - GST \le 2 epoch\_duration + 4\delta$

4.4 Formal proof

This section formally proves the correctness and establishes the complexity of RareSync (Algorithm 2). We start by defining the concept of a process’ behavior and timer history.

Behaviors & timer histories. A behavior of a process $P_i$ is a sequence of (1) message-sending events performed by $P_i$, (2) message-reception events performed by $P_i$, and (3) internal events performed by $P_i$ (e.g., invocations of the $\textsf{measure}(\cdot )$ and $\mathsf {cancel()}$ methods on the local timers). If an event e belongs to a behavior $\beta _i$, we write $e \in \beta _i$; otherwise, we write $e \notin \beta _i$. If an event $e_1$ precedes an event $e_2$ in a behavior $\beta _i$, we write $e_1 {\mathop {\prec }\limits ^{\beta _i}} e_2$. Note that, if $e_1 {\mathop {\prec }\limits ^{\beta _i}} e_2$ and $e_1$ occurs at some time $t_1$ and $e_2$ occurs at some time $t_2$, $t_1 \le t_2$.

A timer history of a process $P_i$ is a sequence of (1) invocations of the $\textsf{measure}(\cdot )$ and $\textsf{cancel}()$ methods on $view\_timer _i$ and $dissemination\_timer _i$, and (2) processed expiration events of $view\_timer _i$ and $dissemination\_timer _i$. Observe that a timer history of a process is a subsequence of the behavior of the process. We further denote by $h_i \mid _{ view }$ the greatest subsequence of $h_i$ associated with $view\_timer _i$, where $h_i$ is a timer history of a process $P_i$. If an expiration event $Exp$ of a timer is associated with an invocation $Inv$ of the $\mathsf {measure(\cdot )}$ method on the timer, we say that $Inv$ produces $Exp$. Note that a single invocation of the $\textsf{measure}(\cdot )$ method can produce at most one expiration event.

Given an execution, we denote by $\beta _i$ and $h_i$ the behavior and the timer history of the process $P_i$, respectively.

4.4.1 Proof of correctness

In order to prove the correctness of RareSync, we need to prove that RareSync ensures the eventual synchronization property (Sect. 4.1).

We start by establishing some basic properties of Algorithm 2. These are encapsulated by several lemmas (specifically, Lemmas 1–8) which can be verified by simple visual code inspection. As such, we summarize them here but delegate their formal proofs to Appendix B.

First, notice that the value of $view _i$ variable at a correct process $P_i$ is never smaller than 1 or greater than $f + 1$.

Lemma 1

Let $P_i$ be a correct process. Then, $1 \le view _i \le f + 1$ throughout the entire execution.

It is also ensured that, if an invocation of the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ produces an expiration event, the expiration event immediately follows the invocation in the timer history $h_i$ of a correct process $P_i$.

Lemma 2

Let $P_i$ be a correct process. Let $Exp _d$ be any expiration event of $dissemination\_timer _i$ that belongs to $h_i$ and let $Inv _d$ be the invocation of the $\textsf{measure}(\cdot )$ method (on $dissemination\_timer _i$) that has produced $Exp _d$. Then, $Exp _d$ immediately follows $Inv _d$ in $h_i$.

The next lemma shows that views entered by a correct process are monotonically increasing, as intended.

Lemma 3

(Monotonically increasing views) Let $P_i$ be a correct process. Let $e_1 = \textsf{advance}(v)$, $e_2 = \textsf{advance}(v')$ and $e_1 {\mathop {\prec }\limits ^{\beta _i}} e_2$. Then, $v' > v$.

The next lemma shows that an invocation of the $\mathsf {measure(\cdot )}$ method cannot be immediately followed by another invocation of the same method in a timer history (of a correct process) associated with $view\_timer _i$.

Lemma 4

Let $P_i$ be a correct process. Let $Inv _v$ be any invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ that belongs to $h_i$. Invocation $Inv _v$ is not immediately followed by another invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ in $h_i \mid _{ view }$.

As a direct consequence of Lemma 4, an expiration event of $view\_timer _i$ immediately follows (in a timer history associated with $view\_timer _i$) the $\mathsf {measure(\cdot )}$ invocation that has produced it.

Lemma 5

Let $P_i$ be a correct process. Let $Exp _v$ be any expiration event that belongs to $h_i \mid _{ view }$ and let $Inv _v$ be the invocation of the $\mathsf {measure(\cdot )}$ method (on $view\_timer _i$) that has produced $Exp _v$. Then, $Exp _v$ immediately follows $Inv _v$ in $h_i \mid _{ view }$.

Consequently, the statement of Lemma 2 also holds for $view\_timer _i$:

Lemma 6

Let $P_i$ be a correct process. Let $Exp _v$ be any expiration event of $view\_timer _i$ that belongs to $h_i$ and let $Inv _v$ be the invocation of the $\textsf{measure}(\cdot )$ method (on $view\_timer _i$) that has produced $Exp _v$. Then, $Exp _v$ immediately follows $Inv _v$ in $h_i$.

Next, we show that the values of the $epoch _i$ and $view _i$ variables of a correct process $P_i$ do not change between an invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ and the processing of the expiration event the invocation produces.

Lemma 7

Let $P_i$ be a correct process. Let $Inv _v$ denote an invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ which produces an expiration event, and let $Exp _v$ denote the expiration event produced by $Inv _v$. Let $epoch _i = e$ and $view _i = v$ when $P_i$ invokes $Inv _v$. Then, when $P_i$ processes $Exp _v$ (line 4), $epoch _i = e$ and $view _i = v$.

Finally, we show that correct processes cannot “jump” into an epoch, i.e., they must go into an epoch by going into its first view.

Lemma 8

Let $P_i$ be a correct process. Let $\textsf{advance}(v) \in \beta _i$, where v is the j-th view of an epoch e and $j > 1$. Then, $\textsf{advance}(v - 1) {\mathop {\prec }\limits ^{\beta _i}} \textsf{advance}(v)$.

With the previous lemmas in place, the basic intended properties of Algorithm 2 are ensured. We now focus on the overarching properties of RareSync, such as the concept of entering an epoch.

We say that a correct process enters an epoch e at time t if and only if the process enters the first view of e (i.e., the view $(e - 1) \cdot (f + 1) + 1$) at time t. Furthermore, a correct process is in epoch e between the time t (including t) at which it enters e and the time $t'$ (excluding $t'$) at which it enters (for the first time after entering e) another epoch $e'$. If another epoch is never entered, the process is in epoch e from time t onward. Recall that, by Lemma 3, a correct process enters each view at most once, which means that a correct process enters each epoch at most once.

The following lemma shows that, if a correct process broadcasts an epoch-completed message for an epoch (line 12), then the process has previously entered that epoch.

Lemma 9

Let a correct process $P_i$ send an epoch-completed message for an epoch e (line 12); let this sending event be denoted by $e_{ send }$. Then, $\textsf{advance}(v) {\mathop {\prec }\limits ^{\beta _i}} e_{ send }$, where v is the first view of the epoch e.

Proof

At the moment of sending the message (line 12), the following holds: (1) $epoch _i = e$, and (2) $view _i = f + 1$ (by the check at line 5 and Lemma 1). We denote by $Inv _v$ the invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ producing the expiration event $Exp _v$ leading to $P_i$ broadcasting the epoch-completed message for e. Note that $Inv _v$ precedes the sending of the epoch-completed message in $\beta _i$.

When processing $Exp _v$ (line 4), the following was the state of $P_i$: $epoch _i = e$ and $view _i = f + 1$. By Lemma 7, when $P_i$ invokes $Inv _v$, $epoch _i = e$ and $view _i = f + 1 > 1$. Therefore, $Inv _v$ must have been invoked at line 8: $Inv _v$ could not have been invoked either at line 2 or at line 29 since $view _i = f + 1 \ne 1$ at that moment. Immediately after invoking $Inv _v$, $P_i$ enters the $(f + 1)$-st view of e (line 9), which implies that $P_i$ enters the $(f + 1)$-st view of e before it sends the epoch-completed message. Therefore, the lemma follows from Lemma 8. $\square$

The next lemma shows that, if a correct process $P_i$ updates its $epoch _i$ variable to $e > 1$, then (at least) $f + 1$ correct processes have previously entered epoch $e - 1$.

Lemma 10

Let a correct process $P_i$ update its $epoch _i$ variable to $e > 1$ at some time t. Then, at least $f + 1$ correct processes have entered $e - 1$ by time t.

Proof

Since $P_i$ updates $epoch _i$ to $e > 1$ at time t, it does so at either:

• Line 15: In this case, $P_i$ has received $2f + 1$ epoch-completed messages for epoch $e - 1$ (line 13), out of which (at least) $f + 1$ were sent by correct processes.

• Line 21: In this case, $P_i$ has received a threshold signature of epoch $e - 1$ (line 19) built out of $2f + 1$ partial signatures, out of which (at least) $f + 1$ must have come from correct processes. Such a partial signature from a correct process can only be obtained by receiving an epoch-completed message for epoch $e - 1$ from that process.

In both cases, $f + 1$ correct processes have sent epoch-completed messages (line 12) for epoch $e - 1$ by time t. By Lemma 9, all these correct processes have entered epoch $e - 1$ by time t. $\square$

Note that a correct process $P_i$ does not enter an epoch immediately upon updating its $epoch _i$ variable, but only upon triggering the $\mathsf {advance(\cdot )}$ indication for the first view of that epoch (line 3 or line 30). We now prove that, if an epoch $e > 1$ is entered by a correct process at some time t, then epoch $e - 1$ is entered by a (potentially different) correct process by time t.

Lemma 11

Let a correct process $P_i$ enter an epoch $e > 1$ at time t. Then, epoch $e - 1$ was entered by a correct process by time t.

Proof

Since $P_i$ enters $e > 1$ at time t (line 30), $epoch _i = e$ at time t. Hence, $P_i$ has updated its $epoch _i$ variable to $e > 1$ by time t. Therefore, the lemma follows directly from Lemma 10. $\square$

The next lemma shows that all epochs are eventually entered by some correct processes. In other words, correct processes keep transiting to new epochs forever.

Lemma 12

Every epoch is eventually entered by a correct process.

Proof

Epoch 1 is entered by a correct process since every correct process initially triggers the $\mathsf {advance(}1\mathsf {)}$ indication (line 3). Therefore, it is left to prove that all epochs greater than 1 are entered by a correct process. By contradiction, let $e + 1$ be the smallest epoch not entered by a correct process, where $e \ge 1$.

Part 1. No correct process $P_i$ ever sets $epoch _i$ to an epoch greater than e.

Since $e + 1$ is the smallest epoch not entered by a correct process, no correct process ever enters any epoch greater than e (by Lemma 11). Furthermore, Lemma 10 shows that no correct process $P_i$ ever updates its $epoch _i$ variable to an epoch greater than $e + 1$.

Finally, $P_i$ never sets $epoch _i$ to $e + 1$ either. By contradiction, suppose that it does. In this case, $P_i$ invokes the $\mathsf {measure(}\delta \mathsf {)}$ method on $dissemination\_timer _i$ (either line 18 or line 24). Since $P_i$ does not update $epoch _i$ to an epoch greater than $e + 1$ (as shown in the previous paragraph), the previously invoked $\mathsf {measure(}\delta \mathsf {)}$ method will never be canceled (neither at line 17 nor at line 23). This implies that $dissemination\_timer _i$ eventually expires (line 25), and $P_i$ enters epoch $e + 1$ (line 30). Hence, a contradiction with the fact that epoch $e + 1$ is never entered by a correct process.

Part 2. Every correct process eventually enters epoch e.

If $e = 1$, every correct process enters e as every correct process eventually executes line 3.

Let $e > 1$. Since $e > 1$ is entered by a correct process (line 30), the process has disseminated an $\textsc {enter-epoch}$ message for e (line 26). This message is eventually received by every correct process since the network is reliable. If a correct process $P_i$ has not previously set its $epoch _i$ variable to e, it does so upon the reception of the enter-epoch message (line 21). Hence, $P_i$ eventually sets its $epoch _i$ variable to e.

Immediately after updating its $epoch _i$ variable to e (line 15 or line 21), $P_i$ invokes $\textsf{measure}(\delta )$ on $dissemination\_timer _i$ (line 18 or line 24). Because $P_i$ never updates $epoch _i$ to an epoch greater than e (by Part 1), $dissemination\_timer _i$ expires while $epoch _i = e$. When this happens (line 25), $P_i$ enters epoch e (line 30). Thus, all correct processes eventually enter epoch e.

Epilogue. By Part 2, a correct process $P_i$ eventually enters epoch e (line 3 or line 30); when $P_i$ enters e, $epoch _i = e$ and $view _i = 1$. Moreover, just before entering e, $P_i$ invokes the $\textsf{measure}(\cdot )$ method on $view\_timer _i$ (line 2 or line 29); let this invocation be denoted by $Inv _v^1$. As $P_i$ never updates its $epoch _i$ variable to an epoch greater than e (by Part 1), $Inv _v^1$ eventually expires. When $P_i$ processes the expiration of $Inv _v^1$ (line 4), $epoch _i = e$ and $view _i = 1 < f + 1$ (by Lemma 7). Hence, $P_i$ then invokes the $\textsf{measure}(\cdot )$ method on $view\_timer _i$ (line 8); when this occurs, $epoch _i = e$ and $view _i = 2$ (by line 6). Following the same argument as for $Inv _v^1$, $view\_timer _i$ expires for each view of epoch e.

Therefore, every correct process $P_i$ eventually broadcasts an epoch-completed message for epoch e (line 12) when $view\_timer _i$ expires for the last view of epoch e. Thus, a correct process $P_j$ eventually receives $2f + 1$ epoch-completed messages for epoch e (line 13), and updates $epoch _j$ to $e + 1$ (line 15). This contradicts Part 1, which implies that the lemma holds. $\square$

We now introduce $e_{ final }$, the first new epoch entered at or after $GST$.

Definition 2

We denote by $e_{ final }$ the smallest epoch such that the first correct process to enter $e_{ final }$ does so at time $t_{e_ final } \ge GST$.

Note that $e_{ final }$ exists due to Lemma 12; recall that, by $GST$, an execution must be finite as no process is able to perform infinitely many steps in finite time. It is stated in Algorithm 1 that $view\_duration = \Delta + 2\delta$ (line 8). However, technically speaking, $view\_duration$ must be greater than $\Delta + 2\delta$ in order to not waste the “very last” moment of a $\Delta + 2\delta$ time period, i.e., we set $view\_duration = \Delta + 2\delta + \epsilon$, where $\epsilon$ is any positive constant. Therefore, in the rest of the section, we assume that $view\_duration = \Delta + 2\delta + \epsilon > \Delta + 2\delta$.

We now show that, if a correct process enters an epoch e at time $t_e \ge GST$ and sends an epoch-completed message for e, the epoch-completed message is sent at time $t_e + epoch\_duration$, where $epoch\_duration = (f + 1) \cdot view\_duration$.

Lemma 13

Let a correct process $P_i$ enter an epoch e at time $t_e \ge GST$ and let $P_i$ send an epoch-completed message for epoch e (line 12). The epoch-completed message is sent at time $t_e + epoch\_duration$.

Proof

We prove the lemma by backwards induction. Let $t^*$ denote the time at which the epoch-completed message for epoch e is sent (line 12).

Base step: The $(f + 1)$-st view of the epoch e is entered by $P_i$ at time $t^{f + 1}$ such that $t^* - t^{f + 1} = 1 \cdot view\_duration$.

When sending the epoch-completed message (line 12), the following holds: $epoch _i = e$ and $view _i = f + 1$ (due to the check at line 5 and Lemma 1). Let $Exp _v^{f + 1}$ denote the expiration event of $view\_timer _i$ processed just before broadcasting the message (line 4). When processing $Exp _v^{f + 1}$, we have that $epoch _i = e$ and $view _i = f + 1$. When $P_i$ has invoked $Inv _v^{f + 1}$, where $Inv _v^{f + 1}$ is the invocation of the $\textsf{measure}(\cdot )$ method which has produced $Exp _v^{f + 1}$, we have that $epoch _i = e$ and $view _i = f + 1$ (by Lemma 7). As $f + 1 \ne 1$, $Inv _v^{f + 1}$ is invoked at line 8 at some time $t^{f + 1} \le t^*$. Finally, $P_i$ enters the $(f + 1)$-st view of the epoch e at line 9 at time $t^{f + 1}$. By Lemma 8, we have that $t^{f + 1} \ge t_e \ge GST$. As local clocks do not drift after $GST$, we have that $t^* - t^{f + 1} = view\_duration$ (due to line 8), which concludes the base step.

Induction step: Let $j \in [1, f]$. The j-th view of the epoch e is entered by $P_i$ at time $t^j$ such that $t^* - t^j = (f + 2 - j)\cdot view\_duration$.

Induction hypothesis: For every $k \in [j + 1, f + 1]$, the k-th view of the epoch e is entered by $P_i$ at time $t^k$ such that $t^* - t^k = (f + 2 - k) \cdot view\_duration$.

Let us consider the $(j + 1)$-st view of the epoch e; note that $j + 1 \ne 1$. Hence, the $(j + 1)$-st view of the epoch e is entered by $P_i$ at some time $t^{j + 1}$ at line 9, where $t^* - t^{j + 1} = (f + 2 - j - 1) \cdot view\_duration = (f + 1 - j) \cdot view\_duration$ (by the induction hypothesis). Let $Exp _v^{j}$ denote the expiration event of $view\_timer _i$ processed at time $t^{j + 1}$ (line 4). When processing $Exp _v^{j}$, we have that $epoch _i = e$ and $view _i = j$ (due to line 6). When $P_i$ has invoked $Inv _v^{j}$ at some time $t^{j}$, where $Inv _v^{j}$ is the invocation of the $\textsf{measure}(\cdot )$ method which has produced $Exp _v^{j}$, we have that $epoch _i = e$ and $view _i = j$ (by Lemma 7). $Inv _v^{j}$ could have been invoked either at line 2, or at line 8, or at line 29:

• Line 2: In this case, $P_i$ enters the j-th view of the epoch e at time $t^j$ at line 3, where $j = 1$ (by line 3). Moreover, we have that $t^{j} \ge GST$ as $t^j = t_e$ (by definition). As local clocks do not drift after $GST$, we have that $t^{j + 1} - t^j = view\_duration$, which implies that $t^* - t^j = t^* - t^{j + 1} + view\_duration = (f + 1 - j + 1) \cdot view\_duration = (f + 2 - j) \cdot view\_duration$. Hence, in this case, the induction step is concluded.

• Line 8: $P_i$ enters the j-th view of the epoch e at line 9 at time $t^j$, where $j > 1$ (by Lemma 1 and line 6). By Lemmas 3 and 8, we have that $t^j \ge t_e \ge GST$. As local clocks do not drift after $GST$, we have that $t^{j + 1} - t^j = view\_duration$, which implies that $t^* - t^j = (f + 2 - j) \cdot view\_duration$. Hence, the induction step is concluded even in this case.

• Line 29: In this case, $P_i$ enters the j-th view of the epoch e at time $t^j$ at line 30, where $j = 1$ as $view _i = 1$ (by line 27). Moreover, $t^j = t_e \ge GST$ (by definition). As local clocks do not drift after $GST$, we have that $t^{j + 1} - t^j = view\_duration$, which implies that $t^* - t^j = t^* - t^{j + 1} + view\_duration = (f + 1 - j + 1) \cdot view\_duration = (f + 2 - j) \cdot view\_duration$. Hence, even in this case, the induction step is concluded.

As the induction step is concluded in all possible scenarios, the backwards induction holds. Therefore, $P_i$ enters the first view of the epoch e (and, thus, the epoch e) at time $t_e$ (recall that the first view of any epoch is entered at most once by Lemma 3) such that $t^* - t_e = (f + 1) \cdot view\_duration = epoch\_duration$, which concludes the proof. $\square$

The following lemma shows that no correct process broadcasts an epoch -completed message for an epoch $\ge e_{ final }$ before time $t_{e_ final } + epoch\_duration$.

Lemma 14

No correct process broadcasts an epoch-completed message for an epoch $e' \ge e_{ final }$ (line 12) before time $t_{e_ final } + epoch\_duration$.

Proof

Let $t^*$ be the first time a correct process, denoted by $P_i$, sends an epoch-completed message for an epoch $e' \ge e_{ final }$ (line 12); if $t^*$ is not defined, the lemma trivially holds. By Lemma 9, $P_i$ has entered epoch $e'$ at some time $t_{e'} \le t^*$. If $e' = e_{ final }$, then $t_{e'} \ge t_{e_{ final }} \ge GST$. If $e' > e_{ final }$, by Lemma 11, $t_{e'} \ge t_{e_{ final }} \ge GST$. Therefore, $t^* = t_{e'} + epoch\_duration$ (by Lemma 13), which means that $t^* \ge t_{e_{ final }} + epoch\_duration$. $\square$

Next, we show during which periods a correct process is in which view of the epoch $e_{ final }$.

Lemma 15

Consider a correct process $P_i$.

• For any $j \in [1, f]$, $P_i$ enters the j-th view of the epoch $e_{ final }$ at some time $t^j$, where $t^j \in \big [t_{e_{ final }} + (j - 1)\cdot view\_duration , t_{e_{ final }} + (j - 1)\cdot view\_duration + 2\delta \big ]$, and stays in the view until (at least) time $t^j + view\_duration$ (excluding time $t^j + view\_duration$).

• For $j = f + 1$, $P_i$ enters the j-th view of the epoch $e_{ final }$ at some time $t^j$, where $t^j \in \big [t_{e_{ final }} + f\cdot view\_duration , t_{e_{ final }} + f\cdot view\_duration + 2\delta \big ]$, and stays in the view until (at least) time $t_{e_{ final }} + epoch\_duration$ (excluding time $t_{e_{ final }} + epoch\_duration$).

Proof

Note that no correct process broadcasts an epoch-completed message for an epoch $\ge e_{ final }$ (line 12) before time $t_{e_{ final }} + epoch\_duration$ (by Lemma 14). We prove the lemma by induction.

Base step: The statement of the lemma holds for $j = 1$.

If $e_{ final } > 1$, every correct process receives an enter-epoch message (line 19) for epoch $e_{ final }$ by time $t_{e_ final } + \delta$ (since $t_{e_ final } \ge GST$). As no correct process broadcasts an epoch-completed message for an epoch $\ge e_{ final }$ before time $t_{e_ final } + epoch\_duration > t_{e_{ final }} + \delta$, $P_i$ sets its $epoch _i$ variable to $e_{ final }$ (line 21) and invokes the $\textsf{measure}(\delta )$ method on $dissemination\_timer _i$ (line 24) by time $t_{e_{ final }} + \delta$. Because of the same reason, the $dissemination\_timer _i$ expires by time $t_{e_{ final }} + 2\delta$ (line 25); at this point in time, $epoch _i = e_{ final }$. Hence, $P_i$ enters the first view of $e_{ final }$ by time $t_{e_{ final }} + 2\delta$ (line 30). Observe that, if $e_{ final } = 1$, $P_i$ enters $e_{ final }$ at time $t_{e_{ final }}$ (as every correct process starts executing Algorithm 2 at $GST = t_{e_{ final }}$). Thus, $t^1 \in [t_{e_{ final }}, t_{e_{ final }} + 2\delta ]$.

Prior to entering the first view of $e_{ final }$, $P_i$ invokes the $\textsf{measure}( view\_duration )$ method on $view\_timer _i$ (line 2 or line 29); we denote this invocation by $Inv _v$. By Lemma 14, $Inv _v$ cannot be canceled (line 16 or line 22) as $t_{e_{ final }} + epoch\_duration > t_{e_{ final }} + 2\delta + view\_duration$. Therefore, $Inv _v$ produces an expiration event $Exp _v$ which is processed by $P_i$ at time $t^1 + view\_duration$ (since $t^1 \ge GST$ and local clocks do not drift after $GST$).

Let us investigate the first time $P_i$ enters another view after entering the first view of $e_{ final }$. This could happen at the following places of Algorithm 2:

• Line 9: By Lemma 6, we conclude that this occurs at time $t^* \ge t^1 + view\_duration$. Therefore, in this case, $P_i$ is in the first view of $e_{ final }$ during the time period $[t^1, t^1 + view\_duration )$. The base step is proven in this case.

• Line 30: By contradiction, suppose that this happens before time $t^1 + view\_duration$. Hence, the $\textsf{measure}(\cdot )$ method was invoked on $dissemination\_timer _i$ (line 18 or line 24) before time $t^1 + view\_ duration$ and after the invocation of $Inv _v$ (by Lemma 2). Thus, $Inv _v$ is canceled (line 16 or line 22), which is impossible (as previously proven). Hence, $P_i$ is in the first view of $e_{ final }$ during (at least) the time period $[t^1, t^1 + view\_duration )$, which implies that the base step is proven even in this case.

Induction step: The statement of the lemma holds for j, where $1 < j \le f + 1$.

Induction hypothesis: The statement of the lemma holds for every $k \in [1, j - 1]$.

Consider the $(j - 1)$-st view of $e_{ final }$ denoted by $v_{j - 1}$. Recall that $t^{j - 1}$ denotes the time at which $P_i$ enters $v_{j - 1}$. Just prior to entering $v_{j - 1}$ (line 3 or line 9 or line 30), $P_i$ has invoked the $\textsf{measure}( view\_duration )$ method on $view\_timer _i$ (line 2 or line 8 or line 29); let this invocation be denoted by $Inv _v$. When $P_i$ invokes $Inv _v$, we have that $epoch _i = e_{ final }$ and $view _i = j - 1$. As in the base step, Lemma 14 shows that $Inv _v$ cannot be canceled (line 16 or line 22) as $t_{e_{ final }} + epoch\_duration > t^{j - 1} + view\_duration$ since $t^{j - 1} \le t_{e_{ final }} + (j - 2)\cdot view\_duration + 2\delta$ (by the induction hypothesis). We denote by $Exp _v$ the expiration event produced by $Inv _v$. By Lemma 7, when $P_i$ processes $Exp _v$ (line 4), we have that $epoch _i = e_{ final }$ and $view _i = j - 1 < f + 1$. Hence, $P_i$ enters the j-th view of $e_{ final }$ at time $t^j = t^{j - 1} + view\_duration$ (line 9), which means that $t^j \in \big [ t_{e_{ final }} + (j - 1) \cdot view\_duration , t_{e_{ final }} + (j - 1) \cdot view\_duration + 2\delta \big ]$.

We now separate two cases:

• Let $j < f + 1$. Just prior to entering the j-th view of $e_{ final }$ (line 9), $P_i$ invokes the $\textsf{measure}( view\_duration )$ method on $view\_timer _i$ (line 8); we denote this invocation by $Inv '_v$. By Lemma 14, $Inv '_v$ cannot be canceled (line 16 or line 22) as $t_{e_{ final }} + epoch\_duration > t_{e_{ final }} + (j - 1) \cdot view\_duration + 2\delta + view\_duration$. Therefore, $Inv '_v$ produces an expiration event $Exp '_v$ which is processed by $P_i$ at time $t^j + view\_duration$ (since $t^j \ge GST$ and local clocks do not drift after $GST$). Let us investigate the first time $P_i$ enters another view after entering the j-th view of $e_{ final }$. This could happen at the following places of Algorithm 2:

  • Line 9: By Lemma 6, we conclude that this occurs at time $\ge t^j + view\_duration$. Therefore, in this case, $P_i$ is in the j-th view of $e_{ final }$ during the time period $[t^j, t^j + view\_duration )$. The induction step is proven in this case.

  • Line 30: By contradiction, suppose that this happens before time $t^j + view\_duration$. Hence, the $\textsf{measure}(\cdot )$ method was invoked on $dissemination\_ timer _i$ (line 18 or line 24) before time $t^j + view\_duration$ and after the invocation of $Inv '_v$ (by Lemma 2). Thus, $Inv '_v$ is canceled (line 16 or line 22), which is impossible (as previously proven). Hence, $P_i$ is in the j-th view of $e_{ final }$ during (at least) the time period $[t^j, t^j + view\_duration )$, which concludes the induction step even in this case.

• Let $j = f + 1$. Just prior to entering the j-th view of $e_{ final }$ (line 9), $P_i$ invokes the $\textsf{measure}( view\_duration )$ method on $view\_timer _i$ (line 8); we denote this invocation by $Inv '_v$. When $Inv _v'$ was invoked, $epoch _i = e_{ final }$ and $view _i = f + 1$. By Lemma 14, we know that the earliest time $Inv _v'$ can be canceled (line 16 or line 22) is $t_{e_{ final }} + epoch\_duration$. Let us investigate the first time $P_i$ enters another view after entering the j-th view of $e_{ final }$. This could happen at the following places of Algorithm 2:

  • Line 9: This means that, when processing the expiration event of $view\_timer _i$ (denoted by $Exp _v^*$) at line 4 (before executing the check at line 5), $view _i < f + 1$. Hence, $Exp _v^*$ is not produced by $Inv _v'$ (by Lemma 7). By contradiction, suppose that $Exp _v^*$ is processed before time $t_{e_{ final }} + epoch\_duration$. In this case, $Exp _v^*$ is processed before the expiration event produced by $Inv _v'$ would (potentially) be processed (which is $t_{e_{ final }} + epoch\_duration$ at the earliest). Thus, $Inv _v'$ must be immediately followed by an invocation of the $\mathsf {cancel()}$ method on $view\_timer _i$ in $h_i \mid _{ view }$ (by Lemmas 4 and 5). As previously shown, the earliest time $Inv '_v$ can be canceled is $t_{e_ final } + epoch\_duration$, which implies that $Exp _v^*$ cannot be processed before time $t_{e_{ final }} + epoch\_duration$. Therefore, $Exp _v^*$ is processed at $t_{e_{ final }} + epoch\_duration$ (at the earliest), which concludes the induction step for this case.

  • Line 30: Suppose that, by contradiction, this happens before time $t_{e_{ final }} + epoch\_duration$. Hence, the $\textsf{measure}(\cdot )$ method was invoked on $dissemination\_ timer _i$ (line 18 or line 24) before time $t_{e_{ final }} + epoch\_duration$ (by Lemma 2) and after $P_i$ has entered the j-th view of $e_{ final }$, which implies that $Inv _v'$ is canceled before time $t_{e_{ final }} + epoch\_duration$ (line 16 or line 22). However, this is impossible as the earliest time for $Inv '_v$ to be canceled is $t_{e_{ final }} + epoch\_duration$. Hence, $P_i$ enters another view at time $t_{e_{ final }} + epoch\_duration$ (at the earliest), which concludes the induction step in this case.

The conclusion of the induction step concludes the proof of the lemma. $\square$

Finally, we prove that RareSync ensures the eventual synchronization property.

Theorem 1

(Eventual synchronization) RareSync ensures eventual synchronization. Moreover, the first synchronization time at or after $GST$ occurs by time $t_{e_ final } + f\cdot view\_duration + 2\delta$.

Proof

Lemma 15 proves that all correct processes overlap in each view of $e_{ final }$ for (at least) $\Delta$ time. As the leader of one view of $e_{ final }$ must be correct (since $\textsf{leader}(\cdot )$ is a round-robin function), the eventual synchronization is satisfied by RareSync: correct processes synchronize in (at least) one of the views of $e_{ final }$. Finally, as the last view of $e_{ final }$ is entered by every correct process by time $t^* = t_{e_{ final }} + f \cdot view\_duration + 2\delta$ (by Lemma 15), the first synchronization time at or after $GST$ must occur by time $t^*$. $\square$

4.4.2 Proof of complexity

We start by showing that, if a correct process sends an epoch-completed message for an epoch e, then the “most recent” epoch entered by the process is e.

Lemma 16

Let $P_i$ be a correct process and let $P_i$ send an epoch-completed message for an epoch e (line 12). Then, e is the last epoch entered by $P_i$ in $\beta _i$ before sending the epoch-completed message.

Proof

By Lemma 9, $P_i$ enters e before sending the epoch-completed message for e. By contradiction, suppose that $P_i$ enters some other epoch $e^*$ after entering e and before sending the epoch-completed message for e. By Lemma 3, $e^* > e$.

When $P_i$ enters $e^*$ (line 30), $epoch _i = e^*$. As the value of the $epoch _i$ variable only increases throughout the execution, $P_i$ does not send the epoch-completed message for e after entering $e^* > e$. Thus, we reach a contradiction, and the lemma holds. $\square$

Next, we show that, if a correct process sends an enter-epoch message for an epoch e at time t, the process enters e at time t.

Lemma 17

Let a correct process $P_i$ send an enter-epoch message (line 26) for an epoch e at time t. Then, $P_i$ enters e at time t.

Proof

When $P_i$ sends the enter-epoch message, we have that $epoch _i = e$. Hence, $P_i$ enters e at time t (line 30). $\square$

Next, we show that a correct process sends (at most) O(n) epoch-completed messages for a specific epoch e.

Lemma 18

For any epoch e and any correct process $P_i$, $P_i$ sends at most O(n) epoch-completed messages for e (line 12).

Proof

Let $Exp _v$ denote the first expiration event of $view\_timer _i$ which $P_i$ processes (line 4) in order to broadcast the epoch-completed message for e (line 12); if $Exp _v$ does not exist, the lemma trivially holds. Hence, let $Exp _v$ exist.

When $Exp _v$ was processed, $epoch _i = e$. Let $Inv '_v$ denote the first invocation of the $\textsf{measure}(\cdot )$ method on $view\_timer _i$ after the processing of $Exp _v$. If $Inv '_v$ does not exist, there does not exist an expiration event of $view\_timer _i$ processed after $Exp _v$ (by Lemma 6), which implies that the lemma trivially holds.

Let us investigate where $Inv '_v$ could have been invoked:

• Line 8: By Lemma 6, we conclude that the processing of $Exp _v$ leads to $Inv '_v$. However, this is impossible as the processing of $Exp _v$ leads to the broadcasting of the epoch-completed messages (see the check at line 5).

• Line 29: In this case, $P_i$ processes an expiration event $Exp _d$ of $dissemination\_timer _i$ (line 25). By Lemma 2, the invocation $Inv _d$ of the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ immediately precedes $Exp _d$ in $h_i$. Hence, $Inv _d$ follows $Exp _v$ in $h_i$ and $Inv _d$ could have been invoked either at line 18 or at line 24. Just before invoking $Inv _d$, $P_i$ changes its $epoch _i$ variable to a value greater than e (line 15 or line 21; the value of $epoch _i$ only increases throughout the execution).

Therefore, when $Inv '_v$ is invoked, $epoch _i > e$. As the value of the $epoch _i$ variable only increases throughout the execution, $P_i$ broadcasts the epoch-completed messages for e at most once (by Lemma 6), which concludes the proof. $\square$

The following lemma shows that a correct process sends (at most) O(n) enter-epoch messages for a specific epoch e.

Lemma 19

For any epoch e and any correct process $P_i$, $P_i$ sends at most O(n) enter-epoch messages for e (line 26).

Proof

Let $Exp _d$ denote the first expiration event of $dissemination\_timer _i$ which $P_i$ processes (line 25) in order to broadcast the enter-epoch message for e (line 26); if $Exp _d$ does not exist, the lemma trivially holds. When $Exp _d$ was processed, $epoch _i = e$. Let $Inv '_d$ denote the first invocation of the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ after the processing of $Exp _d$. If $Inv '_d$ does not exist, there does not exist an expiration event of $dissemination\_timer _i$ processed after $Exp _d$ (by Lemma 2), which implies that the lemma trivially holds.

$Inv '_d$ could have been invoked either at line 18 or at line 24. However, before that (still after the processing of $Exp _d$), $P_i$ changes its $epoch _i$ variable to a value greater than e (line 15 or line 21). Therefore, when $Inv '_d$ is invoked, $epoch _i > e$. As the value of the $epoch _i$ variable only increases throughout the execution, $P_i$ broadcasts the enter-epoch messages for e at most once (by Lemma 2), which concludes the proof. $\square$

Next, we show that, after $GST$, two “epoch-entering” events are separated by at least $\delta$ time.

Lemma 20

Let $P_i$ be a correct process. Let $P_i$ trigger $\textsf{advance}(v)$ at time $t \ge GST$ and let $P_i$ trigger $\textsf{advance}(v')$ at time $t'$ such that (1) $\textsf{advance}(v) {\mathop {\prec }\limits ^{\beta _i}} \textsf{advance}(v')$, and (2) v (resp., $v'$) is the first view of an epoch e (resp., $e'$). Then, $t' \ge t + \delta$.

Proof

Let $\textsf{advance}(v^*)$, where $v^*$ is the first view of an epoch $e^*$, be the first “epoch-entering” event following $\textsf{advance}(v)$ in $\beta _i$ (i.e., $\textsf{advance}(v) {\mathop {\prec }\limits ^{\beta _i}} \textsf{advance}(v^*)$); let $\textsf{advance}(v^*)$ be triggered at time $t^*$. In order to prove the lemma, it suffices to show that $t^* \ge t + \delta$.

The $\textsf{advance}(v^*)$ upcall is triggered at line 30. Let $Exp _d$ denote the processed expiration event of $dissemination\_timer _i$ (line 25) which leads $P_i$ to trigger $\textsf{advance}(v^*)$. Let $Inv _d$ denote the invocation of the $\textsf{measure}(\delta )$ on $dissemination\_timer _i$ that has produces $Exp _d$. By Lemma 2, $Inv _d$ immediately precedes $Exp _d$ in the timer history $h_i$ of $P_i$. Note that $Inv _d$ was invoked after $P_i$ has entered e (this follows from Lemma 2 and the fact that $P_i$ enters e after invoking $\textsf{measure}(\cdot )$ on $view\_timer _i$), which means that $Inv _d$ was invoked at some time $\ge t \ge GST$. As local clocks do not drift after $GST$, $Exp _d$ is processed at some time $\ge t + \delta$, which concludes the proof. $\square$

Next, we define $t_s$ as the first synchronization time at or after $GST$.

Definition 3

We denote by $t_s$ the first synchronization time at or after $GST$ (i.e., $t_s \ge GST$).

The next lemma shows that no correct process enters any epoch greater than $e_{ final }$ by $t_s + \Delta$. This lemma is the consequence of Lemma 14 and Theorem 1.

Lemma 21

No correct process enters an epoch greater than $e_{ final }$ by time $t_s + \Delta$.

Proof

By Lemma 14, no correct process enters an epoch $> e_{ final }$ before time $t_{e_{ final }} + epoch\_duration$. By Theorem 1, we have that $t_s < t_{e_{ final }} + epoch\_duration - \Delta$, which implies that $t_{e_{ final }} + epoch\_duration > t_s + \Delta$. Hence, the lemma. $\square$

Next, we define $e_{ max }$ as the greatest epoch entered by a correct process before time $GST$. Note that $e_{ max }$ is properly defined in any execution as only finite executions are possible until $GST$.

Definition 4

We denote by $e_{ max }$ the greatest epoch entered by a correct process before $GST$. If no such epoch exists, $e_{ max } = 0$.

The next lemma shows that $e_{ final }$ (Definition 2) is $e_{ max } + 1$.

Lemma 22

$e_{ final } = e_{ max } + 1$.

Proof

If $e_{ max } = 0$, then $e_{ final } = 1$. Hence, let $e_{ max } > 0$ in the rest of the proof.

By the definitions of $e_{ final }$ (Definition 2) and $e_{ max }$ (Definition 4) and by Lemma 11, $e_{ final } \ge e_{ max } + 1$. Therefore, we need to prove that $e_{ final } \le e_{ max } + 1$.

By contradiction, suppose that $e_{ final } > e_{ max } + 1$. By Lemma 11, epoch $e_{ final } - 1$ was entered by the first correct process at some time $t_{ prev } \le t_{e_ final }$. Note that $e_{ final } - 1 \ge e_{ max } + 1$. Moreover, $t_{ prev } \ge GST$; otherwise, we would contradict the definition of $e_{ max }$. Thus, the first new epoch to be entered by a correct process at or after $GST$ is not $e_{ final }$, i.e., we contradict Definition 2. Hence, the lemma holds. $\square$

Next, we show that every correct process enters epoch $e_{ max }$ by time $GST + 2\delta$ or epoch $e_{ final } = e_{ max } + 1$ by time $GST + 3\delta$.

Lemma 23

Every correct process (1) enters epoch $e_{ max }$ by $GST + 2\delta$, or (2) enters epoch $e_{ max } + 1$ by $GST + 3\delta$.

Proof

Lemma 22 shows that $e_{ final }$ is $e_{ max } + 1$. Recall that $t_{e_ final } \ge GST$. Consider a correct process $P_i$. If $e_{ max } = 1$ (resp., $e_{ final } = 1$), then $P_i$ enters $e_{ max }$ (resp., $e_{ final }$) by time $GST$, which concludes the lemma. Hence, let $e_{ max } > 1$; thus, $e_{ final } > 1$ by Lemma 22.

Lemma 14 proves that no correct process broadcasts an epoch-completed message for an epoch $\ge e_{ max } + 1$ before time $t_{e_ final } + epoch\_duration \ge GST + epoch\_duration$.

By time $GST + \delta$, every correct process $P_i$ receives an enter-epoch message for epoch $e_{ max } > 1$ (line 19) sent by the correct process which has entered $e_{ max }$ before $GST$ (the message is sent at line 26). Therefore, by time $GST + \delta$, $epoch _i$ is either $e_{ max }$ or $e_{ max } + 1$; note that $epoch _i$ cannot take a value greater than $e_{ max } + 1$ before time $GST + epoch\_duration > GST + \delta$ since no correct process broadcasts an epoch-completed message for an epoch $\ge e_{ max } + 1$ before this time.

Let us consider both scenarios:

• Let $epoch _i = e_{ max } + 1$ by time $GST + \delta$. In this case, $dissemination\_timer _i$ expires in $\delta$ time (line 25), and $P_i$ enters $e_{ max } + 1$ by time $GST + 2\delta$ (line 30) as $GST + epoch\_duration > GST + 2\delta$. Hence, the statement of the lemma is satisfied in this case.

• Let $epoch _i = e_{ max }$ by time $GST + \delta$. If, within $\delta$ time from updating $epoch _i$ to $e_{ max }$, $P_i$ does not cancel its $dissemination\_timer _i$, $dissemination\_timer _i$ expires (line 4), and $P_i$ enters $e_{ max }$ by time $GST + 2\delta$. Otherwise, $epoch _i = e_{ max } + 1$ by time $GST + 2\delta$ as $dissemination\_timer _i$ was canceled; $epoch _i$ cannot take any other value as epoch-completed messages are not broadcast before time $GST + epoch\_duration > GST + 2\delta$. As in the previous case, $dissemination\_timer _i$ expires in $\delta$ time (line 25), and $P_i$ enters $e_{ max } + 1$ by time $GST + 3\delta$ (line 30) as $GST + epoch\_duration > GST + 3\delta$. Hence, the statement of the lemma holds in this case, as well.

Since the lemma is satisfied in both possible scenarios, the proof is concluded. $\square$

The direct consequence of Lemma 22 is that $t_{e_ final } \le GST + epoch\_duration + 4\delta$.

Lemma 24

$t_{e_ final } \le GST + epoch\_duration + 4\delta$.

Proof

By contradiction, let $t_{e_ final } > GST + epoch\_duration + 4\delta$. Lemma 23 proves that every correct process enters epoch $e_{ max }$ by time $GST + 2\delta$ or epoch $e_{ final } = e_{ max } + 1$ by time $GST + 3\delta$. Additionally, Lemma 14 proves that no correct process broadcasts an epoch-completed message for an epoch $\ge e_{ final }$ (line 12) before time $t_{e_ final } + epoch\_duration > GST + 2\cdot epoch\_duration + 4\delta$.

If any correct process enters $e_{ max } + 1$ by time $GST + 3\delta$, we reach a contradiction with the fact that $t_{e_ final } > GST + epoch\_duration + 4\delta$ since $e_{ final } = e_{ max } + 1$ (by Lemma 22). Therefore, all correct processes enter $e_{ max }$ by time $GST + 2\delta$.

Since $t_{e_{ final }} > GST + epoch\_duration + 4\delta$, no correct process $P_i$ updates its $epoch _i$ variable to $e_{ max } + 1$ (at line 15 or line 21) by time $GST + epoch\_duration + 3\delta$ (otherwise, $P_i$ would have entered $e_{ max } + 1$ by time $GST + epoch\_duration + 4\delta$, which contradicts $t_{e_{ final }} > GST + epoch\_duration + 4\delta$). By time $GST + epoch\_duration + 2\delta$, all correct processes broadcast an epoch-completed message for $e_{ max }$ (line 12). By time $GST + epoch\_duration + 3\delta$, every correct process $P_i$ receives $2f + 1$ epoch-completed messages for $e_{ max }$ (line 13), and updates its $epoch _i$ variable to $e_{ max } + 1$ (line 15). This represents a contradiction with the fact that $P_i$ does not update its $epoch _i$ variable to $e_{ max } + 1$ by time $GST + epoch\_duration + 3\delta$, which concludes the proof. $\square$

The final lemma shows that no correct process enters more than O(1) epochs during the time period $[ GST , t_s + \Delta ]$.

Lemma 25

No correct process enters more than O(1) epochs in the time period $[ GST , t_s + \Delta ]$.

Proof

Consider a correct process $P_i$. Process $P_i$ enters epoch $e_{ max }$ by time $GST + 2\delta$ or $P_i$ enters epoch $e_{ max } + 1$ by time $GST + 3\delta$ (by Lemma 23). Lemma 22 shows that $e_{ final } = e_{ max } + 1$. Finally, no correct process enters an epoch greater than $e_{ final } = e_{ max } + 1$ by time $t_s + \Delta$ (by Lemma 21).

Let us consider two scenarios according to Lemma 23:

• 1. By time $GST + 2\delta$, $P_i$ enters $e_{ max }$; let $P_i$ enter $e_{ max }$ at time $t^* \le GST + 2\delta$. By Lemma 3, during the time period $[t^*, t_s + \Delta ]$, $P_i$ enters (at most) $2 = O(1)$ epochs (epochs $e_{ max }$ and $e_{ max } + 1$). Finally, during the time period $[ GST , t^*)$, Lemma 20 shows that $P_i$ enters (at most) $2 = O(1)$ epochs (as $t^* \le GST + 2\delta$). Hence, in this case, $P_i$ enters (at most) $4 = O(1)$ epochs during the time period $[ GST , t_s + \Delta ]$.

• 2. By time $GST + 3\delta$, $P_i$ enters $e_{ max } + 1$; let $P_i$ enter $e_{ max } + 1$ at time $t^* \le GST + 3\delta$. By Lemma 3, during the time period $[t^*, t_s + \Delta ]$, $P_i$ enters (at most) $1 = O(1)$ epoch (epoch $e_{ max } + 1$). Finally, during the time period $[ GST , t^*)$, Lemma 20 shows that $P_i$ enters (at most) $3 = O(1)$ epochs (as $t^* \le GST + 3\delta$). Hence, in this case, $P_i$ enters (at most) $4 = O(1)$ epochs during the time period $[ GST , t_s + \Delta ]$.

Hence, during the time period $[ GST , t_s + \Delta ]$, $P_i$ enters (at most) $4 = O(1)$ epochs. $\square$

Finally, we prove that RareSync achieves $O(n^2)$ communication and $O(f \cdot \delta )$ latency.

Theorem 2

(Complexity) RareSync achieves $O(n^2)$ communication complexity and $O(f \cdot \delta )$ latency complexity.

Proof

Fix a correct process $P_i$. For every epoch e, $P_i$ sends (at most) O(n) epoch-completed and enter-epoch messages for e (by Lemmas 18 and 19). Moreover, if $P_i$ sends an epoch-completed message for an epoch e at time t, then e is the last epoch entered by $P_i$ prior to sending the message (by Lemma 16). $\square$

5 SQuad

This section introduces SQuad, a partially synchronous Byzantine consensus protocol with optimal resilience [9]. SQuad simultaneously achieves (1) $O(n^2)$ communication complexity, matching the Dolev-Reischuk bound [6], and (2) $O(f \cdot \delta )$ latency complexity, matching the Dolev-Strong bound [17].

First, we present Quad, a partially synchronous Byzantine consensus protocol ensuring weak validity (Sect. 5.1). Quad achieves quadratic communication complexity and linear latency complexity. We provide a short overview of the proof of Quad ’s correctness and complexity, followed by the complete formal proof (Sect. 5.2). Then, we construct SQuad by adding a simple preprocessing phase to Quad (Sect. 5.3), which we then formally prove (Sect. 5.4).

5.1 Quad

Quad is a partially synchronous Byzantine consensus protocol satisfying the weak validity property:

• Weak validity: If all processes are correct, then a value decided by a process was proposed.

Quad achieves (1) quadratic communication complexity, and (2) linear latency complexity. Interestingly, the Dolev-Reischuk lower bound [6] does not apply to Byzantine protocols satisfying weak validity; hence, we do not know whether Quad has optimal communication complexity. As explained in Sect. 5.3, we accompany Quad by a preprocessing phase to obtain SQuad.

Quad (Algorithm 3) uses the same view core module as HotStuff [13], i.e., the view logic of Quad is identical to that of HotStuff. Moreover, Quad uses RareSync as its view synchronizer, achieving synchronization with $O(n^2)$ communication. The combination of HotStuff’s view core and RareSync ensures that each correct process sends O(n) words after $GST$ (and before the decision), i.e., $C = O(n)$ in Quad. Following the formula introduced in Sect. 1, Quad indeed achieves $n \cdot C + S = n \cdot O(n) + O(n^2) = O(n^2)$ communication complexity. Due to the linear latency of RareSync, Quad also achieves $O(f \cdot \delta )$ latency complexity.

5.1.1 View core

We now give a brief description of the view core module of Quad. The complete pseudocode of this module can be found in Sect. 5.2 (and in [13]).

Each correct process keeps track of two critical variables: (1) the prepare quorum certificate (QC), and (2) the locked QC. Each of these represents a process’ estimation of the value that will be decided, although with a different degree of certainty. For example, if a correct process decides a value v, it is guaranteed that (at least) $f + 1$ correct processes have v in their locked QC. Moreover, it is ensured that no correct process updates (from this point onward) its prepare or locked QC to any other value, thus ensuring agreement. Lastly, a QC is a (constant-sized) threshold signature.

The structure of a view follows the “all-to-leader, leader-to-all” communication pattern. Specifically, each view is comprised of the following four phases:

• 1. Prepare: A process sends to the leader a view-change message containing its prepare QC. Once the leader receives $2f + 1$ view-change messages, it selects the prepare QC from the “latest” view. The leader sends this QC to all processes via a prepare message. Once a process receives the prepare message from the leader, it supports the received prepare QC if (1) the received QC is consistent with its locked QC, or (2) the received QC is “more recent” than its locked QC. If the process supports the received QC, it acknowledges this by sending a prepare-vote message to the leader.

• 2. Precommit: Once the leader receives $2f + 1$ prepare-vote messages, it combines them into a cryptographic proof $\sigma$ that “enough” processes have supported its “prepare-phase” value; $\sigma$ is a threshold signature. Then, it disseminates $\sigma$ to all processes via a precommit message. Once a process receives the precommit message carrying $\sigma$, it updates its prepare QC to $\sigma$ and sends back to the leader a precommit-vote message.

• 3. Commit: Once the leader receives $2f + 1$ precommit-vote messages, it combines them into a cryptographic proof $\sigma '$ that “enough” processes have adopted its “precommit-phase” value (by updating their prepare QC); $\sigma '$ is a threshold signature. Then, it disseminates $\sigma '$ to all processes via a commit message. Once a process receives the commit message carrying $\sigma '$, it updates its locked QC to $\sigma '$ and sends back to the leader a commit-vote message.

• 4. Decide: Once the leader receives $2f + 1$ commit-vote messages, it combines them into a threshold signature $\sigma ''$, and relays $\sigma ''$ to all processes via a decide message. When a process receives the decide message carrying $\sigma ''$, it decides the value associated with $\sigma ''$.

As a consequence of the “all-to-leader, leader-to-all” communication pattern and the constant size of messages, the leader of a view sends O(n) words, while a non-leader process sends O(1) words.

The view core module provides the following interface:

• Request $\mathsf {start\_executing(View} \text { } v\mathsf {)}$: The view core starts executing the logic of view v and abandons the previous view. Concretely, it stops accepting and sending messages for the previous view, and it starts accepting, sending, and replying to messages for view v. The state of the view core is kept across views (e.g., the prepare and locked QCs).

• Indication $\mathsf {decide(Value} \text { } decision \mathsf {)}$: The view core decides value $decision$ (this indication is triggered at most once).

5.1.2 Protocol description

The protocol (Algorithm 3) amounts to a composition of RareSync and the aforementioned view core. Since the view core requires 8 communication steps in order for correct processes to decide, a synchronous overlap of $8\delta$ is sufficient. Thus, we parameterize RareSync with $\Delta = 8\delta$ (line 3). In short, the view core is subservient to RareSync, i.e., when RareSync triggers the $\mathsf {advance(}v\mathsf {)}$ event (line 7), the view core starts executing the logic of view v (line 8). Once the view core decides (line 9), Quad decides (line 10).

Algorithm 3

Quad: Pseudocode (for process $P_i$)

5.1.3 Proof overview

The agreement and weak validity properties of Quad are ensured by the view core’s implementation. As for the termination property, the view core, and therefore Quad, is guaranteed to decide as soon as processes have synchronized in the same view with a correct leader for $\Delta = 8\delta$ time at or after $GST$. Since RareSync ensures the eventual synchronization property, this eventually happens, which implies that Quad satisfies termination. As processes synchronize within $O(f \cdot \delta )$ time after $GST$, the latency complexity of Quad is $O(f \cdot \delta )$.

As for the total communication complexity, it is the sum of the communication complexity of (1) RareSync, which is $O(n^2)$, and (2) the view core, which is also $O(n^2)$. The view core’s complexity is a consequence of the fact that:

• Each process executes O(1) epochs between $GST$ and the time by which every process decides,

• Each epoch has $f + 1$ views,

• A process can be the leader in only one view of any epoch, and

• A process sends O(n) words in a view if it is the leader, and O(1) words otherwise, for an average of O(1) words per view in any epoch.

Thus, the view core’s communication complexity is $O(n^2) = O(1) \cdot (f+1) \cdot O(1) \cdot n$. Therefore, Quad indeed achieves $O(n^2)$ communication complexity. In summary:

Theorem: Quad is a Byzantine consensus protocol ensuring weak validity with (1) $O(n^2)$ communication complexity, and (2) $O(f \cdot \delta )$ latency complexity.

5.2 Quad: formal proof

In this section, we give the complete pseudocode of Quad ’s view core module (algorithms 4 and 5), and we formally prove that Quad solves consensus (with weak validity) with $O(n^2)$ communication complexity and $O(f \cdot \delta )$ latency complexity.

Algorithm 4

Quad: View core’s utilities (for process $P_i$)

Algorithm 5

Quad: View core (for process $P_i$)

5.2.1 Proof of correctness

In this paragraph, we show that Quad ensures weak validity, termination and agreement. Recall that the main body of Quad is given in Algorithm 3, whereas its view synchronizer RareSync is presented in Algorithm 2 and its view core in Algorithm 5. We underline that the proofs concerned with the view core of Quad can be found in [13], as Quad uses the same view core as HotStuff.

We start by proving that Quad ensures weak validity.

Theorem 3

(Weak validity) Quad ensures weak validity.

Proof

Suppose that all processes are correct. Whenever a correct process updates its $prepareQC$ variable (line 25 of Algorithm 5), it updates it to a quorum certificate vouching for a proposed value. Therefore, leaders always propose a proposed value since the proposed value is “formed” out of $prepareQC$s of processes (line 9 of Algorithm 5). Given that a correct process executes line 43 of Algorithm 5 for a value proposed by the leader of the current view, which is proposed by a process (recall that all processes are correct), the weak validity property is ensured. $\square$

Next, we prove agreement.

Theorem 4

(Agreement) Quad ensures agreement.

Proof

Two conflicting quorum certificates associated with the same view cannot be obtained in the view core of Quad (Algorithm 5); otherwise, a correct process would vote for both certificates, which is not possible according to Algorithm 5. Therefore, two correct processes cannot decide different values from the view core of Quad in the same view. Hence, we need to show that, if a correct process decides v in some view $view$ in the view core (line 43 of Algorithm 5), then no conflicting quorum certificate can be obtained in the future views.

Since a correct process decides v in view $view$ in the view core, the following holds at $f + 1$ correct processes: $lockedQC . value = v$ and $lockedQC . view = view$ (line 34 of Algorithm 5). In order for another correct process to decide a different value in some future view, a prepare quorum certificate for a value different than v must be obtained in a view greater than $view$. However, this is impossible as $f + 1$ correct processes whose $lockedQC . value = v$ and $lockedQC . view = view$ will not support such a prepare quorum certificate (i.e., the check at line 16 of Algorithm 5 will return false). Thus, it is impossible for correct processes to disagree in the view core even across multiple views. The agreement property is ensured by Quad. $\square$

Finally, we prove termination.

Theorem 5

(Termination) Quad ensures termination.

Proof

RareSync ensures that, eventually, all correct processes remain in the same view $view$ with a correct leader for (at least) $\Delta = 8\delta$ time after $GST$. When this happens, all correct processes decide in the view core.

Indeed, the leader of $view$ learns the highest obtained locked quorum certificate through the view-change messages (line 9 of Algorithm 5). Therefore, every correct process supports the proposal of the leader (line 17 of Algorithm 5) as the check at line 16 of Algorithm 5 returns true. After the leader obtains a prepare quorum certificate in $view$, all correct processes vote in the following phases of the same view. Thus, all correct processes decide from the view core (line 43 of Algorithm 5), which concludes the proof. $\square$

Thus, Quad indeed solves the Byzantine consensus problem with weak validity.

Corollary 1

Quad is a partially synchronous Byzantine consensus protocol ensuring weak validity.

5.2.2 Proof of complexity

Next, we show that Quad achieves $O(n^2)$ communication complexity and $O(f \cdot \delta )$ latency complexity. Before we start the proof, we clarify one point about Algorithm 3: as soon as $\textsf{advance}(v)$ is triggered (line 7), for some view v, the process immediately stops accepting and sending messages for the previous view. In other words, it is as if the “stop accepting and sending messages for the previous view” action immediately follows the $\textsf{advance}(\cdot )$ upcall in Algorithm 2.⁷

We begin by proving that, if a correct process sends a message of the view core associated with a view v which belongs to an epoch e, then the last entered epoch prior to sending the message (in the behavior of the process) is e (this result is similar to the one of Lemma 16). A message is a view-core message if it is of the view-change, prepare, precommit, commit or decide type.

Lemma 26

Let $P_i$ be a correct process and let $P_i$ send a view-core message associated with a view v, where v belongs to an epoch e. Then, e is the last epoch entered by $P_i$ in $\beta _i$ before sending the message.

Proof

Process $P_i$ enters the view v before sending the view-core message (since $\mathsf {start\_executing}(v)$ is invoked upon $P_i$ entering v; line 8 of Algorithm 3). By Lemma 8, $P_i$ enters the first view of the epoch e (and, hence, e) before sending the message. By contradiction, suppose that $P_i$ enters another epoch $e'$ after entering e and before sending the view-core message.

By Lemma 3, we have that $e' > e$. However, this means that $P_i$ does not send any view-core messages associated with v after entering $e'$ (since $(e' - 1) \cdot (f + 1) + 1 > v$ and $P_i$ enters monotonically increasing views by Lemma 3). Thus, a contradiction, which concludes the proof. $\square$

Next, we show that a correct process sends (at most) O(n) view-core messages associated with a single epoch.

Lemma 27

Let $P_i$ be a correct process. For any epoch e, $P_i$ sends (at most) O(n) view-core messages associated with views that belong to e.

Proof

Recall that $P_i$ enters monotonically increasing views (by Lemma 3), which means that $P_i$ never invokes $\mathsf {start\_executing}(v)$ (line 8 of Algorithm 3) multiple times for any view v.

Consider a view v that belongs to e. We consider two cases:

• Let $P_i$ be the leader of v. In this case, $P_i$ sends (at most) O(n) view-core messages associated with v.

• Let $P_i$ not be the leader of v. In this case, $P_i$ sends (at most) O(1) view-core messages associated with v.

Given that $P_i$ is the leader of at most one view in every epoch e (since $\mathsf {leader(\cdot )}$ is a round-robin function), $P_i$ sends (at most) $1 \cdot O(n) + f \cdot O(1) = O(n)$ view-core messages associated with views that belong to e. $\square$

Finally, we prove the complexity of Quad.

Theorem 6

(Complexity) Quad achieves $O(n^2)$ communication complexity and $O(f \cdot \delta )$ latency complexity.

Proof

As soon as all correct processes remain in the same view for $8\delta$ time, all correct processes decide from the view core. As RareSync uses $\Delta = 8\delta$ in the implementation of Quad (line 3 of Algorithm 3), all processes decide by time $t_s + 8\delta$, where $t_s$ is the first synchronization time after $GST$ (Definition 3). Given that $t_s + 8\delta - GST$ is the latency of RareSync (see Sect. 4.1) and the latency complexity of RareSync is $O(f \cdot \delta )$ (by Theorem 2), the latency complexity of Quad is indeed $O(f \cdot \delta )$.

Fix a correct process $P_i$. For every epoch e, $P_i$ sends (at most) O(n) view-core messages associated with views that belong to e (by Lemma 27). Moreover, if $P_i$ sends a view-core message associated with a view that belongs to an epoch e, then e is the last epoch entered by $P_i$ prior to sending the message (by Lemma 26). Hence, in the time period $[ GST , t_s + 8\delta ]$, $P_i$ sends view-core messages associated with views that belong to (at most) O(1) epochs (by Lemma 25). Thus, $P_i$ sends (at most) $O(1) \cdot O(n) = O(n)$ view-core messages in the time period $[ GST , t_s + 8\delta ]$, each containing a single word. Moreover, during this time period, the communication complexity of RareSync is $O(n^2)$ (by Theorem 2). Therefore, the communication complexity of Quad is $n \cdot O(n) + O(n^2) = O(n^2)$. $\square$

As a final note, while our definition of communication complexity considers the words exchanged between $GST$ until $t_d(\alpha )$ (i.e., when the last correct process has decided), it is straightforward to extend our results to account for all messages exchanged between $GST$ and infinity. This is achieved by having correct processes halt the sending of messages of the underlying RareSync protocol immediately after deciding, and rebroadcasting (once) the first correct decide message they see. This is because, by the time the first correct process decides, every correct process is also guaranteed to decide regardless of the continued use of RareSync, as termination is now solely dependent on the reception of the decide message. This once-per-process rebroadcast incurs only an additional $O(n^2)$ words exchanged in total, with latency remaining unaffected, so all results continue to hold.

5.3 SQuad: protocol description

At last, we present SQuad, which we derive from Quad.

5.3.1 Deriving SQuad from Quad

Imagine a locally-verifiable, constant-sized cryptographic proof $\sigma _v$ vouching that value v is valid. Moreover, imagine that it is impossible, in the case in which all correct processes propose v to Quad, for any process to obtain a proof for a value different from v:

• Computability: If all correct processes propose v to Quad, then no process (even if faulty) obtains a cryptographic proof $\sigma _{v'}$ for a value $v' \ne v$.

If such a cryptographic primitive were to exist, then the Quad protocol could be modified in the following manner in order to satisfy the validity property introduced in Sect. 1:

• A correct process accompanies each value by a cryptographic proof that the value is valid.

• A correct process ignores any message with a value not accompanied by the value’s proof.

Suppose that all correct processes propose the same value v and that a correct process $P_i$ decides $v'$ from the modified version of Quad. Given that $P_i$ ignores messages with non-valid values, $P_i$ has obtained a proof for $v'$ before deciding. The computability property of the cryptographic primitive guarantees that $v' = v$, implying that validity is satisfied. Given that the proof is of constant size, the communication complexity of the modified version of Quad remains $O(n^2)$.

Therefore, the main challenge in obtaining SQuad from Quad, while preserving Quad ’s complexity, lies in implementing the introduced cryptographic primitive.

5.3.2 Certification phase

SQuad utilizes its certification phase (Algorithm 6) to obtain the introduced constant-sized cryptographic proofs; we call these proofs certificates.⁸ Formally, $\textsf{Certificate}$ denotes the set of all certificates. Moreover, we define a locally computable function $\textsf{verify}\text {: } \textsf{Value} \times \textsf{Certificate} \rightarrow \{ true , false \}$. We require the following properties to hold:

• Computability: If all correct processes propose the same value v to SQuad, then no process (even if faulty) obtains a certificate $\sigma _{v'}$ with $\textsf{verify}(v', \sigma _{v'}) = true$ and $v' \ne v$.

• Liveness: Every correct process eventually obtains a certificate $\sigma _v$ such that $\textsf{verify}(v, \sigma _v) = true$, for some value v.

The computability property states that, if all correct processes propose the same value v to SQuad, then no process (even if Byzantine) can obtain a certificate for a value different from v. The liveness property ensures that all correct processes eventually obtain a certificate. Hence, if all correct processes propose the same value v, all correct processes eventually obtain a certificate for v and no process obtains a certificate for a different value.

In order to implement the certification phase, we assume an $(f + 1, n)$-threshold signature scheme (see Sect. 3) used throughout the entirety of the certification phase. The $(f + 1, n)$-threshold signature scheme allows certificates to count as a single word, as each certificate is a threshold signature. Finally, in order to not disrupt Quad ’s communication and latency, the certification phase itself incurs $O(n^2)$ communication and O(1) latency.

Algorithm 6

Certification Phase: Pseudocode (for process $P_i$)

A certificate $\sigma$ vouches for a value v (the $\textsf{verify}(\cdot )$ function at line 21) if (1) $\sigma$ is a threshold signature of the predefined string “any value” (line 22), or (2) $\sigma$ is a threshold signature of v (line 23). Otherwise, $\textsf{verify}(v, \sigma )$ returns $false$.

Once $P_i$ enters the certification phase (line 1), $P_i$ informs all processes about the value it has proposed by broadcasting a disclose message (line 3). Process $P_i$ includes a partial signature of its proposed value in the message. If $P_i$ receives disclose messages for the same value v from $f + 1$ processes (line 4), $P_i$ combines the received partial signatures into a threshold signature of v (line 6), which represents a certificate for v. To ensure liveness, $P_i$ disseminates the certificate (line 7).

If $P_i$ receives $2f + 1$ disclose messages and there does not exist a “common” value received in $f + 1$ (or more) disclose messages (line 9), the process concludes that it is fine for a certificate for any value to be obtained. Therefore, $P_i$ broadcasts an allow-any message containing a partial signature of the predefined string “any value” (line 11).

If $P_i$ receives $f + 1$ allow-any messages (line 12), it combines the received partial signatures into a certificate that vouches for any value (line 14), and it disseminates the certificate (line 15). Since allow-any messages are received from $f + 1$ processes, there exists a correct process that has verified that it is indeed fine for such a certificate to exist.

If, at any point, $P_i$ receives a certificate (line 18), it adopts the certificate, and disseminates it (line 19) to ensure liveness.

Given that each message of the certification phase contains a single word, the certification phase incurs $O(n^2)$ communication. Moreover, each correct process obtains a certificate after (at most) $2 = O(1)$ rounds of communication. Therefore, the certification phase incurs O(1) latency.

We explain below why the certification phase (Algorithm 6) ensures computability and liveness:

• Computability: If all correct processes propose the same value v to SQuad, all correct processes broadcast a disclose message for v (line 3). Since $2f + 1$ processes are correct, no process obtains a certificate $\sigma _{v'}$ for a value $v' \ne v$ such that $CombinedVerify (v', \sigma _{v'}) = true$ (line 23). Moreover, as every correct process receives $f + 1$ disclose messages for v within any set of $2f + 1$ received disclose messages, no correct process sends an allow-any message (line 11). Hence, no process obtains a certificate $\sigma _{\bot }$ such that $CombinedVerify (\text {``any value''}, \sigma _{\bot }) = true$ (line 22). Thus, computability is ensured.

• Liveness: If a correct process receives $f + 1$ disclose messages for a value v (line 4), the process obtains a certificate for v (line 6). Since the process disseminates the certificate (line 7), every correct process eventually obtains a certificate (line 18), ensuring liveness in this scenario. Otherwise, all correct processes broadcast an allow-any message (line 11). Since there are at least $2f + 1$ correct processes, every correct process eventually receives $f + 1$ allow-any messages (line 12), thus obtaining a certificate. Hence, liveness is satisfied in this case as well.

5.3.3 SQuad = Certification phase + Quad

We obtain SQuad by combining the certification phase with Quad. The pseudocode of SQuad is given in Algorithm 7.

Algorithm 7

SQuad: Pseudocode (for process $P_i$)

A correct process $P_i$ executes the following steps in SQuad:

• 1. $P_i$ starts executing the certification phase with its proposal (line 2).

• 2. Once the process exits the certification phase with a certificate $\sigma _v$ for a value v, it proposes $(v, \sigma _v)$ to $\textsc {Quad} _{ cer }$, a version of Quad “enriched” with certificates (line 5). While executing $\textsc {Quad} _{ cer }$, correct processes ignore messages containing values not accompanied by their certificates.

• 3. Once $P_i$ decides from $\textsc {Quad} _{ cer }$ (line 6), $P_i$ decides the same value from SQuad (line 7).

In summary:

Theorem: SQuad is a Byzantine consensus protocol with (1) $O(n^2)$ communication complexity, and (2) $O(f \cdot \delta )$ latency complexity.

5.4 SQuad: formal proof

First, we show that the certification phase of SQuad ensures computability and liveness.

Lemma 28

(Computability & liveness) Certification phase (Algorithm 6) ensures computability and liveness. Moreover, every correct process sends (at most) O(n) words and obtains a certificate by time $GST + 2\delta$.

Proof

As every correct process broadcasts disclose, certificate or allow-any messages at most once and each message contains a single word, every correct process sends (at most) $3 \cdot n \cdot 1 = O(n)$ words. Next, we prove computability and liveness.

Computability. Let all correct processes propose the same value v to SQuad. Since no correct process broadcasts a disclose message for a value $v' \ne v$, no process ever obtains a certificate $\sigma _{v'}$ for $v'$ such that $CombinedVerify (v', \sigma _{v'}) = true$ (line 23).

Since all correct processes broadcast a disclose message for v (line 3), the rule at line 9 never activates at a correct process. Thus, no correct process ever broadcasts an allow-any message (line 11), which implies that no process obtains a certificate $\sigma _{\bot }$ such that $CombinedVerify (\text {``allow any''}, \sigma _{\bot }) = true$ (line 22). The computability property is ensured.

Liveness. Every correct process receives all disclose messages sent by correct processes by time $GST + \delta$ (since message delays are $\delta$ after $GST$; see Sect. 3). Hence, all correct processes receive (at least) $2f + 1$ disclose messages by time $GST + \delta$. Therefore, by time $GST + \delta$, all correct processes send either (1) a certificate message upon receiving $f + 1$ disclose messages for the same value (line 7), or (2) an allow-any message upon receiving $2f + 1$ disclose messages without a “common value” (line 11). Let us consider two possible scenarios:

• There exists a correct process that has broadcast a certificate message upon receiving $f + 1$ disclose messages for the same value (line 7) by time $GST + \delta$. Every correct process receives this message by time $GST + 2\delta$ (line 18) and obtains a certificate. Liveness is satisfied by time $GST + 2\delta$ in this case.

• Every correct process broadcasts an allow-any message (line 11) by time $GST + \delta$. Hence, every correct process receives $f + 1$ allow-any messages by time $GST + 2\delta$ (line 12) and obtains a certificate (line 14). The liveness property is guaranteed by time $GST + 2\delta$ in this case as well.

The liveness property is ensured by time $GST + 2\delta$. $\square$

Finally, we show that SQuad is a Byzantine consensus protocol with $O(n^2)$ communication complexity and $O(f \cdot \delta )$ latency complexity.

Theorem 7

SQuad is a Byzantine consensus protocol with (1) $O(n^2)$ communication complexity, and (2) $O(f \cdot \delta )$ latency complexity.

Proof

If a correct process decides a value $v'$ and all correct processes have proposed the same value v, then $v' = v$ since (1) correct processes ignore values not accompanied by their certificates (line 5), and (2) the certification phase of SQuad ensures computability (by Lemma 28). Therefore, SQuad ensures validity.

Fix an execution $E_{\textsc {SQuad}}$ of SQuad. We denote by $t_{ last }$ the time the last correct process starts executing $\textsc {Quad} _{ cer }$ (line 5) in $E_{\textsc {SQuad}}$; i.e., by $t_{ last }$ every correct process has exited the certification phase. Moreover, we denote the global stabilization time of $E_{\textsc {SQuad}}$ by $GST _1$. Now, we consider two possible scenarios:

• Let $GST _1 \ge t_{ last }$. $\textsc {Quad} _{ cer }$ solves the Byzantine consensus problem with $O(n^2)$ communication and $O(f \cdot \delta )$ latency (by Theorem 6). As processes send (at most) O(n) words associated with the certification phase (by Lemma 28), consensus is solved in $E_{\textsc {SQuad}}$ with $n \cdot O(n) + O(n^2) = O(n^2)$ communication complexity and $O(f \cdot \delta )$ latency complexity.

• Let $GST _1 < t_{ last }$. Importantly, $t_{ last } - GST _ 1 \le 2\delta$ (by Lemma 28). Now, we create an execution $E_{\textsc {Quad}}$ of the original Quad protocol in the following manner:

  • 1. $E_{\textsc {Quad}} \leftarrow E_{\textsc {SQuad}}$. If a process sends a value with a valid accompanying certificate, then just the certificate is removed in $E_{\textsc {Quad}}$ (i.e., the corresponding message stays in $E_{\textsc {Quad}}$). Otherwise, the entire message is removed. Note that no message sent by a correct process in $E_{\textsc {SQuad}}$ is removed from $E_{\textsc {Quad}}$ as correct processes only send values accompanied by their valid certificates.

  • 2. We remove from $E_{\textsc {Quad}}$ all events associated with the certification phase of SQuad.

  • 3. The global stabilization time of $E_{\textsc {Quad}}$ is set to $t_{ last }$. We denote this time by $GST _2 = t_{ last }$. Note that we can set $GST _2$ to $t_{ last }$ as $t_{ last } > GST _1$.

  In $E_{\textsc {Quad}}$, consensus is solved with $O(n^2)$ communication and $O(f \cdot \delta )$ latency. Therefore, the consensus problem is solved in $E_{\textsc {SQuad}}$. Let us now analyze the complexity of $E_{\textsc {SQuad}}$:

  • The latency complexity of $E_{\textsc {SQuad}}$ is $t_{ last } - GST _1 + O(f \cdot \delta ) = O(f \cdot \delta )$ (as $t_{ last } - GST _1 \le 2\delta$).

  • The communication complexity of $E_{\textsc {SQuad}}$ is the sum of (1) the number of words sent in the time period $[ GST _1, t_{ last })$, and (2) the number of words sent at and after $t_{ last }$ and before the decision, which is $O(n^2)$ since that is the communication complexity of $E_{\textsc {Quad}}$ and each correct process sends (at most) O(n) words associated with the certification phase (by Lemma 28). Fix a correct process $P_i$. Let us take a closer look at the time period $[ GST _1, t_{ last })$:

    • Let $epochs _{\textsc {RareSync}}$ denote the number of epochs for which $P_i$ sends epoch-completed or enter-epoch messages in this time period. By Lemma 20, $P_i$ enters (at most) $2 = O(1)$ epochs in this time period. Hence, $epochs _{\textsc {RareSync}} = O(1)$ (by Lemmas 16 and 17).

    • Let $epochs _{\textsc {Quad} _{ cer }}$ denote the number of epochs for which $P_i$ sends view-core messages in this time period. By Lemma 20, $P_i$ enters (at most) $2 = O(1)$ epochs in this time period. Hence, $epochs _{\textsc {Quad} _{ cer }} = O(1)$ (by Lemma 26).

    For every epoch e, $P_i$ sends (at most) O(n) epoch-completed and enter-epoch messages (by Lemmas 18 and 19). Moreover, for every epoch e, $P_i$ sends (at most) O(n) view-core messages associated with views that belong to e (by Lemma 27).⁹ As each epoch-completed, enter-epoch and view-core message contains a single word and $P_i$ sends at most O(n) words during the certification phase (by Lemma 28), we have that $P_i$ sends (at most) $epochs _{\textsc {RareSync}} \cdot O(n) + epochs _{\textsc {Quad} _{ cer }} \cdot O(n) + O(n) = O(n)$ words during the time period $[ GST _1, t_{ last })$. Therefore, the communication complexity of $E_{\textsc {SQuad}}$ is $n \cdot O(n) + O(n^2) + O(n^2) = O(n^2)$.¹⁰

  Hence, consensus is indeed solved in $E_{\textsc {SQuad}}$ with $O(n^2)$ communication complexity and $O(f \cdot \delta )$ latency complexity.

The theorem holds. $\square$

6 Concluding remarks

This paper shows that the Dolev-Reischuk lower bound can be met by a partially synchronous Byzantine consensus protocol. Namely, we introduce SQuad, an optimally-resilient partially synchronous Byzantine consensus protocol with optimal $O(n^2)$ communication complexity, and optimal $O(f \cdot \delta )$ latency complexity. SQuad owes its complexity to RareSync, an “epoch-based” view synchronizer ensuring synchronization with quadratic communication and linear latency in partial synchrony. In the future, we aim to address the following limitations of RareSync.

6.1 Lack of adaptiveness

RareSync is not adaptive, i.e., its complexity does not depend on the actual number b, but rather on the upper bound f, of Byzantine processes. Consider a scenario S in which all processes are correct; we separate them into three disjoint groups: (1) group A, with $|A| = f$, (2) group B, with $|B| = f$, and (3) group C, with $|C| = f + 1$. At $GST$, group A is in the first view of epoch $e_{ max }$, group B is in the second view of $e_{ max }$, and group C is in the third view of $e_{ max }$.¹¹ Unfortunately, it is impossible for processes to synchronize in epoch $e_{ max }$. Hence, they will need to wait for the end of epoch $e_{ max }$ in order to synchronize in the next epoch: thus, the latency complexity is $O(f \cdot \delta )$ (since $e_{ max }$ has $f + 1$ views) and the communication complexity is $O(n^2)$ (because of the “all-to-all” communication step at the end of $e_{ max }$). In contrast, the view synchronizer presented in [49] achieves O(1) latency and O(n) communication complexity in S. Lastly, since our algorithm is not adaptive in terms of latency, i.e., its latency is $O(f\cdot \delta )$, where (crucially) f denotes the upper bound on the number of tolerated failures, and not the number of actual failures, our algorithm is also not optimistically responsive [13]: the latency of SQuad depends on the maximum network delay $\delta$ and not on the actual speed of the network.

6.2 Suboptimal expected complexity

A second limitation of RareSync is that its expected complexity is the same as its worst-case complexity. Namely, the expected complexity considers a weaker adversary which does not have a knowledge of the $\textsf{leader}(\cdot )$ function. Therefore, this adversary is unable to corrupt f processes that are scheduled to be leaders right after $GST$.

As the previously introduced scenario S does not include any Byzantine process, we can analyze it for the expected complexity of RareSync. Therefore, the expected latency complexity of RareSync is $O(f \cdot \delta )$ and the expected communication complexity of RareSync is $O(n^2)$. On the other hand, the view synchronizer of Naor and Keidar [49] achieves O(1) expected latency complexity and O(n) expected communication complexity.

6.3 Limited clock drift tolerance

A third limitation of RareSync is that its latency is susceptible to clock drifts. Namely, let $\phi > 1$ denote the bound on clock drifts after $GST$. To accommodate for the bounded clock drifts after $GST$, RareSync increases the duration of a view. The duration of the i-th view of an epoch becomes $\phi ^i \cdot view\_duration$ (instead of only $view\_duration$). Thus, the latency complexity of RareSync becomes $O(f \cdot \delta \cdot \phi ^f)$.

Appendices

A Threshold signature scheme: formal definition

This section defines a (k, n)-threshold signature scheme ($k = 2f + 1 = n - f$), which we (informally) introduced in Sect. 3. The threshold signature scheme and its properties are defined with respect to a security parameter $\kappa \in {\mathbb {N}}$. In the rest of the section, we say that a local protocol is efficient if and only if its complexity belongs to $poly (\kappa )$. Moreover, $\textsf{String}$ denotes the set of all strings, ${\mathcal {P}}$ denotes the set of all partial signatures and ${\mathcal {T}}$ denotes the set of all threshold signatures.

Formally, a (k, n)-threshold signature scheme is a tuple consisting of:

• 1. $\textsf{Keys} = \big (\textsf{PK}, \textsf{SK} = ( sk _1,\ldots , sk _n), \textsf{VK} = ( vk _1,\ldots , vk _n) \big )$, where:

  • $\textsf{PK}$ is a public key stored by every correct process.

  • $\textsf{SK}$ is a vector of private key shares such that, for every correct process $P_i$, $P_i$ stores its (and only its) private key share $sk _i$; $sk _i$ is hidden from the adversary.

  • $\textsf{VK}$ is a vector of verification keys and the entire vector is stored by every correct process.

• 2. $ShareSign (m \in \textsf{String}, sk _i)$ is an efficient local (potentially probabilistic) protocol that takes (1) a string m, and (2) the private key share $sk _i$ of a process $P_i$ as the input. The protocol outputs a partial signature $\sigma _i^p \in {\mathcal {P}}$ of (at most) $\kappa$ bits. In the main body of the paper, we used $ShareSign _i(m)$ to abbreviate $ShareSign (m, sk _i)$: $ShareSign _i(m) \equiv ShareSign (m, sk _i)$.

• 3. $ShareVerify (m \in \textsf{String}, vk _i, \sigma _i^p \in {\mathcal {P}})$ is an efficient local deterministic protocol that takes (1) a string m, (2) the verification key $vk _i$ of a process $P_i$, and (3) a partial signature $\sigma _i^p$ as the input. The protocol outputs either $true$ or $false$ depending on whether $\sigma _i^p$ is deemed as a valid partial signature of process $P_i$ for m. In the main body of the paper, we used $ShareVerify _i(m, \sigma _i^p)$ to abbreviate $ShareSign (m, vk _i, \sigma _i^p)$: $ShareVerify _i(m, \sigma _i^p) \equiv ShareVerify (m, vk _i, \sigma _i^p)$.

• 4. $Combine (m \in \textsf{String}, P \subset {\mathcal {P}})$, where P is a set of $\vert P \vert = k$ partial signatures of k distinct processes, is an efficient local protocol that takes (1) a string m, and (2) a set P of $\vert P \vert = k$ partial signatures as the input. The protocol outputs a threshold signature $\sigma ^t \in {\mathcal {T}}$.

• 5. $CombinedVerify (m \in \textsf{String}, \textsf{PK}, \sigma ^t \in {\mathcal {T}})$ is an efficient local deterministic protocol that takes (1) a string m, (2) the public key $\textsf{PK}$, and (3) a threshold signature $\sigma ^t$ as the input. The protocol outputs $true$ or $false$ depending on whether $\sigma ^t$ is deemed as a valid threshold signature for m. In the main body of the paper, we used $CombinedVerify (m, \sigma ^t)$ to abbreviate $CombinedVerify (m, \textsf{PK}, \sigma ^t)$: $CombinedVerify (m, \sigma ^t) \equiv CombinedVerify (m, \textsf{PK}, \sigma ^t)$.

The following guarantees are provided:

• Correctness of partial signatures: For every $i \in [1, n]$, $ShareVerify _i\big (m \in \textsf{String}, ShareSign _i(m) \in {\mathcal {P}} \big )$ returns $true$.

• Unforgeability of partial signatures: If $ShareVerify _i(m \in \textsf{String}, \sigma _i^p \in {\mathcal {P}})$ returns $true$, then (1) $\sigma _i^p \leftarrow ShareSign _i(m)$ has been executed by the process $P_i$, or (2) $P_i$ is faulty.

• Correctness of threshold signatures: Let $m \in \textsf{String}$ be any string and let S be any set of $\vert S \vert = k$ processes. Let $P = \{ \sigma _i^p \,\vert \, \sigma _i^p \leftarrow ShareSign _i(m) \wedge P_i \in S\}$. Then, $CombinedVerify \big ( m, Combine (m, P) \big )$ returns $true$.

• Unforgeability of threshold signatures: If $Verify (m \in \textsf{String}, \sigma ^t \in {\mathcal {T}})$ returns $true$, then there exists a set S of $\vert S \vert = k$ processes such that, for every process $P_i \in S$, (1) $ShareSign _i(m)$ has been executed by $P_i$, or (2) $P_i$ is faulty.

B RareSync: basic properties

This section is dedicated to the correctness of RareSync (Algorithm 2). Concretely, we now formally prove Lemmas 1–8, which are merely stated in Sect. 4.4 without accompanying proofs for brevity.

Lemma 1

Let $P_i$ be a correct process. Then, $1 \le view _i \le f + 1$ throughout the entire execution.

Proof

First, $view _i \ge 1$ throughout the entire execution since (1) the initial value of $view _i$ is 1 (line 3 of Algorithm 1), and (2) the value of $view _i$ either increases (line 6) or is set to 1 (line 27).

By contradiction, suppose that $view _i = F> f + 1 > 1$ at some time during the execution. The update of $view _i$ to $F > f + 1$ must have been done at line 6. This means that, just before executing line 6, $view _i \ge f + 1$. However, this contradicts the check at line 5, which concludes the proof. $\square$

Lemma 2

Let $P_i$ be a correct process. Let $Exp _d$ be any expiration event of $dissemination\_timer _i$ that belongs to $h_i$ and let $Inv _d$ be the invocation of the $\textsf{measure}(\cdot )$ method (on $dissemination\_timer _i$) that has produced $Exp _d$. Then, $Exp _d$ immediately follows $Inv _d$ in $h_i$.

Proof

In order to prove the lemma, we show that only $Exp _d$ can immediately follow $Inv _d$ in $h_i$. We consider the following scenarios:

• Let an invocation $Inv '_d$ of the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ immediately follow $Inv _d$ in $h_i$: $Inv '_d$ could only have been invoked either at line 18 or at line 24. However, an invocation of the $\mathsf {cancel()}$ method on $dissemination\_timer _i$ (line 17 or line 23) must immediately precede $Inv '_d$ in $h_i$, which contradicts the fact that $Inv _d$ immediately precedes $Inv '_d$. Therefore, this scenario is impossible.

• Let an invocation $Inv '_d$ of the $\textsf{cancel}()$ method on $dissemination\_timer _i$ immediately follow $Inv _d$ in $h_i$: $Inv '_d$ could only have been invoked either at line 17 or at line 23. However, an invocation of the $\mathsf {cancel()}$ method on $view\_timer _i$ (line 16 or line 22) must immediately precede $Inv '_d$ in $h_i$, which contradicts the fact that $Inv _d$ immediately precedes $Inv '_d$. Hence, this scenario is impossible, as well.

• Let an expiration event $Exp '_d \ne Exp _d$ of $dissemination\_timer _i$ immediately follow $Inv _d$ in $h_i$: As $Inv _d$ could have been invoked either at line 18 or at line 24, an invocation of the $\mathsf {cancel()}$ method on $dissemination\_timer _i$ (line 17 or line 23) immediately precedes $Inv _d$ in $h_i$. This contradicts the fact that $Exp '_d \ne Exp _d$ is produced and immediately follows $Inv _d$, which renders this scenario impossible.

• Let an invocation $Inv _v$ of the $\textsf{measure}(\cdot )$ method on $view\_timer _i$ immediately follow $Inv _d$ in $h_i$: $Inv _v$ could have been invoked either at line 8 or at line 29. We further consider both cases:

  • If $Inv _v$ was invoked at line 8, then $Inv _v$ is immediately preceded by an expiration event of $view\_timer _i$ (line 4). This case is impossible as $Inv _v$ is not immediately preceded by $Inv _d$.

  • If $Inv _v$ was invoked at line 29, then $Inv _v$ is immediately preceded by an expiration event of $dissemination\_timer _i$ (line 25). This case is also impossible as $Inv _v$ is not immediately preceded by $Inv _d$.

  As neither of the two cases is possible, $Inv _v$ cannot immediately follow $Inv _d$.

• Let an invocation $Inv _v$ of the $\textsf{cancel}()$ method on $view\_timer _i$ immediately follow $Inv _d$ in $h_i$: $Inv _v$ could have been invoked either at line 16 or at line 22. In both cases, an invocation of the $\textsf{cancel}()$ method on $dissemination\_timer$ (line 17 or line 23) immediately follows $Inv _v$ in $h_i$. This contradicts the fact that $Inv _d$ produces $Exp _d$, which implies that this case is impossible.

• Let an expiration event $Exp _v$ of $view\_timer _i$ immediately follow $Inv _d$ in $h_i$: As $Inv _d$ could have been invoked either at line 18 or at line 24, invocations of the $\mathsf {cancel()}$ method on $view\_timer _i$ and $dissemination\_timer _i$ (lines 16, 17 or lines 22, 23) immediately precede $Inv _d$ in $h_i$. This contradicts the fact that $Exp _v$ is produced and immediately follows $Inv _d$, which renders this scenario impossible.

As any other option is impossible, $Exp _d$ must immediately follow $Inv _d$ in $h_i$. Thus, the lemma. $\square$

Lemma 3

(Monotonically increasing views) Let $P_i$ be a correct process. Let $e_1 = \textsf{advance}(v)$, $e_2 = \textsf{advance}(v')$ and $e_1 {\mathop {\prec }\limits ^{\beta _i}} e_2$. Then, $v' > v$.

Proof

Let $epoch _i = e$ and $view _i = j$ when $P_i$ triggers $\textsf{advance}(v)$. Moreover, let $epoch _i = e'$ and $view _i = j'$ when $P_i$ triggers $\textsf{advance}(v')$. As the value of the $epoch _i$ variable only increases throughout the execution (lines 13,  15 and lines 19,  21), $e' \ge e$.

We investigate both possibilities:

• Let $e' > e$. In this case, the lemma follows from Lemma 1 and the fact that $(e' - 1) \cdot (f + 1) + j' > (e - 1) \cdot (f + 1) + j$, for every $j, j' \in [1, f + 1]$.

• Let $e' = e$. Just before triggering $\textsf{advance}(v)$ (line 3 or line 9 or line 30), $P_i$ has invoked the $\textsf{measure}(\cdot )$ method on $view\_timer _i$ (line 2 or line 8 or line 29); we denote this invocation of the $\textsf{measure}(\cdot )$ method by $Inv _v$. Now, we investigate two possible scenarios:

  • Let $P_i$ trigger $\textsf{advance}(v')$ at line 9. By contradiction, suppose that $j' \le j$. Hence, just before triggering $\textsf{advance}(v')$ (i.e., just before executing line 6), we have that $view _i < j$. Thus, line 27 must have been executed by $P_i$ after triggering $\textsf{advance}(v)$ and before triggering $\textsf{advance}(v')$, which means that an expiration event of $dissemination\_timer _i$ (line 25) follows $Inv _v$ in $h_i$. By Lemma 2, the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ was invoked by $P_i$ after the invocation of $Inv _v$. Hence, when the aforementioned invocation of the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ was invoked by $P_i$ (line 18 or line 24), the $epoch _i$ variable had a value greater than e (line 15 or line 21) since $epoch _i \ge e$ when processing line 13 or line 19; recall that the value of the $epoch _i$ variable only increases throughout the execution. Therefore, we reach a contradiction with the fact that $e' = e$, which means that $j' > j$ and the lemma holds in this case.

  • Let $P_i$ trigger $\textsf{advance}(v')$ at line 30. In this case, $P_i$ processes an expiration event of $dissemination\_timer _i$ (line 25); therefore, the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ was invoked by $P_i$ after the invocation of $Inv _v$ (by Lemma 2). As in the previous case, when the aforementioned invocation of the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ was invoked by $P_i$ (line 18 or line 24), the $epoch _i$ variable had a value greater than e (line 15 or line 21); recall that the value of the $epoch _i$ variable only increases throughout the execution. Thus, we reach a contradiction with the fact that $e' = e$, which renders this case impossible.

  In the only possible scenario, we have that $j' > j$, which implies that $v' > v$.

The lemma holds as it holds in both possible cases. $\square$

Lemma 4

Let $P_i$ be a correct process. Let $Inv _v$ be any invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ that belongs to $h_i$. Invocation $Inv _v$ is not immediately followed by another invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ in $h_i \mid _{ view }$.

Proof

We denote by $Inv '_v$ the first invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ after $Inv _v$ in $h_i \mid _{ view }$. If $Inv '_v$ does not exist, the lemma trivially holds. Hence, let $Inv '_v$ exist in the rest of the proof. We examine two possible cases:

• Let $Inv '_v$ be invoked at line 8: In this case, there exists an expiration event of $view\_timer _i$ (line 4) separating $Inv _v$ and $Inv '_v$ in $h_i \mid _{ view }$.

• Let $Inv '_v$ be invoked at line 29: In this case, $Inv '_v$ is immediately preceded by an expiration event $Exp _d$ of $dissemination\_timer _i$ (line 25) in $h_i$. By Lemma 2, an invocation $Inv _d$ of the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ immediately precedes $Exp _d$ in $h_i$. As $Inv _d$ could have been invoked either at line 18 or at line 24, $Inv _d$ is immediately preceded by invocations of the $\mathsf {cancel()}$ methods on $view\_timer _i$ and $dissemination\_timer _i$ (lines 16, 17 or lines 22, 23). Hence, in this case, an invocation of the $\mathsf {cancel()}$ method on $view\_timer _i$ separates $Inv _v$ and $Inv '_v$ in $h_i \mid _{ view }$.

The lemma holds since $Inv '_v$ does not immediately follow $Inv _v$ in $h_i \mid _{ view }$ in any of the two cases. $\square$

A direct consequence of Lemma 4 is that an expiration event of $view\_timer _i$ immediately follows (in a timer history associated with $view\_timer _i$) the $\mathsf {measure(\cdot )}$ invocation that has produced it.

Lemma 5

Let $P_i$ be a correct process. Let $Exp _v$ be any expiration event that belongs to $h_i \mid _{ view }$ and let $Inv _v$ be the invocation of the $\mathsf {measure(\cdot )}$ method (on $view\_timer _i$) that has produced $Exp _v$. Then, $Exp _v$ immediately follows $Inv _v$ in $h_i \mid _{ view }$.

Proof

We prove the lemma by induction.

Base step: Let $Inv _v^1$ be the first invocation of the $\mathsf {measure(\cdot )}$ method in $h_i \mid _{ view }$ that produces an expiration event, and let $Exp _v^1$ be the expiration event produced by $Inv _v^1$. Expiration event $Exp _v^1$ immediately follows $Inv _v^1$ in $h_i \mid _{ view }$.

Since $Inv _v^1$ produces the expiration event $Exp _v^1$, an invocation of the $\mathsf {cancel()}$ method does not immediately follow $Inv _v^1$ in $h_i \mid _{ view }$. Moreover, no invocation of the $\mathsf {measure(\cdot )}$ method immediately follows $Inv _v^1$ in $h_i \mid _{ view }$ (by Lemma 4). Finally, no expiration event produced by a different invocation of the $\mathsf {measure(\cdot )}$ method immediately follows $Inv _v^1$ in $h_i \mid _{ view }$ since $Inv _v^1$ is the first invocation of the method in $h_i \mid _{ view }$ that produces an expiration event. Therefore, the statement of the lemma holds for $Inv _v^1$ and $Exp _v^1$.

Induction step: Let $Inv _v^j$ be the j-th invocation of the $\mathsf {measure(\cdot )}$ method in $h_i \mid _{ view }$ that produces an expiration event, where $j > 1$, and let $Exp _v^j$ be the expiration event produced by $Inv _v^j$. Expiration event $Exp _v^j$ immediately follows $Inv _v^j$ in $h_i \mid _{ view }$.

Induction hypothesis: For every $k \in [1, j - 1]$, the k-th invocation of the $\textsf{measure}(\cdot )$ method in $h_i \mid _{ view }$ that produces an expiration event is immediately followed by the produced expiration event in $h_i \mid _{ view }$.

An invocation of the $\mathsf {cancel()}$ method does not immediately follow $Inv _v^j$ in $h_i \mid _{ view }$ since $Inv _v^j$ produces $Exp _v^j$. Moreover, no invocation of the $\mathsf {measure(\cdot )}$ method immediately follows $Inv _v^j$ in $h_i \mid _{ view }$ (by Lemma 4). Lastly, no expiration event produced by a different invocation of the $\mathsf {measure(\cdot )}$ method immediately follows $Inv _v^j$ in $h_i \mid _{ view }$ by the induction hypothesis. Therefore, the statement of the lemma holds for $Inv _v^j$ and $Exp _v^j$, which concludes the proof. $\square$

Lemma 6

Let $P_i$ be a correct process. Let $Exp _v$ be any expiration event of $view\_timer _i$ that belongs to $h_i$ and let $Inv _v$ be the invocation of the $\textsf{measure}(\cdot )$ method (on $view\_timer _i$) that has produced $Exp _v$. Then, $Exp _v$ immediately follows $Inv _v$ in $h_i$.

Proof

Let us consider all possible scenarios (as in the proof of Lemma 2):

• Let an invocation $Inv _d$ of the $\textsf{measure}(\cdot )$ method on $dissemination\_timer _i$ immediately follow $Inv _v$ in $h_i$: $Inv _d$ could have been invoked either at line 18 or at line 24. However, an invocation of the $\mathsf {cancel()}$ method on $dissemination\_timer _i$ (line 17 or line 23) must immediately precede $Inv _d$ in $h_i$, which contradicts the fact that $Inv _v$ immediately precedes $Inv _d$. Therefore, this scenario is impossible.

• Let an invocation $Inv _d$ of the $\textsf{cancel}()$ method on $dissemination\_timer _i$ immediately follow $Inv _v$ in $h_i$: $Inv _d$ could have been invoked either at line 17 or at line 23. However, an invocation of the $\mathsf {cancel()}$ method on $view\_timer _i$ (line 16 or line 22) must immediately precede $Inv _d$ in $h_i$, which contradicts the fact that $Inv _v$ immediately precedes $Inv _d$. Hence, this scenario is impossible, as well.

• Let an expiration event $Exp _d$ of $dissemination\_timer _i$ immediately follow $Inv _v$ in $h_i$: This is impossible due to Lemma 2.

• Let the event immediately following $Inv _v$ be (1) an invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$, or (2) an invocation of the $\mathsf {cancel()}$ method on $view\_timer _i$, or (3) an expiration event $Exp '_v$ of $view\_timer _i$, where $Exp '_v \ne Exp _v$: This case is impossible due to Lemma 5.

As any other option is impossible, $Exp _v$ must immediately follow $Inv _v$ in $h_i$. $\square$

Lemma 7

Let $P_i$ be a correct process. Let $Inv _v$ denote an invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ which produces an expiration event, and let $Exp _v$ denote the expiration event produced by $Inv _v$. Let $epoch _i = e$ and $view _i = v$ when $P_i$ invokes $Inv _v$. Then, when $P_i$ processes $Exp _v$ (line 4), $epoch _i = e$ and $view _i = v$.

Proof

By contradiction, suppose that $epoch _i \ne e$ or $view _i \ne v$ when $P_i$ processes $Exp _v$. Hence, the value of the variables of $P_i$ must have changed between invoking $Inv _v$ and processing $Exp _v$. Let us investigate all possible lines of Algorithm 2 where $P_i$ could have modified its variables for the first time after invoking $Inv _v$ (the first modification occurs before processing $Exp _v$):

• The $view _i$ variable at line 6: If $P_i$ has modified its $view _i$ variable here, there exists an expiration event of $view\_timer _i$ (line 4) which follows $Inv _v$ in $h_i$. By Lemma 6, this expiration event cannot occur before processing $Exp _v$, which implies that this case is impossible.

• The $epoch _i$ variable at line 15: If $P_i$ updates its $epoch _i$ variable here, an invocation of the $\mathsf {cancel()}$ method on $view\_timer _i$ (line 16) separates $Inv _v$ and $Exp _v$ in $h_i$. However, this is impossible due to Lemma 6, which renders this case impossible.

• The $epoch _i$ variable at line 21: If $P_i$ updates its $epoch _i$ variable here, an invocation of the $\mathsf {cancel()}$ method on $view\_timer _i$ (line 22) separates $Inv _v$ and $Exp _v$ in $h_i$. However, this is impossible due to Lemma 6, which implies that this case is impossible.

• The $view _i$ variable at line 27: If $P_i$ updates its $view _i$ variable here, an expiration event of $dissemination\_timer _i$ (line 25) separates $Inv _v$ and $Exp _v$ in $h_i$, which contradicts Lemma 6.

Given that $P_i$ does not change the value of neither $epoch _i$ nor $view _i$ between invoking $Inv _v$ and processing $Exp _v$, the lemma holds. $\square$

Lemma 8

Let $P_i$ be a correct process. Let $\textsf{advance}(v) \in \beta _i$, where v is the j-th view of an epoch e and $j > 1$. Then, $\textsf{advance}(v - 1) {\mathop {\prec }\limits ^{\beta _i}} \textsf{advance}(v)$.

Proof

Since $P_i$ enters view v, which is not the first view of epoch e, $P_i$ triggers $\textsf{advance}(v)$ at line 9: $P_i$ could not have triggered $\textsf{advance}(v)$ neither at line 3 nor at line 30 since v is not the first view of epoch e. Due to line 4, the $\textsf{measure}(\cdot )$ method was invoked on $view\_timer _i$ before $\textsf{advance}(v)$ is triggered; we denote by $Inv _v$ this specific invocation of the $\mathsf {measure(\cdot )}$ method on $view\_timer _i$ and by $Exp _v$ its expiration event (processed by $P_i$ just before triggering $\textsf{advance}(v)$).

When $P_i$ triggers $\textsf{advance}(v)$ (at line 9), we have that $epoch _i = e$ and $view _i = j$. Moreover, when processing $Exp _v$, we have that $epoch _i = e$ and $view _i = j - 1$ (due to line 6). By Lemma 7, when $P_i$ has invoked $Inv _v$, we had the same state: $epoch _i = e$ and $view _i = j - 1$. Process $P_i$ could have invoked $Inv _v$ either (1) at line 2, or (2) at line 8, or (3) at line 29. Since $P_i$ triggers $\mathsf {advance(\cdot )}$ immediately after (line 3, line 9, or line 30), that $\textsf{advance}(\cdot )$ indication is for $v - 1$ (as $epoch _i = e$ and $view _i = j - 1$ at that time). Hence, $\textsf{advance}(v - 1) {\mathop {\prec }\limits ^{\beta _i}} \textsf{advance}(v)$. $\square$