Classification of repeated measurements using bias corrected Euclidean distance discriminant function

Ngailo, Edward Kanuti; Nadarajah, Saralees

doi:10.1007/s42952-023-00246-z

Classification of repeated measurements using bias corrected Euclidean distance discriminant function

Research Article
Published: 12 December 2023

Volume 53, pages 281–305, (2024)
Cite this article

Journal of the Korean Statistical Society Aims and scope Submit manuscript

Edward Kanuti Ngailo¹ &
Saralees Nadarajah²

71 Accesses
Explore all metrics

Abstract

This paper introduces a novel approach for approximating misclassification probabilities in Euclidean distance classifier when the group means exhibit a bilinear structure such as in the growth curve model first proposed by Potthoff and Roy (Biometrika 51:313–326, 1964). Initially, by leveraging certain statistical relationships, we establish two general results for the improved Euclidean discriminant function in both weighted and unweighted growth curve mean structures. We derive these approximations for the expected misclassification probabilities with respect to the distribution of the improved Euclidean discriminant function. Additionally, we compare the misclassification probabilities of the improved Euclidean discriminant function, the standard Euclidean discriminant function, and the linear discriminant function. It is important to note that in cases where the mean structure is weighted, a higher number of repeated measurements yields better classification results with the improved Euclidean discriminant function and the standard Euclidean discriminant function, allowing for more information to be acquired, as opposed to the linear discriminant function, which performs well with a smaller number of repeated measurements. Furthermore, we evaluate the accuracy of the suggested approximations by Monte Carlo simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Using the growth curve model in classification of repeated measurements

Article 29 March 2024

Generalized Gini linear and quadratic discriminant analyses

Article 15 July 2020

Unequal Priors in Linear Discriminant Analysis

Article 24 July 2019

Availability of data and material

Not applicable.

Code availability

The code used can be obtained from the corresponding author.

References

Batsidis, A., & Zografos, K. (2006). Discrimination of observations into one of two elliptic populations based on monotone training samples. Metrika, 64, 221–241. https://doi.org/10.1007/s00184-006-0046-y
Article MathSciNet Google Scholar
Fisher, R. A. (1936). The use of multiple measurements in taxonomic problems. Annals of Eugenics, 7(2), 179–188. https://doi.org/10.1111/j.1469-1809.1936.tb02137.x
Article Google Scholar
Fisher, R. A. (1938). The statistical utilization of multiple measurements. Annals of Eugenics, 8(4), 376–386. https://doi.org/10.1111/j.1469-1809.1938.tb02189.x
Article Google Scholar
Fujikoshi, Y. (2000). Error bounds for asymptotic approximations of the linear discriminant function when the sample sizes and dimensionality are large. Journal of Multivariate Analysis, 73, 1–17. https://doi.org/10.1006/jmva.1999.1862
Article MathSciNet Google Scholar
Fujikoshi, Y., & Seo, T. (1998). Asymptotic approximations for EPMC’s of the linear and the quadratic discriminant functions when the sample sizes and the dimension are large. Random Operators and Stochastic Equations, 6(3), 269–280. https://doi.org/10.1515/rose.1998.6.3.269
Article MathSciNet Google Scholar
Hotelling, H. (1931). The generalization of Student’s ratio. Annals of Eugenics, 2, 360–378. https://doi.org/10.1111/j.1469-1809.1938.tb02189.x
Article Google Scholar
Koolaard, J. P., & Lawoko, C. R. O. (1996). The linear and Euclidean discriminant functions: A comparison via asymptotic expansions and simulation study. Communications in Statistics - Theory and Methods, 25, 2989–3011. https://doi.org/10.1080/03610929608831882
Article MathSciNet Google Scholar
Lachenbruch, P. A. (1968). On expected probabilities of misclassification in discriminant analysis, necessary sample size, and a relation with the multiple correlation coefficient. Biometrics, 24, 823–834. https://doi.org/10.2307/2528873
Article Google Scholar
Lee, J. C. (1982). Classification of growth curves. Handbook of Statistics, 2, 121–137. https://doi.org/10.1016/S0169-7161(82)02008-2
Article MathSciNet Google Scholar
Levesque, L., Francine, D., Zarit, Z. H., Lise, L., & Francine, G. (2008). Predicting longitudinal patterns of psychological distress in older husband caregivers: Further analysis of existing data. Aging and Mental Health, 12, 333–342.
Article PubMed Google Scholar
Mahalanobis, P. C. (1936). On the generalized distance in statistics. National Institute of Science of India. https://doi.org/10.4236/ojs.2019.91002
Article Google Scholar
Marco, V. R., Young, D. M., & Turner, D. W. (1987). The Euclidean distance classifier: An alternative to the linear discriminant function. Communications in Statistics - Simulation and Computation, 16, 485–505. https://doi.org/10.1080/03610918708812601
Article MathSciNet Google Scholar
Mentz, G. B., & Kshirsagar, A. M. (2005). Classification using growth curves. Communications in Statistics - Theory and Methods, 33, 2487–2502. https://doi.org/10.1081/STA-200031350
Article MathSciNet Google Scholar
Ngailo, E. K., & Chuma, F. (2022). Approximation of misclassification probabilities in linear discriminant analysis based on repeated measurements. Communications in Statistics - Theory and Methods. https://doi.org/10.1080/03610926.2022.2062605
Article Google Scholar
Ngailo, E. K., & Ngaruye, I. (2022). Asymptotic results for expected probability of misclassifications in linear discriminant analysis with repeated measurements. Communications in Statistics - Theory and Methods. https://doi.org/10.1080/03610926.2022.2116286
Article Google Scholar
Ngailo, E. K., Singull, M., & von Rosen, D. (2021). Asymptotic approximation of misclassification probabilities in linear discriminant analysis with repeated measurements. Acta et Commentationes Universitatis Tartuensis de Mathematica. https://doi.org/10.12697/ACUTM.2021.25.05
Article MathSciNet Google Scholar
Okamoto, M. (1963). An asymptotic expansion for the distribution of the linear discriminant function. Annals of Mathematical Statistics, 34, 1286–1301. https://doi.org/10.1214/aoms/1177703864
Article MathSciNet Google Scholar
Pearson, K. (1916). On the probability that two independent distributions of frequency are really samples from the same population. Biometrika, 8, 250–254.
Article Google Scholar
Potthoff, R. F., & Roy, S. N. (1964). A generalized multivariate analysis of variance model useful especially for growth curve problems. Biometrika, 51, 313–326. https://doi.org/10.2307/2334137
Article MathSciNet Google Scholar
Rencher, C. A. (1998). Multivariate statistical inference and applications. Wiley.
Google Scholar
Rencher, C. A., & Christensen, F. W. (2012). Methods of multivariate analysis. Wiley.
Book Google Scholar
Shutoh, N. (2012). An asymptotic approximation for EPMC in linear discriminant analysis based on monotone missing data. Journal of Statistical Planning and Inference, 142, 110–125. https://doi.org/10.1016/j.jspi.2011.07.001
Article MathSciNet Google Scholar
Siotani, M. (1982). Large sample approximations and asymptotic expansions of classification statistics. In P. R. Krishnaiah & L. N. Kanal (Eds.), Handbook of Statistics (pp. 61–100). North-Holland.
Google Scholar
von Rosen, D. (2018). Bilinear regression analysis: An introduction. Springer.
Book Google Scholar

Download references

Funding

No funds received for this research.

Author information

Authors and Affiliations

Department of Physics, Mathematics and Informatics, University of Dar es Salaam, Dar es Salaam, Tanzania
Edward Kanuti Ngailo
Department of Mathematics, University of Manchester, Manchester, M13 9PL, UK
Saralees Nadarajah

Authors

Edward Kanuti Ngailo
View author publications
You can also search for this author in PubMed Google Scholar
Saralees Nadarajah
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Edward Kanuti Ngailo.

Ethics declarations

Conflict of interest

Both authors have no conflicts of interest.

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

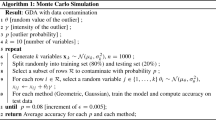
Appendix

In this section, we present the proofs for theorems.

A1: Proof of the theorem when the mean parameter of EDF is unweighted

Theorem 5.1

Consider the Euclidean discriminant function in (5). If ${\widehat{{\textbf{b}}}}_i,$ $i\in \{1, 2\}$ is unweighted, then

$$\begin{aligned} {\mathbb{E}}\left[ \widehat{D}_E|{\varvec{x}}\in \pi _i\right] = (-1)^{i+1}\frac{1}{2}{\boldsymbol{\Delta }}_E^{2}+\frac{1}{2}\Bigg (\frac{1}{n_2}- \frac{1}{n_1}\Bigg )\text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) . \end{aligned}$$

Proof

We present the proof for the moments of $U_i.$ Recall that

$$\begin{aligned} U_i=\left( {{\textbf{b}}}^{i}-\frac{1}{2}\left( \widehat{{{\textbf{b}}}}_{1}+ \widehat{{\textbf{b}}}_{2}\right) \right) ' {{\textbf{A}}}'{{\textbf{A}}}\left( \widehat{{\textbf{b}}}_{1}- \widehat{{{\textbf{b}}}}_{2}\right) . \end{aligned}$$

The expectation of $U_i$ can be calculated as

$$\begin{aligned} {\mathbb{E}}\left[ U_i\right]&=\text{tr}\left\{ {\mathbb{E}}\left[ {{\textbf{A}}} \left( \widehat{{\textbf{b}}}_{1}-\widehat{{{\textbf{b}}}}_{2}\right) \left( \left( {{\textbf{A}}}{\textbf{b}}^{i}\right) '- \frac{1}{2} \left( \widehat{{\textbf{b}}}_{1}+\widehat{{{\textbf{b}}}}_{2} \right) '{{\textbf{A}}}'\right) \right] \right\} \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{b}}_{1} -{{\textbf{b}}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}'- \frac{1}{2}{{\textbf{A}}}\widehat{{{\textbf{b}}}}_{1} \widehat{{\textbf{b}}}'_{1}{{\textbf{A}}}'+ \frac{1}{2}{{\textbf{A}}}\widehat{{\textbf{b}}}_{2} \widehat{{{\textbf{b}}}}'_{2}{{\textbf{A}}}' \right\} \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{b}}_{1} -{{\textbf{b}}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}'- \frac{1}{2}{{\textbf{A}}}{\mathbb{E}}\left[ \widehat{{\textbf{b}}}_{1} \widehat{{{\textbf{b}}}}'_{1}\right] {{\textbf{A}}}'+ \frac{1}{2}{\textbf{A}}{\mathbb{E}}\left[ \widehat{{{\textbf{b}}}}_{2} \widehat{{\textbf{b}}}'_{2}\right] {{\textbf{A}}}' \right\} \\ &= \text{tr}\Big \{{{\textbf{A}}}\left( {{\textbf{b}}}_{1} -{\textbf{b}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}'- \frac{1}{2}{\textbf{A}}\left( \frac{1}{n_1}\left( {{\textbf{A}}}' {{\textbf{A}}}\right) ^{-1} {\textbf{A}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}} \left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}+{\textbf{b}}_{1} {{\textbf{b}}}'_{1}\right) {{\textbf{A}}}'\\ &\quad +\frac{1}{2}{{\textbf{A}}}\left( \frac{1}{n_2} \left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}{{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1} +{{\textbf{b}}}_{2}{\textbf{b}}'_{2}\right) {{\textbf{A}}}'\Big \}\\ &= \text{tr}\Big \{{{\textbf{A}}}\left( {{\textbf{b}}}_{1} -{\textbf{b}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}'- \frac{1}{2}\frac{1}{n_1}{{\textbf{A}}}\left( {{\textbf{A}}}' {{\textbf{A}}}\right) ^{-1} {\textbf{A}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}} \left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}- \frac{1}{2}{{\textbf{A}}}{{\textbf{b}}}_{1}{{\textbf{b}}}'_{1}{{\textbf{A}}}' \end{aligned}$$

$$\begin{aligned} &\quad +\frac{1}{2}\frac{1}{n_2}{\textbf{A}}\left( {{\textbf{A}}}' {{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{\textbf{A}} \left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}+ \frac{1}{2}{{\textbf{A}}}{\textbf{b}}_{2}{{\textbf{b}}}'_{2}{{\textbf{A}}}' \Big \}\\ &= \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{b}}_{1}-{{\textbf{b}}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}'{{\boldsymbol{\Sigma }}}^{-1}- \frac{1}{2}{{\textbf{A}}}{{\textbf{b}}}'_{1}{{\textbf{b}}}'_{1} {{\textbf{A}}}'+ \frac{1}{2}{{\textbf{A}}}{{\textbf{b}}}_{2} {{\textbf{b}}}'_{2}{{\textbf{A}}}'\right\} \\ &\quad -\frac{1}{2}\left( \dfrac{1}{n_1}- \dfrac{1}{n_2}\right) \text{tr}\left\{ {{\textbf{A}}}\left( {{\textbf{A}}}' {\textbf{A}}\right) ^{-1}{{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}} \left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1}{{\textbf{A}}}'\right\} \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( \left( {\textbf{b}}_{1} -{{\textbf{b}}}_{2}\right) {{\textbf{b}}}^{i}- \frac{1}{2} \left( {\textbf{b}}_{1}-{{\textbf{b}}}_{2}\right) \left( {{\textbf{b}}}_{1}+{\textbf{b}}_{2}\right) '\right) {{\textbf{A}}}'\right\} \\ &\quad -\frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{A}}^{\prime } {{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{\textbf{A}} \left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}{{\textbf{A}}}'\right\} \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{b}}_{1}- {{\textbf{b}}}_{2}\right) \left( {{\textbf{b}}}^{i}-\frac{1}{2} \left( {{\textbf{b}}}_{1}+{{\textbf{b}}}_{2}\right) '\right) {\textbf{A}}'\right\} - \frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \end{aligned}$$

$$\begin{aligned} &\quad \cdot \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{A}}^{\prime } {{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{\textbf{A}} \left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}{{\textbf{A}}}'\right\} \\ &= \frac{1}{2}\left( {{\textbf{b}}}_{1}-{\textbf{b}}_{2}\right) ' {{\textbf{A}}}'{{\textbf{A}}}\left( {{\textbf{b}}}_{1}- {\textbf{b}}_{2}\right) (-1)^{i-1} - \frac{1}{2}\left( \dfrac{1}{n_1}- \dfrac{1}{n_2}\right) \\ &\quad \cdot \text{tr}\left\{ {{\textbf{A}}} \left( {\textbf{A}}^{\prime }{{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{\textbf{A}}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}{{\textbf{A}}}'\right\} \\ &= \frac{1}{2}\Delta ^2(-1)^{i-1}-\frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \text{tr}\left( {{\textbf{P}}}_{{{\textbf{A}}}}{{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{\textbf{A}}}\right) \\ &= \frac{1}{2}\Delta ^2(-1)^{i-1}-\frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}{{\textbf{P}}}_{{\textbf{A}}}\right) \\ &= \frac{1}{2}\Delta ^2(-1)^{i-1}-\frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) , \quad {\textbf{P}}_{{{\textbf{A}}}}{{\textbf{P}}}_{{{\textbf{A}}}} ={{\textbf{P}}}_{{{\textbf{A}}}}, \quad i=1, 2. \end{aligned}$$

$\square$

A2: Proof of the theorem when the mean parameter of EDF is weighted

Theorem 5.2

Consider the Euclidean discriminant function in (5). If ${\widehat{{\textbf{b}}}}_i,$ $i\in \{1, 2\}$ is weighted, then

$$\begin{aligned} {\mathbb{E}}\left[ \widehat{D}_E|{\varvec{x}}\in \pi _i\right] = \frac{1}{2}(-1)^{(i-1)}{\boldsymbol{\Delta }}^2_E+\frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1}\text{tr}\left( {\textbf{A}}\left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}\right) ^{-1}{\textbf{A}}'\right) . \end{aligned}$$

Proof

For moments of $U_i,$ ${\mathbb{E}}\left[ U_i\right]$ can be calculated as

$$\begin{aligned} {\mathbb{E}}\left[ U_i\right]&= \text{tr}\left\{ {\mathbb{E}}\left[ \left( \widehat{{\textbf{b}}}_{1}- \widehat{{{\textbf{b}}}}_{2}\right) ' {{\textbf{A}}}'{\varvec{x}}_i- \frac{1}{2}\left( \widehat{{{\textbf{b}}}}_{1}-\widehat{{\textbf{b}}}_{2} \right) ' {{\textbf{A}}}'{{\textbf{A}}}\left( \widehat{{\textbf{b}}}_{1}+ \widehat{{{\textbf{b}}}}_{2}\right) \right] \right\} {\mathbb{E}}_{{\textbf{S}}}\left[ {\mathbb{E}}\left[ U_i|{\widehat{{\textbf{b}}}}_1, \widehat{{\textbf{b}}}_2, {\textbf{S}}\right] \right] \\ &= {\mathbb{E}}_{{\textbf{S}}} \text{tr}\left\{ {\mathbb{E}}\left[ \left( {{\textbf{A}}}\widehat{{{\textbf{b}}}}_{1}-{{\textbf{A}}} \widehat{{{\textbf{b}}}}_{2}\right) \left( \left( {{\textbf{A}}} {{\textbf{b}}}^{i}-\frac{1}{2}\left( {{\textbf{A}}} \widehat{{{\textbf{b}}}}_{1}+ {\textbf{A}}\widehat{{{\textbf{b}}}}_{2}\right) ' \right) | \widehat{{{\textbf{b}}}}_{1}, \widehat{{{\textbf{b}}}}_{2}, {{\textbf{S}}}\right) \right] \right\} \\ &= \left( {{\textbf{b}}}_{1}-{{\textbf{b}}}_{2}\right) ' {\textbf{A}}'{{\textbf{A}}}{{\textbf{b}}}^{i} - \frac{1}{2}\frac{1}{n_1} \text{tr} \left\{ {\mathbb{E}}\left[ {{\textbf{A}}}\left( {{\textbf{A}}}' {\textbf{S}}^{-1}{{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}' {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{\textbf{S}}^{-1}{{\textbf{A}}} \left( {{\textbf{A}}}^{\prime }{{\textbf{S}}}^{-1}{\textbf{A}}\right) ^{-1}{{\textbf{A}}}' \right] \right\} \end{aligned}$$

$$\begin{aligned} &\quad +\frac{1}{2}\frac{1}{n_2}\text{tr}\left\{ {\mathbb{E}}\left[ {{\textbf{A}}}\left( {\textbf{A}}'{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1}{{\textbf{A}}}' {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1} {{\textbf{A}}}\left( {{\textbf{A}}}^{\prime }{\textbf{S}}^{-1}{{\textbf{A}}} \right) ^{-1}{{\textbf{A}}}'\right] \right\} \\ &\quad -\frac{1}{2}\left( \widehat{{\textbf{b}}}_{1}-\widehat{{{\textbf{b}}}}_{2}\right) ' {{\textbf{A}}}'{\textbf{A}}\left( \widehat{{{\textbf{b}}}}_{1}+\widehat{{{\textbf{b}}}}_{2}\right) \\ &= \left( {{\textbf{b}}}_{1}-{{\textbf{b}}}_{2}\right) '{\textbf{A}}'{{\textbf{A}}} \left( {\textbf{b}}_i-\frac{1}{2}\left( {\textbf{b}}_1+{\textbf{b}}_2\right) \right) - \frac{1}{2}\left( \frac{1}{n_1}-\frac{1}{n_2}\right) \\ &\quad \cdot \dfrac{(p-q-1)(p-1)}{(n-q-1)(p-n+q-1)} \text{tr}\left( \left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}\right) ^{-1}\right) \\ &= \frac{1}{2}(-1)^{i+1}\Delta ^2 - \frac{1}{2}\left( \frac{1}{n_1}-\frac{1}{n_2}\right) \text{tr}{\mathbb{E}}\left[ {{\textbf{A}}}\left( {{\textbf{A}}}'{\textbf{S}}^{-1}{{\textbf{A}}} \right) ^{-1} {{\textbf{A}}}' {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1}{{\textbf{A}}} \left( {{\textbf{A}}}^{\prime }{\textbf{S}}^{-1}{{\textbf{A}}} \right) ^{-1}{{\textbf{A}}}' \right] \\ &= (-1)^{i+1}\frac{1}{2}\Delta ^2-\frac{1}{2}\left( \frac{1}{n_1}-\frac{1}{n_2}\right) \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1}\text{tr}\left( {\textbf{A}}\left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}'\right) ^{-1}{\textbf{A}}'\right) . \end{aligned}$$

$\square$

A3: Proof of Theorem 3.3, bias corrected Euclidean discriminant function (unweighted case)

We first present the proof for the moments of $U_i.$ Recall that

$$\begin{aligned} U_i=\left( {{\textbf{b}}}^{i}-\frac{1}{2}\left( \widehat{{{\textbf{b}}}}_{1}+\widehat{{\textbf{b}}}_{2}\right) \right) ' {{\textbf{A}}}'{{\textbf{A}}} \left( \widehat{{\textbf{b}}}_{1}-\widehat{{{\textbf{b}}}}_{2}\right) + \left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) . \end{aligned}$$

Then ${\mathbb{E}}\left[ U_i\right]$ can be calculated as

$$\begin{aligned} {\mathbb{E}}\left[ U_i\right]&= \text{tr}\left\{ {\mathbb{E}}\left[ {{\textbf{A}}}\left( \widehat{{\textbf{b}}}_{1}-\widehat{{{\textbf{b}}}}_{2}\right) \left( \left( {{\textbf{A}}}{\textbf{b}}^{i}\right) ' - \frac{1}{2}\left( \widehat{{\textbf{b}}}_{1}+\widehat{{{\textbf{b}}}}_{2}\right) '{{\textbf{A}}}'\right) \right] \right\} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{b}}_{1}-{{\textbf{b}}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}' - \frac{1}{2}{{\textbf{A}}}\widehat{{{\textbf{b}}}}_{1}\widehat{{\textbf{b}}}'_{1}{{\textbf{A}}}' + \frac{1}{2}{{\textbf{A}}}\widehat{{\textbf{b}}}_{2}\widehat{{{\textbf{b}}}}'_{2}{{\textbf{A}}}' \right\} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{b}}_{1}-{{\textbf{b}}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}' - \frac{1}{2}{{\textbf{A}}}{\mathbb{E}} \left( \widehat{{\textbf{b}}}_{1}\widehat{{{\textbf{b}}}}'_{1}\right) {{\textbf{A}}}'+ \frac{1}{2}{\textbf{A}}{\mathbb{E}} \left( \widehat{{{\textbf{b}}}}_{2}\widehat{{{\textbf{b}}}}'_{2} \right) {{\textbf{A}}}' \right\} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \text{tr}\Big \{{{\textbf{A}}}\left( {{\textbf{b}}}_{1}-{\textbf{b}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}'- \frac{1}{2}{\textbf{A}}\left( \frac{1}{n_1}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1} {\textbf{A}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}} \left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}+{\textbf{b}}_{1}{{\textbf{b}}}'_{1}\right) {{\textbf{A}}}' \\ &\quad +\frac{1}{2}{{\textbf{A}}}\left( \frac{1}{n_2}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1} {\textbf{A}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}+ {\textbf{b}}_{2}{{\textbf{b}}}'_{2}\right) {{\textbf{A}}}'\Big \} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{\textbf{P}}_{{{\textbf{A}}}}\right) \\ &= \text{tr}\Big \{{{\textbf{A}}}\left( {{\textbf{b}}}_{1}-{\textbf{b}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}'- \frac{1}{2}\frac{1}{n_1}{{\textbf{A}}}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1} {\textbf{A}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1} - \frac{1}{2}{{\textbf{A}}}{{\textbf{b}}}_{1}{{\textbf{b}}}'_{1}{{\textbf{A}}}' \\ &\quad +\frac{1}{2}\frac{1}{n_2}{{\textbf{A}}}\left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}}\left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1} + \frac{1}{2}{{\textbf{A}}}{{\textbf{b}}}_{2}{\textbf{b}}'_{2}{{\textbf{A}}}' \Big \} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{b}}_{1}-{{\textbf{b}}}_{2}\right) {{\textbf{b}}}^{i}{{\textbf{A}}}'{{\boldsymbol{\Sigma }}}^{-1} - \frac{1}{2}{{\textbf{A}}}{{\textbf{b}}}'_{1}{{\textbf{b}}}'_{1}{{\textbf{A}}}' + \frac{1}{2}{{\textbf{A}}}{{\textbf{b}}}_{2}{{\textbf{b}}}'_{2}{{\textbf{A}}}'\right\} \\ &\quad -\frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \text{tr}\left\{ {{\textbf{A}}}\left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}}\left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1}{{\textbf{A}}}'\right\} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{\textbf{P}}_{{{\textbf{A}}}}\right) \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( \left( {\textbf{b}}_{1}-{{\textbf{b}}}_{2}\right) {{\textbf{b}}}^{i} - \frac{1}{2}\left( {\textbf{b}}_{1}-{{\textbf{b}}}_{2}\right) \left( {{\textbf{b}}}_{1}+{\textbf{b}}_{2}\right) '\right) {{\textbf{A}}}'\right\} \\ &\quad -\frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{A}}^{\prime }{{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}} \left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}{{\textbf{A}}}'\right\} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{b}}_{1}-{{\textbf{b}}}_{2}\right) \left( {{\textbf{b}}}^{i}-\frac{1}{2}\left( {{\textbf{b}}}_{1}+{{\textbf{b}}}_{2}\right) '\right) {\textbf{A}}'\right\} - \frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \\ &\quad \cdot \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{A}}^{\prime }{{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{\textbf{A}}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1}{{\textbf{A}}}'\right\} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \frac{1}{2}\left( {{\textbf{b}}}_{1}-{\textbf{b}}_{2}\right) ' {{\textbf{A}}}'{{\textbf{A}}} \left( {{\textbf{b}}}_{1}-{\textbf{b}}_{2}\right) (-1)^{i-1}- \frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \\ &\quad \cdot \text{tr}\left\{ {{\textbf{A}}}\left( {\textbf{A}}^{\prime }{{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{\textbf{A}}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'\right\} + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \frac{1}{2}\Delta ^2(-1)^{i-1}-\frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \text{tr}\left( {{\textbf{P}}}_{{{\textbf{A}}}}{{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{\textbf{A}}}\right) + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \frac{1}{2}\Delta ^2(-1)^{i-1}-\frac{1}{2}\left( \dfrac{1}{n_1}-\dfrac{1}{n_2}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}{{\textbf{P}}}_{{\textbf{A}}}\right) + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) \\ &= \frac{1}{2}(-1)^{i+1}\Delta ^2-\frac{1}{2}\left( \frac{1}{n_1}-\frac{1}{n_2}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) - \frac{1}{2}\left( \frac{1}{n_1}-\frac{1}{n_2}\right) \text{tr}\left( {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right) , \end{aligned}$$

(18)

where, in (18), ${{\textbf{P}}}_{{{\textbf{A}}}}{{\textbf{P}}}_{{\textbf{A}}}={{\textbf{P}}}_{{{\textbf{A}}}},$ $i=1, 2.$

Next we provide a derivation for ${\mathbb{E}}\left[ V_0\right]$:

$$\begin{aligned} {\mathbb{E}}\left[ V_0\right]&= {\mathbb{E}}\left[ \left( \widehat{{{\textbf{b}}}}_1-\widehat{{\textbf{b}}}_2\right) ' {{\textbf{A}}}'{{\textbf{A}}} \left( \widehat{{\textbf{b}}}_1-\widehat{{{\textbf{b}}}}_2\right) \right] \\ &= {\mathbb{E}}\left[ \text{tr}\left\{ {{\textbf{A}}}'{\textbf{A}} \left( \widehat{{{\textbf{b}}}}_1-\widehat{{{\textbf{b}}}}_2\right) \left( \widehat{{{\textbf{b}}}}_1-\widehat{{{\textbf{b}}}}_2\right) ' \right\} \right] \\ &= \text{tr}\left\{ {{\textbf{A}}}'{{\textbf{A}}}{\mathbb{E}} \left[ \left( \widehat{{{\textbf{b}}}}_1-\widehat{{{\textbf{b}}}}_2\right) \left( \widehat{{{\textbf{b}}}}_1-\widehat{{{\textbf{b}}}}_2\right) ' \right] \right\} \\ &= \text{tr}\left\{ {{\textbf{A}}}'{{\textbf{A}}}\left( \left( \frac{1}{n_1}+\frac{1}{n_2}\right) \left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1}{{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}} \left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1}+ \left( {{\textbf{b}}}_1-{{\textbf{b}}}_2\right) \left( {\textbf{b}}_1-{{\textbf{b}}}_2\right) '\right) \right\} \\ &= \text{tr}\left\{ {{\textbf{A}}}'{{\textbf{A}}}\left( \frac{1}{n_1}+\frac{1}{n_2}\right) \left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1}{{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}} \left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1}\right\} + \left( {{\textbf{b}}}_1-{{\textbf{b}}}_2\right) '{\textbf{A}}'{{\textbf{A}}} \left( {{\textbf{b}}}_1-{{\textbf{b}}}_2\right) \\ &= \left( \frac{1}{n_1}+\frac{1}{n_2}\right) \text{tr}\left\{ {{\textbf{A}}}\left( {{\textbf{A}}}'{{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}'{{\boldsymbol{\Sigma }}}{{\textbf{A}}} \left( {{\textbf{A}}}'{\textbf{A}}\right) ^{-1}{{\textbf{A}}}'\right\} + \left( {{\textbf{b}}}_1-{\textbf{b}}_2\right) '{{\textbf{A}}}'{{\textbf{A}}} \left( {{\textbf{b}}}_1-{{\textbf{b}}}_2\right) \\ &= \left( \frac{1}{n_1}+\frac{1}{n_2}\right) \text{tr}\left\{ {{\textbf{P}}}_{{{\textbf{A}}}}{{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{\textbf{A}}}\right\} + \left( {{\textbf{b}}}_1-{{\textbf{b}}}_2\right) '{{\textbf{A}}}'{{\textbf{A}}} \left( {{\textbf{b}}}_1-{{\textbf{b}}}_2\right) \\ &= \left( \frac{1}{n_1}+\frac{1}{n_2}\right) \text{tr}\left\{ {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}{{\textbf{P}}}_{{\textbf{A}}}\right\} + \left( {{\textbf{b}}}_1-{{\textbf{b}}}_2\right) '{{\textbf{A}}}'{{\textbf{A}}} \left( {{\textbf{b}}}_1-{{\textbf{b}}}_2\right) \\ &= \left( \frac{1}{n_1}+\frac{1}{n_2}\right) \text{tr}\left\{ {{\boldsymbol{\Sigma }}}{{\textbf{P}}}_{{{\textbf{A}}}}\right\} + \left( {\textbf{b}}_1-{{\textbf{b}}}_2\right) '{{\textbf{A}}}'{{\textbf{A}}} \left( {{\textbf{b}}}_1-{\textbf{b}}_2\right) , \quad {{\textbf{P}}}_{{{\textbf{A}}}}{\textbf{P}}_{{{\textbf{A}}}}={{\textbf{P}}}_{{{\textbf{A}}}}. \end{aligned}$$

A4: Proof of Theorem 3.3

We have

$$\begin{aligned} \left| e(i|j)-\Phi \left( \gamma ^{(i)}_0\right) \right|&= \left| {\mathbb{E}}\left[ \Phi \left( U_i/\sqrt{V_0}\right) \right] - \Phi \left( \gamma ^{(i)}_0\right) \right| , \quad i\in \{1, 2\}, \ i\ne j\\ &= \left| {\mathbb{E}}\left[ \Phi \left( U_i/\sqrt{V_0}\right) -\Phi \left( \gamma ^{(i)}_0\right) \right] \right| \\ &\le {\mathbb{E}}\left[ \left| \Phi \left( U_i/\sqrt{V_0}\right) -\Phi \left( \gamma ^{(i)}_0\right) \right| \right] . \end{aligned}$$

Using Lebesgue’s dominated convergence theorem and Lemma 3.2, we see that the sequence $\left| \Phi \left( U_i/\sqrt{V_0}\right) - \Phi \left( \gamma ^{(i)}_0\right) \right|$ is uniformly integrable. Consequently, under Assumptions A1–A2 and Lemma 3.3, we have

$$\begin{aligned} {\mathbb{E}}\left[ \left| \Phi \left( U_i/\sqrt{V_0}\right) -\Phi \left( \gamma ^{(i)}_0 \right) \right| \right] \rightarrow 0. \end{aligned}$$

Therefore, we can assert that $\Phi \left( \gamma ^{(i)}_0\right)$ provides an asymptotic approximation to e(i|j).

A5: Proof of Theorem 3.5, bias corrected Euclidean discriminant function when the mean parameter ${\widehat{\textbf{B}}}$ is weighted

For moments of ${\widehat{D}}_{EBC_2} \left( {\varvec{x}}\right) ,$ ${\mathbb{E}} \left[ \widehat{D}_{EBC_2}\left( {\varvec{x}}\right) \right]$ can be calculated as

$$\begin{aligned}&{\mathbb{E}}_{{\textbf{S}}}\left[ {\mathbb{E}}\left[ \widehat{D}_{EBC_2}|{\widehat{{\textbf{b}}}}_1, {\widehat{{\textbf{b}}}}_2, {\textbf{S}}\right] \right] \\ &\quad = {\mathbb{E}}_{{\textbf{S}}} \text{tr}\left\{ {\mathbb{E}} \left[ \left( {{\textbf{A}}}\widehat{{{\textbf{b}}}}_{1}-{\textbf{A}}\widehat{{{\textbf{b}}}}_{2}\right) \left( \left( {{\textbf{A}}}{\textbf{b}}^{i}-\frac{1}{2} \left( {{\textbf{A}}}\widehat{{{\textbf{b}}}}_{1}+{\textbf{A}}\widehat{{{\textbf{b}}}}_{2}\right) ' \right) | \widehat{{{\textbf{b}}}}_{1}, \widehat{{{\textbf{b}}}}_{2}, {{\textbf{S}}}\right) \right] \right\} \\ &\qquad +\frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1} \text{tr}\left( {\textbf{A}}\left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}\right) ^{-1}{\textbf{A}}'\right) \\ &\quad = \left( {{\textbf{b}}}_{1}-{{\textbf{b}}}_{2}\right) '{\textbf{A}}'{{\textbf{A}}}{{\textbf{b}}}^{i}- \frac{1}{2}\frac{1}{n_1}\text{tr} {\mathbb{E}}\left[ {{\textbf{A}}}\left( {{\textbf{A}}}'{{\textbf{S}}}^{-1}{\textbf{A}}\right) ^{-1} {{\textbf{A}}}' {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1}{\textbf{A}} \left( {{\textbf{A}}}^{\prime }{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1}{{\textbf{A}}}' \right] \\ &\qquad +\frac{1}{2}\frac{1}{n_2}\text{tr} \left\{ {\mathbb{E}}\left[ {{\textbf{A}}}\left( {{\textbf{A}}}'{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1} {{\textbf{A}}}' {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1}{\textbf{A}} \left( {{\textbf{A}}}^{\prime }{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1}{{\textbf{A}}}'\right] \right\} \\ &\qquad -\frac{1}{2}\left( {{\textbf{b}}}_{1}-{\textbf{b}}_{2}\right) ' {{\textbf{A}}}'{{\textbf{A}}}\left( {{\textbf{b}}}_{1}+{\textbf{b}}_{2}\right) + \frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1} \\ &\qquad \cdot \text{tr}\left( {\textbf{A}}\left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}\right) ^{-1}{\textbf{A}}'\right) \\ &\quad = \left( {{\textbf{b}}}_{1}-{{\textbf{b}}}_{2}\right) '{\textbf{A}}'{{\textbf{A}}} \left( {\textbf{b}}_i-\frac{1}{2}\left( {\textbf{b}}_1+{\textbf{b}}_2\right) \right) - \frac{1}{2}\left( \frac{1}{n_1}-\frac{1}{n_2}\right) \\ &\qquad \cdot \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1} \text{tr}{\mathbb{E}}\left[ {{\textbf{A}}}\left( {{\textbf{A}}}'{\textbf{S}}^{-1}{{\textbf{A}}}\right) ^{-1} {{\textbf{A}}}' {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{\textbf{S}}^{-1}{{\textbf{A}}} \left( {{\textbf{A}}}^{\prime }{{\textbf{S}}}^{-1}{\textbf{A}}\right) ^{-1}{{\textbf{A}}}'\right] \\ &\qquad +\frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1} \text{tr}\left( {\textbf{A}}\left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}\right) ^{-1}{\textbf{A}}'\right) \\ &\quad = \frac{1}{2}(-1)^{i+1}\Delta ^2-\frac{1}{2}\left( \frac{1}{n_1}-\frac{1}{n_2}\right) \text{tr}{\mathbb{E}}\left[ {{\textbf{A}}}\left( {{\textbf{A}}}'{\textbf{S}}^{-1}{{\textbf{A}}} \right) ^{-1} {{\textbf{A}}}' {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1}{{\textbf{A}}} \left( {{\textbf{A}}}^{\prime }{\textbf{S}}^{-1}{{\textbf{A}}} \right) ^{-1}{{\textbf{A}}}' \right] \\ &\qquad +\frac{1}{2}\left( \frac{1}{n_2}-\frac{1}{n_1}\right) \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1} \text{tr}\left( {\textbf{A}}\left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}\right) ^{-1}{\textbf{A}}'\right) \\ &\quad = (-1)^{i+1}\frac{1}{2}\Delta ^2-\frac{1}{2}\left( \frac{1}{n_1}-\frac{1}{n_2}\right) \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1} \text{tr}\left( {\textbf{A}}\left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}'\right) ^{-1}{\textbf{A}}'\right) . \end{aligned}$$

(19)

The result from von Rosen (2018, page 447) has been used to simplify (19).

Next, we calculate the variance of either group $\pi _1$ or $\pi _2$ conditioned on $\widehat{{{\textbf{b}}}}_{1}$ and $\widehat{{\textbf{b}}}_{2}.$ The conditional expectation of ${\mathbb{E}}[V_1]$ given ${{\textbf{S}}}$ is

$$\begin{aligned} {\mathbb{E}}\left[ V_1\right] ={\mathbb{E}}_{{\textbf{S}}}\left[ {\mathbb{E}}\left[ V_1|{\textbf{S}}\right] \right]&= {\mathbb{E}}_{{\textbf{S}}}\left[ {\mathbb{E}}\left[ \left( \widehat{{\textbf{b}}}_1-\widehat{{{\textbf{b}}}}_2\right) ^{\prime } {{\textbf{A}}}^{\prime } {{\boldsymbol{\Sigma }}}{{\textbf{A}}}\left( \widehat{{{\textbf{b}}}}_1-\widehat{{\textbf{b}}}_2\right) |{{\textbf{S}}}\right] \right] \\ &= {\mathbb{E}}_{{\textbf{S}}}\left[ \text{tr}\left( {{\textbf{A}}}^{\prime } {{\boldsymbol{\Sigma }}}{{\textbf{A}}} {\mathbb{E}}\left[ \left( \widehat{{\textbf{b}}}_1-\widehat{{{\textbf{b}}}}_2\right) \left( \widehat{{\textbf{b}}}_1-\widehat{{{\textbf{b}}}}_2\right) ^{\prime }|{{\textbf{S}}} \right] \right) \right] . \end{aligned}$$

(20)

From (20),

$$\begin{aligned}&{\mathbb{E}}_{{\textbf{S}}}\left[ {\mathbb{E}}\left[ V_1|{\textbf{S}}\right] \right] \\ &\quad = {\mathbb{E}}_{{\textbf{S}}} \Big [\text{tr}\Big \{{\textbf{A}}^{\prime } {{\boldsymbol{\Sigma }}}{{\textbf{A}}} \Big ( \frac{1}{n_1}\left( {\textbf{A}}^{\prime } {{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1} {{\textbf{A}}}^{\prime } {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1}{{\textbf{A}}} \left( {\textbf{A}}^{\prime }{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1}\\ &\qquad +\frac{1}{n_2}\left( {{\textbf{A}}}^{\prime } {{\textbf{S}}}^{-1} {{\textbf{A}}} \right) ^{-1} {{\textbf{A}}}^{\prime } {\textbf{S}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1}{{\textbf{A}}} \left( {\textbf{A}}^{\prime }{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1}\Big )+ \left( {\textbf{b}}_1-{{\textbf{b}}}_2\right) \left( {{\textbf{b}}}_1-{\textbf{b}}_2\right) ^{\prime }\Big \}\Big ]\\ &\quad = \frac{n_1+n_2}{n_1 n_2} {\mathbb{E}}_{{\textbf{S}}}\left[ \text{tr}\left\{ {{\textbf{A}}}^{\prime } {{\boldsymbol{\Sigma }}}{{\textbf{A}}}\left( {{\textbf{A}}}^{\prime }{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1} {{\textbf{A}}}^{\prime } {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1} {{\textbf{A}}}\left( {{\textbf{A}}}^{\prime }{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1}\right\} \right] \\ &\qquad +\left( {{\textbf{b}}}_1-{\textbf{b}}_2\right) ^{\prime } {{\textbf{A}}}^{\prime }{{\textbf{A}}} \left( {\textbf{b}}_1-{{\textbf{b}}}_2\right) \\ &\quad = \frac{n_1+n_2}{n_1 n_2} \text{tr}\left\{ {{\boldsymbol{\Sigma }}}{\mathbb{E}}_{{\textbf{S}}} \left[ {{\textbf{A}}} \left( {\textbf{A}}^{\prime }{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1} {{\textbf{A}}}^{\prime } {{\textbf{S}}}^{-1} {{\boldsymbol{\Sigma }}}{{\textbf{S}}}^{-1}{{\textbf{A}}} \left( {\textbf{A}}^{\prime }{{\textbf{S}}}^{-1}{{\textbf{A}}} \right) ^{-1}{\textbf{A}}^{\prime }\right] \right\} \\ &\qquad +\left( {{\textbf{b}}}_1-{\textbf{b}}_2\right) ^{\prime } {{\textbf{A}}}^{\prime }{{\textbf{A}}} \left( {\textbf{b}}_1-{{\textbf{b}}}_2\right) \\ &\quad = \frac{n_1+n_2}{n_1 n_2} \frac{n-r({\textbf{C}})-1}{n-r({\textbf{C}})-p+r({\textbf{A}})-1} \text{tr}\left\{ {{\boldsymbol{\Sigma }}}{\textbf{A}}\left( {\textbf{A}}'{{\boldsymbol{\Sigma }}}^{-1}{\textbf{A}}'\right) ^{-1}\right\} \\ &\qquad +\left( {{\textbf{b}}}_1-{\textbf{b}}_2\right) ^{\prime } {{\textbf{A}}}^{\prime }{{\textbf{A}}} \left( {\textbf{b}}_1-{{\textbf{b}}}_2\right) . \end{aligned}$$

A6: Proof of Theorem 3.5

We have

$$\begin{aligned} \left| e(i|j)-\Phi \left( \gamma ^{(i)}\right) \right|&= \left| {\mathbb{E}}\left[ \Phi \left( U_i/\sqrt{V_1}\right) \right] - \Phi \left( \gamma ^{(i)}\right) \right| = \left| {\mathbb{E}}\left[ \Phi \left( U_i/\sqrt{V_1}\right) -\Phi \left( \gamma ^{(i)}\right) \right] \right| \\ &\le {\mathbb{E}}\left[ \left| \Phi \left( U_i/\sqrt{V_1}\right) -\Phi \left( \gamma ^{(i)}\right) \right| \right] . \end{aligned}$$

By Lebesgue’s dominated convergence theorem, Theorem 3.5 yields that the sequence $\left\{ \left| \Phi \left( U_i/\sqrt{V_1}\right) -\Phi \left( \gamma ^{(i)} \right) \right| \right\}$ is uniformly integrable. Hence, under the Assumptions A1–A2 and Lemma 3.4

$$\begin{aligned} {\mathbb{E}}\left[ \left| \Phi \left( U_i/\sqrt{V_1}\right) -\Phi \left( \gamma ^{(i)} \right) \right| \right] \longrightarrow 0. \end{aligned}$$

Thus, we can see that $\Phi \left( \gamma _0\right)$ provides an asymptotic approximation to e(i|j).

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Cite this article

Ngailo, E.K., Nadarajah, S. Classification of repeated measurements using bias corrected Euclidean distance discriminant function. J. Korean Stat. Soc. 53, 281–305 (2024). https://doi.org/10.1007/s42952-023-00246-z

Download citation

Received: 15 June 2023
Accepted: 26 November 2023
Published: 12 December 2023
Issue Date: March 2024
DOI: https://doi.org/10.1007/s42952-023-00246-z

Keywords

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Classification of repeated measurements using bias corrected Euclidean distance discriminant function

Abstract

Access this article

Similar content being viewed by others

Using the growth curve model in classification of repeated measurements

Generalized Gini linear and quadratic discriminant analyses

Unequal Priors in Linear Discriminant Analysis

Availability of data and material

Code availability

References

Funding

Author information

Authors and Affiliations

Corresponding author

Ethics declarations

Conflict of interest

Ethics approval

Consent to participate

Consent for publication

Additional information

Publisher's Note

Appendix

Theorem 5.1

Proof

Theorem 5.2

Proof

Rights and permissions

About this article

Cite this article

Keywords

Navigation

Classification of repeated measurements using bias corrected Euclidean distance discriminant function

Abstract

Access this article

Similar content being viewed by others

Using the growth curve model in classification of repeated measurements

Generalized Gini linear and quadratic discriminant analyses

Unequal Priors in Linear Discriminant Analysis

Availability of data and material

Code availability

References

Funding

Author information

Authors and Affiliations

Corresponding author

Ethics declarations

Conflict of interest

Ethics approval

Consent to participate

Consent for publication

Additional information

Publisher's Note

Appendix

Appendix

Theorem 5.1

Proof

Theorem 5.2

Proof

Rights and permissions

About this article

Cite this article

Share this article

Keywords

Search

Navigation