Abstract
In this article, we discuss the error analysis for a certain class of monotone finite volume schemes approximating nonlocal scalar conservation laws, modeling traffic flow and crowd dynamics, without any additional assumptions on monotonicity or linearity of the kernel \(\mu \) or the flux f. We first prove a novel Kuznetsov-type lemma for this class of PDEs and thereby show that the finite volume approximations converge to the entropy solution at the rate of \(\sqrt{\Delta t}\) in \(L^1(\mathbb {R})\). To the best of our knowledge, this is the first proof of any type of convergence rate for this class of conservation laws. We also present numerical experiments to illustrate this result.
Similar content being viewed by others
1 Introduction
The celebrated Lighthill–Whitham–Richards (LWR) model [30, 32] given by
with u being the mean traffic density and \(\nu \) the mean traffic speed, is one of the widely used models in traffic flow modeling. However, being a non-linear hyperbolic conservation law, it can have solutions with discontinuities and infinite accelerations, adversely impacting its capability to capture physical traffic phenomena effectively. Thus, over last decade, the parallel class of conservation laws with nonlocal parts in the flux is gaining particular interest in the modeling as well as mathematical community, where a convolution is introduced in the flux to produce Lipschitz-continuous velocities ensuring bounded accelerations. The two most popular strategies are to evaluate the traffic speed, from either averaging the traffic density, or averaging over the velocity, leading to the following two conservation laws,
where \(\nu ,\mu \in (C^2 \cap W^{2,\infty }) (\mathbb {R}),\) and
Such conservation laws have been studied in the recent literature, see [2, 7, 11, 13, 15, 18, 19, 25, 27], and the references therein. From the point of view of modeling, this nonlocal nature is particularly suitable in describing the behavior of traffic, where each vehicle moves according to its evaluation of the density and its variations within its horizon.
The article studies a very general class of these nonlocal conservation laws, namely
where
-
(H1)
\(f\in {{\,\textrm{Lip}\,}}(\mathbb {R})\) with \( f(0)=0,\)
-
(H2)
\(\beta , \nu \in (C^2 \cap {\text {BV}} \cap \, W^{2,\infty }) (\mathbb {R}),\) with \(\beta (0)=0,\)
-
(H3)
\(\mu \in (C^2 \cap {\text {BV}} \cap \, W^{2,\infty }) (\mathbb {R}),\)
with f being non-linear (in contrast to (1.2) or (1.3)). They serve as working models for a variety of real life applications, for example, sedimentation models [6], crowd dynamics models [13,14,15], vehicular traffic [7, 14], biological applications in structured population dynamics [31], supply chain models [14], granular material dynamics [4], as well as conveyor belt dynamics [21].
The wellposedness of this class has been of interest in the last few years. The local counterpart of (1.4)–(1.5) enjoys a rich literature, with [28] as one of the pioneering papers to fix the wellposedness of the entropy solutions for such PDEs. Similar to its local counterpart, since f can be possibly nonlinear, there can be multiple weak solutions of IVP (1.4)–(1.5). Hence, an additional entropy condition is required to single out a unique solution.
Definition 1.1
A function \(u\in C([0,T];L^1(\mathbb {R}))\cap L^{\infty }(\overline{Q}_T)\) is an entropy solution of the IVP (1.4)–(1.5), if for every \(k\in \mathbb {R},\) and for all non-negative \(\phi \in C_c^{\infty }([0,T)\times \mathbb {R})\),
where \(\mathcal {U}(t,x)=\nu (\mu *\beta (u(t))(x))\).
With some appropriate modifications, the proof of [6] can be adapted to prove that any two entropy solutions satisfying Definition 1.1 are equal, while existence of these solutions has been proven in [1, 5] for non linear f and in [9] for linear f, via the convergence of finite volume approximations. These articles dealing with existence of solutions establish that the schemes converge to the entropy solution \(u \in C \left( [0,T];L^1(\mathbb {R})\right) \).
What remains unexplored is to analyze the rate of convergence, i.e., how fast the error \(||u^{\Delta }(T,\, \cdot \,)-u(T,\, \cdot \,)||_{L^1(\mathbb {R})}\) made by the numerical solution \(u^{\Delta }\) in approximating the exact solution u goes to zero as the mesh size \(\Delta x\) goes to zero. That is the precise aim of this article. In other words, we look for an (optimal) \(\alpha \) satisfying
with C being an appropriate positive constant. To achieve this, we first prove a Kuznetsov-type lemma using the entropy formulation (1.6). We further estimate the relative entropy functional involving the solution u and numerical approximation \(u^{\Delta }\) to obtain (1.7) with an optimal \(\alpha =1/2,\) same as the one obtained in [29, 33] for local fluxes (homogeneous). To the best of our knowledge, this is the first result in this direction for such nonlocal conservation laws. It is to be noted that the results of the article hold under no additional assumptions on monotonicity/linearity of the kernel \(\mu \) or the flux f or \(\nu \).
The paper is organized as follows. In Sect. 2, we discuss the wellposedness of (1.4)–(1.5) via convergence of a general class of monotone finite volume approximations. In Sect. 3, we prove the Kuznetsov-type lemma for (1.4)–(1.5) and obtain the rate of convergence as 1/2. In Sect. 4, we also briefly comment on the extensions to higher dimensions. In Sect. 5, we present some numerical experiments which illustrate the theory.
2 Finite volume approximations and wellposedness
We now introduce the notations to be used in the article:
-
i.
\(|u|_{L^\infty _t {\text {BV}}_x}:=\sup \limits _{\begin{array}{c} t\in [0,T] \end{array}} {{\,\textrm{TV}\,}}(u(t,\, \cdot \,)).\)
-
ii.
\(|u|_{{{\,\textrm{Lip}\,}}_t L^1_x}:=\sup \limits _{\begin{array}{c} 0\le t_1<t_2\le T \end{array}}\frac{{\left\| u(t_1,\, \cdot \,)-u(t_2,\, \cdot \,)\right\| }_{L^1(\mathbb {R})}}{|t_1-t_2|}.\)
-
iii.
\(K:=\{u:\overline{Q}_T \rightarrow \mathbb {R}: ||u||_{L^{\infty }(\overline{Q}_T)}+|u|_{L^\infty _t {\text {BV}}_x}<\infty \}.\)
-
iv.
\(\gamma (u,\sigma ):=\sup \limits _{\begin{array}{c} \left| t_1-t_2\right| \le \sigma \\ 0\le t_1< t_2 \le T \end{array}} {\left\| u(t_1,\, \cdot \,)-u(t_2,\, \cdot \,)\right\| }_{L^1(\mathbb {R})}.\)
2.1 Uniqueness of the entropy solution
Any two entropy solutions of the IVP (1.4)–(1.5) are equal. More precisely, we have the following result:
Theorem 2.1
(Uniqueness) Let \(u,v\in C([0,T];L^1(\mathbb {R})) \cap (L^\infty _t {\text {BV}}_x) (\overline{Q}_T)\) be two entropy solutions of the IVP (1.4)–(1.5) corresponding to the initial data \({u_0}\) and \({v_0}\) respectively. Then, there exists a constant
such that
In particular, if \(u_0=v_0,\) then \(u=v\) a.e. in \(\overline{Q}_T\).
Proof
Note that the nonlocal coefficient of the flux function considered in this article is more general than the ones in all the previous results on the uniqueness of nonlinear-nonlocal conservation laws. However, the continuous dependence estimates for the entropy solution of the conservation laws (local) derived in [24, Thm. 1.3] can still be invoked to prove the desired weighted contraction estimates as in [6, Thm. 4.1]. Alternatively, this can also be seen as a consequence of the Kuznetsov-type estimates derived in the sequel (see Lemma 3.2), by sending \(\varepsilon ,\varepsilon _0 \rightarrow 0.\) \(\square \)
2.2 Existence via numerical approximations
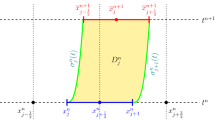
For \(\Delta x,\Delta t>0,\) and \(\lambda :=\Delta t/\Delta x,\) consider equidistant spatial grid points \(x_i:=i\Delta x\) for \(i\in \mathbb {Z}\) and temporal grid points \(t^n:=n\Delta t\) for non-negative integers \(n\le N\), such that \(T =N\Delta t\). Let \(\chi _i(x)\) denote the indicator function of \(C_i:=[x_{i-1/2}, x_{i+1/2})\), where \(x_{i+1/2}=\frac{1}{2}(x_i+x_{i+1})\) and let \(\chi ^n(t)\) denote the indicator function of \(C^{n}:=[t^n,t^{n+1})\). We approximate the initial data according to:
We define a piecewise constant approximate solution \(u^{\Delta }\) to (1.4) by
through the following marching formula:
where the convolution term \(\mu *\beta (u)\) is computed through a standard quadrature formula using the same space mesh, i.e.,
with \(u^{n}_{p+1/2}\) being any convex combination of \(u^{n}_{p}\) and \(u^{n}_{p+1},\) and \(\mu _{i+1/2} = \mu (x_{i+1/2}).\) Further, \(\mathcal {F} (\nu (c^n_{i+1/2}),u_i^{n},u_{i+1}^{n}) \) denotes the numerical approximation of the flux \(f(u) \nu (\mu *\beta (u))\) at the interface \(x=x_{i+1/2}\) for \(i\in \mathbb {Z},\) with H being increasing in the last three arguments. The approximations generated by the scheme, namely \(u_i^{n} \approx u(t^n,x_i)\) are extended to a function defined on \({Q}_T\) via
In general, \(\mathcal {F}\) can be defined as an appropriate nonlocal extension of any monotone numerical flux, meant for local conservation laws. Here, we present examples of celebrated Lax–Friedrichs flux and Godunov flux.
-
1.
Lax–Friedrichs type flux: For any \( \theta \in \left( 0,\frac{2}{3} \right) ,\) define
$$\begin{aligned} \mathcal {F}_\textrm{LF}(a,b,c) = \frac{a}{2}\Big ( f(b) + f(c)\Big ) - \theta \frac{(c-b)}{2\, \lambda }, \end{aligned}$$where \(\Delta t\) is chosen in order to satisfy the CFL condition
$$\begin{aligned} \lambda \le \frac{\min (1, 4-6\theta ,6\theta )}{1+6\left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}{\left\| \nu \right\| }_{L^\infty (\mathbb {R})}}.\end{aligned}$$(2.5) -
2.
Godunov type flux:
$$\begin{aligned} \mathcal {F}_\textrm{Godunov}(a,b,c)= a F_\textrm{Godunov}(b,c), \end{aligned}$$where the function \(F_\textrm{Godunov}\) is the Godunov flux for the corresponding local conservation law \(u_t+f(u)_x=0\), and \(\Delta t\) is chosen in order to satisfy the CFL condition
$$\begin{aligned} \lambda \left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}{\left\| \nu \right\| }_{L^\infty (\mathbb {R})}\le \frac{1}{6}. \end{aligned}$$
Theorem 2.2
(Existence) Assume that (H1)–(H3) hold. For initial data \(u_0\in (L^1\cap BV) (\mathbb {R})\) and \(\Delta x >0,\) there exist constants \(\mathcal {L}_i, i=1,2,3,\) independent of \(\Delta t\) such that the sequence of approximations \(u^n\) defined by (2.2) satisfies the following for all \(i\in \mathbb {Z}, n\in \mathbb {N}\) and \(0\le n \le N\):
-
1.
\(L^{\infty }\) estimate:
$$\begin{aligned} {\left\| u^n\right\| }_{L^{\infty }}\le \exp (\mathcal {L}_1 T){\left\| u^0\right\| }_{L^{\infty }}, \end{aligned}$$(2.6)where \(\mathcal {L}_1 = \mathcal {L}_1\left( {\left| \mu \right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}},{\left\| u_0\right\| }_{L^1(\mathbb {R})},\left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}, \left| \beta \right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})},\left| \nu \right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}\right) .\)
-
2.
\(L^{1}\) estimate:
$$\begin{aligned} {\left\| u^{n}\right\| }_{L^1}{\le }{\left\| u^0\right\| }_{L^1}. \end{aligned}$$(2.7) -
3.
BV estimate:
$$\begin{aligned} {{\,\textrm{TV}\,}}(u^{n}) \le \exp (\mathcal {L}_2T)({{\,\textrm{TV}\,}}(u^{0}) +\mathcal {L}_2), \end{aligned}$$(2.8)where \( \mathcal {L}_2=\mathcal {L}_2({\left\| \mu \right\| }_{W^{2,\infty }(\mathbb {R})}, {\left\| \nu \right\| }_{W^{2,\infty }(\mathbb {R})}, \left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}, {\left\| u_0\right\| }_{L^1(\mathbb {R})}). \)
-
4.
Time continuity:
$$\begin{aligned} \Delta x \sum \limits _{i \in \mathbb {Z}}\left| u_i^m-u_i^n\right| \le \mathcal {L}_3|m-n| \Delta t, \quad \quad m,n \in \mathbb {N}\cup \{0\}, \end{aligned}$$(2.9)where \({\mathcal {L}_3=\mathcal {L}_3({\left\| u_0\right\| }_{L^1(\mathbb {R})}, \left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}, \left| \mu \right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}, {\left\| \nu \right\| }_{W^{1,\infty }(\mathbb {R})}, {{\,\textrm{TV}\,}}(u^n)).}\)
-
5.
Discrete entropy inequality: For any \(k\in \mathbb {R}\) we have
$$\begin{aligned}&{\left| u_i^{n+1}-k\right| }-{\left| u_i^{n}- k\right| }+\lambda \big (\mathcal {G}^{n}_{i+1/2}(u_i^{n} ,u_{i+1}^{n},k )-\mathcal {G}^{n}_{i-1/2}(u_{i-1}^{n} ,u_i^{n},k)\big )\end{aligned}$$(2.10)$$\begin{aligned}&\qquad +\lambda \textrm{sgn}(u_i^{n+1}-k) f(k)(\nu (c_{i+\frac{1}{2}}^{n})-\nu (c_{i-\frac{1}{2}}^{n}))\le 0, \end{aligned}$$(2.11)where \(\mathcal {G}^{n}_{i+1/2}(a,b,k)=\mathcal {F}_{i+1/2}^n(a \vee k,b \vee k)-\mathcal {F}_{i+1/2}^n(a \wedge k,b \wedge k)\) for all \(i\in \mathbb {Z}, n\in \mathbb {N}\).
Furthermore, the finite volume approximations converge to the unique entropy solution u of the IVP (1.4)–(1.5).
Proof
The proof follows by invoking the monotonicity of the scheme and writing it in the incremental form. The details can be worked out exactly on the similar lines of [1, Lem. 2.4–2.7] and [5, Lem. 2.2–2.8] with proper modification in the estimations on the nonlocal coefficient. \(\square \)
The above theorem implies that the entropy solution satisfies the following regularity estimates.
Corollary 2.3
(Regularity of the entropy solution) Assume that (H1)–(H3) hold. For \(0 <t \le T\) and \(u_0\in (L^1\cap BV) (\mathbb {R}),\) the entropy solution u of the IVP (1.4)–(1.5) satisfies the following:
Remark 2.4
In addition, if \(u_i^0\ge 0,\) the numerical approximations defined by (2.2) satisfy \(u_i^n\ge 0,\) see [5, Lem. 2.2] for details of the proof. This further implies that \({\left\| u^n\right\| }_{L^1}={\left\| u^0\right\| }_{L^1},\) since the scheme is conservative. Consequently, if initial data is non-negative, so is the entropy solution.
3 Error estimate
We define \(\Phi : \overline{Q}_T^2 \rightarrow \mathbb {R}\) by
where \(\omega _a(x)=\frac{1}{a}\omega \big (\frac{x}{a}\big ),\) \(a>0\) and \(\omega \) is a standard symmetric mollifier with \({\text {supp}} (\omega ) \subseteq [-1,1].\) Furthermore, we assume that \(\int _\mathbb {R}\omega _a(x) \mathinner {\textrm{d}{x}} =1\) and \(\int _\mathbb {R}\left| \omega '_a(x)\right| \mathinner {\textrm{d}{x}} =\frac{1}{a}.\) Now, it is straight forward to see that \(\Phi \) is symmetric and \(\Phi _x=\omega '_{{\varepsilon }}(x-y)\omega _{\varepsilon _0}(t-s)=-\Phi _y, \Phi _t=\omega _{\varepsilon }(x-y)\omega '_{{\varepsilon }_0}(t-s)=-\Phi _s\). Further, define the following functions.
Definition 3.1
We now state and prove the Kuznetsov-type lemma for nonlocal conservation laws.
Lemma 3.2
Let u be the entropy solution of (1.4)–(1.5) and \(v \in K.\) Then,
where \(\mathcal {K}\) is constant that depends on
and is independent of \(\varepsilon ,\varepsilon _0\).
Proof
Consider the sum \(\Lambda _{\varepsilon ,\varepsilon _0}(u,v)+\Lambda _{\varepsilon ,\varepsilon _0}(v,u)\):
where \(\mathcal {V}(s,y)= \nu (\mu *\beta (v(s))(y)).\) Since \(\Phi _{s}=-\Phi _{t},\Phi _{y}=-\Phi _{x}, \) we have
In other words, we have
with
Since u is the entropy solution of (1.4)–(1.5), we have that \(\Lambda _{\varepsilon ,\varepsilon _0}(u,v)\ge 0, \) and hence,
The terms \(I_0\) and \(I_T\) appear in the local case as well so they can be estimated on the similar lines of [20, 23] to get:
where \(\mathcal {K}_1=\mathcal {K}_1(\left| u\right| _{L^\infty _t {\text {BV}}_x},\left| v\right| _{L^\infty _t {\text {BV}}_x})\). Now, we estimate the other terms one by one. Using integration by parts \(I_{\Phi '}\) can be written as,
Consequently,
Consider the term
Since \(|G_x(u,v)|\le \left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}\left| u_x\right| \) (in the sense of measures, see [8, Lem. A2.1] for details), we have,
Note that the term
Consequently we get:
where \(I^1_{\mathcal {U}},I^2_{\mathcal {U}}\), and \(I^3_{\mathcal {U}}\) satisfy the following estimates.
Collectively, we have
for some appropriate constants \(\mathcal {K}_2\) and \(\mathcal {K}_3\). Now, we consider,
Note that
Now, adding and subtracting \(\nu '((\mu *\beta (v(s)))(y))(\mu '*\beta (v(s)))(x)\) to \(\left| \mathcal {V}_y(s,y)-\mathcal {V}_x(s,x)\right| \), we get
Furthermore,
which implies that
Adding and subtracting \(\nu '((\mu *\beta ((s)))(x))(\mu '*\beta (u(t)))(x)\) to \(\left| \mathcal {V}_x(s,x)-\mathcal {U}_x(t,x)\right| \), we ge
Moreover,
Collecting all terms, we have
Now, it can be observed that \(I_{\mathcal {U}_x}\) can be handled like (3.4), leading to the following estimate:
for some appropriate constants \(\mathcal {K}_4\) and \(\mathcal {K}_5\). Substituting the above estimates in (3.1), we get
Now, the result follows by Gronwall’s inequality. \(\square \)
The remaining of this section is dedicated to estimating the relative entropy functional \(\Lambda _{\varepsilon ,\varepsilon _0}(u^{\Delta },u)\) for which we follow the following notations:
For \(i\in \mathbb {Z}, n\in \mathbb {N}, k\in \mathbb {R},(t,x)\in Q_T,\) define
-
1.
\(\eta _{i}^n(k):=\left| u_i^n-k\right| \),
-
2.
\(C_i^n:=C^n\times C_i\),
-
3.
\(p_i^n(k):=G(u_i^n,k)=\textrm{sgn}(u_i^n-k) (f(u_i^n)-f(k))\),
-
4.
\(\mathcal {U}^{\Delta }(t,x):= \nu (\mu *\beta (u^{\Delta }(t)))(x)\).
Lemma 3.3
The relative entropy functional \(\Lambda _{\varepsilon ,\varepsilon _0} (u^{\Delta },u)\) satisfies:
where \(\mathcal {C}\) is a constant independent of \(\Delta x, \Delta t.\)
Proof
Let \(\sum _{i,n}\) denote the double summation \(\sum _{i\in \mathbb {Z}}\sum _{n=0}^{N-1}.\) For the piecewise constant function \(u^{\Delta }\) (cf. (2.2)–(2.4)) the relative entropy can be written as
Applying the fundamental theorem of calculus, followed by summation by parts, we get
We have
For \((n,i)\in \mathbb {N}\times \mathbb {Z}\) and \((t,x)\in C_i^n\) observe that
Also for \(t \in C^n,\) using (2.9), we have
Now using the Lipschitz continuity of \(\mathcal {U}^{\Delta }\) in the space variable, we have
Furthermore,
Finally, combining all the above estimates we get,
Thus, we have
Now, we consider
The error terms can be estimated as below,
using Theorem 2.2, equation (2.7), and
Furthermore, we have, by applying fundamental theorem of calculus and rearrange the terms,
Apply summation by parts in i to get,
Now, using (3.10), we have
Using (2.9), for \(t\in C^n,\) we have
Consequently,
Finally, combining the above estimates, we get:
Thus, so far we have proved
Recall \(\lambda _1\), cf. (3.6),
by applying the discrete entropy inequality (2.11).
Furthermore, we can rewrite \(\lambda _2'\), cf. (3.7), as follows
by using the fundamental theorem of calculus, followed by summation by parts.
- Claim 1:
-
\(A_2+\lambda _2' =\mathcal {O}\left( \frac{\Delta x}{\varepsilon }+\frac{\Delta t}{\varepsilon _0}\right) \).
Adding and subtracting
we have
Apply summation by parts to get
Note that from the definition of the numerical entropy flux \(G_{i+1/2}^n\) (see Thm. 2.2(5)), it follows that \(v(c_{i+1/2}^n)p_i^n(k)=G_{i+1/2}^n(u_i^n,u_i^n,k).\) Now, invoking the Lipschitz continuity of \(G_{i+1/2}^n\) in its second argument, we get
for \(\mathcal {C}_1=\mathcal {C}_1(\left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})},{\left\| \nu \right\| }_{L^{\infty }(\mathbb {R})}).\) Furthermore,
where the last inequality follows from the Lipschitz continuity of the function \(u \mapsto \textrm{sgn}(u-k)(f(u)-f(k))\) with \(\mathcal {C}_2=\mathcal {C}_2\big (\left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})},{\left\| \nu \right\| }_{L^{\infty }(\mathbb {R})}, {\left\| u^{\Delta }\right\| }_{L^{\infty }(\overline{Q}_T)}\big ).\)
Now, since \(\mu \) has bounded variation, the claim follows because of the following estimates,
which is true because of (2.7) and the estimates
the proofs of which can be found in [23, Ex. 3.17].
- Claim 2:
-
\(A_3+\lambda _3' =\mathcal {O}\left( \frac{\Delta x}{\varepsilon }\right) \).
We find
The terms \(\tilde{\mathcal {E}}_1\) and \(\tilde{\mathcal {E}}_2\) can be estimated as follows:
using (3.18)–(3.19). Furthermore,
Adding and subtracting the term
we have
Now, let us estimate \(\tilde{\mathcal {E}}_{21}\).
Now, let us estimate \(\tilde{\mathcal {E}}_{22}\).
Recall, cf. (2.3), that
which implies
where \({\mathcal {C}_5=\left| \beta \right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}|\mu |_{BV(\mathbb {R})}\mathcal {L}_3},\) by applying (2.9). Therefore,
where \(\mathcal {C}_6=\left| \nu \right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}{\left\| f(u)\right\| }_{L^{\infty }(Q_T)} \mathcal {C}_5\). Finally, estimates on the remaining boundary terms \(\tilde{\mathcal {E}}_{23}\) and \(\tilde{\mathcal {E}}_{24}\), easily follow from (3.18). Specifically,
where \({\mathcal {C}_7=\mathcal {C}_3{\left\| f(u)\right\| }_{L^{\infty }(Q_T)}.}\) Similarly, \(\tilde{\mathcal {E}}_{24} \le \mathcal {C}_7\Delta t \,{\left\| f(u)\right\| }_{L^{\infty }(Q_T)}. \) Substituting the assertions of Claim 1 and Claim 2 in (3.14) we get
where \({\mathcal {C}=\mathcal {C}(T,{\left\| \nu \right\| }_{W^{2,\infty }(\mathbb {R})},\left| \beta \right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})}, \left| f\right| _{{{\,\textrm{Lip}\,}}(\mathbb {R})},\left| \mu \right| _{BV(\mathbb {R})},}{\left\| u_0\right\| }_{L^{1}(\mathbb {R})},\left| u_0\right| _{BV(\mathbb {R})},{\left\| \mu \right\| }_{W^{2,\infty }(\mathbb {R})}).\)
\(\square \)
Now, we state and prove the main result of this paper.
Theorem 3.4
(Rate of Convergence) Let u be the entropy solution of (1.4)–(1.5) and \(u^{\Delta }\) be the numerical solution given by (2.2). Then we have the following convergence rate:
Proof
The CFL condition implies that \(\Delta x =\mathcal {O} (\Delta t).\) Furthermore, the initial approximation (2.1) implies \({\left\| u_0^{\Delta }-u_0\right\| }_{L^1(\mathbb {R})}=\mathcal {O}(\Delta t)\). Now, the desired error estimate follows from Lemma 3.3 and Lemma 3.2 setting \(\varepsilon =\varepsilon _0=\sqrt{\Delta t},\) as \(\gamma (u^{\Delta },\sqrt{\Delta t}) = \mathcal {O}(\sqrt{\Delta t}).\) \(\square \)
4 Extension to multi dimensions
We consider the case of two space dimensions and denote the space variables by \((x,y) \in \mathbb {R}^2\), and consider the following PDE:
Further, for numerical scheme, fix a rectangular grid with sizes \(\Delta x\) and \(\Delta y\) in \(\mathbb {R}^2\) and choose a time step \(\Delta t\). For later use, we also introduce the usual notation
Throughout, we fix initial data \(u_0\in (L^{\infty }\cap {\text {BV}}) (\mathbb {R}^2; \mathbb {R})\) and introduce
We define a piecewise constant approximate solution \(u^{\Delta }\) by
where \(\chi _A\) denotes the indicator function of a set A, through the following marching formula based on dimensional splitting, (see [16, Sec. 3] and [22, Sec. 5] for details):
where \(\mathcal {F}^{x,n}_{i+1/2,j}\) and \(\mathcal {F}^{y,n}_{i,j+1/2}\) denote the numerical approximations of the fluxes \(f^1(u) \nu ^1(\mu ^1*\beta ^1(u))\) and \(f^2(u) \nu ^2(\mu ^2*\beta ^2(u))\) at the interfaces \((x_{i+1/2},y_j)\) and \((x_{i},y_{j+1/2})\), respectively, for \(i,j\in \mathbb {Z}\). The convolution terms are computed through quadrature formula, i.e.,
where, \(u^n_{l+1/2,p}\) is any convex combination of \(u^n_{l,p}\) and \(u^n_{l+1,p}\), with \(\mu ^1_{i+1/2,j} = \mu ^1 (x_{i+1/2}, y_j)\) and \( \mu ^2_{i+1/2,j} = \mu ^2 (x_{i+1/2}, y_j) \,.\) Throughout, we require that \(\Delta t\) is chosen in order to satisfy the CFL conditions
and
with numerical fluxes \(\mathcal {F}^x\) or \(\mathcal {F}^y\) chosen as Lax–Friedrichs flux and Godunov flux, respectively. Extension to other monotone fluxes and for higher dimensions is similar. The numerical scheme can now be shown to converge to entropy solution, see, for example, [1]. The Kuznetsov Lemma and the theorem on error estimate presented in Sect. 3 can now be extended to several space dimensions using dimension splitting arguments (see [23, Sec. 4.3]) with appropriate modifications throughout the proof.
5 Numerical experiments
We now present some numerical experiments to illustrate the theory presented in the previous section. We show the results for the Lax–Friedrichs scheme. The results obtained by Godunov scheme are similar, and are not shown here. Throughout the section, \(\theta =\theta _x=\theta _y\) is chosen to be 0.3333, and \(\lambda \) and \(\lambda _x=\lambda _y\) are chosen to be 0.1286 and 0.2857, respectively, so as to satisfy the CFL condition (2.5) and (4.4), respectively, in one and two dimensions, for any grid size \(\Delta x\) or \(\Delta y\) used in this section.
5.1 One dimension
We employ the nonlocal version of the standard LWR model (1.1), i.e., IVP (1.4)–(1.5), with
where L is such that \(\int _{\mathbb {R}}\mu (x)\mathinner {\textrm{d}{x}}=1\).
Further, \(\beta (r)=r\) and \(\nu (r)=1-r,f(u)=u\). This PDE fits the hypothesis of the article. Further, the domain of integration is chosen to be the interval \([-1.5, 1.5]\) with \(t\in [0, 0.5]\), and
Figure 1 displays the numerical approximations of (1.4), (5.1) generated by the numerical scheme (2.2), with decreasing grid size \(\Delta x\), starting with \(\Delta x =0.00625,\) and \({\eta =0.0625}\). It can be seen that the numerical scheme is able to capture both shocks and rarefactions well. To compute the observed convergence rate of the scheme (2.2) we obtain numerical approximations to (1.4), (5.1) with decreasing grid sizes \(\Delta x\), starting with \(\Delta x =0.00625\). The observed convergence rate \(\alpha \) is then calculated at time \(T=0.5\) by computing the \(L^1\) distance between the numerical solutions \(u_{\Delta x}(T,\, \cdot \,)\) and \( u_{\Delta x/2}(T,\, \cdot \,)\) obtained for the grid size \(\Delta x\) and \(1/2\Delta x\), for each grid size \(\Delta x\). Let \(e_{\Delta x}(T)={\left\| u_{\Delta x}(T,\, \cdot \,)-u_{\Delta x/2}(T,\, \cdot \,)\right\| }_{L^1(\mathbb {R})}.\) The observed convergence rate \(\alpha \) is given by \(\log _{2}(e_{\Delta x}(T)/{e_{\Delta x/2}(T)}).\) The results recorded in Fig. 2 show that \(\alpha >0.5\). The present numerical integration resonates well with the theoretical convergence rate obtained in Theorem 3.4 in this article. It can be seen that the density u goes beyond the maximal initial density 0.5, violating the maximum principle, a phenomenon observed in non-local conservation laws with linear local part, see [6, Ex. 1]. It is to be noted that, in general, for nonlocal conservation laws with linear local part, entropy solutions do not satisfy the invariant region principle, i.e., the density may cross the value 1 even for \(0\le u_0 \le 1\) (see [6, Ex. 1]). On the other hand, for fluxes such as \(f(u)=u(1-u),\) invariant region principle holds but not necessarily the maximum principle (see [6, Ex. 2]). The numerical results for such fluxes can be computed analogously and we do not present them here.
Figure 3 illustrates the nonlocal to local limit, see [10, 12, 26] and references therein, namely that the entropy solutions of the nonlocal conservation laws converge to the entropy solution of the corresponding local conservation law as the radius of the kernel goes to zero.
5.2 Two dimensions
To illustrate our results in two dimensions, we employ the model introduced in [1], modeling crowd dynamics in two dimensions, which fits in the framework of the article. Assume that a group of pedestrians in a square room \([-4,4]^2\), can be described through the density \(u = u (t,x,y)\) that satisfies the nonlocal conservation law
where the smooth, non-negative and compactly supported function \(\mu \) models the way in which each individual averages the density around her/his position to adjust her/his speed.
We choose:
so that \(\iint _{\mathbb {R}^2} \mu (x,y) \mathinner {\textrm{d}{x}} \mathinner {\textrm{d}{y}} =1\).
As initial data, we consider two cases:
-
1.
Annular initial data, where the crowd is concentrated in an annulus:
$$\begin{aligned} u_0 (x,y) = \chi _{ \{(x,y) :4 \le x^2 + y^2\le 9\}} (x,y). \end{aligned}$$(5.4) -
2.
Circular initial data, where the crowd is concentrated in a circle:
$$\begin{aligned} u_0 (x,y) = \chi _{ \{(x,y) :x^2 + y^2\le 4\}} (x,y). \end{aligned}$$(5.5)
The system (5.2) fits into the setting of (4.2) with
The numerical integrations of (5.2), (5.4) and (5.2), (5.5) are obtained by the the algorithm described in Sect. 4 and are shown in Fig. 4. The figures depict that the density does not cross the maximal density 1 and the numerical simulations are able to capture the physical properties well. To compute the convergence rate of the scheme (4.2) with Lax–Friedrichs flux, we apply the algorithm to problem (5.2), (5.4) and (5.2), (5.5) on the domain \([-4, \, 4]^2\) on the time interval [0, 0.5] with different grid sizes with \(\lambda _x = \lambda _y = 0.2857\). The convergence rate \(\alpha \) is then calculated at time \(T=0.5\) by computing the \(L^1\) distance between the numerical solutions \(u_{\Delta x}(T,\, \cdot \,)\) and \( u_{\Delta x/2}(T,\, \cdot \,)\) obtained for the grid size \(\Delta x\) and \(\Delta x/2\), for each grid size \(\Delta x\). The results recorded in Table 1 and Fig. 5 show that the observed convergence rates lie strictly between 0.5 and 1. The present numerical integration resonate well with theoretical convergence rate obtained in Theorem 3.4 in this article.
6 Conclusions
In this article, we have established the convergence rate estimates for scalar nonlocal nonlinear conservation laws, modeling traffic and crowd dynamics. Also, our analysis is not case specific, and covers most of the kernels (irrespective of its monotonicity) considered in traffic modelling such as forward, backward and central kernels.
The rate is shown to be 1/2 which is consistent with its local counterparts. It is interesting to see that the obtained convergence rate of 1/2 is independent of the radius of the convolution matrix and monotonicity of the kernel, with constant in the estimate depending on the radius of the kernel \(\eta .\) For \({\nu (u)=1-u, \beta (u)=u,}\) the nonlocal conservation laws boil down to the local conservation law and hence the convergence rate 1/2 is optimal due to [33].
The extensions of these results to a general coupled system of nonlocal conservation laws, for the convergent finite volume schemes proposed in [1] and for nonlocal conservation laws with discontinuous flux (see [3]), are not straightforward and are works in progress. Furthermore, using the Kuznetsov-type lemma proved in this article, the rate at which the solutions of the nonlocal FTL (see [11, 17]) models converge to its continuum limit, can be explored, which we aim to address in our upcoming article.
References
Aggarwal, A., Colombo, R.M., Goatin, P.: Nonlocal systems of conservation laws in several space dimensions. SIAM J. Numer. Anal. 53(2), 963–983 (2015)
Aggarwal, A., Goatin, P.: Crowd dynamics through non-local conservation laws. Bull. Braz. Math. Soc. (N.S.) 47(1), 37–50 (2016)
Aggarwal, A., Vaidya, G.: Convergence of finite volume approximations and well-posedness: nonlocal conservation laws with rough flux. Preprint (2023)
Amadori, D., Shen, W.: An integro-differential conservation law arising in a model of granular flow. J. Hyperbolic Differ. Equ. 9(1), 105–131 (2012)
Amorim, P., Colombo, R.M., Teixeira, A.: On the numerical integration of scalar nonlocal conservation laws. ESAIM Math. Model. Numer. Anal. 49(1), 19–37 (2015)
Betancourt, F., Bürger, R., Karlsen, K.H., Tory, E.M.: On nonlocal conservation laws modelling sedimentation. Nonlinearity 24(3), 855 (2011)
Blandin, S., Goatin, P.: Well-posedness of a conservation law with non-local flux arising in traffic flow modeling. Numer. Math. 132(2), 217–241 (2016)
Bouchut, F., Perthame, B.: Kruzkov’s estimates for scalar conservation laws revisited. Trans. Am. Math. Soc. 350(7), 2847–2870 (1998)
Boudin, L., Mathiaud, J.: A numerical scheme for the one-dimensional pressureless gases system. Numer. Methods Part. Differ. Equ. 28(6), 1729–1746 (2012)
Bressan, A., Shen, W.: On traffic flow with nonlocal flux: a relaxation representation. Arch. Ration. Mech. Anal. 237(3), 1213–1236 (2020)
Coclite, G.M., Karlsen, K.H., Risebro, N.H.: A nonlocal Lagrangian traffic flow model and the zero-filter limit. arXiv:2302.03889 (2023)
Colombo, M., Crippa, G., Spinolo, L.V.: On the singular local limit for conservation laws with nonlocal fluxes. Arch. Ration. Mech. Anal. 233(3), 1131–1167 (2019)
Colombo, R.M., Garavello, M., Lécureux-Mercier, M.: A class of nonlocal models for pedestrian traffic. Math. Mod. Met. Appl. Sci. 22(4), 1150023 (2012)
Colombo, R.M., Herty, M., Mercier, M.: Control of the continuity equation with a non local flow. ESAIM Control Optim. Calc. Var. 17(2), 353–379 (2011)
Colombo, R.M., Lécureux-Mercier, M.: Nonlocal crowd dynamics models for several populations. Acta Math. Sin. 32(1), 177–196 (2011)
Crandall, M.G., Majda, A.: Monotone difference approximations for scalar conservation laws. Math. Comput. 34(149), 1–21 (1980)
Francesco, M.D., Fagioli, S., Radici, E.: Deterministic particle approximation for nonlocal transport equations with nonlinear mobility. J. Differ. Equ. 266(5), 2830–2868 (2019)
Friedrich, J., Göttlich, S., Keimer, A., Pflug, L.: Conservation laws with nonlocal velocity—the singular limit problem. arXiv:2210.12141 (2022)
Friedrich, J., Kolb, O., Göttlich, S.: A Godunov type scheme for a class of LWR traffic flow models with non-local flux. Netw. Heterog. Media 13(4), 531–547 (2018)
Ghoshal, S.S., Towers, J.D., Vaidya, G.: A Godunov type scheme and error estimates for scalar conservation laws with Panov-type discontinuous flux. Numer. Math. 151, 601–625 (2022)
Göttlich, S., Hoher, S., Schindler, P., Schleper, V., Verl, A.: Modeling, simulation and validation of material flow on conveyor belts. Appl. Math. Model. 38(13), 3295–3313 (2014)
Holden, H., Karlsen, K.H., Lie, K.-A., Risebro, N.H.: Splitting Methods for Partial Differential Equations with Rough Solutions: Analysis and MATLAB Programs. EMS Publishing House, Zürich (2010)
Holden, H., Risebro, N.H.: Front Tracking for Hyperbolic Conservation Laws. Springer, Berlin (2015)
Karlsen, K.H., Risebro, N.H.: On the uniqueness and stability of entropy solutions of nonlinear degenerate parabolic equations with rough coefficients. Discrete Contin. Dyn. Syst. 9(5), 1081 (2003)
Keimer, A., Pflug, L.: Existence, uniqueness and regularity results on nonlocal balance laws. J. Differ. Equ. 263(7), 4023–4069 (2017)
Keimer, A., Pflug, L.: On approximation of local conservation laws by nonlocal conservation laws. J. Math. Anal. Appl. 475(2), 1927–1955 (2019)
Keimer, A., Pflug, L., Spinola, M.: Nonlocal scalar conservation laws on bounded domains and applications in traffic flow. SIAM J. Math. Anal. 50(6), 6271–6306 (2018)
Kružkov, S.N.: First order quasilinear equations in several independent variables. Math. USSR Sbornik 10(2), 217–243 (1970)
Kuznetsov, N.N.: Accuracy of some approximate methods for computing the weak solutions of a first-order quasi-linear equation. USSR Comput. Math. Math. Phys. 16(6), 105–119 (1976)
Lighthill, M.J., Whitham, G.B.: On kinematic waves II a theory of traffic flow on long crowded roads. Proc. Roy. Soc. Lond. Ser. A 229(1178), 317–345 (1955)
Perthame, B.: Transport Equations in Biology. Frontiers in Mathematics, Birkhäuser Verlag, Besal (2007)
Richards, P.I.: Shock waves on the highway. Oper. Res. 4(1), 42–51 (1956)
Sabac, F.: The optimal convergence rate of monotone finite difference methods for hyperbolic conservation laws. SIAM J. Numer. Anal. 34(6), 2306–2318 (1997)
Acknowledgements
The work was carried out during GV’s tenure of the ERCIM ‘Alain Bensoussan’ Fellowship Programme at NTNU. Part of it was carried out during AA’s research visit at NTNU. It was supported in part by the project IMod — Partial differential equations, statistics and data: An interdisciplinary approach to data-based modelling, project number 325114, from the Research Council of Norway, and by AA’s Faculty Development Allowance, funded by IIM Indore.
Funding
Open access funding provided by NTNU Norwegian University of Science and Technology (incl St. Olavs Hospital - Trondheim University Hospital).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aggarwal, A., Holden, H. & Vaidya, G. On the accuracy of the finite volume approximations to nonlocal conservation laws. Numer. Math. 156, 237–271 (2024). https://doi.org/10.1007/s00211-023-01388-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-023-01388-2





 ),
),  ),
),  ) and
) and  )
)

 ); Solution to the nonlocal conservation law (
); Solution to the nonlocal conservation law (
