Skip to main content
SpringerLink
Log in

Tailoring vibrational behavior in hybrid cellular sandwich nanobeams: a multiscale computational study

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

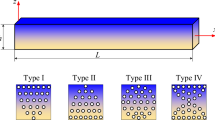
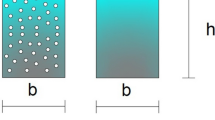
This study presents a novel approach to the design of sandwich nanobeams by investigating the vibrational behavior of a three-layer beam comprised of bi-dimensional functionally graded (2D-FG) porous material as the top and bottom face sheets and a hybrid cellular structure (HCS) as the core layer. The HCS is a unique configuration consisting of two separate parts with different unit cell angles, offering a wide range of Poisson ratios from negative to positive. Aluminum and alumina are assumed for face sheets as metal and ceramic, respectively. Also, aluminum is used as the base material for the cellular structure in the middle layer. An elasticity theory based on Eringen’s nonlocal theory is incorporated to account for the effects at small scales. Modified shear deformation theory (PSDBT) is implemented to derive the equations of motion based on the energy method. Afterward, they are solved by the Galerkin method. The possibility of achieving a unit natural frequency of sandwich HCS nanobeam has been conducted. It will be provided by changing the length of parts of the cellular structure core layer with distinct angles. Poisson’s ratios of the core can be adjusted from negative values to positive by altering the angle of cells. Another significant achievement is that sandwich beams with the same natural frequencies can be designed under different shape modes. By analyzing the effect of various parameters, such as material graduation indexes in both directions of thickness and length, the cellular angle of hybrid core, nonlocal parameter, porosity, and slenderness ratios (L/h), the study offers new insights into the design and potential applications of sandwich nanobeams with hybrid cellular structures.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Vo, T.P., Thai, H.-T., Nguyen, T.-K., Inam, F., Lee, J.: Static behaviour of functionally graded sandwich beams using a quasi-3D theory. Compos. B Eng. 68, 59–74 (2015)

    Article  Google Scholar 

  2. Jing, L.-l, Ming, P.-j, Zhang, W.-p, Fu, L.-r, Cao, Y.-p: Static and free vibration analysis of functionally graded beams by combination Timoshenko theory and finite volume method. Compos. Struct. 138, 192–213 (2016)

    Article  ADS  Google Scholar 

  3. Karamanli, A., Aydogdu, M.: On the vibration of size dependent rotating laminated composite and sandwich microbeams via a transverse shear-normal deformation theory. Compos. Struct. 216, 290–300 (2019)

    Article  Google Scholar 

  4. Li, Z., Wang, Z., Wang, X., Zhou, W.: Bending behavior of sandwich beam with tailored hierarchical honeycomb cores. Thin-Walled Struct. 157, 107001 (2020)

    Article  Google Scholar 

  5. Garg, A., Chalak, H.D., Zenkour, A.M., Belarbi, M.O., Sahoo, R.: Bending and free vibration analysis of symmetric and unsymmetric functionally graded CNT reinforced sandwich beams containing softcore. Thin-Walled Struct. 170, 108626 (2022)

    Article  Google Scholar 

  6. Koizum, M.: The concept of FGM”. Ceram. Trans. Funct. Gradient Mater. 34, 3–10 (1993)

    Google Scholar 

  7. Saleh, B., Jiang, J., Ma, A., Song, D., Yang, D., Xu, Q.: Review on the Influence of different reinforcements on the microstructure and wear behavior of functionally graded aluminum matrix composites by centrifugal casting. Met. Mater. Int. 26, 933–960 (2020)

    Article  CAS  Google Scholar 

  8. Chehel Amirani, M., Khalili, S.M.R., Nemati, N.: Free vibration analysis of sandwich beam with FG core using the element free Galerkin method. Compos. Struct. 90, 373–379 (2009)

    Article  Google Scholar 

  9. Arefi, M., Najafitabar, F.: Buckling and free vibration analyses of a sandwich beam made of a soft core with FG-GNPs reinforced composite face-sheets using Ritz Method. Thin-Walled Struct. 158, 107200 (2021)

    Article  Google Scholar 

  10. Li, X.-F., Wang, B.-L., Han, J.-C.: A higher-order theory for static and dynamic analyses of functionally graded beams. Arch. Appl. Mech. 80, 1197–1212 (2010)

    Article  ADS  Google Scholar 

  11. Le, C.I., Le, N.A.T., Nguyen, D.K.: Free vibration and buckling of bidirectional functionally graded sandwich beams using an enriched third-order shear deformation beam element. Compos. Struct. 261, 113309 (2021)

    Article  Google Scholar 

  12. Nguyen, T.-K., Vo, T.P., Nguyen, B.-D., Lee, J.: An analytical solution for buckling and vibration analysis of functionally graded sandwich beams using a quasi-3D shear deformation theory. Compos. Struct. 156, 238–252 (2016)

    Article  Google Scholar 

  13. Koutoati, K., Mohri, F., Daya, E.M., Carrera, E.: A finite element approach for the static and vibration analyses of functionally graded material viscoelastic sandwich beams with nonlinear material behavior. Compos. Struct. 274, 114315 (2021)

    Article  Google Scholar 

  14. Mehdianfar, P., Shabani, Y., Khorshidi, K.: Natural frequency of sandwich beam structures with two dimensional functionally graded porous layers based on novel formulations. Int. J. Eng. 35, 2092–2101 (2022)

    Article  Google Scholar 

  15. Li, J., Wu, Z., Kong, X., Li, X., Wu, W.: Comparison of various shear deformation theories for free vibration of laminated composite beams with general lay-ups. Compos. Struct. 108, 767–778 (2014)

    Article  Google Scholar 

  16. Mahi, A., Adda Bedia, E.A., Tounsi, A.: A new hyperbolic shear deformation theory for bending and free vibration analysis of isotropic, functionally graded, sandwich and laminated composite plates. Appl. Math. Model. 39, 2489–2508 (2015)

    Article  MathSciNet  Google Scholar 

  17. Li, J., Hu, X., Li, X.: Free vibration analyses of axially loaded laminated composite beams using a unified higher-order shear deformation theory and dynamic stiffness method. Compos. Struct. 158, 308–322 (2016)

    Article  Google Scholar 

  18. Eltaher, M.A., Alshorbagy, A.E., Mahmoud, F.F.: Vibration analysis of Euler–Bernoulli nanobeams by using finite element method. Appl. Math. Model. 37, 4787–4797 (2013)

    Article  MathSciNet  Google Scholar 

  19. Karampour, S., Ghavanloo, E., Fazelzadeh, S.A.: Free vibration analysis of elastic metamaterial circular curved beams with locally resonant microstructures. Arch. Appl. Mech. 93, 323–333 (2023)

    Article  ADS  Google Scholar 

  20. Heshmati, M., Daneshmand, F.: Vibration analysis of non-uniform porous beams with functionally graded porosity distribution. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 233, 1678–1697 (2018)

    Google Scholar 

  21. Chen, S., Geng, R., Li, W.: Vibration analysis of functionally graded beams using a higher-order shear deformable beam model with rational shear stress distribution. Compos. Struct. 277, 114586 (2021)

    Article  Google Scholar 

  22. Zhang, J., Lu, G., You, Z.: Large deformation and energy absorption of additively manufactured auxetic materials and structures: a review. Compos. B Eng. 201, 108340 (2020)

    Article  CAS  Google Scholar 

  23. Wang, T., Li, Z., Wang, L., Hulbert, G.M.: Crashworthiness analysis and collaborative optimization design for a novel crash-box with re-entrant auxetic core. Struct. Multidiscip. Optim. 62, 2167–2179 (2020)

    Article  Google Scholar 

  24. Wang, Y.C., Lakes, R.S.: Composites with inclusions of negative bulk modulus: extreme damping and negative Poisson’s ratio. J. Compos. Mater. 39, 1645–1657 (2005)

    Article  CAS  ADS  Google Scholar 

  25. Bohara, R.P., Linforth, S., Nguyen, T., Ghazlan, A., Ngo, T.: Novel lightweight high-energy absorbing auxetic structures guided by topology optimisation. Int. J. Mech. Sci. 211, 106793 (2021)

    Article  Google Scholar 

  26. Jafari Nedoushan, R., An, Y., Yu, W.-R., Abghary, M.J.: Novel triangular auxetic honeycombs with enhanced stiffness. Compos. Struct. 277, 114605 (2021)

    Article  Google Scholar 

  27. Luo, C., Han, C.Z., Zhang, X.Y., Zhang, X.G., Ren, X., Xie, Y.M.: Design, manufacturing and applications of auxetic tubular structures: a review. Thin-Walled Struct. 163, 107682 (2021)

    Article  Google Scholar 

  28. Shabani, Y., Khorshidi, K.: Free vibration analysis of rectangular doubly curved auxetic-core sandwich panels integrated with CNT-reinforced composite layers using Galerkin method. J. Sci. Technol. Compos. 8, 1686–1777 (2022)

    Google Scholar 

  29. Shukla, S., Behera, B.K.: Auxetic fibrous structures and their composites: a review. Compos. Struct. 290, 115530 (2022)

    Article  Google Scholar 

  30. Shabani, Y., Khorshidi, K.: Buckling analysis of sandwich structures with metamaterials core integrated by graphene nanoplatelets reinforced polymer composite. Mech. Adv. Compos. Struct. 10, 1–10 (2023)

    Google Scholar 

  31. Yin, H., Zhang, W., Zhu, L., Meng, F., Liu, J., Wen, G.: Review on lattice structures for energy absorption properties. Compos. Struct. 304, 116397 (2023)

    Article  CAS  Google Scholar 

  32. Khoshgoftar, M., Abbaszadeh, H.: Experimental and finite element analysis of the effect of geometrical parameters on the mechanical behavior of auxetic cellular structure under static load. J. Strain Anal. Eng. Des. 56, 131–138 (2021)

    Article  Google Scholar 

  33. Dhari, R.S., Javanbakht, Z., Hall, W.: On the inclined static loading of honeycomb re-entrant auxetics. Compos. Struct. 273, 114289 (2021)

    Article  Google Scholar 

  34. Khoshgoftar, M.J., Barkhordari, A., Limuti, M., Buccino, F., Vergani, L., Mirzaali, M.J.: Bending analysis of sandwich panel composite with a re-entrant lattice core using zig–zag theory. Sci. Rep. 12, 15796 (2022)

    Article  CAS  PubMed  PubMed Central  ADS  Google Scholar 

  35. Sorrentino, A., Castagnetti, D., Mizzi, L., Spaggiari, A.: Rotating squares auxetic metamaterials with improved strain tolerance. Smart Mater. Struct. 30, 035015 (2021)

    Article  CAS  ADS  Google Scholar 

  36. Sorrentino, A., Castagnetti, D., Mizzi, L., Spaggiari, A.: Bio-inspired auxetic mechanical metamaterials evolved from rotating squares unit. Mech. Mater. 173, 104421 (2022)

    Article  Google Scholar 

  37. Wang, Z.-P., Wang, Y., Poh, L.H., Liu, Z.: Integrated shape and size optimization of curved tetra-chiral and anti-tetra-chiral auxetics using isogeometric analysis. Compos. Struct. 300, 116094 (2022)

    Article  Google Scholar 

  38. Zhang, X.G., Ren, X., Jiang, W., Zhang, X.Y., Luo, C., Zhang, Y., et al.: A novel auxetic chiral lattice composite: experimental and numerical study. Compos. Struct. 282, 115043 (2022)

    Article  Google Scholar 

  39. Dutta, S., Menon, H.G., Hariprasad, M.P., Krishnan, A., Shankar, B.: Study of auxetic beams under bending: a finite element approach. Mater. Today Proc. 46, 9782–9787 (2021)

    Article  Google Scholar 

  40. Xu, G.-d, Zeng, T., Cheng, S., Wang, X.-h, Zhang, K.: Free vibration of composite sandwich beam with graded corrugated lattice core. Compos. Struct. 229, 111466 (2019)

    Article  Google Scholar 

  41. Li, C., Shen, H.-S., Wang, H.: Nonlinear bending of sandwich beams with functionally graded negative Poisson’s ratio honeycomb core. Compos. Struct. 212, 317–325 (2019)

    Article  Google Scholar 

  42. Zhao, S., Zhang, Y., Wu, H., Zhang, Y., Yang, J., Kitipornchai, S.: Tunable nonlinear bending behaviors of functionally graded graphene origami enabled auxetic metamaterial beams. Compos. Struct. 301, 116222 (2022)

    Article  CAS  Google Scholar 

  43. Reddy, J.N.: Analysis of functionally graded plates. Int. J. Numer. Meth. Eng. 47, 663–684 (2000)

    Article  Google Scholar 

  44. Mirjavadi, S.S., Mohasel Afshari, B., Shafiei, N., Rabby, S., Kazemi, M.: Effect of temperature and porosity on the vibration behavior of two-dimensional functionally graded micro-scale Timoshenko beam. J. Vib. Control 24, 4211–4225 (2018)

    Article  MathSciNet  Google Scholar 

  45. Zhu, X., Zhang, J., Zhang, W., Chen, J.: Vibration frequencies and energies of an auxetic honeycomb sandwich plate. Mech. Adv. Mater. Struct. 26, 1951–1957 (2019)

    Article  Google Scholar 

  46. Aydogdu, M., Taskin, V.: Free vibration analysis of functionally graded beams with simply supported edges. Mater. Des. 28, 1651–1656 (2007)

    Article  Google Scholar 

  47. Simsek, M.: Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories. Nuclear Eng. Des. Nucl. Eng. Des. 240, 697–705 (2010)

    Article  CAS  Google Scholar 

  48. Khorshidi, K., Shabani, Y.: Free vibration analysis of sandwich plates with magnetorheological smart fluid core by using modified shear deformation theory. J. Sci. Technol. Compos. 8, 1826–1835 (2022)

    Google Scholar 

  49. Karama, M., Afaq, K.S., Mistou, S.: Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int. J. Solids Struct. 40, 1525–1546 (2003)

    Article  Google Scholar 

  50. Peddieson, J., Buchanan, G.R., McNitt, R.P.: Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 41, 305–312 (2003)

    Article  Google Scholar 

  51. Li, C., Zhang, N., Li, S., Yao, L.Q., Yan, J.W.: Analytical solutions for bending of nanoscaled bars based on Eringen’s nonlocal differential Law. J. Nanomater. 2019, 8571792 (2019)

    Article  Google Scholar 

  52. Shabani, Y., Mehdianfar, P., Khorshidi, K.: Static buckling and free vibration analysis of bi-dimensional FG metal ceramic porous beam. Mech. Adv. Compos. Struct. 11, 149–158 (2024)

    Google Scholar 

  53. Ghayesh, M.H., Amabili, M., Farokhi, H.: Nonlinear forced vibrations of a microbeam based on the strain gradient elasticity theory. Int. J. Eng. Sci. 63, 52–60 (2013)

    Article  MathSciNet  Google Scholar 

  54. Elmeiche, A., Mohamed, B., Elhannani, A.: Forced vibration analysis of functionally graded beams carrying moving harmonic loads under random boundary conditions. Math. Model. 7, 258–264 (2020)

    Google Scholar 

  55. Wang, Y., Fu, T., Zhang, W.: An accurate size-dependent sinusoidal shear deformable framework for GNP-reinforced cylindrical panels: applications to dynamic stability analysis. Thin-Walled Struct. 160, 107400 (2021)

    Article  Google Scholar 

  56. Ma, G.W., Ye, Z.Q., Shao, Z.S.: Modeling loading rate effect on crushing stress of metallic cellular materials. Int. J. Impact Eng 36, 775–782 (2009)

    Article  Google Scholar 

  57. Şimşek, M., Al-shujairi, M.: Static, free and forced vibration of functionally graded (FG) sandwich beams excited by two successive moving harmonic loads. Compos. B Eng. 108, 18–34 (2017)

    Article  Google Scholar 

  58. Ait Atmane, H., Tounsi, A., Bernard, F.: Effect of thickness stretching and porosity on mechanical response of a functionally graded beams resting on elastic foundations. Int. J. Mech. Mater. Des. 13, 71–84 (2017)

    Article  Google Scholar 

  59. Vo, T.P., Thai, H.-T., Nguyen, T.-K., Maheri, A., Lee, J.: Finite element model for vibration and buckling of functionally graded sandwich beams based on a refined shear deformation theory. Eng. Struct. 64, 12–22 (2014)

    Article  Google Scholar 

  60. Aria, A.I., Friswell, M.I.: Computational hygro-thermal vibration and buckling analysis of functionally graded sandwich microbeams. Compos. B Eng. 165, 785–797 (2019)

    Article  Google Scholar 

  61. Kahya, V., Turan, M.: Vibration and stability analysis of functionally graded sandwich beams by a multi-layer finite element. Compos. B Eng. 146, 198–212 (2018)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering, Arak University, Arak, 38156-88349, Iran

    Yasin Shabani, Pejman Mehdianfar & Mohammad Javad Khoshgoftar

Authors
  1. Yasin Shabani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pejman Mehdianfar
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammad Javad Khoshgoftar
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

M.J.K. contributed to conceptualization; Y.S. performed investigation; P.M. provided methodology; M.J.K. performed project administration, supervision, and writing—review and editing; Y.S. provided software; P.M. performed validation; Y.S. and P.M. performed writing—original draft.

Corresponding author

Correspondence to Mohammad Javad Khoshgoftar.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix 1

$$ N_{xx}^{b,c,t} = A_{1}^{b,c,t} \frac{\partial u\left( x \right)}{{\partial x}} - A_{2}^{b,c,t} \frac{{\partial^{2} w\left( x \right)}}{{\partial x^{2} }} + A_{3}^{b,c,t} \frac{\partial \varphi \left( x \right)}{{\partial x}} $$
(54)
$$ N_{xz}^{b,c,t} = - B_{1}^{b,c,t} \frac{\partial w\left( x \right)}{{\partial x}} + B_{2}^{b,c,t} \varphi \left( x \right) + B_{3}^{b,c,t} \frac{\partial w\left( x \right)}{{\partial x}} $$
(55)
$$ M_{xx}^{b,c,t} = A_{2}^{b,c,t} \frac{\partial u\left( x \right)}{{\partial x}} - C_{1}^{b,c,t} \frac{{\partial^{2} w\left( x \right)}}{{\partial x^{2} }} + C_{2}^{b,c,t} \frac{\partial \varphi \left( x \right)}{{\partial x}} $$
(56)
$$ R_{xx}^{b,c,t} = A_{3}^{b,c,t} \frac{\partial u\left( x \right)}{{\partial x}} - C_{2}^{b,c,t} \frac{{\partial^{2} w\left( x \right)}}{{\partial x^{2} }} + D_{1}^{b,c,t} \frac{\partial \varphi \left( x \right)}{{\partial x}} $$
(57)
$$ S_{xz}^{b,c,t} = - E_{1}^{b,c,t} \frac{\partial w\left( x \right)}{{\partial x}} + E_{2}^{b,c,t} \varphi \left( x \right) + B_{1}^{b,c,t} \frac{\partial w\left( x \right)}{{\partial x}} $$
(58)
$$ T_{xz}^{b,c,t} = - E_{2}^{b,c,t} \frac{\partial w\left( x \right)}{{\partial x}} + H_{1}^{b,c,t} \varphi \left( x \right) + B_{2}^{b,c,t} \frac{\partial w\left( x \right)}{{\partial x}} $$
(59)
$$ A_{1}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {Q_{11}^{b,c,t} } \right){\text{d}}z} $$
(60)
$$ A_{2}^{b,c,t} = - \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {Q_{11}^{b,c,t} g(z)} \right){\text{d}}z} $$
(61)
$$ A_{3}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {Q_{11}^{b,c,t} f(z)} \right){\text{d}}z} $$
(62)
$$ B_{1}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {k_{s} Q_{55}^{b,c,t} \frac{\partial g\left( z \right)}{{\partial z}}} \right){\text{d}}z} $$
(63)
$$ B_{2}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {k_{s} \;Q_{55}^{b,c,t} \frac{\partial f(z)}{{\partial z}}} \right){\text{d}}z} $$
(64)
$$ B_{3}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {k_{s} Q_{55}^{b,c,t} } \right){\text{d}}z} $$
(65)
$$ C_{1}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {Q_{11}^{b,c,t} g^{2} (z)} \right){\text{d}}z} $$
(66)
$$ C_{2}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {Q_{11}^{b,c,t} g(z)f(z)} \right){\text{d}}z} $$
(67)
$$ D_{1}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {Q_{11}^{b,c,t} f^{2} (z)} \right){\text{d}}z} $$
(68)
$$ E_{1}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {k_{s} Q_{55}^{b,c,t} \frac{{\partial^{2} g\left( z \right)}}{{\partial z^{2} }}} \right){\text{d}}z} $$
(69)
$$ E_{2}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {k_{s} \;Q_{55}^{b,c,t} \frac{\partial g\left( z \right)}{{\partial z}}\frac{\partial f(z)}{{\partial z}}} \right){\text{d}}z} $$
(70)
$$ H_{1}^{b,c,t} = \int_{{h_{1,2,3} }}^{{h_{2,3,4} }} {\left( {k_{s} \;Q_{55}^{b,c,t} \frac{{\partial^{2} f(z)}}{{\partial z^{2} }}} \right){\text{d}}z} $$
(71)

Appendix 2

$$ \overline{K}\left[ {1,1} \right] = A_{1} \left( \begin{gathered} \left( {m + 1} \right)mL^{2} x^{m - 1} + \left( {m + 3} \right)\left( {m + 2} \right)x^{m + 1} \hfill \\ - \left( {m + 2} \right)\left( {m + 1} \right)2Lx^{m} \hfill \\ \end{gathered} \right) $$
(72)
$$ \overline{K}\left[ {1,2} \right] = - A_{2} \left( \begin{gathered} \left( {n - 1} \right)\left( {n + 1} \right)nL^{2} x^{n - 2} \hfill \\ + \left( {n + 1} \right)\left( {n + 3} \right)\left( {n + 2} \right)x^{n} \hfill \\ - \left( {n + 2} \right)\left( {n + 1} \right)n2Lx^{n - 1} \hfill \\ \end{gathered} \right) $$
(73)
$$ \overline{K}\left[ {1,3} \right] = A_{3} \left( \begin{gathered} \left( {j + 1} \right)jL^{2} x^{j - 1} \hfill \\ + \left( {j + 3} \right)\left( {j + 2} \right)x^{j + 1} \hfill \\ - \left( {j + 2} \right)\left( {j + 1} \right)2Lx^{j} \hfill \\ \end{gathered} \right) $$
(74)
$$ \overline{K}\left[ {2,1} \right] = A_{2} \left( \begin{gathered} \left( {m - 1} \right)\left( {m + 1} \right)mL^{2} x^{m - 2} \hfill \\ + \left( {m + 1} \right)\left( {m + 3} \right)\left( {m + 2} \right)x^{m} \hfill \\ - \left( {m + 2} \right)\left( {m + 1} \right)m2Lx^{m - 1} \hfill \\ \end{gathered} \right) $$
(75)
$$ \begin{aligned} \overline{K}\left[ {2,2} \right] & = \left( { - B_{1} + B_{3} + E_{1} - B_{1} } \right)\left( \begin{gathered} \left( {n + 1} \right)nL^{2} x^{n - 1} \hfill \\ + \left( {n + 3} \right)\left( {n + 2} \right)x^{n + 1} \hfill \\ - \left( {n + 2} \right)\left( {n + 1} \right)2Lx^{n} \hfill \\ \end{gathered} \right) \\ & \quad - C_{1} \left( \begin{gathered} \left( {n - 2} \right)\left( {n - 1} \right)\left( {n + 1} \right)nL^{2} x^{n - 3} \hfill \\ + n\left( {n + 1} \right)\left( {n + 3} \right)\left( {n + 2} \right)x^{n - 1} \hfill \\ - \left( {n - 1} \right)\left( {n + 2} \right)\left( {n + 1} \right)n2Lx^{n - 2} \hfill \\ \end{gathered} \right) \\ \end{aligned} $$
(76)
$$ \overline{K}\left[ {2,3} \right] = \left( {B_{2} - E_{2} } \right)\left( \begin{gathered} \left( {j + 1} \right)L^{2} x^{j} \hfill \\ + \left( {j + 3} \right)x^{j + 2} \hfill \\ - 2\left( {j + 2} \right)Lx^{j + 1} \hfill \\ \end{gathered} \right) + C_{2} \left( \begin{gathered} \left( {j - 1} \right)\left( {j + 1} \right)jL^{2} x^{j - 2} \hfill \\ + \left( {j + 1} \right)\left( {j + 3} \right)\left( {j + 2} \right)x^{j} \hfill \\ - \left( {j + 2} \right)\left( {j + 1} \right)j2Lx^{j - 1} \hfill \\ \end{gathered} \right) $$
(77)
$$ \overline{K}\left[ {3,1} \right] = A_{3} \left( \begin{gathered} \left( {m + 1} \right)mL^{2} x^{m - 1} \hfill \\ + \left( {m + 3} \right)\left( {m + 2} \right)x^{m + 1} \hfill \\ - \left( {m + 2} \right)\left( {m + 1} \right)2Lx^{m} \hfill \\ \end{gathered} \right) $$
(78)
$$ \overline{K}\left[ {3,2} \right] = - C_{2} \left( \begin{gathered} \left( {n - 1} \right)\left( {n + 1} \right)nL^{2} x^{n - 2} \hfill \\ + \left( {n + 1} \right)\left( {n + 3} \right)\left( {n + 2} \right)x^{n} \hfill \\ - \left( {n + 2} \right)\left( {n + 1} \right)n2Lx^{n - 1} \hfill \\ \end{gathered} \right) + \left( {E_{2} - B_{2} } \right)\left( \begin{gathered} \left( {n + 1} \right)L^{2} x^{n} \hfill \\ + \left( {n + 3} \right)x^{n + 2} \hfill \\ - 2\left( {n + 2} \right)Lx^{n + 1} \hfill \\ \end{gathered} \right) $$
(79)
$$ \overline{K}\left[ {3,3} \right] = D_{1} \left( \begin{gathered} \left( {j + 1} \right)jL^{2} x^{j - 1} \hfill \\ + \left( {j + 3} \right)\left( {j + 2} \right)x^{j + 1} \hfill \\ - \left( {j + 2} \right)\left( {j + 1} \right)2Lx^{j} \hfill \\ \end{gathered} \right) - H_{1} \left( \begin{gathered} L^{2} x^{j + 1} \hfill \\ + x^{j + 3} \hfill \\ - 2Lx^{j + 2} \hfill \\ \end{gathered} \right) $$
(80)
$$ \overline{M}\left[ {1,1} \right] = - I_{1} \left( \begin{gathered} L^{2} x^{m + 1} \hfill \\ + x^{m + 3} \hfill \\ - 2x^{m + 2} L \hfill \\ \end{gathered} \right) + \mu I_{1} \left( \begin{gathered} \left( {m + 1} \right)mL^{2} x^{m - 1} \hfill \\ + \left( {m + 3} \right)\left( {m + 2} \right)x^{m + 1} \hfill \\ - \left( {m + 2} \right)\left( {m + 1} \right)2Lx^{m} \hfill \\ \end{gathered} \right) $$
(81)
$$ \overline{M}\left[ {1,2} \right] = I_{2} \left( \begin{gathered} \left( {n + 1} \right)L^{2} x^{n} \hfill \\ - 2\left( {n + 2} \right)Lx^{n + 1} \hfill \\ + \left( {n + 3} \right)x^{n + 2} \hfill \\ \end{gathered} \right) - \mu I_{2} \left( \begin{gathered} \left( {n - 1} \right)\left( {n + 1} \right)nL^{2} x^{n - 2} \hfill \\ + \left( {n + 1} \right)\left( {n + 3} \right)\left( {n + 2} \right)x^{n} \hfill \\ - \left( {n + 2} \right)\left( {n + 1} \right)n2Lx^{n - 1} \hfill \\ \end{gathered} \right) $$
(82)
$$ \overline{M}\left[ {1,3} \right] = - I_{3} \left( \begin{gathered} L^{2} x^{j + 1} \hfill \\ + x^{j + 3} \hfill \\ - 2x^{j + 2} L \hfill \\ \end{gathered} \right) + \mu I_{3} \left( \begin{gathered} \left( {j - 1} \right)\left( {j + 1} \right)jL^{2} x^{j - 2} \hfill \\ + \left( {j + 1} \right)\left( {j + 3} \right)\left( {j + 2} \right)x^{j} \hfill \\ - \left( {j + 2} \right)\left( {j + 1} \right)j2Lx^{j - 1} \hfill \\ \end{gathered} \right) $$
(83)
$$ \overline{M}\left[ {2,1} \right] = - I_{2} \left( \begin{gathered} \left( {m + 1} \right)L^{2} x^{m} \hfill \\ - 2\left( {m + 2} \right)Lx^{m + 1} \hfill \\ + \left( {m + 3} \right)x^{m + 2} \hfill \\ \end{gathered} \right) + \mu I_{2} \left( \begin{gathered} \left( {m - 1} \right)\left( {m + 1} \right)mL^{2} x^{m - 2} \hfill \\ + \left( {m + 1} \right)\left( {m + 3} \right)\left( {m + 2} \right)x^{m} \hfill \\ - \left( {m + 2} \right)\left( {m + 1} \right)m2Lx^{m - 1} \hfill \\ \end{gathered} \right) $$
(84)
$$ \begin{aligned} \overline{M}\left[ {2,2} \right] & = - I_{1} \left( \begin{gathered} L^{2} x^{n + 1} \hfill \\ + x^{n + 3} \hfill \\ - 2x^{n + 2} L \hfill \\ \end{gathered} \right) + \left( {\mu I_{1} + I_{5} } \right)\left( \begin{gathered} \left( {n - 1} \right)\left( {n + 1} \right)nL^{2} x^{n - 2} \hfill \\ + \left( {n + 1} \right)\left( {n + 3} \right)\left( {n + 2} \right)x^{n} \hfill \\ - \left( {n + 2} \right)\left( {n + 1} \right)n2Lx^{n - 1} \hfill \\ \end{gathered} \right) \\ & \quad - I_{5} \mu \left( \begin{gathered} \left( {n - 2} \right)\left( {n - 1} \right)\left( {n + 1} \right)nL^{2} x^{n - 3} \hfill \\ + n\left( {n + 1} \right)\left( {n + 3} \right)\left( {n + 2} \right)x^{n - 1} \hfill \\ - \left( {n - 1} \right)\left( {n + 2} \right)\left( {n + 1} \right)n2Lx^{n - 2} \hfill \\ \end{gathered} \right) \\ \end{aligned} $$
(85)
$$ \overline{M}\left[ {2,3} \right] = - I_{4} \left( \begin{gathered} \left( {j + 1} \right)L^{2} x^{j} \hfill \\ + \left( {j + 3} \right)x^{j + 2} \hfill \\ - 2\left( {j + 2} \right)Lx^{j + 1} \hfill \\ \end{gathered} \right) + \mu I_{4} \left( \begin{gathered} \left( {j - 1} \right)\left( {j + 1} \right)jL^{2} x^{j - 2} \hfill \\ + \left( {j + 1} \right)\left( {j + 3} \right)\left( {j + 2} \right)x^{j} \hfill \\ - \left( {j + 2} \right)\left( {j + 1} \right)j2Lx^{j - 1} \hfill \\ \end{gathered} \right) $$
(86)
$$ \overline{M}\left[ {3,1} \right] = - I_{3} \left( \begin{gathered} L^{2} x^{m + 1} \hfill \\ + x^{m + 3} \hfill \\ - 2x^{m + 2} L \hfill \\ \end{gathered} \right) + \mu I_{3} \left( \begin{gathered} \left( {m + 1} \right)mL^{2} x^{m - 1} \hfill \\ + \left( {m + 3} \right)\left( {m + 2} \right)x^{m + 1} \hfill \\ - \left( {m + 2} \right)\left( {m + 1} \right)2Lx^{m} \hfill \\ \end{gathered} \right) $$
(87)
$$ \overline{M}\left[ {3,2} \right] = I_{4} \left( \begin{gathered} \left( {n + 1} \right)L^{2} x^{n} \hfill \\ - 2\left( {n + 2} \right)Lx^{n + 1} \hfill \\ + \left( {n + 3} \right)x^{n + 2} \hfill \\ \end{gathered} \right) - \mu I_{4} \left( \begin{gathered} \left( {n - 1} \right)\left( {n + 1} \right)nL^{2} x^{n - 2} \hfill \\ + \left( {n + 1} \right)\left( {n + 3} \right)\left( {n + 2} \right)x^{n} \hfill \\ - \left( {n + 2} \right)\left( {n + 1} \right)n2Lx^{n - 1} \hfill \\ \end{gathered} \right) $$
(88)
$$ \overline{M}\left[ {3,3} \right] = - I_{6} \left( \begin{gathered} L^{2} x^{j + 1} \hfill \\ + x^{j + 3} \hfill \\ - 2x^{j + 2} L \hfill \\ \end{gathered} \right) + \mu I_{6} \left( \begin{gathered} \left( {j - 1} \right)\left( {j + 1} \right)jL^{2} x^{j - 2} \hfill \\ + \left( {j + 1} \right)\left( {j + 3} \right)\left( {j + 2} \right)x^{j} \hfill \\ - \left( {j + 2} \right)\left( {j + 1} \right)j2Lx^{j - 1} \hfill \\ \end{gathered} \right) $$
(89)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shabani, Y., Mehdianfar, P. & Khoshgoftar, M.J. Tailoring vibrational behavior in hybrid cellular sandwich nanobeams: a multiscale computational study. Arch Appl Mech 94, 281–298 (2024). https://doi.org/10.1007/s00419-023-02520-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-023-02520-2

Keywords

Search

Navigation