Time-dependent theory of single-photon scattering from a two-qubit system

Abstract

This paper investigates the manipulation of photon propagation in a one-dimensional waveguide coupled to a system of two identical superconducting qubits. The study focuses on the spatio-temporal distribution of the electric field resulting from the scattering of a single-photon narrow pulse. The method employed extends a previously developed time-dependent theory for a single qubit. Utilizing the Wigner-Weisskopf approximation, the explicit expressions for the forward and backward photon scattering amplitudes are derived. The associated electric fields are calculated for various regions in the 1D space, revealing contributions from the free incoming photon field, spontaneous qubit decay, and steady-state solutions. The findings contribute to understanding the behavior of superconducting qubits in open waveguide, providing insights into their potential applications in quantum devices and information technologies.

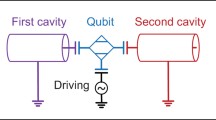
Graphic abstract

Appendices

Appendix A: Derivation of equations for qubits’ amplitudes (16), (17)

Taking the qubits’ amplitudes $\beta _n(t')$ out of integrals in (14), (15) we obtain:

$$\begin{aligned} \frac{{d\beta _1 }}{{dt}}= & {} - i\int \limits _0^\infty {d\omega } g(\omega )\gamma _0 \left( \omega \right) e^{ - i(\omega - \Omega )t} \nonumber \\{} & {} - 2\beta _1 (t)\int \limits _0^\infty {d\omega } g^2 (\omega )I(\omega ,t) \nonumber \\{} & {} - 2\beta _2 (t)\int \limits _0^\infty {d\omega } g^2 (\omega )\cos (k_\omega d)I(\omega ,t), \end{aligned}$$

(A1)

$$\begin{aligned} \frac{{d\beta _2 }}{{dt}}= & {} - i\int \limits _0^\infty {d\omega } g(\omega )\gamma _0 \left( \omega \right) e^{ik_\omega d} e^{ - i(\omega - \Omega )t}\nonumber \\{} & {} - 2\beta _1 (t)\int \limits _0^\infty {d\omega } g^2 (\omega )\cos (k_\omega d)I(\omega ,t) \nonumber \\{} & {} - 2\beta _2 (t)\int \limits _0^\infty {d\omega } g^2 (\omega )I(\omega ,t), \end{aligned}$$

(A2)

where

$$\begin{aligned} I(\omega ,t) = \int \limits _0^t {} e^{ - i\left( {\omega - \Omega } \right) (t - t')} dt'. \end{aligned}$$

(A3)

Next, we change variables in (A3), $t-t'=\tau$, and tend the upper bound of integral to infinity.

$$\begin{aligned} I(\omega ,t)= & {} \int \limits _0^t {dt'} e^{ - i\left( {\omega - \Omega } \right) (t - t')} = \int \limits _0^t {d\tau } e^{ - i\left( {\omega - \Omega } \right) \tau } \nonumber \\{} & {} \approx \int \limits _0^\infty {d\tau } e^{ - i\left( {\omega - \Omega } \right) \tau } = \pi \delta (\omega - \Omega ) - iP\frac{1}{{\omega - \Omega }} ,\nonumber \\ \end{aligned}$$

(A4)

where $P\frac{1}{\omega -\Omega }$ denotes Cauchy’s principal value.

Then, for (A1), (A2) we obtain:

$$\begin{aligned} \frac{{d\beta _1 }}{{dt}}= & {} - i\int \limits _0^\infty {d\omega } g(\omega )\gamma _0 \left( \omega \right) e^{ - i(\omega - \Omega )t} \nonumber \\{} & {} - 2\pi \beta _1 (t)g^2 (\Omega ) - 2\pi \beta _2 (t)g^2 (\Omega )\cos (k_\Omega d) \nonumber \\{} & {} + i2\beta _1 (t)P\int \limits _0^\infty {d\omega } \frac{{g^2 (\omega )}}{{\omega - \Omega }} \nonumber \\ {}{} & {} + i2\beta _2 (t)P\int \limits _0^\infty {d\omega } \frac{{g^2 (\omega )\cos (k_\omega d)}}{{\omega - \Omega }}, \end{aligned}$$

(A5)

$$\begin{aligned} \frac{{d\beta _2 }}{{dt}}= & {} - i\int \limits _0^\infty {d\omega } g(\omega )\gamma _0 \left( \omega \right) e^{ik_\omega d} e^{ - i(\omega - \Omega )t} \nonumber \\{} & {} - 2\pi \beta _1 (t)g^2 (\Omega )\cos (k_\Omega d) - 2\pi \beta _2 (t)g^2 (\Omega ) \nonumber \\{} & {} + i2\beta _1 (t)P\int \limits _0^\infty {d\omega } \frac{{g^2 (\omega )\cos (k_\omega d)}}{{\omega - \Omega }} \nonumber \\ {}{} & {} + i2\beta _2 (t)P \int \limits _0^\infty {d\omega } \frac{{g^2 (\omega )}}{{\omega - \Omega }}. \end{aligned}$$

(A6)

The quantity $P\int \limits _0^\infty {d\omega } \frac{{g^2 (\omega )}}{{\omega - \Omega }}$ results in the shift of the qubit frequency $\Omega$. We assume the shift is small and include it implicitly in the definition of $\Omega$. As the coupling $g(\omega )$ between qubit and the field is effective at the qubit resonance, we take it off the Cauchy principal integral in equations (A5), (A6) at the qubit resonance frequency. Then for the Cauchy principal integral we obtain:

$$\begin{aligned} P\int \limits _0^\infty {d\omega } \frac{{g^2 (\omega )\cos (k_\omega d)}}{{\omega - \Omega }}= & {} g^2 (\Omega )P\int \limits _0^\infty {d\omega } \frac{{\cos (k_\omega d)}}{{\omega - \Omega }} \nonumber \\= & {} - \pi g^2 (\Omega )\sin (k_\Omega d). \end{aligned}$$

(A7)

For two-qubit system the rate of spontaneous emission can be found from Fermi’s golden rule:

$$\begin{aligned} \Gamma = 4\pi g^2 (\Omega ). \end{aligned}$$

(A8)

Combining the equations (A7) and (A8) with equations (A5) and (A6) we obtain the equations (16) and (17) which are given in the main text.

Appendix B: Properties of sine and cosine integrals and some related integrals

Here we use the conventional definitions for sine and cosine integrals [38].

$$\begin{aligned}{} & {} \textrm{si}(xy) = - \int \limits _x^\infty {\frac{{\sin zy}}{z}} dz, \end{aligned}$$

(B1)

$$\begin{aligned}{} & {} \textrm{ci}(xy) = - \int \limits _x^\infty {\frac{{\cos zy}}{z}} dz, \end{aligned}$$

(B2)

$$\begin{aligned}{} & {} {\textrm{Si}}(xy) = \int \limits _0^x {\frac{{\sin zy}}{z}} dz, \end{aligned}$$

(B3)

$$\begin{aligned}{} & {} \int \limits _0^\infty {\frac{{\sin zy}}{z}} dz = \frac{\pi }{2}sign(y), \end{aligned}$$

(B4)

where $\textrm{si}(xy)$ is defined on the whole real axis, while $\textrm{ci}(xy)$ is defined only for $x>0$.

Using these definitions it is not difficult to show that

$$\begin{aligned} \textrm{si}(xy)= & {} \textrm{Si}(xy) - \frac{\pi }{2}sign(y), \end{aligned}$$

(B5)

$$\begin{aligned} \textrm{si}( - xy)= & {} - \int \limits _{ - x}^\infty {\frac{{\sin zy}}{z}} dz = - \textrm{Si}(xy) - \frac{\pi }{2}sign(y). \end{aligned}$$

(B6)

Combining (B5) and (B6) we obtain a useful relation

$$\begin{aligned} \textrm{Si}(xy)+\textrm{Si}(-xy)=-\pi sign(y). \end{aligned}$$

(B7)

From definitions (B1), (B2), and (B3) the parity relations follow:

$$\begin{aligned} \textrm{si}(x(-y))= & {} -\textrm{si}(xy);\,\textrm{ci}(x(-y))=\textrm{ci}(xy);\nonumber \\ \textrm{Si}(x(-y))= & {} -\textrm{Si}(xy). \end{aligned}$$

(B8)

The exponential integral $E_1(z)$ in the expression (36), is defined as follows [37]:

$$\begin{aligned} E_1(z) = \int \limits _z^\infty {\frac{{e^{-t }}}{t}} dt. \end{aligned}$$

(B9)

The behavior of scattered fields at large x and t follows from the asymptote of the exponential integral function, sine, and cosine integrals [38, 39]:

$$\begin{aligned} \textrm{si}(x)\approx -\frac{\cos (x)}{x}-\frac{\sin (x)}{x^2}; \quad \textrm{ci}(x)\approx \frac{\sin (x)}{x}-\frac{\cos (x)}{x^2},\nonumber \\ \end{aligned}$$

(B10)

where $x\gg 1$.

$$\begin{aligned} E_1(z)\approx \frac{e^{-z}}{z}\left( 1-\frac{1}{z}\right) , \end{aligned}$$

(B11)

where $|z|\gg 1$.

Below we illustrate the application of above formulae for the calculation of some integrals which we use throughout the paper.

$$\begin{aligned} I_2 (x,t) = \int \limits _0^\infty {d\omega } \frac{{e^{i(\omega - \omega _S )t} - 1}}{{\omega - \omega _S }}e^{i\frac{\omega }{{v_g }}\left( {x - v_g t} \right) }. \end{aligned}$$

(B12)

This integral, where $x>0$ and $x-v_gt<0$ describes the forward travelling wave between qubits $0<x<d$ as well as behind the second qubit, $x>d$.

Changing the variables in the integrand of (B12), $z=\omega -\omega _S$, $\tau =x/v_g$, $T=(x-v_gt)/v_g$ we obtain

$$\begin{aligned} I_2 (x,t) = e^{i\omega _S T} \left( {\int \limits _{ - \omega _S }^\infty {dz} \frac{{e^{iz\tau } }}{z} - \int \limits _{ - \omega _S }^\infty {dz} \frac{{e^{izT} }}{z}} \right) . \end{aligned}$$

(B13)

The calculation of the first integral in (B13) yields:

$$\begin{aligned}{} & {} \int \limits _{ - \omega _S }^\infty {dz} \frac{{e^{iz\tau } }}{z} = \int \limits _{ - \omega _S }^\infty {dz} \frac{{\cos z\tau }}{z} + i\int \limits _{ - \omega _S }^\infty {dz} \frac{{\sin z\tau }}{z} \nonumber \\{} & {} \quad = \int \limits _{ - \omega _S }^{\omega _S } {dz} \frac{{\cos z\tau }}{z} + \int \limits _{\omega _S }^\infty {dz} \frac{{\cos z\tau }}{z} + i\int \limits _{ - \omega _S }^\infty {dz} \frac{{\sin z\tau }}{z} \nonumber \\{} & {} \quad = - \textrm{ci}(\omega _S \tau ) - i \,\textrm{si}( - \omega _S \tau ). \end{aligned}$$

(B14)

Similar expression we obtain for second integral in (B13):

$$\begin{aligned} \int \limits _{ - \omega _S }^\infty {dz} \frac{{e^{izT} }}{z} = - \textrm{ci}(\omega _S T) - i \,\textrm{si}( - \omega _S T). \end{aligned}$$

(B15)

Therefore, for $I_2(x,t)$ we obtain:

$$\begin{aligned} I_2 (x,t)= & {} e^{i\omega _S T}\left( -\textrm{ci}(\omega _S\tau )-i \,\textrm{si}(-\omega _S\tau )\right. \nonumber \\{} & {} \left. +\textrm{ci}(\omega _ST)+i \,\textrm{si}(-\omega _ST)\right) . \end{aligned}$$

(B16)

Using the relation (B7) we rewrite (B16) as follows:

$$\begin{aligned} I_2 (x,t)= & {} e^{i\omega _S T}\nonumber \\{} & {} \times \left( -\textrm{ci}(\omega _S\tau )+i \,\textrm{si}(\omega _S\tau )+\textrm{ci}(\omega _ST)-i \,\textrm{si}(\omega _ST)\right) \nonumber \\{} & {} +i\pi e^{i\omega _S T}\left( sign(\tau )- sign(T)\right) . \end{aligned}$$

(B17)

Here $\tau >0$, and $T<0$. Therefore, we obtain:

$$\begin{aligned} I_2 (x,t)= & {} e^{i\omega _S T}\nonumber \\{} & {} \times \left( -\textrm{ci}(\omega _S\tau )+i \,\textrm{si}(\omega _S\tau )+\textrm{ci}(\omega _S|T|)+i \,\textrm{si}(\omega _S|T|)\right) \nonumber \\{} & {} +2i\pi e^{i\omega _ST}, \end{aligned}$$

(B18)

where $\tau =x/v_g>0$, $T=(x-v_gt)/v_g<0$.

For integral $I_2(x-d,t)$ which describes the forward travelling wave between qubits, $x-d<0$ we obtain from (B17), where x is replaced with $x-d$:

$$\begin{aligned} I_2 (x-d,t)= & {} e^{i\omega _S T}\left( -\textrm{ci}(\omega _S|\tau |)-i \,\textrm{si}(\omega _S|\tau |)\right. \nonumber \\{} & {} \left. +\textrm{ci}(\omega _S|T|)+i \,\textrm{si}(\omega _S|T|)\right) , \end{aligned}$$

(B19)

where $\tau =(x-d)/v_g<0$, $T=(x-d-v_gt)/v_g<0$.

Next, we consider the integral (55) which describes the backward travelling wave in front of the first qubit $x<0$.

$$\begin{aligned} J_2 (x,t) = \int \limits _0^\infty {d\omega } \frac{{e^{i(\omega - \omega _S )t} - 1}}{{\omega - \omega _S }}e^{ - i\frac{\omega }{{v_g }}\left( {x + v_g t} \right) }, \end{aligned}$$

(B20)

where $x<0$, $x+v_gt>0$.

The calculation of this integral is similar to that of $I_2(x,t)$. For $J_2(x,t$ we obtain the following result:

$$\begin{aligned} J_2 (x,t)= & {} e^{-i\omega _S T}\nonumber \\{} & {} \times \left( -\textrm{ci}(\omega _S\tau )-i \,\textrm{si}(\omega _S\tau )+\textrm{ci}(\omega _ST)+i \,\textrm{si}(\omega _ST)\right) \nonumber \\{} & {} -i\pi e^{-i\omega _S T}\left( sign(\tau )- sign(T)\right) . \end{aligned}$$

(B21)

Therefore, for $J_2(x,t)$ we finally obtain:

$$\begin{aligned} J_2 (x,t)= & {} e^{-i\omega _S T}\nonumber \\{} & {} \times \left( -\textrm{ci}(\omega _S|\tau |)+i \,\textrm{si}(\omega _S|\tau |)+\textrm{ci}(\omega _ST)+i \,\textrm{si}(\omega _ST)\right) \nonumber \\{} & {} +2i\pi e^{-i\omega _S T}, \end{aligned}$$

(B22)

where $\tau =x/v_g<0$, $T=(x+v_gt)/v_g>0$.

There are two integrals which describe the backward travelling wave between qubits, $J_2(x,t)$ where $x>0$, and $J_2(x-d),t$ where $x-d<0$. The quantity $J_2(x,t)$ with $x>0$ follows from (B21) where $\tau =x/v_g>0$:

$$\begin{aligned} J_2 (x,t)= & {} e^{-i\omega _S T}\left( -\textrm{ci}(\omega _S\tau )-i \,\textrm{si}(\omega _S\tau )\right. \nonumber \\{} & {} \left. +\textrm{ci}(\omega _ST)+i \,\textrm{si}(\omega _ST)\right) , \end{aligned}$$

(B23)

where $\tau =x/v_g>0$, $T=(x+v_gt)/v_g>0$.

The integral $J_2(x-d,t)$ is obtained from equation (B22) where x is replaced with $x-d$, and where $\tau =(x-d)/v_g<0$, $T=(x-d+v_gt)/v_g>0$.