Abstract
This paper was inspired by a recent publication by Redžíc (2018 Eur. J. Phys.39 025205) which threw into bold relief the differences between the way Maxwell viewed the current and the way Lorentz visualized it. We make the assumption that for a circuit of laboratory dimensions current (and charge perturbation effects in general) can be assumed to propagate instantaneously around the loop. Our second fundamental assumption is the commonly accepted one that E is the force per unit charge on a stationary charge. We use these facts to make the usual definition of electromotive force more rigorous and to derive the Lorentz force formula.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Introduction
It is a curious fact that many of the fundamental quantities of electromagnetic field theory have not yet received rigorous and logical definitions. [1] One example is the electromotive force or EMF. Redžíc [2] has presented a meticulously written paper comparing Maxwell's view of EMF with current usage and points out that he (Maxwell) rejected the idea of current being a flow of charged particles. Rather, he visualized it as the flow of an incompressible fluid. This view is at odds with that of Lorentz who explicitly assumed that electrons carry the current, even in metallic filamentary conductors where simple calculations show that the drift speed is far too small for this to be the case. Redžíc's paper contains a wealth of references on this issue.
We survey this disparity of views and offer a simple observation about current and the speed of charge perturbation effects which makes the definition of EMF rigorous. We show that the usual Faraday law holds for time-varying loops and then derive the Lorentz force formula. 1
Charge, current, and EMF
Charge and current
Rowland demonstrated in 1876 [5] that electrostatic charge deposited on an insulated disk generated a magnetic field when he gave the disk a spin. Rowland's experiment is often quoted as evidence that moving charge constitutes a current in metallic filamentary conductors, as did Lorentz in his 1906 lectures on the theory of electrons [4]. Lorentz used it to justify writing the conduction current density in the form J = ρ v . Rowland's experiment was an intimation—perhaps—but not logical proof. It only shows that convected charge generates a magnetic field and really says nothing about the mechanism of conduction in metals.
Experiments that are perhaps more germane to this issue were conducted by Tolman and others, the first being [6], by accelerating a wire along its long axis and suddenly stopping it. Charge was detected on the two ends, and computations showed that this charge was consistent with particles having the appropriate charge-to-mass ratio for electrons. These experiments, too, are often quoted as evidence that electrons flowing through a conductor explain the current in it. But this experiment does not provide sufficient evidence that electrons flowing from one end of a wire to the other constitute the current in that wire.
Computation of the drift speed of electrons in a copper wire at room temperature indicates that the flow rate is only on the order of millimeters per second. In fact, as Griffiths puts it (referring to a battery connected to a lightbulb) in his highly respected text Introduction to Electrodynamics [7], 'What is more, given that the charges in a typical wire move (literally) at a snail's pace (see Prob. 5.20), why doesn't it take half an hour for the news to reach the lightbulb?' It is worthwhile noting that Maxwell did not believe that current was constituted of flowing charge, preferring to view it as an incompressible fluid. Here's the way Redžíc puts it in a footnote 2
⋯Maxwell was not inclined to interpret electricity as a collection of charged particles. ⋯when discussing the 'equation of continuity,'
, where j c is the conduction current density and ρ is 'the volume density of free electricity,' he not only refrains from writing j c as ρ v (arts 295, 395), but 'in order to simplify the mathematical process,' he introduces 'mathematical points' as convenient mathematical abstractions (arts 44, 73, 81).
So—who was right, Lorentz or Maxwell? To get a clue to the answer, let us return to a later portion of the Griffiths text, namely page 547, Example 12.13, in a chapter on relativity. Here he discusses the hidden momentum effect on a current dipole, applying the Lorentz contraction to the electrons supposedly flowing around the loop. Any such effect should, of course, be negligible if they are moving at a snail's pace. This inconsistency is one which shows up in virtually all modern textbooks and papers, though very few even address the slow flow of actual electrons as does Griffiths.
In this paper, we will side with Maxwell by considering the current in a wire circuit of lab dimensions to propagate instantaneously around the loop—as do any charge perturbation effects.
Electromagnetic variables 3
Oddly, the fundamental variables of electromagnetic theory have, by and large, not been defined in a rigorous manner for general time-varying fields (see [1]). In particular, many texts fail to discuss potentials at all, and so we will briefly survey a logical approach for defining the fundamental electromagnetic variables ϕ, A , E and B in a rigorous manner. This approach is similar to the one adopted by Wald in his interesting new text [8], which—like the present development—bases electromagnetic theory on the potentials.
We assume that the current density J has been operationally defined, not necessarily as ρ v . For instance in a metallic filamentary conductor we might define it as J = (I/S) e S , where I is the current (assumed to be experimentally determined) and S = S e S is the vector cross-sectional area.
We define the retarded vector potential as

where:
- 1.The integral is over all space, with the integration variable
 and the volume element of integration
and the volume element of integration 
- 2.

- 3.μ0 is the permeability of free space
- 4.c is the speed of light
- 5.
![$\left[{\boldsymbol{J}}({\boldsymbol{r}}^{\prime} ,t)\right]\equiv {\boldsymbol{J}}({\boldsymbol{r}}^{\prime} ,t-R/c)$](data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAAEAAAABCAQAAAC1HAwCAAAAC0lEQVR42mNkYAAAAAYAAjCB0C8AAAAASUVORK5CYII=)
Now let us take the divergence of A . This results in
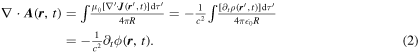
Here, we have used the continuity equation for the divergence of current density, defined the retarded scalar potential by

and noted that μ0
 0 = 1/c2. The commutativity of the operators used in equation (2) depends on an assumed causality of
A
as a function of
J
and is justified in [1]. Due to its importance and implications, a more direct derivation of (2), known in the literature as the Lorenz gauge condition, is given in an
0 = 1/c2. The commutativity of the operators used in equation (2) depends on an assumed causality of
A
as a function of
J
and is justified in [1]. Due to its importance and implications, a more direct derivation of (2), known in the literature as the Lorenz gauge condition, is given in an
Straightforward differentiations show that these potentials obey the wave equations
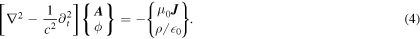
Using the standard identity

defining the magnetic induction by

combining these equations with the top line in equation (4), and applying equation (2) results in
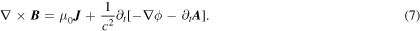
The form of the last term prompts us to define the electric field intensity as

We can then write equation (7) as

which is the Ampére–Maxwell equation. Taking the divergence of (6) results in

Taking the curl of (8) and applying (6) results in

Taking the divergence of (8) and applying the bottom wave equation in (4) results in

Equations (9) through (12) are the Maxwell equations for free space.
Perhaps a word is in order about our use of the continuity equation relating charge to current density. One might object that it relies upon the Lorentz view of current as a flow of charge. It does not. As Wald [8] has pointed out, if the continuity equation does not hold then Maxwell's equations would not be solvable. 4 Hence, we treat it as an independent assumption.
To summarize, in this section we showed how the potentials and the fundamental field variables can be logically defined as causal consequences of the current density. We now consider the definition of the electromotive force or EMF.
Electromotive force (EMF)
The Faraday law for a nonmoving loop
Have a look at figure 1, which shows a closed contour C in space assumed for now to be stationary. We will for the most part think of it as a closed filamentary conductor for intuitive reasons—but this is not necessary. The EMF around this contour is, in the more careful treatments, defined as

where f is the force per unit charge exerted by the electromagnetic field on a small charge placed at a point on the curve and held stationary there. This charge is imagined to be very slowly moved around the contour and so the EMF is the negative of the amount of work per unit charge expended in so doing. 5 But this is ambiguous because it does not address the issue of time—undoubtedly because EMF is often introduced in conjunction with constant currents and fields. Another shortcomng is that, at this stage of our development, we do not yet know what the force supplied by the electromagnetic field is.
Figure 1. A closed contour in space.
Download figure:
Standard image High-resolution imageWe remedy these two defects by writing our definition as

and making the fundamental assumption that the electric field intensity is the force per unit charge exerted by the field on a stationary charge. This permits us to write

This does not yet solve our problem, though, because when we use the electric field intensity we are assuming that our test charge is either stationary or to be moved only very, very slowly. Furthermore, are the values of t on the two sides of this equation the same or different? This question is one which most texts fail to deal with. To do so, we make another fundamental assumption. As we pointed out in an earlier section, we will assume that currents—or the effects of any charge perturbation—propagate instantaneously around the loop. Thus, we can think of freezing all the field variables and their derivatives at the values they assume at the time t, then slowly moving our test charge around the loop. Thus, we can now, with rigor and without ambiguity, define the EMF of our stationary curve C as in equation (15) where t is fixed. Using our definition of E in equation (8), we have
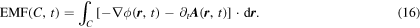
The gradient term integrates to zero around the closed loop—remember that t is fixed!—and, with the usual mathematical caveats about exchange of differentiation and integration, we have

We can now apply the Stokes theorem to write
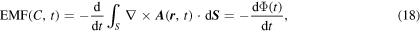
where S is a bounding surface for C whose sense is taken using the right-hand rule and Φ is the magnetic flux through that surface. Equation (18) is known as the Faraday law of induction for a nonmoving loop.
The Faraday law for a moving loop
Now suppose that C moves and/or deforms with time. We parameterize it by

where L = L(t) is the length of the curve at time t. At each time t there is a different contour, and at each value of s the position on the curve is a time function r = r (s, t). Note that we can write the curve as a function of time, C(t).
If we were to not assume that propagation of electrical effects around the loop is instantaneous, the actual curve described by our test charge in space would look something like the one shown in figure 2, where we have assumed that T seconds are required to traverse the curve. Even though r (L, 0) = r (0, 0) for a physical conductor, we might have r (L, T) ≠ r (0, 0) for the trajectory of our test charge in space. Thus, C would perhaps not even be closed, with the attendant problems of defining a bounding surface and the flux through it. Therefore, even though we might possibly define an EMF for such a contour, it would be cumbersome and difficult to work with. The value of work per unit charge would depend upon the particular characteristics of the motion, in particular its velocity at various points along the curve. We will therefore continue with our assumption of instantaneous propagation of electrical effects, assuming the fields and their derivatives to be frozen at the values they assume at time t and continue to use our assumption that the force is that on an almost stationary particle during its slow movement around the loop.
Figure 2. An open contour in space.
Download figure:
Standard image High-resolution imageThe first term in equation (16) still integrates to zero for it is the line integral of a gradient over the closed contour C(t) at the particular time t.
The second term is more problematic because of the dependence of C(t) upon the time. We will begin with a direct computation of the total derivative of this integral, which proceeds as follows. By the definition of derivative, we have
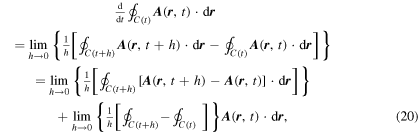
where we have added and subtracted
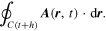
In the first term in the last two lines, we use the mean value theorem of calculus on each component of the integrand, writing
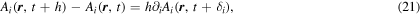
where 0 ≤ ∣δi ∣ ≤ ∣h∣. Using equation (21) in the next to last line of equation (20) we obtain
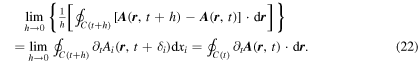
The validity of our last step depends, of course, on continuity conditions of A and C(t).
Our last term requires more work—for which we will find figure 3 helpful. There, we see the contour at time t on the bottom and at time t + h at the top. We have shown the latter reversed to agree with the sense of what we are about to do, which is to connect the two curves by positive and negative segments infinitely close together. We show this idea in the figure exaggerated for clarity. This procedure produces a closed surface bounded by our two original contours and these two small segments. Even though the two contours C(t) and C(t + h) occur at different times, for our construction we will consider the loci of points to coexist at time t because the integrand is evaluated at that time. We can now write the last term in our equation (20) as
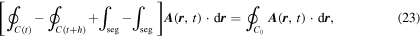
where C0 is the composite curve formed by C(t), C(t + h), seg, and −seg. Here seg refers to the small straight line segment whose vector length is v ( r , t)h as shown in the figure and r is an arbitrary point on C(t). Application of the Stokes theorem to the composite curve C0 gives

where S is the cylindrical side surface and we have written ∇ × A = B . Because seg has infinitesimal length and d S = v ( r , t)h × d r , however, we can approximate this surface integral by the contour integral
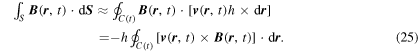
Using this result along with equations (23) and (22) in (20) and taking the limit results in

Rearranging this equation and substituting in equation (16) and recalling that the gradient term integrates to zero gives
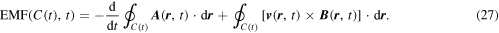
The last term is often called the 'motional EMF.' If we apply the Stokes theorem, we obtain
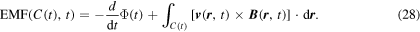
This is the classical Faraday induction law for a moving loop.
Figure 3. A moving contour.
Download figure:
Standard image High-resolution imageThe Lorentz force
Redžíc 6 says that Maxwell '⋯paved the way for the Lorentz force expression.' We will now complete Maxwell's demonstration by showing that it is indeed rigorously valid. We have already made the fundamental (and common) assumption that E is the force per unit charge on a stationary charge. Now we will add the assumption that force due to its motion adds to the force on it when it is stationary.
Consider figure 4. There we see a charged particle moving along an arbitrary trajectory 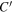 that passes through the point
that passes through the point 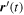 at time t with velocity
v
(t).
7
We imagine an arbitrary open path of points C through
at time t with velocity
v
(t).
7
We imagine an arbitrary open path of points C through 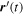 as shown by the dashed line, traversed in the direction defined by the dashed arrow. We imagine this curve to be displaced an infinitesimal distance and replicated and that it is traversed in the opposite direction as indicated by the second arrow, thus forming the arc −C. We also suppose that the two ends of these contours are connected by negligibly short arcs, thus forming a closed curve consisting of C and its negative. We assume that only the first arc passes through
as shown by the dashed line, traversed in the direction defined by the dashed arrow. We imagine this curve to be displaced an infinitesimal distance and replicated and that it is traversed in the opposite direction as indicated by the second arrow, thus forming the arc −C. We also suppose that the two ends of these contours are connected by negligibly short arcs, thus forming a closed curve consisting of C and its negative. We assume that only the first arc passes through 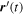 , whereas the second path avoids it. Thus, the closed path C − C is deforming only at the point
, whereas the second path avoids it. Thus, the closed path C − C is deforming only at the point 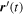 .
8
We can therefore write the velocity of this deforming point as
.
8
We can therefore write the velocity of this deforming point as

where the delta function is a one-dimensional one along the curve; furthermore, the flux enclosed by the curve C − C is zero. Hence, Faraday's law for moving contours in equation (28) becomes
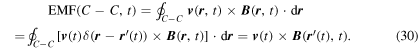
We now note that our contour C − C is an imaginary construction so there is no charge on it anywhere except at 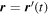 . Therefore, we can write the force as
. Therefore, we can write the force as 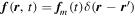 , where
f
m
refers to the force on the moving particle due to its motion. This permits us to write
, where
f
m
refers to the force on the moving particle due to its motion. This permits us to write
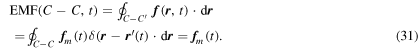
Using this in equation (30) we get

Assuming that the field forces on a charged particle are additive, the total force per unit charge on the moving charge becomes
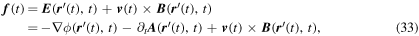
which is of course the Lorentz force law.
Figure 4. A moving point and a zero area contour.
Download figure:
Standard image High-resolution imageSummary
We have made the fundamental observation that propagation of electrical effects around a lab-sized circuit can be considered instantaneous 9 and used that fact to make the usual definition of EMF rigorous and to derive the Lorentz force law. We have also raised some doubt as to the applicability of the Lorentz expression J = ρ v for metallic conductors.
For conventional situations, we have shown that the usual Maxwell theory is valid. However, for short pulses (such as those in ultrawideband communications or EMP studies) or very high frequencies, the fundamental concepts should be reexamined taking into account finite propagation speeds. Undoubtedly, the very concept of EMF is not applicable in such circumstances.
Acknowledgments
The author acknowledges the contributions of the reviewers. Their suggestions materially improved the presentation. He also acknowleges the contributions of Dr Vladimir Onoochin, who brought the Redžíc paper to his attention and reviewed an early form of the mansucript.
Data availability statement
No new data were created or analysed in this study.
: Appendix. Derivation of the Lorenz condition
Consider the retarded integral
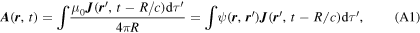
where J is an arbitrary function which satisfies the continuity condition ∇ · J = − ∂t ρ and

In component form, dropping arguments for simplicity, we have

Now
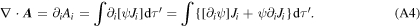
But 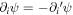 , where the prime denotes differentiation with respect to the ith primed position variable, so
, where the prime denotes differentiation with respect to the ith primed position variable, so
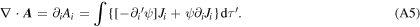
Write

Thus, the integrand of (A5) can be written as

The first term is merely ![$-{\rm{\nabla }}^{\prime} \cdot \left[\psi {\boldsymbol{J}}\right]$](https://content.cld.iop.org/journals/0143-0807/45/1/015202/revision3/ejpad0a9eieqn15.gif) . Inserting it in (A5), integrating over all space, and applying the Stokes theorem causes this term to vanish—assuming the usual regularity conditions on the integrand. Thus, the integrand, equation (A7), becomes
. Inserting it in (A5), integrating over all space, and applying the Stokes theorem causes this term to vanish—assuming the usual regularity conditions on the integrand. Thus, the integrand, equation (A7), becomes

Here, we must exercise a great deal of care because we are subjecting the conventional notation for partial derivatives to some stress. The symbol 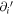 means differentiation with respect to the primed position variables
means differentiation with respect to the primed position variables 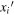 , while ∂i
symbolizes differentiation with respect to the unprimed position variables. Suppose we write
, while ∂i
symbolizes differentiation with respect to the unprimed position variables. Suppose we write 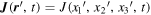 and denote partial differentiation with respect to the first three arguments by
and denote partial differentiation with respect to the first three arguments by 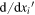 . Taking note that
. Taking note that 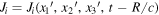 and that R is a function of both primed and unprimed position variables in (A8), we have
and that R is a function of both primed and unprimed position variables in (A8), we have
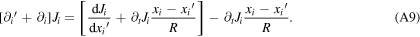
Thus, there is a cancellation of terms, and our integrand becomes

Inserting this into (A4) gives
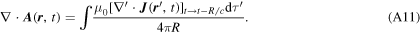
The continuity condition says that 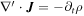 , and the partial time derivative clearly commutes with the computation of the retarded integral, so—applying the condition that μ0
, and the partial time derivative clearly commutes with the computation of the retarded integral, so—applying the condition that μ0
 0 = 1/c2—we have
0 = 1/c2—we have
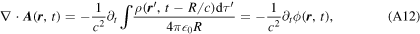
where ϕ is the retarded scalar potential.
Footnotes
- 1
Curiously, Lorentz never gave a satisfactory derivation of his law. The supposed original derivation was in [3], but it assumed an ether, was vaguely structured, and contained a number of errors. Later, in [4] he seemingly disavowed his earlier derivation, passing it off by saying, 'Like our former equations it is got by generalizing the results of electromagnetic experiments.' He never specified which experiments these were. Presumably it was Ampére's experiments to which he was referring.
- 2
Reference [2] footnote 9.
- 3
This section repeats the gist of reference [1], but is presented here in condensed form for clarity of exposition.
- 4
- 5
To move the charge we would have to exert a force which is the negative of the force on it due to the field; hence the negative. The movement is considered to be so slow that it does not affect force computation.
- 6
Reference [2] section 5 'Conclusions'.
- 7
r'(t) = r'(s, t) for some value of the real parameter s, and v(t) =
 tr'(s, t).
tr'(s, t). - 8
Note that v is not the velocity with which we might move a test charge along the C − C, but refers to the actual velocity of the actual charged particle.
- 9
In our derivation of the Lorentz force we can in fact make this assumption with no doubt since our auxiliary curve was only imaginary and hence can be sized to suit our assumption! The Lorentz force law is thus generally valid and does not depend upon any instantaneous propagation of effects.


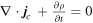
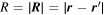
![$\left[{\boldsymbol{J}}({\boldsymbol{r}}^{\prime} ,t)\right]\equiv {\boldsymbol{J}}({\boldsymbol{r}}^{\prime} ,t-R/c)$](https://content.cld.iop.org/journals/0143-0807/45/1/015202/revision3/ejpad0a9eieqn5.gif)