Hall anomalies of the doped Mott insulator

Abstract

The Hall coefficient of the strongly interacting square lattice Hubbard model is calculated for temperatures between the antiferromagnetic interaction and the Mott gap scales. The leading order thermodynamic formula is evaluated for all doping concentrations. Second-order corrections of the thermodynamic formula are calculated and found to be negligible. The Hall coefficient diverges toward the Mott insulator. Below 45% doping the Hall sign is reversed relative to band structure-based Boltzmann’s equation. These results elucidate the effects of the Mott insulator on the charge carriers and their non-Fermi liquid transport.

Introduction

Mott insulators¹ are found in narrow band metals at odd numbers of electrons per unit cell, in the presence of strong electron-electron interactions. When slightly doped, one can often observe a “strange metal” behavior which is inconsistent with well-defined Fermi liquid quasiparticles^2,3,4.

This paper focuses on the Hall coefficient R_H, which is customarily used to define the charge carriers’ density in metals and semiconductors. In cuprates, a positive Hall sign is commonly attributed to hole-like curved Fermi surface due to next-nearest neighbor hopping. However, the apparent divergence of R_H^5,6,7 (or linear vanishing of Hall number⁸) of La_2−xSr_xCuO₄ toward zero doping x → 0, cannot be readily understood by a large Fermi surface curvature, or by its reconstruction, in the absence of translational symmetry breaking. This divergence is presumably related to effects of strong electron-electron interactions which drive the Mott insulator at zero doping. However, the lack of well-controlled transport calculations in this regime has stood in the way of a full understanding of this anomaly.

Thermodynamic formulas (“Thermodynamic formulas” contain static thermodynamic averages and susceptibilities, which can be obtained by derivatives of the equilibrium free energy with respect to static (timeindependent) source fields) for transport coefficients are very useful, as they bypass difficulties of real-time dynamics, and are amenable to well-controlled statistical mechanics methods. Unfortunately, most thermodynamic formulas have restricted applicability. For example, Chern numbers⁹ and Streda formulas¹⁰ for Hall conductivities are limited to low-temperature gapped quantum Hall phases. Shraiman, Shastry, and Singh¹¹ (SSS) have applied a thermodynamic formula to obtain the high-frequency Hall coefficient, but their analysis did not extend to low frequencies. Dynamical conductivity moments are thermodynamic expectation values, but inverting them to obtain the DC conductivity requires biased extrapolation¹².

Here we apply a thermodynamic formula for R_H in the DC limit, which was directly derived^13,14 from the constituent Kubo formulas. It is generally valid for strongly interacting metals. This formula consists of a zeroth order term ${R}_{{{{\rm{H}}}}}^{(0)}$ which is a ratio of two relatively simple current susceptibilities, and an unwieldy correction term ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ which involves a sum of thermodynamic averages of higher order Hamiltonian-current commutators. We have previously argued that under certain circumstances, ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ can be neglected¹⁵. In this paper, we evaluate its leading orders and confirm that they are indeed small throughout the regime of interest of this paper.

${R}_{{{{\rm{H}}}}}^{(0)}$ is calculated for the square lattice Hubbard model (HM)^16,17 using its low energy renormalized tJ-model (tJM). Our calculations are therefore limited to intermediate temperatures (IT): above the antiferromagnetic temperature scale J, but below the Hubbard gap scale U. Here, we do not aim to describe the Hall conductivity at experimentally accessible temperatures of cuprates T < J, where the HM undergoes various orderings (e.g. superconductivity, spin and charge density waves^18,19,20). Nevertheless, the calculated higher temperature Hall coefficient provides insight into the sign and density of the metallic charge carriers, which should also be relevant to transport at lower temperatures.

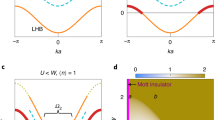
The difference between Figs. 1 and 2 highlights the departures of R_H from Fermi liquid-based Boltzmann transport theory: (1) An interaction-induced sign reversal below ≤45% doping where the Fermi surface is nominally electron-like. (2) R_H divergence toward half filling in the absence of translational symmetry breaking. (3) A temperature-dependent Hall sign reversal at the Hubbard gap energy scale.

Fig. 1: Hall map for the Hubbard model on the square lattice.

The tJ model at T ≥ J is used to compute the Hall coefficient as explained in the Introduction. The anomalous (reddish-brown) region of sign reversal and divergence toward zero doping, is a consequence of the strong Hubbard interaction which projects out doubly occupied states and introduces non-trivial changes in current commutators and the Hall coefficient. Beyond the present analysis, for T ≤ J, we mark the region of antiferromagnetic (AFM) order, and a hypothetical region of d-wave superconductivity (d-SC)^18–20.

Fig. 2: Hall coefficient of non-interacting square lattice.

${R}_{{{{\rm{H}}}}}^{{{{\rm{SL}}}}}$ given by Eq. (5). Very weak temperature dependence is seen, as shown in Supplementary Fig. 1. Note that ${R}_{{{{\rm{H}}}}}^{{{{\rm{SL}}}}} < 0$ for 0 < x < 1, and does not diverge anywhere except at x →   1.

This paper is organized as follows. After introducing the thermodynamic Hall coefficient formula, and the HM and tJM Hamiltonians, we provide a road map to Fig. 1 in Section “Road map to Fig. 1”. The Hall coefficient is calculated using different parts of the Hamiltonian for different temperature regimes. The result of the correction term calculation is given in section “The correction term ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$”. Technical details are supplied in the Supplementary Methods. In the summary, we explain similarities and differences of our results to several previous calculations, and propose comparing our results to transport measurements in cold atoms and strongly correlated flat band superconductors.

Results

The thermodynamic Hall Coefficient formula

The Hall coefficient at vanishing magnetic field B (in the z-direction) is defined by

$${R}_{{{{\rm{H}}}}}\equiv {\left.\frac{d{\sigma }_{xy}}{dB}{\sigma }_{xx}^{-2}\right\vert }_{B = 0},$$

(1)

where σ_αβ is the conductivity tensor and C4 symmetry is assumed. Calculating the DC Kubo formulas for σ_xx, σ_xy can be particularly difficult for strongly interacting models. The thermodynamic formula,

$${R}_{{{{\rm{H}}}}}={R}_{{{{\rm{H}}}}}^{(0)}+{R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}},$$

(2)

was rigorously derived from the Kubo formulas^13,14. ${R}_{{{{\rm{H}}}}}^{(0)}$ is a ratio of the current-magnetization-current (CMC) susceptibility and the conductivity sum rule (CSR) squared:

$$\begin{array}{l}{R}_{{{{\rm{H}}}}}^{(0)}\,\,=\,\frac{{\chi }_{{{{\rm{cmc}}}}}^{}}{{\chi }_{{{{\rm{csr}}}}}^{2}},\\ {\chi }_{{{{\rm{cmc}}}}}\,=\,-2{{{\rm{Re}}}}\langle \left[{P}^{y},[M,{j}^{x}]\right]\rangle ,{\chi }_{{{{\rm{csr}}}}}={{{\rm{Im}}}}\langle \left[{P}^{x},{j}^{x}\right]\rangle ,\end{array}$$

(3)

where 〈 ⋅ 〉 is the thermal expectation value. The operators P^α, j^α are the polarization and current in the α direction, and $M=-\frac{\partial H}{\partial B}$ is the z-magnetization.

The correction term ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ is given by the sum¹⁴,

$${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}=\frac{1}{{\chi }_{{{{\rm{csr}}}}}}\mathop{\sum }\limits_{i,j=0}^{\infty }{R}_{i}{R}_{j}(1-{\delta }_{i,0}{\delta }_{j,0}){M}_{2i,2j}^{{\prime\prime} }.$$

(4)

The prefactors R_i, and hypermagnetization matrix elements M_2i,2j are fully defined in the Supplementary Methods. We emphasize that both ${R}_{{{{\rm{H}}}}}^{(0)}$ and all terms in ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ are constructed solely from thermodynamic (static) expectation values. These are amenable to inverse temperature (β) expansion and quantum Monte-Carlo (QMC) simulation without analytic continuation (Imaginary time QMC conductivities require analytic continuation, which is limited to frequencies higher than temperature (see Appendix B in ref. ²¹). The DC conductivities are often deduced by proxies to the analytical continuation^22,23). Obviously, the correction term is generally very difficult to compute up to high orders in the Krylov basis. In certain cases (such as the case of weakly disordered bands¹⁵), it was shown to be small. In Section IV C, we compute ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ of the tJM up to second order.

We note that in contrast to other thermodynamic formulas for the Hall conductivity^9,10, which are only valid for gapped phases, Eq. (2) applies to gapless metals with σ_xx > 0. ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr(2)}}}}}-delete.$

For the non-interacting square lattice (SL) (with unit lattice constant, and ℏ = 1) with weak disorder, ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ can be neglected¹⁵. ${R}_{{{{\rm{H}}}}}^{(0)}$ reproduces Boltzmann’s Hall coefficient for an isotropic lifetime²⁴,

$${R}_{{{{\rm{H}}}}}^{{{{\rm{SL}}}}}=\frac{\int\frac{{d}^{2}k}{(2{\pi }^{2})}\left(-\frac{df}{d\epsilon }\right){\left(\frac{\partial \epsilon }{\partial {k}_{y}}\right)}^{2}\frac{{\partial }^{2}\epsilon }{{(\partial {k}_{x})}^{2}}}{2ec{\left(\int\frac{{d}^{2}k}{(2{\pi }^{2})}\left(-\frac{df}{d\epsilon }\right){\left(\frac{\partial \epsilon }{\partial {k}_{x}}\right)}^{2}\right)}^{2}},$$

(5)

which is depicted in Fig. 2, and in the Supplementary Figure 1. Here, where ${\epsilon }_{{{{\bf{k}}}}}=-2t\left(\cos ({k}_{x})+\cos ({k}_{y})\right)$ and f(ϵ) is Fermi function, with a chemical potential determined by the doping x. We note that the SL result is negative (electron-like) at all doping x > 0, with very weak temperature dependence up to infinite temperature. The addition of positive next nearest neighbor hopping results in a regime of positive Hall sign at finite doping values, but no divergence toward zero doping.

Models

Interactions which produce a Mott insulator can be modeled by the HM where the hopping energy t is well below the large interaction scale U,

$${H}^{{{{\rm{HM}}}}}=-t\mathop{\sum}\limits_{\langle ij\rangle ,s=\uparrow ,\downarrow }({c}_{is}^{{\dagger} }{c}_{js}+{c}_{js}^{{\dagger} }{c}_{is})+U\mathop{\sum}\limits_{i}{n}_{i\uparrow }{n}_{i\downarrow },$$

(6)

where ${c}_{is}^{{\dagger} }$ creates an electron on site i with spin s. 〈ij〉 are nearest neighbor bonds, and ${n}_{is}={c}_{is}^{{\dagger} }{c}_{is}^{}$. Here we are interested in the strong coupling regime of t \le U, which generates a Mott insulator with a charge gap of order U at zero doping.

At large U/t ≫ 1 the Hilbert space is constrained by a Gutzwiller projection (GP) ${{{{\mathcal{P}}}}}_{{{{\rm{GP}}}}}={\prod }_{i}(1-{n}_{i\uparrow }{n}_{i\downarrow })$. The GP hopping terms are defined by the bond operators,

$$\begin{array}{l}{K}_{ij}^{\pm }\equiv \mathop{\sum}\limits_{s}{\tilde{c}}_{is}^{{\dagger} }{\tilde{c}}_{js}\pm {\tilde{c}}_{js}^{{\dagger} }{\tilde{c}}_{is},\\ {{{{\boldsymbol{\Sigma }}}}}_{ij}^{\pm }\equiv \mathop{\sum}\limits_{s{s}^{{\prime} }}{\tilde{c}}_{is}^{{\dagger} }{\overrightarrow{\sigma }}_{s{s}^{{\prime} }}{\tilde{c}}_{j{s}^{{\prime} }}\pm {\tilde{c}}_{js}^{{\dagger} }{\overrightarrow{\sigma }}_{s{s}^{{\prime} }}{\tilde{c}}_{i{s}^{{\prime} }},\end{array}$$

(7)

where K⁺ (K⁻) describes the kinetic energy (current). The GP electron creation, hole density and spin operators are defined by

$$\begin{array}{rcl}&&{\tilde{c}}_{is}^{{\dagger} }\equiv {c}_{is}^{{\dagger} }(1-{n}_{i,-s}),\quad {n}_{i}^{h}\equiv 1-\mathop{\sum}\limits_{s}{\tilde{c}}_{is}^{{\dagger} }{\tilde{c}}_{is},\\ &&\frac{1}{2}\mathop{\sum}\limits_{s{s}^{{\prime} }}{\tilde{c}}_{is}^{{\dagger} }{\sigma }^{\alpha }{\tilde{c}}_{i{s}^{{\prime} }}\equiv {s}_{i}^{\alpha }(1-{n}_{i}^{h}).\end{array}$$

(8)

${({n}_{i}^{h})}^{2}={n}_{i}^{h}$ is the vacancy number, and s_i are spin half operators. The uniform electric polarization is ${P}^{\alpha }=-e{\sum }_{i}{x}_{i}^{\alpha }{n}_{i}^{h}$, where e is the (negative) electron charge, and x_i is the lattice position of site i.

The effective Hamiltonian in this GP subspace, to leading orders in t/U, is the tJM^25,26. Using the antiferromagnetic interaction J = 4t²/U and the operators of Eq. (7) one can write,

$$\begin{array}{l}{H}^{{{{\rm{tJM}}}}}\,=\,{{{{\mathcal{P}}}}}_{{{{\rm{GP}}}}}\left({H}^{t}+{H}^{J}+{H}^{{J}^{{\prime} }}\right){{{{\mathcal{P}}}}}_{{{{\rm{GP}}}}}+{{{\mathcal{O}}}}({t}^{3}/{U}^{2}),\\ {H}^{t}\quad\,=-t\mathop{\sum}\limits_{\langle ij\rangle }{K}_{ij}^{+},\\ {H}^{J}\;\;\;\,=J\mathop{\sum}\limits_{\langle ij\rangle }{{{{\bf{s}}}}}_{i}\cdot {{{{\bf{s}}}}}_{j}(1-{n}_{i}^{h})(1-{n}_{j}^{h}),\\ {H}^{{J}^{{\prime} }}\;\;\;=-\frac{J}{4}\mathop{\sum}\limits_{\langle ij\rangle \langle jk\rangle }\left({K}_{ik}^{+}-2{{{{\boldsymbol{\Sigma }}}}}_{ik}^{+}\cdot {{{{\bf{s}}}}}_{j}\right)(1-{n}_{j}^{h}).\end{array}$$

(9)

In the IT temperature range, all tJM susceptibilities can be obtained by lower orders of (β)ⁿ, than needed when expanding with the unrenormalized HM. For the present work, we note that transport coefficients are dominated by ${H}^{t},{H}^{{J}^{{\prime} }}$, whereby H^J determines the emergence of antiferromagnetic correlations at lower temperatures.

Road map to Figure 1

To arrive at Fig. 1, we compute ${R}_{{{{\rm{H}}}}}^{(0)}$ analytically as a function of doping for temperatures t < T ≪ U using H^t and expanding up to order (βt)². We neglect ${H}^{J},{H}^{{J}^{{\prime} }}$ in this regime, since they contribute relative corrections of order (t/U), (T/U) ≪ 1. This approximation is validated by a QMC calculation of ${R}_{{{{\rm{H}}}}}^{(0)}$ using the temperature dependent HM Boltzmann weights at large U/t ≫ 1. QMC thus allows us to extend the high temperature expansion of the tJM down to T ≃ J.

At very high temperatures, T → U, doubly occupied sites in the HM proliferate, and the validity of the GP breaks down. Since interactions of the HM become irrelevant, the Hall sign is dominated by the hopping term and therefore becomes negative at all doping levels. Therefore, one expects a crossover from the positive Hall sign at lower temperatures to a negative sign at higher temperatures. Indeed, such a crossover is heralded by the contributions of the second neighbor hopping terms ${H}^{{J}^{{\prime} }}$, which are negligible in the IT regime, but which increase with T. These terms interpolate between red region and the high-temperature blue region in Fig. 1, as also shown in Fig. 5.

The t-Model

At temperatures t ≪ T ≪ U, we can evaluate ${R}_{{{{\rm{H}}}}}^{(0)}$ and ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ by expanding in powers of βt using the current operators of H^t, and neglecting the weaker contributions of order ${{{\mathcal{O}}}}(J)$ in this regime. The current and magnetization are given by,

$$\begin{array}{rcl}&&{j}_{ij}^{\alpha }=-iet\,{K}_{ij;\alpha }^{-},\\ &&M=\frac{1}{2c}\mathop{\sum}\limits_{\langle ij\rangle }{x}_{i}{j}_{ij}^{y}-{y}_{i}{j}_{ij}^{x}.\end{array}$$

(10)

${K}_{ij;\alpha }^{-}$ denotes a directed bond operator in the α direction, and c is the speed of light.

For the CSR, the doping dependence of the two leading powers of β were previously calculated by Jaklic²⁷ and Perepelitsky²⁸. The calculation, shown in the Supplementary Methods, yields

$$\begin{array}{l}{\chi }_{{{{\rm{csr}}}}}^{t}=2\beta {e}^{2}{t}^{2}x(1-x)\\ \qquad+\,\frac{{\beta }^{3}{e}^{2}{t}^{4}}{6}x(1-x)(-9+2x+{x}^{2})+{{{\mathcal{O}}}}({\beta }^{5}{t}^{6}).\end{array}$$

(11)

As depicted in Fig. 3, the CSR of the tJM vanishes toward x → 0, and is suppressed even quite far from the Mott phase. In contrast, the CSR of the non-interacting SL is maximized at half filling where the Fermi surface has the largest volume. The CSR of the tJM is the conductivity integral which is cut off at the Hubbard gap. In the region where the tJM applies, the Hubbard gap is replaced by the Gutzwiller projection, which is why χ_CSR vanishes while R_H diverges as x → 0⁺.

Fig. 3: Doping dependent of Conductivity Sum Rule.

The suppression of the tJM CSR relative to the non-interacting square lattice CSR, affects a large region of doping. Vanishing of the tJM CSR at x → 0 leads to the anomalous divergence of R_H toward the Mott phase, and the diverging resistivity slope.

The CMC of H^t is evaluated up to order β⁴ as shown in the Supplementary Methods,

$$\begin{array}{l}{\chi }_{{{{\rm{cmc}}}}}^{t}=\frac{{\beta }^{2}{t}^{4}{e}^{3}}{2c}x(1-x)(-5+10x+3{x}^{2})\\ \qquad\;\;+\,\frac{{\beta }^{4}{t}^{6}{e}^{3}}{16c}x(1-x)(45-136x+50{x}^{2}+48{x}^{3}-71{x}^{4})\\ \qquad\;\;\,+\,{{{\mathcal{O}}}}({\beta }^{6}{t}^{8}).\end{array}$$

(12)

Thus, the zeroth order Hall coefficient in the IT regime is provided analytically as a function of doping and temperature:

$${R}_{{{{\rm{H}}}}}^{t}=\frac{1}{ec}\left(\frac{-5+10x+3{x}^{2}}{8x(1-x)}+{(\beta t)}^{2}\frac{-45-53x+145{x}^{2}+225{x}^{3}}{192x}\right).$$

(13)

The curves of Eq. (13) are depicted by solid lines in Fig. 4.

Fig. 4: Hall coefficient in the intermediate temperature regime.

Lines depict the high temperature expansion results of ${R}_{{{{\rm{H}}}}}^{(0)}$ for the t-model in Eq. (13). Solid and open circles are QMC results using Boltzmann weights of the HM with two widely different values of U/t. The QMC results are limited to the regions of negligible fermion sign error (see Section IV A). We note that the high temperature expansion agrees with the QMC data down to T ≃ 2t, and the QMC data shows quite weak temperature dependence down to T ≃ 0.5t.

Note: the CSR of the HM is finite as x → 0, but is exponentially suppressed, i.e. ${\chi }_{{{{\rm{CSR}}}}}^{t} \sim \exp (-U/T) \,>\, 0$. In the regime T ≪ U, the divergence of Eq. (13) continues down to exponentially low doping, below which it rapidly vanishes by particle-hole symmetry of the CMC. This effect is not visible in the qualitative color map of Fig. 1.

Discussion

Sign reversal of the Hall coefficient at low doping has been previously obtained by dynamical mean field theory (DMFT)^29,30, QMC²², and determinant QMC³¹. These methods have found evidence of hole pockets in the momentum dependent occupation, which is qualitatively consistent with our results at low doping. References^32,33,34 calculate within DMFT, the Hall conductivity of the Hubbard model at strong magnetic fields. They found that the Hall sign is reversed relative to band theory, near half filling. These effects were attributed to the Chern numbers of the non-interacting Hofstadter’s butterfly bands of the square lattice. It is interesting that these sign changes which were predicted at strong fields, (as measured in strongly correlated flat bands Moiré systems³⁵), are qualitatively similar to the Hall sign we obtain in the weak field limit.

Here however, we find that the sign reversal occurs already at x ≤ 0.45, which may come as a surprise vis-a-vis the widely used band theoretical approaches at much lower doping. The reason is simply related to the spin and charge entangled commutation relations of GP current operators of the tJM,

$$[{K}_{12}^{-},{K}_{23}^{-}]={K}_{13}^{-}\left(\frac{1+{n}_{2}^{h}}{2}\right)+{{{{\boldsymbol{\Sigma }}}}}_{13}^{-}\cdot {{{{\bf{s}}}}}_{2}(1-{n}_{2}^{h}),$$

(14)

which affects the hole density dependence of the CMC, and determines the doping concentration of the sign reversal. The commutators between the GP electron and spin operators can be obtained from the multiplication Supplementary Table I.

Since the hole density operators have coefficients of order unity, it is natural that the sign change occurs at a fraction with a denominator not much larger than unity. The important lesson we can learn from this is that the effects of GP reach far into the high doping and temperature regimes.

Previous QMC calculations of ${R}_{{{{\rm{H}}}}}^{(0)}$ for the HM^22,36 have used our Eq. (2), and neglected ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$. They have also reported a positive Hall sign near half filling (but no apparent divergence) for the square lattice model. However in the regime of U/t ≃ 16, R^corr ∝ ∣∣[H, j^x]∣∣ ~ U/t, is expected to dominate over ${R}_{{{{\rm{H}}}}}^{(0)}$, and hence cannot be ignored.

The difference between ${R}_{{{{\rm{H}}}}}^{(0)}({{{\rm{HM}}}})$³⁶ and ${R}_{{{{\rm{H}}}}}^{(0)}({{{\rm{tJM}}}})$ of Eq. (13), can be explained by the fact that R^corr(tJM) ≪ R^corr(HM) in the IT regime.

We can compare ${R}_{{{{\rm{H}}}}}^{(0)}$ of Eq. (13) to the infinite frequency Hall coefficient of the t-model calculated at leading order in β by SSS¹¹

$${R}_{{{{\rm{H}}}}}^{* }=\frac{d}{dB}\mathop{\lim }\limits_{\beta \to 0,\omega \to \infty }{\rho }_{yx}(\omega )=\frac{1}{ec}\left(-\frac{1}{4x}+\frac{1}{1-x}-\frac{3}{4}\right)$$

(15)

${R}_{{{{\rm{H}}}}}^{* }$ changes sign at x = 1/3 and diverges as 1/(4x) toward the Mott limit. While Eq. (13) changes sign at x = 0.4415 and diverges as 5/(8x) at small x. Still, the qualitative similarity we find between the infinite and zero frequency is surprising, but we cannot infer any general relation from this coincidence. We note that ${R}_{{{{\rm{H}}}}}^{* }$ may be relevant to the optical Kerr effect³⁷.

In summary, we obtain well-controlled analytic results for the DC Hall coefficient as a function of hole doping in the intermediate temperature regime above any ordering instabilities. We conclude that the Mott insulator phase modifies the effective charge carriers in the IT metallic phase which covers a large region of temperature and doping. The nature of these carriers has theoretical implications for superconductivity in cuprates^18,19,20,38 and in flat-band layered graphene^39,40,41. We also propose comparing our results to Hall coefficient measurements in cold atoms⁴². The superconducting order parameter should consist of GP holes, with spin entangled commutation relations (14), rather than quasiparticles confined to the non-interacting Fermi surface. These carrier properties affect the relation between superfluid stiffness and doping⁴³, and the Hall signs in the flux flow regime^44,45.

Methods

Extension to lower temperatures

The QMC extends the calculation of ${R}_{{{{\rm{H}}}}}^{(0)}$ down to lower temperatures J ≤T ≪ U. Using the HM weights, the QMC fully includes the AFM interactions of H^J.

A determinant QMC calculation for lattice fermions with discrete auxiliary fields was implemented using the ALF package⁴⁶. We used HM weights for U/t = 8, 16, 50. The typical system sizes were chosen between 8 × 8 and 12 × 12, with little size dependence of our results, which indicates a short correlation length in the studied temperature regime. The imaginary time step was chosen to render the Trotter errors to be insignificant. The number of Monte Carlo sweeps was generally ~ 10⁵. The statistical fluctuations were well-behaved, and "Jackknife resampling” (a method used for error estimation) revealed sufficiently small error bars. The average sign in the QMC sampling is defined as

$$\langle S\rangle =\langle {{{\rm{sgn}}}}(\det )\rangle .$$

(16)

In the Supplementary Fig. 10, we report the value of 〈S〉 as a function of interaction strength U/t, doping and temperature. We show that quite generally, 〈S〉 approaches unity at higher temperatures where the Fermionic negative weights introduce negligible effects on QMC configuration averaging.

The CMC and CSR susceptibilities of Eq. (3) were computed by sampling products of Green’s functions using Wick’s theorem over QMC equilibrium configurations of the auxiliary fields. In Fig. 4 the QMC results are depicted by circles of larger diameter than the numerical error bars. The displayed data is restricted to the regime of 〈S〉 ≥ 0.8, which for U = 8t and all doping range is satisfied at T ≥ t/2 ≈ J. We note that the data exhibits a weaker temperature dependence than expected by extrapolating the analytic high temperature results.

Extension to very high temperatures

At temperatures T ≫ U, one cannot use the tJM, and the suppression of double occupancies in the HM diminishes. At infinite temperature, the HM density matrix is independent of U and ${R}_{{{{\rm{H}}}}}^{(0)}$ recovers the U = 0 result of Eq. (5) at T → ∞. Expansion in βU of the susceptibilities yields,

$$\begin{array}{rcl}&&{\chi }_{{{{\rm{csr}}}}}^{{{{\rm{HM}}}}} \sim \beta {e}^{2}{t}^{2}n(2-n),\quad {\chi }_{{{{\rm{cmc}}}}}^{{{{\rm{HM}}}}} \sim {\beta }^{2}\frac{{e}^{3}}{c}{t}^{4}n(2-n)(1-n)\\ &&{R}_{{{{\rm{H}}}}}^{(0)}=\frac{2(1-n)}{n(2-n)ec}+{{{\mathcal{O}}}}{(\beta U)}^{2}\simeq {R}_{{{{\rm{H}}}}}^{{{{\rm{SL}}}}}\end{array}$$

(17)

where n = 1 − x is the electron density.

Interestingly, this recovery of the U ≃ 0 behavior at high temperatures is heralded by the effects of the next neighbor hopping term ${H}^{{J}^{{\prime} }}$ in the tJM as shown below. As a kinetic energy term, ${H}^{{J}^{{\prime} }}$ contributes to the currents and magnetization operators of the CMC susceptibility:

$$\begin{array}{l}{{j}^{{\prime} }}_{ijk}^{\alpha }=-ieJ(1-{n}_{j}^{h})\left({K}_{ik;\alpha }^{-}-2{{{{\boldsymbol{\Sigma }}}}}_{ik;\alpha }^{-}\cdot {{{{\bf{s}}}}}_{j}\right),\\\; {M}^{{\prime} }=\frac{1}{2c}\mathop{\sum}\limits_{\langle ijk\rangle }({x}_{i}{{j}^{{\prime} }}_{ijk}^{y}-{y}_{i}{{j}^{{\prime} }}_{ijk}^{x}).\end{array}$$

(18)

Since J ≪ t, these terms are unimportant for the CSR. However, for the CMC they yield an important contribution at very high temperatures:

$${\chi }_{{{{\rm{cmc}}}}}^{{J}^{{\prime} }}=\frac{\beta J{e}^{3}}{2}x(1-x)(1+2x-3{x}^{2}).$$

(19)

${H}^{{J}^{{\prime} }}$ connects across the plaquette diagonals, therefore ${\chi }_{{{{\rm{cmc}}}}}^{{J}^{{\prime} }} \sim \beta J$ while ${\chi }_{{{{\rm{cmc}}}}}^{t} \sim {(\beta t)}^{2}$ in Eq. (12). Thus, at $T \sim U,{\chi }_{{{{\rm{cmc}}}}}^{{J}^{{\prime} }}$ starts to dominate.

Thus we obtain an additional contribution to ${R}_{{{{\rm{H}}}}}^{t}$ of Eq. (13) which becomes large at T ~ U:

$${R}_{{{{\rm{H}}}}}^{{J}^{{\prime} }}=\frac{4T}{ecU}\left(\frac{1+2x-3{x}^{2}}{8x(1-x)}\right).$$

(20)

As shown in Fig. 5, since ${R}_{{{{\rm{H}}}}}^{{J}^{{\prime} }}$ is negative at low doping, it reduces the positive Hall coefficient divergence, and drives the Hall sign change to lower doping values, as also seen in the upper blueish regions of Fig. 1.

Fig. 5: tJM Hall coefficient including next neighbor hopping.

Plots of Eq. (20). The Hall sign reversal is pushed to lower doping, as seen in Fig. 1.

The correction term ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$

We calculate the correction term up to second order

$${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}(2)}=\frac{1}{{\chi }_{{{{\rm{csr}}}}}}\left({\left(\frac{{{{\Delta }}}_{1}}{{{{\Delta }}}_{2}}\right)}^{2}{M}_{2,2}^{{\prime\prime} }-\left(\frac{{{{\Delta }}}_{1}}{{{{\Delta }}}_{2}}\right)\left({M}_{2,0}^{{\prime\prime} }+{M}_{0,2}^{{\prime\prime} }\right)\right).$$

(21)

In the Supplementary Methods, we derive the first two recurrents of H^t at high temperatures,

$${{{\Delta }}}_{1}^{2}={t}^{2}(3-2x-{x}^{2}),{{{\Delta }}}_{2}^{2}={t}^{2}\frac{24(1+x)}{3+x}.$$

(22)

The order of a Krylov hyperstate denotes the maximal number of nested commutators of H and j^α. The high order Krylov operators contain a sum of a rapidly increasing number of operators, which must be stored numerically. The calculation of ${M}_{2,2}^{{\prime\prime} }$ to leading order in (βt) involved traces over up to 10⁵ operator clusters.

In Fig. 6, we plot the final result for ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}(2)}$ for all doping concentrations. We see that in comparison ${R}_{{{{\rm{H}}}}}^{(0)}$, the its quantitative effect is negligible, and maximized toward x → 0 by

$$\mathop{\lim }\limits_{x\to 0}\left\vert {R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}(2)}/{R}_{{{{\rm{H}}}}}^{(0)}\right\vert \to 6 \% .$$

(23)

Order 4 and higher corrections are expected to be even smaller due to the following argument: Generically, the coefficients R_i do not decay rapidly with i⁴⁷. However we expect ${M}_{2i,2j}^{{\prime\prime} }$ to decrease rapidly with i, j, since they involve traces over operator clusters which are generated from different current directions by ${{{{\mathcal{L}}}}}^{2i}{j}^{x}=[H,[H,\ldots ,{j}^{x}]]$ and ${{{{\mathcal{L}}}}}^{2j}{j}^{y}=[H,[H,\ldots ,{j}^{y}]]$.

Fig. 6: Calculation of second order correction term.

A comparison of the high temperature Hall coefficient of the t-model, Eq. (3) (blue line), with its second order correction term (orange line, multiplied by 100 for visibility), as defined in Eq. (21). The ratio of magnitudes vanishes at x → 1, and approaches 0.06 at x → 0.

The number of these clusters increases with i, j faster than exponentially. The operator clusters occupy partially overlapping areas on the lattice. The traces in the matrix elements (including the contributions from ${{{\mathcal{M}}}}$ and (βH)²) vanish unless all the ${\tilde{c}}_{i},{\tilde{c}}_{i}^{{\dagger} },{s}_{i}^{\alpha }$ operators cancel on all sites. Since the Krylov operators are normalized, this condition yields a rapidly decreasing contribution to ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ as already seen in the low order terms. The relative contributions of the remainder of R^corr are therefore expected to be even smaller.

Based on the high temperature result (${{{\mathcal{O}}}}{(\beta t)}^{0}$) in Eq. (23), and the weak temperature dependence found for ${R}_{{{{\rm{H}}}}}^{(0)}$ shown in Fig. 4, we may assume that the correction term remains negligible throughout the IT regime. We note that we have not calculated ${R}_{{{{\rm{H}}}}}^{{{{\rm{corr}}}}}$ for the HM at T ≥ U.