1 Introduction

Collaboration is ubiquitous and essential in various human activities, posing the intriguing subject of building a great team [1–5]. One of the challenges in this goal is that a good team should result in more than the sum of its constituents. For example, assembling the top players on a football team does not guarantee the best performance [6]. The concept of synergy, or team chemistry, therefore, has been debated to explain these discrepancies in diverse fields such as sports and business [7, 8].

Since modern science is also dominated by collaboration [3, 9, 10], revealing synergy in scientific collaboration is crucial. Whether two scientists exhibit synergistic performance can be determined by comparing their individual abilities and their collaborative ability. However, scientific careers are blurred by temporal effects and randomness. Recent studies [11, 12] have shown that the ability of an individual scientist can be untangled from his/her career by ruling out these factors. Specifically, the scientific impact of a paper is conventionally measured by the number of citations it receives [13, 14]. Then, the scientific career of a scientist can be considered as the sequence of the scientific impacts of papers written by him/her. It has been shown that the probability of the appearance of the highest-impact paper is totally random across the career, untangling the role of productivity, called the random-impact rule. In addition, the evolution of individual scientific careers can be described by a stochastic process of one’s own ability and universal randomness, called the Q-model.

While team formation procedures and their linkages to scientific impact have been explored [4, 15–21], much remains unknown about the role of productivity, luck, ability, and synergy in “collaborative” careers. This raises crucial questions: Do the random-impact rule and the Q-model also apply to collaborative careers? How can we determine whether two scientists exhibit synergistic performance in a way that is not blurred by various factors such as luck? Is it possible to predict synergy and reveal its underlying mechanism? These problems are critical for individual scientists seeking better collaborators, as well as for institutions and policymakers looking to support scientific innovation on a global scale.

Here, we investigate quantitative aspects of the nebulous concept of synergy, focusing on pairwise scientific collaboration. We use a large-scale bibliometric dataset to reconstruct the publication histories of 560,689 individual scientists and 1,026,196 pairs of scientists as the most elementary unit of a team. First, we find that the random-impact rule governs the evolution of not only individual but also collaborative careers, which allows us to untangle the role of longevity, luck, and a team’s own ability (as well as an individual scientist’s). Building on this finding, we define the additivity rule of the ability and identify ability discrepancies between two scientists working together and separately, which is not blurred by inherent randomness in scientific careers. Then, each pair’s synergy type is determined in a statistically significant way. Furthermore, we explore the mechanism of synergy based on a network approach. In particular, we detect a nontrivial block structure in synergy networks, which allows us to predict unknown types of synergy between two scientists who have never collaborated. This implies that combinations of certain, yet unknown, individual features are significantly involved in the generative mechanism of synergy. Finally, we investigate the associations between synergy and accessible individual features–gender, ethnicity, academic age, research interests, affiliations, and working countries; research interest is the most relevant to pair synergy, although its diversity does not have a consistent relation with synergy across disciplines.

2 Results

2.1 Evolution of scientific impact in collaborative careers

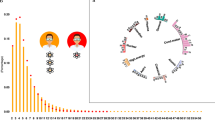
We begin by collecting the publication histories of individual scientists and their pairs in nine disciplines, including medicine, biology, chemistry, physics, psychology, materials science, computer science, geology, and mathematics (see Methods). The scientific impact of each paper is estimated by \(\tilde{c}_{10}\), the rescaled number of citations received within 10 years after publication (see Methods). Figure 1(A) depicts the careers of Dr. Andre Geim and Dr. Konstantin Novoselov, who were jointly awarded the 2010 Nobel Prize in Physics, as well as their individual publication histories. They appear to have synergy based on the fact that their joint publications are typically more influential than their individual publications. In contrast, the case of the other two anonymous scientists (Fig. 1(B)) suggests that their collaboration may yield negative effects on their individual careers. However, to confirm their synergy types, we need to untangle various factors from the scientific impacts, e.g., productivity, luck, individual abilities, and team ability. Since the previous study [11] revealed the evolution of scientific impacts on individual careers, we perform a similar analysis, yet for both individual and collaborative careers.

Figure 1
figure 1

Collaborative careers. (A) The publication histories of Andre Geim and Konstantin Novoselov, who shared the 2010 Nobel Prize in Physics. Each point represents a research paper written by Geim (green triangles), Novoselov (blue inverted triangles), and both of them together (red circles). We measured the impact of a paper, \(\tilde{c}_{10}\), using the normalized citation count for 10 years after its publication (see Methods), and present the distribution of each type of paper on the right along with their geometric means (dashed horizontal lines). At first glance, Geim and Novoselov have tended to produce more impactful publications when they collaborate than when they work separately. (B) The publication histories of the other two anonymous scientists. Each point represents a research paper written by A (green triangles), B (blue inverted triangles), and both of them together (red circles). In contrast to (A), their collaboration seems to result in negative effects, but confirming their synergy type requires untangling confounding factors

Full size image

We find that the distribution of \(t^{*}\), the career age at which each pair publishes its highest-impact paper, obtained from our data cannot be distinguished from the distribution obtained from its randomly shuffled version (Fig. 2). In addition, the relative position of the highest-impact paper \(N^{*}/N\) yields a uniform distribution \(P(N^{*}/N)\) as shown in the inset of Fig. 2. Therefore, the random-impact rule applies to both individual and collaborative careers across disciplines [Fig. S3 and Fig. S6 in the Additional file 1]. These results imply that the shared experience between two scientists does not systematically boost their chances of collaborative success.

Figure 2
figure 2

Impact patterns in collaborative careers. (A) The distribution of the timing of the highest-impact paper \(P(t^{*})\) for collaborative careers (circles) and their shuffled versions (crosses). The trend is almost identical after the shuffling. The inset shows the cumulative distribution of the relative position \(P(\leq N^{*}/N)\), indicating that the highest-impact paper is distributed randomly in a collaborative career. Thus, the decay in \(P(t^{*})\) can be explained by the declining productivity over time. (B) \(\langle \log{ (\tilde{c}_{10} )} \rangle \) as a function of N. Each point in the scatter plot corresponds to a pair of scientists, and the gray circles represent the log-binned mean of the data. The prediction of the Q-model (orange) agrees well with the data, in contrast to the R-model (blue). (C) The collapse of the cumulative distributions \(P(\geq \tilde{c}_{10}/Q)\). Each gray curve corresponds to a pair, and the black curve represents the universal distribution \(P(p)\)

Full size image

Since the random-impact rule suggests that scientific careers are governed by stochastic processes, the simplest scenario could be that the impact of every paper is randomly chosen from a global distribution, known as the R-model [11]. However, this model cannot explain the observed increase in the highest impact of a pair \(\tilde{c}_{10}^{*}\) as a function of the number of publications N (orange line in Fig. 22B). Instead, we find that the impact distributions of pairs differ, which can be described by the Q-model [11]. According to the Q-model, the impact of a paper α published by a duo \(\{i,j\}\) is determined by the multiplicative process as follows:

$$ \tilde{c}_{10, \{i,j\}\alpha} = Q_{\{i,j\}} p_{\alpha}, $$
(1)

where \(Q_{\{i,j\}}\) is the pair’s own ability, and \(p_{\alpha}\) is a stochastic variable interpreted as luck. We estimate the values of Q and p by using a maximum-likelihood approach to calculate \(\log{\tilde{c}_{10}^{*}}\) as a function of N (see section S2.1 in the SI). Our results show that the Q-model explains the data in Fig. 2(B). Moreover, p is nearly independent of Q and N (table S2 in the SI), suggesting that luck is universal and scientist-independent. In this regard, the distributions of the scientific impacts in each career normalized by its ability \(P(\tilde{c}_{10}/Q)\) collapse into a single curve \(P(p)\). This finding is consistent across disciplines (Fig. S7 and Fig. S8 in the SI) as well as individual careers (Fig. S4 and Fig. S5 in the SI). Thus, the Q-model, originally designed to understand the evolution of individual success, also can be applied to success in pairwise scientific collaboration.

2.2 Sum of its parts, luck, and synergy

In the previous section, we observed that pairs of scientists, akin to individuals, had distinct Q values, which serve as indicators of their citation-attracting ability. This finding raises an issue of determining the type of synergy, such as positive or negative, between two scientists i and j based on Q. Generally, positive (negative) synergy means that the effect of interactions between elements is greater (less) than the expected additive effect of the parts [22]. Consequently, our primary goal is to determine the additivity rule of Q. It is reasonable to suppose that the average individual abilities contribute to collaborative performance, while the microscopic mechanism of the emergence of Q is unknown. Thus, we empirically set the expectation value of collaborative Q by the generalized mean [23]. In particular, we can write the expected ability of a pair of i and j, \(Q_{\{i,j\}}^{\text{expect}}\), by taking the generalized mean of the values of Q obtained from the papers written without each other, \(Q_{i-j}\) and \(Q_{j-i}\), as follows:

$$ Q_{\{i,j\}}^{\text{expect}} = \biggl( \frac{Q_{i-j}^{\beta }+ Q_{j-i}^{\beta}}{2} \biggr)^{1/\beta}. $$
(2)

The value of β in this additivity rule is determined by maximizing the coefficient of determination \(R^{2}\) between \(Q^{\text{expect}}\) and the measured Q, \(Q^{\text{measure}}\), i.e., minimizing the sum of the squares of their differences. We obtain the optimal β separately for each discipline because the effects of ability heterogeneity may differ by discipline [24, 25]. Considering the extreme cases, \(\beta = \infty \) corresponds to the maximum in the given values, whereas \(\beta = -\infty \) yields the minimum. Therefore, a larger β value indicates that a pair’s Q depends more on its higher-Q member, and vice versa. We find that the optimal β vary across disciplines (Fig. 3, β ranges from −1.00 to 1.93). For example, in physics, the higher-Q member is the most crucial for greater scientific impact, with \(\beta \approx 1.93\). The observed variation in the values of β might be related to the different practices of disciplines including how practitioners perceive brilliance as important for success [26] or the level of cognitive consensus [27].

Figure 3
figure 3

Quantification of pair synergy. (A) The coefficient of determination \(R^{2}\) between \(Q^{\mathrm{{measure}}}\) and \(Q^{\mathrm{{expect}}}\) as a function of the generalized mean parameter β. The dashed lines represent \(R^{2}\) with varying β values, while the circles with vertical lines represent the optimal β values for each discipline. \(R^{2}\) does not fluctuate abruptly, indicating the robustness of the analysis for the selection of β (for more detailed information, see section S3.3 in the SI). (B) The normalized distributions of \(S/\epsilon _{S}\) for each discipline. The dotted line represents the standard normal distribution, and the inset shows the distributions of S. (C) Classification of pair synergy. The error bars correspond to 95% confidence intervals calculated from the Q-model. As an illustrative example, the synergy between Geim and Novoselov is strongly positive

Full size image

In addition, the moderate values of \(R^{2}\) (0.31–0.51) in Fig. 3(A) indicate significant deviations from the additivity rules. To quantify the ability deviation, we employ the log-ratio \(S = \log (Q^{\text{measure}}/Q^{\text{expect}})\), which is motivated by the heavy-tailed distribution of Q as reported in previous studies [11, 13, 28]. We observe the broad distributions \(P(S)\) (the standard deviation ranges 0.37–0.43, see inset of Fig. 3(B)). However, this does not directly imply the existence of non-additive effects. The limited number of publications in a career yields an inherent uncertainty \(\epsilon _{Q}\) in the measurement of Q due to the stochasticity in the impact sequences. Therefore, even if the data precisely follow the additivity rule, a small number of publications of a pair or its individual members can cause the misinterpretation that the pair is breaking the rule. To address the issue, we normalize S by its uncertainty \(\epsilon _{S}\), which is derived from the error propagation along with \(\epsilon _{Q}\) of each team and its members (see section S3.1 in the SI). If there is no synergy effect in scientific collaboration, i.e., the ability of every pair is determined only by the additivity rule of their individual abilities, the distribution of \(S/\epsilon _{S}\) would follow the standard normal distribution \(\mathcal{N}(0,1)\). Remarkably, we find that there exists a discrepancy between the obtained \(P(S/\epsilon _{S})\) and the standard normal distribution (Fig. 3(B)). The discrepancy can be quantified by the values of kurtosis, which range 0.06–1.83. As a result, the inherent uncertainty in the Q-model is insufficient to explain the observed non-additive effects.

Can the observed deviations now be considered indicative of synergy? One possible factor contributing to these deviations is the inclusion of external coauthors beyond pairs. In other words, the non-additive effects could be an outcome influenced by additional co-authors. To tackle this concern, we use a credit allocation method [29] to subtract the credit share of external co-authors from the careers of pairs. We find that significant ability discrepancies persist even after the credit allocation and show marginal changes (see section S4 and Fig. S9 in the SI). Our findings provide substantial evidence for the existence of synergy, which is unlikely to be influenced by career dynamics or the presence of external co-authors.

Consequently, we classify synergy types of scientist pairs into three major categories: positive, neutral, and negative (Fig. 3(C)). If a pair shows positive (negative) synergy, its value of S is significantly greater (less) than 0. Note that if two scientists have an insufficient number of publications to be categorized as described above, their synergy type is considered inconclusive. By applying the criteria to our data, we discover that not every pair is capable of achieving positive synergy; approximately half of the pairs exhibit neutral, while some are even negative (Fig. S10 in the SI). Returning to the two examples in Fig. 1, our classification results reveal that the pair of Geim and Novoselov presents strongly positive synergy, while the anonymous pair’s synergy type remains inconclusive due to the limited longevity in collaboration. In addition, our measurement of synergy is not highly susceptible to the additivity parameter β (see section S3.3 in the SI).

2.3 Predictability and mechanisms of synergy

Our next question is whether synergy is predictable. In complex interacting systems, novel interactions can be identified by network inference [30, 31]. Especially, drug-drug interactions [30] provide a meaningful analogy to the context of our study, in which interactions between drugs can also be classified into a few types. Since pairwise drug interactions are primarily determined by combinations of intrinsic features of drugs, stochastic block models (SBMs) [32–34], which formalize the idea of group-dependent interactions, can predict the types of unknown interactions. In our case, if pair synergy is determined by combinations of individual features of scientists (e.g., skill set), the same approach can predict unknown synergy types. Therefore the predictability of synergy using SBM inference implies the role of combinations of individual features in the generative mechanism of synergy.

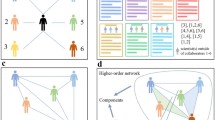
To elaborate further, let us consider the following hypothetical situation. Imagine a synergy network where nodes represent scientists, edges correspond to the conclusive observations of pair synergy, and edge types reflect synergy types (Fig. 4(A)). The assumption that combinations of individual features determine pair synergy means that the edge type between any two nodes is a function of two specific attributes (group memberships) of the nodes. As shown in Fig. 4(A), each node has a hidden categorical attribute representing a feature, and the synergy between two scientists is a function of their features. Inference of the network’s block structure enables us to gain insight into the mechanism and predictability of pair synergy. For instance, we can conclude that the synergy types between groups \(\{B, C, H\}\) and \(\{D, E, F\}\) are negative because nodes within each group share a particular attribute, and these attributes determine the type of pair synergy. In addition, using the inferred block structure, we can predict unknown interactions. Scientists B and F, for instance, have never collaborated, so their edge type is unknown. However, based on the negative nature of the interactions between their affiliated groups, we can predict that B and F will exhibit negative synergy.

Figure 4
figure 4

Block structure in pair synergy networks and its predictability (A) The diagram illustrates a hypothetical synergy network. We hypothesize that the interaction type of a scientist pair is determined by the combination of their attributes. In such a case, we can infer the block structure from the known interactions and estimate the types of unknown interactions. (B and C) We measure the predictability by the area under the receiver operating characteristic curve (AUROC). (B) shows the AUROC for random removal as a function of removal fraction, and (C) displays the AUROC for novel interaction prediction as a function of the difference between the observation year that we use to detect the block structure and the predicted year. The shaded areas correspond to the 95% confidence interval for each discipline

Full size image

We construct a network of the obtained synergy types for each discipline (table S4 in the SI) and investigate the predictability of synergy types based on the SBM inference approach (see Methods). Specifically, we perform two tasks: (i) predicting the types of randomly removed edges, and (ii) predicting the types of newly appearing edges as time evolves. The accuracy of each prediction task is measured by the area under the receiver operating characteristic curve (AUC). Notably, without any information except the observed synergy types of other pairs, our approach can predict the unidentified synergy types (Fig. 4(B) and (C); \(\text{AUC}>0.5\)). Our results emphasize the critical role of combinations of individual features on the establishment of synergy, while the small margins (\(\text{AUC}<0.65\)) imply the possible influence of exogenous factors.

Furthermore, we investigate the effects of specific individual features on pair synergy by collecting six distinct attributes: gender, ethnicity, academic age, research interests, affiliations, and working countries (see section S6 in the SI). First, we examine the Pearson correlation between the probability that two scientists are grouped into the same block during the SBM sampling and the similarity of their individual attributes for each attribute type, which reflects the association between the inferred block structure and metadata (see Methods). In this analysis, we find no attribute strongly associated with the inferred block structure (\(r<0.1\); table S5 in the SI). However, we cannot entirely dismiss the possibility that these attributes are related to pair synergy since the structural pattern captured by metadata may differ from those captured by SBM inference, as discussed in [35]. Therefore, we should examine the relationship between the attributes and synergy types directly without the inferred block structure.

To accomplish this, we employ the Blockmodel Entropy Significance Test (BESTest), a method introduced in Ref. [35] that quantifies the significance of the association between network and node metadata (see Methods). The BESTest compares the entropy of SBMs where the block memberships are determined by given node attributes to that of reshuffled attributes, providing the significance of the explanation power of the node attributes for the corresponding network, quantified by the p-value. As shown in Fig. 5 (upper wedges), while attributes rarely exhibit significant associations, research interest emerges as the most relevant attribute to pair synergy across most disciplines (\(\text{p}<0.012\); except geology, \(\text{p}=0.112\)).

Figure 5
figure 5

Correlations between individual attributes and pair synergy. The results of two statistical analyses describe the relationships between six individual attributes and pair synergy across disciplines. The upper wedge corresponds to the results of the BESTest, and the lower wedge corresponds to the results of ordinal logistic regression with pair synergy as the ordinal outcome and the diversity of each attribute as the explanatory variable (see Methods)

Full size image

Our subsequent focus is on the particular rule linked to the aforementioned individual attributes. One frequently debated hypothesis posits that the combination of diverse or complementary attributes is conducive to achieving successful outcomes [36–41].

To explore the relationship between attribute diversity and pair synergy, we use the Ordinal Logistic Regression (OLR) by considering the synergy type as an ordinal outcome (positive > neutral > negative). The strength of the association is quantified by the odds ratio obtained from the OLR. An odds ratio above 1 indicates that an increase in diversity corresponds to a greater likelihood of more synergistic interaction, while a value below 1 suggests a negative impact of diversity on synergy. As shown in Fig. 5 (lower wedges), the observed association strengths are generally weak (\(|\log _{2}{\text{Odds Ratio}}|<1\); except research interests in medicine with 1.20). In addition, despite the insignificance of the BESTest, it is also worth mentioning the consistent negative effects of age diversity, which could be related to the role of hidden hierarchy [42]. Nonetheless, our feasible conclusion is that there appears no significant simple rule for the feature combination across disciplines. One possible scenario is that pair synergy is indeed established by relatively sophisticated mechanisms (e.g., quadratic relations) rather than solely relying on the simplistic notion of diversity [36–41]. Another one is that the synergy networks are too sparse to detect the simple rules. The sparsity comes from the requirement for obtaining a conclusive synergy type that two scientists have enough publications both together and separately.

3 Discussion

In this paper, we have presented a quantitative and mechanistic analysis of synergy in scientific collaboration, contributing to the field in two key ways. Firstly, we have identified discrepancies in the performance of scientists working together versus separately, which cannot be explained by confounding factors such as career longevity, productivity, or random chance. This finding confirms the existence of synergy between two scientists in terms of their scientific impacts. Secondly, we have adopted a network approach to uncover the underlying mechanisms that drive pair synergy. Our analysis based on the SBM inference highlights the critical role of combinations of individual attributes, resulting in the predictability of unknown synergy types. Moreover, we found that research interest exhibits the strongest association with pair synergy, although its diversity does not consistently lead to complementarity across all disciplines.

Our finding of the random-impact rule that also applies to collaborative careers dispels the hypothesis of shared experience necessarily leading to team success or the existence of a honeymoon phase at the beginning of collaboration. Previous research has observed a correlation between collaboration longevity and team success, prompting the question of whether scientists engage in continued collaboration due to achieving satisfactory outcomes or if their long-lasting ties contribute to their success [15]. The random-impact rule in team careers empirically supports the former scenario, where scientists continue collaborating due to their satisfactory outcomes. In this context, exogenous factors could be influential in the early organization of collaboration until the value of Q solidifies. Examples include communication manner [43], geographical proximity [44], and intrinsic relationship between two scientists, e.g., mento–mentee [45, 46].

While this study focuses on pairwise interactions, scientific collaboration involves higher-order interactions that present a greater challenge to study [47, 48]. Quantifying synergy among more than two scientists presents inherent challenges; however, we believe that these open up promising avenues for future research. For instance, as the team size increases, the longevity of repeat collaboration rapidly diminishes (Fig. S2 in the SI), leading to increased uncertainty in measuring Q. In addition, controlling the effects of each sub-team is necessary to establish the additivity rule for higher-order interactions. Solving these problems will require advanced approaches, such as higher-order network reconstruction [49] or well-controlled social experiments [50].

There are additional possibilities for future research that stem from our work. Here, we adopted the generalized mean to establish the additivity rule of individual abilities. In general, the definition of the additivity rule is a contentious yet vital issue in numerous fields, including viscosity and drug interactions. [22, 51]. While our method for evaluating synergy demonstrates insensitivity to the additivity parameter β, as shown in section S3.3 in the SI, empirical and theoretical support would further strengthen our results. Another crucial issue that calls for further exploration is the definition of scientific impact. The concept of scientific impact can encompass a broad range of factors that extend beyond citation count [52]. In this context, to establish a connection between our findings and existing literature in fields such as psychology or cognitive science, it is imperative to clarify the meaning of Q or citations. Solving a scientific problem involves cognitive processes, explored in collective intelligence research [5, 53, 54]. It is essential to note, however, that the number of citations for a paper does not necessarily indicate the scientific significance of a study; rather, it may also be considered as a popularity measure. Therefore, it may be worthwhile to investigate synergy regarding other facets of scientific impact, e.g., disruptiveness [16] and novelty [41].

Our results have implications for both policymakers and individual scientists. The primary motivation for scientific team building is to enhance collaboration outcomes. In this sense, this work goes beyond previous studies that only predicted future collaboration [55–57]. Our results pave the way for matching underrepresented scientists with unrealized potential, which has the potential to accelerate scientific innovation on a global scale. Finally, we caution against exploiting predictability at the expense of overlooking the unpredictable nature of science [50]. As such, careful consideration must be taken when applying the results in practice.

4 Methods

4.1 Data

We employed the Microsoft Academic Graph (MAG) [58, 59] released in October 2019, which contains 228,996,078 articles and 231,970,249 authors. We reconstruct the publication histories of 560,689 individual scientists and 1,026,196 duos of scientists spanning 9 fields of study. In particular, we classified the main discipline of each scientist based on their papers’ fields and we only considered pairs of scientists who share the same main discipline. To alleviate the error in author identification, we conducted author disambiguation and conflation processes (see the SI for the details). The following pair and individual criteria have been used to select pairs of scientists: i) an individual scientist must have published at least 10 papers (and at least one paper every five years) throughout a career spanning more than ten years, and ii) a pair of scientists must have published at least five papers together throughout a career spanning more than five years. Then, the scientific impact of each paper is calculated based on citations. Specifically, the number of citations received 10 years after its publication \(\tilde{c}_{10}\) is rescaled by the average \(\tilde{c}_{10}\) in its publication year to control the citation inflation.

4.2 Q-Model

The Q-model [11] is a mechanistic model that generates impact sequences based on the random-impact rule, which states that impact is distributed randomly during a career. In this model, a stochastic process \(c_{i\alpha}=Q_{i} p_{\alpha}\) determines the impact \(c_{i\alpha}\) of a paper α produced by scientist i, where \(p_{\alpha}\) corresponds to inherent randomness. The underlying assumption is that the length of the sequence and \(Q_{i}\) are unaffected by \(p_{\alpha}\). To validate this, we calculate the model parameters and see if the correlations between p and N and between p and Q are negligible (table S2 in the SI).

4.3 Prediction via stochastic block model

The stochastic block model (SBM) [32, 33] is a generative network model in which adjacency matrix is generated with probability , where is a block partition vector where entry \(b_{i} \in \{1, \ldots , B\}\) corresponds to the group membership of node i. The posterior distribution of block partitions is written as

(3)

Based on this, we can sample the block partitions of a given network. Specifically, we employ a nonparametric Bayesian approach [30, 34, 60, 61], which allows for the number of partitions to be determined in a principled way rather than being predetermined. The Python library graph-tool (https://graph-tool.skewed.de) provides the code implementation.

Note that our goal is not to predict the occurrence of an edge between two nodes, but rather to predict the specific type of edge that would be present if such an edge were to appear. Our synergy networks possess edge types , where \(x_{ij} \in \) {positive, neutral, negative}. Suppose a set of unknown edge types  [62]. The probability distribution of the edge types can be written as follows:

(4)

where and denote the observed edges and their types. We can make predictions by sampling the posterior distribution .

4.4 Blockmodel entropy significance test

The Blockmodel Entropy Significance Test (BESTest) [35] is a statistical test for determining the significance of the association between a network structure and metadata. The statistic of the BESTest is

$$ \text{p} = \text{Pr}\bigl[\mathcal{S}^{\prime} \leq \mathcal{S}\bigr], $$
(5)

where \(\mathcal{S}\) is the entropy of the SBM with consideration of the metadata as a planted partition, and \(\mathcal{S}^{\prime}\) is the same as \(\mathcal{S}\) but using a random permuted version of the metadata.

For some attributes including research interests, affiliations, and working countries, multiple elements can be assigned to a node. In these cases, we adopt the mixed-membership SBM [31], which allows the block membership of a node to be represented as a vector.

4.5 Diversity

We quantify the diversity for our six attributes. For gender and ethnicity, the diversity is quantified by \(1-\delta _{a_{i}, a_{j}}\) where i’s attribute \(a_{i}\) is a categorical variable and δ is the Kronecker delta function. For academic age, the diversity is quantified by the difference in years \(a_{i} - a_{j}\) where \(a_{i}\) is an integer. For research interests, affiliations, and working countries, the diversity is quantified as \(1 - J(a_{i}, a_{j})\) where \(a_{i}\) is a set of attribute elements and J is the Jaccard index.

We investigate the association between pair synergy and attribute diversity using ordinal logistic regression (ORL). In this analysis, the ordinal outcome is the synergy type, and the explanatory variable is the diversity calculated using the methods described above for each attribute.