Random walk with restart on hypergraphs: fast computation and an application to anomaly detection

Abstract

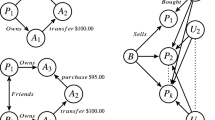
Random walk with restart (RWR) is a widely-used measure of node similarity in graphs, and it has proved useful for ranking, community detection, link prediction, anomaly detection, etc. Since RWR is typically required to be computed separately for a larger number of query nodes or even for all nodes, fast computation of it is indispensable. However, for hypergraphs, the fast computation of RWR has been unexplored, despite its great potential. In this paper, we propose ARCHER, a fast computation framework for RWR on hypergraphs. Specifically, we first formally define RWR on hypergraphs, and then we propose two computation methods that compose ARCHER. Since the two methods are complementary (i.e., offering relative advantages on different hypergraphs), we also develop a method for automatic selection between them, which takes a very short time compared to the total running time. Through our extensive experiments on 18 real-world hypergraphs, we demonstrate (a) the speed and space efficiency of ARCHER, (b) the complementary nature of the two computation methods composing ARCHER, (c) the accuracy of its automatic selection method, and (d) its successful application to anomaly detection on hypergraphs.

Appendices

Appendix A: Experimental datasets

We provide a brief description of the datasets used in this paper.

• EEN and EEU.⁶ These hypergraphs represent sets of email addresses on emails in Enron (EEN) and a European research institution (EEU) where users are nodes and the group of the sender and all receivers of each email is a hyperedge.

• HB and SB.$^{6}$ These represent co-sponsorships of bills in the House of Representatives (HB) and the Senate (SB) where US Congresspersons are nodes, and groups of sponsors and co-sponsors of bills are hyperedges.

• WAL.$^{6}$ This is a hypergraph where products are nodes and hyperedges are sets of co-purchased products at Walmart.

• TRI.$^{6}$ This is a hypergraph where nodes are accommodations (mostly hotels) and hyperedges are sets of accommodations that a user performed “click-out” during the same browsing session at Trivago.

• COD, COG, and COH.$^{6}$ These are co-authorship hypergraphs where authors are nodes and each hyperedge represents the authors of a publication recorded on DBLP (COD), Geology (COG), and History (COH).

• THS, THM, and THU).$^{6}$ These are hypergraphs where users are nodes and each hyperedge represents the group of users associated with a thread at StackOverflow (THS), MathStackOverflow (THM), and AskUbuntu (THU).

• AM.⁷ This is a hypergraph of Amazon (AM) product reviews (spec., those categorized as Movies & TV) where users are nodes and a group of products reviewed by the same user is a hyperedge. Each user has at least 5 reviews.

• YP.⁸ This is a hypergraph of user ratings on locations (e.g., hotels and restaurants) at Yelp (YP) where users are nodes and a group of locations a user rated is a hyperedge. Ratings higher than 3 are considered.

• TW.⁹ This is a hypergraph of social relationships on Twitter (TW) where users are nodes and each hyperedge represents a group of users that compose a ‘circle’ (or ‘list’) together on Twitter.

• ML1, ML10, and ML20.¹⁰ These hypergraphs represent interactions of movies at MovieLens with different sizes of 1 M (ML1), 10 M (ML10), and 20 M (ML20) movie ratings where nodes are movies and a group of movies a user rated is a hyperedge. Ratings higher than 3 are considered.

Appendix B: Application to node retrieval

In this section, we introduce an application of RWR scores on hypergraphs for the task of node retrieval. Additionally, we evaluate the empirical effectiveness of this approach.

Fig. 8

Similar-node-retrieval performance on hypergraphs in terms of AUROC and MAP. The hypergraph RWR using EDNW provides the best accuracy among all the baselines in the SB and HB datasets

Similar node retrieval Given a hypergraph and a query node s, this task is to search for nodes structurally similar to the query node. Specifically, we measure node-to-node proximities for s and use them as ranking scores to sort all nodes except s in the order of the scores. If nodes with the same class of the query node are ranked high, structurally similar nodes are successfully retrieved, which can be evaluated by ranking metrics such as AUROC and MAP. For this task, we compute the hypergraph RWR scores $\varvec{r}$ w.r.t. query node s through ARCHER, and utilize the scores for ranking.

Settings We conduct this experiment on the SB (senate-bills) and HB (house-bills) datasets, which contain binary node labels. The RWR models used in Sect. 5.6 are also used for this task. To introduce edge-dependent node weights (EDNW), we set $\gamma _e(v) = \bar{d}(v)^{-\beta }$, where $\bar{d}(v)$ represents the unweighted degree of node v. We then set $\beta =1.0$ and $\omega (e) = 1$ (refer to Appendix C for the selection of $\beta =1.0$). For EINW, we set $\gamma _e(v) = 1$ and $\omega (e) = 1$. We vary the restart probability c from 0.1 to 0.9 by 0.1.

Results Fig. 8 shows the experimental results on the node retrieval task in terms of AUROC and MAP. As shown in the figure, the RWR using EDNW shows the best performance, especially with high values of restart probability c, among all tested methods. Note that the RWR using EDNW outperforms that using EINW and naive RWR, indicating the edge-dependent node weights are useful also for this task.

Appendix C: Experiments on edge-dependent node weights for applications

In this section, we provide the experimental results regarding the effectiveness of the edge-dependent node weights for applications.

Anomaly detection For anomaly detection in Sect. 5.6, we set edge-dependent node weights $\gamma _e(v) = \bar{d}(v)^{-\beta }$ for hypergraph RWR. For the experiment, we assess the performance of RWR by varying two parameters: $\beta$ and the restart probability c. Specifically, we explore different values of $\beta$ within the range of $\{0.5, 1.0, 2.0\}$, and we also vary c between 0.1 and 0.9 in increments of 0.1. Figure 9 shows the results, $\beta = 0.5$ generally yields the best performance across the tested datasets.

Fig. 9

Anomaly detection performance on hypergraphs in terms of AUROC and MAP with different edge-dependent node weights, i.e., $\gamma _e(v) = \bar{d}(v)^{-\beta }$. When $\beta =0.5$, it provides the best accuracy

Similar node retrieval For node retrieval in Appendix B, we also set $\gamma _e(v) = \bar{d}(v)^{-\beta }$ for hypergraph RWR. We test the node-retrieval performance of RWR by varying the values of $\beta$ and c. Specifically, the list of values tested for $\beta$ is $\{0.5, 1.0, 2.0\}$, while the range for c spans from 0.1 to 0.9. Figure 10 shows the results, and $\beta = 1.0$ leads to the best performance in most cases.

Fig. 10

Similar-node-retrieval performance in terms of AUROC and MAP with different edge-dependent node weights, i.e., $\gamma _e(v) = \bar{d}(v)^{-\beta }$. When $\beta = 1.0$, it provides better performance in most of the cases

Appendix D: Counting of the number of non-zero entries

In this section, we discuss how to compute $\texttt {nnz}({\textbf {H}}_{\mathcal {C}})$ and $\texttt {nnz}({\textbf {H}}_{\star })$ rapidly and space-efficiently. They are used in Eq. (11) by ARCHER to select one between clique- and star-expansion-based methods.

Calculation of ${\texttt {nnz}({\textbf {H}}_{\mathcal {C}})}$ While it is possible to naively count the number of non-zeros in ${\textbf {H}}_{\mathcal {C}}={\textbf {I}}_{n} - (1-c)\tilde{\textbf{P}}^{\top }$, materializing ${\textbf {H}}_{\mathcal {C}}$ typically requires more space than the input data due to its relatively high density. Hence, we suggest a more efficient way based on the following property regarding ${\textbf {H}}_{\mathcal {C}}$:

$$\begin{aligned} \texttt {nnz}({\textbf {H}}_{\mathcal {C}}) = \texttt {nnz}(\tilde{\textbf{P}}) \end{aligned}$$

(D1)

where $\tilde{\textbf{P}} = \tilde{\textbf{W}}\tilde{\textbf{R}}$. The equality is from the fact that the diagonal entries of $\tilde{\textbf{P}}$ are non-zeros because $\tilde{\textbf{P}}$ involves the transition probability that moves from each node v to one of its hyperedges, and goes back to v. Note the sparsity pattern of $\tilde{\textbf{P}}$ is the same as that of the adjacency matrix of the clique-expanded graph $G_{\mathcal {C}}$ (with additional self-loops on every node) of the hypergraph $G_{H}$. Thus, we can calculate $\texttt {nnz}(\tilde{\textbf{P}})$ without materializing $\tilde{\textbf{P}}$, by directly counting the edges that are clique-expanded from each hyperedge.

Algorithm 4 summarizes the procedure for computing $\texttt {nnz}({\textbf {H}}_{\mathcal {C}})$. For each node v (line 2), we find every node u that appears together with v in at least one hyperedge (line 5). Whenever we find such u, it is equivalent to finding an edge (v, u), and thus we increment the count accordingly (line 7). Note that we maintain a set C of such nodes to prevent duplicated counting (lines 3 and 8). Regardless of the input, Algorithm 4 requires $O(|C |)=O(n)$ extra space to maintain the set C. The time complexity is $O(\sum _{v \in \mathcal {V}}\sum _{e \in E(v)}|e |) = O(\sum _{e \in \mathcal {E}}|e |^{2})$ because it requires $|e |$ operations for each node in e.

Algorithm 4

Counting the number of non-zeros of ${\textbf {H}}_{\mathcal {C}}$

Calculation of ${\texttt {nnz}({\textbf {H}}_{\star })}$ Similarly, $\texttt {nnz}({\textbf {H}}_{\star })$ can also be efficiently calculated based on the following equalities:

$$\begin{aligned} \texttt {nnz}({\textbf {H}}_{\star })&= n + m + \texttt {nnz}(\tilde{\textbf{S}}) \nonumber \\&= n + m + \texttt {nnz}(\tilde{\textbf{W}}) + \texttt {nnz}(\tilde{\textbf{R}}) \nonumber \\&= n + m + \texttt {nnz}({\textbf {W}}) + \texttt {nnz}({\textbf {R}}), \end{aligned}$$

(D2)

where ${\textbf {H}}_{\star }={\textbf {I}}_{N}-(1-c)\tilde{\textbf{S}}^{\top }$. Note that ${\textbf {I}}_{N}$ is the identity matrix of size $N = n + m$, occupying $n + m$ non-zeros in ${\textbf {H}}_{\star }$. The matrix $\tilde{\textbf{S}}$ consists of $\tilde{\textbf{W}}$ and $\tilde{\textbf{R}}$ as shown in Eq. (5), and their sparsity patterns are the same as ${\textbf {W}}$ and ${\textbf {R}}$. The time complexity of this approach is dominated by that of counting the numbers of non-zero entries in ${\textbf {W}}$ and ${\textbf {R}}$. If ${\textbf {W}}$ and ${\textbf {R}}$ are in a sparse matrix format, the number of their non-zero entries can be computed in $O(\texttt {nnz}({\textbf {W}})+\texttt {nnz}({\textbf {R}}))=O(\sum _{v \in \mathcal {V}}\bar{d}(v))=O(\sum _{e \in \mathcal {E}}|e |)$ time and even in O(1) time in some formats (e.g., compressed sparse row). With the exception of the inputs (i.e., ${\textbf {W}}$ and ${\textbf {R}}$), this approach requires a constant amount of additional space.

Appendix E: Correlation between data statistics and costs of BePI

In this section, we empirically investigate the correlations between basic data statistics and the costs of BePI, which ARCHER employs for RWR computation. As the data statistics, we use $\texttt {nnz}({\textbf {H}})$ (i.e., $\texttt {nnz}({\textbf {H}}_{\mathcal {C}})$ and $\texttt {nnz}({\textbf {H}}_{\star })$ in clique- and star-expansion-based computations, respectively), density, overlapness, and average hyperedge size. As the costs of the clique- and star-expansion-based computation of BePI, we consider preprocessing time, space cost, and query time. The results obtained across all the datasets (refer to Appendix A) for both clique- and star-expansion-based computations are presented in Fig. 11. As shown in Fig. 11a, there exists a strong positive correlation between $\texttt {nnz}({\textbf {H}})$ and the costs for the calculation of RWR. For other statistics (see Figs. 11b, 11c, and 11d), there is no noticeable correlation between the statistics and the costs.

Fig. 11

Correlations between a basic data statistics and b the costs of RWR computation on hypergraphs in terms of preprocessing time, space cost, and query time. BePI is used for RWR computation. We report the Pearson correlation coefficient for each scatter plot. Note that there is a strong positive correlation between $\texttt {nnz}({\textbf {H}})$ and the costs, whereas other statistics do not exhibit such a correlation