No CrossRef data available.
Article contents
THE CERESA CLASS: TROPICAL, TOPOLOGICAL AND ALGEBRAIC
Part of:
Curves
Published online by Cambridge University Press: 21 December 2023
Abstract
The Ceresa cycle is an algebraic cycle attached to a smooth algebraic curve with a marked point, which is trivial when the curve is hyperelliptic with a marked Weierstrass point. The image of the Ceresa cycle under a certain cycle class map provides a class in étale cohomology called the Ceresa class. Describing the Ceresa class explicitly for nonhyperelliptic curves is in general not easy. We present a ‘combinatorialization’ of this problem, explaining how to define a Ceresa class for a tropical algebraic curve and also for a topological surface endowed with a multiset of commuting Dehn twists (where it is related to the Morita cocycle on the mapping class group). We explain how these are related to the Ceresa class of a smooth algebraic curve over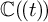 
$\mathbb {C}(\!(t)\!)$ and show that the Ceresa class in each of these settings is torsion.
MSC classification
Secondary:
14H30: Coverings, fundamental group
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
Amini, O., Baker, M., Brugallé, E. and Rabinoff, J., ‘Lifting harmonic morphisms II: Tropical curves and metrized complexes’, Algebra Number Theory 9(2) (2015), 267–315.CrossRefGoogle Scholar
Amini, O., Bloch, S., Burgos Gil, J. I. and Fresán, J., ‘Feynman amplitudes and limits of heights’, Izv. Ross. Akad. Nauk Ser. Mat. 80(5) (2016), 5–40.Google Scholar
Amini, O. and Caporaso, L., ‘Riemann–Roch theory for weighted graphs and tropical curves’, Advances in Mathematics 240 (2013), 1–23.Google Scholar
Asada, M., Matsumoto, M. and Oda, T., ‘Local monodromy on the fundamental groups of algebraic curves along a degenerate stable curve’, J. Pure Appl. Algebra 103(3) (1995), 235–283.Google Scholar
Baker, M. and Norine, S., ‘Harmonic morphisms and hyperelliptic graphs’, Int. Math. Res. Not. IMRN (15) (2009), 2914–2955.Google Scholar
Beauville, A., ‘A non-hyperelliptic curve with torsion Ceresa class’, C. R. Math. Acad. Sci. Paris 359 (2021), 871–872.Google Scholar
Beauville, A. and Schoen, C., ‘A non-hyperelliptic curve with torsion Ceresa cycle modulo algebraic equivalence’, Int. Math. Res. Not. IMRN (5) (2023), 3671–3675.Google Scholar
Betts, L. A. and Litt, D., ‘Semisimplicity of the Frobenius action on
$\unicode{x3c0}$
1’, in p-adic Hodge Theory, Singular Varieties, and Non-Abelian Aspects, edited by Bhatt, Bhargav and Olsson, Martin (Springer International Publishing, Cham, 2023), 17–64.CrossRefGoogle Scholar
$\unicode{x3c0}$
1’, in p-adic Hodge Theory, Singular Varieties, and Non-Abelian Aspects, edited by Bhatt, Bhargav and Olsson, Martin (Springer International Publishing, Cham, 2023), 17–64.CrossRefGoogle ScholarBisogno, D., Li, W., Litt, D. and Srinivasan, P., ‘Group-theoretic Johnson classes and non-hyperelliptic curves with torsion Ceresa class’, Épijournal Géom. Algébrique 7 (2023), Art. 8, 19.Google Scholar
Brannetti, S., Melo, M. and Viviani, F., ‘On the tropical Torelli map’, Adv. Math. 226(3) (2011), 2546–2586.Google Scholar
Brosnan, P. and Pearlstein, G., ‘Jumps in the Archimedean height’, Duke Math. J. 168(10) (2019), 1737–1842.CrossRefGoogle Scholar
Caporaso, L., ‘Algebraic and tropical curves: comparing their moduli spaces’, in Handbook of Moduli. Vol. I, Adv. Lect. Math. (ALM), vol. 24 (Int. Press, Somerville, MA, 2013), 119–160.Google Scholar
Caporaso, L. and Viviani, F., ‘Torelli theorem for graphs and tropical curves’, Duke Math. J. 153(1) (2010), 129–171.Google Scholar
Ceresa, G.,
$^{\prime }C$
is not algebraically equivalent to
${C}^{-}$
in its Jacobian’, Ann. of Math. (2) 117(2) (1983), 285–291.Google Scholar
$^{\prime }C$
is not algebraically equivalent to
${C}^{-}$
in its Jacobian’, Ann. of Math. (2) 117(2) (1983), 285–291.Google ScholarChan, M., ‘Tropical hyperelliptic curves’, J. Algebraic Combin. 37(2) (2013), 331–359.Google Scholar
Chan, M., ‘Lectures on tropical curves and their moduli spaces’, in Moduli of Curves, (Springer, 2017), 1–26.Google Scholar
Corey, D., ‘Tropical curves of hyperelliptic type’, J. Algebraic Combin. 53(4) (2021), 1215–1229.Google Scholar
Farb, B. and Margalit, D., A Primer on Mapping Class Groups, Princeton Mathematical Series, vol. 49 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
Green, M. and Griffiths, P., ‘Algebraic cycles and singularities of normal functions’, Algebraic Cycles and Motives. Vol. 1, London Math. Soc. Lecture Note Ser., vol. 343 (Cambridge Univ. Press, Cambridge, 2007), 206–263.Google Scholar
Hain, R., ‘Normal functions and the geometry of moduli spaces of curves’, Handbook of Moduli. Vol. I, Adv. Lect. Math. (ALM), vol. 24 (Int. Press, Somerville, MA, 2013), 527–578.Google Scholar
Hain, R. and Matsumoto, M., ‘Galois actions on fundamental groups of curves and the cycle
$C-{C}^{-}$
’, J. Inst. Math. Jussieu 4(3) (2005), 363–403.CrossRefGoogle Scholar
$C-{C}^{-}$
’, J. Inst. Math. Jussieu 4(3) (2005), 363–403.CrossRefGoogle ScholarHain, R. and Reed, D., ‘On the Arakelov geometry of moduli spaces of curves’, J. Differential Geom. 67(2) (2004), 195–228.Google Scholar
Harris, B., ‘Homological versus algebraic equivalence in a Jacobian’, Proc. Nat. Acad. Sci. U.S.A. 80(4) (1983), 1157–1158.CrossRefGoogle Scholar
Hensel, S., ‘A primer on handlebody groups’, in Handbook of Group Actions, edited by Ji, Lizhen, Papadopoulos, Athanase and Yau, Shing-Tung (International Press of Boston, Inc., 2020), 143 –178.Google Scholar
Johnson, D., ‘An abelian quotient of the mapping class group
$\mathcal{I}_{\mathrm{g}}$
’, Math. Ann. 249(3) (1980), 225–242.Google Scholar
$\mathcal{I}_{\mathrm{g}}$
’, Math. Ann. 249(3) (1980), 225–242.Google ScholarKnudsen, F. F., ‘The projectivity of the moduli space of stable curves. II. The stacks
${M}_{g,n}$
’, Math. Scand. 52(2) (1983), 161–199.Google Scholar
${M}_{g,n}$
’, Math. Scand. 52(2) (1983), 161–199.Google ScholarLilienfeldt, D. T.-B. G. and Shnidman, A., ‘Experiments with Ceresa classes of cyclic Fermat quotients’, Proc. Amer. Math. Soc. 151(3) (2023), 931–947.Google Scholar
Mikhalkin, G. and Zharkov, I., ‘Tropical eigenwave and intermediate Jacobians’, in Homological Mirror Symmetry and Tropical Geometry, Lect. Notes Unione Mat. Ital., vol. 15 (Springer, Cham, 2014), 309–349.Google Scholar
Morita, S., ‘The extension of Johnson’s homomorphism from the Torelli group to the mapping class group’, Invent. Math. 111(1) (1993), 197–224.Google Scholar
Oda, T., ‘A note on ramification of the Galois representation on the fundamental group of an algebraic curve. II’, J. Number Theory 53(2) (1995), 342–355.Google Scholar
Peters, Chris A. M. and Steenbrink, J. H. M., Mixed Hodge Structures, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 52 (Springer-Verlag, Berlin, 2008).Google Scholar
Pitsch, W., ‘Trivial cocycles and invariants of homology 3-spheres’, Adv. Math. 220(1) (2009), 278–302.CrossRefGoogle Scholar
Powell, J., ‘Two theorems on the mapping class group of a surface’, Proc. Amer. Math. Soc. 68(3) (1978), 347–350.Google Scholar
Putman, A., ‘Cutting and pasting in the Torelli group’, Geom. Topol. 11 (2007), 829–865.Google Scholar
Putman, A., ‘A note on the connectivity of certain complexes associated to surfaces’, Enseign. Math. (2) 54(3–4) (2008), 287–301.Google Scholar
Qiu, C. and Zhang, W., ‘Vanishing results in chow groups for the modified diagonal cycles’, 2022, https://arxiv.org/abs/arXiv:2209.09736.Google Scholar
Top, J., ‘Hecke l-series related with algebraic cycles or with siegel modular forms’, Ph.D. thesis, Utrecht, 1989.Google Scholar
Totaro, B., ‘Complex varieties with infinite Chow groups modulo 2’, Ann. of Math. (2) 183(1) (2016), 363–375.CrossRefGoogle Scholar
Tsuchiya, A., Ueno, K. and Yamada, Y., ‘Conformal field theory on universal family of stable curves with gauge symmetries’, in Integrable Systems in Quantum Field Theory and Statistical Mechanics, Adv. Stud. Pure Math., vol. 19 (Academic Press, Boston, MA, 1989), 459–566.Google Scholar
Zhang, S.-W., ‘Gross–Schoen cycles and dualising sheaves’, Invent. Math. 179(1) (2010), 1–73.CrossRefGoogle Scholar
Zharkov, I., ‘
$C$
is not equivalent to
${C}^{-}$
in its Jacobian: A tropical point of view’, Int. Math. Res. Not. IMRN (3) (2015), 817–829.Google Scholar
$C$
is not equivalent to
${C}^{-}$
in its Jacobian: A tropical point of view’, Int. Math. Res. Not. IMRN (3) (2015), 817–829.Google Scholar