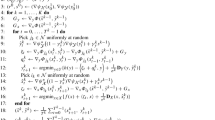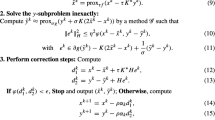An Inexact Primal-Dual Smoothing Framework for Large-Scale Non-Bilinear Saddle Point Problems

Abstract

We develop an inexact primal-dual first-order smoothing framework to solve a class of non-bilinear saddle point problems with primal strong convexity. Compared with existing methods, our framework yields a significant improvement over the primal oracle complexity, while it has competitive dual oracle complexity. In addition, we consider the situation where the primal-dual coupling term has a large number of component functions. To efficiently handle this situation, we develop a randomized version of our smoothing framework, which allows the primal and dual sub-problems in each iteration to be inexactly solved by randomized algorithms in expectation. The convergence of this framework is analyzed both in expectation and with high probability. In terms of the primal and dual oracle complexities, this framework significantly improves over its deterministic counterpart. As an important application, we adapt both frameworks for solving convex optimization problems with many functional constraints. To obtain an $\varepsilon$-optimal and $\varepsilon$-feasible solution, both frameworks achieve the best-known oracle complexities.

Appendix: Technical Proofs

1.1 Proof of Proposition 2.2

First, for any $\lambda \in {\mathbb {E}}_2$, we note that $\nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda )=\nabla _{\lambda }\varPhi ({\widetilde{x}}_{\gamma }(\lambda ),\lambda )$ and $\nabla {\widehat{\psi }}^\textrm{D}(\lambda )=\nabla _{\lambda }\varPhi (x^*(\lambda ),\lambda )$ (cf. Proposition 2.1). Therefore,

$$\begin{aligned} \Vert \nabla _{\lambda }\varPhi ({\widetilde{x}}_{\gamma }(\lambda ),\lambda )-\nabla \psi ^\textrm{D}(\lambda )\Vert ^2_{*}&= \Vert \nabla _{\lambda }\varPhi ({\widetilde{x}}_{\gamma }(\lambda ),\lambda )-\nabla _{\lambda }\varPhi (x^*(\lambda ),\lambda )\Vert ^2_{*} \nonumber \\&{\mathop {\le }\limits ^{\mathrm{(a)}}}L_{\lambda x}^2 \Vert {\widetilde{x}}_{\gamma }(\lambda ) - x^*(\lambda )\Vert ^2\nonumber \\&{\mathop {\le }\limits ^{\mathrm{(b)}}}(2L_{\lambda x}^2/\mu ) \big ({\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda )-{\widehat{S}}^\textrm{P}(x^*(\lambda ),\lambda )\big ){\mathop {\le }\limits ^{\mathrm{(c)}}}2L_{\lambda x}^2\gamma /\mu , \end{aligned}$$

(105)

where in (a) we use (3c), in (b) we use the $\mu$-strong convexity of ${\widehat{S}}^\textrm{P}(\cdot ,\lambda )$ on ${\mathcal {X}}$ and in (c) we use the definition of ${\widetilde{x}}_{\gamma }(\lambda )$ in (19). This proves (28).

We next prove (29). First, for any $\lambda ,\lambda '\in {\mathbb {E}}_2$,

$$\begin{aligned} {\widehat{\psi }}^\textrm{D}(\lambda ') {\mathop {\le }\limits ^{\mathrm{(a)}}}{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda ') {\mathop {\le }\limits ^{\mathrm{(b)}}}{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda ) + \langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda ),\lambda '-\lambda \rangle , \end{aligned}$$

(106)

where (a) follows from (13) and (b) follows from the concavity of ${\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\cdot )$ on ${\mathbb {E}}_2$. This proves the left-hand side (LHS) of (29). To show the right-hand side (RHS), we note that ${\widehat{\psi }}^\textrm{D}$ is concave and $L_\textrm{D}$-smooth on ${\mathbb {E}}_2$ (cf. Proposition 2.1). Thus, we can invoke the descent lemma [3], such that for all $\lambda ,\lambda '\in {\mathbb {E}}_2$,

$$\begin{aligned} {\widehat{\psi }}^\textrm{D}(\lambda ')&\ge {\widehat{\psi }}^\textrm{D}(\lambda )+\langle \nabla {\widehat{\psi }}^\textrm{D}(\lambda ),\lambda '-\lambda \rangle -({L_\textrm{D}}/{2})\Vert \lambda -\lambda '\Vert ^{2}\nonumber \\&\ge {\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda )-\gamma +\langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda ),\lambda '-\lambda \rangle \nonumber \\&\quad +\langle \nabla \psi ^\textrm{D}(\lambda )-\nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda ),\lambda '-\lambda \rangle -({L_\textrm{D}}/{2})\Vert \lambda -\lambda '\Vert ^{2}\nonumber \\&\ge {\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda )-\gamma +\langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda ),\lambda '-\lambda \rangle \nonumber \\&\quad -\Vert \nabla \psi ^\textrm{D}(\lambda )-\nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda )\Vert _{*}\,\Vert \lambda -\lambda '\Vert -({L_\textrm{D}}/{2})\Vert \lambda -\lambda '\Vert ^{2}\nonumber \\&{\mathop {\ge }\limits ^{\mathrm{(a)}}}{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda )-\gamma +\langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda ), \lambda '-\lambda \rangle \nonumber \\&\quad -L_{\lambda x}\sqrt{2\gamma /\mu }\Vert \lambda -\lambda '\Vert -({L_\textrm{D}}/{2})\Vert \lambda -\lambda '\Vert ^2,\nonumber \\&{\mathop {\ge }\limits ^{\mathrm{(b)}}}{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda )-2\gamma +\langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }(\lambda ),\lambda ),\lambda '-\lambda \rangle -{L_\textrm{D}}\Vert \lambda -\lambda '\Vert ^2, \end{aligned}$$

(107)

where (a) follows from (28) and (b) follows from the AM-GM inequality, i.e.,

$$\begin{aligned} L_{\lambda x}\sqrt{2\gamma /\mu }\Vert \lambda -\lambda '\Vert \le (L_{\lambda x}^2/\mu )\Vert \lambda -\lambda '\Vert ^{2}+\gamma \le (L_\textrm{D}/2)\Vert \lambda -\lambda '\Vert ^{2}+\gamma . \qquad \end{aligned}$$

(108)

We then rearrange (107) to obtain the RHS of (29).

1.2 Proof of Lemma 3.1

Fix any $k\in {\mathbb {Z}}_+$. Since ${\widehat{S}}^\textrm{D}_{\rho _{k}}(x^{k},\cdot )$ is $\rho _{k}$-strongly concave on $\varLambda$,

$$\begin{aligned} {\widehat{\psi }}^\textrm{P}_{\rho _{k}}(x^k)-{\widehat{S}}^\textrm{D}_{\rho _{k}}(x^{k},\lambda )&={\widehat{S}}^\textrm{D}_{\rho _{k}}(x^{k},\lambda ^*_{\rho _{k}}(x^{k}))-{\widehat{S}}^\textrm{D}_{\rho _{k}}(x^{k},\lambda ){\ge } \frac{\rho _{k}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2}. \end{aligned}$$

(109)

As a result, for all $\lambda \in \varLambda$, we have

$$\begin{aligned} \varDelta _{\rho _{k}}(x^k,\lambda ^k)&=\psi _{\rho _{k}}^{\textrm{P}}(x^{k})-\psi ^\textrm{D}(\lambda ^{k}) = f(x^k)+g(x^k)+{\widehat{\psi }}^\textrm{P}_{\rho _{k}}(x^k)-\psi ^\textrm{D}(\lambda ^{k})\nonumber \\&{\mathop {\ge }\limits ^{\mathrm{(a)}}}f(x^k)+g(x^k)+ {\widehat{S}}^\textrm{D}_{\rho _{k}}(x^{k},\lambda )+\frac{\rho _{k}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2} -\psi ^\textrm{D}(\lambda ^{k})\nonumber \\&= S(x^{k},\lambda ) - \rho _k\omega (\lambda ) +\frac{\rho _{k}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2} -({\widehat{\psi }}^\textrm{D}(\lambda ^{k}) - h(\lambda ^k))\nonumber \\&= {\widehat{S}}^\textrm{P}(x^{k},\lambda )- h(\lambda )-\rho _k\omega (\lambda ) +\frac{\rho _{k}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2} -{\widehat{\psi }}^\textrm{D}(\lambda ^{k})+h(\lambda ^k), \end{aligned}$$

(110)

where in (a) we use (109). Define $z_k(\lambda )\triangleq \tau _{k}\lambda ^{k}+(1-\tau _{k})\lambda$. We then multiply both sides of (110) by $\tau _k>0$, and obtain

$$\begin{aligned} \tau _{k}\varDelta _{\rho _{k}}(x^k,\lambda ^k)&{\mathop {\ge }\limits ^{\mathrm{(a)}}}\tau _k {\widehat{S}}^\textrm{P}(x^{k},\lambda ) - \tau _k h(\lambda ) - \rho _{k+1}\omega (\lambda )\nonumber \\&\quad +\frac{\rho _{k+1}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2} -\tau _k{\widehat{\psi }}^\textrm{D}(\lambda ^{k})+\tau _k h(\lambda ^k) \nonumber \\&=\tau _k {\widehat{S}}^\textrm{P}(x^{k},\lambda ) + (1-\tau _{k}){\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),\lambda ) - \tau _k h(\lambda ) - \rho _{k+1}\omega (\lambda ) \nonumber \\&\quad +\frac{\rho _{k+1}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2}-\tau _k{\widehat{\psi }}^\textrm{D}(\lambda ^{k}) - (1-\tau _{k}){\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),\lambda )+\tau _k h(\lambda ^k)\nonumber \\&\quad {\mathop {\ge }\limits ^{\mathrm{(b)}}}{\widehat{S}}^\textrm{P}(x^{k+1},\lambda ) - \tau _k h(\lambda ) - \rho _{k+1}\omega (\lambda )+\frac{\rho _{k+1}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2} \nonumber \\&\quad -\tau _k\big ({\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),{\hat{\lambda }}^{k})+\langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),{\hat{\lambda }}^{k}),\,\lambda ^{k}-{\hat{\lambda }}^{k}\rangle \big )\nonumber \\&\quad - (1-\tau _{k})\big ({\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),{\widehat{\lambda }}^k) + \langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),{\hat{\lambda }}^{k}),\,\lambda -{\hat{\lambda }}^{k}\rangle \big )+\tau _k h(\lambda ^k)\nonumber \\&{\mathop {=}\limits ^{\mathrm{(c)}}}S_{\rho _{k+1}}(x^{k+1},\lambda ) +(1- \tau _k) h(\lambda ) -{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),{\hat{\lambda }}^{k})\nonumber \\&\quad +\frac{\rho _{k+1}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2}- \langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),{\hat{\lambda }}^{k}),\,z_k(\lambda )-{\hat{\lambda }}^{k}\rangle +\tau _k h(\lambda ^k)\nonumber \\&{\mathop {\ge }\limits ^{\mathrm{(d)}}}S_{\rho _{k+1}}(x^{k+1},\lambda ) +\frac{\rho _{k+1}}{2}\Vert \lambda -\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2}\nonumber \\&\quad -\big ({\widehat{\psi }}^\textrm{D}(z_k(\lambda )) + L_\textrm{D}\Vert {\widehat{\lambda }}^k-z_k(\lambda )\Vert ^2+2\gamma _k\big )+h(z_k(\lambda )), \end{aligned}$$

(111)

where we use $\tau _k\rho _{k}=\rho _{k+1}$ in (a), the convexity of ${\widehat{S}}^\textrm{P}(\cdot ,\lambda )$, the LHS of (29) and the concavity of ${\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),\cdot )$ in (b), the definition of ${\widehat{S}}^\textrm{P}$ and $S_{\rho _{k+1}}$ [in (13) and (15), respectively] in (c), and the RHS of (29) and the convexity of h in (d). Note that if we take $\lambda ={\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})$, then $z_k(\lambda )=\lambda ^{k+1}$ by step 7. In addition, from steps 2 and 7, we have

$$\begin{aligned} {\widehat{\lambda }}^k-\lambda ^{k+1} = (1-\tau _k)\big ({\widetilde{\lambda }}_{\rho _k,\eta _{k}}(x^{k})- {\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})\big ), \end{aligned}$$

(112)

and from (32) and (109), we have

$$\begin{aligned} \frac{\rho _{k}}{2}\Vert {\widetilde{\lambda }}_{\rho _k,\eta _{k}}(x^{k})-\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2} \le {\widehat{\psi }}^\textrm{P}_{\rho _{k}}(x^k)-{\widehat{S}}^\textrm{D}_{\rho _{k}}(x^{k},{\widetilde{\lambda }}_{\rho _k,\eta _{k}}(x^{k}))\le \eta _k. \end{aligned}$$

(113)

This observation leads us to bound $\Vert {\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})-\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2}$ as

$$\begin{aligned}&\Vert {\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})-\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2}\nonumber \\&\quad {\mathop {\ge }\limits ^{\mathrm{(a)}}}\frac{1}{2}\Vert {\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})-{\widetilde{\lambda }}_{\rho _k,\eta _{k}}(x^{k})\Vert ^{2}-\Vert {\widetilde{\lambda }}_{\rho _k,\eta _{k}}(x^{k})-\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2} \nonumber \\&\quad {\mathop {\ge }\limits ^{\mathrm{(b)}}}\frac{1}{2}\Vert {\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})-{\widetilde{\lambda }}_{\rho _k,\eta _{k}}(x^{k})\Vert ^{2}-\frac{2\eta _{k}}{\rho _{k}}{\mathop {=}\limits ^{\mathrm{(c)}}}\frac{\Vert \lambda ^{k+1}-{\hat{\lambda }}^k\Vert ^2}{2(1-\tau _k)^2}-\frac{2\eta _{k}}{\rho _{k}}, \end{aligned}$$

(114)

where in (a) we use $\left\| a+b\right\| ^2\le 2(\left\| a\right\| ^2+\left\| b\right\| ^2)$, in (b) we use (113) and in (c) we use (112). We then substitute $\lambda ={\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})$ and (114) into (111), and obtain

$$\begin{aligned} \tau _{k}\varDelta _{\rho _{k}}(x^k,\lambda ^k)&\ge S_{\rho _{k+1}}(x^{k+1},{\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})) +\frac{\rho _{k+1}}{2}\bigg (\frac{\Vert \lambda ^{k+1}-{\hat{\lambda }}^k\Vert ^2}{2(1-\tau _k)^2}-\frac{2\eta _{k}}{\rho _{k}}\bigg )\\&\quad -\big (\psi ^\textrm{D}(\lambda ^{k+1}) + L_\textrm{D}\Vert {\widehat{\lambda }}^k-\lambda ^{k+1}\Vert ^2+2\gamma _k\big )\\&{\mathop {\ge }\limits ^{\mathrm{(a)}}}\psi ^\textrm{P}_{\rho _{k+1}}(x^{k+1}) - (1+\tau _k)\eta _k\\&\quad +\bigg (\frac{\rho _{k+1}}{4(1-\tau _k)^2} - L_\textrm{D}\bigg )\Vert \lambda ^{k+1}-{\hat{\lambda }}^k\Vert ^2-\psi ^\textrm{D}(\lambda ^{k+1}) - 2\gamma _k\\&{\mathop {\ge }\limits ^{\mathrm{(b)}}}\varDelta _{\rho _{k+1}}(x^{k+1},\lambda ^{k+1}) - 2\eta _k-2\gamma _k, \end{aligned}$$

where we use (34) in (a) and $\tau _k\in (0,1)$ and ${\rho _{k+1}}\ge {4(1-\tau _{k})^{2}}L_\textrm{D}$ in (b).

1.3 Proof of Theorem 3.2

Since $\gamma _k=\varepsilon /(4(k+3))=O(\varepsilon /k)$ [cf. (57)], based on (41), we have

$$\begin{aligned} C_{\textsf{det}}^\textrm{P}&= {\sum }_{k=1}^{K_{\textsf{det}}} \; O\left( n\sqrt{\kappa _{\mathcal {X}}}\log \big ((L+L_{xx})k/\varepsilon \big )\right) \nonumber \\&= O\left( n\sqrt{\kappa _{\mathcal {X}}}\Big (K_{\textsf{det}}\log \big (\kappa _{\mathcal {X}}\big )+\log \big (K_{\textsf{det}}!\big )\Big )\right) \nonumber \\&{\mathop {=}\limits ^{\mathrm{(a)}}}O\left( n\sqrt{\kappa _{\mathcal {X}}}\sqrt{L_\textrm{D}/\varepsilon }\Big (\log \big ((L+L_{xx})/\varepsilon \big )+\log \big ({L_\textrm{D}/\varepsilon }\big )\Big ) \right) \nonumber \\&= O\left( n\sqrt{\kappa _{\mathcal {X}}L_\textrm{D}/\varepsilon }\log \big ((L+L_{xx})L_\textrm{D}/\varepsilon \big )\right) , \end{aligned}$$

(115)

where in (a) we use the fact that $\log (K!)\!=\!\Theta (K\log K)$ for any $K\in {\mathbb {N}}$ and (62).

Similarly, we can analyze the dual oracle complexity for solving (32). Since $\rho _k=O(L_\textrm{D}/k^2)$ [cf. (60)] and $\eta _k=O(\varepsilon /k)$ [cf. (57)], based on (40), we have

$$\begin{aligned} C_{{\textsf{det}},1}^\textrm{D}&= {\sum }_{k=1}^{K_{\textsf{det}}} \; O\Big (n\sqrt{L_{\lambda \lambda }k^2/L_\textrm{D}}\log (L_{\lambda \lambda }k/\varepsilon )\Big )\nonumber \\&= O\Big (n\sqrt{L_{\lambda \lambda }/L_\textrm{D}} \Big (\log (L_{\lambda \lambda }/\varepsilon ){\sum }_{k=1}^{K_{\textsf{det}}}k + {\sum }_{k=1}^{K_{\textsf{det}}}\; k\log k\Big )\Big )\nonumber \\&{\mathop {=}\limits ^{\mathrm{(a)}}}O\Big (n\sqrt{L_{\lambda \lambda }/L_\textrm{D}} ({L_\textrm{D}/\varepsilon })\Big (\log (L_{\lambda \lambda }/\varepsilon ) + \log ({L_\textrm{D}/\varepsilon }) \Big )\Big )\nonumber \\&= O\Big (n\sqrt{L_{\lambda \lambda }L_\textrm{D}}/\varepsilon \log (L_{\lambda \lambda }L_\textrm{D}/\varepsilon )\Big ), \end{aligned}$$

(116)

where in (a) we use $\sum _{k=1}^K k =\Theta (K^2)$, $\sum _{k=1}^K k\log k =\Theta (K^2\log K)$ and (62). We can repeat this analysis to conclude that the dual oracle complexity for solving (34), i.e., $C_{{\textsf{det}},2}^\textrm{D}$ has the same order as $C_{{\textsf{det}},1}^\textrm{D}$. Since $C_{\textsf{det}}^\textrm{D}=C_{{\textsf{det}},1}^\textrm{D}+ C_{{\textsf{det}},2}^\textrm{D}$, the proof is complete.

1.4 Proof of Lemma 4.1

To prove this lemma, one needs to properly incorporate the inexact criteria in (65)–(67) (which involve conditional expectations) into the proof of Lemma 3.1. The key steps are: i) taking conditional expectation over the steps in the proof of Lemma 3.1 by using the measurability results in (69) and ii) applying the tower property of conditional expectation by using the nested relation in (68). Specifically, at the k-th iteration, we first modify the proof of Proposition 2.1 and show that

$$\begin{aligned} {\mathbb {E}}[{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }({\widehat{\lambda }}^k),{\widehat{\lambda }}^k)&-{\widehat{\psi }}^\textrm{D}(\lambda ^{k+1})+\big \langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }({\widehat{\lambda }}^k),{\widehat{\lambda }}^k),\lambda ^{k+1}-{\widehat{\lambda }}^k\big \rangle \,|\,{\mathcal {F}}_{k,1}]\nonumber \\&\le L_\textrm{D}{\mathbb {E}}[\Vert {\widehat{\lambda }}^k-\lambda ^{k+1}\Vert ^2\,|\,{\mathcal {F}}_{k,1}]+2\gamma _k. \end{aligned}$$

(117)

(For notational brevity, we omit ‘a.s.’ here and for all the inequalities below.) Furthermore, since ${\mathcal {F}}_{k,0}\subseteq {\mathcal {F}}_{k,1}$, if we take ${\mathbb {E}}[\cdot |{\mathcal {F}}_{k,0}]$ over (117), then we have

$$\begin{aligned}&{\mathbb {E}}[{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }({\widehat{\lambda }}^k),{\widehat{\lambda }}^k)-{\widehat{\psi }}^\textrm{D}(\lambda ^{k+1})+\big \langle \nabla _{\lambda }{\widehat{S}}^\textrm{P}({\widetilde{x}}_{\gamma }({\widehat{\lambda }}^k),{\widehat{\lambda }}^k),\lambda ^{k+1}-{\widehat{\lambda }}^k\big \rangle \,|\,{\mathcal {F}}_{k,0}]\nonumber \\&\quad \le L_\textrm{D}{\mathbb {E}}[\Vert {\widehat{\lambda }}^k-\lambda ^{k+1}\Vert ^2\,|\,{\mathcal {F}}_{k,0}]+2\gamma _k. \end{aligned}$$

(118)

In addition, from (114), we have

$$\begin{aligned} {\mathbb {E}}[\Vert {\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})-\lambda ^*_{\rho _{k}}(x^{k})\Vert ^{2}\,|\,{\mathcal {F}}_{k,0}]\ge \frac{{\mathbb {E}}[\Vert \lambda ^{k+1}-{\hat{\lambda }}^k\Vert ^2\,|\,{\mathcal {F}}_{k,0}]}{2(1-\tau _k)^2}-\frac{2\eta _{k}}{\rho _{k}}. \end{aligned}$$

(119)

Now, we can take ${\mathbb {E}}[\cdot |{\mathcal {F}}_{k,0}]$ over Equation (c) in (111), and use (118), (119) and the fact that $x^k,\lambda ^k\in {\mathcal {F}}_{k,0}$ to obtain

$$\begin{aligned} \tau _{k}\varDelta _{\rho _{k}}(x^k,\lambda ^k)&\ge {\mathbb {E}}[S_{\rho _{k+1}}(x^{k+1},{\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1})) +\frac{\rho _{k+1}\Vert \lambda ^{k+1}-{\hat{\lambda }}^k\Vert ^2}{4(1-\tau _k)^2}-\tau _k\eta _{k}\nonumber \\&\quad -\big (\psi ^\textrm{D}(\lambda ^{k+1}) + L_\textrm{D}\Vert {\widehat{\lambda }}^k-\lambda ^{k+1}\Vert ^2+2\gamma _k\big )\,|\,{\mathcal {F}}_{k,0}]. \end{aligned}$$

(120)

Again, since ${\mathcal {F}}_{k,0}\subseteq {\mathcal {F}}_{k,2}$, if we take ${\mathbb {E}}[\cdot |{\mathcal {F}}_{k,0}]$ over (67), then we have

$$\begin{aligned} {\mathbb {E}}\big [\psi _{\rho _{k+1}}^{\textrm{P}}(x^{k+1})-S_{\rho _{k+1}}(x^{k+1},{\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1}))\,\big \vert \,{\mathcal {F}}_{k,0}\big ]\le \eta _{k}. \end{aligned}$$

(121)

We then substitute (121) into (120), and use the condition ${\rho _{k+1}}\ge {4(1-\tau _{k})^{2}}L_\textrm{D}$ to get

$$\begin{aligned} \tau _{k}\varDelta _{\rho _{k}}(x^k,\lambda ^k) \ge {\mathbb {E}}[\varDelta _{\rho _{k+1}}(x^{k+1},\lambda ^{k+1})\,|\,{\mathcal {F}}_{k,0}] - 2\eta _k-2\gamma _k. \end{aligned}$$

(122)

1.5 Proof of Theorem 4.2

The proof follows the same argument as that of Theorem 3.2, hence we only outline the important steps. Based on the choice of $\gamma _k$ in (57) and the complexity of ${{\textsf{M}}}_2$ in (73),

$$\begin{aligned} C_{\textsf{stoc}}^\textrm{P}&= {\sum }_{k=1}^{K_{\textsf{stoc}}} \; O\big ((n+\sqrt{n\kappa _{\mathcal {X}}})\log \big ((L+L_{xx})(n+\sqrt{n\kappa _{\mathcal {X}}})k/(\mu \varepsilon )\big )\big )\\&= O\left( (n+\sqrt{n\kappa _{\mathcal {X}}})\Big (K_{\textsf{stoc}}\log \big ((L+L_{xx})(n+\sqrt{n\kappa _{\mathcal {X}}})/(\mu \varepsilon )\big )+\log \big (K_{\textsf{stoc}}!\big )\Big )\right) \\&= O\left( (n+\sqrt{n\kappa _{\mathcal {X}}})\sqrt{L_\textrm{D}/\varepsilon }\Big (\log \big ((L+L_{xx})(n+\sqrt{n\kappa _{\mathcal {X}}})/(\mu \varepsilon )\big )+\log \big ({L_\textrm{D}/\varepsilon }\big )\Big )\right) \\&= O\big ((n+\sqrt{n\kappa _{\mathcal {X}}})\sqrt{L_\textrm{D}/\varepsilon }\log \big ((L+L_{xx})L_\textrm{D}(n+\sqrt{n\kappa _{\mathcal {X}}})/(\mu \varepsilon )\big )\big ). \end{aligned}$$

Using the same reasoning as in the proof of Theorem 3.2, the dual oracle complexities for solving both (65) and (67) have the same order, so it suffices to only analyze the complexity for solving (65). Specifically, based on (72), we have

$$\begin{aligned} C_{{\textsf{stoc}},1}^\textrm{D}&= \textstyle {\sum }_{k=1}^{K_{\textsf{stoc}}} \; O\Big (\big (n+\sqrt{nL_{\lambda \lambda }k^2/L_\textrm{D}}\big )\log \big (L_{\lambda \lambda }(n+\sqrt{nL_{\lambda \lambda }k^2/L_\textrm{D}})k/(L_\textrm{D}\varepsilon )\big )\Big )\\&{\mathop {=}\limits ^{\mathrm{(a)}}}\textstyle {\sum }_{k=1}^{K_{\textsf{stoc}}} \; O\Big (\big (n+k\sqrt{nL_{\lambda \lambda }/L_\textrm{D}}\big )\big (\log \big (L_{\lambda \lambda }(n+\sqrt{nL_{\lambda \lambda }/L_\textrm{D}})/(L_\textrm{D}\varepsilon )\big )+\log k\big )\Big )\\&= O\Big (\big (K_{\textsf{stoc}}n+\sqrt{nL_{\lambda \lambda }/L_\textrm{D}}\textstyle {\sum }_{k=1}^{K_{\textsf{stoc}}}k\big )\log \big (L_{\lambda \lambda }(n+\sqrt{nL_{\lambda \lambda }/L_\textrm{D}})/(L_\textrm{D}\varepsilon )\big )\\&\quad +\big (n\textstyle {\sum }_{k=1}^{K_{\textsf{stoc}}}\log k+\sqrt{L_{\lambda \lambda }/L_\textrm{D}}\textstyle {\sum }_{k=1}^{K_{\textsf{stoc}}}k\log k\big )\Big )\\&= O\Big (\big (n\sqrt{L_\textrm{D}/\varepsilon }+\sqrt{nL_{\lambda \lambda }L_\textrm{D}}/\varepsilon \big )\log \big (L_{\lambda \lambda }(n+\sqrt{nL_{\lambda \lambda }/L_\textrm{D}})/(L_\textrm{D}\varepsilon )\big )\\&\quad +\,\sqrt{L_\textrm{D}/\varepsilon }\log ({L_\textrm{D}/\varepsilon })(n+\sqrt{nL_{\lambda \lambda }/\varepsilon })\Big )\\&= O\Big (\big (n\sqrt{L_\textrm{D}/\varepsilon }+\sqrt{nL_{\lambda \lambda }L_\textrm{D}}/\varepsilon \big )\log \big (L_{\lambda \lambda }(n+\sqrt{nL_{\lambda \lambda }/L_\textrm{D}})/\varepsilon \big )\Big ), \end{aligned}$$

where (a) holds since $n\le kn$. We obtain (76) by noting that $C_{{\textsf{stoc}}}^\textrm{D}=\Theta \big (C_{{\textsf{stoc}},1}^\textrm{D}\big )$.

1.6 Proof of Theorem 4.3

First, let us define the events ${\mathcal {A}}_{0,0}\triangleq \varOmega$, and for any $k\in {\mathbb {Z}}_+$,

$$\begin{aligned} {\mathcal {A}}_{k,1}&\triangleq \{\psi _{\rho _{k}}^{\textrm{P}}(x^{k})-S_{\rho _{k}}(x^{k},{\widetilde{\lambda }}_{\rho _k,\eta _{k}}(x^{k}))\le \eta _k\},\, {\mathcal {A}}_{k,2}\triangleq \{S({\widetilde{x}}_{\gamma _{k}}({\hat{\lambda }}^{k}),{\hat{\lambda }}^{k})-\psi ^\textrm{D}({\hat{\lambda }}^{k})\le \gamma _k\},\\ {\mathcal {A}}_{k+1,0}&\triangleq \{\psi _{\rho _{k+1}}^{\textrm{P}}(x^{k+1})-S_{\rho _{k+1}}(x^{k+1},{\widetilde{\lambda }}_{\rho _{k+1},\eta _{k}}(x^{k+1}))\le \eta _k\}. \end{aligned}$$

Also, for any measurable event ${\mathcal {A}}$, denote its complement as ${\mathcal {A}}^\textrm{c}$ and its indicator function as ${\mathbb {I}}_{{\mathcal {A}}}$, i.e., ${\mathbb {I}}_{{\mathcal {A}}}(z)=1$ if $z\in {\mathcal {A}}$ and 0 otherwise.

Fix any $k\in \{0,\ldots ,K-1\}$. From Markov’s inequality and (77), we have

$$\begin{aligned} \Pr \big \{{\mathcal {A}}^\textrm{c}_{k,1}\,\big \vert \,{\mathcal {F}}_{k,0}\big \} \le {\mathbb {E}}\big [\psi _{\rho _{k}}^{\textrm{P}}(x^{k})-S_{\rho _{k}}(x^{k},{\widetilde{\lambda }}_{\rho _k,\eta _{k}}(x^{k}))\,\big \vert \,{\mathcal {F}}_{k,0}\big ]/\eta _k\le \delta /(3K)\quad \text{ a.s. } \end{aligned}$$

(123)

Since $\bigcup _{i=0}^{k-1}\{{\mathcal {A}}_{i,1},{\mathcal {A}}_{i,2},{\mathcal {A}}_{i+1,0}\}\subseteq {\mathcal {F}}_{k,0}$, we have that

$$\begin{aligned} {{\mathcal {C}}_{k,0}}\in {\mathcal {F}}_{k,0},\quad \text{ where } \quad {\mathcal {C}}_{k,0}\triangleq \textstyle {\bigcap }_{i=0}^{k-1}\;\big ({\mathcal {A}}_{i,1}\cap {\mathcal {A}}_{i,2}\cap {\mathcal {A}}_{i+1,0}\big ). \end{aligned}$$

(124)

(When $k=0$, define ${\mathcal {C}}_{0,0}\triangleq {\mathcal {A}}_{0,0}$.) In addition, note that $\Pr \{{\mathcal {C}}_{k,0}\}>0$, since

$$\begin{aligned} \Pr \big \{{\mathcal {C}}_{k,0}^\textrm{c}\big \} = \Pr \big \{\textstyle {\bigcup }_{i=0}^{k-1}\big ({\mathcal {A}}_{k-1,1}^\textrm{c}\cup {\mathcal {A}}_{k-1,2}^\textrm{c}\cup {\mathcal {A}}_{k,0}^\textrm{c}\big )\big \}\le (3k)\delta /(3K) \le \delta <1. \end{aligned}$$

(125)

We then take conditional expectation ${\mathbb {E}}[\cdot \,|\,{{\mathcal {C}}_{k,0}}]$ in (123) to obtain

$$\begin{aligned} {\mathbb {E}}\big [\Pr \big \{{\mathcal {A}}_{k,1}\,\big \vert \,{\mathcal {F}}_{k,0}\big \}\,|\,{{\mathcal {C}}_{k,0}}\big ]\ge 1-\delta /(3K). \end{aligned}$$

(126)

On the other hand,

$$\begin{aligned} {\mathbb {E}}\big [\Pr \big \{{\mathcal {A}}_{k,1}\,\big \vert \,{\mathcal {F}}_{k,0}\big \}\,|\,{{\mathcal {C}}_{k,0}}\big ]&= {\mathbb {E}}\big [\Pr \big \{{\mathcal {A}}_{k,1}\,\big \vert \,{\mathcal {F}}_{k,0}\big \}{\mathbb {I}}_{{\mathcal {C}}_{k,0}}\big ]/{\mathbb {P}}({\mathcal {C}}_{k,0})\\&{\mathop {=}\limits ^{\mathrm{(a)}}}{\mathbb {E}}\big [{\mathbb {I}}_{{\mathcal {A}}_{k,1}}{\mathbb {I}}_{{\mathcal {C}}_{k,0}}\big ]/{\mathbb {P}}({\mathcal {C}}_{k,0}) = \Pr \big \{{\mathcal {A}}_{k,1}\,|\,{\mathcal {C}}_{k,0}\big \}, \end{aligned}$$

where (a) follows since ${{\mathcal {C}}_{k,0}}\in {\mathcal {F}}_{k,0}$. Therefore, we have

$$\begin{aligned} \Pr \{{\mathcal {A}}_{k,1}\,|\,{\mathcal {C}}_{k,0}\}\ge 1-\delta /(3K). \end{aligned}$$

(127)

Similarly, if we define ${\mathcal {C}}_{k,1}\triangleq {\mathcal {C}}_{k,0}\cap {\mathcal {A}}_{k,1}$ and ${\mathcal {C}}_{k,2}\triangleq {\mathcal {C}}_{k,1}\cap {\mathcal {A}}_{k,2}$, then we also have

$$\begin{aligned}&\Pr \{{\mathcal {A}}_{k,2}\,|\,{{\mathcal {C}}_{k,1}}\}\ge 1-\delta /(3K),\quad \Pr \{{\mathcal {A}}_{k+1,0}\,|\,{{\mathcal {C}}_{k,2}}\}\ge 1-\delta /(3K). \end{aligned}$$

(128)

From Theorem 3.1, we know that if $K=K_{\textsf{det}}'$ and the event $\bigcap _{k=0}^{K-1}\big ({\mathcal {A}}_{k,1}\cap {\mathcal {A}}_{k,2}\cap {\mathcal {A}}_{k+1,0}\big )$ occurs, then $\varDelta _{\rho _K}(x^K,\lambda ^K)\le \varepsilon$. Therefore,

$$\begin{aligned} \Pr \big \{\varDelta _{\rho _K}(x^K,\lambda ^K)\le \varepsilon \big \}&\ge \Pr \big \{\textstyle {\bigcap }_{k=0}^{K-1}\big ({\mathcal {A}}_{k,1}\cap {\mathcal {A}}_{k,2}\cap {\mathcal {A}}_{k+1,0}\big )\big \}\\&= \textstyle {\prod }_{k=0}^{K-1} \Pr \big \{{\mathcal {A}}_{k+1,0}\,|\,{{\mathcal {C}}_{k,2}}\big \}\Pr \big \{{\mathcal {A}}_{k,2}\,|\,{{\mathcal {C}}_{k,1}}\big \}\Pr \{{\mathcal {A}}_{k,1}\,|\,{{\mathcal {C}}_{k,0}}\}\\&{\mathop {\ge }\limits ^{\mathrm{(a)}}}\big (1-\delta /(3K)\big )^{3K}{\mathop {\ge }\limits ^{\mathrm{(b)}}}1-\delta , \end{aligned}$$

where (a) follows from (127) and (128) and (b) follows from Bernoulli’s inequality. By the same reasoning, we can also show that if $K=K_{\textsf{det}}$, then (80) holds.

1.7 Proof of Lemma 5.1

Since $\lambda ^*\in {\mathbb {R}}_+^n$ is an optimal solution of $\max _{\lambda \in {\mathbb {R}}_+^n}\psi ^\textrm{D}(\lambda )$, we have that $\psi ^\textrm{D}({\overline{\lambda }})\le \psi ^\textrm{D}(\lambda ^*)$. This implies $\varDelta _{\rho }({\overline{x}},{\lambda ^*})\le \varDelta _{\rho }({\overline{x}},{\overline{\lambda }}) \le \epsilon$. From the definition of $\varDelta _\rho$ in (23), we have

$$\begin{aligned} \epsilon \ge \varDelta _{\rho }({\overline{x}},{\lambda ^*})&\ge S({\bar{x}},\lambda )-({\rho }/{2})\Vert \lambda \Vert _{2}^{2}-S(x,{\lambda ^*}), \quad \forall \,x\in {\mathcal {X}},\quad \forall \,\lambda \in {\mathbb {R}}_{+}^{m}. \end{aligned}$$

(129)

We then choose $x\!=\!x^{*}$ and $\lambda \!=\!0$ in (129) to obtain

$$\begin{aligned} \epsilon \ge S({\bar{x}},0)-S(x^{*},{\lambda ^*}) =f({\bar{x}})-\left( f(x^{*})+\textstyle {\sum }_{i=1}^n\lambda ^*_i g_i(x^*)\right) \ge f({\bar{x}})-f(x^{*}), \end{aligned}$$

(130)

where the last step follows from $\lambda ^*_i\ge 0$ and $g_i(x^*)\le 0$, for any $i\in [n]$.

Now, fix any $\theta >0$ and $i\in [n]$. Let $e_i\in {\mathbb {R}}^{n}$ denote the i-th standard basis vector, i.e., $(e_i)_i=1$ and $(e_i)_j=0$ for any $j\!\in \![n]\setminus \{i\}$. In (129), if we choose $x=x^{*}$ and $\lambda =\lambda ^*+\theta _i e_i$, where $\theta _i=\theta$ if $g_i({\overline{x}})>0$ and 0 otherwise, then

$$\begin{aligned} \epsilon&\ge S({\bar{x}},\lambda ^*)+\theta _i g_{i}({\bar{x}})-({\rho }/{2})\Vert \lambda ^*+\theta _i e_i\Vert _{2}^{2}-S(x^*,{\lambda ^*}) \\&\ge \theta _i g_{i}({\bar{x}})-({\rho }/{2})\Vert \lambda ^*+\theta _i e_i\Vert _{2}^{2}\ge \theta [g_{i}({\bar{x}})]_+-({\rho }/{2})\Vert \lambda ^*+\theta e_i\Vert _{2}^{2}, \end{aligned}$$

where in the last step we use $\lambda ^*\ge 0$ and $\theta \ge \theta _i\ge 0$. After rearranging, we have

$$\begin{aligned} \begin{aligned} {[}g_i({\bar{x}})]_+&\le \rho \lambda _i^*+{\rho \theta }/{2}+({\rho \Vert \lambda ^*\Vert ^2_2+2\epsilon })/({2\theta }){\mathop {\le }\limits ^{\mathrm{(a)}}}\rho \lambda _i^* + \sqrt{\rho ({\rho \Vert \lambda ^*\Vert ^2_2+2\epsilon })}\\&{\mathop {\le }\limits ^{\mathrm{(b)}}}(\lambda _i^*+\Vert \lambda ^*\Vert _2) \rho + \sqrt{2\epsilon \rho }, \end{aligned} \end{aligned}$$

(131)

where we take the infimum over $\theta >0$ in (a) and use $\sqrt{a+b}\le \sqrt{a}+\sqrt{b}$, $\forall \, a,b\ge 0$ in (b).

1.8 Proof of Theorem 5.3

Similar to the analysis in Sect. 3.4, we have

$$\begin{aligned} {\overline{C}}_{\textsf{det}}&{\mathop {=}\limits ^{\mathrm{(a)}}}O\Big (n{\sum }_{k=1}^{K_{\textsf{cons}}}\sqrt{(L+\alpha )/\mu +k\alpha \sqrt{\varepsilon }/(M\sqrt{\mu })}\log \big (k\big ((L+\alpha )/\varepsilon +k\alpha \sqrt{\mu }/(M\sqrt{\varepsilon })\big )\big )\Big )\\&{\mathop {=}\limits ^{\mathrm{(b)}}}O\Big (n{\sum }_{k=1}^{K_{\textsf{cons}}}\big (\sqrt{(L+\alpha )/\mu }+\sqrt{k\alpha /M}({\varepsilon }/{\mu })^{1/4}\big )(\log k+\log \big ((L+\alpha ){\mu }/(M\varepsilon )\big )\big )\Big )\\&{\mathop {=}\limits ^{\mathrm{(c)}}}O\Big (n\big (\sqrt{(L+\alpha )/\mu }K_{\textsf{cons}}\big (\log K_{\textsf{cons}}+ \log \big ((L+\alpha ){\mu }/(M\varepsilon )\big )\big )\\&\quad +\,\sqrt{\alpha /M}({\varepsilon }/{\mu })^{1/4}K_{\textsf{cons}}^{3/2}(\log K_{\textsf{cons}}+ \log \big ((L+\alpha ){\mu }/(M\varepsilon )\big )\big )\Big )\\&= O\Big (n\big (M\sqrt{L+\alpha }/(\mu \sqrt{\varepsilon })+M\sqrt{\alpha }/(\mu \sqrt{\varepsilon })\big )\log \big ((L+\alpha )/\varepsilon \big )\Big ), \end{aligned}$$

where in (a) we use $\gamma _k=\Theta (\varepsilon /k)$, in (b) we use $\alpha /\sqrt{\varepsilon }=O((L+\alpha )/\varepsilon )$ and in (c) we use $\sum _{k=1}^K k^\nu \log k = \Theta (K^{\nu +1}\log K)$, for any $\nu \ge 0$. By noting that $\alpha \le L+\alpha$, we obtain (103).