1 Introduction

Electron beams (EB) have various uses and a diverse range of applications in multiple fields such as material research, compact torus construction, x-ray and microwave generation, ion acceleration, and others where a long-term energy source is required.

The use of EB in the heating of magnetically confined plasma to high temperatures has garnered significant interest in research and practical implementation, both theoretically [1,2,3,4,5,6,7,8] and empirically [9,10,11]. Some linear density profiles within the system have been identified and validated in previous articles [12,13,14]. When an EB travels through plasma, its kinetic energy is converted to thermal energy, which heats the plasma [1].

The instabilities arising from the interaction of charged particle beams with plasma have been notably stimulated by the fact that, apart from their negative effects such as anomalous diffusion due to low-frequency oscillations or constraints on the highest attainable currents in plasma accelerators and other devices, there exists a great number of useful applications for these instabilities.

The effect of an external static magnetic field on the linear interaction of relativistic electron beam with inhomogeneous cold bounded plasma was previously investigated [4, 5, 14, 17].

In this paper, we investigate the linear interaction of inhomogeneous warm EB and inhomogeneous, collisional cold plasma.

Differential equations of second order are the field equations that describe the system.

Starting with the linear density formula to solve the field equation:

$$ N_{0b} = n_{0b} \left( {1 + \frac{x}{L}} \right),\,V_{0b} = v_{0b} \left( {1 + \frac{x}{L}} \right) $$

where \(L\) is the length scale of the variation (\(L > > x\)), the electric field of the interaction is calculated. It is shown that waves are excited more strongly in this case compared to the case of an inhomogeneous cold electron beam with an unmagnetized cold plasma.

2 Fundamental waves

The initial linearized pair of equations (the equation of motion and the continuity equation) for electron beam oscillations in 1-D is:

$$ \frac{{\partial \,\vec{V}_{b} }}{\partial \,t} + (\vec{V}_{b} \cdot \vec{\nabla })\,\vec{V}_{b} ) = - \frac{e}{m}\,\vec{E} - \frac{1}{{n_{b} \,m}}\nabla P;\quad \vec{V}_{b} = \vec{V}_{0b} + \vec{V}_{1b} ,\quad \vec{V}_{0b} = V_{0b} \,\,\vec{e}_{z} $$
(1)
$$ \frac{{\partial \;N_{b} }}{\partial \;t} + \vec{\nabla } \cdot (N_{b} \;\vec{V}_{b} \,) = 0;\quad N_{b} = n_{0b} + n_{1b} $$
(2)

For an inhomogeneous collisional plasma in the oscillating electric field, the initial linearized set of equations (the equation of motion and the continuity equation) defining the oscillations in 1-D is:

$$ \frac{{\partial \;\,\vec{V}_{P} }}{\partial \;\,t} + (\vec{V}_{P} \cdot \vec{\nabla })\,\;\vec{V}_{P} \, = - \frac{e}{m}\;\,\,\vec{E} - \upsilon \,\vec{V}_{P} $$
(3)
$$ \frac{{\partial \;N_{P} }}{\partial \;t} + \vec{\nabla } \cdot (N_{P} \;\vec{V}_{P} \,) = 0\;\quad ;\;\,\,\quad N_{P} = n_{0P} + n_{1P} $$
(4)

In Eqs. (1–4) \(V_{0b} \,\) and \(\,\;n_{0\,b}\) are the unperturbed velocity and density of the beam while \(n_{0\,P} ,\,\;\) and \(n_{1\,P}\) are the unperturbed and perturbed density of the plasma, respectively. P is the beam pressure, and \(\upsilon\) is the collision of plasma electrons with other plasma particles. All other terms have their usual meaning.

From Eqs. (1) and (2), we obtain the following expressions for the warm EB:

$$ V_{1b} = \frac{ - e}{{m\,V_{0b} }}\exp \left( {\frac{i\omega }{{V_{0b} }}x} \right).\int {\exp (\frac{ - i\omega }{{V_{0b} }}x)\,\,E(x)\,dx} - \frac{{V_{{T_{e} }}^{2} }}{{V_{0b} }}\exp \left( {\frac{i\omega }{{V_{0b} }}x} \right)\,\int {\frac{1}{{n_{0b} }}\exp \left( {\frac{ - i\omega }{{V_{0b} }}x} \right)\frac{{\partial \,n_{0b} }}{\partial \,x}dx} $$
(5)
$$ \begin{gathered} n_{1b} = n_{0b} \left[ {\frac{e}{{m\,V_{0b}^{2} }}\exp \left( {\frac{i\omega }{{V_{0b} }}x} \right).\int {\exp \left( {\frac{ - i\omega }{{V_{0b} }}x} \right)\,\,E(x)\,dx - 1} } \right] - \frac{i\omega }{{V_{0b} }}\exp \left( {\frac{i\omega }{{V_{0b} }}x} \right).\int {n_{0b} \exp \left( {\frac{ - i\omega }{{V_{0b} }}x} \right)\,\,\,dx} \hfill \\ + \frac{i\omega \,e}{{V_{{_{0b} }}^{3} }}\exp \left( {\frac{i\omega }{{V_{0b} }}x} \right)\left[ {\int {n_{0b} } .\left( {\int {\exp \left( {\frac{ - i\omega }{{V_{0b} }}x} \right)\,\,E(x)\,dx} } \right)\,dx} \right] + \frac{{V_{{T_{e} }}^{2} }}{{V_{{_{0b} }}^{2} }}n_{0b} \exp \left( {\frac{i\omega }{{V_{0b} }}x} \right)\,\int {\frac{1}{{n_{0b} }}\exp \left( {\frac{ - i\omega }{{V_{0b} }}x} \right)\frac{{\partial \,n_{0b} }}{\partial \,x}dx} \hfill \\ \end{gathered} $$
(6)

where \(V_{{T_{e} }}^{{}} = \sqrt {\frac{{kT_{e} }}{m}}\) is the electron thermal velocity.

Using Poisson's equation

$$ \frac{{dE}}{{dx}} = - 4\pi \;e\,(n_{{1P}} + n_{{1b}} ) $$
(7)

and substituting (5) and (6) into (7), we obtain the expressions describing the perturbed plasma velocity \(V_{1P}\) and density \(n_{1P}\)

$$ V_{1P} = \frac{ - ie}{{m\tilde{\omega }}}\;E(x) $$

\(n_{1P} = \frac{ - e}{{m\omega \,\tilde{\omega }}}\frac{\partial }{\partial \;x}\left[ {n_{0P} (x)\,\;E(x)} \right]\) where, \(\tilde{\omega } = \omega + i\upsilon\).

Introducing \(n_{1P}\) and \(n_{1b}\) into Poisson's equation, we obtain the following differential equation

$$ \left( {V_{0b} \frac{\partial }{\partial \,x} - i\,\omega } \right)^{2} \left( {\varepsilon \,E(x)} \right) + \omega_{b}^{2} E(x) = R_{1b} $$
(8)

where,

$$ R_{1b} = R_{b} - 4\pi \,e\,\left( {V_{0b} \frac{\partial }{\partial \,x} - i\,\omega } \right)^{2} \left[ {\frac{{V_{{T_{e} }}^{2} }}{{V_{{_{0b} }}^{2} }}\int {\left( {n_{0b} \exp \left( {\frac{i\omega }{{V_{0b} }}x} \right)\,\int {\frac{1}{{n_{0b} }}\exp \left( {\frac{ - i\omega }{{V_{0b} }}x} \right)\frac{{\partial \,n_{0b} }}{\partial \,x}dx} } \right)\,dx} } \right] $$
(9)
$$ R_{b} = 4\pi \,e\,V_{{_{0b} }}^{2} \,\left( {\frac{\partial }{\partial \,x} - \frac{i\,\omega }{{V_{0b} }}} \right)^{2} \int {\left( {n_{0b} + \frac{i\,\omega }{{V_{0b} }}\exp \left( {\frac{i\omega }{{V_{0b} }}x} \right)\,\int {n_{0b} \exp \left( {\frac{ - i\omega }{{V_{0b} }}x} \right)\,dx} } \right)\,dx} $$
(10)

Equation (8) can be solved in the region \(0 \le x \le a\) by the same method in Ref. [18] to get:

$$ E(x) = \frac{{\exp \left( {\frac{i\omega }{{V_{0b} }}x} \right)}}{\varepsilon }\left[ {\frac{1}{{V_{0b}^{2} }}\int\limits_{0}^{a} {d\,x^{\prime}} \int\limits_{0}^{{x^{\prime}}} {R_{1b} } \exp \left( {\frac{ - i\omega }{{V_{0b} }}x} \right)\,d\,x + C} \right] $$
(11)

where \(\varepsilon = 1 - \frac{{\omega_{{P_{e} }}^{2} }}{{\omega \tilde{\omega }}}\), \(\omega_{{P_{e} ,b}}^{2} (x) = \frac{{4\;\pi \,\,e^{2} n_{{0,(\,P_{e} ,b\,)}} (x)}}{m}\).

The dielectric \(\varepsilon (x)\) is not affected by warmness of the beam, while the electric field amplification is affected by the warmness of the beam. In the case of a cold beam, \(V_{{T_{e} }}^{{}} = 0 \Rightarrow R_{1b} \to R_{b}\) and Eq. (8) gives the same result as ref. [6, 12].

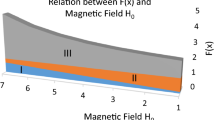
We show below a plot of the curve of Eq. (11) in Fig. 1, presenting the relationship between the electric field wave and the ratio [Vth/Vob]2 for \({n}_{p}\)=3 \(\times {10}^{11}\) c \({\mathrm{m}}^{-3}\) and \({n}_{b}\)=10 \(\times {10}^{11}\) c \({\mathrm{m}}^{-3}\).

Fig.1
figure 1

Electric field E(x) × 10^6 V/cm with [Vth/Vob]2

Full size image

Our observations indicate that as the electron thermal velocity Vth and the temperature of the warm electron beam increase, the electric field decreases. The highest electric field value is found in the cold plasma region, where Vth = 0.

3 Conclusions

In this paper, we investigated the interaction of the inhomogeneous warm electron beam with a non-homogeneous cold unmagnetized collisional plasma. It is shown that the linear effects play an important role in the process of energy transfer from the beam to the plasma as compared to the linear cases at \(\upsilon = 0\) and cold electron beam \(V_{{T_{e} }} = 0\). This leads to the fact that the dielectric \(\varepsilon (x)\) is not affected by warmness of the beam, while the electric field amplification is affected by the warmness of the beam. It is found that the electric field decreases with the increase in the thermal velocity and then, with the increase in the temperature of warm electron beam.

It is also found that the inhomogeneous electron beam has an effect on the waves and hence on the power absorbed by the plasma. In addition, the term of collision plasma plays an important role in the energy transfer between the beam and the plasma.