1 Introduction

Moderate or intense low oxygen dilution (MILD) offers an environmentally friendly and energy efficient combustion methodology (Wünning and Wünning 1997; Katsuki and Hasegawa 1998; Cavaliere and de Joannon 2004). MILD combustion can be defined as the combustion process at which the reactants’ initial temperature (\({T}_{0}\)) is higher than the autoignition temperature \({T}_{ign}\) of the reacting mixture and the maximum temperature rise due to combustion is smaller than the autoignition temperature \(\Delta T<{T}_{ign}\) (Cavaliere and de Joannon 2004). Previous experimental investigations using OH Planar Laser-Induced pre-dissociative Fluorescence (OH-PLIF) showed the existence of disconnected reaction zones inside the combustor, while the appearance of distributed combustion was observed through temperature measurements using Rayleigh thermometry (Plessing et al. 1998). DNS studies of MILD combustion have reported that the interaction between the thin reaction zones is the main reason for the observed distributed combustion in homogeneous mixture MILD combustion (Minamoto et al. 2014b). Minamoto et al. (2013) suggested that premixed flame models could be extended to homogeneous mixture MILD combustion if it considers reaction zone interactions. Recently, Awad et al. (2021) compared the evolution of the reactive scalar gradient in the homogeneous mixture MILD combustion case with a typical premixed flame and revealed important differences between the scalar gradient statistics in MILD combustion and those found in conventional premixed flames. The reactive scalar gradient (e.g. reaction progress variable gradient) is often used to evaluate the flame surface area (Klein et al. 2020) and to characterise flame surface interactions (Griffiths et al. 2015). Therefore, it is worthwhile to assess whether the fundamental building blocks of premixed flame modelling, such as Damköhler’s hypotheses which relate the volume-integrated burning rate to flame surface area and the ratio of eddy to molecular diffusivities, remain valid for MILD combustion of homogeneous (i.e. constant equivalence ratio) mixtures.

According to Damköhler (1940, 1947), under the limit of large-scale turbulence, when all turbulent eddies are larger than the flame thickness, the augmentation in the turbulent burning rate in comparison to the laminar burning rate takes place in proportion to the increase in flame area generation under turbulence in premixed flames. This leads to the mathematical expression of Damköhler’s first hypothesis (DH1), which is expressed as (Damköhler 1940, 1947):

$${S}_{T}/{S}_{L}={A}_{T}/{A}_{L}$$
(1)

In Eq. 1, \({S}_{L}\) is the unstretched laminar burning velocity, whereas \({A}_{T}\) and \({A}_{L}\) represent the turbulent flame surface area and the projected area in the direction of flame propagation, respectively. Although Damköhler’s first hypothesis was proposed for the corrugated flamelets regime (Peters 2000), several DNS studies for statistically planar premixed flames with unity Lewis number revealed that DH1 remains valid in the thin reaction zone regime (Aspden et al. 2011; Ahmed et al. 2019; Varma et al. 2021). Klein et al. (2020) considered multi-step chemistry DNS data of hydrogen/air flames and reported that DH1 remains valid in an order of magnitude sense even in the broken-reaction zone regime (Peters 2000). Moreover, some experimental analyses utilised Eq. 1 to extract \({S}_{T}/{S}_{L}\) from \({A}_{T}/{A}_{L}\) measurements in the past (Muppala et al. 2005; Dinkelacker et al. 2011). On the other hand, several recent experimental studies reported discrepancies between \({S}_{T}/{S}_{L}\) and \({A}_{T}/{A}_{L}\) values for high values of Karlovitz number (i.e. \(Ka\gg 1\)) (Yuan and Gülder 2010; Wang et al. 2019; Driscoll et al. 2020). Therefore, it is useful to assess the applicability of Eq. 1 in homogeneous mixture MILD combustion, which is representative of high Karlovitz number (i.e. \(Ka\gg 1\)) combustion and can potentially exhibit attributes of distributed burning (Minamoto et al. 2013, 2014a, b; Minamoto and Swaminathan 2014, 2015).

Damköhler (1940, 1947) also suggested an alternative expression for \({S}_{T}/{S}_{L}\) for conditions where the integral length scale of turbulence is smaller than the thermal flame thickness by considering that the chemical timescale remains identical for both laminar and turbulent conditions, but the diffusive effects are augmented by turbulent transport. This expression is known as Damköhler’s second hypothesis (DH2), which is given by (Damköhler 1940, 1947):

$${S}_{T}/{S}_{L}=\sqrt{{D}_{t}/D}$$
(2)

where \({D}_{t}\) is the turbulent diffusivity and \(D\) is the molecular diffusivity of the reaction progress variable. Ahmed et al. (2021) reported that DH2 remains valid in an order of magnitude sense for statistically planar premixed flames, with unity Lewis number, in the thin reaction zone combustion regime (Peters 2000) with the turbulent integral length scale being greater than the thermal flame thickness.

The applicability of DH1 and DH2 for homogeneous mixture (i.e. constant equivalence ratio) MILD combustion is yet to be assessed and this gap is addressed in the current analysis by utilising a three-dimensional DNS database, conducted with a skeletal methane-air chemical mechanism containing 16 species and 25 reactions (Smooke and Giovangigli 1991), for homogenous mixture MILD combustion at different turbulence intensities and dilution levels (\({{\text{O}}}_{2}\) concentrations of 3.5% and 4.8% by volume). The main objectives of the present study are: (1) to assess the applicability of DH1 and DH2 in homogeneous mixture MILD combustion; (2) to analyse the influence of dilution, turbulence intensity and the definition of the reaction progress variable on the applicability of both DH1 and DH2 in homogeneous mixture MILD combustion.

The paper is structured as follows. The numerical implementation is presented in the next section. This is followed by the presentation of results and their discussion. Finally, main findings are summarised, and conclusions are drawn.

2 Numerical Implementation

A well-known DNS code SENGA2 (Cant 2012) has been used to conduct the simulations analysed in this paper. In SENGA2, the standard conservative equations of compressible turbulent reacting flows are solved. The spatial derivatives are approximated using a high-order finite-difference scheme (i.e. 10th order central difference scheme for internal grid points with the order of accuracy gradually reducing to a one-sided fourth-order scheme at non-periodic boundaries). A fourth order Runge–Kutta scheme is used for explicit time advancement. A skeletal chemical mechanism consisting of 16 species (i.e. CH4, O2, CO2, H2O, H, O, OH, HO2, H2, CO, H2O2, HCO, CH2O, CH3, CH3O and N2) and 25 reactions (Smooke and Giovangigli 1991) has been employed to represent the chemical kinetics of methane-air combustion. The present simulation uses a cubic domain of size 10 mm × 10 mm × 10 mm. An equidistant Cartesian grid of 252 × 252 × 252 is used to discretise the computational domain which ensures that at least 12 grid points reside within the thermal flame thickness \({\delta }_{th}=({T}_{ad}-{T}_{0})/{max\left|\nabla T\right|}_{L}\) (with \(T, {T}_{ad}\) and \({T}_{0}\) being the instantaneous, adiabatic flame and reactant temperatures, respectively, and the subscript ‘L’ indicating the values in the corresponding 1D unstretched laminar premixed flame) and the Kolmogorov length scale \(\eta\) is resolved by at least 1.5 grid points for all turbulent cases. The Navier–Stokes Characteristic Boundary Conditions (NSCBC) approach (Poinsot and Lele 1992) has been utilised to specify the boundary conditions. A turbulent inflow with specified density and velocity is used at the left x-direction, whereas a partially non-reflecting outflow is specified at the right x-direction. All other transverse boundaries are subjected to periodic boundary conditions.

In this study, two dilution levels (\({{\text{O}}}_{2}\) concentrations of 3.5% and 4.8% by volume) have been considered. For the present discussion, LD refers to the lower dilution case (higher \({{\text{O}}}_{2}\) concentration) and HD refers to the higher dilution case (lower \({{\text{O}}}_{2}\) concentration). To ensure a meaningful comparison between LD and HD cases, the simulations are performed under atmospheric pressure and identical values of equivalence ratio (i.e. \(\phi =0.8\)), turbulence intensities \({u}^{\prime}/{S}_{L}\) and length scale ratios \(l/{\delta }_{th}\), where \({u}^{\prime}\) is the root-mean-square turbulent velocity and \(l\) is the integral length scale of turbulence. The thermochemical conditions for the 1D unstretched laminar flames which are used for the purpose of initialisation are listed in Table 1. The data within Table 1 includes the mole fractions of the reactants (i.e. \({X}_{{{\text{O}}}_{2}}\), \({X}_{{{\text{CO}}}_{2}}{,X}_{{{\text{H}}}_{2}{\text{O}}}{,X}_{{\text{CH}}4}\) and \({X}_{{{\text{N}}}_{2}}\), since CH4, O2, CO2, H2O and N2 constitute the reactants’ mixture for the 1D laminar flames), the unburned gas temperature and the thermodynamic pressure.

Table 1 Thermochemical conditions for the unstretched laminar premixed flames used in the generation of the simulations’ initial fields
Full size table

The conditions summarised in Table 1 indicate that the mole fraction of O2 remains smaller than 5% for all operating conditions. The autoignition temperature for the conditions presented in Table 1 is around 1100 K in a perfectly stirred reactor configuration (Cavaliere and De Joannon 2004). The maximum temperature rise \(\Delta T\) for a 1D premixed flame under the conditions summarised in Table 1 remains smaller than 400 K (Minamoto et al. 2014a). Thus, the conditions analysed here can be taken to satisfy the requirements of \({T}_{0}>{T}_{ign}\) and \(\Delta T<{T}_{ign}\) outlined by Cavaliere and De Joannon (2004). The conditions considered in this analysis are comparable to those used by Minamoto et al. (2014a, b) for DNS of MILD combustion in the past and also are representative of the experimental analysis of Suzukawa et al. (1997).

The initial turbulence intensities, length scale ratios, the values of Damköhler number \(Da=l{S}_{L}/{u}^{\prime}{\delta }_{th}\) and Karlovitz number \(Ka={\left({u}^{\prime}/{S}_{L}\right)}^{3/2}{\left(l/{\delta }_{th}\right)}^{-1/2}\) for the investigated cases are shown in Table 2.

Table 2 Turbulence parameters for the current simulations
Full size table

The current DNS of homogeneous mixture MILD combustion has been conducted using a canonical configuration that splits the simulation into two phases following Minamoto et al. (2013, 2014a, b), as schematically summarised in Fig. 1. The first phase is designed to mimic the mixing of combustion products with the reactant mixture, in a similar fashion to the mixing in an EGR combustor, while the second phase simulates the MILD combustion phenomena (Minamoto et al. 2013, 2014a, b; Minamoto and Swaminathan 2014, 2015). Thus, the first phase provides both the initial and inflow fields for the second phase. The mixture in phase 1 is prepared according to the following steps (Minamoto et al. 2013):

  1. (1)

    Initial turbulence fields of freely decaying homogenous isotropic turbulence are generated using a pseudo-spectral method (Rogallo 1981) following the Batchelor-Townsend spectrum (Batchelor and Townsend 1948) of turbulent kinetic energy.

  2. (2)

    The thermochemical conditions, summarised in Table 1, are used to simulate a 1D laminar premixed flame at \(\phi =0.8\) and \({T}_{0}=1500{\text{K}}\) for each case. These simulation parameters (initial temperature and mixture compositions) are similar to those used in the experimental analysis of Suzukawa et al. (1997). The 1D laminar profiles of each species mass fraction are then specified as functions of the progress variable based on fuel mass fraction \({c}_{{Y}_{F}}=(1-{Y}_{F}/{Y}_{F0})\) where \({Y}_{F}\) is the fuel mass fraction and \({Y}_{F0}\) is its value in the unburned reactants.

  3. (3)

    An initial 3D scalar field for \({c}_{{Y}_{F}}\) with bimodal distribution of \({c}_{{Y}_{F}}\) is then developed using the pseudo-spectral methodology proposed by Eswaran and Pope (1988) such that the mean of \({c}_{{Y}_{F}}\) remains close to 0.5 and \({c}_{{Y}_{F}}\) varies between 0.0 and 1.0 (i.e. \(0.0\le {c}_{{Y}_{F}}\le 1.0\)).

  4. (4)

    The functions generated in Step 2 are then utilised to populate the bimodal \({c}_{{Y}_{F}}\) field from Step 3 with values of the mass fractions for all reactive scalars (i.e. 16 species mass fractions) that correspond to the local value of \({c}_{{Y}_{F}}\) in the 3D field. Thus, the resulting scalar field has 16 species mass fractions.

  5. (5)

    The fields from Step 4 are then subjected to initial turbulence without reaction for about one turnover time \({(l}_{o}/{u}^{\mathrm{{\prime}}})\) in a periodic domain, which mimics the mixing process due to exhaust gas recirculation (EGR) in a MILD combustor. At the end of this step, the mean and variance of the pre-processed \(c\) fields are \(\langle c\rangle \approx 0.50\) and \(\langle {c}^{{\prime}2}\rangle \approx 0.09\) respectively.

Fig. 1
figure 1

Schematic diagram for the two stages of the MILD combustion simulation

Full size image

Thus, the initial species field for the turbulent reacting flow simulations has non-zero values of all 16 species mass fractions despite having only five species in the reactants of the 1D unstretched laminar flame. The aforementioned methodology was proposed and used in several previous analyses (Minamoto et al. 2013, 2014a, b; Minamoto and Swaminathan 2014, 2015) and the same practice is followed here.

In order to ensure that the initial transients have left the domain, the simulations are continued for 2.5 flow-through times (i.e. \({2.5L}_{x}/{U}_{in}\) where \({L}_{x}\) is the domain length in the x-direction and \({U}_{in}=20 \, m/s\) is the mean inlet velocity).

It is still computationally expensive to simulate MILD combustion processes using DNS. Since MILD combustion is realised only for a small window in terms of O2 concentration, \({T}_{0}\) and \(\Delta T\), the parametric analysis is carried out only for parameters, such as the extent of dilution and turbulence intensities, which are expected to significantly affect the behaviour of MILD combustion.

Beyond a certain level of \({T}_{0}\), an increase in \({T}_{0}\) gives rise to a drop in \(\Delta T\) under MILD conditions (Cavaliere and de Joannon 2004). This is the case at \({T}_{0}\)=1500 K chosen for this analysis. Thus, the variations of \({T}_{0}\) and \(\Delta T\) have competing effects in terms of determining temperature and species gradients and the maximum values of chemical reaction rate. Moreover, an increase in \({T}_{0}\) also enhances in the species diffusivity and, thus, strengthens the diffusive transport. The statistical behaviours of the chemical reaction rate and molecular diffusion term for MILD combustion of n-heptane with \({T}_{0}\)=1100 K (Abo-Amsha and Chakraborty 2023) have been found to be qualitatively similar to those for MILD combustion of methane with \({T}_{0}\)=1500 K (Awad et al. 2021), as considered in this analysis. The similar qualitative results for two different fuels, under different compositions and different \({T}_{0}\), provides some level of confidence that the reaction–diffusion (im)balance will not be altered significantly by an alteration of the initial temperature \({T}_{0}\) for MILD combustion. Hence, the variation of the unburned gas temperature was not considered as part of the parametric analysis.

It is worth noting that the validity of DH1 for conventional premixed combustion was demonstrated for different values of unburned gas temperature (i.e. Aspden et al. 2011; Chakraborty and Cant 2005; Ahmed et al. 2019; Varma et al. 2021). Thus, it can be postulated that the qualitative behaviour of the combustion process discussed in this paper is unlikely to change with the unburned gas temperature if MILD combustion is realised. The conditions analysed here can be taken to be representative of homogeneous mixture MILD combustion and, thus, an assessment of the validity of Damköhler’s hypotheses, or lack thereof, can be obtained from the cases considered here. However, it is not practical at this point to make any conclusive remark regarding any possible revisions to Damköhler’s hypotheses for MILD combustion based on the limited number of cases considered here.

3 Results and Discussion

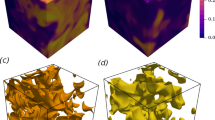
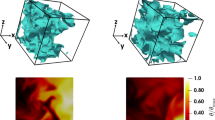
Figure 2 shows the instantaneous temperature field and \(c=0.8\) isosurface (based on \({{\text{CH}}}_{4}\) mass fraction) for both LD and HD cases at \({u}^{\mathrm{{\prime}}}/{S}_{L}=8.0\). The heat release rate assumes the maximum value for the present thermochemistry close to \(c=0.8\) (for \(c\) based on \({{\text{CH}}}_{4}\) mass fraction). Thus, the \(c=0.8\) isosurface is taken as representative of the flame surface. Figure 2 reveals a significant amount of flame self-interaction throughout the domain in the shown cases and the same qualitative behaviour was observed for \({u}^{\prime}/{S}_{L}=4.0\) cases. Moreover, it can be seen from Fig. 2 (1st row) that the temperature rise is insignificant, as expected in MILD combustion (Minamoto et al. 2013, 2014a, b; Minamoto and Swaminathan 2014, 2015; Awad et al. 2021), and the HD case exhibits lower temperature rise with smoother temperature gradients than the LD case. The HD case shows about 48% reduction in the temperature rise in comparison to the LD case. This could be due to the lower heat release rate and the higher mixture specific heat capacity arising from higher \({{\text{H}}}_{2}{\text{O}}\) and \({{\text{CO}}}_{2}\) concentrations in the HD case. The interacting reaction zones extend to about 50% of the computational domain for the LD case, whereas it extends throughout most of the domain in the HD case, suggesting that the reaction process continues further in the domain in the HD case in comparison to the LD case.

Fig. 2
figure 2

Instantaneous views of the temperature field (1st row), \(c=0.8\) isosurface (based on \({{\text{CH}}}_{4}\) mass fraction) coloured by the local temperature (2nd row) and the normalised OH mole fraction-based information \({I}^{{\text{OH}}}/{\left[{I}^{{\text{OH}}}\right]}_{max, L}\) (3rd row) for LD (left) and HD (right) at \({u}^{\prime}/{S}_{L}\)=8.0

Full size image

Figure 2 (3rd row) also shows the OH mole fraction-based information \({I}^{{\text{OH}}}\) for initial \({u}^{\prime}/{S}_{L}=8.0\) case normalised by the maximum value of \({I}^{{\text{OH}}}\) in the corresponding steady unstretched laminar premixed combustion (i.e. \({\left[{I}^{{\text{OH}}}\right]}_{max, L}\)) for both LD and HD conditions where \({I}^{{\text{OH}}}\) is evaluated from the DNS data as (Minamoto and Swaminathan 2014; Awad et al. 2021): \({I}^{{\text{OH}}}\propto {X}_{{\text{OH}}}{T}^{-\beta }\). For the temperature range between \(1000{\text{K}}\le T\le 1800{\text{K}}\), \(\beta\) ranges between − 2.6 and 1.0 (i.e. \(-2.6\le \beta \le 1.0\)) and it is taken here to be 0.0 (i.e. \(\beta =0.0\)) following previous studies (Minamoto and Swaminathan 2014; Awad et al. 2021). The distribution of \({I}^{{\text{OH}}}/{\left[{I}^{{\text{OH}}}\right]}_{max, L}\) provides an impression of more distributed reaction zone in the HD case than in the LD case. The observations made from Fig. 2 are also qualitatively valid for both LD and HD cases at \({u}^{\prime}/{S}_{L}=4.0\), which are not shown here for the sake of conciseness.

3.1 Applicability of DH1 for Homogeneous Mixture MILD Combustion

The turbulent burning velocity \({S}_{T}\) can be defined based on a major species \(\alpha\) in the following manner (Poinsot and Veynante 2001):

$${S}_{T}={[\rho }_{0}{A}_{L}({Y}_{\alpha P}-{Y}_{\alpha R}){]}^{-1}\int_{V}{\dot{w}}_{\alpha }dV$$
(3)

where \({\dot{w}}_{\alpha }\) is the reaction rate of species \(\alpha\). This suggests that the magnitude of \({S}_{T}\) is dependent on the choice of the major species \(\alpha\) in a multispecies framework. For the ease of discussion, it is useful to consider normalised mass fractions of the major species in the form of a reaction progress variable. The reaction progress variable \(c\) for a major species \(\alpha\) can be defined as:

$$c=({Y}_{\alpha }-{Y}_{\alpha R})/({Y}_{\alpha P}-{Y}_{\alpha R}),$$
(4)

where \({Y}_{\alpha }\) is the mass fraction of species \(\alpha\) upon which the reaction progress variable is defined and the subscripts R and P refer to values in unburned reactants and burned products, respectively. Using Eqs. 3 and 4, the turbulent burning velocity can be expressed as: \({S}_{T}={\left({\rho }_{0}{A}_{L}\right)}^{-1}\int_{V}{\dot{w}}_{c}dV\) for homogeneous mixture combustion (since \(({Y}_{\alpha P}-{Y}_{\alpha R})\) is a constant for a homogeneous mixture) where \({\dot{w}}_{c}\) is defined as: \({\dot{w}}_{c}={\dot{w}}_{\alpha }/({Y}_{\alpha P}-{Y}_{\alpha R})\). In the present analysis \(\alpha ={{\text{CH}}}_{4}, {{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) are considered. The Lewis numbers of the major species, based on which the reaction progress variables are defined, are given as \(L{e}_{C{H}_{4}}=0.97,L{e}_{{O}_{2}}=1.10,L{e}_{C{O}_{2}}=1.39\) and \(L{e}_{{H}_{2}O}=0.89\) (Smooke and Giovangigli 1991). The Lewis numbers of all the species in the chemical mechanism used here can be found in Smooke and Giovangigli (1991) and the Lewis numbers of the transported species range from 0.18 to 1.39. It is worth noting that the definition of reaction progress variable can play an important role when calculating the mass burning rate using the flame generated manifold (FGM) method, as shown by Gupta et al. (2021).

Two methods for determining the flame surface area have been adopted in this work: (1) based on the volume integral of \(|\nabla c|\) (i.e. \(A=\int_{V}|\nabla c|dV=\int_{V}|\nabla {Y}_{\alpha }|dV/({Y}_{\alpha P}-{Y}_{\alpha R})\) but the normalisation factor \(({Y}_{\alpha P}-{Y}_{\alpha R})\) cancels out while evaluating \({A}_{T}/{A}_{L}\)), (2) based on the area of the sharpened \({I}^{OH}\) isosurface. Klein et al. (2020) suggested that the first method is more robust (especially when based on a well-chosen \(c\) isosurface) than other alternatives which can result in an error of more than 40% when calculating the flame surface area in the broken reaction zone region of the premixed combustion regime diagram (Peters 2000). However, the second method of area evaluation is also accounted for in this analysis for the sake of completeness. The OH mole fraction-based information shown in Fig. 2 (3rd row) is sharpened using a Heaviside function in terms of \([{I}^{OH}-0.5[{I}^{{\text{OH}}}{]}_{L}^{max}]\) (i.e. \(H[{I}^{{\text{OH}}}-0.5[{I}^{{\text{OH}}}{]}_{L}^{max}]=0.5+0.5 \tanh[k\{{I}^{{\text{OH}}}-0.5[{I}^{{\text{OH}}}{]}_{L}^{max}\}]\) with \(k={10}^{6}\) as \(k\ge {10}^{6}\) does not affect the result). The flame surface area \({A}_{T}^{{\text{OH}}}\) is calculated using the surface area of the isosurfaces of \(H[{I}^{{\text{OH}}}-0.5[{I}^{{\text{OH}}}{]}_{L}^{max}]=0.5\).

The above discussion suggests that it is worthwhile to assess the validity of DH1 and DH2 for different choices of \(c\) (i.e. different choices of major species for turbulent burning velocity and flame surface area evaluations).

In order to assess the applicability of DH1, the volume-integrated burning rate and the turbulent flame surface area in MILD combustion conditions normalised by the corresponding quantities under steady unstretched laminar premixed combustion given by Table 1 (i.e. \(\Omega ={\int_{V}{\dot{w}}_{c}dV/\left[\int_{V}{\dot{w}}_{c}dV\right]}_{L}\), \(S={\int_{V}|\nabla c|dV/\left[\int_{V}|\nabla c|dV\right]}_{L}\) and \({S}^{{\text{OH}}}={A}_{T}^{{\text{OH}}}/{A}_{L}\)) are presented in Fig. 3 for all cases considered (both LD and HD conditions with initial \({u}^{\prime}/{S}_{L}\) = 4.0 and 8.0) and for different definitions of \(c\). The denominators of \(\Omega\), \(S\) and \({S}^{{\text{OH}}}\) are independent of the choices of \(c\), as they are expressed as \({\left[\int_{V}{\dot{w}}_{c}dV\right]}_{L}={\rho }_{0}{S}_{L}{A}_{L}\) and \({\left[\int_{V}\left|\nabla c\right|dV\right]}_{L}={A}_{L}\).

Fig. 3
figure 3

Variations of \(\Omega ={\int_{V}{\dot{w}}_{c}dV/\left[\int_{V}{\dot{w}}_{c}dV\right]}_{L}\), \(S={\int_{V}|\nabla c|dV/\left[\int_{V}|\nabla c|dV\right]}_{L}\) and \({S}^{{\text{OH}}}={A}_{T}^{{\text{OH}}}/{A}_{L}\) for \(c\) definitions using \({{\text{CH}}}_{4}, {{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fractions for different initial values of \({u}^{\prime}/{S}_{L}\) for both LD and HD (1st–2nd row)

Full size image

It can be seen from Fig. 3 that \(S\) assumes a value greater than one for both LD and HD cases and all definitions of \(c\) for both turbulence intensities considered here. Figure 3 further shows that \(S\) defined in terms of \({{\text{CO}}}_{2}\) mass fraction-based reaction progress variable assumes the highest value among all the different choices of \(c\). By contrast, \(\Omega\) based on \({{\text{CO}}}_{2}\) mass fraction-based reaction progress variable assumes the smallest value among all the different choices of \(c\). This trend is stronger for the HD case than in the LD case. The \(S\) values of \({{\text{CH}}}_{4}\) and \({{\text{H}}}_{2}{\text{O}}\) based reaction progress variables remain comparable for both LD and HD cases but \(S\) values of \({{\text{O}}}_{2}\) mass fraction-based reaction progress variable remain greater than those in case of \({{\text{CH}}}_{4}\) and \({{\text{H}}}_{2}{\text{O}}\) based reaction progress variables. The main reaction affecting the production of \({{\text{CO}}}_{2}\) is \({\text{CO}}+{\text{OH}}\leftrightarrow {{\text{CO}}}_{2}+{\text{H}}\). In MILD combustion, there is a significant amount of dilution, which includes \({{\text{CO}}}_{2}\), resulting in high \({{\text{CO}}}_{2}\) concentrations. This, in turn, results in a reduction in the forward reaction of \({\text{CO}}+{\text{OH}}\leftrightarrow {{\text{CO}}}_{2}+{\text{H}}\) and the backward reaction of \({\text{CO}}+{\text{OH}}\leftrightarrow {{\text{CO}}}_{2}+{\text{H}}\) is favoured. Thus, the net production rate of \({{\text{CO}}}_{2}\) and consequently, the reaction rate based on \({{\text{CO}}}_{2}\) is significantly reduced compared to other definitions. The reduced reaction rate of the reaction progress variable based on \({{\text{CO}}}_{2}\) mass fraction compared to other definitions was also observed in laminar premixed flames with high strain rates (Coriton et al. 2010) and high \(Ka\) \({{\text{CH}}}_{4}\)/air premixed jet flames in regions where the flame is affected by the pilot (Wang et al. 2017). As the \({{\text{CO}}}_{2}\) concentration remains higher in HD cases than the LD cases (see Table 1), the forward reaction of \({\text{CO}}+{\text{OH}}\leftrightarrow {{\text{CO}}}_{2}+{\text{H}}\) is further reduced resulting in a lower net production rate of \({{\text{CO}}}_{2}\) and consequently smaller values of \(\Omega\) based on \({{\text{CO}}}_{2}\) mass fraction are obtained for the HD cases.

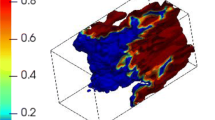
The magnitude of the reaction progress variable gradient (\(|\nabla c|\)) based on \({{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fractions conditioned upon \(|\nabla c|\) based on \({{\text{CH}}}_{4}\) mass fraction is exemplarily shown for LD and HD cases at \({u}^{\prime}/{S}_{L}=4.0\) and 8.0 in Fig. 4. It can be seen from Fig. 4 that \(|\nabla c|\) based on \({{\text{CO}}}_{2}\) mass fraction assumes non-negligible values at small values of \(|\nabla c|\) based on \({{\text{CH}}}_{4}\) mass fraction, which can further be confirmed from Fig. 5 where the \(|\nabla c|\) fields based on \({{\text{CH}}}_{4}\) and \({{\text{CO}}}_{2}\) mass fractions for the LD and HD cases are exemplarily shown. It can be seen from Fig. 5 that \(|\nabla c|\) for \(c\) based on \({{\text{CO}}}_{2}\) mass fraction is more distributed throughout the domain compared to the \(|\nabla c|\) for \(c\) based on \({{\text{CH}}}_{4}\) mass fraction. This suggests that the non-negligible values of \(|\nabla c|\) in the case of \(c\) based on \({{\text{CO}}}_{2}\) mass fraction occupy a significantly larger volume of the domain than the volume over which non-zero values of \(|\nabla c|\) for \(c\) based on \({{\text{CH}}}_{4}\) mass fraction are obtained. The same qualitative behaviour is observed for the HD cases irrespective of \({u}^{\prime}/{S}_{L}\). This, in turn, results in higher \(S\) values for the \(c\) definition based on \({{\text{CO}}}_{2}\) compared to other definitions for both LD and HD cases. Furthermore, it can be seen from Fig. 3 that \(\Omega\) and \(S\) are not significantly affected by changing the turbulence intensity within the range tested in this work for both LD and HD cases suggesting that \(\Omega\) and \(S\) values are predominantly affected by the level of dilution. It can also be seen from Fig. 3 that \({S}^{{\text{OH}}}\) overpredicts the \(S\) values compared to those calculated from \(|\nabla {c}_{{\text{CH}}4}|\) (i.e. using the reaction progress variable definition based on \({{\text{CH}}}_{4}\) mass fraction) for the LD case, especially for \({u}^{\prime}/{S}_{L}=8.0\), whereas it underpredicts the \(S\) values in comparison to \({S}_{{\text{CH}}4}\) for the HD case. Estimation of the flame surface area based on the sharpened \({S}^{{\text{OH}}}\) isosurfaces gives rise to about 32% and 47% maximum deviation in comparison to that obtained based on \(|\nabla {c}|_{{\text{CH}}4}\) for LD and HD cases, respectively. This is consistent with previous findings in the broken-reaction zone regime (Klein et al. 2020).

Fig. 4
figure 4

Profiles of the mean values of \(\left|\nabla c\right|\times {\delta }_{th}\) for \({{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fraction based \(c\) definitions conditioned upon \(|\nabla c|\times {\delta }_{th}\) for \({{\text{CH}}}_{4}\) mass fraction based \(c\) definition for both LD (left) and HD (right) cases at \({u}^{\prime}/{S}_{L}\)=4.0 (top row) and \({u}^{\prime}/{S}_{L}\)=8.0 (bottom row)

Full size image
Fig. 5
figure 5

Instantaneous fields of \(\left|\nabla c\right|\times {\delta }_{th}\) based on \({{\text{CH}}}_{4}\) (left) and \({{\text{CO}}}_{2}\) (right) at 2.5 flowthrough time for the lower dilution (LD) case at \({u}^{\prime}/{S}_{L}\) = 4.0 (top row) and 8.0 (bottom row)

Full size image

Figure 6 shows the values of \({T}_{I}=\Omega /S\) and \({T}_{I}^{{\text{OH}}}=\Omega /{S}^{{\text{OH}}}\) for \(c\) definitions based on \({{\text{CH}}}_{4}, {{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fractions for both LD and HD cases with initial \({u}^{\prime}/{S}_{L}=4.0\) and 8.0. A unity value of \({T}_{I}\) and \({T}_{I}^{{\text{OH}}}\) indicates the validity of Damköhler’s first hypothesis (i.e., Eq. 1). It is observed from Fig. 6 that \({T}_{I}\) remains of the order of unity for both LD and HD cases for \({{\text{CH}}}_{4}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fraction-based reaction progress variables. However, \({T}_{I}\) assumes values significantly smaller than one for \({{\text{O}}}_{2}\) and \({{\text{CO}}}_{2}\) mass fraction-based reaction progress variables. The changes in turbulence intensity do not seem to affect \({T}_{I}\) for both LD and HD conditions. Moreover, \({T}_{I}\) remains smaller in the HD cases for all \(c\) definitions compared to the LD cases. It can be seen from Fig. 6 that 6% reduction in \({T}_{I}\) for the HD case is obtained in comparison to the LD case for the \(c\) definition based on \({{\text{CH}}}_{4}\) mass fraction. By contrast, there are about 30%, 58% and 15% reduction in \({T}_{I}\) for the HD cases in comparison to the corresponding LD cases for \(c\) definitions based on \({{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fractions, respectively. This suggests that the \({{\text{CH}}}_{4}\) based definition of \(c\) is the least sensitive to dilution level compared to other definitions.

Fig. 6
figure 6

Variations of \({T}_{I}=\Omega /S\) (1st column) and \({T}_{I}^{{\text{OH}}}=\Omega /{S}^{{\text{OH}}}\) (2nd column) for \({{\text{CH}}}_{4}, {{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fraction based \(c\) definitions for different initial values of \({u}^{\prime}/{S}_{L}\) for LD and HD (1st–2nd row)

Full size image

The present analysis shows that the values of \({T}_{I}\) are found to be less than unity (with \({S}_{\alpha }\) calculated from \(\left|\nabla {c}\right|_{\alpha }\)) for reaction progress variables based on \({{\text{O}}}_{2}\) and \({{\text{CO}}}_{2}\) mass fractions for which Lewis numbers are greater than unity (i.e. \(L{e}_{{\text{O}}2}=1.10\) and \(L{e}_{{\text{CO}}2}=1.39\)). The Lewis numbers of \({{\text{CH}}}_{4}\) and \({{\text{H}}}_{2}{\text{O}}\) are close to unity and the current findings show that \({T}_{I}\) is close to unity for the reaction progress variable based on \({{\text{CH}}}_{4}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fractions. This is consistent with previous simple chemistry DNS results for conventional premixed flames where \({T}_{I}\approx 1.0\) was obtained when the Lewis number of reaction progress variable is unity (i.e. \(Le=1.0\)), and \({T}_{I}\) was less than unity (i.e. \({T}_{I}<1.0\)) for Lewis number of reaction progress variable greater than unity (i.e. \(Le>1\)) (Chakraborty and Cant 2005, 2011).

It is important to note that the differential diffusion effects induced by non-unity Lewis number affect both chemical reaction and molecular diffusion rates. The reaction rate is indeed different for different species and the differences in the reaction zone thickness also affect the sharpness of the reaction progress variable gradient. However, Awad et al. (2021) demonstrated that the reaction effects in MILD combustion are markedly weaker than those in conventional premixed combustion, but remain important, nonetheless. Moreover, it is worth noting that even in the context of single-step chemistry, an increase in Lewis number gives rise to a drop in the magnitude of the reactive scalar gradient, which in turn affects the value of \({A}_{T}\) (Chakraborty and Cant 2005; Chakraborty and Klein 2008). Thus, the effects of Lewis number play an important role, in addition to the chemical effects, in the observed behaviour. Interested readers are referred to Awad et al. (2021) for the discussion of the relative roles of reaction and diffusion on the evolution of \(|\nabla c|\) in MILD combustion and its contrast with respect to conventional premixed flame cases.

Moreover, \({T}_{I}<1.0\) was also reported in \({{\text{H}}}_{2}\)-air premixed flames at an equivalence ratio of 0.7 (for which \({{\text{H}}}_{2}\)-air mixture is nominally thermo-diffusively neutral) using multi-step chemistry DNS in the broken reaction zone regime (Klein et al. 2020). Since the distributed nature of the reaction zone increases with dilution (Minamoto et al. 2013, 2014a, 2014b), the decreasing values of \({T}_{I}\) with increasing dilution levels (shown in Fig. 6) are qualitatively consistent with previous findings for conventional premixed flames within the broken reaction zones regime (Klein et al. 2020).

The findings from Fig. 6 indicate that DH1 is valid in an order of magnitude sense in MILD combustion provided that the species based on which the reaction progress variable (\(c\)) is defined has a Lewis number close to unity. This is despite DH1 not being originally proposed for MILD combustion (Damköhler 1940, 1947). However, the level of validity of DH1, even in the order of magnitude sense and for reaction progress variable definitions with Lewis number close to unity, deteriorates with increasing dilution level.

The variation of \({T}_{I}^{{\text{OH}}}\) with different \(c\) definitions can be explained by the variation of \(\Omega\) with different \(c\) definitions because it is divided by identical flame surface area \({S}^{{\text{OH}}}\). The values of \({T}_{I}\) and \({T}_{I}^{{\text{OH}}}\) are comparable for the LD case for \({u}^{\prime}/{S}_{L}=4.0\) but \({T}_{I}^{{\text{OH}}}\) remains smaller than \({T}_{I}\) for the LD case at \({u}^{\prime}/{S}_{L}=8.0\). By contrast, \({T}_{I}^{{\text{OH}}}\)>\({T}_{I}\) is obtained for all the HD cases but the qualitative behaviours of \({T}_{I}\) and \({T}_{I}^{{\text{OH}}}\) for different \(c\) definitions remain identical.

It is important to note that the experimental analyses by Yuan and Gülder (2010), Wang et al. (2019) and Driscoll et al. (2020), which have been carried out for conventional turbulent premixed flames, reported \({T}_{I}\) to be much greater than unity (~ 5–7). This contrasts with the current findings in the case of MILD combustion where \({T}_{I}\) values for reaction progress variable definitions based on \({{\text{O}}}_{2}\) and \({{\text{CO}}}_{2}\) mass fractions remain smaller than unity. It was demonstrated by Chakraborty et al. (2019) that the ratio \({T}_{I}\) is expected to be equal to 1.0 under the assumption of unity Lewis number for statistically planar flames but this ratio can assume a value greater than unity for flames which are concavely curved towards the reactants in a mean sense (e.g., Bunsen burner premixed flames). It was further demonstrated by Ozel-Erol et al. (2021) that this ratio can be smaller than 1.0 even under unity Lewis number conditions for flames which are convex towards the reactants in a mean sense (e.g., spherically expanding premixed flame kernels). The ratio \({T}_{I}\) increases significantly with decreasing characteristic Lewis number, and \({T}_{I}\) assumes values greater (smaller) than unity for characteristic Lewis numbers smaller (greater) than unity (Chakraborty and Cant 2005, 2011; Ozel-Erol et al. 2021; Mohan et al. 2023). It is worth noting that a recent detailed chemistry-based analysis for stoichiometric and fuel-lean statistically planar methane-air premixed flames by Awad et al. (2021) reported \({T}_{I}\) values which are slightly smaller than 1.0 for reaction progress variables based on \({{{\text{CH}}}_{4, }{\text{O}}}_{2},{{\text{H}}}_{2}{\text{O}}\) and \({{\text{CO}}}_{2}\) mass fractions, where differential diffusion due to non-unity Lewis number plays a key role.

3.2 Applicability of DH2 for Homogeneous Mixture MILD Combustion

The assessment of the applicability of DH2 requires the evaluation of the turbulent eddy diffusivity \({D}_{t}\). According to the gradient hypothesis, the turbulent scalar flux \(\widetilde{{u}_{1}^{{\prime}{\prime}}{c}^{{\prime}{\prime}}}\) is often modelled as (Veynante et al. 1997):

$$\widetilde{{u}_{i}^{\prime \prime}{c}^{\prime \prime}}= -{D}_{t} (\partial \widetilde{c}/\partial {x}_{i})$$
(5)

where \(\overline{q }\), \(\widetilde{q}=\overline{\rho q }/\overline{\rho }\) and \({q}^{{\prime}{\prime}}=q-\widetilde{q}\) are the Reynolds averaged, Favre-averaged and Favre fluctuation of a general quantity \(q\), respectively. In this analysis, the quantities are time averaged between 1.5 and 2.5 throughpass times following the procedure used previously by Minamoto et al. (2013, 2014a, b). The gradient hypothesis remains valid when the effects of turbulent velocity fluctuations dominate over the effects of flame normal acceleration due to thermal expansion (Veynante et al. 1997). Awad et al. (2021) demonstrated that the magnitude of dilatation rate \(\nabla .\overrightarrow{u}\) arising from thermal expansion remains negligible compared to turbulent straining due to the small change in density under MILD combustion conditions. Veynante et al. (1997) argued that the gradient hypothesis is obtained when the Bray number \({N}_{B}\propto \tau {S}_{L}/{u}^{{\prime}}\) is smaller than unity where \(\tau ={\rho }_{u}/{\rho }_{b}-1\) with \({\rho }_{u}\) and \({\rho }_{b}\) being the unburned and burned gas densities, respectively. In MILD combustion, the gas density does not change significantly, due to the negligible temperature rise, and thus \(\tau\) and \({N}_{B}\) remain small indicating a gradient type of transport. In the current cases, \(\tau\) amounts to 0.124 and 0.13 (0.068 and 0.07) and \({N}_{B}\) amounts to 0.031 and 0.016 (0.017 and \({8.7\times 10}^{-3}\)) for the LD (HD) cases with initial \({u}^{{\prime}}/{S}_{L}=4.0\) and 8.0, respectively. For a gradient transport, \(\widetilde{{u}_{1}^{{\prime}{\prime}}{c}^{{\prime}{\prime}}}\times (\partial \widetilde{c}/\partial {x}_{1})\) assumes negative values (i.e. \(-{D}_{t} (\partial \widetilde{c}/\partial {x}_{1}{)}^{2}\)). It can indeed be seen from Fig. 7a that negative values of \(\widetilde{{u}_{1}^{{\prime}{\prime}}{c}^{{\prime}{\prime}}}\times (\partial \widetilde{c}/\partial {x}_{1})\) are obtained throughout the flame brush for all cases considered here. Accordingly, \({D}_{t}\) can be estimated using Eq. 5 (i.e., \({D}_{t}=-\widetilde{{u}_{1}^{{\prime}{\prime}}{c}^{{\prime}{\prime}}}/ (\partial \widetilde{c}/\partial {x}_{1})\)). The variation of \({D}_{t}/{D}_{0}\) (where \({D}_{0}\) is the unburned gas diffusivity) with \(\tilde{c}\) for all cases are shown in Fig. 7b, which shows \({D}_{t}\) varies within the flame brush and its magnitude increases with increasing \({u}^{\prime}/{S}_{L}\).

Fig. 7
figure 7

Variations of (a) \(\widetilde{{u}_{1}^{{\prime}{\prime}}{c}^{{\prime}{\prime}}}(\partial \widetilde{c}/\partial {x}_{1})\times {\delta }_{th}/{S}_{L}\) and (b) \({D}_{t}/{D}_{0}\) based on Eq. 5 (black) and Eq. 6 (red) with \(\tilde{c}\) for all cases considered here

Full size image

In the context of RANS, \({D}_{t}\) is often modelled as (Pope 2000):

$${D}_{t}={\nu }_{t}/S{c}_{t}={C}_{\mu } {\widetilde{k}}^{2}/(S{c}_{t}\widetilde{\varepsilon }),$$
(6)

where \({\nu }_{t}\) is the kinematic eddy viscosity, \(S{c}_{t}\) is the turbulent Schmidt number, and \({C}_{\mu }=0.09\) is a model parameter. The turbulent Schmidt number remains of the order of unity and \(S{c}_{t}=1.0\) is taken for the following analysis in this paper. Here, \(\widetilde{k}=\overline{\rho {u }_{i}^{{\prime}{\prime}}{u}_{i}^{{\prime}{\prime}}}/2\overline{\rho }\) and \(\widetilde{\varepsilon }=\overline{\mu (\partial {u}_{i}^{\prime \prime}/\partial {x}_{j})(\partial {u}_{i}^{\prime \prime}/\partial {x}_{j})}/\overline{\rho }\) are the Favre-averaged turbulent kinetic energy and its dissipation rate, respectively. The values of \({D}_{t}\) predicted using Eq. 6 are shown in Fig. 7b. It can be seen from Fig. 7b that the predictions of Eq. 6 do not capture the qualitative behaviour of \({D}_{t}=-\widetilde{{u}_{1}^{\prime \prime}{c}^{\prime \prime}}/ (\partial \widetilde{c}/\partial {x}_{1})\) extracted from DNS data as well as underpredicting the levels of \({D}_{t}\).

The prediction of \({{T}_{II}=(S}_{T}/{S}_{L})/\sqrt{\left[-\overline{\rho {u }_{1}^{\prime \prime}{c}^{\prime \prime}}/\left\{\overline{\rho }D\left(\partial \widetilde{c}/\partial {x}_{1}\right)\right\}\right]}\) and \({T}_{II}^{M}=({S}_{T}/{S}_{L})/\sqrt{{(C}_{\mu }Sc/S{c}_{t})\left[\overline{\rho } {\widetilde{k}}^{2}/\mu \widetilde{\varepsilon }\right]}\) (with \({D}_{t}\) evaluated based on Eq. 6) are shown in Fig. 8 for both LD and HD cases at initial \({u}^{{\prime}}/{S}_{L}\) = 4.0 and 8.0 and for \(c\) definitions based on \({{\text{CH}}}_{4}, {{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fractions. For the results shown in Fig. 8, the values of \({D}_{t}\) and \(D\) conditionally averaged at \(\widetilde{c}=0.5\) are used, but the qualitative behaviours shown in Fig. 8 do not change significantly if conditional averaging is done at different values of \(\widetilde{c}\) (not shown for brevity). It can be seen in Fig. 8 that \({T}_{II}\) and \({T}_{II}^{M}\) remain of the order of unity for the LD cases, but \({T}_{II}\) assumes the smallest value for \({{\text{CO}}}_{2}\) mass fraction-based reaction progress variable. Both \({T}_{II}\) and \({T}_{II}^{M}\) deviate significantly from unity for the \({{\text{O}}}_{2}\) and \({{\text{CO}}}_{2}\) mass fraction-based reaction progress variables in the HD cases. Even for the reaction progress variable definitions based on \({{\text{CH}}}_{4}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fractions, \({T}_{II}\) and \({T}_{II}^{M}\) assume values greater than unity for the HD case with initial \({u}^{{\prime}}/{S}_{L}\) = 4.0, but the values of \({T}_{II}\) and \({T}_{II}^{M}\) remain closer to unity for these definitions of \(c\) for the HD case with initial \({u}^{{\prime}}/{S}_{L}\) = 8.0.

Fig. 8
figure 8

Variations of \({{T}_{II}=(S}_{T}/{S}_{L})/\sqrt{{\left[-\overline{\rho {u }_{1}^{{\prime}{\prime}}{c}^{{\prime}{\prime}}}/\left\{\overline{\rho }D\left(\partial \widetilde{c}/\partial {x}_{1}\right)\right\}\right]}_{\widetilde{c}=0.5}}\) (1st column) \({T}_{II}^{M}=({S}_{T}/{S}_{L})/\sqrt{{(C}_{\mu }Sc/S{c}_{t}){\left[\overline{\rho } {\widetilde{k}}^{2}/\mu \widetilde{\varepsilon }\right]}_{\widetilde{c}=0.5}}\) (2nd column) for \({{\text{CH}}}_{4}, {{\text{O}}}_{2},\mathrm{ C}{{\text{O}}}_{2}\) and \({{\text{H}}}_{2}{\text{O}}\) mass fraction based \(c\) definitions for different initial values of \({u}^{\prime}/{S}_{L}\) for LD and HD (1st–2nd row) cases

Full size image

In the present analysis, the extent of the validity of Damköhler’s hypotheses has been quantified in terms of \({T}_{I}=\Omega /S\) and \({{T}_{II}=(S}_{T}/{S}_{L})/\sqrt{{\left[-\overline{\rho {u }_{1}^{{\prime}{\prime}}{c}^{{\prime}{\prime}}}/\left\{\overline{\rho }D\left(\partial \widetilde{c}/\partial {x}_{1}\right)\right\}\right]}_{\widetilde{c}=0.5}}\), which are presented in Figs. 6 and 8, respectively. The findings from Figs. 6 and 8 reveal that DH1 and DH2 can be taken to hold in homogeneous mixture MILD combustion only in an order of magnitude sense for \({{\text{CH}}}_{4}\) mass fraction-based reaction progress variable, which has a Lewis number close to unity (i.e., \(Le{}_{{\text{CH}}4}=0.97\)). The present analysis is based on DNS data, which is computationally expensive, so only a limited number of simulations can be conducted. Therefore, it is not practical at this point to provide a quantitative conclusion regarding a functional relation between the extent of validity of the hypotheses and Lewis number based on the limited number of data points analysed in this study. However, this aspect can form the foundation for further analyses in the future.

4 Conclusions

The applicability of Damköhler’s first and second hypotheses for homogenous mixture (i.e. constant equivalence ratio) Moderate or Intense Low-Oxygen Dilution (MILD) combustion processes (with \({{\text{CH}}}_{4}\) as the fuel) has been assessed using three-dimensional Direct Numerical Simulations (DNS) with a skeletal chemical mechanism for methane-air combustion. The effects of turbulence intensity, dilution level (\({{\text{O}}}_{2}\) concentrations of 3.5% and 4.8% by volume) and the definition of the reaction progress variable on the applicability of Damköhler’s hypotheses in MILD combustion have also been investigated.

It is found that Damköhler’s first and second hypotheses are valid only in an order of magnitude sense in MILD combustion, and only for a reaction progress variable definition based on the mass fraction of a species which has a Lewis number close to unity (e.g., \({{\text{CH}}}_{4}\)). The deviation from Damköhler’s hypotheses increases when the Lewis number of the species, based on which the reaction progress variable is defined, deviates significantly from unity (e.g., \({{\text{CO}}}_{2}\)). Moreover, it has been found that the level of validity of Damköhler’s first and second hypotheses deteriorate with increasing dilution level, even if the progress variable has been defined based on a species with unity Lewis number. It is shown that the flame surface area calculation based on OH mole fraction-based information can lead to significant departures from Damköhler’s first hypothesis. Finally, it has been found that changing the turbulence intensity in the range considered here does not affect the applicability of Damköhler’s hypotheses in the considered MILD combustion cases.

Most existing methodologies for homogeneous mixture combustion implicitly assume the validity of at least one of Damköhler’s hypotheses (especially the first hypothesis). The current findings suggest that Damköhler’s first hypothesis works reasonably well when the reaction progress variable is defined based on a species with a Lewis number close to unity. This suggests that a reaction progress variable based on a species with a Lewis number close to unity is advantageous from the point of view of modelling turbulent MILD combustion. The validity of the current findings of the current analysis needs to be assessed for broader range of parameters involving turbulence intensity, O2 dilution and initial reactant temperature, which will form the basis of future investigations.