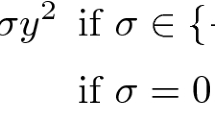Skip to main content
SpringerLink
Log in

Ellipses and polynomial-to-polynomial mapping of weighted Szegő projections

  • Published:
Analysis and Mathematical Physics Aims and scope Submit manuscript

Abstract

We take a look at weighted Szegő projections on ellipses and ellipsoids in light of some known results of real and complex potential theory. We show that on planar ellipses there is a weighted Szegő projection taking polynomials to polynomials without increasing degree.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Khavinson, D., Shapiro, H.: Dirichlet’s problem when the data is an entire function. Bull. Lond. Math. Soc. 24, 456–468 (1992)

    Article  MathSciNet  Google Scholar 

  2. Lundberg, E., Render, H.: The Khavinson–Shapiro conjecture and polynomial decompositions. J. Math. Anal. Appl. 376(2), 506–513 (2011)

    Article  MathSciNet  Google Scholar 

  3. Render, H.: Real Bargmann spaces, Fischer decompositions, and sets of uniqueness for polyharmonic functions. Duke Math. J. 142(2), 313–352 (2008)

    Article  MathSciNet  Google Scholar 

  4. Render, H.: A characterization of the Khavinson–Shapiro conjecture via Fischer operators. Potential Anal. 45, 539–543 (2016)

    Article  MathSciNet  Google Scholar 

  5. Shapiro, H.: An algebraic theorem of E. Fischer, and the holomorphic Goursat problem. Bull. Lond. Math. Soc. 21, 513–537 (1989)

    Article  MathSciNet  Google Scholar 

  6. Fischer, E.: Über die differentiationsprozesse der algebra. J. Reine Angew. Math. (Crelles J.) 148, 1–78 (1918)

    Google Scholar 

  7. Khavinson, D., Lundberg, E.: A tale of ellipsoids in potential theory. Not. Am. Math. Soc. 61(2), 148–156 (2014)

    Article  MathSciNet  Google Scholar 

  8. Legg, A.: The Khavinson–Shapiro conjecture and the Bergman projection in one and several complex variables. Comput. Methods Funct. Theory 16, 231–242 (2016)

    Article  MathSciNet  Google Scholar 

  9. Ligocka, E.: A characterization of ellipsoids and balls in \(C^N\). Proc. Am. Math. Soc. 110(1), 103–107 (1990)

    Google Scholar 

  10. Khavinson, D., Stylianopoulos, N.: Recurrence relations for orthogonal polynomials and algebraicity of solutions of the Dirichlet problem. In: Laptev, A. (ed.) Around the Research of Vladimir Maz’ya II: Partial Differential Equations, pp. 219–228. Springer, New York (2010)

    Chapter  Google Scholar 

  11. Baratchart, L., Saff, B., Stylianopoulos, N.: On finite-term recurrence relations for Bergman and Szegő polynomials. Comput. Methods Funct. Theory 12, 393–402 (2012)

    Article  MathSciNet  Google Scholar 

  12. Putinar, M., Stylianopoulos, N.: Finite-term relations for planar orthogonal polynomials. Complex Anal. Oper. Theory 1, 447–456 (2007)

    Article  MathSciNet  Google Scholar 

  13. Krantz, S.: Function Theory of Several Complex Variables, 2nd edn. AMS Chelsea Publishing, Providence (1992)

    Google Scholar 

  14. Bell, S.: The Cauchy Transform, Potential Theory and Conformal Mapping, 2nd edn. CRC Press, Boca Raton (2016)

    Google Scholar 

  15. Barrett, D., Bolt, M.: The Cauchy–Leray operator for convex domains. In: Krantz, S. (ed.) Handbook of Complex Analysis, Ch. 2, pp. 19–39. CRC Press, Boca Raton (2022)

    Chapter  Google Scholar 

  16. Bolt, M.: A geometric characterization: complex ellipsoids and the Bochner–Martinelli kernel. Illinois J. Math. 49(3), 811–826 (2005)

    Article  MathSciNet  Google Scholar 

  17. Bell, S., Gustafsson, B., Sylvan, Z.: Szegő coordinates, quadrature domains, and double quadrature domains. Comput. Methods Funct. Theory 11, 25–44 (2009)

    Article  Google Scholar 

  18. Gustafsson, B.: Application of half-order differentials on Riemann surfaces to quadrature identities for arc-length. J. d’Anal. Math. 49, 54–89 (1987)

    Article  MathSciNet  Google Scholar 

  19. Dong, R., Treuer, J., Zhang, Y.: Rigidity theorems by capacities and kernels. Int. Math. Res. Not. (2022). https://doi.org/10.1093/imrn/rnac290

    Article  Google Scholar 

Download references

Acknowledgements

I thank an anonymous referee for valuable comments that greatly improved the exposition.

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Purdue University Fort Wayne, Fort Wayne, 46805, IN, USA

    Alan R. Legg

Authors
  1. Alan R. Legg
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Manuscript prepared entirely by the sole author A.R.L.

Corresponding author

Correspondence to Alan R. Legg.

Ethics declarations

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Legg, A.R. Ellipses and polynomial-to-polynomial mapping of weighted Szegő projections. Anal.Math.Phys. 14, 5 (2024). https://doi.org/10.1007/s13324-023-00864-0

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s13324-023-00864-0

Keywords

Mathematics Subject Classification

Search

Navigation