CompTrails: comparing hypotheses across behavioral networks

Abstract

The term Behavioral Networks describes networks that contain relational information on human behavior. This ranges from social networks that contain friendships or cooperations between individuals, to navigational networks that contain geographical or web navigation, and many more. Understanding the forces driving behavior within these networks can be beneficial to improving the underlying network, for example, by generating new hyperlinks on websites, or by proposing new connections and friends on social networks. Previous approaches considered different hypotheses on a single network and evaluated which hypothesis fits best. These hypotheses can represent human intuition and expert opinions or be based on previous insights. In this work, we extend these approaches to enable the comparison of a single hypothesis between multiple networks. We unveil several issues of naive approaches that potentially impact comparisons and lead to undesired results. Based on these findings, we propose a framework with five flexible components that allow addressing specific analysis goals tailored to the application scenario. We show the benefits and limits of our approach by applying it to synthetic data and several real-world datasets, including web navigation, bibliometric navigation, and geographic navigation. Our work supports practitioners and researchers with the aim of understanding similarities and differences in human behavior between environments.

1 Introduction

Social data is often available in the form of attributed behavioral networks representing, for example, friendships in social networks, physical contacts, or collaborations between authors. Additionally, sequential behavioral data, e.g., on human navigation, is often modeled as networks by focusing on direct transitions between individual states in the spirit of a first-order Markov-Chain model. Analyzing and understanding the processes underlying such datasets can provide crucial insights for scientific, economic, and societal questions and issues. To couple the analysis of complex processes with existing theories and knowledge in the context of human behavior it has been proposed to investigate and compare hypotheses (Singer et al. 2015; Noboa et al. 2017).

Hypotheses represent formalized beliefs in aggregated human behavior that can arise from previous studies, (social) theory, or intuition; for example, in web navigation, a hypothesis can capture the general assumption that users navigate to thematically more focused pages in the network periphery rather than pages in the network center (Dimitrov et al. 2017). Existing work allows to rank several such hypotheses on the same underlying network using the Bayesian approach HypTrails (Singer et al. 2015). However, with existing methods, it is not directly possible to compare the same hypothesis across different networks.

Fig. 1

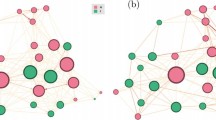
Hypothesis comparison across behavioral networks. A first approach towards comparing an abstract hypothesis H on different behavioral networks $g_o$ and $g_p$ given as multigraphs (e.g., each edge represents a single co-authored work of two researchers). Metadata is given in the form of node attributes (see tables on the left), e.g., the type of scientist [computer scientists (CS) and biologists (B)] or geographic location (Geo) of their workplace (e.g., Germany, California, etc.). Hypotheses represent an explanation of behavior, i.e., they attempt to explain the edge distribution. For example, hypothesis H assumes that only researchers in the same field collaborate. An instantiation for each network can be derived ($h_o$ and $h_p$), mathematically represented as edge-occurrence probability matrices. CompTrails compares the adjacency matrices of each network with its respective hypothesis instance to produce a comparable score indicating how well the hypothesis matches the actual data in each network

The general goal of this work is to narrow this gap by proposing a novel framework called CompTrails that takes several steps towards formally comparing hypotheses across several behavioral networks. The idea is to score and rank networks according to how well the respective hypothesis is in line with (and can explain) the behavior captured in the network. We illustrate our approach in Fig. 1. Figure 1a consists of two behavioral networks that represent co-authorship. Both networks $g_o$ (representing Europe) and $g_p$ (representing USA) have two types of actors, biologists (B) or computer scientists (CS), but they represent data from different origins, for example, researchers from different continents such as Europe and USA. Nodes on the graph represent researchers, and the number of edges between researchers represents the frequency with which these researchers cooperated in this network. A potential hypothesis H for these behavioral networks could be that collaboration exists only between researchers in the same topical domain. This idea represents an abstract hypothesis that will be instantiated for each network, resulting in hypothesis instances $h_p$ and $h_o$ in Fig. 1a. Using the CompTrails framework, we can then compute a score for a given network and its respective hypothesis instance. The main goal is to achieve scores that are comparable across networks.

In this paper, we discuss the following factors that can lead to incomparable scores and make the comparison of cross-network hypotheses challenging: (1) Different amount of nodes in each (graph) data, (2) different amount of (multi-)edges, (3) different distributions of edges per node, i.e., normally distributed and skewed distribution. We propose a framework with five steps (see Fig. 1b) that aims to mitigate these factors. Each component addresses one or more of the above factors and helps to approach comparability of hypotheses across differently structured networks. We illustrate and discuss the capabilities and limitations of CompTrails based on several synthetic and different real-world datasets. The code is available under https://github.com/LSX-UniWue/CompTrails.

2 Background and related work

Next, we provide the necessary background information on behavioral networks and hypotheses in behavioral networks. We then formally define metrics that can be used to evaluate the performance of a given hypothesis in explaining the underlying data. Finally, we review previous work on data-driven navigational analysis and hypothesis comparison in behavioral networks.

2.1 Behavioral networks

A behavioral network is a graph-based model that captures human behavior as relations or transitions between entities/nodes that can provide insight into the decision-making processes of individuals. Behavioral networks can be represented as directed or undirected multigraphs, that is, networks that allow multiple edges between nodes. These could also be represented as integer weights at the edges. In the following, we focus on directed multigraphs. However, the concept is easily transferred to the undirected case by replacing each undirected edge with two directed edges in opposite directions. For example, a network that captures web navigation is represented as a directed multigraph, while a coauthorship network is represented as an undirected multigraph.

Furthermore, sequential behavioral data (e.g., Wikipedia (Dimitrov et al. 2019; Scaria et al. 2014) or geospatial traces (Becker et al. 2015)) can be transformed into a multigraph representation by defining a set of nodes (e.g., Wikipedia pages or geographic locations) and representing direct transitions between nodes as edges. Similarly, bibliometric networks (Noboa et al. 2017) can be represented as multigraphs, where nodes represent authors, and an edge between nodes represents coauthorship in a peer-reviewed publication. By representing behavioral networks as multigraphs, we can apply the methods discussed in this paper to analyze and compare multiple datasets.

Formally, a multigraph g consists of a set of nodes S and edges E, where multiple edges are allowed between two given nodes. This graph can be represented by an adjacency matrix $t \in {\mathbb {Z}}^{\Vert S\Vert \times \Vert S\Vert }$ with $\Vert S\Vert$ denoting the number of nodes. This matrix represents the edge counts between all nodes. Furthermore, metadata for nodes is often available in these networks. For example, given a bibliometric network, this may include research orientation or affiliation of authors (network nodes). We will use such metadata to formalize abstract hypotheses representing explanations for behavior. In the context of scientific collaboration, an abstract hypothesis could be: “Collaboration within the same affiliation is more likely than between affiliations”. We will refer to such abstract hypotheses as H.

For the intuition captured in H, we can create a specific hypothesis instances for each network g. Such hypothesis instances are represented as an edge-occurrence probability matrix h. An entry $h^{i,j}$ in h defines the probability that an edge of node i ends at a specific node j in the network. Thus, the dimensionality of any hypothesis instantiation for a network is identical to the network adjacency matrix, and each row of the hypothesis instance h sums up to 1. To construct hypothesis instances h, we use metadata analogously for all networks to be compared.

2.2 Hypothesis comparison

Given an observed network as a multigraph g and a hypothesis instantiation h for this multigraph, we can use different metrics to score how well they align. A well-known potential approach is entropy-based, namely the Jensen-Shannon (JS) divergence. It is an information-theoretic measure that quantifies the difference between the probability distributions defined by the data and the hypothesis. It uses the Kullback-Leibler divergence: $D_{KL}({\hat{t}} \mid h) = \frac{1}{\mid S \mid }\sum _{s \in S} {\hat{t}}_s log \left( \frac{{\hat{t}}_s}{h_s} \right)$ with ${\hat{t}}$ being the row-wise normalized adjacency matrix of one network, and h representing the respective hypothesis instance matrix. JS divergence is the symmetric counterpart of Kullback-Leibler divergence and calculates $D_{KL}$ from a mean matrix $m = \frac{1}{2}({\hat{t}} + h)$ to both original matrices. $D_{JS}({\hat{t}} \mid h) = \frac{1}{2} D_{KL}({\hat{t}} \mid m) + \frac{1}{2} D_{KL}(h \mid m)$. As an overall score for the network, we calculate the mean row-wise JS divergence. The downside of entropy-based approaches is the loss of information about the actual edge counts, since it reduces each row of the adjacency matrix to probabilities.

An alternative approach, HypTrails (Singer et al. 2015), uses Bayesian inference and the sensitivity of the likelihood with respect to the data given different priors defined by hypothesis instances. The approach then uses the resulting marginal likelihood for each prior and creates a ranking of hypotheses. Furthermore, the degree of belief in a hypothesis can be taken into account by varying a so-called concentration factor k. Intuitively, this factor represents the belief in the hypothesis, that is, as k increases, the hypothesis must be very accurate to result in high scores. Mathematically, the evidence is calculated as follows:

$$\begin{aligned} P(t \mid \alpha ) = \prod _i \frac{\Gamma ( \sum _j \alpha _{i,j} )}{\prod _j \Gamma ( \alpha _{i,j} ) } \frac{\prod _j \Gamma ( \alpha _{i,j} + t_{i,j} )}{\Gamma ( \sum _j ( \alpha _{i,j} + t_{i,j}) ) }, \end{aligned}$$

where t represent the actual transitions in our network and $\alpha$ are Dirichlet parameters that incorporate the prior h. The concentration factor k directly influences the $\alpha$ counts (Dirichlet parameters), where an increased concentration factor leads to a stronger belief in the hypothesis. For further details on this approach, we refer the reader to Singer et al. (2015).

These evidence and divergence scores can be used to compare different hypotheses for a dataset. As we will show in Sect. 4, by default, it is not possible to use any of these metrics to compare one hypothesis with multiple heterogeneous datasets with different amounts and distributions of edges and nodes.

2.3 Related work

This section will first describe existing techniques for data-driven behavioral analysis and its different settings. Then, we will cover related work with respect to hypothesis testing on networks and explain the differences with respect to our framework.

Hypotheses-driven behavioral analysis: A fundamental work to analyze human behavior, more specifically navigation behavior, and explain their driving forces, is HypTrails (Singer et al. 2015). It introduces a Bayesian inference approach to compare different hypotheses about human navigation on sequence-structured data. Based on this method, different settings have already been evaluated, for example, geographic navigation (Becker et al. 2015), tag navigation (Dimitrov et al. 2018; Niebler et al. 2016), web navigation (Dimitrov et al. 2019) and many more (Becker et al. 2015). Further related work has extended the method, for example, by allowing it to scale to large data (Becker et al. 2016), to allow the analysis of any kind of graph-structured data instead of sequential data (Noboa et al. 2017) or by allowing the analysis of different groups of users within a single dataset (Becker et al. 2017). None of these methods is suitable for comparing a hypothesis between networks.

Network similarity testing: This research domain is not restricted to the handling of navigational data, but provides methods for testing any kind of hypothesis on network structures. Moreno and Neville (2013) propose an algorithm using mixed Kronecker product graph models to determine whether two observed networks are significantly different. Other previous work uses different regression methods, such as QAP (Hubert and Schultz 1976) or the quadratic regression assignment procedure (Krackhardt 1988). They permute nodes while keeping the network intact to test when the networks are significantly different. An alternative approach to hypothesis comparison in networks based on a generalization of classic configuration models has been presented (Casiraghi et al. 2016). Furthermore, general network measures such as centrality, graph distance, and number of triangles could be used to characterize and compare graph topologies (Wills and Meyer 2020). However, all of these approaches are used to compare two network instances and do not allow us to compare the same abstract hypothesis H between different networks, especially with different sizes and distributions. Again, none of these methods allows for comparing a hypothesis across networks.

3 Comparing hypotheses across behavioral networks

Given a set of behavioral networks $G = \{g_1, \dots , g_{\mid G \mid }\}$, an abstract hypothesis H, and the respective instances of the hypothesis $H = \{h_1, \dots , h_{\mid H \mid }\}$ for each network, the question is, which behavioral network $g \in G$ is best explained by the hypothesis H. In the introductory example in Fig. 1a, $G = \{g_o, g_p\}$ represented co-authorship networks with researchers from Europe and the United States, respectively. Hypothesis H represents the notion that cooperation occurs exclusively between researchers in the same domain (CS/CS or B/B). The question is whether this exclusive collaboration will be more applicable to Europe or the US. To answer this question, for both networks $g_o$ and $g_p$, the respective hypothesis instances ($h_o$, $h_p$) are derived. Then a comparison score needs to be calculated for each network $g_i$ that quantifies its fit with the corresponding hypothesis instance $h_i$. These scores can then be compared across different networks. As we will show, applying commonly known metrics will not lead to comparable scores across networks (cf. Fig. 2). Therefore, we provide a novel computational framework.

General setting and abstract hypothesis. As introduced in Sect. 2.2, we consider two measures to quantify the fit between a network and a hypothesis instance: JS and the HypTrails metric. However, naively applying these metrics as a comparison score does not work: we demonstrate this with an example of three synthetic networks of different sizes with 10, 100, or 1000 nodes that could, e.g., represent three differently sized websites of two types of pages, where we investigate an abstract hypothesis H that represents the intuition that transitions occur mainly between pages of the same type.

Network generation. To create these networks, we start by generating an underlying link structure using the Barabasi–Albert model (Barabási and Albert 1999). Barabasi–Albert graphs are scale-free networks that are more connected in the center and less connected in the periphery. They grow incrementally by preferential attachment, where new nodes are more likely to connect to existing nodes with high degrees. This results in a power-law degree distribution, with a few highly connected nodes (hubs) and many low-degree nodes. The parameter defining the number of edges added per new node will be called m. For this synthetic experiment, we set $m_{10}=5$, $m_{100}=25$, and $m_{1000}=125$, which leads to the same density across the networks. Scale-free networks represent a typical structure for many behavioral networks, e.g. social networks or websites.

Navigation behavior. On these link structures, we simulate navigation behavior with a biased random walker with different factors driving navigation behavior depending on the size of the network. For networks $g_{10}$ and $g_{1000}$ the biased random walker uses fully random transitions given the graph structure, regardless of the type of website. For $g_{100}$, the random walker only travels between the same type of websites. For both network and hypothesis instances, we disregard self-loops. By construction, the network $g_{100}$ should best fit the hypothesis (transitions occur mainly between pages of the same type). In contrast, $g_{10}$ and $g_{1000}$ have a worse fit and should perform equally since they are generated by the same underlying process. The random walker starts 5 times from each node and creates a biased random walk of length 5.

Results for HypTrails. Figure 2a shows the results when HypTrails is applied, and we can observe that the hypothesis of the network $g_{10}$ (blue line) and $g_{100}$ (red line) has the highest evidence for all concentration factors k. However, we aim to produce similar scores for networks $g_{10}$ and $g_{1000}$, since they were created with the same generative process and only differ in size. Furthermore, the network $g_{100}$ should have the highest evidence, which is not the case. This is due to the node-wise product of probabilities to calculate the marginal likelihood. Therefore, larger networks lead to less evidence, even if the hypothesis by construction better explains the network. Additionally, a naive normalization of the evidence by node degree also does not lead to the desired results.

Results for JS divergence. When using the JS divergence as metric (see Fig. 2b), we can observe a similar behavior as for HypTrails. $g_{10}$ and $g_{100}$ have the lowest divergence and $g_{1000}$ has a higher divergence. Again, based on the construction process, we expect $g_{100}$ to have the lowest divergence. The JS divergence produces extreme values, if the incoming distribution is very skewed (that is, a value containing the majority of probability mass and all other values containing close to zero probability mass). Thus, for sparse networks such as $g_{1000}$, the divergence is higher than for less sparse networks such as $g_{10}$. Analogous to the previous example, this shows the need for adjustments that we incorporate in our CompTrails framework.

Influence factors on naive hypothesis comparison metrics. In general, previous examples show that a naive comparison of hypotheses across networks can be biased even if the network generation process is strictly controlled. In particular, in this paper, we establish three influence factors that can influence the metrics used. (1) a different number of nodes across networks (e.g., HypTrails), (2) a different number of edges, and (3) a different distribution of edges. Figure 2 shows the impact of the first factor. We show the impact of the other two factors in the Appendix. While these aspects cover important aspects of network variability, other factors may still influence the hypothesis comparison process (see Sect. 7 for a discussion).

Summary. To approach these sources of bias, we propose CompTrails. Figure 2c shows the result of applying specific steps of CompTrails. By doing so, $g_{100}$ has the lowest divergence and $g_{10}$ and $g_{1000}$ are very close to each other.

Fig. 2

Naive metrics versus CompTrails. Each panel compares the same abstract hypothesis H across three differently sized datasets with 10, 100 and 1000 nodes, respectively, based on a different comparison method. $g_{100}$ was created to be best explained by the hypotheses. Furthermore, Network $g_{10}$ and $g_{1000}$ are generated by the same process and should fit the hypothesis equally poorly. HypTrails fails to rank $g_{100}$ first (see Fig. 2a). At the same time, JS ranks the smaller network to have a better fit to the hypothesis (see Fig. 2b). CompTrails ranks the network $g_{100}$ correctly and illustrates that network $g_{10}$ and $g_{1000}$ perform similarly as illustrated by the overlapping standard error intervals (see Fig. 2c). We applied the components of GSF, NS with Snowball Sampling on the transitions, and ES

4 The CompTrails framework

The CompTrails framework (see Fig. 1b) facilitates the comparison of hypotheses across behavioral networks. It consists of five flexible components that we will introduce in this section: (1) Network abstraction (NA), (2) graph structure filtering (GSF), (3) node synchronization (NS), (4) edge synchronization (ES), and (5) evaluation metric flexibility. Each component is optional and allows different aspects of the analysis to be considered, each having specific effects on the analysis. The CompTrails procedure is summarized in Algorithm 1.

4.1 Network abstraction (NA)

Behavioral data is given on a fine-grained level represented by multi-edges between individual nodes in a network. However, behavioral hypotheses can be defined on different abstraction levels taking into account node categories rather than individual nodes. The idea of network abstraction (NA) is to take advantage of such abstraction levels and to collapse nodes of the same category into a single node. For example, in Fig. 1a, the nodes represent authors that can be categorized as computer scientists (CS) and biologists (B). Thus, for the abstract hypothesis H that only researchers within the same research domain (CS or B) cooperate, the edge occurrence and hypothesis instance matrices reduce to dimensions of $2 \times 2$. For example, the hypothesis instances reduce to ${\hat{h}}_o = {\hat{h}}_p = \big ({\begin{matrix} 1 &{} 0 \\ 0 &{} 1 \end{matrix}}\big )$.

NA is a powerful concept that can be applied to a wide range of hypotheses (cf. Sect. 6). Apart from the technical advantages outlined below, network abstraction influences hypothesis semantics. When instantiating the previously defined hypothesis H using network abstraction, the hypothesis instances model the cooperation probabilities between the actual categories of researchers and not between the individual researchers. However, when formulating H in a network of individual researchers, the hypothesis implicitly assumes that the probability of collaboration between a single researcher and any researcher of the same category is equal. Depending on the use case, one approach may be more appropriate than the other.

A significant technical advantage of NA lies in reducing the sparsity of the network by combining nodes and edges, resulting in more stable sampling procedures (cf. Sects. 4.3 and 4.4). Additionally, if the node categories in the compared networks are equivalent, network abstraction can render node sampling obsolete since nodes are already synchronized (cf. Sect. 4.3). In the previous example, this is the case (${\hat{h}}_o = {\hat{h}}_p$) since both networks exclusively contain the same two researcher categories (CS and B). A limitation of network abstraction is that it significantly reduces the level of detail for the defined hypotheses. In the previous example, nodes are collapsed into research domains, thus losing the ability to express collaboration characteristics between individual researchers. Consequently, combining hypotheses, e.g., using a domain-based and an individual component, becomes infeasible.

The choice to apply network abstraction can play an important role in the analysis process. In particular, it allows one to formulate hypotheses on different semantic levels. Overall, applying NA aims to achieve several objectives: (1) preserving the flexibility to express hypotheses effectively, (2) maximizing the accuracy of semantics, and (3) minimizing the occurrence of sparse edges.

4.2 Graph structure filtering (GSF)

For many behavioral networks, the set of edges that plausibly occur regularly are restricted. For example, when observing navigation behavior between websites, edges typically occur between sites that link to each other. Without considering this underlying graph structure, hypothesis instances assign significant probability masses to implausible edges. If the sparsity is too prominent, the results will be highly biased toward whether edges exist rather than their probability distribution. The idea of graph structure filtering (GSF) is to explicitly set the probabilities of non-plausible (or highly improbable) edges to zero in the hypothesis instances. Thus, under the assumption that plausible edges are similarly sparse across datasets, GSF can improve comparability.

In practice, there are two approaches to derive graph structures that can be used for GSF. The first is based on background information, such as the link structure between websites, cf. Dimitrov et al. (2017). Alternatively, in a data-driven approach, edge probabilities in a hypothesis instance can be set to zero if they have never been observed in the data. We will refer to the latter as the inferred graph structure.

Semantically, GSF enables us to focus on the probability distributions of existing or plausible edges. However, using unfiltered hypotheses allows us to place emphasis on whether edges exist, in contrast to emphasizing the distribution of existing edges. Finally, by neglecting irrelevant node connections, GSF can be a helpful step in comparing sparse behavioral networks.

4.3 Node synchronization (NS)

As illustrated in Fig. 1a, a hypothesis H can be applied to behavioral networks with different numbers of nodes. However, the example in Fig. 2 clearly shows that comparing networks with different numbers of nodes can heavily bias comparison metrics and produce potentially misleading results. To address this, CompTrails suggests a sampling-based node synchronization (NS) procedure.

Algorithm 1

Pseudo-code of sampling approach. The input to this algorithm is a set of graphs and their respective hypothesis instances. The return value is a list of scores.

For a given pair of network and hypothesis instances $(g_i, h_i)$, NS samples a fixed number of nodes $N_{nodes}$ (with replacement). Since the networks are very small, we set $N_{nodes}$ to the smallest number of nodes in all the compared networks (e.g., 4 in Fig. 1). For large networks, we suggest sampling a smaller number of nodes for computational efficiency. This results in a sampled subnetwork. Subsequently, edge counts from the data and edge probabilities from the hypothesis instance of the original network are projected onto this subnetwork. For example, if the 4 nodes [1, 2, 4, 6] are sampled from network $g_o$, after projection, the number of outgoing edges would be [5, 3, 6, 2] (counts derived from the figure). The hypothesis instance is adjusted analogously. The evaluation metric (cf. Sect. 4.5) is then applied to this sample. Repetition of $N_{runs}$ times yields a distribution with the mean and standard deviation of the metric for the given pair of network and hypothesis instance $(g_i, h_i)$.

In general, NS ensures the comparison of networks based on an equal number of nodes. Additionally, since networks are typically very sparse, unguided random sampling of nodes often results in disconnected subnets with many isolated nodes. Therefore, we suggest employing advanced node sample strategies such as snowball sampling (Goodman 1961) to preserve coherent behavioral substructures of the network. In our experiments, we use a variant of snowball sampling as a probabilistic sampling technique where initially, one seed node is chosen randomly, then additional nodes are added in breadth-first search order. We do two iterations of the neighborhood collection and then use another random starting point until the required number of nodes is collected. If the current node has more neighbors than the nodes we want to sample, we randomly choose the number of nodes required from the current neighborhood. In our real-world experiments, we perform snowball sampling on adjacency matrices t if these matrices are sparse (see Wikispeedia Sect. 6.1), and we use random sampling for dense datasets such as Flickr (see Sect. 6.2). Overall, our node synchronization step adjusts for differences in the metric that arise directly from different overall sizes of the network. The sampling approach should be chosen with care, taking into account the respective network characteristics (see Appendix B.2).

4.4 Edge synchronization (ES)

Evaluation metrics can be sensitive to the number of observed edges, potentially biasing results. Especially for the JS metric, a lower number of edges may underestimate the match between a hypothesis and the network. Therefore, CompTrails provides an edge synchronization (ES) step that balances edge counts across networks using a sampling approach. This approach is designed to maximize the number of edges sampled. For each network $g_i$, ES first orders the nodes by their number of outgoing edges. This allows ES to match nodes across all networks according to their corresponding rank. For each rank r, ES stores the minimum number of outgoing edges $n_r$ of all nodes with rank r in all networks. For example, for Fig. 1, in the network $g_o$, node 1 has rank 1 with 8 outgoing edges. In $g_p$, all nodes have 4 outgoing edges and are ranked randomly. Let us assume that node 4 is ranked first. $n_r$ is set to 4. Subsequently, ES samples the minimum number of edges $n_r$ for each node in each network according to its rank r. The resulting matrices are then compared using the chosen evaluation metric (cf. Sect. 4.5).

An optional extension of this step could weight the rows in the comparison according to their number of sampled edges $n_r$ instead of treating every node as equally important. While initial experiments have shown limited effects, we see a full exploration of the consequences as a topic for future research. Overall, ES is an essential component of CompTrails as it balances the distribution of transition counts between networks.

4.5 Evaluation metric

CompTrails can in principle, be used with a variety of evaluation metrics to score the match of a hypothesis H to networks G (potentially abstracted, filtered and/or synchonized). For a frequentist approach, the symmetric JS divergence calculates an entropy measure. This approach only makes use of the transition probabilities and loses information about the overall transition count. Alternatively, HypTrails represents a Bayesian approach, deriving a Bayes factor between the evidence scores of a hypothesis and a network.

Our explorative experiments (Sect. 2.2) did not indicate a qualitative difference between the different metrics. Since HypTrails relies on a hyperparameter (the concentration factor k) which in theory can change the interpretation of hypotheses drastically, we chose JS divergence for the remainder of the work for a more unambiguous interpretation of the results. Nevertheless, it is plausible to integrate other metrics into our framework as alternatives to JS scoring.

5 Synthetic experiments

In the following, we explore the effectiveness of the CompTrails components using synthetic networks with controlled behavioral properties.

Table 1 Overview of behavioral networks used in the experiments

5.1 Experimental setup

To create synthetic networks with controlled behavioral properties, we apply a set of biased random walkers to generated graph structures. The graph structures are generated on the basis of the Barabasi–Albert model (Barabási and Albert 1999). These are scale-free networks representing a typical structure for many behavioral networks. Since our framework explicitly aims to compare navigational behavior across networks of different sizes, we create two graphs with 200 and 1000 nodes, respectively, and set $m_{200}=5$ and $m_{1000}=25$ to create roughly equal dense underlying graph structures.

Biased random walker. Based on these graphs, we generate synthetic behavioral networks using biased random walkers. These walkers produce navigational sequences (lists of nodes being traversed) aggregated into multigraphs (Singer et al. 2015; Noboa et al. 2017) by counting transitions between nodes. The biased random walker can be described with the following stochastic process: Our graphs have two types of nodes: "even" E and "odd" O. The following transition probabilities parametrize the biased random walk:

$$\begin{aligned} P(X_{t+1}= & {} E) = {\mathcal {P}}_E \quad \text {(probability of transitioning to even)} \\ P(X_{t+1}= & {} O) = 1 - {\mathcal {P}}_E \quad \text {(probability of transitioning to odd)} \end{aligned}$$

where ${\mathcal {P}}_E$ is the probability of transitioning to an even node, and $X_t$ denotes the type of the visited node at time t. At each time step t, the walker chooses the type of the next node to visit. This selection is based solely on the transition probabilities $P(X_{t+1}$) and is independent of the current node type. After selecting the node type, the walker randomly selects a node of that type as the next node to visit. We set the biased random walker to start 5 and 25 times (for the two networks) at each node for the differently sized networks, respectively, and create walks of length 5 for both networks. If the neighborhood does not contain such a node, the next node will be randomly selected from the entire neighborhood.

Generating synthetic behavioral networks. To show the applicability of our approach, we generate a range of different behavioral networks with different mixtures of the navigational behavior mentioned above (adjusting $P_E$). For both Barabasi–Albert graphs, we create 11 networks with a biased random walker starting from 100% even biased navigation ($P_E=1$), then mix the navigational bias in 10% steps. Table 1 shows statistics for the resulting behavioral networks (see row “Barabasi”).

Hypothesis definition. As hypotheses H, we use the same two navigational biases even and odd, and an additional hypothesis uniform stating that all transitions are equally likely. For each hypothesis, we create a hypothesis instance dependent on the respective underlying graph structure. We show in the appendix that not applying GSF can produce misleading results. Therefore, we recommend applying this component if possible and in line with the hypothesis analyzed. The hypothesis instances only allow transitions to adjacent nodes in the graph and no teleportation to any even/odd node in the graph. On the basis of these matrices for transitions and hypotheses, we will show the effectiveness of our framework in this ongoing section.

5.2 Applying CompTrails

This section shows two exemplary ways to apply different components of our framework to compare navigational behavior in the synthetic datasets explained above. The first approach applies components 2 (GSF), 3 (NS), and 4 (ES), which we suggest as the default approach, and the second approach uses component 1 (NA), where we abstract the nodes to their respective type. Additional studies, e.g., using random node sampling in the NS step or not applying the GSF component, are provided in the Appendix. In a controlled setting, we use this section to show the applicability and limits of CompTrails for comparing differently structured networks.

Fig. 3

Applying CompTrails on synthetic networks with shifting behavioral bias. Each panel shows the JS divergence (y-axis) of 11 behavioral networks with shifting behavioral biases (x-axis) for CompTrails with graph structure filtering (GSF), node synchronization(NS), and edge synchronization (ES). The JS divergence is shown as a line plot with standard deviation intervals. The shifting behavioral bias is based on biased random walkers

5.3 Comparison across differently sized networks

The goal of this experiment is to compare the navigation behavior between networks of different sizes. In the previously generated networks, the divergence should increase when adding more bias towards the other node type. We apply components 2 (GSF), 3 (NS) and 4 (ES) of our framework. We apply the sampling steps $N_{runs} = 100$ times and sample 10% of the nodes of the smallest network ($N_{nodes} = 20$) in the NS component. These values have proven to be good default settings, while very small networks should use the size of the entire smallest network for $N_{nodes}$. Furthermore, we apply NS using snowball sampling with a two-hop proximity due to rather sparse edge matrices. The metric used is JS; therefore, a lower divergence represents better coverage of the hypothesis. The three graphs in Fig. 3 show the different hypotheses that represent behavior even, odd, and uniform (from left to right). The results for the networks $t_{200}$ are represented by the blue line, and those for the networks $t_{1000}$ are represented by the red line. Within each graph, the network bias is printed on the x-axis, where the network with only even bias is shown farther left in the graph and the network with only odd bias in the right; those between are mixed behavior networks.

For hypothesis even (left part of Fig. 3), for both network sizes, the JS divergence continuously increased from left to right (even bias to odd bias), which is perfectly in line with our expectations mentioned above. The standard deviations intervals (shaded area in the plot) of the sampling procedure overlap, which indicates that the framework is able to adjust for the varying network setups and can thus analyze the behavior of the random walker within the networks. Analogous results can be observed for the hypothesis odd, which is desired since the hypothesis states the opposing behavior. For hypothesis uniform, the divergence is very low for all our networks with completely even or completely odd transition behavior, which are the scores most right-hand and most left-hand. This seems unintuitive at first glance since the uniform hypothesis should not explain a biased random walker behavior with a strong bias towards either one of the node types. A possible explanation for this is: Given that our network contains bias 100% towards even nodes, the walker only transitions towards even nodes, and hence the edge-occurrence matrix contains barely any edges with the odd node type. Therefore, snowball sampling mostly samples even states. Then, the transition behavior within these states is nearly uniform since mostly even states have been sampled. Similarly, we expected the divergence to be lowest for the network with 50% even and 50% odd behavior, which is the center value of the graph. However, the divergence values across the networks stay consistently low across networks (except for the edges explained above). We found indicators that this phenomenon also occurs due to the snowball sampling step (cf. Fig. 10 in the Appendix). However, analyzing the exact underlying process will require more in-depth experiments in future work. Furthermore, we found our method to be sensitive with respect to discrepancies in the entropy of transition and hypothesis instance distributions (see Appendix, Fig. 9 for details) that can originate, e.g., from differently dense underlying graph structures. Thus, we show that CompTrails overall mitigates many of the biases introduced by network characteristics, but we also point out that the current sampling approach can, in some cases, produce undesired artifacts that have to be taken into account in practical applications and future work (also see Sect. 7). Network abstraction (see Sects. 4.1 and 5.2) is a viable alternative to sampling and can reduce the previously mentioned sampling artifacts depending on the network and hypothesis structure.

5.4 Comparison on different abstraction levels

As a second way to compare networks of different sizes, we show the effect of network abstraction (Sect. 4.1). In contrast to the previous section, where the hypothesis stated that a transition between all nodes of the same type is equally likely, here we analyze that transitions between any nodes of the same type are likely. We expect our experiments to produce the same results as before; networks with the same creation process should have the lowest divergence for the respective hypothesis. We abstract the networks into only two states, which means that each node is classified as even or odd. Since both abstracted networks have a size of 2, we can refrain from applying the NS and ES components.

Figure 4 contains the same three hypotheses and structure as before; each graph has two overlapping lines for all networks. The divergence increases across all eleven networks (see the plot on the left), which is expected. The uniform hypothesis has a “V” shape, which has the lowest divergence at 0.5. In contrast to the previous approach, we do not have the issue of sampling only nodes from one type. Therefore, we do not observe the same phenomenon.

Fig. 4

CompTrails results when abstracting states to state types odd/even on synthetic data. The lines for both network configurations are effectively identical over all samples

This example reduces the state space to two states which is an extreme case. We show different reductions in our real-world experiments using bibliometric networks (see Sect. 6.3). In general, network abstraction can be a viable alternative to sampling steps (see Sects. 4.3 and 4.4) depending on the structure of the network and hypothesis.

6 Real-world data

Next, we show the application of our framework to several real-world datasets. These applications are illustrative applications and do not aim to gather new scientific insights in the corresponding research domains. When interpreting the results, it is important to consider the aspects discussed in Sect. 7, e.g., potential biases due to different densities. Table 1 gives an overview of the networks we analyze and their dimensionalities. The following sections introduce the respective dataset, the investigated hypothesis, the chosen components of CompTrails, and discuss the corresponding results.

Table 2 Overview of datasets with applied components from CompTrails. We leave out component 5, the metric, which is always JS divergence

Fig. 5

Application of our framework CompTrails on different real-world data sets. See Table 2 for the utilized components

6.1 WikiSpeedia

WikiSpeedia¹ is a dataset based on the equally named game (West and Leskovec 2012; West et al. 2009). It uses a subset of Wikipedia that contains 4604 pages. Starting from a randomly selected page, the goal of the game is to find the shortest path to another randomly selected page. For our approach, we apply the same filtering and pre-processing steps as in Becker et al. (2017): 1. We only consider games that have been successfully completed (51 318). 2. Games are filtered by an optimal click sequence length of 3 between the start and target pages, which filters games equally difficult to solve. 3. Sequences shorter than 3 and longer than 8 clicks are filtered because these are considered as not seriously played games. This leads to 26 842 sequences.

Networks: A typical game has two phases. The randomly selected start page is most likely a node on the periphery of the network. Previous work (Koopmann et al. 2019; Scaria et al. 2014) has shown that players tend to click on the links to the nodes to a greater degree at the beginning to locate their current position, which is referred to as the zoom-out phase. In the second phase, transitions to nodes semantically more similar to the target node are used. This is called a zoom-in phase (Koopmann et al. 2019). The networks contain the transitions of each phase in all the games. Each sequence is individually split at the middle node (we add the middle node to the first phase for sequences of odd length). This results in two networks out and in with 4604 nodes each.

Hypothesis: The hypothesis used is the Degree hypothesis, representing the intuition that players transition to neighbors with high degrees more likely. This represents the out phase of a WikiSpeedia game. Edge probabilities are calculated proportionally to the degree of neighboring nodes. Nodes not in the neighborhood do not have any transition probability. Since this hypothesis should explain the first phase (out) of a typical game, we expect to see a higher divergence for the in-phase.

Framework: For this dataset, we use the graph structure filtering (GSF) of our framework and apply the graph structure given from Wikipedia. We apply NS and ES and set $N_{runs} = 1000$ and $N_{Nodes} = 460$ which is 10%. Additionally, we use snowball sampling on the edge network.

Results: As expected, the out network is better explained by the hypothesis (mean divergence of 0.49), since it prefers transitions to high-degree nodes (see Fig. 5a).

6.2 Flickr PhotoTrails

Flickr PhotoTrails is a dataset that contains sequences of photos taken in different cities posted on Flickr (Becker et al. 2015). Since these photos contain geospatial locations and time stamps, it is possible to construct navigational sequences of users (Becker et al. 2015).

Networks: We analyze five cities, namely Vancouver, Washington, Los Angelos, London, and New York City. According to previous work (Becker et al. 2015), we assume that the pictures are taken of attractions (network nodes) within each city. Therefore, we compute the shortest distance from any attraction for each photo and assign it accordingly. We extracted all attractions from DBPedia for the respective cities with their GPS coordinates for this. This allows us to derive sequences of attractions from photo sequences, which we accumulate into a behavioral network. Edges represent the next photographed attractions.

Hypothesis: The analyzed center hypothesis represents the intuition that people are moving more often towards the city center. The center is computed using the center of all attractions on the network.

Framework: To account for different node and edge counts across networks, we apply NS & ES with $N_{runs} = 1000$ and $N_{nodes} = 11$, which is the number of states of the smallest network due to the small size of the network. Since the networks are very dense, we can apply random sampling.

Results: The results show that tourists in Vancouver with a mean divergence of 0.48 and New York with 0.54 fit the hypothesis best. This can be explained by the assumption that attractions within these cities are closer to the city center. In contrast, cities such as LA are rather widespread and therefore do not fit the centrality hypothesis well.

Fig. 6

Application of CompTrails on bibliometric networks. Figure 6a applies snowball sampling using the hypotheses network, due to sparse meta-data. Figure 6b applies the network abstraction step by abstracting authors into their respective countries. Hypotheses represent the intuition of authors cooperating, if they are in the same country, or cooperation occurs more likely if the countries are geographically closer. Figure 6c is the counterpart using affiliations as abstract node types

6.3 Bibliometric dataset

This dataset uses bibliometric social graphs, also known as co-author graphs. Here, nodes represent authors, and edges describe cooperations between these authors, specifically co-published peer-reviewed publications.

Networks: For our experiments, we use networks that represent different subdomains to compare different hypotheses between them. We use Google’s ranking system² for scientific conferences in the domain of engineering and computer science and choose different subdomains with their respective top 20 conferences. We extracted all publications from these conferences using the pipeline from Stubbemann and Koopmann (2020). Subdomains are created for the domains of artificial intelligence (AI), Software Systems (SS), Signal Processing (SP), Data Mining (DM), Robotics (R) and human-computer interactions (HCI). We analyze whether and why researchers cooperate differently in research domains.

Hypothesis: Geographical proximity is one of the major driving factors for scientific cooperation (Koopmann et al. 2021). Therefore, our hypothesis represents the intuition that cooperation within the same country is more likely. An author has a country assigned if he was affiliated with this country for any publication. This allows authors to be associated to multiple countries if the authors switched affiliations. The similarity of the two authors is calculated using the number of overlapping countries reported.

Framework: Due to sparsity, we apply the inferred graph structure to all hypotheses (using the GSF component of CompTrails). Furthermore, we use NS and ES and set $N_{runs} = 1000$ and $N_{nodes} = 10\%$. Here, we employ snowball sampling because metadata, i.e., the assignments of authors to countries, is sparse and leads to sparse networks.

Results: Our results (see Fig. 6a) show that the domains of Artificial Intelligence AI and Signal Processing SP particularly fit the hypothesis of cooperating with authors from the same country. On the contrary, Software Systems SS has the highest divergence. The differences between the different domains are substantial.

6.4 Bibliometric dataset with network abstraction

We further extend the experimental setting in Sect. 6.3, by applying network abstraction (Sect. 4.1), in two different ways.

Abstraction by country: First, to define nodes, we categorize all authors according to their respective country (see Fig. 6b). Authors with multiple country associated are categorized to all the countries. As a hypothesis, we used the geographical distance between countries. Based on this, authors are more likely to cooperate with authors from other countries geographically close to each other. This hypothesis represents a more abstract scenario compared to Sect. 6.3 as it does not consider individual authors. Furthermore, while the initial hypothesis solely considers country overlaps, the current hypothesis uses more complex edge probabilities by incorporating the geographic distance between different countries. We calculate the geographic distance of countries as the distance of their central locations derived from DBPedia. Since each network contains authors from a different number of countries, we still apply the NS and ES steps.

Abstraction by affiliation: Furthermore, we use a second abstraction approach by categorizing the authors by their respective affiliations to derive nodes. Authors associated with multiple affiliations are categorized to all the affiliations. The hypothesis represents the same intuition as for countries where authors of affiliations geographically closer are more likely to cooperate. If geographic information for an affiliation is unavailable, we use the respective information of the affiliation’s country. As before, since each network contains different affiliations, the resulting abstracted networks have different numbers of nodes. Hence, our method’s NS and ES components are applied to allow for fair comparison across these networks.

Results: The abstraction approach produces a very similar divergence for all datasets (see Fig. 6b), i.e., the difference between the best-explained datasets (SS, DM, and SP) and the worst (HCI) is only 0.04 for the country abstraction. However, the application of CompTrails allows us to detect these small effects. Abstracting to affiliations (see Fig. 6c leads to sparse matrices since not all authors provide affiliations in the dataset. Therefore, the error bars have a wider margin. No significant differences between networks can be observed regarding the abstraction of countries.

7 Discussion

CompTrails provides tools to facilitate the comparison of hypotheses across networks. Each component of CompTrails targets specific characteristics of hypothesis semantics (Sect. 4.1), graph structure (Sect. 4.2), number of network nodes (Sect. 4.3), and number of network edges (Sect. 4.4). By providing these components, CompTrails enables a more accurate formulation of hypotheses, as well as the comparison of metrics across networks, where the naive application of existing approaches, such as JS divergence, produces skewed comparisons. In addition, we demonstrate throughout our examples and applications how CompTrails can be flexibly adjusted to specific graph and hypothesis characteristics. In the following, we summarize the underlying principles and effects as well as the scope of these adjustments and highlight directions for future work.

One challenge of hypothesis comparison, in general, is that the “best” fit of a hypothesis is inherently underspecified. For example, the practitioner may be more interested in whether the overall edge distribution follows a given hypothesis, whether the edge distribution in every node individually follows the given hypothesis, or whether the network provides overall higher evidence to reject a hypothesis. This may lead to different weighting, scaling, and metric choices. Consequently, the components of CompTrails inherently change the semantics of the comparison, and the corresponding results are non-exhaustive. Therefore, depending on the specific scenarios and the goal of the practitioner, the different steps must be chosen appropriately as illustrated throughout our experiments, and additional steps or adaptations may be adequate.

CompTrails specifically aims to address diversity in node and edge distributions between networks. In particular, we adjust metrics considering the number of nodes and the number of edges between networks. These factors can lead to a drastic bias in the comparison of hypotheses if not adjusted (see Fig. 12). However, other differences, such as the densities of underlying graph structures, still lead to challenges. An example of this can be seen in the results in the additional study visualized in Appendix, cf. Fig. 9. Furthermore, users must consider the potential side effects or artifacts of sampling approaches, as demonstrated with the uniform hypothesis in Fig. 3. Currently, CompTrails does not always fully adjust for such effects. Therefore, detailed studies, e.g., on the mitigation of different sparsity characteristics, will be required in the future to account for such effects in a more principled manner.

In contrast to previous measures, CompTrails has the advantage that it provides a distribution of result scores instead of a single result, through sampling. This allows quantifying uncertainties, for example caused by different numbers of edges across nodes. Consequently, measures of effect size (such as Standardized Mean Difference or Cohens’d) can be computed to estimate the strength of the comparison. Note that traditional statistical hypothesis tests are not applicable since they can be arbitrarily adjusted by increasing the number of runs (through a hyperparameter).

8 Conclusions

Overall, CompTrails, provides a powerful set of tools for comparing hypotheses across behavioral networks by counteracting hypothesis and graph characteristics that would otherwise bias or invalidate existing approaches, such as naively applying JS divergence. We show the positive impact of the different framework components using synthetic as well as real-world examples. However, we also identified specific settings in which our proposed adjustments currently may result in artifacts complicating an unbiased hypothesis comparison, and discussed them critically. An in-depth study of such effects, e.g., also based on graph-theoretic analysis, and controlling for additional biasing factors will be a key topic in future work. In that sense, we consider CompTrails to open a broader, complex research topic that will enhance our understanding of the underlying processes of behavior across datasets.

Appendix

This appendix reports on additional experiments we conducted to understand the effects and challenges of this work. First, we will show the influence of the number of edges (see Fig. 7) and the density of the edge distribution (see Fig. 8). Afterward, we report several parameter and ablation studies conducted on the synthetic datasets. We conclude with an exemplary real-world example, in which we chose inaccurate settings, yielding misleading results.

1.1 A: Effects of influence factors

As discussed in Sect. 3, a naive comparison of networks of different sizes does not produce the expected results. In general, we identified three main influence factors. (1) The number of nodes in each network, (2) the number of (multi-)edges, (3) and the distribution of edges per node, i.e., normally distributed versus skewed distributions. An example of the effect of the first factor, a different number of nodes, is shown in Fig. 2 in the main manuscript. Now, we add constructed examples to showcase the effect of the remaining two factors, which are different numbers of edges (see Fig. 7), and different distributions of edges per node (see Fig. 8). For Fig. 7, we construct three networks with 100 nodes using underlying Barabasi–Albert graphs created by the same process. To create different numbers of edges, we created random walks of lengths of 10 (sparse), 20 (middle), and 30 (dense), respectively, which produces three behavioral networks of the same size but with different amount of edges. The hypothesis and network biases are identical to Fig. 2. For Fig. 8, the underlying Barabasi–Albert graphs were constructed with $m_{10}=5$, $m_{100}=25$ and $m_{1000}=50$, respectively, which leads to fewer possible transitions for the respective random walker. As in Fig. 2, by construction, the middle (orange) network was fully generated according to the hypothesis, while the other two were generated as a mixture of the hypothesis and a uniform random walker. Thus, the desired outcome would be to have a lower divergence for the middle network and the same, higher divergence for the two others. We can see for both experiments, that applying the plain metrics directly does not produce the expected results. When applying the appropriate steps of CompTrails, which are NS and ES, the divergence of the orange networks is the lowest, and for the blue and green networks, the divergences are approximately equal.

Fig. 7

Evaluating the impact of different numbers of edges on the comparison. All three networks have 100 nodes each and have the same connectivity ($m=25$). The biased random walker has a length of 10 (sparse), 20 (middle), and 30 (dense) steps, which results in 4500, 9500, and 14,500 transitions

Fig. 8

Evaluating the impact of different edge distributions. All three networks have 100 nodes each and the same number of edges, hence the random walker has identical properties. We constructed the underlying Barabasi–Albert graph with $m_{10}=5$, $m_{100}=25$ and $m_{1000}=50$ respectively, which leads to fewer possible transitions for the respective random walker. We used the same walker settings as in Fig. 2, which means that we start 5 times from each node with a walk length of 5

1.2 B: Parameter and ablation studies—analyzing different components of comptrails on synthetic networks

In Sect. 5.2, we apply CompTrails on our created synthetic datasets with specific component settings. Here, we report additional experiments with modified parameters, either for the construction of the synthetic networks, or with respect to the choice of CompTrails components. The underlying data generation process and base configuration are equivalent to Sect. 5.2. Modifications are elaborated in each section.

Fig. 9

Applying CompTrails on synthetic networks. The underlying Barabasi–Albert graphs are constructed using $m=5$. This leads to underlying graphs with different densities. We observe small differences between networks of different densities also after adjustments

1.2.1 B.1: Understanding the impact of different densities

In the first experiment, we used the same approach as in Sect. 5 except for the process of generating the underlying Barabasi–Albert graphs. We use $m=5$ for both graphs, which generates a relatively dense graph for the smaller network with 200 nodes and a sparser graph for the larger network with 1000 nodes. The biased random walker applies the same transition probabilities, leading to the results in Fig. 9.

While with CompTrails, we can still compare the even and odd hypothesis well across the different networks of one density, our method is unable to fully adjust w.r.t. different densities, which means that the divergence for the same bias of the random walker is not identical on networks of different densities. We relate this to the different entropies in the transition and/or hypothesis instance distribution that originate from differently dense underlying graph structures. Here, we see the potential for extensions of our framework in future research that make hypotheses better comparable in such settings. However, these differences can also be interpreted as plausible: Specifically for nodes with few transition, on an instance-level the hypothesis after graph structure filtering is potentially more "precise" in predicting where the transitions will take place in the sparser graph, and thus could also be considered as better. For the uniform hypothesis, we observe similar artifacts as in the main experiment, see Sect. 5.

A possible explanation of this phenomenon could be related to the Edge Sampling step for networks with different density. When the ES step is applied in the smaller graph, there are more possible nodes to sample an edge, as it is more dense by construction. Even if the number of sampled transitions is adjusted in our method, the number of possible nodes after graph structure filtering is higher for the small graph. We assume that this will lead to differences in the entropy of hypothesis instantiations and/or observed edge distributions, even after we finish our sampling step, which we can see in Fig. 9.

Fig. 10

Applying random node sampling instead of snowball sampling during the NS component. Sampled matrices are sparse and produce greater standard deviations in the divergences

1.2.2 B.2: Random node sampling versus snowball sampling

The CompTrails framework allows for different options to sample nodes. In our main experiments with synthetic data, see Sect. 5.2, we apply snowball sampling on the transition network in the node synchronization component. In the following, we show results using random sampling instead. The results are shown in Fig. 10. We observe that random sampling leads to large standard deviations in the result scores. This can be explained by the sparser sampled transition matrices, which are generated by random sampling.

1.2.3 B.3: Effects of graph structure filtering

Fig. 11

Not using GSF with the underlying graph structure. Networks with an opposite behavior as the hypothesis have a high divergence, which is correct. All other networks arrange themselves on a similar divergence level as the uniform hypothesis

Next, we demonstrate the effect of GSF in our framework, see the results in Fig. 11. Here, networks created using biased random walkers with the same or similar transition probabilities as the hypothesis produce very similar divergences. This makes the approach unable to clearly differentiate between the different degrees of agreement with the hypothesis. This clearly shows the benefit of including GSF in the framework in this case. On the other hand, for very dense networks (results not shown here), GSF is not necessary to apply, since nearly all edges of the network occur in the underlying graph structure.

1.2.4 B.4: Overall effects of node and edge synchronization

Fig. 12

Not applying the core components of our framework, namely the NS and ES steps. Since we do not sample, no standard deviation plots are shown. Divergence scores for different network sizes diverge, which shows the necessity of our approach

Next, we conducted a brief experiment, where we did not apply the core components of our work, namely node sampling and edge sampling. The results can be seen in Fig. 12. As explained, directly applying JSD is not capable of producing comparable divergence scores when comparing matrices of different sizes and densities. However, for the uniform hypothesis, the degree of agreement with respect to a single network is more evident compared to the CompTrails approach.

1.2.5 B.5: Number of nodes sampled

Fig. 13

Parameter study on the percentage of nodes sampled in the NS step. As expected, fewer nodes sampled lead to larger standard deviations

To analyze the impact of the percentage of nodes sampled in the node synchronization step, we conducted a parameter study, in which we varied the percentage of nodes sampled from 10% (which is our default setting) up to 50% of the size of the smallest network (here from 200 nodes in the blue networks (see Fig. 13). For this, we created behavioral networks using underlying Barabasi–Albert using $m=2$, and biased random walker as in the settings before. Increasing the number of sampled nodes led to smaller standard deviations between runs and improved similarity between the corresponding networks, as we can see in Fig. 13c). However, it is important to acknowledge the trade-off involved, as sampling all nodes can potentially result in memory and runtime constraints.

1.2.6 B.6: Number of runs

Fig. 14

Parameter study on the amount of runs conducted. The result for 100 runs can be seen in Fig. 10. Random fluctuations can occur if the number of runs is too small

We conducted a small parameter study on the number of runs, i.e., how many times we run our proposed method. The results can be seen in Fig. 14. For a small number of runs, the mean of the divergence scores becomes very unstable, as shown in Fig. 14a. Sampling more often leads to smoother result. The shaded areas show the standard deviation, which is not influenced by the number of runs.

1.3 C: Example of misconfiguration of CompTrails in a real world setting

Fig. 15

Applying snowball sampling on the transitions of our bibliometric dataset. We can not observe any differences in the results since the dataset has few metadata and hence the resulting sampled hypothesis matrices have many zero values, which leads to non-interpretable results

Finally, we demonstrate the results of not configuring CompTrails correctly: In the bibliometric dataset case study, the meta-data, and therefore the hypothesis are very sparse. In the main part of our study, we applied snowball sampling to the hypotheses to handle this dataset limitation. The application of snowball sampling helps to sample a coherent structure. The outcome of applying snowball sampling to the transitions is depicted in Fig. 15. Since the transitions exhibit a high density, we selected states in which numerous zero values were present in the respective hypotheses. Consequently, the analysis leads to a similar divergence for each network within the dataset. Although this behavior is in line with our chosen approach, it does not provide valuable insight to the researcher.