Introduction

Several examples in condensed matter systems are not easily observable through conventional experimental techniques. Such hidden orders have been in debate for several decades and have been waiting to be discovered1,2,3,4,5,6,7. In particular, unusual higher rank multipole moments, beyond the conventional electric and magnetic dipole moments, have been suggested as a key player to exhibit various hidden orders8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33. Multipolar degrees of freedom are renowned for not only generating hidden orders, but also contributing to a range of other intriguing and intricate phenomena. For example, in heavy fermion materials, multipolar degrees of freedom can lead to the emergence of unconventional superconductivity and non-Fermi liquid behavior with exotic Kondo physics34,35,36,37,38,39,40,41,42,43,44,45. In addition, exotic ground states, known as multipolar quantum spin liquids, can emerge from the magnetic frustration between the multipolar moments46,47,48,49. Therefore, the investigation of multipolar physics properties has been the primary objective of extensive research with significant implications and fresh insights that could potentially lead to various applications50,51,52,53,54,55,56. However, there are few such examples, and many of the magnetic systems contain not only multipoles but also magnetic dipoles at the same time.

Finding multipolar degrees of freedom in the magnetic systems requires a delicate combination of spin-orbit couplings and crystalline electric field (CEF) splitting based on the point group symmetries33,57,58,59. In conventional crystals, the point group symmetry, which should be compatible with the translational symmetry, limits the exploration of pure multipolar degrees of freedom in the magnetic systems57. On the other hand, the quasicrystals, and their approximants could exhibit the point group symmetries beyond the space group such as pentagonal rotational symmetry, due to their ordered structure lacking spatial periodicity60,61,62. Thus, quasicrystalline materials provide a good platform for finding multipolar degrees. Several rare-earth magnetic quasicrystals exhibit icosahedral symmetry, but their multipolar physics and related exotic phenomena have yet to be investigated63,64,65,66,67,68.

In this paper, we consider the non-crystallographic 5-fold rotational symmetry and icosahedral symmetry with f-orbital electrons of the rare earth atoms. First, we classify all possible multipole degrees of freedom found in rare-earth magnetic quasicrystals in the presence of noncrystallographic 5-fold symmetry. We note that this generally leads to the higher order multipoles of the pseudospin x and y components, and magnetic dipoles of the Ising moments. More interestingly, if magnetic quasicrystals with Yb3+ ions are in a perfect icosahedral crystal field symmetry, they host the Kramers doublet that carries pure magnetic octupole moments without magnetic dipole moments. On symmetry grounds, the generic spin Hamiltonian is introduced for both Kramers and non-Kramers doublet. In the antiferromagnetic Ising limit, we first discuss the degenerate ground state resulting from the geometrically frustrated icosahedron structure. Subsequently, with the introduction of quantum fluctuations, a distinctive ground state is established, which has non-zero entanglement. In this case, depending on (anti-) ferromagnetic XY interaction, the specific linear combination of the degenerate ground states found in the Ising limit becomes a non-degenerate ground state. Our work provides a perspective for finding multipolar degrees of freedom and their magnetic frustration originated from noncrystallographic symmetries. Furthermore, it opens a paradigm for enriching hidden orders, spin liquids and Kondo effects in quasicrystals.

Results

Multipolar degrees of freedom in icosahedral magnetic quasicrystals

In this section, we begin by categorizing all potential multipolar degrees of freedom for rare-earth magnetic systems with noncrystallographic 5-fold symmetry and icosahedral symmetry. We then shift our attention to a scenario wherein magnetic dipoles are absent, and pure magnetic octupole moments are present. We examine the characteristics of such moments.

The most general CEF Hamiltonian in a 5-fold rotational symmetry is given as follows, using the Stevens operators,

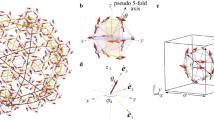
$${H}_{{{{\rm{CEF}}}}}={B}_{60}{O}_{6}^{0}+{B}_{65}{O}_{6}^{5}+{B}_{20}{O}_{2}^{0}+{B}_{40}{O}_{4}^{0}$$
(1)

Here, Bnm = −γnmqCnm〈rn〉θn are the Stevens coefficients obtained by the radial integrals, where γnm is a term calculated from the ligand environment expressed in terms of tesseral harmonics. q is the charge of the central atom, Cnm are the normalization factors of the spherical harmonics, r is the radial position, θn are constants associated with electron orbitals of the magnetic ion69. Here, we assume the point charge model. We neglect the finite extent of the charges on the ions, the overlap of the wave functions of the magnetic ions with those of neighboring ions, and the complex effects of the screening of the magnetic electrons by the outer electron shells of the magnetic ion. Nevertheless, we emphasize that it serves as a first approximation to illustrate the principles involved, and can be used to calculate the ratios of terms of the same degree in the Hamiltonian for lattice sites of high symmetry, since these ratios are independent of the models and are determined solely on symmetry grounds70. Note that the z-axis is a 5-fold rotational symmetry axis. The \({O}_{n}^{m}\) are Stevens operators with respect to the total angular momentum operators (See Supplementary Methods for the detailed forms of \({O}_{n}^{m}\).). When we consider the full icosahedral symmetry, which has 5-fold rotational symmetry plus mirror reflection symmetries, it leads to B20 = B40 = 0, and B65 = − 42B60. We examine two cases one where perfect icosahedral symmetry exists, and another where only 5-fold symmetry exists. These cases are applicable to different situations. The latter case can be taken into account using the charge defects which breaks the icosahedral symmetry down to C5v. In this case, the charge defect on a ligand is placed on a z-axis as q → q(1 + α). As a result, the Stevens coefficients, B65, B20, B40 are changing as a function of α. Since \({B}_{nm}=-\alpha {\gamma }_{nm}^{{\prime} }q{C}_{nm}\langle {r}^{n}\rangle {\theta }_{n}\) for a single point charge defect, B60 is unchanged if the charge defect is placed on the z-axis. Most of the binary, ternary and complex Al-TM (TM = transition metal) icosahedral quasicrystals, similar to the Al-Mn or Al-Mn-Si compounds, belong to the Mackay-type of icosahedral quasicrystals which have perfect icosahedral symmetry. In contrast, for instance, Ce15Au65Sn20 has only C5v point group symmetry around its magnetic atom, Ce61.

For both full icosahedral symmetry, Ih and 5-fold rotational symmetry, C5v with nonzero α, we summarize the CEF states in Figs. 1 and 2 for half-integer J and integer J values, respectively. For α = 0, the point group symmetry restores the full icosahedral symmetry and multiple degenerate levels appear. It is noteworthy that for J = 7/2 which is the case for Yb3+, the (Kramers) doublet exists under the perfect icosahedral symmetry group as shown in the red box of Fig. 1a. Specifically, there are two eigenspaces of HCEF, the Kramers doublet and the sextet71. On the other hand, for any given α ≠ 0, the CEF states under 5-fold symmetry are split into doublets or singlets for all given values of the total angular momentum J of the rare earth atom. In both Figs. 1 and 2, the tentative orders of the energy levels are given for α = 0.5. Given α ≠ 0, every energy levels for half-integer J are Kramers doublet due to the time-reversal symmetry. However, for integer J, some singlets are allowed. Notably, in all cases, the pseudospins of the doublets exhibit magnetic dipoles along the z-component, while typically showing multipoles such as quadrupoles, octupoles, and higher orders along the x and y-components. For half-integer values of J, Σx(y) could be dipole, octupole and dotriacontapole (see Fig. 1), whereas for integer values of J, the doublets carry either quadrupole or hexadecapole Σx(y) (see Fig. 2). Again, it is because of the time-reversal symmetry. It is interesting to note that for the low lying Kramers doublet, Σx(y) for J = 7/2 always represents magnetic octupoles originated from the Kramers doublet, whereas, Σx(y) for J = 9/2 and J = 15/2 could take magnetic octupoles or dotriacontapoles. We also note that for the low lying non-Kramers doublets, Σx(y) for J = 4 and J = 6 take either quadrupole or hexadecapole, while for J = 8, it could take only quadrupole (see Fig. 2c).

Fig. 1: Summary of the CEF states and multipoles under non-crystallographic point group symmetries for given half-integer values of J.
figure 1

a J = 7/2 (Yb3+) (b) J = 9/2 (Nd3+) and (c) J = 15/2 (Dy3+). Under the icosahedral symmetry Ih, the CEF states are split into several multiplets. Particularly, note that J = 7/2 which is the case for Yb3+ has a Kramers doublet and it hosts pure magnetic octupoles without magnetic dipoles or quadrupoles, as shown in the red box. Whereas, for C5v where the mirror reflection of Ih is absent, all the multiplets are split into Kramers doublets. In this case, the z-component of the pseudospin, Σz is dipole for any Kramers doublets. In contrast, the x, y-components, Σx,y, could be not only dipoles but also octupoles and dotriacontapoles. Depending on the energy scale of the breaking of the mirror symmetry, the order of energy could change. d Dipoles (black-copper), octupoles (red-white) and dotriacontapoles (red-yellow). See the main text for more details.

Full size image
Fig. 2: Summary of the CEF states and multipoles under non-crystallographic point group symmetries for given integer values of J.
figure 2

a J = 4 (Pr3+) (b) J = 6 (Tb3+) and (c) J = 8 (Ho3+). Unlike the icosahedral symmetry Ih where the CEF states are split into several multiplets. the five-fold symmetry C5v symmetry splits all the multiplets into either non-Kramers doublets or singlets. Under C5v, the z-components of the pseudospin, Σz are magnetic dipoles for each doublet. On the other hand, the x, y-components, Σx,y represent either quadrupoles or hexadecapoles. Depending on the energy scale of the breaking of mirror symmetry, the order of energy could change. d Singlet (black), quadrupoles (blue-skyblue) and hexadecapoles (violet-skyblue). See the main text for more details.

Full size image

We emphasize that the loss of translational symmetry generally allows such unconventional multipolar degrees of freedom. The aperiodic system allows the non-crystallographic point group symmetries which give rise to the unconventional terms of CEF Hamiltonian. For instance, 5-fold rotational symmetry leads to the \({O}_{6}^{5}\) term in Eq. (1). Note that the \({O}_{6}^{5}\) term relates \(\left\vert {J}_{{{{\rm{z}}}}}=m\right\rangle\) and \(\left\vert {J}_{{{{\rm{z}}}}}=m\pm 5\right\rangle\) states, which are not related to each others in the conventional periodic systems. This allows us to obtain the multipolar degrees of freedom in the aperiodic system.

From now on, we focus on the special case where the lowest Kramers doublet is represented by pure octupoles, i.e. J = 7/2 in an icosahedral crystal field symmetry and discuss their characteristics. Then, in the following subsections, we discuss the generic spin Hamiltonian, geometrical frustration and quantum fluctuation effects. It is important to note that all these arguments are generally applicable to any cases of multipolar physics with J listed in Figs. 1 and 2.

Let us define the Kramers doublet as \(\left\vert \pm \right\rangle\), which are written in terms of the eigenstates of the Jz operator,

$$\begin{array}{l}\left\vert +\right\rangle =-\sqrt{\frac{7}{10}}\left\vert {J}_{{{{\rm{z}}}}}=-\frac{3}{2}\right\rangle +\sqrt{\frac{3}{10}}\left\vert +\frac{7}{2}\right\rangle \\ \left\vert -\right\rangle =\sqrt{\frac{3}{10}}\left\vert -\frac{7}{2}\right\rangle +\sqrt{\frac{7}{10}}\left\vert +\frac{3}{2}\right\rangle .\end{array}$$
(2)

With respect to the Yb3+ ion, it is established that B6 < 0, thus the ground eigenspace of the CEF Hamiltonian is the Kramers doublet, which is well separated from the sextet72,73. The CEF energy gap is given by 25200∣B60∣ ~ \({{{\mathcal{O}}}}\) (10meV), where detailed numerical value depends on icosahedral magnetic materials with Yb. Since the energy scale of spin exchanges between rare-earth ions are generally much smaller than the crystal field splittings, one can expect the magnetic properties at low temperature are explained within this Kramers doublet. From Eq. (2), one can easily find that 〈 ± ∣Ji∣ ∓ 〉 and 〈 ± ∣Ji∣ ± 〉 vanish where i = x, y, z. Importantly, Jz also vanishes due to the symmetric coefficients of the states. This confirms that there is no magnetic dipole moment. Thus, one should consider the multipolar degrees of freedom given by the irreducible tensor operators. However, since \(\left\vert \pm \right\rangle\) are the Kramers doublet, the time-reversal even operators such as quadrupole moments vanish. Hence, it is reasonable to anticipate the presence of higher-order degrees of freedom, such as octupoles, in the absence of dipolar or quadrupolar degrees of freedom.

To show that the Kramers doublet, \(\left\vert \pm \right\rangle\) in Eq. (2), describes the octupolar degrees of freedom, let us define the pseudospin ladder operators, Σ±, as follows.

$${\Sigma }^{+}=\left\vert +\right\rangle \left\langle -\right\vert \,\,\,\,\,{\Sigma }^{-}={({\Sigma }^{+})}^{{\dagger} },$$
(3)

and Σz = [Σ+, Σ−]/2. Now define the octupolar operators as the rank 3 spherical tensor operators, \({T}_{m}^{(3)}\) in terms of J+, J− and Jz. Note that octupolar operators are time-reversal odd. Thus, under the time-reversal transformation, \({{{\mathcal{T}}}}\), we have \({{{\mathcal{T}}}}{\Sigma }^{\pm }{{{{\mathcal{T}}}}}^{-1}=-{\Sigma }_{\mp }\), \({{{\mathcal{T}}}}{\Sigma }^{{{{\rm{z}}}}}{{{{\mathcal{T}}}}}^{-1}=-{\Sigma }^{{{{\rm{z}}}}}\). As a result, \({\Sigma }^{{{{\rm{z}}}}} \sim {T}_{0}^{(3)}\) and \({\Sigma }^{\pm } \sim {T}_{m}^{(3)}\) for non-zero m. However, \({T}_{1}^{(3)}\) and \({T}_{-1}^{(3)}\) vanish because \({T}_{\pm 1}^{(3)}\left\vert \pm \right\rangle\) is not in the doublet eigenspace. Note that \({T}_{\pm 1}^{(3)}\) changes the eigenvalue of the Jz operator by ±1. Similarly, since \({J}_{\pm }^{2}\left\vert \pm \right\rangle\) and \({J}_{\pm }^{3}\left\vert \mp \right\rangle\) are not in the doublet, the only non-trivial matrix elements are \(\langle \pm | {T}_{\pm 2}^{(3)}| \mp \rangle\) and \(\langle \mp | {T}_{\pm 3}^{(3)}| \pm \rangle\). This leads to \({T}_{\pm 2,\mp 3}^{(3)} \sim {\Sigma }^{\pm }\). In detail, one can represent the octupolar pseudospin operators in the doublet as,

$${\Sigma }^{z}\equiv {T}_{0}^{(3)},\,\,\,{\Sigma }^{\pm }\equiv \frac{1}{2}\sqrt{\frac{2}{15}}{T}_{\pm 2}^{(3)}\mp \frac{1}{2}\sqrt{\frac{1}{5}}{T}_{\mp 3}^{(3)}.$$
(4)

Specifically, \({T}_{\pm 2}^{(3)}=\displaystyle\frac{1}{4}\sqrt{\frac{105}{\pi }}\overline{{J}_{\pm }^{2}{J}_{{{{\rm{z}}}}}}\), \({T}_{\pm 3}^{(3)}=\mp \displaystyle\frac{1}{8}\sqrt{\frac{35}{\pi }}{J}_{\pm }^{3}\), and \({T}_{0}^{(3)}=\displaystyle\frac{1}{4}\sqrt{\frac{7}{\pi }}(5{J}_{{{{\rm{z}}}}}^{3}-3{J}_{{{{\rm{z}}}}}{J}^{2})\), where \(\overline{{{{\mathcal{O}}}}}\) is the symmetrization of the operator \({{{\mathcal{O}}}}\)74. Each pseudospin operator is a linear combination of rank 3 tensors. From Eq. (4), one can write,

$${\Sigma }_{{{{\rm{x(y)}}}}}=\frac{1}{4}\left[\sqrt{\frac{2}{15}}\left({T}_{2}^{(3)}\pm {T}_{-2}^{(3)}\right)\pm \sqrt{\frac{1}{5}}\left({T}_{3}^{(3)}-{T}_{-3}^{(3)}\right)\right],$$
(5)

where x(y) takes + (−) sign in Eq. (5), respectively. Note that the octupole moment is restricted to the 2-sphere, which represents the set of possible expectation values of the three pseudospin operators, Σz and Σx(y).

Generic spin Hamiltonian on symmetry grounds

By applying the symmetry transformation of the icosahedron group (Ih) and the time reversal symmetry transformation, one can find the generic spin Hamiltonian of the nearest neighbor interactions. Let us define the local z-axis pointing to the center of the icosahedron shell. Then, under the 5-fold rotational symmetries of Ih, we have \({\Sigma }_{i}^{\pm }\to {e}^{\mp 4{{{\rm{i}}}}\pi /5}{\Sigma }_{j}^{\pm }\), where i and j are the nearest neighboring sites. This leads to the bond dependent phase factors in the Hamiltonian, such as \({\Sigma }_{i}^{+}{\Sigma }_{j}^{+}\) or \({\Sigma }_{i}^{+}{\Sigma }_{j}^{z}\) terms. As a result, the generic symmetry allowed Hamiltonian under the icosahedral symmetry contains four independent parameters, J±±, J±z, J± and Jzz, and is given as,

$$\begin{array}{l}H\,=\,\mathop{\sum}\limits_{\langle i,j\rangle }\left[{J}_{{{{\rm{zz}}}}}{\Sigma }_{i}^{{{{\rm{z}}}}}{\Sigma }_{j}^{{{{\rm{z}}}}}+{J}_{\pm }\left({\Sigma }_{i}^{+}{\Sigma }_{j}^{-}+{\Sigma }_{i}^{-}{\Sigma }_{j}^{+}\right)\right.\\ \qquad +\,{J}_{\pm \pm }\left({\alpha }_{ij}{\Sigma }_{i}^{+}{\Sigma }_{j}^{+}+{\alpha }_{ij}^{* }{\Sigma }_{i}^{-}{\Sigma }_{j}^{-}\right)\\ \qquad +\,\left.{J}_{\pm {{{\rm{z}}}}}\left({\Sigma }_{i}^{{{{\rm{z}}}}}\left({\beta }_{ij}{\Sigma }_{j}^{+}+{\beta }_{ij}^{* }{\Sigma }_{j}^{-}\right)+i\leftrightarrow j\right)\right].\end{array}$$
(6)

Here, αij takes the values 1, e±i2π/5 and e±i4π/5 depending on the bond orientation due to the 5-fold rotational symmetry, and \({\beta }_{ij}={({\alpha }_{ij}^{* })}^{2}\). The Hamiltonian in Eq. (6) is expressed in terms of local coordinate axes, where the local z-axis for each site is parallel to a high-symmetry axis of the icosahedron (See Supplementary Methods for detailed derivation of the effective pseudospin Hamiltonian and local axes.). The magnitudes of these spin exchange parameters will vary depending on the case. Here, for the simplest case, we first study the Ising limit with a finite Jzz and then consider the quantum fluctuations in the presence of J±.

Remarkably, we should emphasize that the spin Hamiltonian, H in Eq. (6), could be used to argue general characteristics of the multipolar pseudospin models even for the C5v symmetry rather than Ih. This is because the constraints on the Hamiltonian have their origin in the mirror reflection symmetry shared by the C5v and Ih groups. See Supplementary Methods and Supplementary Fig. 1 for detailed information. The Hamiltonian in Eq. (6) would be applicable for any Kramers or non-Kramers doublets with half-integer or integer values of J. The only difference between Kramers and non-Kramers doublets is the presence and the absence of the parameter J±z. This is originated from the fact that for non-Kramers doublet, z components represent magnetic dipoles, whereas x, y components represent quadrupoles or hexadecapoles, thus the coupling between Σz and Σ± is forbidden under the time reversal symmetry.

Geometrical frustration

Let us first consider the Ising model, where only Jzz is non-zero in Eq. (6). Figure 3 represents the structure of icosahedral quasicrystal descended from 6-dimensional hyperspace by the cut-and-project scheme60. As shown in Fig. 3, the distances between the centers of the icosahedrons vary. Particularly, the orthographic projection view of Fig. 3 shows that if we connect two sites of the magnetic atom whose distance is less than or equal to the length of an edge of the icosahedron shell, then there are many isolated icosahedron shells. See Supplementary Methods for detailed cut-and-project scheme for the icosahedral quasicrystal. In real-world materials, the distances between shells may vary depending on the structures of quasicrystals and approximants63,64,65,66,75. Furthermore, it is known that the inter-shell distance can be also controlled in terms of the external pressure63,76,77. Thus, for general argument, we mainly focus on the nearest neighboring sites in a single icosahedron and discuss the magnetic states. For ferromagnetic Jzz, it is obvious there are only two degenerate ground states, where every octupole points in local + z and − z directions, respectively.

Fig. 3: Icosahedral quasicrystal generated by the cut-and-project scheme from 6-dimensional hyperspace.
figure 3

Red dots represent the sites of the magnetic atom. We draw the sites forming the icosahedron shells only for visibility. The projection view is drawn to emphasize the high-symmetry of the icosahedral quasicrystal. The shortest distance between the centers of the icosahedrons has different values for each icosahedron shell in the quasicrystal. In the projection view, any pair of two sites are connected by the sky-blue line if their distance is less than or equal to the length of an edge of an icosahedron shell. There are many isolated icosahedron shells which have no connection to the other icosahedron shells. For the antiferromagnetic, Jzz, there is geometrical frustration on each icosahedron.

Full size image

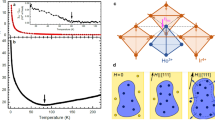
For the antiferromagnetic Ising model, where Jzz is positive, the presence of triangular faces in the icosahedron leads to geometric frustration. In this case, there exist 72 degenerate states that are classified into two groups based on symmetry grounds (i) 60 degenerate states without 5-fold rotational symmetry, (ii) 12 degenerate states with 5-fold rotational symmetry. Figure 4a shows an example of the first group of ground states. Note the octupolar moments arranged on the icosahedron in Fig. 4a do not have a 5-fold rotational symmetry axis. Since there are 6 independent choices for the Z-axis, by applying 5-fold rotational transformation around each Z-axis, we have 30 degenerate states. In addition, for each 30 degenerate states, the energy is invariant under the swap of two octupoles on the sites Q and R in Fig. 4a and c. Hence Mσ, the spatial mirror reflection with respect to the σ-plane depicted in Fig. 4c doubles the number of degenerate states with no 5-fold rotational symmetry, resulting in total 60 degenerate states. (See Supplementary Note for detailed discussion of the symmetry argument.). Figure 4b, d illustrate 5-fold rotational symmetric ground state. There are 12 independent choices for the rotational symmetry axis, Z-axis in Fig. 4b of the second group.

Fig. 4: Two distinct groups of octupolar ground states on an icosahedron for antiferromagnetic Jzz based on the symmetry ground.
figure 4

a 60 degenerate states with no 5-fold rotational symmetry. b 12 degenerate states with 5-fold symmetry. Z-axis is the 5-fold rotational symmetry axis in (b). c, d Top view along Z-axis in (a, b), respectively. (c) Mirror reflection with respect to σ plane containing Z-axis swaps the octupoles on the sites Q and R. This leads to another degenerate state which lacks the 5-fold symmetry. d The state depicted in (b) possesses 5-fold rotational symmetry along Z-axis.

Full size image

Quantum fluctuation

Now let us consider non-zero but small J± and study the effect of quantum fluctuations. To study the fluctuation effects, we introduce three subsets of the 72 degenerate states, A,B and C in terms of the orientation preserving icosahedral rotation group, I ⊴ Ih. Specifically, the subsets A and C are generated by applying the spatial rotations in I to the states in Fig. 4a, b, respectively. While, the subset B is generated by applying the coset, \({{{{\rm{IM}}}}}_{\sigma }=\{{{{\rm{g}}}}{{{{\rm{M}}}}}_{\sigma }| {{{\rm{g}}}}\in {{{\rm{I}}}}\}\) to the state in Fig. 4a. Thus, for \({H}_{\pm }={J}_{\pm }{\sum }_{\langle i,j\rangle }({\Sigma }_{i}^{+}{\Sigma }_{j}^{-}+{\Sigma }_{i}^{-}{\Sigma }_{j}^{+})\), two states in the same subset admit zero matrix element of H±. One can let \(\left\vert {\psi }_{{{{{\rm{A}}}}}_{n}}\right\rangle\), \(\left\vert {\psi }_{{{{{\rm{B}}}}}_{l}}\right\rangle\) and \(\left\vert {\psi }_{{{{{\rm{C}}}}}_{r}}\right\rangle\), where 1 ≤ n, l ≤ 30 and 1 ≤ r ≤ 12 be the states in A,B and C, respectively. Hence, in the sub-Hilbert space of the 72 Ising ground states, H± has the matrix representation, \({[{H}_{\pm }]}_{{{{\rm{A}}}},{{{\rm{B}}}},{{{\rm{C}}}}}\), given by

$${[{H}_{\pm }]}_{{{{\rm{A}}}},{{{\rm{B}}}},{{{\rm{C}}}}}=\left(\begin{array}{ccc}0&{T}_{{{{\rm{AB}}}}}&{T}_{{{{\rm{AC}}}}}\\ {T}_{{{{\rm{BA}}}}}&0&{T}_{{{{\rm{BC}}}}}\\ {T}_{{{{\rm{CA}}}}}&{T}_{{{{\rm{CB}}}}}&0\end{array}\right)$$
(7)

where \({T}_{{{{\rm{BA}}}}}={T}_{{{{\rm{AB}}}}}^{{\dagger} }\) is a 30 × 30 matrix, while \({T}_{{{{\rm{AC}}}}}={T}_{{{{\rm{CA}}}}}^{{\dagger} }\) and \({T}_{{{{\rm{BC}}}}}={T}_{{{{\rm{CB}}}}}^{{\dagger} }\) are 30 × 12 matrices. Here, each non-zero matrix element is J±. On symmetry grounds, we can write the general form of the ground state, \(\left\vert {{{\rm{GS}}}}\right\rangle\), as,

$$\left\vert {{{\rm{GS}}}}\right\rangle =a\mathop{\sum }\limits_{n=1}^{30}\left\vert {\psi }_{{{{{\rm{A}}}}}_{n}}\right\rangle +b\mathop{\sum }\limits_{l=1}^{30}\left\vert {\psi }_{{{{{\rm{B}}}}}_{l}}\right\rangle +c\mathop{\sum }\limits_{r=1}^{12}\left\vert {\psi }_{{{{{\rm{C}}}}}_{r}}\right\rangle ,$$
(8)

where we have only three real coefficients, a, b and c for \(\left\vert {\psi }_{{{{{\rm{A}}}}}_{n}}\right\rangle\), \(\left\vert {\psi }_{{{{{\rm{B}}}}}_{l}}\right\rangle\) and \(\left\vert {\psi }_{{{{{\rm{C}}}}}_{r}}\right\rangle\), respectively (See Supplementary Note for detailed discussion for the perturbative method.). The energy correction is E(a, b, c) = 〈GS∣H ± ∣GS〉.

First, considering J± < 0, the Lagrange multiplier method leads to \(a=b=(1+\sqrt{6})c/5\) for the ground state. Next, if J± > 0, E(a, b, c) is minimized when a = − b and c = 0. Remarkably, we have no degeneracy in either cases. Thus, any small quantum fluctuation given by H± leads to a ground state with particular superpositions of degenerate states (See Supplementary Note for detailed derivation).

To capture the entanglement, we compute the entanglement negativity of the state defined by \({{{{\mathcal{N}}}}}_{{{{\rm{E}}}}}={\sum }_{i}(\left\vert {\lambda }_{i}\right\vert -{\lambda }_{i})/2\), where λi are all eigenvalues of the partial transpose of the density matrix of the ground state, ρ78. \({{{{\mathcal{N}}}}}_{{{{\rm{E}}}}}=0\) if ρ is separable, while \({{{{\mathcal{N}}}}}_{{{{\rm{E}}}}} \,>\, 0\) for an entangled state. For the icosahedron shell, \({{{{\mathcal{N}}}}}_{{{{\rm{E}}}}}\) is computed by partitioning 12 vertices into two hemispherical region (one of them is highlighted as the blue shaded region in the inset of Fig. 5). Figure 5a illustrates the entanglement is instantaneously generated for non-zero J±.

Fig. 5: Quantum fluctuation effect of nonzero J±.
figure 5

a For nonzero J±, the entanglement negativity of the ground state, \({{{{\mathcal{N}}}}}_{{{{\rm{E}}}}}\), becomes finite. The blue shaded region of the icosahedron, as depicted in the inset, defines the sub-Hilbert space. Red arrows accentuate the local z axes. When J± = 0 (represented by the triangle), the state is separable. For J± > 0 (square, (b)), the ground state is composed of the states in A and B subsets without 5-fold symmetry, with equal probability but opposite sign. When J± < 0 (circle, (c)), all 72 degenerate states are combined in the ground state, as shown in (c).

Full size image

The quantum fluctuation effects originated from J±± and J±z appear in higher-order. In detail, let D and PD be the subspace of the degenerate ground states of the Ising model (either Jzz < 0 or Jzz > 0) and the projection operator to D, respectively. For additional terms in the Hamiltonian, say \({H}_{\pm \pm }={\sum }_{\langle i,j\rangle }[{J}_{\pm \pm }{\Sigma }_{i}^{+}{\Sigma }_{j}^{+}+h.c.]\) or \({H}_{\pm {{{\rm{z}}}}}={\sum }_{\langle i,j\rangle }[{J}_{\pm {{{\rm{z}}}}}{\Sigma }_{i}^{+}{\Sigma }_{j}^{{{{\rm{z}}}}}+h.c.]\), we have PDH±±PD = PDH±zPD = 0. This is because J ±±  and J±z terms do not preserve the total Σz. Thus, the degeneracy is not lifted at the first-order in perturbation theory. This implies that the quantum fluctuations originated from the J++ or J+z terms appear in higher-orders, for instance PDH ±± QDH±±PD, where QD = 1 − PD. On the other hand, J± terms in the Hamiltonian lift the degeneracy at the first-order because PDH±PD ≠ 0. As a result, compared to the J± term, J±± and J±z select a distinct linear superposition of the degenerate subspace of an icosahedron shell.

Influence of the inter-icosahedron interaction

Now let us discuss the inter-icosahedral interaction effect. See Supplementary Fig. 3 for the case of the ferromagnetic intra-icosahedron Ising interaction. Here, we consider the case of antiferromagnetic intra-icosahedron Ising interaction. Based on the self-similarity of the icosahedral quasicrystal, we have an enlarged icosahedral structure composed of 12 icosahedron clusters. Taking into account the nearest neighboring sites between the clusters, the interacting sites between the clusters form triangles. These are shown in Fig. 6a, b drawn as orange lines. Since these triangles are not shared, the energy for inter-clusters interaction should be minimized for each triangle. We also note that only 5 sites out of 12 sites in an icosahedron cluster interact with neighboring sites that belong to other icosahedron clusters. Hence, for each icosahedron, there are 7 sites which do not interact with other clusters. The configurations of these 7 sites are only determined by the local intra-cluster interactions. Let us consider the inter-clusters Ising interaction,

$${H}_{{{{\rm{inter}}}}}=\mathop{\sum}\limits_{\langle i,j\rangle }{J}_{{{{\rm{inter}}}}}{\Sigma }_{i}^{{{{\rm{z}}}}}{\Sigma }_{j}^{{{{\rm{z}}}}}.$$
(9)

For both Jinter > 0 and Jinter < 0, the inter-cluster interactions reduce the whole degeneracy of the enlarged icosahedron structure from 7212, that is composed of 12 icosahedrons. Figure 6a, b show the examples of the ground state configurations of ferromagnetic and antiferromagnetic inter-cluster Ising interaction, respectively. For instance, when Jinter < 0, every octupole connected by the orange lines should point either outside or inside of their icosahedron clusters (See the middle and right panels of Fig. 6a). On the other hand, for Jinter > 0, additional frustration effect exists on each orange triangle. Figure 6c shows an example of such geometrical frustration due to Jinter > 0. In this case, there are more number of frustrated configurations. We emphasize that such geometrical frustration emerges in the enlarged self-similar icosahedral structures in the quasicrystal.

Fig. 6: Examples of the classical octupolar configurations when the intra Ising interaction is antiferromagnetic, Jzz > 0.
figure 6

a Jinter < 0 and (b) Jinter > 0. The orange lines are drawn for emphasizing the inter-cluster interactions. a For each orange triangles, three octupoles should point either all-outside or all-inside of their icosahedron. c An example of the degenerate ground state due to the frustration of the antiferromagnetic inter-cluster interactions. For Jinter > 0, three octupoles for each orange triangles should satisfy 2-in-1-out or 1-in-2-out, which leads to the geometrical frustration on the enlarged spatial scale.

Full size image

Remarkably, even for the ferromagnetic inter-cluster interaction, the degeneracy of each icosahedron shell is reduced due to the inter-cluster interaction. Once the configuration of a single icosahedron shell is fixed, the configurations of the nearest neighboring icosahedron shells (five of them) are also partially determined due to the ferromagnetic inter-cluster interaction. For instance, if the icosahedron shell has the configuration belong to C group whose inter-cluster interacting sites are all pointing out of the icosahedron (red circles in Fig. 7), then at least two inter-cluster interacting octupoles in each neighboring icosahedron also points out of the icosahedron. This reduces the allowed manifold of the antiferromagnetic ground states on the neighboring icosahedron clusters. Refer to Fig. 7 for a specific example of this reduction.

Fig. 7: An example of the frustration on an icosahedron due to the ferromagnetic inter-cluster interactions.
figure 7

a For simplicity, we slice an icosahedron into 4 layers, each layer contains 1, 5, 5 and 1 octupoles, respectively. Red (silver) circles represent the octupoles pointing outside (inside) of the icosahedron shell. Half circles emphasize two-fold degrees of freedom. Here, we assume that due to the inter-cluster interactions, two neighboring octupoles are fixed as pointing outside of the icosahedron shell. Then, the octupole located at the bottom in the figure should be pointing inside of the icosahedron. There are three kinds of the configurations on the 5 sites that are interacting with the other icosahedrons. Configuration (b) which has all pointing outside configuration belongs to the C group, and hence it determiines a configuration in other sites. On the other hand, other two kinds of configurations have further frustrated degrees of freedom. In detail, the configuration (c) admits 3 × 2 = 6-fold degeneracy, while the configuration (d) admits 3 + 2 = 5-fold degeneracy. In total, only 12 fold degeneracy is survived under the inter-cluster interactions.

Full size image

One may ask the influence of the quantum fluctuation under the inter-icosahedron interaction. To address it, we consider ∣Jinter∣ > Δ where Δ is the gap of the first excited state of an isolated icosahedron shell with intra-shell J±. See Supplementary Fig. 4 for detailed information of the gap. First of all, for both cases of the sign of Jinter, it selects particularly degenerate manifold among 72 states. This is because the inter-shell interaction (partially) selects the configurations of the sites in neighboring icosahedrons. For instance, for Jinter < 0, each separated orange triangles in the right panel of Fig. 6a should admit either all-in- or all-out octupole configurations. This reduces the ground state manifold of the enlarged icosahedral structure from 7212 dimensions, which is realized in the absence of inter-shell interaction. Note that without quantum fluctuations on each icosahedron shell, the allowed ground states could be written as the product state i.e. \(\left\vert {{{\rm{GS}}}}\right\rangle ={\otimes }_{i = 1}^{12}\left\vert {\psi }_{{k}_{i}}^{(i)}\right\rangle\). Here, 1 ≤ ki ≤ 72 is the index of 72 kinds of allowed antiferromagnetic frustrated ground configurations on an isolated icosahedron shell. However, importantly, only certain set of ki is selected if we take into account Jinter.

To address quantum fluctuations, let us consider the intra-shell, J± term. We neglect the inter-shell interaction J±, because it would be much smaller than both inter-shell Ising interactions and intra-shell quantum fluctuations. Since intra-shell J± term only flips two neighboring octupoles in the same icosahedron shell, two ground states, say \(\left\vert {{{{\rm{GS}}}}}_{{{{\rm{a}}}}}\right\rangle\) and \(\left\vert {{{{\rm{GS}}}}}_{{{{\rm{b}}}}}\right\rangle\) such that 〈GSa∣H±∣GSb〉 ≠ 0 have to be obtained by flipping two neighboring octupoles in an icosahedron shell, keeping all other octupoles unchanged. However, for Jinter < 0, if we flip an octupole on an icosahedron shell that is interacting with neighboring icosahedron shells, then the octupoles in different icosahedron shells also should be flipped due to the inter-shell interaction. Thus, \(\left\vert {{{{\rm{GS}}}}}_{{{{\rm{a}}}}}\right\rangle\) and \(\left\vert {{{{\rm{GS}}}}}_{{{{\rm{b}}}}}\right\rangle\) should share the same configuration of the 60 inter-shell interacting sites. Hence, one can classify the state that are mixed due to J± in terms of the configurations of the 60 inter-shell interacting sites.

Figure 8 explains how the ground states are chosen in the presence of both the inter-shell interactions and intra-shell quantum fluctuations. Although we assume Jinter < 0, here, the similar argument would be applicable for Jinter > 0 along with additional frustration effects on the orange triangle. Note that Jinter restricts the possible octupole configurations on each separated triangles as shown in Fig. 8a. Here, blue and red triangles represent all-in-, and all-out-pointing octupoles configurations, as exemplified in the right panel of Fig. 8a. Thus, the classical ground states are classified in terms of the configurations of these 20 triangles, red or blue colored. Based on the duality of the icosahedron, the configurations of 20 triangles are mapped onto the sites in the dodecahedrons as shown in Fig. 8b. In detail, the red and blue dots in Fig. 8b correspond to the red and blue triangles in Fig. 8a. The dashed lines are drawn if there are the sites connected by the intra-shell interactions in neighboring triangles. The Hilbert space is factorized into many sub-Hilbert spaces classified in terms of the configurations of the dodecahedron i.e. inter-shell interacting 60 sites, and hence the Hamiltonian, H is now block diagonalized as shown in Fig. 8c. The ground state is originated from the largest dimensional sub-Hilbert space. In Fig. 7a–c, we see that the maximal dimension of a sub-Hilbert space is 520 when all the icosahedron shells correspond to the case of Fig. 7c. Indeed, Fig. 8b shows two examples of the doedcahedrons correspond to the 520-dimensional sub-Hilbert spaces. Figure 8c represents these maximal dimensional sub-Hilbert space as the green squares. Furthermore, since the quantum fluctuation is intra-shell interaction, the ground state of the sub-Hilbert space is given by the product state of the ground state of each icosahedron shell. The intra-shell J± Hamiltonian on an icosahedron shell is given by 5 × 5 matrix which is much smaller than the case of the isolated icosahedron shell, 72 × 72 matrix. Explicit forms of the H± matrix and the ground state (assuming J± > 0) is shown in Fig. 8d, e, respectively. Here, ν and μ are the indices of the sub-Hilbert space and icosahedron shells, respectively. \(\phi =(1+\sqrt{5})/2\) is the golden ratio. As a result, we have a ground state given \(\left\vert {{{{\rm{GS}}}}}^{(\nu )}\right\rangle ={\otimes }_{\mu = 1}^{\mu = 12}\left\vert {{{{\rm{gs}}}}}_{\mu }^{(\nu )}\right\rangle\) for each ν-th sub-Hilbert spaces. Thus, we have large degeneracy of the ground states. Note that such degeneracy would be lifted by the inter-shell J± that is small compared to other parameters in general. We emphasize that the inter-shell interactions reduce the ground state manifold, and hence the ground state on each icosahedron shell is changed.

Fig. 8: Selection of the ground state in the presence of both Jinter and intra-shell quantum fluctuation.
figure 8

a Geometrical structure of the inter-shell interactions (orange lines). For Jinter < 0, ferromagnetic Ising inter-shell interactions, each separated triangles of orange lines should admit either all-in- or all-out octupole configurations as exemplified in the right panel. In the left panel, we assign red and blue colors on some triangles as the all-in-, and all-out-pointing configurations, respectively. b 60 inter-shell interacting sites and their interactions mapped onto a dodecahedron, which is a dual of the icosahedron. Here, red and blue dots correspond to the red and blue triangles including three octupoles in (a). Dashed black lines connect two dots if these two dots (originally red or blue triangles) contain the sites belonging to original single icosahedron shell. c Block diagonalized Hamiltonian including intra-shell Jzz, J± and inter-shell Ising interaction, Jinter. The blocks of the Hamiltonian are classified in terms of the configurations of the 60 inter-shell i.e. the configurations on the dodecahedrons in (b). The maximal dimension of the sub-Hilbert space is 512 which is much smaller than the total dimension, 7212 (the case for Jinter = 0). d Effective Hamiltonian for the quantum fluctuation on μ-th icosahedron for ν-th 512-dimensional sub-Hilbert space, written as \({H}_{\pm }^{\mu ,\nu }\). The basis are chosen as the 5-types of configurations on a shell (See Fig. 6(c)). e The ground state of \({H}_{\pm }^{\mu ,\nu }\) for J± > 0 for μ-th icosahedron, \(\left\vert {{{{\rm{gs}}}}}_{\mu }^{(\nu )}\right\rangle\). Here, \(\phi =(1+\sqrt{5})/2\) is the golden ratio. The ground state defined in the enlarged icosahedral structure is classified by the configurations of 60 inter-shell interacting octupoles as \(\left\vert {{{{\rm{GS}}}}}^{(\nu )}\right\rangle ={\otimes }_{\mu = 1}^{12}\left\vert {{{{\rm{gs}}}}}_{\mu }^{(\nu )}\right\rangle\).

Full size image

Lastly, let us briefly explain the potential influence of the further neighbor interactions. First, further inter-cluster interactions between neighbors affect the sites that do not interact with neighboring icosahedrons. This further reduces the degeneracy. Second, isolated icosahedron clusters also begin to interact via further neighbor interactions and should be considered. Nevertheless, we suspect that our discussion of the nearest neighbor inter-cluster interaction can be applied analogously to investigate the configurations of the more extended icosahedral structures based on the repetitive self-similar structure of the quasicrystal.

Discussion

In summary, our findings indicate that magnetic quasicrystalline systems contain multipolar degrees of freedom, which arise from the interplay between spin-orbit coupling and CEF splitting of the icosahedral point group symmetry. Despite extensive prior research on magnetic properties in quasicrystals, the presence and significance of multipolar degrees of freedom have yet to be identified. In our study, we demonstrate for the first time that noncrystallographic point group symmetry can accommodate unconventional degrees of freedom and we examine their characteristics. The multipole degrees of freedom are clarified for different values of J, depending on whether there is perfect icosahedral symmetry Ih or five-fold symmetry C5v. Strikingly, it has been demonstrated that pure octupolar degrees of freedom emerge for J = 7/2 under Ih symmetry. In this case, the Kramers doublet has zero expectation values for both magnetic dipoles and quadrupoles, but the rank 3 tensors describing the octupole degrees of freedom have nonzero expectation values. Based on the symmetry transformation, we further clarify each component of the pseudospin-1/2 in terms of magnetic octupoles as discussed in Eq. (4). On symmetry grounds, we also derive the spin Hamiltonian with four independent parameters. For antiferromagnetic Ising model, magnetic frustration leads to 72 degenerate states for a single icosahedron. For a small but finite J±, quantum fluctuations make a particular mixture of these degenerate states. It makes different but non-degenerate ground state for (anti-) ferromagnetic J±, producing a finite entanglement even for arbitrary small J±. In addition, we show that the inter-icosahedron interaction prefers a particularly degenerate manifold among the 72 states in each icosahedron shell, and thus selects a different mixture of the Ising states under the intra-shell interaction J±. Depending on the inter-shell distances, possible macroscopic degeneracy and entanglement of octupoles would be an interesting future work. The self-similarity of the quasicrystals would allow the real-space renormalization group approach to explore potential quantum phase transitions. Note that such self-similar structures are absent in the periodic approximants. Also, the studies in the presence of J±± and J±z, which do not preserve the total Σz, can be explored which we leave as a future work.

Such octupolar degrees of freedom can be found in rare-earth based magnetic quasicrystals and approximants such as Au-Al alloys, Cd-Mg alloys including rare earth ions and etc6,49,62,63,64,68,71,79,80,81,82,83,84,85. However, many of the currently known magnetic quasicrystals have problems with intermediate valences and some mixed sites between non-rare earth atoms79,80,82,85,86,87,88,89,90,91,92. It makes imperfect symmetries, allowing small deviations from perfect non-crystallographic point group symmetries. Nevertheless, it is expected that advances in chemical synthesis techniques could make the successful synthesis of finely controlled icosahedral quasicrystals possible80,83,87,93, and it may give us a chance to discover pure magnetic octupoles or even higher order multipolar degrees of freedom and their intriguing physics.

To detect the pure octupolar orders, one can use the symmetry allowed higher order time-reversal odd fields. For instance, one can detect the z component of the octupoles by coupling to the magnetic field tensor which has the same symmetry as \(5{B}_{{{{\rm{z}}}}}^{3}-3{B}_{{{{\rm{z}}}}}({{{\bf{B}}}}\cdot {{{\bf{B}}}})\), where B is the external magnetic field and Bz is its z component. Also, one can use the magnetostriction effect as discussed in refs. 59,94,95.

Our work shows that the multipolar degrees of freedom arise naturally in icosahedral quasicrystals. It breaks the ground in the magnetism of quasicrystals and raises several interesting questions. One could explore magnetic quasicrystals looking for hidden phases, magnetic frustration induced long-range entanglement such as spin liquids and non-Fermi liquids due to the exotic Kondo effect6,96,97,98,99,99,100,101. Our study motivates to experimentally find rare-earth icosahedral quasicrystals beyond conventional magnetism in periodic crystals. The field of magnetic quasicrystals is an interesting research area, and continuous progress in both experimental and theoretical studies is leading us to discover anomalous magnetic phenomena in quasicrystals.

Methods

Exploration of the multipoles

To construct the crystal electric field (CEF) Hamiltonian, we utilized the simplified point charge model. In this model, point charge ligands are positioned on each of the 12 vertices of the icosahedron that surrounds the rare earth atom. For the charge impurity model, where the icosahedral point group symmetry breaks down to the C5v, we place the charge impurity at the ligand site on the local z-axis. The Stevens parameter is calculated using numerical values of the Stevens factors and radial integrals of rare-earth ions, as presented in102. Our method involves block diagonalizing the CEF Hamiltonians and searching for possible doublet eigenspaces and their corresponding multipolar degrees of freedom. We determine the presence of higher-order multipolar degrees of freedom by examining the vanishing of lower magnetic or electric multipole operators. To construct the spin Hamiltonian that is allowed by symmetry on the icosahedral quasicrystal, we apply both the icosahedral point group symmetry and time-reversal symmetry to the octupolar pseudospin operators. Further details are described in the Supplementary Methods.

Construction of the icosahedral quasicrystal

The icosahedral quasicrystal is constructed using the standard cut-and-project scheme explained in detail in the Supplementary Methods. To find the ground states of the Ising model under open boundary conditions, we utilized the exact diagonalization method and symmetry ground. Using quantum fluctuation, we have conducted an analytical study on the entangled pure ground state and computed its entanglement negativity on the single icosahedron shell through the exact diagonalization method.