Introduction

The discovery of topological insulators and topological superconductors completely revolutionized the usual classification of the phases of matter, shedding light on the fact that the Ginzburg-Landau classification was but a partial description1. Starting from the first feasible proposal for a topological insulator2, in less than two decades the field has undergone several major breakthroughs, like the classification of topological phases by symmetry classes3, the discovery of higher order topology4 and, very recently, of non-Hermitian topology5. In this context, the dimensionality of the systems plays a crucial role for the definition of the topological invariants. Indeed, these are typically defined relative to systems compactified in all directions. The bulk boundary correspondence, then, suggests that when the system is non-trivial, and is made semi-infinite in one direction, metallic states appear at the boundary. These metallic states persist as long as the uncompactified dimension of the system does not become comparable with their decay length.

The improvement in the nanostructuration of topological phases of matter has made it possible to realize samples in which this condition is not met6,7. In this regard, a very active branch of research is nowadays related to the study of finite size effects on topological phases6,7,8,9,10,11,12,13,14,15,16,17,18. Indeed, dimensional crossovers between topological phases is a promising way to engineer novel topological systems19,20. In this context, the way has been paved by the extensive studies performed on graphene nanoribbons (GNRs), that have revealed an extremely rich phenomenology. For instance, it was found that these systems, depending on the nanoribbon width and on the nature of its terminations, can host robust topological bound states21,22 amenable to detection with local probes23,24,25.

Taking a step back, even before the first theoretical proposal for a symmetry protected topological insulator was conceived, many topologically non-trivial systems had been object of study, first of all the quantum Hall system26. In that context, a milestone for the comprehension of topological phases had been conceived: the Haldane model27. Dated back to 1988, it represented the first theoretical proposal for a system realizing a quantum anomalous Hall phase and is now regarded as the most famous model for a Chern insulator. Even more importantly, the time reversal doubling of the Haldane model results in the Kane-Mele model which, describing spinful fermions on a honeycomb lattice with strong spin-orbit interaction, is the prototypical model of a time reversal protected topological phase28,29. Although the Kane-Mele model was originally proposed to describe the electrons in graphene, where the predicted spin Hall phase cannot be observed since the spin-orbit coupling is too small to yield a sizable topological gap, it has recently found a direct experimental realization in Bismuthene30 and Germanene31, and is hence receiving renewed attention.

In light of this, Haldane model nanoribbons represent a significant model for studying the physics of these newly discovered honeycomb-based topological materials. Even more importantly, they configure themselves as the optimal theoretical playground for merging the physics of nanostructured topological insulators and the one inherited from GNRs. In this paper, we focus on zigzag Haldane nanoribbons and assess the effects of dimensional reduction on the topological phase of the Haldane model. We find that, for thin enough strips, there are multiple regions of the parameter space in which the chiral edge states gap out and, correspondingly, degenerate pairs of quasi zero-dimensional (0D) end-states appear whose energy lies inside the gap. Such regions however are intercalated, through topological quantum phase transitions, to phases without bound states. We hence unveil a complex, width-dependent, reentrant quantum phase diagram, which we characterize by numerically computing a well established indicator for the classification of topological phases in (effectively) one-dimensional systems, that is, the Zak phase32,33,34. Moreover, we explain the mechanism leading to the mass inversion via a phenomenological low energy theory, effectively modeling the chiral edge states coupling. Finally, we show that domain walls in the on-site staggered potential distribution can localize quasi 0D bound states. These Jackiw-Rebbi like states35, ubiquitous in topological phases of matter11,36,37,38,39, retain a fractional charge of \(\pm \frac{e}{2}\) (e the electron charge) and are found to be robust against the introduction of random on-site disorder. More generally, our results demonstrate that the physics of coupled topological edges can be way richer than what is expected from naive low energy theories.

Results

Haldane model on zigzag nanoribbons

The Haldane model27 describes spinless fermions on a honeycomb lattice, pierced by an orthogonal periodic magnetic field and having the full symmetry of the lattice and zero net flux over the unit cell. Time reversal symmetry is broken for the model, so that the transverse Hall conductance can be non-trivially quantized40. We denote the two sublattices of the honeycomb lattice as A and B and we choose as primitive vectors a1 = a(1, 0) and \({{{{\bf{a}}}}}_{2}=a(\frac{1}{2},\frac{\sqrt{3}}{2})\). Moreover, we place the unit cell origin on the A sites, so that the basis vectors are given by δa = (0, 0) and \({{{{\boldsymbol{\delta }}}}}_{b}=a(\frac{1}{2},\frac{1}{2\sqrt{3}})\). The Hamiltonian is thus given by

$$\begin{array}{lll}{{{\mathcal{H}}}}={t}_{1}\left(\mathop{\sum}\limits_{l,n}{a}_{ln}^{{\dagger} }{b}_{ln}+{a}_{ln}^{{\dagger} }{b}_{l-1n}+{a}_{ln}^{{\dagger} }{b}_{ln-1}\right)+\,{{\mbox{h.c.}}}\,\\\qquad\;+\,{t}_{2}{{{{\rm{e}}}}}^{{{{\rm{i}}}}\phi }\left(\mathop{\sum}\limits_{l,n}{a}_{ln}^{{\dagger} }{a}_{l+1n}+{a}_{ln}^{{\dagger} }{a}_{l-1n+1}+{a}_{ln}^{{\dagger} }{a}_{ln-1}\right)+\,{{\mbox{h.c.}}}\,\\ \qquad\;+\,{t}_{2}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}\phi }\left(\mathop{\sum}\limits_{l,n}{b}_{ln}^{{\dagger} }{b}_{l+1n}+{b}_{ln}^{{\dagger} }{b}_{l-1n+1}+{b}_{ln}^{{\dagger} }{b}_{ln-1}\right)+\,{{\mbox{h.c.}}}\,\\\qquad\; +\,m\left(\mathop{\sum}\limits_{l,n}{a}_{ln}^{{\dagger} }{a}_{ln}-{b}_{ln}^{{\dagger} }{b}_{ln}\right),\end{array}$$
(1)

where aln (bln) destroys a fermion at la1 + na2 + δa(b); t1 and t2 parameterize the intensity of the nearest and next to nearest neighbor hoppings respectively; ϕ is a phase accounting for the staggered magnetic flux inside the unit cell and m tunes a term of staggered on-site potential breaking inversion symmetry. In the topological phase, that occurs for \(| m/{t}_{2}| < 3\sqrt{3}\sin \phi\), the bulk bands are gapped and the Chern number40 has a non-trivial value (c = ± 1)27.

Correspondingly, in a strip geometry chiral modes localized on opposite edges and with gapless dispersion relation occur, in accordance with the bulk boundary correspondence. This can be explicitly seen by imposing periodic boundary conditions (PBC) in the a1 direction and going in k-space. For a strip of length L = Na, the Fourier transformation is defined as

$${a}_{ln}=\frac{1}{\sqrt{N}}\mathop{\sum}\limits_{k}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}k{x}_{ln}^{a}}{a}_{n}(k)\qquad {x}_{ln}^{a}=la+\frac{n}{2}a,$$
(2)
$${b}_{ln}=\frac{1}{\sqrt{N}}\mathop{\sum}\limits_{k}{{{{\rm{e}}}}}^{-{{{\rm{i}}}}k{x}_{ln}^{b}}{b}_{n}(k)\qquad {x}_{ln}^{b}=la+\frac{n+1}{2}a,$$
(3)

with the Bloch momenta discretized as \({k}_{j}=\frac{2\pi }{Na}j,\,j=0,\ldots ,N-1\). The Bloch Hamiltonian is found to be of the form (see also41)

$${{{\mathcal{H}}}}(k)=\left[\begin{array}{cccccccc}g(\tilde{k},\phi )+m&2{t}_{1}\cos \left(\frac{\tilde{k}}{2}\right)&g\left(\frac{\tilde{k}}{2},-\phi \right)&0&0&0&\cdots \,&0\\ 2{t}_{1}\cos \left(\frac{\tilde{k}}{2}\right)&g\left(\tilde{k},-\phi \right)-m&{t}_{1}&g\left(\frac{\tilde{k}}{2},\phi \right)&0&0&\cdots \,&0\\ g\left(\frac{\tilde{k}}{2},-\phi \right)&{t}_{1}&g\left(\tilde{k},\phi \right)+m&2{t}_{1}\cos \left(\frac{\tilde{k}}{2}\right)&g\left(\frac{\tilde{k}}{2},-\phi \right)&0&\cdots \,&0\\ 0&g\left(\frac{\tilde{k}}{2},\phi \right)&2{t}_{1}\cos \left(\frac{\tilde{k}}{2}\right)&g\left(\tilde{k},-\phi \right)-m&{t}_{1}&g\left(\frac{\tilde{k}}{2},\phi \right)&\ddots &0\\ \vdots &\ddots &\ddots &\ddots &\ddots &\ddots &\cdots \,&\vdots \end{array}\right],$$
(4)

with \(g(\tilde{k},\phi )=2{t}_{2}\cos (\tilde{k}+\phi )\) and \(\tilde{k}=ka\).

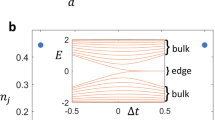
In Fig. 1a is shown a schematic representation of a strip with zigzag edges, Ny = 60 sites in the vertical direction, and PBC along the a1 direction. In Fig. 1b are reported the corresponding energy bands, obtained via numerical tight-binding diagonalization. Inside the bulk gap are clearly visible the two modes corresponding to the chiral edge states characterizing the topological phase.

Fig. 1: Haldane chiral modes in a wide zigzag nanoribbon.
figure 1

a Scheme of the lattice with PBC along the a1 direction. The dashed red lines at the two ends of the strip mark the sites that are connected by PBC. b Bands of the Haldane model in a strip configuration with zigzag edges, with PBC along the a1 direction and Ny = 60 sites in the y (or a2) direction. The parameters are set as t1 = 1, t2 = 0.3, m = 0, ϕ = π/2.

Full size image

It can be expected that by reducing the strip width, the chiral edge states may hybridize because of spatial overlap, giving rise to a gap opening in the edge spectrum. The length scale at which this phenomenon becomes relevant is defined by the decay length of the edge states, that, for the Haldane model on zigzag nanoribbons, has been found to be42,43

$${\xi }_{{{{\rm{loc}}}}}\approx \frac{\sqrt{3}}{2}{\left[\log \left\{\sqrt{1+{\left(\frac{{t}_{1}}{4{t}_{2}}\right)}^{2}}+\frac{{t}_{1}}{4{t}_{2}}\right\}\right]}^{-1}.$$
(5)

This kind of behavior has been explicitly proven in several contexts8,44. In spite of this, an analysis of the topological character of the gapped phases originated by finite size effects is still missing in the context of Chern insulators. In the next section, the results of such a study are presented.

Emerging quasi 1D topological phase diagram

We start by numerically computing the amplitude of the gap Δ as a function of the staggered on-site potential m. We set the energy scale to t1 = 1, and we impose t2 = 0.3 and ϕ = π/2, so that the topological bulk gap of the Haldane model is maximized. We perform our analysis for the Haldane strip with PBC for the different widths Ny = 4, 6, 8, 10. The results are reported in Fig. 2.

Fig. 2: Energy gap and Zak phase.
figure 2

Gap width Δ (top panels) and Zak phase φ (bottom panels) as a function of the staggered on-site potential m, computed for strips of various widths: (a, e) Ny = 4; (b, f) Ny = 6; (c, g) Ny = 8; (d, h) Ny = 10. The model parameters are set to t1 = 1, t2 = 0.3 and ϕ = π/2. For Ny = 6 and Ny = 10 the system is gapless at m = 0. In correspondence of every gap closing the Zak phase jumps of π.

Full size image

By comparing the top panels (Fig. 2a–d) it appears that the number of gap closings and reopenings grows monotonically with the strip width. This non trivial pattern hints to the fact that a topological phase transition may be associated with the gap closings. Interestingly, for the strips whose number of sites in the vertical direction is given by Ny = 4M + 2, the edge spectrum is gapless for m = 0: in these cases, despite the wave functions of the chiral modes on opposite edges are brought in close proximity, they do not hybridize with each other. This counterintuitive behavior is proven analytically in Supplementary Note 1.

In order to characterize the topology of the zigzag Haldane strips, we use a well established tool for assessing the topological properties of 1D solids: the Zak phase32, i.e., the natural open-loop extension of the Berry phase45 when the parameter space is the Brillouin zone. The Zak phase associated with an isolated band was originally defined in terms of the cell-periodic Bloch functions \(\left\vert {u}_{k}\right\rangle\) as32:

$$\varphi ={{{\rm{i}}}}\int\nolimits_{0}^{2\pi /a}{{{\rm{d}}}}k\langle {u}_{k}| {\partial }_{k}| {u}_{k}\rangle .$$
(6)

However, the above definition cannot be applied in the present case. Indeed, we are dealing with a multiband system in which the valence bands may cross each other and whose Hamiltonian can only be diagonalized numerically. Thus, we follow the prescription given in46 for the multi-band case. Given a discretization of the Brillouin zone \({k}_{j}=\frac{2\pi }{a}\frac{j}{N},\,j\in \{0,\ldots ,N-1\}\), for each momentum kj we compute a basis of eigenstates of the Hamiltonian in Eq. (4) for the occupied bands. The resulting Ny-dimensional vectors will be denoted as \(\left\vert {u}_{n{k}_{0}}\right\rangle ,\ldots ,\left\vert {u}_{n{k}_{N-1}}\right\rangle\), n being the band index. Then we enforce the periodic gauge, by defining46

$${\left\vert {u}_{n{k}_{N}}\right\rangle }_{\ell }={{{{\rm{e}}}}}^{-{{{\rm{i}}}}\frac{2\pi }{a}{t}_{\ell }}{\left\vert {u}_{n{k}_{0}}\right\rangle }_{\ell },$$
(7)

where \({\left\vert {u}_{n{k}_{j}}\right\rangle }_{\ell }\) is the ℓ-th component of the eigenvector \(\left\vert {u}_{n{k}_{j}}\right\rangle\) and tℓ the x position of the ℓ-th site inside the strip unit cell47, whose origin we place on the A site at the bottom edge. The Zak phase for the occupied bands is thus defined as46,47,48

$$\varphi =-\Im \log \det \mathop{\prod }\limits_{j=0}^{N-1}S({k}_{j},{k}_{j+1}),$$
(8)

with the overlap matrix S given by46,47,48

$$S{({k}_{j},{k}_{j+1})}_{mn}=\langle {u}_{m{k}_{j}}| {u}_{n{k}_{j+1}}\rangle .$$
(9)

This formula is unaffected by any erratic behavior of the phase randomly appended to the eigenvectors by the numerical diagonalization routine48. It must be noted that since the Hamiltonian in Eq. (4) is real, the Zak phase can only be 0 or π. The values obtained for the Zak phase at different values of m are reported in the bottom panels of Fig. 2, below the corresponding plots of the energy gap. We find that the Zak phases jump of π at each gap closing, confirming that some kind of topological phase transition actually occurs.

In order to gain any insight about which phase is trivial and which is topological we need to make some more physical considerations. As a matter of fact, the Zak phase itself does not have an absolute meaning33,49,50, since its value depends on the choice of the unit cell origin in real space. However, the difference between the values of the Zak phases in two regions of the parameter space is uniquely defined (modulo 2π).

In the large m limit, the system at half filling is expected to be a trivial insulator: in fact, in this scenario the electrons localize on the sublattice which is lower in energy (depending on the sign of m) and the hoppings between sites are suppressed. In view of this, we expect the regions of parameter space characterized by a value of the Zak phase differing by π (0) from that of the large m limit to be topologically non-trivial (trivial). It is worth pointing out that for Ny = 6 and Ny = 10 the limits m → ± ∞ correspond to different values of the Zak phase. We prove analytically in Supplementary Note 2 that this is a general fact for Ny = 4M + 2. In these cases, the comparison of the Zak phases should be made with the m → − ∞ limit for negative values of m and with the m → ∞ limit for positive ones. The phase diagram emerging from this argument is depicted in Fig. 3, where for each of the widths considered a star is drawn in every region of the parameter space which is expected to be topologically non-trivial. By virtue of bulk boundary correspondence, quasi 0D bound states should occur when the quasi 1D strips are considered under open boundary conditions (OBC) along the a1 direction and the parameters fall inside one of the topological regions depicted in Fig. 3.

Fig. 3: Emerging phase diagram.
figure 3

Phase diagram of the model as a function of the staggered on-site potential m for different widths: (a) Ny = 4; (b) Ny = 6; (c) Ny = 8; (d) Ny = 10. The model parameters are set to t1 = 1, t2 = 0.3 and ϕ = π/2. The regions of the parameter space where a star is drawn, are those expected to be topologically non trivial. The yellow and red dots in (d) mark the two phases inspected in Fig. 6.

Full size image

To check our predictions we perform numerical diagonalization of the model in an uncompactified geometry along the a1 direction and we inspect the low energy spectra in the different regions of the parameter space. The OBC strips are cropped with a rectangular geometry, with the long edges parallel to a1. In Fig. 4, for each of the widths taken into account, the bands in PBC geometry (Panels a–d) and the corresponding low energy spectra in the OBC case (Panels e–h) are reported. The values of m at which the diagonalization was performed for each strip, were chosen close to the point of the topological regions where the gap was maximum (cf. Fig. 2a–d). The spectra of the finite size systems present two degenerate eigenvalues located inside the gap. In Panels i–l we report the 1D profile of the probability density distributions corresponding to the eigenvalue n∘10 (marked in orange) of the spectra in Panels e–h respectively as a function of the position, together with insets representing the corresponding unprojected probability densities directly on the strips. From the localization pattern of these states, we conclude that the in-gap doublets characterizing the topological phases depicted in Fig. 3 correspond to quasi zero-dimensional bound states exponentially localized at the two ends of the strips. We numerically checked the robustness of these 0D bound states against the introduction of random on-site disorder finding that, though their energy is inevitably slightly shifted, they survive as long as the disorder strength does not become comparable with the gap width (see Supplementary Note 3).

Fig. 4: Topological quasi 0D bound states.
figure 4

Results from numerical diagonalization in topologically non-trivial regions for different widths: (a, e, i) Ny = 4; (b, f, j) Ny = 6; (c, g, k) Ny = 8; (d, h, l) Ny = 10. For different values of m for each of the widths considered (respectively 0, 0.5, 0.8, 0.92), the top row reports the bands of the strips with PBC along x (a1) and the mid row reports the low energy spectra of the corresponding OBC counterparts, obtained for strips of length 20a (e), 40a (f), 80a (g), 160a (h). The values of m chosen for each strip belong to the regions marked with a star in Fig. 3. A doublet of degenerate modes (marked in blue and orange) is visible inside each gap of the OBC spectra: these correspond to bound states localized at the ends of the strips. The 1D probability density profiles of the states associated to the eigenvalue n∘10 (marked in orange) of each of the spectra (e–h) are reported in the bottom row (i–l) as a function of the position for the left half of the various strips (x < 0). For each of these plots, the insets show the unprojected probability densities. The model parameters are set to t1 = 1, t2 = 0.3 and ϕ = π/2.

Full size image

The results just discussed prove that the dimensional reduction of the Haldane model, when operated on a strip with zigzag edges, gives rise to a reentrant topological phase diagram, characterized by the emergence of degenerate doublets of in-gap 0D end states. Quite curiously, such phenomenology has no counterpart in the case of armchair nanoribbons, at least in the parameter range we numerically inspected. A qualitative motivation of this peculiar asymmetry is given by the end of the next subsection, where we interpret our results through an effective model.

Low energy theory

In order to understand our findings, we frame them into an effective low energy theory. The minimal low energy model describing the coupling between the two counter-propagating edge states in a zigzag Haldane nanoribbon would be

$${H}_{{{{\rm{edge}}}}}=\left[{v}_{F}^{{{{\rm{ZZ}}}}}(k-\pi )+\tilde{m}\right]{\tau }_{z}+{{{\mathcal{M}}}}{\tau }_{x},$$
(10)

where42

$${v}_{F}^{{{{\rm{ZZ}}}}}\approx \frac{6{t}_{2}{t}_{1}}{\sqrt{{t}_{1}^{2}+16{t}_{2}^{2}}},\qquad \tilde{m}\approx \frac{m{t}_{1}}{\sqrt{{t}_{1}^{2}+16{t}_{2}^{2}}}.$$

Unfortunately, here \({{{\mathcal{M}}}}\) is an effective coupling induced by the spatial proximity between the two zigzag edges in the thin strip limit. As such, in principle it depends in a non trivial way on all of the model parameters, as well as on the Bloch momentum k. This severely hinders the derivation of a reliable low energy theory for the present model. Nevertheless, we can still achieve some qualitative predictions– at least for m = 0 –by the following hand waving argument. To effectively describe the coupling of the chiral edge states, we consider two 1D chains, representing the two edges of the zigzag nanoribbon. We assume that the sites of the two chains are connected via a coupling which decreases exponentially with the distance, as it is usually done when modeling proximity effects. However, we add a crucial physical input: We introduce a sharp cutoff in the hopping range, effectively coupling only sites that in the actual nanoribbon are connected by the minimum amount of first neighbor hoppings. The motivation behind this choice, is that the coupling between any other pair of edge sites would represent a higher order (negligible) correction.

Omitting the details of the derivation, for which we refer the interested reader to Supplementary Note 4, we find for the two classes considered (Ny = 4M or Ny = 4M + 2) and assuming m = 0

$${N}_{y}=4M:\qquad {{{{\mathcal{M}}}}}^{{{{\rm{teo}}}}}(k)=\tilde{\Delta }\left[1+\mathop{\sum }\limits_{j=1}^{M}2\cos (kj){{{{\rm{e}}}}}^{-\left(\sqrt{{w}^{2}+{j}^{2}}-w\right)/\xi }\right],$$
(11)
$${N}_{y}=4M+2:\quad {{{{\mathcal{M}}}}}^{{{{\rm{teo}}}}}(k)=\tilde{\Delta }\mathop{\sum }\limits_{j=0}^{M}2\cos (k(j+1/2)){{{{\rm{e}}}}}^{-\left(\sqrt{{w}^{2}+{(j+1/2)}^{2}}-w\right)/\xi },$$
(12)

where \(w=\frac{\sqrt{3}}{2}\frac{{N}_{y}}{2}-\frac{1}{\sqrt{3}}\) is the strip width and ξ is of the order of the chiral edge states localization length (Eq. (5)).

To benchmark our results, we extract the low energy bands directly from the exact numerical diagonalization. Let us denote by \({E}_{{N}_{y}}(m;k)\) the lowest (positive) energy band for a strip of width Ny (all the other parameters of the model fixed). We can assume that, close to the Dirac point, \({E}_{{N}_{y}}(m;k)\) is well described by the spectrum of the low energy model in Eq. (10), with a certain unknown function \({{{\mathcal{M}}}}\). Thus, noting that the hybridization between the chiral modes is exponentially suppressed with the strip width– i.e.,\({{{\mathcal{M}}}}{\longrightarrow }^{{N}_{y}\to \infty }0\) –we can recover (the modulus of) \({{{\mathcal{M}}}}\) for a given Ny as

$$| {{{\mathcal{M}}}}(m;k)| =\sqrt{{E}_{{N}_{y}}{(m;k)}^{2}-{E}_{\infty }{(m;k)}^{2}}.$$
(13)

In Fig. 5a–d are shown the plots of \({{{{\mathcal{M}}}}}^{{{{\rm{teo}}}}}(k)\) as a function of k for the different widths considered, with ξ set to twice the localization length of the edge states (ξloc) for t2 = 0.3 (assuming t1 = 1). In Panels e–h instead, are reported the corresponding plots of \(| {{{\mathcal{M}}}}(0;k)|\), obtained numerically as described in Eq. (13). Note that the points in k space where \({{{\mathcal{M}}}}\) stops oscillating and steeply goes up correspond to the points where the edge states of the reference strip (Ny → ∞) merge with the bulk states. Beyond this limit, the low energy Hamiltonian in Eq. (10) is no longer valid, since it does not account for the bulk degrees of freedom.

Fig. 5: Effective toy model validation.
figure 5

Comparison between the effective mass term derived analytically in Eqs. (11) and (12) (a–d) and the ones obtained numerically according to Eq. (13), for m = 0 (e–h) and m = 0.5 (i–l) with the other parameters set to \({t}_{1}=1,\,{t}_{2}=0.3,\,\phi =\frac{\pi }{2}\). The dashed vertical line in the plots (e–l) indicates the position of the Dirac point, which varies with m according to \({k}_{{{{\rm{D}}}}}=\pi -\frac{m}{6{t}_{2}}\) (cf. Eq. (10)). The y-axis in (a–d) are in arbitrary units.

Full size image

By comparison between the two rows of plots, one can see that the effective mass term in Eqs. (11) and (12) correctly reproduce some qualitative features of the one obtained numerically for m = 0. More specifically, setting the parameter t2 in the range [0.1–0.3], we correctly recover the number of nodes of \({{{\mathcal{M}}}}(0;k)\) for the different widths, the fact that the mass term spreads in k-space as t2 is increased and, crucially, the fact that \({{{\mathcal{M}}}}(0;\pi )=0\) for Ny = 4M + 2. Further support to these statements can be found in Supplementary Figs. 4, 5 and 6, where, for each of the widths considered, we report the plots of \(| {{{\mathcal{M}}}}|\) as a function of k for different values of m and t2. It is worth mentioning that the shape of \({{{\mathcal{M}}}}(0;k)\) more closely resembles that of a sinusoidal-like function for smaller values of t2 (t2 ~ 0.1−0.2). The deviations from the sinusoidal pattern predicted by the effective low energy theory observed in Fig. 5e–n (t2 = 0.3), are probably due to the fact that the first has been derived taking into account first neighbor hoppings only. That being the case, it is expected to be more reliable for smaller values of t2.

Furthermore, the numerical results for \({{{\mathcal{M}}}}\) show that, at least at a qualitative level, for m > 0 the mass term is shifted to the right in the Brillouin zone (see Fig. 5i–l and Supplementary Figs. 4, 5 and 6). On the other hand, we know that for m > 0 the Dirac point moves to the left (dashed vertical lines in Fig. 5i–l). Therefore, there must be a (set of) value(s) of m for which the nodes of \({{{\mathcal{M}}}}(m;k)\) coincide with the shifted Dirac point. This mechanism qualitatively explains the mass inversion in our model and, consequently, the reentrant topological phase diagram retrieved numerically.

Finally, we briefly address the reason why armchair nanoribbons do not share this kind of phenomenology. In the Haldane model on armchair nanoribbons the Dirac point is at k = 0, and is insensitive to variation of the staggered mass. This can be understood by noticing that, in contrast with the zigzag case, each armchair edge has the same number of A and B sites. Thus, varying m does not shift the energy of the edge states. This hints to the fact that in the case of armchair geometry, the properties of the edge states are less likely to be tuned by varying the staggered mass m. Moreover, the edge states in zigzag Haldane nanoribbons present a peculiar property: as shown by Eq. (5), ξloc grows with t2 in the zigzag case. On the other hand, the Haldane edge states on armchair nanoribbons have their localization length inversely proportional to t243. Thus, in the zigzag case, bigger values of t2 lead both to a wider topological bulk gap in the 2D limit, and to a larger localization length of the edge states. This feature, which is not shared by armchair nanoribbons, elects thin zigzag nanoribbons as the optimal playground to inspect the finite size effects on the Haldane edge states.

Jackiw-Rebbi like bound states

Interestingly, if we consider a setup of our model in which the staggered mass term m interpolates between two values in adjacent regions of the phase diagram with different Zak phases, we observe the occurrence of a bound state, localized at the transition point and with energy lying inside the gap. Thus, leaning on the results from Jackiw and Rebbi35, we can conclude that such bound state retains a fractional charge of \(\pm \frac{e}{2}\) 36,51. Strikingly, the bound state is present even when the mass m interpolates between two regions that, despite having different Zak phases, do not host bound states against the vacuum (more details in Supplementary Note 5).

In Fig. 6 we report an explicit example for a strip with Ny = 10 and L = 200a, in which the on-site staggered potential is set to ± 0.3 for the A and B sites respectively on the left part and to ± 0.3 on the right part (with m = 0 at the interface to smoothen out the jump). These two regions of the phase diagram are marked with a yellow and red dot respectively in Fig. 3d. All the other parameters of the model are left unchanged. In Panel a is reported a density plot of the on-site potential close to the transition point, where the sign of m switches for the two sublattices. By performing real space numerical diagonalization we obtain the low energy spectrum and the corresponding eigenvectors. The first is shown in Panel b, where an isolated eigenvalue is clearly visible inside the gap: this corresponds to a bound state localized at the point where m switches its sign, as demonstrated by the plot of its probability density in Panel c. From Fig. 2d, we see that from m = − 0.3 to m = + 0.3 the Zak phase jumps of π, so that the occurrence of a bound state at the domain wall is actually expected according to our analysis.

Fig. 6: Jackiw-Rebbi bound states at domain walls.
figure 6

Results obtained via numerical diagonalization for a strip with Ny = 10 and L = 200a with spatially varying on-site potential. According to Jackiw-Rebbi theory, a bound state is expected in correspondence of mass inversion (which we identify as a jump of π in the Zak phase). The model parameters are set to t1 = 1, t2 = 0.3 and ϕ = π/2. a: Representation of the on-site potential for the central region of the strip. The left side of the strip (x < 0) has m = − 0.3, while the right side (x > 0) has m = 0.3 (cf. yellow and red dot of Fig. 3d). The Zak phases in the two regions differ of π. b: Low energy spectrum obtained via numerical diagonalization. An isolated eigenvalue is visible inside the gap (marked in orange). c: 1D profile of the probability density of the state associated with the in-gap eigenvalue for − 50a < x < 50a, with an inset showing the corresponding unprojected probability distribution directly on the strip. The state appears to be exponentially localized at the domain wall.

Full size image

Discussion

In this paper we have studied the role of finite size effects on the Haldane model. We have shown that, in the case of zigzag strip geometry, the chiral edge modes can, as expected, hybridize and develop a gap. Surprisingly, however, such gap can be both trivial or topological in the sense that, in the uncompactified geometry, bound states can be present or absent depending on the value of the trivial mass, even in the topological phase of the Haldane model. In other words, we unveiled a phase diagram which presents a width-dependent reentrant behavior with respect to the tuning of the on-site staggered potential. Moreover, we have reinterpreted such reentrant structure within an effective minimal model describing the coupling between the chiral edge states of the Haldane model in zigzag nanoribbons.

We have then proven that, when present, the bound states are robust against on-site random disorder. Besides, we have shown that they also occur in correspondence of domain walls in the on-site staggered potential and, consequently, that they bear a fractional charge of \(\pm \frac{e}{2}\). The topological nature of the bound states is witnessed by the behavior of the Zak phase. Indeed, we can hence conclude that the mass associated to the tunneling between the edges competes in a definitely non-trivial fashion with the other masses of the model, generating a rich phenomenology.

The implications of our results are diverse. In the context of two-dimensional topological insulators and Chern insulators they imply, for instance, that the transport properties of setups where constrictions are present might be affected by the presence of zero modes, and hence show resonances. Moreover, given that a similar gap structure also characterizes the 2D Kitaev model19,52 for topological superconductivity, the impact of our results bears also consequences on the field of Majorana zero modes53,54,55 and parafermions56,57,58, paving the way to new possibilities for implementing such non-abelian excitations.

Methods

Numerical diagonalization tools

The finite size model construction and the numerical diagonalization have been performed using the package Pybinding59.

Numerical computation of the Zak phase

The computation of the gaps and of the Zak phase as a function of the staggered on-site potential have been performed with an original code and the results for the Zak phase have been benchmarked with existing packages.