Inverse Vertex/Absolute Quickest 1-Center Location Problem on a Tree Under Weighted $l_1$ Norm

Abstract

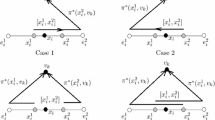
Given an undirected tree $T=(V,E)$ and a value $\sigma >0$, every edge $e\in E$ has a lead time l(e) and a capacity c(e). Let $P_{st}$ be the unique path connecting s and t. A transmission time of sending $\sigma$ units data from s to $t\in V$ is $Q(s,t,\sigma )=l(P_{st})+\frac{\sigma }{c(P_{st})}$, where $l(P_{st})=\sum _{e\in P_{st}}l(e)$ and $c(P_{st})=\min _{e\in P_{st}} c(e)$. A vertex (an absolute) quickest 1-center problem is to determine a vertex $s^*\in V$ (a point $s^*\in T$, which is either a vertex or an interior point in some edge) whose maximum transmission time is minimum. In an inverse vertex (absolute) quickest 1-center problem on a tree T, we aim to modify a capacity vector with minimum cost under weighted $l_1$ norm such that a given vertex (point) becomes a vertex (an absolute) quickest 1-center. We first introduce a maximum transmission time balance problem between two trees $T_1$ and $T_2$, where we reduce the maximum transmission time of $T_1$ and increase the maximum transmission time of $T_2$ until the maximum transmission time of the two trees become equal. We present an analytical form of the objective function of the problem and then design an $O(n_1^2n_2)$ algorithm, where $n_i$ is the number of vertices of $T_i$ with $i=1, 2$. Furthermore, we analyze some optimality conditions of the two inverse problems, which support us to transform them into corresponding maximum transmission time balance problems. Finally, we propose two $O(n^3)$ algorithms, where n is the number of vertices in T.