1 Introduction

The constant demand for faster and more efficient RF transistors has led to the increased usage of III-V semiconductors as they exhibit superior electronic properties compared to silicon, including higher mobilities, saturation velocities, and larger breakdown fields [1]. In contrast to silicon-based devices, TCAD tools for III-V semiconductors fail to provide an accurate prediction of the electrical device behavior, which is a major drawback for the technology development [2]. Efforts have recently been made to overcome these limitations by improving the drift-diffusion (DD) model for III-V HBTs [3], but it remains unknown whether this could lead to an accurate prediction of the device behavior. At small length scales, the DD approximation becomes questionable [4], and a more physically concise transport model is needed, at least to assess the accuracy of the DD model. The semiclassical Boltzmann transport equation (BTE) is best suited for this purpose since it captures important quantum mechanical effects such as band structure, all relevant scattering mechanisms, and the Pauli exclusion principle [5], while its simulation time remains in a feasible range, unlike those of quantum transport models when scattering is included and consistency with the Poisson equation (PE) is required [6]. However, solving the BTE still requires large simulation times due to its seven-dimensional phase space.

It is the objective of this paper to present a numerically stable simulation approach for solving the BTE under stationary, small-signal and transient conditions in III-V semiconductor devices, exemplarily demonstrated for a GaAs \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure.

The most common approach for solving the BTE with a high-dimensional phase space, the Monte Carlo (MC) method [5], has many disadvantages due to its stochastic and inherently transient nature [7]. Its most important drawback in the case of III-V semiconductor devices is the difficulty to include the Pauli exclusion principle, which is very important due to the low mass of the \(\Gamma\) valley. The Pauli exclusion principle can be included by sampling the full distribution function in the phase space [8], but this results in large CPU times. Approximations of the Pauli exclusion principle have been developed for the scattering integral (e.g., [9]), but they may cause large errors [10]. Moreover, slow processes (e.g., generation/recombination) might require prohibitively long simulations. Deterministic BTE solvers, on the other hand, can directly obtain stationary and small-signal solutions for arbitrary low frequencies [11]. Inclusion of the Pauli exclusion principle causes no problem because the distribution function is known in the whole phase space. Furthermore, deterministic BTE solvers have many numerical similarities with the conventional device simulation codes and can be much more easily integrated in a TCAD suite.

The most popular deterministic method to solve the BTE is based on a spherical harmonic expansion (SHE) together with the H-transformation [12]. In covalent semiconductors the corresponding system matrix can be formulated in such a way that it has the M-property resulting in a numerically very robust system of equations [11]. Unfortunately, we have found that the SHE approach leads to stability issues when devices consisting of III-V semiconductors are simulated. The reason is that angular-dependent scattering by the polar-optical phonons present in III-V semiconductors leads to the loss of the M-property. Consequently, the distribution function may become negative when solving the BTE and the entire simulation becomes unstable. This problem can be avoided by solving the BTE directly in the \({\textbf {k}}\)-space (e.g., [13,14,15,16]).

The free-streaming operator of the BTE has properties that lead to wave-like behavior of the distribution function, which can be handled with methods developed for computational fluid dynamics [17]. We adapt a deterministic approach based on Godunov’s scheme with a constant reconstruction of the distribution function within a finite volume of the real space [18], which has already been successfully applied to a silicon nanowire with a one-dimensional real and \({\textbf {k}}\)-space [19]. This first-order scheme has the advantage, that it is linear in the distribution function in contrast to higher order schemesFootnote 1 (e.g., Ref. [21]), which in turn makes it easier to apply the Newton–Raphson method to the coupled BTE and PE, and to perform small-signal analysis and transient simulations based on implicit schemes. As shown in [22], the approach ensures the nonnegativity of the distribution function independent of the scattering rates and even allows the simulation of the ballistic case, in contrast to approaches based on odd/even splitting of the distribution function (e.g., SHE) [19]. The discrete scattering integral can be formulated such that it is particle number conserving and satisfies the principle of detailed balance together with the Pauli principle. This ensures that at equilibrium the distribution function corresponds to the Fermi–Dirac distribution for the lattice temperature. Moreover, it should be emphasized that the Riemann problems arising from the application of Godunov’s scheme are solved under the condition of conservation of total energy and particle flux, and thus, both are ensured by the construction of our approach through the entire device.

We modify the Godunov-type stabilization scheme (GSS) for the three-dimensional \({\textbf {k}}\)-space, but we do not use the H-transformation. Although this results in spurious diffusion in the \({\textbf {k}}\)-space, it has the advantage of a simpler implementation of the self-consistent Newton–Raphson scheme owing to the \({\textbf {k}}\)-space grid, which does not depend on the quasistatic potential. In [22], it was shown that the impact of the spurious diffusion in the \({\textbf {k}}\)-space is rather small at room temperature, and even the H-transformation cannot suppress spurious diffusion in the case of a transient simulation.

The proposed simulation approach based on the GSS has already been successfully applied to a state-of-the-art InP/InGaAs double heterojunction bipolar transistor (DHBT) to demonstrate its physically rigorous modeling of III-V devices, achieving reasonable agreement with current–voltage characteristic and cut-off frequency measurements  [23]. Due to the properties of heterojunctions, the simulation of HBTs based on drift-diffusion or hydrodynamic models is even more difficult than in the homogeneous case, as was shown for Si/SiGe HBTs in [24].

This paper proceeds as follows. Section 2 shows the adaption of the Godunov-type stabilization scheme for a three-dimensional \({\textbf {k}}\)-space together with the band structure model and the discretization used. The implementation is then verified in Sect. 3 by comparing the velocity-field characteristics of a GaAs bulk simulation with various measurements. In the further course of Sect. 3, the results of the DD model and BTE for a GaAs \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure are compared for equilibrium, and finally, the results of transient and small-signal analysis are presented.

2 Simulation approach

In the following, arguments such as time t, wave vector \({\textbf {k}}\), valley index \(\upsilon\), etc., of solution variables are not given in each equation for the sake of brevity. It goes without saying that quantities and solution variables, once so defined, depend on these arguments in the further course of this paper.

2.1 Phase space

The numerical effort can be reduced by exploiting symmetries of the devices in the real space. For example, the essential transport phenomena of HBTs can be simulated based on a one-dimensional model [25]. This limits the transport model to a 1D real space, which is mapped onto a grid with the grid nodes \(z_i\) for \(i = 1,\dots ,N_z\), where \(N_z\) is the number of grid nodes. The ith cell of the real space grid is given by \(z_i \le z \le z_{i+1}\) and has the length

$$\begin{aligned} \Delta z_i = z_{i+1} -z_i \ . \end{aligned}$$
(1)

We assume that the semiconductor material is constant within a cell of the real space. Since the electron mobility is usually much larger than the hole mobility in III-V semiconductors, most devices are based on electron transport [1] and we will apply the BTE only to the conduction bands. If holes are to be consideredFootnote 2, they are described by the piecewise constant quasi-Fermi-level approximation [26]. The conduction bands are approximated by three valleys for III-V semiconductors [5] and the relation between the band energy \(\varepsilon _{\upsilon }\) and wave vector \({\textbf {k}}\) for these valleys \(\upsilon = \mathrm {\Gamma }, \, \textrm{L}, \, \textrm{X}\) is given by spherical, nonparabolic dispersion relations

$$\begin{aligned} \varepsilon _{\upsilon }= \varepsilon _{\upsilon , \, \text {min}}+\frac{1}{2 \alpha _{\upsilon }} \left[ \sqrt{1+2 \alpha _{\upsilon }\frac{\hbar ^2 {\textbf {k}}^2}{m_{\upsilon }^{*}}}-1\right] , \end{aligned}$$
(2)

where \(m_{\upsilon }^{*}\) is the effective mass, \(\alpha _{\upsilon }\) the non-parabolicity factor, and \(\varepsilon _{\upsilon , \, \text {min}}\) the energy minimum of the considered valley.

Owing to the one-dimensional real space and the spherical valleys, the distribution function is rotationally symmetric around the \(k_z\) axis. This symmetry can be efficiently represented by cylindrical coordinates \(k_\rho\), \(k_\phi\) and \(k_z\) in the \({\textbf {k}}\)-space, where the distribution function does not depend on the angle \(k_\phi\), reducing the computational effort enormously [14].

The \({\textbf {k}}\)-space is discretized along equienergy spheres according to Eq. (2), where the energy is mapped onto a 1D equidistant grid

$$\begin{aligned} \varepsilon _{\upsilon ,j} = \varepsilon _{\upsilon , \, \text {min}}+ j \, \Delta \varepsilon \quad \text { for } j=0,1,\dots , N_{\text {max}} \ . \end{aligned}$$
(3)

The angle between the \(k_{\rho }\) and \(k_{z}\) axes is divided into \(N_{\theta }\) parts and triangulation finally yields the \({\textbf {k}}\)-grid shown in Fig. 1, which is rotationally symmetric w.r.t. the \(k_z\) axis.

Fig. 1
figure 1

Schematic representation of the \({\textbf {k}}\)-grid with \(N_{\theta }=4\). The triangles rotated around the \(k_z\) axis are the so-called \({\textbf {k}}\)-boxes of the 3D \({\textbf {k}}\)-space

Full size image

The grid is symmetric w.r.t. to the \(k_\rho\) axis to ease the calculation of the \({\textbf {k}}\)-vector after a reflection w.r.t. the z direction (see Sect. 2.3). Two nodes of a triangle lie on one equienergy surface, while the third one lies on an adjacent surface. The energy is interpolated linearly over a triangle resulting in a constant group velocity within a \({\textbf {k}}\)-box. Since adjacent triangles share two grid nodes, the energy interpolation is continuous in the whole \({\textbf {k}}\)-space. The group velocity has cylindrical symmetry and its magnitude and z-component do not depend on the angle \(k_\phi\). For all valleys of the different semiconductor materials \({\textbf {k}}\)-space grids are generated. \(T_{i}^{\upsilon ,j}\) is the jth \({\textbf {k}}\)-box of the \(\upsilon\)th valley in the ith cell of the real space. Its volume in the 3D \({\textbf {k}}\)-space is \(\Omega _{i}^{\upsilon ,j}\).Footnote 3

2.2 Boltzmann and Poisson equations

The BTE characterizes the spatiotemporal evolution of electrons by the distribution function

$$\begin{aligned} \textrm{d}N^\upsilon (z,\, {\textbf {k}},\, t) = \frac{2}{\left( 2\pi \right) ^3} \, f^{\upsilon }(z,\, {\textbf {k}},\, t) \, \textrm{d}z \, \textrm{d}^3 k \, , \end{aligned}$$
(4)

which is by definition the density of the phase space [27]. The electron density, for example, is given by [5]

$$\begin{aligned} n(z,t) = \frac{2}{\left( 2\pi \right) ^3} \, \sum _\upsilon \int f^{\upsilon }(z,{\textbf {k}},t) \, \textrm{d}^3 k \ . \end{aligned}$$
(5)

Taking into account that the grid of the phase space has been reduced to 5 dimensions (3D \({\textbf {k}}\)-space, 1D real space and time), the BTE has the form

$$\begin{aligned} \frac{\partial {f^\upsilon }}{\partial {t}} + v^{\, \upsilon }_z\frac{\partial {f^\upsilon }}{\partial {z}} + \frac{1}{\hbar } F^\upsilon _z \frac{\partial {f^\upsilon }}{\partial {k_z}} = \mathcal{S}^\upsilon \, , \end{aligned}$$
(6)

where \(v^{\, \upsilon }_z(z,{\textbf {k}})\) is the z-component of the group velocity, and \(F^\upsilon _z(z,t)\) is the force in the z-direction

$$\begin{aligned} F^\upsilon _z = \frac{\partial {(q\varphi -\varepsilon _{\upsilon , \, \text {min}})}}{\partial {z}} \ . \end{aligned}$$
(7)

with the positive elementary charge q. The scattering integral \(\mathcal{S}^\upsilon (z,{\textbf {k}},t)\) is given by

$$\begin{aligned}&\mathcal{S}^\upsilon ({\textbf {k}}) = \frac{\Omega _{\text {sys}}}{\left( 2\pi \right) ^3} \sum _{\upsilon '} \nonumber \\ \int&\left[ 1-f^{\upsilon }({\textbf {k}})\right] W_{\upsilon ,{\upsilon '}}({\textbf {k}} ,{\textbf {k}}') f'^{\upsilon }({\textbf {k}}') \nonumber \\ -&\left[ 1-f'^{\upsilon }({\textbf {k}}')\right] W_{{\upsilon '},\upsilon }({\textbf {k}}',{\textbf {k}}) f^{\upsilon }({\textbf {k}}) \, \textrm{d}^3 k' \end{aligned}$$
(8)

and accounts for all local and instantaneous scattering events from the initial states \((\upsilon ',{\textbf {k}}')\) into the final ones \((\upsilon ,{\textbf {k}})\) and their inverse processes, while the Pauli principle is taken into account [28]. \(\Omega _{\text {sys}}\) is the system volume and \(W_{\upsilon ,\upsilon '}(z,{\textbf {k}},{\textbf {k}}')\) the corresponding transition rate of a scattering event. The transition rate takes into account all scattering processes relevant for III-V semiconductors, i.e., scattering by acoustic, polar-optical, intervalley phonons, impurities and alloy fluctuations. Their formulations can be found in [5]. The 3D integral in Eq. (8) can be analytically calculated within the \({\textbf {k}}\)-boxes based on the linear energy interpolation and cylindrical symmetry. Since the energy on the spherical surfaces is not constant when integrating the collision terms in cylindrical coordinates, an additional variable transformation to equienergy lines in \({\textbf {k}}\)-space is performed, where each \({\textbf {k}}\)-box is parameterized by equienergy lines parallel to \({\textbf {k}}\)-box boundaries.

When choosing the finite volume for the real space, it must be considered that the distribution function is defined, inter alia, on the \({\textbf {k}}\)-space, which depends on the material considered. Material junctions or material-contact interfaces are located on grid points in real space, making it inappropriate to define the finite volume around a grid point. Instead, the grid cells \((z_i, z_{i+1})\) are chosen as finite volumes in real space, since they are always associated with only one material. In consequence, (almost) all solution variables and physical quantities are defined on the grid cells; in particular, this definition for the electric potential is uncommon in the literature, but is more appropriate when applying the Godunov-type stabilization scheme, as explained later below (Fig. 2).

Fig. 2
figure 2

Potential definitions on the real space grid

Full size image

The PE must therefore be solved for the cell’s potential \(\varphi _{i}\) and the finite volume method yields

$$\begin{aligned} \epsilon _i \, \left( E^\text {R}_{z,i}-E^\text {L}_{z,i}\right) = \Delta z_{i} \, \rho _{i} \end{aligned}$$
(9)

for the ith real-space cell with the space charge \(\rho _i(t) = q(p_i(t) - n_i(t) + N_{\text {D},i} - N_{\text {A},i})\). n, p are the electron and hole densities, respectively, and \(N_{\text {D}}\), \(N_{\text {A}}\) the donor and acceptor concentrations, respectively. The electric fields \(E^\text {L}_{z,i}\), \(E^\text {R}_{z,i}\) at the left and right boundaries of the ith cell, respectively, can be calculated based on the continuity of the normal component of the electric flux density at the interface between the two cells for zero interface charge [29]

$$\begin{aligned} \epsilon _{i} E^\text {R}_{z,i} =&\epsilon _{i} \frac{\varphi _i-\varphi ^\text {R}_i}{\frac{\Delta z_i}{2}} \nonumber \\ =&\epsilon _{i+1} \frac{\varphi ^\text {L}_{i+1}-\varphi _{i+1}}{\frac{\Delta z_{i+1}}{2}} = \epsilon _{i+1} E^\text {L}_{z,i+1} \ , \end{aligned}$$
(10)

where \(\varphi ^\text {R}_i\) is the potential at the right boundary of the ith cell and \(\varphi ^\text {L}_{i+1}\) the one at the left boundary. The potential is continuous at the interface between two cells [29] and we obtain

$$\begin{aligned} \varphi ^\text {R}_i = \varphi ^\text {L}_{i+1} = \frac{ \frac{\epsilon _i}{\Delta z_i} \varphi _i + \frac{\epsilon _{{i+1}}}{\Delta z_{i+1}} \varphi _{i+1} }{\frac{\epsilon _i}{\Delta z_i} + \frac{\epsilon _{{i+1}}}{\Delta z_{i+1}}} \ . \end{aligned}$$
(11)

With the above two equations we can derive an expression for \(E^\text {R}_{z,i}\) that depends only on the cell potentials \(\varphi _i\), \(\varphi _{i+1}\). A similar expression can be derived for \(E^\text {L}_{z,i}\) and with Eq. (9) the PE for the cell potentials can be obtained.

As is readily apparent from Eqs. 7 to 5, the BTE and PE are coupled and their solutions must be calculated self-consistently. Self-consistency is achieved by treating the BTE and PE as one system of equations, which can then be solved by the Newton–Raphson method. The initial guess is obtained by a Gummel iteration, similar to [30], where the PE and BTE are solved iteratively until the change in potential is less than 1m V.

2.3 Godunov-type stabilization scheme

The basic idea is to improve the numerical stability of the BTE by separating the drift term from the scattering and diffusion terms without explicitly introducing operator splitting [19]. The problematic drift term is moved to the interfaces at \(z_{i}\) by assuming that the band energy is constant within a cell of the real-space grid and changes abruptly at the interface due to a change in material or potential by

$$\begin{aligned} \Delta \varepsilon _{\upsilon ,i} =&\varepsilon _{\upsilon , \text {min}, i} - \varepsilon _{\upsilon , \text {min}, i-1} \nonumber \\&- q \left( \varphi _{i} - \varphi _{i-1} \right) \ . \end{aligned}$$
(12)

As a result, the force term vanishes within the cell and the BTE simplifies to

$$\begin{aligned} \frac{\partial {f}}{\partial {t}} + v_z \frac{\partial {f}}{\partial {z}} = \mathcal{S}\, . \end{aligned}$$
(13)

The derivative w.r.t. z in Eq. (13) is then evaluated by Godunov’s scheme [18] for the ith cell of the real space

$$\begin{aligned} \frac{\partial {\bar{f}_{i}}}{\partial {t}} + \frac{\mathcal{F}_{\text {R},i}-\mathcal{F}_{\text {L},i}}{\Delta z_{i}} = \bar{\mathcal{S}}_{i} \, , \end{aligned}$$
(14)

where we also integrated over the \({\textbf {k}}\)-box \(T_{i}^{\upsilon ,j}\). When the Pauli exclusion principle is taken into account in the scattering term, the Godunov-type stabilization scheme ensures that the distribution function is non-negative and cannot be greater than one, regardless of the scattering rate, as shown in  [22]. We use a constant reconstruction of the distribution function \(\bar{f}^{\upsilon ,j}_{i}(t )\) within a finite volume of the phase space

$$\begin{aligned} \bar{f}^{\upsilon ,j}_{i} = \frac{1}{\Delta z_{i} \Omega ^{\upsilon ,j}_{i}} \, \int \limits _{z_i}^{z_{i+1}} \int \limits _{T^{\upsilon ,j}_{i}} f^{\upsilon }\left( z, {\textbf {k}}\right) \, \textrm{d}^3 k \textrm{d}z \, . \end{aligned}$$
(15)

Similarly, the scattering integral Eq. (8) is averaged over a phase space cell and \(\bar{\mathcal{S}}^{\upsilon ,j}_{i}\) is a function of \(\bar{f}^{\upsilon ,j}_{i}\) [22]. \(\mathcal{F}^{\upsilon ,j}_{\text {L},i}(t)\) and \(\mathcal{F}^{\upsilon ,j}_{\text {R},i}\) are the electron fluxes at the left and right boundaries of the ith cell in real space, respectively. Their computation is nontrivial since the reconstruction of the distribution function is discontinuous at each interface, while flux conservation requires a single unique flux shared by two adjacent cells [17]. Interpolation of the distribution function at the interface results in spurious oscillations because it does not take the direction of the electron flow into account. Godunov solved this issue by using a suitable Riemann solver at the discontinuities, where the flux should be upwinded [18]. In the case of the BTE, we further assume for the Riemann solver that the total energy, the part of the wave vector parallel to the interface, and the electron flux at each interface \(z_i\) are conserved. With these assumptions, an exact solution to the Riemann problem for the two-dimensional \({\textbf {k}}\)-grid can be found, as described in detail below.

In order to upwind the electron flux, a case distinction must be made according to the sign of the group velocity in the \({\textbf {k}}\)-box [17, 19, 22]. For the right interface of the ith grid cell at \(z_{i+1}\), this implies that the flux of a \({\textbf {k}}\)-box \(T^{\upsilon ,j}_{i}\) with \(v^{\upsilon ,j}_{z,i} > 0\) originates from the interior of the cell and is therefore given by

$$\begin{aligned} \mathcal{F}^{\upsilon ,j}_{\text {R},i} =&\int _{T^{\upsilon ,j}_{i}} v_{z,i}^{\upsilon ,j} \, f^\upsilon (z_{i+1},{\textbf {k}}) \, \textrm{d}^3 k \nonumber \\ =&\Omega ^{\upsilon ,j}_{i} v^{\upsilon ,j}_{z,i} \, \bar{f}^{\upsilon ,j}_{i} \text { for } v^{\upsilon ,j}_{z,i} > 0 \end{aligned}$$
(16)

due to the constant group velocity and constant reconstruction of the distribution function within the phase-space cells. On the other hand, the flux for a \({\textbf {k}}\)-box with \(v_z < 0\) arises either from a reflection of electrons with positive velocity from within the ith real-space cell, when their kinetic energy is not sufficient to pass the energy barrier of the interface at \(z_{i+1}\), or from electrons transmitted from the \((i+1)\)th cell, which is the adjacent cell to the right,

$$\begin{aligned} \mathcal{F}^{\upsilon ,j}_{\text {R},i} =&\sum _{j'}t_{\text {R},i}^{\upsilon ,j,j'} \, \bar{f}^{\upsilon ,j'}_{i+1} \nonumber \\&+ r_{\text {R},i}^{\upsilon ,j} \, \bar{f}^{\upsilon ,-j}_{i} \text { for } v^{\upsilon ,j}_{z,i} < 0 \, . \end{aligned}$$
(17)

The transmission coefficient \(t_{\text {R},i}^{\upsilon ,j,j'}\) accounts for electrons moving from the \({\textbf {k}}\)-space cell \(T^{\upsilon ,j'}_{i+1}\) into \(T^{\upsilon ,j}_{i}\). The reflection coefficient \(r_{\text {R},i}^{\upsilon ,j}\) is the factor for electrons being reflected at the right interface. Due to the symmetry of the \({\textbf {k}}\)-space grid (Fig. 1), the electrons are reflected from cell \(T^{\upsilon ,-j}_{i}\) into \(T^{\upsilon ,j}_{i}\) with \(v^{\upsilon ,j}_{z,i} = - v^{\upsilon ,-j}_{z,i}\). The flux on the left side of the cell follows analogously

$$\begin{aligned}&\mathcal{F}^{\upsilon ,j}_{\text {L},i} \nonumber \\&= {\left\{ \begin{array}{ll} \sum _{j'}t_{\text {L},i}^{\upsilon ,j,j'} \, \bar{f}^{\upsilon ,j'}_{i-1} + r_{\text {L},i}^{\upsilon ,j} \, \bar{f}^{\upsilon ,-j}_{i} &{} v^{\upsilon ,j}_{z,i} > 0 \\ \Omega ^{\upsilon ,j}_{i} \, v^{\upsilon ,j}_{z,i} \, \bar{f}^{\upsilon ,j}_{i} &{} v^{\upsilon ,j}_{z,i} < 0 \end{array}\right. } \end{aligned}$$
(18)

with the transmission factor \(t_{\text {L},i}^{\upsilon ,j,j'}\) and reflection factor \(r_{\text {L},i}^{\upsilon ,j}\) for the left interface.

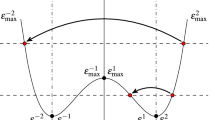
The calculation of the transmission coefficients is rather complex, because the change in the band edge (see  Eq. (12)) at the interface can lead to a change in the \({\textbf {k}}\)-space box when an electron moves through the interface. To evaluate the electron flux into the final \({\textbf {k}}\)-box \(T^{\upsilon ,j}_{i}\), we have to determine the initial \({\textbf {k}}\)-boxes \(T^{\upsilon ,j'}_{i-1}\) from which the electrons stem. These are found by back propagation under conservation of the total electron energy and transverse momentum. We start with a corner of the final \({\textbf {k}}\)-box in the ith cell (\(T^{4}_{i}\) in the right \({\textbf {k}}\)-grid of Fig. 3) and determine into which initial \({\textbf {k}}\)-box in the \((i-1)\)th cell it falls (\({\textbf {k}}\)-boxes \(T^{j'}_{i-1}\) in the left \({\textbf {k}}\)-grid of Fig. 3). For example, the upper corner of \(T^{4}_i\) in the right \({\textbf {k}}\)-grid falls into \(T^{1}_{i-1}\) of the left \({\textbf {k}}\)-grid. In order to determine the area of \(P^{4,1'}_{i-1}\) in the \((i-1)\)th cell, the other corners of the triangle \(T^{4}_{i}\) are mapped to the left \({\textbf {k}}\)-grid using the linear interpolation of the band structure within \(T^{1}_{i-1}\). In general, the final \({\textbf {k}}\)-box does not coincide with an initial \({\textbf {k}}\)-box and the two additional mapped vertices of \(T^{4}_i\) are mapped outside of \(T^{1'}_{i-1}\), where its interpolation of the band structure is not accurate enough. However, the two additional mapped vertices of \(T^{4}_i\) are then only used to calculate the area of the polygon \(P^{4,1'}_{i-1}\) as the overlap of two triangles, which is determined by the Sutherland–Hodgman algorithm [31]. The procedure is repeated until all overlaps with the initial \({\textbf {k}}\)-boxes are found. Thus, the final \({\textbf {k}}\)-box is in general linked to multiple initial \({\textbf {k}}\)-boxes.Footnote 4 The transmission factor of the flux from the initial \({\textbf {k}}\)-box \(T^{\upsilon ,j'}_{i-1}\) into the final \({\textbf {k}}\)-box \(T^{\upsilon ,j}_{i}\) is given by integration of the group velocity over the overlap area in the final \({\textbf {k}}\)-box

$$\begin{aligned} t_{\text {L},i}^{\upsilon ,j,j'} = v_{z,i}^{\upsilon ,j} 2\pi \int _{P_{i,i-1}^{\upsilon ,j,j'}} k_\rho \, \textrm{d}^2 k \ , \end{aligned}$$
(19)

where the factor \(2\pi k_\rho\) stems from the integral over the angle \(k_\phi\).

Fig. 3
figure 3

Schematic partitioning of the final \({\textbf {k}}\)-box \(T^4\) in the ith cell of the real space by polygons \(P^{j,j'}\) resulting from the mapping of the initial \({\textbf {k}}\)-boxes \(T^{j'}\) in the \((i-1)\)th cell

Full size image

In the case that the minimum energy of the final \({\textbf {k}}\)-box is below the band edge of the \((i-1)\)th cell (\(\Delta \varepsilon _{\upsilon ,i} < 0\)), the transmitted electrons have an energy in the final \({\textbf {k}}\)-box, which is larger than its minimal energy. The electron flux in the energy range from the minimum to the band edge of the adjacent cell is then due to reflection. The reflected flux stems solely from the initial \({\textbf {k}}\)-box \(T^{\upsilon ,-j}_{i}\) in the same cell of the real space

$$\begin{aligned} r_{\text {L},i}^{\upsilon ,j} = v_{z,i}^{\upsilon ,j} 2\pi \int _{P_{i,i}^{\upsilon ,j,-j}} k_\rho \, \textrm{d}^2 k \end{aligned}$$
(20)

due to the symmetry of the \({\textbf {k}}\)-grid.

3 Simulation results

For simulations of the homogeneous (bulk) case with a constant electric field, the spatial dependence of the distribution function is eliminated by assuming that the flux entering the cell from the left side is equal to the flux leaving the cell on the right side. Therefore, the BTE is solved only for a single grid cell and the Riemann problem is solved at a single interface, where the potential barrier Eq.  (12) is given by the product of the applied electric field and the cell length. The band structure and scattering parameters for GaAs are taken from [32], while the parameters for the bandgap narrowing of GaAs can be found in [33]. For all following simulations, the Pauli exclusion principle is taken into account and the \({\textbf {k}}\)-space is discretized along equi-energy spheres up to 2 eV with a constant energy spacing of 5 meV, while the angle \(\theta\) between the \(k_{z}\)-axis and \({\textbf {k}}\) is divided into \(N_{\theta } = 8\) parts (see Fig. 1). This results in triangular \({\textbf {k}}\)-grids for \(\mathrm {\Gamma }, \, \textrm{L}, \, \textrm{X}\) valley with 12784, 10704 and 9488 triangles.

Fig. 4
figure 4

Comparison of drift velocities determined from the BTE with measurements by Ruch and Kino [34], Ashida [35], and Houston and Evans [36]

Full size image

In Fig. 4, the drift velocity of the BTE simulation is compared with various measurements from the literature [34,35,36]. A maximum deviation of 5.5% from these measurements is observed near the peak of the drift velocity, which is within the range of the deviation of the measurements from each other and thus within an acceptable error range.

For the simulation of III-V devices, the Riemann problems at the grid nodes \(z_i\) depend on the potential profile (see Eq. (12)) and the PE must be solved in a coupled manner with the BTE (see Sect. 2.2), ensuring the consistency of the distribution function and the quasistatic potential. The resulting system of equations, consisting of the PE and BTE, is solved exemplarily for the unipolar GaAs \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)structure with the doping profile shown in Fig. 5 and a constant grid spacing of \(\Delta z= {2.5}{\textrm{nm}}\) is assumed in real space for all following simulations, unless otherwise stated.

The Pauli exclusion principle increases the mean energy of the electrons, and in the case of a low density of states (\(\Gamma\) valley) and high electron densities this effect is strong. In the \(N^+\) regions of the device the mean energy at equilibrium is about 4 times higher than in the N region (Fig. 5), clearly demonstrating the importance of the Pauli exclusion principle.

Fig. 5
figure 5

Donor concentration, electron density, and mean energy of the \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure at \(V = 0\textrm{V}\)

Full size image

Under steady-state conditions, this results in a system of equations with over 2 million unknowns and over 440 million nonzero entries in the corresponding system matrix. Thanks to its quadratic convergence near the solution, the Newton–Raphson method needs at most 6 Newton iterations per bias point. The I-V characteristics of the \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)structure are shown in Fig. 6, demonstrating the ability of the GSS approach to find numerically stable solutions under steady-state conditions.

Fig. 6
figure 6

I-V characteristic and real part of admittance for \(f = {0}\,{\textrm{Hz}}\) of the \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure

Full size image
Fig. 7
figure 7

Occupation of \(\Gamma\), L, X valley in \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure at \(V = 1{\textrm{V}}\)

Full size image

In Fig. 7, the occupation of the \(\Gamma\), L, X valleys is illustrated for an applied voltage of 1 V. The electrons move from left to right and in the range 100 nm to 150 nm against the electric field, which results in a cooling of the electron gas and a reduction of the L valley occupancy. After passing the barrier at about 150 nm, the electrons gain energy and rapidly populate the higher valleys. Even for this rather simple device, the single valley approximation made by most TCAD tools [2] is highly questionable since the electrons in the L and X valleys have a significant influence on the behavior of the device. Exemplary, this is shown for the drift velocity in Fig. 8. It is noteworthy that the extension of the DD model proposed in [3, 37] does not explicitly model the X valley, but uses a single valley L’ to account for the two valleys L and X. This approximation may lead to deviations from the BTE results depending on the device and the operating point considered.

Fig. 8
figure 8

Drift velocity of \(\Gamma\), L, X valley in \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure at \(V = 1\textrm{V}\)

Full size image

A comprehensive comparison between the BTE and various formulations of the DD model for III-V semiconductors is beyond the scope of this work. However, we will show that even in the linear response regime the BTE model yields for this \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure currents quite different from the DD model. In the linear response regime the conductance of the DD model including Fermi–Dirac statistics is given for the 1D \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure without further approximations by

$$\begin{aligned} G_{\textrm{eq}}= \frac{q}{\int _{0}^{L} \frac{1}{n_{\textrm{eq}}(z) \, \mu _{\textrm{eq}}(z, \, N_{\text {D}})} \, \textrm{d}z} \end{aligned}$$
(21)

with the equilibrium electron density \(n_{\textrm{eq}}(z)\) (see Fig. 5) and the equilibrium mobility \(\mu _{\textrm{eq}}(z, \, N_{\text {D}})\), which are the same for the BTE and DD models. The conductances in the linear response regime of the BTE and DD models differ by about a factor of three at room temperature (DD: 128.1 mS, BTE: 45.8 mS). A similar behavior was observed for a silicon \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure, which was attributed to a failure of the DD approximation [38, 39]; in particular, the approximation of the electron temperature by the lattice temperature, which fails if considerable built-in fields are present (Fig. 9). These lead to a linear response of the electron energy which in turn reduces the conductance by thermodiffusion. This effect cannot be modeled by real ohmic contacts with a surface recombination velocity [40], because it is due to the N\(^+\)N junctions inside the device, where the electron density is much lower than at the contacts.

Fig. 9
figure 9

Electrical field strength and small-signal response of the kinetic energy at \(V = 1\,{\mu V}\) with \(\Delta z= {1.0}{\textrm{nm}}\)

Full size image

Next, the transient case is considered. As the GSS approach proposed in this work utilizes a time-independent \({\textbf {k}}\)-grid, the time integration of Eq. (14) is straightforward and several transient methods are conceivable. Implicit methods directly take into account the consistency of the quasistatic potential and the distribution function when solving the system of equations for the next point in time. In the case of A-stable methods, the length of the time steps is not limited, and, after the fast transients have vanished, rather long time steps can be used in the case of slow processes (e.g., recombination) [41]. The implicit methods, however, are memory- and CPU-intensive. This can be avoided by using explicit methods such as the forward Euler scheme, in which the time steps are limited by a CFL condition [14]. As proposed in [19], the BTE is then solved together with the PE in time, but the time steps for the PE are split into shorter time steps for the BTE similar to MC simulations [9]. Since the matrices of the BTE are constant during a time step of the PE (due to the constant potential), the application of the forward Euler scheme is reduced to a few matrix–vector operations and very short time steps, that solve the BTE with a very low error, can be chosen at minor additional computational cost. Due to the upwind property of the GSS stability is obtained even without scattering [19]. This is in contrast to the MC method, which relies on scattering to achieve stability [42].

Fig. 10
figure 10

Current evolution when instantaneously changing V from 0 to 1 V for the \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure with \(\Delta z= {5}\,{\textrm{nm}}\) and \(\Delta t = {0.5}{\textrm{fs}}\) for the BDF2 scheme, while the forward Euler scheme (FE) employs \(\Delta t = {0.1}{\textrm{fs}}\) for the BTE and \(\Delta t = {0.5}{\textrm{fs}}\) for the PE

Full size image

Exemplarily, Fig. 10 depicts the current evolution for an instantaneous change of voltage from 0 to 1V when using the forward Euler and BDF2 methods [41]. Due to the fixed time step of 0.5 fs for the BDF2 scheme and the PE step of the forward Euler approach, the plasma oscillations are well resolved. The forward Euler scheme shows the usual weaker damping inherent to that method. Since the transients vanish within a few hundred femtoseconds the explicit Euler scheme is faster than the implicit BDF2 method and requires much less memory. On the other hand, in the case of slow processes with relaxation times of the order of nanoseconds or longer, the only feasible approach would be an A-stable scheme with time-step control.

Direct solutions of the BTE have the advantage that they can be easily extended to the small-signal case [43]. Equation (14) and the PE are linearized around the steady state by a first-order Taylor series w.r.t. the small-signal variables whose time dependence is assumed to be harmonic. Figure 6 shows the small-signal results for \(\mathfrak {R}\left\{ \underline{Y}\right\}\) at \(f = {0}\,\textrm{Hz}\) (red triangles). There is negligible deviation from the results obtained by finite differences of the steady-state currents (black curve) and the results of the steady-state and small-signal analysis are consistent.

In Fig. 11, the real and imaginary part of the admittance \(\underline{Y}\) of the \({\textrm{N}}^{+}{\textrm{NN}}^{+}\)-structure is depicted as a function of frequency for \(V = 1{\textrm{m V}}, \, 1 \textrm{V}\).

Fig. 11
figure 11

Real (solid) and imaginary part (dashed) of admittance \(\underline{Y}\) over frequency for \(V = {1}\,{mV}, \, {1}\,{V}\)

Full size image

As expected, \(\mathfrak {R}\left\{ \underline{Y}\right\}\) is non-negative over the entire frequency range, indicating that the simulation is asymptotically stable. For frequencies below 1 THz, \(\mathfrak {R}\left\{ \underline{Y}\right\}\) is nearly constant and corresponds to the steady-state admittance, as shown in Fig. 6. Around 16 THz, a plasma resonance is observed for both voltages, which matches the frequency of the current oscillations in Fig. 10. At frequencies beyond 16THz, \(\mathfrak {R}\left\{ \underline{Y}\right\}\) decreases, but reaches a nonzero saturation value. As already pointed out by Noei et al. [19], this nonphysical behavior can be attributed to the numerical damping that Godunov’s scheme introduces and which depends on the grid spacing. However, the effect occurs only at high frequencies and the damping is negligible for the technically relevant frequency range.

4 Conclusion

We have presented a stabilization scheme based on Godunov’s approach for directly solving the BTE in the three-dimensional \({\textbf {k}}\)-space, which leads to a physically rigorous modeling of the electron transport in III-V devices. The main advantage of the scheme is that it ensures the nonnegativity of the distribution function regardless of the scattering mechanisms and strengths considered, resulting in excellent numerical stability under steady-state, small-signal, and transient conditions. Moreover, the scheme utilizes a time-independent \({\textbf {k}}\)-grid that makes it easier to perform small-signal analysis and transient simulations. For the latter explicit and implicit methods can be used.

While Monte Carlo simulations are widely used in literature due to their shorter simulation time, deterministic solutions of the BTE, as proposed in this paper, provide higher accuracy of the distribution function and its moments. They also enable accurate small-signal analysis at all technically relevant frequencies and inclusion of the Pauli principle, which is not negligible for the doping concentrations in today’s transistors.

It is important to point out that the simulation time of the BTE solver is not competitive with those of TCAD tools and there is a need for the development of novel, faster TCAD tools based on the drift-diffusion or hydrodynamic model for III-V devices. However, the BTE solver could be used as a reliable reference and basis in the development of these TCAD tools, since the drift-diffusion and hydrodynamic models can be derived from the BTE under certain approximations, their parameters can be generated by the BTE, and their accuracy can be checked using the BTE.