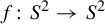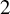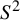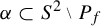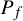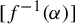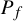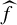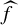1 Introduction
In this paper, we consider Thurston maps and the dynamics of the induced pull-back operation on Jordan curves on the underlying
![]() $2$
-sphere. By definition, a Thurston map is a branched covering map
$2$
-sphere. By definition, a Thurston map is a branched covering map
![]() $f\colon S^2\rightarrow S^2$
on a topological
$f\colon S^2\rightarrow S^2$
on a topological
![]() $2$
-sphere
$2$
-sphere
![]() $S^2$
such that f is not a homeomorphism and every critical point of f (points where f is not a local homeomorphism) has a finite orbit under iteration of f. These maps are named after William Thurston who introduced them in his quest for a better understanding of the dynamics of postcritically-finite rational maps on the Riemann sphere. We refer to [Reference Bonk and MeyerBM17, Ch. 2] for general background on Thurston maps and related concepts.
$S^2$
such that f is not a homeomorphism and every critical point of f (points where f is not a local homeomorphism) has a finite orbit under iteration of f. These maps are named after William Thurston who introduced them in his quest for a better understanding of the dynamics of postcritically-finite rational maps on the Riemann sphere. We refer to [Reference Bonk and MeyerBM17, Ch. 2] for general background on Thurston maps and related concepts.
For a branched covering map
![]() $f\colon S^2\rightarrow S^2$
, we denote by
$f\colon S^2\rightarrow S^2$
, we denote by
![]() ${C_f}$
the set of critical points of f and by
${C_f}$
the set of critical points of f and by
![]() $f^n$
the nth iterate of f for
$f^n$
the nth iterate of f for
![]() $n\in \mathbb {N}$
. Then the postcritical set of f is defined as
$n\in \mathbb {N}$
. Then the postcritical set of f is defined as
For a Thurston map f, this set has finite cardinality
![]() $2\le \#{P_f}<\infty $
(for the first inequality, see [Reference Bonk and MeyerBM17, Corollary 2.13]).
$2\le \#{P_f}<\infty $
(for the first inequality, see [Reference Bonk and MeyerBM17, Corollary 2.13]).
A Thurston map f often admits a description in purely combinatorial-topological terms. In this context, it is an interesting question whether f can be realized (in a suitable sense) by a rational map with the same combinatorics. Roughly speaking, this means that f is conjugate to a rational map ‘up to isotopy’ (see §3 for the precise definition).
It is not hard to see that each Thurston map with two or three postcritical points is realized. The situation is much more complicated for Thurston maps f with
![]() $\#{P_f}\ge 4$
. William Thurston found a necessary and sufficient condition when a Thurston map can be realized by a rational map [Reference Douady and HubbardDH93]. Namely, if f has an associated hyperbolic orbifold (this is always true apart from some well-understood exceptional maps), then f is realized if and only if f has no (Thurston) obstruction. Such an obstruction is given by a finite collection of disjoint Jordan curves in
$\#{P_f}\ge 4$
. William Thurston found a necessary and sufficient condition when a Thurston map can be realized by a rational map [Reference Douady and HubbardDH93]. Namely, if f has an associated hyperbolic orbifold (this is always true apart from some well-understood exceptional maps), then f is realized if and only if f has no (Thurston) obstruction. Such an obstruction is given by a finite collection of disjoint Jordan curves in
![]() ${S^{2}}\smallsetminus {P_f}$
(up to isotopy) with certain invariance properties (see §3.2 for more discussion).
${S^{2}}\smallsetminus {P_f}$
(up to isotopy) with certain invariance properties (see §3.2 for more discussion).
The ‘if’ part of this statement gives a positive criterion for f to be realized, but it is very hard to apply in practice, because, at least in principle, it involves the verification of infinitely many conditions for the map f. For this reason, in each individual case, a successful verification for a map, or a class of maps, is difficult and usually constitutes an interesting result in its own right.
We mention two results in this direction. The first one is the ‘arcs intersecting obstructions’ theorem by Pilgrim and Tan Lei [Reference Pilgrim and LeiPL98, Theorem 3.2] that gives control on the position of an obstruction and has many applications in holomorphic dynamics (see, for instance, [Reference Drach, Mikulich, Rückert and SchleicherDMRS19, Reference Pilgrim and LeiPL98]). The other one is the ‘mating criterion’ by Tan Lei, Rees, and Shishikura that addresses the question when two postcritically-finite quadratic polynomials can be topologically glued together to form a rational map (see [Reference LeiLei92, Reference ReesRee92, Reference Shishikura and LeiShi00]).
The investigation of obstructions of a Thurston map
![]() $f\colon S^2\rightarrow S^2$
is closely related to the study of the pull-back operation on Jordan curves. It is easy to show that if
$f\colon S^2\rightarrow S^2$
is closely related to the study of the pull-back operation on Jordan curves. It is easy to show that if
![]() ${\alpha \subset S^2 \smallsetminus {P_f}}$
is a Jordan curve, then the isotopy class
${\alpha \subset S^2 \smallsetminus {P_f}}$
is a Jordan curve, then the isotopy class
![]() $[f^{-1}(\alpha )]$
(relative to
$[f^{-1}(\alpha )]$
(relative to
![]() ${P_f}$
) only depends on the isotopy class
${P_f}$
) only depends on the isotopy class
![]() $[\alpha ]$
(see Lemma 3.4). Intuitively, the number of postcritical points of a Thurston map can be seen as a measure of its combinatorial complexity. In this paper, we focus on the simplest non-trivial case, namely Thurston maps f with
$[\alpha ]$
(see Lemma 3.4). Intuitively, the number of postcritical points of a Thurston map can be seen as a measure of its combinatorial complexity. In this paper, we focus on the simplest non-trivial case, namely Thurston maps f with
![]() $\#{P_f}=4$
. In this case, the pull-back operation gives rise to a well-defined map, the slope map, on these isotopy classes
$\#{P_f}=4$
. In this case, the pull-back operation gives rise to a well-defined map, the slope map, on these isotopy classes
![]() $[\alpha ]$
(we will discuss this in more detail below). The search for obstructions of f amounts to understanding the fixed points of the slope map.
$[\alpha ]$
(we will discuss this in more detail below). The search for obstructions of f amounts to understanding the fixed points of the slope map.
There exist various natural constructions that allow one to combine or modify given (rational) Thurston maps to obtain a new dynamical system. The most studied constructions are mating (see [Reference LeiLei92, Reference Shishikura and LeiSL00]), tuning (see [Reference ReesRee92]), and capture (see [Reference HeadHea88, Reference LeiLei97]). In this paper, we study the operation of blowing up arcs, originally introduced by Pilgrim and Tan Lei in [Reference Pilgrim and LeiPL98]. This operation can be applied to an arbitrary Thurston map f and results in a new Thurston map
![]() $\widehat f$
that is of higher degree, but combinatorially closely related to the original map f. In particular, f and
$\widehat f$
that is of higher degree, but combinatorially closely related to the original map f. In particular, f and
![]() $\widehat f$
have the same set of postcritical points and the same dynamics on them. Nevertheless, the dynamical behavior of Jordan curves under the pull-back operation for the original map f and the new map
$\widehat f$
have the same set of postcritical points and the same dynamics on them. Nevertheless, the dynamical behavior of Jordan curves under the pull-back operation for the original map f and the new map
![]() $\widehat f$
may differ drastically.
$\widehat f$
may differ drastically.
We show that if a Thurston map
![]() $f\colon S^2\rightarrow S^2$
with
$f\colon S^2\rightarrow S^2$
with
![]() $\#{P_f}=4$
has an obstruction
$\#{P_f}=4$
has an obstruction
![]() $\alpha $
, then one can naturally modify f by blowing up certain arcs to produce a new Thurston map
$\alpha $
, then one can naturally modify f by blowing up certain arcs to produce a new Thurston map
![]() $\widehat f$
for which this obstruction
$\widehat f$
for which this obstruction
![]() $\alpha $
is eliminated. The main result of this paper is the fact that then, no new obstructions arise for
$\alpha $
is eliminated. The main result of this paper is the fact that then, no new obstructions arise for
![]() $\widehat f$
and so it is realized by a rational map.
$\widehat f$
and so it is realized by a rational map.
Theorem 1.1. Let
![]() $f\colon {S^{2}}\to {S^{2}}$
be a Thurston map with
$f\colon {S^{2}}\to {S^{2}}$
be a Thurston map with
![]() $\#{P_f}=4$
and a hyperbolic orbifold. Suppose that f has an obstruction represented by a Jordan curve
$\#{P_f}=4$
and a hyperbolic orbifold. Suppose that f has an obstruction represented by a Jordan curve
![]() $\alpha \subset S^2\smallsetminus {P_f}$
, and
$\alpha \subset S^2\smallsetminus {P_f}$
, and
![]() $E\ne \emptyset $
is a finite set of arcs in
$E\ne \emptyset $
is a finite set of arcs in
![]() $({S^{2}},f^{-1}({P_f}))$
that satisfy the
$({S^{2}},f^{-1}({P_f}))$
that satisfy the
![]() $\alpha $
-restricted blow-up conditions.
$\alpha $
-restricted blow-up conditions.
Let
![]() $\widehat {f}$
be a Thurston map obtained from f by blowing up arcs in E (with some multiplicities) so that
$\widehat {f}$
be a Thurston map obtained from f by blowing up arcs in E (with some multiplicities) so that
![]() $\unicode{x3bb} _{\widehat {f}}(\alpha )<1$
. Then
$\unicode{x3bb} _{\widehat {f}}(\alpha )<1$
. Then
![]() $\widehat {f}$
is realized by a rational map.
$\widehat {f}$
is realized by a rational map.
The technical verbiage and the notation in this formulation will be explained in subsequent sections (see in particular equation (3.3) for the definition of the ‘eigenvalue’
![]() $\unicode{x3bb} _{\widehat {f}}(\alpha )$
and Definition 6.5 for
$\unicode{x3bb} _{\widehat {f}}(\alpha )$
and Definition 6.5 for
![]() $\alpha $
-restricted blow-up conditions).
$\alpha $
-restricted blow-up conditions).
Recently, Dylan Thurston provided a positive characterization when a Thurston map is realized, at least in the case when each critical point eventually lands in a critical cycle under iteration. He proved that such a Thurston map f is realized by a rational map if and only if there is an ‘elastic spine’ (that is, a planar embedded graph in
![]() ${S^{2}}\smallsetminus {P_f}$
with a suitable metric on it) that gets ‘looser’ under backwards iteration (see [Reference ThurstonThu16, Reference ThurstonThu20] for more details). In concrete cases, especially for Thurston maps that should be realized by rational maps with Julia sets homeomorphic to the Sierpiński carpet, the application of Dylan Thurston’s criterion is not so straightforward. Moreover, his criterion is only valid for Thurston maps with periodic critical points. In contrast, for some maps for which Dylan Thurston’s criterion is not applicable or hard to apply, Theorem 1.1 can be used to verify that the maps are realized. In particular, many maps obtained by blowing up Lattès maps (see below) are of this type.
${S^{2}}\smallsetminus {P_f}$
with a suitable metric on it) that gets ‘looser’ under backwards iteration (see [Reference ThurstonThu16, Reference ThurstonThu20] for more details). In concrete cases, especially for Thurston maps that should be realized by rational maps with Julia sets homeomorphic to the Sierpiński carpet, the application of Dylan Thurston’s criterion is not so straightforward. Moreover, his criterion is only valid for Thurston maps with periodic critical points. In contrast, for some maps for which Dylan Thurston’s criterion is not applicable or hard to apply, Theorem 1.1 can be used to verify that the maps are realized. In particular, many maps obtained by blowing up Lattès maps (see below) are of this type.
1.1 Blowing up Lattès maps
We will now discuss a special case of Theorem 1.1 in detail to give the reader some intuition for the geometric ideas behind this statement and its proof.
Let
![]() $\mathbb {P}$
be a pillow obtained from two copies of the unit square
$\mathbb {P}$
be a pillow obtained from two copies of the unit square
![]() $[0,1]^2\subset \mathbb {R}^2\cong \mathbb {C}$
glued together along their boundaries. We consider the two copies of
$[0,1]^2\subset \mathbb {R}^2\cong \mathbb {C}$
glued together along their boundaries. We consider the two copies of
![]() $[0,1]^2$
in
$[0,1]^2$
in
![]() $\mathbb {P}$
as the front and back side of
$\mathbb {P}$
as the front and back side of
![]() $\mathbb {P}$
and call them the tiles of level
$\mathbb {P}$
and call them the tiles of level
![]() $0$
or simply
$0$
or simply
![]() $0$
-tiles. We denote by
$0$
-tiles. We denote by ![]() the lower left corner of
the lower left corner of
![]() $\mathbb {P}$
(see the right part of Figure 1). The pillow
$\mathbb {P}$
(see the right part of Figure 1). The pillow
![]() $\mathbb {P}$
is a topological
$\mathbb {P}$
is a topological
![]() $2$
-sphere. Actually, if we consider
$2$
-sphere. Actually, if we consider
![]() $\mathbb {P}$
as an abstract polyhedral surface, then
$\mathbb {P}$
as an abstract polyhedral surface, then
![]() $\mathbb {P}$
carries a conformal structure making
$\mathbb {P}$
carries a conformal structure making
![]() $\mathbb {P}$
conformally equivalent to the Riemann sphere
$\mathbb {P}$
conformally equivalent to the Riemann sphere
![]() $\widehat {\mathbb {C}}$
. See §2.4 for more discussion.
$\widehat {\mathbb {C}}$
. See §2.4 for more discussion.

Figure 1 The
![]() $(4\times 4)$
-Lattès map.
$(4\times 4)$
-Lattès map.
We now fix
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n\ge 2$
. We subdivide each of the two
$n\ge 2$
. We subdivide each of the two
![]() $0$
-tiles of
$0$
-tiles of
![]() $\mathbb {P}$
into
$\mathbb {P}$
into
![]() $n^2$
small squares of sidelength
$n^2$
small squares of sidelength
![]() $1/n$
, called the
$1/n$
, called the
![]() $1$
-tiles. We color these
$1$
-tiles. We color these
![]() $1$
-tiles in a checkerboard fashion black and white so that the
$1$
-tiles in a checkerboard fashion black and white so that the
![]() $1$
-tile in the front
$1$
-tile in the front
![]() $0$
-tile that contains the vertex A on its boundary is colored white (see the left part of Figure 1). We map this white
$0$
-tile that contains the vertex A on its boundary is colored white (see the left part of Figure 1). We map this white
![]() $1$
-tile to the front
$1$
-tile to the front
![]() $0$
-tile of the right-hand pillow by an orientation-preserving Euclidean similarity that fixes the vertex A. This similarity scales distances by the factor n. We can uniquely extend the similarity by a successive Schwarz reflection process to the whole pillow
$0$
-tile of the right-hand pillow by an orientation-preserving Euclidean similarity that fixes the vertex A. This similarity scales distances by the factor n. We can uniquely extend the similarity by a successive Schwarz reflection process to the whole pillow
![]() $\mathbb {P}$
to obtain a continuous map
$\mathbb {P}$
to obtain a continuous map
![]() $\mathcal {L}_n\colon \mathbb {P}\rightarrow \mathbb {P}$
. Then on each
$\mathcal {L}_n\colon \mathbb {P}\rightarrow \mathbb {P}$
. Then on each
![]() $1$
-tile S, the map
$1$
-tile S, the map
![]() $\mathcal {L}_n$
is a Euclidean similarity that sends S to the front or back
$\mathcal {L}_n$
is a Euclidean similarity that sends S to the front or back
![]() $0$
-tile of
$0$
-tile of
![]() $\mathbb {P}$
depending on whether S is white or black. We call
$\mathbb {P}$
depending on whether S is white or black. We call
![]() $\mathcal {L}_n$
the
$\mathcal {L}_n$
the
![]() $(n\times n)$
-Lattès map, because under a suitable conformal equivalence
$(n\times n)$
-Lattès map, because under a suitable conformal equivalence
![]() $\mathbb {P}\cong \widehat {\mathbb {C}}$
, the map
$\mathbb {P}\cong \widehat {\mathbb {C}}$
, the map
![]() $\mathcal {L}_n$
is conjugate to a rational map obtained from n-multiplication of a Weierstrass
$\mathcal {L}_n$
is conjugate to a rational map obtained from n-multiplication of a Weierstrass
![]() $\wp $
-function. See Figure 1 for an illustration of the map
$\wp $
-function. See Figure 1 for an illustration of the map
![]() $\mathcal {L}_4$
. Here, the marked points on the left pillow
$\mathcal {L}_4$
. Here, the marked points on the left pillow
![]() $\mathbb {P}$
(the domain of the map) correspond to the preimage points
$\mathbb {P}$
(the domain of the map) correspond to the preimage points
![]() $\mathcal {L}_4^{-1}(A)$
. Note that there is exactly one preimage of A in the interior of the back side of the pillow.
$\mathcal {L}_4^{-1}(A)$
. Note that there is exactly one preimage of A in the interior of the back side of the pillow.
It is easy to see that the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n\colon \mathbb {P}\rightarrow \mathbb {P}$
is a Thurston map with four postcritical points, namely, the four corners of the pillow
$\mathcal {L}_n\colon \mathbb {P}\rightarrow \mathbb {P}$
is a Thurston map with four postcritical points, namely, the four corners of the pillow
![]() $\mathbb {P}$
. The map
$\mathbb {P}$
. The map
![]() $\mathcal {L}_n$
is realized by a rational map, because it is even conjugate to such a map.
$\mathcal {L}_n$
is realized by a rational map, because it is even conjugate to such a map.
We now modify the map
![]() $\mathcal {L}_n$
by gluing in vertical or horizontal flaps to
$\mathcal {L}_n$
by gluing in vertical or horizontal flaps to
![]() $\mathbb {P}$
. This is a special case of the more general construction of blowing up arcs mentioned above. We will describe this in detail in §4, but will illustrate the procedure in Figure 2, where we show how to glue in one horizontal flap.
$\mathbb {P}$
. This is a special case of the more general construction of blowing up arcs mentioned above. We will describe this in detail in §4, but will illustrate the procedure in Figure 2, where we show how to glue in one horizontal flap.

Figure 2 Gluing in a flap.
We cut the pillow
![]() $\mathbb {P}$
open along a horizontal side e of one of the
$\mathbb {P}$
open along a horizontal side e of one of the
![]() $1$
-tiles. Note that in this process, e is ‘doubled’ into two arcs
$1$
-tiles. Note that in this process, e is ‘doubled’ into two arcs
![]() $ e'$
and
$ e'$
and
![]() $e"$
with common endpoints. We then take two disjoint copies of the Euclidean square
$e"$
with common endpoints. We then take two disjoint copies of the Euclidean square
![]() $[0,1/{n}]^2$
and identify them along three corresponding sides to obtain a flap F. It has two ‘free’ sides on its boundary. We glue each free side to one of the arcs
$[0,1/{n}]^2$
and identify them along three corresponding sides to obtain a flap F. It has two ‘free’ sides on its boundary. We glue each free side to one of the arcs
![]() $ e'$
and
$ e'$
and
![]() $ e"$
of the cut in the obvious way.
$ e"$
of the cut in the obvious way.
In general, one can repeat this construction and glue several flaps at the location given by the arc e. We assume that this has been done simultaneously for
![]() $n_h\ge 0$
flaps along horizontal edges and
$n_h\ge 0$
flaps along horizontal edges and
![]() $n_v\ge 0$
flaps along vertical edges. By this procedure, we obtain a ‘flapped’ pillow
$n_v\ge 0$
flaps along vertical edges. By this procedure, we obtain a ‘flapped’ pillow
![]() $\widehat {\mathbb {P}}$
, which is still a topological
$\widehat {\mathbb {P}}$
, which is still a topological
![]() $2$
-sphere (see the left part of Figure 3). By construction, it is tiled by
$2$
-sphere (see the left part of Figure 3). By construction, it is tiled by
![]() $2n^2+2(n_h+n_v)$
squares of sidelength
$2n^2+2(n_h+n_v)$
squares of sidelength
![]() $1/n$
, which we consider as the
$1/n$
, which we consider as the
![]() $1$
-tiles of
$1$
-tiles of
![]() $\widehat {\mathbb {P}}$
. The checkerboard coloring of the base surface
$\widehat {\mathbb {P}}$
. The checkerboard coloring of the base surface
![]() $\mathbb {P}$
extends in a unique way to the new surface
$\mathbb {P}$
extends in a unique way to the new surface
![]() $\widehat {\mathbb {P}}$
. The original
$\widehat {\mathbb {P}}$
. The original
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n\colon \mathbb {P}\rightarrow \mathbb {P}$
can naturally be ‘extended’ to a continuous map
$\mathcal {L}_n\colon \mathbb {P}\rightarrow \mathbb {P}$
can naturally be ‘extended’ to a continuous map
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
so that each
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
so that each
![]() $1$
-tile S of
$1$
-tile S of
![]() $\widehat {\mathbb {P}}$
is mapped to the front or back
$\widehat {\mathbb {P}}$
is mapped to the front or back
![]() $0$
-tile of
$0$
-tile of
![]() $\mathbb {P}$
(depending on the color of S) by a Euclidean similarity scaling distances by the factor n. See Figure 3 for an illustration of a map
$\mathbb {P}$
(depending on the color of S) by a Euclidean similarity scaling distances by the factor n. See Figure 3 for an illustration of a map
![]() $\widehat {\mathcal {L}}$
obtained from the Lattès map
$\widehat {\mathcal {L}}$
obtained from the Lattès map
![]() $\mathcal {L}_4$
by gluing in flaps at a vertical and a horizontal edge. Similarly as in Figure 1, on the left, we marked the preimages of A under
$\mathcal {L}_4$
by gluing in flaps at a vertical and a horizontal edge. Similarly as in Figure 1, on the left, we marked the preimages of A under
![]() $\widehat {\mathcal {L}}$
.
$\widehat {\mathcal {L}}$
.

Figure 3 An example of a map
![]() $\widehat {\mathcal {L}}$
obtained from
$\widehat {\mathcal {L}}$
obtained from
![]() $\mathcal {L}_4$
by gluing in flaps.
$\mathcal {L}_4$
by gluing in flaps.
To obtain a Thurston map
![]() $f\colon \mathbb {P}\rightarrow \mathbb {P}$
from this construction, we need to choose a homeomorphism
$f\colon \mathbb {P}\rightarrow \mathbb {P}$
from this construction, we need to choose a homeomorphism
![]() $\phi \colon \widehat {\mathbb {P}}\rightarrow \mathbb {P}$
. Roughly speaking,
$\phi \colon \widehat {\mathbb {P}}\rightarrow \mathbb {P}$
. Roughly speaking,
![]() $\phi $
is a homeomorphism that identifies
$\phi $
is a homeomorphism that identifies
![]() $ \widehat {\mathbb {P}}$
with
$ \widehat {\mathbb {P}}$
with
![]() $\mathbb {P}$
and fixes each corner of the pillow. The precise choice of
$\mathbb {P}$
and fixes each corner of the pillow. The precise choice of
![]() $\phi $
is somewhat technical and so we refer to §4.2 for the details. Then, one easily observes that the postcritical set
$\phi $
is somewhat technical and so we refer to §4.2 for the details. Then, one easily observes that the postcritical set
![]() ${P_f}$
consists of the four corners of the pillow
${P_f}$
consists of the four corners of the pillow
![]() $\mathbb {P}$
. The map f is uniquely determined up to Thurston equivalence (see Definition 3.2) independently of the choice of
$\mathbb {P}$
. The map f is uniquely determined up to Thurston equivalence (see Definition 3.2) independently of the choice of
![]() $\phi $
under suitable restrictions. We refer to f as a Thurston map obtained from the
$\phi $
under suitable restrictions. We refer to f as a Thurston map obtained from the
![]() $(n\times n)$
-Lattès map by gluing
$(n\times n)$
-Lattès map by gluing
![]() $n_h$
horizontal and
$n_h$
horizontal and
![]() $n_v$
vertical flaps to
$n_v$
vertical flaps to
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Now the following statement is true. As we will explain, it can be seen as a special case of our main result.
Theorem 1.2. Let
![]() $n\in \mathbb {N}$
with
$n\in \mathbb {N}$
with
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $f\colon \mathbb {P}\to \mathbb {P}$
be a Thurston map obtained from the
$f\colon \mathbb {P}\to \mathbb {P}$
be a Thurston map obtained from the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
by gluing
$\mathcal {L}_n$
by gluing
![]() $n_h\ge 0$
horizontal and
$n_h\ge 0$
horizontal and
![]() $n_v\ge 0$
vertical flaps to
$n_v\ge 0$
vertical flaps to
![]() $\mathbb {P}$
, where
$\mathbb {P}$
, where
![]() $n_h+n_v>0$
. Then the map f has a hyperbolic orbifold. It has an obstruction if and only if
$n_h+n_v>0$
. Then the map f has a hyperbolic orbifold. It has an obstruction if and only if
![]() $n_h=0$
or
$n_h=0$
or
![]() $n_v=0$
. In particular, if
$n_v=0$
. In particular, if
![]() $n_h>0$
and
$n_h>0$
and
![]() $n_v>0$
, then f is realized by a rational map.
$n_v>0$
, then f is realized by a rational map.
If
![]() $n_h=n_v=0$
, then no flaps were glued to
$n_h=n_v=0$
, then no flaps were glued to
![]() $\mathbb {P}$
and the map f coincides with the original
$\mathbb {P}$
and the map f coincides with the original
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
(strictly speaking, only if we choose the homeomorphism
$\mathcal {L}_n$
(strictly speaking, only if we choose the homeomorphism
![]() $\phi $
used in the construction above to be the identity on
$\phi $
used in the construction above to be the identity on
![]() $\mathbb {P}$
, as we may). Then
$\mathbb {P}$
, as we may). Then
![]() $f=\mathcal {L}_n$
has a parabolic orbifold. Therefore, Thurston’s criterion as formulated in §3.2 does not apply.
$f=\mathcal {L}_n$
has a parabolic orbifold. Therefore, Thurston’s criterion as formulated in §3.2 does not apply.
If
![]() $n_h=0$
or
$n_h=0$
or
![]() $n_v=0$
, but
$n_v=0$
, but
![]() $n_h+n_v>0$
as in Theorem 1.2, then it is immediate to see that f has an obstruction (see §5.1) and therefore f cannot be realized by a rational map. So the interesting part of Theorem 1.2 is the claim that if
$n_h+n_v>0$
as in Theorem 1.2, then it is immediate to see that f has an obstruction (see §5.1) and therefore f cannot be realized by a rational map. So the interesting part of Theorem 1.2 is the claim that if
![]() $n_h>0$
and
$n_h>0$
and
![]() $n_v> 0$
, then f has no obstruction.
$n_v> 0$
, then f has no obstruction.
Even though Theorem 1.2 follows from our more general statement formulated in Theorem 1.1, we will give a complete proof. We will argue by contradiction and assume that a map f with
![]() $n_h>0$
and
$n_h>0$
and
![]() $n_v> 0$
has an obstruction. In principle, there are infinitely many candidates represented by essential isotopy classes of Jordan curves
$n_v> 0$
has an obstruction. In principle, there are infinitely many candidates represented by essential isotopy classes of Jordan curves
![]() $\alpha \subset \mathbb {P}\smallsetminus {P_f}$
. These isotopy classes in turn are distinguished by different slopes in
$\alpha \subset \mathbb {P}\smallsetminus {P_f}$
. These isotopy classes in turn are distinguished by different slopes in
![]() $\widehat {\mathbb {Q}} =\mathbb {Q}\cup \{\infty \}$
(as will be explained in §2.5). For such an isotopy class represented by
$\widehat {\mathbb {Q}} =\mathbb {Q}\cup \{\infty \}$
(as will be explained in §2.5). For such an isotopy class represented by
![]() $\alpha $
to be an obstruction, it has to be f-invariant in the sense that
$\alpha $
to be an obstruction, it has to be f-invariant in the sense that
![]() $f^{-1}(\alpha )$
should contain a component
$f^{-1}(\alpha )$
should contain a component
![]() $\widetilde {\alpha }$
isotopic to
$\widetilde {\alpha }$
isotopic to
![]() $\alpha $
relative to
$\alpha $
relative to
![]() ${P_f}$
. It seems to be a very intricate problem to find all slopes in
${P_f}$
. It seems to be a very intricate problem to find all slopes in
![]() $\widehat {\mathbb {Q}}$
that give an invariant isotopy class for f. Since we have been able to decide this question only for very simple maps f, we proceed in a more indirect manner.
$\widehat {\mathbb {Q}}$
that give an invariant isotopy class for f. Since we have been able to decide this question only for very simple maps f, we proceed in a more indirect manner.
We assume that the Jordan curve
![]() $\alpha \subset \mathbb {P}\smallsetminus {P_f}$
is f-invariant and gives an obstruction. We then investigate the mapping degrees of f on components of
$\alpha \subset \mathbb {P}\smallsetminus {P_f}$
is f-invariant and gives an obstruction. We then investigate the mapping degrees of f on components of
![]() $f^{-1}(\alpha )$
and consider intersection numbers of some relevant curves together with a careful counting argument. We heavily use the fact that the horizontal and vertical Jordan curves (see (2.4)) are f-invariant. Ultimately, we arrive at a contradiction. See §5 for the details of this argument.
$f^{-1}(\alpha )$
and consider intersection numbers of some relevant curves together with a careful counting argument. We heavily use the fact that the horizontal and vertical Jordan curves (see (2.4)) are f-invariant. Ultimately, we arrive at a contradiction. See §5 for the details of this argument.
Our idea to use intersection numbers (as in Lemma 5.5) to control possible locations of obstructions and dynamics on curves is not new (see, for example, [Reference Pilgrim and LeiPL98, Theorem 3.2], [Reference Cui, Peng and LeiCPL16, §8], and [Reference ParryPar18]). However, the previously available results do not provide sharp enough estimates applicable in our situation.
One can think of Theorem 1.2 in the following way. Suppose that instead of directly passing from the Lattès map
![]() $\mathcal {L}_n$
to a map, let us now call it
$\mathcal {L}_n$
to a map, let us now call it
![]() $\widehat f$
, obtained by gluing
$\widehat f$
, obtained by gluing
![]() $n_h>0$
horizontal and
$n_h>0$
horizontal and
![]() $n_v>0$
vertical flaps to
$n_v>0$
vertical flaps to
![]() $\mathbb {P}$
, we first create an intermediate map f obtained by gluing
$\mathbb {P}$
, we first create an intermediate map f obtained by gluing
![]() $n_h>0$
horizontal, but no vertical flaps. Then f has a hyperbolic orbifold and an obstruction given by a ‘horizontal’ Jordan curve
$n_h>0$
horizontal, but no vertical flaps. Then f has a hyperbolic orbifold and an obstruction given by a ‘horizontal’ Jordan curve
![]() $\alpha $
. In the passage from f to
$\alpha $
. In the passage from f to
![]() $\widehat f$
, we kill this obstruction, because we glue additional vertical flaps that serve as obstacles and increase the mapping degree on some pullbacks of
$\widehat f$
, we kill this obstruction, because we glue additional vertical flaps that serve as obstacles and increase the mapping degree on some pullbacks of
![]() $\alpha $
. Theorem 1.1 then says that no other obstructions arise for
$\alpha $
. Theorem 1.1 then says that no other obstructions arise for
![]() $\widehat f$
. Therefore, Theorem 1.1 generalizes Theorem 1.2 if we interpret it in the way just described. The proof of Theorem 1.1 is based on the ideas that we use to establish Theorem 1.2, but substantial refinements and extensions are required.
$\widehat f$
. Therefore, Theorem 1.1 generalizes Theorem 1.2 if we interpret it in the way just described. The proof of Theorem 1.1 is based on the ideas that we use to establish Theorem 1.2, but substantial refinements and extensions are required.
1.2 The global curve attractor problem
The mapping properties of Jordan curves play an important role in Thurston’s characterization of rational maps. The original proof of this statement associates with a given Thurston map
![]() $f\colon {S^{2}}\to {S^{2}}$
with a hyperbolic orbifold a certain Teichmüller space
$f\colon {S^{2}}\to {S^{2}}$
with a hyperbolic orbifold a certain Teichmüller space
![]() $\mathcal {T}_f$
and an analytic map
$\mathcal {T}_f$
and an analytic map
![]() $\sigma _f\colon \mathcal {T}_f\to \mathcal {T}_f$
, called Thurston’s pullback map. One can show that the map f is realized by a rational map if and only if
$\sigma _f\colon \mathcal {T}_f\to \mathcal {T}_f$
, called Thurston’s pullback map. One can show that the map f is realized by a rational map if and only if
![]() $\sigma _f$
has a fixed point [Reference Douady and HubbardDH93]. This reduction to a fixed point problem in a Teichmüller space has also been successfully applied by Thurston in other contexts such as uniformization problems and the theory of
$\sigma _f$
has a fixed point [Reference Douady and HubbardDH93]. This reduction to a fixed point problem in a Teichmüller space has also been successfully applied by Thurston in other contexts such as uniformization problems and the theory of
![]() $3$
-manifolds (there is a rich literature on the subject; see, for example, [Reference Fathi, Laudenbach and PoénaruFLP12, Reference HubbardHub16, Reference ThurstonThu88, Reference ThurstonThu98, Reference OtalOta01]).
$3$
-manifolds (there is a rich literature on the subject; see, for example, [Reference Fathi, Laudenbach and PoénaruFLP12, Reference HubbardHub16, Reference ThurstonThu88, Reference ThurstonThu98, Reference OtalOta01]).
In recent years, the pullback map
![]() $\sigma _f$
and its dynamical properties have been subject to deeper investigations (see, for example, [Reference Koch, Pilgrim and SelingerKPS16, Reference LodgeLod13, Reference PilgrimPil12, Reference SelingerSel12]). In particular, Selinger showed in [Reference SelingerSel12] that
$\sigma _f$
and its dynamical properties have been subject to deeper investigations (see, for example, [Reference Koch, Pilgrim and SelingerKPS16, Reference LodgeLod13, Reference PilgrimPil12, Reference SelingerSel12]). In particular, Selinger showed in [Reference SelingerSel12] that
![]() $\sigma _f$
extends to the Weil–Petersson boundary of
$\sigma _f$
extends to the Weil–Petersson boundary of
![]() $\mathcal {T}_f$
. The behavior of
$\mathcal {T}_f$
. The behavior of
![]() $\sigma _f$
on this boundary is closely related to the behavior of Jordan curves under pull-back by f. This in turn leads to the following difficult open question in holomorphic dynamics, called the global curve attractor problem (see [Reference LodgeLod13, §9]).
$\sigma _f$
on this boundary is closely related to the behavior of Jordan curves under pull-back by f. This in turn leads to the following difficult open question in holomorphic dynamics, called the global curve attractor problem (see [Reference LodgeLod13, §9]).
Conjecture. Let
![]() $f\colon S^2\to S^2$
be a Thurston map with a hyperbolic orbifold that is realized by a rational map. Then there exists a finite set
$f\colon S^2\to S^2$
be a Thurston map with a hyperbolic orbifold that is realized by a rational map. Then there exists a finite set
![]() $\mathscr {A}(f)$
of Jordan curves in
$\mathscr {A}(f)$
of Jordan curves in
![]() $S^2\smallsetminus {P_f}$
such that for every Jordan curve
$S^2\smallsetminus {P_f}$
such that for every Jordan curve
![]() $\gamma \subset S^2\smallsetminus {P_f}$
, all pullbacks
$\gamma \subset S^2\smallsetminus {P_f}$
, all pullbacks
![]() $\widetilde \gamma $
of
$\widetilde \gamma $
of
![]() $\gamma $
under
$\gamma $
under
![]() $f^n$
are contained in
$f^n$
are contained in
![]() $\mathscr {A}(f)$
up to isotopy relative to
$\mathscr {A}(f)$
up to isotopy relative to
![]() ${P_f}$
for all sufficiently large
${P_f}$
for all sufficiently large
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
A set of Jordan curves
![]() $\mathscr {A}(f)$
, as in this conjecture, is called a global curve attractor of f. We will give a solution of this problem for maps as in Theorem 1.2 with
$\mathscr {A}(f)$
, as in this conjecture, is called a global curve attractor of f. We will give a solution of this problem for maps as in Theorem 1.2 with
![]() $n=2$
and
$n=2$
and
![]() $n_h, n_v\ge 1$
. Unfortunately, our methods only apply for
$n_h, n_v\ge 1$
. Unfortunately, our methods only apply for
![]() $n=2$
and not for
$n=2$
and not for
![]() $n\ge 3$
.
$n\ge 3$
.
Theorem 1.3. Let
![]() $f\colon \mathbb {P}\rightarrow \mathbb {P}$
be a Thurston map obtained from the
$f\colon \mathbb {P}\rightarrow \mathbb {P}$
be a Thurston map obtained from the
![]() $(2\times 2)$
-Lattès map by gluing
$(2\times 2)$
-Lattès map by gluing
![]() $n_h\geq 1$
horizontal and
$n_h\geq 1$
horizontal and
![]() $n_v\geq 1$
vertical flaps to the pillow
$n_v\geq 1$
vertical flaps to the pillow
![]() $\mathbb {P}$
. Then f has a global curve attractor
$\mathbb {P}$
. Then f has a global curve attractor
![]() $\mathscr {A}(f)$
.
$\mathscr {A}(f)$
.
One can show that the Julia set of a rational map, as provided by Theorem 1.2, is either a Sierpiński carpet or the whole Riemann sphere depending on whether the map has periodic critical points or not (see Proposition 9.1). Accordingly, Theorem 1.3 provides the first examples of maps with Sierpiński carpet Julia set for which an answer to the global curve attractor problem is known. In fact, we obtain such maps with arbitrarily large degrees.
Recently, Belk et al proved the existence of a finite global curve attractor for all postcritically finite polynomials [Reference Belk, Lanier, Margalit and WinarskiBLMW22]. The conjecture is also known to be true for all critically fixed rational maps (that is, rational maps for which each critical point is fixed) and some nearly Euclidean Thurston maps (that is, Thurston maps with exactly four postcritical points and only simple critical points); see [Reference Floyd, Kelsey, Koch, Lodge, Parry, Pilgrim and SaenzFKK+17, Reference HlushchankaHlu19, Reference LodgeLod13]. In [Reference Kelsey and LodgeKL19], Kelsey and Lodge verified the conjecture for all quadratic non-Lattès maps with four postcritical points. However, for general postcritcally finite rational maps, the conjecture remains wide open.
Since the maps we consider have four postcritical points, it is convenient to reformulate the global curve attractor problem by introducing the slope map (it is closely related to the Thurston pull-back map
![]() $\sigma _f$
on the Weil–Petersson boundary of
$\sigma _f$
on the Weil–Petersson boundary of
![]() $\mathcal {T}_f$
). To define it in the special case relevant for us, we consider the marked pillow
$\mathcal {T}_f$
). To define it in the special case relevant for us, we consider the marked pillow
![]() $(\mathbb {P},V)$
, where V is the set consisting of the four corners of
$(\mathbb {P},V)$
, where V is the set consisting of the four corners of
![]() $\mathbb {P}$
, and assume that
$\mathbb {P}$
, and assume that
![]() $f\colon \mathbb {P}\to \mathbb {P}$
is a Thurston map with
$f\colon \mathbb {P}\to \mathbb {P}$
is a Thurston map with
![]() ${P_f}=V$
. Up to topological conjugacy, every Thurston map with four postcritical points can be assumed to have this form.
${P_f}=V$
. Up to topological conjugacy, every Thurston map with four postcritical points can be assumed to have this form.
As we already mentioned, there is a bijective correspondence between isotopy classes
![]() $[\alpha ]$
of essential Jordan curves
$[\alpha ]$
of essential Jordan curves
![]() $\alpha $
in
$\alpha $
in
![]() $(\mathbb {P},V)$
and slopes
$(\mathbb {P},V)$
and slopes
![]() $r/s\in \widehat {\mathbb {Q}}$
(see Lemma 2.3). We introduce the additional symbol
$r/s\in \widehat {\mathbb {Q}}$
(see Lemma 2.3). We introduce the additional symbol
![]() $\odot $
to represent peripheral Jordan curves in
$\odot $
to represent peripheral Jordan curves in
![]() $(\mathbb {P},V)$
. We now define the slope map
$(\mathbb {P},V)$
. We now define the slope map
![]() $\mu _f\colon \widehat {\mathbb {Q}}\cup \{\odot \} \rightarrow \widehat {\mathbb {Q}}\cup \{\odot \} $
associated with f as follows. We set
$\mu _f\colon \widehat {\mathbb {Q}}\cup \{\odot \} \rightarrow \widehat {\mathbb {Q}}\cup \{\odot \} $
associated with f as follows. We set ![]() . This corresponds to the fact that each pullback of a peripheral Jordan curve
. This corresponds to the fact that each pullback of a peripheral Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $(\mathbb {P},V)$
under f is peripheral (see Corollary 3.5(i)). If
$(\mathbb {P},V)$
under f is peripheral (see Corollary 3.5(i)). If
![]() $r/s\in \widehat {\mathbb {Q}}$
is an arbitrary slope, then we choose a Jordan curve
$r/s\in \widehat {\mathbb {Q}}$
is an arbitrary slope, then we choose a Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $(\mathbb {P},V)$
whose isotopy class
$(\mathbb {P},V)$
whose isotopy class
![]() $[\alpha ]$
is represented by
$[\alpha ]$
is represented by
![]() $r/s$
. If all pullbacks of
$r/s$
. If all pullbacks of
![]() $\alpha $
under f are peripheral, we set
$\alpha $
under f are peripheral, we set ![]() . Otherwise, there exists an essential pullback
. Otherwise, there exists an essential pullback
![]() $\widetilde \alpha $
of
$\widetilde \alpha $
of
![]() $\alpha $
under f. Then the isotopy class
$\alpha $
under f. Then the isotopy class
![]() $[\widetilde \alpha ]$
is independent of the choice of the essential pullback
$[\widetilde \alpha ]$
is independent of the choice of the essential pullback
![]() $\widetilde \alpha $
(see Corollary 3.5(ii)) and so it is represented by a unique slope
$\widetilde \alpha $
(see Corollary 3.5(ii)) and so it is represented by a unique slope
![]() $r'/s'\in \widehat {\mathbb {Q}}$
. In this case, we set
$r'/s'\in \widehat {\mathbb {Q}}$
. In this case, we set ![]() . In this way,
. In this way,
![]() $\mu _f(x)\in \widehat {\mathbb {Q}}\cup \{\odot \}$
is defined for all
$\mu _f(x)\in \widehat {\mathbb {Q}}\cup \{\odot \}$
is defined for all
![]() $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
. Since the map
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
. Since the map
![]() $\mu _f$
has the same source and target, we can iterate it. If
$\mu _f$
has the same source and target, we can iterate it. If
![]() $n\in \mathbb {N}_0$
, then we denote by
$n\in \mathbb {N}_0$
, then we denote by
![]() $\mu ^n_f$
the nth iterate of
$\mu ^n_f$
the nth iterate of
![]() $\mu _f$
. We will then prove the following statement.
$\mu _f$
. We will then prove the following statement.
Theorem 1.4. Let
![]() $f\colon \mathbb {P}\rightarrow \mathbb {P}$
be a Thurston map obtained from the
$f\colon \mathbb {P}\rightarrow \mathbb {P}$
be a Thurston map obtained from the
![]() $(2\times 2)$
-Lattès map by gluing
$(2\times 2)$
-Lattès map by gluing
![]() $n_h\geq 1$
horizontal and
$n_h\geq 1$
horizontal and
![]() $n_v\geq 1$
vertical flaps to the pillow
$n_v\geq 1$
vertical flaps to the pillow
![]() $\mathbb {P}$
. Then there exists a finite set
$\mathbb {P}$
. Then there exists a finite set
![]() $S\subset \widehat {\mathbb {Q}}\cup \{\odot \}$
with the following property: for each
$S\subset \widehat {\mathbb {Q}}\cup \{\odot \}$
with the following property: for each
![]() $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
, there exists
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
, there exists
![]() $N\in \mathbb {N}_0$
such that
$N\in \mathbb {N}_0$
such that
![]() $ \mu ^n_f(x)\in S$
for all
$ \mu ^n_f(x)\in S$
for all
![]() $n\ge N$
.
$n\ge N$
.
Note that
![]() ${P_f}=V$
in this case; so our previous considerations apply and the map
${P_f}=V$
in this case; so our previous considerations apply and the map
![]() $\mu _f$
is defined. It is clear that the previous theorem leads to the solution of the global curve attractor problem for the maps f considered.
$\mu _f$
is defined. It is clear that the previous theorem leads to the solution of the global curve attractor problem for the maps f considered.
Proof of Theorem 1.3 based on Theorem 1.4
To obtain a finite attractor
![]() $\mathscr {A}(f)$
, pick a Jordan curve in each isotopy class represented by a slope in S and add five Jordan curves that represent the isotopy classes of peripheral Jordan curves in
$\mathscr {A}(f)$
, pick a Jordan curve in each isotopy class represented by a slope in S and add five Jordan curves that represent the isotopy classes of peripheral Jordan curves in
![]() $(\mathbb {P},V)$
(one for null-homotopic curves and one for each corner of
$(\mathbb {P},V)$
(one for null-homotopic curves and one for each corner of
![]() $\mathbb {P}$
).
$\mathbb {P}$
).
For the proof of Theorem 1.4, we will establish a certain monotonicity property of the slope map
![]() $\mu _f$
for a map f as in the statement (see Proposition 8.1). Roughly speaking, this monotonicity means that up to isotopy relative to
$\mu _f$
for a map f as in the statement (see Proposition 8.1). Roughly speaking, this monotonicity means that up to isotopy relative to
![]() ${P_f}=V$
, complicated essential Jordan curves in
${P_f}=V$
, complicated essential Jordan curves in
![]() $(\mathbb {P}, V)$
get ‘simpler’ and ‘less twisted’ if we take successive preimages under f and eventually end up in the global curve attractor.
$(\mathbb {P}, V)$
get ‘simpler’ and ‘less twisted’ if we take successive preimages under f and eventually end up in the global curve attractor.
Our methods again rely on the consideration of intersection numbers. The algebraic methods for solving the global curve attractor problem developed in [Reference PilgrimPil12] (specifically, [Reference PilgrimPil12, Theorem 1.4]) do not apply in general for the maps considered in Theorem 1.3 (see the discussion in §9.3).
Some of our ideas can also be used for the study of the global dynamics of the slope map for Thurston maps that are not covered by Theorem 1.4. In particular, we are able to describe the iterative behavior of
![]() $\mu _f$
for a specific obstructed Thurston map f obtained by blowing up the
$\mu _f$
for a specific obstructed Thurston map f obtained by blowing up the
![]() $(2\times 2)$
-Lattès map (see §9.2 for the details). This provides an answer to a question by Pilgrim.
$(2\times 2)$
-Lattès map (see §9.2 for the details). This provides an answer to a question by Pilgrim.
While it is straightforward to compute
![]() $\mu _f(x)$
for individual values
$\mu _f(x)$
for individual values
![]() $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
, we have been unable to give an explicit formula for
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
, we have been unable to give an explicit formula for
![]() $\mu _f$
for the maps f we consider. In general, these slope maps show very complicated behavior. Currently, very few explicit computations of slope maps are known in the literature. Except for some very special situations (for example, when the slope map is constant, that is, when
$\mu _f$
for the maps f we consider. In general, these slope maps show very complicated behavior. Currently, very few explicit computations of slope maps are known in the literature. Except for some very special situations (for example, when the slope map is constant, that is, when
![]() $\mu _f(x)=\odot $
for all
$\mu _f(x)=\odot $
for all
![]() $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
), we are only aware of computations of slope maps for nearly Euclidian Thurston maps in [Reference Cannon, Floyd, Parry and PilgrimCFPP12, §5] and [Reference LodgeLod13, §6]. See also [Reference Floyd, Parry and PilgrimFPP18] for some general properties of the slope map
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
), we are only aware of computations of slope maps for nearly Euclidian Thurston maps in [Reference Cannon, Floyd, Parry and PilgrimCFPP12, §5] and [Reference LodgeLod13, §6]. See also [Reference Floyd, Parry and PilgrimFPP18] for some general properties of the slope map
![]() $\mu _f$
.
$\mu _f$
.
An undergraduate student at UCLA, Darragh Glynn, performed some computer experiments to compute
![]() $\mu _f$
for maps f as in Theorem 1.2 for
$\mu _f$
for maps f as in Theorem 1.2 for
![]() $n\ge 3$
(and
$n\ge 3$
(and
![]() $n_h,n_v\ge 1$
corresponding to the rational case). His results show that in these cases, the map
$n_h,n_v\ge 1$
corresponding to the rational case). His results show that in these cases, the map
![]() $\mu _f$
does not have the monotonicity property as for
$\mu _f$
does not have the monotonicity property as for
![]() $n=2$
, but indicate that these maps f still have a global curve attractor (see §9.2 for more discussion).
$n=2$
, but indicate that these maps f still have a global curve attractor (see §9.2 for more discussion).
1.3 Organization of this paper
Our paper is organized as follows. In the next two sections, we review some background. In §2, we fix notation and state some basic definitions. We also discuss isotopy classes of Jordan curves in spheres with four marked points, how isotopy classes of such curves correspond to slopes in
![]() $\widehat {\mathbb {Q}}$
, as well as some relevant facts about intersection numbers. Even though all of this is fairly standard, we give complete proofs in the appendix, because it is hard to track down this material in the literature with a detailed exposition.
$\widehat {\mathbb {Q}}$
, as well as some relevant facts about intersection numbers. Even though all of this is fairly standard, we give complete proofs in the appendix, because it is hard to track down this material in the literature with a detailed exposition.
In §3, we recall some basics about Thurston maps and the relevant concepts for a precise formulation of Thurston’s characterization of rational maps for Thurston maps with four postcritical points—the only case relevant for us (see §3.2).
We explain the blow-up procedure for arcs in §4 and relate this to the procedure of gluing flaps to the pillow
![]() $\mathbb {P}$
(see §4.2). The proof of Theorem 1.2 is then given in §5.
$\mathbb {P}$
(see §4.2). The proof of Theorem 1.2 is then given in §5.
The proof of our main result, Theorem 1.1, requires more preparation. This is the purpose of §6. There we introduce the concept of essential circuit length that will allow us to formulate tight estimates for the number of essential pullbacks of a Jordan curve under a Thurston map with four postcritical points. This is formulated in the rather technical Lemma 6.2 which is of crucial importance though. The proof of Theorem 1.1 is then given in §7.
Section 8 is devoted to the proof of Theorem 1.4. In §9, we discuss some further directions related to this work. As we already mentioned, the appendix is devoted to the discussion of isotopy classes and intersection numbers of Jordan curves in spheres with four marked points.
2 Preliminaries
In this section, we discuss background relevant for the rest of the paper.
2.1 Notation and basic concepts
We denote by
![]() $\mathbb {N}=\{1,2,\ldots \}$
the set of natural numbers and by
$\mathbb {N}=\{1,2,\ldots \}$
the set of natural numbers and by
![]() $\mathbb {N}_0=\{0,1, 2, \ldots \}$
the set of natural numbers including
$\mathbb {N}_0=\{0,1, 2, \ldots \}$
the set of natural numbers including
![]() $0$
. The sets of integers, real numbers, and complex numbers are denoted by
$0$
. The sets of integers, real numbers, and complex numbers are denoted by
![]() $\mathbb {Z}$
,
$\mathbb {Z}$
,
![]() $\mathbb {R}$
, and
$\mathbb {R}$
, and
![]() $\mathbb {C}$
, respectively. We write i for the imaginary unit in
$\mathbb {C}$
, respectively. We write i for the imaginary unit in
![]() $\mathbb {C}$
, and
$\mathbb {C}$
, and
![]() $\text {Im}(z)$
for the imaginary part of a complex number
$\text {Im}(z)$
for the imaginary part of a complex number
![]() $z\in \mathbb {C}$
.
$z\in \mathbb {C}$
.
As usual, ![]() is the Euclidean plane and
is the Euclidean plane and ![]() is the Riemann sphere. Here and elsewhere, we write
is the Riemann sphere. Here and elsewhere, we write ![]() for emphasis when an object A is defined to be another object B. When we consider two objects A and B, and there is a natural identification between them that is clear from the context, we write
for emphasis when an object A is defined to be another object B. When we consider two objects A and B, and there is a natural identification between them that is clear from the context, we write
![]() $A\cong B$
. For example,
$A\cong B$
. For example,
![]() $\mathbb {R}^2\cong \mathbb {C}$
if we identify a point
$\mathbb {R}^2\cong \mathbb {C}$
if we identify a point
![]() $(x,y)\in \mathbb {R}^2$
with
$(x,y)\in \mathbb {R}^2$
with
![]() $x+ iy \in \mathbb {C}$
. We will freely switch back and forth between these different viewpoints of
$x+ iy \in \mathbb {C}$
. We will freely switch back and forth between these different viewpoints of
![]() $\mathbb {R}^2\cong \mathbb {C}$
.
$\mathbb {R}^2\cong \mathbb {C}$
.
We use the notation ![]() for the closed unit interval,
for the closed unit interval, ![]() for the open unit disk in
for the open unit disk in
![]() $\mathbb {C}$
, and
$\mathbb {C}$
, and ![]() for the square lattice in
for the square lattice in
![]() $\mathbb {C}$
. If
$\mathbb {C}$
. If
![]() $z,w\in ~\mathbb {C}$
, then we write
$z,w\in ~\mathbb {C}$
, then we write ![]() for the line segment in
for the line segment in
![]() $\mathbb {C}$
joining z and w. We also use the notation
$\mathbb {C}$
joining z and w. We also use the notation ![]() and
and ![]() .
.
The cardinality of a set X is denoted by
![]() $\#X\in \mathbb {N}_0\cup \{\infty \}$
and the identity map on X by
$\#X\in \mathbb {N}_0\cup \{\infty \}$
and the identity map on X by
![]() $\operatorname {id}_X$
. If X is a topological space and
$\operatorname {id}_X$
. If X is a topological space and
![]() $M\subset X$
, then
$M\subset X$
, then
![]() $\operatorname {cl}(M)$
denotes the closure,
$\operatorname {cl}(M)$
denotes the closure,
![]() $\operatorname {int}(M)$
the interior, and
$\operatorname {int}(M)$
the interior, and
![]() $\partial M$
the boundary of M in X.
$\partial M$
the boundary of M in X.
Let
![]() $f\colon X\to Y$
be a map between sets X and Y. If
$f\colon X\to Y$
be a map between sets X and Y. If
![]() $M\subset X$
, then
$M\subset X$
, then
![]() $f|M$
stands for the restriction of f to M. If
$f|M$
stands for the restriction of f to M. If
![]() $N\subset Y$
, then
$N\subset Y$
, then ![]() is the preimage of N in X. Similarly,
is the preimage of N in X. Similarly, ![]() is the preimage of a point
is the preimage of a point
![]() $y\in Y$
.
$y\in Y$
.
Let
![]() $f\colon X\rightarrow X$
be a map. For
$f\colon X\rightarrow X$
be a map. For
![]() $n\in \mathbb {N}$
, we denote by
$n\in \mathbb {N}$
, we denote by
the nth iterate of f. It is convenient to define ![]() . For
. For
![]() $n\in \mathbb {N}_0$
, we denote by
$n\in \mathbb {N}_0$
, we denote by ![]() and
and ![]() the preimages of a set
the preimages of a set
![]() $M\subset X$
and a point
$M\subset X$
and a point
![]() $p\in X$
under
$p\in X$
under
![]() $f^n$
, respectively.
$f^n$
, respectively.
A surface S is a connected and oriented topological
![]() $2$
-manifold. We denote its Euler characteristic by
$2$
-manifold. We denote its Euler characteristic by
![]() $\chi (S)$
. Note that
$\chi (S)$
. Note that
![]() $\chi (S)\in \{2, 1,0, -1, \ldots \} \cup \{-\infty \}$
. Throughout this paper, we use the notation
$\chi (S)\in \{2, 1,0, -1, \ldots \} \cup \{-\infty \}$
. Throughout this paper, we use the notation
![]() ${S^{2}}$
for a (topological)
${S^{2}}$
for a (topological)
![]() $2$
-sphere, that is,
$2$
-sphere, that is,
![]() ${S^{2}}$
indicates a surface homeomorphic to the Riemann sphere
${S^{2}}$
indicates a surface homeomorphic to the Riemann sphere
![]() $\widehat {\mathbb {C}}$
. An annulus is a surface homeomorphic to
$\widehat {\mathbb {C}}$
. An annulus is a surface homeomorphic to
![]() $\{ z\in \mathbb {C}: 1<|z|<2\}$
.
$\{ z\in \mathbb {C}: 1<|z|<2\}$
.
A Jordan curve
![]() $\alpha $
in a surface S is the image
$\alpha $
in a surface S is the image
![]() $\alpha =\eta (\partial \mathbb {D})$
of a (topological) embedding
$\alpha =\eta (\partial \mathbb {D})$
of a (topological) embedding
![]() $\eta \colon \partial \mathbb {D} \rightarrow S$
of the unit circle
$\eta \colon \partial \mathbb {D} \rightarrow S$
of the unit circle
![]() $\partial \mathbb {D}=\{z\in \mathbb {C}: |z|=1\}$
into S. An arc e in S is the image
$\partial \mathbb {D}=\{z\in \mathbb {C}: |z|=1\}$
into S. An arc e in S is the image
![]() $e=\iota (\mathbb {I})$
of an embedding
$e=\iota (\mathbb {I})$
of an embedding
![]() $\iota \colon \mathbb {I}\to S$
. Then
$\iota \colon \mathbb {I}\to S$
. Then
![]() $\iota (0)$
and
$\iota (0)$
and
![]() $\iota (1)$
are the endpoints of e, and we define
$\iota (1)$
are the endpoints of e, and we define ![]() . The set
. The set ![]() is called the interior of e. The notions of endpoints and interior of e only depend on e and not on the choice of the embedding
is called the interior of e. The notions of endpoints and interior of e only depend on e and not on the choice of the embedding
![]() $\iota $
. Note that the notation
$\iota $
. Note that the notation
![]() $\partial e$
and
$\partial e$
and
![]() $\operatorname {int}(e)$
is ambiguous, because it should not be confused with the boundary and interior of e as a subset of S. For arcs e in a surface S, we will only use
$\operatorname {int}(e)$
is ambiguous, because it should not be confused with the boundary and interior of e as a subset of S. For arcs e in a surface S, we will only use
![]() $\partial e$
and
$\partial e$
and
![]() $\operatorname {int}(e)$
with the meaning just defined.
$\operatorname {int}(e)$
with the meaning just defined.
A subset U of a surface S is called an open or closed Jordan region if there exists a topological embedding
![]() $\eta \colon \operatorname {cl}(\mathbb {D})=\{z\in \mathbb {C}: |z|\le 1\}\rightarrow S$
such that
$\eta \colon \operatorname {cl}(\mathbb {D})=\{z\in \mathbb {C}: |z|\le 1\}\rightarrow S$
such that
![]() $U=\eta (\mathbb {D})$
or
$U=\eta (\mathbb {D})$
or
![]() ${U=\eta (\operatorname {cl}(\mathbb {D}))}$
, respectively. In both cases,
${U=\eta (\operatorname {cl}(\mathbb {D}))}$
, respectively. In both cases,
![]() $\partial U=\eta (\partial \mathbb {D})$
is a Jordan curve in S. A crosscut e in an open or closed Jordan region U is an arc
$\partial U=\eta (\partial \mathbb {D})$
is a Jordan curve in S. A crosscut e in an open or closed Jordan region U is an arc
![]() $e\subset \operatorname {cl}(U)$
such that
$e\subset \operatorname {cl}(U)$
such that
![]() $\operatorname {int}(e)\subset \operatorname {int}(U)$
and
$\operatorname {int}(e)\subset \operatorname {int}(U)$
and
![]() $\partial e\subset \partial U$
.
$\partial e\subset \partial U$
.
A path
![]() $\gamma $
in a surface S is a continuous map
$\gamma $
in a surface S is a continuous map
![]() $\gamma \colon [a,b]\rightarrow S$
, where
$\gamma \colon [a,b]\rightarrow S$
, where
![]() $[a,b]\subset \mathbb {R}$
is a compact (non-degenerate) interval. As is common, we will use the same notation
$[a,b]\subset \mathbb {R}$
is a compact (non-degenerate) interval. As is common, we will use the same notation
![]() $\gamma $
for the image
$\gamma $
for the image
![]() $\gamma ([a,b])$
of the path if no confusion can arise. The path
$\gamma ([a,b])$
of the path if no confusion can arise. The path
![]() $\gamma $
joins two sets
$\gamma $
joins two sets
![]() $M,N\subset S$
if
$M,N\subset S$
if
![]() $\gamma (a) \in M$
and
$\gamma (a) \in M$
and
![]() $\gamma (b)\in N$
, or vice versa. A loop in S based at
$\gamma (b)\in N$
, or vice versa. A loop in S based at
![]() $p\in S$
is a path
$p\in S$
is a path
![]() $\gamma \colon [a,b] \rightarrow S$
such that
$\gamma \colon [a,b] \rightarrow S$
such that
![]() $\gamma (a)=\gamma (b)=p$
. The loop
$\gamma (a)=\gamma (b)=p$
. The loop
![]() $\gamma $
is called simple if
$\gamma $
is called simple if
![]() $\gamma $
is injective on
$\gamma $
is injective on
![]() $[a,b)$
. So essentially, a simple loop is a Jordan curve run through with some parameterization.
$[a,b)$
. So essentially, a simple loop is a Jordan curve run through with some parameterization.
Let
![]() $M,N,K$
be subsets of a surface S. We say that K separates M and N if every path in S joining M and N meets K. Note that here, K is not necessarily disjoint from M or N. We say that K separates a point
$M,N,K$
be subsets of a surface S. We say that K separates M and N if every path in S joining M and N meets K. Note that here, K is not necessarily disjoint from M or N. We say that K separates a point
![]() $p\in S$
from a set
$p\in S$
from a set
![]() $M\subset S$
if K separates
$M\subset S$
if K separates
![]() $\{p\}$
and M.
$\{p\}$
and M.
Let
![]() $Z\subset S$
be a finite set of points in a surface S. Then we refer to the pair
$Z\subset S$
be a finite set of points in a surface S. Then we refer to the pair
![]() $(S, Z)$
as a marked surface, and the points in Z as the marked points in S. The most important case for us will be when
$(S, Z)$
as a marked surface, and the points in Z as the marked points in S. The most important case for us will be when
![]() $S=S^2$
is a
$S=S^2$
is a
![]() $2$
-sphere and
$2$
-sphere and
![]() $Z\subset S^2$
consists of four points.
$Z\subset S^2$
consists of four points.
A Jordan curve
![]() $\alpha $
in a marked surface
$\alpha $
in a marked surface
![]() $(S,Z)$
is a Jordan curve
$(S,Z)$
is a Jordan curve
![]() $\alpha \subset S\smallsetminus Z$
. An arc e in
$\alpha \subset S\smallsetminus Z$
. An arc e in
![]() $(S,Z)$
is an arc
$(S,Z)$
is an arc
![]() $e\subset S$
with
$e\subset S$
with
![]() $\partial e\subset Z$
and
$\partial e\subset Z$
and
![]() $\operatorname {int}(e)\subset S\smallsetminus Z$
. We say that a Jordan curve
$\operatorname {int}(e)\subset S\smallsetminus Z$
. We say that a Jordan curve
![]() $\alpha $
in a marked sphere
$\alpha $
in a marked sphere
![]() $({S^{2}}, Z)$
is essential if each of the two connected components of
$({S^{2}}, Z)$
is essential if each of the two connected components of
![]() ${S^{2}}\smallsetminus \alpha $
contains at least two points of Z; otherwise, we say that
${S^{2}}\smallsetminus \alpha $
contains at least two points of Z; otherwise, we say that
![]() $\alpha $
is peripheral.
$\alpha $
is peripheral.
Let
![]() $({S^{2}},Z)$
be a marked sphere with
$({S^{2}},Z)$
be a marked sphere with
![]() $\#Z = 4$
. A core arc of an essential Jordan curve
$\#Z = 4$
. A core arc of an essential Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $({S^{2}},Z)$
is an arc in
$({S^{2}},Z)$
is an arc in
![]() $({S^{2}},Z)$
that is contained in one of the two connected components of
$({S^{2}},Z)$
that is contained in one of the two connected components of
![]() ${S^{2}}\smallsetminus \alpha $
and joins the two points in Z that lie in this component.
${S^{2}}\smallsetminus \alpha $
and joins the two points in Z that lie in this component.
Let A be an annulus. Then a core curve of A is a Jordan curve
![]() $\beta \subset A$
such that under some homeomorphism
$\beta \subset A$
such that under some homeomorphism
![]() $\varphi \colon A\rightarrow A'$
, the curve
$\varphi \colon A\rightarrow A'$
, the curve
![]() $\beta '=\varphi (\beta )$
separates the boundary components of
$\beta '=\varphi (\beta )$
separates the boundary components of
![]() $A'=\{z\in \mathbb {C}: 1<|z|<2\}$
.
$A'=\{z\in \mathbb {C}: 1<|z|<2\}$
.
2.2 Branched covering maps
Let X and Y be surfaces. Then a continuous map
![]() ${f\colon X\to Y}$
is called a branched covering map if for each point
${f\colon X\to Y}$
is called a branched covering map if for each point
![]() $q\in Y$
, there exists an open set
$q\in Y$
, there exists an open set
![]() $V\subset Y$
homeomorphic to
$V\subset Y$
homeomorphic to
![]() $\mathbb {D}$
with
$\mathbb {D}$
with
![]() $q\in V$
that is evenly covered in the following sense: for some index set
$q\in V$
that is evenly covered in the following sense: for some index set
![]() $J\ne \emptyset $
, we can write
$J\ne \emptyset $
, we can write
![]() $f^{-1}(V)$
as a disjoint union
$f^{-1}(V)$
as a disjoint union
 $$ \begin{align} f^{-1}(V)= \bigcup_{j\in J}U_j \end{align} $$
$$ \begin{align} f^{-1}(V)= \bigcup_{j\in J}U_j \end{align} $$
of open sets
![]() $U_j\subset X$
such that
$U_j\subset X$
such that
![]() $U_j$
contains precisely one point
$U_j$
contains precisely one point
![]() $p_j\in f^{-1}(q)$
. Moreover, we require that for each
$p_j\in f^{-1}(q)$
. Moreover, we require that for each
![]() $j\in J$
, there exists
$j\in J$
, there exists
![]() $d_j\in \mathbb {N}$
and orientation-preserving homeomorphisms
$d_j\in \mathbb {N}$
and orientation-preserving homeomorphisms
![]() $\varphi _j\colon U_j\rightarrow \mathbb {D}$
with
$\varphi _j\colon U_j\rightarrow \mathbb {D}$
with
![]() $\varphi _j(p_j)=0$
and
$\varphi _j(p_j)=0$
and
![]() $\psi _j\colon V\rightarrow \mathbb {D}$
with
$\psi _j\colon V\rightarrow \mathbb {D}$
with
![]() $\psi _j(q)=0$
such that
$\psi _j(q)=0$
such that
for all
![]() $z\in \mathbb {D}$
(see [Reference Bonk and MeyerBM17, §A.6] for more background on branched covering maps). For given f, the number
$z\in \mathbb {D}$
(see [Reference Bonk and MeyerBM17, §A.6] for more background on branched covering maps). For given f, the number
![]() $d_j$
is uniquely determined by
$d_j$
is uniquely determined by
![]() $p=p_j$
, and called the local degree of f at p and denoted by
$p=p_j$
, and called the local degree of f at p and denoted by
![]() $\deg (f,p)$
. A point
$\deg (f,p)$
. A point
![]() $p\in X$
with
$p\in X$
with
![]() $\deg (f,p) \geq 2$
is called a critical point of f. The set of all critical points of f is a discrete set in X and denoted by
$\deg (f,p) \geq 2$
is called a critical point of f. The set of all critical points of f is a discrete set in X and denoted by
![]() ${C_f}$
. If f is a branched covering map, then it is a covering map (in the usual sense) from
${C_f}$
. If f is a branched covering map, then it is a covering map (in the usual sense) from
![]() $X\smallsetminus f^{-1}(f({C_f}))$
onto
$X\smallsetminus f^{-1}(f({C_f}))$
onto
![]() $Y\smallsetminus f({C_f})$
.
$Y\smallsetminus f({C_f})$
.
In the following, suppose X and Y are compact surfaces, and
![]() $f\colon X\rightarrow Y$
is a branched covering map. Then
$f\colon X\rightarrow Y$
is a branched covering map. Then
![]() ${C_f}\subset X$
is a finite set. Moreover, if
${C_f}\subset X$
is a finite set. Moreover, if
![]() $\deg (f)\in \mathbb {N}$
denotes the topological degree of f, then
$\deg (f)\in \mathbb {N}$
denotes the topological degree of f, then
 $$ \begin{align*}\sum_{p\in f^{-1}(q)} \deg(f,p)=\deg(f)\end{align*} $$
$$ \begin{align*}\sum_{p\in f^{-1}(q)} \deg(f,p)=\deg(f)\end{align*} $$
for each
![]() $q\in Y$
.
$q\in Y$
.
If
![]() $\gamma \colon [a,b]\rightarrow Y$
is a path, then we call a path
$\gamma \colon [a,b]\rightarrow Y$
is a path, then we call a path
![]() $\widetilde \gamma \colon [a,b]\rightarrow X$
a lift of
$\widetilde \gamma \colon [a,b]\rightarrow X$
a lift of
![]() $\gamma $
(under f) if
$\gamma $
(under f) if
![]() $f\circ \widetilde \gamma =\gamma $
. Every path
$f\circ \widetilde \gamma =\gamma $
. Every path
![]() $\gamma $
in Y has a lift
$\gamma $
in Y has a lift
![]() $\widetilde \gamma $
in X (see [Reference Bonk and MeyerBM17, Lemma A.18]), but in general,
$\widetilde \gamma $
in X (see [Reference Bonk and MeyerBM17, Lemma A.18]), but in general,
![]() $\widetilde \gamma $
is not unique. If
$\widetilde \gamma $
is not unique. If
![]() $\gamma ([a,b))\subset Y\smallsetminus f({C_f})$
and
$\gamma ([a,b))\subset Y\smallsetminus f({C_f})$
and
![]() $x_0\in f^{-1}(\gamma (a))$
, then there exists a unique lift
$x_0\in f^{-1}(\gamma (a))$
, then there exists a unique lift
![]() $\widetilde \gamma \colon [a,b]\rightarrow X$
of
$\widetilde \gamma \colon [a,b]\rightarrow X$
of
![]() $\gamma $
under f with
$\gamma $
under f with
![]() $\widetilde \gamma (a)=x_0$
. This easily follows from standard existence and uniqueness theorems for lifts under covering maps (see [Reference Bonk and MeyerBM17, Lemma A.6]).
$\widetilde \gamma (a)=x_0$
. This easily follows from standard existence and uniqueness theorems for lifts under covering maps (see [Reference Bonk and MeyerBM17, Lemma A.6]).
If
![]() $e\subset Y$
is an arc, then an arc
$e\subset Y$
is an arc, then an arc
![]() $\widetilde e\subset X$
is called a lift of e (under f) if
$\widetilde e\subset X$
is called a lift of e (under f) if
![]() $f|\widetilde e$
is a homeomorphism of
$f|\widetilde e$
is a homeomorphism of
![]() $\widetilde e$
onto e. It easily follows from the existence and uniqueness statements for lifts of paths just discussed that if e is an arc in
$\widetilde e$
onto e. It easily follows from the existence and uniqueness statements for lifts of paths just discussed that if e is an arc in
![]() $(Y, f({C_f}))$
,
$(Y, f({C_f}))$
,
![]() $y_0\in \operatorname {int}(e)$
, and
$y_0\in \operatorname {int}(e)$
, and
![]() ${x_0\in f^{-1}(y_0)}$
, then there exists a unique lift
${x_0\in f^{-1}(y_0)}$
, then there exists a unique lift
![]() $\widetilde e\subset X$
of e with
$\widetilde e\subset X$
of e with
![]() $x_0\in \widetilde e$
.
$x_0\in \widetilde e$
.
Let
![]() $V\subset Y$
be an open and connected set, and
$V\subset Y$
be an open and connected set, and
![]() $U\subset f^{-1}(V)$
be a (connected) component of
$U\subset f^{-1}(V)$
be a (connected) component of
![]() $f^{-1}(V)$
. Then
$f^{-1}(V)$
. Then
![]() $f|U\colon U \rightarrow V$
is also a branched covering map. Each point
$f|U\colon U \rightarrow V$
is also a branched covering map. Each point
![]() $q\in V$
has the same number
$q\in V$
has the same number
![]() $d\in \mathbb {N}$
of preimages under
$d\in \mathbb {N}$
of preimages under
![]() $f|U$
counting local degrees. We set
$f|U$
counting local degrees. We set ![]() . If the Euler characteristic
. If the Euler characteristic
![]() $\chi (V)$
is finite, then
$\chi (V)$
is finite, then
![]() $\chi (U)$
is also finite and we have the Riemann–Hurwitz formula
$\chi (U)$
is also finite and we have the Riemann–Hurwitz formula
 $$ \begin{align} \chi(U)+\sum_{p\in U \cap {C_f}}(\deg(f,p)-1)=\deg(f|U)\cdot \chi(V). \end{align} $$
$$ \begin{align} \chi(U)+\sum_{p\in U \cap {C_f}}(\deg(f,p)-1)=\deg(f|U)\cdot \chi(V). \end{align} $$
2.3 Planar embedded graphs
A planar embedded graph in a sphere
![]() $S^2$
is a pair
$S^2$
is a pair
![]() ${G=(V,E)}$
, where V is a finite set of points in
${G=(V,E)}$
, where V is a finite set of points in
![]() ${S^{2}}$
and E is a finite set of arcs in
${S^{2}}$
and E is a finite set of arcs in
![]() $({S^{2}},V)$
with pairwise disjoint interiors. The sets V and E are called the vertex and edge sets of G, respectively. Note that our notion of a planar embedded graph does not allow loops, that is, edges that connect a vertex to itself, but it does allow multiple edges, that is, distinct edges that join the same pair of vertices. The degree of a vertex v in G, denoted
$({S^{2}},V)$
with pairwise disjoint interiors. The sets V and E are called the vertex and edge sets of G, respectively. Note that our notion of a planar embedded graph does not allow loops, that is, edges that connect a vertex to itself, but it does allow multiple edges, that is, distinct edges that join the same pair of vertices. The degree of a vertex v in G, denoted
![]() $\deg _G(v)$
, is the number of edges of G incident to v. Note that
$\deg _G(v)$
, is the number of edges of G incident to v. Note that
![]() $2\cdot \#E = \sum _{v\in V} \deg _G(v)$
.
$2\cdot \#E = \sum _{v\in V} \deg _G(v)$
.
The realization of G is the subset
![]() $\mathcal {G}$
of
$\mathcal {G}$
of
![]() ${S^{2}}$
given by
${S^{2}}$
given by
A face of G is a connected component of
![]() ${S^{2}}\smallsetminus \mathcal {G}$
. Usually, we conflate a planar embedded graph G with its realization
${S^{2}}\smallsetminus \mathcal {G}$
. Usually, we conflate a planar embedded graph G with its realization
![]() $\mathcal {G}$
. Then it is understood that
$\mathcal {G}$
. Then it is understood that
![]() $\mathcal {G}$
contains a finite set
$\mathcal {G}$
contains a finite set
![]() $V\subset \mathcal {G}$
of distinguished points that are the vertices of the graph. Its edges are the closures of the components of
$V\subset \mathcal {G}$
of distinguished points that are the vertices of the graph. Its edges are the closures of the components of
![]() $\mathcal {G}\smallsetminus V$
.
$\mathcal {G}\smallsetminus V$
.
A subgraph of a planar embedded graph
![]() $G=(V,E)$
is a planar embedded graph
$G=(V,E)$
is a planar embedded graph
![]() ${G'=(V',E')}$
with
${G'=(V',E')}$
with
![]() $V'\subset V$
and
$V'\subset V$
and
![]() $E'\subset E$
. A path of length n between vertices v and
$E'\subset E$
. A path of length n between vertices v and
![]() $v'$
in G is a sequence
$v'$
in G is a sequence
![]() $v_0,e_0,v_1,e_1,\ldots ,e_{n-1},v_n$
, where
$v_0,e_0,v_1,e_1,\ldots ,e_{n-1},v_n$
, where
![]() $v_0=v$
,
$v_0=v$
,
![]() $v_n=v'$
, and
$v_n=v'$
, and
![]() $e_k$
is an edge incident to the vertices
$e_k$
is an edge incident to the vertices
![]() $v_{k}$
and
$v_{k}$
and
![]() $v_{k+1}$
for
$v_{k+1}$
for
![]() $k=0,\ldots ,n-1$
. A path that does not repeat vertices is called a simple path.
$k=0,\ldots ,n-1$
. A path that does not repeat vertices is called a simple path.
A path
![]() $v_0,e_0, v_1,e_1,\ldots ,e_{n-1},v_n$
with
$v_0,e_0, v_1,e_1,\ldots ,e_{n-1},v_n$
with
![]() $v_0=v_n$
and
$v_0=v_n$
and
![]() $n\geq 2$
is called a circuit of length n in G and is denoted by
$n\geq 2$
is called a circuit of length n in G and is denoted by
![]() $(e_0,e_1,\ldots ,e_{n-1})$
. Such a circuit is called a simple cycle if all vertices
$(e_0,e_1,\ldots ,e_{n-1})$
. Such a circuit is called a simple cycle if all vertices
![]() $v_k$
,
$v_k$
,
![]() $k = 0,\ldots ,n-1$
, are distinct.
$k = 0,\ldots ,n-1$
, are distinct.
A planar embedded graph G is called connected if any two distinct vertices of G can be joined by a path in G. Equivalently, G is connected if its realization
![]() $\mathcal {G}$
is connected as a subset of
$\mathcal {G}$
is connected as a subset of
![]() ${S^{2}}$
. Note that if G is connected, then each face of G is simply connected.
${S^{2}}$
. Note that if G is connected, then each face of G is simply connected.
As follows from [Reference DiestelDie05, Lemma 4.2.2], the topological boundary
![]() $\partial U$
of each face U of G may be viewed as the realization of a subgraph of G. Moreover, a walk around any connected component of the boundary
$\partial U$
of each face U of G may be viewed as the realization of a subgraph of G. Moreover, a walk around any connected component of the boundary
![]() $\partial U$
traces a circuit
$\partial U$
traces a circuit
![]() $(e_0,e_1,\ldots ,e_{n-1})$
in G such that each edge of G appears zero, one, or two times in the sequence
$(e_0,e_1,\ldots ,e_{n-1})$
in G such that each edge of G appears zero, one, or two times in the sequence
![]() $e_0,e_1,\ldots ,e_{n-1}$
. We will say that the circuit
$e_0,e_1,\ldots ,e_{n-1}$
. We will say that the circuit
![]() $(e_0,e_1,\ldots ,e_{n-1})$
traces (a connected component of) the boundary
$(e_0,e_1,\ldots ,e_{n-1})$
traces (a connected component of) the boundary
![]() $\partial U$
. If U is simply connected, then
$\partial U$
. If U is simply connected, then
![]() $\partial U$
is connected, and the length of the (essentially unique) circuit that bounds U is called the circuit length of U in G.
$\partial U$
is connected, and the length of the (essentially unique) circuit that bounds U is called the circuit length of U in G.
A planar embedded graph
![]() $(V,E)$
is called bipartite if we can split V into two disjoint subsets
$(V,E)$
is called bipartite if we can split V into two disjoint subsets
![]() $V_1$
and
$V_1$
and
![]() $V_2$
such that each edge
$V_2$
such that each edge
![]() $e\in E$
has one endpoint in
$e\in E$
has one endpoint in
![]() $V_1$
and one in
$V_1$
and one in
![]() $V_2$
.
$V_2$
.
2.4 The Euclidean square pillow
As discussed in the introduction, we consider a square pillow
![]() $\mathbb {P}$
obtained from gluing two identical copies of the unit square
$\mathbb {P}$
obtained from gluing two identical copies of the unit square
![]() $\mathbb {I}^2\subset \mathbb {R}^2$
along their boundaries by the identity map. Then
$\mathbb {I}^2\subset \mathbb {R}^2$
along their boundaries by the identity map. Then
![]() $\mathbb {P}$
is a topological
$\mathbb {P}$
is a topological
![]() $2$
-sphere. We equip
$2$
-sphere. We equip
![]() $\mathbb {P}$
with the induced path metric that agrees with the Euclidean metric on each of the two copies of the unit square. We call this metric space
$\mathbb {P}$
with the induced path metric that agrees with the Euclidean metric on each of the two copies of the unit square. We call this metric space
![]() $\mathbb {P}$
the Euclidean square pillow. The vertices and edges of the unit square
$\mathbb {P}$
the Euclidean square pillow. The vertices and edges of the unit square
![]() $\mathbb {I}^2$
in
$\mathbb {I}^2$
in
![]() $\mathbb {P}$
are called the vertices and edges of
$\mathbb {P}$
are called the vertices and edges of
![]() $\mathbb {P}$
. One copy of
$\mathbb {P}$
. One copy of
![]() $\mathbb {I}^2$
in
$\mathbb {I}^2$
in
![]() $\mathbb {P}$
is called the front and the other copy the back side of
$\mathbb {P}$
is called the front and the other copy the back side of
![]() $\mathbb {P}$
. In a dynamical context, we also refer to these two copies of
$\mathbb {P}$
. In a dynamical context, we also refer to these two copies of
![]() $\mathbb {I}^2$
as the
$\mathbb {I}^2$
as the
![]() $0$
-tiles of
$0$
-tiles of
![]() $\mathbb {P}$
. We color the front side of
$\mathbb {P}$
. We color the front side of
![]() $\mathbb {P}$
white, and its back side black. Finally, we equip
$\mathbb {P}$
white, and its back side black. Finally, we equip
![]() $\mathbb {P}$
with the orientation that agrees with the standard orientation on the front side
$\mathbb {P}$
with the orientation that agrees with the standard orientation on the front side
![]() $\mathbb {I}^2$
of
$\mathbb {I}^2$
of
![]() $\mathbb {P}$
(represented by the positively oriented standard flag
$\mathbb {P}$
(represented by the positively oriented standard flag
![]() $((0,0), \mathbb {I}\times \{0\}, \mathbb {I}^2)$
; see [Reference Bonk and MeyerBM17, Appendix A.4]).
$((0,0), \mathbb {I}\times \{0\}, \mathbb {I}^2)$
; see [Reference Bonk and MeyerBM17, Appendix A.4]).
We label the vertices and edges of
![]() $\mathbb {P}$
in counterclockwise order by
$\mathbb {P}$
in counterclockwise order by
![]() $A,B,C,D$
and
$A,B,C,D$
and
![]() $a,b,c,d$
, respectively, so that
$a,b,c,d$
, respectively, so that
![]() $A\in \mathbb {P}$
corresponds to the vertex
$A\in \mathbb {P}$
corresponds to the vertex
![]() $(0,0)\in \mathbb {I}^2$
and the edge
$(0,0)\in \mathbb {I}^2$
and the edge
![]() $a\subset \mathbb {P}$
corresponds to
$a\subset \mathbb {P}$
corresponds to
![]() $[0,1]\times \{0\}\subset \mathbb {I}^2$
. Then a has the endpoints A and B. We can view the boundary
$[0,1]\times \{0\}\subset \mathbb {I}^2$
. Then a has the endpoints A and B. We can view the boundary
![]() $\partial \mathbb {I}^2$
of
$\partial \mathbb {I}^2$
of
![]() $\mathbb {I}^2$
as a planar embedded graph in
$\mathbb {I}^2$
as a planar embedded graph in
![]() $\mathbb {P}$
with the vertex set
$\mathbb {P}$
with the vertex set ![]() and the edge set
and the edge set ![]() . We call a and c the horizontal edges, and b and d the vertical edges of
. We call a and c the horizontal edges, and b and d the vertical edges of
![]() $\mathbb {P}$
; see Figure 4.
$\mathbb {P}$
; see Figure 4.

Figure 4 The Euclidean square pillow
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
The pillow
![]() $\mathbb {P}$
is an example of a Euclidean polyhedral surface, that is, a surface obtained by gluing Euclidean polygons along boundary edges by using isometries. Note that the metric on
$\mathbb {P}$
is an example of a Euclidean polyhedral surface, that is, a surface obtained by gluing Euclidean polygons along boundary edges by using isometries. Note that the metric on
![]() $\mathbb {P}$
is locally flat except at its vertices, which are Euclidean conic singularities. So
$\mathbb {P}$
is locally flat except at its vertices, which are Euclidean conic singularities. So
![]() $\mathbb {P}$
is an orbifold (see, for example, [Reference MilnorMil06a, Appendix E] and [Reference Bonk and MeyerBM17, Appendix A.9]).
$\mathbb {P}$
is an orbifold (see, for example, [Reference MilnorMil06a, Appendix E] and [Reference Bonk and MeyerBM17, Appendix A.9]).
An alternative description for the pillow
![]() $\mathbb {P}$
can be given as follows. We consider the unit square
$\mathbb {P}$
can be given as follows. We consider the unit square
![]() $\mathbb {I}^2\subset \mathbb {R}^2\cong \mathbb {C}$
and map it to the upper half-plane in
$\mathbb {I}^2\subset \mathbb {R}^2\cong \mathbb {C}$
and map it to the upper half-plane in
![]() $\widehat {\mathbb {C}}$
by a conformal map, normalized so that the vertices
$\widehat {\mathbb {C}}$
by a conformal map, normalized so that the vertices
![]() $0,1,1+i, i$
are mapped to
$0,1,1+i, i$
are mapped to
![]() $0, 1, \infty , -1$
, respectively. By Schwarz reflection, this map can be extended to a meromorphic function
$0, 1, \infty , -1$
, respectively. By Schwarz reflection, this map can be extended to a meromorphic function
![]() $\wp \colon \mathbb {C}\to \widehat {\mathbb {C}}$
. Then
$\wp \colon \mathbb {C}\to \widehat {\mathbb {C}}$
. Then
![]() $\wp $
is a Weierstrass
$\wp $
is a Weierstrass
![]() $\wp $
-function (up to a postcomposition with a Möbius transformation) that is doubly periodic with respect to the lattice
$\wp $
-function (up to a postcomposition with a Möbius transformation) that is doubly periodic with respect to the lattice ![]() . Actually, for
. Actually, for
![]() $z, w\in \mathbb {C}$
, we have
$z, w\in \mathbb {C}$
, we have
We can push forward the Euclidean metric on
![]() $\mathbb {C}$
to the Riemann sphere
$\mathbb {C}$
to the Riemann sphere
![]() $\widehat {\mathbb {C}}$
by
$\widehat {\mathbb {C}}$
by
![]() $\wp $
. With respect to this metric, called the canonical orbifold metric for
$\wp $
. With respect to this metric, called the canonical orbifold metric for
![]() $\wp $
, the sphere
$\wp $
, the sphere
![]() $\widehat {\mathbb {C}}$
is isometric to the Euclidean square pillow
$\widehat {\mathbb {C}}$
is isometric to the Euclidean square pillow
![]() $\mathbb {P}$
. In the following, we identify the pillow
$\mathbb {P}$
. In the following, we identify the pillow
![]() $\mathbb {P}$
with
$\mathbb {P}$
with
![]() $\widehat {\mathbb {C}}$
by the orientation-preserving isometry that maps the vertices
$\widehat {\mathbb {C}}$
by the orientation-preserving isometry that maps the vertices
![]() $A,B,C,D$
to
$A,B,C,D$
to
![]() $0, 1, \infty , -1$
, respectively. Then we can consider
$0, 1, \infty , -1$
, respectively. Then we can consider
![]() $\wp \colon \mathbb {C}\to \widehat {\mathbb {C}} \cong \mathbb {P}$
as a map onto the pillow
$\wp \colon \mathbb {C}\to \widehat {\mathbb {C}} \cong \mathbb {P}$
as a map onto the pillow
![]() $\mathbb {P}$
. Actually,
$\mathbb {P}$
. Actually,
![]() $\wp $
is the universal orbifold covering map for
$\wp $
is the universal orbifold covering map for
![]() $\mathbb {P}$
(see [Reference Bonk and MeyerBM17, §A.9] for more background). A very intuitive description of this map can be given if we color the squares
$\mathbb {P}$
(see [Reference Bonk and MeyerBM17, §A.9] for more background). A very intuitive description of this map can be given if we color the squares
![]() $[k,k+1]\times [n,n+1]$
,
$[k,k+1]\times [n,n+1]$
,
![]() $k,n\in \mathbb {Z}$
, in checkerboard manner black and white so that
$k,n\in \mathbb {Z}$
, in checkerboard manner black and white so that
![]() $[0,1]\times [0,1]$
is white. Restricted to such a square S, the map
$[0,1]\times [0,1]$
is white. Restricted to such a square S, the map
![]() $\wp $
is an isometry that sends S to the white
$\wp $
is an isometry that sends S to the white
![]() $0$
-tile of
$0$
-tile of
![]() $\mathbb {P}$
if S is white, and to the black
$\mathbb {P}$
if S is white, and to the black
![]() $0$
-tile
$0$
-tile
![]() $\mathbb {P}$
if S is black; see Figure 5 for an illustration. Here, the points in the complex plane
$\mathbb {P}$
if S is black; see Figure 5 for an illustration. Here, the points in the complex plane
![]() $\mathbb {C}$
marked by a black dot (on the left) are mapped to A by
$\mathbb {C}$
marked by a black dot (on the left) are mapped to A by
![]() $\wp $
and are elements of
$\wp $
and are elements of
![]() $\wp ^{-1}(A)= 2\mathbb {Z}^2$
.
$\wp ^{-1}(A)= 2\mathbb {Z}^2$
.

Figure 5 The map
![]() $\wp \colon \mathbb {C}\to \mathbb {P}$
.
$\wp \colon \mathbb {C}\to \mathbb {P}$
.
2.5 Isotopies and intersection numbers
Let X and Y be topological spaces. Then a continuous map
![]() $H\colon X\times \mathbb {I}\to Y$
is called a homotopy from X to Y. For
$H\colon X\times \mathbb {I}\to Y$
is called a homotopy from X to Y. For
![]() $t\in \mathbb {I}$
, we denote by
$t\in \mathbb {I}$
, we denote by ![]() the time-t map of the homotopy. The homotopy H is called an isotopy if
the time-t map of the homotopy. The homotopy H is called an isotopy if
![]() $H_t$
is a homeomorphism from X onto Y for each
$H_t$
is a homeomorphism from X onto Y for each
![]() $t\in \mathbb {I}$
. If
$t\in \mathbb {I}$
. If
![]() $Z\subset X$
, then a homotopy
$Z\subset X$
, then a homotopy
![]() $H\colon X\times \mathbb {I}\to Y$
is said to be a homotopy relative to Z if
$H\colon X\times \mathbb {I}\to Y$
is said to be a homotopy relative to Z if
![]() $H_t(p) = H_0(p)$
for all
$H_t(p) = H_0(p)$
for all
![]() $p\in Z$
and
$p\in Z$
and
![]() $t\in \mathbb {I}$
. In other words, the image of each point in Z remains fixed during the homotopy H. Isotopies relative to Z are defined in a similar way.
$t\in \mathbb {I}$
. In other words, the image of each point in Z remains fixed during the homotopy H. Isotopies relative to Z are defined in a similar way.
Two homeomorphisms
![]() $h_0, h_1 \colon X \rightarrow Y $
are called isotopic (relative to
$h_0, h_1 \colon X \rightarrow Y $
are called isotopic (relative to
![]() $Z\subset X$
) if there exists an isotopy
$Z\subset X$
) if there exists an isotopy
![]() $H\colon X\times \mathbb {I}\to Y$
(relative to Z) with
$H\colon X\times \mathbb {I}\to Y$
(relative to Z) with
![]() $H_0 = h_0$
and
$H_0 = h_0$
and
![]() $H_1 = h_1$
. Given
$H_1 = h_1$
. Given
![]() $M,N,Z\subset X$
, we say that M is isotopic to N relative to Z (or M can be isotoped into N relative to Z), denoted by
$M,N,Z\subset X$
, we say that M is isotopic to N relative to Z (or M can be isotoped into N relative to Z), denoted by
![]() $M\sim N$
relative to Z, if there exists an isotopy
$M\sim N$
relative to Z, if there exists an isotopy
![]() $H\colon X\times \mathbb {I} \to X$
relative to Z with
$H\colon X\times \mathbb {I} \to X$
relative to Z with
![]() $H_0 = \operatorname {id}_{X}$
and
$H_0 = \operatorname {id}_{X}$
and
![]() $H_1(M) = N$
. Recall that
$H_1(M) = N$
. Recall that
![]() $\operatorname {id}_{X}$
is the identity map on X.
$\operatorname {id}_{X}$
is the identity map on X.
Let
![]() $(S,Z)$
be a marked surface (with a finite, possibly empty set
$(S,Z)$
be a marked surface (with a finite, possibly empty set
![]() $Z\subset S$
of marked points). If
$Z\subset S$
of marked points). If
![]() $\alpha $
is a Jordan curve in
$\alpha $
is a Jordan curve in
![]() $(S,Z)$
, then its isotopy class
$(S,Z)$
, then its isotopy class
![]() $ [\alpha ]$
(with
$ [\alpha ]$
(with
![]() $(S,Z)$
understood) consists of all Jordan curves
$(S,Z)$
understood) consists of all Jordan curves
![]() $\beta $
in
$\beta $
in
![]() $(S,Z)$
such that
$(S,Z)$
such that
![]() $\alpha \sim \beta $
relative to Z.
$\alpha \sim \beta $
relative to Z.
The following statement gives a sufficient condition for two Jordan curves in
![]() $(S,Z)$
to be isotopic relative to Z.
$(S,Z)$
to be isotopic relative to Z.
Lemma 2.1. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be disjoint Jordan curves in a marked surface
$\beta $
be disjoint Jordan curves in a marked surface
![]() $(S,Z)$
. Suppose there is an annulus
$(S,Z)$
. Suppose there is an annulus
![]() $U\subset S \smallsetminus Z$
such that
$U\subset S \smallsetminus Z$
such that
![]() $\partial U=\alpha \cup \beta $
. Then
$\partial U=\alpha \cup \beta $
. Then
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are isotopic relative to Z.
$\beta $
are isotopic relative to Z.
Proof. This is standard and we will only give a sketch of the proof. Since Jordan curves in surfaces are tame, one can slightly enlarge the annulus U to an annulus
![]() $U'\subset S^2\smallsetminus Z$
that contains
$U'\subset S^2\smallsetminus Z$
that contains
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Then
$\beta $
. Then
![]() $\alpha $
can be isotoped into
$\alpha $
can be isotoped into
![]() $\beta $
by an isotopy on
$\beta $
by an isotopy on
![]() $U'$
that is the identity near
$U'$
that is the identity near
![]() $\partial U'$
. This isotopy on
$\partial U'$
. This isotopy on
![]() $U'$
can be extended to an isotopy on
$U'$
can be extended to an isotopy on
![]() $S^2$
relative to Z that isotopes
$S^2$
relative to Z that isotopes
![]() $\alpha $
into
$\alpha $
into
![]() $\beta $
.
$\beta $
.
Let
![]() $(S,Z)$
be a marked surface. If
$(S,Z)$
be a marked surface. If
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are arcs or Jordan curves in
$\beta $
are arcs or Jordan curves in
![]() $(S, Z)$
, we define their (unsigned) intersection number as
$(S, Z)$
, we define their (unsigned) intersection number as
The relevant marked surface
![]() $(S,Z)$
here will be understood from the context, and we suppress it from our notation for intersection numbers. If we want to emphasize it, we will say that we consider intersection numbers in
$(S,Z)$
here will be understood from the context, and we suppress it from our notation for intersection numbers. If we want to emphasize it, we will say that we consider intersection numbers in
![]() $(S,Z)$
. The intersection number is always finite, because we can always reduce to the case when
$(S,Z)$
. The intersection number is always finite, because we can always reduce to the case when
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are piecewise geodesic with respect to some Riemannian metric on S (see [Reference BuserBus10, Lemma A.8]). If
$\beta $
are piecewise geodesic with respect to some Riemannian metric on S (see [Reference BuserBus10, Lemma A.8]). If
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
satisfy
$\beta $
satisfy
![]() $\mathrm {i}(\alpha \cap \beta ) =\# (\alpha \cap \beta )$
, then we say that
$\mathrm {i}(\alpha \cap \beta ) =\# (\alpha \cap \beta )$
, then we say that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are in minimal position (in their isotopy classes relative to Z).
$\beta $
are in minimal position (in their isotopy classes relative to Z).
Suppose
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are arcs or Jordan curves in
$\beta $
are arcs or Jordan curves in
![]() $(S, Z)$
. Then we say that
$(S, Z)$
. Then we say that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
meet transversely at a point
$\beta $
meet transversely at a point
![]() $p\in \alpha \cap \beta \cap (S\smallsetminus Z)$
(or
$p\in \alpha \cap \beta \cap (S\smallsetminus Z)$
(or
![]() $\alpha $
crosses
$\alpha $
crosses
![]() $\beta $
at p) if p is an isolated point in
$\beta $
at p) if p is an isolated point in
![]() $\alpha \cap \beta $
and if the following condition is true for a (small) arc
$\alpha \cap \beta $
and if the following condition is true for a (small) arc
![]() $\sigma \subset \alpha $
containing p as an interior point such that
$\sigma \subset \alpha $
containing p as an interior point such that
![]() $\sigma \cap \beta =\{p\}$
: let
$\sigma \cap \beta =\{p\}$
: let
![]() $\sigma ^L$
and
$\sigma ^L$
and
![]() $\sigma ^R$
be the two subarcs of
$\sigma ^R$
be the two subarcs of
![]() $\sigma $
into which
$\sigma $
into which
![]() $\sigma $
is split by p, then with suitable orientation of
$\sigma $
is split by p, then with suitable orientation of
![]() $\beta $
near p, the arc
$\beta $
near p, the arc
![]() $\sigma ^L$
lies to the left and
$\sigma ^L$
lies to the left and
![]() $\sigma ^R$
to the right of
$\sigma ^R$
to the right of
![]() $\beta $
. We say that
$\beta $
. We say that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
meet transversely or have transverse intersection if the set
$\beta $
meet transversely or have transverse intersection if the set
![]() $\alpha \cap \beta $
is finite and if
$\alpha \cap \beta $
is finite and if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
meet transversely at each point
$\beta $
meet transversely at each point
![]() $p\in \alpha \cap \beta \cap (S\smallsetminus Z)$
.
$p\in \alpha \cap \beta \cap (S\smallsetminus Z)$
.
Lemma 2.2. Suppose
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are Jordan curves or arcs in a marked surface
$\beta $
are Jordan curves or arcs in a marked surface
![]() $(S,Z)$
. If
$(S,Z)$
. If
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are in minimal position, then
$\beta $
are in minimal position, then
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
meet transversely.
$\beta $
meet transversely.
Proof. This is essentially a standard fact (see, for example, [Reference BuserBus10, pp. 416–417]), and we will only give an outline of the proof.
Since
![]() $ \# (\alpha \cap \beta )=\mathrm {i}(\alpha \cap \beta )$
, the set
$ \# (\alpha \cap \beta )=\mathrm {i}(\alpha \cap \beta )$
, the set
![]() $\alpha \cap \beta $
consists of finitely many isolated points. To reach a contradiction, suppose that
$\alpha \cap \beta $
consists of finitely many isolated points. To reach a contradiction, suppose that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
do not meet transversely at some point
$\beta $
do not meet transversely at some point
![]() ${p\in \alpha \cap \beta \cap (S\smallsetminus Z)}$
. Then there exists an arc
${p\in \alpha \cap \beta \cap (S\smallsetminus Z)}$
. Then there exists an arc
![]() $\sigma \subset \alpha $
containing p as an interior point such that
$\sigma \subset \alpha $
containing p as an interior point such that
![]() $\sigma \cap \beta =\{p\}$
and with the following property: if
$\sigma \cap \beta =\{p\}$
and with the following property: if
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
denote the two subarcs of
$\sigma _2$
denote the two subarcs of
![]() $\sigma $
into which
$\sigma $
into which
![]() $\sigma $
is split by p, then
$\sigma $
is split by p, then
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
lie on the same side of
$\sigma _2$
lie on the same side of
![]() $\beta $
(equipped with some orientation locally near p). In other words,
$\beta $
(equipped with some orientation locally near p). In other words,
![]() $\alpha $
touches
$\alpha $
touches
![]() $\beta $
locally near p from one side and does not cross
$\beta $
locally near p from one side and does not cross
![]() $\beta $
at p.
$\beta $
at p.
We can then modify the curve
![]() $\alpha $
near p by an isotopy that pulls the subarc
$\alpha $
near p by an isotopy that pulls the subarc
![]() $\sigma $
away from
$\sigma $
away from
![]() $\beta $
so that the new curve
$\beta $
so that the new curve
![]() $\alpha $
does not have the intersection point p with
$\alpha $
does not have the intersection point p with
![]() $\beta $
while no new intersection points of
$\beta $
while no new intersection points of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
arise. This contradicts our assumption that for the original curve
$\beta $
arise. This contradicts our assumption that for the original curve
![]() $\alpha $
, we have
$\alpha $
, we have
![]() $\# (\alpha \cap \beta )=\mathrm {i}(\alpha \cap \beta )$
.
$\# (\alpha \cap \beta )=\mathrm {i}(\alpha \cap \beta )$
.
2.6 Jordan curves in spheres with four marked points
If
![]() $(S^2,Z)$
is a marked sphere where
$(S^2,Z)$
is a marked sphere where
![]() $Z\subset S^2$
consists of exactly four points, then, up to homeomorphism, we may assume that
$Z\subset S^2$
consists of exactly four points, then, up to homeomorphism, we may assume that
![]() $S^2$
is equal to the pillow
$S^2$
is equal to the pillow
![]() $\mathbb {P}$
, and
$\mathbb {P}$
, and
![]() $Z=V=\{A,B,C,D\}$
consists of the four vertices of
$Z=V=\{A,B,C,D\}$
consists of the four vertices of
![]() $\mathbb {P}$
. We will freely switch back and forth between a general marked sphere
$\mathbb {P}$
. We will freely switch back and forth between a general marked sphere
![]() $(S^2, Z)$
with
$(S^2, Z)$
with
![]() $\#Z=4$
and
$\#Z=4$
and
![]() $(\mathbb {P},V)$
.
$(\mathbb {P},V)$
.
We need some statements about isotopy classes of Jordan curves and arcs in
![]() $(\mathbb {P},V)$
and their intersections numbers. They are ‘well known’, but unfortunately we have been unable to track down a comprehensive account in the literature. Accordingly, we will provide a complete treatment. This may be of independent interest apart from the main objective of the paper. We will give the statements in this section, but will provide the details of the proofs in the appendix.
$(\mathbb {P},V)$
and their intersections numbers. They are ‘well known’, but unfortunately we have been unable to track down a comprehensive account in the literature. Accordingly, we will provide a complete treatment. This may be of independent interest apart from the main objective of the paper. We will give the statements in this section, but will provide the details of the proofs in the appendix.
As we will see, there is a natural way to define a bijection between the set of isotopy classes
![]() $[\gamma ]$
of essential Jordan curves
$[\gamma ]$
of essential Jordan curves
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P}, V)$
and the set of extended rational numbers
$(\mathbb {P}, V)$
and the set of extended rational numbers ![]() . Throughout this paper, whenever we write
. Throughout this paper, whenever we write
![]() $r/s\in \widehat {\mathbb {Q}}$
, we assume that
$r/s\in \widehat {\mathbb {Q}}$
, we assume that
![]() ${r\in \mathbb {Z}}$
and
${r\in \mathbb {Z}}$
and
![]() $s\in \mathbb {N}_0$
are two relatively prime integers. We allow
$s\in \mathbb {N}_0$
are two relatively prime integers. We allow
![]() $s=0$
here, in which case we assume
$s=0$
here, in which case we assume
![]() $r= 1$
. Then
$r= 1$
. Then ![]() .
.
We say that a (straight) line
![]() $\ell \subset \mathbb {C}$
has slope
$\ell \subset \mathbb {C}$
has slope
![]() $r/s\in \widehat {\mathbb {Q}}$
if it is given as
$r/s\in \widehat {\mathbb {Q}}$
if it is given as
for some
![]() $z_0\in \mathbb {C}$
. We use the notation
$z_0\in \mathbb {C}$
. We use the notation
![]() $\ell _{r/s}(z_0)$
for the unique line in
$\ell _{r/s}(z_0)$
for the unique line in
![]() $\mathbb {C}$
with slope
$\mathbb {C}$
with slope
![]() $r/s$
passing through
$r/s$
passing through
![]() $z_0\in \mathbb {C}$
, and the notation
$z_0\in \mathbb {C}$
, and the notation
![]() $\ell _{r/s}$
(when the point
$\ell _{r/s}$
(when the point
![]() $z_0$
is not important) for any line in
$z_0$
is not important) for any line in
![]() $\mathbb {C}$
with slope
$\mathbb {C}$
with slope
![]() $r/s$
.
$r/s$
.
Let
![]() $\ell _{r/s}\subset \mathbb {C}$
be any line with slope
$\ell _{r/s}\subset \mathbb {C}$
be any line with slope
![]() $r/s \in \widehat {\mathbb {Q}}$
. If
$r/s \in \widehat {\mathbb {Q}}$
. If
![]() $\ell _{r/s}$
does not contain any point in the lattice
$\ell _{r/s}$
does not contain any point in the lattice
![]() $\mathbb {Z}^2=\wp ^{-1}(V)$
and so
$\mathbb {Z}^2=\wp ^{-1}(V)$
and so
![]() $\ell _{r/s}\subset \mathbb {C} \smallsetminus \mathbb {Z}^2$
, then
$\ell _{r/s}\subset \mathbb {C} \smallsetminus \mathbb {Z}^2$
, then ![]() is a Jordan curve in
is a Jordan curve in
![]() $\mathbb {P}\smallsetminus V$
. Actually,
$\mathbb {P}\smallsetminus V$
. Actually,
![]() $\tau _{r/s}$
is a simple closed geodesic in the Euclidean square pillow
$\tau _{r/s}$
is a simple closed geodesic in the Euclidean square pillow
![]() $\mathbb {P}$
(see Figure 6 for an illustration). If
$\mathbb {P}$
(see Figure 6 for an illustration). If
![]() $\ell _{r/s}$
contains a point in
$\ell _{r/s}$
contains a point in
![]() $\mathbb {Z}^2$
, then
$\mathbb {Z}^2$
, then ![]() is a geodesic arc in
is a geodesic arc in
![]() $(\mathbb {P}, V)$
.
$(\mathbb {P}, V)$
.

Figure 6 A line
![]() $\ell _{2}$
and the corresponding Jordan curve
$\ell _{2}$
and the corresponding Jordan curve
![]() $\tau _2=\wp (\ell _2)$
in
$\tau _2=\wp (\ell _2)$
in
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
It is easy to see that every simple closed geodesic or geodesic arc
![]() $\tau $
in
$\tau $
in
![]() $(\mathbb {P}, V)$
has the form
$(\mathbb {P}, V)$
has the form
![]() $\tau =\wp (\ell _{r/s})$
for a line
$\tau =\wp (\ell _{r/s})$
for a line
![]() $\ell _{r/s}\subset \mathbb {C}$
with some slope
$\ell _{r/s}\subset \mathbb {C}$
with some slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. In the following, we use the notation
$r/s\in \widehat {\mathbb {Q}}$
. In the following, we use the notation
![]() $\tau _{r/s}$
for a simple closed geodesic and
$\tau _{r/s}$
for a simple closed geodesic and
![]() $\xi _{r/s}$
for a geodesic arc obtained in this way.
$\xi _{r/s}$
for a geodesic arc obtained in this way.
It follows from (2.3) that for fixed
![]() $r/s \in \widehat {\mathbb {Q}} $
, we obtain precisely two distinct arcs
$r/s \in \widehat {\mathbb {Q}} $
, we obtain precisely two distinct arcs
![]() $\xi _{r/s}$
and
$\xi _{r/s}$
and
![]() $\xi ^{\prime }_{r/s}$
of the form
$\xi ^{\prime }_{r/s}$
of the form
![]() $\wp (\ell _{r/s}(z_0))$
depending on
$\wp (\ell _{r/s}(z_0))$
depending on
![]() $z_0\in \mathbb {Z}^2$
. For each simple closed geodesic
$z_0\in \mathbb {Z}^2$
. For each simple closed geodesic
![]() $\tau _{r/s}$
, the arcs
$\tau _{r/s}$
, the arcs
![]() $\xi _{r/s}$
and
$\xi _{r/s}$
and
![]() $\xi ^{\prime }_{r/s}$
are core arcs of
$\xi ^{\prime }_{r/s}$
are core arcs of
![]() $\tau _{r/s}$
lying in different components of
$\tau _{r/s}$
lying in different components of
![]() $\mathbb {P}\smallsetminus \tau _{r/s}$
(see the appendix for more details). In particular,
$\mathbb {P}\smallsetminus \tau _{r/s}$
(see the appendix for more details). In particular,
![]() $\tau _{r/s}$
is always an essential Jordan curve in
$\tau _{r/s}$
is always an essential Jordan curve in
![]() $(\mathbb {P}, V)$
.
$(\mathbb {P}, V)$
.
It turns out that the isotopy classes of essential Jordan curves in
![]() $(\mathbb {P},V)$
are closely related to the simple closed geodesics
$(\mathbb {P},V)$
are closely related to the simple closed geodesics
![]() $\tau _{r/s}$
.
$\tau _{r/s}$
.
Lemma 2.3. Let
![]() $\gamma $
be an essential Jordan curve in
$\gamma $
be an essential Jordan curve in
![]() $(\mathbb {P},V)$
. Then there exists a unique slope
$(\mathbb {P},V)$
. Then there exists a unique slope
![]() $r/s\in \widehat {\mathbb {Q}}$
with the following property. Let
$r/s\in \widehat {\mathbb {Q}}$
with the following property. Let
![]() $\ell _{r/s}$
be any line in
$\ell _{r/s}$
be any line in
![]() $\mathbb {C}$
with slope
$\mathbb {C}$
with slope
![]() $r/s$
and
$r/s$
and
![]() $\ell _{r/s}\subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
, and set
$\ell _{r/s}\subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
, and set ![]() . Then
. Then
![]() $\tau _{r/s}$
is an essential Jordan curve in
$\tau _{r/s}$
is an essential Jordan curve in
![]() $(\mathbb {P},V)$
with
$(\mathbb {P},V)$
with
![]() $\gamma \sim \tau _{r/s}$
relative to V. Moreover, the map
$\gamma \sim \tau _{r/s}$
relative to V. Moreover, the map
![]() $[\gamma ]\mapsto r/s$
gives a bijection between isotopy classes
$[\gamma ]\mapsto r/s$
gives a bijection between isotopy classes
![]() $[\gamma ]$
of essential Jordan curves
$[\gamma ]$
of essential Jordan curves
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P},V)$
and slopes
$(\mathbb {P},V)$
and slopes
![]() $r/s\in \widehat {\mathbb {Q}}$
.
$r/s\in \widehat {\mathbb {Q}}$
.
While this is well known (see, for example, [Reference Farb and MargalitFM12, Proposition 2.6] or [Reference Keen and SeriesKS94, Proposition 2.1]), we find the available proofs too sketchy. This is the reason why we provide a detailed proof in the appendix. Implicit in Lemma 2.3 is the fact that the isotopy class
![]() $[\tau _{r/s}]$
of
$[\tau _{r/s}]$
of
![]() $\tau _{r/s} =\wp (\ell _{r/s})$
only depends on
$\tau _{r/s} =\wp (\ell _{r/s})$
only depends on
![]() $r/s$
and not on the specific choice of the line
$r/s$
and not on the specific choice of the line
![]() $\ell _{r/s}$
with
$\ell _{r/s}$
with
![]() $\ell _{r/s} \subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
(see Lemma A.7 for an explicit statement).
$\ell _{r/s} \subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
(see Lemma A.7 for an explicit statement).
Recall that a, c denote the horizontal, and b, d the vertical edges of
![]() $\mathbb {P}$
. In the following, we denote by
$\mathbb {P}$
. In the following, we denote by
![]() $\alpha ^h= \tau _{0}$
a horizontal essential Jordan curve in
$\alpha ^h= \tau _{0}$
a horizontal essential Jordan curve in
![]() $(\mathbb {P},V)$
(corresponding to slope
$(\mathbb {P},V)$
(corresponding to slope
![]() $0$
and separating the edges a and c of
$0$
and separating the edges a and c of
![]() $\mathbb {P}$
) and by
$\mathbb {P}$
) and by
![]() $\alpha ^v =\tau _{\infty }$
a vertical essential Jordan curve in
$\alpha ^v =\tau _{\infty }$
a vertical essential Jordan curve in
![]() $(\mathbb {P},V)$
(corresponding to slope
$(\mathbb {P},V)$
(corresponding to slope
![]() $\infty $
and separating b from d). To be specific, we set
$\infty $
and separating b from d). To be specific, we set
The following lemma summarizes the intersection properties of essential Jordan curves and arcs in
![]() $(\mathbb {P},V)$
.
$(\mathbb {P},V)$
.
Lemma 2.4. Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be essential Jordan curves in
$\beta $
be essential Jordan curves in
![]() $(\mathbb {P},V)$
and
$(\mathbb {P},V)$
and
![]() $r/s, r'/s'\in \widehat {\mathbb {Q}}$
be the unique slopes such that
$r/s, r'/s'\in \widehat {\mathbb {Q}}$
be the unique slopes such that
![]() $\alpha \sim \tau _{r/s}$
and
$\alpha \sim \tau _{r/s}$
and
![]() $\beta \sim \tau _{r'/s'}$
relative to V, where
$\beta \sim \tau _{r'/s'}$
relative to V, where
![]() $\tau _{r/s}$
and
$\tau _{r/s}$
and
![]() $\tau _{r'/s'}$
are simple closed geodesics in
$\tau _{r'/s'}$
are simple closed geodesics in
![]() $(\mathbb {P},V)$
with slopes
$(\mathbb {P},V)$
with slopes
![]() $r/s$
and
$r/s$
and
![]() $r'/s'$
, respectively. Let
$r'/s'$
, respectively. Let
![]() $\xi $
be a core arc of
$\xi $
be a core arc of
![]() $\beta $
, and
$\beta $
, and
![]() $\xi _{r'/s'}$
be a geodesic arc in
$\xi _{r'/s'}$
be a geodesic arc in
![]() $(\mathbb {P}, V)$
with slope
$(\mathbb {P}, V)$
with slope
![]() $r'/s'$
. Then the following statements are true for intersection numbers in
$r'/s'$
. Then the following statements are true for intersection numbers in
![]() $(\mathbb {P}, V)$
:
$(\mathbb {P}, V)$
:
-
(i) if
 $r/s=r'/s'$
, then
$r/s=r'/s'$
, then
 $\mathrm {i}(\alpha ,\beta )=0$
, and if
$\mathrm {i}(\alpha ,\beta )=0$
, and if
 $r/s\ne r'/s'$
, then
$r/s\ne r'/s'$
, then
 $\mathrm {i}(\alpha , \beta )= \#(\tau _{r/s}\cap \tau _{r'/s'}) =2|rs'-sr'|>0$
;
$\mathrm {i}(\alpha , \beta )= \#(\tau _{r/s}\cap \tau _{r'/s'}) =2|rs'-sr'|>0$
; -
(ii)
 $\mathrm {i}(\alpha , \xi )= \#(\tau _{r/s}\cap \xi _{r'/s'}) =\tfrac 12 \mathrm {i}(\alpha , \beta ) =|rs'-sr'|$
;
$\mathrm {i}(\alpha , \xi )= \#(\tau _{r/s}\cap \xi _{r'/s'}) =\tfrac 12 \mathrm {i}(\alpha , \beta ) =|rs'-sr'|$
; -
(iii)
 $\mathrm {i}(\alpha ,a)= \#(\tau _{r/s}\cap a )=|r|, \ \mathrm {i}(\alpha ,c)= \#( \tau _{r/s}\cap c)=|r|$
;
$\mathrm {i}(\alpha ,a)= \#(\tau _{r/s}\cap a )=|r|, \ \mathrm {i}(\alpha ,c)= \#( \tau _{r/s}\cap c)=|r|$
; -
(iv)
 $\mathrm {i}(\alpha , b)= \#(\tau _{r/s}\cap b)=s,\ \mathrm {i}(\alpha , d)=\#(\tau _{r/s}\cap d)=s$
;
$\mathrm {i}(\alpha , b)= \#(\tau _{r/s}\cap b)=s,\ \mathrm {i}(\alpha , d)=\#(\tau _{r/s}\cap d)=s$
; -
(v)
 $\mathrm {i}( \alpha , \alpha ^h) =2|r|$
and
$\mathrm {i}( \alpha , \alpha ^h) =2|r|$
and
 $\mathrm {i}( \alpha , \alpha ^v) =2s$
.
$\mathrm {i}( \alpha , \alpha ^v) =2s$
.
We will prove this lemma in the appendix. Note that Figure 7 illustrates statements (iii) and (v) when
![]() $\alpha =\tau _2$
. It follows from the lemma that
$\alpha =\tau _2$
. It follows from the lemma that
![]() $\tau _{r/s}$
for
$\tau _{r/s}$
for
![]() $r/s\ne 0, \infty $
is in minimal position with each of the curves
$r/s\ne 0, \infty $
is in minimal position with each of the curves
![]() $a,b,c,d, \alpha ^h, \alpha ^v$
.
$a,b,c,d, \alpha ^h, \alpha ^v$
.

Figure 7 Counting intersections of
![]() $\tau _2$
with the horizontal curve
$\tau _2$
with the horizontal curve
![]() $\alpha ^h$
and the horizontal edges a and c.
$\alpha ^h$
and the horizontal edges a and c.
Let
![]() $\gamma $
be a Jordan curve or an arc in a surface S, and
$\gamma $
be a Jordan curve or an arc in a surface S, and
![]() $M_1, M_2\subset S$
be two disjoint sets with
$M_1, M_2\subset S$
be two disjoint sets with
![]() $0<\#(\gamma \cap M_j)<\infty $
for
$0<\#(\gamma \cap M_j)<\infty $
for
![]() $j=1,2$
. We say that the points in
$j=1,2$
. We say that the points in
![]() $\gamma \cap M_1\ne \emptyset $
and
$\gamma \cap M_1\ne \emptyset $
and
![]() $\gamma \cap M_2\ne \emptyset $
alternate on
$\gamma \cap M_2\ne \emptyset $
alternate on
![]() $\gamma $
if any two points in one of the sets are separated by the other, that is, any subarc
$\gamma $
if any two points in one of the sets are separated by the other, that is, any subarc
![]() $\sigma \subset \gamma $
with both endpoints in either of the sets
$\sigma \subset \gamma $
with both endpoints in either of the sets
![]() $\gamma \cap M_1$
or
$\gamma \cap M_1$
or
![]() $\gamma \cap M_2$
must contain a point in the other set.
$\gamma \cap M_2$
must contain a point in the other set.
More intuitively, this situation when the points in
![]() $\gamma \cap M_1$
and
$\gamma \cap M_1$
and
![]() $\gamma \cap M_2$
alternate on an arc
$\gamma \cap M_2$
alternate on an arc
![]() $\gamma $
can be described as follows. Suppose we traverse
$\gamma $
can be described as follows. Suppose we traverse
![]() $\gamma $
in some (injective) parameterization starting from one of its endpoints. Then we will first meet a point in either
$\gamma $
in some (injective) parameterization starting from one of its endpoints. Then we will first meet a point in either
![]() $M_1$
or
$M_1$
or
![]() $M_2$
, say in
$M_2$
, say in
![]() $M_1$
. Then as we continue along
$M_1$
. Then as we continue along
![]() $\gamma $
, we will meet a point in
$\gamma $
, we will meet a point in
![]() $M_2$
, then a point in
$M_2$
, then a point in
![]() $M_1$
, etc. A similar remark applies when
$M_1$
, etc. A similar remark applies when
![]() $\gamma $
is a Jordan curve. Note that is this case
$\gamma $
is a Jordan curve. Note that is this case
![]() $\#(\gamma \cap M_1)= \#(\gamma \cap M_2)$
.
$\#(\gamma \cap M_1)= \#(\gamma \cap M_2)$
.
Lemma 2.5. Let
![]() $\tau =\wp (\ell _{r/s})$
be a simple closed geodesic or a geodesic arc in
$\tau =\wp (\ell _{r/s})$
be a simple closed geodesic or a geodesic arc in
![]() $(\mathbb {P},V)$
obtained from a line
$(\mathbb {P},V)$
obtained from a line
![]() $\ell _{r/s}\subset \mathbb {C}$
with slope
$\ell _{r/s}\subset \mathbb {C}$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. If
$r/s\in \widehat {\mathbb {Q}}$
. If
![]() $r/s\ne 0$
, then the sets
$r/s\ne 0$
, then the sets
![]() $a\cap \tau $
and
$a\cap \tau $
and
![]() $c\cap \tau $
are non-empty and finite, and the points in
$c\cap \tau $
are non-empty and finite, and the points in
![]() $a\cap \tau $
and
$a\cap \tau $
and
![]() $c\cap \tau $
alternate on
$c\cap \tau $
alternate on
![]() $\tau $
.
$\tau $
.
A similar statement is true if
![]() $r/s\ne \infty $
and we replace
$r/s\ne \infty $
and we replace
![]() $a,c$
with
$a,c$
with
![]() $b,d$
, respectively. Lemma 2.5 is related to a similar statement in a more general setting that is the key to proving Lemma 2.3 (see Lemma A.3).
$b,d$
, respectively. Lemma 2.5 is related to a similar statement in a more general setting that is the key to proving Lemma 2.3 (see Lemma A.3).
Proof. Define ![]() . Suppose first that
. Suppose first that
![]() $\tau =\wp (\ell _{r/s})$
is a simple closed geodesic. Then
$\tau =\wp (\ell _{r/s})$
is a simple closed geodesic. Then
![]() $ \tau =\wp ([z_0, w_0])$
, where
$ \tau =\wp ([z_0, w_0])$
, where
![]() $z_0\in \ell _{r/s} \subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
and
$z_0\in \ell _{r/s} \subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
and
![]() $w_0=z_0+2\omega $
, and the map
$w_0=z_0+2\omega $
, and the map
![]() $u\in [0,1]\mapsto \wp (uz_0+ (1-u)w_0)$
provides a parameterization of
$u\in [0,1]\mapsto \wp (uz_0+ (1-u)w_0)$
provides a parameterization of
![]() $\tau $
as a simple loop as follows from (2.3).
$\tau $
as a simple loop as follows from (2.3).
Now the set
![]() $\wp ^{-1}(a\cup c)$
consists precisely of the lines
$\wp ^{-1}(a\cup c)$
consists precisely of the lines
![]() $\ell _0(ni)=\{ z\in \mathbb {C}: \text {Im} (z)=n\}$
,
$\ell _0(ni)=\{ z\in \mathbb {C}: \text {Im} (z)=n\}$
,
![]() $n\in \mathbb {Z}$
. These lines alternate in the sense that
$n\in \mathbb {Z}$
. These lines alternate in the sense that
![]() $\wp $
maps
$\wp $
maps
![]() $\ell _0(ni)$
onto a or c depending on whether
$\ell _0(ni)$
onto a or c depending on whether
![]() $n\in \mathbb {Z}$
is even or odd, respectively. Since
$n\in \mathbb {Z}$
is even or odd, respectively. Since
![]() $r/s\ne 0$
, we have
$r/s\ne 0$
, we have
![]() $r\in \mathbb {Z}\smallsetminus \{0\}$
, and so
$r\in \mathbb {Z}\smallsetminus \{0\}$
, and so
![]() $\text {Im} (w_0-z_0)=\text {Im}(2\omega )=2r$
is a non-zero even integer. This implies that the line segment
$\text {Im} (w_0-z_0)=\text {Im}(2\omega )=2r$
is a non-zero even integer. This implies that the line segment
![]() $ [z_0, w_0]\subset \ell _{r/s}$
has non-empty intersections (consisting of finitely many points) with each of the sets
$ [z_0, w_0]\subset \ell _{r/s}$
has non-empty intersections (consisting of finitely many points) with each of the sets
![]() $\wp ^{-1}(a)$
and
$\wp ^{-1}(a)$
and
![]() $\wp ^{-1}(c)$
. Moreover, the points in these intersections alternate on the segment
$\wp ^{-1}(c)$
. Moreover, the points in these intersections alternate on the segment
![]() $[z_0, w_0]$
. From this, together with the fact that
$[z_0, w_0]$
. From this, together with the fact that
the statement follows (the latter fact is needed to argue that the points in
![]() $a\cap \tau $
and
$a\cap \tau $
and
![]() $c\cap \tau $
alternate on the simple closed geodesic
$c\cap \tau $
alternate on the simple closed geodesic
![]() $\tau $
).
$\tau $
).
If
![]() $\tau $
is a geodesic arc, then there exists
$\tau $
is a geodesic arc, then there exists
![]() $z_0\in \mathbb {Z}^2$
such that
$z_0\in \mathbb {Z}^2$
such that
![]() $ \tau =\wp ([z_0, w_0])$
, where
$ \tau =\wp ([z_0, w_0])$
, where
![]() $w_0=z_0+\omega $
. The map
$w_0=z_0+\omega $
. The map
![]() $\wp $
sends
$\wp $
sends
![]() $[z_0, w_0]$
homeomorphically onto
$[z_0, w_0]$
homeomorphically onto
![]() $\tau $
. Again,
$\tau $
. Again,
![]() $ [z_0, w_0]$
has non-empty intersections consisting of finitely many points with each of the sets
$ [z_0, w_0]$
has non-empty intersections consisting of finitely many points with each of the sets
![]() $\wp ^{-1}(a)$
and
$\wp ^{-1}(a)$
and
![]() $\wp ^{-1}(c)$
. Moreover, the points in the sets
$\wp ^{-1}(c)$
. Moreover, the points in the sets
![]() $\wp ^{-1}(a)\cap [z_0, w_0]\ne \emptyset $
and
$\wp ^{-1}(a)\cap [z_0, w_0]\ne \emptyset $
and
![]() ${\wp ^{-1}(c)\cap [z_0, w_0]\ne \emptyset }$
alternate on the segment
${\wp ^{-1}(c)\cap [z_0, w_0]\ne \emptyset }$
alternate on the segment
![]() $[z_0, w_0]$
. The statement also follows in this case.
$[z_0, w_0]$
. The statement also follows in this case.
We conclude this section with a statement related to the previous considerations formulated for an arbitrary sphere with four marked points.
Lemma 2.6. Let
![]() $({S^{2}}, Z)$
be a marked sphere with
$({S^{2}}, Z)$
be a marked sphere with
![]() $\# Z = 4$
, and
$\# Z = 4$
, and
![]() $\alpha , \gamma $
be essential Jordan curves in
$\alpha , \gamma $
be essential Jordan curves in
![]() $({S^{2}}, Z)$
. Suppose that
$({S^{2}}, Z)$
. Suppose that
![]() $a_\alpha $
and
$a_\alpha $
and
![]() $c_\alpha $
are core arcs of
$c_\alpha $
are core arcs of
![]() $\alpha $
that lie in different components of
$\alpha $
that lie in different components of
![]() ${S^{2}}\smallsetminus \alpha $
. Then the following statements are true:
${S^{2}}\smallsetminus \alpha $
. Then the following statements are true:
-
(i)
 $\mathrm {i}(\alpha , \gamma )= 2 \mathrm {i}(a_\alpha , \gamma ) = 2 \mathrm {i}(c_\alpha , \gamma )$
;
$\mathrm {i}(\alpha , \gamma )= 2 \mathrm {i}(a_\alpha , \gamma ) = 2 \mathrm {i}(c_\alpha , \gamma )$
; -
(ii) if
 $\mathrm {i}(\alpha , \gamma )>0$
, then there exists a Jordan curve
$\mathrm {i}(\alpha , \gamma )>0$
, then there exists a Jordan curve
 $\gamma '$
in
$\gamma '$
in
 $({S^{2}},Z)$
with
$({S^{2}},Z)$
with
 $ \gamma ' \sim \gamma $
relative to Z such that
$ \gamma ' \sim \gamma $
relative to Z such that
 $\gamma '$
is in minimal position with
$\gamma '$
is in minimal position with
 $\alpha $
,
$\alpha $
,
 $a_\alpha $
,
$a_\alpha $
,
 $c_\alpha $
and the points in
$c_\alpha $
and the points in
 $a_\alpha \cap \gamma '\ne \emptyset $
and
$a_\alpha \cap \gamma '\ne \emptyset $
and
 $c_\alpha \cap \gamma '\ne \emptyset $
alternate on
$c_\alpha \cap \gamma '\ne \emptyset $
alternate on
 $\gamma '$
.
$\gamma '$
.
Proof. We may identify the marked sphere
![]() $({S^{2}}, Z)$
with the pillow
$({S^{2}}, Z)$
with the pillow
![]() $(\mathbb {P},V)$
by a homeomorphism that sends
$(\mathbb {P},V)$
by a homeomorphism that sends
![]() $\alpha $
,
$\alpha $
,
![]() $a_\alpha $
,
$a_\alpha $
,
![]() $c_\alpha $
to
$c_\alpha $
to
![]() $\alpha ^h$
, a, c, respectively. Then, by Lemma 2.3, the curve
$\alpha ^h$
, a, c, respectively. Then, by Lemma 2.3, the curve
![]() $\gamma $
is isotopic to a simple closed geodesic
$\gamma $
is isotopic to a simple closed geodesic
![]() $\tau _{r/s}$
with slope
$\tau _{r/s}$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. Statement (i) then follows from Lemma 2.4(iii) and (v).
$r/s\in \widehat {\mathbb {Q}}$
. Statement (i) then follows from Lemma 2.4(iii) and (v).
If
![]() $\mathrm {i}(\alpha , \gamma )=\mathrm {i}(\alpha ^h,\tau _{r/s})=2|r|>0$
, then we can choose
$\mathrm {i}(\alpha , \gamma )=\mathrm {i}(\alpha ^h,\tau _{r/s})=2|r|>0$
, then we can choose
![]() $\gamma '=\tau _{r/s}$
in statement (ii). Indeed, then
$\gamma '=\tau _{r/s}$
in statement (ii). Indeed, then
![]() $\gamma '=\tau _{r/s}\sim \gamma $
relative to
$\gamma '=\tau _{r/s}\sim \gamma $
relative to
![]() $V=Z$
, and
$V=Z$
, and
![]() $\gamma '=\tau _{r/s}$
is in minimal position with
$\gamma '=\tau _{r/s}$
is in minimal position with
![]() $\alpha ^h=\tau _0$
,
$\alpha ^h=\tau _0$
,
![]() $a_\alpha =a$
,
$a_\alpha =a$
,
![]() $c_\alpha =c$
as follows from Lemma 2.4 (i) and (iii). Since
$c_\alpha =c$
as follows from Lemma 2.4 (i) and (iii). Since
![]() $r/s\ne 0$
in this case, the statement about alternation follows from Lemma 2.5.
$r/s\ne 0$
in this case, the statement about alternation follows from Lemma 2.5.
3 Thurston maps
Here we provide a very brief summary of some relevant definitions and facts. For more details, we refer the reader to [Reference Bonk and MeyerBM17, Ch. 2].
Let
![]() $f\colon S^2\to S^2$
be a branched covering map of a topological
$f\colon S^2\to S^2$
be a branched covering map of a topological
![]() $2$
-sphere
$2$
-sphere
![]() $S^2$
. A point
$S^2$
. A point
![]() $p\in {S^{2}}$
is called periodic (for f) if
$p\in {S^{2}}$
is called periodic (for f) if
![]() $f^n(p)=p$
for some
$f^n(p)=p$
for some
![]() $n\in \mathbb {N}$
. Recall that
$n\in \mathbb {N}$
. Recall that
![]() ${C_f}$
denotes the set of all critical points of f. The union
${C_f}$
denotes the set of all critical points of f. The union
of the orbits of critical points is called the postcritical set of f. Note that
The map f is said to be postcritically finite if its postcritical set
![]() ${P_f}$
is finite, in other words, if every critical point of f has a finite orbit under iteration.
${P_f}$
is finite, in other words, if every critical point of f has a finite orbit under iteration.
Definition 3.1. A Thurston map is a postcritically finite branched covering map
![]() ${f\colon S^2 \to S^2}$
of topological degree
${f\colon S^2 \to S^2}$
of topological degree
![]() $\deg (f)\geq 2$
.
$\deg (f)\geq 2$
.
Natural examples of Thurston maps are given by rational Thurston maps, that is, postcritically finite rational maps on the Riemann sphere
![]() $\widehat {\mathbb {C}}$
.
$\widehat {\mathbb {C}}$
.
The ramification function of a Thurston map
![]() $f\colon {S^{2}}\to {S^{2}}$
is a function
$f\colon {S^{2}}\to {S^{2}}$
is a function
![]() $\alpha _{f} \colon {S^{2}} \to \mathbb {N}\cup \{\infty \}$
such that
$\alpha _{f} \colon {S^{2}} \to \mathbb {N}\cup \{\infty \}$
such that
![]() $\alpha _{f}(p)$
for
$\alpha _{f}(p)$
for
![]() $p\in S^2$
is the lowest common multiple of all local degrees
$p\in S^2$
is the lowest common multiple of all local degrees
![]() $\deg (f^n,q)$
, where
$\deg (f^n,q)$
, where
![]() $q\in f^{-n}(p)$
and
$q\in f^{-n}(p)$
and
![]() $n\in \mathbb {N}$
are arbitrary. In particular,
$n\in \mathbb {N}$
are arbitrary. In particular,
![]() $\alpha _{f}(p) = 1$
for
$\alpha _{f}(p) = 1$
for
![]() $p\in {S^{2}} \smallsetminus {P_f}$
and
$p\in {S^{2}} \smallsetminus {P_f}$
and
![]() $\alpha _{f}(p) \ge 2$
for
$\alpha _{f}(p) \ge 2$
for
![]() $p\in {P_f}$
.
$p\in {P_f}$
.
Definition 3.2. Two Thurston maps
![]() $f\colon S^2\to S^2$
and
$f\colon S^2\to S^2$
and
![]() $g\colon \widehat {S}^2\to \widehat {S}^2$
, where
$g\colon \widehat {S}^2\to \widehat {S}^2$
, where
![]() $ \widehat {S}^2$
is another topological
$ \widehat {S}^2$
is another topological
![]() $2$
-sphere, are called Thurston equivalent if there are homeomorphisms
$2$
-sphere, are called Thurston equivalent if there are homeomorphisms
![]() $h_0,h_1\colon S^2\to \widehat {S}^2$
that are isotopic relative to
$h_0,h_1\colon S^2\to \widehat {S}^2$
that are isotopic relative to
![]() ${P_f}$
such that
${P_f}$
such that
![]() $h_0 \circ f = g \circ h_1$
.
$h_0 \circ f = g \circ h_1$
.
We say that a Thurston map is realized (by a rational map) if it is Thurston equivalent to a rational map. Otherwise, we say that it is obstructed.
The orbifold
![]() $\mathcal {O}_f$
associated with a Thurston map f is the pair
$\mathcal {O}_f$
associated with a Thurston map f is the pair
![]() $(S^2,\alpha _f)$
. The Euler characteristic of
$(S^2,\alpha _f)$
. The Euler characteristic of
![]() $\mathcal {O}_f$
is
$\mathcal {O}_f$
is

Here we set ![]() .
.
The Euler characteristic of the orbifold
![]() $\mathcal {O}_f$
satisfies
$\mathcal {O}_f$
satisfies
![]() $\chi (\mathcal {O}_f) \leq 0$
. We call
$\chi (\mathcal {O}_f) \leq 0$
. We call
![]() $\mathcal {O}_f$
hyperbolic if
$\mathcal {O}_f$
hyperbolic if
![]() $\chi (\mathcal {O}_f)<0$
, and parabolic if
$\chi (\mathcal {O}_f)<0$
, and parabolic if
![]() $\chi (\mathcal {O}_f)=0$
.
$\chi (\mathcal {O}_f)=0$
.
If
![]() $f\colon S^2\rightarrow S^2$
is a Thurston map, then
$f\colon S^2\rightarrow S^2$
is a Thurston map, then
![]() $f(C_f\cup P_f)\subset P_f$
, which implies
$f(C_f\cup P_f)\subset P_f$
, which implies
![]() $C_f\cup P_f\subset f^{-1}(P_f)$
. The reverse inclusion is related to the parabolicity of
$C_f\cup P_f\subset f^{-1}(P_f)$
. The reverse inclusion is related to the parabolicity of
![]() $\mathcal {O}_f$
.
$\mathcal {O}_f$
.
Lemma 3.3. Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map. If f has a parabolic orbifold, then
$f\colon S^2\rightarrow S^2$
be a Thurston map. If f has a parabolic orbifold, then
![]() $f^{-1}(P_f)=C_f\cup P_f$
. Moreover, conversely, if
$f^{-1}(P_f)=C_f\cup P_f$
. Moreover, conversely, if
![]() $\#{P_f}\ge 4$
and
$\#{P_f}\ge 4$
and
![]() $f^{-1}({P_f})\subset {C_f} \cup {P_f}$
, then f has a parabolic orbifold.
$f^{-1}({P_f})\subset {C_f} \cup {P_f}$
, then f has a parabolic orbifold.
The second part follows from [Reference Douady and HubbardDH93, Lemma 2], but for the convenience of the reader, we will provide the simple proof. Here the assumption
![]() $\#{P_f}\ge 4$
cannot be omitted as some examples with
$\#{P_f}\ge 4$
cannot be omitted as some examples with
![]() $\#P_f=3$
show (such as the Thurston map arising from the ‘barycentric subdivision rule’; see [Reference Bonk and MeyerBM17, Example 12.21]).
$\#P_f=3$
show (such as the Thurston map arising from the ‘barycentric subdivision rule’; see [Reference Bonk and MeyerBM17, Example 12.21]).
Proof. Let
![]() $\alpha _f$
be the ramification function of f. Then
$\alpha _f$
be the ramification function of f. Then
![]() $p\in P_f$
if and only if
$p\in P_f$
if and only if
![]() $\alpha _f(p)\ge 2$
.
$\alpha _f(p)\ge 2$
.
First suppose that f has a parabolic orbifold. Then
![]() $\alpha _f(q)\cdot \deg (f,q)= \alpha _f(f(q))$
for all
$\alpha _f(q)\cdot \deg (f,q)= \alpha _f(f(q))$
for all
![]() $q\in S^2$
(see [Reference Bonk and MeyerBM17, Proposition 2.14]). So if
$q\in S^2$
(see [Reference Bonk and MeyerBM17, Proposition 2.14]). So if
![]() $q\in f^{-1}(P_f)$
, then
$q\in f^{-1}(P_f)$
, then
![]() $f(q)\in P_f$
which implies
$f(q)\in P_f$
which implies
This is only possible if
![]() $\alpha _f(q)\ge 2$
in which case
$\alpha _f(q)\ge 2$
in which case
![]() $q\in P_f$
, or if
$q\in P_f$
, or if
![]() $\deg (f,q)\ge 2$
in which case
$\deg (f,q)\ge 2$
in which case
![]() $q\in C_f$
. Hence,
$q\in C_f$
. Hence,
![]() $q\in C_f\cup P_f$
, and so
$q\in C_f\cup P_f$
, and so
![]() $f^{-1}(P_f)\subset C_f\cup P_f$
. Since the reverse inclusion is true for all Thurston maps, we see that
$f^{-1}(P_f)\subset C_f\cup P_f$
. Since the reverse inclusion is true for all Thurston maps, we see that
![]() $f^{-1}(P_f)=C_f\cup P_f$
if f has a parabolic orbifold.
$f^{-1}(P_f)=C_f\cup P_f$
if f has a parabolic orbifold.
For the converse, suppose that
![]() $f\colon S^2\rightarrow S^2$
is an arbitrary Thurston map with
$f\colon S^2\rightarrow S^2$
is an arbitrary Thurston map with
![]() $\#{P_f}\ge 4$
and
$\#{P_f}\ge 4$
and
![]() $f^{-1}({P_f})\subset {C_f} \cup {P_f}$
. Let
$f^{-1}({P_f})\subset {C_f} \cup {P_f}$
. Let ![]() . Note that
. Note that
![]() $f^{-1}(P_f)\subset (C_f\smallsetminus P_f)\cup P_f$
by our hypotheses.
$f^{-1}(P_f)\subset (C_f\smallsetminus P_f)\cup P_f$
by our hypotheses.
Each point
![]() $p\in S^2$
has precisely d preimages counting multiplicities, that is,
$p\in S^2$
has precisely d preimages counting multiplicities, that is,
 $$ \begin{align*}d=\sum_{q\in f^{-1}(p)}\deg(f,q).\end{align*} $$
$$ \begin{align*}d=\sum_{q\in f^{-1}(p)}\deg(f,q).\end{align*} $$
Furthermore, since
![]() $C_f\subset f^{-1}(P_f)$
and
$C_f\subset f^{-1}(P_f)$
and
![]() $\deg (f,q)\ge 2$
for
$\deg (f,q)\ge 2$
for
![]() $q\in S^2$
if and only if
$q\in S^2$
if and only if
![]() $q\in C_f$
, the Riemann–Hurwitz formula implies
$q\in C_f$
, the Riemann–Hurwitz formula implies
 $$ \begin{align*} \#(C_f\smallsetminus P_f) \le \#C_f&\le \sum_{c\in C_f}(\deg(f,c)-1) =\sum_{q\in f^{-1}(P_f)}(\deg(f,q)-1) \\ &= 2d-2. \end{align*} $$
$$ \begin{align*} \#(C_f\smallsetminus P_f) \le \#C_f&\le \sum_{c\in C_f}(\deg(f,c)-1) =\sum_{q\in f^{-1}(P_f)}(\deg(f,q)-1) \\ &= 2d-2. \end{align*} $$
It follows that
 $$ \begin{align*} d\cdot \#P_f &= \sum_{q\in f^{-1}(P_f)}\deg(f,q)= \sum_{q\in f^{-1}(P_f)}(\deg(f,q)-1)+ \#f^{-1}(P_f)\\ &= (2d-2)+ \#f^{-1}(P_f)\le (2d-2) +\# (C_f\smallsetminus P_f)+\# P_f\\ &\le 4(d-1) +\#P_f. \end{align*} $$
$$ \begin{align*} d\cdot \#P_f &= \sum_{q\in f^{-1}(P_f)}\deg(f,q)= \sum_{q\in f^{-1}(P_f)}(\deg(f,q)-1)+ \#f^{-1}(P_f)\\ &= (2d-2)+ \#f^{-1}(P_f)\le (2d-2) +\# (C_f\smallsetminus P_f)+\# P_f\\ &\le 4(d-1) +\#P_f. \end{align*} $$
Hence,
![]() $(d-1)\cdot \#P_f\le 4(d-1)$
and so
$(d-1)\cdot \#P_f\le 4(d-1)$
and so
![]() $4\le \#P_f\le 4$
. This implies
$4\le \#P_f\le 4$
. This implies
![]() $\#P_f=4$
and that all the previous inequalities must be equalities. In particular,
$\#P_f=4$
and that all the previous inequalities must be equalities. In particular,
![]() $\# (C_f\smallsetminus P_f)=2d-2$
, which shows that at all critical points, the local degree of f is equal to
$\# (C_f\smallsetminus P_f)=2d-2$
, which shows that at all critical points, the local degree of f is equal to
![]() $2$
and no critical points belong to
$2$
and no critical points belong to
![]() $P_f$
.
$P_f$
.
As a consequence, under iteration of f, the orbit of any point
![]() $p\in S^2$
passes through at most one critical point. It follows that we have
$p\in S^2$
passes through at most one critical point. It follows that we have
![]() $\alpha _f(p)=1$
for
$\alpha _f(p)=1$
for
![]() $p\in S^2\smallsetminus P_f$
and
$p\in S^2\smallsetminus P_f$
and
![]() $\alpha _f(p)= 2$
for
$\alpha _f(p)= 2$
for
![]() $p\in P_f$
. This implies that the Euler characteristic (see equation (3.1)) of the orbifold
$p\in P_f$
. This implies that the Euler characteristic (see equation (3.1)) of the orbifold
![]() $\mathcal {O}_f$
associated with f is equal to
$\mathcal {O}_f$
associated with f is equal to
 $$ \begin{align*} \chi(\mathcal{O}_f) = 2 - \sum_{p\in P_f}\bigg(1-\frac{1}{\alpha_f(p)}\bigg) = 2-(1/2+1/2+1/2+1/2)=0. \end{align*} $$
$$ \begin{align*} \chi(\mathcal{O}_f) = 2 - \sum_{p\in P_f}\bigg(1-\frac{1}{\alpha_f(p)}\bigg) = 2-(1/2+1/2+1/2+1/2)=0. \end{align*} $$
We conclude that f has a parabolic orbifold.
3.1 The
 $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
In general, a Lattès map is a rational Thurston map with parabolic orbifold that does not have periodic critical points. Here we provide the analytic definition for the Lattès maps that we use in this paper and interpret this from a more geometric perspective. See [Reference Milnor, Hjorth and PetersenMil06b] and [Reference Bonk and MeyerBM17, Ch. 3] for a general discussion of Lattès maps.
Let
![]() $\mathbb {P}\cong \widehat {\mathbb {C}}$
be the Euclidean square pillow and
$\mathbb {P}\cong \widehat {\mathbb {C}}$
be the Euclidean square pillow and
![]() $\wp \colon \mathbb {C}\to \mathbb {P}$
be its universal orbifold covering map, as discussed in §2.4. Fix a natural number
$\wp \colon \mathbb {C}\to \mathbb {P}$
be its universal orbifold covering map, as discussed in §2.4. Fix a natural number
![]() $n\geq 2$
. It follows from (2.3) that there is a unique (and well-defined) map
$n\geq 2$
. It follows from (2.3) that there is a unique (and well-defined) map
![]() $\mathcal {L}_n\colon \mathbb {P}\to \mathbb {P}$
such that
$\mathcal {L}_n\colon \mathbb {P}\to \mathbb {P}$
such that
We call
![]() $\mathcal {L}_n$
the
$\mathcal {L}_n$
the
![]() $(n\times n)$
-Lattès map. In fact,
$(n\times n)$
-Lattès map. In fact,
![]() $\mathcal {L}_n$
is a rational map under the identification
$\mathcal {L}_n$
is a rational map under the identification
![]() $\mathbb {P}\cong \widehat {\mathbb {C}}$
as discussed in §2.4.
$\mathbb {P}\cong \widehat {\mathbb {C}}$
as discussed in §2.4.
Alternatively, we can describe the map
![]() $\mathcal {L}_n$
in a combinatorial fashion as follows. Recall that the front side of
$\mathcal {L}_n$
in a combinatorial fashion as follows. Recall that the front side of
![]() $\mathbb {P}$
is colored white, and the back side black. These are the two
$\mathbb {P}$
is colored white, and the back side black. These are the two
![]() $0$
-tiles of
$0$
-tiles of
![]() $\mathbb {P}$
, and we subdivide each of them into
$\mathbb {P}$
, and we subdivide each of them into
![]() $n^2$
squares of sidelength
$n^2$
squares of sidelength
![]() $1/n$
. We refer to these small squares as
$1/n$
. We refer to these small squares as
![]() $1$
-tiles (with n understood), and color them in a checkerboard fashion black and white so that the
$1$
-tiles (with n understood), and color them in a checkerboard fashion black and white so that the
![]() $1$
-tile S in the white side of
$1$
-tile S in the white side of
![]() $\mathbb {P}$
with the vertex A on its boundary is colored white. We map S to the white side of the pillow
$\mathbb {P}$
with the vertex A on its boundary is colored white. We map S to the white side of the pillow
![]() $\mathbb {P}$
by an orientation-preserving Euclidean similarity (that scales by the factor n) so that the vertex A is fixed. If we extend this map by reflection to the whole pillow, we get the
$\mathbb {P}$
by an orientation-preserving Euclidean similarity (that scales by the factor n) so that the vertex A is fixed. If we extend this map by reflection to the whole pillow, we get the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
(see Figure 1 for
$\mathcal {L}_n$
(see Figure 1 for
![]() $n=4$
). The map
$n=4$
). The map
![]() $\mathcal {L}_n$
sends each black or white
$\mathcal {L}_n$
sends each black or white
![]() $1$
-tile homeomorphically (by a similarity) onto the
$1$
-tile homeomorphically (by a similarity) onto the
![]() $0$
-tile in
$0$
-tile in
![]() $\mathbb {P}$
of the same color.
$\mathbb {P}$
of the same color.
Based on this combinatorial description, it is easy to see that each critical point of
![]() $\mathcal {L}_n$
has local degree
$\mathcal {L}_n$
has local degree
![]() $2$
and that the postcritical set of
$2$
and that the postcritical set of
![]() $\mathcal {L}_n$
coincides with the set of vertices of
$\mathcal {L}_n$
coincides with the set of vertices of
![]() $\mathbb {P}$
, that is,
$\mathbb {P}$
, that is,
![]() $P_{\mathcal {L}_n}=\{A,B,C,D\}=V$
. One can also check that for the ramification function of
$P_{\mathcal {L}_n}=\{A,B,C,D\}=V$
. One can also check that for the ramification function of
![]() $\mathcal {L}_n$
, we have
$\mathcal {L}_n$
, we have
![]() $\alpha _{\mathcal {L}_n}(p)=2$
for each
$\alpha _{\mathcal {L}_n}(p)=2$
for each
![]() $p\in P_{\mathcal {L}_n}$
. Substituting this into equation (3.1), we see that
$p\in P_{\mathcal {L}_n}$
. Substituting this into equation (3.1), we see that
![]() $\chi (\mathcal {O}_{\mathcal {L}_n})=0$
. Thus,
$\chi (\mathcal {O}_{\mathcal {L}_n})=0$
. Thus,
![]() $\mathcal {L}_n$
has a parabolic orbifold.
$\mathcal {L}_n$
has a parabolic orbifold.
3.2 Thurston’s characterization of rational maps
Thurston maps can often be described from a combinatorial viewpoint as the Lattès map
![]() $\mathcal {L}_n$
in §3.1 (see, for instance, [Reference Cannon, Floyd, Kenyon and ParryCFKP03] and [Reference Bonk and MeyerBM17, Ch. 12]). The question whether a given Thurston map f can be realized by a rational map is usually difficult to answer except in some special cases. William Thurston provided a sharp, purely topological criterion that answers this question. The formulation and proof of this celebrated result can be found in [Reference Douady and HubbardDH93]. In this section, we introduce the necessary concepts and formulate the result only when
$\mathcal {L}_n$
in §3.1 (see, for instance, [Reference Cannon, Floyd, Kenyon and ParryCFKP03] and [Reference Bonk and MeyerBM17, Ch. 12]). The question whether a given Thurston map f can be realized by a rational map is usually difficult to answer except in some special cases. William Thurston provided a sharp, purely topological criterion that answers this question. The formulation and proof of this celebrated result can be found in [Reference Douady and HubbardDH93]. In this section, we introduce the necessary concepts and formulate the result only when
![]() $\#{P_f}=4$
, which is the relevant case for this paper.
$\#{P_f}=4$
, which is the relevant case for this paper.
In the following, let
![]() $f\colon {S^{2}}\to {S^{2}}$
be a Thurston map. The map f defines a natural pullback operation on Jordan curves in
$f\colon {S^{2}}\to {S^{2}}$
be a Thurston map. The map f defines a natural pullback operation on Jordan curves in
![]() $({S^{2}},{P_f})$
: a pullback of a Jordan curve
$({S^{2}},{P_f})$
: a pullback of a Jordan curve
![]() ${\gamma \subset {S^{2}}\smallsetminus {P_f}}$
under f is a connected component
${\gamma \subset {S^{2}}\smallsetminus {P_f}}$
under f is a connected component
![]() $\widetilde {\gamma }$
of
$\widetilde {\gamma }$
of
![]() $f^{-1}(\gamma )$
. Since f is a covering map from
$f^{-1}(\gamma )$
. Since f is a covering map from
![]() $S^2\smallsetminus f^{-1}({P_f})$
onto
$S^2\smallsetminus f^{-1}({P_f})$
onto
![]() $S^2\smallsetminus {P_f}$
, each pullback
$S^2\smallsetminus {P_f}$
, each pullback
![]() $\widetilde {\gamma }$
of
$\widetilde {\gamma }$
of
![]() $\gamma $
is a Jordan curve in
$\gamma $
is a Jordan curve in
![]() $({S^{2}},{P_f})$
. Moreover,
$({S^{2}},{P_f})$
. Moreover,
![]() $f|\widetilde {\gamma }\colon \widetilde {\gamma }\rightarrow \gamma $
is a covering map. For some
$f|\widetilde {\gamma }\colon \widetilde {\gamma }\rightarrow \gamma $
is a covering map. For some
![]() $k\in \mathbb {N}$
with
$k\in \mathbb {N}$
with
![]() $1\le k\le \deg (f)$
, each point
$1\le k\le \deg (f)$
, each point
![]() $p\in \gamma $
has precisely k distinct preimages in
$p\in \gamma $
has precisely k distinct preimages in
![]() $ \widetilde {\gamma }$
. Here k is the (unsigned) mapping degree of
$ \widetilde {\gamma }$
. Here k is the (unsigned) mapping degree of
![]() $f|\widetilde {\gamma }$
which we denote by
$f|\widetilde {\gamma }$
which we denote by
![]() $\deg (f\colon \widetilde {\gamma } \to \gamma )$
.
$\deg (f\colon \widetilde {\gamma } \to \gamma )$
.
Recall that a Jordan curve
![]() $\gamma \subset {S^{2}}\smallsetminus {P_f}$
is called essential if each of the two connected components of
$\gamma \subset {S^{2}}\smallsetminus {P_f}$
is called essential if each of the two connected components of
![]() ${S^{2}}\smallsetminus \gamma $
contains at least two points from
${S^{2}}\smallsetminus \gamma $
contains at least two points from
![]() ${P_f}$
, and is called peripheral otherwise.
${P_f}$
, and is called peripheral otherwise.
We will need the following standard facts.
Lemma 3.4. Let
![]() $f\colon S^2\rightarrow S^2 $
be a Thurston map and let
$f\colon S^2\rightarrow S^2 $
be a Thurston map and let
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
be Jordan curves in
$\gamma '$
be Jordan curves in
![]() $(S^2, {P_f})$
with
$(S^2, {P_f})$
with
![]() $\gamma '\sim \gamma $
relative to
$\gamma '\sim \gamma $
relative to
![]() ${P_f}$
. Then there is a bijection
${P_f}$
. Then there is a bijection
![]() $\widetilde \gamma \leftrightarrow \widetilde \gamma '$
between the pullbacks
$\widetilde \gamma \leftrightarrow \widetilde \gamma '$
between the pullbacks
![]() $\widetilde \gamma $
of
$\widetilde \gamma $
of
![]() $\gamma $
and the pullbacks
$\gamma $
and the pullbacks
![]() $\widetilde \gamma '$
of
$\widetilde \gamma '$
of
![]() $\gamma '$
under f such that for all pullbacks corresponding under this bijection, we have
$\gamma '$
under f such that for all pullbacks corresponding under this bijection, we have
![]() $\widetilde \gamma \sim \widetilde \gamma '$
relative to
$\widetilde \gamma \sim \widetilde \gamma '$
relative to
![]() ${P_f}$
and
${P_f}$
and
![]() $\deg (f\colon \widetilde \gamma \rightarrow \gamma )=\deg (f\colon \widetilde \gamma '\rightarrow \gamma ')$
.
$\deg (f\colon \widetilde \gamma \rightarrow \gamma )=\deg (f\colon \widetilde \gamma '\rightarrow \gamma ')$
.
For the proof, see [Reference Bonk and MeyerBM17, Lemma 6.9]. A consequence of this statement is that the isotopy classes of curves in
![]() $f^{-1}(\gamma )$
relative to
$f^{-1}(\gamma )$
relative to
![]() ${P_f}$
only depend on the isotopy class
${P_f}$
only depend on the isotopy class
![]() $[\gamma ]$
relative to
$[\gamma ]$
relative to
![]() $ {P_f}$
and not on the specific choice of
$ {P_f}$
and not on the specific choice of
![]() $\gamma $
.
$\gamma $
.
Corollary 3.5. Let
![]() $f\colon S^2\rightarrow S^2 $
be a Thurston map, and
$f\colon S^2\rightarrow S^2 $
be a Thurston map, and
![]() $\gamma $
be a Jordan curve in
$\gamma $
be a Jordan curve in
![]() $(S^2, {P_f})$
.
$(S^2, {P_f})$
.
-
(i) If
 $\gamma $
is peripheral, then every pullback of
$\gamma $
is peripheral, then every pullback of
 $\gamma $
under f is also peripheral.
$\gamma $
under f is also peripheral. -
(ii) Suppose that
 $\#{P_f} = 4$
and let
$\#{P_f} = 4$
and let
 $\widetilde \gamma $
be a pullback of
$\widetilde \gamma $
be a pullback of
 $\gamma $
under f. If
$\gamma $
under f. If
 $\gamma $
and
$\gamma $
and
 $\widetilde \gamma $
are essential, then the isotopy class
$\widetilde \gamma $
are essential, then the isotopy class
 $[\widetilde \gamma ]$
relative to
$[\widetilde \gamma ]$
relative to
 $ {P_f}$
only depends on the isotopy class
$ {P_f}$
only depends on the isotopy class
 $[\gamma ]$
relative to
$[\gamma ]$
relative to
 $ {P_f}$
and not on the specific choice of
$ {P_f}$
and not on the specific choice of
 $\gamma $
and its essential pullback
$\gamma $
and its essential pullback
 $\widetilde \gamma $
.
$\widetilde \gamma $
.
Proof. (i) Since
![]() $\gamma $
is peripheral,
$\gamma $
is peripheral,
![]() $\gamma $
can be isotoped (relative to
$\gamma $
can be isotoped (relative to
![]() ${P_f}$
) into a Jordan curve
${P_f}$
) into a Jordan curve
![]() $\gamma '$
inside a small open Jordan region
$\gamma '$
inside a small open Jordan region
![]() $V\subset {S^{2}}$
such that
$V\subset {S^{2}}$
such that
![]() $\# (V \cap {P_f}) \leq 1$
and V is evenly covered by the branched covering map f as in equation (2.1).
$\# (V \cap {P_f}) \leq 1$
and V is evenly covered by the branched covering map f as in equation (2.1).
Then for each component
![]() $U_j$
of
$U_j$
of
![]() $f^{-1}(V)$
, the map
$f^{-1}(V)$
, the map
![]() $f|U_j\colon U_j\to V$
is given by
$f|U_j\colon U_j\to V$
is given by
![]() $z\in \mathbb {D}\mapsto z^{d_j}\in \mathbb {D}$
for some
$z\in \mathbb {D}\mapsto z^{d_j}\in \mathbb {D}$
for some
![]() $d_j\in \mathbb {N}$
after orientation-preserving homeomorphic coordinate changes in the source and target. This implies that
$d_j\in \mathbb {N}$
after orientation-preserving homeomorphic coordinate changes in the source and target. This implies that
![]() $\# (U_j \cap {P_f}) \leq 1$
and that each pullback of
$\# (U_j \cap {P_f}) \leq 1$
and that each pullback of
![]() $\gamma '$
in
$\gamma '$
in
![]() $U_j$
is peripheral. Hence, all pullbacks of
$U_j$
is peripheral. Hence, all pullbacks of
![]() $\gamma '$
under f are peripheral and the same is true for the pullbacks of
$\gamma '$
under f are peripheral and the same is true for the pullbacks of
![]() $\gamma $
as follows from Lemma 3.4.
$\gamma $
as follows from Lemma 3.4.
(ii) Suppose
![]() $\widetilde \gamma $
and
$\widetilde \gamma $
and
![]() $\widetilde \gamma '$
are two distinct essential pullbacks of
$\widetilde \gamma '$
are two distinct essential pullbacks of
![]() $\gamma $
under f. Since these are components of
$\gamma $
under f. Since these are components of
![]() $f^{-1}(\gamma )$
, the Jordan curves
$f^{-1}(\gamma )$
, the Jordan curves
![]() $\widetilde \gamma $
and
$\widetilde \gamma $
and
![]() $\widetilde \gamma '$
are disjoint. Then the set
$\widetilde \gamma '$
are disjoint. Then the set
![]() $S^2\smallsetminus (\widetilde \gamma \cup \widetilde \gamma ')$
is a disjoint union
$S^2\smallsetminus (\widetilde \gamma \cup \widetilde \gamma ')$
is a disjoint union
![]() $S^2\smallsetminus (\widetilde \gamma \cup \widetilde \gamma ')=V\cup U\cup V' $
, where
$S^2\smallsetminus (\widetilde \gamma \cup \widetilde \gamma ')=V\cup U\cup V' $
, where
![]() $V,V'\subset S^2$
are Jordan regions and
$V,V'\subset S^2$
are Jordan regions and
![]() $U\subset S^2$
is an annulus with
$U\subset S^2$
is an annulus with
![]() $\partial U=\widetilde \gamma \cup \widetilde \gamma '$
. Since
$\partial U=\widetilde \gamma \cup \widetilde \gamma '$
. Since
![]() $\widetilde \gamma $
and
$\widetilde \gamma $
and
![]() $\widetilde \gamma '$
are essential, both V and
$\widetilde \gamma '$
are essential, both V and
![]() $V'$
must contain at least two postcritical points. Now
$V'$
must contain at least two postcritical points. Now
![]() $\#{P_f}=4$
, and so
$\#{P_f}=4$
, and so
![]() $U\cap {P_f} =\emptyset $
. Lemma 2.1 then implies that
$U\cap {P_f} =\emptyset $
. Lemma 2.1 then implies that
![]() $\widetilde \gamma $
and
$\widetilde \gamma $
and
![]() $\widetilde \gamma '$
are isotopic relative to
$\widetilde \gamma '$
are isotopic relative to
![]() ${P_f}$
.
${P_f}$
.
It follows that the isotopy class
![]() $[\widetilde \gamma ]$
relative to
$[\widetilde \gamma ]$
relative to
![]() ${P_f}$
does not depend on the choice of the essential pullback
${P_f}$
does not depend on the choice of the essential pullback
![]() $\widetilde \gamma $
of
$\widetilde \gamma $
of
![]() $\gamma $
. At the same time, Lemma 3.4 implies that
$\gamma $
. At the same time, Lemma 3.4 implies that
![]() $[\widetilde \gamma ]$
only depends on the isotopy class
$[\widetilde \gamma ]$
only depends on the isotopy class
![]() $[\gamma ]$
, as desired.
$[\gamma ]$
, as desired.
For a general Thurston map f the concept of an invariant multicurve is important to decide whether f is realized or obstructed. By definition, a multicurve is a non-empty finite family
![]() $\Gamma $
of essential Jordan curves in
$\Gamma $
of essential Jordan curves in
![]() ${S^{2}}\smallsetminus {P_f}$
that are pairwise disjoint and pairwise non-isotopic relative to
${S^{2}}\smallsetminus {P_f}$
that are pairwise disjoint and pairwise non-isotopic relative to
![]() ${P_f}$
.
${P_f}$
.
Suppose now that
![]() $\#{P_f}=4$
. Then any two essential Jordan curves in
$\#{P_f}=4$
. Then any two essential Jordan curves in
![]() ${S^{2}}\smallsetminus {P_f}$
are either isotopic relative to
${S^{2}}\smallsetminus {P_f}$
are either isotopic relative to
![]() ${P_f}$
or have a non-empty intersection (as follows from the argument in the proof of Corollary 3.5(ii)). Thus, in this case, each multicurve
${P_f}$
or have a non-empty intersection (as follows from the argument in the proof of Corollary 3.5(ii)). Thus, in this case, each multicurve
![]() $\Gamma $
consists of a single essential Jordan curve
$\Gamma $
consists of a single essential Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() ${S^{2}}\smallsetminus {P_f}$
. We say that an essential Jordan curve
${S^{2}}\smallsetminus {P_f}$
. We say that an essential Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() ${S^{2}}\smallsetminus {P_f}$
is f-invariant if each essential pullback of
${S^{2}}\smallsetminus {P_f}$
is f-invariant if each essential pullback of
![]() $\gamma $
under f is isotopic to
$\gamma $
under f is isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() ${P_f}$
.
${P_f}$
.
Definition 3.6. Let
![]() $f\colon {S^{2}}\to {S^{2}}$
be a Thurston map with
$f\colon {S^{2}}\to {S^{2}}$
be a Thurston map with
![]() $\#{P_f}=4$
and let
$\#{P_f}=4$
and let
![]() $\gamma \subset {S^{2}}\smallsetminus {P_f} $
be an essential f-invariant Jordan curve. We denote by
$\gamma \subset {S^{2}}\smallsetminus {P_f} $
be an essential f-invariant Jordan curve. We denote by
![]() $\gamma _1,\ldots ,\gamma _n$
for
$\gamma _1,\ldots ,\gamma _n$
for
![]() $n\in \mathbb {N}_0$
all the essential pullbacks of
$n\in \mathbb {N}_0$
all the essential pullbacks of
![]() $\gamma $
under f and define
$\gamma $
under f and define

Then
![]() $\gamma $
is called a (Thurston) obstruction for f if
$\gamma $
is called a (Thurston) obstruction for f if
![]() $\unicode{x3bb} _f(\gamma ) \geq 1$
.
$\unicode{x3bb} _f(\gamma ) \geq 1$
.
Note that if
![]() $n=0$
, then the sum in equation (3.3) is the empty sum and so
$n=0$
, then the sum in equation (3.3) is the empty sum and so
![]() $\unicode{x3bb} _f(\gamma )=0$
. It immediately follows from Lemma 3.4 that whether or not
$\unicode{x3bb} _f(\gamma )=0$
. It immediately follows from Lemma 3.4 that whether or not
![]() $\gamma $
is an obstruction for f only depends on the isotopy class
$\gamma $
is an obstruction for f only depends on the isotopy class
![]() $[\gamma ]$
relative to
$[\gamma ]$
relative to
![]() ${P_f}$
.
${P_f}$
.
The following theorem gives a criterion when a Thurston map f with
![]() $\#{P_f}=4$
is realized.
$\#{P_f}=4$
is realized.
Theorem 3.7. (Thurston’s criterion)
Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map with
$f\colon S^2\rightarrow S^2$
be a Thurston map with
![]() $\#{P_f}=4$
and suppose that f has a hyperbolic orbifold. Then f is realized by a rational map if and only if f has no obstruction.
$\#{P_f}=4$
and suppose that f has a hyperbolic orbifold. Then f is realized by a rational map if and only if f has no obstruction.

Figure 8 The two pullbacks of a curve
![]() $\gamma =\tau _2$
under
$\gamma =\tau _2$
under
![]() $\mathcal {L}_2$
.
$\mathcal {L}_2$
.
With a suitable definition of an obstruction (as an invariant multicurve that satisfies certain mapping properties), this statement is also true for general Thurston maps with a hyperbolic orbifold; see [Reference Douady and HubbardDH93] or [Reference Bonk and MeyerBM17, §2.6].
The example of the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n\colon \mathbb {P}\to \mathbb {P}$
with
$\mathcal {L}_n\colon \mathbb {P}\to \mathbb {P}$
with
![]() $n\ge 2$
shows that Theorem 3.7 is false if f has a parabolic orbifold. Indeed, let
$n\ge 2$
shows that Theorem 3.7 is false if f has a parabolic orbifold. Indeed, let
![]() $\gamma $
be any essential Jordan curve in
$\gamma $
be any essential Jordan curve in
![]() $(\mathbb {P}, P_{\mathcal {L}_n})$
, where
$(\mathbb {P}, P_{\mathcal {L}_n})$
, where
![]() $P_{\mathcal {L}_n}=V=\{A,B,C,D\}$
consists of the vertices of the pillow
$P_{\mathcal {L}_n}=V=\{A,B,C,D\}$
consists of the vertices of the pillow
![]() $\mathbb {P}$
. Since only the isotopy class
$\mathbb {P}$
. Since only the isotopy class
![]() $[\gamma ]$
relative to V matters, by Lemma 2.3, we may assume without loss of generality that
$[\gamma ]$
relative to V matters, by Lemma 2.3, we may assume without loss of generality that
![]() $\gamma =\tau _{r/s}=\wp (\ell _{r/s}(z_0))$
with
$\gamma =\tau _{r/s}=\wp (\ell _{r/s}(z_0))$
with
![]() $z_0\in \mathbb {C}$
,
$z_0\in \mathbb {C}$
,
![]() $r/s\in \widehat {\mathbb {Q}}$
, and
$r/s\in \widehat {\mathbb {Q}}$
, and
![]() $\ell _{r/s}(z_0)\subset \mathbb {C} \smallsetminus \mathbb {Z}^2$
. Here r and s are relatively prime integers and so there exist
$\ell _{r/s}(z_0)\subset \mathbb {C} \smallsetminus \mathbb {Z}^2$
. Here r and s are relatively prime integers and so there exist
![]() $p,q\in \mathbb {Z}$
such that
$p,q\in \mathbb {Z}$
such that
![]() $pr+qs=1$
. Let
$pr+qs=1$
. Let ![]() . Using (2.3) and (3.2), one can verify that under
. Using (2.3) and (3.2), one can verify that under
![]() $\mathcal {L}_n$
, the curve
$\mathcal {L}_n$
, the curve
![]() $\gamma $
has exactly n distinct pullbacks
$\gamma $
has exactly n distinct pullbacks
Moreover, each curve
![]() $\gamma _j$
is isotopic to
$\gamma _j$
is isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() $P_{\mathcal {L}_n}=V$
and
$P_{\mathcal {L}_n}=V$
and
![]() $\deg (\mathcal {L}_n\colon \gamma _j\to \gamma )=n$
for all
$\deg (\mathcal {L}_n\colon \gamma _j\to \gamma )=n$
for all
![]() $j=1,\ldots , n$
; see Figure 8 for an illustration. Thus,
$j=1,\ldots , n$
; see Figure 8 for an illustration. Thus,
![]() $\unicode{x3bb} _{\mathcal {L}_n}(\gamma )=1$
and
$\unicode{x3bb} _{\mathcal {L}_n}(\gamma )=1$
and
![]() $\gamma $
is an obstruction.
$\gamma $
is an obstruction.
4 Blowing up arcs
Here, we describe the operation of ‘blowing up arcs’, originally introduced by Pilgrim and Tan Lei in [Reference Pilgrim and LeiPL98, §2.5]. This operation allows us to define and modify various Thurston maps and plays a crucial role in this paper. We will first describe the general construction and then illustrate it for Lattès maps. As we will explain, the procedure of ‘gluing a flap’ that we introduced in §1.1 can be viewed as a special case of blowing up arcs for Lattès maps.
The construction of blowing up arcs will involve a finite collection E of arcs with pairwise disjoint interiors in a
![]() $2$
-sphere
$2$
-sphere
![]() $S^2$
. We denote by V the set of endpoints of these arcs and consider
$S^2$
. We denote by V the set of endpoints of these arcs and consider
![]() $(V,E)$
as an embedded graph in
$(V,E)$
as an embedded graph in
![]() $S^2$
. In the construction, we will make various topological choices. The following general statement guarantees that we do not run into topological difficulties. In the formulation, we equip
$S^2$
. In the construction, we will make various topological choices. The following general statement guarantees that we do not run into topological difficulties. In the formulation, we equip
![]() $S^2$
with a ‘nice’ metric d so that
$S^2$
with a ‘nice’ metric d so that
![]() $(S^2,d)$
is isometric to
$(S^2,d)$
is isometric to
![]() $\widehat {\mathbb {C}}$
carrying the spherical metric with length element
$\widehat {\mathbb {C}}$
carrying the spherical metric with length element
![]() $ds=2|dz|/(1+|z|^2)$
.
$ds=2|dz|/(1+|z|^2)$
.
Proposition 4.1. Let
![]() $G=(V,E)$
be a planar embedded graph in
$G=(V,E)$
be a planar embedded graph in
![]() $S^2$
and
$S^2$
and
![]() $\mathcal {G}\subset S^2$
be its realization. Then there exists a planar embedded graph
$\mathcal {G}\subset S^2$
be its realization. Then there exists a planar embedded graph
![]() $G'=(V,E')$
in
$G'=(V,E')$
in
![]() $S^2$
with the same vertex set such that its realization
$S^2$
with the same vertex set such that its realization
![]() $\mathcal {G}'$
is isotopic to
$\mathcal {G}'$
is isotopic to
![]() $\mathcal {G}$
relative to V and such that each edge of
$\mathcal {G}$
relative to V and such that each edge of
![]() $G'$
is a piecewise geodesic arc in
$G'$
is a piecewise geodesic arc in
![]() $({S^{2}},d)$
.
$({S^{2}},d)$
.
An outline of the proof is given in [Reference BollobásBol79, Ch. I, §4]; the proposition also follows from [Reference BuserBus10, Lemma A.8].
4.1 The general construction
Before we provide a formal definition, we give some rough idea of how to ‘blow up’ arcs. In the following,
![]() $f\colon {S^{2}}\to {S^{2}}$
is a fixed Thurston map. Let e be an arc in
$f\colon {S^{2}}\to {S^{2}}$
is a fixed Thurston map. Let e be an arc in
![]() ${S^{2}}$
such that the restriction
${S^{2}}$
such that the restriction
![]() $f|e$
is a homeomorphism onto its image. We cut the sphere
$f|e$
is a homeomorphism onto its image. We cut the sphere
![]() ${S^{2}}$
open along e and glue in a closed Jordan region D along the boundary. In this way, we obtain a new
${S^{2}}$
open along e and glue in a closed Jordan region D along the boundary. In this way, we obtain a new
![]() $2$
-sphere on which we can define a branched covering map
$2$
-sphere on which we can define a branched covering map
![]() $\widehat {f}$
as follows:
$\widehat {f}$
as follows:
![]() $\widehat {f}$
maps the complement of
$\widehat {f}$
maps the complement of
![]() $\operatorname {int}(D)$
in the same way as the original map f and it maps
$\operatorname {int}(D)$
in the same way as the original map f and it maps
![]() $\operatorname {int}(D)$
to the complement of
$\operatorname {int}(D)$
to the complement of
![]() $f(e)$
by a homeomorphism that matches the map
$f(e)$
by a homeomorphism that matches the map
![]() $f|e$
. We say that
$f|e$
. We say that
![]() $\widehat {f}$
is obtained from f by blowing up the arc e with multiplicity
$\widehat {f}$
is obtained from f by blowing up the arc e with multiplicity
![]() $1$
.
$1$
.
Now we proceed to give a rigorous definition of the blow-up operation in the general case, where several arcs e are blown up simultaneously with possibly different multiplicities
![]() $m_e\ge 1$
resulting in a new Thurston map
$m_e\ge 1$
resulting in a new Thurston map
![]() $\widehat f$
. To this end, let E be a finite set of arcs in
$\widehat f$
. To this end, let E be a finite set of arcs in
![]() $({S^{2}},f^{-1}({P_f}))$
with pairwise disjoint interiors such that the restriction
$({S^{2}},f^{-1}({P_f}))$
with pairwise disjoint interiors such that the restriction
![]() $f|e\colon e\to f(e)$
is a homeomorphism for each
$f|e\colon e\to f(e)$
is a homeomorphism for each
![]() $e\in E$
. In this case, we say that E satisfies the blow-up conditions.
$e\in E$
. In this case, we say that E satisfies the blow-up conditions.
We assume that each arc
![]() $e\in E$
has an assigned multiplicity
$e\in E$
has an assigned multiplicity
![]() $m_e\in \mathbb {N}$
. Since each
$m_e\in \mathbb {N}$
. Since each
![]() $e\in E$
is an arc in
$e\in E$
is an arc in
![]() $({S^{2}},f^{-1}({P_f}))$
, its interior
$({S^{2}},f^{-1}({P_f}))$
, its interior
![]() $\operatorname {int}(e)$
is disjoint from
$\operatorname {int}(e)$
is disjoint from
![]() $f^{-1}({P_f}) \supset {P_f}$
and so
$f^{-1}({P_f}) \supset {P_f}$
and so
![]() $\operatorname {int}(e)$
does not contain any critical or postcritical point of f.
$\operatorname {int}(e)$
does not contain any critical or postcritical point of f.
For each arc
![]() $e\in E$
, we choose an open Jordan region
$e\in E$
, we choose an open Jordan region
![]() $W_e\subset S^2$
so that the following conditions hold:
$W_e\subset S^2$
so that the following conditions hold:
-
(A1) the open Jordan regions
 $W_e$
,
$W_e$
,
 $e\in E$
, are pairwise disjoint;
$e\in E$
, are pairwise disjoint; -
(A2) for distinct arcs
 $e_1,e_2\in E$
, we have
$e_1,e_2\in E$
, we have
 $\operatorname {cl}{(W_{e_1})} \cap \operatorname {cl}({W_{e_2})}=\partial e_1\cap \partial e_2$
;
$\operatorname {cl}{(W_{e_1})} \cap \operatorname {cl}({W_{e_2})}=\partial e_1\cap \partial e_2$
; -
(A3)
 $\operatorname {int}(e)\subset W_e$
and
$\operatorname {int}(e)\subset W_e$
and
 $\partial e\subset \partial W_e$
for each
$\partial e\subset \partial W_e$
for each
 $e\in E$
;
$e\in E$
; -
(A4)
 $\operatorname {cl}(W_e)\cap f^{-1}({P_f}) = e\cap f^{-1}({P_f})=\partial e$
for each
$\operatorname {cl}(W_e)\cap f^{-1}({P_f}) = e\cap f^{-1}({P_f})=\partial e$
for each
 $e\in E$
;
$e\in E$
; -
(A5)
 $f|\operatorname {cl}(W_{e})$
is a homeomorphism onto its image for each
$f|\operatorname {cl}(W_{e})$
is a homeomorphism onto its image for each
 $e\in E$
.
$e\in E$
.
The existence of such a choice (and also of the choices below) can easily be justified based on Proposition 4.1 and we will skip the details.
Let
![]() $e\in E$
and
$e\in E$
and
![]() $W_e$
be chosen as above. Then we choose a closed Jordan region
$W_e$
be chosen as above. Then we choose a closed Jordan region
![]() $D_e$
so that e is a crosscut in
$D_e$
so that e is a crosscut in
![]() $D_e$
and
$D_e$
and
![]() $D_e\smallsetminus \partial e \subset W_e$
. The two endpoints of e lie on the Jordan curve
$D_e\smallsetminus \partial e \subset W_e$
. The two endpoints of e lie on the Jordan curve
![]() $\partial D_e$
and partition it into two arcs, which we denote by
$\partial D_e$
and partition it into two arcs, which we denote by
![]() $\partial D_e^+$
and
$\partial D_e^+$
and
![]() $\partial D_e^-$
. One can think of
$\partial D_e^-$
. One can think of
![]() $D_e$
as the resulting region if e has been ‘opened up’. This is illustrated in the left and middle parts of Figure 9.
$D_e$
as the resulting region if e has been ‘opened up’. This is illustrated in the left and middle parts of Figure 9.

Figure 9 Setup for blowing up the arcs
![]() $e_1$
and
$e_1$
and
![]() $e_2$
(in the sphere on the left) with the multiplicities
$e_2$
(in the sphere on the left) with the multiplicities
![]() $m_{e_1}=1$
and
$m_{e_1}=1$
and
![]() $m_{e_2}=2$
.
$m_{e_2}=2$
.
To define the desired Thurston map
![]() $\widehat f$
, we want to collapse
$\widehat f$
, we want to collapse
![]() $D_e$
back to e. For this, we choose a continuous map
$D_e$
back to e. For this, we choose a continuous map
![]() $h\colon {S^{2}}\times \mathbb {I}\to {S^{2}}$
with the following properties:
$h\colon {S^{2}}\times \mathbb {I}\to {S^{2}}$
with the following properties:
-
(B1) h is a pseudo-isotopy, that is,
 is a homeomorphism on
is a homeomorphism on
 ${S^{2}}$
for each
${S^{2}}$
for each
 $t\in [0,1)$
;
$t\in [0,1)$
; -
(B2)
 $h_0$
is the identity map on
$h_0$
is the identity map on
 ${S^{2}}$
;
${S^{2}}$
; -
(B3)
 $h_t$
is the identity map on
$h_t$
is the identity map on
 ${S^{2}}\smallsetminus \bigcup _{e\in E}{W_e}$
for each
${S^{2}}\smallsetminus \bigcup _{e\in E}{W_e}$
for each
 $t\in [0,1]$
;
$t\in [0,1]$
; -
(B4)
 $h_1$
is a homeomorphism of
$h_1$
is a homeomorphism of
 $S^2\smallsetminus \bigcup _{e\in E}{D_e}$
onto
$S^2\smallsetminus \bigcup _{e\in E}{D_e}$
onto
 $S^2\smallsetminus \bigcup _{e\in E}{e}$
, and
$S^2\smallsetminus \bigcup _{e\in E}{e}$
, and
 $h_1$
maps
$h_1$
maps
 $\partial D_e^+$
and
$\partial D_e^+$
and
 $\partial D_e^-$
homeomorphically onto e for each
$\partial D_e^-$
homeomorphically onto e for each
 $e\in E$
.
$e\in E$
.
It is easy to see that if we equip
![]() $S^2$
with some metric, then the set
$S^2$
with some metric, then the set
![]() $h_t(D_e)$
Hausdorff converges to e as
$h_t(D_e)$
Hausdorff converges to e as
![]() $t\to 1^-$
. This implies that
$t\to 1^-$
. This implies that
![]() $h_1(D_e)=e$
. So intuitively, the deformation process described by h collapses each closed Jordan region
$h_1(D_e)=e$
. So intuitively, the deformation process described by h collapses each closed Jordan region
![]() $D_e$
to e at time
$D_e$
to e at time
![]() $1$
so that the points in
$1$
so that the points in
![]() ${S^{2}}\smallsetminus \bigcup _{e\in E}{W_e}$
remain fixed.
${S^{2}}\smallsetminus \bigcup _{e\in E}{W_e}$
remain fixed.
We now make yet another choice. For a fixed arc
![]() $e\in E$
, let
$e\in E$
, let
![]() $m=m_e$
. We choose
$m=m_e$
. We choose
![]() ${m-1}$
crosscuts
${m-1}$
crosscuts
![]() $e^1,\ldots ,e^{m-1}$
in
$e^1,\ldots ,e^{m-1}$
in
![]() $D_e$
with the same endpoints as e such that these crosscuts have pairwise disjoint interiors. We set
$D_e$
with the same endpoints as e such that these crosscuts have pairwise disjoint interiors. We set ![]() and
and ![]() . The arcs
. The arcs
![]() $e^0,\ldots ,e^{m}$
subdivide the closed Jordan region
$e^0,\ldots ,e^{m}$
subdivide the closed Jordan region
![]() $D_e$
into m closed Jordan regions
$D_e$
into m closed Jordan regions
![]() $D_e^1, \ldots , D_e^m$
, called components of
$D_e^1, \ldots , D_e^m$
, called components of
![]() $D_e$
. This is illustrated in the right-hand part of Figure 9.
$D_e$
. This is illustrated in the right-hand part of Figure 9.
We may assume that the labeling is such that
![]() $\partial D_e^k=e^{k-1}\cup e^k$
for
$\partial D_e^k=e^{k-1}\cup e^k$
for
![]() $k=1, \ldots , m$
. For each
$k=1, \ldots , m$
. For each
![]() $k=1, \ldots , m$
, we now choose a continuous map
$k=1, \ldots , m$
, we now choose a continuous map
![]() $\varphi _k\colon D_e^k \rightarrow S^2$
with the following properties:
$\varphi _k\colon D_e^k \rightarrow S^2$
with the following properties:
-
(C1)
 $\varphi _k$
is an orientation-preserving homeomorphism of
$\varphi _k$
is an orientation-preserving homeomorphism of
 $\operatorname {int}(D_e^k)$
onto
$\operatorname {int}(D_e^k)$
onto
 $S^2\smallsetminus f(e)$
and maps
$S^2\smallsetminus f(e)$
and maps
 $ e^{k-1}$
and
$ e^{k-1}$
and
 $ e^k$
homeomorphically onto
$ e^k$
homeomorphically onto
 $f(e)$
;
$f(e)$
; -
(C2)
 $\varphi _1|e^0=f\circ h_1|e^0$
,
$\varphi _1|e^0=f\circ h_1|e^0$
,
 $\varphi _m|e^m=f\circ h_1|e^m$
, and
$\varphi _m|e^m=f\circ h_1|e^m$
, and
 $\varphi _k|e^k=\varphi _{k+1}|e^k$
for
$\varphi _k|e^k=\varphi _{k+1}|e^k$
for
 $k=1, \ldots , m-1$
.
$k=1, \ldots , m-1$
.
Note that by the earlier discussion,
![]() $h_1$
maps
$h_1$
maps
![]() $e^0=\partial D^+_e$
and
$e^0=\partial D^+_e$
and
![]() $e^m=\partial D^-_e$
homeomorphically onto e and f is a homeomorphism of e onto
$e^m=\partial D^-_e$
homeomorphically onto e and f is a homeomorphism of e onto
![]() $f(e)$
. These choices of the maps
$f(e)$
. These choices of the maps
![]() $\varphi _k$
depend on e, but we suppress this in our notation for simplicity.
$\varphi _k$
depend on e, but we suppress this in our notation for simplicity.

Figure 10 The map
![]() $\widehat f$
is obtained from f by blowing up the arcs
$\widehat f$
is obtained from f by blowing up the arcs
![]() $e_1$
and
$e_1$
and
![]() $e_2$
with multiplicities
$e_2$
with multiplicities
![]() $m_{e_1}=1$
and
$m_{e_1}=1$
and
![]() $m_{e_2}=2$
.
$m_{e_2}=2$
.
A map
![]() $\widehat {f}\colon {S^{2}}\to {S^{2}}$
can now be defined as follows:
$\widehat {f}\colon {S^{2}}\to {S^{2}}$
can now be defined as follows:
-
(D1) if
 $p\in {S^{2}}\smallsetminus \bigcup _{e\in E} \operatorname {int}(D_e)$
, we set
$p\in {S^{2}}\smallsetminus \bigcup _{e\in E} \operatorname {int}(D_e)$
, we set
 $\widehat {f}(p)=f(h_1(p))$
;
$\widehat {f}(p)=f(h_1(p))$
; -
(D2) if
 $p\in D_e$
for some
$p\in D_e$
for some
 $e\in E$
, then p lies in one of the components
$e\in E$
, then p lies in one of the components
 $D_e^k$
of
$D_e^k$
of
 $D_e$
and we set
$D_e$
and we set
 $\widehat {f}(p)=\varphi _k(p)$
.
$\widehat {f}(p)=\varphi _k(p)$
.
The matching conditions in property (C2) above immediately imply that
![]() $\widehat {f}$
is well defined and continuous.
$\widehat {f}$
is well defined and continuous.
Definition 4.2. We say that the map
![]() $\widehat {f}\colon S^2\rightarrow S^2$
as described above is obtained from the Thurston map f by blowing up each arc
$\widehat {f}\colon S^2\rightarrow S^2$
as described above is obtained from the Thurston map f by blowing up each arc
![]() $e\in E$
with multiplicity
$e\in E$
with multiplicity
![]() $m_e$
.
$m_e$
.
Figure 10 illustrates the construction of
![]() $\widehat {f}$
. Here, we blow up the arcs
$\widehat {f}$
. Here, we blow up the arcs
![]() $e_1$
and
$e_1$
and
![]() $e_2$
from Figure 9 with multiplicities
$e_2$
from Figure 9 with multiplicities
![]() $m_{e_1}=1$
and
$m_{e_1}=1$
and
![]() $m_{e_2}=2$
. The arcs
$m_{e_2}=2$
. The arcs
![]() $f(e_1)$
and
$f(e_1)$
and
![]() $f(e_2)$
share an endpoint (since
$f(e_2)$
share an endpoint (since
![]() $e_1$
and
$e_1$
and
![]() $e_2$
do), but in general, they could have more points in common or even coincide. For simplicity, we chose to draw them with disjoint interiors.
$e_2$
do), but in general, they could have more points in common or even coincide. For simplicity, we chose to draw them with disjoint interiors.
By construction,
![]() $\widehat f$
acts in a similar way as f outside the closed Jordan regions
$\widehat f$
acts in a similar way as f outside the closed Jordan regions
![]() ${D_{e_1}=D^1_{e_1}}$
and
${D_{e_1}=D^1_{e_1}}$
and
![]() $D_{e_2}=D^1_{e_2}\cup D^2_{e_2}$
. More precisely, the map
$D_{e_2}=D^1_{e_2}\cup D^2_{e_2}$
. More precisely, the map
![]() $\widehat f$
equals
$\widehat f$
equals
![]() $f \circ h_1$
on
$f \circ h_1$
on
![]() ${S^{2}}{\kern-1pt}\smallsetminus{\kern-1pt} (\operatorname {int}({\kern-0.5pt}D_{e_1}{\kern-0.5pt}) {\kern-1pt}\cup{\kern-1pt} \operatorname {int}(D_{e_2}{\kern-0.5pt}))$
, where
${S^{2}}{\kern-1pt}\smallsetminus{\kern-1pt} (\operatorname {int}({\kern-0.5pt}D_{e_1}{\kern-0.5pt}) {\kern-1pt}\cup{\kern-1pt} \operatorname {int}(D_{e_2}{\kern-0.5pt}))$
, where
![]() $h_1$
collapses the closed Jordan regions
$h_1$
collapses the closed Jordan regions
![]() $D_{e_1}$
and
$D_{e_1}$
and
![]() $D_{e_2}$
onto
$D_{e_2}$
onto
![]() $e_1$
and
$e_1$
and
![]() $e_2$
, respectively. At the same time,
$e_2$
, respectively. At the same time,
![]() $\widehat f$
maps
$\widehat f$
maps
![]() $\operatorname {int}(D_{e_1})$
homeomorphically onto
$\operatorname {int}(D_{e_1})$
homeomorphically onto
![]() ${S^{2}}\smallsetminus f(e_1)$
, and each of the regions
${S^{2}}\smallsetminus f(e_1)$
, and each of the regions
![]() $\operatorname {int}(D^1_{e_2})$
and
$\operatorname {int}(D^1_{e_2})$
and
![]() $\operatorname {int}(D^2_{e_2})$
homeomorphically onto
$\operatorname {int}(D^2_{e_2})$
homeomorphically onto
![]() ${S^{2}}\smallsetminus f(e_2)$
.
${S^{2}}\smallsetminus f(e_2)$
.
In the next section, we want to relate ‘blowing up arcs’ with ‘gluing flaps’ as discussed in the introduction. To set this up, we consider the
![]() $(2\times 2)$
-Lattès map
$(2\times 2)$
-Lattès map
![]() $f=\mathcal {L}_2$
. We choose two edges
$f=\mathcal {L}_2$
. We choose two edges
![]() $e_1$
and
$e_1$
and
![]() $e_2$
of a
$e_2$
of a
![]() $1$
-tile in
$1$
-tile in
![]() $\mathbb {P}$
as shown in the pillow on the left in Figure 11. Note that f sends
$\mathbb {P}$
as shown in the pillow on the left in Figure 11. Note that f sends
![]() $e_1$
and
$e_1$
and
![]() $e_2$
homeomorphically onto the edges c and b of
$e_2$
homeomorphically onto the edges c and b of
![]() $\mathbb {P}$
, respectively. Thus, the set
$\mathbb {P}$
, respectively. Thus, the set
![]() $E=\{e_1,e_2\}$
satisfies the blow-up conditions. Figure 11 illustrates the setup for blowing up these arcs
$E=\{e_1,e_2\}$
satisfies the blow-up conditions. Figure 11 illustrates the setup for blowing up these arcs
![]() $e_1$
and
$e_1$
and
![]() $e_2$
with the multiplicities
$e_2$
with the multiplicities
![]() $m_{e_1}=1$
and
$m_{e_1}=1$
and
![]() $m_{e_2}=2$
. The resulting map
$m_{e_2}=2$
. The resulting map
![]() $\widehat f\colon \mathbb {P}\to \mathbb {P}$
is shown in Figure 12. The points marked by a dot on the left pillow
$\widehat f\colon \mathbb {P}\to \mathbb {P}$
is shown in Figure 12. The points marked by a dot on the left pillow
![]() $\mathbb {P}$
(the domain of the map) correspond to the preimage points
$\mathbb {P}$
(the domain of the map) correspond to the preimage points
![]() $\widehat f^{-1}(V)$
. The pillow on the left is subdivided into closed Jordan regions alternately colored black and white. The map
$\widehat f^{-1}(V)$
. The pillow on the left is subdivided into closed Jordan regions alternately colored black and white. The map
![]() $\widehat f$
sends each of these closed Jordan regions U homeomorphically onto the back side or front side of the pillow
$\widehat f$
sends each of these closed Jordan regions U homeomorphically onto the back side or front side of the pillow
![]() $\mathbb {P}$
depending on whether U is black or white.
$\mathbb {P}$
depending on whether U is black or white.

Figure 11 Setup for blowing up the arc set
![]() $E=\{e_1, e_2\}$
(on the left pillow) with
$E=\{e_1, e_2\}$
(on the left pillow) with
![]() $m_{e_1}=1$
and
$m_{e_1}=1$
and
![]() $m_{e_2}=2$
.
$m_{e_2}=2$
.

Figure 12 The map
![]() $\widehat {f}$
obtained from
$\widehat {f}$
obtained from
![]() $f=\mathcal {L}_2$
by blowing up the arcs in the set
$f=\mathcal {L}_2$
by blowing up the arcs in the set
![]() $E=\{e_1, e_2\}$
illustrated in Figure 11 with
$E=\{e_1, e_2\}$
illustrated in Figure 11 with
![]() $m_{e_1}=1$
and
$m_{e_1}=1$
and
![]() $m_{e_2}=2$
.
$m_{e_2}=2$
.
The following statement summarizes the main properties of maps
![]() $\widehat {f}$
as in Definition 4.2.
$\widehat {f}$
as in Definition 4.2.
Lemma 4.3. Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map and E be a set of arcs in
$f\colon S^2\rightarrow S^2$
be a Thurston map and E be a set of arcs in
![]() $(S^2, f^{-1}({P_f}))$
satisfying the blow-up conditions. Suppose
$(S^2, f^{-1}({P_f}))$
satisfying the blow-up conditions. Suppose
![]() $\widehat {f}\colon S^2\rightarrow S^2$
is the map obtained by blowing up each arc
$\widehat {f}\colon S^2\rightarrow S^2$
is the map obtained by blowing up each arc
![]() $e\in E$
with multiplicity
$e\in E$
with multiplicity
![]() $m_e\in \mathbb {N}$
.
$m_e\in \mathbb {N}$
.
Then
![]() $\widehat f$
is a Thurston map with
$\widehat f$
is a Thurston map with
![]() $P_{\widehat f}={P_f}$
. Moreover, the map
$P_{\widehat f}={P_f}$
. Moreover, the map
![]() $\widehat f$
is uniquely determined up to Thurston equivalence independently of the choices in the above construction. More precisely, up to Thurston equivalence
$\widehat f$
is uniquely determined up to Thurston equivalence independently of the choices in the above construction. More precisely, up to Thurston equivalence
![]() $\widehat f$
depends only on the original map f, the isotopy classes of the arcs in E relative to
$\widehat f$
depends only on the original map f, the isotopy classes of the arcs in E relative to
![]() $f^{-1}({P_f})$
, and the multiplicities
$f^{-1}({P_f})$
, and the multiplicities
![]() $m_e$
for
$m_e$
for
![]() $e\in E$
.
$e\in E$
.
Proof. By construction,
![]() $\widehat f$
is an orientation-preserving local homeomorphism near each point
$\widehat f$
is an orientation-preserving local homeomorphism near each point
![]() $p\in S^2\smallsetminus f^{-1}({P_f})$
. By considering the number of preimages of a generic point in
$p\in S^2\smallsetminus f^{-1}({P_f})$
. By considering the number of preimages of a generic point in
![]() $S^2$
, we see that the topological degree of
$S^2$
, we see that the topological degree of
![]() $\widehat {f}$
is equal to
$\widehat {f}$
is equal to
![]() $\deg (f)+ \sum _{e\in E} m_{e}>0.$
The fact that
$\deg (f)+ \sum _{e\in E} m_{e}>0.$
The fact that
![]() $\widehat {f}\colon {S^{2}}\to {S^{2}}$
is a branched covering map can now be deduced from [Reference Bonk and MeyerBM17, Corollary A.14].
$\widehat {f}\colon {S^{2}}\to {S^{2}}$
is a branched covering map can now be deduced from [Reference Bonk and MeyerBM17, Corollary A.14].
We have
![]() $\deg (\widehat f, p)=1$
for
$\deg (\widehat f, p)=1$
for
![]() $p\in S^2\smallsetminus f^{-1}({P_f})$
and
$p\in S^2\smallsetminus f^{-1}({P_f})$
and
 $$ \begin{align*}\deg(\widehat f, p) =\deg(f,p)+ \sum_{\{e\in E:\ p\in e\}} m_e \end{align*} $$
$$ \begin{align*}\deg(\widehat f, p) =\deg(f,p)+ \sum_{\{e\in E:\ p\in e\}} m_e \end{align*} $$
for
![]() $p\in f^{-1}({P_f})$
. This implies
$p\in f^{-1}({P_f})$
. This implies
![]() ${C_f} \subset C_{\widehat f} \subset f^{-1}({P_f})$
. Since on the set
${C_f} \subset C_{\widehat f} \subset f^{-1}({P_f})$
. Since on the set
![]() $f^{-1}({P_f})$
the maps f and
$f^{-1}({P_f})$
the maps f and
![]() $\widehat f$
agree, it follows that
$\widehat f$
agree, it follows that
![]() $P_{\widehat f}={P_f}$
. So
$P_{\widehat f}={P_f}$
. So
![]() $\widehat f$
has a finite postcritical set, and we conclude that
$\widehat f$
has a finite postcritical set, and we conclude that
![]() $\widehat f$
is indeed a Thurston map.
$\widehat f$
is indeed a Thurston map.
We omit a detailed justification of the second claim that
![]() $\widehat f$
is uniquely determined up to Thurston equivalence by f, the isotopy classes of the arcs E, and their multiplicities. A proof can be given along the lines of [Reference Pilgrim and LeiPL98, Proposition 2].
$\widehat f$
is uniquely determined up to Thurston equivalence by f, the isotopy classes of the arcs E, and their multiplicities. A proof can be given along the lines of [Reference Pilgrim and LeiPL98, Proposition 2].
Remark 4.4. If in the previous statement
![]() $E\ne \emptyset $
and
$E\ne \emptyset $
and
![]() $\# P_f\ge 3$
, then
$\# P_f\ge 3$
, then
![]() $\widehat f$
has a hyperbolic orbifold. To see this, pick an arc
$\widehat f$
has a hyperbolic orbifold. To see this, pick an arc
![]() $e\in E$
. Then
$e\in E$
. Then
![]() $f(e)$
has at most two points in common with
$f(e)$
has at most two points in common with
![]() $P_f$
, and so we can find a point
$P_f$
, and so we can find a point
![]() $p\in P_f\smallsetminus f(e)\subset P_{\widehat f}$
. Then it follows from the construction of
$p\in P_f\smallsetminus f(e)\subset P_{\widehat f}$
. Then it follows from the construction of
![]() $\widehat f$
that there exists a point q in the interior of the region
$\widehat f$
that there exists a point q in the interior of the region
![]() $D_e$
associated with e such that
$D_e$
associated with e such that
![]() $\widehat f(q)=p$
and
$\widehat f(q)=p$
and
![]() $\deg (\widehat f, q)=1$
. Then
$\deg (\widehat f, q)=1$
. Then
![]() $q\not \in C_{\widehat f}$
, but we also have
$q\not \in C_{\widehat f}$
, but we also have
This shows that
![]() $q\in \widehat f^{-1}(p)\subset \widehat f^{-1}(P_{\widehat f})$
, but
$q\in \widehat f^{-1}(p)\subset \widehat f^{-1}(P_{\widehat f})$
, but
![]() $q\not \in C_{\widehat f}\cup P_{\widehat f}$
, and so
$q\not \in C_{\widehat f}\cup P_{\widehat f}$
, and so
![]() $\widehat f$
must have a hyperbolic orbifold by the first part of Lemma 3.3.
$\widehat f$
must have a hyperbolic orbifold by the first part of Lemma 3.3.
4.2 Blowing up the
 $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
Let
![]() $\mathbb {P}$
be the Euclidean square pillow and
$\mathbb {P}$
be the Euclidean square pillow and
![]() $ \mathcal {L}_n\colon \mathbb {P}\to \mathbb {P}$
be the
$ \mathcal {L}_n\colon \mathbb {P}\to \mathbb {P}$
be the
![]() $(n\times n)$
-Lattès map for fixed
$(n\times n)$
-Lattès map for fixed
![]() $n\geq 2$
. We denote by
$n\geq 2$
. We denote by
![]() $\mathcal {C}\subset \mathbb {P}$
the common boundary of the two sides of
$\mathcal {C}\subset \mathbb {P}$
the common boundary of the two sides of
![]() $\mathbb {P}$
. The set
$\mathbb {P}$
. The set
![]() $\mathcal {C}$
may be viewed as a planar embedded graph with the vertex set
$\mathcal {C}$
may be viewed as a planar embedded graph with the vertex set
![]() $V= \{A,B,C,D\}$
and the edge set
$V= \{A,B,C,D\}$
and the edge set
![]() $\{a, b,c,d\}$
in the notation from §2.4. Let
$\{a, b,c,d\}$
in the notation from §2.4. Let ![]() be the preimage of
be the preimage of
![]() $\mathcal {C}$
under
$\mathcal {C}$
under
![]() $\mathcal {L}_n$
, viewed as a planar embedded graph with the vertex set
$\mathcal {L}_n$
, viewed as a planar embedded graph with the vertex set
![]() $\mathcal {L}_n^{-1}(V)$
. In the next section, we will study the question whether a Thurston map is realized by a rational map if it is obtained from
$\mathcal {L}_n^{-1}(V)$
. In the next section, we will study the question whether a Thurston map is realized by a rational map if it is obtained from
![]() $\mathcal {L}_n$
by blowing up edges of
$\mathcal {L}_n$
by blowing up edges of
![]() $\widetilde {\mathcal {C}}$
. To facilitate this discussion, we will provide a more concrete combinatorial model for these maps.
$\widetilde {\mathcal {C}}$
. To facilitate this discussion, we will provide a more concrete combinatorial model for these maps.
By the definition of the map
![]() $\mathcal {L}_n$
, the graph
$\mathcal {L}_n$
, the graph
![]() $\widetilde {\mathcal {C}}$
subdivides the pillow
$\widetilde {\mathcal {C}}$
subdivides the pillow
![]() $\mathbb {P}$
into
$\mathbb {P}$
into
![]() $2n^2$
$2n^2$
![]() $1$
-tiles, which are squares of sidelength
$1$
-tiles, which are squares of sidelength
![]() $1/n$
. The edges of the embedded graph
$1/n$
. The edges of the embedded graph
![]() $\widetilde {\mathcal {C}}$
are precisely the sides of these squares. We call them the
$\widetilde {\mathcal {C}}$
are precisely the sides of these squares. We call them the
![]() $1$
-edges of
$1$
-edges of
![]() $\mathbb {P}$
(for given n). The map
$\mathbb {P}$
(for given n). The map
![]() $\mathcal {L}_n$
sends each
$\mathcal {L}_n$
sends each
![]() $1$
-edge e of
$1$
-edge e of
![]() $\mathbb {P}$
homeomorphically onto one of the edges a, b, c, d of
$\mathbb {P}$
homeomorphically onto one of the edges a, b, c, d of
![]() $\mathcal {C}$
. We call e horizontal if
$\mathcal {C}$
. We call e horizontal if
![]() $\mathcal {L}_n$
maps it onto a or c, and vertical if
$\mathcal {L}_n$
maps it onto a or c, and vertical if
![]() $\mathcal {L}_n$
maps it onto b or d.
$\mathcal {L}_n$
maps it onto b or d.
We take two disjoint copies of the Euclidean square
![]() $[0,1/n]^2\subset \mathbb {R}^2$
and identify the points on three of their sides, say the sides
$[0,1/n]^2\subset \mathbb {R}^2$
and identify the points on three of their sides, say the sides
![]() $\{0\}\times [0, 1/n]$
,
$\{0\}\times [0, 1/n]$
,
![]() $[0,1/n] \times \{1/n\}$
, and
$[0,1/n] \times \{1/n\}$
, and
![]() $\{1/n\}\times [0,1/n]$
. We call the object obtained a flap F. Note that it is homeomorphic to the closed unit disk and has two ‘free’ sides corresponding to the two copies of
$\{1/n\}\times [0,1/n]$
. We call the object obtained a flap F. Note that it is homeomorphic to the closed unit disk and has two ‘free’ sides corresponding to the two copies of
![]() $[0,1/n] \times \{0\}$
in F.
$[0,1/n] \times \{0\}$
in F.
We can cut the pillow
![]() $\mathbb {P}$
open along one of the edges of
$\mathbb {P}$
open along one of the edges of
![]() $\widetilde {\mathcal {C}}$
and glue in a flap F to the pillow by identifying each copy of
$\widetilde {\mathcal {C}}$
and glue in a flap F to the pillow by identifying each copy of
![]() $[0,1/n]\times \{0\}$
in the flap with one side of the slit by an isometry (see Figure 2). In this way, we get a new polyhedral surface homeomorphic to
$[0,1/n]\times \{0\}$
in the flap with one side of the slit by an isometry (see Figure 2). In this way, we get a new polyhedral surface homeomorphic to
![]() ${S^{2}}$
. One can also glue multiple copies of the flap to the slit by an isometry and obtain a polyhedral surface
${S^{2}}$
. One can also glue multiple copies of the flap to the slit by an isometry and obtain a polyhedral surface
![]() $\widehat {\mathbb {P}}$
homeomorphic to
$\widehat {\mathbb {P}}$
homeomorphic to
![]() ${S^{2}}$
. This can be described more concretely as follows. Let e be an edge in
${S^{2}}$
. This can be described more concretely as follows. Let e be an edge in
![]() $\widetilde {\mathcal {C}}$
and
$\widetilde {\mathcal {C}}$
and
![]() $F_1, \ldots , F_m$
be
$F_1, \ldots , F_m$
be
![]() $m\geq 1$
copies of the flap. For each
$m\geq 1$
copies of the flap. For each
![]() $k=1,\ldots ,m$
, we denote the two copies of
$k=1,\ldots ,m$
, we denote the two copies of
![]() $[0,1/n]\times \{0\}$
in the flap
$[0,1/n]\times \{0\}$
in the flap
![]() $F_k$
by
$F_k$
by
![]() $e_k'$
and
$e_k'$
and
![]() $e_k"$
. We now construct a new polyhedral surface
$e_k"$
. We now construct a new polyhedral surface
![]() $\widehat {\mathbb {P}}$
in the following way.
$\widehat {\mathbb {P}}$
in the following way.
-
(i) First, we cut the original pillow
 $\mathbb {P}$
open along the edge e.
$\mathbb {P}$
open along the edge e. -
(ii) Then, for each
 $k=1,\ldots , m-1$
, we identify the edge
$k=1,\ldots , m-1$
, we identify the edge
 $e_k"$
of
$e_k"$
of
 $F_k$
with the edge
$F_k$
with the edge
 $e_{k+1}'$
of
$e_{k+1}'$
of
 $F_{k+1}$
by an isometry. We get a polyhedral surface
$F_{k+1}$
by an isometry. We get a polyhedral surface
 $D_e$
homeomorphic to a closed disk, whose boundary consists of two edges
$D_e$
homeomorphic to a closed disk, whose boundary consists of two edges
 $e_1'$
and
$e_1'$
and
 $e_m"$
.
$e_m"$
. -
(iii) Finally, we glue the disk
 $D_e$
to the pillow
$D_e$
to the pillow
 $\mathbb {P}$
cut open along e by identifying the edges
$\mathbb {P}$
cut open along e by identifying the edges
 $e_1'$
and
$e_1'$
and
 $e_m"$
in
$e_m"$
in
 $\partial D_e$
with the two sides of the slit by an isometry so that
$\partial D_e$
with the two sides of the slit by an isometry so that
 $e_1'$
and
$e_1'$
and
 $e_m"$
are identified with different sides of the slit. We obtain a polyhedral surface
$e_m"$
are identified with different sides of the slit. We obtain a polyhedral surface
 $\widehat {\mathbb {P}}$
that is homeomorphic to a
$\widehat {\mathbb {P}}$
that is homeomorphic to a
 $2$
-sphere.
$2$
-sphere.
More generally, we can cut open
![]() $\mathbb {P}$
simultaneously along several edges e of
$\mathbb {P}$
simultaneously along several edges e of
![]() $\widetilde {\mathcal {C}}$
and, by the method described, glue
$\widetilde {\mathcal {C}}$
and, by the method described, glue
![]() $m_e\in \mathbb {N}$
copies of the flap to the slit obtained from each edge e. If these edges e of
$m_e\in \mathbb {N}$
copies of the flap to the slit obtained from each edge e. If these edges e of
![]() $\widetilde {\mathcal {C}}$
with their multiplicities
$\widetilde {\mathcal {C}}$
with their multiplicities
![]() $m_e$
are given, then there is essentially only one way of gluing flaps so that the resulting object is a polyhedral surface homeomorphic to
$m_e$
are given, then there is essentially only one way of gluing flaps so that the resulting object is a polyhedral surface homeomorphic to
![]() ${S^{2}}$
.
${S^{2}}$
.
Let
![]() $\widehat {\mathbb {P}}$
be the polyhedral surface obtained from
$\widehat {\mathbb {P}}$
be the polyhedral surface obtained from
![]() $\mathbb {P}$
by gluing a total number of
$\mathbb {P}$
by gluing a total number of
![]() $n_h\geq 0$
horizontal flaps (that is, flaps glued along horizontal edges of
$n_h\geq 0$
horizontal flaps (that is, flaps glued along horizontal edges of
![]() $\widetilde {\mathcal {C}}$
) and a total number of
$\widetilde {\mathcal {C}}$
) and a total number of
![]() $n_v\geq 0 $
vertical flaps (that is, flaps glued along vertical edges of
$n_v\geq 0 $
vertical flaps (that is, flaps glued along vertical edges of
![]() $\widetilde {\mathcal {C}}$
). We call this surface a flapped pillow. We denote by E the set of all edges in
$\widetilde {\mathcal {C}}$
). We call this surface a flapped pillow. We denote by E the set of all edges in
![]() $\widetilde {\mathcal {C}}$
along which flaps were glued and by
$\widetilde {\mathcal {C}}$
along which flaps were glued and by
![]() $m_e$
,
$m_e$
,
![]() $e\in E$
, the corresponding multiplicities. See the left part of Figure 13 for an example of a flapped pillow
$e\in E$
, the corresponding multiplicities. See the left part of Figure 13 for an example of a flapped pillow
![]() $\widehat {\mathbb {P}}$
obtained by gluing one horizontal and two vertical flaps at the edges
$\widehat {\mathbb {P}}$
obtained by gluing one horizontal and two vertical flaps at the edges
![]() $e_1$
and
$e_1$
and
![]() $e_2$
from Figure 11.
$e_2$
from Figure 11.

Figure 13 A branched covering map
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}}\rightarrow \mathbb {P}$
induced by the flapped pillow
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}}\rightarrow \mathbb {P}$
induced by the flapped pillow
![]() $\widehat {\mathbb {P}}$
on the left.
$\widehat {\mathbb {P}}$
on the left.
The polyhedral surface
![]() $\widehat {\mathbb {P}}$
is naturally subdivided into
$\widehat {\mathbb {P}}$
is naturally subdivided into
squares of sidelength
![]() $1/n$
, called the
$1/n$
, called the
![]() $1$
-tiles of the flapped pillow
$1$
-tiles of the flapped pillow
![]() $\widehat {\mathbb {P}}$
. The vertices and the edges of these squares are called the
$\widehat {\mathbb {P}}$
. The vertices and the edges of these squares are called the
![]() $1$
-vertices and
$1$
-vertices and
![]() $1$
-edges of
$1$
-edges of
![]() $\widehat {\mathbb {P}}$
. There is a natural path metric on
$\widehat {\mathbb {P}}$
. There is a natural path metric on
![]() $\widehat {\mathbb {P}}$
that agrees with the Euclidean metric on each
$\widehat {\mathbb {P}}$
that agrees with the Euclidean metric on each
![]() $1$
-tile. The surface
$1$
-tile. The surface
![]() $\widehat {\mathbb {P}}$
equipped with this metric is locally Euclidean with conic singularities at some of the
$\widehat {\mathbb {P}}$
equipped with this metric is locally Euclidean with conic singularities at some of the
![]() $1$
-vertices. Such a conic singularity arises at a
$1$
-vertices. Such a conic singularity arises at a
![]() $1$
-vertex
$1$
-vertex
![]() $v\in \widehat {\mathbb {P}}$
if v is contained in
$v\in \widehat {\mathbb {P}}$
if v is contained in
![]() $k_v\ne 4$
distinct
$k_v\ne 4$
distinct
![]() $1$
-tiles.
$1$
-tiles.
We will assume that
![]() $\widehat {\mathbb {P}}$
has at least one flap, that is,
$\widehat {\mathbb {P}}$
has at least one flap, that is,
![]() $n_h+n_v\geq 1$
. Let
$n_h+n_v\geq 1$
. Let
![]() $F_j$
,
$F_j$
,
![]() $j=1,\ldots , n_h+n_v$
, be the collection of flaps glued to
$j=1,\ldots , n_h+n_v$
, be the collection of flaps glued to
![]() $\mathbb {P}$
. Each flap
$\mathbb {P}$
. Each flap
![]() $F_j$
consists of two
$F_j$
consists of two
![]() $1$
-tiles in
$1$
-tiles in
![]() $\widehat {\mathbb {P}}$
. We call the four
$\widehat {\mathbb {P}}$
. We call the four
![]() $1$
-vertices that belong to
$1$
-vertices that belong to
![]() $F_j$
the vertices of the flap
$F_j$
the vertices of the flap
![]() $F_j$
. The boundary
$F_j$
. The boundary
![]() $\partial F_j$
is a Jordan curve in
$\partial F_j$
is a Jordan curve in
![]() $\widehat {\mathbb {P}}$
composed of two
$\widehat {\mathbb {P}}$
composed of two
![]() $1$
-edges
$1$
-edges
![]() $e^{\prime }_j$
and
$e^{\prime }_j$
and
![]() $e^{\prime \prime }_j$
, which we call the base edges of
$e^{\prime \prime }_j$
, which we call the base edges of
![]() $F_j$
. The
$F_j$
. The
![]() $1$
-edge in
$1$
-edge in
![]() $F_j$
that is opposite to the base edges is called the top edge of the flap
$F_j$
that is opposite to the base edges is called the top edge of the flap
![]() $F_j$
. Note that
$F_j$
. Note that
![]() $\partial e^{\prime }_j=\partial e^{\prime \prime }_j$
consists of two vertices of
$\partial e^{\prime }_j=\partial e^{\prime \prime }_j$
consists of two vertices of
![]() $F_j$
.
$F_j$
.
We now define the base
![]() $B(\widehat {\mathbb {P}})\subset \widehat {\mathbb {P}}$
of the flapped pillow as
$B(\widehat {\mathbb {P}})\subset \widehat {\mathbb {P}}$
of the flapped pillow as

In other words,
![]() $B(\widehat {\mathbb {P}})$
is obtained from
$B(\widehat {\mathbb {P}})$
is obtained from
![]() $\widehat {\mathbb {P}}$
by removing all flaps
$\widehat {\mathbb {P}}$
by removing all flaps
![]() $F_j$
from
$F_j$
from
![]() $\widehat {\mathbb {P}}$
, except that we keep the two vertices in
$\widehat {\mathbb {P}}$
, except that we keep the two vertices in
![]() $\partial e^{\prime }_j\subset F_j$
from each flap. There is a natural identification
$\partial e^{\prime }_j\subset F_j$
from each flap. There is a natural identification
This means that we can consider the base
![]() $B(\widehat {\mathbb {P}})$
both as a subset of
$B(\widehat {\mathbb {P}})$
both as a subset of
![]() $\widehat {\mathbb {P}}$
and of
$\widehat {\mathbb {P}}$
and of
![]() $\mathbb {P}$
. Figure 14 illustrates these two viewpoints. This is slightly imprecise, but this point of view will be extremely convenient in the following.
$\mathbb {P}$
. Figure 14 illustrates these two viewpoints. This is slightly imprecise, but this point of view will be extremely convenient in the following.

Figure 14 The base
![]() $B(\widehat {\mathbb {P}})$
of the flapped pillow
$B(\widehat {\mathbb {P}})$
of the flapped pillow
![]() $\widehat {\mathbb {P}}$
from Figure 13 depicted in two different ways: as a subset of
$\widehat {\mathbb {P}}$
from Figure 13 depicted in two different ways: as a subset of
![]() $\widehat {\mathbb {P}}$
and as the subset
$\widehat {\mathbb {P}}$
and as the subset
![]() $\mathbb {P}\smallsetminus \bigcup _{e\in E} \operatorname {int}(e)$
of
$\mathbb {P}\smallsetminus \bigcup _{e\in E} \operatorname {int}(e)$
of
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
We choose the orientation on
![]() $\widehat {\mathbb {P}}$
so that the induced orientation on
$\widehat {\mathbb {P}}$
so that the induced orientation on
![]() $B(\widehat {\mathbb {P}})$
considered as a subset of
$B(\widehat {\mathbb {P}})$
considered as a subset of
![]() $\widehat {\mathbb {P}}$
coincides with the orientation on
$\widehat {\mathbb {P}}$
coincides with the orientation on
![]() $B(\widehat {\mathbb {P}})$
considered as a subset of the oriented sphere
$B(\widehat {\mathbb {P}})$
considered as a subset of the oriented sphere
![]() $\mathbb {P}$
(if we represent orientations on surfaces by flags, as described in [Reference Bonk and MeyerBM17, §A.4], then we simply pick a positively oriented flag contained in
$\mathbb {P}$
(if we represent orientations on surfaces by flags, as described in [Reference Bonk and MeyerBM17, §A.4], then we simply pick a positively oriented flag contained in
![]() $B(\widehat {\mathbb {P}})\subset \mathbb {P}$
and declare it to be positively oriented in
$B(\widehat {\mathbb {P}})\subset \mathbb {P}$
and declare it to be positively oriented in
![]() $\widehat {\mathbb {P}}\supset B(\widehat {\mathbb {P}})$
).
$\widehat {\mathbb {P}}\supset B(\widehat {\mathbb {P}})$
).
The set
![]() $ B(\widehat {\mathbb {P}})\cong \mathbb {P}\smallsetminus \bigcup _{e\in E} \operatorname {int}(e)$
contains the vertex set
$ B(\widehat {\mathbb {P}})\cong \mathbb {P}\smallsetminus \bigcup _{e\in E} \operatorname {int}(e)$
contains the vertex set
![]() $\mathcal {L}_n^{-1}(V)\subset \mathbb {P}$
of the graph
$\mathcal {L}_n^{-1}(V)\subset \mathbb {P}$
of the graph
![]() $ {\widetilde {\mathcal {C}} =\mathcal {L}_n^{-1}(\mathcal {C})\subset \mathbb {P}}$
. This means that we can naturally view each vertex of
$ {\widetilde {\mathcal {C}} =\mathcal {L}_n^{-1}(\mathcal {C})\subset \mathbb {P}}$
. This means that we can naturally view each vertex of
![]() $\widetilde {\mathcal {C}} $
also as a
$\widetilde {\mathcal {C}} $
also as a
![]() $1$
-vertex in
$1$
-vertex in
![]() $\widehat {\mathbb {P}}$
. Let
$\widehat {\mathbb {P}}$
. Let
![]() $\widehat {A},\,\widehat {B},\, \widehat {C},\,\widehat {D}$
be the
$\widehat {A},\,\widehat {B},\, \widehat {C},\,\widehat {D}$
be the
![]() $1$
-vertices of
$1$
-vertices of
![]() $\widehat {\mathbb {P}}$
that correspond to the vertices
$\widehat {\mathbb {P}}$
that correspond to the vertices
![]() $A,\,B,\,C,\,D$
of the original pillow, respectively. We set
$A,\,B,\,C,\,D$
of the original pillow, respectively. We set ![]() and call
and call
![]() $\widehat {A},\,\widehat {B},\,\widehat {C},\,\widehat {D}$
the vertices of
$\widehat {A},\,\widehat {B},\,\widehat {C},\,\widehat {D}$
the vertices of
![]() $\widehat {\mathbb {P}}$
.
$\widehat {\mathbb {P}}$
.
Recall from §3.1 that the faces of the embedded graph
![]() $\widetilde {\mathcal {C}}\subset \mathbb {P}$
are colored black and white in a checkerboard manner. This coloring induces a checkerboard coloring on the
$\widetilde {\mathcal {C}}\subset \mathbb {P}$
are colored black and white in a checkerboard manner. This coloring induces a checkerboard coloring on the
![]() $1$
-tiles of the flapped pillow
$1$
-tiles of the flapped pillow
![]() $\widehat {\mathbb {P}}$
. The original map
$\widehat {\mathbb {P}}$
. The original map
![]() $ \mathcal {L}_n\colon \mathbb {P}\to \mathbb {P}$
can now be naturally extended to a continuous map
$ \mathcal {L}_n\colon \mathbb {P}\to \mathbb {P}$
can now be naturally extended to a continuous map
![]() $\widehat { \mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
by reflection so that it preserves the coloring:
$\widehat { \mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
by reflection so that it preserves the coloring:
![]() $\widehat { \mathcal {L}}$
maps each
$\widehat { \mathcal {L}}$
maps each
![]() $1$
-tile of
$1$
-tile of
![]() $\widehat {\mathbb {P}}$
by a Euclidean similarity (scaling distances by the factor n) onto the
$\widehat {\mathbb {P}}$
by a Euclidean similarity (scaling distances by the factor n) onto the
![]() $0$
-tile of
$0$
-tile of
![]() $\mathbb {P}$
with the same color; see Figure 13 for an illustration. On the base
$\mathbb {P}$
with the same color; see Figure 13 for an illustration. On the base
![]() $B(\widehat {\mathbb {P}})$
, the map
$B(\widehat {\mathbb {P}})$
, the map
![]() $\widehat {\mathcal {L}}$
agrees with the original
$\widehat {\mathcal {L}}$
agrees with the original
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
(if we consider
$\mathcal {L}_n$
(if we consider
![]() $B(\widehat {\mathbb {P}})$
as a subset of
$B(\widehat {\mathbb {P}})$
as a subset of
![]() $\mathbb {P}$
by the identification in (4.2)).
$\mathbb {P}$
by the identification in (4.2)).
It is clear that
![]() $\widehat { \mathcal {L}}\colon \widehat {\mathbb {P}}\rightarrow \mathbb {P}$
is a branched covering map. This map is essentially the Thurston map obtained from
$\widehat { \mathcal {L}}\colon \widehat {\mathbb {P}}\rightarrow \mathbb {P}$
is a branched covering map. This map is essentially the Thurston map obtained from
![]() $\mathcal {L}_n$
by blowing up each arc
$\mathcal {L}_n$
by blowing up each arc
![]() $e\in E$
with multiplicity
$e\in E$
with multiplicity
![]() $m_e$
. To make this more precise, we need a suitable identification of the source
$m_e$
. To make this more precise, we need a suitable identification of the source
![]() $\widehat {\mathbb {P}}$
with the target
$\widehat {\mathbb {P}}$
with the target
![]() $\mathbb {P}$
of
$\mathbb {P}$
of
![]() $\widehat { \mathcal {L}}$
so that we obtain a self-map on
$\widehat { \mathcal {L}}$
so that we obtain a self-map on
![]() $\mathbb {P}$
. For this, we choose a natural homeomorphism
$\mathbb {P}$
. For this, we choose a natural homeomorphism
![]() $\phi \colon \widehat {\mathbb {P}}\to \mathbb {P}$
, which we will now define.
$\phi \colon \widehat {\mathbb {P}}\to \mathbb {P}$
, which we will now define.
We view the set ![]() as a planar embedded graph, whose vertices and edges are precisely the
as a planar embedded graph, whose vertices and edges are precisely the
![]() $1$
-vertices and the
$1$
-vertices and the
![]() $1$
-edges of the flapped pillow
$1$
-edges of the flapped pillow
![]() $\widehat {\mathbb {P}}$
. Each
$\widehat {\mathbb {P}}$
. Each
![]() $1$
-edge of
$1$
-edge of
![]() $\widehat {\mathbb {P}}$
is homeomorphically mapped by
$\widehat {\mathbb {P}}$
is homeomorphically mapped by
![]() $\widehat {\mathcal {L}}$
onto one of the edges of
$\widehat {\mathcal {L}}$
onto one of the edges of
![]() $\mathbb {P}$
. Similarly as before, the
$\mathbb {P}$
. Similarly as before, the
![]() $1$
-edges of
$1$
-edges of
![]() $\widehat {\mathbb {P}}$
that are mapped by
$\widehat {\mathbb {P}}$
that are mapped by
![]() $\widehat {\mathcal {L}}$
onto a or c are called horizontal, while the
$\widehat {\mathcal {L}}$
onto a or c are called horizontal, while the
![]() $1$
-edges of
$1$
-edges of
![]() $\widehat {\mathbb {P}}$
that are mapped by
$\widehat {\mathbb {P}}$
that are mapped by
![]() $\widehat {\mathcal {L}}$
onto b or d are called vertical.
$\widehat {\mathcal {L}}$
onto b or d are called vertical.
There is a simple path of length n in the graph
![]() $\widehat {\mathcal {C}}$
that connects the vertices
$\widehat {\mathcal {C}}$
that connects the vertices
![]() $\widehat A$
and
$\widehat A$
and
![]() $\widehat B$
. Clearly, any such path consists only of horizontal
$\widehat B$
. Clearly, any such path consists only of horizontal
![]() $1$
-edges in
$1$
-edges in
![]() $\widehat {\mathbb {P}}$
. We denote by
$\widehat {\mathbb {P}}$
. We denote by
![]() $\widehat a$
the realization of the chosen path in the sphere
$\widehat a$
the realization of the chosen path in the sphere
![]() $\widehat {\mathbb {P}}$
, which is an arc in
$\widehat {\mathbb {P}}$
, which is an arc in
![]() $(\widehat {\mathbb {P}}, \widehat V)$
. The arc
$(\widehat {\mathbb {P}}, \widehat V)$
. The arc
![]() $\widehat a$
may not be uniquely determined (namely, if flaps have been glued to slits obtained from edges
$\widehat a$
may not be uniquely determined (namely, if flaps have been glued to slits obtained from edges
![]() $e\subset a$
), but any two such arcs are isotopic relative to
$e\subset a$
), but any two such arcs are isotopic relative to
![]() $\widehat V$
. We define
$\widehat V$
. We define
![]() $\widehat b$
,
$\widehat b$
,
![]() $\widehat c$
,
$\widehat c$
,
![]() $\widehat d$
in a similar way and call
$\widehat d$
in a similar way and call
![]() $\widehat a,\, \widehat c$
the horizontal edges, and
$\widehat a,\, \widehat c$
the horizontal edges, and
![]() $\widehat b,\, \widehat d$
the vertical edges of
$\widehat b,\, \widehat d$
the vertical edges of
![]() $\widehat {\mathbb {P}}$
.
$\widehat {\mathbb {P}}$
.
We now choose an orientation-preserving homeomorphism
![]() $\phi \colon \widehat {\mathbb {P}}\to \mathbb {P}$
that sends
$\phi \colon \widehat {\mathbb {P}}\to \mathbb {P}$
that sends
![]() $\widehat {A},\,\widehat {B},\,\widehat {C},\, \widehat {D}$
to
$\widehat {A},\,\widehat {B},\,\widehat {C},\, \widehat {D}$
to
![]() $A,\,B,\,C,\, D$
, and
$A,\,B,\,C,\, D$
, and
![]() $\widehat a, \,\widehat b, \,\widehat c, \,\widehat d$
to
$\widehat a, \,\widehat b, \,\widehat c, \,\widehat d$
to
![]() $a, \,b, \,c, \,d$
, respectively. We define
$a, \,b, \,c, \,d$
, respectively. We define ![]() , which is a self-map on
, which is a self-map on
![]() $\mathbb {P}$
. Clearly, f is a branched covering map on
$\mathbb {P}$
. Clearly, f is a branched covering map on
![]() $\mathbb {P}$
. To refer to this map, we say that
$\mathbb {P}$
. To refer to this map, we say that
![]() $f\colon \mathbb {P} \to \mathbb {P}$
is obtained from the
$f\colon \mathbb {P} \to \mathbb {P}$
is obtained from the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
by gluing
$\mathcal {L}_n$
by gluing
![]() $n_h$
horizontal and
$n_h$
horizontal and
![]() $n_v$
vertical flaps to
$n_v$
vertical flaps to
![]() $\mathbb {P}$
. More informally, we call both maps f and
$\mathbb {P}$
. More informally, we call both maps f and
![]() $\widehat {\mathcal {L}}$
a blown-up Lattès map.
$\widehat {\mathcal {L}}$
a blown-up Lattès map.
A point in
![]() $\widehat {\mathbb {P}}$
is a critical point for
$\widehat {\mathbb {P}}$
is a critical point for
![]() $\widehat { \mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
if and only if it is on the boundary of at least four
$\widehat { \mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
if and only if it is on the boundary of at least four
![]() $1$
-tiles subdividing
$1$
-tiles subdividing
![]() $\widehat {\mathbb {P}}$
. This implies that the set
$\widehat {\mathbb {P}}$
. This implies that the set
![]() $C_{\widehat {\mathcal {L}}}$
of critical points of
$C_{\widehat {\mathcal {L}}}$
of critical points of
![]() $\widehat {\mathcal {L}}$
consists of
$\widehat {\mathcal {L}}$
consists of
![]() $1$
-vertices of
$1$
-vertices of
![]() $\widehat {\mathbb {P}}$
and that each critical point of
$\widehat {\mathbb {P}}$
and that each critical point of
![]() $\mathcal {L}_n$
is also a critical point for
$\mathcal {L}_n$
is also a critical point for
![]() $\widehat { \mathcal {L}}$
(recall that we can view each point in
$\widehat { \mathcal {L}}$
(recall that we can view each point in
![]() $\mathcal {L}_n^{-1}(V)\supset C_{\mathcal {L}_n}$
as a
$\mathcal {L}_n^{-1}(V)\supset C_{\mathcal {L}_n}$
as a
![]() $1$
-vertex in
$1$
-vertex in
![]() $\widehat {\mathbb {P}}$
). Moreover, if a
$\widehat {\mathbb {P}}$
). Moreover, if a
![]() $1$
-vertex of
$1$
-vertex of
![]() $\widehat {\mathbb {P}}$
is a critical point of
$\widehat {\mathbb {P}}$
is a critical point of
![]() $\widehat {\mathcal {L}}$
, but not of
$\widehat {\mathcal {L}}$
, but not of
![]() $\mathcal {L}_n$
, then it must be one of the points in
$\mathcal {L}_n$
, then it must be one of the points in
![]() $\widehat V$
. For example,
$\widehat V$
. For example,
![]() $\widehat A\in \widehat V$
is a critical point of
$\widehat A\in \widehat V$
is a critical point of
![]() $\widehat { \mathcal {L}}$
if and only if a flap was glued to an edge of
$\widehat { \mathcal {L}}$
if and only if a flap was glued to an edge of
![]() $\widetilde {\mathcal {C}}$
incident to
$\widetilde {\mathcal {C}}$
incident to
![]() $A\cong \widehat A$
. In any case, since
$A\cong \widehat A$
. In any case, since
![]() $\widehat {\mathcal {L}}$
sends the
$\widehat {\mathcal {L}}$
sends the
![]() $1$
-vertices of
$1$
-vertices of
![]() $\widehat {\mathbb {P}}$
to the vertices of
$\widehat {\mathbb {P}}$
to the vertices of
![]() $\mathbb {P}$
, the postcritical set of
$\mathbb {P}$
, the postcritical set of
![]() $f=\widehat { \mathcal {L}}\circ \phi ^{-1}$
coincides with the vertex set V. Thus, f is a Thurston map.
$f=\widehat { \mathcal {L}}\circ \phi ^{-1}$
coincides with the vertex set V. Thus, f is a Thurston map.
Since we assumed that
![]() $\widehat {\mathbb {P}}$
contains at least one flap (that is,
$\widehat {\mathbb {P}}$
contains at least one flap (that is,
![]() $n_h+n_v>0$
), the orbifold of the Thurston map f is hyperbolic. Indeed, each
$n_h+n_v>0$
), the orbifold of the Thurston map f is hyperbolic. Indeed, each
![]() $1$
-vertex of
$1$
-vertex of
![]() $\widehat {\mathbb {P}}$
that is a critical point of
$\widehat {\mathbb {P}}$
that is a critical point of
![]() $\mathcal {L}_n$
is also a critical point of
$\mathcal {L}_n$
is also a critical point of
![]() $\widehat {\mathcal {L}}$
with the same or larger local degree. Since we glued at least one flap, there is at least one
$\widehat {\mathcal {L}}$
with the same or larger local degree. Since we glued at least one flap, there is at least one
![]() $1$
-vertex v contained in six or more
$1$
-vertex v contained in six or more
![]() $1$
-tiles of
$1$
-tiles of
![]() $\widehat {\mathbb {P}}$
. Then
$\widehat {\mathbb {P}}$
. Then
![]() $\deg (\widehat {\mathcal {L}},v)=\deg (f,v') \ge 3$
, where
$\deg (\widehat {\mathcal {L}},v)=\deg (f,v') \ge 3$
, where
![]() $v'=\phi (v)$
. Now
$v'=\phi (v)$
. Now
and so for the ramification function
![]() $\alpha _f$
of f, we have
$\alpha _f$
of f, we have
![]() $\alpha _f(X)\ge 3$
. However, for all other points
$\alpha _f(X)\ge 3$
. However, for all other points
![]() $Y\in V={P_f}$
, we have
$Y\in V={P_f}$
, we have
![]() $\alpha _{f}(Y)\ge \alpha _{\mathcal {L}_n}(Y)\ge 2$
. It then follows from equation (3.1) that
$\alpha _{f}(Y)\ge \alpha _{\mathcal {L}_n}(Y)\ge 2$
. It then follows from equation (3.1) that
![]() $\chi (\mathcal {O}_f)<0$
, and so f has indeed a hyperbolic orbifold.
$\chi (\mathcal {O}_f)<0$
, and so f has indeed a hyperbolic orbifold.
The homeomorphism
![]() $\phi $
chosen in the definition of f is not unique, but any two such homeomorphisms are isotopic relative to
$\phi $
chosen in the definition of f is not unique, but any two such homeomorphisms are isotopic relative to
![]() $\widehat V$
(this easily follows from [Reference BuserBus10, Theorem A.5]). This implies that f is uniquely determined up to Thurston equivalence. This map may be viewed (up to Thurston equivalence) as the result of the blowing up operation introduced in §4.1 applied to the edges
$\widehat V$
(this easily follows from [Reference BuserBus10, Theorem A.5]). This implies that f is uniquely determined up to Thurston equivalence. This map may be viewed (up to Thurston equivalence) as the result of the blowing up operation introduced in §4.1 applied to the edges
![]() $e \in E$
with the multiplicities
$e \in E$
with the multiplicities
![]() $m_e$
. In particular, if we run the procedure for the map
$m_e$
. In particular, if we run the procedure for the map
![]() $\widehat { \mathcal {L}}$
indicated in Figure 13, then we obtain the map
$\widehat { \mathcal {L}}$
indicated in Figure 13, then we obtain the map
![]() $\widehat f$
illustrated in Figure 12 (up to Thurston equivalence).
$\widehat f$
illustrated in Figure 12 (up to Thurston equivalence).
5 Realizing blown-up Lattès maps
The goal of this section is to determine when a blown-up Lattès map is realized by a rational map. In particular, we will apply Thurston’s criterion to prove Theorem 1.2. The strategies and techniques used in the proof will highlight the main ideas needed for establishing the more general Theorem 1.1.
We fix
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $n_h, n_v\ge 0$
, and follow the notation introduced in §4.2. In particular, we denote by
$n_h, n_v\ge 0$
, and follow the notation introduced in §4.2. In particular, we denote by
![]() $\widehat {\mathbb {P}}$
a flapped pillow with
$\widehat {\mathbb {P}}$
a flapped pillow with
![]() $n_h$
horizontal and
$n_h$
horizontal and
![]() $n_v$
vertical flaps, by
$n_v$
vertical flaps, by
![]() $\widehat { \mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
the respective blown-up
$\widehat { \mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
the respective blown-up
![]() $(n\times n)$
-Lattès map, and by
$(n\times n)$
-Lattès map, and by
![]() $\phi \colon \widehat {\mathbb {P}}\to \mathbb {P}$
the identifying homeomorphism. Then
$\phi \colon \widehat {\mathbb {P}}\to \mathbb {P}$
the identifying homeomorphism. Then
![]() $f\colon \mathbb {P}\to \mathbb {P}$
given as
$f\colon \mathbb {P}\to \mathbb {P}$
given as
![]() $f=\widehat { \mathcal {L}}\circ \phi ^{-1}$
is the Thurston map under consideration. We will assume that
$f=\widehat { \mathcal {L}}\circ \phi ^{-1}$
is the Thurston map under consideration. We will assume that
![]() $n_h+n_v>0$
, and so
$n_h+n_v>0$
, and so
![]() $\widehat {\mathbb {P}}$
has at least one flap. In this case, f has a hyperbolic orbifold as we have seen, and so we can apply Thurston’s criterion. For this, we consider essential Jordan curves
$\widehat {\mathbb {P}}$
has at least one flap. In this case, f has a hyperbolic orbifold as we have seen, and so we can apply Thurston’s criterion. For this, we consider essential Jordan curves
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P},{P_f})=(\mathbb {P},V)$
and study their (essential) pullbacks under f.
$(\mathbb {P},{P_f})=(\mathbb {P},V)$
and study their (essential) pullbacks under f.
If
![]() $\gamma $
is such a curve, then the homeomorphism
$\gamma $
is such a curve, then the homeomorphism
![]() $\phi $
sends the pullbacks of
$\phi $
sends the pullbacks of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat {\mathcal {L}}$
to the pullbacks of
$\widehat {\mathcal {L}}$
to the pullbacks of
![]() $\gamma $
under f. So to understand the isotopy types and mapping properties of the pullbacks under f, we will instead look at the pullbacks of
$\gamma $
under f. So to understand the isotopy types and mapping properties of the pullbacks under f, we will instead look at the pullbacks of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat {\mathcal {L}}$
. In particular, if
$\widehat {\mathcal {L}}$
. In particular, if
![]() $\widehat {\gamma }$
is a pullback of
$\widehat {\gamma }$
is a pullback of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat {\mathcal {L}}$
, then
$\widehat {\mathcal {L}}$
, then
![]() $\deg (\widehat {\mathcal {L}}\colon \widehat {\gamma } \to \gamma ) = \deg (f\colon \phi (\widehat {\gamma }) \to \gamma )$
and
$\deg (\widehat {\mathcal {L}}\colon \widehat {\gamma } \to \gamma ) = \deg (f\colon \phi (\widehat {\gamma }) \to \gamma )$
and
![]() $\phi (\widehat {\gamma })$
is essential in
$\phi (\widehat {\gamma })$
is essential in
![]() $(\mathbb {P},{P_f})=(\mathbb {P},V)$
if and only if
$(\mathbb {P},{P_f})=(\mathbb {P},V)$
if and only if
![]() $\widehat {\gamma }$
is essential in
$\widehat {\gamma }$
is essential in
![]() $(\widehat {\mathbb {P}}, \widehat V)$
, where
$(\widehat {\mathbb {P}}, \widehat V)$
, where
![]() $\widehat V$
denotes the vertex set of the flapped pillow
$\widehat V$
denotes the vertex set of the flapped pillow
![]() $\widehat {\mathbb {P}}$
.
$\widehat {\mathbb {P}}$
.
Since the mapping
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
is a similarity map on each
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
is a similarity map on each
![]() $1$
-tile of
$1$
-tile of
![]() $\widehat {\mathbb {P}}$
, the preimage
$\widehat {\mathbb {P}}$
, the preimage
![]() $\widehat {\mathcal {L}}^{-1} (\gamma )$
of a Jordan curve
$\widehat {\mathcal {L}}^{-1} (\gamma )$
of a Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P},{P_f})$
(or of any subset
$(\mathbb {P},{P_f})$
(or of any subset
![]() $\gamma $
of
$\gamma $
of
![]() $\mathbb {P}$
), can be obtained in the following intuitive way: we rescale and copy the part of
$\mathbb {P}$
), can be obtained in the following intuitive way: we rescale and copy the part of
![]() $\gamma $
that belongs to the white
$\gamma $
that belongs to the white
![]() $0$
-tile of
$0$
-tile of
![]() $\mathbb {P}$
into each white
$\mathbb {P}$
into each white
![]() $1$
-tile of
$1$
-tile of
![]() $\widehat {\mathbb {P}}$
and the part of
$\widehat {\mathbb {P}}$
and the part of
![]() $\gamma $
that belongs to the black
$\gamma $
that belongs to the black
![]() $0$
-tile of
$0$
-tile of
![]() $\mathbb {P}$
into each black
$\mathbb {P}$
into each black
![]() $1$
-tile.
$1$
-tile.
5.1 The horizontal and vertical curves
Recall that
![]() $\alpha ^h$
and
$\alpha ^h$
and
![]() $\alpha ^v$
(see (2.4)) denote the Jordan curves in
$\alpha ^v$
(see (2.4)) denote the Jordan curves in
![]() $(\mathbb {P},V)=(\mathbb {P},{P_f})$
that separate the two horizontal and the two vertical edges of
$(\mathbb {P},V)=(\mathbb {P},{P_f})$
that separate the two horizontal and the two vertical edges of
![]() $\mathbb {P}$
, respectively. These two curves are invariant under f and will play a crucial role in the considerations of this section.
$\mathbb {P}$
, respectively. These two curves are invariant under f and will play a crucial role in the considerations of this section.
Lemma 5.1. Let
![]() $f=\widehat {\mathcal {L}} \circ \phi ^{-1} \colon \mathbb {P} \to \mathbb {P}$
be a Thurston map obtained from the
$f=\widehat {\mathcal {L}} \circ \phi ^{-1} \colon \mathbb {P} \to \mathbb {P}$
be a Thurston map obtained from the
![]() ${(n\times n)}$
-Lattès map,
${(n\times n)}$
-Lattès map,
![]() $n\ge 2$
, by gluing
$n\ge 2$
, by gluing
![]() $n_h\ge 0$
horizontal and
$n_h\ge 0$
horizontal and
![]() $n_v\ge 0$
vertical flaps to
$n_v\ge 0$
vertical flaps to
![]() $\mathbb {P}$
. Then the following statements are true.
$\mathbb {P}$
. Then the following statements are true.
-
(i) The Jordan curve
 $\alpha ^h$
has
$\alpha ^h$
has
 $n+n_h$
pullbacks under f. Exactly n of these pullbacks are essential. Each of these essential pullbacks is isotopic to
$n+n_h$
pullbacks under f. Exactly n of these pullbacks are essential. Each of these essential pullbacks is isotopic to
 $\alpha ^h$
relative to
$\alpha ^h$
relative to
 ${P_f}$
.
${P_f}$
. -
(ii) If
 $\widetilde {\alpha }$
is one of the n essential pullbacks of
$\widetilde {\alpha }$
is one of the n essential pullbacks of
 $\alpha ^h$
, then
$\alpha ^h$
, then
 $\deg (f\colon \widetilde {\alpha }\to \alpha ^h)=n+n_{\widetilde {\alpha }}$
, where
$\deg (f\colon \widetilde {\alpha }\to \alpha ^h)=n+n_{\widetilde {\alpha }}$
, where
 $n_{\widetilde {\alpha }}\ge 0$
is the number of distinct vertical flaps in
$n_{\widetilde {\alpha }}\ge 0$
is the number of distinct vertical flaps in
 $\widehat {\mathbb {P}}$
that
$\widehat {\mathbb {P}}$
that
 $ \phi ^{-1} (\widetilde {\alpha })$
meets.
$ \phi ^{-1} (\widetilde {\alpha })$
meets. -
(iii) We have
where the sum is taken over all essential pullbacks
 $\widetilde \alpha $
of
$\widetilde \alpha $
of
 $\alpha ^h$
under f.
$\alpha ^h$
under f.
Analogous statements are true for the curve
![]() $\alpha ^v$
.
$\alpha ^v$
.

Figure 15 Pullbacks of
![]() $\alpha ^h$
for a blown-up
$\alpha ^h$
for a blown-up
![]() $(4\times 4)$
-Lattès map with
$(4\times 4)$
-Lattès map with
![]() $n_h=n_v=1$
.
$n_h=n_v=1$
.
Proof. Figure 15 illustrates the proof. It is obvious that the curve
![]() $\alpha ^h$
has exactly
$\alpha ^h$
has exactly
![]() $n+n_h$
distinct pullbacks under
$n+n_h$
distinct pullbacks under
![]() $\widehat {\mathcal {L}}$
. Among them, there are n essential pullbacks
$\widehat {\mathcal {L}}$
. Among them, there are n essential pullbacks
![]() $\widehat \alpha _1,\ldots , \widehat \alpha _n$
that separate the two horizontal edges of
$\widehat \alpha _1,\ldots , \widehat \alpha _n$
that separate the two horizontal edges of
![]() $\widehat {\mathbb {P}}$
and thus are isotopic to each other relative to the vertex set
$\widehat {\mathbb {P}}$
and thus are isotopic to each other relative to the vertex set
![]() $\widehat V$
of
$\widehat V$
of
![]() $\widehat {\mathbb {P}}$
. For each
$\widehat {\mathbb {P}}$
. For each
![]() $j=1,\ldots , n$
, the image
$j=1,\ldots , n$
, the image ![]() is isotopic to
is isotopic to
![]() $\alpha ^h$
. Moreover, we have
$\alpha ^h$
. Moreover, we have
![]() $\deg (\widehat {\mathcal {L}}\colon \widehat \alpha _j\to \alpha ^h)=n+n_{{\alpha }_j}$
. The other
$\deg (\widehat {\mathcal {L}}\colon \widehat \alpha _j\to \alpha ^h)=n+n_{{\alpha }_j}$
. The other
![]() $n_h$
pullbacks of
$n_h$
pullbacks of
![]() $\alpha ^h$
under
$\alpha ^h$
under
![]() $\widehat {\mathcal {L}}$
are each contained in one of the horizontal flaps and thus are peripheral in
$\widehat {\mathcal {L}}$
are each contained in one of the horizontal flaps and thus are peripheral in
![]() $(\widehat {\mathbb {P}}, \widehat V)$
. Consequently,
$(\widehat {\mathbb {P}}, \widehat V)$
. Consequently,

This completes the proof of the lemma for the curve
![]() $\alpha ^h$
. The proof for the curve
$\alpha ^h$
. The proof for the curve
![]() $\alpha ^v$
follows from similar considerations.
$\alpha ^v$
follows from similar considerations.
The following corollary is an immediate consequence of the previous lemma.
Corollary 5.2. Let
![]() $f=\widehat {\mathcal {L}} \circ \phi ^{-1} \colon \mathbb {P} \to \mathbb {P}$
be a Thurston map obtained from the
$f=\widehat {\mathcal {L}} \circ \phi ^{-1} \colon \mathbb {P} \to \mathbb {P}$
be a Thurston map obtained from the
![]() ${(n\times n)}$
-Lattès map,
${(n\times n)}$
-Lattès map,
![]() $n\ge 2$
, by gluing
$n\ge 2$
, by gluing
![]() $n_h\ge 0$
horizontal and
$n_h\ge 0$
horizontal and
![]() $n_v\ge 0$
vertical flaps to
$n_v\ge 0$
vertical flaps to
![]() $\mathbb {P}$
. Then
$\mathbb {P}$
. Then
![]() $\alpha ^h$
is an obstruction (for f) if and only if
$\alpha ^h$
is an obstruction (for f) if and only if
![]() $n_v=0$
, and
$n_v=0$
, and
![]() $\alpha ^v$
is an obstruction if and only if
$\alpha ^v$
is an obstruction if and only if
![]() $n_h=0$
.
$n_h=0$
.
Proof. Let us first suppose that
![]() $n_v=0$
, that is,
$n_v=0$
, that is,
![]() $\widehat {\mathbb {P}}$
does not have any vertical flaps. Then by Lemma 5.1,
$\widehat {\mathbb {P}}$
does not have any vertical flaps. Then by Lemma 5.1,
![]() $\alpha ^h$
has n essential pullbacks under f, each of which is mapped onto
$\alpha ^h$
has n essential pullbacks under f, each of which is mapped onto
![]() $\alpha ^h$
with degree n (this is illustrated in Figure 16 in a special case). Consequently,
$\alpha ^h$
with degree n (this is illustrated in Figure 16 in a special case). Consequently,
![]() $\unicode{x3bb} _f(\alpha ^h)= n\cdot (1/n)=1$
, which means
$\unicode{x3bb} _f(\alpha ^h)= n\cdot (1/n)=1$
, which means
![]() $\alpha ^h$
is an obstruction for f.
$\alpha ^h$
is an obstruction for f.

Figure 16 Pullbacks of
![]() $\alpha ^h$
for a blown up
$\alpha ^h$
for a blown up
![]() $(4\times 4)$
-Lattès map with
$(4\times 4)$
-Lattès map with
![]() $n_h=1$
and
$n_h=1$
and
![]() $n_v=0$
.
$n_v=0$
.
If
![]() $n_v>0$
, the flapped pillow
$n_v>0$
, the flapped pillow
![]() $\widehat {\mathbb {P}}$
has at least one vertical flap. Then
$\widehat {\mathbb {P}}$
has at least one vertical flap. Then
![]() $n_{\widetilde {\alpha }}>0$
for at least one essential pullback
$n_{\widetilde {\alpha }}>0$
for at least one essential pullback
![]() $\widetilde {\alpha }$
of
$\widetilde {\alpha }$
of
![]() $\alpha ^h$
. Lemma 5.1 implies that
$\alpha ^h$
. Lemma 5.1 implies that
and so
![]() $\alpha ^h$
is not an obstruction for f.
$\alpha ^h$
is not an obstruction for f.
The proof for the vertical curve
![]() $\alpha ^v$
is completely analogous.
$\alpha ^v$
is completely analogous.
The above corollary can be read as follows: the obstruction
![]() $\alpha ^h$
for the
$\alpha ^h$
for the
![]() $(n\times n)$
-Lattès map can be eliminated by gluing a vertical flap to
$(n\times n)$
-Lattès map can be eliminated by gluing a vertical flap to
![]() $\mathbb {P}$
. Similarly, the obstruction
$\mathbb {P}$
. Similarly, the obstruction
![]() $\alpha ^v$
can be eliminated by gluing a horizontal flap. We will show momentarily that if both of these obstructions are eliminated (that is, if there are both horizontal and vertical flaps), then no other obstructions are present and so the map f is realized.
$\alpha ^v$
can be eliminated by gluing a horizontal flap. We will show momentarily that if both of these obstructions are eliminated (that is, if there are both horizontal and vertical flaps), then no other obstructions are present and so the map f is realized.
5.2 Ruling out other obstructions
Now we discuss what happens with the essential curves in
![]() $(\mathbb {P},{P_f})$
that are not isotopic to the horizontal curve
$(\mathbb {P},{P_f})$
that are not isotopic to the horizontal curve
![]() $\alpha ^h$
or the vertical curve
$\alpha ^h$
or the vertical curve
![]() $\alpha ^v$
.
$\alpha ^v$
.
Theorem 5.3. Let
![]() $f=\widehat {\mathcal {L}} \circ \phi ^{-1} \colon \mathbb {P} \to \mathbb {P}$
be a Thurston map obtained from the
$f=\widehat {\mathcal {L}} \circ \phi ^{-1} \colon \mathbb {P} \to \mathbb {P}$
be a Thurston map obtained from the
![]() ${(n\times n)}$
-Lattès map,
${(n\times n)}$
-Lattès map,
![]() $n\ge 2$
, by gluing
$n\ge 2$
, by gluing
![]() $n_h\ge 0$
horizontal and
$n_h\ge 0$
horizontal and
![]() $n_v\ge 0$
vertical flaps to
$n_v\ge 0$
vertical flaps to
![]() $\mathbb {P}$
and assume that
$\mathbb {P}$
and assume that
![]() $n_h+n_v>0$
. If
$n_h+n_v>0$
. If
![]() $\gamma \subset \mathbb {P}\smallsetminus {P_f} $
is an essential Jordan curve that is not isotopic to either
$\gamma \subset \mathbb {P}\smallsetminus {P_f} $
is an essential Jordan curve that is not isotopic to either
![]() $\alpha ^h$
or
$\alpha ^h$
or
![]() $\alpha ^v$
, then
$\alpha ^v$
, then
![]() $\gamma $
is not an obstruction for f.
$\gamma $
is not an obstruction for f.
Before we turn to the proof of this theorem, we first record how it implies Theorem 1.2 stated in the introduction.
Proof of Theorem 1.2
Let n, f,
![]() $n_h$
, and
$n_h$
, and
![]() $n_v$
with
$n_v$
with
![]() $n_h+n_v>0$
be as in the statement. We have seen in §4.2 that then f has a hyperbolic orbifold. If
$n_h+n_v>0$
be as in the statement. We have seen in §4.2 that then f has a hyperbolic orbifold. If
![]() $n_h=0$
or
$n_h=0$
or
![]() $n_v=0$
, then by Corollary 5.2, the curve
$n_v=0$
, then by Corollary 5.2, the curve
![]() $\alpha ^v$
or the curve
$\alpha ^v$
or the curve
![]() $\alpha ^h$
is an obstruction, respectively.
$\alpha ^h$
is an obstruction, respectively.
If
![]() $n_h>0$
and
$n_h>0$
and
![]() $n_v>0$
, then f has no obstruction as follows from Corollary 5.2 and Theorem 5.3. Since f has a hyperbolic orbifold, in this case, f is realized by a rational map according to Theorem 3.7.
$n_v>0$
, then f has no obstruction as follows from Corollary 5.2 and Theorem 5.3. Since f has a hyperbolic orbifold, in this case, f is realized by a rational map according to Theorem 3.7.
Corollary 5.2 and Theorem 5.3 also imply that if
![]() $n_h=0$
, then
$n_h=0$
, then
![]() $\alpha ^v$
is the only obstruction for f (up to isotopy relative to
$\alpha ^v$
is the only obstruction for f (up to isotopy relative to
![]() ${P_f}$
). Similarly,
${P_f}$
). Similarly,
![]() $\alpha ^h$
is the only obstruction if
$\alpha ^h$
is the only obstruction if
![]() $n_v=0$
.
$n_v=0$
.
Before we go into the details, we will give an outline for the proof of Theorem 5.3. We argue by contradiction and assume that f has an obstruction given by an essential Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P},{P_f})$
that is isotopic to neither
$(\mathbb {P},{P_f})$
that is isotopic to neither
![]() $\alpha ^h$
nor
$\alpha ^h$
nor
![]() $\alpha ^v$
relative to
$\alpha ^v$
relative to
![]() ${P_f}$
. Then
${P_f}$
. Then
![]() $\unicode{x3bb} _f(\gamma )\geq 1$
. Let
$\unicode{x3bb} _f(\gamma )\geq 1$
. Let
![]() $ \gamma _1,\ldots , \gamma _k$
for some
$ \gamma _1,\ldots , \gamma _k$
for some
![]() $k\in \mathbb {N}$
be all the essential pullbacks of
$k\in \mathbb {N}$
be all the essential pullbacks of
![]() $\gamma $
under f, which must be isotopic to
$\gamma $
under f, which must be isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() ${P_f}$
.
${P_f}$
.
Using facts about intersection numbers and the mapping properties of f, one can show that for the number of essential pullbacks of
![]() $\gamma $
, we have
$\gamma $
, we have
![]() $k \le n$
and that the corresponding mapping degrees satisfy
$k \le n$
and that the corresponding mapping degrees satisfy
![]() $\deg (f\colon \gamma _j\to \gamma )\geq n$
for all
$\deg (f\colon \gamma _j\to \gamma )\geq n$
for all
![]() $j=1,\ldots , k$
. Since
$j=1,\ldots , k$
. Since
![]() $\unicode{x3bb} _f(\gamma )\geq 1$
, it follows that there are exactly
$\unicode{x3bb} _f(\gamma )\geq 1$
, it follows that there are exactly
![]() $k=n$
essential pullbacks and that
$k=n$
essential pullbacks and that
![]() $\deg (f\colon \gamma _j\to \gamma )=n$
for each
$\deg (f\colon \gamma _j\to \gamma )=n$
for each
![]() $j=1, \ldots , n$
.
$j=1, \ldots , n$
.
This in turn implies that none of the essential pullbacks ![]() of
of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat {\mathcal {L}}$
goes over a flap in
$\widehat {\mathcal {L}}$
goes over a flap in
![]() $\widehat {\mathbb {P}}$
. Then all the n pullbacks
$\widehat {\mathbb {P}}$
. Then all the n pullbacks
![]() $\widehat {\gamma }_1,\ldots , \widehat {\gamma }_n$
belong to the base
$\widehat {\gamma }_1,\ldots , \widehat {\gamma }_n$
belong to the base
![]() $B(\widehat {\mathbb {P}})$
of
$B(\widehat {\mathbb {P}})$
of
![]() $\widehat {\mathbb {P}}$
. This means that each
$\widehat {\mathbb {P}}$
. This means that each
![]() $\widehat {\gamma }_j$
can be thought of as a pullback of
$\widehat {\gamma }_j$
can be thought of as a pullback of
![]() $\gamma $
under the original
$\gamma $
under the original
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
. However, there are only n pullbacks of
$\mathcal {L}_n$
. However, there are only n pullbacks of
![]() $\gamma $
under
$\gamma $
under
![]() $\mathcal {L}_n$
, which cross all the edges of the graph
$\mathcal {L}_n$
, which cross all the edges of the graph
![]() $\mathcal {L}_n^{-1}(\mathcal {C})$
, where
$\mathcal {L}_n^{-1}(\mathcal {C})$
, where
![]() $\mathcal {C}$
is the common boundary of the
$\mathcal {C}$
is the common boundary of the
![]() $0$
-tiles in
$0$
-tiles in
![]() $\mathbb {P}$
. Consequently, the pullbacks
$\mathbb {P}$
. Consequently, the pullbacks
![]() $\widehat {\gamma }_1,\ldots , \widehat {\gamma }_n$
cross all the
$\widehat {\gamma }_1,\ldots , \widehat {\gamma }_n$
cross all the
![]() $1$
-edges in the closure of the base
$1$
-edges in the closure of the base
![]() $B(\widehat {\mathbb {P}})$
. It follows that one of the pullbacks
$B(\widehat {\mathbb {P}})$
. It follows that one of the pullbacks
![]() $\widehat {\gamma }_j$
must cross one of the base edges of a flap F in
$\widehat {\gamma }_j$
must cross one of the base edges of a flap F in
![]() $\widehat {\mathbb {P}}$
, which would necessarily mean that
$\widehat {\mathbb {P}}$
, which would necessarily mean that
![]() $\widehat {\gamma }_j$
goes over the flap F. This gives the desired contradiction and Theorem 5.3 follows.
$\widehat {\gamma }_j$
goes over the flap F. This gives the desired contradiction and Theorem 5.3 follows.
In the remainder of this section, we will fill in the details for this outline. First, we establish several general facts about degrees and intersection numbers.
Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $f\colon X\rightarrow Y$
be a map between two sets X and Y. We say that f is at most n-to-
$f\colon X\rightarrow Y$
be a map between two sets X and Y. We say that f is at most n-to-
![]() $1$
if
$1$
if
![]() $\#f^{-1}(y)\le n$
for each
$\#f^{-1}(y)\le n$
for each
![]() $y\in Y$
. We say that f is n-to-
$y\in Y$
. We say that f is n-to-
![]() $1$
if
$1$
if
![]() $\#f^{-1}(y)= n$
for each
$\#f^{-1}(y)= n$
for each
![]() $y\in Y$
.
$y\in Y$
.
Lemma 5.4. Let
![]() $f\colon X\rightarrow Y$
be a map between two sets X and Y. Suppose
$f\colon X\rightarrow Y$
be a map between two sets X and Y. Suppose
![]() $M\subset X$
,
$M\subset X$
,
![]() $N\subset Y$
, and
$N\subset Y$
, and
![]() $f|M\colon M\to f(M)$
is at most n-to-
$f|M\colon M\to f(M)$
is at most n-to-
![]() $1$
for some
$1$
for some
![]() $n\in \mathbb {N}$
. Then
$n\in \mathbb {N}$
. Then
Proof. The map f sends each point in
![]() $M \cap f^{-1}(N)$
to a point in
$M \cap f^{-1}(N)$
to a point in
![]() $f(M)\cap N$
. Moreover, each point in
$f(M)\cap N$
. Moreover, each point in
![]() $f(M)\cap N$
has at most n preimages in
$f(M)\cap N$
has at most n preimages in
![]() $M\cap f^{-1}(N)$
under f. The statement follows.
$M\cap f^{-1}(N)$
under f. The statement follows.
Lemma 5.5. Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map with
$f\colon S^2\rightarrow S^2$
be a Thurston map with
![]() $\#{P_f}=4$
, and
$\#{P_f}=4$
, and
![]() $\gamma $
be an essential Jordan curve in
$\gamma $
be an essential Jordan curve in
![]() $(S^2, {P_f})$
. Suppose that
$(S^2, {P_f})$
. Suppose that
![]() $\widetilde \alpha $
is an essential Jordan curve or an arc in
$\widetilde \alpha $
is an essential Jordan curve or an arc in
![]() $(S^2,{P_f})$
such that:
$(S^2,{P_f})$
such that:
-
(i)
 $f(\widetilde \alpha )$
and
$f(\widetilde \alpha )$
and
 $\widetilde \alpha $
are isotopic relative to
$\widetilde \alpha $
are isotopic relative to
 ${P_f}$
;
${P_f}$
; -
(ii) the map
 $f|\widetilde \alpha : \widetilde \alpha \to f( \widetilde \alpha )$
is at most n-to-
$f|\widetilde \alpha : \widetilde \alpha \to f( \widetilde \alpha )$
is at most n-to-
 $1$
, where
$1$
, where
 $n\in \mathbb {N}$
;
$n\in \mathbb {N}$
; -
(iii)
 $\mathrm {i}(f(\widetilde \alpha ), \gamma )= \#(f(\widetilde \alpha )\cap \gamma )>0$
.
$\mathrm {i}(f(\widetilde \alpha ), \gamma )= \#(f(\widetilde \alpha )\cap \gamma )>0$
.
Then
![]() $k \le n$
, where
$k \le n$
, where
![]() $k\in \mathbb {N}_0$
denotes the number of distinct pullbacks of
$k\in \mathbb {N}_0$
denotes the number of distinct pullbacks of
![]() $\gamma $
under f that are isotopic to
$\gamma $
under f that are isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() ${P_f}$
. Moreover, if
${P_f}$
. Moreover, if
![]() $\widetilde \alpha $
meets a peripheral pullback of
$\widetilde \alpha $
meets a peripheral pullback of
![]() $\gamma $
, then
$\gamma $
, then
![]() $k<n$
.
$k<n$
.
In the formulation and the ensuing proof, intersection numbers are with respect to
![]() $(S^2, P_f)$
. Note that since
$(S^2, P_f)$
. Note that since
![]() $f(\widetilde \alpha )$
and
$f(\widetilde \alpha )$
and
![]() $\widetilde \alpha $
are isotopic relative to
$\widetilde \alpha $
are isotopic relative to
![]() ${P_f}$
by assumption,
${P_f}$
by assumption,
![]() $f(\widetilde \alpha )$
is of the same type as
$f(\widetilde \alpha )$
is of the same type as
![]() $\widetilde \alpha $
, that is, a Jordan curve or an arc in
$\widetilde \alpha $
, that is, a Jordan curve or an arc in
![]() $(S^2,{P_f})$
.
$(S^2,{P_f})$
.
Proof. Let
![]() $\gamma _1,\ldots , \gamma _k$
be the distinct pullbacks of
$\gamma _1,\ldots , \gamma _k$
be the distinct pullbacks of
![]() $\gamma $
under f that are isotopic to
$\gamma $
under f that are isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() ${P_f}$
. Since
${P_f}$
. Since
![]() $f|\widetilde \alpha \colon \widetilde \alpha \rightarrow f(\widetilde \alpha )$
is at most n-to-
$f|\widetilde \alpha \colon \widetilde \alpha \rightarrow f(\widetilde \alpha )$
is at most n-to-
![]() $1$
, we can apply Lemma 5.4 and conclude that
$1$
, we can apply Lemma 5.4 and conclude that
However,
 $$ \begin{align} \!\!\!\!n\cdot \mathrm{i} (f(\widetilde \alpha) , \gamma)\ge \#(\widetilde \alpha \cap f^{-1}(\gamma))\geq \sum_{j=1}^k \#(\widetilde \alpha \cap \gamma_j ) \geq \sum_{j=1}^k \mathrm{i}(\widetilde \alpha, \gamma_j)= k \cdot \mathrm{i}(f(\widetilde \alpha) , \gamma).\ \end{align} $$
$$ \begin{align} \!\!\!\!n\cdot \mathrm{i} (f(\widetilde \alpha) , \gamma)\ge \#(\widetilde \alpha \cap f^{-1}(\gamma))\geq \sum_{j=1}^k \#(\widetilde \alpha \cap \gamma_j ) \geq \sum_{j=1}^k \mathrm{i}(\widetilde \alpha, \gamma_j)= k \cdot \mathrm{i}(f(\widetilde \alpha) , \gamma).\ \end{align} $$
Since
![]() $\mathrm {i}(f(\widetilde \alpha ) ,\gamma )>0$
, we see that
$\mathrm {i}(f(\widetilde \alpha ) ,\gamma )>0$
, we see that
![]() $k \le n$
. If
$k \le n$
. If
![]() $\widetilde \alpha $
meets a peripheral pullback of
$\widetilde \alpha $
meets a peripheral pullback of
![]() $\gamma $
, then the second inequality in (5.1) is strict and we actually have
$\gamma $
, then the second inequality in (5.1) is strict and we actually have
![]() $k <n$
.
$k <n$
.
The next result will lead to the strict inequality from Lemma 5.5 in the proof of Theorem 5.3.
Lemma 5.6. As before, let
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
be the blown-up
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
be the blown-up
![]() $(n\times n)$
-Lattès map, and suppose
$(n\times n)$
-Lattès map, and suppose
![]() $\gamma =\tau _{r/s}$
is a simple closed geodesic in
$\gamma =\tau _{r/s}$
is a simple closed geodesic in
![]() $\mathbb {P}$
with slope
$\mathbb {P}$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}\smallsetminus \{0,\infty \}$
. Let
$r/s\in \widehat {\mathbb {Q}}\smallsetminus \{0,\infty \}$
. Let
![]() $\widehat {\gamma }$
be a pullback of
$\widehat {\gamma }$
be a pullback of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat {\mathcal {L}}$
. If
$\widehat {\mathcal {L}}$
. If
![]() $\widehat {\gamma }$
intersects the interior of a base edge of a flap F in
$\widehat {\gamma }$
intersects the interior of a base edge of a flap F in
![]() $\widehat {\mathbb {P}}$
, then
$\widehat {\mathbb {P}}$
, then
![]() $\widehat {\gamma }$
also intersects the top edge of F.
$\widehat {\gamma }$
also intersects the top edge of F.
Proof. We have
![]() $\gamma =\wp (\ell _{r/s})$
, where
$\gamma =\wp (\ell _{r/s})$
, where
![]() $\ell _{r/s}\subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
is a straight line with slope
$\ell _{r/s}\subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
is a straight line with slope
![]() ${r/s\ne 0,\infty }$
. Then
${r/s\ne 0,\infty }$
. Then
![]() $\gamma $
is an essential Jordan curve in
$\gamma $
is an essential Jordan curve in
![]() $(\mathbb {P}, V)$
. Let
$(\mathbb {P}, V)$
. Let
![]() $\widehat \gamma \subset \widehat {\mathbb {P}}$
be as in the statement. As in §2.4, we denote by
$\widehat \gamma \subset \widehat {\mathbb {P}}$
be as in the statement. As in §2.4, we denote by
![]() $a,b,c,d$
the edges of the pillow
$a,b,c,d$
the edges of the pillow
![]() $\mathbb {P}$
. Let
$\mathbb {P}$
. Let
![]() $e'\subset \widehat {\mathbb {P}}$
be a base edge of a flap F in
$e'\subset \widehat {\mathbb {P}}$
be a base edge of a flap F in
![]() $\widehat {\mathbb {P}}$
such that
$\widehat {\mathbb {P}}$
such that
![]() $\widehat {\gamma }\cap \operatorname {int}(e') \neq \emptyset $
. We will assume that F is a horizontal flap. Then
$\widehat {\gamma }\cap \operatorname {int}(e') \neq \emptyset $
. We will assume that F is a horizontal flap. Then
![]() $\widehat {\mathcal {L}}(e')=a$
or
$\widehat {\mathcal {L}}(e')=a$
or
![]() $\widehat {\mathcal {L}}(e')=c$
. We will make the further assumption that
$\widehat {\mathcal {L}}(e')=c$
. We will make the further assumption that
![]() $\widehat {\mathcal {L}}(e')=a$
. The other cases, when
$\widehat {\mathcal {L}}(e')=a$
. The other cases, when
![]() $\widehat {\mathcal {L}}(e')=c$
or when F is a vertical flap, can be treated in a way that is completely analogous to the ensuing argument.
$\widehat {\mathcal {L}}(e')=c$
or when F is a vertical flap, can be treated in a way that is completely analogous to the ensuing argument.
Let
![]() $e"\subset F$
be the base edge of F different from
$e"\subset F$
be the base edge of F different from
![]() $e'$
, and
$e'$
, and
![]() $\widetilde e$
be the top edge of F. Then
$\widetilde e$
be the top edge of F. Then
![]() $\widehat {\mathcal {L}}(e")=a$
and
$\widehat {\mathcal {L}}(e")=a$
and
![]() $\widehat {\mathcal {L}}(\widetilde e)=c$
. Moreover,
$\widehat {\mathcal {L}}(\widetilde e)=c$
. Moreover,
We have
![]() $\gamma =\wp (\ell _{r/s})$
with
$\gamma =\wp (\ell _{r/s})$
with
![]() $r/s\ne 0$
, and so by Lemma 2.5, the sets
$r/s\ne 0$
, and so by Lemma 2.5, the sets
![]() $a\cap \gamma $
and
$a\cap \gamma $
and
![]() $c\cap \gamma $
are finite and non-empty and the points in these sets alternate on
$c\cap \gamma $
are finite and non-empty and the points in these sets alternate on
![]() $\gamma $
. Since
$\gamma $
. Since
![]() $\widehat {\mathcal {L}}$
is a covering map from
$\widehat {\mathcal {L}}$
is a covering map from
![]() $\widehat {\gamma }$
onto
$\widehat {\gamma }$
onto
![]() $\gamma $
, we conclude that the sets
$\gamma $
, we conclude that the sets
![]() $\widehat {\gamma } \cap \widehat {\mathcal {L}}^{-1}(a) $
and
$\widehat {\gamma } \cap \widehat {\mathcal {L}}^{-1}(a) $
and
![]() $\widehat {\gamma } \cap \widehat {\mathcal {L}}^{-1}(c)$
are also finite and non-empty and the points in these sets alternate on
$\widehat {\gamma } \cap \widehat {\mathcal {L}}^{-1}(c)$
are also finite and non-empty and the points in these sets alternate on
![]() $\widehat {\gamma }$
.
$\widehat {\gamma }$
.

Figure 17 A pullback
![]() $\widehat {\gamma }$
going over a horizontal flap in
$\widehat {\gamma }$
going over a horizontal flap in
![]() $\widehat {\mathbb {P}}$
.
$\widehat {\mathbb {P}}$
.
We choose a point
![]() $p\in \widehat {\gamma } \cap \operatorname {int}(e')$
. Since
$p\in \widehat {\gamma } \cap \operatorname {int}(e')$
. Since
![]() $\gamma =\wp (\ell _{r/s})$
, the curve
$\gamma =\wp (\ell _{r/s})$
, the curve
![]() $\gamma $
has transverse intersections with
$\gamma $
has transverse intersections with
![]() $\operatorname {int}(a)$
. It follows that the pullback
$\operatorname {int}(a)$
. It follows that the pullback
![]() $\widehat \gamma $
has a transverse intersection with
$\widehat \gamma $
has a transverse intersection with
![]() $\operatorname {int}(e')$
at p, and so
$\operatorname {int}(e')$
at p, and so
![]() $\widehat {\gamma } $
crosses into the interior of the flap F at p. Therefore, if we travel along
$\widehat {\gamma } $
crosses into the interior of the flap F at p. Therefore, if we travel along
![]() $\widehat {\gamma } $
starting at
$\widehat {\gamma } $
starting at
![]() $p\in \widehat {\gamma } \cap \widehat {\mathcal {L}}^{-1}(a)$
and traverse into the interior of the flap F, we must meet
$p\in \widehat {\gamma } \cap \widehat {\mathcal {L}}^{-1}(a)$
and traverse into the interior of the flap F, we must meet
![]() $\widehat {\mathcal {L}}^{-1}(c)$
before we possibly exit F through its boundary
$\widehat {\mathcal {L}}^{-1}(c)$
before we possibly exit F through its boundary
![]() $\partial F=e'\cup e"=F\cap \widehat {\mathcal {L}}^{-1}(a)$
(see equation (5.2)). Now
$\partial F=e'\cup e"=F\cap \widehat {\mathcal {L}}^{-1}(a)$
(see equation (5.2)). Now
![]() $F\cap \widehat {\mathcal {L}}^{-1}(c)=\widetilde e$
and so this implies that the pullback
$F\cap \widehat {\mathcal {L}}^{-1}(c)=\widetilde e$
and so this implies that the pullback
![]() $\widehat {\gamma }$
meets the top edge
$\widehat {\gamma }$
meets the top edge
![]() $\widetilde e$
(see Figure 17 for an illustration). The statement follows.
$\widetilde e$
(see Figure 17 for an illustration). The statement follows.
We are now ready to prove the main result of this section.
Proof of Theorem 5.3
Let
![]() $f\colon \mathbb {P}\rightarrow \mathbb {P}$
be a Thurston map as in the statement, obtained from the
$f\colon \mathbb {P}\rightarrow \mathbb {P}$
be a Thurston map as in the statement, obtained from the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
,
$\mathcal {L}_n$
,
![]() $n\ge 2$
, by gluing
$n\ge 2$
, by gluing
![]() $n_h\ge 0$
horizontal and
$n_h\ge 0$
horizontal and
![]() $n_v\ge 0$
vertical flaps, where we assume
$n_v\ge 0$
vertical flaps, where we assume
![]() $n_h+n_v>0$
. As described in the beginning of this section, then
$n_h+n_v>0$
. As described in the beginning of this section, then
![]() $f=\widehat {\mathcal {L}} \circ \phi ^{-1}$
, where
$f=\widehat {\mathcal {L}} \circ \phi ^{-1}$
, where
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
is a branched covering map on the associated flapped pillow
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
is a branched covering map on the associated flapped pillow
![]() $ \widehat {\mathbb {P}}$
and
$ \widehat {\mathbb {P}}$
and
![]() $\phi \colon \widehat {\mathbb {P}} \rightarrow \mathbb {P}$
is an identifying homeomorphism as discussed in §4.2. Note that
$\phi \colon \widehat {\mathbb {P}} \rightarrow \mathbb {P}$
is an identifying homeomorphism as discussed in §4.2. Note that
![]() $ \widehat {\mathbb {P}}$
has at least one flap, since
$ \widehat {\mathbb {P}}$
has at least one flap, since
![]() $n_h+n_v>0$
. Following the notation from §4.2, we denote by
$n_h+n_v>0$
. Following the notation from §4.2, we denote by
![]() $\widehat a$
,
$\widehat a$
,
![]() $\widehat b$
,
$\widehat b$
,
![]() $\widehat c$
,
$\widehat c$
,
![]() $\widehat d$
the arcs in
$\widehat d$
the arcs in
![]() $(\widehat {\mathbb {P}}, \widehat V)$
that, under
$(\widehat {\mathbb {P}}, \widehat V)$
that, under
![]() $\phi $
, correspond to the edges a, b, c, d of
$\phi $
, correspond to the edges a, b, c, d of
![]() $\mathbb {P}$
, respectively.
$\mathbb {P}$
, respectively.
We now argue by contradiction and assume that there exists an essential Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P}, {P_f})=(\mathbb {P},V)$
that is not isotopic to
$(\mathbb {P}, {P_f})=(\mathbb {P},V)$
that is not isotopic to
![]() $\alpha ^h$
or
$\alpha ^h$
or
![]() $\alpha ^v$
relative to
$\alpha ^v$
relative to
![]() ${P_f}=V$
, but is an obstruction for f, that is,
${P_f}=V$
, but is an obstruction for f, that is,
![]() $\unicode{x3bb} _f(\gamma ) \geq 1$
. Since we can replace
$\unicode{x3bb} _f(\gamma ) \geq 1$
. Since we can replace
![]() $\gamma $
with any curve in the same isotopy class, by Lemma 2.3, we may assume that
$\gamma $
with any curve in the same isotopy class, by Lemma 2.3, we may assume that
![]() $\gamma = \wp (\ell _{r/s})$
for a straight line
$\gamma = \wp (\ell _{r/s})$
for a straight line
![]() $\ell _{r/s}\subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
with slope
$\ell _{r/s}\subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. Since
$r/s\in \widehat {\mathbb {Q}}$
. Since
![]() $\gamma $
is not isotopic to
$\gamma $
is not isotopic to
![]() $\alpha ^h$
or
$\alpha ^h$
or
![]() $\alpha ^v$
relative to V, we have
$\alpha ^v$
relative to V, we have
![]() $r/s\ne 0,\infty $
, and so
$r/s\ne 0,\infty $
, and so
![]() $r,s\ne 0$
. Then it follows from Lemma 2.4(iii) and (iv) that
$r,s\ne 0$
. Then it follows from Lemma 2.4(iii) and (iv) that
 $$ \begin{align} \#(a\cap \gamma)= \mathrm{i}(a, \gamma)= |&r|= \mathrm{i}(c, \gamma) =\#(c\cap \gamma)>0, \nonumber\\ \#(b\cap \gamma)=\mathrm{i}(b,\gamma) =&s = \mathrm{i} (d,\gamma) =\#(d\cap \gamma) >0. \end{align} $$
$$ \begin{align} \#(a\cap \gamma)= \mathrm{i}(a, \gamma)= |&r|= \mathrm{i}(c, \gamma) =\#(c\cap \gamma)>0, \nonumber\\ \#(b\cap \gamma)=\mathrm{i}(b,\gamma) =&s = \mathrm{i} (d,\gamma) =\#(d\cap \gamma) >0. \end{align} $$
In particular,
![]() $\gamma \subset \mathbb {P}\smallsetminus V$
intersects the interiors of all four edges of
$\gamma \subset \mathbb {P}\smallsetminus V$
intersects the interiors of all four edges of
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
Let
![]() $\gamma _1, \ldots , \gamma _k$
for some
$\gamma _1, \ldots , \gamma _k$
for some
![]() $k\in \mathbb {N}$
denote all the pullbacks of
$k\in \mathbb {N}$
denote all the pullbacks of
![]() $\gamma $
under f that are isotopic to
$\gamma $
under f that are isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() ${P_f}$
. By construction of the blown-up map, the arc
${P_f}$
. By construction of the blown-up map, the arc
![]() $\widehat a=\phi ^{-1}(a) $
consists of n
$\widehat a=\phi ^{-1}(a) $
consists of n
![]() $1$
-edges in
$1$
-edges in
![]() $\widehat {\mathbb {P}}$
, each of which is homeomorphically mapped onto a by
$\widehat {\mathbb {P}}$
, each of which is homeomorphically mapped onto a by
![]() $\widehat {\mathcal {L}}$
. This implies that the map
$\widehat {\mathcal {L}}$
. This implies that the map
![]() $f|a\colon a\to a$
is at most n-to-
$f|a\colon a\to a$
is at most n-to-
![]() $1$
. By (5.3), we can apply Lemma 5.5 to a and
$1$
. By (5.3), we can apply Lemma 5.5 to a and
![]() $\gamma $
and conclude that
$\gamma $
and conclude that
![]() $k\leq n$
.
$k\leq n$
.
By Lemma 5.1, the horizontal curve
![]() $\alpha ^h$
has n distinct pullbacks under f that are isotopic to
$\alpha ^h$
has n distinct pullbacks under f that are isotopic to
![]() $\alpha ^h$
relative to
$\alpha ^h$
relative to
![]() ${P_f}$
. Since
${P_f}$
. Since
by Lemma 2.4(i), we can apply Lemma 5.5 again, this time to
![]() $\gamma _j$
and
$\gamma _j$
and
![]() $\alpha ^h$
(in the roles of
$\alpha ^h$
(in the roles of
![]() $\widetilde \alpha $
and
$\widetilde \alpha $
and
![]() $\gamma $
, respectively), and conclude that
$\gamma $
, respectively), and conclude that
![]() $n\leq \deg (f\colon \gamma _j\to \gamma )$
for all
$n\leq \deg (f\colon \gamma _j\to \gamma )$
for all
![]() $j=1,\ldots ,k$
.
$j=1,\ldots ,k$
.
Then

Therefore,
![]() $k=n$
and
$k=n$
and
![]() $\deg (f\colon \gamma _j\to \gamma )= n$
for each
$\deg (f\colon \gamma _j\to \gamma )= n$
for each
![]() $j=1,\ldots ,n$
.
$j=1,\ldots ,n$
.
This shows that the curve
![]() $\gamma $
has exactly n essential pullbacks under
$\gamma $
has exactly n essential pullbacks under
![]() $\widehat {\mathcal {L}}$
given by
$\widehat {\mathcal {L}}$
given by ![]() . Here, the isotopy classes are considered with respect to the vertex set
. Here, the isotopy classes are considered with respect to the vertex set
![]() $\widehat V$
of
$\widehat V$
of
![]() $\widehat {\mathbb {P}}$
. We will now use the second part of Lemma 5.5 to show that none of these pullbacks goes over a flap in
$\widehat {\mathbb {P}}$
. We will now use the second part of Lemma 5.5 to show that none of these pullbacks goes over a flap in
![]() $\widehat {\mathbb {P}}$
.
$\widehat {\mathbb {P}}$
.
Claim. For each flap F in
![]() $\widehat {\mathbb {P}}$
and each pullback
$\widehat {\mathbb {P}}$
and each pullback
![]() $\widehat {\gamma }_j$
,
$\widehat {\gamma }_j$
,
![]() $j=1,\ldots ,n$
, we have
$j=1,\ldots ,n$
, we have
![]() $F\cap \widehat {\gamma }_j = \emptyset $
.
$F\cap \widehat {\gamma }_j = \emptyset $
.
To see that the claim is true, suppose some pullback
![]() $\widehat {\gamma }_j$
meets a flap F in
$\widehat {\gamma }_j$
meets a flap F in
![]() $\widehat {\mathbb {P}}$
. We may assume that F is a horizontal flap; the other case, when F is vertical, can be treated by similar considerations. Then F contains a peripheral pullback
$\widehat {\mathbb {P}}$
. We may assume that F is a horizontal flap; the other case, when F is vertical, can be treated by similar considerations. Then F contains a peripheral pullback
![]() $\widehat \alpha ^h$
of
$\widehat \alpha ^h$
of
![]() $\alpha ^h$
under
$\alpha ^h$
under
![]() $\widehat {\mathcal {L}}$
, which separates the union
$\widehat {\mathcal {L}}$
, which separates the union
![]() $\partial F$
of the two base edges of F from the top edge of F. We will first show that
$\partial F$
of the two base edges of F from the top edge of F. We will first show that
![]() $\widehat {\gamma }_j$
intersects
$\widehat {\gamma }_j$
intersects
![]() $\widehat \alpha ^h$
.
$\widehat \alpha ^h$
.
Note that
![]() $\partial F$
is a Jordan curve and that
$\partial F$
is a Jordan curve and that
![]() $\operatorname {int}(F)$
does not contain any point from the vertex set
$\operatorname {int}(F)$
does not contain any point from the vertex set
![]() $\widehat V$
of
$\widehat V$
of
![]() $\widehat {\mathbb {P}}$
. It follows that the curve
$\widehat {\mathbb {P}}$
. It follows that the curve
![]() $\widehat {\gamma }_j$
must intersect
$\widehat {\gamma }_j$
must intersect
![]() $\partial F$
, because
$\partial F$
, because
![]() $\widehat {\gamma }_j$
is essential in
$\widehat {\gamma }_j$
is essential in
![]() $(\widehat {\mathbb {P}}, \widehat V)$
. Since the curve
$(\widehat {\mathbb {P}}, \widehat V)$
. Since the curve
![]() $\gamma $
does not pass through
$\gamma $
does not pass through
![]() ${P_f}=V$
, its pullback
${P_f}=V$
, its pullback
![]() $\widehat {\gamma }_j$
under
$\widehat {\gamma }_j$
under
![]() $\widehat {\mathcal {L}}$
does not pass through any
$\widehat {\mathcal {L}}$
does not pass through any
![]() $1$
-vertex in
$1$
-vertex in
![]() $\widehat {\mathbb {P}}$
. Consequently,
$\widehat {\mathbb {P}}$
. Consequently,
![]() $\widehat {\gamma }_j$
must meet the interior of one of the two base edges of F, which compose the boundary
$\widehat {\gamma }_j$
must meet the interior of one of the two base edges of F, which compose the boundary
![]() $\partial F$
. Lemma 5.6 now implies that
$\partial F$
. Lemma 5.6 now implies that
![]() $\widehat {\gamma }_j$
also meets the top edge of F. Therefore,
$\widehat {\gamma }_j$
also meets the top edge of F. Therefore,
![]() $\widehat {\gamma }_j$
meets the peripheral pullback
$\widehat {\gamma }_j$
meets the peripheral pullback
![]() $\widehat \alpha ^h$
in F.
$\widehat \alpha ^h$
in F.
It follows that
![]() $\gamma _j=\phi (\widehat {\gamma }_j)$
meets the peripheral pullback
$\gamma _j=\phi (\widehat {\gamma }_j)$
meets the peripheral pullback
![]() $\phi (\widehat \alpha ^h)$
of
$\phi (\widehat \alpha ^h)$
of
![]() $\alpha ^h$
under f. Lemma 5.5 now implies that
$\alpha ^h$
under f. Lemma 5.5 now implies that
![]() $n< \deg (f\colon \gamma _j\to \gamma )=n$
, which is a contradiction. This finishes the proof of the claim.
$n< \deg (f\colon \gamma _j\to \gamma )=n$
, which is a contradiction. This finishes the proof of the claim.
The claim implies that each essential pullback
![]() $\widehat {\gamma }_j$
,
$\widehat {\gamma }_j$
,
![]() $j=1,\ldots , n$
, belongs to the base
$j=1,\ldots , n$
, belongs to the base
![]() $B(\widehat {\mathbb {P}})$
of
$B(\widehat {\mathbb {P}})$
of
![]() $\widehat {\mathbb {P}}$
. By (4.2), we can identify
$\widehat {\mathbb {P}}$
. By (4.2), we can identify
![]() $B(\widehat {\mathbb {P}})$
with the subset
$B(\widehat {\mathbb {P}})$
with the subset
![]() $\mathbb {P}\smallsetminus \bigcup _{e\in E} \operatorname {int}(e)$
of the original pillow
$\mathbb {P}\smallsetminus \bigcup _{e\in E} \operatorname {int}(e)$
of the original pillow
![]() $\mathbb {P}$
, where E denotes the non-empty subset of all
$\mathbb {P}$
, where E denotes the non-empty subset of all
![]() $1$
-edges of
$1$
-edges of
![]() $\mathbb {P}$
along which flaps were glued in the construction of
$\mathbb {P}$
along which flaps were glued in the construction of
![]() $\widehat {\mathbb {P}}$
.
$\widehat {\mathbb {P}}$
.
Under this identification, the map
![]() $\widehat {\mathcal {L}}$
on
$\widehat {\mathcal {L}}$
on
![]() $B(\widehat {\mathbb {P}})$
coincides with the
$B(\widehat {\mathbb {P}})$
coincides with the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
. Thus, we may view
$\mathcal {L}_n$
. Thus, we may view
![]() $\widehat {\gamma }_1, \ldots , \widehat {\gamma }_n$
as pullbacks of
$\widehat {\gamma }_1, \ldots , \widehat {\gamma }_n$
as pullbacks of
![]() $\gamma $
under
$\gamma $
under
![]() $\mathcal {L}_n$
on the original pillow
$\mathcal {L}_n$
on the original pillow
![]() $\mathbb {P}$
. Now
$\mathbb {P}$
. Now
![]() $\gamma $
has exactly n pullbacks under
$\gamma $
has exactly n pullbacks under
![]() $\mathcal {L}_n$
(see equation (3.4)). This implies that
$\mathcal {L}_n$
(see equation (3.4)). This implies that
Since
![]() $\gamma $
meets the interior of every edge of
$\gamma $
meets the interior of every edge of
![]() $\mathbb {P}$
, the set
$\mathbb {P}$
, the set
![]() $\mathcal {L}_n^{-1}(\gamma )=\widehat \gamma _1\cup \cdots \cup \widehat {\gamma }_n $
meets the interior of every
$\mathcal {L}_n^{-1}(\gamma )=\widehat \gamma _1\cup \cdots \cup \widehat {\gamma }_n $
meets the interior of every
![]() $1$
-edge of
$1$
-edge of
![]() $\mathbb {P}$
. This is impossible, because
$\mathbb {P}$
. This is impossible, because
does not meet the interior of any
![]() $1$
-edge in
$1$
-edge in
![]() $E\ne \emptyset $
. This is a contradiction and the statement follows.
$E\ne \emptyset $
. This is a contradiction and the statement follows.
6 Essential circuit length
To prove our main result, Theorem 1.1, we need some preparation, in particular, a refined version of Lemma 5.5. We will also address the question how blowing up arcs modifies the pullbacks of a curve
![]() $\alpha $
under natural restrictions on the blown-up arcs. First, we introduce some terminology and establish some auxiliary facts.
$\alpha $
under natural restrictions on the blown-up arcs. First, we introduce some terminology and establish some auxiliary facts.
Let
![]() $U\subset S^2$
be an open and connected set, and
$U\subset S^2$
be an open and connected set, and
![]() $\sigma \subset S^2$
be an arc. We say that
$\sigma \subset S^2$
be an arc. We say that
![]() $\sigma $
is an arc in U ending in
$\sigma $
is an arc in U ending in
![]() $\partial U$
if there exists an endpoint p of
$\partial U$
if there exists an endpoint p of
![]() $\sigma $
such that
$\sigma $
such that
![]() $\sigma \smallsetminus \{p\}\subset U$
and
$\sigma \smallsetminus \{p\}\subset U$
and
![]() $p\in \partial U$
.
$p\in \partial U$
.
Let
![]() $\mathcal {G}$
be a connected planar embedded graph in
$\mathcal {G}$
be a connected planar embedded graph in
![]() $S^2$
and U be one of its faces. Then U is simply connected, and so we can find a homeomorphism
$S^2$
and U be one of its faces. Then U is simply connected, and so we can find a homeomorphism
![]() $\varphi \colon \mathbb {D}\to U$
. Since we want some additional properties of
$\varphi \colon \mathbb {D}\to U$
. Since we want some additional properties of
![]() $\varphi $
here, it is easiest to equip
$\varphi $
here, it is easiest to equip
![]() $S^2$
with a complex structure and choose a conformal map
$S^2$
with a complex structure and choose a conformal map
![]() $\varphi \colon \mathbb {D}\to U$
.
$\varphi \colon \mathbb {D}\to U$
.
Since
![]() $\partial U$
is a finite union of edges of
$\partial U$
is a finite union of edges of
![]() $\mathcal {G}$
, this set is locally connected and so the conformal map
$\mathcal {G}$
, this set is locally connected and so the conformal map
![]() $\varphi $
extends to a surjective continuous map
$\varphi $
extends to a surjective continuous map
![]() $\varphi \colon \operatorname {cl}(\mathbb {D}) \rightarrow \operatorname {cl}(U)$
[Reference PommerenkePom92, Theorem 2.1]. This extension has the following property: if
$\varphi \colon \operatorname {cl}(\mathbb {D}) \rightarrow \operatorname {cl}(U)$
[Reference PommerenkePom92, Theorem 2.1]. This extension has the following property: if
![]() $\sigma $
is an arc in U ending in
$\sigma $
is an arc in U ending in
![]() $\partial U$
, then
$\partial U$
, then
![]() $\varphi ^{-1}(\sigma )$
is an arc in
$\varphi ^{-1}(\sigma )$
is an arc in
![]() $\mathbb {D}$
ending in
$\mathbb {D}$
ending in
![]() $\partial \mathbb {D}$
(see [Reference PommerenkePom92, Proposition 2.14]). For given
$\partial \mathbb {D}$
(see [Reference PommerenkePom92, Proposition 2.14]). For given
![]() $\mathcal {G}$
and U, we fix, once and for all, such a map
$\mathcal {G}$
and U, we fix, once and for all, such a map
![]() $\varphi =\varphi _{\mathcal {G}, U}$
from
$\varphi =\varphi _{\mathcal {G}, U}$
from
![]() $\operatorname {cl}(\mathbb {D})$
onto
$\operatorname {cl}(\mathbb {D})$
onto
![]() $\operatorname {cl}(U)$
.
$\operatorname {cl}(U)$
.
Let
![]() $(e_1,e_2,\ldots ,e_{n})$
be a circuit in
$(e_1,e_2,\ldots ,e_{n})$
be a circuit in
![]() $\mathcal {G}$
that traces the boundary
$\mathcal {G}$
that traces the boundary
![]() $\partial U$
. Recall from §2.3 that the number n is called the circuit length of U in
$\partial U$
. Recall from §2.3 that the number n is called the circuit length of U in
![]() $\mathcal {G}$
, and each edge
$\mathcal {G}$
, and each edge
![]() $e\in \partial U$
appears exactly once or twice in the sequence
$e\in \partial U$
appears exactly once or twice in the sequence
![]() $e_1,e_2,\ldots ,e_{n}$
depending on whether the face U lies on one or both sides of e, respectively. Then there is a corresponding decomposition
$e_1,e_2,\ldots ,e_{n}$
depending on whether the face U lies on one or both sides of e, respectively. Then there is a corresponding decomposition
![]() $\partial \mathbb {D}=\sigma _1\cup \cdots \cup \sigma _n$
of the unit circle
$\partial \mathbb {D}=\sigma _1\cup \cdots \cup \sigma _n$
of the unit circle
![]() $\partial \mathbb {D}$
into non-overlapping subarcs
$\partial \mathbb {D}$
into non-overlapping subarcs
![]() $\sigma _1, \ldots , \sigma _n$
of
$\sigma _1, \ldots , \sigma _n$
of
![]() $\partial \mathbb {D}$
such that
$\partial \mathbb {D}$
such that
![]() $\varphi =\varphi _{\mathcal {G}, U}$
is a homeomorphism of
$\varphi =\varphi _{\mathcal {G}, U}$
is a homeomorphism of
![]() $\sigma _m$
onto
$\sigma _m$
onto
![]() $e_m$
for each
$e_m$
for each
![]() $m=1, \ldots , n$
.
$m=1, \ldots , n$
.
Let
![]() $0<{\epsilon } < 1$
. We say that a Jordan curve
$0<{\epsilon } < 1$
. We say that a Jordan curve
![]() $\beta \subset U$
is an
$\beta \subset U$
is an
![]() ${\epsilon }$
-boundary of U with respect to
${\epsilon }$
-boundary of U with respect to
![]() $\mathcal {G}$
if
$\mathcal {G}$
if ![]() , and
, and
![]() $\beta '$
separates
$\beta '$
separates
![]() $0$
from
$0$
from
![]() $\partial \mathbb {D}$
. Then
$\partial \mathbb {D}$
. Then
![]() $\beta '$
is a core curve of the annulus
$\beta '$
is a core curve of the annulus
![]() $A_{\epsilon }$
.
$A_{\epsilon }$
.
For the remainder of this section,
![]() $f\colon S^2\rightarrow S^2$
is a Thurston map. All isotopies on
$f\colon S^2\rightarrow S^2$
is a Thurston map. All isotopies on
![]() $S^2$
are relative to
$S^2$
are relative to
![]() $P_f$
, and we consider intersection numbers in
$P_f$
, and we consider intersection numbers in
![]() $(S^2, P_f)$
.
$(S^2, P_f)$
.
Let e be an arc in
![]() $(S^2, {P_f})$
. Then we can naturally view the set
$(S^2, {P_f})$
. Then we can naturally view the set ![]() as a planar embedded graph with the vertex set
as a planar embedded graph with the vertex set
![]() $f^{-1}(\partial e)$
and the edges given by the lifts of e under f. Note that
$f^{-1}(\partial e)$
and the edges given by the lifts of e under f. Note that
![]() $\mathcal {G}$
is bipartite.
$\mathcal {G}$
is bipartite.
Lemma 6.1. Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map, e be an arc and
$f\colon S^2\rightarrow S^2$
be a Thurston map, e be an arc and
![]() $\gamma $
be a Jordan curve in
$\gamma $
be a Jordan curve in
![]() $(S^2, {P_f})$
with
$(S^2, {P_f})$
with
![]() $\#(e\cap \gamma )=\mathrm {i}(e,\gamma )$
. Suppose that
$\#(e\cap \gamma )=\mathrm {i}(e,\gamma )$
. Suppose that
![]() $\mathcal {H}$
is a connected subgraph of
$\mathcal {H}$
is a connected subgraph of
![]() $\mathcal {G}=f^{-1}(e)$
and U is a face of
$\mathcal {G}=f^{-1}(e)$
and U is a face of
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $2n$
with
$2n$
with
![]() $n\in \mathbb {N}$
be the circuit length of U in
$n\in \mathbb {N}$
be the circuit length of U in
![]() $\mathcal {H}$
. Then for each
$\mathcal {H}$
. Then for each
![]() $0<{\epsilon }<1$
, there exists an
$0<{\epsilon }<1$
, there exists an
![]() ${\epsilon }$
-boundary
${\epsilon }$
-boundary
![]() $\beta $
of U with respect to
$\beta $
of U with respect to
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $\#(\beta \cap f^{-1}(\gamma )) = 2n \cdot \mathrm {i}(e,\gamma ).$
$\#(\beta \cap f^{-1}(\gamma )) = 2n \cdot \mathrm {i}(e,\gamma ).$
Note that the circuit length of U in
![]() $\mathcal {H}$
is even since
$\mathcal {H}$
is even since
![]() $\mathcal {H}$
is a bipartite graph.
$\mathcal {H}$
is a bipartite graph.
Proof. Let ![]() . Then e and
. Then e and
![]() $\gamma $
have exactly s distinct points in common, say
$\gamma $
have exactly s distinct points in common, say
![]() $p_1, \ldots , p_s\in e\cap \gamma $
. Each point
$p_1, \ldots , p_s\in e\cap \gamma $
. Each point
![]() $p_j$
lies in
$p_j$
lies in
![]() $\operatorname {int}(e)$
, because
$\operatorname {int}(e)$
, because
![]() $\partial e\subset {P_f}$
and
$\partial e\subset {P_f}$
and
![]() $\gamma \subset S^2\smallsetminus {P_f}$
. Since e and
$\gamma \subset S^2\smallsetminus {P_f}$
. Since e and
![]() $\gamma $
are in minimal position, they meet transversely (see Lemma 2.2), that is, if we travel along
$\gamma $
are in minimal position, they meet transversely (see Lemma 2.2), that is, if we travel along
![]() $\gamma $
toward one of the points
$\gamma $
toward one of the points
![]() $p_j$
(according to some orientation of
$p_j$
(according to some orientation of
![]() $\gamma $
), then near
$\gamma $
), then near
![]() $p_j$
, we stay on one side of e, but cross over to the other side of e if we pass
$p_j$
, we stay on one side of e, but cross over to the other side of e if we pass
![]() $p_j$
.
$p_j$
.
This implies that we can find disjoint subarcs
![]() $\sigma _1, \ldots , \sigma _s$
of
$\sigma _1, \ldots , \sigma _s$
of
![]() $\gamma $
such that each arc
$\gamma $
such that each arc
![]() $\sigma _j$
contains
$\sigma _j$
contains
![]() $p_j$
in its interior, but contains no other point in
$p_j$
in its interior, but contains no other point in
![]() $e\cap \gamma $
. Moreover,
$e\cap \gamma $
. Moreover,
![]() $p_j$
splits
$p_j$
splits
![]() $\sigma _j$
into two non-overlapping subarcs
$\sigma _j$
into two non-overlapping subarcs
![]() $\sigma _j^L$
and
$\sigma _j^L$
and
![]() $\sigma _j^R$
with the common endpoint
$\sigma _j^R$
with the common endpoint
![]() $p_j$
so that with some fixed orientation of e, the arc
$p_j$
so that with some fixed orientation of e, the arc
![]() $\sigma _j^L$
lies to the left and
$\sigma _j^L$
lies to the left and
![]() $\sigma _j^R$
lies to the right of e. Note that if
$\sigma _j^R$
lies to the right of e. Note that if ![]() , then
, then
![]() $e\cap \gamma '=\emptyset $
.
$e\cap \gamma '=\emptyset $
.
For the given face U of
![]() $\mathcal {H}$
, we fix a map
$\mathcal {H}$
, we fix a map
![]() $\varphi =\varphi _{\mathcal {H},U}\colon \operatorname {cl}(\mathbb {D}) \rightarrow \operatorname {cl}(U)$
as discussed in the beginning of this section. Let
$\varphi =\varphi _{\mathcal {H},U}\colon \operatorname {cl}(\mathbb {D}) \rightarrow \operatorname {cl}(U)$
as discussed in the beginning of this section. Let
![]() $(e_1,\ldots ,e_{2n})$
be a circuit in
$(e_1,\ldots ,e_{2n})$
be a circuit in
![]() $\mathcal {H}$
that traces the boundary
$\mathcal {H}$
that traces the boundary
![]() $\partial U$
. As we have already pointed out, the number of edges in the circuit is even, because
$\partial U$
. As we have already pointed out, the number of edges in the circuit is even, because
![]() $\mathcal {H}$
is a bipartite graph. With suitable orientation of each arc
$\mathcal {H}$
is a bipartite graph. With suitable orientation of each arc
![]() $e_m$
, the face U lies on the left of
$e_m$
, the face U lies on the left of
![]() $e_m$
. If an arc appears twice in the list
$e_m$
. If an arc appears twice in the list
![]() $e_1,\ldots ,e_{2n}$
, then it will carry opposite orientations in its two occurrences.
$e_1,\ldots ,e_{2n}$
, then it will carry opposite orientations in its two occurrences.
We want to investigate the set
![]() $f^{-1}(\gamma )\cap \operatorname {cl}(U)$
near
$f^{-1}(\gamma )\cap \operatorname {cl}(U)$
near
![]() $\partial U$
. Note that f maps each arc
$\partial U$
. Note that f maps each arc
![]() $e_m$
homeomorphically onto e. This implies that f is a homeomorphism on a suitable Jordan region that contains
$e_m$
homeomorphically onto e. This implies that f is a homeomorphism on a suitable Jordan region that contains
![]() $e_m$
as a crosscut. It follows that we can pull back the local picture near points in
$e_m$
as a crosscut. It follows that we can pull back the local picture near points in
![]() $e\cap \gamma $
to a similar local picture for points in
$e\cap \gamma $
to a similar local picture for points in
![]() $e_m\cap f^{-1}(\gamma )$
. So if we choose the arcs
$e_m\cap f^{-1}(\gamma )$
. So if we choose the arcs
![]() $\sigma _j$
small enough, as we may assume, and pull them back by f, then it is clear that
$\sigma _j$
small enough, as we may assume, and pull them back by f, then it is clear that
![]() $f^{-1}(\gamma )\cap \operatorname {cl}(U)$
can be represented in the form
$f^{-1}(\gamma )\cap \operatorname {cl}(U)$
can be represented in the form
 $$ \begin{align*} f^{-1}(\gamma)\cap \operatorname{cl}(U)=K \cup \bigcup_{m=1}^{2n} \bigcup_{j=1}^s \sigma_{m,j},\end{align*} $$
$$ \begin{align*} f^{-1}(\gamma)\cap \operatorname{cl}(U)=K \cup \bigcup_{m=1}^{2n} \bigcup_{j=1}^s \sigma_{m,j},\end{align*} $$
where K has positive distance to
![]() $\partial U=e_1\cup \cdots \cup e_{2n}$
(with respect to some base metric on
$\partial U=e_1\cup \cdots \cup e_{2n}$
(with respect to some base metric on
![]() $S^2$
). Moreover, each
$S^2$
). Moreover, each
![]() $\sigma _{m,j}$
is an arc in U ending in
$\sigma _{m,j}$
is an arc in U ending in
![]() $e_m\subset \partial U$
such that f is a homeomorphism from
$e_m\subset \partial U$
such that f is a homeomorphism from
![]() $\sigma _{m,j}$
onto
$\sigma _{m,j}$
onto
![]() $\sigma _{j}^L$
or
$\sigma _{j}^L$
or
![]() $\sigma _{j}^R$
depending on whether
$\sigma _{j}^R$
depending on whether
![]() $f|e_m\colon e_m\rightarrow e$
is orientation-preserving or orientation-reversing. If we remove from each arc
$f|e_m\colon e_m\rightarrow e$
is orientation-preserving or orientation-reversing. If we remove from each arc
![]() $\sigma _{m,j}$
its endpoint in
$\sigma _{m,j}$
its endpoint in
![]() $e_m$
, then the half-open arcs obtained are all disjoint. Two arcs
$e_m$
, then the half-open arcs obtained are all disjoint. Two arcs
![]() $\sigma _{m,j}$
and
$\sigma _{m,j}$
and
![]() $\sigma _{m',j'}$
share an endpoint precisely when
$\sigma _{m',j'}$
share an endpoint precisely when
![]() $j=j'$
and they arise from edges
$j=j'$
and they arise from edges
![]() $e_m$
and
$e_m$
and
![]() $e_{m'}$
with the same underlying set, but with opposite orientations. In this case, f sends one of these arcs to
$e_{m'}$
with the same underlying set, but with opposite orientations. In this case, f sends one of these arcs to
![]() $\sigma ^L_j$
, and the other one to
$\sigma ^L_j$
, and the other one to
![]() $\sigma ^R_j$
.
$\sigma ^R_j$
.
Since K has positive distance to
![]() $\partial U$
, it is clear that if
$\partial U$
, it is clear that if
![]() $\beta $
is an
$\beta $
is an
![]() ${\epsilon }$
-boundary of U with respect to
${\epsilon }$
-boundary of U with respect to
![]() $\mathcal {H}$
for
$\mathcal {H}$
for
![]() ${\epsilon }>0$
small enough (as we may assume), then
${\epsilon }>0$
small enough (as we may assume), then
![]() $\beta \cap K=\emptyset $
. So to control
$\beta \cap K=\emptyset $
. So to control
![]() $\#(\beta \cap f^{-1}(\gamma ))$
, we have to worry only about the intersections of
$\#(\beta \cap f^{-1}(\gamma ))$
, we have to worry only about the intersections of
![]() $\beta $
with the arcs
$\beta $
with the arcs
![]() $\sigma _{m,j}$
.
$\sigma _{m,j}$
.
Note that there are exactly
![]() $2n\cdot s=2n\cdot \mathrm {i}(e,\gamma )$
of these arcs. If we pull them back by the map
$2n\cdot s=2n\cdot \mathrm {i}(e,\gamma )$
of these arcs. If we pull them back by the map
![]() $\varphi $
, then we obtain pairwise disjoint arcs in
$\varphi $
, then we obtain pairwise disjoint arcs in
![]() $\mathbb {D}$
ending in
$\mathbb {D}$
ending in
![]() $\partial \mathbb {D}$
. The statement now follows from the following fact, whose precise justification we leave to the reader: if
$\partial \mathbb {D}$
. The statement now follows from the following fact, whose precise justification we leave to the reader: if
![]() $\alpha _1, \ldots , \alpha _M$
with
$\alpha _1, \ldots , \alpha _M$
with
![]() $M\in \mathbb {N}_0$
are pairwise disjoint arcs in
$M\in \mathbb {N}_0$
are pairwise disjoint arcs in
![]() $\mathbb {D}$
ending in
$\mathbb {D}$
ending in
![]() $\partial \mathbb {D}$
, then for each
$\partial \mathbb {D}$
, then for each
![]() $0<{\epsilon }<1$
, there exists a core curve
$0<{\epsilon }<1$
, there exists a core curve
![]() $\beta '$
of the annulus
$\beta '$
of the annulus
![]() $A_{\epsilon }= \{z\in \mathbb {C}: 1-{\epsilon }<|z|<1\}$
such that
$A_{\epsilon }= \{z\in \mathbb {C}: 1-{\epsilon }<|z|<1\}$
such that
![]() $ \# (\beta '\cap (\alpha _1\cup \cdots \cup \alpha _M))=M$
.
$ \# (\beta '\cap (\alpha _1\cup \cdots \cup \alpha _M))=M$
.
Now we are ready to provide a refined version of Lemma 5.5.
Lemma 6.2. Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map with
$f\colon S^2\rightarrow S^2$
be a Thurston map with
![]() $\#{P_f}=4$
,
$\#{P_f}=4$
,
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
be essential Jordan curves in
$\gamma $
be essential Jordan curves in
![]() $(S^2, {P_f})$
, c be a core arc of
$(S^2, {P_f})$
, c be a core arc of
![]() $\alpha $
, and assume that
$\alpha $
, and assume that
![]() $\#(c \cap \gamma ) =\mathrm {i}(c, \gamma )>0$
.
$\#(c \cap \gamma ) =\mathrm {i}(c, \gamma )>0$
.
Let
![]() $\mathcal {H}$
be a connected subgraph of
$\mathcal {H}$
be a connected subgraph of ![]() , and U be a face of
, and U be a face of
![]() $\mathcal {H}$
such that for small enough
$\mathcal {H}$
such that for small enough
![]() ${\epsilon }>0$
, each
${\epsilon }>0$
, each
![]() ${\epsilon }$
-boundary
${\epsilon }$
-boundary
![]() $\beta $
of U with respect to
$\beta $
of U with respect to
![]() $\mathcal {H}$
is isotopic to
$\mathcal {H}$
is isotopic to
![]() $\alpha $
relative to
$\alpha $
relative to
![]() ${P_f}$
. Let
${P_f}$
. Let
![]() $2n$
with
$2n$
with
![]() $n \in \mathbb {N}$
be the circuit length of U in
$n \in \mathbb {N}$
be the circuit length of U in
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Then
![]() $k\le n$
, where
$k\le n$
, where
![]() $k\in N_0$
denotes the number of pullbacks of
$k\in N_0$
denotes the number of pullbacks of
![]() $\gamma $
under f that are isotopic to
$\gamma $
under f that are isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() ${P_f}$
. Moreover, if
${P_f}$
. Moreover, if
![]() $\partial U\subset \mathcal {H}$
meets a peripheral pullback of
$\partial U\subset \mathcal {H}$
meets a peripheral pullback of
![]() $\gamma $
under f, then
$\gamma $
under f, then
![]() $k<n$
.
$k<n$
.
Proof. Let
![]() $\gamma _1,\ldots , \gamma _k$
be the pullbacks of
$\gamma _1,\ldots , \gamma _k$
be the pullbacks of
![]() $\gamma $
under f that are isotopic to
$\gamma $
under f that are isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() ${P_f}$
. Then by Lemma 6.1, for sufficiently small
${P_f}$
. Then by Lemma 6.1, for sufficiently small
![]() ${\epsilon }> 0$
, we can find an
${\epsilon }> 0$
, we can find an
![]() ${\epsilon }$
-boundary
${\epsilon }$
-boundary
![]() $\beta $
of U with respect to
$\beta $
of U with respect to
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $\beta \sim \alpha $
relative to
$\beta \sim \alpha $
relative to
![]() ${P_f}$
and
${P_f}$
and
where the last equality follows from Lemma 2.6. Hence, we have
 $$ \begin{align} n\cdot \mathrm{i} (\alpha, \gamma) = \#( \beta\cap f^{-1}(\gamma)) \geq \sum_{j=1}^k \#( \beta \cap\gamma_j ) \geq \sum_{j=1}^k \mathrm{i}(\beta, \gamma_j)=k \cdot \mathrm{i}(\alpha,\gamma). \end{align} $$
$$ \begin{align} n\cdot \mathrm{i} (\alpha, \gamma) = \#( \beta\cap f^{-1}(\gamma)) \geq \sum_{j=1}^k \#( \beta \cap\gamma_j ) \geq \sum_{j=1}^k \mathrm{i}(\beta, \gamma_j)=k \cdot \mathrm{i}(\alpha,\gamma). \end{align} $$
Since
![]() $\mathrm {i}(\alpha ,\gamma )=2\cdot \mathrm {i}(c, \gamma )>0$
, we conclude that
$\mathrm {i}(\alpha ,\gamma )=2\cdot \mathrm {i}(c, \gamma )>0$
, we conclude that
![]() $k\le n$
, as desired.
$k\le n$
, as desired.
To see the second statement, we have to revisit the proof of Lemma 6.1. There we identified
![]() $2n\cdot \mathrm {i}(c,\gamma )=n\cdot \mathrm {i}(\alpha ,\gamma ) $
distinct arcs
$2n\cdot \mathrm {i}(c,\gamma )=n\cdot \mathrm {i}(\alpha ,\gamma ) $
distinct arcs
![]() $\sigma $
in U ending in
$\sigma $
in U ending in
![]() $\partial U$
(they were called
$\partial U$
(they were called
![]() $\sigma _{m,j}$
in the proof). These arcs were subarcs of
$\sigma _{m,j}$
in the proof). These arcs were subarcs of
![]() $f^{-1}(\gamma )$
and accounted for all possible intersections of
$f^{-1}(\gamma )$
and accounted for all possible intersections of
![]() $\beta $
with
$\beta $
with
![]() $f^{-1}(\gamma )$
for sufficiently small
$f^{-1}(\gamma )$
for sufficiently small
![]() ${\epsilon }>0$
; with a suitable choice of
${\epsilon }>0$
; with a suitable choice of
![]() $\beta $
, each of these arcs
$\beta $
, each of these arcs
![]() $\sigma $
gave precisely one such intersection point. Now if a peripheral pullback
$\sigma $
gave precisely one such intersection point. Now if a peripheral pullback
![]() $ \widetilde \gamma \subset f^{-1}(\gamma )$
of
$ \widetilde \gamma \subset f^{-1}(\gamma )$
of
![]() $\gamma $
under f meets
$\gamma $
under f meets
![]() $\partial U$
, then one of these arcs
$\partial U$
, then one of these arcs
![]() $\sigma $
is a subarc of
$\sigma $
is a subarc of
![]() $ \widetilde \gamma $
. It follows that the first inequality in (6.1) must be strict and so
$ \widetilde \gamma $
. It follows that the first inequality in (6.1) must be strict and so
![]() $k<n$
.
$k<n$
.
For the rest of this section, we fix a Thurston map
![]() $f\colon S^2\rightarrow S^2$
with
$f\colon S^2\rightarrow S^2$
with
![]() $\#{P_f}=4$
, an essential Jordan curve
$\#{P_f}=4$
, an essential Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $(S^2, {P_f})$
, and core arcs a and c of
$(S^2, {P_f})$
, and core arcs a and c of
![]() $\alpha $
that lie in different components of
$\alpha $
that lie in different components of
![]() ${S^{2}}\smallsetminus \alpha $
. We can view the set
${S^{2}}\smallsetminus \alpha $
. We can view the set ![]() as a planar embedded graph in
as a planar embedded graph in
![]() $S^2$
with the set of vertices
$S^2$
with the set of vertices
![]() $f^{-1}({P_f})$
, and the edge set consisting of the lifts of a and c under f. Then
$f^{-1}({P_f})$
, and the edge set consisting of the lifts of a and c under f. Then
![]() $\mathcal {G}$
is a bipartite graph.
$\mathcal {G}$
is a bipartite graph.
Let U be the unique connected component of
![]() ${S^{2}}\smallsetminus (a\cup c)$
. Then U is an annulus and
${S^{2}}\smallsetminus (a\cup c)$
. Then U is an annulus and
![]() $\alpha $
is its core curve. The connected components
$\alpha $
is its core curve. The connected components
![]() $\widetilde {U}$
of
$\widetilde {U}$
of
![]() $f^{-1}(U)$
are precisely the complementary components of
$f^{-1}(U)$
are precisely the complementary components of
![]() $\mathcal {G}=f^{-1}(a \cup c)$
in
$\mathcal {G}=f^{-1}(a \cup c)$
in
![]() $S^2$
. It easily follows from the Riemann–Hurwitz formula (see equation (2.2)) that each
$S^2$
. It easily follows from the Riemann–Hurwitz formula (see equation (2.2)) that each
![]() $\widetilde {U}$
is an annulus, and that
$\widetilde {U}$
is an annulus, and that
![]() $f\colon \widetilde {U} \rightarrow U$
is a covering map. Moreover, each such annulus contains precisely one pullback
$f\colon \widetilde {U} \rightarrow U$
is a covering map. Moreover, each such annulus contains precisely one pullback
![]() $\widetilde \alpha $
of
$\widetilde \alpha $
of
![]() $\alpha $
under f.
$\alpha $
under f.
This setup is illustrated in Figure 18. The points marked in black indicate the four postcritical points of f. The sphere on the right contains two core arcs a and c of a Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $({S^{2}},P_f)$
. On the left, the lifts of a and c under f are shown in blue and magenta colors, respectively, and the pullbacks of
$({S^{2}},P_f)$
. On the left, the lifts of a and c under f are shown in blue and magenta colors, respectively, and the pullbacks of
![]() $\alpha $
in green.
$\alpha $
in green.

Figure 18 A Thurston map f. The sphere on the right shows a Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $({S^{2}}, P_f)$
and two core arcs a and c. The sphere on the left shows the pullbacks of
$({S^{2}}, P_f)$
and two core arcs a and c. The sphere on the left shows the pullbacks of
![]() $\alpha $
under f and the planar embedded graph
$\alpha $
under f and the planar embedded graph
![]() $\mathcal {G}=f^{-1}(a\cup c)$
.
$\mathcal {G}=f^{-1}(a\cup c)$
.
We call a connected component
![]() $ \widetilde {U}$
of
$ \widetilde {U}$
of
![]() $f^{-1}(U)=S^2\smallsetminus \mathcal {G}$
essential or peripheral, depending on whether the unique pullback
$f^{-1}(U)=S^2\smallsetminus \mathcal {G}$
essential or peripheral, depending on whether the unique pullback
![]() $\widetilde \alpha $
of
$\widetilde \alpha $
of
![]() $\alpha $
contained in
$\alpha $
contained in
![]() $ \widetilde {U}$
is essential or peripheral in
$ \widetilde {U}$
is essential or peripheral in
![]() $(S^2, {P_f})$
, respectively. Each boundary
$(S^2, {P_f})$
, respectively. Each boundary
![]() $\partial \widetilde {U}$
has exactly two connected components. One of them is mapped by f to a and the other one to c; accordingly, we denote them by
$\partial \widetilde {U}$
has exactly two connected components. One of them is mapped by f to a and the other one to c; accordingly, we denote them by
![]() $\partial _a \widetilde U$
and
$\partial _a \widetilde U$
and
![]() $\partial _c \widetilde U$
, respectively. Then we have
$\partial _c \widetilde U$
, respectively. Then we have
The sets
![]() $\partial _a \widetilde {U}$
and
$\partial _a \widetilde {U}$
and
![]() $\partial _c \widetilde {U}$
are subgraphs of
$\partial _c \widetilde {U}$
are subgraphs of
![]() $\mathcal {G}$
. Since
$\mathcal {G}$
. Since
![]() $\widetilde {U}$
is a connected subset of
$\widetilde {U}$
is a connected subset of
![]() $S^2\smallsetminus \mathcal {G}\subset S^2\smallsetminus \partial _a \widetilde {U}$
, there exists a unique face
$S^2\smallsetminus \mathcal {G}\subset S^2\smallsetminus \partial _a \widetilde {U}$
, there exists a unique face
![]() $V_a$
of
$V_a$
of
![]() $\partial _a \widetilde {U} $
(considered as a subgraph of
$\partial _a \widetilde {U} $
(considered as a subgraph of
![]() $\mathcal {G}$
) such that
$\mathcal {G}$
) such that
![]() $\widetilde U\subset V_a$
. Similarly, there exists a unique face
$\widetilde U\subset V_a$
. Similarly, there exists a unique face
![]() $V_c$
of
$V_c$
of
![]() $\partial _c \widetilde U$
with
$\partial _c \widetilde U$
with
![]() $\widetilde U\subset V_c$
. By definition, the circuit length of
$\widetilde U\subset V_c$
. By definition, the circuit length of
![]() $\partial _a \widetilde U$
or of
$\partial _a \widetilde U$
or of
![]() $\partial _c \widetilde U$
is the circuit length of
$\partial _c \widetilde U$
is the circuit length of
![]() $V_a$
in
$V_a$
in
![]() $\partial _a \widetilde {U}$
or of
$\partial _a \widetilde {U}$
or of
![]() $V_c$
in
$V_c$
in
![]() $\partial _c \widetilde {U}$
, respectively.
$\partial _c \widetilde {U}$
, respectively.
Then the following statement is true.
Lemma 6.3. The circuit lengths of
![]() $\partial _a \widetilde {U}$
and
$\partial _a \widetilde {U}$
and
![]() $\partial _c \widetilde {U}$
are both equal to
$\partial _c \widetilde {U}$
are both equal to
![]() $2\cdot \deg (f\colon \widetilde {U} \rightarrow U)$
.
$2\cdot \deg (f\colon \widetilde {U} \rightarrow U)$
.
We call the identical circuit lengths of
![]() $\partial _a \widetilde {U}$
and
$\partial _a \widetilde {U}$
and
![]() $\partial _c \widetilde {U}$
the circuit length of
$\partial _c \widetilde {U}$
the circuit length of
![]() $\widetilde {U}$
(for fixed f,
$\widetilde {U}$
(for fixed f,
![]() $\alpha $
, a, and c).
$\alpha $
, a, and c).
Proof. It is clear that the subgraph
![]() $\partial _a \widetilde {U}$
of
$\partial _a \widetilde {U}$
of
![]() $\mathcal {G}$
is bipartite, and so
$\mathcal {G}$
is bipartite, and so
![]() $\partial _a \widetilde {U}$
has even circuit length
$\partial _a \widetilde {U}$
has even circuit length
![]() $2n$
with
$2n$
with
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let ![]() . It is enough to show that
. It is enough to show that
![]() $2n=2d$
, because the roles of
$2n=2d$
, because the roles of
![]() $\partial _a \widetilde {U}$
and
$\partial _a \widetilde {U}$
and
![]() $\partial _c \widetilde {U}$
are symmetric, and so the same identity will then also be true for the circuit length of
$\partial _c \widetilde {U}$
are symmetric, and so the same identity will then also be true for the circuit length of
![]() $\partial _c \widetilde {U}$
.
$\partial _c \widetilde {U}$
.
To see that
![]() $2n=2d$
, we use a similar idea as in the proof of Lemma 6.1. We choose a point
$2n=2d$
, we use a similar idea as in the proof of Lemma 6.1. We choose a point
![]() $p\in \operatorname {int}(a)$
and an arc
$p\in \operatorname {int}(a)$
and an arc
![]() $\sigma \subset S^2\smallsetminus c$
with
$\sigma \subset S^2\smallsetminus c$
with
![]() $p\in \operatorname {int}(\sigma )$
that meets a transversely in p, but has no other point with a in common. Then p splits
$p\in \operatorname {int}(\sigma )$
that meets a transversely in p, but has no other point with a in common. Then p splits
![]() $\sigma $
into two non-overlapping subarcs
$\sigma $
into two non-overlapping subarcs
![]() $\sigma ^L$
and
$\sigma ^L$
and
![]() $\sigma ^R$
with the common endpoint p so that with some fixed orientation of a, the arc
$\sigma ^R$
with the common endpoint p so that with some fixed orientation of a, the arc
![]() $\sigma ^L$
lies to the left and
$\sigma ^L$
lies to the left and
![]() $\sigma ^R$
lies to the right of a.
$\sigma ^R$
lies to the right of a.
Let
![]() $(e_1,\ldots ,e_{2n})$
be a circuit in
$(e_1,\ldots ,e_{2n})$
be a circuit in
![]() $\partial _a \widetilde U$
that traces the boundary
$\partial _a \widetilde U$
that traces the boundary
![]() $\partial V_a=\partial _a \widetilde U$
, where
$\partial V_a=\partial _a \widetilde U$
, where
![]() $V_a$
is the unique face of
$V_a$
is the unique face of
![]() $\partial _a \widetilde U$
with
$\partial _a \widetilde U$
with
![]() $\widetilde U\subset V_a$
. With suitable orientation of each arc
$\widetilde U\subset V_a$
. With suitable orientation of each arc
![]() $e_m$
, the face
$e_m$
, the face
![]() $\widetilde U$
lies on the left of
$\widetilde U$
lies on the left of
![]() $e_m$
. We now consider the set
$e_m$
. We now consider the set
![]() $f^{-1}(\sigma )\cap \operatorname {cl}(\widetilde U)$
near
$f^{-1}(\sigma )\cap \operatorname {cl}(\widetilde U)$
near
![]() $\partial _a \widetilde U$
. If we choose
$\partial _a \widetilde U$
. If we choose
![]() $\sigma $
small enough (as we may), then as in the proof of Lemma 6.1, we see that
$\sigma $
small enough (as we may), then as in the proof of Lemma 6.1, we see that
 $$ \begin{align} f^{-1}(\sigma)\cap \operatorname{cl}( \widetilde U)= \bigcup_{m=1}^{2n} \sigma_{m},\end{align} $$
$$ \begin{align} f^{-1}(\sigma)\cap \operatorname{cl}( \widetilde U)= \bigcup_{m=1}^{2n} \sigma_{m},\end{align} $$
where each
![]() $\sigma _{m}$
is an arc in
$\sigma _{m}$
is an arc in
![]() $\widetilde U$
ending in
$\widetilde U$
ending in
![]() $e_m\subset \partial _a \widetilde U$
such that f is a homeomorphism from
$e_m\subset \partial _a \widetilde U$
such that f is a homeomorphism from
![]() $\sigma _{m}$
to
$\sigma _{m}$
to
![]() $\sigma ^L$
or
$\sigma ^L$
or
![]() $\sigma ^R$
depending on whether
$\sigma ^R$
depending on whether
![]() $f|e_m\colon e_m\rightarrow a$
is orientation-preserving or orientation-reversing. If we remove from each arc
$f|e_m\colon e_m\rightarrow a$
is orientation-preserving or orientation-reversing. If we remove from each arc
![]() $\sigma _{m}$
its endpoint in
$\sigma _{m}$
its endpoint in
![]() $e_m$
, then the half-open arcs obtained are all disjoint. However, since
$e_m$
, then the half-open arcs obtained are all disjoint. However, since
![]() $f\colon \widetilde U \to U$
is a d-to-
$f\colon \widetilde U \to U$
is a d-to-
![]() $1$
covering map, there are precisely d distinct lifts of
$1$
covering map, there are precisely d distinct lifts of
![]() $\sigma ^L\smallsetminus \{p\}$
and d distinct lifts of
$\sigma ^L\smallsetminus \{p\}$
and d distinct lifts of
![]() $\sigma ^R\smallsetminus \{p\}$
under f contained in
$\sigma ^R\smallsetminus \{p\}$
under f contained in
![]() $\widetilde U$
. These must be precisely the half-open arcs obtained from
$\widetilde U$
. These must be precisely the half-open arcs obtained from
![]() $\sigma _{m}$
,
$\sigma _{m}$
,
![]() $m=1, \ldots , 2n$
. It follows that
$m=1, \ldots , 2n$
. It follows that
![]() $2n=2d$
, as desired.
$2n=2d$
, as desired.
Suppose
![]() $\widetilde U$
is an essential component of
$\widetilde U$
is an essential component of
![]() $f^{-1}(U)$
. We consider a circuit in
$f^{-1}(U)$
. We consider a circuit in
![]() $\partial \widetilde {U}\subset \mathcal {G}$
and denote by
$\partial \widetilde {U}\subset \mathcal {G}$
and denote by
![]() $\mathcal {H}\subset \mathcal {G}$
the underlying graph of the circuit. In the following, we will often conflate the circuit with its underlying graph
$\mathcal {H}\subset \mathcal {G}$
the underlying graph of the circuit. In the following, we will often conflate the circuit with its underlying graph
![]() $\mathcal {H}$
, where we think of
$\mathcal {H}$
, where we think of
![]() $\mathcal {H}$
as traversed as a circuit in some way. Since
$\mathcal {H}$
as traversed as a circuit in some way. Since
![]() $\widetilde {U}$
is a connected set in
$\widetilde {U}$
is a connected set in
![]() $S^2\smallsetminus \mathcal {G}\subset S^2\smallsetminus \mathcal {H}$
, there exists a unique face V of
$S^2\smallsetminus \mathcal {G}\subset S^2\smallsetminus \mathcal {H}$
, there exists a unique face V of
![]() $\mathcal {H}$
such that
$\mathcal {H}$
such that
![]() $\widetilde U\subset V$
. By definition, for
$\widetilde U\subset V$
. By definition, for
![]() $0<{\epsilon }<1$
, an
$0<{\epsilon }<1$
, an
![]() ${\epsilon }$
-boundary
${\epsilon }$
-boundary
![]() $\beta $
of
$\beta $
of
![]() $\widetilde U$
with respect to
$\widetilde U$
with respect to
![]() $\mathcal {H}$
is an
$\mathcal {H}$
is an
![]() ${\epsilon }$
-boundary of V with respect to
${\epsilon }$
-boundary of V with respect to
![]() $\mathcal {H}$
. This is an abuse of terminology, because even for small
$\mathcal {H}$
. This is an abuse of terminology, because even for small
![]() ${\epsilon }>0$
, such an
${\epsilon }>0$
, such an
![]() ${\epsilon }$
-boundary
${\epsilon }$
-boundary
![]() $\beta $
may not lie in
$\beta $
may not lie in
![]() $\widetilde U$
, but it is convenient in the following. Note that for small enough
$\widetilde U$
, but it is convenient in the following. Note that for small enough
![]() ${\epsilon }>0$
, such
${\epsilon }>0$
, such
![]() ${\epsilon }$
-boundaries for fixed
${\epsilon }$
-boundaries for fixed
![]() $\mathcal {H}$
have the same isotopy type relative to
$\mathcal {H}$
have the same isotopy type relative to
![]() ${P_f}$
.
${P_f}$
.
By definition, the essential circuit length of
![]() $\widetilde {U}$
is the minimal length of all circuits
$\widetilde {U}$
is the minimal length of all circuits
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\partial \widetilde {U}$
such that for all small enough
$\partial \widetilde {U}$
such that for all small enough
![]() ${\epsilon }>0$
, each
${\epsilon }>0$
, each
![]() ${\epsilon }$
-boundary of
${\epsilon }$
-boundary of
![]() $\widetilde {U}$
with respect to
$\widetilde {U}$
with respect to
![]() $\mathcal {H}$
is isotopic to a core curve of
$\mathcal {H}$
is isotopic to a core curve of
![]() $\widetilde {U}$
relative to
$\widetilde {U}$
relative to
![]() ${P_f}$
. As we will see momentarily, if we run through
${P_f}$
. As we will see momentarily, if we run through
![]() $\partial _a \widetilde {U}$
and
$\partial _a \widetilde {U}$
and
![]() $\partial _c \widetilde {U}$
as circuits, then they have this property and so the essential circuit length of
$\partial _c \widetilde {U}$
as circuits, then they have this property and so the essential circuit length of
![]() $\widetilde {U}$
is well defined. We call a circuit
$\widetilde {U}$
is well defined. We call a circuit
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\partial \widetilde U$
that realizes the essential circuit length an essential circuit for
$\partial \widetilde U$
that realizes the essential circuit length an essential circuit for
![]() $\widetilde {U}$
.
$\widetilde {U}$
.
Lemma 6.4. We have the inequality
For example, consider the annulus
![]() $\widetilde U$
containing the pullback
$\widetilde U$
containing the pullback
![]() $\widetilde \alpha $
in Figure 18. Then the circuit length of
$\widetilde \alpha $
in Figure 18. Then the circuit length of
![]() $ \widetilde U$
equals
$ \widetilde U$
equals
![]() $6$
, while the essential circuit length of
$6$
, while the essential circuit length of
![]() $ \widetilde U$
equals
$ \widetilde U$
equals
![]() $4$
.
$4$
.
Proof. Consider
![]() $\partial _a \widetilde {U}$
as a circuit in
$\partial _a \widetilde {U}$
as a circuit in
![]() $\partial \widetilde {U}$
. Let
$\partial \widetilde {U}$
. Let
![]() $V_a$
be the unique face of
$V_a$
be the unique face of
![]() $\partial _a \widetilde U$
that contains
$\partial _a \widetilde U$
that contains
![]() $\widetilde U$
. Then, for sufficiently small
$\widetilde U$
. Then, for sufficiently small
![]() ${\epsilon }>0$
, each
${\epsilon }>0$
, each
![]() ${\epsilon }$
-boundary
${\epsilon }$
-boundary
![]() $\beta $
of
$\beta $
of
![]() $V_a$
with respect to
$V_a$
with respect to
![]() $\partial _a \widetilde U$
necessarily separates
$\partial _a \widetilde U$
necessarily separates
![]() $\partial _a \widetilde {U}$
and
$\partial _a \widetilde {U}$
and
![]() $\partial _c \widetilde {U}$
, and is thus a core curve of
$\partial _c \widetilde {U}$
, and is thus a core curve of
![]() $\widetilde {U}$
. The statement follows.
$\widetilde {U}$
. The statement follows.
Let
![]() $\widehat f$
be a Thurston map obtained from f by blowing up some set of arcs E in
$\widehat f$
be a Thurston map obtained from f by blowing up some set of arcs E in
![]() ${S^2\smallsetminus f^{-1}({P_f})}$
. Under certain natural assumptions on the arcs in E, we want to describe the components of
${S^2\smallsetminus f^{-1}({P_f})}$
. Under certain natural assumptions on the arcs in E, we want to describe the components of
![]() $\widehat f^{-1}(U)$
and their properties in terms of the components of
$\widehat f^{-1}(U)$
and their properties in terms of the components of
![]() $f^{-1}(U)$
. We first formulate suitable conditions that allow such a comparison.
$f^{-1}(U)$
. We first formulate suitable conditions that allow such a comparison.
Definition 6.5. (
 $\alpha $
-restricted blow-up conditions)
$\alpha $
-restricted blow-up conditions)
Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map with
$f\colon S^2\rightarrow S^2$
be a Thurston map with
![]() $\#{P_f}=4$
,
$\#{P_f}=4$
,
![]() $\alpha $
be an essential Jordan curve in
$\alpha $
be an essential Jordan curve in
![]() $(S^2, {P_f})$
, and a and c be core arcs of
$(S^2, {P_f})$
, and a and c be core arcs of
![]() $\alpha $
that lie in different components of
$\alpha $
that lie in different components of
![]() ${S^{2}}\smallsetminus \alpha $
. Suppose
${S^{2}}\smallsetminus \alpha $
. Suppose
![]() $E\ne \emptyset $
is a finite set of arcs in
$E\ne \emptyset $
is a finite set of arcs in
![]() $({S^{2}},f^{-1}({P_f}))$
satisfying the blow-up conditions, that is, the interiors of the arcs in E are disjoint and
$({S^{2}},f^{-1}({P_f}))$
satisfying the blow-up conditions, that is, the interiors of the arcs in E are disjoint and
![]() $f\colon e\to f(e)$
is a homeomorphism for each
$f\colon e\to f(e)$
is a homeomorphism for each
![]() $e\in E$
.
$e\in E$
.
We say that E satisfies the
![]() $\alpha $
-restricted blow-up conditions if
$\alpha $
-restricted blow-up conditions if
for each
![]() $e\in E$
.
$e\in E$
.
In other words, for each
![]() $e\in E$
, the arc
$e\in E$
, the arc
![]() $f(e)$
is in minimal position with respect to
$f(e)$
is in minimal position with respect to
![]() $\alpha $
and intersects
$\alpha $
and intersects
![]() $\alpha $
only once, and
$\alpha $
only once, and
![]() $f(\operatorname {int}(e))=\operatorname {int}(f(e))$
belongs to the annulus
$f(\operatorname {int}(e))=\operatorname {int}(f(e))$
belongs to the annulus
![]() $U=S^2\smallsetminus (a\cup c)$
. Note that the endpoints of
$U=S^2\smallsetminus (a\cup c)$
. Note that the endpoints of
![]() $f(e)$
lie in
$f(e)$
lie in
![]() ${P_f}\subset a\cup c=\partial U$
; see Figure 19 for an illustration.
${P_f}\subset a\cup c=\partial U$
; see Figure 19 for an illustration.

Figure 19 The Thurston map f from Figure 18 and a set
![]() $E=\{e_1,e_2\}$
of arcs in
$E=\{e_1,e_2\}$
of arcs in
![]() $({S^{2}},f^{-1}({P_f}))$
satisfying the
$({S^{2}},f^{-1}({P_f}))$
satisfying the
![]() $\alpha $
-restricted blow-up conditions.
$\alpha $
-restricted blow-up conditions.
The condition in (6.3) is somewhat artificial, because it depends not only on
![]() $\alpha $
, but also on the choices of a and c. One can show that up to isotopy, it can be replaced by the more natural condition
$\alpha $
, but also on the choices of a and c. One can show that up to isotopy, it can be replaced by the more natural condition
![]() $\mathrm {i}(f(e),\alpha )=1$
for all
$\mathrm {i}(f(e),\alpha )=1$
for all
![]() $e\in E$
. Since the justification of this claim involves some topological machinery that is beyond the scope of the paper, we prefer to work with (6.3).
$e\in E$
. Since the justification of this claim involves some topological machinery that is beyond the scope of the paper, we prefer to work with (6.3).
Now the following statement is true.
Lemma 6.6. Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map with
$f\colon S^2\rightarrow S^2$
be a Thurston map with
![]() $\#{P_f}=4$
,
$\#{P_f}=4$
,
![]() $\alpha $
be an essential Jordan curve in
$\alpha $
be an essential Jordan curve in
![]() $(S^2, {P_f})$
, a and c be core arcs of
$(S^2, {P_f})$
, a and c be core arcs of
![]() $\alpha $
that lie in different components of
$\alpha $
that lie in different components of
![]() ${S^{2}}\smallsetminus \alpha $
. Suppose a set E of arcs in
${S^{2}}\smallsetminus \alpha $
. Suppose a set E of arcs in
![]() $({S^{2}},f^{-1}({P_f}))$
satisfies the
$({S^{2}},f^{-1}({P_f}))$
satisfies the
![]() $\alpha $
-restricted blow-up conditions and we are given multiplicities
$\alpha $
-restricted blow-up conditions and we are given multiplicities
![]() $m_e\in \mathbb {N}$
for
$m_e\in \mathbb {N}$
for
![]() $e\in E$
.
$e\in E$
.
Then the Thurston map
![]() $\widehat f$
obtained from f by blowing up each arc
$\widehat f$
obtained from f by blowing up each arc
![]() $e\in E$
with multiplicity
$e\in E$
with multiplicity
![]() $m_e$
can be constructed so that it satisfies the following conditions.
$m_e$
can be constructed so that it satisfies the following conditions.
-
(i)
 $\mathcal {G}=f^{-1}(a\cup c)$
is a subgraph of
$\mathcal {G}=f^{-1}(a\cup c)$
is a subgraph of  .
. -
(ii) Each complementary annulus
 $\widehat U$
of
$\widehat U$
of
 $\widehat {\mathcal {G}}$
is contained in a unique complementary annulus
$\widehat {\mathcal {G}}$
is contained in a unique complementary annulus
 $\widetilde U$
of
$\widetilde U$
of
 $\mathcal {G}$
. Moreover, the assignment
$\mathcal {G}$
. Moreover, the assignment
 $\widehat U\mapsto \widetilde U$
is a bijection between the complementary annuli of
$\widehat U\mapsto \widetilde U$
is a bijection between the complementary annuli of
 $\widehat {\mathcal {G}}$
and of
$\widehat {\mathcal {G}}$
and of
 $\mathcal {G}$
.
$\mathcal {G}$
.
Let
![]() $\widehat U$
and
$\widehat U$
and
![]() $\widetilde U$
be corresponding annuli as in condition (ii). Then the following statements are true.
$\widetilde U$
be corresponding annuli as in condition (ii). Then the following statements are true.
-
(iii) The core curves of
 $\widehat U$
and of
$\widehat U$
and of
 $\widetilde U$
are isotopic relative to
$\widetilde U$
are isotopic relative to
 ${P_f}=P_{\widehat f}$
. In particular,
${P_f}=P_{\widehat f}$
. In particular,
 $\widehat U$
is essential if and only if
$\widehat U$
is essential if and only if
 $\widetilde U$
is essential.
$\widetilde U$
is essential. -
(iv) If
 $\widehat U$
(and hence also
$\widehat U$
(and hence also
 $\widetilde U$
) is essential, then the essential circuit lengths of
$\widetilde U$
) is essential, then the essential circuit lengths of
 $\widehat U$
and
$\widehat U$
and
 $\widetilde U$
are the same. Moreover, if
$\widetilde U$
are the same. Moreover, if
 $\mathcal {H}$
is an essential circuit for
$\mathcal {H}$
is an essential circuit for
 $\widehat U$
, then
$\widehat U$
, then
 $\mathcal {H}$
is an essential circuit for
$\mathcal {H}$
is an essential circuit for
 $\widetilde U$
. In particular,
$\widetilde U$
. In particular,
 $\mathcal {H}\subset \partial \widetilde U\subset \partial \widehat U$
.
$\mathcal {H}\subset \partial \widetilde U\subset \partial \widehat U$
.
In condition (i), it is understood that the planar embedded graph
![]() $\mathcal {G}=f^{-1}(a\cup c)\subset S^2$
has the vertex set
$\mathcal {G}=f^{-1}(a\cup c)\subset S^2$
has the vertex set
![]() $f^{-1}(P_f)$
and that
$f^{-1}(P_f)$
and that
![]() $\widehat {\mathcal {G}}=\widehat f^{-1}(a\cup c)$
has the vertex set
$\widehat {\mathcal {G}}=\widehat f^{-1}(a\cup c)$
has the vertex set
![]() $\widehat {f}^{-1}(P_{\widehat {f}})\supset f^{-1}(P_f)$
.
$\widehat {f}^{-1}(P_{\widehat {f}})\supset f^{-1}(P_f)$
.
To illustrate the lemma, we consider the Thurston map
![]() $\widehat f$
that is indicated in Figure 20 and obtained from the Thurston map f in Figure 18 by blowing up the arcs
$\widehat f$
that is indicated in Figure 20 and obtained from the Thurston map f in Figure 18 by blowing up the arcs
![]() $e_1$
and
$e_1$
and
![]() $e_2$
in Figure 19 with multiplicities
$e_2$
in Figure 19 with multiplicities
![]() $m_{e_1}=2$
and
$m_{e_1}=2$
and
![]() $m_{e_2}=1$
. Here, the lifts of a and c under the blown-up map
$m_{e_2}=1$
. Here, the lifts of a and c under the blown-up map
![]() $\widehat f$
are shown in blue and magenta colors on the left sphere, respectively. Comparing these figures, we immediately see that in this case, the statements of the lemma are true.
$\widehat f$
are shown in blue and magenta colors on the left sphere, respectively. Comparing these figures, we immediately see that in this case, the statements of the lemma are true.
Proof. Let
![]() $e\in E$
be arbitrary. Since E satisfies the conditions in Definition 6.5, the set
$e\in E$
be arbitrary. Since E satisfies the conditions in Definition 6.5, the set
![]() $f(e)$
is an arc in
$f(e)$
is an arc in
![]() $(S^2, P_f)$
, and so
$(S^2, P_f)$
, and so
![]() $f(e)$
has its endpoints in
$f(e)$
has its endpoints in
![]() $P_f$
. By (6.3), the arc
$P_f$
. By (6.3), the arc
![]() $f(e)$
meets
$f(e)$
meets
![]() $\alpha $
precisely once and is in minimal position with respect to
$\alpha $
precisely once and is in minimal position with respect to
![]() $\alpha $
. In particular,
$\alpha $
. In particular,
![]() $f(e)$
meets
$f(e)$
meets
![]() $\alpha $
transversely by Lemma 2.2. This implies that the endpoints of
$\alpha $
transversely by Lemma 2.2. This implies that the endpoints of
![]() $f(e)$
lie in different core arcs of
$f(e)$
lie in different core arcs of
![]() $\alpha $
, and so one endpoint of
$\alpha $
, and so one endpoint of
![]() $f(e)$
lies in a and the other one in c. It follows that e has one endpoint in
$f(e)$
lies in a and the other one in c. It follows that e has one endpoint in
![]() $f^{-1}(a)$
and the other one in
$f^{-1}(a)$
and the other one in
![]() $f^{-1}(c)$
.
$f^{-1}(c)$
.
The set
![]() $\operatorname {int}(e)$
belongs to a unique annulus
$\operatorname {int}(e)$
belongs to a unique annulus
![]() $\widetilde U$
obtained as a complementary component of
$\widetilde U$
obtained as a complementary component of
![]() $\mathcal {G}=f^{-1}(a\cup c)$
. Then one endpoint of e is in
$\mathcal {G}=f^{-1}(a\cup c)$
. Then one endpoint of e is in
![]() $\partial _a \widetilde U=f^{-1}(a)\cap \partial \widetilde U$
and the other one in
$\partial _a \widetilde U=f^{-1}(a)\cap \partial \widetilde U$
and the other one in
![]() $\partial _c \widetilde U=f^{-1}(c)\cap \partial \widetilde U$
. In the blow-up construction described in §4.1, we can choose the open Jordan region
$\partial _c \widetilde U=f^{-1}(c)\cap \partial \widetilde U$
. In the blow-up construction described in §4.1, we can choose the open Jordan region
![]() $W_e$
so that
$W_e$
so that
![]() $W_e \subset \widetilde U$
for each
$W_e \subset \widetilde U$
for each
![]() $e\in E$
(of course, here the annulus
$e\in E$
(of course, here the annulus
![]() $\widetilde U$
depends on e). Now we make choices of the subsequent ingredients in the blow-up construction as discussed in §4.1. That is, for each fixed arc
$\widetilde U$
depends on e). Now we make choices of the subsequent ingredients in the blow-up construction as discussed in §4.1. That is, for each fixed arc
![]() $e\in E$
, we choose a closed Jordan region
$e\in E$
, we choose a closed Jordan region
![]() $D_e$
inside
$D_e$
inside
![]() $W_e$
. It is subdivided into
$W_e$
. It is subdivided into
![]() $m=m_e$
components
$m=m_e$
components
![]() $D_e^1,\ldots , D_e^m$
. In addition, we also choose a pseudo-isotopy
$D_e^1,\ldots , D_e^m$
. In addition, we also choose a pseudo-isotopy
![]() $h\colon {S^{2}}\times \mathbb {I}\to {S^{2}}$
satisfying conditions (B1)–(B4), as well as maps
$h\colon {S^{2}}\times \mathbb {I}\to {S^{2}}$
satisfying conditions (B1)–(B4), as well as maps
![]() $\varphi _k\colon D_e^k\to {S^{2}}$
,
$\varphi _k\colon D_e^k\to {S^{2}}$
,
![]() $k=1,\ldots , m=m_e$
, satisfying conditions (C1) and (C2). Let
$k=1,\ldots , m=m_e$
, satisfying conditions (C1) and (C2). Let
![]() $\widehat f$
be the Thurston map obtained by blowing up each arc
$\widehat f$
be the Thurston map obtained by blowing up each arc
![]() $e\in E$
with multiplicity
$e\in E$
with multiplicity
![]() $m_e$
according to these choices. We claim that
$m_e$
according to these choices. We claim that
![]() $\widehat f$
satisfies all the conditions in the statement.
$\widehat f$
satisfies all the conditions in the statement.
It immediately follows from condition (B3) and the definition of
![]() $\widehat f$
that
$\widehat f$
that
![]() $\mathcal {G}=f^{-1}(a\cup c)$
is a subgraph of
$\mathcal {G}=f^{-1}(a\cup c)$
is a subgraph of ![]() , and so statement (i) is true.
, and so statement (i) is true.
We have
![]() $\widehat {\mathcal {G}}\smallsetminus \mathcal {G} \subset \bigcup _{e\in E} D_e$
. Condition (C1) now implies that for each
$\widehat {\mathcal {G}}\smallsetminus \mathcal {G} \subset \bigcup _{e\in E} D_e$
. Condition (C1) now implies that for each
![]() $e\in E$
and each
$e\in E$
and each
![]() $k=1,\ldots , m=m_e$
, the set
$k=1,\ldots , m=m_e$
, the set
![]() $\widehat {\mathcal {G}} \cap D^k_e$
consists of two disjoint edges, one of which is homeomorphically mapped onto a and the other one onto c by
$\widehat {\mathcal {G}} \cap D^k_e$
consists of two disjoint edges, one of which is homeomorphically mapped onto a and the other one onto c by
![]() $\widehat f$
. We will call these edges a-sticks and c-sticks, respectively. Each closed Jordan region
$\widehat f$
. We will call these edges a-sticks and c-sticks, respectively. Each closed Jordan region
![]() $D_e$
contains exactly
$D_e$
contains exactly
![]() $m_e$
a-sticks, which have a common endpoint in
$m_e$
a-sticks, which have a common endpoint in
![]() $\partial e \cap f^{-1}(a)$
, and exactly
$\partial e \cap f^{-1}(a)$
, and exactly
![]() $m_e$
c-sticks with a common endpoint in
$m_e$
c-sticks with a common endpoint in
![]() $\partial e \cap f^{-1}(c)$
. The edge set of
$\partial e \cap f^{-1}(c)$
. The edge set of
![]() $\widehat {\mathcal {G}}$
consists of all the edges of
$\widehat {\mathcal {G}}$
consists of all the edges of
![]() $\mathcal {G}$
together with all the a-sticks and c-sticks.
$\mathcal {G}$
together with all the a-sticks and c-sticks.
Each complementary component
![]() $\widehat U$
of
$\widehat U$
of
![]() $\widehat {\mathcal {G}}$
is equal to a unique complementary component
$\widehat {\mathcal {G}}$
is equal to a unique complementary component
![]() $\widetilde U$
of
$\widetilde U$
of
![]() $\mathcal {G}$
with all the a- and c-sticks removed that are contained in
$\mathcal {G}$
with all the a- and c-sticks removed that are contained in
![]() $\operatorname {cl}(\widetilde U)$
. Statement (ii) follows. Furthermore, since
$\operatorname {cl}(\widetilde U)$
. Statement (ii) follows. Furthermore, since
![]() ${P_f}\cap \widetilde U = \emptyset $
, statement (iii) follows as well.
${P_f}\cap \widetilde U = \emptyset $
, statement (iii) follows as well.
To prove statement (iv), let
![]() $\widetilde U$
and
$\widetilde U$
and
![]() $\widehat U$
be corresponding essential annuli as in statement (ii). Viewing
$\widehat U$
be corresponding essential annuli as in statement (ii). Viewing
![]() $\partial \widetilde U$
as a subgraph of
$\partial \widetilde U$
as a subgraph of
![]() $\mathcal {G} $
and
$\mathcal {G} $
and
![]() $\partial \widehat U$
as a subgraph of
$\partial \widehat U$
as a subgraph of
![]() $\widehat {\mathcal {G}}$
, we see that
$\widehat {\mathcal {G}}$
, we see that
![]() $\partial \widetilde U$
is a subgraph of
$\partial \widetilde U$
is a subgraph of
![]() $\partial \widehat U$
. The additional edges of
$\partial \widehat U$
. The additional edges of
![]() $\partial \widehat U$
are exactly the a- and c-sticks contained in
$\partial \widehat U$
are exactly the a- and c-sticks contained in
![]() $\operatorname {cl}(\widetilde U)$
. It follows from the definition that the essential circuit length of
$\operatorname {cl}(\widetilde U)$
. It follows from the definition that the essential circuit length of
![]() $\widehat U$
is greater than or equal to the essential circuit length of
$\widehat U$
is greater than or equal to the essential circuit length of
![]() $\widetilde U$
.
$\widetilde U$
.
Let
![]() $\mathcal {H}$
be an essential circuit for
$\mathcal {H}$
be an essential circuit for
![]() $\widehat U$
and suppose
$\widehat U$
and suppose
![]() $\mathcal {H}$
contains an a- or c-stick
$\mathcal {H}$
contains an a- or c-stick
![]() $\sigma $
. Then one of the endpoints of
$\sigma $
. Then one of the endpoints of
![]() $\sigma $
has degree
$\sigma $
has degree
![]() $1$
in
$1$
in
![]() $\partial \widehat U$
, and so
$\partial \widehat U$
, and so
![]() $\sigma $
must appear in two consecutive positions in the circuit
$\sigma $
must appear in two consecutive positions in the circuit
![]() $\mathcal {H}$
. Omitting these two occurrences of
$\mathcal {H}$
. Omitting these two occurrences of
![]() $\sigma $
from
$\sigma $
from
![]() $\mathcal {H}$
, we get a shorter circuit
$\mathcal {H}$
, we get a shorter circuit
![]() $\mathcal {H}'$
in
$\mathcal {H}'$
in
![]() $\partial \widehat U$
such that for all small enough
$\partial \widehat U$
such that for all small enough
![]() ${\epsilon }>0$
, each
${\epsilon }>0$
, each
![]() ${\epsilon }$
-boundary of
${\epsilon }$
-boundary of
![]() $\widehat U$
with respect to
$\widehat U$
with respect to
![]() $\mathcal {H}'$
is isotopic to a core curve of
$\mathcal {H}'$
is isotopic to a core curve of
![]() $\widehat {U}$
relative to
$\widehat {U}$
relative to
![]() $P_{\widehat f} ={P_f}$
. This contradicts the choice of
$P_{\widehat f} ={P_f}$
. This contradicts the choice of
![]() $\mathcal {H}$
, and it follows that
$\mathcal {H}$
, and it follows that
![]() $\mathcal {H}$
does not contain any a- or c-sticks. Consequently,
$\mathcal {H}$
does not contain any a- or c-sticks. Consequently,
![]() $\mathcal {H}\subset \partial \widetilde U \subset \partial \widehat U$
, and the definition of the essential circuit length together with statement (iii) imply that
$\mathcal {H}\subset \partial \widetilde U \subset \partial \widehat U$
, and the definition of the essential circuit length together with statement (iii) imply that
![]() $\mathcal {H}$
is an essential circuit for
$\mathcal {H}$
is an essential circuit for
![]() $\widetilde U$
. Statement (iv) follows.
$\widetilde U$
. Statement (iv) follows.
7 Eliminating obstructions by blowing up arcs
The goal of this section is to show that the blow-up surgery can be applied to an obstructed Thurston map f with four postcritical points in such a way that the resulting map
![]() $\widehat {f}$
is realized by a rational map. The precise formulation is given in Theorem 1.1 (see also Remark 7.2). We will prove this statement by contradiction. For this, we assume that
$\widehat {f}$
is realized by a rational map. The precise formulation is given in Theorem 1.1 (see also Remark 7.2). We will prove this statement by contradiction. For this, we assume that
![]() $\widehat {f}$
has an obstruction, and will carefully analyze some related mapping degrees. This leads to a very tight situation, where in some inequalities, we actually have equality. From this, we want to conclude that f has a parabolic orbifold, in contradiction to our hypotheses in Theorem 1.1. We first formulate a related criterion for parabolicity.
$\widehat {f}$
has an obstruction, and will carefully analyze some related mapping degrees. This leads to a very tight situation, where in some inequalities, we actually have equality. From this, we want to conclude that f has a parabolic orbifold, in contradiction to our hypotheses in Theorem 1.1. We first formulate a related criterion for parabolicity.
Lemma 7.1. Let
![]() $f\colon S^2\rightarrow S^2$
be a Thurston map with
$f\colon S^2\rightarrow S^2$
be a Thurston map with
![]() $\#{P_f}=4$
. Suppose there exists a Jordan curve
$\#{P_f}=4$
. Suppose there exists a Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $(S^2, {P_f})$
such that the following conditions are true:
$(S^2, {P_f})$
such that the following conditions are true:
-
(i)
 $\alpha $
is an obstruction for f;
$\alpha $
is an obstruction for f; -
(ii)
 $\alpha $
has no peripheral pullbacks under f;
$\alpha $
has no peripheral pullbacks under f; -
(iii) if we choose core arcs a and c of
 $\alpha $
in different components of
$\alpha $
in different components of
 $S^2\smallsetminus \alpha $
and consider the graph
$S^2\smallsetminus \alpha $
and consider the graph
 $\mathcal {G}=f^{-1}(a\cup c)$
, then
$\mathcal {G}=f^{-1}(a\cup c)$
, then
 $\mathcal {G}$
has precisely
$\mathcal {G}$
has precisely
 $n\in \mathbb {N}$
essential complementary components
$n\in \mathbb {N}$
essential complementary components
 $U_1, \ldots , U_n$
with core curves isotopic to
$U_1, \ldots , U_n$
with core curves isotopic to
 $\alpha $
relative to
$\alpha $
relative to
 ${P_f}$
. Moreover, we assume the essential circuit length of
${P_f}$
. Moreover, we assume the essential circuit length of
 $U_j$
is equal to
$U_j$
is equal to
 $2n$
for each
$2n$
for each
 $j=1, \ldots , n$
.
$j=1, \ldots , n$
.
Then f has a parabolic orbifold.
Proof. Each
![]() $U_j$
contains precisely one pullback
$U_j$
contains precisely one pullback
![]() $\alpha _j$
of
$\alpha _j$
of
![]() $\alpha $
under f. The curves
$\alpha $
under f. The curves
![]() $\alpha _1, \ldots , \alpha _n$
are all the pullbacks of
$\alpha _1, \ldots , \alpha _n$
are all the pullbacks of
![]() $\alpha $
under f. Then it follows from our assumptions that
$\alpha $
under f. Then it follows from our assumptions that
 $$ \begin{align*} 2\deg(f\colon \alpha_j \rightarrow \alpha)&=2\deg(f\colon U_j\rightarrow U)\\ &= \text {circuit length of } U_j \quad \text{(by Lemma}\ 6.3) \\ &\ge \text {essential circuit length of } U_j \quad \text{(by Lemma }\ 6.4) \\ &= 2n, \end{align*} $$
$$ \begin{align*} 2\deg(f\colon \alpha_j \rightarrow \alpha)&=2\deg(f\colon U_j\rightarrow U)\\ &= \text {circuit length of } U_j \quad \text{(by Lemma}\ 6.3) \\ &\ge \text {essential circuit length of } U_j \quad \text{(by Lemma }\ 6.4) \\ &= 2n, \end{align*} $$
and so
![]() $\deg (f\colon \alpha _j \rightarrow \alpha )\ge n$
for
$\deg (f\colon \alpha _j \rightarrow \alpha )\ge n$
for
![]() $j=1, \ldots , n$
. However,
$j=1, \ldots , n$
. However,
![]() $\alpha $
is an obstruction for f, and so
$\alpha $
is an obstruction for f, and so

It follows that we have equality in all previous inequalities. In particular,
for
![]() $j=1, \ldots , n$
.
$j=1, \ldots , n$
.
We want to apply the second part of Lemma 3.3, that is, we want to show that
![]() $f^{-1}({P_f})\subset {C_f} \cup {P_f}$
. To see this, let
$f^{-1}({P_f})\subset {C_f} \cup {P_f}$
. To see this, let
![]() $v\in f^{-1}({P_f})$
be arbitrary. Then v is a vertex of
$v\in f^{-1}({P_f})$
be arbitrary. Then v is a vertex of
![]() $\mathcal {G}=f^{-1}(a\cup c)$
. If v is incident with two or more edges in
$\mathcal {G}=f^{-1}(a\cup c)$
. If v is incident with two or more edges in
![]() $\mathcal {G}$
, then
$\mathcal {G}$
, then
![]() $v\in {C_f}$
.
$v\in {C_f}$
.
Otherwise, v is the endpoint of precisely one edge e in
![]() $\mathcal {G}$
, and so
$\mathcal {G}$
, and so
![]() $\deg _{\mathcal {G}}(v)=1$
. We claim that then
$\deg _{\mathcal {G}}(v)=1$
. We claim that then
![]() $v\in {P_f}$
; to see this, we argue by contradiction and assume that
$v\in {P_f}$
; to see this, we argue by contradiction and assume that
![]() $v\not \in {P_f}$
. Since
$v\not \in {P_f}$
. Since
![]() $\alpha $
has no peripheral pullbacks, we have
$\alpha $
has no peripheral pullbacks, we have
 $$ \begin{align*} e\subset \mathcal{G} =\bigcup_{j=1}^n \partial U_j, \end{align*} $$
$$ \begin{align*} e\subset \mathcal{G} =\bigcup_{j=1}^n \partial U_j, \end{align*} $$
and so
![]() $e\subset \partial U_j$
for some
$e\subset \partial U_j$
for some
![]() $U_j$
. Then e is contained in a circuit
$U_j$
. Then e is contained in a circuit
![]() $(e_1,\ldots , e_{2n})$
of length
$(e_1,\ldots , e_{2n})$
of length
![]() $2n$
that traces one of the components of
$2n$
that traces one of the components of
![]() $\partial U_j$
. Since
$\partial U_j$
. Since
![]() $\deg _{\mathcal {G}}(v)=1$
, the circuit must traverse e twice with opposite orientations, that is, the edge e appears precisely in two consecutive entries in the cycle
$\deg _{\mathcal {G}}(v)=1$
, the circuit must traverse e twice with opposite orientations, that is, the edge e appears precisely in two consecutive entries in the cycle
![]() $(e_1,\ldots , e_{2n})$
. Erasing these two occurrences from the cycle, we obtain a new circuit in
$(e_1,\ldots , e_{2n})$
. Erasing these two occurrences from the cycle, we obtain a new circuit in
![]() $\partial U_j\subset \mathcal {G}$
with length
$\partial U_j\subset \mathcal {G}$
with length
![]() $2n-2$
. Let
$2n-2$
. Let
![]() $\mathcal {H}$
denote the underlying subgraph of
$\mathcal {H}$
denote the underlying subgraph of
![]() $\mathcal {G}$
corresponding to this shortened circuit and let U be the face of
$\mathcal {G}$
corresponding to this shortened circuit and let U be the face of
![]() $\mathcal {H}$
that contains
$\mathcal {H}$
that contains
![]() $U_j$
. Since the endpoint v of e does not belong to
$U_j$
. Since the endpoint v of e does not belong to
![]() ${P_f}$
, for every small enough
${P_f}$
, for every small enough
![]() ${\epsilon }>0$
, the
${\epsilon }>0$
, the
![]() ${\epsilon }$
-boundary of
${\epsilon }$
-boundary of
![]() $\mathcal {H}$
with respect to U is isotopic to the curve
$\mathcal {H}$
with respect to U is isotopic to the curve
![]() $\alpha _j$
relative to
$\alpha _j$
relative to
![]() ${P_f}$
. Then the essential circuit length of
${P_f}$
. Then the essential circuit length of
![]() $U_j$
is
$U_j$
is
![]() $\le 2n-2$
, contradicting the fact that
$\le 2n-2$
, contradicting the fact that
![]() $2n$
is the essential circuit length of
$2n$
is the essential circuit length of
![]() $U_j$
by our hypotheses. So we must have
$U_j$
by our hypotheses. So we must have
![]() $v\in {P_f}$
.
$v\in {P_f}$
.
It follows that
![]() $f^{-1}({P_f})\subset {C_f} \cup {P_f}$
, and so f has a parabolic orbifold by Lemma 3.3.
$f^{-1}({P_f})\subset {C_f} \cup {P_f}$
, and so f has a parabolic orbifold by Lemma 3.3.
We are now ready to prove our main result.
Proof of Theorem 1.1
As in the statement, suppose
![]() $f\colon {S^{2}}\to {S^{2}}$
is a Thurston map with
$f\colon {S^{2}}\to {S^{2}}$
is a Thurston map with
![]() $\#{P_f}=4$
and a hyperbolic orbifold. We assume that f has an obstruction given by a Jordan curve
$\#{P_f}=4$
and a hyperbolic orbifold. We assume that f has an obstruction given by a Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $(S^2, {P_f})$
. We choose core arcs a and c for
$(S^2, {P_f})$
. We choose core arcs a and c for
![]() $\alpha $
that lie in different components of
$\alpha $
that lie in different components of
![]() $S^2\smallsetminus \alpha $
, and assume that
$S^2\smallsetminus \alpha $
, and assume that
![]() $E\ne \emptyset $
is a finite set of arcs in
$E\ne \emptyset $
is a finite set of arcs in
![]() $({S^{2}},f^{-1}({P_f}))$
that satisfies the
$({S^{2}},f^{-1}({P_f}))$
that satisfies the
![]() $\alpha $
-restricted blow-up conditions as in Definition 6.5.
$\alpha $
-restricted blow-up conditions as in Definition 6.5.
We assume that we obtained a Thurston map
![]() $\widehat {f}\colon S^2\rightarrow S^2$
by blowing up arcs in E (with some multiplicities) so that
$\widehat {f}\colon S^2\rightarrow S^2$
by blowing up arcs in E (with some multiplicities) so that
![]() $\unicode{x3bb} _{\widehat {f}}(\alpha )<1$
. Then
$\unicode{x3bb} _{\widehat {f}}(\alpha )<1$
. Then
![]() $P_{\widehat {f}}={P_f}$
and
$P_{\widehat {f}}={P_f}$
and
![]() $\widehat {f}$
has a hyperbolic orbifold (see Lemma 4.3 and Remark 4.4). Up to replacing
$\widehat {f}$
has a hyperbolic orbifold (see Lemma 4.3 and Remark 4.4). Up to replacing
![]() $\widehat {f}$
with a Thurston equivalent map, we may also assume that the statements in Lemma 6.6 are true for the map
$\widehat {f}$
with a Thurston equivalent map, we may also assume that the statements in Lemma 6.6 are true for the map
![]() $\widehat {f}$
. We now argue by contradiction and assume that
$\widehat {f}$
. We now argue by contradiction and assume that
![]() $\widehat {f}$
is not realized by a rational map. Then by Theorem 3.7, the map
$\widehat {f}$
is not realized by a rational map. Then by Theorem 3.7, the map
![]() $\widehat {f}$
has an obstruction given by a Jordan curve
$\widehat {f}$
has an obstruction given by a Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() $(S^2, {P_f})$
.
$(S^2, {P_f})$
.
We set
![]() $U=S^2\smallsetminus (a\cup c)$
. Since E satisfies the
$U=S^2\smallsetminus (a\cup c)$
. Since E satisfies the
![]() $\alpha $
-restricted blow-up conditions, we have
$\alpha $
-restricted blow-up conditions, we have
![]() $\#(f(e)\cap \alpha ) = 1$
and
$\#(f(e)\cap \alpha ) = 1$
and
![]() $f(\operatorname {int}(e)) \cap a = f(\operatorname {int}(e))\cap c = \emptyset $
for each
$f(\operatorname {int}(e)) \cap a = f(\operatorname {int}(e))\cap c = \emptyset $
for each
![]() $e\in E$
. In other words,
$e\in E$
. In other words,
![]() $f(e)$
intersects
$f(e)$
intersects
![]() $\alpha $
only once and
$\alpha $
only once and
![]() $\operatorname {int}(f(e))$
belongs to U. Then each arc in E intersects only one pullback of
$\operatorname {int}(f(e))$
belongs to U. Then each arc in E intersects only one pullback of
![]() $\alpha $
and only once.
$\alpha $
and only once.
Since
![]() $\gamma $
is an obstruction for
$\gamma $
is an obstruction for
![]() $\widehat f$
, but
$\widehat f$
, but
![]() $\alpha $
is not, the curves
$\alpha $
is not, the curves
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
are not isotopic relative to
$\gamma $
are not isotopic relative to
![]() $P_{\widehat {f}}={P_f}$
. So we have
$P_{\widehat {f}}={P_f}$
. So we have
![]() $\mathrm {i}(\alpha , \gamma )>0$
for intersection numbers in
$\mathrm {i}(\alpha , \gamma )>0$
for intersection numbers in
![]() $(S^2, P_f)$
as follows from Lemma 2.1. By Lemma 2.6(i), we have
$(S^2, P_f)$
as follows from Lemma 2.1. By Lemma 2.6(i), we have
As follows from Lemma 2.6(ii), by replacing
![]() $\gamma $
with an isotopic curve relative to
$\gamma $
with an isotopic curve relative to
![]() $P_{\widehat {f}}={P_f}$
if necessary, we may also assume that
$P_{\widehat {f}}={P_f}$
if necessary, we may also assume that
and that the points in the non-empty and finite sets
![]() $a\cap \gamma $
and
$a\cap \gamma $
and
![]() $c\cap \gamma $
alternate on
$c\cap \gamma $
alternate on
![]() $\gamma $
.
$\gamma $
.
We denote by
![]() $\alpha _1,\ldots ,\alpha _n$
with
$\alpha _1,\ldots ,\alpha _n$
with
![]() $n\in \mathbb {N}$
the pullbacks of
$n\in \mathbb {N}$
the pullbacks of
![]() $\alpha $
under f that are isotopic to
$\alpha $
under f that are isotopic to
![]() $\alpha $
relative to
$\alpha $
relative to
![]() ${P_f}$
. Now we consider the graphs
${P_f}$
. Now we consider the graphs
![]() $ \mathcal {G}= f^{-1}(a\cup c)$
and
$ \mathcal {G}= f^{-1}(a\cup c)$
and
![]() $\widehat {\mathcal {G}}=\widehat f^{-1}(a\cup c)$
as in §6. By Lemma 6.6,
$\widehat {\mathcal {G}}=\widehat f^{-1}(a\cup c)$
as in §6. By Lemma 6.6,
![]() $\mathcal {G}$
is a subgraph of
$\mathcal {G}$
is a subgraph of
![]() $\widehat {\mathcal {G}}$
. Moreover, the following facts are true for their complementary components. Each
$\widehat {\mathcal {G}}$
. Moreover, the following facts are true for their complementary components. Each
![]() $\alpha _j$
is a core curve in an essential annulus
$\alpha _j$
is a core curve in an essential annulus
![]() $U_j$
that is a component of
$U_j$
that is a component of
![]() $S^2\smallsetminus \mathcal {G}$
. Each
$S^2\smallsetminus \mathcal {G}$
. Each
![]() $U_j$
contains precisely one component
$U_j$
contains precisely one component
![]() $\widehat U_j$
of
$\widehat U_j$
of
![]() $S^2\smallsetminus \widehat {\mathcal {G}}$
. This component is essential and contains precisely one essential pullback
$S^2\smallsetminus \widehat {\mathcal {G}}$
. This component is essential and contains precisely one essential pullback
![]() $\widehat \alpha _j$
of
$\widehat \alpha _j$
of
![]() $\alpha $
under
$\alpha $
under
![]() $\widehat f$
. The essential circuit length of
$\widehat f$
. The essential circuit length of
![]() $U_j$
is the same as the essential circuit length of
$U_j$
is the same as the essential circuit length of
![]() $\widehat U_j$
. The curves
$\widehat U_j$
. The curves
![]() $\widehat \alpha _1, \ldots , \widehat \alpha _n$
are precisely all the distinct essential pullbacks of
$\widehat \alpha _1, \ldots , \widehat \alpha _n$
are precisely all the distinct essential pullbacks of
![]() $\alpha $
under
$\alpha $
under
![]() $\widehat f$
. They are isotopic to
$\widehat f$
. They are isotopic to
![]() $\alpha $
relative to
$\alpha $
relative to
![]() ${P_f}$
.
${P_f}$
.
Let
![]() $\gamma _1,\ldots ,\gamma _k$
with
$\gamma _1,\ldots ,\gamma _k$
with
![]() $k\in \mathbb {N}$
be the pullbacks of
$k\in \mathbb {N}$
be the pullbacks of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat {f}$
that are isotopic to
$\widehat {f}$
that are isotopic to
![]() $\gamma $
relative to
$\gamma $
relative to
![]() $P_{\widehat {f}}={P_f}$
. Applying Lemmas 6.3 and 6.2 (for the latter, equations (7.1) and (7.2) are important) to an essential circuit for
$P_{\widehat {f}}={P_f}$
. Applying Lemmas 6.3 and 6.2 (for the latter, equations (7.1) and (7.2) are important) to an essential circuit for
![]() $\widehat U_j$
, we see that
$\widehat U_j$
, we see that
 $$ \begin{align} \deg(f\colon \alpha_j\rightarrow \alpha)&= \deg(f\colon U_j\rightarrow U)\nonumber\\ &=\tfrac12\cdot\text{circuit length of } U_j \nonumber \\ &\ge \tfrac12\cdot \text{essential circuit length of } U_j \nonumber \\& = \tfrac12\cdot \text{essential circuit length of } \widehat U_j\nonumber \\ &\ge k \end{align} $$
$$ \begin{align} \deg(f\colon \alpha_j\rightarrow \alpha)&= \deg(f\colon U_j\rightarrow U)\nonumber\\ &=\tfrac12\cdot\text{circuit length of } U_j \nonumber \\ &\ge \tfrac12\cdot \text{essential circuit length of } U_j \nonumber \\& = \tfrac12\cdot \text{essential circuit length of } \widehat U_j\nonumber \\ &\ge k \end{align} $$
for
![]() $j=1, \ldots , n$
.
$j=1, \ldots , n$
.
However,
![]() $\alpha $
has n distinct essential pullbacks
$\alpha $
has n distinct essential pullbacks
![]() $\widehat \alpha _1, \ldots , \widehat \alpha _n$
under
$\widehat \alpha _1, \ldots , \widehat \alpha _n$
under
![]() $\widehat f$
, and so Lemma 5.5 implies that
$\widehat f$
, and so Lemma 5.5 implies that
![]() $\deg (\widehat f\colon \gamma _m\to \gamma )\ge n $
for
$\deg (\widehat f\colon \gamma _m\to \gamma )\ge n $
for
![]() $m=1,\ldots , k$
(again equations (7.1) and (7.2) are used here). Since
$m=1,\ldots , k$
(again equations (7.1) and (7.2) are used here). Since
![]() $\alpha $
and
$\alpha $
and
![]() $\gamma $
are obstructions for f and
$\gamma $
are obstructions for f and
![]() $\widehat {f}$
, respectively, we conclude that
$\widehat {f}$
, respectively, we conclude that

and

It follows that
![]() $k=n$
, which forces
$k=n$
, which forces
![]() $\deg (f\colon \alpha _j\to \alpha )=\deg (\widehat {f}\colon \gamma _j\to \gamma )=n$
for
$\deg (f\colon \alpha _j\to \alpha )=\deg (\widehat {f}\colon \gamma _j\to \gamma )=n$
for
![]() ${j=1,\ldots ,n}$
. If we combine this with (7.3), then we also see that
${j=1,\ldots ,n}$
. If we combine this with (7.3), then we also see that
 $$ \begin{align} \text{circuit length of } U_j &= \text{essential circuit length of } U_j \notag\\ &= \text {essential circuit length of } \widehat U_j =2n \end{align} $$
$$ \begin{align} \text{circuit length of } U_j &= \text{essential circuit length of } U_j \notag\\ &= \text {essential circuit length of } \widehat U_j =2n \end{align} $$
for
![]() $j=1, \ldots , n$
.
$j=1, \ldots , n$
.
We now want to apply Lemma 7.1 to our map f and the obstruction
![]() $\alpha $
. To verify the hypotheses of Lemma 7.1, it remains to show that
$\alpha $
. To verify the hypotheses of Lemma 7.1, it remains to show that
![]() $\alpha $
has no peripheral pullbacks under f, or equivalently, no peripheral pullbacks under
$\alpha $
has no peripheral pullbacks under f, or equivalently, no peripheral pullbacks under
![]() $\widehat f$
(see Lemma 6.6(iii)).
$\widehat f$
(see Lemma 6.6(iii)).
We argue by contradiction and assume that
![]() $\alpha $
has some peripheral pullbacks under
$\alpha $
has some peripheral pullbacks under
![]() $\widehat f$
. Then there exists at least one peripheral annulus in the complement of
$\widehat f$
. Then there exists at least one peripheral annulus in the complement of
![]() $\widehat {\mathcal {G}}$
. Such an annulus is disjoint from each annulus
$\widehat {\mathcal {G}}$
. Such an annulus is disjoint from each annulus
![]() $\widehat U_j$
. We can then travel from a point p of such a peripheral annulus to a point in the set
$\widehat U_j$
. We can then travel from a point p of such a peripheral annulus to a point in the set
![]() $\widehat U_1 \cup \cdots \cup \widehat U_n$
along an arc
$\widehat U_1 \cup \cdots \cup \widehat U_n$
along an arc
![]() $\sigma $
in
$\sigma $
in
![]() $S^2\smallsetminus \widehat f^{-1} (P_{\widehat {f}})$
that crosses each edge in the graph
$S^2\smallsetminus \widehat f^{-1} (P_{\widehat {f}})$
that crosses each edge in the graph
![]() $\widehat {\mathcal {G}}$
transversely. Then there is a first point q on
$\widehat {\mathcal {G}}$
transversely. Then there is a first point q on
![]() $\sigma $
where we enter the closure M of
$\sigma $
where we enter the closure M of
![]() $\widehat U_1 \cup \cdots \cup \widehat U_n$
. The point q is necessarily an interior point of an edge e of
$\widehat U_1 \cup \cdots \cup \widehat U_n$
. The point q is necessarily an interior point of an edge e of
![]() $\widehat {\mathcal {G}}$
contained in the boundary
$\widehat {\mathcal {G}}$
contained in the boundary
![]() $\partial \widehat U_j$
for some
$\partial \widehat U_j$
for some
![]() $j\in \{1, \ldots , n\}$
. Interior points of the subarc of
$j\in \{1, \ldots , n\}$
. Interior points of the subarc of
![]() $\sigma $
between p and q that are close to q do not lie in
$\sigma $
between p and q that are close to q do not lie in
![]() $M\cup \widehat {\mathcal {G}}$
. Hence, such points must belong to a peripheral component
$M\cup \widehat {\mathcal {G}}$
. Hence, such points must belong to a peripheral component
![]() $\widehat U$
of
$\widehat U$
of
![]() $\widehat {\mathcal {G}}$
. Then necessarily,
$\widehat {\mathcal {G}}$
. Then necessarily,
![]() $e\subset \partial \widehat U$
.
$e\subset \partial \widehat U$
.
In other words, there exists an edge e in the graph
![]() $ \widehat {\mathcal {G}}$
that belongs to the boundary of an essential annulus
$ \widehat {\mathcal {G}}$
that belongs to the boundary of an essential annulus
![]() $\widehat U_j$
and a peripheral annulus
$\widehat U_j$
and a peripheral annulus
![]() $\widehat U$
. Clearly,
$\widehat U$
. Clearly,
![]() $\widehat f(e)=a$
or
$\widehat f(e)=a$
or
![]() $\widehat f(e)=c$
. In the following, we will assume that
$\widehat f(e)=c$
. In the following, we will assume that
![]() $\widehat f(e)=c$
, that is,
$\widehat f(e)=c$
, that is,
![]() $e\subset \partial _c \widehat U_j\cap \partial _c \widehat U$
; the other case,
$e\subset \partial _c \widehat U_j\cap \partial _c \widehat U$
; the other case,
![]() $\widehat f(e)=a$
, is completely analogous.
$\widehat f(e)=a$
, is completely analogous.
Since
![]() $\mathrm {i}(c,\gamma ) = \#(c \cap \gamma )>0$
, there exists a pullback
$\mathrm {i}(c,\gamma ) = \#(c \cap \gamma )>0$
, there exists a pullback
![]() $\widehat {\gamma }$
of
$\widehat {\gamma }$
of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat f$
that meets e transversely. Consequently, this pullback
$\widehat f$
that meets e transversely. Consequently, this pullback
![]() $\widehat {\gamma }$
meets both
$\widehat {\gamma }$
meets both
![]() $\widehat U_j$
and
$\widehat U_j$
and
![]() $\widehat U$
. Since
$\widehat U$
. Since
![]() $\widehat f\colon \widehat {\gamma } \rightarrow \gamma $
is a covering map and the points in
$\widehat f\colon \widehat {\gamma } \rightarrow \gamma $
is a covering map and the points in
![]() $a\cap \gamma \ne \emptyset $
and
$a\cap \gamma \ne \emptyset $
and
![]() $c\cap \gamma \ne \emptyset $
alternate on
$c\cap \gamma \ne \emptyset $
alternate on
![]() $\gamma $
, the points in
$\gamma $
, the points in
![]() $\widehat f^{-1}(a) \cap \widehat {\gamma }\ne \emptyset $
and
$\widehat f^{-1}(a) \cap \widehat {\gamma }\ne \emptyset $
and
![]() $\widehat f^{-1}(c) \cap \widehat {\gamma }\ne \emptyset $
alternate on
$\widehat f^{-1}(c) \cap \widehat {\gamma }\ne \emptyset $
alternate on
![]() $\widehat {\gamma }$
. This implies that the curve
$\widehat {\gamma }$
. This implies that the curve
![]() $\widehat {\gamma }$
also meets the sets
$\widehat {\gamma }$
also meets the sets
![]() $\partial _a \widehat U_j$
and
$\partial _a \widehat U_j$
and
![]() $\partial _a \widehat U$
, and hence both components of the boundary of
$\partial _a \widehat U$
, and hence both components of the boundary of
![]() $\widehat U_j$
and of
$\widehat U_j$
and of
![]() $\widehat U$
. We conclude that
$\widehat U$
. We conclude that
![]() $\widehat {\gamma }$
meets the core curve
$\widehat {\gamma }$
meets the core curve
![]() $\widehat \alpha _j$
of
$\widehat \alpha _j$
of
![]() $\widehat U_j$
and the core curve
$\widehat U_j$
and the core curve
![]() $\widehat \alpha $
of
$\widehat \alpha $
of
![]() $\widehat U$
. Note that
$\widehat U$
. Note that
![]() $\widehat \alpha $
is a peripheral pullback of
$\widehat \alpha $
is a peripheral pullback of
![]() $\alpha $
under
$\alpha $
under
![]() $\widehat f$
. To show that this is impossible, we consider two cases.
$\widehat f$
. To show that this is impossible, we consider two cases.
Case 1:
![]() $\widehat {\gamma }$
is an essential pullback of
$\widehat {\gamma }$
is an essential pullback of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat f$
, say
$\widehat f$
, say
![]() $\widehat {\gamma }=\gamma _m$
for some
$\widehat {\gamma }=\gamma _m$
for some
![]() $m\in \{1, \ldots , n\}$
. Then Lemma 5.5 (for the map
$m\in \{1, \ldots , n\}$
. Then Lemma 5.5 (for the map
![]() $\widehat f$
, and
$\widehat f$
, and
![]() $\alpha $
,
$\alpha $
,
![]() $\widehat {\gamma }$
in the roles of
$\widehat {\gamma }$
in the roles of
![]() $\gamma $
,
$\gamma $
,
![]() $\widetilde \alpha $
, respectively) shows
$\widetilde \alpha $
, respectively) shows
![]() $n<\deg (\widehat f\colon \widehat {\gamma } \rightarrow \gamma )$
, because
$n<\deg (\widehat f\colon \widehat {\gamma } \rightarrow \gamma )$
, because
![]() $\alpha $
has n essential pullbacks and
$\alpha $
has n essential pullbacks and
![]() $ \widehat {\gamma } $
meets a peripheral pullback of
$ \widehat {\gamma } $
meets a peripheral pullback of
![]() $\alpha $
. However, we know that
$\alpha $
. However, we know that
![]() $\deg (\widehat f\colon \widehat {\gamma } \rightarrow \gamma )=\deg (\widehat f\colon \gamma _m \rightarrow \gamma )=n$
. This is a contradiction.
$\deg (\widehat f\colon \widehat {\gamma } \rightarrow \gamma )=\deg (\widehat f\colon \gamma _m \rightarrow \gamma )=n$
. This is a contradiction.
Case 2:
![]() $\widehat {\gamma }$
is a peripheral pullback of
$\widehat {\gamma }$
is a peripheral pullback of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat f$
. Let
$\widehat f$
. Let ![]() . Then it follows from Lemma 6.6 that
. Then it follows from Lemma 6.6 that
![]() $\mathcal {H} \subset \partial _c \widehat U_j$
. Moreover, equation (7.4) implies that
$\mathcal {H} \subset \partial _c \widehat U_j$
. Moreover, equation (7.4) implies that
![]() $\mathcal {H}$
(considered as a circuit) realizes the essential circuit lengths of
$\mathcal {H}$
(considered as a circuit) realizes the essential circuit lengths of
![]() $U_j$
and
$U_j$
and
![]() $\widehat U_j$
, which are both equal to
$\widehat U_j$
, which are both equal to
![]() $2n$
.
$2n$
.
Now
![]() $e\subset \partial _c U_j=\mathcal {H}$
, and so
$e\subset \partial _c U_j=\mathcal {H}$
, and so
![]() $\mathcal {H}$
meets the peripheral pullback
$\mathcal {H}$
meets the peripheral pullback
![]() $\widehat {\gamma }$
of
$\widehat {\gamma }$
of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat f$
. The second part of Lemma 6.2 applied to
$\widehat f$
. The second part of Lemma 6.2 applied to
![]() $\mathcal {H}$
implies that the number k of essential pullbacks of
$\mathcal {H}$
implies that the number k of essential pullbacks of
![]() $\gamma $
under
$\gamma $
under
![]() $\widehat f$
is less than n, contradicting
$\widehat f$
is less than n, contradicting
![]() $k=n$
.
$k=n$
.
To summarize, these contradictions show that
![]() $\alpha $
has no peripheral pullbacks under
$\alpha $
has no peripheral pullbacks under
![]() $\widehat f$
, and hence no peripheral pullbacks under f by Lemma 6.6(iii). So we can apply Lemma 7.1 and conclude that f has a parabolic orbifold. This is yet another contradiction, because f has a hyperbolic orbifold by our hypotheses. This shows that our initial assumption that
$\widehat f$
, and hence no peripheral pullbacks under f by Lemma 6.6(iii). So we can apply Lemma 7.1 and conclude that f has a parabolic orbifold. This is yet another contradiction, because f has a hyperbolic orbifold by our hypotheses. This shows that our initial assumption that
![]() $\widehat f$
has an obstruction is false. Hence,
$\widehat f$
has an obstruction is false. Hence,
![]() $\widehat f$
is realized by a rational map. This completes the proof of Theorem 1.1.
$\widehat f$
is realized by a rational map. This completes the proof of Theorem 1.1.
Remark 7.2. Let
![]() $f\colon S^2 \rightarrow S^2$
be a Thurston map with
$f\colon S^2 \rightarrow S^2$
be a Thurston map with
![]() $\#P_f=4$
and a hyperbolic orbifold, and suppose f has an obstruction represented by a Jordan curve
$\#P_f=4$
and a hyperbolic orbifold, and suppose f has an obstruction represented by a Jordan curve
![]() $\alpha $
in
$\alpha $
in
![]() $(S^2, P_f)$
. Then there always exist a set of arcs
$(S^2, P_f)$
. Then there always exist a set of arcs
![]() $E\neq \emptyset $
in
$E\neq \emptyset $
in
![]() $(S^2, f^{-1}(P_f))$
satisfying the
$(S^2, f^{-1}(P_f))$
satisfying the
![]() $\alpha $
-restricted blow-up conditions and multiplicities
$\alpha $
-restricted blow-up conditions and multiplicities
![]() $m_e$
,
$m_e$
,
![]() $e\in E$
, such that the corresponding blown-up map
$e\in E$
, such that the corresponding blown-up map
![]() $\widehat f$
satisfies
$\widehat f$
satisfies
![]() $\unicode{x3bb} _{\widehat f}(\alpha ) < 1$
. We are then exactly in the setup of Theorem 1.1.
$\unicode{x3bb} _{\widehat f}(\alpha ) < 1$
. We are then exactly in the setup of Theorem 1.1.
To see this, we first fix some core arcs a and c of
![]() $\alpha $
lying in different components of
$\alpha $
lying in different components of
![]() $S^2\smallsetminus \alpha $
. We now choose an arc
$S^2\smallsetminus \alpha $
. We now choose an arc
![]() $e_0$
in
$e_0$
in
![]() $(S^2,P_f)$
with
$(S^2,P_f)$
with
![]() $\mathrm {i}(e_0,\alpha )=\#(e_0 \cap \alpha ) = 1$
and
$\mathrm {i}(e_0,\alpha )=\#(e_0 \cap \alpha ) = 1$
and
![]() $\operatorname {int}(e_0)\subset {S^{2}}\smallsetminus (a\cup c)$
. Let E be the (non-empty) set of all lifts of
$\operatorname {int}(e_0)\subset {S^{2}}\smallsetminus (a\cup c)$
. Let E be the (non-empty) set of all lifts of
![]() $e_0$
under f. Then E is a set of arcs in
$e_0$
under f. Then E is a set of arcs in
![]() $(S^2, f^{-1}(P_f))$
and it is clear that E satisfies the
$(S^2, f^{-1}(P_f))$
and it is clear that E satisfies the
![]() $\alpha $
-restricted blow-up conditions. If
$\alpha $
-restricted blow-up conditions. If
![]() $\widetilde \alpha $
is any pullback of
$\widetilde \alpha $
is any pullback of
![]() $\alpha $
under f, then there exists at least one arc
$\alpha $
under f, then there exists at least one arc
![]() $ e \in E$
that meets
$ e \in E$
that meets
![]() $\widetilde \alpha $
(necessarily in an interior point of e). Blowing up the arc e with some multiplicity
$\widetilde \alpha $
(necessarily in an interior point of e). Blowing up the arc e with some multiplicity
![]() $m_e\in \mathbb {N}$
increases the mapping degree for the corresponding pullback
$m_e\in \mathbb {N}$
increases the mapping degree for the corresponding pullback
![]() $\widehat \alpha $
under
$\widehat \alpha $
under
![]() $\widehat f$
by
$\widehat f$
by
![]() $m_e$
and does not change the isotopy class of this pullback, that is,
$m_e$
and does not change the isotopy class of this pullback, that is,
![]() $[\widehat \alpha ] = [\widetilde \alpha ]$
relative to
$[\widehat \alpha ] = [\widetilde \alpha ]$
relative to
![]() $P_{\widehat f}= P_f$
(this easily follows from Lemma 6.6 and its proof). Note that each pullback
$P_{\widehat f}= P_f$
(this easily follows from Lemma 6.6 and its proof). Note that each pullback
![]() $\widehat \alpha $
of
$\widehat \alpha $
of
![]() $\alpha $
under
$\alpha $
under
![]() $\widehat f$
corresponds to a pullback
$\widehat f$
corresponds to a pullback
![]() $\widetilde \alpha $
of
$\widetilde \alpha $
of
![]() $\alpha $
under f (this is essentially Lemma 6.6(ii)). It follows that if we choose the multiplicities
$\alpha $
under f (this is essentially Lemma 6.6(ii)). It follows that if we choose the multiplicities
![]() $m_e$
,
$m_e$
,
![]() $e\in E$
, large enough, then for the Thurston map
$e\in E$
, large enough, then for the Thurston map
![]() $\widehat f$
, we will have
$\widehat f$
, we will have
![]() $\unicode{x3bb} _{\widehat f}(\alpha ) < 1$
and so
$\unicode{x3bb} _{\widehat f}(\alpha ) < 1$
and so
![]() $\alpha $
is not an obstruction for
$\alpha $
is not an obstruction for
![]() $\widehat f$
. By Theorem 1.1, the map
$\widehat f$
. By Theorem 1.1, the map
![]() $\widehat f$
is actually realized by a rational map. So by a suitable blow-up operation, an obstructed Thurston map f (with
$\widehat f$
is actually realized by a rational map. So by a suitable blow-up operation, an obstructed Thurston map f (with
![]() $P_f=4$
and a hyperbolic orbifold) can be turned into a Thurston map
$P_f=4$
and a hyperbolic orbifold) can be turned into a Thurston map
![]() $\widehat f$
that is realized.
$\widehat f$
that is realized.
8 Global curve attractors
In this section, we will prove Theorem 1.4. We consider the pillow
![]() $\mathbb {P}$
with its vertex set
$\mathbb {P}$
with its vertex set
![]() ${V= \{A,B,C,D\}}$
. For the remainder of this section,
${V= \{A,B,C,D\}}$
. For the remainder of this section,
![]() $f\colon \mathbb {P}\to \mathbb {P}$
is a Thurston map obtained from the
$f\colon \mathbb {P}\to \mathbb {P}$
is a Thurston map obtained from the
![]() $(2\times 2)$
-Lattès map by gluing
$(2\times 2)$
-Lattès map by gluing
![]() $n_h\geq 1$
horizontal and
$n_h\geq 1$
horizontal and
![]() $n_v\geq 1$
vertical flaps to
$n_v\geq 1$
vertical flaps to
![]() $\mathbb {P}$
. Then f is Thurston equivalent to a rational map by Theorem 1.2. In the following, all isotopies on
$\mathbb {P}$
. Then f is Thurston equivalent to a rational map by Theorem 1.2. In the following, all isotopies on
![]() $\mathbb {P}$
are considered relative to
$\mathbb {P}$
are considered relative to
![]() ${P_f}=V$
.
${P_f}=V$
.
To prove Theorem 1.4, we want to show that Jordan curves in
![]() $(\mathbb {P},V)$
are getting ‘less twisted’ under taking preimages under f. To formalize this, we define the complexity
$(\mathbb {P},V)$
are getting ‘less twisted’ under taking preimages under f. To formalize this, we define the complexity
![]() $\| x \|$
of
$\| x \|$
of
![]() $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
as
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
as ![]() for
for
![]() $x= \odot $
and
$x= \odot $
and ![]() for
for
![]() $x=r/s\in \widehat {\mathbb {Q}}$
. Recall that
$x=r/s\in \widehat {\mathbb {Q}}$
. Recall that
![]() $\odot $
represents the isotopy classes of all peripheral curves, and that for a slope
$\odot $
represents the isotopy classes of all peripheral curves, and that for a slope
![]() $r/s\in \widehat {\mathbb {Q}}$
, we use the convention that the numbers
$r/s\in \widehat {\mathbb {Q}}$
, we use the convention that the numbers
![]() $r\in \mathbb {Z}$
and
$r\in \mathbb {Z}$
and
![]() $s\in \mathbb {N}_0$
are relatively prime and that
$s\in \mathbb {N}_0$
are relatively prime and that
![]() $r=1$
if
$r=1$
if
![]() $s=0$
. Note that
$s=0$
. Note that
![]() $\| x \|=0$
for
$\| x \|=0$
for
![]() $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
if and only if
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
if and only if
![]() $x=\odot $
.
$x=\odot $
.
The complexity admits a natural interpretation in terms of intersection numbers. To see this, recall that
![]() $\alpha ^h$
and
$\alpha ^h$
and
![]() $\alpha ^v$
(see (2.4)) represent simple closed geodesics in
$\alpha ^v$
(see (2.4)) represent simple closed geodesics in
![]() $(\mathbb {P}, V)$
that separate the two horizontal and the two vertical edges of
$(\mathbb {P}, V)$
that separate the two horizontal and the two vertical edges of
![]() $\mathbb {P}$
, respectively. Suppose the slope
$\mathbb {P}$
, respectively. Suppose the slope
![]() $r/s \in \widehat {\mathbb {Q}}$
corresponds to the isotopy class
$r/s \in \widehat {\mathbb {Q}}$
corresponds to the isotopy class
![]() $[\gamma ]$
of a (necessarily essential) Jordan curve
$[\gamma ]$
of a (necessarily essential) Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P},V)$
. Then by Lemma 2.4(v),
$(\mathbb {P},V)$
. Then by Lemma 2.4(v),
Moreover, if
![]() $\gamma $
is peripheral, then
$\gamma $
is peripheral, then
![]() $\mathrm {i}(\gamma ,\alpha ^h)+ \mathrm {i}(\gamma ,\alpha ^v)=0$
, which agrees with the fact that
$\mathrm {i}(\gamma ,\alpha ^h)+ \mathrm {i}(\gamma ,\alpha ^v)=0$
, which agrees with the fact that
![]() $\| {\odot } \|=0$
.
$\| {\odot } \|=0$
.
As we will see, under the slope map
![]() $\mu _f$
(as defined in §1.2), complexities do not increase, and actually strictly decrease unless the slope belongs to a certain finite set. More precisely, we will show the following statement.
$\mu _f$
(as defined in §1.2), complexities do not increase, and actually strictly decrease unless the slope belongs to a certain finite set. More precisely, we will show the following statement.
Proposition 8.1. Let
![]() $f\colon \mathbb {P}\to \mathbb {P}$
be a Thurston map obtained from the
$f\colon \mathbb {P}\to \mathbb {P}$
be a Thurston map obtained from the
![]() $(2\times 2)$
-Lattès map by gluing
$(2\times 2)$
-Lattès map by gluing
![]() $n_h\geq 1$
horizontal and
$n_h\geq 1$
horizontal and
![]() $n_v\geq 1$
vertical flaps to the pillow
$n_v\geq 1$
vertical flaps to the pillow
![]() $\mathbb {P}$
. Then the following statements are true:
$\mathbb {P}$
. Then the following statements are true:
-
(i)
 $\|\mu _f(x) \| \leq \|x \|$
for all
$\|\mu _f(x) \| \leq \|x \|$
for all
 $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
;
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
; -
(ii)
 $\|\mu _f(x) \| < \|x \|$
for all
$\|\mu _f(x) \| < \|x \|$
for all
 $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
with
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
with
 $\|x\|> 8.$
$\|x\|> 8.$
Since the set
![]() $ \{x \in \widehat {\mathbb {Q}}\cup \{\odot \} : \|x\|\leq 8\}$
is finite, we actually have the strict inequality in statement (i) with at most finitely many exceptions. The proof of the proposition will show that
$ \{x \in \widehat {\mathbb {Q}}\cup \{\odot \} : \|x\|\leq 8\}$
is finite, we actually have the strict inequality in statement (i) with at most finitely many exceptions. The proof of the proposition will show that
![]() $\|\mu _f(x) \| =\|x \|$
if and only if
$\|\mu _f(x) \| =\|x \|$
if and only if
![]() $\mu _f(x)=x$
(see Remark 8.6). As we will see below, Theorem 1.4 easily follows from Proposition 8.1.
$\mu _f(x)=x$
(see Remark 8.6). As we will see below, Theorem 1.4 easily follows from Proposition 8.1.
Before we proceed with the proof of this proposition, we will establish several auxiliary results. As in §2.4,
![]() $a, b, c, d$
are the edges of the pillow
$a, b, c, d$
are the edges of the pillow
![]() $\mathbb {P}$
, and
$\mathbb {P}$
, and
![]() $\wp \colon \mathbb {C}\to \mathbb {P}$
denotes the Weierstrass function that is doubly periodic with respect to the lattice
$\wp \colon \mathbb {C}\to \mathbb {P}$
denotes the Weierstrass function that is doubly periodic with respect to the lattice
![]() $2\mathbb {Z}^2$
.
$2\mathbb {Z}^2$
.
We are interested in simple closed geodesics and geodesic arcs
![]() $\tau $
in
$\tau $
in
![]() $(\mathbb {P}, V)$
. Recall that every such geodesic has the form
$(\mathbb {P}, V)$
. Recall that every such geodesic has the form
![]() $\tau =\wp (\ell _{r/s})$
for a line
$\tau =\wp (\ell _{r/s})$
for a line
![]() $\ell _{r/s}\subset \mathbb {C}$
with slope
$\ell _{r/s}\subset \mathbb {C}$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. If
$r/s\in \widehat {\mathbb {Q}}$
. If
![]() $\ell _{r/s}\subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
, then
$\ell _{r/s}\subset \mathbb {C}\smallsetminus \mathbb {Z}^2$
, then
![]() $\tau =\wp (\ell _{r/s})$
is a simple closed geodesic in
$\tau =\wp (\ell _{r/s})$
is a simple closed geodesic in
![]() $(\mathbb {P},V)$
, that is,
$(\mathbb {P},V)$
, that is,
![]() $\tau \subset \mathbb {P}\smallsetminus V$
. If
$\tau \subset \mathbb {P}\smallsetminus V$
. If
![]() $\ell _{r/s}$
contains a point in
$\ell _{r/s}$
contains a point in
![]() $\mathbb {Z}^2$
, then
$\mathbb {Z}^2$
, then
![]() $\tau =\wp (\ell _{r/s})$
is a geodesic arc in
$\tau =\wp (\ell _{r/s})$
is a geodesic arc in
![]() $(\mathbb {P},V)$
, that is, its interior lies in
$(\mathbb {P},V)$
, that is, its interior lies in
![]() $\mathbb {P}\smallsetminus V$
and its endpoints are in V.
$\mathbb {P}\smallsetminus V$
and its endpoints are in V.
Lemma 8.2. Let
![]() $\tau $
be a simple closed geodesic or a geodesic arc in
$\tau $
be a simple closed geodesic or a geodesic arc in
![]() $(\mathbb {P},V)$
with slope
$(\mathbb {P},V)$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. We consider the
$r/s\in \widehat {\mathbb {Q}}$
. We consider the
![]() $1$
-edges of
$1$
-edges of
![]() $\mathbb {P}$
with respect to the
$\mathbb {P}$
with respect to the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
,
$\mathcal {L}_n$
,
![]() $n\ge 2$
, that is, the lifts of the edges
$n\ge 2$
, that is, the lifts of the edges
![]() $a,b,c,d$
of
$a,b,c,d$
of
![]() $\mathbb {P}$
under
$\mathbb {P}$
under
![]() $\mathcal {L}_n$
. Then the following statements are true.
$\mathcal {L}_n$
. Then the following statements are true.
-
(i) If
 $|r|>2n$
, then
$|r|>2n$
, then
 $ \tau $
intersects the interior of every horizontal
$ \tau $
intersects the interior of every horizontal
 $1$
-edge of
$1$
-edge of
 $\mathbb {P}$
.
$\mathbb {P}$
. -
(ii) If
 $s>2n$
, then
$s>2n$
, then
 $ \tau $
intersects the interior of every vertical
$ \tau $
intersects the interior of every vertical
 $1$
-edge of
$1$
-edge of
 $\mathbb {P}$
.
$\mathbb {P}$
.
Proof. We will only show the first part of the statement. The proof of the second part is completely analogous.
Let
![]() $\tau $
be a simple closed geodesic or a geodesic arc in
$\tau $
be a simple closed geodesic or a geodesic arc in
![]() $(\mathbb {P},V)$
with slope
$(\mathbb {P},V)$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
, where
$r/s\in \widehat {\mathbb {Q}}$
, where
![]() $|r|>2n$
. Suppose that e is a horizontal
$|r|>2n$
. Suppose that e is a horizontal
![]() $1$
-edge and
$1$
-edge and
![]() $\widetilde e$
is a lift of e under
$\widetilde e$
is a lift of e under
![]() $\wp $
. Then the arc
$\wp $
. Then the arc
![]() $\widetilde e$
is a line segment of length
$\widetilde e$
is a line segment of length
![]() $1/n$
contained in a line
$1/n$
contained in a line
![]() $\ell _0\subset \mathbb {C}$
parallel to the real axis. To show that
$\ell _0\subset \mathbb {C}$
parallel to the real axis. To show that
![]() $\tau $
meets
$\tau $
meets
![]() $\operatorname {int}(e)$
, it suffices to represent the given geodesic
$\operatorname {int}(e)$
, it suffices to represent the given geodesic
![]() $\tau $
in the form
$\tau $
in the form
![]() $\tau =\wp (\ell _{r/s})$
for a line
$\tau =\wp (\ell _{r/s})$
for a line
![]() $\ell _{r/s}\subset \mathbb {C}$
with
$\ell _{r/s}\subset \mathbb {C}$
with
![]() $ \ell _{r/s} \cap \operatorname {int}(\widetilde e) \ne \emptyset $
.
$ \ell _{r/s} \cap \operatorname {int}(\widetilde e) \ne \emptyset $
.
For this, we choose
![]() $p, q\in \mathbb {Z}$
such that
$p, q\in \mathbb {Z}$
such that
![]() $pr+qs=1$
and define
$pr+qs=1$
and define ![]() and
and ![]() . The numbers
. The numbers
![]() $\omega $
and
$\omega $
and
![]() $\widetilde \omega $
form a basis of the period lattice
$\widetilde \omega $
form a basis of the period lattice
![]() $2\mathbb {Z}^2$
of
$2\mathbb {Z}^2$
of
![]() $\wp $
. In particular, if
$\wp $
. In particular, if
![]() $\tau =\wp (\ell _{r/s}(z_0))$
for some
$\tau =\wp (\ell _{r/s}(z_0))$
for some
![]() $z_0\in \mathbb {C}$
, then
$z_0\in \mathbb {C}$
, then
![]() $\tau = \wp (\ell _{r/s}(z_0+j \widetilde \omega ))$
for all
$\tau = \wp (\ell _{r/s}(z_0+j \widetilde \omega ))$
for all
![]() $j\in \mathbb {Z}$
. The lines
$j\in \mathbb {Z}$
. The lines
![]() $\ell _{r/s}(z_0+j \widetilde \omega )$
,
$\ell _{r/s}(z_0+j \widetilde \omega )$
,
![]() $j\in \mathbb {Z}$
, are parallel and equally spaced. Actually, two consecutive lines in this family differ by a translation by
$j\in \mathbb {Z}$
, are parallel and equally spaced. Actually, two consecutive lines in this family differ by a translation by
![]() $\widetilde \omega $
. Since
$\widetilde \omega $
. Since
![]() $r\ne 0$
, these lines are not parallel to the real axis and so they will cut out subsegments of equal length on the line
$r\ne 0$
, these lines are not parallel to the real axis and so they will cut out subsegments of equal length on the line
![]() $\ell _0$
that contains
$\ell _0$
that contains
![]() $\widetilde e$
. To determine the length of these segments, we write
$\widetilde e$
. To determine the length of these segments, we write
![]() $\widetilde \omega $
in the form
$\widetilde \omega $
in the form
with
![]() $u,v\in \mathbb {R}$
. It is easy to see that equation (8.1) implies that
$u,v\in \mathbb {R}$
. It is easy to see that equation (8.1) implies that
![]() $u=-2/r$
(multiply equation (8.1) by the complex conjugate of
$u=-2/r$
(multiply equation (8.1) by the complex conjugate of
![]() $\omega $
and take imaginary parts), and so the lines in our family cut
$\omega $
and take imaginary parts), and so the lines in our family cut
![]() $\ell _0$
into subsegments of length
$\ell _0$
into subsegments of length
![]() $|u|=2/|r|$
. Since
$|u|=2/|r|$
. Since
![]() $|u|=2/|r|<1/n$
by our hypotheses, one of these lines meets
$|u|=2/|r|<1/n$
by our hypotheses, one of these lines meets
![]() $\operatorname {int}(\widetilde e)$
. This implies that
$\operatorname {int}(\widetilde e)$
. This implies that
![]() $\tau \cap \operatorname {int}(e)\ne \emptyset $
, as desired.
$\tau \cap \operatorname {int}(e)\ne \emptyset $
, as desired.
We now want to see what happens to a geodesic arc
![]() $\xi $
in
$\xi $
in
![]() $(\mathbb {P},V)$
if we take preimages under a map f as in Proposition 8.1. Unless
$(\mathbb {P},V)$
if we take preimages under a map f as in Proposition 8.1. Unless
![]() $\xi $
has slope in a finite exceptional set, suitable sets
$\xi $
has slope in a finite exceptional set, suitable sets
![]() $ \mathcal {H}$
in the preimage
$ \mathcal {H}$
in the preimage
![]() $f^{-1}(\xi )$
will meet the interior of a flap glued to the pillow
$f^{-1}(\xi )$
will meet the interior of a flap glued to the pillow
![]() $\mathbb {P}$
, and consequently a peripheral pullback of the horizontal curve
$\mathbb {P}$
, and consequently a peripheral pullback of the horizontal curve
![]() $\alpha ^h\subset \mathbb {P}$
or of the vertical curve
$\alpha ^h\subset \mathbb {P}$
or of the vertical curve
![]() $\alpha ^v\subset \mathbb {P}$
. We will formulate some relevant statements in a slightly more general situation. We first introduce some terminology.
$\alpha ^v\subset \mathbb {P}$
. We will formulate some relevant statements in a slightly more general situation. We first introduce some terminology.
Suppose
![]() $Z\subset S^2$
consists of four distinct points. We say that
$Z\subset S^2$
consists of four distinct points. We say that
![]() $K\subset S^2$
essentially separates Z if we can split Z into two disjoint subsets
$K\subset S^2$
essentially separates Z if we can split Z into two disjoint subsets
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
consisting of two points each such that K separates
$Z_2$
consisting of two points each such that K separates
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
. Note that K trivially has this property if
$Z_2$
. Note that K trivially has this property if
![]() $K\cap Z$
consists of two or more points.
$K\cap Z$
consists of two or more points.
Now let
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $n\ge 2$
, and consider the
$n\ge 2$
, and consider the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n\colon \mathbb {P}\rightarrow \mathbb {P}$
. If
$\mathcal {L}_n\colon \mathbb {P}\rightarrow \mathbb {P}$
. If
![]() $\xi $
is a geodesic arc in
$\xi $
is a geodesic arc in
![]() $(\mathbb {P},V)$
, then the preimage
$(\mathbb {P},V)$
, then the preimage
![]() $\mathcal {L}_n^{-1}(\xi )$
is a disjoint union of simple closed geodesics and geodesic arcs in
$\mathcal {L}_n^{-1}(\xi )$
is a disjoint union of simple closed geodesics and geodesic arcs in
![]() $(\mathbb {P}, V)$
. Note that each connected component of
$(\mathbb {P}, V)$
. Note that each connected component of
![]() $\mathcal {L}_n^{-1}(\xi )$
essentially separates V, but no proper subset of such a component does. It follows that if
$\mathcal {L}_n^{-1}(\xi )$
essentially separates V, but no proper subset of such a component does. It follows that if
![]() $K\subset \mathcal {L}_n^{-1}(\xi )$
is a connected set, then it essentially separates V if and only if K is a simple closed geodesic or a geodesic arc in
$K\subset \mathcal {L}_n^{-1}(\xi )$
is a connected set, then it essentially separates V if and only if K is a simple closed geodesic or a geodesic arc in
![]() $(\mathbb {P},V)$
.
$(\mathbb {P},V)$
.
Let
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
be a branched covering map obtained from the
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
be a branched covering map obtained from the
![]() $(n\times n)$
-Lattès map by gluing flaps to
$(n\times n)$
-Lattès map by gluing flaps to
![]() $\mathbb {P}$
. As in §4.2, we denote by
$\mathbb {P}$
. As in §4.2, we denote by
![]() $\widehat V$
the vertex set and by
$\widehat V$
the vertex set and by
![]() $B(\widehat {\mathbb {P}})$
the base of the flapped pillow
$B(\widehat {\mathbb {P}})$
the base of the flapped pillow
![]() $\widehat {\mathbb {P}}$
. By construction,
$\widehat {\mathbb {P}}$
. By construction,
![]() $\widehat {\mathcal {L}}$
maps each
$\widehat {\mathcal {L}}$
maps each
![]() $1$
-tile of
$1$
-tile of
![]() $\widehat {\mathbb {P}}$
by a Euclidean similarity (with scaling factor n) onto a
$\widehat {\mathbb {P}}$
by a Euclidean similarity (with scaling factor n) onto a
![]() $0$
-tile of
$0$
-tile of
![]() $\mathbb {P}$
. We also recall that we can naturally view the base
$\mathbb {P}$
. We also recall that we can naturally view the base
![]() $B(\widehat {\mathbb {P}})$
as a subset of
$B(\widehat {\mathbb {P}})$
as a subset of
![]() $\mathbb {P}$
(see (4.2)) and, with such an identification, the map
$\mathbb {P}$
(see (4.2)) and, with such an identification, the map
![]() $\widehat {\mathcal {L}}$
coincides with
$\widehat {\mathcal {L}}$
coincides with
![]() $\mathcal {L}_n$
on
$\mathcal {L}_n$
on
![]() $B(\widehat {\mathbb {P}})$
.
$B(\widehat {\mathbb {P}})$
.
Suppose that a geodesic arc
![]() $\xi $
in
$\xi $
in
![]() $(\mathbb {P},V)$
joins two distinct points
$(\mathbb {P},V)$
joins two distinct points
![]() $X,Y\in V$
. We consider
$X,Y\in V$
. We consider ![]() as a planar embedded graph in
as a planar embedded graph in
![]() $\widehat {\mathbb {P}}$
with the set of vertices
$\widehat {\mathbb {P}}$
with the set of vertices
![]() $\widehat {\mathcal {L}}^{-1}(\{X,Y\})$
and the edges given by the lifts of
$\widehat {\mathcal {L}}^{-1}(\{X,Y\})$
and the edges given by the lifts of
![]() $\xi $
under
$\xi $
under
![]() $\widehat {\mathcal {L}}$
.
$\widehat {\mathcal {L}}$
.
Lemma 8.3. Let
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
be a branched covering map obtained from the
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \to \mathbb {P}$
be a branched covering map obtained from the
![]() $(n\times n)$
-Lattès map with
$(n\times n)$
-Lattès map with
![]() $n\ge 2$
by gluing
$n\ge 2$
by gluing
![]() $n_h\geq 1$
horizontal and
$n_h\geq 1$
horizontal and
![]() $n_v\geq 1$
vertical flaps to
$n_v\geq 1$
vertical flaps to
![]() $\mathbb {P}$
. Suppose
$\mathbb {P}$
. Suppose
![]() $\xi $
is a geodesic arc in
$\xi $
is a geodesic arc in
![]() $(\mathbb {P},V)$
with slope
$(\mathbb {P},V)$
with slope
![]() $r/s \in \widehat {\mathbb {Q}} \smallsetminus \{0,\infty \}$
and
$r/s \in \widehat {\mathbb {Q}} \smallsetminus \{0,\infty \}$
and
![]() $\widehat \xi $
is a lift of
$\widehat \xi $
is a lift of
![]() $\xi $
under
$\xi $
under
![]() $\widehat {\mathcal {L}}$
.
$\widehat {\mathcal {L}}$
.
Let F be a flap in
![]() $\widehat {\mathbb {P}}$
with the base edges
$\widehat {\mathbb {P}}$
with the base edges
![]() $e'$
and
$e'$
and
![]() $e"$
. If
$e"$
. If
then
![]() $\widehat \xi $
meets a base edge and the top edge of the flap F.
$\widehat \xi $
meets a base edge and the top edge of the flap F.
Proof. The proof is similar to the proof of Lemma 5.6. Recall that
![]() $a,b,c,d$
denote the edges of the pillow
$a,b,c,d$
denote the edges of the pillow
![]() $\mathbb {P}$
. Suppose
$\mathbb {P}$
. Suppose
![]() $\xi \subset \mathbb {P}$
,
$\xi \subset \mathbb {P}$
,
![]() $\widehat \xi \subset \widehat {\mathbb {P}}$
, and
$\widehat \xi \subset \widehat {\mathbb {P}}$
, and
![]() $e',e"\subset F$
are as in the statement of the lemma. Let
$e',e"\subset F$
are as in the statement of the lemma. Let
![]() $\widetilde e\subset F$
be the top edge of F.
$\widetilde e\subset F$
be the top edge of F.
Without loss of generality, we will assume that F is a horizontal flap. Then
![]() $\widehat {\mathcal {L}}(e')=a$
or
$\widehat {\mathcal {L}}(e')=a$
or
![]() $\widehat {\mathcal {L}}(e')=c$
. We will make the further assumption that
$\widehat {\mathcal {L}}(e')=c$
. We will make the further assumption that
![]() $\widehat {\mathcal {L}}(e')=a$
. The other cases, when
$\widehat {\mathcal {L}}(e')=a$
. The other cases, when
![]() $\widehat {\mathcal {L}}(e')=c$
or when F is a vertical flap, can be treated in a way that is completely analogous to the ensuing argument. Then
$\widehat {\mathcal {L}}(e')=c$
or when F is a vertical flap, can be treated in a way that is completely analogous to the ensuing argument. Then
![]() $\widehat {\mathcal {L}}(e")=a$
and
$\widehat {\mathcal {L}}(e")=a$
and
![]() $\widehat {\mathcal {L}}(\widetilde e)=c$
. Moreover,
$\widehat {\mathcal {L}}(\widetilde e)=c$
. Moreover,
Since
![]() $\xi $
is a geodesic arc in
$\xi $
is a geodesic arc in
![]() $(\mathbb {P}, V)$
with slope
$(\mathbb {P}, V)$
with slope
![]() $r/s\ne 0$
, by Lemma 2.5, the sets
$r/s\ne 0$
, by Lemma 2.5, the sets
![]() $a\cap \xi $
and
$a\cap \xi $
and
![]() $c\cap \xi $
are non-empty and finite, and the points in these sets alternate on
$c\cap \xi $
are non-empty and finite, and the points in these sets alternate on
![]() $\xi $
. We claim that there is a point
$\xi $
. We claim that there is a point
![]() $p\in \widehat \xi \cap \operatorname {int}(F)$
. By our hypotheses, this can only fail if
$p\in \widehat \xi \cap \operatorname {int}(F)$
. By our hypotheses, this can only fail if
![]() $\widehat \xi $
meets either
$\widehat \xi $
meets either
![]() $\operatorname {int}(e')$
or
$\operatorname {int}(e')$
or
![]() $\operatorname {int}(e")$
in a point q. Since the arc
$\operatorname {int}(e")$
in a point q. Since the arc
![]() $\xi $
has a transverse intersection with
$\xi $
has a transverse intersection with
![]() $\operatorname {int}(a)$
at
$\operatorname {int}(a)$
at
![]() $\widehat {\mathcal {L}} (q)$
, the arc
$\widehat {\mathcal {L}} (q)$
, the arc
![]() $\widehat \xi $
has a transverse intersection with
$\widehat \xi $
has a transverse intersection with
![]() $\operatorname {int}(e')$
or
$\operatorname {int}(e')$
or
![]() $\operatorname {int}(e")$
at q. Then
$\operatorname {int}(e")$
at q. Then
![]() $\widehat \xi $
meets
$\widehat \xi $
meets
![]() $\operatorname {int}(F)$
in a point p in any case.
$\operatorname {int}(F)$
in a point p in any case.
Since the points in
![]() $a\cap \xi \ne \emptyset $
and
$a\cap \xi \ne \emptyset $
and
![]() $c\cap \xi \ne \emptyset $
alternate on
$c\cap \xi \ne \emptyset $
alternate on
![]() $\xi $
, the points in
$\xi $
, the points in
![]() ${\widehat \xi \cap \widehat {\mathcal {L}}^{-1}(a)\ne \emptyset }$
and
${\widehat \xi \cap \widehat {\mathcal {L}}^{-1}(a)\ne \emptyset }$
and
![]() $\widehat \xi \cap \widehat {\mathcal {L}}^{-1}(c)\ne \emptyset $
alternate on
$\widehat \xi \cap \widehat {\mathcal {L}}^{-1}(c)\ne \emptyset $
alternate on
![]() $\widehat \xi $
. Note that
$\widehat \xi $
. Note that
![]() $F\cap \widehat {\mathcal {L}}^{-1}(c)=\widetilde e$
and
$F\cap \widehat {\mathcal {L}}^{-1}(c)=\widetilde e$
and
![]() $F\cap \widehat {\mathcal {L}}^{-1}(a)= \partial F = e' \cup e"$
. So, if we trace the arc
$F\cap \widehat {\mathcal {L}}^{-1}(a)= \partial F = e' \cup e"$
. So, if we trace the arc
![]() $\widehat \xi $
starting from p in two different directions, we must meet a base edge of F in one direction and the top edge of F in the other direction. The statement follows.
$\widehat \xi $
starting from p in two different directions, we must meet a base edge of F in one direction and the top edge of F in the other direction. The statement follows.
Now the following fact is true.
Lemma 8.4. Let
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
be a branched covering map obtained from the
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}}\to \mathbb {P}$
be a branched covering map obtained from the
![]() $(n\times n)$
-Lattès map with
$(n\times n)$
-Lattès map with
![]() $n\ge 2$
by gluing
$n\ge 2$
by gluing
![]() $n_h\geq 1$
horizontal and
$n_h\geq 1$
horizontal and
![]() $n_v\geq 1$
vertical flaps to
$n_v\geq 1$
vertical flaps to
![]() $\mathbb {P}$
. Suppose that
$\mathbb {P}$
. Suppose that
![]() $\xi $
is a geodesic arc in
$\xi $
is a geodesic arc in
![]() $(\mathbb {P},V)$
with slope
$(\mathbb {P},V)$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
and
$r/s\in \widehat {\mathbb {Q}}$
and
![]() $ \mathcal {H}$
is any connected subgraph of
$ \mathcal {H}$
is any connected subgraph of
![]() $ \widehat {\mathcal {G}}=\widehat {\mathcal {L}}^{-1}(\xi )$
that essentially separates
$ \widehat {\mathcal {G}}=\widehat {\mathcal {L}}^{-1}(\xi )$
that essentially separates
![]() $\widehat V\subset \widehat {\mathbb {P}}$
. If
$\widehat V\subset \widehat {\mathbb {P}}$
. If
![]() $|r|+s> 4n$
, then
$|r|+s> 4n$
, then
![]() $\mathcal {H}$
meets a base edge and the top edge of a flap in
$\mathcal {H}$
meets a base edge and the top edge of a flap in
![]() $\widehat {\mathbb {P}}$
.
$\widehat {\mathbb {P}}$
.
Proof. Suppose
![]() $\xi $
is a geodesic arc in
$\xi $
is a geodesic arc in
![]() $(\mathbb {P},V)$
with slope
$(\mathbb {P},V)$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
, where
$r/s\in \widehat {\mathbb {Q}}$
, where
![]() $|r|+s> 4n$
, and
$|r|+s> 4n$
, and
![]() $ \mathcal {H}$
is a connected subgraph of
$ \mathcal {H}$
is a connected subgraph of
![]() $\widehat {\mathcal {G}}=\widehat {\mathcal {L}}^{-1}(\xi )$
that essentially separates the vertex set
$\widehat {\mathcal {G}}=\widehat {\mathcal {L}}^{-1}(\xi )$
that essentially separates the vertex set
![]() $\widehat V$
of
$\widehat V$
of
![]() $\widehat {\mathbb {P}}$
. Note that then
$\widehat {\mathbb {P}}$
. Note that then
![]() $r/s\ne 0,\infty $
, which will allow us to apply Lemma 8.3. Each edge of the graph
$r/s\ne 0,\infty $
, which will allow us to apply Lemma 8.3. Each edge of the graph
![]() $\widehat {\mathcal {G}}=\widehat {\mathcal {L}}^{-1}(\xi )$
is a lift
$\widehat {\mathcal {G}}=\widehat {\mathcal {L}}^{-1}(\xi )$
is a lift
![]() $\widehat \xi $
of
$\widehat \xi $
of
![]() $\xi $
as in this lemma.
$\xi $
as in this lemma.
We now argue by contradiction and suppose that there is no flap F in
![]() $\widehat {\mathbb {P}}$
such that
$\widehat {\mathbb {P}}$
such that
![]() $\mathcal {H}$
meets both a base edge and the top edge of F. By the definition of
$\mathcal {H}$
meets both a base edge and the top edge of F. By the definition of
![]() $B(\widehat {\mathbb {P}})$
(see (4.1)) and Lemma 8.3, this means that each edge of
$B(\widehat {\mathbb {P}})$
(see (4.1)) and Lemma 8.3, this means that each edge of
![]() $\mathcal {H}$
, and thus the graph
$\mathcal {H}$
, and thus the graph
![]() $ \mathcal {H}$
itself, is contained in
$ \mathcal {H}$
itself, is contained in
![]() $B(\widehat {\mathbb {P}})$
. Consequently, we can consider
$B(\widehat {\mathbb {P}})$
. Consequently, we can consider
![]() $ \mathcal {H}$
as a connected subset of
$ \mathcal {H}$
as a connected subset of
![]() $\mathbb {P}\supset B(\widehat {\mathbb {P}})$
. On
$\mathbb {P}\supset B(\widehat {\mathbb {P}})$
. On
![]() $B(\widehat {\mathbb {P}})$
, the maps
$B(\widehat {\mathbb {P}})$
, the maps
![]() $\widehat {\mathcal {L}}$
and
$\widehat {\mathcal {L}}$
and
![]() $\mathcal {L}_n$
are identical. Therefore, we can also regard
$\mathcal {L}_n$
are identical. Therefore, we can also regard
![]() $ \mathcal {H}$
as a connected subset of
$ \mathcal {H}$
as a connected subset of
![]() $\mathcal {L}_n^{-1}(\xi )$
.
$\mathcal {L}_n^{-1}(\xi )$
.
The set
![]() $\mathcal {H}$
, now considered as a subset of
$\mathcal {H}$
, now considered as a subset of
![]() $\mathbb {P}$
, essentially separates
$\mathbb {P}$
, essentially separates
![]() $V\subset \mathbb {P}$
. To see this, let
$V\subset \mathbb {P}$
. To see this, let
![]() $\widehat V_1, \widehat V_2\subset \widehat V\subset \widehat {\mathbb {P}}$
be two pairs of vertices separated by
$\widehat V_1, \widehat V_2\subset \widehat V\subset \widehat {\mathbb {P}}$
be two pairs of vertices separated by
![]() $ \mathcal {H}$
in
$ \mathcal {H}$
in
![]() $\widehat {\mathbb {P}}$
. We can identify
$\widehat {\mathbb {P}}$
. We can identify
![]() $\widehat V_1$
with a pair
$\widehat V_1$
with a pair
![]() $V_1$
and
$V_1$
and
![]() $\widehat V_2$
with a pair
$\widehat V_2$
with a pair
![]() $V_2$
of vertices of
$V_2$
of vertices of
![]() $\mathbb {P}$
. We claim that
$\mathbb {P}$
. We claim that
![]() $V_1$
and
$V_1$
and
![]() $V_2$
are separated by
$V_2$
are separated by
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\mathbb {P}$
. Indeed, if this was not the case, then we could find a path
$\mathbb {P}$
. Indeed, if this was not the case, then we could find a path
![]() $\beta $
in
$\beta $
in
![]() $\mathbb {P}$
that joins
$\mathbb {P}$
that joins
![]() $V_1$
and
$V_1$
and
![]() $V_2$
without meeting
$V_2$
without meeting
![]() $\mathcal {H}$
. This path can be modified as follows to a path
$\mathcal {H}$
. This path can be modified as follows to a path
![]() $\widehat \beta $
in
$\widehat \beta $
in
![]() $\widehat {\mathbb {P}}$
that joins
$\widehat {\mathbb {P}}$
that joins
![]() $\widehat V_1$
and
$\widehat V_1$
and
![]() $\widehat V_2$
and does not meet
$\widehat V_2$
and does not meet
![]() $\mathcal {H}\subset \widehat {\mathbb {P}}$
: if
$\mathcal {H}\subset \widehat {\mathbb {P}}$
: if
![]() $\beta $
meets some
$\beta $
meets some
![]() $1$
-edge e of
$1$
-edge e of
![]() $\mathbb {P}$
to which one or several flaps are glued, then on
$\mathbb {P}$
to which one or several flaps are glued, then on
![]() $\beta $
, there is a first point
$\beta $
, there is a first point
![]() $p\in e$
and a last point
$p\in e$
and a last point
![]() $q\in e$
. We now replace the part of
$q\in e$
. We now replace the part of
![]() $\beta $
between p and q by a path that joins points corresponding to p and q in
$\beta $
between p and q by a path that joins points corresponding to p and q in
![]() $\widehat {\mathbb {P}}$
, travels on these flaps, and does not meet
$\widehat {\mathbb {P}}$
, travels on these flaps, and does not meet
![]() $\mathcal {H}$
. If we make such replacements for all these edges e consecutively, then we obtain a path
$\mathcal {H}$
. If we make such replacements for all these edges e consecutively, then we obtain a path
![]() $\widehat \beta $
that joins
$\widehat \beta $
that joins
![]() $\widehat V_1$
and
$\widehat V_1$
and
![]() $\widehat V_2$
, but is disjoint from
$\widehat V_2$
, but is disjoint from
![]() $\mathcal {H}$
. However, such a path
$\mathcal {H}$
. However, such a path
![]() $\widehat \beta $
cannot exist, because
$\widehat \beta $
cannot exist, because
![]() $ \mathcal {H}$
separates
$ \mathcal {H}$
separates
![]() $\widehat V_1$
and
$\widehat V_1$
and
![]() $\widehat V_2$
in
$\widehat V_2$
in
![]() $\widehat {\mathbb {P}}$
.
$\widehat {\mathbb {P}}$
.
We see that
![]() $ \mathcal {H}\subset \mathcal {L}_n^{-1}(\xi )$
indeed essentially separates V. Since
$ \mathcal {H}\subset \mathcal {L}_n^{-1}(\xi )$
indeed essentially separates V. Since
![]() $\mathcal {H}$
is connected, the discussion above (after the definition of essential separation) implies that
$\mathcal {H}$
is connected, the discussion above (after the definition of essential separation) implies that
![]() $ \mathcal {H}$
is a simple closed geodesic or a geodesic arc in
$ \mathcal {H}$
is a simple closed geodesic or a geodesic arc in
![]() $(\mathbb {P},V)$
with slope
$(\mathbb {P},V)$
with slope
![]() $r/s$
. Since
$r/s$
. Since
![]() $|r|+s>4n$
, either
$|r|+s>4n$
, either
![]() $|r|>2n$
or
$|r|>2n$
or
![]() $s>2n$
. Thus, by Lemma 8.2, the geodesic
$s>2n$
. Thus, by Lemma 8.2, the geodesic
![]() $\mathcal {H}$
meets each horizontal
$\mathcal {H}$
meets each horizontal
![]() $1$
-edge of
$1$
-edge of
![]() $\mathbb {P}$
in the first case or each vertical
$\mathbb {P}$
in the first case or each vertical
![]() $1$
-edge of
$1$
-edge of
![]() $\mathbb {P}$
in the second case. Since
$\mathbb {P}$
in the second case. Since
![]() $n_h\geq 1$
and
$n_h\geq 1$
and
![]() $n_v\geq 1$
, in either case,
$n_v\geq 1$
, in either case,
![]() $\mathcal {H}$
must meet the interior of a
$\mathcal {H}$
must meet the interior of a
![]() $1$
-edge along which a flap is glued and hence cannot be a subset of
$1$
-edge along which a flap is glued and hence cannot be a subset of
![]() $B(\widehat {\mathbb {P}})$
. This is a contradiction and the lemma follows.
$B(\widehat {\mathbb {P}})$
. This is a contradiction and the lemma follows.
Remark 8.5. Suppose we are in the setup of Lemma 8.4. Then the connected set
![]() $\mathcal {H}$
meets a base edge and the top edge of a flap, say a horizontal flap F. Then there exists a peripheral pullback
$\mathcal {H}$
meets a base edge and the top edge of a flap, say a horizontal flap F. Then there exists a peripheral pullback
![]() $\widehat \alpha $
of the horizontal curve
$\widehat \alpha $
of the horizontal curve
![]() $\alpha ^h$
under the map
$\alpha ^h$
under the map
![]() $ \widehat {\mathcal {L}}$
that is contained in F. Let
$ \widehat {\mathcal {L}}$
that is contained in F. Let
![]() $e'$
and
$e'$
and
![]() $e"$
be the base edges of F, and
$e"$
be the base edges of F, and
![]() $\widetilde e$
be the top edge of F. Then the curve
$\widetilde e$
be the top edge of F. Then the curve
![]() $\widehat \alpha $
separates
$\widehat \alpha $
separates
![]() $\partial F = e'\cup e"$
from
$\partial F = e'\cup e"$
from
![]() $\widetilde e\subset F$
. Since
$\widetilde e\subset F$
. Since
![]() $\mathcal {H}$
is connected and meets both
$\mathcal {H}$
is connected and meets both
![]() $\widetilde e$
and
$\widetilde e$
and
![]() $e'\cup e"$
, we conclude that
$e'\cup e"$
, we conclude that
![]() $\mathcal {H} \cap \widehat \alpha \ne \emptyset $
. If
$\mathcal {H} \cap \widehat \alpha \ne \emptyset $
. If
![]() $\beta $
is a connected set that traces
$\beta $
is a connected set that traces
![]() $\mathcal {H}$
closely, then it will also have points close to
$\mathcal {H}$
closely, then it will also have points close to
![]() $\widetilde e$
and close to
$\widetilde e$
and close to
![]() $e'\cup e"$
. Again this will imply that
$e'\cup e"$
. Again this will imply that
![]() $\beta \cap \widehat \alpha \ne \emptyset $
. This remark will become important in the proof of Proposition 8.1.
$\beta \cap \widehat \alpha \ne \emptyset $
. This remark will become important in the proof of Proposition 8.1.
A completely analogous statement to Lemma 8.4 is true (with a very similar proof) if we assume that
![]() $\xi $
is a simple closed geodesic in
$\xi $
is a simple closed geodesic in
![]() $(\mathbb {P},V)$
and
$(\mathbb {P},V)$
and
![]() $ \mathcal {H}$
is an essential pullback of
$ \mathcal {H}$
is an essential pullback of
![]() $\xi $
under
$\xi $
under
![]() $\widehat {\mathcal {L}}$
.
$\widehat {\mathcal {L}}$
.
We now turn to the proof of Proposition 8.1.
Proof of Proposition 8.1
Let
![]() $f\colon \mathbb {P}\to \mathbb {P}$
be a Thurston map obtained from the
$f\colon \mathbb {P}\to \mathbb {P}$
be a Thurston map obtained from the
![]() ${(2\times 2)}$
-Lattès map by gluing
${(2\times 2)}$
-Lattès map by gluing
![]() $n_h\geq 1$
horizontal and
$n_h\geq 1$
horizontal and
![]() $n_v\geq 1$
vertical flaps to
$n_v\geq 1$
vertical flaps to
![]() $\mathbb {P}$
. Then
$\mathbb {P}$
. Then
![]() ${P_f}=V$
, where
${P_f}=V$
, where
![]() $V=\{A,B,C,D\}$
is the set of vertices of
$V=\{A,B,C,D\}$
is the set of vertices of
![]() $\mathbb {P}$
, and A is the unique point in
$\mathbb {P}$
, and A is the unique point in
![]() ${P_f}=V$
that is fixed by f.
${P_f}=V$
that is fixed by f.
To prove the first statement, let
![]() $x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
be arbitrary. If
$x\in \widehat {\mathbb {Q}}\cup \{\odot \}$
be arbitrary. If
![]() $x=\odot $
, then
$x=\odot $
, then
![]() $\mu _f(\odot )=\odot $
and
$\mu _f(\odot )=\odot $
and
![]() $\|\mu _f(\odot )\|=\|{\odot }\|=0$
. So in the following, we will assume that
$\|\mu _f(\odot )\|=\|{\odot }\|=0$
. So in the following, we will assume that
![]() $x=r/s\in \widehat {\mathbb {Q}}$
. Let
$x=r/s\in \widehat {\mathbb {Q}}$
. Let
![]() $\gamma \subset \mathbb {P}\smallsetminus V$
be a simple closed geodesic with slope
$\gamma \subset \mathbb {P}\smallsetminus V$
be a simple closed geodesic with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. Then
$r/s\in \widehat {\mathbb {Q}}$
. Then
![]() $\gamma $
is an essential Jordan curve and so each of the two complementary components of
$\gamma $
is an essential Jordan curve and so each of the two complementary components of
![]() $\gamma $
in
$\gamma $
in
![]() $\mathbb {P}$
contains precisely two postcritical points of f. Let
$\mathbb {P}$
contains precisely two postcritical points of f. Let
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
be core arcs of
$\xi '$
be core arcs of
![]() $\gamma $
belonging to different components of
$\gamma $
belonging to different components of
![]() $\mathbb {P}\smallsetminus \gamma $
. Here we may assume that
$\mathbb {P}\smallsetminus \gamma $
. Here we may assume that
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
are geodesic arcs in
$\xi '$
are geodesic arcs in
![]() $(\mathbb {P},V)$
with slope
$(\mathbb {P},V)$
with slope
![]() $r/s$
.
$r/s$
.
As before, we denote by
![]() $\alpha ^h$
and
$\alpha ^h$
and
![]() $\alpha ^v$
simple closed geodesics in
$\alpha ^v$
simple closed geodesics in
![]() $(\mathbb {P}, V)$
that separate the two horizontal and the two vertical edges of
$(\mathbb {P}, V)$
that separate the two horizontal and the two vertical edges of
![]() $\mathbb {P}$
, respectively. Then, by Lemma 2.4, we have
$\mathbb {P}$
, respectively. Then, by Lemma 2.4, we have
 $$ \begin{align*} \mathrm{i}(\gamma,\alpha^h)&=2 \mathrm{i}(\xi, \alpha^h)=\#(\gamma\cap\alpha^h)=2|r|,\\ \mathrm{i}(\gamma,\alpha^v)&=2 \mathrm{i}(\xi, \alpha^v)=\#(\gamma\cap\alpha^v)=2s, \\ \|x\| &=|r|+s = \tfrac12 \mathrm{i}(\gamma, \alpha^h)+ \tfrac12 \mathrm{i}(\gamma, \alpha^v). \end{align*} $$
$$ \begin{align*} \mathrm{i}(\gamma,\alpha^h)&=2 \mathrm{i}(\xi, \alpha^h)=\#(\gamma\cap\alpha^h)=2|r|,\\ \mathrm{i}(\gamma,\alpha^v)&=2 \mathrm{i}(\xi, \alpha^v)=\#(\gamma\cap\alpha^v)=2s, \\ \|x\| &=|r|+s = \tfrac12 \mathrm{i}(\gamma, \alpha^h)+ \tfrac12 \mathrm{i}(\gamma, \alpha^v). \end{align*} $$
We call a point
![]() $p\in \mathbb {P}$
a
$p\in \mathbb {P}$
a
![]() $1$
-vertex if
$1$
-vertex if
![]() $f(p) \in {P_f}=\{A,B,C,D\}$
. We say that a
$f(p) \in {P_f}=\{A,B,C,D\}$
. We say that a
![]() $1$
-vertex is of type A, B, C, or D if it is a preimage of A, B, C, or D under f, respectively.
$1$
-vertex is of type A, B, C, or D if it is a preimage of A, B, C, or D under f, respectively.
Without loss of generality, we may assume that the core arc
![]() $\xi $
connects the point A with a point
$\xi $
connects the point A with a point
![]() $X\in \{B,C,D\}$
. Then
$X\in \{B,C,D\}$
. Then
![]() $\xi '$
joins the two points in
$\xi '$
joins the two points in
![]() $\{B,C,D\}\smallsetminus \{X\}$
. Let
$\{B,C,D\}\smallsetminus \{X\}$
. Let
![]() $\mathcal {G}=f^{-1}(\xi \cup \xi ')$
, which we view as a planar embedded graph with the set of vertices
$\mathcal {G}=f^{-1}(\xi \cup \xi ')$
, which we view as a planar embedded graph with the set of vertices
![]() $f^{-1}(V)$
. Note that the degree of a vertex p in
$f^{-1}(V)$
. Note that the degree of a vertex p in
![]() $\mathcal {G}$
is equal to the local degree of the map f at p. In addition, the graph
$\mathcal {G}$
is equal to the local degree of the map f at p. In addition, the graph
![]() $\mathcal {G}$
has the following properties.
$\mathcal {G}$
has the following properties.
-
(P1)
 $\mathcal {G}$
is a bipartite graph. In particular,
$\mathcal {G}$
is a bipartite graph. In particular,
 $1$
-vertices of type A are connected only to
$1$
-vertices of type A are connected only to
 $1$
-vertices of type X and vice versa.
$1$
-vertices of type X and vice versa. -
(P2) Each postcritical point of f is a
 $1$
-vertex of type A. If a
$1$
-vertex of type A. If a
 $1$
-vertex of type A has degree
$1$
-vertex of type A has degree
 $\ge 2$
in
$\ge 2$
in
 $\mathcal {G}$
, then it must be a postcritical point.
$\mathcal {G}$
, then it must be a postcritical point.
The analog of property (P1) is valid for arbitrary Thurston maps with four postcritical points. To see that property (P2) is true, note that the
![]() $(2\times 2)$
-Lattès map sends each of the four vertices of
$(2\times 2)$
-Lattès map sends each of the four vertices of
![]() $\mathbb {P}$
to A. This remains true if we glue any number of flaps to
$\mathbb {P}$
to A. This remains true if we glue any number of flaps to
![]() $\mathbb {P}$
. Moreover, gluing additional flaps can only create additional preimages of A of degree
$\mathbb {P}$
. Moreover, gluing additional flaps can only create additional preimages of A of degree
![]() $1$
in
$1$
in
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
If every pullback of
![]() $\gamma $
under f is peripheral, then
$\gamma $
under f is peripheral, then
![]() $\mu _f(x)=\odot $
, and so
$\mu _f(x)=\odot $
, and so
Suppose
![]() $\gamma $
has an essential pullback
$\gamma $
has an essential pullback
![]() $\widetilde {\gamma }$
under f. Then
$\widetilde {\gamma }$
under f. Then
![]() $\mu _f(x)\in \widehat {\mathbb {Q}}$
is the slope corresponding to the isotopy class of
$\mu _f(x)\in \widehat {\mathbb {Q}}$
is the slope corresponding to the isotopy class of
![]() $\widetilde \gamma $
. By the discussion in §6, the pullback
$\widetilde \gamma $
. By the discussion in §6, the pullback
![]() $\widetilde {\gamma }$
belongs to a unique component
$\widetilde {\gamma }$
belongs to a unique component
![]() $\widetilde {U}$
of
$\widetilde {U}$
of
![]() $\mathbb {P}\smallsetminus \mathcal {G}$
. We use the notation
$\mathbb {P}\smallsetminus \mathcal {G}$
. We use the notation ![]() . Then
. Then
![]() $\partial _\xi \widetilde {U}$
is a subgraph of
$\partial _\xi \widetilde {U}$
is a subgraph of
![]() $\mathcal {G}$
that only contains
$\mathcal {G}$
that only contains
![]() $1$
-vertices of type A and X. Since
$1$
-vertices of type A and X. Since
![]() $\widetilde {\gamma }$
is essential,
$\widetilde {\gamma }$
is essential,
![]() $\partial _\xi \widetilde {U}$
satisfies:
$\partial _\xi \widetilde {U}$
satisfies:
-
(P3)
 $\#(\partial _\xi \widetilde {U}\cap {P_f}) \leq 2$
.
$\#(\partial _\xi \widetilde {U}\cap {P_f}) \leq 2$
.
Our goal now is to simplify the pullback
![]() $\widetilde {\gamma }$
using an isotopy depending on the combinatorics of
$\widetilde {\gamma }$
using an isotopy depending on the combinatorics of
![]() $\partial _\xi \widetilde {U}$
. More precisely, we will construct a curve
$\partial _\xi \widetilde {U}$
. More precisely, we will construct a curve
![]() $\beta $
that is isotopic to
$\beta $
that is isotopic to
![]() $\widetilde {\gamma }$
, but has fewer intersections with
$\widetilde {\gamma }$
, but has fewer intersections with
![]() $\alpha ^h$
and
$\alpha ^h$
and
![]() $\alpha ^v$
. To obtain a suitable curve
$\alpha ^v$
. To obtain a suitable curve
![]() $\beta $
, we now distinguish several cases that exhaust all possibilities.
$\beta $
, we now distinguish several cases that exhaust all possibilities.
Case 1:
![]() $\partial _\xi \widetilde {U}$
does not contain any simple cycle. Then
$\partial _\xi \widetilde {U}$
does not contain any simple cycle. Then
![]() $\partial _\xi \widetilde {U}$
is a tree and, since
$\partial _\xi \widetilde {U}$
is a tree and, since
![]() $\widetilde {\gamma }$
is essential, there are exactly two postcritical points in
$\widetilde {\gamma }$
is essential, there are exactly two postcritical points in
![]() $\partial _\xi \widetilde {U}$
. These are
$\partial _\xi \widetilde {U}$
. These are
![]() $1$
-vertices of type A by property (P2). Let
$1$
-vertices of type A by property (P2). Let
![]() $\mathcal {H}\subset \partial _\xi \widetilde {U}$
be the unique simple path that joins these two postcritical points in
$\mathcal {H}\subset \partial _\xi \widetilde {U}$
be the unique simple path that joins these two postcritical points in
![]() $\partial _\xi \widetilde {U}$
. By property (P1), the path
$\partial _\xi \widetilde {U}$
. By property (P1), the path
![]() $\mathcal {H}$
must have length
$\mathcal {H}$
must have length
![]() $\ge 2$
, because the endpoints of
$\ge 2$
, because the endpoints of
![]() $\mathcal {H}$
have type A and the vertices of types A and X alternate on
$\mathcal {H}$
have type A and the vertices of types A and X alternate on
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
If the length of
![]() $\mathcal {H}$
was
$\mathcal {H}$
was
![]() $\ge 3$
, then
$\ge 3$
, then
![]() $\mathcal {H}$
would contain at least one additional point p of type A apart from its endpoints. Then
$\mathcal {H}$
would contain at least one additional point p of type A apart from its endpoints. Then
![]() $\deg _{\mathcal {H}}(p)=2$
, so
$\deg _{\mathcal {H}}(p)=2$
, so
![]() $\deg _{\mathcal {G}}(p)\geq 2$
, which means p must be a postcritical point by property (P2). However, then
$\deg _{\mathcal {G}}(p)\geq 2$
, which means p must be a postcritical point by property (P2). However, then
![]() $\mathcal {H}\subset \partial _\xi \widetilde {U}$
contains at least three postcritical points, which contradicts property (P3). We conclude that
$\mathcal {H}\subset \partial _\xi \widetilde {U}$
contains at least three postcritical points, which contradicts property (P3). We conclude that
![]() $\mathcal {H}$
has length
$\mathcal {H}$
has length
![]() $2$
; see Figure 21 (Case 1).
$2$
; see Figure 21 (Case 1).

Figure 21 Different combinatorial types of the graph
![]() $\partial _\xi \widetilde U$
. The subgraph in magenta corresponds to the appropriate choice of
$\partial _\xi \widetilde U$
. The subgraph in magenta corresponds to the appropriate choice of
![]() $\mathcal {H}$
in each case. The vertices in black indicate the postcritical points.
$\mathcal {H}$
in each case. The vertices in black indicate the postcritical points.
Let
![]() $\widehat {U}=S^2\smallsetminus \mathcal {H}$
. Then the annulus between
$\widehat {U}=S^2\smallsetminus \mathcal {H}$
. Then the annulus between
![]() $\widetilde {\gamma }$
and
$\widetilde {\gamma }$
and
![]() $\mathcal {H}$
contains no postcritical points of f, and hence for sufficiently small
$\mathcal {H}$
contains no postcritical points of f, and hence for sufficiently small
![]() $\epsilon $
, each
$\epsilon $
, each
![]() $\epsilon $
-boundary
$\epsilon $
-boundary
![]() $\beta $
of
$\beta $
of
![]() $\widehat {U}$
with respect to
$\widehat {U}$
with respect to
![]() $\mathcal {H}$
is isotopic to
$\mathcal {H}$
is isotopic to
![]() $\widetilde {\gamma }$
, as follows from Lemma 2.1.
$\widetilde {\gamma }$
, as follows from Lemma 2.1.
Case 2:
![]() $\partial _\xi \widetilde {U}$
contains a simple cycle. Then by property (P1), one of the vertices of such a cycle must be of type A. Since this vertex has degree equal to
$\partial _\xi \widetilde {U}$
contains a simple cycle. Then by property (P1), one of the vertices of such a cycle must be of type A. Since this vertex has degree equal to
![]() $2$
in the cycle, and hence degree
$2$
in the cycle, and hence degree
![]() $\ge 2$
in
$\ge 2$
in
![]() $\mathcal {G}$
, it must be a postcritical point by property (P2). It follows that
$\mathcal {G}$
, it must be a postcritical point by property (P2). It follows that
![]() $\#(\partial _\xi \widetilde {U}\cap {P_f})\geq 1$
. So by property (P3), either
$\#(\partial _\xi \widetilde {U}\cap {P_f})\geq 1$
. So by property (P3), either
![]() $\#(\partial _\xi \widetilde {U}\cap {P_f}) = 1$
or
$\#(\partial _\xi \widetilde {U}\cap {P_f}) = 1$
or
![]() $\#(\partial _\xi \widetilde {U}\cap {P_f}) = 2$
.
$\#(\partial _\xi \widetilde {U}\cap {P_f}) = 2$
.
Case 2a:
![]() $\#(\partial _\xi \widetilde {U}\cap {P_f}) = 1$
. Since
$\#(\partial _\xi \widetilde {U}\cap {P_f}) = 1$
. Since
![]() $\widetilde {\gamma }$
is essential, there are exactly two postcritical points in the component of
$\widetilde {\gamma }$
is essential, there are exactly two postcritical points in the component of
![]() $S^2\smallsetminus \widetilde {\gamma }$
that contains
$S^2\smallsetminus \widetilde {\gamma }$
that contains
![]() $\partial _\xi \widetilde {U}$
. One of them belongs to
$\partial _\xi \widetilde {U}$
. One of them belongs to
![]() $\partial _\xi \widetilde {U}$
, while the other one belongs to a face of
$\partial _\xi \widetilde {U}$
, while the other one belongs to a face of
![]() $\partial _\xi \widetilde {U}$
disjoint from
$\partial _\xi \widetilde {U}$
disjoint from
![]() $\widetilde U$
. This postcritical point then necessarily belongs to a face of a simple cycle
$\widetilde U$
. This postcritical point then necessarily belongs to a face of a simple cycle
![]() $\mathcal {H}$
in
$\mathcal {H}$
in
![]() $\partial _\xi \widetilde {U}$
. This simple cycle
$\partial _\xi \widetilde {U}$
. This simple cycle
![]() $\mathcal {H}$
then necessarily contains the unique postcritical point in
$\mathcal {H}$
then necessarily contains the unique postcritical point in
![]() $\partial _\xi \widetilde {U}$
as we have seen above. Moreover,
$\partial _\xi \widetilde {U}$
as we have seen above. Moreover,
![]() $\mathcal {H}$
must have length
$\mathcal {H}$
must have length
![]() $2$
, because otherwise,
$2$
, because otherwise,
![]() $\mathcal {H}$
has an even length
$\mathcal {H}$
has an even length
![]() $\ge 4$
by property (P1). However, then
$\ge 4$
by property (P1). However, then
![]() $\mathcal {H}$
contains another
$\mathcal {H}$
contains another
![]() $1$
-vertex of type A with degree
$1$
-vertex of type A with degree
![]() $\ge 2$
, which is necessarily a postcritical point by property (P2). Then
$\ge 2$
, which is necessarily a postcritical point by property (P2). Then
![]() $\mathcal {H}\subset \partial _\xi \widetilde {U}$
contains at least two postcritical points, which contradicts our assumption for this case. So
$\mathcal {H}\subset \partial _\xi \widetilde {U}$
contains at least two postcritical points, which contradicts our assumption for this case. So
![]() $\mathcal {H}$
has indeed length
$\mathcal {H}$
has indeed length
![]() $2$
; see Figure 21 (Case 2a).
$2$
; see Figure 21 (Case 2a).
Let
![]() $\widehat {U}$
denote the face of
$\widehat {U}$
denote the face of
![]() $\mathcal {H}$
that contains
$\mathcal {H}$
that contains
![]() $\widetilde {U}$
. Then again, the annulus between
$\widetilde {U}$
. Then again, the annulus between
![]() $\widetilde {\gamma }$
and
$\widetilde {\gamma }$
and
![]() $\mathcal {H}$
contains no postcritical points of f, and hence each
$\mathcal {H}$
contains no postcritical points of f, and hence each
![]() $\epsilon $
-boundary
$\epsilon $
-boundary
![]() $\beta $
of
$\beta $
of
![]() $\widehat {U}$
with respect to
$\widehat {U}$
with respect to
![]() $\mathcal {H}$
is isotopic to
$\mathcal {H}$
is isotopic to
![]() $\widetilde {\gamma }$
for sufficiently small
$\widetilde {\gamma }$
for sufficiently small
![]() $\epsilon $
.
$\epsilon $
.
Case 2b:
![]() $\#(\partial _\xi \widetilde {U}\cap {P_f}) = 2$
. Let
$\#(\partial _\xi \widetilde {U}\cap {P_f}) = 2$
. Let
![]() $\mathcal {H}$
be a simple path in
$\mathcal {H}$
be a simple path in
![]() $\partial _\xi \widetilde {U}$
that joins the two postcritical points in
$\partial _\xi \widetilde {U}$
that joins the two postcritical points in
![]() $\partial _\xi \widetilde {U}$
. By the same reasoning as in Case 1,
$\partial _\xi \widetilde {U}$
. By the same reasoning as in Case 1,
![]() $\mathcal {H}$
has length
$\mathcal {H}$
has length
![]() $2$
; see Figure 21 (Case 2b). Let
$2$
; see Figure 21 (Case 2b). Let
![]() $\widehat {U}=S^2\smallsetminus \mathcal {H}$
. Since
$\widehat {U}=S^2\smallsetminus \mathcal {H}$
. Since
![]() $\widetilde \gamma $
is essential, there are no postcritical points in the annulus between
$\widetilde \gamma $
is essential, there are no postcritical points in the annulus between
![]() $\widetilde \gamma $
and
$\widetilde \gamma $
and
![]() $\mathcal {H}$
. Thus, each
$\mathcal {H}$
. Thus, each
![]() $\epsilon $
-boundary
$\epsilon $
-boundary
![]() $\beta $
of
$\beta $
of
![]() $\widehat {U}$
with respect to
$\widehat {U}$
with respect to
![]() $\mathcal {H}$
is isotopic to
$\mathcal {H}$
is isotopic to
![]() $\widetilde {\gamma }$
for sufficiently small
$\widetilde {\gamma }$
for sufficiently small
![]() $\epsilon $
.
$\epsilon $
.
Note that in all cases,
![]() $\mathcal {H}$
essentially separates
$\mathcal {H}$
essentially separates
![]() $V={P_f}$
, because in all cases,
$V={P_f}$
, because in all cases,
![]() $\mathcal {H}$
separates the pairs of points in V contained in different complementary components of
$\mathcal {H}$
separates the pairs of points in V contained in different complementary components of
![]() $\widetilde \gamma $
. Moreover, by our choice, the circuit length of
$\widetilde \gamma $
. Moreover, by our choice, the circuit length of
![]() $\widehat U$
is equal to
$\widehat U$
is equal to
![]() $4$
in Cases 1 and 2b, and equal to
$4$
in Cases 1 and 2b, and equal to
![]() $2$
in Case 2a. So in each case, it is
$2$
in Case 2a. So in each case, it is
![]() $\le 4$
. Since
$\le 4$
. Since
![]() $\xi $
and
$\xi $
and
![]() $\alpha ^h$
are in minimal position, as follows from Lemma 2.4, we can apply Lemma 6.1 to the face
$\alpha ^h$
are in minimal position, as follows from Lemma 2.4, we can apply Lemma 6.1 to the face
![]() $\widehat U$
of
$\widehat U$
of
![]() $\mathcal {H}$
. Hence, for each sufficiently small
$\mathcal {H}$
. Hence, for each sufficiently small
![]() ${\epsilon }>0$
, we can always find an
${\epsilon }>0$
, we can always find an
![]() ${\epsilon }$
-boundary
${\epsilon }$
-boundary
![]() $\beta $
of
$\beta $
of
![]() $\widehat U$
with respect to
$\widehat U$
with respect to
![]() $\mathcal {H}$
that is isotopic to
$\mathcal {H}$
that is isotopic to
![]() $\widetilde {\gamma }$
and satisfies
$\widetilde {\gamma }$
and satisfies
![]() $\#(\beta \cap f^{-1} (\alpha ^h))\leq 4 \mathrm {i} (\xi , \alpha ^h)$
.
$\#(\beta \cap f^{-1} (\alpha ^h))\leq 4 \mathrm {i} (\xi , \alpha ^h)$
.
Let
![]() $\widetilde {\alpha }_{1}$
and
$\widetilde {\alpha }_{1}$
and
![]() $\widetilde {\alpha }_{2}$
be the two pullbacks of
$\widetilde {\alpha }_{2}$
be the two pullbacks of
![]() $\alpha ^h$
under f that are isotopic to
$\alpha ^h$
under f that are isotopic to
![]() $\alpha ^h$
(there are exactly two such pullbacks by Lemma 5.1). Then in all cases, we have
$\alpha ^h$
(there are exactly two such pullbacks by Lemma 5.1). Then in all cases, we have
 $$ \begin{align} 2\mathrm{i}(\widetilde \gamma, \alpha^h)&= 2\mathrm{i}(\beta, \alpha^h)=\mathrm{i}(\beta,\widetilde{\alpha}_{1})+ \mathrm{i}(\beta,\widetilde{\alpha}_{2}) \notag\\ & \leq \# (\beta\cap\widetilde{\alpha}_{1}) + \#(\beta\cap\widetilde{\alpha}_{2}) \notag \\&\leq \#(\beta\cap f^{-1} (\alpha^h)) \notag \\ & \leq 4 \mathrm{i} (\xi, \alpha^h) \notag \\ & = 2 \mathrm{i} (\gamma, \alpha^h). \end{align} $$
$$ \begin{align} 2\mathrm{i}(\widetilde \gamma, \alpha^h)&= 2\mathrm{i}(\beta, \alpha^h)=\mathrm{i}(\beta,\widetilde{\alpha}_{1})+ \mathrm{i}(\beta,\widetilde{\alpha}_{2}) \notag\\ & \leq \# (\beta\cap\widetilde{\alpha}_{1}) + \#(\beta\cap\widetilde{\alpha}_{2}) \notag \\&\leq \#(\beta\cap f^{-1} (\alpha^h)) \notag \\ & \leq 4 \mathrm{i} (\xi, \alpha^h) \notag \\ & = 2 \mathrm{i} (\gamma, \alpha^h). \end{align} $$
Thus,
![]() $\mathrm {i}(\widetilde \gamma , \alpha ^h) \leq \mathrm {i}(\gamma , \alpha ^h)$
. The same reasoning (with a possibly different choice of
$\mathrm {i}(\widetilde \gamma , \alpha ^h) \leq \mathrm {i}(\gamma , \alpha ^h)$
. The same reasoning (with a possibly different choice of
![]() $\beta $
) also shows
$\beta $
) also shows
![]() $\mathrm {i}(\widetilde \gamma , \alpha ^v) \leq \mathrm {i}(\gamma , \alpha ^v).$
Combining these inequalities, we conclude
$\mathrm {i}(\widetilde \gamma , \alpha ^v) \leq \mathrm {i}(\gamma , \alpha ^v).$
Combining these inequalities, we conclude
This completes the proof of the first part of the statement.
Note that the second inequality in (8.4) is strict if
![]() $\beta $
intersects a peripheral pullback of
$\beta $
intersects a peripheral pullback of
![]() $\alpha ^h$
. A similar statement is also true for the analogous inequality for the curve
$\alpha ^h$
. A similar statement is also true for the analogous inequality for the curve
![]() $\alpha ^v$
. We now assume that
$\alpha ^v$
. We now assume that
![]() $x=r/s\in \widehat {\mathbb {Q}}$
satisfies
$x=r/s\in \widehat {\mathbb {Q}}$
satisfies
![]() $\|x\|>8$
. We will argue that then either the inequality in (8.4) or the analogous inequality for
$\|x\|>8$
. We will argue that then either the inequality in (8.4) or the analogous inequality for
![]() $\alpha ^v$
is strict. This will lead to
$\alpha ^v$
is strict. This will lead to
![]() $\|\mu _f(x)\|< \|x\|. $
$\|\mu _f(x)\|< \|x\|. $
To see this, first note that
![]() $f=\widehat {\mathcal {L}} \circ \phi ^{-1}$
, where
$f=\widehat {\mathcal {L}} \circ \phi ^{-1}$
, where
![]() $\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \rightarrow \mathbb {P} $
is the associated branched covering map obtained by blowing up the
$\widehat {\mathcal {L}}\colon \widehat {\mathbb {P}} \rightarrow \mathbb {P} $
is the associated branched covering map obtained by blowing up the
![]() $(2\times 2)$
-Lattès map and
$(2\times 2)$
-Lattès map and
![]() $\phi \colon \widehat {\mathbb {P}} \rightarrow \mathbb {P}$
is a suitable homeomorphism (see §4.2 for the details). We proceed as in the first part of the proof and again represent x by a simple closed geodesic
$\phi \colon \widehat {\mathbb {P}} \rightarrow \mathbb {P}$
is a suitable homeomorphism (see §4.2 for the details). We proceed as in the first part of the proof and again represent x by a simple closed geodesic
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P},V)$
with slope
$(\mathbb {P},V)$
with slope
![]() $x=r/s$
. We may assume that
$x=r/s$
. We may assume that
![]() $\gamma $
has an essential pullback
$\gamma $
has an essential pullback
![]() $\widetilde \gamma $
under f, because otherwise, we have the desired strict inequality by (8.3).
$\widetilde \gamma $
under f, because otherwise, we have the desired strict inequality by (8.3).
We choose a geodesic core arc
![]() $\xi $
in
$\xi $
in
![]() $(\mathbb {P},V)$
and a connected set
$(\mathbb {P},V)$
and a connected set
![]() $\mathcal {H}\subset f^{-1}(\xi )$
as before and define
$\mathcal {H}\subset f^{-1}(\xi )$
as before and define ![]() . Then
. Then
![]() $\widehat {\mathcal {H}}$
is a connected subset of
$\widehat {\mathcal {H}}$
is a connected subset of
![]() $\widehat {\mathcal {L}}^{-1}(\xi )$
that essentially separates
$\widehat {\mathcal {L}}^{-1}(\xi )$
that essentially separates
![]() $\widehat V$
, where
$\widehat V$
, where
![]() $\widehat V= \phi ^{-1}(V)$
is the set of vertices of the flapped pillow
$\widehat V= \phi ^{-1}(V)$
is the set of vertices of the flapped pillow
![]() $\widehat {\mathbb {P}}$
. Since
$\widehat {\mathbb {P}}$
. Since
![]() $\|x\|=|r|+s>8$
, we can apply Lemma 8.4 (with
$\|x\|=|r|+s>8$
, we can apply Lemma 8.4 (with
![]() $n=2$
) and conclude that the set
$n=2$
) and conclude that the set
![]() $\widehat {\mathcal {H}}$
will meet a base edge and the top edge of some flap F in
$\widehat {\mathcal {H}}$
will meet a base edge and the top edge of some flap F in
![]() $\widehat {\mathbb {P}}$
. We will assume that F is a horizontal flap, the case of a vertical flap being completely analogous.
$\widehat {\mathbb {P}}$
. We will assume that F is a horizontal flap, the case of a vertical flap being completely analogous.
If
![]() ${\epsilon }$
is small enough, then the
${\epsilon }$
is small enough, then the
![]() ${\epsilon }$
-boundary
${\epsilon }$
-boundary
![]() $\beta $
constructed above traces
$\beta $
constructed above traces
![]() $\mathcal {H}$
very closely in the sense that for each point in
$\mathcal {H}$
very closely in the sense that for each point in
![]() $\mathcal {H}$
, there is a nearby point in
$\mathcal {H}$
, there is a nearby point in
![]() $\beta $
. The same is true for
$\beta $
. The same is true for ![]() and
and
![]() $\widehat {\mathcal {H}}$
. Using Remark 8.5, this implies that if
$\widehat {\mathcal {H}}$
. Using Remark 8.5, this implies that if
![]() ${\epsilon }$
is sufficiently small (as we may assume), then
${\epsilon }$
is sufficiently small (as we may assume), then
![]() $\widehat \beta $
will meet the peripheral pullback
$\widehat \beta $
will meet the peripheral pullback
![]() $\widehat \alpha $
of
$\widehat \alpha $
of
![]() $\alpha ^h$
under
$\alpha ^h$
under
![]() $\widehat {\mathcal {L}}$
that is contained in the horizontal flap F. Consequently,
$\widehat {\mathcal {L}}$
that is contained in the horizontal flap F. Consequently,
![]() $\beta $
meets the peripheral pullback
$\beta $
meets the peripheral pullback
![]() $\phi (\widehat \alpha )$
of
$\phi (\widehat \alpha )$
of
![]() $\alpha ^h$
under f. As we already pointed out, this leads to a strict inequality in (8.4) and thus also in (8.5). The statement follows.
$\alpha ^h$
under f. As we already pointed out, this leads to a strict inequality in (8.4) and thus also in (8.5). The statement follows.
The proof of Theorem 1.4 is now easy.
Proof of Theorem 1.4
Let
![]() $f\colon \mathbb {P} \rightarrow \mathbb {P}$
be a Thurston map as in the statement. Then Proposition 8.1 implies that if
$f\colon \mathbb {P} \rightarrow \mathbb {P}$
be a Thurston map as in the statement. Then Proposition 8.1 implies that if
![]() $x\in \widehat {\mathbb {Q}} \cup \{\odot \} $
is arbitrary, then the complexities of the elements
$x\in \widehat {\mathbb {Q}} \cup \{\odot \} $
is arbitrary, then the complexities of the elements
![]() $x,\, \mu _f(x),\, \mu ^2_f(x),\, \ldots $
of the orbit of x under iteration of
$x,\, \mu _f(x),\, \mu ^2_f(x),\, \ldots $
of the orbit of x under iteration of
![]() $\mu _f$
strictly decrease until this orbit eventually reaches the finite set
$\mu _f$
strictly decrease until this orbit eventually reaches the finite set ![]() . From this point on, the orbit of x stays in S. The statement follows.
. From this point on, the orbit of x stays in S. The statement follows.
Remark 8.6. The proofs of Theorems 1.3 and 1.4 show that a global curve attractor
![]() $\mathcal {A}(f)$
for f can be obtained from Jordan curves corresponding to slopes in the finite set
$\mathcal {A}(f)$
for f can be obtained from Jordan curves corresponding to slopes in the finite set
![]() ${S= \{x \in \widehat {\mathbb {Q}}\cup \{\odot \} : \|x\|\leq 8\}}$
. Actually, (8.4) and (8.5) imply that
${S= \{x \in \widehat {\mathbb {Q}}\cup \{\odot \} : \|x\|\leq 8\}}$
. Actually, (8.4) and (8.5) imply that
![]() $\|\mu _f(x)\|=\|x\|$
if and only if
$\|\mu _f(x)\|=\|x\|$
if and only if
![]() $\mu _f(x)=x$
. Therefore, the minimal global curve attractor
$\mu _f(x)=x$
. Therefore, the minimal global curve attractor
![]() $\mathcal {A}(f)$
corresponds to the set
$\mathcal {A}(f)$
corresponds to the set
![]() $\{x \in \widehat {\mathbb {Q}}\cup \{\odot \} : \mu _f(x)=x\} \subset S$
. In other words, the minimal
$\{x \in \widehat {\mathbb {Q}}\cup \{\odot \} : \mu _f(x)=x\} \subset S$
. In other words, the minimal
![]() $\mathcal {A}(f)$
consists of peripheral curves and essential curves that are invariant under f (up to isotopy).
$\mathcal {A}(f)$
consists of peripheral curves and essential curves that are invariant under f (up to isotopy).
In principle, a global curve attractor for a map f, as in Theorem 1.4, depends on the locations of the flaps. By Remark 8.6, for each concrete case, one can easily determine the exact attractor by checking if a slope
![]() $x \in \widehat {\mathbb {Q}}$
with
$x \in \widehat {\mathbb {Q}}$
with
![]() $\|x\|\leq 8$
is invariant. For example, by using a computer program written by Darragh Glynn, we verified that for the map f corresponding to the flapped pillow in Figure 22 (with one horizontal flap and one vertical flap glued at the two
$\|x\|\leq 8$
is invariant. For example, by using a computer program written by Darragh Glynn, we verified that for the map f corresponding to the flapped pillow in Figure 22 (with one horizontal flap and one vertical flap glued at the two
![]() $1$
-edges of
$1$
-edges of
![]() $\mathbb {P}$
incident to the vertex B), the invariant slopes are
$\mathbb {P}$
incident to the vertex B), the invariant slopes are
![]() $0$
,
$0$
,
![]() $\infty $
,
$\infty $
,
![]() $1$
,
$1$
,
![]() $-1$
.
$-1$
.

Figure 22 A flapped pillow.
9 Further discussion
In this section, we briefly discuss some additional topics related to the investigations in this paper.
9.1 Julia sets of blown-up Lattès maps
An obvious question is what we can say about the Julia sets of the rational maps provided by Theorem 1.2 (for the definitions of the Julia and Fatou sets of rational maps and other basic notions in complex dynamics, see [Reference MilnorMil06a]).
Proposition 9.1. Let
![]() $g\colon \widehat {\mathbb {C}} \rightarrow \widehat {\mathbb {C}}$
be a rational map that is Thurston equivalent to a map
$g\colon \widehat {\mathbb {C}} \rightarrow \widehat {\mathbb {C}}$
be a rational map that is Thurston equivalent to a map
![]() $f\colon \mathbb {P}\rightarrow \mathbb {P}$
obtained from the
$f\colon \mathbb {P}\rightarrow \mathbb {P}$
obtained from the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
with
$\mathcal {L}_n$
with
![]() $n\ge 2$
by gluing
$n\ge 2$
by gluing
![]() $n_h\ge 1$
horizontal and
$n_h\ge 1$
horizontal and
![]() $n_v\ge 1$
vertical flaps to the pillow
$n_v\ge 1$
vertical flaps to the pillow
![]() $\mathbb {P}$
. Then the following statements are true.
$\mathbb {P}$
. Then the following statements are true.
-
(i) The Julia set of g is equal to
 $\widehat {\mathbb {C}}$
if n is even and the vertex A is not contained in a flap, or if n is odd and none of the points in V is contained in a flap.
$\widehat {\mathbb {C}}$
if n is even and the vertex A is not contained in a flap, or if n is odd and none of the points in V is contained in a flap. -
(ii) The Julia set of g is equal to a Sierpiński carpet in
 $\widehat {\mathbb {C}}$
if n is even and A is contained in a flap, or if n is odd and at least one of the points in V is contained in a flap.
$\widehat {\mathbb {C}}$
if n is even and A is contained in a flap, or if n is odd and at least one of the points in V is contained in a flap.
Obviously, these cases cover all possibilities and so the Julia set of g is either the whole Riemann sphere
![]() $\widehat {\mathbb {C}}$
or a Sierpiński carpet, that is, a subset of
$\widehat {\mathbb {C}}$
or a Sierpiński carpet, that is, a subset of
![]() $\widehat {\mathbb {C}}$
homeomorphic to the standard
$\widehat {\mathbb {C}}$
homeomorphic to the standard
![]() $1/3$
-Sierpiński carpet fractal. As we will see, in the first case, the map g has no periodic critical points, while it has periodic critical points (namely critical fixed points) in the second case.
$1/3$
-Sierpiński carpet fractal. As we will see, in the first case, the map g has no periodic critical points, while it has periodic critical points (namely critical fixed points) in the second case.
Proof. Let g be a rational map as in the statement. To see what the Julia set of g is, we will check whether g has periodic critical points or not, and verify in the former case that g has no Levy arcs (see below for the definition). These conditions are invariant under Thurston equivalence and therefore it is enough to consider the map f. Then
![]() ${P_f}=V$
, where
${P_f}=V$
, where
![]() $V=\{A,B,C,D\}$
is the set of vertices of
$V=\{A,B,C,D\}$
is the set of vertices of
![]() $\mathbb {P}$
. By definition of the
$\mathbb {P}$
. By definition of the
![]() $(n\times n)$
-Lattès map
$(n\times n)$
-Lattès map
![]() $\mathcal {L}_n$
, for each
$\mathcal {L}_n$
, for each
![]() $X\in V$
, we have
$X\in V$
, we have
![]() $\mathcal {L}_n(X)=A$
if n is even and
$\mathcal {L}_n(X)=A$
if n is even and
![]() $\mathcal {L}_n(X)=X$
if n is odd. Since
$\mathcal {L}_n(X)=X$
if n is odd. Since
![]() $f|V$
agrees with
$f|V$
agrees with
![]() $\mathcal {L}_n|V$
, this implies that for each
$\mathcal {L}_n|V$
, this implies that for each
![]() $X\in V$
, we also have
$X\in V$
, we also have
![]() $f(X)=A$
if n is even and
$f(X)=A$
if n is even and
![]() $f(X)=X$
if n is odd.
$f(X)=X$
if n is odd.
Since the orbit of each critical point under iteration of f passes through the set
![]() $P_f=V$
, this shows that any periodic critical point of f must be equal to the point A if n is even or must belong to V if n is odd. Now for
$P_f=V$
, this shows that any periodic critical point of f must be equal to the point A if n is even or must belong to V if n is odd. Now for
![]() $X\in V$
, we have
$X\in V$
, we have
![]() $\deg _{\mathcal {L}_n}(X)=1$
and so
$\deg _{\mathcal {L}_n}(X)=1$
and so
where
![]() $n_X\in \mathbb {N}_0$
is the number of flaps that contain X. These considerations show that f, and hence also g, has no periodic critical points in case (i). Hence, the Julia set of g is the whole Riemann sphere
$n_X\in \mathbb {N}_0$
is the number of flaps that contain X. These considerations show that f, and hence also g, has no periodic critical points in case (i). Hence, the Julia set of g is the whole Riemann sphere
![]() $\widehat {\mathbb {C}}$
in this case (see [Reference MilnorMil06a, Corollary 19.8]).
$\widehat {\mathbb {C}}$
in this case (see [Reference MilnorMil06a, Corollary 19.8]).
In case (ii), the map f, and hence also g, has a critical fixed point, and so the Fatou set of g is non-empty. To show that its Julia set is a Sierpiński carpet, we use the following criterion that follows from [Reference Bartholdi and DudkoBD18, Lemma 4.16]: the Julia set of g is a Sierpiński carpet if and only if g, or equivalently f, has no Levy arcs. Here a Levy arc of f is a path
![]() $\alpha $
in
$\alpha $
in
![]() $\mathbb {P}$
satisfying the following conditions:
$\mathbb {P}$
satisfying the following conditions:
-
(L1)
 $\alpha $
is an arc in
$\alpha $
is an arc in
 $(\mathbb {P}, V)$
, or
$(\mathbb {P}, V)$
, or
 $\alpha $
is a simple loop based at a point
$\alpha $
is a simple loop based at a point
 $X\in V$
such that
$X\in V$
such that
 ${\alpha \smallsetminus \{X\}\subset \mathbb {P}\smallsetminus V}$
and each component of
${\alpha \smallsetminus \{X\}\subset \mathbb {P}\smallsetminus V}$
and each component of
 $\mathbb {P}\smallsetminus \alpha $
contains at least one point in V;
$\mathbb {P}\smallsetminus \alpha $
contains at least one point in V; -
(L2) there exist
 $k\in \mathbb {N}$
and a lift
$k\in \mathbb {N}$
and a lift
 $\widetilde \alpha $
of
$\widetilde \alpha $
of
 $\alpha $
under
$\alpha $
under
 $f^k$
such that
$f^k$
such that
 $\alpha $
and
$\alpha $
and
 $\widetilde \alpha $
are isotopic relative to V.
$\widetilde \alpha $
are isotopic relative to V.
Now suppose that f has a Levy arc
![]() $\alpha $
with
$\alpha $
with
![]() $\widetilde \alpha $
and
$\widetilde \alpha $
and
![]() $k\in \mathbb {N}$
as in condition (L2). Then
$k\in \mathbb {N}$
as in condition (L2). Then
![]() $f^k|\widetilde \alpha $
is a
$f^k|\widetilde \alpha $
is a
![]() $1$
-to-
$1$
-to-
![]() $1$
map and either
$1$
map and either
![]() $\mathrm {i}(\alpha , \alpha ^h)>0 $
or
$\mathrm {i}(\alpha , \alpha ^h)>0 $
or
![]() $\mathrm {i}(\alpha , \alpha ^v)>0$
. Without loss of generality, we may assume that
$\mathrm {i}(\alpha , \alpha ^v)>0$
. Without loss of generality, we may assume that
![]() $\mathrm {i}(\alpha , \alpha ^h)=\#(\alpha \cap \alpha ^h)>0$
. If
$\mathrm {i}(\alpha , \alpha ^h)=\#(\alpha \cap \alpha ^h)>0$
. If
![]() $\alpha $
is an arc in
$\alpha $
is an arc in
![]() $(\mathbb {P}, V)$
, then we can apply Lemma 5.5 with
$(\mathbb {P}, V)$
, then we can apply Lemma 5.5 with ![]() ,
, ![]() , and
, and ![]() and conclude that the number of distinct pullbacks of
and conclude that the number of distinct pullbacks of
![]() $\alpha ^h$
under
$\alpha ^h$
under
![]() $f^k$
that are isotopic to
$f^k$
that are isotopic to
![]() $\alpha ^h$
is at most
$\alpha ^h$
is at most
![]() $1$
. This is also true if
$1$
. This is also true if
![]() $\alpha $
is a simple loop as in condition (L1) by the argument in the proof of Lemma 5.5.
$\alpha $
is a simple loop as in condition (L1) by the argument in the proof of Lemma 5.5.
We reach a contradiction, because it follows from Lemma 5.1 that
![]() $\alpha ^h$
has
$\alpha ^h$
has
![]() $n^k>1$
such pullbacks. Consequently, f and g do not have any Levy arcs and so the Julia set of g is a Sierpiński carpet.
$n^k>1$
such pullbacks. Consequently, f and g do not have any Levy arcs and so the Julia set of g is a Sierpiński carpet.
9.2 The global curve attractor problem
We were able to prove the existence of a finite global curve attractor only for blown-up
![]() $(n\times n)$
-Lattès maps with
$(n\times n)$
-Lattès maps with
![]() $n=2$
. The proof of Theorem 1.4 crucially relies on Proposition 8.1, which says that the (naturally defined) complexity of curves does not increase under the pullback operation. The latter statement is false in general for blown-up
$n=2$
. The proof of Theorem 1.4 crucially relies on Proposition 8.1, which says that the (naturally defined) complexity of curves does not increase under the pullback operation. The latter statement is false in general for blown-up
![]() $(n\times n)$
-Lattès maps with
$(n\times n)$
-Lattès maps with
![]() $n\geq 3$
.
$n\geq 3$
.
Numerical computations by Darragh Glynn suggest that for some blown-up
![]() ${(3\times 3)}$
-Lattès map f, one can have infinitely many slopes
${(3\times 3)}$
-Lattès map f, one can have infinitely many slopes
![]() $x\in \widehat {\mathbb {Q}}$
such that
$x\in \widehat {\mathbb {Q}}$
such that
![]() $\|\mu _f(x) \|> \| x \|$
. For example, consider the map f obtained from the
$\|\mu _f(x) \|> \| x \|$
. For example, consider the map f obtained from the
![]() $(3\times 3)$
-Lattès map by blowing up once the horizontal and vertical edges incident to the vertex B of
$(3\times 3)$
-Lattès map by blowing up once the horizontal and vertical edges incident to the vertex B of
![]() $\mathbb {P}$
. Then one can prove the following general relation for the slope map
$\mathbb {P}$
. Then one can prove the following general relation for the slope map
![]() $\mu _f$
:
$\mu _f$
:
Based on this, one can show that
![]() $\|\mu _f(x) \|> \| x\|$
for all
$\|\mu _f(x) \|> \| x\|$
for all
Actually, it seems that in this case, the slope map
![]() $\mu _f$
has orbits with arbitrarily many strict increases of complexity. For instance, we have two jumps of complexity for the orbit of slope
$\mu _f$
has orbits with arbitrarily many strict increases of complexity. For instance, we have two jumps of complexity for the orbit of slope
![]() $1/9$
under
$1/9$
under
![]() $\mu _f$
:
$\mu _f$
:
Note that this orbit stabilizes at the fixed point
![]() $1/5$
of
$1/5$
of
![]() $\mu _f$
. The numerical computations by Darragh Glynn also show that there are examples of blown-up
$\mu _f$
. The numerical computations by Darragh Glynn also show that there are examples of blown-up
![]() $(n\times n)$
-Lattès maps with
$(n\times n)$
-Lattès maps with
![]() $n\geq 5$
for which the slope map has periodic cycles of length
$n\geq 5$
for which the slope map has periodic cycles of length
![]() $\geq 2$
.
$\geq 2$
.
It is natural to ask what one can say about the behavior of the slope map
![]() $\mu _f$
for an obstructed Thurston map f (with
$\mu _f$
for an obstructed Thurston map f (with
![]() $\#P_f=4$
). It was already observed in [Reference Koch, Pilgrim and SelingerKPS16] that for a blown-up
$\#P_f=4$
). It was already observed in [Reference Koch, Pilgrim and SelingerKPS16] that for a blown-up
![]() $(2\times 2)$
-Lattès map f with only vertical flaps glued to the pillow
$(2\times 2)$
-Lattès map f with only vertical flaps glued to the pillow
![]() $\mathbb {P}$
, there are infinitely many (non-isotopic) invariant essential Jordan curves. Indeed, for such a map f, the curve
$\mathbb {P}$
, there are infinitely many (non-isotopic) invariant essential Jordan curves. Indeed, for such a map f, the curve
![]() $\alpha ^v$
is f-invariant and satisfies
$\alpha ^v$
is f-invariant and satisfies
![]() $\unicode{x3bb} _f(\alpha ^v)=1$
. One can use this to show that f commutes with
$\unicode{x3bb} _f(\alpha ^v)=1$
. One can use this to show that f commutes with
![]() $T^2$
(up to isotopy relative to
$T^2$
(up to isotopy relative to
![]() $P_f$
), where T is a Dehn twist about
$P_f$
), where T is a Dehn twist about
![]() $\alpha ^v$
. This implies that each curve
$\alpha ^v$
. This implies that each curve
![]() $T^{2n}(\alpha ^h)$
is f-invariant. In fact, it is easy to verify directly that each essential Jordan curve with slope
$T^{2n}(\alpha ^h)$
is f-invariant. In fact, it is easy to verify directly that each essential Jordan curve with slope
![]() $x\in \mathbb {Z} \cup \{\infty \}$
is f-invariant, or equivalently, that
$x\in \mathbb {Z} \cup \{\infty \}$
is f-invariant, or equivalently, that
![]() $\mu _f(x)=x$
for
$\mu _f(x)=x$
for
![]() $x\in \mathbb {Z} \cup \{\infty \}$
.
$x\in \mathbb {Z} \cup \{\infty \}$
.
However, for such a blown-up
![]() $(2\times 2)$
-Lattès map f with only vertical flaps glued to the pillow
$(2\times 2)$
-Lattès map f with only vertical flaps glued to the pillow
![]() $\mathbb {P}$
, the general behavior of the slope map
$\mathbb {P}$
, the general behavior of the slope map
![]() $\mu _f$
under iteration has not been analyzed before. The considerations in the proof of the first part of Proposition 8.1 also apply in this situation. In particular, (8.4) and (8.5) are still true and show that the orbit of an arbitrary
$\mu _f$
under iteration has not been analyzed before. The considerations in the proof of the first part of Proposition 8.1 also apply in this situation. In particular, (8.4) and (8.5) are still true and show that the orbit of an arbitrary
![]() $x\in \widehat {\mathbb {Q}} \cup \{\infty \}$
under
$x\in \widehat {\mathbb {Q}} \cup \{\infty \}$
under
![]() $\mu _f$
eventually lands in a fixed point of
$\mu _f$
eventually lands in a fixed point of
![]() $\mu _f$
. Moreover, results in §8 provide a method to determine all fixed slopes for
$\mu _f$
. Moreover, results in §8 provide a method to determine all fixed slopes for
![]() $\mu _f$
.
$\mu _f$
.
The easiest case is the map f obtained from the
![]() $(2\times 2)$
-Lattès map
$(2\times 2)$
-Lattès map
![]() $\mathcal {L}_2$
by gluing at least one vertical flap to each of the four vertical
$\mathcal {L}_2$
by gluing at least one vertical flap to each of the four vertical
![]() $1$
-edges in the ‘middle’ of the pillow
$1$
-edges in the ‘middle’ of the pillow
![]() $\mathbb {P}$
. If
$\mathbb {P}$
. If
![]() $\xi $
is a geodesic arc in
$\xi $
is a geodesic arc in
![]() $(\mathbb {P},V)$
with an endpoint in
$(\mathbb {P},V)$
with an endpoint in
![]() $A\in V$
and slope
$A\in V$
and slope
![]() $x\in \mathbb {Q}\smallsetminus \mathbb {Z}$
, then each component of
$x\in \mathbb {Q}\smallsetminus \mathbb {Z}$
, then each component of
![]() $\mathcal {L}_2^{-1}(\xi )$
must pass through the interior of one of the four vertical
$\mathcal {L}_2^{-1}(\xi )$
must pass through the interior of one of the four vertical
![]() $1$
-edges in the middle of
$1$
-edges in the middle of
![]() $\mathbb {P}$
. Consequently, we can apply the considerations in the proof of Lemma 8.4 and in the second part of the proof of Proposition 8.1, and conclude that
$\mathbb {P}$
. Consequently, we can apply the considerations in the proof of Lemma 8.4 and in the second part of the proof of Proposition 8.1, and conclude that
![]() ${\| \mu _f(x)\| < \| x\| }$
for
${\| \mu _f(x)\| < \| x\| }$
for
![]() $x\in \mathbb {Q} \smallsetminus \mathbb {Z}$
. Thus, the orbit of each
$x\in \mathbb {Q} \smallsetminus \mathbb {Z}$
. Thus, the orbit of each
![]() $x\in \widehat {\mathbb {Q}} \cup \{\odot \}$
under
$x\in \widehat {\mathbb {Q}} \cup \{\odot \}$
under
![]() $\mu _f$
eventually lands in
$\mu _f$
eventually lands in
![]() $\mathbb {Z} \cup \{\infty , \odot \}$
(that is, in a fixed point of
$\mathbb {Z} \cup \{\infty , \odot \}$
(that is, in a fixed point of
![]() $\mu _f$
). Since the map f is easily seen to be expanding (see [Reference Bonk and MeyerBM17, Definition 2.2 and Theorem 14.1]), this provides an answer to a question raised by Pilgrim of whether there is an obstructed expanding Thurston map for which one has a complete understanding of the global dynamics of the slope map.
$\mu _f$
). Since the map f is easily seen to be expanding (see [Reference Bonk and MeyerBM17, Definition 2.2 and Theorem 14.1]), this provides an answer to a question raised by Pilgrim of whether there is an obstructed expanding Thurston map for which one has a complete understanding of the global dynamics of the slope map.
9.3 Twisting problems
Many natural problems related to Thurston equivalence remain rather mysterious and are often very difficult to solve. Twisting problems are examples of this nature.
To explain this, suppose we are given a rational Thurston map
![]() $f\colon \widehat {\mathbb {C}}\to \widehat {\mathbb {C}}$
. Let
$f\colon \widehat {\mathbb {C}}\to \widehat {\mathbb {C}}$
. Let
![]() $\phi \colon \widehat {\mathbb {C}}\to \widehat {\mathbb {C}}$
be an orientation-preserving homeomorphism that fixes the postcritical set
$\phi \colon \widehat {\mathbb {C}}\to \widehat {\mathbb {C}}$
be an orientation-preserving homeomorphism that fixes the postcritical set
![]() $P_f$
pointwise. We now consider the branched covering map
$P_f$
pointwise. We now consider the branched covering map ![]() on
on
![]() $\widehat {\mathbb {C}}$
, called the
$\widehat {\mathbb {C}}$
, called the
![]() $\phi $
-twist of f. Then
$\phi $
-twist of f. Then
![]() $C_g=C_f$
and g has the same dynamics on
$C_g=C_f$
and g has the same dynamics on
![]() $C_f$
as f. In particular,
$C_f$
as f. In particular,
![]() $P_g=P_f$
; so g has a finite postcritical set and is a Thurston map.
$P_g=P_f$
; so g has a finite postcritical set and is a Thurston map.
This leads us to the natural questions: Is g realized? And if yes, to which rational map is g equivalent depending on the isotopy type of
![]() $\phi $
? In fact, there are only finitely many rational maps g (up to Möbius conjugation) that can arise in this way from a fixed map f. A famous instance of this question, called the ‘twisted rabbit problem’, was solved by Bartholdi and Nekrashevych in [Reference Bartholdi and NekrashevychBN06] (see also [Reference Belk, Lanier, Margalit and WinarskiBLMW22, Reference LodgeLod13]).
$\phi $
? In fact, there are only finitely many rational maps g (up to Möbius conjugation) that can arise in this way from a fixed map f. A famous instance of this question, called the ‘twisted rabbit problem’, was solved by Bartholdi and Nekrashevych in [Reference Bartholdi and NekrashevychBN06] (see also [Reference Belk, Lanier, Margalit and WinarskiBLMW22, Reference LodgeLod13]).
In our context, we can ask which twists of maps, as in Theorem 1.2, are realized. We do not have an answer to this question, but it seems that this leads to non-trivial and difficult problems. For example, consider the blown-up
![]() $(2\times 2)$
-Lattès map
$(2\times 2)$
-Lattès map
![]() $f\colon \mathbb {P}\to \mathbb {P}$
corresponding to the flapped pillow
$f\colon \mathbb {P}\to \mathbb {P}$
corresponding to the flapped pillow
![]() $\widehat {\mathbb {P}}$
as in Figure 22. Then
$\widehat {\mathbb {P}}$
as in Figure 22. Then
![]() $\widehat {\mathbb {P}}$
has one horizontal and one vertical flap, and so f is realized by Theorem 1.2. One can check that the Jordan curve
$\widehat {\mathbb {P}}$
has one horizontal and one vertical flap, and so f is realized by Theorem 1.2. One can check that the Jordan curve ![]() has exactly two essential pullbacks
has exactly two essential pullbacks
![]() $\gamma _1, \gamma _2 \sim \wp (\ell _{1/3})$
under f with
$\gamma _1, \gamma _2 \sim \wp (\ell _{1/3})$
under f with
![]() $\deg (f\colon \gamma _1\to \gamma )=1$
and
$\deg (f\colon \gamma _1\to \gamma )=1$
and
![]() $\deg (f\colon \gamma _2\to \gamma )=2$
. We now choose an orientation-preserving homeomorphism
$\deg (f\colon \gamma _2\to \gamma )=2$
. We now choose an orientation-preserving homeomorphism
![]() $\phi \colon \mathbb {P}\to \mathbb {P}$
that maps
$\phi \colon \mathbb {P}\to \mathbb {P}$
that maps
![]() $\gamma $
onto
$\gamma $
onto
![]() $\gamma _1$
, while fixing each point in
$\gamma _1$
, while fixing each point in
![]() $V=P_f$
. Then the curve
$V=P_f$
. Then the curve
![]() $\gamma _1$
is an obstruction for the twisted map
$\gamma _1$
is an obstruction for the twisted map ![]() with
with
![]() $\unicode{x3bb} _g( \gamma _1)=3/2$
. An analogous construction applies to some other essential Jordan curves, for instance, with slopes
$\unicode{x3bb} _g( \gamma _1)=3/2$
. An analogous construction applies to some other essential Jordan curves, for instance, with slopes
![]() $3/23$
and
$3/23$
and
![]() $3/49$
, and gives twists of f with an obstruction.
$3/49$
, and gives twists of f with an obstruction.
It follows from this discussion that the mapping class biset associated with the map f above is not contracting (see [Reference Bartholdi and DudkoBD17, Reference Bartholdi and DudkoBD18] for the definitions). Thus, the algebraic methods for solving the global curve attractor problem developed in [Reference PilgrimPil12] (see, specifically, [Reference PilgrimPil12, Theorem 1.4]) do not apply in general for the maps considered in Theorem 1.2.
9.4 Thurston maps with more than four postcritical points
While in this paper we only discuss the case of Thurston maps
![]() $f\colon {S^{2}}\to {S^{2}}$
with
$f\colon {S^{2}}\to {S^{2}}$
with
![]() $\#{P_f}=4$
, it is natural to ask if one can adapt Theorem 1.1 to the case when
$\#{P_f}=4$
, it is natural to ask if one can adapt Theorem 1.1 to the case when
![]() $\#{P_f}>4$
. The main difficulty is that an obstruction in this case is in general not given by a unique essential Jordan curve in
$\#{P_f}>4$
. The main difficulty is that an obstruction in this case is in general not given by a unique essential Jordan curve in
![]() $({S^{2}},{P_f})$
, but by a multicurve. Of course, this fact complicates the analysis of pullback properties of curves and their intersection numbers. However, we expect that one can naturally generalize our result for an arbitrary Thurston map: given an obstructed Thurston map f, one can eliminate all possible multicurve obstructions by successively applying the blow-up operation and obtain a Thurston map that is realized.
$({S^{2}},{P_f})$
, but by a multicurve. Of course, this fact complicates the analysis of pullback properties of curves and their intersection numbers. However, we expect that one can naturally generalize our result for an arbitrary Thurston map: given an obstructed Thurston map f, one can eliminate all possible multicurve obstructions by successively applying the blow-up operation and obtain a Thurston map that is realized.
9.5 Other combinatorial constructions of rational maps
The dynamical behavior of curves under the pullback operation is an important topic in holomorphic dynamics. While in this paper we only study the realization and the global curve attractor problems, one is led to similar considerations, for example, in the study of iterated monodromy groups (see [Reference Hlushchanka and MeyerHM18]). For these investigations, it is important to have explicit classes of rational maps at hand that are constructed in combinatorial fashion and against which conjectures can be tested or which lead to the discovery of general phenomena. The maps provided by Theorem 1.1 may be useful in this respect. Another interesting class of maps worthy of further investigation are Thurston maps constructed from tilings of the Euclidean or hyperbolic plane as in [Reference Bonk and MeyerBM17, Example 12.25].
Acknowledgements
The authors would like to thank Kostya Drach, Dima Dudko, Daniel Meyer, Kevin Pilgrim, and Dylan Thurston for various useful comments and remarks. We are grateful to Darragh Glynn for allowing us to incorporate some of his numerical findings in this paper.
M.B. was partially supported by NSF grant DMS-1808856. M.H. was partially supported by the ERC advanced grant ‘HOLOGRAM’. A.I. was partially supported by the Swiss National Science Foundation (project no. 181898).
A Appendix. Isotopy classes of Jordan curves in spheres with four marked points
In this appendix, we will provide proofs for Lemmas 2.3 and 2.4. Our presentation is rather detailed. We need some additional auxiliary facts that we will discuss first. Throughout, we will rely on the notation and terminology established in §2.
In the following, we will consider a marked sphere
![]() $(S^2, Z)$
, where
$(S^2, Z)$
, where
![]() $Z\subset S^2$
consists of precisely four points. If
$Z\subset S^2$
consists of precisely four points. If
![]() $M\subset S^2$
and
$M\subset S^2$
and
![]() $\alpha $
is a Jordan curve in
$\alpha $
is a Jordan curve in
![]() $(S^2, Z)$
, then we say that
$(S^2, Z)$
, then we say that
![]() $\alpha $
is in minimal position with the set M if
$\alpha $
is in minimal position with the set M if
![]() $\#(\alpha \cap M)\le \#(\alpha '\cap M)$
for all Jordan curves
$\#(\alpha \cap M)\le \#(\alpha '\cap M)$
for all Jordan curves
![]() $\alpha '$
in
$\alpha '$
in
![]() $(S^2, Z)$
with
$(S^2, Z)$
with
![]() $\alpha \sim \alpha '$
relative to Z.
$\alpha \sim \alpha '$
relative to Z.
Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be Jordan curves or arcs in
$\beta $
be Jordan curves or arcs in
![]() $(S^2,Z)$
. We say that subarcs
$(S^2,Z)$
. We say that subarcs
![]() $\alpha '\subset \alpha $
and
$\alpha '\subset \alpha $
and
![]() $\beta '\subset \beta $
form a bigon U in
$\beta '\subset \beta $
form a bigon U in
![]() $(S^2,Z)$
if
$(S^2,Z)$
if
![]() $\alpha '$
and
$\alpha '$
and
![]() $\beta '$
have the same endpoints, but disjoint interiors, and if
$\beta '$
have the same endpoints, but disjoint interiors, and if
![]() $U\subset S^2$
is an open Jordan region with
$U\subset S^2$
is an open Jordan region with
![]() $\partial U= \alpha '\cup \beta '$
and
$\partial U= \alpha '\cup \beta '$
and
![]() $U\subset S^2\smallsetminus Z$
.
$U\subset S^2\smallsetminus Z$
.
Lemma A.1. Let
![]() $\gamma $
be a Jordan curve in a marked sphere
$\gamma $
be a Jordan curve in a marked sphere
![]() $({S^{2}}, Z)$
with
$({S^{2}}, Z)$
with
![]() $\# Z = 4$
, and let a and c be disjoint arcs in
$\# Z = 4$
, and let a and c be disjoint arcs in
![]() $({S^{2}},Z)$
. Suppose
$({S^{2}},Z)$
. Suppose
![]() $\gamma $
is in minimal position with the set
$\gamma $
is in minimal position with the set
![]() $a\cup c$
. Then
$a\cup c$
. Then
![]() $\gamma $
meets each of the arcs a and c transversely and no subarcs of
$\gamma $
meets each of the arcs a and c transversely and no subarcs of
![]() $\gamma $
and of a or c form a bigon U in
$\gamma $
and of a or c form a bigon U in
![]() $(S^2, Z)$
with
$(S^2, Z)$
with
![]() $U\cap (\gamma \cup a \cup c)=\emptyset $
.
$U\cap (\gamma \cup a \cup c)=\emptyset $
.
Proof. These facts are fairly standard in contexts like this (see, for example, [Reference Farb and MargalitFM12, §1.2.4]), and so we will only give an outline of the proof.
Our assumptions imply that
![]() $\gamma $
meets each arc a and c transversally and has only finitely many intersections with
$\gamma $
meets each arc a and c transversally and has only finitely many intersections with
![]() $a\cup c$
(Lemma 2.1 and its proof apply mutatis mutandis to our situation). We now argue by contradiction and assume that a subarc
$a\cup c$
(Lemma 2.1 and its proof apply mutatis mutandis to our situation). We now argue by contradiction and assume that a subarc
![]() $\gamma '\subset \gamma $
and a subarc
$\gamma '\subset \gamma $
and a subarc
![]() $\sigma $
of a or c form a bigon U in
$\sigma $
of a or c form a bigon U in
![]() $(S^2,Z)$
with
$(S^2,Z)$
with
![]() $U\cap (\gamma \cup a \cup c)=\emptyset $
. Note that then,
$U\cap (\gamma \cup a \cup c)=\emptyset $
. Note that then,
![]() $\operatorname {cl}(U)\subset S^2\smallsetminus Z$
. Hence, we can modify the curve
$\operatorname {cl}(U)\subset S^2\smallsetminus Z$
. Hence, we can modify the curve
![]() $\gamma $
near U by an isotopy in
$\gamma $
near U by an isotopy in
![]() $S^2\smallsetminus Z$
that pulls the subarc
$S^2\smallsetminus Z$
that pulls the subarc
![]() $\gamma '$
of
$\gamma '$
of
![]() $\gamma $
through U and away from
$\gamma $
through U and away from
![]() $\sigma $
so that the new Jordan curve
$\sigma $
so that the new Jordan curve
![]() $\gamma $
does not intersect
$\gamma $
does not intersect
![]() $\sigma \subset a\cup c$
and no new intersection points with
$\sigma \subset a\cup c$
and no new intersection points with
![]() $a\cup c$
arise. This leads to a contradiction, because the original curve
$a\cup c$
arise. This leads to a contradiction, because the original curve
![]() $\gamma $
was in minimal position with
$\gamma $
was in minimal position with
![]() $a\cup c$
.
$a\cup c$
.
A topological space D is called a closed topological disk if there exists a homeomorphism
![]() $\eta \colon \operatorname {cl}(\mathbb {D})\rightarrow D$
of the closed unit disk
$\eta \colon \operatorname {cl}(\mathbb {D})\rightarrow D$
of the closed unit disk
![]() $\operatorname {cl}(\mathbb {D})\subset \mathbb {C}$
onto D. This is an abstract version of the notion of a closed Jordan region contained in a surface. The set
$\operatorname {cl}(\mathbb {D})\subset \mathbb {C}$
onto D. This is an abstract version of the notion of a closed Jordan region contained in a surface. The set ![]() is a Jordan curve independent of
is a Jordan curve independent of
![]() $\eta $
and called the boundary of D. The interior of D is defined as
$\eta $
and called the boundary of D. The interior of D is defined as ![]() .
.
Similarly as for closed Jordan regions, an arc
![]() $\alpha $
contained in a closed topological disk D is called a crosscut (in
$\alpha $
contained in a closed topological disk D is called a crosscut (in
![]() $D)$
if
$D)$
if
![]() $\partial \alpha \subset \partial D$
and
$\partial \alpha \subset \partial D$
and
![]() $\operatorname {int}(\alpha )\subset \operatorname {int}(D)$
. A crosscut
$\operatorname {int}(\alpha )\subset \operatorname {int}(D)$
. A crosscut
![]() $\alpha $
splits D into two compact and connected sets S and
$\alpha $
splits D into two compact and connected sets S and
![]() $S'$
called the sides of
$S'$
called the sides of
![]() $\alpha $
(in
$\alpha $
(in
![]() $D)$
such that
$D)$
such that
![]() $D=S\cup S'$
and
$D=S\cup S'$
and
![]() $S\cap S'=\alpha $
. With suitable orientations of
$S\cap S'=\alpha $
. With suitable orientations of
![]() $\alpha $
and D, one side of
$\alpha $
and D, one side of
![]() $\alpha $
lies on the left and the other side on the right of
$\alpha $
lies on the left and the other side on the right of
![]() $\alpha $
. Each non-empty connected set
$\alpha $
. Each non-empty connected set
![]() $c\subset D$
that does not meet
$c\subset D$
that does not meet
![]() $\alpha $
is contained in precisely one side of
$\alpha $
is contained in precisely one side of
![]() $\alpha $
.
$\alpha $
.
If
![]() $\alpha _1, \ldots , \alpha _n$
for
$\alpha _1, \ldots , \alpha _n$
for
![]() $n\in \mathbb {N}$
are pairwise disjoint crosscuts in a closed topological disk D, then we can define an abstract graph
$n\in \mathbb {N}$
are pairwise disjoint crosscuts in a closed topological disk D, then we can define an abstract graph
![]() $G=(V,E)$
in the following way: we consider each component U of
$G=(V,E)$
in the following way: we consider each component U of
![]() $D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
as a vertex of G. We join two distinct vertices represented by components U and
$D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
as a vertex of G. We join two distinct vertices represented by components U and
![]() $U'$
by an edge if one of the crosscuts
$U'$
by an edge if one of the crosscuts
![]() $\alpha _j$
is contained in the boundary of both U and
$\alpha _j$
is contained in the boundary of both U and
![]() $U'$
. Accordingly, the edges of G are in bijective correspondence with the crosscuts
$U'$
. Accordingly, the edges of G are in bijective correspondence with the crosscuts
![]() $\alpha _1, \ldots , \alpha _n$
.
$\alpha _1, \ldots , \alpha _n$
.
Lemma A.2. Let
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\alpha _1, \ldots , \alpha _n$
be pairwise disjoint crosscuts in a closed topological disk D, and let G be the graph obtained from the components of the set
$\alpha _1, \ldots , \alpha _n$
be pairwise disjoint crosscuts in a closed topological disk D, and let G be the graph obtained from the components of the set
![]() $D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
as described. The the following statements are true.
$D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
as described. The the following statements are true.
-
(i) The graph G is a finite tree with at least two vertices.
-
(ii) Let
 $c\subset D$
be a connected set and suppose that
$c\subset D$
be a connected set and suppose that
 $c\cap \alpha _k=\emptyset $
for some
$c\cap \alpha _k=\emptyset $
for some
 $k\in \{1, \ldots , n\}$
. Then there exists
$k\in \{1, \ldots , n\}$
. Then there exists
 $m\in \{1,\ldots , n\}$
and a side S of
$m\in \{1,\ldots , n\}$
and a side S of
 $\alpha _m$
such that
$\alpha _m$
such that
 $S\smallsetminus \alpha _m $
is disjoint from all the sets c,
$S\smallsetminus \alpha _m $
is disjoint from all the sets c,
 $\alpha _1, \ldots , \alpha _n$
.
$\alpha _1, \ldots , \alpha _n$
.
If
![]() $\alpha =\alpha _m$
and S are as in statement (ii), then there exists a subarc
$\alpha =\alpha _m$
and S are as in statement (ii), then there exists a subarc
![]() $\beta $
of
$\beta $
of
![]() $\partial D$
with the same endpoints as
$\partial D$
with the same endpoints as
![]() $\partial \alpha \subset D$
such that
$\partial \alpha \subset D$
such that
![]() $\partial S=\alpha \cup \beta $
. Then
$\partial S=\alpha \cup \beta $
. Then ![]() is an open Jordan region bounded by the union of the arcs
is an open Jordan region bounded by the union of the arcs
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
whose only common points are their endpoints. This region U does not meet c nor any of the arcs
$\beta $
whose only common points are their endpoints. This region U does not meet c nor any of the arcs
![]() $\alpha _1, \ldots , \alpha _n$
. In the proof of Lemma A.3, we will use such a region U to obtain a bigon in an appropriate context.
$\alpha _1, \ldots , \alpha _n$
. In the proof of Lemma A.3, we will use such a region U to obtain a bigon in an appropriate context.
Proof. (i) This is intuitively clear, and we leave the details to the reader. By induction on the number n of crosscuts, one can show that G is a finite connected graph with at least two vertices. Since a crosscut splits D into two sides, it easily follows that the removal of any edge from G disconnects it. Hence, G cannot contain any simple cycle and must be a tree.
(ii) The graph G is a tree; so if we remove the edge corresponding to the crosscut
![]() $\alpha _k$
from G, then we obtain two disjoint non-empty subgraphs
$\alpha _k$
from G, then we obtain two disjoint non-empty subgraphs
![]() $G_1$
and
$G_1$
and
![]() $G_2$
of G. The connected components of
$G_2$
of G. The connected components of
![]() $D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
corresponding to the vertices of
$D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
corresponding to the vertices of
![]() $G_1$
are contained in one side
$G_1$
are contained in one side
![]() $S'$
of
$S'$
of
![]() $\alpha _k$
, while the other connected components of
$\alpha _k$
, while the other connected components of
![]() $D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
corresponding to the vertices of
$D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
corresponding to the vertices of
![]() $G_2$
lie in the other side
$G_2$
lie in the other side
![]() $S"$
of
$S"$
of
![]() $\alpha _k$
. Since c is connected and does not meet
$\alpha _k$
. Since c is connected and does not meet
![]() $\alpha _k$
, it must be contained in one of the sides of
$\alpha _k$
, it must be contained in one of the sides of
![]() $\alpha _k$
, say
$\alpha _k$
, say
![]() $c\subset S"$
. Then c is disjoint from
$c\subset S"$
. Then c is disjoint from
![]() $S'$
and hence from all the sets that correspond to vertices in
$S'$
and hence from all the sets that correspond to vertices in
![]() $G_1$
.
$G_1$
.
The tree G has a leaf v in
![]() $G_1\ne \emptyset $
, that is, there exists a vertex v of
$G_1\ne \emptyset $
, that is, there exists a vertex v of
![]() $G_1$
such that v is connected to the rest of G by precisely one edge. Then the connected component of
$G_1$
such that v is connected to the rest of G by precisely one edge. Then the connected component of
![]() $D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
corresponding to v has exactly one of the crosscuts, say
$D\smallsetminus (\alpha _1 \cup \cdots \cup \alpha _n)$
corresponding to v has exactly one of the crosscuts, say
![]() $\alpha _m$
with
$\alpha _m$
with
![]() ${m\in \{1,\ldots , n\}}$
, on its boundary. Then this component has the form
${m\in \{1,\ldots , n\}}$
, on its boundary. Then this component has the form
![]() $S\smallsetminus \alpha _m$
, where S is the unique side of
$S\smallsetminus \alpha _m$
, where S is the unique side of
![]() $\alpha _m$
contained in
$\alpha _m$
contained in
![]() $S'$
. Then
$S'$
. Then
![]() $S\smallsetminus \alpha _m$
is disjoint from
$S\smallsetminus \alpha _m$
is disjoint from
![]() $c\subset S"$
and from all the crosscuts
$c\subset S"$
and from all the crosscuts
![]() $\alpha _1, \ldots , \alpha _n$
.
$\alpha _1, \ldots , \alpha _n$
.
We can now prove a statement that is the key to the understanding of isotopy classes of Jordan curves in a sphere with four marked points.
Lemma A.3. Let
![]() $\gamma $
be a Jordan curve in a marked sphere
$\gamma $
be a Jordan curve in a marked sphere
![]() $({S^{2}}, Z)$
with
$({S^{2}}, Z)$
with
![]() $\# Z = 4$
, and let a and c be disjoint arcs in
$\# Z = 4$
, and let a and c be disjoint arcs in
![]() $({S^{2}},Z)$
. Suppose
$({S^{2}},Z)$
. Suppose
![]() $\gamma $
is in minimal position with the set
$\gamma $
is in minimal position with the set
![]() $a\cup c$
. Then the sets
$a\cup c$
. Then the sets
![]() $a\cap \gamma $
and
$a\cap \gamma $
and
![]() $c\cap \gamma $
are non-empty and finite, and the points in these sets alternate on
$c\cap \gamma $
are non-empty and finite, and the points in these sets alternate on
![]() $\gamma $
unless
$\gamma $
unless
![]() $\gamma $
is peripheral or
$\gamma $
is peripheral or
![]() $\gamma \cap (a\cup c) =\emptyset $
.
$\gamma \cap (a\cup c) =\emptyset $
.
Proof. In the given setup, each of the disjoint sets
![]() $\partial a$
and
$\partial a$
and
![]() $\partial c$
contains two points in Z. Since
$\partial c$
contains two points in Z. Since
![]() $\#Z=4$
, it follows that a connects two of the points in Z, while c connects the other two points.
$\#Z=4$
, it follows that a connects two of the points in Z, while c connects the other two points.
We may assume that
![]() $\gamma $
is essential and that at least one of the arcs a or c meets
$\gamma $
is essential and that at least one of the arcs a or c meets
![]() $\gamma $
, say
$\gamma $
, say
![]() $a\cap \gamma \ne \emptyset $
, because otherwise, we are in an exceptional situation as in the statement.
$a\cap \gamma \ne \emptyset $
, because otherwise, we are in an exceptional situation as in the statement.
If none of the arcs a and c meets
![]() $\gamma $
in more than two points, then
$\gamma $
in more than two points, then
![]() $\# (a \cap \gamma ) =1$
and
$\# (a \cap \gamma ) =1$
and
![]() $\# (c \cap \gamma ) \le 1$
. Now a and
$\# (c \cap \gamma ) \le 1$
. Now a and
![]() $\gamma $
meet transversely by Lemma A.1. This implies that the endpoints of a lie in different components of
$\gamma $
meet transversely by Lemma A.1. This implies that the endpoints of a lie in different components of
![]() $S^2\smallsetminus \gamma $
. Since
$S^2\smallsetminus \gamma $
. Since
![]() $\gamma $
is essential, each of these components contains precisely two points of
$\gamma $
is essential, each of these components contains precisely two points of
![]() $Z=\partial a\cup \partial c$
. Hence, the endpoints of c also lie in different components of
$Z=\partial a\cup \partial c$
. Hence, the endpoints of c also lie in different components of
![]() $S^2\smallsetminus \gamma $
. This implies that
$S^2\smallsetminus \gamma $
. This implies that
![]() $c\cap \gamma \ne \emptyset $
and so
$c\cap \gamma \ne \emptyset $
and so
![]() $\# (c \cap \gamma ) =1$
in the case under consideration. So both a and c meet
$\# (c \cap \gamma ) =1$
in the case under consideration. So both a and c meet
![]() $\gamma $
in exactly one point. It follows that the statement is true in this case.
$\gamma $
in exactly one point. It follows that the statement is true in this case.
We are reduced to the situation where at least one of the arcs a or c meets
![]() $\gamma $
in at least two (but necessarily finitely many) points, say
$\gamma $
in at least two (but necessarily finitely many) points, say ![]() . We now endow
. We now endow
![]() $\gamma $
and a with some orientations. With the given orientation, we denote the initial point of a by
$\gamma $
and a with some orientations. With the given orientation, we denote the initial point of a by
![]() $x_0$
and its terminal point by
$x_0$
and its terminal point by
![]() $x_1$
. Let
$x_1$
. Let
![]() $y_1, \ldots , y_{n}, y_{n+1}=y_1$
denote the
$y_1, \ldots , y_{n}, y_{n+1}=y_1$
denote the
![]() $n\ge 2$
intersection points of
$n\ge 2$
intersection points of
![]() $\gamma $
with a that we encounter while traversing
$\gamma $
with a that we encounter while traversing
![]() $\gamma $
once starting from some point in
$\gamma $
once starting from some point in
![]() $\gamma \smallsetminus a $
. The same n points also appear on a. We denote them by
$\gamma \smallsetminus a $
. The same n points also appear on a. We denote them by
![]() $p_1, \ldots , p_n$
in the order they appear if we traverse a starting from
$p_1, \ldots , p_n$
in the order they appear if we traverse a starting from
![]() $x_0$
. For
$x_0$
. For
![]() $k=1, \ldots , n$
, we denote by
$k=1, \ldots , n$
, we denote by
![]() $\gamma [y_k, y_{k+1}]$
the subarc of
$\gamma [y_k, y_{k+1}]$
the subarc of
![]() $\gamma $
obtained from traversing
$\gamma $
obtained from traversing
![]() $\gamma $
with the given orientation from
$\gamma $
with the given orientation from
![]() $y_k$
to
$y_k$
to
![]() $y_{k+1}$
.
$y_{k+1}$
.
Claim.
![]() $c\cap \gamma [y_k, y_{k+1}]\ne \emptyset $
for each
$c\cap \gamma [y_k, y_{k+1}]\ne \emptyset $
for each
![]() $k=1, \ldots , n$
.
$k=1, \ldots , n$
.
To see this, we argue by contradiction and assume that
![]() $c\cap \gamma [y_k, y_{k+1}] = \emptyset $
for some
$c\cap \gamma [y_k, y_{k+1}] = \emptyset $
for some
![]() $k\in \{1, \ldots , n\}$
. Our goal now is to show that some subarcs of a and
$k\in \{1, \ldots , n\}$
. Our goal now is to show that some subarcs of a and
![]() $\gamma $
form a bigon U in
$\gamma $
form a bigon U in
![]() $(S^2, Z)$
with
$(S^2, Z)$
with
![]() $U\cap (\gamma \cup a\cup c)=\emptyset $
. This is a contradiction with Lemma A.1, because
$U\cap (\gamma \cup a\cup c)=\emptyset $
. This is a contradiction with Lemma A.1, because
![]() $\gamma $
and
$\gamma $
and
![]() $a\cup c$
are in minimal position.
$a\cup c$
are in minimal position.
To produce such bigon U, we want to apply Lemma A.2. To do this, we slit the sphere
![]() $S^2$
open along the arc a. This results in a closed topological disk D whose boundary
$S^2$
open along the arc a. This results in a closed topological disk D whose boundary
![]() $\partial D$
consists of two copies
$\partial D$
consists of two copies
![]() $a^+$
and
$a^+$
and
![]() $a^-$
of the arc a. The set
$a^-$
of the arc a. The set
![]() $S^2\smallsetminus \operatorname {int}(a)$
can be identified with
$S^2\smallsetminus \operatorname {int}(a)$
can be identified with
![]() $\operatorname {int}(D)$
, while each point in
$\operatorname {int}(D)$
, while each point in
![]() $\operatorname {int}(a)$
is doubled into one corresponding point in
$\operatorname {int}(a)$
is doubled into one corresponding point in
![]() $a^+$
and one in
$a^+$
and one in
![]() $a^-$
.
$a^-$
.
The arcs
![]() $a^+$
and
$a^+$
and
![]() $a^-$
have their endpoints
$a^-$
have their endpoints
![]() $x_0$
and
$x_0$
and
![]() $x_1$
in common. We identify
$x_1$
in common. We identify
![]() $a^+$
with the original arc a with the same orientation. Then we can think of the intersection points
$a^+$
with the original arc a with the same orientation. Then we can think of the intersection points
![]() $p_1, \ldots , p_n$
of
$p_1, \ldots , p_n$
of
![]() $\gamma $
with a as lying on
$\gamma $
with a as lying on
![]() $a^+=a$
, while each of the points
$a^+=a$
, while each of the points
![]() $p_j$
has a corresponding point
$p_j$
has a corresponding point
![]() $q_j$
on
$q_j$
on
![]() $a^{-}$
.
$a^{-}$
.
Each arc
![]() $\gamma [y_j, y_{j+1}]$
corresponds to a crosscut
$\gamma [y_j, y_{j+1}]$
corresponds to a crosscut
![]() $\gamma _j$
in D for
$\gamma _j$
in D for
![]() $j=1, \ldots , n$
. These crosscuts have their endpoints in the set
$j=1, \ldots , n$
. These crosscuts have their endpoints in the set
![]() $P\cup Q$
, where
$P\cup Q$
, where ![]() and
and ![]() . Moreover, the crosscuts
. Moreover, the crosscuts
![]() $\gamma _1, \ldots , \gamma _n$
are pairwise disjoint. Indeed, the only possible common intersection point of two of these arcs could be a common endpoint of two consecutive arcs
$\gamma _1, \ldots , \gamma _n$
are pairwise disjoint. Indeed, the only possible common intersection point of two of these arcs could be a common endpoint of two consecutive arcs
![]() $\gamma _j$
and
$\gamma _j$
and
![]() $\gamma _{j+1}$
(where
$\gamma _{j+1}$
(where ![]() ) corresponding to
) corresponding to
![]() $y_{j+1}\in a$
; but in the process of creating D, the point
$y_{j+1}\in a$
; but in the process of creating D, the point
![]() $y_{j+1}$
is doubled into the points
$y_{j+1}$
is doubled into the points
![]() $p_{\ell }$
and
$p_{\ell }$
and
![]() $q_{\ell }$
for some
$q_{\ell }$
for some
![]() $\ell \in \{1, \ldots , n\}$
. Since
$\ell \in \{1, \ldots , n\}$
. Since
![]() $\gamma $
meets a transversely, one of these points will be the terminal point of
$\gamma $
meets a transversely, one of these points will be the terminal point of
![]() $\gamma _j$
, while the other one will be the initial point of
$\gamma _j$
, while the other one will be the initial point of
![]() $\gamma _{j+1}$
, and so actually,
$\gamma _{j+1}$
, and so actually,
![]() $\gamma _j\cap \gamma _{j+1}=\emptyset $
. It follows that the hypotheses of Lemma A.2 are satisfied.
$\gamma _j\cap \gamma _{j+1}=\emptyset $
. It follows that the hypotheses of Lemma A.2 are satisfied.
It is clear that the arc c, now considered as a subset of D, does not meet the crosscut
![]() $\gamma _k$
corresponding to
$\gamma _k$
corresponding to
![]() $\gamma [y_k,y_{k+1}]$
. Hence, by Lemma A.2, there exists
$\gamma [y_k,y_{k+1}]$
. Hence, by Lemma A.2, there exists
![]() $m\in \{1, \ldots , n\}$
and a side S of
$m\in \{1, \ldots , n\}$
and a side S of
![]() $\gamma _m$
in D such that
$\gamma _m$
in D such that
![]() $S\smallsetminus \gamma _m$
is disjoint from c and all the arcs
$S\smallsetminus \gamma _m$
is disjoint from c and all the arcs
![]() $\gamma _1, \ldots , \gamma _n$
. Then there exists an arc
$\gamma _1, \ldots , \gamma _n$
. Then there exists an arc
![]() $\beta \subset \partial D=a^+\cup a^-$
with the same endpoints as
$\beta \subset \partial D=a^+\cup a^-$
with the same endpoints as
![]() $\gamma _m$
such that
$\gamma _m$
such that
![]() $\partial S=\gamma _m\cup \beta $
. The set
$\partial S=\gamma _m\cup \beta $
. The set
![]() $S\smallsetminus \gamma _m$
is disjoint from
$S\smallsetminus \gamma _m$
is disjoint from
![]() $\gamma _1\cup \cdots \cup \gamma _n\supset P\cup Q$
, and so the arc
$\gamma _1\cup \cdots \cup \gamma _n\supset P\cup Q$
, and so the arc
![]() $\beta $
has its endpoints in the set
$\beta $
has its endpoints in the set
![]() $P\cup Q$
, but no other points in common with
$P\cup Q$
, but no other points in common with
![]() $P\cup Q$
.
$P\cup Q$
.
This implies that neither
![]() $x_0$
nor
$x_0$
nor
![]() $x_1$
are contained in
$x_1$
are contained in
![]() $\beta $
; indeed, suppose
$\beta $
; indeed, suppose
![]() $x_0\in \beta $
, for example. Then the endpoints of
$x_0\in \beta $
, for example. Then the endpoints of
![]() $\beta $
and hence of
$\beta $
and hence of
![]() $\gamma _m$
are necessarily the points
$\gamma _m$
are necessarily the points
![]() $p_1$
and
$p_1$
and
![]() $q_1$
. Collapsing D back to
$q_1$
. Collapsing D back to
![]() $S^2$
, we see that the endpoints
$S^2$
, we see that the endpoints
![]() $y_m$
and
$y_m$
and
![]() $y_{m+1}$
of
$y_{m+1}$
of
![]() $\gamma [y_m, y_{m+1}]$
are the same. This is a contradiction (here the assumption
$\gamma [y_m, y_{m+1}]$
are the same. This is a contradiction (here the assumption
![]() $n\ge 2$
is crucial). We arrive at a similar contradiction (using the points
$n\ge 2$
is crucial). We arrive at a similar contradiction (using the points
![]() $p_n$
and
$p_n$
and
![]() $q_n$
) if we assume
$q_n$
) if we assume
![]() $x_1\in \beta $
. It follows that
$x_1\in \beta $
. It follows that
![]() $\beta \subset \operatorname {int}(a^+)$
or
$\beta \subset \operatorname {int}(a^+)$
or
![]() $\beta \subset \operatorname {int}(a^-)$
.
$\beta \subset \operatorname {int}(a^-)$
.
These considerations imply that if we pass back to
![]() $S^2$
by identifying corresponding points in
$S^2$
by identifying corresponding points in
![]() $a^+$
and
$a^+$
and
![]() $a^-$
, then from
$a^-$
, then from
![]() $\operatorname {int}(S)$
, we obtain a bigon
$\operatorname {int}(S)$
, we obtain a bigon
![]() $U\subset S^2$
bounded by the subarc
$U\subset S^2$
bounded by the subarc
![]() $\gamma [y_m, y_{m+1}]$
of
$\gamma [y_m, y_{m+1}]$
of
![]() $\gamma $
and a subarc
$\gamma $
and a subarc
![]() $\widetilde \beta $
of a, where U is disjoint from
$\widetilde \beta $
of a, where U is disjoint from
![]() $ \gamma \cup a\cup c$
. This is impossible by Lemma A.1 since
$ \gamma \cup a\cup c$
. This is impossible by Lemma A.1 since
![]() $\gamma $
is in minimal position with
$\gamma $
is in minimal position with
![]() $a\cup c$
. This contradiction shows that the claim is indeed true.
$a\cup c$
. This contradiction shows that the claim is indeed true.
The claim implies that c has at least
![]() $n\ge 2$
intersection points with
$n\ge 2$
intersection points with
![]() $\gamma $
. Hence, we can reverse the roles of a and c and get a similar statement as the claim also for the arc c. This implies that the (finitely many) points in
$\gamma $
. Hence, we can reverse the roles of a and c and get a similar statement as the claim also for the arc c. This implies that the (finitely many) points in
![]() $a\cap \gamma \ne \emptyset $
and
$a\cap \gamma \ne \emptyset $
and
![]() $c\cap \gamma \ne \emptyset $
alternate on
$c\cap \gamma \ne \emptyset $
alternate on
![]() $\gamma $
.
$\gamma $
.
As in §2.4, we now consider the pillow
![]() $\mathbb {P}$
with its set V of vertices as the marked points, and the Weierstrass function
$\mathbb {P}$
with its set V of vertices as the marked points, and the Weierstrass function
![]() $\wp \colon \mathbb {C}\to \mathbb {P}$
that is doubly periodic with respect to the lattice
$\wp \colon \mathbb {C}\to \mathbb {P}$
that is doubly periodic with respect to the lattice
![]() $2\mathbb {Z}^2$
. We will now revert to the notation a and c for the horizontal edges of
$2\mathbb {Z}^2$
. We will now revert to the notation a and c for the horizontal edges of
![]() $\mathbb {P}$
. Recall that
$\mathbb {P}$
. Recall that
![]() $\mathbb {I}=[0,1]$
.
$\mathbb {I}=[0,1]$
.
Lemma A.4. Let
![]() $\alpha \colon \mathbb {I}\rightarrow \mathbb {C}$
be a simple loop or a homeomorphic parameterization of an arc. Suppose that the endpoints
$\alpha \colon \mathbb {I}\rightarrow \mathbb {C}$
be a simple loop or a homeomorphic parameterization of an arc. Suppose that the endpoints
![]() $z_0=\alpha (0)$
and
$z_0=\alpha (0)$
and
![]() $w_0=\alpha (1)$
of
$w_0=\alpha (1)$
of
![]() $\alpha $
lie in
$\alpha $
lie in
![]() $\mathbb {C}\smallsetminus \wp ^{-1}(a\cup c)$
and that
$\mathbb {C}\smallsetminus \wp ^{-1}(a\cup c)$
and that
![]() $\wp (z_0)=\wp (w_0)$
. Suppose further that either
$\wp (z_0)=\wp (w_0)$
. Suppose further that either
![]() $\alpha \cap \wp ^{-1} (a\cup c)=\emptyset $
, or all of the following conditions are true:
$\alpha \cap \wp ^{-1} (a\cup c)=\emptyset $
, or all of the following conditions are true:
![]() $\alpha $
meets each of the lines in
$\alpha $
meets each of the lines in
![]() $\wp ^{-1} (a\cup c)$
transversely, we have
$\wp ^{-1} (a\cup c)$
transversely, we have
and the points in
![]() $ \alpha \cap \wp ^{-1} (a) $
and
$ \alpha \cap \wp ^{-1} (a) $
and
![]() $ \alpha \cap \wp ^{-1} (c)$
alternate on
$ \alpha \cap \wp ^{-1} (c)$
alternate on
![]() $\alpha $
.
$\alpha $
.
Then
![]() $w_0-z_0\in 2\mathbb {Z}^2$
. Here
$w_0-z_0\in 2\mathbb {Z}^2$
. Here
![]() $w_0-z_0\ne 0$
unless
$w_0-z_0\ne 0$
unless
![]() $\alpha \cap \wp ^{-1} (a\cup c)=\emptyset $
.
$\alpha \cap \wp ^{-1} (a\cup c)=\emptyset $
.
Proof. Note that the set
![]() $\wp ^{-1}(a\cup c)$
consists precisely of the lines
$\wp ^{-1}(a\cup c)$
consists precisely of the lines ![]() ,
,
![]() $n\in \mathbb {Z}$
. Moreover, such a line
$n\in \mathbb {Z}$
. Moreover, such a line
![]() $L_n$
is mapped to a or c depending on whether n is even or odd, respectively.
$L_n$
is mapped to a or c depending on whether n is even or odd, respectively.
We consider the second case first when
![]() $\alpha \cap \wp ^{-1} (a\cup c)\ne \emptyset $
. We denote by
$\alpha \cap \wp ^{-1} (a\cup c)\ne \emptyset $
. We denote by
![]() ${0<u_1<\cdots < u_k<1}$
,
${0<u_1<\cdots < u_k<1}$
,
![]() $k\in \mathbb {N}$
, all the (finitely many) u-parameter values with
$k\in \mathbb {N}$
, all the (finitely many) u-parameter values with
![]() $\alpha (u_j)\in \wp ^{-1} (a\cup c)$
for
$\alpha (u_j)\in \wp ^{-1} (a\cup c)$
for
![]() $j=1, \ldots , k$
. Since
$j=1, \ldots , k$
. Since
![]() $\alpha $
meets each line
$\alpha $
meets each line
![]() $L_n$
transversely and the points in
$L_n$
transversely and the points in
![]() $ {\alpha \cap \wp ^{-1} (a)\ne \emptyset }$
and
$ {\alpha \cap \wp ^{-1} (a)\ne \emptyset }$
and
![]() $ \alpha \cap \wp ^{-1} (c) \ne \emptyset $
alternate on
$ \alpha \cap \wp ^{-1} (c) \ne \emptyset $
alternate on
![]() $\alpha $
, it is clear that the values
$\alpha $
, it is clear that the values
![]() $\text {Im} (\alpha (u_j))$
either strictly increase by
$\text {Im} (\alpha (u_j))$
either strictly increase by
![]() $1$
in each step
$1$
in each step
![]() $j=1, \ldots , k$
, or strictly decrease by
$j=1, \ldots , k$
, or strictly decrease by
![]() $1$
in each step. Here we have strict increase if
$1$
in each step. Here we have strict increase if
![]() $\text {Im} (\alpha (u_1)-\alpha (0))>0$
, and strict decrease if
$\text {Im} (\alpha (u_1)-\alpha (0))>0$
, and strict decrease if
![]() $\text {Im} (\alpha (u_1)-\alpha (0))<0$
. This implies that
$\text {Im} (\alpha (u_1)-\alpha (0))<0$
. This implies that
![]() $k>0$
is precisely the number of lines
$k>0$
is precisely the number of lines
![]() $L_n$
,
$L_n$
,
![]() $n\in \mathbb {Z}$
, that separate
$n\in \mathbb {Z}$
, that separate
![]() $z_0$
and
$z_0$
and
![]() $w_0$
. So
$w_0$
. So
![]() $z_0$
and
$z_0$
and
![]() $w_0$
lie in different components of
$w_0$
lie in different components of
![]() $\mathbb {C}\smallsetminus \wp ^{-1}(a\cup c)$
which shows that
$\mathbb {C}\smallsetminus \wp ^{-1}(a\cup c)$
which shows that
![]() $z_0\ne w_0$
.
$z_0\ne w_0$
.
By our hypotheses,
![]() $\# (\alpha \cap \wp ^{-1} (a))=\# (\alpha \cap \wp ^{-1} (c))$
, which implies that the number k of intersection points of
$\# (\alpha \cap \wp ^{-1} (a))=\# (\alpha \cap \wp ^{-1} (c))$
, which implies that the number k of intersection points of
![]() $\alpha $
with
$\alpha $
with
![]() $\wp ^{-1} (a\cup c)$
is even. Since
$\wp ^{-1} (a\cup c)$
is even. Since
![]() $\wp (z_0)=\wp (w_0)$
, by (2.3), we have
$\wp (z_0)=\wp (w_0)$
, by (2.3), we have
![]() $w_0=\pm z_0+v_0$
with
$w_0=\pm z_0+v_0$
with
![]() $v_0\in 2\mathbb {Z}^2$
. We have to rule out the minus sign here.
$v_0\in 2\mathbb {Z}^2$
. We have to rule out the minus sign here.
We argue by contradiction and assume that
![]() $w_0=-z_0+v_0$
. Then
$w_0=-z_0+v_0$
. Then ![]() , and so the endpoints
, and so the endpoints
![]() $z_0$
and
$z_0$
and
![]() $w_0$
of
$w_0$
of
![]() $\alpha $
are in symmetric position to the point
$\alpha $
are in symmetric position to the point
![]() $v_1\in \mathbb {Z}^2$
. This implies that the number k of lines
$v_1\in \mathbb {Z}^2$
. This implies that the number k of lines
![]() $L_n$
,
$L_n$
,
![]() $n\in \mathbb {Z}$
, separating
$n\in \mathbb {Z}$
, separating
![]() $z_0$
and
$z_0$
and
![]() $w_0$
is odd, contradicting what we have just seen. We conclude
$w_0$
is odd, contradicting what we have just seen. We conclude
![]() $w_0=z_0+v_0$
with
$w_0=z_0+v_0$
with
![]() $v_0\in 2\mathbb {Z}^2$
, and the statement follows in this case. Note that the exact same argument leading to
$v_0\in 2\mathbb {Z}^2$
, and the statement follows in this case. Note that the exact same argument leading to
![]() $w_0-z_0\in 2\mathbb {Z}^2$
also applies if
$w_0-z_0\in 2\mathbb {Z}^2$
also applies if
![]() $\alpha \cap \wp ^{-1} (a\cup c)=\emptyset $
.
$\alpha \cap \wp ^{-1} (a\cup c)=\emptyset $
.
We call a Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P}, V)$
null-homotopic in
$(\mathbb {P}, V)$
null-homotopic in
![]() $(\mathbb {P}, V)$
if
$(\mathbb {P}, V)$
if
![]() $\gamma $
can be homotoped in
$\gamma $
can be homotoped in
![]() $\mathbb {P}\smallsetminus V$
to a point, that is, if there exists a homotopy
$\mathbb {P}\smallsetminus V$
to a point, that is, if there exists a homotopy
![]() $H\colon \partial \mathbb {D}\times \mathbb {I}\rightarrow \mathbb {P}\smallsetminus V$
such that
$H\colon \partial \mathbb {D}\times \mathbb {I}\rightarrow \mathbb {P}\smallsetminus V$
such that
![]() $H_0$
is a homeomorphism of
$H_0$
is a homeomorphism of
![]() $\partial \mathbb {D}$
onto
$\partial \mathbb {D}$
onto
![]() $\gamma $
and
$\gamma $
and
![]() $H_1$
is a constant map.
$H_1$
is a constant map.
Lemma A.5. Let
![]() $\gamma $
be an essential Jordan curve in
$\gamma $
be an essential Jordan curve in
![]() $(\mathbb {P}, V)$
. Then
$(\mathbb {P}, V)$
. Then
![]() $\gamma $
is not null-homotopic in
$\gamma $
is not null-homotopic in
![]() $(\mathbb {P}, V)$
.
$(\mathbb {P}, V)$
.
This statement sounds somewhat tautological, because in topology, ‘essential’ is often defined as ‘not null-homotopic’. Recall though that in our context
![]() $\gamma $
is called essential if each of the two components of
$\gamma $
is called essential if each of the two components of
![]() $\mathbb {P}\smallsetminus \gamma $
contains precisely two of the points in V. In the proof, we will use some standard facts about winding numbers; see [Reference BurckelBur79, Ch. 4] for the basic definitions and background.
$\mathbb {P}\smallsetminus \gamma $
contains precisely two of the points in V. In the proof, we will use some standard facts about winding numbers; see [Reference BurckelBur79, Ch. 4] for the basic definitions and background.
Proof. On an intuitive level, every homotopy contracting
![]() $\gamma $
to a point must slide over all the points in one of the complementary components of
$\gamma $
to a point must slide over all the points in one of the complementary components of
![]() $\gamma $
. Hence, it cannot stay in
$\gamma $
. Hence, it cannot stay in
![]() $\mathbb {P}\smallsetminus V$
, and so
$\mathbb {P}\smallsetminus V$
, and so
![]() $\gamma $
is not null-homotopic in
$\gamma $
is not null-homotopic in
![]() $(\mathbb {P}, V)$
.
$(\mathbb {P}, V)$
.
To make this more rigorous, we argue by contradiction. By the Schönflies theorem, we may identify
![]() $\mathbb {P}$
with
$\mathbb {P}$
with
![]() $\widehat {\mathbb {C}}$
and
$\widehat {\mathbb {C}}$
and
![]() $\gamma $
with
$\gamma $
with
![]() $\partial \mathbb {D}$
and assume that
$\partial \mathbb {D}$
and assume that
![]() $0$
and
$0$
and
![]() $\infty $
belong to the set
$\infty $
belong to the set
![]() $Z\subset \widehat {\mathbb {C}}$
of marked points corresponding to the points in V. We now argue by contradiction and assume that there exists a homotopy
$Z\subset \widehat {\mathbb {C}}$
of marked points corresponding to the points in V. We now argue by contradiction and assume that there exists a homotopy
![]() $H\colon \partial \mathbb {D} \times \mathbb {I}\rightarrow \widehat {\mathbb {C}} \smallsetminus Z\subset \mathbb {C}\smallsetminus \{0\}$
such that
$H\colon \partial \mathbb {D} \times \mathbb {I}\rightarrow \widehat {\mathbb {C}} \smallsetminus Z\subset \mathbb {C}\smallsetminus \{0\}$
such that
![]() $H_0$
is a homeomorphism on
$H_0$
is a homeomorphism on
![]() $\partial \mathbb {D}$
and
$\partial \mathbb {D}$
and
![]() $H_1$
is a constant map. Then for each
$H_1$
is a constant map. Then for each
![]() $t\in \mathbb {I}$
, the map
$t\in \mathbb {I}$
, the map ![]() is a loop in
is a loop in
![]() $\mathbb {C}\smallsetminus \{0\}$
. Each loop
$\mathbb {C}\smallsetminus \{0\}$
. Each loop
![]() $\alpha _t$
,
$\alpha _t$
,
![]() $t\in \mathbb {I}$
, has the same winding number
$t\in \mathbb {I}$
, has the same winding number
![]() $\text {ind}_{\alpha _t}(0)$
around
$\text {ind}_{\alpha _t}(0)$
around
![]() $0$
, because this winding number is invariant under homotopies in
$0$
, because this winding number is invariant under homotopies in
![]() $\mathbb {C}\smallsetminus \{0\}$
(see [Reference BurckelBur79, Theorem 4.12]). However,
$\mathbb {C}\smallsetminus \{0\}$
(see [Reference BurckelBur79, Theorem 4.12]). However,
![]() $\text {ind}_{\alpha _0}(0)=\pm 1$
, because
$\text {ind}_{\alpha _0}(0)=\pm 1$
, because
![]() $\alpha _0$
is a simple loop (see [Reference BurckelBur79, Theorem 4.42]), while
$\alpha _0$
is a simple loop (see [Reference BurckelBur79, Theorem 4.42]), while
![]() $\text {ind}_{\alpha _1}(0)=0$
, because
$\text {ind}_{\alpha _1}(0)=0$
, because
![]() $\alpha _1$
is a constant loop. This is a contradiction.
$\alpha _1$
is a constant loop. This is a contradiction.
An element x of a rank-2 lattice
![]() $\Gamma $
(such as
$\Gamma $
(such as
![]() $2\mathbb {Z}^2$
) in
$2\mathbb {Z}^2$
) in
![]() $\mathbb {C}$
is called primitive if it cannot be represented in the form
$\mathbb {C}$
is called primitive if it cannot be represented in the form
![]() $x=ny$
with
$x=ny$
with
![]() $y\in \Gamma $
and
$y\in \Gamma $
and
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $n\ge 2$
. Note that then,
$n\ge 2$
. Note that then,
![]() $x\ne 0$
.
$x\ne 0$
.
Lemma A.6. Let
![]() $\gamma $
be a Jordan curve in
$\gamma $
be a Jordan curve in
![]() $(\mathbb {P},V)$
parameterized as a simple loop
$(\mathbb {P},V)$
parameterized as a simple loop
![]() $\beta \colon \mathbb {I}\rightarrow \mathbb {P}$
, and let
$\beta \colon \mathbb {I}\rightarrow \mathbb {P}$
, and let
![]() $\alpha \colon \mathbb {I}\rightarrow \mathbb {C}$
be a lift of
$\alpha \colon \mathbb {I}\rightarrow \mathbb {C}$
be a lift of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
.
$\wp $
.
-
(i) If
 $\alpha (0)=\alpha (1)$
and
$\alpha (0)=\alpha (1)$
and
 $\alpha $
is a path in a convex subset of
$\alpha $
is a path in a convex subset of
 $\mathbb {C}\smallsetminus \mathbb {Z}^2$
, then
$\mathbb {C}\smallsetminus \mathbb {Z}^2$
, then
 $\gamma $
is null-homotopic in
$\gamma $
is null-homotopic in
 $(\mathbb {P}, V)$
.
$(\mathbb {P}, V)$
. -
(ii) If
 $\gamma $
is essential, then
$\gamma $
is essential, then
 $\alpha (1)-\alpha (0)$
is a primitive element of
$\alpha (1)-\alpha (0)$
is a primitive element of
 $2\mathbb {Z}^2$
. It is uniquely determined up to sign by the isotopy class
$2\mathbb {Z}^2$
. It is uniquely determined up to sign by the isotopy class
 $[\gamma ]$
of
$[\gamma ]$
of
 $\gamma $
relative to V.
$\gamma $
relative to V.
Here we call
![]() $\alpha $
a lift of
$\alpha $
a lift of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
if
$\wp $
if
![]() $\beta =\wp \circ \alpha $
. In this lemma and its proof, we will carefully distinguish between a path and its image set (unlike elsewhere in the paper).
$\beta =\wp \circ \alpha $
. In this lemma and its proof, we will carefully distinguish between a path and its image set (unlike elsewhere in the paper).
Proof. Note that since
![]() $\beta (\mathbb {I})=\gamma \subset \mathbb {P}\smallsetminus V$
and
$\beta (\mathbb {I})=\gamma \subset \mathbb {P}\smallsetminus V$
and
![]() $\wp $
is a covering map over
$\wp $
is a covering map over
![]() $ \mathbb {P}\smallsetminus V$
, a lift
$ \mathbb {P}\smallsetminus V$
, a lift
![]() $\alpha $
of
$\alpha $
of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
exists. Moreover, for each choice of
$\wp $
exists. Moreover, for each choice of
![]() $z_0\in \wp ^{-1}(\beta (0))$
, there exists a unique lift
$z_0\in \wp ^{-1}(\beta (0))$
, there exists a unique lift
![]() $\alpha $
of
$\alpha $
of
![]() $\beta $
such that
$\beta $
such that
![]() $\alpha (0)=z_0$
(for these standard facts see [Reference HatcherHat02, §1.3, Proposition 1.30]). We will use this uniqueness property of lifts repeatedly in the following.
$\alpha (0)=z_0$
(for these standard facts see [Reference HatcherHat02, §1.3, Proposition 1.30]). We will use this uniqueness property of lifts repeatedly in the following.
(i) The idea for the first part is very simple. We use a ‘straight-line homotopy’ between
![]() $\alpha $
and the constant path
$\alpha $
and the constant path
![]() $u\in \mathbb {I}\mapsto \alpha (0)$
and push it to
$u\in \mathbb {I}\mapsto \alpha (0)$
and push it to
![]() $\mathbb {P}\smallsetminus V$
by applying
$\mathbb {P}\smallsetminus V$
by applying
![]() $\wp $
.
$\wp $
.
More precisely, we define
for
![]() $u,t\in \mathbb {I}$
. Since the path
$u,t\in \mathbb {I}$
. Since the path
![]() $\alpha $
lies in a convex set
$\alpha $
lies in a convex set
![]() $K\subset \mathbb {C} \smallsetminus \mathbb {Z}^2$
, we have
$K\subset \mathbb {C} \smallsetminus \mathbb {Z}^2$
, we have
for all
![]() $u,t\in \mathbb {I}$
, and so
$u,t\in \mathbb {I}$
, and so
![]() $H(\mathbb {I}\times \mathbb {I})\subset \wp (\mathbb {C}\smallsetminus \mathbb {Z}^2)=\mathbb {P}\smallsetminus V$
. Hence, H is a homotopy in
$H(\mathbb {I}\times \mathbb {I})\subset \wp (\mathbb {C}\smallsetminus \mathbb {Z}^2)=\mathbb {P}\smallsetminus V$
. Hence, H is a homotopy in
![]() $\mathbb {P}\smallsetminus V$
. Moreover,
$\mathbb {P}\smallsetminus V$
. Moreover,
![]() $H_t(u)=(\wp \circ \alpha _t)(u)$
for all
$H_t(u)=(\wp \circ \alpha _t)(u)$
for all
![]() $u\in \mathbb {I}$
, and so
$u\in \mathbb {I}$
, and so
![]() $H_t=\wp \circ \alpha _t$
for all
$H_t=\wp \circ \alpha _t$
for all
![]() $t\in \mathbb {I}$
. In particular,
$t\in \mathbb {I}$
. In particular,
![]() $H_0=\wp \circ \alpha _0=\wp \circ \alpha =\beta $
. Moreover,
$H_0=\wp \circ \alpha _0=\wp \circ \alpha =\beta $
. Moreover,
![]() $H_1(u)=\alpha (0)$
for
$H_1(u)=\alpha (0)$
for
![]() $u\in \mathbb {I}$
, and so
$u\in \mathbb {I}$
, and so
![]() $H_1$
is a constant path.
$H_1$
is a constant path.
For all
![]() $t\in \mathbb {I}$
, we have
$t\in \mathbb {I}$
, we have
Hence,
![]() $\wp (\alpha _t(1)){\kern-1pt}={\kern-1pt}\wp (\alpha _t(0))$
for
$\wp (\alpha _t(1)){\kern-1pt}={\kern-1pt}\wp (\alpha _t(0))$
for
![]() $t{\kern-1pt}\in{\kern-1pt} \mathbb {I}$
, and so
$t{\kern-1pt}\in{\kern-1pt} \mathbb {I}$
, and so
![]() $H_t{\kern-1pt}={\kern-1pt}\wp \circ \alpha _t$
is a loop in
$H_t{\kern-1pt}={\kern-1pt}\wp \circ \alpha _t$
is a loop in
![]() $\mathbb {P}\smallsetminus V$
for all
$\mathbb {P}\smallsetminus V$
for all
![]() $t{\kern-1pt}\in{\kern-1pt} \mathbb {I}$
. By identifying the points
$t{\kern-1pt}\in{\kern-1pt} \mathbb {I}$
. By identifying the points
![]() $(0,{\kern-1pt}t)$
and
$(0,{\kern-1pt}t)$
and
![]() $(1,{\kern-1pt}t)$
for each
$(1,{\kern-1pt}t)$
for each
![]() $t{\kern-1pt}\in{\kern-1pt} \mathbb {I}$
, we get a homotopy
$t{\kern-1pt}\in{\kern-1pt} \mathbb {I}$
, we get a homotopy
![]() $\overline H\colon{\kern-1.2pt} \partial \mathbb {D}{\kern-1pt}\times{\kern-1pt} \mathbb {I}{\kern-1pt}\rightarrow{\kern-1.2pt} \mathbb {P}\smallsetminus V$
such that
$\overline H\colon{\kern-1.2pt} \partial \mathbb {D}{\kern-1pt}\times{\kern-1pt} \mathbb {I}{\kern-1pt}\rightarrow{\kern-1.2pt} \mathbb {P}\smallsetminus V$
such that
for all
![]() $u,t\in \mathbb {I}$
. Since
$u,t\in \mathbb {I}$
. Since
![]() $\overline H_0(e^{2\pi iu})=H_0(u)=\beta (u)$
for
$\overline H_0(e^{2\pi iu})=H_0(u)=\beta (u)$
for
![]() $u\in \mathbb {I}$
, we see that
$u\in \mathbb {I}$
, we see that
![]() $\overline H_0$
is a homeomorphism of
$\overline H_0$
is a homeomorphism of
![]() $\partial \mathbb {D}$
onto
$\partial \mathbb {D}$
onto
![]() $\beta (\mathbb {I})=\gamma $
. However,
$\beta (\mathbb {I})=\gamma $
. However,
![]() $\overline H_1$
is a constant map. Hence,
$\overline H_1$
is a constant map. Hence,
![]() $\gamma $
is null-homotopic in
$\gamma $
is null-homotopic in
![]() $(\mathbb {P}, V)$
.
$(\mathbb {P}, V)$
.
(ii) The proof is somewhat tedious as we have to worry about different choices of the curve in
![]() $[\gamma ]$
, its different parameterizations as a simple loop, and the different lifts of these parameterizations under
$[\gamma ]$
, its different parameterizations as a simple loop, and the different lifts of these parameterizations under
![]() $\wp $
.
$\wp $
.
To prove the statement, we first consider a special case, namely we choose a Jordan curve
![]() $\gamma _0$
in
$\gamma _0$
in
![]() $(\mathbb {P}, V)$
that lies in the same isotopy class relative to V as
$(\mathbb {P}, V)$
that lies in the same isotopy class relative to V as
![]() $\gamma $
with the additional property that
$\gamma $
with the additional property that
![]() $\gamma _0$
is in minimal position with the set
$\gamma _0$
is in minimal position with the set
![]() $a\cup c$
. Since
$a\cup c$
. Since
![]() $\gamma _0$
cannot be a subset of
$\gamma _0$
cannot be a subset of
![]() $a\cup c$
, we can parameterize
$a\cup c$
, we can parameterize
![]() $\gamma _0$
as a simple loop
$\gamma _0$
as a simple loop
![]() $\beta _0\colon \mathbb {I}\rightarrow \mathbb {P}$
such that
$\beta _0\colon \mathbb {I}\rightarrow \mathbb {P}$
such that
![]() $\beta _0(0)=\beta _0(1)\not \in a\cup c$
. We now consider a lift
$\beta _0(0)=\beta _0(1)\not \in a\cup c$
. We now consider a lift
![]() $\alpha _0\colon \mathbb {I}\rightarrow \mathbb {C}$
of
$\alpha _0\colon \mathbb {I}\rightarrow \mathbb {C}$
of
![]() $\beta _0$
under
$\beta _0$
under
![]() $\wp $
. Note that
$\wp $
. Note that
![]() $\alpha _0$
is a simple loop or a homeomorphic parameterization on an arc in
$\alpha _0$
is a simple loop or a homeomorphic parameterization on an arc in
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Since
![]() $\gamma $
is essential, the Jordan curve
$\gamma $
is essential, the Jordan curve
![]() $\gamma _0$
is also essential. Indeed, under an isotopy relative to V that deforms
$\gamma _0$
is also essential. Indeed, under an isotopy relative to V that deforms
![]() $\gamma $
into
$\gamma $
into
![]() $\gamma _0$
, the complementary components of
$\gamma _0$
, the complementary components of
![]() $\gamma $
in
$\gamma $
in
![]() $\mathbb {P}$
are deformed into the complementary components of
$\mathbb {P}$
are deformed into the complementary components of
![]() $\gamma _0$
while the points in V stay fixed. Therefore, each of the two components of
$\gamma _0$
while the points in V stay fixed. Therefore, each of the two components of
![]() $\mathbb {P}\smallsetminus \gamma _0$
contains precisely two points of V.
$\mathbb {P}\smallsetminus \gamma _0$
contains precisely two points of V.
It follows from Lemma A.1 that
![]() $\gamma _0$
meets a and c transversely. Moreover, by Lemma A.3, either
$\gamma _0$
meets a and c transversely. Moreover, by Lemma A.3, either
![]() $\gamma _0\cap (a\cup c)=\emptyset $
, or the sets
$\gamma _0\cap (a\cup c)=\emptyset $
, or the sets
![]() $a\cap \gamma _0$
and
$a\cap \gamma _0$
and
![]() $c\cap \gamma _0$
are non-empty and finite, and the points in these sets alternate on
$c\cap \gamma _0$
are non-empty and finite, and the points in these sets alternate on
![]() $\gamma _0$
. We now define
$\gamma _0$
. We now define ![]() . Then
. Then
![]() $\overline \alpha _0$
is a Jordan curve or an arc in
$\overline \alpha _0$
is a Jordan curve or an arc in
![]() $\mathbb {C}$
. Moreover, we either have
$\mathbb {C}$
. Moreover, we either have
![]() $\overline \alpha _0\cap \wp ^{-1}(a\cup c)=\emptyset $
, or
$\overline \alpha _0\cap \wp ^{-1}(a\cup c)=\emptyset $
, or
![]() $\overline \alpha _0$
meets each of the lines in
$\overline \alpha _0$
meets each of the lines in
![]() $\wp ^{-1}(a\cup c)$
transversely,
$\wp ^{-1}(a\cup c)$
transversely,
and the points in
![]() $\overline \alpha _0 \cap \wp ^{-1} (a)$
and
$\overline \alpha _0 \cap \wp ^{-1} (a)$
and
![]() $\overline \alpha _0 \cap \wp ^{-1} (c)$
alternate on
$\overline \alpha _0 \cap \wp ^{-1} (c)$
alternate on
![]() $ \overline \alpha _0$
. Let
$ \overline \alpha _0$
. Let ![]() and
and ![]() . Then
. Then
and by the choice of
![]() $\beta _0$
, we have
$\beta _0$
, we have
![]() $z_0, w_0\not \in \wp ^{-1}(a\cup c)$
. Therefore, we are exactly in the situation of Lemma A.4.
$z_0, w_0\not \in \wp ^{-1}(a\cup c)$
. Therefore, we are exactly in the situation of Lemma A.4.
It follows that ![]() . Here
. Here
![]() $v_0\ne 0$
. Indeed, otherwise
$v_0\ne 0$
. Indeed, otherwise
![]() $z_0=w_0$
. Then the second part of Lemma A.4 implies that the arc
$z_0=w_0$
. Then the second part of Lemma A.4 implies that the arc
![]() $\overline \alpha _0$
does not meet
$\overline \alpha _0$
does not meet
![]() $\wp ^{-1}(a\cup c)$
and so it lies in a connected component of
$\wp ^{-1}(a\cup c)$
and so it lies in a connected component of
![]() $\mathbb {C}\smallsetminus \wp ^{-1}(a\cup c)$
. This component is an infinite strip, and hence a convex set, contained in
$\mathbb {C}\smallsetminus \wp ^{-1}(a\cup c)$
. This component is an infinite strip, and hence a convex set, contained in
![]() $\mathbb {C}\smallsetminus \mathbb {Z}^2$
. Now part (i) implies that
$\mathbb {C}\smallsetminus \mathbb {Z}^2$
. Now part (i) implies that
![]() $\gamma _0$
is null-homotopic in
$\gamma _0$
is null-homotopic in
![]() $(\mathbb {P}, V)$
. By Lemma A.5, this contradicts the fact that
$(\mathbb {P}, V)$
. By Lemma A.5, this contradicts the fact that
![]() $\gamma _0$
is essential. We conclude that indeed
$\gamma _0$
is essential. We conclude that indeed
![]() $v_0=w_0-z_0\ne 0$
.
$v_0=w_0-z_0\ne 0$
.
This shows that
![]() $\alpha _0(1)-\alpha _0(0)=w_0-z_0$
is a non-zero element of the lattice
$\alpha _0(1)-\alpha _0(0)=w_0-z_0$
is a non-zero element of the lattice
![]() $2\mathbb {Z}^2$
. We claim that
$2\mathbb {Z}^2$
. We claim that
![]() $w_0-z_0$
is actually a primitive element of
$w_0-z_0$
is actually a primitive element of
![]() $2\mathbb {Z}^2$
. To see this, we argue by contradiction and assume that
$2\mathbb {Z}^2$
. To see this, we argue by contradiction and assume that
![]() $w_0-z_0=ny_0$
with
$w_0-z_0=ny_0$
with
![]() $y_0\in 2\mathbb {Z}^2\smallsetminus \{0\}$
and
$y_0\in 2\mathbb {Z}^2\smallsetminus \{0\}$
and
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $n\ge 2$
.
$n\ge 2$
.
We now consider the path
![]() $\sigma \colon \mathbb {I}\rightarrow \mathbb {C}\smallsetminus \{0\}$
given as
$\sigma \colon \mathbb {I}\rightarrow \mathbb {C}\smallsetminus \{0\}$
given as
![]() $\sigma (u)=\exp ( ({2\pi i}/{y_0}) \alpha _0(u))$
for
$\sigma (u)=\exp ( ({2\pi i}/{y_0}) \alpha _0(u))$
for
![]() $u\in \mathbb {I}$
. This is a loop with winding number
$u\in \mathbb {I}$
. This is a loop with winding number
around
![]() $0$
. Now a simple loop in
$0$
. Now a simple loop in
![]() $\mathbb {C}\smallsetminus \{0\}$
has winding number
$\mathbb {C}\smallsetminus \{0\}$
has winding number
![]() $0$
or
$0$
or
![]() $\pm 1$
around
$\pm 1$
around
![]() $0$
(see [Reference BurckelBur79, Theorem 4.42]), and so
$0$
(see [Reference BurckelBur79, Theorem 4.42]), and so
![]() $\sigma $
cannot be simple. This implies that there are numbers
$\sigma $
cannot be simple. This implies that there are numbers
![]() $0\le u<u'<1$
such that
$0\le u<u'<1$
such that
![]() $\sigma (u)=\sigma (u')$
. This in turn means that
$\sigma (u)=\sigma (u')$
. This in turn means that
![]() $\alpha _0(u')-\alpha _0(u)=ky_0$
for some
$\alpha _0(u')-\alpha _0(u)=ky_0$
for some
![]() $k\in \mathbb {Z}$
. Since
$k\in \mathbb {Z}$
. Since
![]() $y_0\in 2\mathbb {Z}^2$
, it follows that
$y_0\in 2\mathbb {Z}^2$
, it follows that
This is impossible, since
![]() $\beta _0$
is injective on
$\beta _0$
is injective on
![]() $[0,1)$
.
$[0,1)$
.
We have shown the first part of the statement for a particular Jordan curve
![]() $\gamma _0$
in
$\gamma _0$
in
![]() $[\gamma ]$
with a special parameterization
$[\gamma ]$
with a special parameterization
![]() $\beta _0$
, and a choice of a lift
$\beta _0$
, and a choice of a lift
![]() $\alpha _0$
of
$\alpha _0$
of
![]() $\beta _0$
under
$\beta _0$
under
![]() $\wp $
. We now have to show that the number
$\wp $
. We now have to show that the number
![]() $v_0 =w_0-z_0=\alpha _0(1)-\alpha _0(0)$
obtained in this way only depends on
$v_0 =w_0-z_0=\alpha _0(1)-\alpha _0(0)$
obtained in this way only depends on
![]() $[\gamma ]$
up to sign. For this, we pick an arbitrary Jordan curve in
$[\gamma ]$
up to sign. For this, we pick an arbitrary Jordan curve in
![]() $[\gamma ]$
which we will simply call
$[\gamma ]$
which we will simply call
![]() $\gamma $
.
$\gamma $
.
Since
![]() $\gamma _0\sim \gamma $
relative to V, there exists an isotopy
$\gamma _0\sim \gamma $
relative to V, there exists an isotopy
![]() $H\colon \mathbb {P} \times \mathbb {I}\rightarrow \mathbb {P}$
relative to V with
$H\colon \mathbb {P} \times \mathbb {I}\rightarrow \mathbb {P}$
relative to V with
![]() $H_0=\operatorname {id}_{\mathbb {P}}$
and
$H_0=\operatorname {id}_{\mathbb {P}}$
and
![]() $H_1(\gamma _0)=\gamma $
. We now define a homotopy
$H_1(\gamma _0)=\gamma $
. We now define a homotopy
![]() $\overline H\colon \mathbb {I}\times \mathbb {I}\rightarrow \mathbb {P}\smallsetminus V$
by setting
$\overline H\colon \mathbb {I}\times \mathbb {I}\rightarrow \mathbb {P}\smallsetminus V$
by setting
for
![]() $u,t\in \mathbb {I}$
. Note that
$u,t\in \mathbb {I}$
. Note that
![]() $ \overline H$
maps into
$ \overline H$
maps into
![]() $ \mathbb {P} \smallsetminus V$
as follows from the facts that
$ \mathbb {P} \smallsetminus V$
as follows from the facts that
![]() $\gamma _0\subset \mathbb {P} \smallsetminus V$
and H is an isotopy relative to V.
$\gamma _0\subset \mathbb {P} \smallsetminus V$
and H is an isotopy relative to V.
The time-
![]() $0$
map
$0$
map
![]() $\overline H(\cdot , 0)=\beta _0$
of the homotopy
$\overline H(\cdot , 0)=\beta _0$
of the homotopy
![]() $\overline H$
is the parameterization of the loop
$\overline H$
is the parameterization of the loop
![]() $\gamma _0$
, while the time-
$\gamma _0$
, while the time-
![]() $1$
map
$1$
map ![]() gives some parameterization of
gives some parameterization of
![]() $\gamma =H_1(\gamma _0)$
as a simple loop.
$\gamma =H_1(\gamma _0)$
as a simple loop.
By the homotopy lifting theorem (see [Reference HatcherHat02, Proposition 1.30]), there exists a homotopy
![]() $\widetilde H\colon \mathbb {I}\times \mathbb {I}\rightarrow \mathbb {C}\smallsetminus \mathbb {Z}^2$
such that
$\widetilde H\colon \mathbb {I}\times \mathbb {I}\rightarrow \mathbb {C}\smallsetminus \mathbb {Z}^2$
such that
![]() $\overline H= \wp \circ \widetilde H$
and
$\overline H= \wp \circ \widetilde H$
and
![]() $\widetilde H_0= \widetilde H (\cdot , 0) =\alpha _0$
. Then
$\widetilde H_0= \widetilde H (\cdot , 0) =\alpha _0$
. Then ![]() is a lift of
is a lift of
![]() $\beta =\overline H (\cdot , 1)$
under
$\beta =\overline H (\cdot , 1)$
under
![]() $\wp $
. We want to show that
$\wp $
. We want to show that
![]() $\alpha (1)-\alpha (0)=v_0= w_0-z_0$
.
$\alpha (1)-\alpha (0)=v_0= w_0-z_0$
.
To see this, we consider the paths
![]() $\sigma ,\tau \colon \mathbb {I}\rightarrow \mathbb {C}\smallsetminus \mathbb {Z}^2$
defined as
$\sigma ,\tau \colon \mathbb {I}\rightarrow \mathbb {C}\smallsetminus \mathbb {Z}^2$
defined as
![]() $\sigma (t)=\widetilde H(0,t)$
and
$\sigma (t)=\widetilde H(0,t)$
and
![]() $\tau (t)=\widetilde H(1,t)$
for
$\tau (t)=\widetilde H(1,t)$
for
![]() $t\in \mathbb {I}$
. Then
$t\in \mathbb {I}$
. Then

for
![]() $t\in \mathbb {I}$
. Note also that
$t\in \mathbb {I}$
. Note also that
This implies that the paths
![]() $\tau $
and
$\tau $
and
![]() $t\in \mathbb {I}\mapsto \sigma (t)+v_0$
have the same initial points. Since
$t\in \mathbb {I}\mapsto \sigma (t)+v_0$
have the same initial points. Since
![]() $v_0\in 2\mathbb {Z}^2$
, it follows from (2.3) and (A.1) that the map
$v_0\in 2\mathbb {Z}^2$
, it follows from (2.3) and (A.1) that the map
![]() $\wp $
sends them both to
$\wp $
sends them both to
![]() $\overline \sigma =\wp \circ \sigma =\wp \circ \tau $
, which is a path in
$\overline \sigma =\wp \circ \sigma =\wp \circ \tau $
, which is a path in
![]() $\mathbb {P}\smallsetminus V$
. It follows from the uniqueness of lifts under
$\mathbb {P}\smallsetminus V$
. It follows from the uniqueness of lifts under
![]() $\wp $
that
$\wp $
that
![]() $\tau (t)=\sigma (t)+v_0$
for all
$\tau (t)=\sigma (t)+v_0$
for all
![]() $t\in \mathbb {I}$
.
$t\in \mathbb {I}$
.
This implies that
as desired.
Note that for a given parameterization
![]() $\beta $
of
$\beta $
of
![]() $\gamma $
, the difference
$\gamma $
, the difference
![]() $\alpha (1)-\alpha (0)$
is independent up to sign of the choice of the lift
$\alpha (1)-\alpha (0)$
is independent up to sign of the choice of the lift
![]() $\alpha $
of
$\alpha $
of
![]() $\beta $
. Indeed, suppose
$\beta $
. Indeed, suppose
![]() $\alpha '$
is another lift of
$\alpha '$
is another lift of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
. Then
$\wp $
. Then
and so by (2.3), we have
for some (fixed) choice of the sign
![]() $\pm $
and
$\pm $
and
![]() $m_0\in 2\mathbb {Z}^2$
. Then
$m_0\in 2\mathbb {Z}^2$
. Then
![]() $t\in \mathbb {I}\mapsto \pm \alpha (t)+m_0$
is a lift of
$t\in \mathbb {I}\mapsto \pm \alpha (t)+m_0$
is a lift of
![]() $\beta $
with the same initial point as
$\beta $
with the same initial point as
![]() $\alpha '$
and so we see that
$\alpha '$
and so we see that
for all
![]() $t\in \mathbb {I}$
. This implies that
$t\in \mathbb {I}$
. This implies that
as desired.
It remains to show that up to sign
![]() $\alpha (1)-\alpha (0)$
is independent of the choice of the parameterization
$\alpha (1)-\alpha (0)$
is independent of the choice of the parameterization
![]() $\beta $
of
$\beta $
of
![]() $\gamma $
. For this, we consider another parameterization
$\gamma $
. For this, we consider another parameterization
![]() $\beta '$
of
$\beta '$
of
![]() $\gamma $
as a simple loop. We first assume that
$\gamma $
as a simple loop. We first assume that
![]() $\beta '(0)=\beta (0)$
. Then there exists a homeomorphism
$\beta '(0)=\beta (0)$
. Then there exists a homeomorphism
![]() $h\colon \mathbb {I}\rightarrow \mathbb {I}$
such that
$h\colon \mathbb {I}\rightarrow \mathbb {I}$
such that
![]() $\beta '=\beta \circ h$
. Here h fixes the endpoints
$\beta '=\beta \circ h$
. Here h fixes the endpoints
![]() $0$
and
$0$
and
![]() $1$
of
$1$
of
![]() $\mathbb {I}$
or interchanges them depending on whether
$\mathbb {I}$
or interchanges them depending on whether
![]() $\beta '$
parameterizes
$\beta '$
parameterizes
![]() $\gamma $
with the same or opposite orientation as
$\gamma $
with the same or opposite orientation as
![]() $\beta $
, respectively. In any case,
$\beta $
, respectively. In any case,
![]() $\alpha '=\alpha \circ h$
is a lift of
$\alpha '=\alpha \circ h$
is a lift of
![]() $\beta '$
under
$\beta '$
under
![]() $\wp $
. It follows that
$\wp $
. It follows that
as desired. As we now know, this relation is independent of the specific choice of the lift
![]() $\alpha '$
of
$\alpha '$
of
![]() $\beta '$
.
$\beta '$
.
Finally, we have to consider the case where
![]() $\beta '$
has a possibly different initial point than
$\beta '$
has a possibly different initial point than
![]() $\beta $
, say
$\beta $
, say ![]() . By what we have seen, to establish (A.2), we can choose any parameterization
. By what we have seen, to establish (A.2), we can choose any parameterization
![]() $\beta '$
of
$\beta '$
of
![]() $\gamma $
as a simple loop with
$\gamma $
as a simple loop with
![]() $\beta '(0)=p_0$
and any lift
$\beta '(0)=p_0$
and any lift
![]() $\alpha '$
of
$\alpha '$
of
![]() $\beta '$
.
$\beta '$
.
We can extend our parameterization
![]() $\beta $
on
$\beta $
on
![]() $\mathbb {I}$
periodically to a continuous map
$\mathbb {I}$
periodically to a continuous map
![]() ${\beta \colon \mathbb {R} \rightarrow \gamma }$
such that
${\beta \colon \mathbb {R} \rightarrow \gamma }$
such that
![]() $\beta (u+1)=\beta (u)$
for all
$\beta (u+1)=\beta (u)$
for all
![]() $u\in \mathbb {R}$
. Then
$u\in \mathbb {R}$
. Then
![]() $\beta $
lifts under
$\beta $
lifts under
![]() $\wp $
to a continuous map
$\wp $
to a continuous map
![]() $\alpha \colon \mathbb {R} \rightarrow \mathbb {C}$
which agrees with the original lift
$\alpha \colon \mathbb {R} \rightarrow \mathbb {C}$
which agrees with the original lift
![]() $\alpha $
on
$\alpha $
on
![]() $\mathbb {I}$
. Then
$\mathbb {I}$
. Then
![]() $u\in \mathbb {R} \mapsto \alpha (u+1)-v_0$
is also a lift of
$u\in \mathbb {R} \mapsto \alpha (u+1)-v_0$
is also a lift of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
. The initial point of this lift corresponding to
$\wp $
. The initial point of this lift corresponding to
![]() $u=0$
is equal to
$u=0$
is equal to
![]() $\alpha (0)$
. The uniqueness of lifts implies that this lift and the original lift
$\alpha (0)$
. The uniqueness of lifts implies that this lift and the original lift
![]() $\alpha $
are the same paths and so
$\alpha $
are the same paths and so
for all
![]() $u\in \mathbb {R}$
.
$u\in \mathbb {R}$
.
We can find
![]() $u_0\in [0,1)$
such that
$u_0\in [0,1)$
such that
![]() $\beta (u_0)=p_0$
. Then
$\beta (u_0)=p_0$
. Then
![]() $\beta '\colon \mathbb {I}\rightarrow \gamma $
defined as
$\beta '\colon \mathbb {I}\rightarrow \gamma $
defined as
![]() $\beta '(u)=\beta (u_0+u)$
for
$\beta '(u)=\beta (u_0+u)$
for
![]() $u\in \mathbb {I}$
is a parameterization of
$u\in \mathbb {I}$
is a parameterization of
![]() $\gamma $
as a simple loop with the initial point
$\gamma $
as a simple loop with the initial point
![]() $p_0$
. Under
$p_0$
. Under
![]() $\wp $
, this path
$\wp $
, this path
![]() $\beta '$
has the lift
$\beta '$
has the lift
![]() $\alpha '\colon \mathbb {I}\rightarrow \mathbb {C}$
given by
$\alpha '\colon \mathbb {I}\rightarrow \mathbb {C}$
given by
![]() $\alpha '(u)=\alpha (u+u_0)$
for
$\alpha '(u)=\alpha (u+u_0)$
for
![]() $u\in \mathbb {I}$
. Then equation (A.3) implies that
$u\in \mathbb {I}$
. Then equation (A.3) implies that
as desired. The proof is complete.
We are now almost ready to prove Lemma 2.3. Before we get to this, it is useful to discuss an alternative way to view our pillow
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
We consider a slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. Then we can choose
$r/s\in \widehat {\mathbb {Q}}$
. Then we can choose
![]() $p, q\in \mathbb {Z}$
such that
$p, q\in \mathbb {Z}$
such that
![]() $pr+qs=1$
and define
$pr+qs=1$
and define ![]() and
and ![]() . The numbers
. The numbers
![]() $\omega $
and
$\omega $
and
![]() $\widetilde \omega $
form a basis of
$\widetilde \omega $
form a basis of
![]() $\mathbb {C}\cong \mathbb {R}^2$
over
$\mathbb {C}\cong \mathbb {R}^2$
over
![]() $\mathbb {R}$
, and so every point
$\mathbb {R}$
, and so every point
![]() $z\in \mathbb {C}$
can be uniquely written in the form
$z\in \mathbb {C}$
can be uniquely written in the form
![]() $z=u \widetilde \omega +v \omega $
with
$z=u \widetilde \omega +v \omega $
with
![]() $u,v\in \mathbb {R}$
. Accordingly, the map
$u,v\in \mathbb {R}$
. Accordingly, the map ![]() for
for
![]() $u,v\in \mathbb {R}$
is a well-defined ‘skew-reflection’ R on
$u,v\in \mathbb {R}$
is a well-defined ‘skew-reflection’ R on
![]() $\mathbb {C}$
. Note also that
$\mathbb {C}$
. Note also that
![]() $\mathbb {Z}^2=\{n\widetilde \omega +k\omega : n,k\in \mathbb {Z}\}$
.
$\mathbb {Z}^2=\{n\widetilde \omega +k\omega : n,k\in \mathbb {Z}\}$
.
We consider the parallelogram ![]() . Then it follows from (2.3) that
. Then it follows from (2.3) that
![]() $\wp (Q)=\mathbb {P}$
. Moreover, for
$\wp (Q)=\mathbb {P}$
. Moreover, for
![]() $z,w\in Q$
,
$z,w\in Q$
,
![]() $z\ne w$
, we have
$z\ne w$
, we have
![]() $\wp (z)=\wp (w)$
if and only if
$\wp (z)=\wp (w)$
if and only if
![]() $z,w\in \partial Q$
and
$z,w\in \partial Q$
and
![]() $w=R(z)$
. Intuitively, this means that the pillow
$w=R(z)$
. Intuitively, this means that the pillow
![]() $\mathbb {P}$
can be obtained from Q by ‘folding’ Q in its middle segment
$\mathbb {P}$
can be obtained from Q by ‘folding’ Q in its middle segment
![]() $[0, \widetilde \omega ]\subset Q$
and identifying the points on
$[0, \widetilde \omega ]\subset Q$
and identifying the points on
![]() $\partial Q$
that correspond to each other under the skew-reflection R. The map
$\partial Q$
that correspond to each other under the skew-reflection R. The map
![]() $\wp $
sends the set
$\wp $
sends the set
![]() $\{0, \widetilde \omega , \widetilde \omega +\omega , \omega \}$
bijectively onto the set
$\{0, \widetilde \omega , \widetilde \omega +\omega , \omega \}$
bijectively onto the set
![]() $\{A,B,C,D\}$
of vertices of
$\{A,B,C,D\}$
of vertices of
![]() $\mathbb {P}$
(but not necessarily in that order).
$\mathbb {P}$
(but not necessarily in that order).
From this geometric picture, it is clear that for each
![]() $t\in (0,1)$
, the set
$t\in (0,1)$
, the set
is a simple closed geodesic in
![]() $(\mathbb {P},V)$
. Moreover, the sets
$(\mathbb {P},V)$
. Moreover, the sets
are geodesic core arcs of
![]() $\tau _{r/s}$
lying in different components of
$\tau _{r/s}$
lying in different components of
![]() $\mathbb {P}\smallsetminus \tau _{r/s}$
. In particular,
$\mathbb {P}\smallsetminus \tau _{r/s}$
. In particular,
![]() $\tau _{r/s}$
is an essential Jordan curve in
$\tau _{r/s}$
is an essential Jordan curve in
![]() $(\mathbb {P}, V)$
.
$(\mathbb {P}, V)$
.
It follows from (2.3) that
![]() $\wp (\ell _{r/s}(t\widetilde \omega ))\cap \wp (\ell _{r/s}(t'\widetilde \omega )) \ne \emptyset $
for
$\wp (\ell _{r/s}(t\widetilde \omega ))\cap \wp (\ell _{r/s}(t'\widetilde \omega )) \ne \emptyset $
for
![]() $t,t'\in \mathbb {R}$
if and only if
$t,t'\in \mathbb {R}$
if and only if
![]() $t'-t \in 2\mathbb {Z}$
or
$t'-t \in 2\mathbb {Z}$
or
![]() $t'+t\in 2\mathbb {Z}$
. In this case, we have
$t'+t\in 2\mathbb {Z}$
. In this case, we have
![]() $\wp (\ell _{r/s}(t\widetilde \omega ))=\wp (\ell _{r/s}(t'\widetilde \omega ))$
. Moreover,
$\wp (\ell _{r/s}(t\widetilde \omega ))=\wp (\ell _{r/s}(t'\widetilde \omega ))$
. Moreover,
![]() $\tau =\wp (\ell _{r/s}(t\widetilde \omega ))$
is a simple closed geodesic
$\tau =\wp (\ell _{r/s}(t\widetilde \omega ))$
is a simple closed geodesic
![]() $\tau _{r/s}$
in
$\tau _{r/s}$
in
![]() $(\mathbb {P}, V)$
if
$(\mathbb {P}, V)$
if
![]() $t\in \mathbb {R}\smallsetminus \mathbb {Z}$
, it is equal to the geodesic arc
$t\in \mathbb {R}\smallsetminus \mathbb {Z}$
, it is equal to the geodesic arc
![]() $\xi _{r/s}$
if t is an even integer, and is equal to the geodesic arc
$\xi _{r/s}$
if t is an even integer, and is equal to the geodesic arc
![]() $\xi ^{\prime }_{r/s}$
if t is an odd integer. Note that
$\xi ^{\prime }_{r/s}$
if t is an odd integer. Note that
![]() $\ell _{r/s}(t\widetilde \omega )$
for
$\ell _{r/s}(t\widetilde \omega )$
for
![]() $t\in \mathbb {R}$
contains a point in
$t\in \mathbb {R}$
contains a point in
![]() $\mathbb {Z}^2=\{n\widetilde \omega +k\omega : n,k\in \mathbb {Z}\}$
if and only if
$\mathbb {Z}^2=\{n\widetilde \omega +k\omega : n,k\in \mathbb {Z}\}$
if and only if
![]() $t\in \mathbb {Z}$
.
$t\in \mathbb {Z}$
.
Lemma A.7. Let
![]() $\tau _{r/s}$
and
$\tau _{r/s}$
and
![]() $\tau ^{\prime }_{r/s}$
be two distinct simple closed geodesics in
$\tau ^{\prime }_{r/s}$
be two distinct simple closed geodesics in
![]() $(\mathbb {P}, V)$
with slope
$(\mathbb {P}, V)$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. Then
$r/s\in \widehat {\mathbb {Q}}$
. Then
![]() $\tau _{r/s}$
and
$\tau _{r/s}$
and
![]() $\tau ^{\prime }_{r/s}$
are isotopic relative to V.
$\tau ^{\prime }_{r/s}$
are isotopic relative to V.
Proof. The previous considerations imply that we may assume that the geodesics are represented in the form
![]() $\tau _{r/s} =\wp (\ell _{r/s}(t\widetilde \omega ))$
and
$\tau _{r/s} =\wp (\ell _{r/s}(t\widetilde \omega ))$
and
![]() $\tau ^{\prime }_{r/s} =\wp (\ell _{r/s}(t'\widetilde \omega ))$
with
$\tau ^{\prime }_{r/s} =\wp (\ell _{r/s}(t'\widetilde \omega ))$
with
![]() $t,t'\in (0,1)$
,
$t,t'\in (0,1)$
,
![]() $t\ne t'$
. We may assume
$t\ne t'$
. We may assume
![]() $t<t'$
. Then
$t<t'$
. Then
is an annulus contained in
![]() $\mathbb {P}\smallsetminus V$
with
$\mathbb {P}\smallsetminus V$
with
![]() $\partial U=\tau _{r/s}\cup \tau ^{\prime }_{r/s}$
. It follows from Lemma 2.1 that
$\partial U=\tau _{r/s}\cup \tau ^{\prime }_{r/s}$
. It follows from Lemma 2.1 that
![]() $\tau _{r/s}$
and
$\tau _{r/s}$
and
![]() $\tau ^{\prime }_{r/s}$
are isotopic relative to V.
$\tau ^{\prime }_{r/s}$
are isotopic relative to V.
Proof of Lemma 2.3
Let
![]() $\gamma $
be an essential Jordan curve in
$\gamma $
be an essential Jordan curve in
![]() $(\mathbb {P}, V)$
. If we parameterize
$(\mathbb {P}, V)$
. If we parameterize
![]() $\gamma $
as a simple loop
$\gamma $
as a simple loop
![]() $\beta \colon \mathbb {I}\rightarrow \mathbb {P}$
and lift
$\beta \colon \mathbb {I}\rightarrow \mathbb {P}$
and lift
![]() $\beta $
to a path
$\beta $
to a path
![]() $\alpha \colon \mathbb {I}\rightarrow \mathbb {C}$
under
$\alpha \colon \mathbb {I}\rightarrow \mathbb {C}$
under
![]() $\wp $
, then by Lemma A.6, we know that
$\wp $
, then by Lemma A.6, we know that
![]() $\alpha (1)-\alpha (0)$
is a primitive element of
$\alpha (1)-\alpha (0)$
is a primitive element of
![]() $2\mathbb {Z}^2$
uniquely determined by
$2\mathbb {Z}^2$
uniquely determined by
![]() $[\gamma ]$
up to sign. Hence, we can find relatively prime integers
$[\gamma ]$
up to sign. Hence, we can find relatively prime integers
![]() $r,s\in \mathbb {Z}$
such that
$r,s\in \mathbb {Z}$
such that
By switching signs here, which corresponds to parameterizing
![]() $\gamma $
with opposite orientation, we may assume that
$\gamma $
with opposite orientation, we may assume that
![]() $r\in \mathbb {Z}$
,
$r\in \mathbb {Z}$
,
![]() $s\in \mathbb {N}_0$
, and that
$s\in \mathbb {N}_0$
, and that
![]() $r=1$
if
$r=1$
if
![]() $s=0$
. Note that with these restrictions on r and s, the primitive element
$s=0$
. Note that with these restrictions on r and s, the primitive element
![]() $2 (s+ir)$
of
$2 (s+ir)$
of
![]() $2\mathbb {Z}^2$
corresponds to the unique slope
$2\mathbb {Z}^2$
corresponds to the unique slope
![]() $r/s\in \widehat {\mathbb {Q}}$
, and every slope in
$r/s\in \widehat {\mathbb {Q}}$
, and every slope in
![]() $ \widehat {\mathbb {Q}}$
arises from a unique primitive element of
$ \widehat {\mathbb {Q}}$
arises from a unique primitive element of
![]() $2\mathbb {Z}^2$
in this form.
$2\mathbb {Z}^2$
in this form.
As before, define ![]() and
and ![]() , where
, where
![]() $p, q\in \mathbb {Z}$
are chosen so that
$p, q\in \mathbb {Z}$
are chosen so that
![]() $pr+qs=1$
. We know that
$pr+qs=1$
. We know that ![]() and
and ![]() are disjoint geodesic arcs in
are disjoint geodesic arcs in
![]() $(\mathbb {P},V)$
. The sets
$(\mathbb {P},V)$
. The sets
![]() $\wp ^{-1}(\xi )$
and
$\wp ^{-1}(\xi )$
and
![]() $\wp ^{-1} (\xi ')$
consist of parallel lines with slope
$\wp ^{-1} (\xi ')$
consist of parallel lines with slope
![]() $r/s$
, and these lines alternate in the following sense: each component of
$r/s$
, and these lines alternate in the following sense: each component of
![]() $\mathbb {C}\smallsetminus \wp ^{-1}(\xi \cup \xi ')$
is an infinite strip whose boundary contains one line in
$\mathbb {C}\smallsetminus \wp ^{-1}(\xi \cup \xi ')$
is an infinite strip whose boundary contains one line in
![]() $\wp ^{-1}(\xi )$
and one line in
$\wp ^{-1}(\xi )$
and one line in
![]() $\wp ^{-1} (\xi ')$
.
$\wp ^{-1} (\xi ')$
.
We may assume that
![]() $\gamma $
is in minimal position with
$\gamma $
is in minimal position with
![]() $\xi \cup \xi '$
. Moreover, we may assume that the parameterization
$\xi \cup \xi '$
. Moreover, we may assume that the parameterization
![]() $\beta $
of
$\beta $
of
![]() $\gamma $
as a simple loop was chosen so that
$\gamma $
as a simple loop was chosen so that
![]() $\beta (0)=\beta (1) \not \in \xi \cup \xi '$
.
$\beta (0)=\beta (1) \not \in \xi \cup \xi '$
.
Then by Lemmas A.1 and A.3, we know that either
![]() $\xi \cap \gamma =\emptyset =\xi '\cap \gamma $
, or the following conditions are true:
$\xi \cap \gamma =\emptyset =\xi '\cap \gamma $
, or the following conditions are true:
![]() $\gamma $
meets
$\gamma $
meets
![]() $\xi $
and
$\xi $
and
![]() $\xi '$
transversely, the sets
$\xi '$
transversely, the sets
![]() $\xi \cap \gamma $
and
$\xi \cap \gamma $
and
![]() $\xi '\cap \gamma $
are non-empty and finite, and the points in these sets alternate on
$\xi '\cap \gamma $
are non-empty and finite, and the points in these sets alternate on
![]() $\gamma $
. We claim that the latter is not possible.
$\gamma $
. We claim that the latter is not possible.
Otherwise, we choose a lift
![]() $\alpha $
of
$\alpha $
of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
. Then
$\wp $
. Then
![]() $\alpha $
intersects the lines in
$\alpha $
intersects the lines in
![]() $\wp ^{-1}(\xi \cup \xi ')$
transversely, we have
$\wp ^{-1}(\xi \cup \xi ')$
transversely, we have
and the points in
![]() $\alpha \cap \wp ^{-1}(\xi )\ne \emptyset $
and
$\alpha \cap \wp ^{-1}(\xi )\ne \emptyset $
and
![]() $\alpha \cap \wp ^{-1}(\xi ')\ne \emptyset $
alternate on
$\alpha \cap \wp ^{-1}(\xi ')\ne \emptyset $
alternate on
![]() $\alpha $
. An argument very similar to the proof of Lemma A.4 then shows that
$\alpha $
. An argument very similar to the proof of Lemma A.4 then shows that
![]() $2k>0$
is the number of lines in the set
$2k>0$
is the number of lines in the set
![]() $\wp ^{-1}(\xi \cup \xi ')$
that separate
$\wp ^{-1}(\xi \cup \xi ')$
that separate
![]() $\alpha (0)$
from
$\alpha (0)$
from
![]() $\alpha (1)$
. However, we know that
$\alpha (1)$
. However, we know that
![]() ${\alpha (1)-\alpha (0)= 2 (s+ir)}$
, and so
${\alpha (1)-\alpha (0)= 2 (s+ir)}$
, and so
![]() $\alpha (1)$
and
$\alpha (1)$
and
![]() $\alpha (0)$
lie on a line with slope
$\alpha (0)$
lie on a line with slope
![]() $r/s$
and are not separated by any line in
$r/s$
and are not separated by any line in
![]() $\wp ^{-1}(\xi \cup \xi ')$
. This is a contradiction.
$\wp ^{-1}(\xi \cup \xi ')$
. This is a contradiction.
This shows that
![]() $\xi \cap \gamma =\emptyset =\xi '\cap \gamma $
. Now consider a simple closed geodesic
$\xi \cap \gamma =\emptyset =\xi '\cap \gamma $
. Now consider a simple closed geodesic
![]() ${\tau _{r/s}=\wp (\ell _{r/s}(t\widetilde \omega ))}$
with slope
${\tau _{r/s}=\wp (\ell _{r/s}(t\widetilde \omega ))}$
with slope
![]() $r/s$
and
$r/s$
and
![]() $0<t<1$
. Since
$0<t<1$
. Since
![]() $\xi \cap \gamma =\emptyset $
, we can choose t very close to
$\xi \cap \gamma =\emptyset $
, we can choose t very close to
![]() $0$
so that
$0$
so that
![]() $\tau _{r/s}\cap \gamma =\emptyset $
. Now we can apply considerations very similar to the proof of Corollary 3.5(ii). The complement of
$\tau _{r/s}\cap \gamma =\emptyset $
. Now we can apply considerations very similar to the proof of Corollary 3.5(ii). The complement of
![]() $\tau _{r/s} \cup \gamma $
in
$\tau _{r/s} \cup \gamma $
in
![]() $\mathbb {P}$
is a disjoint union
$\mathbb {P}$
is a disjoint union
![]() $\mathbb {P} \smallsetminus (\tau _{r/s} \cup \gamma )=W\cup U\cup W' $
, where
$\mathbb {P} \smallsetminus (\tau _{r/s} \cup \gamma )=W\cup U\cup W' $
, where
![]() $W,W'\subset \mathbb {P}$
are open Jordan regions and
$W,W'\subset \mathbb {P}$
are open Jordan regions and
![]() $U\subset \mathbb {P}$
is an annulus with
$U\subset \mathbb {P}$
is an annulus with
![]() $\partial U=\tau _{r/s} \cup \gamma $
. Since
$\partial U=\tau _{r/s} \cup \gamma $
. Since
![]() $\tau _{r/s}$
and
$\tau _{r/s}$
and
![]() $\gamma $
are essential, both W and
$\gamma $
are essential, both W and
![]() $W'$
must contain at least two points in V. Since
$W'$
must contain at least two points in V. Since
![]() $\#V=4$
, we have
$\#V=4$
, we have
![]() $U\cap V =\emptyset $
. Lemma 2.1 now implies that
$U\cap V =\emptyset $
. Lemma 2.1 now implies that
![]() $\tau _{r/s}$
and
$\tau _{r/s}$
and
![]() $\gamma $
are isotopic relative to V. By Lemma A.7, the curve
$\gamma $
are isotopic relative to V. By Lemma A.7, the curve
![]() $\gamma $
is actually isotopic to each closed geodesic
$\gamma $
is actually isotopic to each closed geodesic
![]() $\tau _{r/s}$
with slope
$\tau _{r/s}$
with slope
![]() $r/s$
.
$r/s$
.
The map
![]() $[\gamma ]\mapsto r/s$
that sends each isotopy class
$[\gamma ]\mapsto r/s$
that sends each isotopy class
![]() $[\gamma ]$
to a slope
$[\gamma ]$
to a slope
![]() $r/s\in \widehat {\mathbb {Q}}$
obtained from a primitive element in
$r/s\in \widehat {\mathbb {Q}}$
obtained from a primitive element in
![]() $2\mathbb {Z}^2$
associated with
$2\mathbb {Z}^2$
associated with
![]() $[\gamma ]$
according to Lemma A.6 is well defined. It is clear that it is surjective, because the isotopy class
$[\gamma ]$
according to Lemma A.6 is well defined. It is clear that it is surjective, because the isotopy class
![]() $[\tau _{r/s}]$
of a geodesic
$[\tau _{r/s}]$
of a geodesic
![]() $\tau _{r/s}$
with slope
$\tau _{r/s}$
with slope
![]() $r/s\in \widehat {\mathbb {Q}}$
is sent to
$r/s\in \widehat {\mathbb {Q}}$
is sent to
![]() $r/s$
. To see that it is injective, suppose two isotopy classes
$r/s$
. To see that it is injective, suppose two isotopy classes
![]() $[\gamma ]$
and
$[\gamma ]$
and
![]() $[\gamma ']$
are sent to the same slope
$[\gamma ']$
are sent to the same slope
![]() $r/s\in \widehat {\mathbb {Q}}$
by this map. If
$r/s\in \widehat {\mathbb {Q}}$
by this map. If
![]() $\tau _{r/s}$
is a closed geodesic with slope
$\tau _{r/s}$
is a closed geodesic with slope
![]() $r/s$
, then by our previous discussion, we have
$r/s$
, then by our previous discussion, we have
![]() $ \gamma \sim \tau _{r/s}\sim \gamma '$
relative to V. Hence,
$ \gamma \sim \tau _{r/s}\sim \gamma '$
relative to V. Hence,
![]() $[\gamma ]=[\gamma ']$
. It follows that the map
$[\gamma ]=[\gamma ']$
. It follows that the map
![]() $[\gamma ]\mapsto r/s$
is indeed a bijection.
$[\gamma ]\mapsto r/s$
is indeed a bijection.
Remark A.8. Suppose
![]() $\gamma $
is an essential Jordan curve in
$\gamma $
is an essential Jordan curve in
![]() $(\mathbb {P},V)$
and its isotopy class
$(\mathbb {P},V)$
and its isotopy class
![]() $[\gamma ]$
relative to V corresponds to slope
$[\gamma ]$
relative to V corresponds to slope
![]() $r/s\in \widehat {\mathbb {Q}}$
according to Lemma 2.3. Let
$r/s\in \widehat {\mathbb {Q}}$
according to Lemma 2.3. Let
![]() $\beta \colon \mathbb {I} \rightarrow \gamma $
be a parameterization of
$\beta \colon \mathbb {I} \rightarrow \gamma $
be a parameterization of
![]() $\gamma $
as a simple loop, and
$\gamma $
as a simple loop, and
![]() $\alpha \colon \mathbb {I}\rightarrow \mathbb {C}$
be a lift of
$\alpha \colon \mathbb {I}\rightarrow \mathbb {C}$
be a lift of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
. Then equation (A.4) in the proof of Lemma A.6 shows that we always have
$\wp $
. Then equation (A.4) in the proof of Lemma A.6 shows that we always have
![]() $\alpha (1)-\alpha (0)=\pm 2(s+ir)$
.
$\alpha (1)-\alpha (0)=\pm 2(s+ir)$
.
A similar statement is true for arcs in
![]() $(\mathbb {P}, V)$
.
$(\mathbb {P}, V)$
.
Corollary A.9. Let
![]() $\xi $
be an arc in
$\xi $
be an arc in
![]() $(\mathbb {P}, V)$
. Then
$(\mathbb {P}, V)$
. Then
![]() $\xi $
is isotopic relative to V to a geodesic arc
$\xi $
is isotopic relative to V to a geodesic arc
![]() $\xi _{r/s}$
for some slope
$\xi _{r/s}$
for some slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. Moreover, if
$r/s\in \widehat {\mathbb {Q}}$
. Moreover, if
![]() $\beta \colon \mathbb {I}\rightarrow \xi $
is a homeomorphic parameterization of
$\beta \colon \mathbb {I}\rightarrow \xi $
is a homeomorphic parameterization of
![]() $\xi $
and
$\xi $
and
![]() $\alpha $
is any lift of
$\alpha $
is any lift of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
, then
$\wp $
, then
![]() $\alpha (1)-\alpha (0)=\pm (s+ir)$
.
$\alpha (1)-\alpha (0)=\pm (s+ir)$
.
Proof. The arc
![]() $\xi $
joins two of the points in V, while the other two points in V do not lie on
$\xi $
joins two of the points in V, while the other two points in V do not lie on
![]() $\xi $
. Hence, we may ‘surround’
$\xi $
. Hence, we may ‘surround’
![]() $\xi $
by an essential Jordan curve
$\xi $
by an essential Jordan curve
![]() $\gamma $
in
$\gamma $
in
![]() $(\mathbb {P}, V)$
such that
$(\mathbb {P}, V)$
such that
![]() $\xi $
is a core arc of
$\xi $
is a core arc of
![]() $\gamma $
. By Lemma 2.3, we know that
$\gamma $
. By Lemma 2.3, we know that
![]() $\gamma $
is isotopic relative to V to a closed geodesic
$\gamma $
is isotopic relative to V to a closed geodesic
![]() $\tau _{r/s}$
in
$\tau _{r/s}$
in
![]() $\mathbb {P}$
with some slope
$\mathbb {P}$
with some slope
![]() $r/s\in \widehat {\mathbb {Q}}$
. Hence,
$r/s\in \widehat {\mathbb {Q}}$
. Hence,
![]() $\xi $
is isotopic relative to V to a core arc
$\xi $
is isotopic relative to V to a core arc
![]() $\xi '$
of
$\xi '$
of
![]() $\tau _{r/s}$
.
$\tau _{r/s}$
.
Now any two arcs in the interior of a closed topological disk D with the same endpoints are isotopic by an isotopy that fixes the endpoints of these arcs and the points in
![]() $\partial D$
(see [Reference BuserBus10, Theorem A.6(ii)]). This implies that any two core arcs of an essential Jordan curve in
$\partial D$
(see [Reference BuserBus10, Theorem A.6(ii)]). This implies that any two core arcs of an essential Jordan curve in
![]() $(\mathbb {P}, V)$
are isotopic relative to V if the core arcs have the same endpoints. We know that the closed geodesic
$(\mathbb {P}, V)$
are isotopic relative to V if the core arcs have the same endpoints. We know that the closed geodesic
![]() $\tau _{r/s}$
has precisely two geodesic arcs with slope
$\tau _{r/s}$
has precisely two geodesic arcs with slope
![]() $r/s$
as core arcs in different components of
$r/s$
as core arcs in different components of
![]() $\mathbb {P}\smallsetminus \tau _{r/s}$
. Therefore,
$\mathbb {P}\smallsetminus \tau _{r/s}$
. Therefore,
![]() $\xi '$
, and hence also
$\xi '$
, and hence also
![]() $\xi $
, is isotopic relative to V to a geodesic arc
$\xi $
, is isotopic relative to V to a geodesic arc
![]() $\xi _{r/s}$
with slope
$\xi _{r/s}$
with slope
![]() $r/s$
. This proves the first part of the statement.
$r/s$
. This proves the first part of the statement.
Let
![]() $\beta \colon \mathbb {I} \rightarrow \xi $
be a homeomorphic parameterization of
$\beta \colon \mathbb {I} \rightarrow \xi $
be a homeomorphic parameterization of
![]() $\xi $
and
$\xi $
and
![]() $\alpha \colon \mathbb {I} \rightarrow \mathbb {C}$
be a lift of
$\alpha \colon \mathbb {I} \rightarrow \mathbb {C}$
be a lift of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
. By what we have seen, we can choose an isotopy
$\wp $
. By what we have seen, we can choose an isotopy
![]() $H\colon \mathbb {P}\times \mathbb {I}\rightarrow \mathbb {P}$
relative to V with
$H\colon \mathbb {P}\times \mathbb {I}\rightarrow \mathbb {P}$
relative to V with
![]() $H_0=\operatorname {id}_{\mathbb {P}}$
and
$H_0=\operatorname {id}_{\mathbb {P}}$
and
![]() $H_1(\xi )=\xi _{r/s}$
. We use this to define a homotopy
$H_1(\xi )=\xi _{r/s}$
. We use this to define a homotopy
![]() $\overline H\colon \mathbb {I}\times \mathbb {I}\rightarrow \mathbb {P}$
by setting
$\overline H\colon \mathbb {I}\times \mathbb {I}\rightarrow \mathbb {P}$
by setting
for
![]() $u,t\in \mathbb {I}$
. Note that
$u,t\in \mathbb {I}$
. Note that
![]() $ \overline H_t$
for
$ \overline H_t$
for
![]() $t\in \mathbb {I}$
gives a homeomorphic parameterization of an arc in
$t\in \mathbb {I}$
gives a homeomorphic parameterization of an arc in
![]() $(\mathbb {P}, V)$
. These arcs have all the same endpoints. In particular,
$(\mathbb {P}, V)$
. These arcs have all the same endpoints. In particular, ![]() gives a homeomorphic parameterization of
gives a homeomorphic parameterization of
![]() $H_1(\xi )=\xi _{r/s}$
.
$H_1(\xi )=\xi _{r/s}$
.
We can lift
![]() $ \overline H_t$
under
$ \overline H_t$
under
![]() $\wp $
to find a homotopy
$\wp $
to find a homotopy
![]() $\widetilde H\colon \mathbb {I}\times \mathbb {I} \rightarrow \mathbb {C}$
such that
$\widetilde H\colon \mathbb {I}\times \mathbb {I} \rightarrow \mathbb {C}$
such that
![]() $\widetilde H_0=\alpha $
and
$\widetilde H_0=\alpha $
and
![]() $\wp \circ \widetilde H_t=\overline H_t$
for all
$\wp \circ \widetilde H_t=\overline H_t$
for all
![]() $t\in \mathbb {I}$
. To see this, one first applies the standard homotopy lifting theorem (see [Reference HatcherHat02, Proposition 1.30]) to the homotopy
$t\in \mathbb {I}$
. To see this, one first applies the standard homotopy lifting theorem (see [Reference HatcherHat02, Proposition 1.30]) to the homotopy
![]() $\overline H$
restricted
$\overline H$
restricted
![]() $(0,1)\times \mathbb {I}$
and the covering map
$(0,1)\times \mathbb {I}$
and the covering map
![]() $\wp \colon \mathbb {C}\smallsetminus \mathbb {Z}^2\rightarrow \mathbb {P}\smallsetminus V\supset \overline H((0,1)\times \mathbb {I})$
to obtain a unique homotopy
$\wp \colon \mathbb {C}\smallsetminus \mathbb {Z}^2\rightarrow \mathbb {P}\smallsetminus V\supset \overline H((0,1)\times \mathbb {I})$
to obtain a unique homotopy
![]() $\widetilde H\colon (0,1)\times \mathbb {I}\rightarrow \mathbb {C}$
with
$\widetilde H\colon (0,1)\times \mathbb {I}\rightarrow \mathbb {C}$
with
![]() $\widetilde H_0=\alpha |(0,1)$
. Now as
$\widetilde H_0=\alpha |(0,1)$
. Now as
![]() $u_0\to 0^+$
, the set
$u_0\to 0^+$
, the set
![]() $\overline H((0,u_0]\times \mathbb {I})$
shrinks to the point
$\overline H((0,u_0]\times \mathbb {I})$
shrinks to the point
![]() $\beta (0)\in V$
, and so the connected set
$\beta (0)\in V$
, and so the connected set
![]() $\widetilde H((0,u_0]\times \mathbb {I})$
shrinks to a unique point in
$\widetilde H((0,u_0]\times \mathbb {I})$
shrinks to a unique point in
![]() $\wp ^{-1}(V)=\mathbb {Z}^2$
. This point can only be
$\wp ^{-1}(V)=\mathbb {Z}^2$
. This point can only be
![]() $\alpha (0)$
. Hence,
$\alpha (0)$
. Hence,
![]() $\overline H(u,t)\to \alpha (0)$
uniformly for
$\overline H(u,t)\to \alpha (0)$
uniformly for
![]() $t\in \mathbb {I}$
as
$t\in \mathbb {I}$
as
![]() $u\to 0^+$
, and similarly
$u\to 0^+$
, and similarly
![]() $\overline H(u,t)\to \alpha (1)$
uniformly for
$\overline H(u,t)\to \alpha (1)$
uniformly for
![]() $t\in \mathbb {I}$
as
$t\in \mathbb {I}$
as
![]() $u\to 1^-$
. This implies that we can continuously extend
$u\to 1^-$
. This implies that we can continuously extend
![]() $\widetilde H$
to a homotopy on
$\widetilde H$
to a homotopy on
![]() $\mathbb {I}\times \mathbb {I}$
with the desired properties by setting
$\mathbb {I}\times \mathbb {I}$
with the desired properties by setting
![]() $\widetilde H(0,t)=\alpha (0)$
and
$\widetilde H(0,t)=\alpha (0)$
and
![]() $\widetilde H(1,t)=\alpha (1)$
for
$\widetilde H(1,t)=\alpha (1)$
for
![]() $t\in \mathbb {I}$
.
$t\in \mathbb {I}$
.
Then ![]() is a lift of
is a lift of
![]() $\beta '$
, because
$\beta '$
, because
![]() $\wp \circ \alpha '= \wp \circ \widetilde H_1 =\overline H_1=\beta '$
. Since
$\wp \circ \alpha '= \wp \circ \widetilde H_1 =\overline H_1=\beta '$
. Since
![]() $\beta '$
is a homeomorphic parameterization of the geodesic arc
$\beta '$
is a homeomorphic parameterization of the geodesic arc
![]() $\xi _{r/s}$
, the path
$\xi _{r/s}$
, the path
![]() $\alpha '$
sends
$\alpha '$
sends
![]() $\mathbb {I}$
homeomorphically onto a subsegment of a line
$\mathbb {I}$
homeomorphically onto a subsegment of a line
![]() $\ell _{r/s}\subset \mathbb {C}$
. Since
$\ell _{r/s}\subset \mathbb {C}$
. Since
![]() $\alpha '$
has its endpoints in
$\alpha '$
has its endpoints in
![]() $\mathbb {Z}^2$
and
$\mathbb {Z}^2$
and
![]() $\alpha '((0,1))$
is disjoint from
$\alpha '((0,1))$
is disjoint from
![]() $\mathbb {Z}^2$
, this implies
$\mathbb {Z}^2$
, this implies
![]() $\alpha '(1)-\alpha '(0)=\pm (s+ir)$
. Since
$\alpha '(1)-\alpha '(0)=\pm (s+ir)$
. Since
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
have the same endpoints, the statement follows.
$\alpha '$
have the same endpoints, the statement follows.
Proof of Lemma 2.4
In the proof all isotopies, isotopy classes, intersection numbers, etc. are for isotopies on
![]() $\mathbb {P}$
relative to V. We will use the facts about the geodesics on
$\mathbb {P}$
relative to V. We will use the facts about the geodesics on
![]() $(\mathbb {P}, V)$
discussed before Lemma A.7 without further reference.
$(\mathbb {P}, V)$
discussed before Lemma A.7 without further reference.
(i) Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be essential Jordan curves in
$\beta $
be essential Jordan curves in
![]() $(\mathbb {P},V)$
as in the statement. As before, we define
$(\mathbb {P},V)$
as in the statement. As before, we define
![]() $\omega =s+ir$
and
$\omega =s+ir$
and
![]() $\widetilde \omega =-p+iq$
, where
$\widetilde \omega =-p+iq$
, where
![]() $p,q\in \mathbb {Z}$
and
$p,q\in \mathbb {Z}$
and
![]() $pr+qs=1$
.
$pr+qs=1$
.
First suppose that
![]() $r/s=r'/s'$
. Then in the isotopy class
$r/s=r'/s'$
. Then in the isotopy class
![]() $[\alpha ]=[\beta ]$
, we can find simple closed geodesics with slope
$[\alpha ]=[\beta ]$
, we can find simple closed geodesics with slope
![]() $r/s$
that are disjoint, for example, the curves
$r/s$
that are disjoint, for example, the curves
![]() ${\tau _{r/s} =\wp (\ell _{r/s}(\widetilde \omega /3))}$
and
${\tau _{r/s} =\wp (\ell _{r/s}(\widetilde \omega /3))}$
and
![]() $\tau ^{\prime }_{r/s} =\wp (\ell _{r/s}(2\widetilde \omega /3))$
. It follows that
$\tau ^{\prime }_{r/s} =\wp (\ell _{r/s}(2\widetilde \omega /3))$
. It follows that
![]() $\mathrm {i}(\alpha , \beta )=0$
in this case.
$\mathrm {i}(\alpha , \beta )=0$
in this case.
We now assume that
![]() $r/s\ne r'/s'$
. To determine
$r/s\ne r'/s'$
. To determine
![]() $\mathrm {i}(\alpha , \beta )$
, we have to find the minimum of all numbers
$\mathrm {i}(\alpha , \beta )$
, we have to find the minimum of all numbers
![]() $\#(\alpha \cap \beta )$
, where
$\#(\alpha \cap \beta )$
, where
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
range over the given isotopy classes. By applying a suitable isotopy, we can reduce to the case where
$\beta $
range over the given isotopy classes. By applying a suitable isotopy, we can reduce to the case where
![]() $\alpha $
is a fixed curve in its isotopy class and we only have to take variations over
$\alpha $
is a fixed curve in its isotopy class and we only have to take variations over
![]() $\beta $
. So by Lemma 2.3, we may assume that
$\beta $
. So by Lemma 2.3, we may assume that
![]() ${\alpha =\tau _{r/s}=\wp (\ell _{r/s})}$
is a simple closed geodesic as in the statement. Then
${\alpha =\tau _{r/s}=\wp (\ell _{r/s})}$
is a simple closed geodesic as in the statement. Then
![]() $\tau _{r/s}= \wp (\ell _{r/s}(t_0\widetilde \omega ))$
for some
$\tau _{r/s}= \wp (\ell _{r/s}(t_0\widetilde \omega ))$
for some
![]() $t_0\in (0,1)$
. The preimage
$t_0\in (0,1)$
. The preimage
![]() $\wp ^{-1}(\tau _{r/s})$
of
$\wp ^{-1}(\tau _{r/s})$
of
![]() $\tau _{r/s}$
under
$\tau _{r/s}$
under
![]() $\wp $
consists of the two disjoint families
$\wp $
consists of the two disjoint families
of distinct lines with slope
![]() $r/s$
.
$r/s$
.
Now let
![]() $\widetilde \beta \colon \mathbb {I}\rightarrow \mathbb {C}$
be a lift of
$\widetilde \beta \colon \mathbb {I}\rightarrow \mathbb {C}$
be a lift of
![]() $\beta $
under
$\beta $
under
![]() $\wp $
, where we think of
$\wp $
, where we think of
![]() $\beta $
as a simple closed loop in a parameterization with suitable orientation. Then if
$\beta $
as a simple closed loop in a parameterization with suitable orientation. Then if ![]() and
and ![]() , we have
, we have
![]() $w_0-z_0=2(s'+ir')$
as follows from Remark A.8. By changing the basepoint of
$w_0-z_0=2(s'+ir')$
as follows from Remark A.8. By changing the basepoint of
![]() $\beta $
if necessary, we may assume that
$\beta $
if necessary, we may assume that
![]() $\widetilde \beta (0),\widetilde \beta (1)\not \in \wp ^{-1}(\tau _{r/s})$
. If
$\widetilde \beta (0),\widetilde \beta (1)\not \in \wp ^{-1}(\tau _{r/s})$
. If ![]() , then we can write
, then we can write
![]() $\omega '$
uniquely in the form
$\omega '$
uniquely in the form
where
![]() $k,n\in \mathbb {Z}$
. Note that then,
$k,n\in \mathbb {Z}$
. Note that then, ![]() (to see this, multiply equation (A.6) by the complex conjugate of
(to see this, multiply equation (A.6) by the complex conjugate of
![]() $\omega $
and take imaginary parts).
$\omega $
and take imaginary parts).
Now each family
![]() $\mathcal {F}_j$
,
$\mathcal {F}_j$
,
![]() $j=1, 2$
, consists of equally spaced parallel lines with slope
$j=1, 2$
, consists of equally spaced parallel lines with slope
![]() $r/s$
such that consecutive lines in each family differ by a translation by
$r/s$
such that consecutive lines in each family differ by a translation by
![]() $2\widetilde \omega $
. This implies that the points
$2\widetilde \omega $
. This implies that the points
![]() $z_0$
and
$z_0$
and
![]() $w_0=z_0+2\omega '$
are separated by precisely N lines from each of the families
$w_0=z_0+2\omega '$
are separated by precisely N lines from each of the families
![]() $\mathcal {F}_j$
,
$\mathcal {F}_j$
,
![]() $j=1, 2$
. So
$j=1, 2$
. So
![]() $\widetilde \beta $
must have at least
$\widetilde \beta $
must have at least
![]() $2N$
points in common with
$2N$
points in common with
![]() $\wp ^{-1}(\tau _{r/s})$
. Since
$\wp ^{-1}(\tau _{r/s})$
. Since
![]() $\wp \circ \widetilde \beta $
maps
$\wp \circ \widetilde \beta $
maps
![]() $[0,1)$
injectively onto
$[0,1)$
injectively onto
![]() $\beta $
, we conclude that
$\beta $
, we conclude that
![]() $\beta =\wp (\widetilde \beta )$
has at least
$\beta =\wp (\widetilde \beta )$
has at least
![]() $2N$
points in common with
$2N$
points in common with
![]() $\tau _{r/s}$
. If
$\tau _{r/s}$
. If
![]() $\beta =\tau _{r'/s'}$
, then
$\beta =\tau _{r'/s'}$
, then
![]() $\widetilde \beta $
is a parameterization of the line segment
$\widetilde \beta $
is a parameterization of the line segment
![]() $[z_0, w_0]$
, and so
$[z_0, w_0]$
, and so
![]() $\widetilde \beta $
meets
$\widetilde \beta $
meets
![]() $\wp ^{-1}(\tau _{r/s})$
in precisely
$\wp ^{-1}(\tau _{r/s})$
in precisely
![]() $2N$
points. This means that
$2N$
points. This means that
![]() $\tau _{r/s}$
and
$\tau _{r/s}$
and
![]() $\tau _{r'/s'}$
have exactly
$\tau _{r'/s'}$
have exactly
![]() $2N$
points in common.
$2N$
points in common.
It follows that for all
![]() $\beta $
, we have
$\beta $
, we have
and so
![]() $ 2N\le \mathrm {i}(\alpha ,\beta )\le \#(\tau _{r/s}\cap \tau _{r'/s'})=2N. $
Thus, we have equality here and the statement follows.
$ 2N\le \mathrm {i}(\alpha ,\beta )\le \#(\tau _{r/s}\cap \tau _{r'/s'})=2N. $
Thus, we have equality here and the statement follows.
(ii) This is a variant of the argument in statement (i) and we use the same notation.
Since
![]() $\beta \sim \tau _{r'/s'}$
, the core arc
$\beta \sim \tau _{r'/s'}$
, the core arc
![]() $\xi $
of
$\xi $
of
![]() $\beta $
is isotopic to a core arc of
$\beta $
is isotopic to a core arc of
![]() $ \tau _{r'/s'}$
. Now two core arcs of a given essential Jordan curve in
$ \tau _{r'/s'}$
. Now two core arcs of a given essential Jordan curve in
![]() $(\mathbb {P}, V)$
are isotopic relative to V if they have the same endpoints (this was pointed out in the proof of Corollary A.9). It follows that
$(\mathbb {P}, V)$
are isotopic relative to V if they have the same endpoints (this was pointed out in the proof of Corollary A.9). It follows that
![]() $\xi \sim \xi ^{\prime }_{r'/s'}$
, where
$\xi \sim \xi ^{\prime }_{r'/s'}$
, where
![]() $\xi ^{\prime }_{r'/s'}$
is one of the two geodesic core arcs of
$\xi ^{\prime }_{r'/s'}$
is one of the two geodesic core arcs of
![]() $ \tau _{r'/s'}$
. In particular,
$ \tau _{r'/s'}$
. In particular,
![]() $\xi ^{\prime }_{r'/s'}=\wp (\ell _{r'/s'})$
for a line
$\xi ^{\prime }_{r'/s'}=\wp (\ell _{r'/s'})$
for a line
![]() $\ell _{r'/s'}\subset \mathbb {C}$
that contains a point in
$\ell _{r'/s'}\subset \mathbb {C}$
that contains a point in
![]() $\mathbb {Z}^2$
. Note that
$\mathbb {Z}^2$
. Note that
![]() $\xi ^{\prime }_{r'/s'}$
possibly differs from the geodesic arc
$\xi ^{\prime }_{r'/s'}$
possibly differs from the geodesic arc
![]() $\xi _{r'/s'}$
as in the statement (if
$\xi _{r'/s'}$
as in the statement (if
![]() $\xi ^{\prime }_{r'/s'}$
and
$\xi ^{\prime }_{r'/s'}$
and
![]() $\xi _{r'/s'}$
lie in different components of
$\xi _{r'/s'}$
lie in different components of
![]() $\mathbb {P}\smallsetminus \tau _{r'/s'}$
).
$\mathbb {P}\smallsetminus \tau _{r'/s'}$
).
If
![]() $\widetilde \xi \colon \mathbb {I}\rightarrow \mathbb {C}$
is a lift of
$\widetilde \xi \colon \mathbb {I}\rightarrow \mathbb {C}$
is a lift of
![]() $\xi $
under
$\xi $
under
![]() $\wp $
in suitable orientation, and
$\wp $
in suitable orientation, and ![]() ,
, ![]() , then it follows from Corollary A.9 that
, then it follows from Corollary A.9 that
![]() $w_1-z_1=\omega '=s'+ir'$
. Now equation (A.6) implies that there are exactly
$w_1-z_1=\omega '=s'+ir'$
. Now equation (A.6) implies that there are exactly
![]() $N=|n|= |rs'-sr'|$
lines in
$N=|n|= |rs'-sr'|$
lines in
![]() $ \mathcal {F}_1\cup \mathcal {F}_2$
that separate
$ \mathcal {F}_1\cup \mathcal {F}_2$
that separate
![]() $z_1$
and
$z_1$
and
![]() $w_1$
(essentially, this follows from the fact that the set
$w_1$
(essentially, this follows from the fact that the set
![]() $[0,n]\cap \{2j\pm t_0:j\in \mathbb {Z}\}$
, where
$[0,n]\cap \{2j\pm t_0:j\in \mathbb {Z}\}$
, where
![]() $t_0\in (0,1)$
, contains precisely
$t_0\in (0,1)$
, contains precisely
![]() $N=|n|$
points).
$N=|n|$
points).
Let ![]() , where
, where
![]() $p',q'\in \mathbb {Z}$
and
$p',q'\in \mathbb {Z}$
and
![]() $p'r'+q's'=1$
. Then, by the discussion before Lemma A.7, the map
$p'r'+q's'=1$
. Then, by the discussion before Lemma A.7, the map
![]() $\wp $
sends one of the segments
$\wp $
sends one of the segments
![]() $[z_1, w_1]$
and
$[z_1, w_1]$
and
![]() ${[z_1+\widetilde \omega ', w_1+ \widetilde \omega ']}$
homeomorphically onto
${[z_1+\widetilde \omega ', w_1+ \widetilde \omega ']}$
homeomorphically onto
![]() $\xi _{r'/s'}$
depending on whether
$\xi _{r'/s'}$
depending on whether
![]() $\xi ^{\prime }_{r'/s'}= \xi _{r'/s'}$
or
$\xi ^{\prime }_{r'/s'}= \xi _{r'/s'}$
or
![]() $\xi ^{\prime }_{r'/s'}\ne \xi _{r'/s'}$
, respectively. In either case, each segment meets exactly N lines in
$\xi ^{\prime }_{r'/s'}\ne \xi _{r'/s'}$
, respectively. In either case, each segment meets exactly N lines in
![]() $ \mathcal {F}_1\cup \mathcal {F}_2$
.
$ \mathcal {F}_1\cup \mathcal {F}_2$
.
Arguing as before, we see that
This leads to
![]() $ N\le \mathrm {i}(\alpha ,\xi )\le \#(\tau _{r/s}\cap \xi _{r'/s'})=N. $
So we have equality here and the statement follows.
$ N\le \mathrm {i}(\alpha ,\xi )\le \#(\tau _{r/s}\cap \xi _{r'/s'})=N. $
So we have equality here and the statement follows.
(iii)–(v) These are special cases of statements (i) and (ii). For example,
![]() $a=\wp (\mathbb {R}\times \{0\}) =\wp (\ell _0(0))$
is a core arc of
$a=\wp (\mathbb {R}\times \{0\}) =\wp (\ell _0(0))$
is a core arc of
![]() $\alpha ^h$
corresponding to slope
$\alpha ^h$
corresponding to slope
![]() $r'/s'=0/1=0$
. Hence, by statement (ii), we have
$r'/s'=0/1=0$
. Hence, by statement (ii), we have
The other statements follow from similar considerations.