Polyhedral Approximation of Spectrahedral Shadows via Homogenization

Abstract

This article is concerned with the problem of approximating a not necessarily bounded spectrahedral shadow, a certain convex set, by polyhedra. By identifying the set with its homogenization, the problem is reduced to the approximation of a closed convex cone. We introduce the notion of homogeneous $\delta$-approximation of a convex set and show that it defines a meaningful concept in the sense that approximations converge to the original set if the approximation error $\delta$ diminishes. Moreover, we show that a homogeneous $\delta$-approximation of the polar of a convex set is immediately available from an approximation of the set itself under mild conditions. Finally, we present an algorithm for the computation of homogeneous $\delta$-approximations of spectrahedral shadows and demonstrate it on examples.

1 Introduction

Polyhedral approximation of convex sets is a profound method in convex analysis with applications ranging through various branches of mathematics. In the 1903 article [21], Minkowski argues that every compact convex set in three-dimensional Euclidean space can be approximated arbitrarily well by polyhedra, i.e. intersections of finitely many closed halfspaces. Although it is not explicitly stated in the article, his line of argumentation also applies to general n-dimensional Euclidean spaces. This is later mentioned by Bonnesen and Fenchel in [4].

Since then, polyhedral approximation has been applied in mathematical programming, in particular in multiple objective optimization, see, for example, [9, 20, 28], in approximation methods for general convex optimization problems [2, 27] and for mixed-integer convex programmes [19, 30]. Other areas of application include machine learning [11, 31] and large deviation probability theory [23].

In [17], Kamenev introduces a class of approximation algorithms that compute outer and inner polyhedral approximations of a compact convex set called cutting and augmenting schemes, respectively, by iteratively improving upon a current approximation. The prevalent method of quantifying the approximation error in these algorithms is via the Hausdorff distance. Kamenev proves that under certain conditions the sequence of polyhedral approximations generated by such a scheme converges to the original set in the Hausdorff distance and derives explicit bounds for the Hausdorff distance between an approximation and the set to be approximated. These general schemes subsume many of the polyhedral approximation algorithms in the literature.

The literature concerned with polyhedral approximation of not necessarily bounded sets is scarce. The reason appears to be the fact that the Hausdorff distance only defines a metric on the family of nonempty compact subsets of $\mathbb {R}^n$ but not on the larger family of nonempty closed subsets. In fact, restrictive conditions need to be satisfied for polyhedral approximation of unbounded sets in the Hausdorff distance to be possible. For instance, the recession cones of the approximation and the original set need to coincide, which limits approximation to sets with polyhedral recession cones. A characterization of those sets that are approximable by polyhedra in the Hausdorff distance is due to Ney and Robinson [23]. Similar results are obtained in [26] in the context of convex multiple objective optimization. Evidently, the Hausdorff distance is no suitable measure of approximation quality in the unbounded case. One of the authors recently introduced the notion of $(\varepsilon ,\delta )$-approximation, a concept of polyhedral outer approximation of closed convex sets containing no lines, see [6]. One feature is that these approximations bound the so-called truncated Hausdorff distance, a metric on the family of closed cones in $\mathbb {R}^n$, between the recession cones, but allow them to differ. Here, we present another notion of polyhedral approximation that is not limited to outer approximation, applicable to a larger class of sets and exhibits elegant behaviour under polarity not present for $(\varepsilon ,\delta )$-approximations. These approximations, denoted homogeneous $\delta$-approximations, are motivated by the fact that every closed convex set in $\mathbb {R}^n$ can be identified with a closed convex cone in $\mathbb {R}^{n+1}$, called its homogenization, and that it can also be recovered therefrom. They are defined via the truncated Hausdorff distance between the homogenizations of the approximation and the original set.

This article is structured as follows. In the next section, we introduce necessary notation and basic definitions. Section 3 presents the notion of homogeneous $\delta$-approximation for the polyhedral approximation of a convex set C. We show that homogeneous $\delta$-approximations converge to ${{\,\textrm{cl}\,}}C$ in the sense of Painlevé–Kuratowski if the approximation error $\delta$ tends to zero. Moreover, we prove that a polyhedron P is a homogeneous $\delta$-approximation of C given that the Hausdorff distance between P and C is finite and compute the approximation error $\delta$ in terms of this distance. This shows that the concept of homogeneous $\delta$-approximation is more general than polyhedral approximation with respect to the Hausdorff distance. Finally, we investigate the behaviour of homogeneous $\delta$-approximations under polarity and show that a homogeneous $\delta$-approximation of the polar set ${C}^{\circ }$ can be obtained from a homogeneous $\delta$-approximation of C under mild assumptions. In the last section, an algorithm for the computation of outer and inner homogeneous $\delta$-approximations for a special class of convex sets called spectrahedral shadows is presented. These sets are the images of spectrahedra, the feasible regions of semidefinite programmes, under linear transformations and are special in the sense that their homogenizations can easily be described explicitly as spectrahedral shadows at least up to closure. The algorithm is based on a recently presented algorithm for the computation of polyhedral approximations of the recession cone of a spectrahedral shadow, see [8]. Two examples illustrating the algorithm are presented.

2 Preliminaries

Given a set $C \subseteq \mathbb {R}^n$, we denote by ${{\,\textrm{cl}\,}}C$, ${{\,\textrm{int}\,}}C$ and ${{\,\textrm{conv}\,}}C$ the closure, interior and convex hull of C, respectively. The Euclidean unit ball of appropriate dimension is written as B. A nonempty set C is called a cone if $\mu x \in C$ for every $x \in C$ and $\mu \geqslant 0$, i.e. C is closed under nonnegative scalar multiplication. For convex C, its recession cone is , denoted by $0^{\infty }{C}$. If $x \in {{\,\textrm{cl}\,}}C$, then , see [24, Theorem 8.3]. The smallest, with respect to inclusion, convex cone containing C is called the conical hull of C and written ${{\,\textrm{cone}\,}}C$. We use the convention . Furthermore, a point $x \in C$ is called an extreme point of C if is convex. The set of extreme points of C is written ${{\,\textrm{ext}\,}}C$. We denote the hyperplane with normal vector $\omega \in \mathbb {R}^n$ and offset $\gamma \in \mathbb {R}$ by $H(\omega , \gamma )$, i.e. , and the lower closed halfspace by $H^-(\omega ,\gamma )$. A polyhedron $P \subseteq \mathbb {R}^n$ is the intersection of finitely many such halfspaces. Its extreme points are called vertices and are denoted by ${{\,\textrm{vert}\,}}P$. According to the well-known Weyl–Minkowski theorem, see [13, Theorem 14.3], every polyhedron can alternatively be expressed as the Minkowski sum of the convex hull of finitely many points and the conical hull of finitely many directions, i.e. for suitable $v_1,\dots ,v_m \in \mathbb {R}^n$ and . The polar ${C}^{\circ }$ and polar cone ${C}^*$ of C are defined as for $\gamma =1$ and $\gamma =0$, respectively. It is easily verified that ${\left( {{\,\textrm{cone}\,}}C\right) }^{\circ }={C}^*$.

We define as the Euclidean distance between x and C. If C is closed and convex, the infimum is uniquely attained, see, for example, [15]. In this case, the point at which the infimum is attained is called the projection of x onto C and denoted by . Now, the Hausdorff distance between sets $C_1, C_2 \subseteq \mathbb {R}^n$ is then expressed as

The function $d_{\textsf{H}}$ defines a metric on the class of nonempty compact subsets of $\mathbb {R}^n$. For convex cones $K_1, K_2 \subseteq \mathbb {R}^n$, the truncated Hausdorff distance between $K_1$ and $K_2$, denoted $d_{\textsf{tH}}\left( {K_1},{K_2}\right)$, is defined as

$$ d_{\textsf{H}}\left( {K_1 \cap B},{K_2 \cap B}\right) . $$

That is, it is the usual Hausdorff distance between $K_1$ and $K_2$ restricted to B. Since cones contain the origin, $d_{\textsf{tH}}\left( {K_1},{K_2}\right) \leqslant 1$ always holds. The truncated Hausdorff distance provides a metric on the class of closed convex cones in $\mathbb {R}^n$, see [29].

3 Approximation Concept for Convex Sets

In this section, we present a concept of polyhedral approximation of a convex set $C \subseteq \mathbb {R}^n$ that need not be bounded. The truncated Hausdorff distance being a metric between closed convex cones is the motivation for our approach. In order to work in a conic setting, we assign to C a convex cone from $\mathbb {R}^{n+1}$ called its homogenization.

Definition 3.1

Let $C \subseteq \mathbb {R}^n$ be a convex set. The homogenization or conification of C, denoted ${{\,\textrm{homog}\,}}{C}$, is the cone

Every closed convex set $C \subseteq \mathbb {R}^n$ can be identified with its homogenization because C can be recovered from ${{\,\textrm{homog}\,}}{C}$. In particular,

(1)

i.e. intersecting ${{\,\textrm{homog}\,}}{C}$ with the hyperplane $H(e_{n+1},1) = \{x \in \mathbb {R}^{n+1} \mid x_{n+1}=1\}$ and projecting the result onto the first n variables yield the original set C. In the general case, the right-hand side set in Equation (1) equals ${{\,\textrm{cl}\,}}C$ because ${{\,\textrm{homog}\,}}{C} = {{\,\textrm{homog}\,}}{{{\,\textrm{cl}\,}}C}$, cf. Proposition 3.8. Thus, we can identify convex sets with their homogenizations up to closures. Using this correspondence, one can work with convex cones entirely. This is a standard tool in convex analysis to study problems in a conic framework, see, for example, [5, 24, 25]. Here, we use it to reduce the problem of approximating convex sets to the problem of approximating convex cones.

Definition 3.2

For a convex set $C \subseteq \mathbb {R}^n$ and $\delta \geqslant 0$, a polyhedron $P \subseteq \mathbb {R}^n$ is called a homogeneous $\delta$-approximation of C if

$$ d_{\textsf{tH}}\left( {{{\,\textrm{homog}\,}}{P}},{{{\,\textrm{homog}\,}}{C}}\right) \leqslant \delta . $$

Clearly, if P is a homogeneous $\delta$-approximation of C, it is also one of ${{\,\textrm{cl}\,}}C$ because ${{\,\textrm{homog}\,}}{C}={{\,\textrm{homog}\,}}{{{\,\textrm{cl}\,}}C}$. The notion of homogeneous $\delta$-approximation can be understood as a relative error measure between the involved sets. Consider a convex set $C \subseteq \mathbb {R}^n$ and a polyhedron $P \subseteq \mathbb {R}^n$. If $x \in P$ with $d\left( {x},{C}\right) \leqslant \varepsilon$, then the distance of the corresponding direction of ${{\,\textrm{homog}\,}}{P}$ to ${{\,\textrm{homog}\,}}{C}$ obeys the relation

In particular, the distance depends inversely on $\left\Vert {x} \right\Vert$. Hence, if P is a homogeneous $\delta$-approximation of C, then points of one set that are far from the origin are allowed a larger distance to the other set than points closer to the origin.

This observation is explained from the fact that the distinction between points and directions of a closed convex set C collapses when transitioning to its homogenization. One has the identity

(2)

see [24, Theorem 8.2], i.e. points as well as directions of C correspond to directions of ${{\,\textrm{homog}\,}}{C}$. Thus, a convergent sequence of directions of ${{\,\textrm{homog}\,}}{C}$ does not necessarily yield a convergent sequence in C itself. For instance, if converges to a direction $(\bar{x},0)^{\textsf{T}}$ and provided all $\mu _k$ are positive, then the sequence is unbounded. This means that closeness of homogenizations with respect to the truncated Hausdorff distance does not imply closeness of the sets themselves with respect to the Hausdorff distance. In fact, the Hausdorff distance, which measures absolute distances, between a homogeneous $\delta$-approximation P of C and C may be infinite for arbitrary $\delta \in (0,1]$.

Example 3.1

Let $C = [0,\infty )$ and define $P_{\delta } = \left[ 0,\sqrt{1-\delta ^2}/\delta \right]$ for $\delta \in (0,1]$. Then, $0^{\infty }{C} = C$ and $P_{\delta }$ is compact for every $\delta \in (0,1]$, but one has

The second equality is evident by taking into account that the projection of $(1,0)^{\textsf{T}}$ onto ${{\,\textrm{homog}\,}}{P_{\delta }}$ is attained on the ray generated by $\left( \sqrt{1-\delta ^2}/\delta ,1\right) ^{\textsf{T}}$. Hence, $P_{\delta }$ is a homogeneous $\delta$-approximation of C with $d_{\textsf{H}}\left( {P_{\delta }},{C}\right) = \infty$.

A converse relation does hold.

Proposition 3.1

Let $C \subseteq \mathbb {R}^n$ be a closed convex set and $P \subseteq \mathbb {R}^n$ be a polyhedron. If $d_{\textsf{H}}\left( {P},{C}\right) \leqslant \varepsilon$, then P is a homogeneous $\varepsilon$-approximation of C.

Proof

Consider the alternative formula for the Hausdorff distance

see [25]. By assumption, it holds $P \subseteq C+\varepsilon B$ and $C \subseteq P+\varepsilon B$. We only show the inclusion ${{\,\textrm{homog}\,}}{P} \cap B \subseteq {{\,\textrm{homog}\,}}{C} \cap B + \varepsilon B$. The other inclusion is derived identically by interchanging the roles of P and C. It holds

(3)

Let x be an element from the right-hand side set. Then, there exist $c \in C$, $\mu \in [0,1]$ and $d \in B$ such that $x=\mu (c+\varepsilon d,1)^{\textsf{T}}$. Define . Then,

$$ \left\Vert {x-\bar{x}} \right\Vert = d\left( {x},{{{\,\textrm{homog}\,}}{C}}\right) \leqslant \left\Vert {x-\mu (c,1)^{\textsf{T}}} \right\Vert \leqslant \mu \varepsilon \leqslant \varepsilon . $$

Moreover, $\left\Vert {\bar{x}} \right\Vert \leqslant \left\Vert {x} \right\Vert \leqslant 1$, because the projection mapping onto ${{\,\textrm{homog}\,}}{C}$ is nonexpansive, see [15, Proposition 3.1.3]. Thus, $x = \bar{x}+(x-\bar{x}) \in {{\,\textrm{homog}\,}}{C} \cap B+\varepsilon B$. Using (3), we obtain the inclusion and, because the latter set is closed, also ${{\,\textrm{homog}\,}}{P} \cap B \subseteq {{\,\textrm{homog}\,}}{C} \cap B + \varepsilon B$. $\square$

The above proposition and Example 3.1 show that the concept of homogeneous $\delta$-approximation is more general than approximation with respect to the Hausdorff distance. Moreover, homogeneous $\delta$-approximations provide a meaningful notion of approximation in the sense that a sequence of homogeneous $\delta$-approximations of C converge to C if $\delta$ tends to 0. The common notion of convergence in this scenario is that of Painlevé–Kuratowski, a theory of convergence for sequences of sets that applies to a broader class than Hausdorff convergence but coincides with it in a compact setting. It is discussed in detail in the book [25] by Rockafellar and Wets, and we adhere to the notation therein. Let $\mathcal {N}_{\infty }$ and ${\mathcal {N}}^\#_{\infty }$ denote the collections and of subsets of $\mathbb {N}$, respectively. The set ${\mathcal {N}}_{\infty }$ can be regarded as the set of subsequences of $\mathbb {N}$ that contain all natural numbers larger than some $\bar{n} \in \mathbb {N}$ and ${\mathcal {N}}^\#_{\infty }$ as the set of all subsequences of $\mathbb {N}$. Obviously, ${\mathcal {N}}_{\infty } \subseteq {\mathcal {N}}^\#_{\infty }$.

Definition 3.3

For a sequence of subsets of $\mathbb {R}^n$, the outer limit is the set

denoted by $\limsup _{k \rightarrow \infty } M_k$, and the inner limit $\liminf _{k \rightarrow \infty } M_k$ is the set

The outer limit of a sequence can be paraphrased as the set of all points for which every open neighbourhood intersects infinitely many elements $M_k$ of the sequence. Similarly, the inner limit is the set for which the same is true but for all elements $M_k$ beyond some $\bar{k} \in \mathbb {N}$. In particular, both sets are closed.

Definition 3.4

A sequence of subsets of $\mathbb {R}^n$ is said to converge to a set $M \subseteq \mathbb {R}^n$ in the sense of Painlevé–Kuratowski or PK-converge, written $M_k \rightarrow M$, if

$$ M = \limsup _{k \rightarrow \infty } M_k = \liminf _{k \rightarrow \infty } M_k. $$

Now, homogeneous $\delta$-approximations define a suitable notion of approximation for closed convex sets because PK-convergence can be characterized in terms of homogenizations and the truncated Hausdorff distance.

Proposition 3.2

(cf. [25, Corollary 4.47]) Let be a sequence of closed convex subsets of $\mathbb {R}^n$ and $C \subseteq \mathbb {R}^n$ be a closed convex set. Then, the following are equivalent:

• (i) $C_k \rightarrow C$,

• (ii) $d_{\textsf{tH}}\left( {{{\,\textrm{homog}\,}}{C_k}},{{{\,\textrm{homog}\,}}{C}}\right) \rightarrow 0$.

Hence, if is a sequence of homogeneous $\delta _k$-approximations of C and $\lim _{k \rightarrow \infty } \delta _k = 0$, then PK-converges to C.

We will now emphasize another property of homogeneous $\delta$-approximations that is not present for approximations in the Hausdorff distance. Surprisingly, the polar set of a homogeneous $\delta$-approximation of C is a homogeneous $\delta$-approximation of ${C}^{\circ }$ provided the origin is contained in the sets. This is different from the compact case. If $d_{\textsf{H}}\left( {P},{C}\right) \leqslant \delta$, then in general it holds

$$ d_{\textsf{H}}\left( {{P}^{\circ }},{{C}^{\circ }}\right) \leqslant \frac{\delta }{r_0(P)r_0(C)}, $$

where $r_0(P)$ and $r_0(C)$ are the radius of the largest Euclidean ball centred at the origin that is contained in P and C, respectively, see [18, Lemma 1]. In particular, the Hausdorff distance between ${P}^{\circ }$ and ${C}^{\circ }$ does not only depend on $\varepsilon$ but also on constants related to the geometry of C. In order to establish the result, we need a connection between the polar cone of ${{\,\textrm{homog}\,}}{C}$ and ${C}^{\circ }$. The following result is originally presented as [1, Theorem 3.1] for closed convex sets C. Here, we prove a slight generalization.

Proposition 3.3

Let $C \subseteq \mathbb {R}^n$ be a convex set containing the origin. Then,

Proof

The first equality is proved in [1, Theorem 3.1] for C being closed and convex. However, it also holds for arbitrary convex sets C because ${C}^{\circ }={\left( {{\,\textrm{cl}\,}}C\right) }^{\circ }$ and ${{\,\textrm{homog}\,}}{C} = {{\,\textrm{homog}\,}}{{{\,\textrm{cl}\,}}C}$. The inclusion ${{\,\textrm{homog}\,}}{C} \subseteq {{\,\textrm{homog}\,}}{{{\,\textrm{cl}\,}}C}$ is immediate from $C \subseteq {{\,\textrm{cl}\,}}C$. For the other direction, consider a point

that means we fix $\mu \geqslant 0$ and $x \in {{\,\textrm{cl}\,}}C$. Thus, there exists a sequence converging to x. For every $k \in \mathbb {N}$, it holds . Therefore, . This implies

and by taking closures

$$ {{\,\textrm{homog}\,}}{{{\,\textrm{cl}\,}}C} \subseteq {{\,\textrm{homog}\,}}{C}. $$

To show the second equation in the original statement, we compute

The penultimate line follows from [24, Theorem 9.1]. $\square$

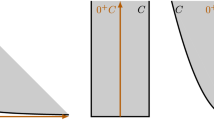
Figure 1 illustrates Proposition 3.3 for the set .

Fig. 1

Homogenization of the set and its polar cone. According to Proposition 3.3, the polar cone is the closure of the cone generated by

Theorem 3.1

Let $C \subseteq \mathbb {R}^n$ be a convex set containing the origin. If P is a homogeneous $\delta$-approximation of C containing the origin, then ${P}^{\circ }$ is a homogeneous $\delta$-approximation of ${C}^{\circ }$.

Proof

Let $M :\mathbb {R}^{n+1} \rightarrow \mathbb {R}^{n+1}$ denote the isometry defined by

Now, we compute

$$ \begin{aligned} d_{\textsf{tH}}\left( {{{\,\textrm{homog}\,}}{\left( {P}^{\circ }\right) }},{{{\,\textrm{homog}\,}}{\left( {C}^{\circ }\right) }}\right)&= d_{\textsf{tH}}\left( {M\left[ {{\,\textrm{homog}\,}}{\left( {P}^{\circ }\right) }\right] },{M\left[ {{\,\textrm{homog}\,}}{\left( {C}^{\circ }\right) }\right] }\right) \\&= d_{\textsf{tH}}\left( {-{{\,\textrm{homog}\,}}{\left( -{P}^{\circ }\right) }},{-{{\,\textrm{homog}\,}}{\left( -{C}^{\circ }\right) }}\right) \\&= d_{\textsf{tH}}\left( {{{{\,\textrm{homog}\,}}{\left( P\right) }}^*},{{{{\,\textrm{homog}\,}}{\left( C\right) }}^*}\right) \\&= d_{\textsf{tH}}\left( {{{\,\textrm{homog}\,}}{P}},{{{\,\textrm{homog}\,}}{C}}\right) \\&\leqslant \delta . \end{aligned} $$

The first equation is true by [16, Proposition 2.1]. The second and third follow from Proposition 3.3 using the fact that $0 \in P \cap C$. Theorem 1 of [29] yields the equality in line 4. Finally, the inequality holds because P is a homogeneous $\delta$-approximation of C. Thus, ${P}^{\circ }$ is a homogeneous $\delta$-approximation of ${C}^{\circ }$. $\square$

4 Computing Homogeneous $\delta$-Approximations of Spectrahedral Shadows

In this section, we present an algorithm for the computation of a homogeneous $\delta$-approximation of a convex sets C. In order to do this, we need to be able to explicitly describe the set ${{\,\textrm{homog}\,}}{C}$. Therefore, we restrict ourselves to a certain class of convex sets for which this is possible called spectrahedral shadows. Let $\mathcal {S}^{\ell }$ denote the linear space of real symmetric $\ell \times \ell$-matrices. If $X \in \mathcal {S}^{\ell }$ is positive semidefinite and positive definite, it is written as $X \succcurlyeq 0$ and $X \succ 0$, respectively. Moreover, for $X,Y \in \mathcal {S}^{\ell }$ an inner product is defined by the trace of the matrix product, i.e. . Now, a spectrahedral shadow $S \subseteq \mathbb {R}^n$ can be represented as

for $A_0 \in \mathcal {S}^{\ell }$ and linear functions $\mathcal {A}:\mathbb {R}^n \rightarrow \mathcal {S}^{\ell }$, $\mathcal {B}:\mathbb {R}^m \rightarrow \mathcal {S}^{\ell }$. Every linear function $\mathcal {A}$ between $\mathbb {R}^n$ and $\mathcal {S}^{\ell }$ can be defined as $\mathcal {A}(x) = \sum _{i=1}^n A_ix_i$ for suitable $A_1,\dots ,A_n \in \mathcal {S}^{\ell }$, see [10]. Spectrahedral shadows are the images of spectrahedra, the feasible regions of semidefinite programmes, under orthogonal projections. They are closed under many set operations, e.g. intersections, Minkowski sums, linear transformations, taking polar or conical hulls, see, for instance, [3, 7, 12, 14, 22].

The algorithm we present is based on an algorithm for the polyhedral approximation of recession cones of convex sets that was recently and independently developed in [6] and [28]. Given a spectrahedral shadow S and an error tolerance $\delta > 0$, Algorithm 2 of [8] computes polyhedral cones $K_{\textsf{O}}$ and $K_{\textsf{I}}$ such that $K_{\textsf{I}} \subseteq 0^{\infty }{{{\,\textrm{cl}\,}}S} \subseteq K_{\textsf{O}}$, $d_{\textsf{tH}}\left( {K_{\textsf{O}}},{0^{\infty }{{{\,\textrm{cl}\,}}S}}\right) \leqslant \delta$ and $d_{\textsf{tH}}\left( {K_{\textsf{I}}},{0^{\infty }{{{\,\textrm{cl}\,}}S}}\right) \leqslant \delta$. It is shown that the algorithm works correctly and terminates after finitely many steps under the following assumptions:

• (A1) A point $p \in \mathbb {R}^n$ is known for which there exists $y_p \in \mathbb {R}^m$ such that $A_0+\mathcal {A}(x)+\mathcal {B}(y_p) \succ 0$,

• (A2) A direction $\bar{d} \in {{\,\textrm{int}\,}}0^{\infty }{S} \cap B$ is known.

For ease of reference, we recall the algorithm here as Algorithm 1. Therefore, the following primal/dual pair of semidefinite programmes depending on parameters $p,d \in \mathbb {R}^n$ and a spectrahedral shadow S is needed.

Here, $\mathcal {A}^{\textsf{T}}$ and $\mathcal {B}^{\textsf{T}}$ are the adjoints of $\mathcal {A}$ and $\mathcal {B}$, respectively. It holds and the corresponding for $\mathcal {B}^{\textsf{T}}$, see [10, Lemma 4.5.3]. Typically, we assume that $p \in S$ and d is a direction. Then, problem can be motivated as follows. Starting at the point $p \in S$, the maximum distance is to be determined that can be moved in direction d without leaving the set. If S is compact, then the maximum distance will be attained in the point where halfline intersects the boundary of S. A solution to the dual programme, if it exists, gives rise to a supporting hyperplane of ${{\,\textrm{cl}\,}}S$. The following proposition is a slight variation of [7, Proposition 3.11].

Proposition 4.1

Let $S \subseteq \mathbb {R}^n$ be a spectrahedral shadow and $p \in S$. Then, the following hold:

• (i) If is unbounded, then $d \in 0^{\infty }{{{\,\textrm{cl}\,}}S}$,

• (ii) If is strictly feasible with finite optimal value $t^*$, then an optimal solution $(V^*,w^*)$ to exists and the hyperplane $H(w^*,w^{*\textsf{T}}p+t^*)$ supports ${{\,\textrm{cl}\,}}S$ at $p+t^*d$.

Algorithm 1

Approximation algorithm for recession cones of spectrahedral shadows

After finding initial outer and inner approximations $K_{\textsf{O}}$ and $K_{\textsf{I}}$ or determining that S is the whole space in lines 1–9, Algorithm 1 iteratively shrinks $K_{\textsf{O}}$ or enlarges $K_{\textsf{I}}$ until the truncated Hausdorff distance between them is certifiably not larger than $\delta$. To this end, in every iteration of the main loop in lines 10–25 a new search direction d is chosen in line 14 and the problem is investigated. If it is unbounded, then $d \in 0^{\infty }{{{\,\textrm{cl}\,}}S}$ according to Proposition 4.1(i) and $K_{\textsf{I}}$ is updated as . Otherwise, a solution $(V_d,w_d)$ to exists and $H(w_d,w_d^{\textsf{T}}p+t_d)$ is a supporting hyperplane of ${{\,\textrm{cl}\,}}S$ for the optimal value $t_d$ of according to Proposition 4.1(ii). Therefore, $H(w_d,0)$ supports $0^{\infty }{{{\,\textrm{cl}\,}}S}$ and the current outer approximation is updated as $K_{\textsf{O}} \cap H^-(w_d,0)$. After an update of either approximation occurs, a new search direction is computed. For more details about the algorithm, we refer the reader to [8].

In order to apply Algorithm 1 to the problem of computing homogeneous $\delta$-approximations of S, observe that every convex cone is its own recession cone. This suggests we could apply Algorithm 1 to ${{\,\textrm{homog}\,}}{S}$ and obtain a homogeneous $\delta$-approximation of S by undoing the homogenization. This approach presupposes that S satisfies suitable assumptions such that the requirements of Algorithm 1 are fulfilled for ${{\,\textrm{homog}\,}}{S}$ and, more importantly, that ${{\,\textrm{homog}\,}}{S}$ is a spectrahedral shadow for which a representation is available or can be computed from a representation of S. The following proposition shows that the latter is possible.

Proposition 4.2

Let . Then, the homogenization ${{\,\textrm{homog}\,}}{S}$ is the closure of the spectrahedral shadow

Proof

The Cartesian product is the set $\{(x,x_{n+1})^{\textsf{T}}\in \mathbb {R}^{n+1}\mid \exists \;y\in \mathbb {R}^m:A_0+\mathcal {A}(x)+\mathcal {B}(y) \succcurlyeq 0, x_{n+1} \geqslant 1, -x_{n+1} \geqslant -1\}$. This set is a spectrahedral shadow because the three inequalities can be expressed as one matrix inequality using block diagonal matrices, i.e.

(4)

According to [22, Proposition 4.3.1] is the spectrahedral shadow

Using the implicit equality $x_{n+1}=\mu$, we eliminate $\mu$ from the description of the set. The resulting spectrahedral shadow differs from the claimed set only through the occurrence of the matrix inequalities

(5)

for $i=1,\dots ,n+1$. Now, there exists $t \in \mathbb {R}$ such that (5) holds for $i=1,\dots ,n+1$ if and only if the same is true but for $i=1,\dots ,n$. Indeed, if $x_{n+1}=0$, then positive definiteness in (5) implies $x=0$ and we can choose $t=0$ in both cases. Otherwise, if $x_{n+1} > 0$, then (5) holds for some i, if and only if $t \geqslant x_{n+1}^{-1}x_i^2$ according to the Schur complement, see [32]. Thus, we can set in both cases. The case $x_{n+1} < 0$ does not occur as it violates the positive semidefiniteness in (5). By a similar argument using Schur complement, there exists $t \in \mathbb {R}$ such that (5) holds for all $i=1,\dots ,n$ if and only if there exists $t \in \mathbb {R}$ such that

where I denotes the identity matrix of size n. $\square$

Proposition 4.2 and its preceding paragraph motivate the formulation of the following algorithm for the computation of homogeneous $\delta$-approximations of S.

Algorithm 2

homogeneous $\delta$-approximation algorithm for spectrahedral shadows

The function $\pi _{\mathbb {R}^n} :\mathbb {R}^{n+1} \rightarrow \mathbb {R}^n$ in lines 3 and 4 denotes the projection given by

Theorem 4.1

Algorithm 2 works correctly; in particular, it terminates with an outer homogeneous $\delta$-approximation $P_{\textsf{O}}$ and an inner homogeneous $\delta$-approximation $P_{\textsf{I}}$ of S.

Proof

Since $\bar{x}$ satisfies Assumption (A1) for S, the point $p = \left( \bar{x}^{\textsf{T}},1\right) ^{\textsf{T}}$ satisfies analogous conditions for K. This is seen from a direct calculation using the description of K derived in Proposition 4.2. Similarly, $\bar{x} \in {{\,\textrm{int}\,}}S$ implies $\left( \bar{x}^{\textsf{T}},1\right) ^{\textsf{T}}\in {{\,\textrm{int}\,}}K$. In particular,

satisfies Assumption (A2) for K because $K = 0^{\infty }{K}$. From the correctness of Algorithm 1, see [8, Theorem 4.4], it follows that line 2 of Algorithm 2 works correctly and returns polyhedral cones $K_{\textsf{O}}$ and $K_{\textsf{I}}$ satisfying

$$\begin{aligned} K_{\textsf{I}} \subseteq 0^{\infty }{{{\,\textrm{cl}\,}}{K}} = {{\,\textrm{cl}\,}}K = {{\,\textrm{homog}\,}}{S} \subseteq K_{\textsf{O}} \end{aligned}$$

(6)

as well as $d_{\textsf{tH}}\left( {K_{\textsf{O}}},{{{\,\textrm{homog}\,}}{S}}\right) \leqslant \delta$ and $d_{\textsf{tH}}\left( {K_{\textsf{I}}},{{{\,\textrm{homog}\,}}{S}}\right) \leqslant \delta$. For the sets $P_{\textsf{O}}$ and $P_{\textsf{I}}$ in lines 3 and 4, it holds

$$ {{\,\textrm{homog}\,}}{P_{\textsf{O}}} = K_{\textsf{O}} \cap H^+(e_{n+1},0) \quad \text {and}\quad {{\,\textrm{homog}\,}}{P_{\textsf{I}}} = K_{\textsf{I}}. $$

The difference arises from the inclusions in (6) and the fact that homogenizations are contained in the halfspace $H^+(e_{n+1},0)$ by definition. However,

$$ d_{\textsf{tH}}\left( {K_{\textsf{O}} \cap H^+(e_{n+1},0)},{{{\,\textrm{homog}\,}}{S}}\right) \leqslant d_{\textsf{tH}}\left( {K_{\textsf{O}}},{{{\,\textrm{homog}\,}}{S}}\right) \leqslant \delta $$

holds due to the inclusion ${{\,\textrm{homog}\,}}{S} \subseteq K_{\textsf{O}} \cap H^+(e_{n+1},0)$. Therefore, $P_{\textsf{O}}$ and $P_{\textsf{I}}$ are homogeneous $\delta$-approximations of S.

The finiteness of Algorithm 2 is implied by the finiteness of Algorithm 1, see [8, Theorem 4.4]. $\square$

Remark 4.1

The inner homogeneous $\delta$-approximation $P_{\textsf{I}}$ of S computed by Algorithm 2 is always compact. Due to the containment of its homogenization $K_{\textsf{I}}$ in the set , one has $\mu > 0$ whenever . Thus, every direction of $K_{\textsf{I}}$ corresponds to a point of $P_{\textsf{I}}$, in particular

according to Eq. (2).

We conclude this section with two examples.

Example 4.1

Algorithm 2 is applied to the spectrahedral shadow

which is the Minkowski sum of the epigraphs of the functions $x \mapsto x^{-1}$ restricted to $\mathbb {R}_{++}$ and $x \mapsto x^2$. As input parameters, we set $\delta =0.01$ and $\bar{x} \approx (1.8846,1.8846)^{\textsf{T}}$. Figure 2 depicts $P_{\textsf{O}}$ as well as the determined inner homogeneous $\delta$-approximation $P_{\textsf{I}}$. In total, 534 semidefinite programmes are solved during the execution of Algorithm 2 for finding $P_{\textsf{O}}$ and $P_{\textsf{I}}$.

Fig. 2

Depicted are the outer and inner homogeneous $\delta$-approximation $P_{\textsf{O}}$ and $P_{\textsf{I}}$ of the set from Example 4.1 computed by Algorithm 2 with $\delta =0.01$ in red and blue, respectively. On the left is a section around the origin with vertices marked by black dots. Note that the distance between vertices of $P_{\textsf{O}}$ and $P_{\textsf{I}}$ increases with their distance to the origin. The right figure shows the scale of $P_{\textsf{I}}$, which is compact

Example 4.2

Consider the spectrahedral shadow S consisting of points $x \in \mathbb {R}^3$ that admit the existence of $y^1, y^2 \in \mathbb {R}^3$ and $Z \in \mathcal {S}^3$, $Z \succcurlyeq 0$, such that the system

is satisfied. Algorithm 2 with $\delta =0.03$ and $\bar{x}=0$ requires the solutions to 1989 problems of type , where . The resulting outer approximation $P_{\textsf{O}}$ has 92 vertices and 24 extreme directions, while the compact inner approximation $P_{\textsf{I}}$ is composed of 177 vertices. According to Theorem 3.1, their polar sets ${P}^{\circ }_{\textsf{O}}$ and ${P}^{\circ }_{\textsf{I}}$ are an inner and outer homogeneous $\delta$-approximation of ${S}^{\circ }$, respectively. They are both compact with 94 and 232 vertices each. Sets $P_{\textsf{O}}$ and $P_{\textsf{I}}$ as well as their polars are shown in Fig. 3. The polyhedra in Fig. 3 are plotted using the function Poly3DCollection provided by the Python library Matplotlib. This requires the vertex-facet incidences of the polyhedra, which can be computed using the library pycddlib.

Fig. 3

The top row shows homogeneous $\delta$-approximations $P_{\textsf{O}}$ and $P_{\textsf{I}}$ of the set S from Example 4.2 for $\delta =0.03$ restricted to balls of radius 7 and 100, respectively. Their polar sets, which are homogeneous $\delta$-approximations of ${S}^{\circ }$, are depicted in the bottom row. Both are contained in a ball of radius 1.02

5 Conclusions

We have introduced the notion of homogeneous $\delta$-approximation for the polyhedral approximation of convex sets, which uses the common concept of homogenization of a convex set. The advantage of this approach compared to approximation with respect to the Hausdorff distance is its compatibility with sets that are unbounded. Moreover, we have shown that homogeneous $\delta$-approximations behave well under polarity in the sense that the polar of a homogeneous $\delta$-approximation of a convex set is a homogeneous $\delta$-approximation of the polar set under mild assumptions. This behaviour is not encountered when working with the Hausdorff distance. Finally, we have presented an algorithm for the computation of homogeneous $\delta$-approximations of spectrahedral shadows, a subclass of convex sets. The algorithm is shown to be correct and finite, and its practicability is demonstrated on two examples.