Transverse foliations in the rotating Kepler problem

Abstract

We construct finite energy foliations and transverse foliations of neighbourhoods of the circular orbits in the rotating Kepler problem for all negative energies. This paper would be a first step towards our ultimate goal that is to recover and refine McGehee’s results on homoclinics [23] and to establish a theoretical foundation to the numerical demonstration of the existence of a homoclinic–heteroclinic chain in the planar circular restricted three-body problem [20], using pseudoholomorphic curves.

1 Introduction

The rotating Kepler problem is the Kepler problem in rotating coordinates, obtained from the planar circular restricted three-body problem (PCR3BP) by setting the mass of one of the primaries to zero. Its Hamiltonian $H :T^*( {\mathbb {R}}^2 {\setminus } \{ 0 \} ) \rightarrow {\mathbb {R}}$ is given by

$$\begin{aligned} \begin{aligned} H(q_1, q_2, p_1,p_2)&= \frac{1}{2} |p |^2 - \frac{1}{ |q |} - p_2 q_1 + p_1 q_2 \\&= \frac{1}{2} ( (p_1 +q_2)^2 + (p_2 - q_1)^2) - \frac{1}{|q|}- \frac{1}{2} |q |^2, \end{aligned} \end{aligned}$$

(1.1)

where $q=(q_1, q_2)$ and $p=(p_1, p_2).$ It admits two integrals of motion

$$\begin{aligned} E = \frac{1}{2} |p \vert ^2 - \frac{1}{ |q |}, \quad \quad L = q_1 p_2 - q_2 p_1, \end{aligned}$$

(1.2)

called the Kepler energy and the angular momentum, respectively. Throughout the paper, we tacitly assume that the Kepler energy is negative, so that its trajectories projected to the q-plane are ellipses. We call such trajectories Kepler ellipses.

The Hamiltonian H admits a unique critical value $c = -\frac{3}{2}.$ If $c<-\frac{3}{2},$ then the energy level $H^{-1}(c)$ consists of two connected components, denoted by $\Sigma _c^b$ and $\Sigma _c^u.$ They are called the bounded and the unbounded components, respectively. It is important to mention that the component $\Sigma _c^b$ is not bounded as a set. Indeed, the point $(q_1, q_2, p_1,p_2)=( \frac{1}{a}, 0, \sqrt{ 2(a+c)}, 0)$ lies on $\Sigma _c^b$ for any value of $a>-c.$ We stick to our nomenclature though as its projection to the q-plane is bounded. If $c>-\frac{3}{2},$ then the energy level $H^{-1}(c)$ consists of a single unbounded component whose projection to the q-plane is the whole ${\mathbb {R}}^2 \setminus \{ 0\}.$

Periodic orbits will be referred to as circular orbits if the projections to the q-plane are circular. A circular orbit is called direct and retrograde if it is rotating in the same direction as the coordinate system and in opposite direction to the coordinate system, respectively. If $c<-\frac{3}{2},$ then there are precisely two circular orbits $\gamma _{\textrm{retro}}^b$ and $\gamma _{\textrm{direct}}^b$ on $\Sigma _c^b$ and a unique circular orbit $\gamma _{\textrm{direct}}^u$ on $\Sigma _c^u.$ The circular orbit $\gamma _{\textrm{retro}}^b$ is retrograde and the other two are direct. When $c = -\frac{3}{2},$ the two direct circular orbits degenerate into a circle of critical points. In the case $c>-\frac{3}{2},$ there is a unique circular orbit $\gamma _{\textrm{retro}}^u$ on $H^{-1}(c)$ that is retrograde.

Fix $c<-\frac{3}{2}.$ The angular momentum L,  restricted to $\Sigma _c^b,$ takes values in the interval $[L^b_{\textrm{retro}}, L^b_{\textrm{direct}}],$ where $L^b_{\textrm{retro}}<0$ and $L^b_\textrm{direct}>0$ are angular momenta of $\gamma _{\textrm{retro}}^b$ and $\gamma _{\textrm{direct}}^b,$ respectively. See Sect. 3. Each $L \in (L^b_{\textrm{retro}}, L^b_{\textrm{direct}})$ corresponds to a Liouville torus. The three-dimensional manifold $\Sigma _c^b$ is not compact due to collisions. Note that along all collision orbits, we have $L=0.$ However, two-body collisions can always be regularised, see for example [25, Section 2] and also [8, Section 4.1], and hence $\Sigma _c^b$ can be compactified to form a closed three-dimensional manifold $\overline{\Sigma }_c^b,$ diffeomorphic to ${\mathbb {R}}P^3.$

Consider two solid tori

$$\begin{aligned} \Sigma _{\textrm{retro}} ^b&= \{ (q,p) \in \overline{\Sigma }_c^b : (q,p) \text{ lies } \text{ on } \text{ an } \text{ orbit } \text{ with } L \in [L_{\textrm{retro}}^b, 0 ]\},\\ \Sigma _{\textrm{direct}}^b&= \{ (q,p) \in \overline{\Sigma }_c^b : (q,p) \text{ lies } \text{ on } \text{ an } \text{ orbit } \text{ with } L \in [0,L_{\textrm{direct}}^b] \}. \end{aligned}$$

Each solid torus is foliated into embedded discs, whose boundaries lie on the boundary torus consisting only of collision orbits and whose interiors are transverse to the Hamiltonian flow. The circular orbit corresponds to a unique fixed point of the associated first return map. To see this, we first note that there is a contact form on $\overline{\Sigma }_c^b$ that is dynamically convex, i.e., every contractible periodic orbit has Conley-Zehnder index at least three. See [3, Proposition 3.2] and [2, Theorem 1.1]. Then, an application of a result from [17] implies that $\gamma _\textrm{retro}^b$ binds a rational open book decomposition whose pages are disc-like global surfaces of section for the Hamiltonian flow. Since every $L \in [0,L_{\textrm{direct}}^b]$ corresponds to a Liouville torus that is tangent to the Hamiltonian flow, each of the pages of this rational open book decomposition intersects $\Sigma _\textrm{direct}^b$ transversally in closed discs that determine the above-mentioned disc foliation of $\Sigma _{\textrm{direct}}^b$. The same holds for $\gamma _{\textrm{direct}}^b$ and $\Sigma _{\textrm{retro}}^b.$

The goal of this paper is to show that similar assertions hold in neighbourhoods of $\gamma _{\textrm{direct}}^u$ and $\gamma _\textrm{retro}^u,$ as stated below.

Theorem 1.1

The following assertions hold.

• (1) Assume that $c<-\frac{3}{2}.$ Then, there is a subset $\Sigma _{\textrm{direct}}^u$ of the unbounded component $\Sigma _c^u \subset H^{-1}(c)$ satisfying the following properties:

  • (a) It is diffeomorphic to a solid torus whose core is $\gamma _{\textrm{direct}}^u$ and whose boundary is a Liouville torus.

  • (b) It is foliated into embedded discs whose boundaries lie on the boundary torus and whose interiors are transverse to the Hamiltonian flow.

  • (c) A unique fixed point of the associated first return map corresponds to the direct circular orbit $\gamma _{\textrm{direct}}^u.$

• (2) If $-\frac{3}{2}<c<0,$ then there is a subset $\Sigma _{\textrm{retro}}^u \subset H^{-1}(c)$ having the same properties as above, with $\gamma _{\textrm{direct}}^u$ being replaced by $\gamma _{\textrm{retro}}^u.$

More precise descriptions for the subsets $\Sigma _{\textrm{direct}}^u$ and $\Sigma _{\textrm{retro}}^u$ in the statement above will be given in Sects. 5 and 6, respectively.

Remark 1.2

Here are a couple of remarks on the theorem above.

• (1) The reason why we consider only negative energies is that we would not like to regularise the collisions. See Sect. 3.

• (2) The subset $\Sigma ^u_{\textrm{direct}}$ can be arbitrarily large. See Remark 5.1.

• (3) Pick any embedded disc ${\mathscr {D}}$ described in (b) above. Since the rotating Kepler problem is completely integrable, the solid torus $\Sigma _{\textrm{direct}}^u$ is foliated by Liouville tori. This Liouville foliation induces a foliation of the disc ${\mathscr {D}}$ into concentric circles whose centre corresponds to the direct circular orbit $\gamma _{\textrm{direct}}^u$. The same holds for $\Sigma _{\textrm{retro}}^u$ with $\gamma _{\textrm{direct}}^u$ being replaced by $\gamma _{\textrm{retro}}^u.$

The motivation of this paper comes from results on the PCR3BP by McGehee [23] and by Koon, Lo, Marsden, and Ross [20]. We briefly state below these results for readers’ convenience.

The PCR3BP studies the motion of an infinitesimal body under the gravitational influence of two massive bodies moving along circular orbits around their centre of mass. The infinitesimal body, denoted by C,  is assumed to move in the plane spanned by the orbits of the two massive bodies, denoted by S and J. We rescale the total mass of the system to one, so that the mass of S equals $1-\mu$ and the mass of J equals $\mu$ for some $\mu \in [0,1].$ If the centre of mass is located at the origin, then the Hamiltonian of the PCR3BP in a rotating frame is given by

$$\begin{aligned} H_{\mu }(q_1, q_2, p_1,p_2) = \frac{1}{2} |p |^2 - \frac{1-\mu }{|q-S|} - \frac{ \mu }{|q - J |} - p_2 q_1 + p_1 q_2, \end{aligned}$$

where $S = ( -\mu , 0)$ and $J = (1-\mu ,0)$ denote the positions of S and J,  respectively. Note that in the case $\mu =0,$ this becomes the Hamiltonian of the rotating Kepler problem; see (1.1).

We assume $\mu < \frac{1}{2},$ so that S is heavier than J. The Hamiltonian $H_{\mu }$ admits five equilibria $L_j, j=1,2,3,4,5$, ordered by action in the following way:

$$\begin{aligned} H_{\mu }(L_1)<H_{\mu }(L_2)<H_{\mu }(L_3)<H_{\mu }(L_4)=H_{\mu }(L_5). \end{aligned}$$

These values tend to $-\frac{3}{2},$ the critical value of the rotating Kepler problem, as $\mu \rightarrow 0.$ We are interested in energies slightly above the first two critical values $H_\mu (L_1)$ and $H_\mu (L_2).$ The corresponding Hill’s regions are illustrated in Fig. 1.

Fig. 1

Hill’s regions corresponding to energies slightly above $H_\mu (L_1)$ (left) and $H_\mu (L_2)$ (right). The darkly shaded regions indicate the projection of invariant tori

Since $L_1$ and $L_2$ are of saddle-centre type, a theorem of Lyapunoff [21] shows that for energy slightly above $H_\mu (L_j),$ the energy level carries a unique hyperbolic periodic orbit near $L_j,$ called the Lyapunoff orbit, $j=1,2.$

In his dissertation [23], McGehee established the presence of invariant tori on the energy level, as in Fig. 1, for $\mu >0$ small enough, in other words, for J sufficiently light. By making use of these tori, he was able to find a homoclinic orbit to the Lyapunoff orbit associated with $L_1$ or $L_2.$ See Fig. 2.

Using McGehee’s result, Koon, Lo, Marsden, and Ross provided a numerical demonstration of the existence of a homoclinic–heteroclinic chain in the Sun–Jupiter system [20]: let the mass $\mu$ of J be that of Jupiter and the energy be that of comet Oterma, so that it is slightly above $H_\mu (L_2).$ For these values, the authors showed that the energy level carries the Lyapunoff orbits near $L_1$ and $L_2$ and a heteroclinic orbit between the two Lyapunoff orbits. These three periodic orbits consist of a so-called homoclinic–heteroclinic chain, which might be used to design spacecraft orbits exploring the interior and exterior regions, as illustrated in Fig. 2.

Fig. 2

A homoclinic–heteroclinic chain in the PCR3BP. The inner and outer black curves denote homoclinic orbits to the Lyapunoff orbits (red curves) near $L_1$ and $L_2$, respectively. The blue curve indicates a heteroclinic orbit (color figure online)

Our ultimate goal is to recover and refine McGehee’s results and to establish a theoretical foundation to the numerical demonstration by Koon–Lo–Marsden–Ross, using pseudoholomorphic curves. As compactness is crucial in pseudoholomorphic curve theory, to achieve this goal, one first has to find an efficient way to deal with non-compact energy levels. This paper would provide a way to construct finite energy foliations of regions in the non-compact energy level in the case $\mu =0,$ i.e., in the rotating Kepler problem, so it would be a first step towards our final goal.

Outline of the paper. We start by recollecting relevant facts about Reeb dynamics and pseudoholomorphic curves in symplectisations in Sect. 2. Then, in Sect. 3, we review results on the rotating Kepler problem that will be needed in our argument later on. In Sect. 4, we recall the definition and some properties of Poincaré’s coordinates, a modification of the well-known Delaunay coordinates that are not valid for the circular orbits. Constructions of finite energy folations and transverse foliations are provided in Sects. 5 and 6. We present in Appendix 6 an alternative way to obtain a transverse foliation whose pages are annuli.

2 Basic notions in contact geometry

2.1 Periodic orbits

Let $\Sigma =K^{-1}(0) \subset {\mathbb {R}}^4$ be a regular energy level of a Hamiltonian $K :{\mathbb {R}}^4 \rightarrow {\mathbb {R}}.$ We endow ${\mathbb {R}}^4$ with coordinates $(x_1, x_2, y_1, y_2).$ A periodic orbit (of K) on $\Sigma$ will be denoted by a pair $P=(w,T),$ where $w :{\mathbb {R}}\rightarrow \Sigma$ solves the differential equation $\dot{w} = X_K \circ w,$ where $X_K$ denotes the Hamiltonian vector field of K,  defined as $\omega _0 (X_K, \cdot ) = -dK,$ and $T>0$ is a period. Here, $\omega _0 = dy_1 \wedge \textrm{d}x_1 + \textrm{d}y_2 \wedge \textrm{d}x_2$ denotes the standard symplectic form on ${\mathbb {R}}^4.$ By abuse of notation, we may also denote by P the trace $w({\mathbb {R}}) \subset \Sigma .$ If T is minimal, then P is called simple. Throughout the paper, when we consider a periodic orbit, then we tacitly assume that it is simple. If two periodic orbits $P_1=(w_1, T_1)$ and $P_2=(w_2, T_2)$ satisfy $w_1({\mathbb {R}}) = w_2({\mathbb {R}})$ and $T_1 = T_2,$ then they are identified, and we write $P_1 =P_2.$

Suppose that K is invariant under an anti-symplectic involution $\rho :{\mathbb {R}}^4 \rightarrow {\mathbb {R}}^4$, meaning that $\rho$ is an involution satisfying $\rho ^* \omega _0 = -\omega _0.$ The Hamiltonian vector field satisfies $\rho _* X_K = -X_K,$ so that

$$\begin{aligned} \phi _K^t = \rho \circ \phi _K^{-t} \circ \rho , \end{aligned}$$

where $\phi _K^t$ indicates the flow of $X_K,$ called the Hamiltonian flow of K. This shows that if $P=(w,T)$ is a periodic orbit, then $P_\rho = (w_\rho , T),$ defined as

$$\begin{aligned} w_\rho :{\mathbb {R}}\rightarrow \Sigma , \quad w_\rho (t) = \rho \circ w(T-t), \end{aligned}$$

is a periodic orbit, as well. In the case that $w({\mathbb {R}}) = w_\rho ({\mathbb {R}}),$ we write $P = P_\rho$ and call it a symmetric periodic orbit (with respect to $\rho$). Note that every symmetric periodic orbit intersects the fixed point set $\textrm{Fix}(\rho ),$ which is assumed to be non-empty, precisely at two points.

Assume that $\Sigma$ is compact and of contact type, i.e., there is a Liouville vector field Y that is transverse to $\Sigma .$ The one-form $\lambda = \omega _0(Y, \cdot )$ restricts to a contact form on $\Sigma ,$ still denoted by $\lambda .$ Denote by $R=R_\lambda$ the Reeb vector field of $\lambda .$ Note that the Hamiltonian vector field $X_K$ and the Reeb vector field R are related by

$$\begin{aligned} R = \frac{1}{\lambda (X_K)}X_K, \end{aligned}$$

implying that their flows coincide up to reparametrisation. The Reeb period of a periodic orbit P is defined as the period of P with respect to the Reeb flow.

If the Liouville vector field Y is invariant under $\rho$, i.e., it satisfies $\rho _* Y =Y,$ then $\rho$ becomes exact, meaning that it satisfies $\rho ^* \lambda = - \lambda .$ In this case, $\rho$ restricts to an anti-contact involution on the contact manifold $(\Sigma , \lambda ),$ again denoted by $\rho .$ The triple $(\Sigma , \lambda , \rho )$ is said to be a real contact manifold. Note that the Reeb vector field R and the Reeb flow $\phi _R^t$ satisfy

$$\begin{aligned} \rho _* R = -R, \quad \phi _R^t = \rho \circ \phi _R^{-t} \circ \rho . \end{aligned}$$

Therefore, given a periodic orbit $P=(w,T),$ the Reeb periods of P and $P_{\rho }$ coincide.

2.2 Conley–Zehnder index

As before, let $\Sigma =K^{-1}(0) \subset {\mathbb {R}}^4$ be a compact energy level of $K :{\mathbb {R}}^4 \rightarrow {\mathbb {R}},$ equipped with a transverse Liouville vector field Y. The corresponding contact form is denoted again by $\lambda .$

For every $z =(x_1, x_2, y_1, y_2) \in \Sigma$, the tangent space $T_z \Sigma$ is spanned by the orthogonal vectors $X_1, X_2, X_3$, defined as

$$\begin{aligned} X_j = A_j \nabla K, \quad j=1,2,3, \end{aligned}$$

(2.1)

where the $4 \times 4$ matrices $A_j, j=1,2,3,$ are given by

$$\begin{aligned} A_1 = \left( \begin{array}{cc} 0 &{}\quad J \\ J &{}\quad 0 \end{array} \right) , \ \ \ A_2 =\left( \begin{array}{cc} J &{} \quad 0 \\ 0 &{}\quad -J \end{array} \right) ,\ \ \ A_3 = \left( \begin{array}{cc} 0 &{}\quad I \\ -I &{}\quad 0 \end{array} \right) , \end{aligned}$$

with

$$\begin{aligned} I = \left( \begin{array}{cc} 1 &{}\quad 0 \\ 0 &{}\quad 1 \end{array} \right) , \ \ \ \ J = \left( \begin{array}{cc} 0 &{}\quad 1 \\ -1 &{}\quad 0 \end{array} \right) . \end{aligned}$$

Note that $X_3=A_3 \nabla K = X_K$ is parallel to the Reeb vector field R. The projection $\pi :T\Sigma \rightarrow \xi = \ker \lambda$ along R restricted to the tangent plane distribution $\textrm{span} \{X_1, X_2\}$ induces an isomorphism from $\textrm{span} \{X_1, X_2\}$ to the contact structure $\xi .$ In particular, the latter is spanned by the vector fields

$$\begin{aligned} \begin{aligned} {\overline{X}}_1&= \pi (X_1) = X_1 - \lambda (X_1)R,\\ {\overline{X}}_2&= \pi (X_2) = X_2 - \lambda (X_2)R. \end{aligned} \end{aligned}$$

(2.2)

Let $\mathfrak {T}$ denote the unitary trivialisation of $T \Sigma / {\mathbb {R}}X_3,$ induced by $X_1$ and $X_2.$ Set

$$\begin{aligned} \kappa _{ij}:= \langle {\textrm{Hess}}K \cdot X_i, X_j \rangle , \quad i,j=1,2,3. \end{aligned}$$

In the trivialisation $\mathfrak {T}$, the transverse linearised flow of the Hamiltonian vector field $X_K$ along a periodic trajectory $P=(w,T)$ on $\Sigma$ is described by solutions $\alpha (t)=(\alpha _1(t), \alpha _2(t)) \in {\mathbb {R}}^2$ to the ODE

$$\begin{aligned} \begin{pmatrix} {\dot{\alpha }}_1(t) \\ {\dot{\alpha }}_2(t) \end{pmatrix} = \begin{pmatrix} -\kappa _{12} &{} - \kappa _{22} - \kappa _{33} \\ \kappa _{11} + \kappa _{33} &{} \kappa _{12} \end{pmatrix} \bigg |_{w(t)} \begin{pmatrix} \alpha _1(t) \\ \alpha _2(t) \end{pmatrix}. \end{aligned}$$

(2.3)

Let $\vartheta (t)$ be any continuous argument of a non-vanishing solution $\alpha (t),$ i.e., $\alpha _1(t)+ i\alpha _2(t) \in {\mathbb {R}}_+ e^{i \vartheta (t)}.$ Define the rotation interval of P as

$$\begin{aligned} I = \{ \vartheta (T) - \vartheta (0) \mid \alpha (0)\ne 0 \}, \end{aligned}$$

(2.4)

which depends only on the initial condition $\alpha (0)\ne 0.$ It is a compact connected interval with length strictly less than $\pi .$ The periodic orbit P is non-degenerate if and only if $\partial I \cap 2 \pi {\mathbb {Z}}= \emptyset .$ Given $\varepsilon >0$ small enough, we set $I_\varepsilon := I - \varepsilon .$ Then, the Conley–Zehnder index of P is defined as

$$\begin{aligned} \mu _{\textrm{CZ}}(P) = {\left\{ \begin{array}{ll} 2k+1 &{} \text{ if } I_\varepsilon \subset ( 2k\pi , 2(k+1)\pi ), \\ 2k &{} \text{ if } 2k\pi \in \textrm{int}(I_\varepsilon ).\end{array}\right. } \end{aligned}$$

Note that, in this definition, the Conley–Zehnder index is lower semi-continuous with respect to the $C^0$-topology.

Suppose that the Hamiltonian K is invariant under an anti-symplectic involution $\rho :{\mathbb {R}}^4 \rightarrow {\mathbb {R}}^4,$ and the Liouville vector field Y satisfies $\rho _*Y=Y,$ so that $\rho$ restricts to an anti-contact involution of $\Sigma ,$ denoted again by $\rho$, as in the previous section. Since

$$\begin{aligned} \rho _* X_j = X_j, \quad j =1,2,3, \end{aligned}$$

we find by the definition of the Conley–Zehnder index that

$$\begin{aligned} \mu _{\textrm{CZ}}(P_\rho ) = \mu _{\textrm{CZ}}(P). \end{aligned}$$

2.3 Pseudoholomorphic curves in symplectisations

Let $(\Sigma ,\lambda )$ be a closed contact three-manifold. We denote by $\mathcal {J}(\lambda )$ the set of $d\lambda$-compatible almost complex structures on $\xi =\ker \lambda$. We extend each $J \in \mathcal {J}(\lambda )$ to a $d(e^r\lambda )$-compatible almost complex structure ${\tilde{J}}$ on $T({\mathbb {R}}\times \Sigma )$ that is given by

$$\begin{aligned} {\tilde{J}} :\partial _r \mapsto R, \quad {\tilde{J}}|_{\xi }=J, \end{aligned}$$

(2.5)

where r denotes the coordinate on ${\mathbb {R}}.$ Note that ${\tilde{J}}$ is ${\mathbb {R}}$-invariant.

Given a closed Riemann surface (S, j) and a finite set $\Gamma \subset S,$ we consider a smooth map ${\tilde{u}} = (a,u) :S {\setminus } \Gamma \rightarrow {\mathbb {R}}\times \Sigma ,$ satisfying $d{\tilde{u}} \circ j = {\tilde{J}} \circ d {\tilde{u}}$ and a finite energy condition

$$\begin{aligned} 0< E({\tilde{u}}):= \sup _{\phi } \int _{S \setminus \Gamma } {\tilde{u}}^* d(\phi \lambda )<\infty , \end{aligned}$$

where the supremum is taken over all monotone increasing smooth functions $\phi :{\mathbb {R}}\rightarrow [0,1].$ In this paper, we only consider the case $S=S^2$ and $\# \Gamma \in \{ 1, 2 \}.$ If $\# \Gamma = 1$ or $\# \Gamma =2,$ then such a map is called a finite energy plane or a finite energy cylinder, respectively.

Points in $\Gamma$ are called punctures of ${\tilde{u}}= (a,u).$ If a is bounded in a small neighbourhood of a puncture $z_0 \in \Gamma ,$ then $z_0$ is called removable. In this case, ${\tilde{u}}$ can be smoothly extended over $z_0$. See [9]. Otherwise, either $a(z) \rightarrow +\infty$ or $a(z) \rightarrow -\infty$ as $z \rightarrow z_0.$ Then, the puncture $z_0$ is called positive or negative, respectively. In the following, we assume that every puncture is not removable, so that the set $\Gamma$ is decomposed into $\Gamma = \Gamma ^+ \sqcup \Gamma ^-,$ where $\Gamma ^\pm$ consist only of positive/negative punctures, respectively. We assign $\varepsilon \in \{ \pm 1\}$ to each puncture $z_0 \in \Gamma ^\pm$ according to its sign.

The following statement is taken from [9] and [11].

Theorem 2.1

Given $z_0 \in \Gamma$, choose a holomorphic chart $\varphi :( \mathbb {D} {\setminus } \partial \mathbb {D}, 0) \rightarrow (\varphi (\mathbb {D} {\setminus } \partial \mathbb {D}), z_0)$ centred at $z_0.$ Abbreviate ${\tilde{u}}(s,t) = {\tilde{u}} \circ \varphi ( e^{-2\pi (s+it)}), (s,t) \in [0,+\infty ) \times {\mathbb {R}}/ {\mathbb {Z}}.$ Then, every sequence $s_n \rightarrow +\infty$ admits a subsequence $s_{n_k}$ and a $\tau$-periodic orbit x of the Reeb vector field, such that $u(s_{n_k}, t) \rightarrow x(\varepsilon \tau t+d)$ in $C^{\infty } ({\mathbb {R}}/ {\mathbb {Z}}, \Sigma )$ as $k \rightarrow +\infty ,$ for some $d \in {\mathbb {R}}.$ In the case x is non-degenerate, $u(s, t) \rightarrow x(\varepsilon \tau t+d)$ in $C^{\infty } ({\mathbb {R}}/ {\mathbb {Z}}, \Sigma )$ as $s \rightarrow +\infty .$

The periodic orbit x in the theorem above is called an asymptotic limit of ${\tilde{u}}$ at the puncture $z_0 \in \Gamma .$ If the puncture $z_0$ is positive or negative, the corresponding asymptotic limit is also called positive or negative, respectively. A finite energy curve is called non-degenerate if its every asymptotic limit is non-degenerate. The theorem above shows that a non-degenerate finite energy plane admits a unique asymptotic limit.

We now assume that $(\Sigma , \lambda )$ is equipped with an anti-contact involution $\rho .$ It defines the exact anti-symplectic involution ${{\tilde{\rho }}}:= \textrm{Id}_{\mathbb {R}}\times \rho$ on $({\mathbb {R}}\times \Sigma , d( e^r \lambda )),$ meaning that ${{\tilde{\rho }}}^* ( e^r \lambda ) = -e^r \lambda .$ An almost complex structure $J \in \mathcal {J}(\lambda )$ is said to be $\rho$-anti-invariant if

$$\begin{aligned} D\rho |_\xi \circ J \circ ( D\rho |_\xi )^{-1}=-J. \end{aligned}$$

(2.6)

Denote by $\mathcal {J}_\rho (\lambda ) \subset \mathcal {J}(\lambda )$ the set of $d\lambda$-compatible and $\rho$-anti-invariant almost complex structures on $\xi .$ If $J \in \mathcal {J}_\rho (\lambda ),$ then the associated $d(e^r \lambda )$-compatible almost complex structure ${\tilde{J}}$ as in (2.5) is $\tilde{\rho }$-anti-invariant. It follows that if ${\tilde{u}} = (a,u)$ is a finite energy ${\tilde{J}}$-holomorphic curve, then ${\tilde{u}}_{\rho }:= \rho \circ {\tilde{u}} \circ I,$ where $I(z) = {\bar{z}}$, is a finite energy ${\tilde{J}}$-holomorphic curve with Hofer energy $E(\tilde{u}_\rho ) = E({\tilde{u}}).$ Moreover, if x is a positive or negative asymptotic limit of ${\tilde{u}}$ at $z_0 \in \Gamma$, then $x_\rho$ is a positive or negative asymptotic limit of ${\tilde{u}}_\rho$ at $\bar{z}_0 \in I(\Gamma ),$ respectively. If ${\tilde{u}} = \tilde{u}_\rho ,$ then it is said to be invariant (with respect to $\rho$). Note that every asymptotic limit of invariant finite energy planes and cylinders has to be a symmetric periodic orbit. For more information on the behaviour of pseudoholomorphic curves under the symmetry, we refer the reader to [7, 19].

2.4 Transverse foliations

Let $\psi ^t$ be a smooth flow on an oriented closed three-manifold $\Sigma .$ A transverse foliation $\mathcal {F}$ of $\Sigma$ adapted to $\psi ^t$ is formed by the following data:

• (1) the singular set $\mathcal {P}$ which consists of finitely many simple periodic orbits, called binding orbits.

• (2) a smooth foliation of $\Sigma \setminus \cup _{P \in \mathcal {P}}P$ by properly embedded surfaces transverse to the flow. Each leaf $\mathring{F} \in \mathcal {F}$ has an orientation induced by the flow and the orientation of $\Sigma$. The closure F of $\mathring{F}$ is a compact embedded surface in $\Sigma$ whose boundary is a subset of $\mathcal {P}.$ Each end z of $\mathring{F}$ is called a puncture. Every puncture z is associated with a binding orbit $P_z \in \mathcal {P},$ called the asymptotic limit of $\mathring{F}$ at z. The asymptotic limit $P_z$ at z has two orientations, one induced by $\mathring{F}$ and the other induced by the flow. If the two orientations coincide with each other, then the puncture z is said to be positive. Otherwise, it is negative.

In the case where $\Sigma$ has a non-empty boundary that is tangent to the flow, then we extend the definition of a transverse foliation in such a way that every binding orbit is required to be contained in the interior of $\Sigma$ and each regular leaf is transverse to the boundary of $\Sigma$.

Assume that the flow $\psi ^t$ is anti-invariant under a smooth involution $\rho :\Sigma \rightarrow \Sigma ,$ meaning that $\psi ^t = \rho \circ \psi ^{-t} \circ \rho .$ A transverse foliation $\mathcal {F}$ is said to be symmetric (with respect to $\rho$) if $P_\rho \in \mathcal {P},$ $\forall P \in \mathcal {P},$ and $\mathring{F}_\rho :=\rho (\mathring{F}) \in \mathcal {F},$ $\forall \mathring{F} \in \mathcal {F}.$

2.5 Finite energy foliations

Let $\lambda$ be a contact form on the tight three-sphere $(S^3, \xi _0)$ and $J \in \mathcal {J}(\lambda ).$

Definition 2.2

A (stable) finite energy foliation for $(S^3, \lambda , J)$ is a two-dimensional smooth foliation $\tilde{\mathcal {F}}$ of ${\mathbb {R}}\times S^3$ satisfying the following properties:

• (1) Every leaf ${\tilde{F}} \in \tilde{\mathcal {F}}$ is the image of an embedded finite energy ${\tilde{J}}$-holomorphic curve ${\tilde{u}}_{{\tilde{F}}}=(a_{{\tilde{F}}}, u_{{\tilde{F}}})$ having only one positive puncture. The number of negative punctures is any finite number. The energies of such finite energy surfaces are uniformly bounded.

• (2) Every asymptotic limit of ${\tilde{F}}$ is unknotted and has Conley–Zehnder index 1, 2 or 3,  where asymptotic limits of a leaf ${\tilde{F}}$ is defined to be asymptotic limits of ${\tilde{u}}_{{\tilde{F}}}$.

• (3) A map $T :{\mathbb {R}}\times \tilde{\mathcal {F}} \rightarrow \tilde{\mathcal {F}}$

  $$\begin{aligned} T(c,{\tilde{F}}) = \{ (c + a, z) \in {\mathbb {R}}\times S^3 \mid (a, z) \in {\tilde{F}} \} \end{aligned}$$

  defines an ${\mathbb {R}}$-action on $\tilde{\mathcal {F}}.$ If ${\tilde{F}}$ is a fixed point of T, i.e., $T(c, {\tilde{F}}) = {\tilde{F}}, \forall c \in {\mathbb {R}},$ then its Fredholm index $\textrm{Ind}({\tilde{F}}):= \textrm{Ind}({\tilde{u}}_{{\tilde{F}}})$ is equal to 0 and ${\tilde{u}}_{\tilde{F}}$ is a cylinder over a periodic orbit. Here, the Fredholm index $\textrm{Ind}({\tilde{u}}_{{\tilde{F}}})$ represents the local dimension of the moduli space of unparametrised ${\tilde{J}}$-holomorphic curves near ${\tilde{u}}_{{\tilde{F}}}$ having the same asymptotic limits. In the case ${\tilde{F}}$ is not a fixed point, then $\textrm{Ind}(\tilde{F}) \in \{ 1, 2\}$ and $u_{{\tilde{F}}}$ is embedded and transverse to the Reeb flow of $\lambda .$

Every non-degenerate contact form $\lambda$ admits a finite energy foliation, as stated below.

Theorem 2.3

(Hofer, Wysocki and Zehnder [14]) Let $\lambda$ be a non-degenerate contact form on $(S^3, \xi _0).$ Then, for a generic J,  there is a finite energy foliation for $(S^3, \lambda , J).$

The projection of a finite energy foliation, obtained in the theorem above, to $S^3$ provides a transverse foliation adapted to the Reeb flow of $\lambda .$

Suppose that $(S^3, \lambda )$ admits an anti-contact involution $\rho$ and that $J \in \mathcal {J}_\rho (\lambda ).$ A finite energy foliation $\tilde{\mathcal {F}}$ is said to be symmetric (with respect to $\rho$) if ${\tilde{\rho }}(\tilde{\mathcal {F}}) = \tilde{\mathcal {F}}.$ The projection of a symmetric finite energy foliation to $S^3$ produces a symmetric transverse foliation.

3 The rotating Kepler problem

Recall that the Hamiltonian of the rotating Kepler problem is given by

$$\begin{aligned} H(q_1, q_2, p_1,p_2) = \frac{1}{2} ( (p_1 +q_2)^2 + (p_2 - q_1)^2) - \frac{1}{|q|}- \frac{1}{2} |q |^2. \end{aligned}$$

Consider a smooth function

$$\begin{aligned} f(r) = -\frac{1}{ r} - \frac{1}{2}r^2, \quad r>0. \end{aligned}$$

It is strictly increasing for $r<1$ and decreasing for $r>1$ and attains a unique global maximum $-\frac{3}{2}$ at $r=1.$ Therefore, for every $c<-\frac{3}{2}$, the equation $f(r)=c$ has precisely two roots $r_c^b< 1 < r_c^u.$ It follows that for every $c<-\frac{3}{2}$, the energy level $H^{-1}(c)$ consists of two components, $\Sigma _c^b$ that projects to $\{ q \in {\mathbb {R}}^2 {\setminus } \{ 0 \}: |q |\le r_c^b\}$ and $\Sigma _c^u$ that projects to $\{ q \in {\mathbb {R}}^2 {\setminus } \{ 0 \}: |q |\ge r_c^u\}.$ If $-\frac{3}{2}< c < 0$, then $H^{-1}(c)$ is connected and projects to ${\mathbb {R}}^2 \setminus \{ 0 \}.$

Since $\{ E, L \} =0$, where the Kepler energy E and the angular momentum L are as in (1.2), the Hamiltonian flows of E and L commute

$$\begin{aligned} \phi _H^t = \phi _{E-L}^t= \phi _E^t \circ \phi _{-L}^t = \phi _{-L}^t \circ \phi _E^t = \phi _L^{-t} \circ \phi _E^t. \end{aligned}$$

See, for instance, [8, Theorem 3.1.7]. Therefore, given a trajectory $\gamma (t)$ of H, i.e., a trajectory of the Hamiltonian vector field $X_H,$ there exists a Kepler ellipse $\alpha (t)$, such that

$$\begin{aligned} \gamma (t) = \exp (- it)\alpha (t). \end{aligned}$$

(3.1)

Note that $\gamma$ is not necessarily periodic. It is periodic if and only if the period of $\alpha$ and $2 \pi$ are ${\mathbb {Q}}$-commensurable. In other words, if we denote the period of $\alpha$ by $T>0$, then $\gamma$ is periodic if and only if

$$\begin{aligned} kT = 2 \pi l \quad \text { for some coprime positive integers } k,l. \end{aligned}$$

(3.2)

Let $\alpha (t)$ be a Kepler ellipse that projects to a circular orbit. Then, $\gamma (t),$ as in (3.1), is circular as well. This happens if and only if $X_E$ and $X_L$ are parallel along $\alpha (t)$. To study circular orbits, recall that the eccentricity e of a Kepler ellipse satisfies

$$\begin{aligned} e^2 = 2EL^2 +1. \end{aligned}$$

(3.3)

Since circular orbits have $e=0$, we obtain

$$\begin{aligned} 0 = 2 E ( H-E)^2+1. \end{aligned}$$

(3.4)

Fix $H=c$. If $c< -\frac{3}{2}$, then Eq. (3.4) has three solutions

$$\begin{aligned} E_{\textrm{retro}}^b< E_{\textrm{direct}}^b< - \frac{1}{2}< E_\textrm{direct}^u <0, \end{aligned}$$

implying that $H^{-1}(c)$ carries precisely three circular orbits: $\gamma _{\textrm{retro}}^b$ with $E= E_{\textrm{retro}}^b$ and $\gamma _{\textrm{direct}}^b$ with $E = E_{\textrm{direct}}^b,$ both lying on $\Sigma _c^b,$ and $\gamma _{\textrm{direct}}^u$ with $E = E_\textrm{direct}^u,$ lying on $\Sigma _c^u.$ Their angular momenta are

$$\begin{aligned} L _{\textrm{retro}}^b = - \frac{1}{\sqrt{ -2 E_{\textrm{retro}}^b}}, \quad L _{\textrm{direct}}^b = \frac{1}{\sqrt{ -2 E_{\textrm{direct}}^b}}, \quad L _{\textrm{direct}}^u = \frac{1}{\sqrt{ -2 E_{\textrm{direct}}^u}}, \end{aligned}$$

respectively. Note that our coordinate system rotates in the counterclockwise direction. Therefore, $\gamma _{\textrm{retro}}^b$ rotates in opposite direction to the coordinate system and $\gamma _{\textrm{direct}}^b$ and $\gamma _{\textrm{direct}}^u$ rotate in the same direction with the coordinate system. For this reason, $\gamma _{\textrm{retro}}^b$ is called the retrograde circular orbit and $\gamma _{\textrm{direct}}^b$ and $\gamma _{\textrm{direct}}^u$ are called the direct circular orbits.

Assume that $-\frac{3}{2}< c < 0$. In this case, Eq. (3.4) has a unique solution $E = E_{\textrm{retro}} ^u\in (-2,0)$, implying that $H^{-1}(c)$ carries a unique circular orbit, denoted by $\gamma _{\textrm{retro}}^u$, whose angular momentum is given by

$$\begin{aligned} L _{\textrm{retro}}^u = - \frac{1}{\sqrt{ -2 E_{\textrm{retro}}^u}} \in \Bigg ( -\frac{1}{\root 3 \of {2}}, - \frac{1}{2}\Bigg ). \end{aligned}$$

This unique circular orbit is retrograde. See Fig. 3.

Suppose that $\alpha (t)$ is a non-circular Kepler ellipse and let $\gamma (t)$ be the corresponding periodic trajectory of H, satisfying (3.1) and (3.2). Since L generates rotation, it implies that $\gamma (t)$ lies in an $S^1$-family of periodic trajectories of H satisfying the same condition. For this reason, we call a periodic trajectory of H satisfying (3.2) a $T_{k,l}$-type orbit and an $S^1$-family of $T_{k,l}$-type orbits a $T_{k,l}$-torus.

The Kepler energy is constant along each $T_{k,l}$-torus. Indeed, Kepler’s third law implies

$$\begin{aligned} T^2 = \frac{ (2\pi )^2}{(-2E)^3}, \end{aligned}$$

and hence, using (3.2), we obtain

$$\begin{aligned} E_{k,l}:= -\frac{1}{2} \left( \frac{k}{l} \right) ^{\frac{2}{3}}. \end{aligned}$$

One can easily check that in the case $c<-\frac{3}{2}$, all $T_{k,l}$-type orbits satisfy $k>l$ on $\Sigma _c^b$ and $k<l$ on $\Sigma _c^u.$

For a fixed coprime $k,l \in {\mathbb {N}},$ identifying (3.3) determines a one-parameter family of $T_{k,l}$-tori. Either the eccentricity e, the angular momentum L, or the total energy $H=c$ can be regarded as the parameter of such a family. We call this family the $T_{k,l}$-torus family. See Fig. 4.

Fig. 3

The solution set of (left) $2E(c-E)^2+1=0$; (right) $2(c+L)L^2+1=0$ is the union of two graphs. The left and right curves indicate the retrograde and direct circular orbits, respectively

Fig. 4

Some $T_{k,l}$-tori with $k=9.$ The dashed line indicates the tori consisting only of collision orbits

Observe that along every $T_{k,l}$-torus family, there is a unique $T_{k,l}$-torus containing a collision orbit (and hence it consists only of collision orbits). Indeed, a $T_{k,l}$-type orbit $\gamma (t)$ is a collision orbit if and only if a Kepler ellipse $\alpha (t)$ is a collision orbit. This happens precisely at $e=1,$ and in view of (3.3), this implies $L=0,$ or equivalently $H=E.$ A $T_{k,l}$-type orbit is said to be direct or retrograde if it satisfies $L>0$ or $L<0,$ respectively.

We summarize the discussion so far in the following. Recall that we consider orbits with $E<0$.

Lemma 3.1

Let $c < -\frac{3}{2}$. When projected to $\Sigma _c^b,$ the Kepler energy E satisfies

$$\begin{aligned} E_{\textrm{retro}}^b \le E \le E_{\textrm{direct}}^b <-\frac{1}{2}, \end{aligned}$$

and the angular momentum L satisfies

$$\begin{aligned} L_{\textrm{retro}}^b \le L \le L_{\textrm{direct}}^b <1. \end{aligned}$$

When projected to $\Sigma _c^u$, we have

$$\begin{aligned} -\frac{1}{2}< E_{\textrm{direct}}^u \le E<0, \quad \ \ 1< L _{\textrm{direct}}^u \le L <-c. \end{aligned}$$

In the case $-\frac{3}{2}< c < 0$, we have

$$\begin{aligned} -2< E_{\textrm{retro}}^u \le E<0, \quad \ \ -\frac{1}{\root 3 \of {2}}< L _{\textrm{retro}}^u \le L <-c. \end{aligned}$$

4 Poincaré’s coordinates

We briefly recall the definition of Poincaré’s coordinates. For more details, we refer the reader to [1, Chapter 9] and [24, Section 8.9].

Consider the following open subset of $T^* ( {\mathbb {R}}^2 {\setminus } \{ 0 \})$:

$$\begin{aligned} \mathcal {E} = \{ (q,p) \in T^* ( {\mathbb {R}}^2 \setminus \{ 0 \} ): E(q,p)< 0< e(q,p)<1, \ L(q,p)>0 \}, \end{aligned}$$

called the direct elliptical domain (recall that we have $L>0$ along direct orbits, see Sect. 3), and define smooth maps $\alpha , \beta :\mathcal {E} \rightarrow {\mathbb {R}}/ 2\pi {\mathbb {Z}}$ and $a :\mathcal {E} \rightarrow {\mathbb {R}}$ as follows. Choose $(q,p) \in \mathcal {E}$ and let $\gamma$ denote the Kepler ellipse on which the point (q, p) lies. Then, $\alpha = \alpha (q,p)$ is defined as the argument of the position q,  and $\beta = \beta (q,p)$ is defined to be the argument of the perihelion, i.e., the point, lying on the projection of $\gamma$ to the q-plane, that is nearest to the origin. Finally, $a = a(q,p)$ is defined to be the semi-major axis of the Kepler ellipse $\gamma .$ Note that $a = -\frac{1}{2E},$ where $E<0$ indicates the Kepler energy of $\gamma .$ See Fig. 5.

Set $\mathcal {K}= {\mathbb {R}}/ 2\pi {\mathbb {Z}}\times {\mathbb {R}}/ 2\pi {\mathbb {Z}}\times S,$ where $S = \{ (x, y) \in {\mathbb {R}}^2: x>0, y \in (0,1) \}.$ Then, there is a diffeomorphism

$$\begin{aligned} {\mathscr {K}} :\mathcal {E} \rightarrow \mathcal {K}, \quad (q_1,q_2,p_1,p_2) \mapsto (\alpha , \beta , a,e), \end{aligned}$$

called the Kepler map. This implies that the domain $\mathcal {E}$ is a thickened two-torus.

Theorem 4.1

(Lagrange, 1808) The Kepler map ${\mathscr {K}}$ satisfies

$$\begin{aligned} {\mathscr {K}} _* ( dp_1 \wedge dq_1 + dp_2 \wedge dq_2) = d \sqrt{ a (1-e^2)} \wedge d \beta + d \sqrt{a} \wedge d(\alpha - \beta ). \end{aligned}$$

Fig. 5

Some quantities associated with a Kepler ellipse of Kepler energy $E<0$. The quantity a is the semi-major axis that is equal to $-\frac{1}{2E}.$ The quantity $\alpha$ is given by the argument of the present position, and $\beta$ is given by the argument of the perihelion

Suggested by this result, Delaunay (1860) considered a diffeomorphism

$$\begin{aligned} {\mathscr {D}} :\mathcal {K} \rightarrow \mathcal {D}, \quad (\alpha , \beta , a, e) \mapsto ( \beta , \alpha - \beta , \sqrt{ a ( 1-e^2)}, \sqrt{ a}), \end{aligned}$$

where

$$\begin{aligned} \mathcal {D}:= {\mathbb {R}}/ 2 \pi {\mathbb {Z}}\times {\mathbb {R}}/ 2 \pi {\mathbb {Z}}\times \mathcal {O}, \quad \mathcal {O}=\{ (x,y) \in {\mathbb {R}}^2: 0<x<y \}. \end{aligned}$$

Write

$$\begin{aligned} (l, k, L, K) = ( \beta , \alpha - \beta , \sqrt{ a ( 1-e^2)}, \sqrt{ a}) \end{aligned}$$

and define

$$\begin{aligned} \Delta = {\mathscr {D}} \circ {\mathscr {K}} :\mathcal {E} \rightarrow \mathcal {D}, \quad (q_1, q_2,p_1,p_2) \mapsto (l, k, L, K), \end{aligned}$$

called the Delaunay map. Theorem 4.1 implies that $\Delta$ is a symplectomorphism, namely, it satisfies

$$\begin{aligned} \Delta _* ( dp_1 \wedge dq_1 + dp_2 \wedge dq_2 ) = d L \wedge dl + dK \wedge dk. \end{aligned}$$

However, since the argument of the perihelion is undefined for a circular orbit, the Delaunay map cannot be used to study the dynamics in a neighbourhood of a circular orbit.

Remark 4.2

The classical notations of the Delaunay variables are (g, l, G, L), not (l, k, L, K). However, we stick to our choice, since we would like to denote the angular momentum by L.

To remedy this problem, Poincaré introduced new coordinates as follows. Define

$$\begin{aligned} \Pi :\mathcal {D} \rightarrow {\mathbb {R}}\times {\mathbb {R}}/ 2 \pi {\mathbb {Z}}\times {\mathbb {R}}\times {\mathbb {R}}, \quad (l, k, L, K) \mapsto (\eta , \lambda , \xi , \Lambda ), \end{aligned}$$

where

$$\begin{aligned} \eta&= - \sqrt{ 2(K-L)} \sin l, \\ \lambda&= l + k ,\\ \xi&= \sqrt{ 2 (K-L) } \cos l,\\ \Lambda&= K. \end{aligned}$$

It turned out that $\Pi$ is a symplectomorphism onto its image $\mathcal {P} = \Pi (\mathcal {D}).$ We then define the Poincaré mapping

$$\begin{aligned} {\mathscr {P}} = \Pi \circ \Delta = \Pi \circ {\mathscr {D}} \circ {\mathscr {K}} :\mathcal {E} \rightarrow \mathcal {P}, \end{aligned}$$

which is a symplectomorphism as well. Namely, it satisfies

$$\begin{aligned} {\mathscr {P}} ^* ( d\xi \wedge d\eta + d\Lambda \wedge d\lambda ) = dp_1 \wedge dq_1 + dp_2 \wedge dq_2. \end{aligned}$$

We shall now add the circular orbits. Recall that for the circular orbits, we have $e=0, \alpha = \beta$ and $L=K.$ Let

$$\begin{aligned} \overline{\mathcal {E}}&= \mathcal {E} \cup \{ (q,p) \in T^* ( {\mathbb {R}}\setminus \{ 0 \} ) : E(q,p)< 0 = e(q,p), \ L(q,p)>0 \} \\&= \{ (q,p) \in T^* ( {\mathbb {R}}\setminus \{ 0 \} ) : E(q,p)< 0 \le e(q,p)<1, \ L(q,p)>0 \} \end{aligned}$$

and

$$\begin{aligned} \overline{\mathcal {P}} = \mathcal {P} \cup \{ ( 0, \lambda , 0, \Lambda ): \lambda \in {\mathbb {R}}/ 2 \pi {\mathbb {Z}}, \Lambda >0 \}. \end{aligned}$$

If $e(q_1, q_2, p_1,p_2) =0,$ then we set

$$\begin{aligned} {{\mathscr {P}}} (q_1, q_2, p_1,p_2) = (0, \lambda , 0, \Lambda ) \end{aligned}$$

by defining $\lambda =\alpha$ and $\Lambda = L=K.$ This extends the Poincaré mapping to a symplectomorphism ${{\mathscr {P}}} :\overline{\mathcal {E}} \rightarrow \overline{\mathcal {P}}.$ We conclude that in the study of direct orbits, i.e., orbits with $L>0,$ we can work with the transformed Hamiltonian ${{\mathscr {P}}}_*H :\overline{\mathcal {P}} \rightarrow {\mathbb {R}}.$

We now consider

$$\begin{aligned} \overline{\mathcal {E}}' = \{ (q,p) \in T^* ( {\mathbb {R}}^2 \setminus \{ 0 \} ): E(q,p)< 0 \le e(q,p)<1, \ L(q,p)<0 \}, \end{aligned}$$

and note that $\psi ( \overline{\mathcal {E}}') =\overline{\mathcal {E}},$ where $\psi ( q_1,q_2,p_1,p_2) = (q_ 1,q_2,-p_1,-p_2).$ Define $\phi :\overline{\mathcal {P}} \rightarrow \overline{\mathcal {P}}':= \phi (\overline{\mathcal {P}})$ by

$$\begin{aligned} \phi ( \eta , \lambda ,\xi , \Lambda ) = (\eta , \lambda , -\xi , -\Lambda ). \end{aligned}$$

Then, we obtain a symplectomorphism

$$\begin{aligned} {\mathscr {P}}':=\phi \circ {\mathscr {P}} \circ \psi :\overline{\mathcal {E}}' \rightarrow \overline{\mathcal {P}}'. \end{aligned}$$

It follows that in the study of retrograde orbits, i.e., orbits with $L<0,$ we can work with the transformed Hamiltonian ${\mathscr {P}}'_*H :\overline{\mathcal {P}}' \rightarrow {\mathbb {R}}.$

5 Below the critical energy

Throughout the section, we fix $c<-\frac{3}{2}$ and $E_0 \in (E_{\textrm{direct}}^u, 0).$ We shall prove the assertion of Theorem 1.1 for the set

$$\begin{aligned} \Sigma _{\textrm{direct}}^u = \{\text {all periodic orbits of } X_H \text { with} E \in [E_{\textrm{direct}}^u, E_0]\} \subset \Sigma _c^u, \end{aligned}$$

diffeomorphic to a solid torus with core being the direct circular orbit $\gamma _{\textrm{direct}}^u.$ Note that it contains only direct orbits and no collision orbits. Indeed, every periodic orbit on $\Sigma _{\textrm{direct}}^u$ has $L>0.$ See Lemma 3.1.

Remark 5.1

The neighbourhood $\Sigma ^u_{\textrm{direct}}$ of $\gamma ^u_{\textrm{direct}}$ could be arbitrarily large: just take $E_0 \in (E^u_{\textrm{direct}}, 0)$ to be sufficiently close to 0.

We shall work in Poincaré’s coordinates. For simplicity, we write $(x_1, x_2, y_1, y_2) = (\eta , \lambda , \xi , \Lambda ).$ Note that

$$\begin{aligned} y_2 = \sqrt{a} = \frac{1}{\sqrt{-2E}}, \quad x_1^2 +y_1^2 = 2(y_2-L). \end{aligned}$$

Then, the Hamiltonian (1.1) is given in Poincaré’s coordinates by

$$\begin{aligned} H (x_1, x_2, y_1, y_2) = - \frac{1}{2y_2^2} - y_2 + \frac{1}{2} ( x_1 ^2 + y_1 ^2) \end{aligned}$$

(5.1)

for $(x_1, x_2, y_1, y_2) \in \overline{\mathcal {P}} \subset {\mathbb {R}}\times {\mathbb {R}}/ 2 \pi {\mathbb {Z}}\times {\mathbb {R}}\times {\mathbb {R}}_+.$ We set

$$\begin{aligned} H_1(x_1, y_1) = \frac{1}{2}(x_1^2 + y_1^2), \quad H_2( y_2) = - \frac{1}{2y_2^2}-y_2, \end{aligned}$$

(5.2)

so that $H = H_1 + H_2.$

Since $E_0 \in ( E_{\textrm{direct}}^u, 0)$ is fixed and we consider the subset $\Sigma _{\textrm{direct}}^u \subset \Sigma _c^u,$ we have

$$\begin{aligned} y_2 \in [\Lambda _1, \Lambda _2] \quad \; \; \text{ on } \; \; \Sigma _{\textrm{direct}}^u, \end{aligned}$$

where $\Lambda _1 = \sqrt{ -\frac{1}{2E_{\textrm{direct}}^u}}$ and $\Lambda _2 = \sqrt{ - \frac{1}{2E_0}}.$ Since $E_{\textrm{direct}}^u >- \frac{1}{2},$ see Lemma 3.1, we have $\Lambda _1>1.$

5.1 Disc foliation

It is easy to construct a disc foliation of $\Sigma _{\textrm{direct}}^u$ transverse to the Hamiltonian flow by looking at the negative gradient flow lines of $H_2.$ These are solutions to the ODE

$$\begin{aligned} \dot{x}_2 = - (H_2)_{x_2} = 0, \quad \dot{y}_2 = - (H_2)_{y_2} = -\frac{1}{ y_2^3}+1 >0. \end{aligned}$$

Therefore, along every negative gradient flow line, the $x_2$-component is constant and the $y_2$-component is strictly increasing. See Fig. 6.

Fig. 6

Negative gradient flow lines of $H_2.$ Dashed lines indicate Hamiltonian trajectories

Pick any $x_2 \in {\mathbb {R}}/ 2 \pi {\mathbb {Z}}$ and let $h_{x_2}$ be the corresponding negative gradient flow line of $H_2.$ Denote by $\Pi :\Sigma _{\textrm{direct}}^u \rightarrow {\mathbb {R}}^2$ the projection $(x_1, x_2, y_1, y_2) \mapsto (x_2, y_2).$ Then, the preimage $\Pi ^{-1}(h_{x_2})$ is an embedded disc in $\Sigma _{\textrm{direct}}^u$ that is transverse to the Hamiltonian flow. The point $\Pi ^{-1}(x_2, \Lambda _1)$ is the intersection of the disc $\Pi ^{-1}(h_{x_2})$ and the direct circular orbit $\gamma _{\textrm{direct}}^u.$ By varying $x_2 \in {\mathbb {R}}/ 2 \pi {\mathbb {Z}},$ we obtain the desired disc foliation.

Below we shall embed $\Sigma _{\textrm{direct}}^u$ into a weakly convex three-sphere and construct a symmetric finite energy foliation of the three-sphere. We then obtain a disc foliation as the intersection of the projection of the finite energy foliation with $\Sigma _{\textrm{direct}}^u.$

5.2 Interpolation

Fix $\Lambda _3 \in (\Lambda _2, +\infty )$ and $0< \varepsilon _0 < \frac{1}{2} ( \Lambda _3 - \Lambda _2).$

Consider

$$\begin{aligned} F( x_2, y_2) = \frac{1}{2} ( y_2 - \Lambda _3)^2 - \cos \frac{x_2}{2} +B, \end{aligned}$$

where $(x_2, y_2) \in {\mathbb {R}}/ 4\pi {\mathbb {Z}}\times {\mathbb {R}}_+$, and the constant B satisfies

$$\begin{aligned} B< - \frac{1}{2 ( \Lambda _2+\varepsilon _0)^2} - (\Lambda _2 + \varepsilon _0) - \frac{1}{2} ( \Lambda _2 + \varepsilon _0 - \Lambda _3)^2 -1 \end{aligned}$$

(5.3)

and define

$$\begin{aligned} K(x_2, y_2) = \left( 1 - f(y_2) \right) H_2( y_2) + f(y_2) F(x_2, y_2), \end{aligned}$$

(5.4)

where $f:{\mathbb {R}}\rightarrow [0,1]$ is a non-decreasing function satisfying $f(y_2) =0$ for $y_2 < \Lambda _2 + \varepsilon _0$ and $f(y_2)=1$ for $y_2 > \Lambda _2 +2\varepsilon _0.$ See Fig. 7.

Set

$$\begin{aligned} \bar{H}(x_1, x_2, y_1, y_2) = H_1(x_1, y_1) + K(x_2, y_2), where (x_2, y_2) \in {\mathbb {R}}/ 4\pi {\mathbb {Z}}\times {\mathbb {R}}_+, \end{aligned}$$

and denote by ${\bar{\Sigma }}$ the connected component of $\bar{H}^{-1}(c)$ that contains a double cover $\bar{\Sigma }^u_\textrm{direct}$ of $\Sigma _\textrm{direct}^u.$ Note that ${\bar{H}}$ is invariant under the anti-symplectic involution

$$\begin{aligned} \rho ( x_1, x_2, y_1, y_2) = ( -x_1, 4 \pi - x_2, y_1, y_2). \end{aligned}$$

(5.5)

We claim that for $y_2 \ge \Lambda _1,$ the smooth function K has precisely two critical points $(0, \Lambda _3)$ that is a saddle and $(2\pi , \Lambda _3)$ that is a global minimum. In fact, we show that

$$\begin{aligned} K_{y_2}<0, \ \forall y_2 < \Lambda _3 \quad \text { and } \quad K_{y_2}>0, \ \forall y_2 > \Lambda _3. \end{aligned}$$

(5.6)

It suffices to show that K is strictly decreasing in $y_2,$ provided $y_2 \in [\Lambda _2+\varepsilon _0, \Lambda _2 +2\varepsilon _0].$ We assume that $y_2 \in [\Lambda _2+\varepsilon _0, \Lambda _2 +2\varepsilon _0]$ and find that

$$\begin{aligned} K_{y_2}&= f' \cdot \left( \frac{1}{2 y_2^2 } + y_2+ \frac{1}{2} ( y_2 - \Lambda _3)^2 - \cos \frac{x_2}{2} + B\right) \\&\quad + (1-f) \cdot \left( \frac{1}{y_2^3}-1\right) + f \cdot ( y_2 - \Lambda _3 ). \end{aligned}$$

The first term in the right-hand side is non-positive due to the choice of the constant B. See (5.3). The second term is non-positive, since $1<\Lambda _2,$ and the last term is also non-positive because of the choice of $\varepsilon _0.$ Note that at least one of the three terms is non-zero. This implies that K admits a critical point only if $y_2 = \Lambda _3,$ provided $y_2 \ge \Lambda _1.$ The rest of the claim is straightforward.

Given $x_2,$ define

$$\begin{aligned} \Lambda _{\max } = \Lambda _{\max }(x_2):= \max \{ y_2 \mid (x_1, x_2, y_1, y_2) \in \bar{\Sigma } \}. \end{aligned}$$

Notice that it satisfies $K (x_2, \Lambda _{\max })=c$ and that

$$\begin{aligned} \Lambda _1 = \min \{ y_2 \mid (x_1, x_2, y_1, y_2) \in \bar{\Sigma } \}. \end{aligned}$$

We now introduce

$$\begin{aligned} G(x_2, y_2) = \frac{1}{2} x_2^2 + \frac{1}{2}( y_2 - \Lambda _3)^2. \end{aligned}$$

Given $\varepsilon _1>0,$ choose any non-decreasing smooth function $g:{\mathbb {R}}\rightarrow [0,1]$ satisfying $g(x_2) =0$ for $x_2 < - 2\varepsilon _1$ and $g(x_2)=1$ for $x_2 > -\varepsilon _1$ and define

$$\begin{aligned} {\tilde{K}}(x_2, y_2) = \left( 1 - g(x_2) \right) G(x_2, y_2) + g(x_2) K(x_2, y_2). \end{aligned}$$

We repeat a similar business for $x_2 \ge 4 \pi$ in a symmetric way (note that the function K is symmetric in $x_2$ with respect to $x_2 =2\pi$). Namely, we interpolate between the smooth functions ${\tilde{K}}$ and

$$\begin{aligned} {\tilde{G}} (x_2, y_2) = \frac{1}{2} ( x _2 - 4\pi )^2 + \frac{1}{2} ( y_2 - \Lambda _3)^2 \end{aligned}$$

using the non-increasing function ${\tilde{g}} (x_2):= g( 4 \pi - x_2).$ This produces a smooth function ${\tilde{H}}_2 (x_2, y_2),$ which is still symmetric in $x_2$ with respect to $x_2 = 2\pi .$ Note that we have broken the periodicity in $x_2.$ See Fig. 7.

Fig. 7

Interpolations for $y_2$(left) and $x_2$(right)

Lemma 5.2

The function ${\tilde{H}}_2$ admits precisely three critical points $(x_2, y_2) = (0,\Lambda _3), (2\pi , \Lambda _3)$ and $(4\pi , \Lambda _3).$

Proof

By the definition and symmetry of ${\tilde{H}}_2,$ it suffices to show that there are no critical points of ${\tilde{H}}_2$ in $\{ -2 \varepsilon _1< x_2 < - \varepsilon _1 \}.$

We assume $-2 \varepsilon _1< x_2 < - \varepsilon _1$ and find that

$$\begin{aligned} ({\tilde{H}}_2)_{x_2}&= \left( 1-g(x_2) \right) x_2 + \frac{ f(x_2)g(x_2)}{2} \sin \frac{x_2}{2}+ g'(x_2)(K-G),\\ ({\tilde{H}}_2)_{y_2}&= \left( 1-g(x_2)\right) (y_2 - \Lambda _3) + g(x_2) K_{y_2}. \end{aligned}$$

If $y_2 \ge \Lambda _1,$ then we obtain in view of (5.6) that

$$\begin{aligned} ({\tilde{H}}_2)_{y_2}<0,\; \forall y_2 <\Lambda _3, \quad (\tilde{H}_2)_{y_2}>0, \; \forall y_2 >\Lambda _3, \end{aligned}$$

and hence, $({\tilde{H}}_2)_{y_2}$ vanishes only if $y_2=\Lambda _3.$ We then compute

$$\begin{aligned} K(x_2, \Lambda _3) - G(x_2, \Lambda _3) = -\cos \frac{x_2}{2} - \frac{1}{2} x_2^2 + B <0, \end{aligned}$$

so that $( {\tilde{H}}_2)_{x_2} |_{ y_2 = \Lambda _3} <0.$

Suppose that $y_2 < \Lambda _1,$ so that

$$\begin{aligned} ({\tilde{H}}_2)_{x_2}&= \left( 1-g(x_2) \right) x_2 + g'(x_2)\left( - \frac{1}{2 y_2^2}-y_2 - \frac{1}{2}x_2^2 - \frac{1}{2}(y_2-\Lambda _3)^2 \right) ,\\ ({\tilde{H}}_2)_{y_2}&= \left( 1 - g(x_2) \right) (y_2- \Lambda _3) + g(x_2) \left( \frac{1}{y_2^3}-1 \right) . \end{aligned}$$

Note that $({\tilde{H}}_2)_{y_2}$ may vanish for $y_2 <1.$ For $y_2 >0,$ a global minimum of the function $\frac{1}{2 y_2^2} + y_2 + \frac{1}{2}(y_2-\Lambda _3)^2$ is positive, and hence, we have $({\tilde{H}}_2)_{x_2}<0,$ provided $y_2<1.$

We conclude that there exist no critical points of ${\tilde{H}}_2$ in $\{ -2 \varepsilon _1< x_2 < - \varepsilon _1 \},$ from which the lemma follows. $\square$

We define the modified Hamiltonian

$$\begin{aligned} {\tilde{H}}(x_1, x_2, y_1, y_2) = H_1(x_1, y_2) + {\tilde{H}}_2(x_2, y_2). \end{aligned}$$

The anti-symplectic involution $\rho$ in (5.5) induces an anti-symplectic involution on ${\mathbb {R}}^3 \times {\mathbb {R}}_+,$ again denoted by $\rho .$ Note that ${\tilde{H}}$ is $\rho$-invariant.

The previous lemma implies that the Hamiltonian ${\tilde{H}}$ admits precisely three critical points

$$\begin{aligned} p_{c1} = (0, 0, 0, \Lambda _3), \quad p_{c2} = (0,2\pi ,0,\Lambda _3), \quad p_{c3} = (0,4\pi , 0,\Lambda _3). \end{aligned}$$

(5.7)

Since ${\tilde{H}}(p_{c1}) = {\tilde{H}}( p_{c3}) = -1+B< {\tilde{H}}( p_{c2}) = 1+B<c$ and $p_{c2}$ has Morse index 1 as a critical point of ${\tilde{H}},$ it follows from standard Morse theory that the energy level ${\tilde{H}}^{-1}(c)$ contains a unique connected component, denoted by $\Sigma ,$ which is diffeomorphic to $S^3.$ Note that $\Sigma$ is $\rho$-invariant.

For later use, we prove the following assertion.

Lemma 5.3

Along $\Sigma$, we have $y_2>1,$ and hence

$$\begin{aligned} {\tilde{H}}_{y_2}<0, \ \forall y_2 < \Lambda _3, \quad {\tilde{H}}_{y_2}>0, \ \forall y_2 > \Lambda _3. \end{aligned}$$

Proof

By the definition and symmetry of ${\tilde{H}}_2$, without loss of generality, we may assume that $-2 \varepsilon _1< x_2 < - \varepsilon _1.$

Fix $-2 \varepsilon _1< x_2 < - \varepsilon _1$ and consider the smooth function

$$\begin{aligned} Q( y_2)= \frac{1}{2}\left( 1 - g(x_2) \right) (y_2- \Lambda _3)^2 + g(x_2) \left( - \frac{1}{2 y_2^2}-y_2\right) , \quad y_2>0. \end{aligned}$$

There is $a=a(x_2)\in (0,1)$, such that the function Q is strictly increasing for $y_2 \in (0,a)$ and is strictly decreasing for $y_2 \in (a, \Lambda _2 + \varepsilon _0).$

Every point $(x_1, x_2, y_1, y_2) \in \Sigma$ with $y_2 < \Lambda _2 + \varepsilon _0$ satisfies

$$\begin{aligned} Q( y_2)= c - \frac{1}{2}x_2^2 \left( 1 - g(x_2) \right) - \frac{1}{2}(x_1^2+ y_1^2), \end{aligned}$$

and hence, we find

$$\begin{aligned} Q(y_2)&\le c - \frac{1}{2}x_2^2 \left( 1 - g(x_2)\right) \\&< - \frac{3}{2}g(x_2) +\frac{1}{2} \left( 1 - g(x_2) \right) (1- \Lambda _3)^2 \\&= Q( 1). \end{aligned}$$

This together with compactness of $\Sigma$ implies that for any $(x_1, x_2, y_1, y_2) \in \Sigma$ with $x_2 \in (-2 \varepsilon _1, - \varepsilon _1)$, the component $y_2$ is bigger than 1. The rest of the lemma is straightforward. This finishes the proof. $\square$

5.3 Construction of a contact form

In this section, we construct a $\rho$-invariant Liouville vector field Y that is transverse to $\Sigma .$ Then, the restriction of the one-form $\omega _0(Y, \cdot )$ to $\Sigma$ defines a contact form on $\Sigma$, denoted by $\lambda .$ The anti-symplectic involution $\rho :{\mathbb {R}}^4 \rightarrow {\mathbb {R}}^4$ restricts to an anti-contact involution on $\Sigma ,$ still denoted by $\rho .$ Consequently, we obtain a real contact manifold $(\Sigma , \lambda , \rho ).$ Recall from Sect. 2.3 that $\rho$ provides the exact anti-symplectic involution ${{\tilde{\rho }}} = \textrm{Id}_{{\mathbb {R}}} \times \rho$ on $( {\mathbb {R}}\times \Sigma , d(e^r \lambda )).$

We first claim that the radial vector field with respect to $p_{c1}$

$$\begin{aligned} Y_0 = \frac{1}{2} \left( x_1 \partial _{x_1} + x_2 \partial _{x_2} + y_1\partial _{y_1} + (y_2 - \Lambda _3)\partial _{y_2} \right) \end{aligned}$$

is transverse to $\Sigma$ along $\{ x_2 < 2\pi \}.$ By the definition of ${\tilde{H}},$ it suffices to consider the region $\{ - 2 \varepsilon _1< x_2 < 2 \pi \}.$ We find that

$$\begin{aligned} \begin{aligned} d{\tilde{H}}(Y_0)&= \frac{1}{2} ( x_1^2 +y_1^2) +\frac{1}{2} \left( 1-g(x_2) \right) \left( x_2^2 + (y_2 - \Lambda _3)^2 \right) \\&\ \ \ + \frac{1}{2}g(x_2) \left( x_2 K_{x_2} + (y_2 - \Lambda _3) K_{y_2} \right) + \frac{1}{2} x_2 g'(x_2)(K-G). \end{aligned} \end{aligned}$$

The first two terms in the right-hand side are non-negative. The third term is also non-negative because of Lemma 5.3 and (5.6). For the last term, we find that

$$\begin{aligned}&\ \ \ K(x_2, y_2) - G(x_2, y_2) \\&= \left( 1 - f(y_2) \right) \left( - \frac{1}{2 y_2^2} - y_2 - \frac{1}{2}(y_2 - \Lambda _3)^2 \right) + f(y_2) \left( B - \cos \frac{x_2}{2} \right) -\frac{1}{2}x_2^2. \end{aligned}$$

By the choice of the constant B (see (5.3)), it is negative. This proves the claim.

We now consider the Liouville vector field

$$\begin{aligned} Y_1 = \frac{1}{2} ( x_1 \partial _{x_1} + y_1 \partial _{y_1})+ \frac{1}{4} \sin \frac{x_2}{2} \partial _{x_2} + ( y_2 - \Lambda _3) \left( 1 - \frac{1}{8} \cos \frac{x_2}{2} \right) \partial _{y_2}. \end{aligned}$$

Using (5.6) it is straightforward to see that $d\tilde{H}(Y_1)>0$ along $\Sigma \cap \{ 0< x_2 < 4 \pi \}.$

To interpolate between the two Liouville vector fields $Y_0$ and $Y_1,$ we define a smooth function

$$\begin{aligned} \ell (x_2, y_2) = ( y_2 - \Lambda _3) \left( \frac{1}{4} \sin \frac{x_2}{2} - \frac{1}{2}x_2 \right) , \end{aligned}$$

so that $X_{\ell } = Y_1 - Y_0.$ Fix $\varepsilon _2>0$ small enough and pick any non-decreasing smooth function $h :{\mathbb {R}}\rightarrow [0,1]$ satisfying $h(x_2)=0$ for $x_2 < 2\pi - 2 \varepsilon _2$ and $h(x_2) = 1$ for $x_2 > 2 \pi - \varepsilon _2.$ Define

$$\begin{aligned} {\tilde{Y}} = Y_0 + X_{h\ell }, \end{aligned}$$

(5.8)

where $X_{h\ell }$ indicates the Hamiltonian vector field associated with $h\!(x_2)\ell \!(x_2,\! y_2).$

We claim that the Liouville vector field ${\tilde{Y}}$ is transverse to $\Sigma$ along $\{ x_2 < 4 \pi \}.$ In view of the argument above, it suffices to consider the region $\{ 2\pi - 2\varepsilon _2< x_2 < 2 \pi - \varepsilon _2\}.$ We find that

$$\begin{aligned} d {\tilde{H}} ( {\tilde{Y}} ) = (1-h) d {\tilde{H}}(Y_0) + h d \tilde{H}(Y_1)+\ell d {\tilde{H}} ( X_h). \end{aligned}$$

The sum of the first two terms in the right-hand side above is positive. For the last term, we find

$$\begin{aligned} \ell d{\tilde{H}}(X_h) = - h'(x_2) \cdot \left( \frac{1}{4} \sin \frac{x_2}{2} - \frac{1}{2} x_2 \right) ( y_2 - \Lambda _3) K_{y_2}. \end{aligned}$$

This is non-negative because of (5.6). This proves the claim.

We now repeat the same business as above in the region $\{ x_2 > 2\pi \}.$ More precisely, we consider the radial vector field with respect to $p_{c2}$

$$\begin{aligned} Y_2 = \frac{1}{2} \left( x_1 \partial _{x_1} + (x_2- 4 \pi ) \partial _{x_2} + y_1\partial _{y_1} + (y_2 - \Lambda _3)\partial _{y_2} \right) \end{aligned}$$

and interpolate between ${\tilde{Y}}$ and $Y_2$ using the non-increasing function ${\tilde{h}}(x_2):= h( 4 \pi - x_2).$ This provides the Liouville vector field Y that is transverse to $\Sigma .$ By construction, it is invariant under $\rho .$

5.4 Periodic orbits

Let $\gamma (t) = (x_1(t), x_2(t), y_1(t), y_2(t))$ be a periodic orbit of ${\tilde{H}}.$ Denote by

$$\begin{aligned} \gamma _1(t) = (x_1(t), y_1(t)), \quad \gamma _2(t) = (x_2(t), y_2(t)) \end{aligned}$$

the projections of $\gamma (t)$ to the $(x_1, y_1$)-plane and to the $(x_2, y_2)$-plane, respectively. Then, the periodic orbit $\gamma$ belongs to one of the following three categories:

• $\gamma _1$ is constant; the green curve in Fig. 8.

• $\gamma _2$ is constant; the red and blue curves in Fig.  8.

• Both $\gamma _1$ and $\gamma _2$ are non-constant; the black curves in Fig. 8.

Consider the first case, so that we have $\gamma _1 \equiv (0,0),$ and hence, ${\tilde{H}}_2(\gamma _2(t))=c, \forall t.$ The corresponding periodic orbit will be denoted by $P_0.$

We now assume that $\gamma _2$ is constant, so that we have either $\gamma _2 \equiv (0, \Lambda _3),$ $\gamma _2 \equiv (2\pi , \Lambda _3)$ or $\gamma _2 \equiv (4\pi , \Lambda _3).$ See Lemma 5.2. The corresponding periodic orbits $\gamma$ will be denoted by $P_3 = (w_3, 2\pi ), P_2=(w_2, 2\pi )$ and $P_3' = (w_3', 2\pi ),$ where

$$\begin{aligned} w_3(t)&= ( r_3 \sin t, 0, r_3 \cos t, \Lambda _3), \\ w_2(t)&= ( r_2 \sin t,2 \pi , r_2 \cos t, \Lambda _3),\\ w_3'(t)&= ( r_3 \sin t, 4\pi , r_3 \cos t, \Lambda _3), \end{aligned}$$

respectively, with

$$\begin{aligned} r_2 = \sqrt{ 2 ( c-1-B)}< r_3 = \sqrt{ 2 ( c + 1 - B)}. \end{aligned}$$

(5.9)

Note that $P_2$ is a symmetric periodic orbit and that $P_3'=(P_3)_{\rho }.$ Since

$$\begin{aligned} R = \frac{1}{\lambda (X_{{\tilde{H}}})}X_{{\tilde{H}}}, \end{aligned}$$

the Reeb periods of $P_2, P_3$ and $P_3'$ are given by

$$\begin{aligned} \tau _2 = \pi r_2^2, \quad \tau _3 = \tau _3' = \pi r_3^2, \end{aligned}$$

respectively.

Fig. 8

Phase portraits of $K_1$(left) and $K_2$(right)

In the last case, i.e., both $\gamma _1$ and $\gamma _2$ are non-constant, the periodic orbit $\gamma$ lies in an $S^1$-family of periodic orbits.

5.5 Conley–Zehnder indices

We shall prove

Proposition 5.4

The contact form $\lambda$ on $\Sigma ,$ constructed in Sect. 5.3, is weakly convex. More precisely, the periodic orbits $P_2,P_3$, and $P_3'$ are non-degenerate and satisfy $\mu _\textrm{CZ}(P_2)=2$ and $\mu _{\textrm{CZ}}(P_3)= \mu _{\textrm{CZ}}(P_3')=3.$ The other periodic orbits have the Conley-Zehnder indices at least 3. In particular, $P_2$ is a unique periodic orbit having $\mu _\textrm{CZ}=2.$

Proof

We follow [26].

We first consider the periodic orbits $P_2,P_3$ and $P_3'.$ Since $\mu _{\textrm{CZ}}( P_3' ) = \mu _{\textrm{CZ}}(P_3),$ see Sect. 2.2, we may consider only $P_2$ and $P_3$ along which we have

$$\begin{aligned} X_1 = (0, - r_i \cos t, 0, - r_i \sin t), \quad X_2 = ( 0, - r_i \sin t, 0, r_i \cos t), \quad i=2,3, \end{aligned}$$

where $X_1$ and $X_2$ are as in (2.1). As before, we denote by $\mathfrak {T}$ the trivialisation of $( T \Sigma / {\mathbb {R}}X_K) |_{P_i}$ induced by $X_1$ and $X_2.$ We choose another trivialisation $\Phi$ that is induced by the canonical basis

$$\begin{aligned} V_1 = (0,1,0,0), \quad V_2 = (0,0,0,1). \end{aligned}$$

In this trivialisation, the linearised Hamiltonian flow along $P_i$ restricted to $( T \Sigma / {\mathbb {R}}X_K) |_{P_i}$ is described by a solution to the ODE

$$\begin{aligned} {\dot{\alpha }}_i(s) = A \alpha _i(s), \quad A = \begin{pmatrix} 0 &{} 1 \\ -\frac{1}{4} \cos \frac{x_2}{2} &{} 0 \end{pmatrix}. \end{aligned}$$

If $i=2,$ then we have $x_2 = 2\pi ,$ and hence

$$\begin{aligned} A \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ \frac{1}{4} \end{pmatrix}, \quad \quad A \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}. \end{aligned}$$

This implies that the rotation interval (see (2.4)) of any non-trivial solution to the ODE above contains 0 as an interior point. Since the winding number of the projection of $X_1$ (and hence also of $X_2$) to the $(x_2,y_2)$-plane are equal to 1,  it follows that the rotation interval of any non-trivial solution to ODE (2.3) contains $2\pi$ as an interior point. We conclude from the definition of the Conley–Zehnder index that $P_2$ is non-degenerate and satisfies

$$\begin{aligned} \mu _{\textrm{CZ}}(P_2) = 2. \end{aligned}$$

Consider $P_3,$ so that $x_2 = 0.$ Then, a continuous argument of any non-vanishing solution $\alpha$ to the ODE above is of the form

$$\begin{aligned} \vartheta (s) = -\frac{1}{2}s + \vartheta _0 \end{aligned}$$

for some constant $\vartheta _0 \in {\mathbb {R}}.$ Since the Hamiltonian period of $P_3$ equals $2\pi ,$ the rotation interval of $\alpha$ is contained in $(-2\pi , 0).$ Since the basis $\{ X_1, X_2 \}$ has the negative orientation with respect to the basis $\{ V_1, V_2\},$ and the winding number of the projection of $X_1$ to the $(x_2,y_2)$-plane equals 1,  as in the previous case, this implies that the rotation interval of any non-trivial solution to ODE (2.3) is contained in $(2\pi , 4\pi )$ from which we obtain that $P_3$ is non-degenerate and satisfies

$$\begin{aligned} \mu _{\textrm{CZ}}(P_3)=3. \end{aligned}$$

Let $P=(w,T)$ be a periodic orbit not corresponding to the critical points of ${\tilde{H}}_2.$ See Fig. 8. We write $w(t) = (x_1(t), x_2(t), y_1(t), y_2(t))$ and denote by $w_1(t)=(x_1(t), y_1(t))$ and $w_2(t)=(x_2(t), y_2(t))$ the projections of w(t) to the $(x_1, y_1)$-plane and $(x_2, y_2)$-plane, respectively. Note that

$$\begin{aligned} {\dot{w}}_2(t) = ( {\dot{x}}_2(t), {\dot{y}}_2(t) ) = \left( \tilde{H}_{y_2}(w(t)), - {\tilde{H}}_{x_2}( w(t) ) \right) . \end{aligned}$$

For $j=1,2,$ $w_j(t)$ is a closed curve which is oriented in the clockwise direction, and hence, its winding number with respect to the standard basis is given by

$$\begin{aligned} \textrm{wind}\left( t \mapsto {\dot{w}}_j(t) \right) \le -1, \end{aligned}$$

where the equality holds if and only if $w_j(t)$ is a simple closed curve.

We abbreviate by

$$\begin{aligned} Y_1(t) = \left( {\tilde{H}}_{y_2} (w(t)), {\tilde{H}}_{x_2}(w(t)) \right) , \quad Y_2(t) = \left( {\tilde{H}}_{x_2}(w(t)), -\tilde{H}_{y_2}(w(t))\right) , \end{aligned}$$

which are the projections of $X_1$ and $X_2$ along P to the $(x_1, y_1)$-plane. Since P does not correspond to the critical points of ${\tilde{H}}_2,$ these vectors are non-vanishing and linearly independent. Hence, we may compute the rotation interval associated with the transverse linearised flow of $X_K$ along P using the trivialisation of the $(x_1, y_1)$-plane induced by $Y_1$ and $Y_2.$ We find the winding numbers of $Y_1$ and $Y_2$ with respect to the standard basis

$$\begin{aligned} \begin{aligned}\textrm{wind}\left( t \mapsto Y_1(t)\right)&= \textrm{wind}\left( t \mapsto Y_2(t)\right) \\&= \textrm{wind}\left( t \mapsto ( {\tilde{H}}_{y_2} ( w(t)), {\tilde{H}}_{x_2}(w(t)))\right) \\&= - \textrm{wind}\left( t \mapsto ( {\tilde{H}}_{y_2} ( w(t)), -{\tilde{H}}_{x_2}(w(t)))\right) \\&= - \textrm{wind} \left( t \mapsto {\dot{w}}_2(t) \right) \\&\ge 1. \end{aligned} \end{aligned}$$

(5.10)

Suppose that P corresponds to a black curve in Fig. 8, so that ${\dot{w}}_1(t)$ is non-vanishing. Since ${\dot{w}}_1(t)$ is preserved by the linearised flow projected to the $(x_1, y_1)$-plane, there is a solution $\alpha (t)$ to ODE (2.3) whose projection to the $(x_1, y_1)$-plane equals ${\dot{w}}_1(t).$ We denote such a projection by $\bar{\alpha }(t)$ and then compute its winding number with respect to the basis $\mathfrak {B} = \{ Y_1(t), Y_2(t)\}$

$$\begin{aligned} \textrm{wind}\left( t \mapsto \bar{\alpha }(t) ; \mathfrak {B} \right)&= \textrm{wind}\left( t \mapsto Y_1(t) \right) - \textrm{wind}\left( t \mapsto \bar{\alpha }(t) \right) \\&= \textrm{wind}\left( t \mapsto Y_1(t) \right) - \textrm{wind}\left( t \mapsto {\dot{w}}_1(t) \right) \\&\ge 2, \end{aligned}$$

where we have used the fact that the basis $\mathfrak {B}$ has negative orientation with respect to the standard basis. This implies that the rotation interval of P contains $4\pi ,$ from which we conclude that $\mu _{\textrm{CZ}}(P) \ge 3.$

We now assume that P corresponds to the green curve in Fig. 8, so that $w_1(t) \equiv (0,0).$ In this case, the linearised Hamiltonian flow along P restricted to the $(x_1, y_1)$-plane is described by a solution to the ODE

$$\begin{aligned} {\dot{\beta }} = \begin{pmatrix} 0 &{}\quad 1 \\ -1 &{}\quad 0 \end{pmatrix} \beta . \end{aligned}$$

As in the case of $P_3,$ this implies that the rotation interval of $\beta$ is contained in $(-\infty , 0),$ and hence, we find using (5.10) that the rotation interval of any non-trivial solution to ODE (2.3) is contained in $(2\pi ,+\infty ).$ Consequently, we have $\mu _{\textrm{CZ}}(P) \ge 3.$

This finishes the proof. $\square$

5.6 Construction of a finite energy foliation

Let $\overline{X}_1, \overline{X}_2$ be the two vector fields that span the contact structure $\xi = \ker \lambda$; see (2.2). We define the $d\lambda$-compatible almost complex structure $J :\xi \rightarrow \xi$ by

$$\begin{aligned} J ( {\overline{X}}_1 ) = {\overline{X}}_2. \end{aligned}$$

(5.11)

Note that it is $\rho$-anti-invariant. See (2.6).

Abbreviate $S^1 = {\mathbb {R}}/{\mathbb {Z}}.$ Let ${\tilde{u}} = (a,u) :{\mathbb {R}}\times S^1 \rightarrow {\mathbb {R}}\times \Sigma$ be a ${\tilde{J}}$-holomorphic curve, where ${\tilde{J}}$ is given as in (2.5). Being $\tilde{J}$-holomorphic, ${\tilde{u}}$ satisfies

$$\begin{aligned} {\left\{ \begin{array}{ll} \pi u_s + J(u) \pi u_t= 0,\\ \lambda ( u_t) = a_s,\\ \lambda ( u_s)= -a_t, \end{array}\right. } \end{aligned}$$

(5.12)

where $\pi :T\Sigma \rightarrow \xi$ is the projection along R. We make the following Ansatz:

Ansatz. The $\Sigma$-part u of ${\tilde{u}}$ takes the form

$$\begin{aligned} u(s,t) = ( r(s) \sin 2\pi t, x_2(s), r(s) \cos 2 \pi t, y_2(s)) \end{aligned}$$

(5.13)

             with $r(s) \ne 0$ and $\dot{r} (s) \ne 0.$

We only consider the case that we have $x_2 \equiv 0, x_2\equiv 2 \pi , x_2 \equiv 4 \pi$ or $y_2 \equiv \Lambda _3$ with $0 \le x_2(s) \le 4 \pi , \forall s.$ Recall that in this case, we have ${\tilde{H}}_2 = K,$ where the latter is as in (5.4). Since $u(s,t) \in \Sigma ,$ this implies that

$$\begin{aligned} \frac{1}{2} r(s)^2 + K( x_2(s), y_2(s) ) = c. \end{aligned}$$

(5.14)

Following the argument given in [6, Chapter 5], we shall show that the corresponding ${\tilde{u}}$ is a finite energy plane asymptotic to $P_2, P_3$ or $P_3'$ or a finite energy cylinder asymptotic to $P_3$ or $P_3'$ at its positive puncture and to $P_2$ at its negative puncture.

We first assume the case where $x_2(s) \in [0, 2 \pi ],\forall s,$ so that the Liouville vector field is given by $Y = Y_0 + X_{h \ell },$ see (5.8), and hence, the contact form $\lambda$ equals

$$\begin{aligned} \lambda&= \frac{1}{2} \left( y_1 \textrm{d}x_1 + (y_2 - \Lambda _3)\textrm{d}x_2 - x_1 \textrm{d}y_1 - x_2 \textrm{d}y_2 \right) - d(h\ell )\\&= \frac{1}{2} y_1 \textrm{d}x_1 - \frac{1}{2}x_1 \textrm{d}y_1 - \frac{1}{2} \Bigg ( x_2 + h(x_2) \Bigg (\frac{1}{2} \sin \frac{x_2}{2} - x_2 \Bigg ) \Bigg ) \textrm{d}y_2 \\&\ \ \ + \frac{1}{2} (y_2 - \Lambda _3)\Bigg ( 1 - h'(x_2) \Bigg ( \frac{1}{2}\sin \frac{x_2}{2} - x_2 \Bigg ) - h(x_2) \Bigg ( \frac{1}{4}\cos \frac{x_2}{2} -1 \Bigg ) \Bigg ) \textrm{d}x_2. \end{aligned}$$

We compute

$$\begin{aligned} \nonumber \lambda (u_t)&= \pi r^2,\\ \lambda (u_s)&= - \frac{1}{2} \Bigg ( x_2 + h(x_2) \Bigg (\frac{1}{2} \sin \frac{x_2}{2} - x_2 \Bigg )\Bigg )\dot{y}_2 \\&\ \ \ + \frac{1}{2} (y_2 - \Lambda _3)( 1 - h'(x_2) \Bigg ( \frac{1}{2}\sin \frac{x_2}{2} - x_2 \Bigg ) - h(x_2) \Bigg ( \frac{1}{4}\cos \frac{x_2}{2} -1 ) \Bigg ) \dot{x}_2. \end{aligned}$$

Since $x_2 \equiv 0,$ $x_2 \equiv 2 \pi$ or $y_2 \equiv \Lambda _3,$ we obtain

$$\begin{aligned} \lambda (u_s)=0. \end{aligned}$$

This together with the last identity of (5.12) implies that a is independent of t, so we may choose

$$\begin{aligned} a(s,t) = a(s) = \int _0^s \pi r( u)^2 d u, \end{aligned}$$

(5.15)

from which we see that $a \rightarrow \pm \infty$ as $s \rightarrow \pm \infty .$

The first identity of (5.12) implies that $\pi u_s$ and $\pi u_t$ are linearly independent, so that there exist A, B, C and D, such that

$$\begin{aligned} {\overline{X}}_1 = A \pi u_s + B \pi u_t \quad \text { and } \quad {\overline{X}}_2 = C \pi u_s + D \pi u_t. \end{aligned}$$

By definition of J,  we have $A= D$ and $B=-C,$ and hence

$$\begin{aligned} {\overline{X}}_1 = A \pi u_s + B \pi u_t \quad \text { and } \quad {\overline{X}}_2 = -B \pi u_s + A \pi u_t. \end{aligned}$$

(5.16)

Let $P :{\mathbb {R}}^4 \rightarrow {\mathbb {R}}^2$ be the projection $(x_1, x_2, y_1, y_2) \mapsto (x_2, y_2)$ and denote

$$\begin{aligned} P( {\overline{X}}_1)= \begin{pmatrix} \square _1 \\ \square _2 \end{pmatrix}, \quad P({\overline{X}}_2) = \begin{pmatrix} \triangle _1 \\ \triangle _2 \end{pmatrix}, \quad P( \pi u_s) =\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}, \quad P(\pi u_t) = \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}. \end{aligned}$$

A direct computation using (5.14) shows that

$$\begin{aligned} a_1 b_2 - a_2 b_1 = - \frac{ \pi r^3\dot{r} }{k} \ne 0, \end{aligned}$$

where

$$\begin{aligned} k&= \lambda (X_{{\tilde{H}}})\\&= \frac{r^2}{2} + \frac{1}{2} (y_2 - \Lambda _3) ( 1 - h'(x_2) \Bigg ( \frac{1}{2}\sin \frac{x_2}{2} - x_2 \Bigg ) - h(x_2) \Bigg ( \frac{1}{4}\cos \frac{x_2}{2} -1 ) \Bigg ) K_{y_2} \\&\ \ \ + \frac{1}{2} \Bigg ( x_2 + h(x_2) \Bigg (\frac{1}{2} \sin \frac{x_2}{2} - x_2 \Bigg ) \Bigg ) K_{x_2}. \end{aligned}$$

By means of (5.16), we obtain

$$\begin{aligned} \frac{1}{ a_1 b_2 - a_2 b_1} \begin{pmatrix} b_2 &{} - b_1 \\ - a_2 &{} a_1 \end{pmatrix} \begin{pmatrix} \square _1 \\ \square _2 \end{pmatrix} = \begin{pmatrix} A \\ B \end{pmatrix} = \frac{1}{ a_1 b_2 - a_2 b_1} \begin{pmatrix} -a_2 &{} a_1 \\ - b_2 &{} b_1 \end{pmatrix} \begin{pmatrix} \triangle _1 \\ \triangle _2 \end{pmatrix}, \end{aligned}$$

and hence

$$\begin{aligned} \begin{aligned} b_2 \square _1 - b_1 \square _2&= -a_2 \triangle _1 + a_1 \triangle _2,\\ -a_2 \square _1 + a_1 \square _2&= -b_2 \triangle _1 + b_1 \triangle _2. \end{aligned} \end{aligned}$$

(5.17)

We compute that

$$\begin{aligned} \triangle _1 \square _2 - \triangle _2 \square _1 = \frac{ r^2 ( r^2 + K _{x_2} ^2 + K_{y_2} ^2)}{2k } > 0. \end{aligned}$$

Then, solving (5.17) provides

$$\begin{aligned} \begin{aligned} \begin{pmatrix} \dot{x}_2 \\ \dot{y}_2 \end{pmatrix}&= \frac{1}{ \triangle _1 \square _2 - \triangle _2 \square _1 } \begin{pmatrix} - \square _1 &{} \triangle _1 \\ - \square _2 &{} \triangle _2 \end{pmatrix} \begin{pmatrix} b_2 \square _1 - b_1 \square _2 \\ -b_2 \triangle _1 + b_1\triangle _2 \end{pmatrix} \\&= \frac{1}{ \triangle _1 \square _2 - \triangle _2 \square _1 } \begin{pmatrix} -b_2 ( \triangle _1^2 + \square _1^2) + b_1 ( \triangle _1 \triangle _2 + \square _1 \square _2) \\ b_1 ( \triangle _2^2 + \square _2^2) -b_2 ( \triangle _1 \triangle _2 + \square _1 \square _2) \end{pmatrix}. \end{aligned} \end{aligned}$$

(5.18)

Suppose first that $x_2 \equiv 0.$ Using (5.14) and (5.18), we find

$$\begin{aligned} \dot{y}_2 (s) = \frac{ - 2 \pi r(s)^2 K_{y_2} (0, y_2(s)) }{ ( K_{y_2} (0, y_2(s)) )^2 + r(s)^2 } = \frac{ - 4 \pi (c - K (0, y_2(s)) ) K_{y_2} (0, y_2(s)) }{ ( K_{y_2} (0, y_2(s)) )^2 + 2 (c - K (0, y_2(s)) ) },\nonumber \\ \end{aligned}$$

(5.19)

which may be seen as a differential equation of the type

$$\begin{aligned} \dot{y}_2 (s) = P( y_2(s)). \end{aligned}$$

(5.20)

Here, $P=P(y_2)$ is a smooth function defined on the interval $[y_2^-, y_2^+],$ where $(y_2^-, y_2^+ ) = (\Lambda _1, \Lambda _3)$ or $(y_2^-, y_2^+ ) = (\Lambda _3, \Lambda _{\max }).$ It follows from (5.6) that the function P satisfies the following properties:

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} P(y_2) = 0 &{} \quad y_2 = \Lambda _1, \Lambda _3, \Lambda _{\max } ,\\ P(y_2)>0 &{} \quad y_2 \in (\Lambda _1, \Lambda _3),\\ P(y_2)<0 &{} \quad y_2 \in (\Lambda _3, \Lambda _{\max }). \end{array}\right. } \end{aligned} \end{aligned}$$

(5.21)

Thus, any solution $y_2=y_2(s)$ to ODE (5.19) with initial condition $y_2(0) \in (\Lambda _1, \Lambda _3)$ is strictly increasing and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } y_2(s) =\Lambda _1 \quad \text { and } \quad \lim _{s \rightarrow +\infty } y_2(s) = \Lambda _3, \end{aligned}$$

and any solution with $y_2(0) \in (\Lambda _3, \Lambda _{\max })$ is strictly decreasing and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } y_2(s) =\Lambda _{\max } \quad \text { and } \quad \lim _{s \rightarrow +\infty } y_2(s) = \Lambda _3. \end{aligned}$$

By construction, such a solution yields a solution

$$\begin{aligned} u(s,t) = ( r(s) \sin 2 \pi t, 0, r(s) \cos 2 \pi t, y_2(s)), \; (s,t) \in {\mathbb {R}}\times S^1 \end{aligned}$$

(5.22)

to the first equation in (5.12). Here, the radius r(s) is determined by relation (5.14) with $x_2(s) = 0$ and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } r(s) = 0, \quad \lim _{s \rightarrow +\infty } r (s) = r_3, \end{aligned}$$

where $r_3$ is as in (5.9). This, together with a(s, t),  defined in (5.15), produces a ${\tilde{J}}$-holomorphic curve ${\tilde{u}} = (a, u ) :{\mathbb {R}}\times S^1 \rightarrow {\mathbb {R}}\times \Sigma .$ Note that this solution depends on the choice of the initial condition $y_2 (0) \in (\Lambda _1, \Lambda _3) \cup (\Lambda _3, \Lambda _{\max }).$

For any $N>0$ and for any $\phi :{\mathbb {R}}\rightarrow [0,1]$ with $\phi ' \ge 0,$ we have

$$\begin{aligned} \int _{[-N,N] \times S^1} d \tilde{u} ^* ( \phi \lambda ) = \phi ( a (N) ) \pi r (N)^2 - \phi ( a (-N)) \pi r (-N)^2, \end{aligned}$$

and hence

$$\begin{aligned} E({\tilde{u}} ) =\tau _3= \pi r_3^2. \end{aligned}$$

Moreover, the mass of ${\tilde{u}}$ at $-\infty$ is given by

$$\begin{aligned} m(-\infty )= \lim _{N \rightarrow -\infty } \int _{\{ N \} \times S^1} u ^* \lambda = \lim _{ N \rightarrow -\infty } \pi r (N)^2 = 0, \end{aligned}$$

implying that $-\infty$ is a removable puncture of ${\tilde{u}}$. See [10, Section 1]. After removing it, we obtain an embedded finite energy ${\tilde{J}}$-holomorphic plane ${\tilde{u}} = (a, u) :{\mathbb {C}}\rightarrow {\mathbb {R}}\times \Sigma$ asymptotic to $P_3$ at its positive puncture $s=+\infty .$

In the case $x_2 \equiv 2 \pi ,$ we obtain

$$\begin{aligned} \dot{y}_2 (s) = \frac{ - 4 \pi (c - K (2 \pi , y_2(s)) ) K_{y_2}(2 \pi , y_2(s))}{ ( K_{y_2}(2 \pi , y_2(s)) )^2 + 2 (c - K (2 \pi , y_2(s)) ) }, \end{aligned}$$

(5.23)

which may be seen as a differential equation satisfying the same properties as above. See (5.20) and (5.21). Note that the radius r(s), determined by (5.14) with $x_2(s) = 2\pi$, satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } r(s) = 0, \quad \lim _{s \rightarrow +\infty } r (s) = r_2, \end{aligned}$$

where $r_2$ is as in (5.9). Then, arguing in a similar manner, we find an embedded finite energy ${\tilde{J}}$-holomorphic plane ${\tilde{u}}$, depending on the initial condition $y_2 (0) \in (\Lambda _1, \Lambda _3) \cup (\Lambda _3, \Lambda _{\max }),$ asymptotic to $P_2$ at its positive puncture $s=+\infty$ and having energy equal to $\tau _2=\pi r_2^2.$ Note that it is invariant, i.e., ${\tilde{u}} = {\tilde{u}}_{\rho }$. See Sect. 2.3.

Finally, assume that $y_2 \equiv \Lambda _3$ with $0 \le x_2(s) \le 2\pi , \forall s,$ so that

$$\begin{aligned} \dot{x}_2 (s) = \frac{ - 4 \pi ( c - K ( x_2(s), \Lambda _3) )K_{x_2}(x_2(s), \Lambda _3)}{ (K_{x_2}(x_2(s), \Lambda _3))^2 +2(c - K (x_2(s), \Lambda _3))}, \end{aligned}$$

(5.24)

which may be seen as a differential equation of the type

$$\begin{aligned} \dot{x}_2 (s) = Q(x_2(s)). \end{aligned}$$

Here, $Q = Q(x_2)$ is a smooth function defined on $[0, 2\pi ].$ Notice that

$$\begin{aligned} {\left\{ \begin{array}{ll} Q(x_2) =0 &{} \quad x_2 = 0, 2\pi , \\ Q(x_2)<0 &{} \quad 0<x_2 < 2\pi , \end{array}\right. } \end{aligned}$$

from which we see that any solution $x_2 = x_2(s)$ to ODE (5.24) with the initial condition $x_2(0) \in (0, 2\pi )$ is strictly decreasing and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } x_2(s) = 2\pi \quad \text { and } \quad \lim _{s \rightarrow +\infty } x_2(s) = 0. \end{aligned}$$

In view of the construction, such a solution gives rise to a solution

$$\begin{aligned} u(s,t) = ( r(s) \sin 2 \pi t, x_2(s), r(s) \cos 2 \pi t, \Lambda _3), \ (s,t) \in {\mathbb {R}}\times S^1 \end{aligned}$$

(5.25)

to the first equation in (5.12). The radius r(s) is determined by (5.14) with $y_2(s) = \Lambda _3$ and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } r(s) = r_2 \quad \text { and } \quad \lim _{s \rightarrow +\infty } r (s) = r_3, \end{aligned}$$

where $r_2$ and $r_3$ are as in (5.9). This together with a(s, t),  defined in (5.15), produces a $\tilde{J}$-holomorphic curve ${\tilde{u}} = (a, u ) :{\mathbb {R}}\times S^1 \rightarrow {\mathbb {R}}\times \Sigma ,$ depending on the choice of the initial condition $x_2 (0) \in (0, 2 \pi ).$ The Hofer energy is given by $\tau _3$ and the mass of ${\tilde{u}}$ at $-\infty$ is equal to $\tau _2=\pi r_2^2,$ implying that $-\infty$ is non-removable. Thus, we obtain an embedded finite energy ${\tilde{J}}$-holomorphic cylinder ${\tilde{v}} = (b, v) :{\mathbb {R}}\times S^1 \rightarrow {\mathbb {R}}\times \Sigma$ asymptotic to $P_3$ at its positive puncture $s=+\infty$ and to $P_2$ at its negative puncture $s=-\infty .$

We now consider the case $x_2 \equiv 4\pi$ or $y_2 \equiv \Lambda _3$ with $2\pi \le x_2(s) \le 4\pi , \forall s.$ Instead of the direct construction as above, we shall use the symmetry induced by the anti-contact involution $\rho .$

Let ${\tilde{u}} = (a,u) :{\mathbb {C}}\rightarrow {\mathbb {R}}\times \Sigma ,$ where u(s, t) is as in (5.22), be a finite energy $\tilde{J}$-holomorphic plane, corresponding to $x_2 \equiv 0.$ It is asymptotic to $P_3$ at its positive puncture. The discussion above shows that ${\tilde{u}}_{\rho }(s,t) = \left( a_{\rho }(s,t), u_{\rho }(s, t) )\right) ,$ where

$$\begin{aligned} a_{\rho }(s,t) = a(s,-t) \quad \text { and } \quad u_{\rho }(s,t) = ( r(s) \sin 2 \pi t, 4\pi , r(s) \cos 2 \pi t, y_2(s) ), \end{aligned}$$

is a finite energy ${\tilde{J}}$-holomorphic plane asymptotic to $P_3' = (P_3)_{\rho }.$ As above, if $y_2(0) \in (\Lambda _1, \Lambda _3),$ then $y_2(s)$ is strictly increasing and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } y_2(s) =\Lambda _1 \quad \text { and } \quad \lim _{s \rightarrow +\infty } y_2(s) = \Lambda _3, \end{aligned}$$

and if $y_2(0) \in (\Lambda _3, \Lambda _{\max }),$ then $y_2(s)$ is strictly decreasing and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } y_2(s) =\Lambda _{\max } \quad \text { and } \quad \lim _{s \rightarrow +\infty } y_2(s) = \Lambda _3. \end{aligned}$$

In a similar manner, if ${\tilde{u}} = (a,u) :{\mathbb {R}}\times S^1 \rightarrow {\mathbb {R}}\times \Sigma ,$ where u(s, t) is as in (5.25) and $0\le x_2(s) \le 2 \pi , \forall s,$ is a finite energy ${\tilde{J}}$-holomorphic cylinder, then $\tilde{u}_{\rho }(s,t) = \left( a_{\rho }(s,t), u_{\rho }(s, t) )\right) ,$ where $a_{\rho }$ is as above and

$$\begin{aligned} u_{\rho }(s,t) = ( r(s) \sin 2 \pi t, 4\pi - x_2(s), r(s) \cos 2 \pi t, \Lambda _3 ), \end{aligned}$$

is a finite energy ${\tilde{J}}$-holomorphic cylinder, asymptotic to $P_3' = (P_3)_{\rho }$ at its positive puncture and to $P_2 = (P_2)_\rho$ at its negative puncture. Moreover, if $4 \pi - x_2(s)$ has the initial condition $4\pi - x_2(0) \in ( 2\pi , 4 \pi ),$ then it is strictly increasing and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } 4 \pi - x_2(s) = 2\pi \quad \text { and } \quad \lim _{s \rightarrow +\infty } 4 \pi - x_2(s) = 4\pi . \end{aligned}$$

We have constructed the following embedded finite energy $\tilde{J}$-holomorphic curves:

• finite energy planes ${\tilde{u}}_{3,1}$ and ${\tilde{u}}_{3,2},$ which corresponds to $x_2 \equiv 0$ and initial conditions $y_2(0) \in (\Lambda _1, \Lambda _3)$ and $y_2(0) \in (\Lambda _3, \Lambda _{\max }),$ respectively. They are both asymptotic to $P_3.$

• finite energy planes ${\tilde{u}}_{2,1}$ and ${\tilde{u}}_{2,2},$ corresponding to $x_2 \equiv 2 \pi$ and initial conditions $y_2(0) \in (\Lambda _1, \Lambda _3)$ and $y_2(0) \in (\Lambda _3, \Lambda _{\max }),$ respectively. They are invariant and asymptotic to $P_2.$

• finite energy planes ${\tilde{u}}_{3,1}' = ({\tilde{u}}_{3,1})_\rho$ and ${\tilde{u}}_{3,2}'=({\tilde{u}}_{3,2})_\rho ,$ which corresponds to $x_2 \equiv 4\pi$ and initial conditions $y_2(0) \in (\Lambda _1, \Lambda _3)$ and $y_2(0) \in (\Lambda _3, \Lambda _{\max }),$ respectively. They are both asymptotic to $P_3'= (P_3)_\rho .$

• finite energy cylinders ${\tilde{v}}_1$ and ${\tilde{v}}_2 = ({\tilde{v}}_1)_\rho ,$ corresponding to $y_2 \equiv \Lambda _3$ and initial conditions $x_2(0) \in (0, 2\pi )$ and $x_2(0) \in (2 \pi , 4 \pi ),$ respectively. The cylinder ${\tilde{v}}_1$ is asymptotic to $P_3$ at $+\infty$ and to $P_2$ at $-\infty ,$ and ${\tilde{v}}_2$ is asymptotic to $P_3'=(P_3)_\rho$ at $+\infty$ and to $P_2=(P_2)_\rho$ at $-\infty .$

The following statement is taken from [12, Theorem 1.5] and [28, Theorem 4.5.44]. Note that J is not required to be generic.

Theorem 5.5

[Hofer-Wysocki-Zehnder, Wendl] Let a closed three-manifold M be equipped with a contact form $\lambda$ and a $d\lambda$-compatible almost complex structure J. Assume that ${\tilde{u}} = (a, u) :{\mathbb {C}}\rightarrow {\mathbb {R}}\times M$ is an embedded finite energy ${\tilde{J}}$-holomorphic plane, asymptotic to a non-degenerate periodic orbit $P=(x,T)$ having $\mu _{\textrm{CZ}}(P)=3.$ Then, there exists an $\delta >0$ and an embedding

$$\begin{aligned} {{\tilde{\Phi }}} :{\mathbb {R}}\times (-\delta , \delta ) \times {\mathbb {C}}\rightarrow {\mathbb {R}}\times M, \ (\sigma , \tau , z) \mapsto ( a_\tau (z) + \sigma , u_\tau (z)), \end{aligned}$$

having the following properties:

• (1) For each $\sigma \in {\mathbb {R}}$ and $\tau \in (-\delta , \delta )$, the map ${\tilde{u}}_{\sigma , \tau }= {{\tilde{\Phi }}}( \sigma , \tau , \cdot )$ is up to parametrisation an embedded finite energy ${\tilde{J}}$-holomorphic plane and ${\tilde{u}}_{0,0} = {\tilde{u}}.$

• (2) The map $u_{\cdot }(\cdot ) :(-\delta , \delta ) \times {\mathbb {C}}\rightarrow M$ is an embedding and its image is disjoint from the asymptotic limit P. In particular, the maps $u_{\tau } :{\mathbb {C}}\rightarrow M$ are embeddings for all $\tau \in (-\delta , \delta ),$ with mutually disjoint images that do not intersect their asymptotic limit P.

• (3) For any sequence ${\tilde{u}}_k = (a_k, u_k)$ of finite energy ${\tilde{J}}$-holomorphic planes, such that they are all asymptotic to P and satisfy ${\tilde{u}}_k \rightarrow {\tilde{u}}$ in $C^{\infty }_{\textrm{loc}}({\mathbb {C}})$ for all k sufficiently large, there exists a sequence $(\sigma _k, \tau _k) \in {\mathbb {R}}\times (-\delta , \delta )$ converging to (0, 0) and a sequence $\varphi _k :{\mathbb {C}}\!\rightarrow {\mathbb {C}}$ of biholomorphic reparametrisations of ${\mathbb {C}}$ of the form $z \mapsto bz+c$ with constants $b, c \in {\mathbb {C}},$ such that ${\tilde{u}}_k = {\tilde{u}}_{\sigma _k, \tau _k} \circ \varphi _k.$

An application of the previous theorem to the finite energy plane ${\tilde{u}}_{3,1}$ (recall that $P_3$ is non-degenerate and satisfies $\mu _{\textrm{CZ}}(P_3)=3,$ see Proposition 5.4) yields a maximal one-parameter family of embedded finite energy $\tilde{J}$-holomorphic planes

$$\begin{aligned} {\tilde{u}}_{\tau } = (a_\tau , u_\tau ) :{\mathbb {C}}\rightarrow {\mathbb {R}}\times \Sigma , \quad \tau \in (\tau _-, \tau _+), \end{aligned}$$

all asymptotic to $P_3.$ This family is non-compact. Indeed, otherwise, there is $\tau _1 \ne \tau _2$ with $u_{\tau _1}({\mathbb {C}}) \cap u_{\tau _2}({\mathbb {C}}) \ne \emptyset .$ Then, it follows from [10, Theorem 1.4] that $u_{\tau _1}({\mathbb {C}}) = u_{\tau _2}({\mathbb {C}}),$ and hence, we find an open book decomposition of $\Sigma$ with binding $P_3$ and disc-like pages. By the usual argument, every page is transverse to the Reeb vector field, implying that every periodic orbit other than $P_3$ is linked to $P_3.$ This contradicts to the presence of $P_2$ and $P_3'.$

We now take a look at the breaking of the family $\{ \tilde{u}_\tau \}$ as $\tau \rightarrow \tau _\pm .$ For simplicity, we write $\tau _-=0$ and $\tau _+=1.$ We assume that $\tau$ strictly increases in the direction of the Reeb vector field.

Pick a sequence $\tau _n \rightarrow 0^+$ as $n \rightarrow +\infty$ and write ${\tilde{u}}_n:= {\tilde{u}}_{\tau _n}, n \in {\mathbb {N}}.$ By a standard argument (see [6, 14, 16]), we find that ${\tilde{u}}_n$ converges to a holomorphic building with height 2. The top consists of an embedded finite energy ${\tilde{J}}$-holomorphic cylinder ${\tilde{v}}=(b,v) :{\mathbb {C}}{\setminus } \{ 0 \} \rightarrow {\mathbb {R}}\times \Sigma$ asymptotic to $P_3$ at its positive puncture $+\infty$ and to an index 2 orbit Q at at its negative puncture 0. The bottom consists of an embedded finite energy ${\tilde{J}}$-holomorphic plane ${\tilde{u}}=(a,u) :{\mathbb {C}}\rightarrow {\mathbb {R}}\times \Sigma$ asymptotic to Q. Moreover, given a neighbourhood $U \subset \Sigma$ of $v({\mathbb {C}}\setminus \{0\}) \cup Q \cup u({\mathbb {C}}),$ we have $u_n({\mathbb {C}}) \subset U$ for n sufficiently large. See [13] and also [6, Proposition 9.5]. Since $P_2$ is a unique index 2 orbit, see Proposition 5.4, we have $Q=P_2.$ The uniqueness property of finite energy planes asymptotic to $P_2$ and finite energy cylinders asymptotic to $P_3$ at $+\infty$ and to $P_2$ at 0 (see [6, Proposition C.-3]), based on Siefring’s intersection theory [27], implies that $\tilde{v} = {\tilde{v}}_1$ or ${\tilde{v}}={\tilde{v}}_2$ and ${\tilde{u}} = \tilde{u}_{2,1}$ or ${\tilde{u}} = {\tilde{u}}_{2,2},$ up to reparametrisation and ${\mathbb {R}}$-translation.

We now choose a sequence $\tau _n' \rightarrow 1^-$ as $n \rightarrow +\infty$ and do a similar business with ${\tilde{u}}_n':= {\tilde{u}}_{\tau _n'}.$ This sequence also converges to a holomorphic building with height 2 whose top level consists of an embedded finite energy cylinder ${\tilde{v}}' = (b',v') :{\mathbb {C}}{\setminus } \{ 0 \} \rightarrow {\mathbb {R}}\times \Sigma$ asymptotic to $P_3$ at its positive puncture $+\infty$ and to $P_2$ at its negative puncture 0 and whose bottom consists of an embedded finite energy plane ${\tilde{u}}' = (a',u') :{\mathbb {C}}\rightarrow {\mathbb {R}}\times \Sigma$ asymptotic to $P_2.$ By uniqueness, we have ${\tilde{v}}' = {\tilde{v}}_1$ or ${\tilde{v}}'={\tilde{v}}_2$ and ${\tilde{u}} '= {\tilde{u}}_{2,1}$ or ${\tilde{u}} '= {\tilde{u}}_{2,2},$ up to reparametrisation and ${\mathbb {R}}$-translation. Moreover, given a neighbourhood $U' \subset \Sigma$ of $v'({\mathbb {C}}{\setminus }\{0\}) \cup P_2 \cup u'({\mathbb {C}}),$ we have $u_n'({\mathbb {C}}) \subset U'$ for n sufficiently large.

Lemma 5.6

$v({\mathbb {C}}{\setminus } \{ 0 \} )= v' ( {\mathbb {C}}{\setminus } \{ 0 \} ) = v_1({\mathbb {C}}{\setminus } \{ 0 \}),$ $u({\mathbb {C}}) = u_{2,1}({\mathbb {C}})$ and $u'({\mathbb {C}}) = u_{2,2}({\mathbb {C}}).$

Proof

Arguing indirectly, we assume that $v({\mathbb {C}}{\setminus } \{ 0 \} ) = v_2 ( {\mathbb {C}}{\setminus } \{ 0 \}).$ Recall that it is obtained as the $\Sigma$-part of a limit of the sequence ${\tilde{u}}_{\tau _n} = ( a_{\tau _n}, u_{\tau _n})$ with $\tau _n \rightarrow 0^+.$ Given a neighbourhood U of $v_2({\mathbb {C}}{\setminus } \{ 0 \}) \cup P_2 \cup u ({\mathbb {C}})$, we have $u_{\tau _n}({\mathbb {C}}) \subset U$ for all n sufficiently large. Since the $x_2$-components of ${\tilde{u}}_{3,1}$, ${\tilde{v}}_2$ and ${\tilde{u}}$ satisfy $x_2 \equiv 0$, $2\pi< x_2 < 4\pi$ and $x_2 \equiv 2\pi ,$ respectively, this implies that there is $\tau _0 \in (0,1)$, such that $u_{\tau _0}$ admits a point with $x_2 = 2\pi .$ Thus, $u_{\tau _0}$ intersects $u_{2,1}$ or $u_{2,2},$ contradicting the stability and positivity of intersections of immersed pseudoholomorphic curves (see [22, Appendix E]). We conclude that $v({\mathbb {C}}{\setminus } \{ 0 \} ) = v_1({\mathbb {C}}{\setminus } \{ 0 \}).$ By the same reasoning, we obtain $v'({\mathbb {C}}{\setminus } \{ 0 \}) = v_1({\mathbb {C}}{\setminus } \{ 0 \}).$

We now show that the planes u and $u'$ are disjoint. We follow the argument given in the proof of [4, Proposition 3.17]. Assume by contradiction that they have a non-empty intersection. Then, Theorem 2.4 in [27] shows that $u({\mathbb {C}}) = u'({\mathbb {C}}).$ Pick any point $q \in \Sigma {\setminus } \left( P_3 \cup v({\mathbb {C}}{\setminus } \{ 0 \}) \cup P_2 \cup u({\mathbb {C}}) \right)$ and take a small neighbourhood $\mathcal {U}$ of $P_3 \cup v({\mathbb {C}}{\setminus } \{ 0 \} ) \cup P_2 \cup u({\mathbb {C}}),$ not containing q. Then, there exists $\tau _0$ and $\tau _1$ contained in (0, 1),  close enough to 0 and 1,  respectively, such that $u_{\tau _0} ({\mathbb {C}}), u_{\tau _1} ({\mathbb {C}}) \subset \mathcal {U}.$ By Jordan–Brouwer separation theorem, the piecewise smooth embedded two-sphere $S = u_{\tau _0}({\mathbb {C}}) \cup P_3 \cup u_{\tau _1}({\mathbb {C}})$ divides $\Sigma$ into two components $C_1$ and $C_2$ having boundary S. It follows from the choice of the point q that one of the two components, say $C_1,$ contains q in its interior and the other contains $P_3 \cup v({\mathbb {C}}{\setminus } \{ 0 \}) \cup P_2 \cup u({\mathbb {C}}).$

We claim that the set $A= \left( \bigcup _{\tau \in (0,1)} u_{\tau }({\mathbb {C}}) \right) \cap \textrm{int}(C_1)$ is non-empty, open, and closed in $\textrm{int}(C_1).$ In view of Theorem 5.5, it is non-empty and open. To achieve the closedness of A, take a sequence $w_n \in A.$ Since $w_n$ is contained the closed subset $C_1,$ a limit of the sequence $w_n$ is contained in $C_1.$ On the other hand, since $w_n$ is also contained in the union $\bigcup _{\tau \in (0,1)} u_{\tau }({\mathbb {C}}),$ the compactness property of the family $\{u_{\tau }\}_{\tau \in (0,1)}$ described above implies that its limit is contained either in $\bigcup _{\tau \in (0,1)} u_{\tau }({\mathbb {C}}),$ in $P_3,$ or in $v({\mathbb {C}}{\setminus } \{ 0 \} ) \cup P_2 \cup u({\mathbb {C}}).$ The last option does not occur, because $v({\mathbb {C}}\setminus \{ 0 \} ) \cup P_2 \cup u({\mathbb {C}})$ is contained in the interior of $C_2.$ Therefore, a limit of the sequence $w_n$ is contained in $\left( \bigcup _{\tau \in (0,1)} u_{\tau }({\mathbb {C}}) \cup P_3 \right) \cap C_1,$ from which we see that the set $\left( \bigcup _{\tau \in (0,1)} u_{\tau }({\mathbb {C}}) \cup P_3 \right) \cap C_1$ is closed in $\Sigma .$ This proves the claim.

The claim above implies that $q \in \bigcup _{\tau \in (0,1)} u_{\tau }({\mathbb {C}}).$ It follows from the choice of q that:

$$\begin{aligned} \Sigma = P_3 \cup v({\mathbb {C}}\setminus \{ 0 \}) \cup P_2 \cup u({\mathbb {C}}) \cup \bigcup _{\tau \in (0,1)} u_{\tau }({\mathbb {C}}), \end{aligned}$$

and hence, there exists $\tau _0 \in (0,1)$, such that $u_{\tau _0}$ admits a point with $x_2 = 2\pi ,$ which derives a contradiction as above. Consequently, we find $u({\mathbb {C}}) \cap u'({\mathbb {C}}) = \emptyset .$ Since $\tau$ increases in the direction of the Reeb vector field, we have $u({\mathbb {C}}) = u_{2,1}({\mathbb {C}})$ and $u'({\mathbb {C}}) = u_{2,2}({\mathbb {C}}).$ This completes the proof. $\square$

Abbreviate

$$\begin{aligned} \mathfrak {B}= \{ (x_1, x_2, y_1, y_2) \in \Sigma \mid x_2 \le 2\pi \}, \end{aligned}$$

whose boundary is the piecewise smooth embedded two-sphere $u_{2,1}({\mathbb {C}}) \cup P_2 \cup u_{2,2}({\mathbb {C}}).$ The proof of the previous lemma shows that the images of the planes $u_{2,1}, u_{2,2}$ and $u_{\tau }, \tau \in (0,1)$ and the cylinder $v_1$ determine a smooth foliation of $\mathfrak {B} \setminus ( P_2 \cup P_3).$ Since the finite energy plane ${\tilde{u}}_{3,2}$ corresponds to $x_2 \equiv 0,$ we have $u_{3,2}({\mathbb {C}}) \subset \mathfrak {B}{\setminus } ( P_2 \cup P_3).$ Therefore, there is $\tau _* \in (0,1)$, such that $u_{\tau _*}({\mathbb {C}}) \cap u_{3,2}({\mathbb {C}}) \ne \emptyset .$ We find again by [10, Theorem 1.4] that $u_{\tau _*}({\mathbb {C}}) = u_{3,2}({\mathbb {C}}).$

Note that

$$\begin{aligned} \rho (\mathfrak {B} ) = \overline{ \Sigma \setminus \mathfrak {B}} = \{ (x_1, x_2, y_1, y_2) \in \Sigma \mid x_2 \ge 2\pi \}. \end{aligned}$$

We then push all the data above to the region $\rho (\mathfrak {B} ).$ More precisely, we have a one-parameter family of embedded finite energy ${\tilde{J}}$-holomorphic planes

$$\begin{aligned} ({\tilde{u}}_{\tau })_{\rho } :{\mathbb {C}}\rightarrow {\mathbb {R}}\times \Sigma , \quad \tau \in (\tau _-, \tau _+), \end{aligned}$$

all asymptotic to $P_3 ' = \rho (P_3).$ Note that $(u_{\tau _*})_\rho ({\mathbb {C}}) = u_{3,2}'({\mathbb {C}}).$ This family breaks onto ${\tilde{v}}_2 =({\tilde{v}}_1)_\rho$ and ${\tilde{u}}_{2,1} = (\tilde{u}_{2,1})_\rho$ at one end and onto ${\tilde{v}}_2$ and ${\tilde{u}}_{2,2} = ({\tilde{u}}_{2,2})_\rho$ at the other end. The images of maps $u_{2,1},u_{2,2}, (u_{\tau })_\rho , \tau \in (\tau _-, \tau _+)$ and $v_2$ fill the three-ball $\rho (\mathfrak {B}).$

We have constructed a stable finite energy foliation $\tilde{\mathcal {F}}$ of ${\mathbb {R}}\times \Sigma ,$ which is symmetric with respect to the exact anti-symplectic involution ${{\tilde{\rho }}}$ and whose leaves are embedded finite energy planes and cylinders. Denote by $\mathcal {F}$ the projection of $\tilde{\mathcal {F}}$ to $\Sigma ,$ which is symmetric with respect to the anti-contact involution $\rho .$ Since finite energy planes in $\tilde{\mathcal {F}}$ are asymptotic to $P_2$ or $P_3,$ their $\Sigma$-projections are transverse to the Reeb vector field [15]. See also [8, Section 13.6]. It is straightforward to see that the $\Sigma$-parts $v_1, v_2$ of the cylinders ${\tilde{v}}_1, {\tilde{v}}_2$ are transverse to the Reeb vector field, as well. Therefore, $\mathcal {F}$ determines a transverse foliation of $\Sigma$ whose binding orbits are $P_2,P_3$, and $P_3'$ and whose regular leaves are embedded planes and cylinders. See Fig. 9.

Fig. 9

The projection of the transverse foliation $\mathcal {F}$ to the $(x_2,y_2)$-plane. The black curves indicate the families of planes

Remark 5.7

A transverse foliation satisfying the properties above is called a weakly convex foliation. For more details, see [5].

We now cut the energy level $\Sigma$ along the two spheres

$$\begin{aligned} B&= \{ (x_1, x_2, y_1, y_2) \in \Sigma \mid x_2 = 0 \} = u_{3,1}({\mathbb {C}}) \cup P_3 \cup u_{3,2}({\mathbb {C}}),\\ \rho (B)&= \{ (x_1, x_2, y_1, y_2) \in \Sigma \mid x_2 = 4 \pi \} = u_{3,1}'({\mathbb {C}}) \cup P_3' \cup u_{3,2}'({\mathbb {C}}). \end{aligned}$$

Denote by $\Sigma _0$ a unique component whose boundary is given by $B \cup \rho (B).$ It is diffeomorphic to $S^2 \times I,$ where I is a closed interval. We then identify B and $\rho (B),$ providing us with $\bar{\Sigma } \cong S^2 \times S^1.$ Recall that $\bar{\Sigma }$ is a unique connected component of $\bar{H}^{-1}(c)$ which contains $\bar{\Sigma }^u_\textrm{direct},$ the double cover of ${\Sigma }^u_\textrm{direct}$. See Sect. 5.2. The contact form $\lambda ,$ constructed in Sect. 5.3, induces a contact form $\bar{\lambda }$ on $\bar{\Sigma },$ and the anti-contact involution $\rho$ induces an anti-contact involution on the contact manifold $(\bar{\Sigma }, \bar{\lambda }).$ We denote it again by $\rho .$ The unique index-2 periodic orbit $P_2$ still lies on $\bar{\Sigma },$ and the two index-3 binding orbits $P_3$ and $P_3'$ now provide a single symmetric periodic index-3 orbit, still denoted by $P_3.$ The periodic orbit $P_0$ yields two periodic orbits, one satisfies $y_2 = \Lambda _{\max }$ and the other satisfies $y_2 \equiv \Lambda _1.$ Note that the latter is the second iterate of the direct circular orbit $\gamma _\textrm{direct}^u.$

The almost complex structure $J :\xi \rightarrow \xi$ as in (5.11) induces a $d\bar{\lambda }$-compatible and $\rho$-anti-invariant almost complex structure ${\bar{J}} :\bar{\xi } \rightarrow \bar{\xi },$ where $\bar{\xi } = \ker \bar{\lambda }.$ Hence, the finite energy foliation $\tilde{\mathcal {F}}$ of ${\mathbb {R}}\times \Sigma$ induces a finite energy foliation of ${\mathbb {R}}\times \bar{\Sigma }$ consisting of the following:

• finite energy planes ${\tilde{u}}_{3,1}$ and ${\tilde{u}}_{3,2},$ corresponding to $x_2 \equiv 0$ (mod $4\pi$) and initial conditions $y_2(0) \in (\Lambda _1, \Lambda _3)$ and $y_2(0) \in (\Lambda _3, \Lambda _{\max }),$ respectively. They satisfy ${\tilde{u}}_{3,j} = ( {\tilde{u}}_{3,j})_\rho , j=1,2$ and are both asymptotic to $P_3.$

• finite energy planes ${\tilde{u}}_{2,1}$ and ${\tilde{u}}_{2,2},$ corresponding to $x_2 \equiv 2 \pi$ (mod $4\pi$) and initial conditions $y_2(0) \in (\Lambda _1, \Lambda _3)$ and $y_2(0) \in (\Lambda _3, \Lambda _{\max }),$ respectively. They satisfy ${\tilde{u}}_{2,j} = ( {\tilde{u}}_{2,j})_\rho , j=1,2$ and are both asymptotic to $P_2.$

• finite energy cylinders ${\tilde{v}}_1$ and ${\tilde{v}}_2 = ({\tilde{v}}_1)_\rho ,$ which corresponds to $y_2 \equiv \Lambda _3$ and initial conditions $x_2(0) \in (0, 2\pi )$ and $x_2(0) \in (2 \pi , 4 \pi ),$ respectively. They are both asymptotic to $P_3$ at $+\infty$ and to $P_2$ at $-\infty .$

• two families of finite energy planes $(\tilde{u}_{j, \tau }),$ $\tau \in (0,1).$ For each $j=1,2,$ the family $(\tilde{u}_{j, \tau })$ breaks onto ${\tilde{v}}_1$ and ${\tilde{u}}_{2,j}$ at the one end and onto ${\tilde{v}}_2$ and ${\tilde{u}}_{2,j}$ at the other end.

The projection of the finite energy foliation above defines a transverse foliation $\bar{\mathcal {F}}$ of $\bar{\Sigma },$ whose binding orbits are $P_2$ and $P_3$ and whose regular leaves are embedded planes and cylinders.

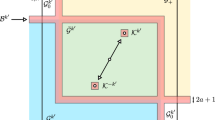
Denote by $\mathcal {T}$ the compact subset of the energy level ${\bar{\Sigma }}$, which projects into the $(x_2, y_2)$-plane (modulo $4\pi$ in $x_2$) as the set

$$\begin{aligned} \{ (x_2, y_2) \mid x_2 \in {\mathbb {R}}/ 4 \pi {\mathbb {Z}},\ \Lambda _1 \le y_2 \le \Lambda _3\}. \end{aligned}$$

Note that the set $\Sigma _{\textrm{direct}}^u$ under the double cover $\bar{\Sigma }^u_\textrm{direct}$ is contained in $\mathcal {T}$ and that $\mathcal {T}$ is diffeomorphic to a solid torus and has boundary

$$\begin{aligned} \partial \mathcal {T}= P_3 \cup P_2 \cup v_1({\mathbb {C}}\setminus \{ 0 \}) \cup v_2 ( {\mathbb {C}}\setminus \{ 0 \}) \end{aligned}$$

lying over the set $\{ (x_2, \Lambda _3) \mid x_2 \in {\mathbb {R}}/ 4 \pi {\mathbb {Z}}\}.$ The interior of $\mathcal {T}$ is filled with the images of planes $u_{2,1}$ and $u_{\tau }=u_{1,\tau }, \tau \in (0,1).$ The core of this solid torus is the second iterate of the direct circular orbit $\gamma ^u_\textrm{direct}.$

Let $F \in \bar{\mathcal {F}}$ be a plane asymptotic to $P_3$ that is not rigid and contained in $\mathcal {T}_1.$ For $j=1,2,$ denote $\Pi _j (x_1, x_2, y_1, y_2) = (x_j, y_j), (x_1, x_2, y_1, y_2) \in {\bar{\Sigma }}.$

Then, $\Pi _1(F)$ is a closed disc of radius $r_3$ centred at the origin and $\Pi _2(F)$ is an arc connecting $(x_2, \Lambda _1)$ for some $x_2 \in (0,4\pi )$ and $(0, \Lambda _3) \equiv ( 4\pi , \Lambda _3).$ If $(x_1, x_2, y_1, y_2) \in \bar{\Sigma }$ is such that $(x_2, y_2) \in \Pi _2(F)$ with $y_2 <\Lambda _2,$ then $(x_1, y_1)$ lies along the circle

$$\begin{aligned} x_1^2 + y_1^2 = 2\left( c + \frac{1}{2y_2^2}+y_2\right) . \end{aligned}$$

(5.26)

See (5.1). Note that the right-hand side above equals zero if and only if $y_2 =\Lambda _1.$

To show that $\bar{\mathcal {F}}$ intersects the set $\bar{\Sigma }^u_\textrm{direct}$ in embedded discs, we have to rule out the presence of a regular leaf $F \in \bar{\mathcal {F}}$ having the property that there is $y_2 <\Lambda _2$, such that $\# [\Pi _2(F)\cap \{ (x_2, y_2) \mid 0<x_2<4\pi \}]>1,$ as illustrated in Fig. 10.

Fig. 10

An unpleasant scenario that is not the case

To this end, fix a regular leaf $F \in \bar{\mathcal {F}},$ asymptotic to $P_3$ and contained in $\mathcal {T} {\setminus } \partial \mathcal {T}.$ Let ${\tilde{u}} = (a,u)$ be a corresponding finite energy plane. Denote $u(s,t) = (x_1(s,t), x_2(s,t), y_1(s,t), y_2(s,t))$ as before. Assume by contradiction that there is $(s_0, t_0)$, such that $\Lambda _1 < y_2(s_0, t_0) \le \Lambda _2$ and $(y_2)_s(s_0, t_0) = ( y_2)_t(s_0, t_0)=0.$ Introduce polar coordinates $(r, \vartheta )$ in the $(x_1, y_1)$-plane. By means of (5.26), we find that

$$\begin{aligned} r(s,t) r_\sigma (s, t) = - (y_2)_\sigma (s,t) \left( \frac{1}{y_2(s,t)^3} -1\right) , \quad \sigma = s, t. \end{aligned}$$

Since $y_2(s_0, t_0)> \Lambda _1 >1,$ we find $r(s_0,t_0)>0,$ and hence, $r_s(s_0,t_0) = r_t(s_0,t_0)=0.$ Let $\gamma (t) = (x_1(t), x_2(t), y_1(t), y_2(t))$ be a Hamiltonian trajectory that intersects F at $u(s_0,t_0).$ Since $y_2 \le \Lambda _2,$ without loss of generality, we may assume that $\bar{H} = H,$ where the latter is as in (5.1). Since H is free of the variable $x_2,$ we find using Hamilton’s equations that $y_2(t) = y_2(s_0, t_0), \forall t.$ Moreover, $\Pi _1(\gamma (t))$ moves along the circle of radius $r(s_0,t_0).$ The discussion so far shows that F and $\gamma$ have a non-empty tangent intersection at $u(s_0, t_0),$ contradicting the fact that F is transverse to the Hamiltonian flow. This shows that the transverse foliation $\bar{\mathcal {F}}$ of $\bar{\Sigma }$ intersects $\bar{\Sigma }^u_\textrm{direct}$ in embedded discs, providing a disc foliation of $\bar{\Sigma }^u_\textrm{direct}$ that is invariant under $\rho .$ This yields a disc foliation of $\Sigma ^u_\textrm{direct}$ satisfying the first two properties of Theorem 1.1 (1).

It remains to show that the associated first return map admits a unique fixed point corresponding to the direct circular orbit $\gamma _{\textrm{direct}}^u.$ It is obvious that $\gamma _{\textrm{direct}}^u$ corresponds to a fixed point. Recall that every periodic orbit $\gamma \ne \gamma _{\textrm{direct}}^u$ in $\Sigma _{\textrm{direct}}^u$ is a $T_{k,l}$-type orbit for some coprime positive integers k, l. See Sect. 3. It is easy to see that $k<l$ on $\Sigma _{\textrm{direct}}^u.$ See for instance [2, Section 6] or [18, Section 3]. This implies that the periods of $\Pi _1\gamma$ and $\Pi _2 \gamma$ do not coincide, and hence, every $T_{k,l}$-type orbit intersects each leaf at least twice. This finishes the proof of Theorem 1.1 for energies below the critical value.

Remark 5.8

In Appendix 6, we will embed $\Sigma _{\textrm{direct}}^u$ into a closed three-manifold ${\hat{\Sigma }} \cong S^2 \times S^1$ and then construct its finite energy foliation, projecting to an open book decomposition of ${\hat{\Sigma }}$ with annulus-like pages. The intersection of this open book decomposition with $\Sigma _\textrm{direct}^u$ provides a foliation of $\Sigma _{\textrm{direct}}^u$ into annuli, whose inner boundaries are the direct circular orbit $\gamma _{\textrm{direct}}^u$ and the outer boundaries lie on the boundary torus $\partial \Sigma _{\textrm{direct}}^u.$ The construction is explicit and does not require the implicit function theorem and compactness argument.

6 Above the critical energy

Fix $-\frac{3}{2}<c<0$ and let $E_0 \in (E_{\textrm{retro}}^u,c).$ Recall that $E =c$ corresponds to the collision orbits. This section is devoted to prove the assertion of Theorem 1.1 for the set

$$\begin{aligned} \Sigma _{\textrm{retro}}^u = \{\text {all periodic orbits of } X_H \text { with} E \in [E_{\textrm{retro}}^u, E_0]\} \subset \Sigma _c^u, \end{aligned}$$

which is diffeomorphic to a solid torus with core being the retrograde circular orbit $\gamma _{\textrm{retro}}^u.$ Note that it contains only retrograde orbits and no collision orbits.

In this case, the transformed Hamiltonian is given by

$$\begin{aligned} H (x_1, x_2, y_1, y_2) = - \frac{1}{2y_2^2} - y_2 - \frac{1}{2} ( x_1 ^2 + y_1 ^2) \end{aligned}$$

for $(x_1, x_2, y_1, y_2) \in \overline{\mathcal {P}}' \subset {\mathbb {R}}\times {\mathbb {R}}/ 2 \pi {\mathbb {Z}}\times {\mathbb {R}}\times {\mathbb {R}}_-.$ For convenience, we shall work with $-H$ instead of H,  so that every orbit is oriented in the opposite direction. Note that the qualitative behaviour of the dynamics does not change. By abuse of notation, we denote $-H$ again by H,  namely, we have

$$\begin{aligned} \begin{aligned} H (x_1, x_2 , y_1, y_2)&= \frac{1}{2y_2^2} + y_2 + \frac{1}{2} ( x_1 ^2 + y_1 ^2) \\&= H_1(x_1, y_2) - H_2(y_2), \end{aligned} \end{aligned}$$

where $H_1$ and $H_2$ are as in (5.2). Note that

$$\begin{aligned} y_2 \in [\nu _2, \nu _1] \quad \text { on } \ \Sigma _{\textrm{retro}}^u, \end{aligned}$$

where $\nu _1 = - \sqrt{ - \frac{1}{ 2E_{\textrm{retro}}^u}} \in ( - \frac{1}{\root 3 \of {2}}, -\frac{1}{2})$ and $\nu _2 = - \sqrt{ - \frac{1}{2E_0}}.$

Arguing as in Sect. 5.1, one can construct a disc foliation of $\Sigma _{\textrm{retro}}^u$ by looking at the negative gradient flow lines of $-H_2.$ See Fig. 11.

Fig. 11

Negative gradient flow lines of $-H_2.$ Dashed lines indicate Hamiltonian trajectories

Let $h_{x_2}$ be the negative gradient flow line of $-H_2$ corresponding to $x_2 \in {\mathbb {R}}/ 2\pi {\mathbb {Z}}.$ Its preimage $\Pi ^{-1}(h_{x_2})$ under the projection $\Pi (x_1, x_2, y_1, y_2) = (x_2, y_2), (x_1, x_2, y_1, y_2) \in \Sigma _{\textrm{retro}}^u$ is an embedded disc, transverse to the Hamiltonian flow. By varying $x_2$ in ${\mathbb {R}}/ 2 \pi {\mathbb {Z}},$ we find a disc foliation of $\Sigma _\textrm{retro}^u.$

Fix $\nu _3 \in (-\infty , \nu _2)$ and $0< \varepsilon _0 < \frac{1}{2} (\nu _2 - \nu _3).$ Consider

$$\begin{aligned} U(x_2, y_2) = \frac{1}{2} ( y_2 - \nu _3)^2 - \cos \frac{x_2}{2} +D, \end{aligned}$$

where $(x_2, y_2) \in {\mathbb {R}}/ 4\pi {\mathbb {Z}}\times {\mathbb {R}}_+$, and D is a constant satisfying

$$\begin{aligned} D< \min \left\{ 0, \frac{1}{2 ( \nu _2-\varepsilon _0)^2} + (\nu _2 - \varepsilon _0) - \frac{1}{2} ( \nu _2 - \varepsilon _0 - \nu _3)^2 -1 \right\} . \end{aligned}$$

Set

$$\begin{aligned} V(x_2, y_2) =- \left( 1-f(y_2) \right) H_2(y_2) + f(y_2) U(x_2, y_2), \end{aligned}$$

where a non-increasing smooth function $f :{\mathbb {R}}\rightarrow [0,1]$ satisfies $f(y_2) = 1, \forall y_2 < \nu _2 - 2\varepsilon _0$ and $f(y_2)=0, \forall y_2 > \nu _2 - \varepsilon _0.$ See Fig. 12.

Fig. 12

Interpolation for variable $y_2$

Because of the choice of the constant D,  we have

$$\begin{aligned} V_{y_2}<0, \ \forall y_2< \nu _3 \quad \text { and } \quad V_{y_2} >0, \forall y_2 < \nu _3, \end{aligned}$$

and $(0, \nu _3)$ and $(2\pi , \nu _3)$ are the only critical points of V. Given $x_2,$ denote by $\nu _{\min } = \nu _{\min }(x_2)$ the value of $y_2$ satisfying $V(x_2, \nu _{\min })=-c.$

We define

$$\begin{aligned} \bar{H}(x_1, x_2, y_1, y_2) = H_1(x_1, y_1) + V(x_2, y_2), \end{aligned}$$

where $(x_2, y_2) \in {\mathbb {R}}/ 4\pi {\mathbb {Z}}\times {\mathbb {R}}_+$, and note that it is invariant under the anti-symplectic involution $\rho$ as in (5.5).

We now break the periodicity in $x_2$ precisely as in Sect. 5.2. Namely, we consider

$$\begin{aligned} W(x_2, y_2)=\frac{1}{2}x_2^2 + \frac{1}{2} (y_2 -\nu _3)^2 \end{aligned}$$

and interpolate

$$\begin{aligned} {\tilde{V}} (x_2, y_2) = \left( (1-g(x_2) \right) W(x_2, y_2) + g(x_2) V(x_2, y_2), \end{aligned}$$

where g is a non-decreasing smooth function $g:{\mathbb {R}}\rightarrow [0,1]$, such that $g(x_2)=0, \forall x_2 < -2\varepsilon _1$ and $g(x_2) =1, \forall x_2 >-\varepsilon _1$ with $\varepsilon _1>0$ small enough. By repeating in a similar manner for $x_2 \ge 2\pi$ in a symmetric way, we obtain a smooth function ${\tilde{H}}_2(x_2, y_2).$ Note that it is symmetric in $x_2$ with respect to $x_2 =2\pi .$

We then obtain a modified Hamiltonian

$$\begin{aligned} {\tilde{H}} (x_1, x_2, y_1, y_2) = H_1(x_1, y_1) + {\tilde{H}}_2( x_2, y_2). \end{aligned}$$

It is easy to see that ${\tilde{H}}$ admits exactly three critical points given in (5.7) and satisfies

$$\begin{aligned} {\tilde{H}}_{y_2}<0, \ \forall y_2 < \nu _3, \quad {\tilde{H}}_{y_2}>0, \ \forall y_2 >\nu _3. \end{aligned}$$

This implies that there is a connected component $\Sigma \cong S^3$ of the energy level ${\tilde{H}}^{-1}(-c).$ The anti-symplectic involution $\rho$ induces an anti-symplectic involution of ${\mathbb {R}}^3 \times {\mathbb {R}}_-,$ still denoted by $\rho .$ Since ${\tilde{H}}$ is invariant under $\rho$, so is $\Sigma .$

The rest of the proof is analogous to the previous case, so we omit it. This finishes the proof.

Appendix A: Annulus foliations

As announced in Remark  5.8, we shall construct a foliation of $\Sigma _{\textrm{direct}}^u$ (when $c<-\frac{3}{2}$) different from the one given in Sect. 5. An annulus foliation of $\Sigma _{\textrm{retro}}^u$ (when $c \in (-\frac{3}{2},0)$) can be constructed in a similar manner.

We fix $c<-\frac{3}{2}$ and $E_0 \in (E_{\textrm{direct}}^u,0)$ and define $\Sigma _{\textrm{direct}}^u \subset \Sigma _c^u$ as before. Consider $\Lambda _3 > \Lambda _2$ and $0< \varepsilon < \frac{1}{2}( \Lambda _3 -\Lambda _2),$ where $\Lambda _2$ is as in Sect. 5. Let

$$\begin{aligned} V(y_2) = \frac{1}{2} (y_2 - \Lambda _3)^2 +B, \end{aligned}$$

where the constant B is given as in (5.3), and define

$$\begin{aligned} {\hat{H}}_2 (y_2) = ( 1 - f(y_2)) H_2(y_2) + f(y_2) V(y_2), \end{aligned}$$

where $f :{\mathbb {R}}\rightarrow [0,1]$ is a non-decreasing function satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} f(y_2) =0 &{} y_2 < \Lambda _2+ \varepsilon ,\\ f(y_2)=1 &{} y_2 > \Lambda _2 + 2\varepsilon . \end{array}\right. } \end{aligned}$$

Arguing as in Sect. 5.2, we see that

$$\begin{aligned} {\hat{H}}_2'<0, \ \forall y_2 < \Lambda _3 \quad \text { and } \quad {\hat{H}}_2'>0, \ \forall y_2 > \Lambda _3. \end{aligned}$$

(A.1)

We introduce

$$\begin{aligned} {\hat{H}} (x_1, x_2, y_1, y_2)= H_1(x_1, y_1)+ \hat{H}_2 (y_2). \end{aligned}$$

Note that ${\hat{H}}$ is free of the variable $x_2.$ The energy level ${\hat{H}}^{-1}(c)$ contains a connected component ${\hat{\Sigma }} \cong S^1 \times S^2,$ containing $\Sigma _{\textrm{direct}}^u,$ where we have identified $S^1 \equiv {\mathbb {R}}/2 \pi {\mathbb {Z}}.$ If $(x_1, x_2, y_1, y_2) \in {\hat{\Sigma }},$ then

$$\begin{aligned} \Lambda _1 \le y_2 \le \Lambda _{\max }:= \sqrt{2(c-B)} +\Lambda _3. \end{aligned}$$

The Liouville vector field

$$\begin{aligned} {\hat{Y}} = \frac{1}{2} ( x_1 \partial _{x_1} + y_1 \partial _{y_1} ) + (y_2 - \Lambda _3) \partial _{y_2} \end{aligned}$$

satisfies $d\hat{H}({\hat{Y}})>0,$ implying that it is transverse to ${\hat{\Sigma }}.$ Therefore, we obtain a contact form ${\hat{\lambda }}$

$$\begin{aligned} {\hat{\lambda }} = \omega _0 ( {\hat{Y}}, \cdot )|_{{\hat{\Sigma }}} = \frac{1}{2} ( y_1 \textrm{d}x_1 - x_1 \textrm{d}y _1 ) + ( y_2 - \Lambda _3) \textrm{d}x_2. \end{aligned}$$

Consider the periodic orbits $Q_1 = (w_1, T_1)$ and $Q_2=(w_2, T_2),$ where

$$\begin{aligned} w_1(t)&= ( 0, ( \frac{1}{ \Lambda _1^3} -1)t, 0, \Lambda _1) , \quad T_1 = \frac{ 2 \pi }{1- 1/\Lambda _1^3 }\\ w_2(t)&= (0, \sqrt{ 2 ( c-B)}t, 0, \Lambda _{\max }), \quad T_2 = \frac{ 2\pi }{\sqrt{ 2 ( c-B)}}. \end{aligned}$$

Note that $Q_1$ corresponds to the direct circular orbit $\gamma _{\textrm{direct}}^u.$ Since

$$\begin{aligned} \lambda (X_{\hat{H}})={\left\{ \begin{array}{ll} ( \Lambda _1 - \Lambda _3)( \frac{1}{\Lambda _1^3}-1) &{} \text { along } Q_1,\\ 2(c-B) &{} \text { along } Q_2, \end{array}\right. } \end{aligned}$$

their Reeb periods are $2\pi (\Lambda _3-\Lambda _1)$ and $2 \pi \sqrt{ 2(c-B)},$ respectively.

Introduce polar coordinates $(r, \vartheta )$ in the $(x_1, y_1)$-plane. Note that $r = \sqrt{ 2(c-\hat{H}_2)},$ showing that the variable r takes the minimum $r=0$ when $\hat{H}_2=c,$ or equivalently, $y_2 \in \{ \Lambda _1, \Lambda _{\max }\},$ and the maximum $r = r_{\max }$ when $y_2 = \Lambda _3.$ Fix $\vartheta \in {\mathbb {R}}/ 2 \pi {\mathbb {Z}}$ and consider $u_\vartheta (s) = (r(s) \cos \vartheta , r(s) \sin \vartheta )$, such that r(s) satisfies

$$\begin{aligned} \lim _{ s \rightarrow \pm \infty } r(s) = 0, \quad r(0) = r_{\max }. \end{aligned}$$

Denote $\Pi ( x_1, x_2, y_1, y_2) = (x_1, y_1).$ Then, $\Pi ^{-1}(u_\vartheta )$ is an embedded annulus in $\Sigma$ that is transverse to the Hamiltonian flow and asymptotic to $Q_1$ and $Q_2.$ By varying $\vartheta \in {\mathbb {R}}/2 \pi {\mathbb {Z}},$ we obtain an open book decomposition of $\Sigma$ with annulus-like pages. Each annulus, restricted to the $(x_1, y_1, y_2)$-space, is an arc asymptotic to the points $(0,0,\Lambda _1)$ and $(0,0,\Lambda _{\max })$ that correspond to the binding orbits $Q_1$ and $Q_2,$ respectively. See Fig. 13.

Fig. 13

An open book decomposition of $\Sigma$ with annulus-like pages

To construct a finite energy foliation of ${\hat{\Sigma }}$ projecting to the above-described open book decomposition, choose J as in Sect. 5.6. We fix $\vartheta \in {\mathbb {R}}/ 2 \pi {\mathbb {Z}}$ and let ${\tilde{w}}_\vartheta = (d_\vartheta ,w_\vartheta ) :{\mathbb {R}}\times S^1 \rightarrow {\mathbb {R}}\times \Sigma$ be a ${\tilde{J}}$-holomorphic curve. We make the following Ansatz:

Ansatz. The $\Sigma$-part $w_\vartheta$ is of the form

$$\begin{aligned} w_\vartheta (s,t) = ( r(s) \cos \vartheta , 2 \pi t, r(s) \sin \vartheta , y_2(s)), \end{aligned}$$

where r(s) satisfies $\lim _{s \rightarrow \pm \infty }r(s)=0.$

In view of $\hat{H} = c,$ we find

$$\begin{aligned} \frac{1}{2}r(s)^2 +\hat{H}_2(y_2(s))=c. \end{aligned}$$

(A.2)

Proceeding as before, we find

$$\begin{aligned} \dot{y}_2 (s) = \frac{ 2 \pi r(s)^2 }{ r(s)^2+ \hat{H}_2'(y_2(s)) ^2} = \frac{ 4 \pi (c- \hat{H}_2(y_2(s)) ) }{ 2(c-\hat{H}_2(y_2(s)))+ \hat{H}_2'(y_2(s)) ^2}, \end{aligned}$$

(A.3)

which might be seen as a differential equation of type

$$\begin{aligned} \dot{y}_2 (s) = P(y_2(s)). \end{aligned}$$

Here, $P=P(y_2)$ is a smooth function on $[ \Lambda _1, \Lambda _{\max }],$ which vanishes precisely at $y_2 = \Lambda _1, \Lambda _{\max }.$ Since $P(y_2)>0, \forall y_2 \in (\Lambda _1,\Lambda _{\max }),$ we conclude that a solution $y_2=y_2(s)$ to ODE (A.3) with initial condition $y_2(0) \in (\Lambda _1, \Lambda _{\max })$ is strictly increasing and satisfies

$$\begin{aligned} \lim _{s \rightarrow -\infty } y_2(s) = \Lambda _1, \quad \lim _{s \rightarrow +\infty } y_2(s) = \Lambda _{\max }. \end{aligned}$$

We now find using (A.2) and (A.3) that

$$\begin{aligned} \dot{r} (s) = - \frac{2 \pi r(s)\hat{H}_2'( y_2(s))}{ r(s)^2+ \hat{H}_2'(y_2(s)) ^2} = {\left\{ \begin{array}{ll} \sqrt{ ( 2 \pi - \dot{y}_2 (s)) \dot{y}_2 (s)} &{} \textrm{if } \; \hat{H}_2'(y_2(s)) \le 0,\\ - \sqrt{ ( 2 \pi -\dot{y}_2 (s)) \dot{y}_2 (s)} &{} \textrm{if } \; \hat{H}_2'(y_2(s)) >0. \end{array}\right. } \end{aligned}$$

In view of (A.1), we conclude that $r=r(s)$ is increasing for $s \in (-\infty , s_0)$ and decreasing for $s \in (s_0, +\infty ),$ where $s_0$ denotes the time at which $y_2(s_0) =\Lambda _3.$ In particular, $r(s) \rightarrow 0$ as $s \rightarrow \pm \infty .$

We also find

$$\begin{aligned} ( d_\vartheta )_s = \hat{\lambda }( (w_\vartheta )_t)= 2 \pi ( y_2 - \Lambda _3), \quad ( d_\vartheta )_t = \hat{\lambda }( (w_\vartheta )_s) = 0. \end{aligned}$$

This implies that d is independent of t, and hence, we may write

$$\begin{aligned} d_\vartheta (s,t) = 2 \pi \int _0^s ( y_2( u ) - \Lambda _3) d u. \end{aligned}$$

Note that $d_\vartheta (s,t) \rightarrow +\infty$ as $s \rightarrow \pm \infty .$

We have constructed a finite energy ${\tilde{J}}$-holomorphic cylinder ${\tilde{w}}_\vartheta = (d_\vartheta , w_\vartheta ):{\mathbb {R}}\times S^1 \rightarrow {\mathbb {R}}\times \Sigma$ that is asymptotic to $Q_1$ and $Q_2$ at ${\mp } \infty ,$ respectively. Note that both asymptotic limits are positive. Its Hofer energy equals the sum of the Reeb periods of $Q_1$ and $Q_2.$

Since the above argument is independent of the choice of $\vartheta \in {\mathbb {R}}/ 2 \pi {\mathbb {Z}},$ by varying $\vartheta$, we obtain a finite energy foliation of ${\mathbb {R}}\times {\hat{\Sigma }},$ which projects the open book decomposition of ${\hat{\Sigma }}$ with annulus-like pages, described above. Its intersection with the set $\Sigma _{\textrm{direct}}^u$ yields the desired annulus foliation. Namely, the solid torus $\Sigma _{\textrm{direct}}^u$ is foliated into annuli transverse to the Hamiltonian flow restricted to $\Sigma _{\textrm{direct}}^u.$ The outer boundary of each annulus lies on the boundary torus $\partial \Sigma _{\textrm{direct}}^u.$ The inner boundary coincides with the direct circular orbit $\gamma _{\textrm{direct}}^u$ (Fig. 14).

Fig. 14

A slice of the annulus foliation. The dot and the dotted curves correspond to the direct circular orbit and annuli, respectively. The blue curve points in the direction of the Hamiltonian flow