Bio-inspired design of next-generation ultrapermeable membrane systems

Abstract

Ultrapermeable membranes (UPMs) have the potential of improving water production efficiency. However, operating at high water fluxes will intensify concentration polarization and membrane fouling. Inspired by the V-formation of birds in nature we propose a transformative membrane module that enables a doubled mass transfer coefficient with a moderately increased friction loss coefficient. Moreover, we present a practical technological pathway for the UPM systems to achieve 338% improvement of average water flux and 18% energy savings relative to state-of-the-art seawater desalination plants. The work makes it practical to operate at a high average water flux of 84 L m⁻² h⁻¹ with a controlled concentration polarization for the UPM systems. It breaks through the module development bottlenecks for the next-generation UPM systems and has enormous potential application for alleviating water scarcity crisis in the coming decades.

Introduction

Global water usage has increased more than six-fold over the past 100 years.¹ Approximately 10% of the world’s population is facing serious water shortage problems, and that number continues to rise.² Studies predict that more than half of the world’s population will face the water stress to varying extents by the year of 2050.¹ Desalination of seawater and brackish water and wastewater reuse are both effective ways to alleviate the water supply deficit in the coming decades.³ Cumulative desalination capacity has increased more than 8-fold in the past 30 years, reaching up to 100 million m³/day, out of which 57% and 20% are from seawater and brackish water resources, respectively.⁴ In the past 40 years, the specific energy consumption (SEC) of seawater reverse osmosis (SWRO) has declined markedly from more than 8 kWh m⁻³ to about 2 kWh m⁻³,⁵ due to technological developments, e.g., the use of more advanced membrane materials and energy recovery devices and the continuous improvement of pump efficiency.⁶ Compared with concentration-driven (e.g., forward osmosis, osmotic distillation) and temperature-driven (e.g., membrane distillation) desalination technologies, RO as a pressure-driven membrane technology is the state-of-the-art,⁷ accounting for 69% of the total installed capacity.⁸ The thermodynamic minimum SEC is 1.08 kWh m⁻³ for SWRO (based on a feed salinity of 35,000 ppm and a recovery of 50%) and 0.24 kWh m⁻³ for brackish water RO (BWRO) (based on a feed salinity 5800 ppm and a recovery of 75%) (Supplementary Fig. 1a). The actual SEC in RO plants is higher because of pump efficiency, design flux requirement, concentration polarization (CP) and friction loss.

In recent years, high permeable membranes or ultrapermeable membranes (UPMs) based on advanced materials, e.g., graphene,⁹ graphene oxide,^10,11,12,13 carbon nanotube,¹⁴ conjugated-polymer,¹⁵ nanochannel¹⁶ and enhanced polyamide^17,18 have shown potential applications in next-generation RO or nanofiltration systems. For example, the graphene oxide membranes reported by Zhang et al.¹³ have a stable porous structure, and their water permeability can reach up to 60 L m⁻² h⁻¹ bar⁻¹ (lmh bar⁻¹). Unfortunately, the increment of energy saving diminishes as the water permeability goes beyond 3 lmh bar⁻¹ (Supplementary Fig. 1b). In such a case, system design becomes more important in improving energy efficiency.¹⁹ On the other hand, the use of UPMs may reduce the required membrane area for a given permeate production, however, high water fluxes will intensify CP and membrane fouling.²⁰ The study of Shi et al.²¹ indicates that it is impractical using the current membrane module to acquire significant benefit from the UPM systems, and that module and process optimization is essential. Furthermore, McGovern and Lienhard²² show that the limiting flux for an UPM system is correlated linearly with the mass transfer coefficient for single stage and batch ROs. Hence, enhancing mass transfer is crucial for maximizing the prospects of the UPM systems.

Results

Potential evaluation of UPM module design

The study of Fane et al.²⁰ indicated that it is crucial to limit the modified Péclet number (J* = J_W/k) for reducing CP in UPMs. For one RO element, J* can be expressed as:²² ${J}^{\ast }({R}_{{\rm{r}}})=({L}_{{\rm{p}}}/k)[(\Delta {P}_{0}-\Delta {P}_{{\rm{c}}})-{\pi }_{0}/(1-{R}_{{\rm{r}}}){e}^{{J}^{\ast }({R}_{{\rm{r}}})}]$ (R_r is recovery rate; L_p is water permeability; k is mass transfer coefficient; $\Delta {P}_{0}$ is inlet transmembrane pressure; $\Delta {P}_{{\rm{c}}}$ is axial pressure drop; ${\pi }_{0}$ is inlet osmotic pressure). Therefore, the real challenge lies in improving k with a controlled axial pressure drop penalty, which is crucial to enhance the permeation flux (${J}_{{\rm{W}}}$) and to limit the CP factor, CPF = ${e}^{{J}_{{\rm{W}}}/k}$. For a typical conventional membrane module with 28 mil feed spacer²³ studied in this work, the mass transfer coefficient and the pressure drop per unit length in the feed channel are correlated as functions of the cross velocity ($\bar{u}$) using computational fluid dynamics (CFD) simulations: ${\bar{k}}_{{\rm{m}},0}=2.53\times {10}^{-4}\,{\bar{u}}\,^{0.49}$ and $\varDelta {P}_{{\rm{c}},0}/{L}_{0}=3.41\,{\bar{u}}\,^{1.54}$. Doubling ${\bar{k}}_{{\rm{m}},0}$ requires the cross-flow velocity ($\bar{u}$) to be quadrupled, which in turn, leads to a 9-fold friction loss that must be overcome by the pump. Apparently, manipulating cross-flow alone to greatly enhance mass transfer with a moderate pressure drop penalty is difficult.

Module design, or feed spacer design is another way to enhance mass transfer. Considering a hypothetical case where the mass transfer coefficient correlation follows ${\bar{k}}_{{\rm{m}}}=2.53\,K\times {10}^{-4}\,{\bar{u}}\,^{0.49}$ ($K=1,\,2,\,5,\,5\times {10}^{22}$) while the pressure drop correlation remains the same, the estimated average water flux with respect to water permeability is shown in Supplementary Fig. 1c. An arbitrarily large value of K ($K=5\times {10}^{22}$) is used here to gauge the theoretical maximum of average water flux for a given water permeability. For UPM systems, a significant improvement on average water flux (or reducing the required membrane area) can be achieved if the mass transfer coefficient is doubled (from K = 1 to K = 2).

As K continues to increase, a further improvement on average water flux is limited, however, it may suppress CP (Supplementary Fig. 1d) and reduce the risk of membrane fouling. Hence, in order to match the high water flux, improving the mass transfer coefficient 2- to 5-fold with a moderate pressure drop penalty could maximize the benefit from the UPMs. Lin et al.²⁴ reviewed the development of feed spacer in spiral wound membrane modules in the past twenty years and highlighted the significance and potential of novel spacer designs. Liu et al.²⁵ adopted experimental data to testify that the mass transfer coefficient of the static mixing spacer is 20% higher than that of a conventional spacer under a low cross-flow velocity. Li et al.²⁶ used additive manufacturing technology to prepare a few feed spacers, out of which the optimized multi-layer spacer achieved a 30% enhancement of mass transfer relative to conventional spacers. The simulated results by Chong et al.²⁷ indicated that the mass transfer (or Sherwood number) of column node spacers was enhanced by 25% at the cost of a 44% higher flow resistance. Despite efforts in module design aided by CFD^28,29,30,31 and experiments^32,33, even doubling the mass transfer coefficient without significant pressure drop penalty is a challenge.²⁰

Herein we propose a transformative approach inspired by the V-formation of birds for UPM systems that breaks through the membrane module development bottlenecks: the tradeoff between mass transfer and flow resistance. Utilizing an optimization framework presented in this work, a V-shape feed spacer is designed, corresponding to the mass transfer coefficient correlation (${\bar{k}}_{{\rm{m}}}=4.37\times {10}^{-4}\,{\bar{u}}\,^{0.55}$) and the pressure drop per unit length correlation ($\Delta {P}_{{\rm{c}}}/L=2.19\,{\bar{u}}\,^{1.59}$). Using the proposed membrane module, enhancing ${\bar{k}}_{{\rm{m}}}$ 2-fold only leads to a 21% increase in pressure drop per unit length, in comparison to those in the conventional membrane module. This paves the way for UPM systems for RO desalination.

Bio-inspired design of UPM systems

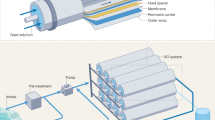
In order to design the next-generation UPM modules with compatible fluid and mass transfer characteristics, we borrow ideas from nature. It is well-known that many birds, such as migrating ibises,^34,35 pelicans,³⁶ and geese³⁷ fly in a ‘V’ formation to save energy. By this formation, pelicans flown in a vortex wake can extend their glide time or reduce their wingbeat frequency that enables a total energy saving of 11.4–14.0%.³⁶ Inspired by this, we develop a fundamentally different spiral wound module (Fig. 1) with V-shape feed spacers for use in conjunction with advanced RO membranes. Furthermore, we propose a hierarchical optimization framework (Supplementary Fig. 2) for RO module and system design. In module design, a power exponent (β) is used in the objective function (see “Methods” section) to control the relative importance of flow resistance and mass transfer. A larger value of β means it is more important to enhance mass transfer than to suppress friction loss. Herein, three representative feed spacers are obtained by solving three-dimensional (3D) CFD model constrained optimization problems with β = 4, 6, and 8 and their system performance is evaluated and compared in the next section. The genetic algorithm is used to solve optimization problem for a given average inlet velocity magnitude (0.1 m s⁻¹) and β. This algorithm does not need derivative information or a good initial estimate and has better global convergence than traditional optimization algorithms.³⁸ More details about the multi-physics model and module design can be found in “Methods” section and in our previous work.³⁹

Fig. 1: A bio-inspired module design for UPM systems.

a Two-stage RO. b V-formation of geese. c A small piece of spacer sheet inspired by the V-formation of geese. d Computational domain for CFD. e A small piece of ultrapermeable membrane. f A spacer cell.

The convergence curves and the optimized spacer geometries with various tradeoff parameters of β (4, 6, and 8) are presented in Supplementary Fig. 3a and 3b–d respectively. As β increases, the optimized feed spacer exhibits a stronger enhancement of mass transfer at the expense of an increased flow resistance. The estimated local mass transfer coefficient (${k}_{\rm{m}}$), velocity and pressure distributions are shown in Figs. 2, 3 and Supplementary Fig. 4 respectively for the optimized spacers (β = 4, 6, and 8) and the conventional spacer. The enhanced mass transfer coefficients in V-shape spacers (shown in Fig. 2) attributes to vortex flow in the transverse section (Fig. 3a–c), which is significantly different from the commercial one (Fig. 3d). The flow pattern coincides with the theoretical optimal velocity to enhance heat and mass transfer for a given viscous dissipation.^40,41 However, the pressure drop coefficient also remarkably increases with β (Supplementary Fig. 4a–c).

Fig. 2: Mass transfer coefficient distributions in the optimized spacers and the conventional spacer.

a β = 4, b β = 6 and c β = 8. d Conventional spacer. The average inlet velocity magnitude is 0.2 m s⁻¹.

Fig. 3: Velocity and streamline distributions in the optimized spacers and the conventional spacer.

a β = 4, b β = 6 and c β = 8. d Conventional spacer. The average inlet velocity magnitude is 0.2 m s⁻¹.

The correlations of the Sherwood number (Sh) and the Darcy friction factor (f) as functions of the Reynolds number (Re) are commonly used to evaluate the mass transfer and hydrodynamic characteristics in membrane modules. Such correlations for the optimized spacers in this work, commercial spacers, and the reported results in literature^{28,29,30,31,42,43} are presented in Fig. 4a, b. Under the same Reynolds number of 200, the Sherwood numbers (Sh = 144, 141, and 164) improve by 95%, 91% and 121% while the Darcy friction factors (f = 1.51, 2.08, and 4.70) increase by 19%, 63% and 268% for the optimized V-shape spacers (β = 4, 6, and 8) compared with that of the commercial one (Sh = 74, f = 1.28). Overall, the V-shape spacer with β = 4 has a good balance between mass transfer and flow resistance. Its mass transfer is significantly enhanced while the friction loss is comparable to or even less than those reported in literature.^{28,29,30,31,42,43} One drawback of the proposed spacers, though, is that the channel is increased, will lowers the membrane areal packing density in membrane modules.

Fig. 4: The estimated hydrodynamics and mass transfer correlations.

The Sherwood number and Darcy friction factor correlations using the optimized spacers and the conventional spacer in this work and previously published correlations.^{28,29,30,31,42,43} a Sh versus Re. b f versus Re.

System design at industrial-scale

Furthermore, the system design at industrial-scale is performed using an optimization framework (Supplementary Fig. 2) based on the optimized feed spacers. The framework enables a customized solution for given input parameters, e.g., recovery rate, minimum average permeation flux, maximum average permeate salinity, maximum CPF at system inlet that is crucial to mitigate fouling and scaling. A two-stage configuration is adopted in this work. It has a lower pressure at the entrance than that in the standard one-stage configuration, which helps reduce flux and CP on lead elements. The objective function contains two terms – SEC (i.e., operating cost) and required membrane area (i.e., capital cost). Membrane cost per m², c_m is a tradeoff parameter used to control the weight of both terms.⁴⁴ By solving a nonlinear mixed-integer programming problem, we can obtain the optimized design that includes module configurations, operating pressures at each stage and desired membrane properties (water and salt permeabilities). More detailed information for the system design can be found in “Methods” section and in our previous work.³⁹ Our previous study on BWRO desalination indicated that the deviations between multiscale model predictions and measurements of pressure and flow at various locations are all less than 5%.⁴⁵

In order to analyze the effect of c_m on the SEC and the required membrane area, the optimization solutions with various c_m (40, 100, 160, 220, 280, 340, 400 $ m⁻²) are obtained for SWRO (feed salinity ${w}_{{\rm{b}},0}$ = 35,000 ppm, recovery rate ${R}_{{\rm{r}},0}$ = 50%, inlet flow rate ${Q}_{0}$ = 300 m³ h⁻¹) and BWRO (${w}_{{\rm{b}},0}$ = 5800 ppm, ${R}_{{\rm{r}},0}$ = 75%, ${Q}_{0}$ = 300 m³ h⁻¹). The Pareto optimal front to visualize the tradeoff between the SEC and the membrane area for SWRO and BWRO is shown in Fig. 5. It is worth pointing out that the optimization solutions have practical engineering significance even when c_m for UPMs is much higher than that of the commercial one because the energy cost dominates in the objective function. Moreover, one advantage of UPM systems lies on miniaturization of plant footprint. For SWRO, there is little difference between β = 4 and 6 in terms of energy consumption and plant size. Both appear to be superior to the case where β = 8 when the maximum CPF at system inlet (CPF_max) is constrained to be no more than 1.20. In industrial RO desalination, the CPF is typically about 1.1–1.2.²⁰ If CPF_max is relaxed to 1.30, the advantage of using β = 4 or 6 becomes greater. For BWRO, the system performance using β = 8 is evidently better than the other two cases if CPF_maxis 1.20. However, the three cases are very close if CPF_max is relaxed to 1.30. The reason for this discrepancy between BWRO and SWRO is that the effect of mass transfer on the BWRO is greater than that of the SWRO if CPF_max is 1.20. When the CPF_max is relaxed to 1.30, the reduction of the number of the pressure vessels will increase the cross velocity, and thus remarkably increase the pressure drop, which defeats the benefits of enhanced mass transfer.

Fig. 5: Tradeoff between SEC and membrane area.

a SWRO (feed salinity of 35,000 ppm; recovery rate of 50%; pump efficiency of 85%; energy recovery efficiency of 95%). b BWRO (feed salinity of 5800 ppm; recovery rate of 75%; pump efficiency of 85%).

Next, we use the optimized spacer (β = 4) as an example to further analyze how much benefit can be obtained from the UPM systems for SWRO. The maximum CPF at system inlet is controlled to 1.20. The optimized SEC (1.65, 1.88, and 2.00 kWh m⁻³) with various values of the c_m parameter (40, 280, and 400 $ m⁻²) reduces by 28%, 18%, and 13% respectively compared with the calculated SEC (2.30 kWh m⁻³) under typical engineering conditions that is consistent with the reported SEC (2.26 kWh m⁻³) for the SWRO system (feed salinity of 35,000 mg L⁻¹; recovery rate of 50%; pump efficiency of 85%; energy recovery efficiency of 95%).⁴⁶ Accordingly, the average water flux (34, 84, and 103 lmh) enhances by 77%, 338% and 435% and the required membrane area (4411, 1777, and 1454 m²) reduces by 43%, 77%, and 81% compared with the estimated results in modern plants (19 lmh, 7804 m²). The average permeate salinity in all cases is no more than 500 ppm that meets the potable water requirements.⁴⁷ If the maximum CPF at system inlet is relaxed to 1.30, more benefit can be obtained from the UPM systems. For example, the SEC (1.63, 1.81, and 1.86 kWh m⁻³) can reduce by 29%, 21% and 19%. The average water flux (48, 111, and 129 lmh) enhances by 149%, 477% and 569% and the required membrane area (3110, 1349, and 1163 m²) reduces by 60%, 83%, and 85% respectively.

The estimated profiles of mass transfer coefficient, pressure drop per unit length, water flux and transmembrane pressure versus recovery rate are shown in Supplementary Fig. 5a, b and Supplementary Fig. 6a, b respectively for c_m = 280 $ m⁻². The mass transfer coefficient using the optimized spacer (β = 8) is higher than the other two cases (β = 4 and 6), which enables the use of more permeable membranes (20.00 lmh bar⁻¹ vs. 11.88 and 11.66 lmh bar⁻¹), operation under higher water flux (Supplementary Fig. 6a) and a pressure closer to the thermodynamic equilibrium (Supplementary Fig. 6b). However, the pressure drop per unit length of the former one is more than triple of the latter two spacers (Supplementary Fig. 5b), which cancels the benefit of using UPMs for energy saving. Overall, the reductions in SEC and membrane area are considerable with β = 4 and 6 (CPF_max = 1.20). For BWRO, the conclusion is just the opposite. Finally, we illustrate how the CP is greatly suppressed at high water fluxes using the case of β = 4. On the one hand, the bio-inspired module design can achieve significant improvement on mass transfer with a controlled flow resistance penalty. On the other hand, the optimized cross velocity at inlet (0.32 m s⁻¹) in system design is much higher than that in the baseline case (0.19 m s⁻¹), which further enhances the mass transfer. Moreover, the two-stage design reduces the applied pressure (first-stage: 48.1 bar, second-stage: 61.7 bar v.s. commercial one-stage SWRO: 66.0 bar), which also contributes to the reduced CP. Using these strategies, the mass transfer coefficient is enhanced by 130% at a cost of 35% increased axial pressure drop per unit length at system inlet. The system pressure drop increases from 1.0 bar to 1.8 bar. Overall, the maximum CPF at a high average water flux of 84 lmh can be controlled to be no more than 1.20 whereas state-of-the-art seawater desalination plants have a CPF about 1.09 at an average water flux of 19 lmh. More detailed results before and after optimization for SWRO with various β are listed in Supplementary Table 1 (c_m = 280 $ m⁻²).

Discussion

Although UPMs are limited on reducing energy consumption in water desalination, they have significant potential in reducing membrane area. However, the fluid mechanics and mass transfer characteristics must be compatible for UPMs to prevent aggravated CP and membrane fouling at high water fluxes. In this work, we evaluate the effect of module design for the UPM systems, and the simulated results indicate that enhancing the mass transfer coefficient by 2–5 times with a moderate pressure drop penalty maximizes system performance. However, to double the mass transfer coefficient using conventional methods is a difficult task. Inspired by the V-formation of birds, we designed three transformative spacers and further provided the optimization solutions (membrane properties, module configurations, and operating pressures) using the proposed hierarchical optimization framework. The designed two-stage UPM RO systems was able to achieve a doubled mass transfer with a moderate pressure drop penalty, and to reach up to 338% improvement of average water flux (or 77% reduction of the required membrane area) and 18% of energy savings compared with the calculated results under typical engineering conditions.

In further work, it would be meaningful to find the optimal feed spacer with the best tradeoff between mass transfer and flow resistance using the multiscale design optimization framework proposed in our previous work³⁹ that couples machine learning with high-performance computing. Furthermore, we will adopt emerging 3D printing technology to prepare the designed spacers and verify their performance on hydrodynamics, mass transfer and mechanical stability. Moreover, it is noted that higher permeation fluxes may lead to higher permeation drag and more compressed foulant layers.⁴⁸ To address this, the proposed optimization strategy may be integrated with other methods, e.g., enhanced pretreatment, unsteady-state shear⁴⁹ and batch operation.⁵⁰ Finally, precise design and fabrication of the UPM suggested in this work would require a clear understanding of water transport mechanism across the RO membrane. Interested readers are referred to the recently proposed solution-friction model⁵¹ for governing factors that impact the water permeability.

Methods

3D multi-physics simulations

In typical spiral wound membrane systems, each module includes more than 1 million feed spacer cells. Therefore, it is computationally impractical for simulation of each membrane module using the 3D multi-physics model. Fortunately, previous work^43,52 indicated that “periodic fully-developed” flow and mass transfer reached in just several cells. Therefore, it is possible to capture the local hydrodynamic and transport characteristics using a computational domain that consists of a few feed spacer cells. The average mass transfer coefficient and the axial pressure drop per unit length at various locations along feed direction are calculated by changing the feed velocity at the inlet of the computational domain. In this work, the established 3D multi-physics model (direct problem) considers the fluid flow (1) and mass transport (2) in five unit cells ($\varOmega$; Fig. 1d) that can be mathematically described as

$$\left\{\begin{array}{ll}\rho ({\mathbf{u}}\cdot \nabla ){\mathbf{u}}-\nabla \cdot [-P{\mathbf{I}}+\mu (\nabla {\bf{u}}+{(\nabla {\bf{u}})}^{{\rm{T}}})]=0,\,&{\rm{in}}\,\Omega ,\\ \nabla \cdot (\rho {\mathbf{u}})=0,\,&{\rm{in}}\,\Omega ,\end{array}\right.$$

(1)

and

$$\nabla \cdot ({D}_{{\rm{s}}}\nabla c)-{\bf{u}}\cdot \nabla c=0,\qquad\qquad\,{\rm{in}}\,\Omega$$

(2)

respectively. The location of the inlet cross-section for the computational domain (Fig. 1d) is chosen arbitrarily to guarantee generality. ρ, μ, ${D}_{{\rm{s}}}$ are fluid density, viscosity, and salt diffusivity. More detailed information, e.g., boundary conditions, model parameters for the multi-physics model was reported in our previous work.³⁹ Pressure drop per unit length $\frac{\Delta {P}_{{\rm{c}}}}{L}$ is calculated by

$$\frac{\Delta {P}_{{\rm{c}}}}{L}=\frac{{P}_{{\rm{in}}}-{P}_{{\rm{out}}}}{L}$$

(3)

where ${P}_{{\rm{in}}}$ and ${P}_{{\rm{out}}}$ denote average pressure at inlet and outlet respectively, and L is the length of computational domain (Fig. 1d). The Darcy friction factor is estimated by²⁹

$$f=\frac{2{D}_{{\rm{H}}}\varDelta {P}_{{\rm{c}}}}{\rho {\bar{u}}^{2}L}.$$

(4)

The hydraulic diameter, ${D}_{{\rm{H}}}$ is calculated by the formula from the literature.⁴³ The Sherwood number, $Sh$ can be obtained using

$$Sh={\bar{k}}_{{\rm{m}}}\frac{{D}_{{\rm{H}}}}{{D}_{{\rm{s}}}}.$$

(5)

The cell-average mass transfer coefficient on membrane walls (Fig. 1d), ${\bar{k}}_{{\rm{m}}}$ is estimated by

$${\bar{k}}_{{\rm{m}}}=\frac{{\int }_{0}^{L}{\rm{d}\it{y}}{\int }_{0}^{W}(\frac{-{D}_{{\rm{s}}}}{{c}_{{\rm{r}}}-{c}_{{\rm{w}}}}\cdot \frac{\partial c}{\partial z}){\rm{d}\it{x}}}{{\int }_{0}^{L}{\rm{d}\it{y}}{\int }_{0}^{W}{\rm{d}\it{x}}}.$$

(6)

${c}_{{\rm{r}}}$ denotes solute concentration at bulk of retentate that is equal to inlet concentration (${c}_{0}$). ${c}_{{\rm{w}}}$ is solute concentration at membrane wall.

Module design

The inverse design problem of feed spacer can be mathematically expressed as

$$\begin{array}{c}\mathop{\min }\limits_{{{{\bf{\upbeta}}}}_{1}}{F}_{1}\\ s.t.\,{{{\bf{H}}}_{1}=\bf{0}},\end{array}$$

(7)

where the design variables are spacer geometric parameters, ${\bf{\upbeta}}_{1}=[{L}_{1},\,{W}_{1},\,{H}_{1},\,\alpha ,\,{L}_{\rm{S}},\,{W}_{\rm{S}}]$ (Fig. 1c, d, f). The inlet cross-flow velocity is fixed ($\bar{u}$ = 0.1 m s⁻¹). The optimized spacer parameters (${\bf{\upbeta }}_{1,{\rm{opt}}}$) can be obtained (Supplementary Fig. 2) by solving 3D nonlinear partial differential Eqs. (1, 2; ${{\bf{H}}}_{1}\,=\,\bf{0}$) constrained optimization problem. For the objective function of ${F}_{1}=\frac{(\Delta {P}_{{\rm{c}}}/L)/(\Delta {P}_{{\rm{c}},0}/{L}_{0})}{{({\bar{k}}_{{\rm{m}},{\rm{imp}}}/{\bar{k}}_{{\rm{m}},{\rm{imp}},0})}^{\beta }}$, the $\Delta {P}_{{\rm{c}}}/L$ and $\varDelta {P}_{{\rm{c}},0}/{L}_{0}$ denote axial pressure drop per unit length for the designed membrane module of this work and the conventional module respectively. The detailed geometric parameters for the latter one were reported in our previous work.⁴⁵ ${\bar{k}}_{{\rm{m}},{\rm{imp}}}$ and ${\bar{k}}_{{\rm{m}},{\rm{imp}},0}$ denote cell-average mass transfer coefficients using the impermeable wall model for the designed and conventional modules respectively that can be converted to the cell-average mass transfer coefficient on permeable wall using reported relations.⁵³ Detailed quantitative analysis indicated that the estimated error using both permeable and impermeable wall models is less than 10% even under a high water flux condition of 200 lmh at system inlet while the latter requires significantly shorter computational time. The power exponent (β) is used to control the tradeoff between flow resistance and mass transfer. The genetic algorithm toolbox, GATBX³⁸ is used to solve the optimization problem due to its superior performance on global convergence.

Based on the optimized spacers (β = 4, 6, 8), we further obtain the correlations of Sherwood number and Darcy friction factor

$$S{h}_{{\rm{imp}}}=kR{e}^{t},$$

(8)

$$f=\mathop{\sum }\limits_{i=1}^{8}({a}_{i}R{e}^{i}+{b}_{0}),$$

(9)

using the CFD simulations with various Reynolds numbers (Re = 50, 62.5, 75…1,000) (Supplementary Fig. 2). The cross velocity ($\bar{u}$) is calculated by

$$\bar{u}=\frac{\mu Re}{\rho {D}_{{\rm{H}}}}.$$

(10)

These correlations (8) and (9) enable a quantitative description of mass transfer and flow resistance, which can be used for system design.

System modeling at industrial-scale

The ${k}^{{\rm{th}}}$ stage of the RO process at industrial-scale can be mathematically expressed by one-dimensional (1D) differential algebraic equations (DAEs),³⁹ as follows.

$$\begin{array}{ll}\left\{\begin{array}{l}\frac{{\rm{d}}Q}{{\rm{d}}X}=-{J}_{{\rm{W}}}\cdot {A}_{k}\\ \frac{{\rm{d}}(\varDelta {{P}})}{{\rm{d}}{X}}=-\frac{\rho{\bar{u}}^{2}f}{2{D}_{\rm{{H}}}}\cdot ({\eta }_{\rm{mem,{k}}}\cdot {l}_{y})\\ \frac{d{w}_{b}}{dX}={J}_{\rm{W}}\cdot \frac{{{{A}}}_{{{k}}}}{Q}({w}_{\rm{b}}-{w}_{\rm{p}})\\ {J}_{\rm{w}}={L}_{\rm{p}}(\varDelta {P}-\sigma \cdot \varphi {R}_{\rm{salt}}{w}_{\rm{w}})\end{array}\right. & \begin{array}{l}X=k-1,Q={Q}_{{k-1}},\\ X=k-1,\varDelta P=\varDelta {P}_{k-1},\\ X=k-1,{w}_{\rm{b}}={w}_{\rm{b,k-1}},\end{array}\end{array}$$

(11)

In Eq. (11), the variables to be evaluated include flow rate ($Q$), transmembrane pressure ($\Delta P$), water flux (${J}_{{\rm{W}}}$), salinities at bulk of retentate (${w}_{{\rm{b}}}$), bulk of permeate (${w}_{{\rm{p}}}$), and membrane wall (${w}_{{\rm{w}}}$) that vary with respect to dimensionless length, $X$ ($\in [k-1,k]$). The $Q$ is calculated by

$$Q={N}_{{\rm{pv}},k}{n}_{{\rm{sp}}}{l}_{x}H\varepsilon \bar{u},$$

(12)

where ${N}_{{\rm{pv}},k}$, ${n}_{{\rm{sp}}}$ denote number of pressure vessels for the ${k}^{{\rm{th}}}$ stage and number of spacer sheets per module respectively. ${l}_{x}$, $H$, $\varepsilon$ are length of membrane sheet perpendicular to the feed direction (x direction, Fig. 1), height of each feed channel and feed channel porosity. Membrane area for the ${k}^{{\rm{th}}}$ stage, ${A}_{k}$ can be calculated by

$${A}_{k}={N}_{{\rm{pv}},k}\cdot {n}_{{\rm{mem}},k}\cdot {A}_{0}\cdot {l}_{y}/{l}_{y,0},$$

(13)

where ${n}_{{\rm{mem}},k}$ are number of modules for the ${k}^{{\rm{th}}}$ stage. ${l}_{y}$, ${l}_{y,0}$ denote lengths of membrane sheet parallel to the feed direction (y direction, Fig. 1) for the optimized module (0.5 m) and commercial module (1 m) respecively.³⁹ ${A}_{0}$ is membrane area of each commercial module.³⁹ Reflection coefficient ($\sigma$) and osmotic pressure coefficient ($\varphi$) are constant. ${R}_{{\rm{salt}}}$ denotes membrane intrinsic rejection. ${w}_{{\rm{p}}}$ and ${w}_{{\rm{w}}}$ can be calculated by³⁹

$${w}_{{\rm{p}}}={w}_{{\rm{b}}}/[\exp\, \left(\mathrm{ln}\,\frac{{J}_{{\rm{W}}}}{B}-\frac{{J}_{{\rm{W}}}}{{\bar{k}}_{{\rm{m}},{\rm{per}}}}\right)+1],$$

(14)

and

$${w}_{{\rm{w}}}=\frac{{w}_{{\rm{p}}}}{1-{R}_{{\rm{salt}}}},$$

(15)

respectively. The detailed derivation of Eq. (14) can be found in our previous work.³⁹ ${\bar{k}}_{{\rm{m}},{\rm{per}}}$ denotes cell-average mass transfer coefficient on permeable wall that can be estimated by the Eqs. (16), (17),⁵³ as follows

$${\bar{k}}_{{\rm{m}},{\rm{per}}}={\bar{k}}_{{\rm{m}},{\rm{imp}}}[\psi +{(1+0.26{\psi }^{1.4})}^{-1.7}],\,(\psi < 20)$$

(16)

$$\psi =\frac{{J}_{{\rm{W}}}}{{\bar{k}}_{{\rm{m}},{\rm{imp}}}},$$

(17)

where ${\bar{k}}_{{\rm{m}},{\rm{imp}}}$ for a given $\bar{u}$ can be calculated by Eqs. (6), (8), and (10) based on the CFD simulations. Combining with Eqs. (3)–(17), the variables at system-level ($Q$, $\Delta P$, ${J}_{{\rm{W}}}$, ${w}_{{\rm{b}}}$, ${w}_{{\rm{p}}}$, ${w}_{{\rm{w}}}$) can be solved. The SEC for RO system is calculated by

$$SEC=\left\{\begin{array}{ll}\frac{{Q}_{0}\Delta {P}_{0}-{\eta }_{{\rm{R}}}{Q}_{1}\Delta {P}_{1}}{36{\eta }_{{\rm{pump}}}{Q}_{{\rm{p}}}},\qquad\qquad\qquad\,for\,one-stage\,RO\\ \frac{{Q}_{0}\Delta {P}_{0}\,+\,{Q}_{1}({P}_{1,{\rm{in}}}-{P}_{1,{\rm{out}}})-{\eta }_{{\rm{R}}}{Q}_{2}\Delta {P}_{2}}{36{\eta }_{{\rm{pump}\,}}{Q}_{{\rm{p}}}},\quad for\,two-stage\,RO\end{array}\right.$$

(18)

where ${Q}_{0}$, ${Q}_{1}$, ${Q}_{2}$ are flow rates at inlet of the first-stage (X = 0), outlet of the first-stage (X = 1) and outlet of the second-stage (X = 2). $\Delta {P}_{0}$, $\Delta {P}_{1}$, $\Delta {P}_{2}$ are transmembrane pressures at inlet of the first-stage (X = 0), outlet of the first-stage (X = 1) and outlet of the second-stage (X = 2). ${P}_{1,{\rm{in}}}$, ${P}_{1,{\rm{out}}}$ denote operating pressures at inlet of the second-stage (X = 1) and outlet of the first-stage (X = 1). ${Q}_{{\rm{p}}}$ is flow rate of permeate. In this work, pump efficiency (${\eta }_{{\rm{pump}}}$ = 85%) and energy recovery device efficiency (${\eta }_{{\rm{R}}}$ = 95%) are specified for the SWRO system. For the BWRO system, ${\eta }_{{\rm{pump}}}$ = 85% and ${\eta }_{{\rm{R}}}$ = 0 (without energy recovery device).

System design

In system design, the optimization problem with equality constraints (${{\bf{H}}}_{2}=\bf{0}$; Eqs. (3)–(17)) and inequality constraints (${\bf{J}}\le \bf{0}$) can be mathematically formulated as

$$\begin{array}{c}\mathop{\min }\limits_{{{{\bf{\upbeta}}}}_{2}}{F}_{2}\\ s.t.\,{{\bf{H}}}_{2}\,={\bf{0}},\\ {\bf{J}}\le {\bf{0}}.\end{array}$$

(19)

The minimized objective (${F}_{2}$) includes the annualized capital cost of the membrane and energy cost per m³ permeate, as below.

$${F}_{2}=\frac{{A}_{{\rm{tot}}}{c}_{{\rm{m}}}{F}_{{\rm{a}}}}{{Q}_{{\rm{p}}}{t}_{{\rm{op}}}}+{c}_{{\rm{e}}}\cdot SEC,$$

(20)

In this work, membrane cost per m² (${c}_{{\rm{m}}}$) is used to control the tradeoff between SEC and the required total membrane area (${A}_{{\rm{tot}}}$). ${c}_{{\rm{e}}}$, ${F}_{{\rm{a}}}$ and ${t}_{{\rm{op}}}$ denote energy cost per kWh, amortization factor of each year and operating time of each year. The values of these parameters are obtained from the previous work.⁴⁴ Inequality constraints consist of e.g., maximum CPF, maximum average permeate salinity, minimum average water flux, minimum and maximum of design variables.

The design variables (β₂, Supplementary Fig. 2) consist of water permeability (L_P) and salt permeability (B), number of pressure vessels (${N}_{{\rm{pv}},1}$, ${N}_{{\rm{pv}},2}$), number of modules per pressure vessel (${n}_{{\rm{mem}},1}$, ${n}_{{\rm{mem}},2}$) and inlet transmembrane pressure (ΔP₀, ΔP₁) at each stage, and number of spacer sheets per module (n_sp). The mass transfer coefficient and pressure drop at each location can be estimated by the obtained correlations in the section of “Module design”. The optimized system parameters (β_2,opt) can be obtained by solving the multi-objective optimization problem that is constrained by the 1D DAEs, which belongs to the class of nonlinear mixed-integer programming. We used the genetic algorithm toolbox, GATBX³⁸ to solve the optimization problem. More details about system design can be found in our previous work.³⁹