No CrossRef data available.
Article contents
On the Extension of Bounded Holomorphic Maps from Gleason Parts of the Maximal Ideal Space of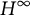 
$H^\infty $
Part of:
Commutative Banach algebras and commutative topological algebras
Spaces and algebras of analytic functions
Published online by Cambridge University Press: 08 January 2024
Abstract
Let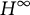 
$H^\infty $ be the algebra of bounded holomorphic functions on the open unit disk, and let 
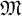$\mathfrak M$ be its maximal ideal space. Let 
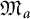$\mathfrak M_a$ be the union of nontrivial Gleason parts (analytic disks) of 
$\mathfrak M$. In this paper, we study the problem of extensions of bounded Banach-valued holomorphic functions and holomorphic maps with values in Oka manifolds from Gleason parts of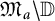 
$\mathfrak M_a\setminus \mathbb {D}$. The resulting extensions satisfy the uniform boundedness principle in the sense that their norms are bounded by constants that do not depend on the choice of the Gleason part. The results extend fundamental results of D. Suárez on the characterization of the algebra of restrictions of Gelfand transforms of functions in 
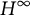$H^\infty $ to Gleason parts of 
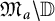$ \mathfrak M_a\setminus \mathbb {D}$. The proofs utilize our recent advances on 
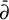$\bar \partial $-equations on quasi-interpolating sets and Runge-type approximations.
MSC classification
Secondary:
46J20: Ideals, maximal ideals, boundaries
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
Research is supported in part by NSERC.
References
Akhiezer, D. N.,
Homogeneous complex manifolds
. In: Gindikin, S. G. and Khenkin, G. M. (eds), Several complex variables IV, Encyclopaedia of Mathematical Sciences, 10, Springer, New York, 1990.Google Scholar
Brudnyi, A.,
Stein-like theory for Banach-valued holomorphic functions on the maximal ideal space of
${H}^{\infty }$
. Invent. Math. 193(2013), 187–227.CrossRefGoogle Scholar
${H}^{\infty }$
. Invent. Math. 193(2013), 187–227.CrossRefGoogle ScholarBrudnyi, A., Dense stable rank and Runge type approximation theorems for
${H}^{\infty }$
maps. J. Aust. Math. Soc. 113(2022), no. 3, 289–317.CrossRefGoogle Scholar
${H}^{\infty }$
maps. J. Aust. Math. Soc. 113(2022), no. 3, 289–317.CrossRefGoogle ScholarBrudnyi, A.,
${L}^{\infty }$
estimates for the Banach-valued
$\overline{\partial}$
-problem in a disk
. Anal. Math. Phys. 13(2023), 21.CrossRefGoogle Scholar
${L}^{\infty }$
estimates for the Banach-valued
$\overline{\partial}$
-problem in a disk
. Anal. Math. Phys. 13(2023), 21.CrossRefGoogle ScholarCarleson, L.,
Interpolation of bounded analytic functions and the corona problem
. Ann. of Math. (2) 76(1962), 547–559.CrossRefGoogle Scholar
Forstnerič, F.,
Complements of Runge domains and holomorphic hulls
. Michigan Math. J. 41(1993), 297–308.Google Scholar
Forstnerič, F., Stein manifolds and holomorphic maps, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 56, Springer, Heidelberg, 2011.CrossRefGoogle Scholar
Hoffman, K.,
Bounded analytic functions and Gleason parts
. Ann. of Math. (2) 86(1967), 74–111.CrossRefGoogle Scholar
Hu, S.-T.,
Some homotopy properties of topological groups and homogeneous spaces
. Ann. of Math. (2) 49(1948), 67–74.CrossRefGoogle Scholar
Kusakabe, Y., Oka properties of complements of holomorphically convex sets. Preprint, 2020. arXiv:2005.08247.Google Scholar
Suárez, D., Čech cohomology and covering dimension for the
${H}^{\infty }$
maximal ideal space. J. Funct. Anal. 123(1994), 233–263.CrossRefGoogle Scholar
${H}^{\infty }$
maximal ideal space. J. Funct. Anal. 123(1994), 233–263.CrossRefGoogle ScholarSuárez, D.,
Homeomorphic analytic maps into the maximal ideal space of
${H}^{\infty }$
. Canad. J. Math. 51(1999), no. 1, 147–163.CrossRefGoogle Scholar
${H}^{\infty }$
. Canad. J. Math. 51(1999), no. 1, 147–163.CrossRefGoogle ScholarSuárez, D., On the analytic structure of the
${H}^{\infty }$
maximal ideal space. Int. J. Math. Game Theory Algebra 11(2001), no. 1, 15–32.Google Scholar
${H}^{\infty }$
maximal ideal space. Int. J. Math. Game Theory Algebra 11(2001), no. 1, 15–32.Google ScholarZiskind, S.,
Interpolating sequences and the Shilov boundary of
${H}^{\infty}(\varDelta)$
. J. Funct. Anal. 21(1976), no. 4, 380–388.CrossRefGoogle Scholar
${H}^{\infty}(\varDelta)$
. J. Funct. Anal. 21(1976), no. 4, 380–388.CrossRefGoogle Scholar