Hostname: page-component-76fb5796d-vvkck Total loading time: 0 Render date: 2024-04-27T06:03:37.981Z Has data issue: false hasContentIssue false
  • English
  • Français

Equal-Sum-Product problem II

Part of: Diophantine equations

Published online by Cambridge University Press:  13 September 2023

Maciej Zakarczemny Open the ORCID record for Maciej Zakarczemny [Opens in a new window]
Maciej Zakarczemny*
Affiliation:
Department of Applied Mathematics, Cracow University of Technology, Warszawska 24, 31-155 Kraków, Poland
*
e-mail: mzakarczemny@pk.edu.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we present the results related to a problem posed by Andrzej Schinzel. Does the number 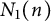$N_1(n)$ of integer solutions of the equation

$$ \begin{align*}x_1+x_2+\cdots+x_n=x_1x_2\cdot\ldots\cdot x_n,\,\,x_1\ge x_2\ge\cdots\ge x_n\ge 1\end{align*} $$
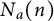tend to infinity with n? Let a be a positive integer. We give a lower bound on the number of integer solutions, $N_a(n)$, to the equation
$$ \begin{align*}x_1+x_2+\cdots+x_n=ax_1x_2\cdot\ldots\cdot x_n,\,\, x_1\ge x_2\ge\cdots\ge x_n\ge 1.\end{align*} $$
We show that if $N_2(n)=1$, then the number 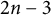$2n-3$ is prime. The average behavior of 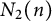$N_2(n)$ is studied. We prove that the set 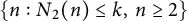$\{n:N_2(n)\le k,\,n\ge 2\}$ has zero natural density.

Keywords

Equal-sum-productexceptional setnatural density

MSC classification

Primary: 11D72: Equations in many variables 11D45: Counting solutions of Diophantine equations
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cassels, J. W. S., An introduction to Diophantine approximation, Chap. II, Cambridge University Press, Cambridge, 1957.Google Scholar
Cojocaru, A. C. and Murty, M. R., An introduction to sieve methods and their applications, Cambridge University Press, Cambridge, 2005.Google Scholar
Ecker, M. W., When does a sum of positive integers equal their product? Math. Mag. 75(2002), no. 1, 41–47.Google Scholar
Guy, R. K., Unsolved problems in number theory (Section D24), Springer, New York–Heidelberg–Berlin, 2004.Google Scholar
Hurwitz, A., Über eine Aufgabe der unbestimmten analysis . Arch. Math. Phys. 3(1907), 185–196.Google Scholar
Kurlandchik, L. and Nowicki, A., When the sum equals the product . Math. Gaz. 84(2000), no. 499, 91–94.Google Scholar
Markoff, A. A., Sur les formes binaires indéfinies . Math. Ann. 17(1880), 379–399.Google Scholar
Nyblom, M. A., Sophie Germain primes and the exceptional values of the equal-sum-and-product problem . Fibonacci Quart. 50(2012), no. 1, 58–61.Google Scholar
Sándor, J., Mitrinović, D. S., and Crstici, B., Handbook of number theory I, Springer, Dordrecht, 2006.Google Scholar
Schinzel, A., Sur une propriété du nombre de diviseurs . Publ. Math. Debrecen 3(1954), 261–262.Google Scholar
Schinzel, A., Selecta. Unsolved problems and unproved conjectures, Vol. 2, American Mathematical Society, Providence, RI, 2007, 1367.Google Scholar
Shiu, P., On Erdös’s last equation . Amer. Math. Mon. 126(2019), no. 9, 802–808.Google Scholar
Takeda, W., On solutions to Erdős’ last equation . Integers 21(2021), A117.Google Scholar
Tolev, D. I., On the division problem in arithmetic progressions . C. R. Acad. Bulg. Sci. 41(1988), 33–36.Google Scholar
Zakarczemny, M., On the equal sum and product problem . Acta Math. Univ. Comenian. 90(2021), no. 4, 387–402.Google Scholar