Quadratic Crofton and sets that see themselves as little as possible

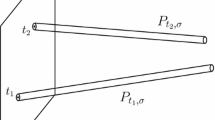
Abstract

Let $\Omega \subset \mathbb {R}^2$ and let $\mathcal {L} \subset \Omega$ be a one-dimensional set with finite length $L =|\mathcal {L}|$. We are interested in minimizers of an energy functional that measures the size of a set projected onto itself in all directions: we are thus asking for sets that see themselves as little as possible (suitably interpreted). Obvious minimizers of the functional are subsets of a straight line but this is only possible for $L \le \text{ diam }(\Omega )$. The problem has an equivalent formulation: the expected number of intersections between a random line and $\mathcal {L}$ depends only on the length of $\mathcal {L}$ (Crofton’s formula). We are interested in sets $\mathcal {L}$ that minimize the variance of the expected number of intersections. We solve the problem for convex $\Omega$ and slightly less than half of all values of L: there, a minimizing set is the union of copies of the boundary and a line segment.