Abstract
The aim of this paper is to prove two results concerning the rigidity of complete, immersed, orientable, stable minimal hypersurfaces: we show that they are hyperplane in R4, while they do not exist in positively curved closed Riemannian (n+1)-manifold when n≤5; in particular, there are no stable minimal hypersurfaces in Sn+1 when n≤5. The first result was recently proved also by Chodosh and Li, and the second is a consequence of a more general result concerning minimal surfaces with finite index. Both theorems rely on a conformal method, inspired by a classical work of Fischer-Colbrie.
Similar content being viewed by others
1 Introduction
It is well-known that a minimal surface  is a critical point of the area functional \(\mathcal{A}_{t}\) for all compactly supported variations, i. e. \(\left .\frac{d}{d t} \right |_{t=0}\mathcal{A}_{t}=0\); equivalently, M2 is minimal if and only if the mean curvature H, i.e. the (normalized) trace of the second fundamental form, is identically zero, or if and only if M2 can be expressed, locally, as the graph Γ(u) of a solution u of the minimal surfaces equation
is a critical point of the area functional \(\mathcal{A}_{t}\) for all compactly supported variations, i. e. \(\left .\frac{d}{d t} \right |_{t=0}\mathcal{A}_{t}=0\); equivalently, M2 is minimal if and only if the mean curvature H, i.e. the (normalized) trace of the second fundamental form, is identically zero, or if and only if M2 can be expressed, locally, as the graph Γ(u) of a solution u of the minimal surfaces equation
In 1914, S. Bernstein showed that an entire (i.e., defined on the whole plane  ) minimal graph in
) minimal graph in  is necessarily a plane; the so-called “Bernstein problem” in higher dimension can be then stated in the following way: if the graph Γ(u) of a function
is necessarily a plane; the so-called “Bernstein problem” in higher dimension can be then stated in the following way: if the graph Γ(u) of a function  is a minimal hypersurface in
is a minimal hypersurface in  , does Γ(u) have to be necessarily a hyperplane? Many famous mathematicians worked on this problem in the Sixties, in particular Fleming [Fle62] (who gave a new proof in the case n=2), De Giorgi [Gio65] (case n=3), Almgren [Alm66] (case n=4), Simons [Sim68] (the three remaining cases for n≤7) and, eventually, Bombieri, De Giorgi and Giusti [BGG69], who showed that, for n≥8, there are minimal entire graphs that are not hyperplanes. We explicitly remark that a minimal graph is area-minimizing, i.e. it is not only a critical point of the area functional, but also a minimum, while this is not true for minimal hypersurfaces that are “non-graphical”, and also that area-minimizing implies stability, that is the non-negativity of the second variation for the area functional \(\left .\frac{d^{2}}{d t^{2}} \right |_{t=0}\mathcal{A}_{t}\geq 0\) for all compactly supported variations.
, does Γ(u) have to be necessarily a hyperplane? Many famous mathematicians worked on this problem in the Sixties, in particular Fleming [Fle62] (who gave a new proof in the case n=2), De Giorgi [Gio65] (case n=3), Almgren [Alm66] (case n=4), Simons [Sim68] (the three remaining cases for n≤7) and, eventually, Bombieri, De Giorgi and Giusti [BGG69], who showed that, for n≥8, there are minimal entire graphs that are not hyperplanes. We explicitly remark that a minimal graph is area-minimizing, i.e. it is not only a critical point of the area functional, but also a minimum, while this is not true for minimal hypersurfaces that are “non-graphical”, and also that area-minimizing implies stability, that is the non-negativity of the second variation for the area functional \(\left .\frac{d^{2}}{d t^{2}} \right |_{t=0}\mathcal{A}_{t}\geq 0\) for all compactly supported variations.
A natural generalization of the classical Bernstein problem, thus, is the stable Bernstein problem, that is: if  is a complete, orientable, isometrically immersed, stable minimal hypersurface, does M have to be necessarily a hyperplane? In the case n=2 the (positive) answer was given in three different papers, which appeared between 1979 and 1981 (see do Carmo and Peng [CP79], Fischer-Colbrie and Schoen [FS80] and Pogorelov [Pog81]).
is a complete, orientable, isometrically immersed, stable minimal hypersurface, does M have to be necessarily a hyperplane? In the case n=2 the (positive) answer was given in three different papers, which appeared between 1979 and 1981 (see do Carmo and Peng [CP79], Fischer-Colbrie and Schoen [FS80] and Pogorelov [Pog81]).
In higher dimensions, the aforementioned result of Bombieri, De Giorgi and Giusti implies that there exist non-flat orientable, complete, stable minimal hypersurfaces in  for n≥8, while for n≤5 the stable Bernstein theorems is true with some additional assumptions (for instance, if one requires bounds on the volume growth of geodesic balls, see e.g. [SSY75]; see also [CP82], [CSZ97], [Che01], [NS07] and references therein for other interesting results in the same spirit). Moreover, by [BGG69] and [HS85], we also note that there are non-flat area-minimizing (and thus minimal and stable) complete orientable hypersurfaces
for n≥8, while for n≤5 the stable Bernstein theorems is true with some additional assumptions (for instance, if one requires bounds on the volume growth of geodesic balls, see e.g. [SSY75]; see also [CP82], [CSZ97], [Che01], [NS07] and references therein for other interesting results in the same spirit). Moreover, by [BGG69] and [HS85], we also note that there are non-flat area-minimizing (and thus minimal and stable) complete orientable hypersurfaces  .
.
Up until recently, without additional hypothesis, the remaining cases (3≤n≤6) were still open, even if the study of minimal (in particular stable or in general with finite index) hypersurfaces immersed into a Riemannian manifold (not only the Euclidean space, then) is a very active field and has attracted a lot of interest. Then, in 2021, Chodosh and Li [CL24] (see also [CL23]) showed that a complete, orientable, isometrically immersed, stable minimal immersion  is a hyperplane. Their proof, clever and highly non-trivial, is based on the non-parabolicity of M: they perform careful estimates for the quantity
is a hyperplane. Their proof, clever and highly non-trivial, is based on the non-parabolicity of M: they perform careful estimates for the quantity
(here u is a positive Green’s function for the Laplacian and Σt is the t-level set of u), relating it to \(\int _{\Sigma _{t}}{\left |A_{M}\right |}^{2}\) (AM is the second fundamental form of M).
In this paper we provide a completely different proof of Chodosh and Li result, based on a conformal deformation of the metric, a comparison result and integral estimates, and we also prove another rigidity result when the ambient space is a complete Riemannian manifold with non-negative sectional curvature and either uniformly positive bi-Ricci curvature or uniformly positive Ricci curvature. To be precise, and to fix the notation, we consider smooth, complete, connected, orientable, isometrically immersed hypersurfaces Mn↪(Xn+1,h), n≥2, where (Xn+1,h) is a (complete) Riemannian manifold of dimension n+1 endowed with metric h. We denote with g the induced metric on M and with H the mean curvature of M; we have that M is minimal if H≡0 on M. In this latter case we say that M is stable if
where A=AM is the second fundamental form of Mn, ν is a unit normal vector to M in X and dVg is the volume form of g.
As we recalled before, stability is related to the non-negativity of the second variation or, equivalently, the non-positivity of the Jacobi operator
The first result is thus the following:
Theorem 1.1
A complete, orientable, immersed, stable minimal hypersurface  is a hyperplane.
is a hyperplane.
The second result concerns minimal hypersurfaces with finite index. We recall that a minimal immersion Mn↪(Xn+1,h) has finite index if the number of negative eigenvalues (counted with multiplicity) of the Jacobi operator LM on every compact domain in M with Dirichlet boundary conditions is finite; in particular stability implies finite (equal zero) index. Before presenting our next result, we need to recall the notion of bi-Ricci curvature tensor introduced in [SY96]: given two orthonormal tangent vectors u,v we define
where Secth(u,v) denotes the sectional curvature of the plane spanned by u and v. Our second result is the following:
Theorem 1.2
If (Xn+1,h) is a complete (n+1)-dimensional, n≤5, manifold with non-negative sectional curvature and either uniformly positive bi-Ricci curvature or uniformly positive Ricci curvature, then every complete, orientable, immersed, minimal hypersurface Mn↪(Xn+1,h) with finite index must be compact.
As a byproduct we have the
Corollary 1.3
If (Xn+1,h) is a complete (n+1)-dimensional, n≤5, manifold with non-negative sectional curvature and uniformly positive Ricci curvature, then there is no complete, orientable, immersed, stable minimal hypersurface Mn↪(Xn+1,h).
In particular, there is no complete, orientable, immersed, stable minimal hypersurface of the round spheres \(M^{n}\hookrightarrow (\mathbb{S}^{n+1},g_{\text{std}})\), provided n≤5. In dimension n=2 this follows from a more general result proved in [SY82], while, in dimension n=3, it was recently proved in [CLS22, Corollary 1.5]. We mention that Theorem 1.2 holds also for complete, orientable, immersed, stable minimal hypersurface of the cylinder \(M^{n}\hookrightarrow (\mathbb{R}\times \mathbb{S}^{n},g_{\text{std}})\) (observe that in this case Sect≥0 and BRic≥1), provided n≤5. As far as we know, Corollary 1.3 is new in the cases n=4,5 (see [Che08] where the same technique is used). We do not know if Theorem 1.2 and Corollary 1.3 hold also in dimension greater than five. We note that, in the same spirit, in [SY96] the authors obtained a compactness result for stable minimal hypersurfaces of dimension n≤4 immersed in space with uniformly positive bi-Ricci curvature.
2 Proof of Theorem 1.1
In this section we give an alternative proof of [CL24, Theorem 1] (see Theorem 1.1). The main idea is to use a weighted volume comparison for a suitable conformal metric \(\widetilde{g}\) together with a new weighted integral estimate inspired by [SSY75].
Let  be a complete, connected, orientable, isometrically immersed, stable minimal hypersurface.
be a complete, connected, orientable, isometrically immersed, stable minimal hypersurface.
2.1 Conformal change
It is well known (see e.g. [Fis85, Proposition 1]) that, since  is stable, then there exists a positive function 0<u∈C∞(M) satisfying
is stable, then there exists a positive function 0<u∈C∞(M) satisfying
Following the line in [Fis85] (see also [ENR07]), let k>0 and consider the conformal metric
where g=ı∗h is the induced metric on M (and ı denotes the inclusion). First of all we prove the following lower bound for a modified Bakry-Emery-Ricci curvature of \(\widetilde{g}\). In particular, this implies the non-negativity of the 2-Bakry-Emery-Ricci curvature of \(\widetilde{g}\) for a suitable k.
Lemma 2.1
Let f:=k(n−2)logu. Then the Ricci tensor of the metric \(\widetilde{g}=u^{2k} g\) satisfies
in the sense of quadratic forms. In particular, if n=3 and \(k=\frac {2}{3}\), then the 2-Bakry-Emery-Ricci tensor \(\mathrm{Ric}_{\widetilde{g}}^{2,f}:=\mathrm{Ric}_{\widetilde{g}}+ \nabla ^{2}_{\widetilde{g}}f-\frac{1}{2} df\otimes df\) satisfies
Proof
Since f=k(n−2)logu, we have
and
which implies
On the other hand, from the standard formulas for a conformal change of the metric \(\tilde{g}=e^{2\varphi}g\), φ∈C∞(M), φ>0 we get
and
Note that, in our case, φ=klogu; now we exploit the facts that u is a solution of equation (2.1) to write
From the Cauchy-Schwarz inequality we have
thus
from Gauss equations in the minimal case we get Ricg=−A2; since A is traceless we have the inequality
and substituting in the previous relation we conclude
□
2.2 Completeness
In this subsection we are going to prove that the conformal metric \(\widetilde{g}= u^{2k} g\) is complete, provided n=3 and \(k=\frac {2}{3}\). In order to do this we follow the strategy in [Fis85] and we use some computations in [ENR07]. First, we recall that in the proof of [Fis85, Theorem 1], given a reference point O∈Mn, the author showed the existence of a \(\widetilde{g}\)-minimizing geodesic,
where s is the g-arclength and  is the usual complete, connected, orientable, isometrically immersed, stable minimal hypersurface. For the sake of completeness, we report the argument here. First of all, for every R>0, we consider the geodesic ball (of g) centered at O of radius R, BR(O). Then, we first claim that there exists a \(\widetilde{g}\)-minimizing geodesic, γR, joining O to any boundary point of BR(O). Indeed, consider uR:=u+η, where η is a smooth function such that η≡0 in BR(O) and η≡1 in Mn∖BR+1(O). Since uR is bounded below, the metric
is the usual complete, connected, orientable, isometrically immersed, stable minimal hypersurface. For the sake of completeness, we report the argument here. First of all, for every R>0, we consider the geodesic ball (of g) centered at O of radius R, BR(O). Then, we first claim that there exists a \(\widetilde{g}\)-minimizing geodesic, γR, joining O to any boundary point of BR(O). Indeed, consider uR:=u+η, where η is a smooth function such that η≡0 in BR(O) and η≡1 in Mn∖BR+1(O). Since uR is bounded below, the metric
is complete, and these geodesics exist. Therefore, for every Ri>0, since \(\partial B_{R_{i}}(O)\) is compact, there exists \(x_{i}\in \partial B_{R_{i}}(O)\) so that xi is closest (in \(\widetilde{g}_{R}\)) to O. Let γi be the \(\widetilde{g}_{R}\)-minimizing geodesic joining O to xi. Note that \(\gamma _{i}\subset B_{R_{i}}(O)\) or another point would be closer to O. Since \(u_{R_{i}}=u\) in \(B_{R_{i}}(O)\), then γi is a \(\widetilde{g}\)-minimizing geodesic. We parametrize γi with respect to g-arclength. In particular, since \(|\dot{\gamma}_{i}(s)|_{g}=1\) for every s, up to subsequences, the sequence \(\dot{\gamma}_{i}(0)\) converges to a limit vector as Ri→∞. Thus, by ODE theory and Ascoli-Arzelà, γi converges on compact sets of [0,∞) to a limiting curve γ which is a \(\widetilde{g}\)-minimizing geodesic and is parametrized by g-arclength.
Remark 2.2
(i) We observe that the completeness of the metric \(\widetilde{g}= u^{2k} g\) will follow if we can show that the \(\widetilde{g}\)-length of γ is infinite, i.e.
Indeed, by construction, the \(\widetilde{g}\)-length of every other divergent geodesic starting from O (i.e. its image does not lie in any ball BR(O)) must be greater or equal than the one of γ.
(ii) Note that γ has unit speed with respect to g and to \(\widetilde{g}\), when it is parametrized by the arclength s and \(\tilde{s}\), respectively.
From now on
Lemma 2.3
The metric \(\widetilde{g}=u^{\frac{4}{3}} g\) is complete.
Proof
We do part of the computations for every n. We consider the \(\widetilde{g}\)-minimizing geodesic γ just constructed and as observed in Remark 2.2 the completeness of \(\widetilde{g}\) is equivalent to prove that γ has infinite \(\widetilde{g}\) length, i.e.
Since γ is minimizing, by the second variation formula, following the computations in the proof of Theorem 1 (with H=0) in [ENR07], we obtain
for every smooth function φ with compact support in (0,+∞) and for every k>0. Since A is trace-free, we have
thus
In particular, if
we have
Using this estimate, the fact that |∇u|2≥(us)2 and integrating by parts, we obtain
Let now φ=ukψ, with ψ smooth with compact support in (0,+∞). We have
and substituting in the previous relation we get
Let
thus we have
Moreover, for every t>1 and using Young’s inequality for every ε>0, we have
Assuming
and choosing
we obtain
From (2.3) we get
for every t>1 and every k satisfying (2.2) and (2.4). Let
and choose \(k=\frac{n-1}{n}\). It is easy to see that P(t) is negative for some t>1 if n=3: indeed
Therefore, if n=3, \(k=\frac {2}{3}\) and \(t=\frac {3}{2}\), we deduce
for every ψ smooth with compact support in (0,+∞). Now we choose ψ=sη with η smooth with compact support in (0,+∞): thus
and we get
Choose η such that η≡1 on [0,R], η≡0 on [2R,+∞) and with |ηs| and |ηss| bounded by C/R and C/R2, respectively, for R≤s≤2R (C is a positive constant). Then
for some C>0 independent of R. We conclude that
i.e. \(\widetilde{g}=u^{\frac {4}{3}} g\) is complete. □
2.3 Weighted integral estimates
From lemma 2.1 and lemma 2.3 we have that the metric \(\widetilde{g}=u^{\tfrac{4}{3}}g\) is complete and it has non-negative 2-Bakry-Emery-Ricci curvature. Using well known comparison results (see [Qia97]) we immediately obtain the following weighted Bishop-Gromov volume estimate for a geodesic ball \(B^{\widetilde{g}}_{R}(x_{0})\) centered at x0∈M, of radius R, with respect to the metric \(\widetilde{g}\).
Corollary 2.4
Let x0∈M3. Then, for every R>0, there exists C>0 such that the f-volume
where \(f=\frac{2}{3} \log u\). Equivalently, in terms of u and the volume form of g,
The last ingredient that we need in the proof of Theorem 1.1 is the following weighted integral inequality in the spirit of [SSY75, Theorem 1].
Lemma 2.5
For every \(0<\delta <\frac{1}{100}\), there exists C>0 such that
Proof
Again, we do part of the computations for every n. From [SSY75] we get
for every \(p\in [4,4+\sqrt{8/n}]\) and for some C=C(n,p)>0. For the sake of completeness we report here the proof of (2.5). We take φ=|A|1+qψ, q≥0, with \(\psi \in C^{\infty}_{0}(M)\), in the stability inequality (1.1) obtaining
for every ε>0, where we used Young’s inequality. On the other hand, multiplying Simons’ inequality (see [CM11, Lemma 2.1] for a proof)
by |A|2qψ2 and integrating by parts, we get
for every ε>0, where we used again Young’s inequality. Since q≥0, for ε>0 sufficiently small, we obtain
Let \(q:=\frac{p-4}{2}\). For ε>0 small enough, we have
if \(p\in [4,4+\sqrt{8/n}]\) and we finally obtain
Taking ψ=φp/2, by Holder’s inequality we get (2.5).
Take φ=uαψ, with ψ smooth with compact support, u the solution of (2.1) and α<0. Since, from Cauchy-Schwarz and Young’s inequalities,
then (2.5) becomes
Now we tackle the first integral on the right-hand side of (2.8) firstly integrating by parts
secondly we use the fact that
together with Cauchy-Schwarz and Young’s inequalities to get
for all ε>0. From (2.1) we find
i.e.
Now, since
then, from Cauchy-Schwarz and Young’s inequalities we obtain
for every t1>0. Now, multiplying by |A|p−4f2 the Simons’ inequality (2.6), integrating by parts and using Young’s inequality we obtain
for every t2>0. Choosing f=uαψ we get
for every ε>0, since
Now let δ>0. Using (2.10) in (2.9) with
we obtain
for all ε,t1,t2>0. Let
we obtain
and
Thus
for all ε>0. Choosing 0<δ<1/100 and ε small enough we obtain
for some C>0. From (2.8) and Young’s inequality we get
for all ε′>0 and \(\psi \in C^{\infty}_{0}(M)\). Therefore
The conclusion now follows immediately by replacing ψ with \(\psi ^{\frac{2}{5+\delta}}\). □
2.4 Final estimate
Combining Lemma 2.5 with Corollary 2.4 we can conclude the proof of Theorem 1.1. More precisely, let x0∈M and let \(\widetilde{r}\) the distance function from x0 with respect to the metric \(\widetilde{g}=u^{\frac {4}{3}} g\). We choose \(\psi :=\eta (\widetilde{r})\) with 0≤η≤1, η≡1 on [0,R], η≡0 on [2R,+∞) and |η′|≤C/R on [R,2R], for some C>0 and R>0. From Lemma 2.5, for some 0<δ<1/100, we have
where we used the fact that \(|\tilde{\nabla}\widetilde{r}|_{\widetilde{g}}\equiv 1\) and Corollary 2.4. Since δ>0, letting R→+∞ we get
and this concludes the proof of Theorem 1.1.
3 Proof of Theorem 1.2
Proof of Theorem 1.2
Let (Xn+1,h) be a complete n-dimensional, n≤5, manifold with non-negative sectional curvature and either uniformly positive bi-Ricci curvature or uniformly positive Ricci curvature and consider an orientable, immersed, minimal hypersurface Mn→(Xn+1,h) with finite index. Suppose, by contradiction, that M is non-compact. It is well known (see [Fis85, Proposition 1]) that there exist 0<u∈C∞(M) and a compact subset K⊂M such that u solves
Let k>0 and consider the conformal metric
where g is the induced metric on M. Let s be the arc length with respect to the metric g. Following the construction in [Fis85, Theorem 1], we can construct a minimizing geodesic \(\widetilde{\gamma}(s):[0,+\infty )\to M\setminus K\) in the metric \(\widetilde{g}\) which has infinite length in the metric g. Now we can argue exactly as in the proof of estimate (6) in [ENR07], using H≡0, obtaining
for every smooth function φ such that φ(0)=φ(a)=0 and for every k>0. Arguing as in [SY96, Section 2] we have the following identity
Since (Nn+1,h) is with non-negative sectional curvature and either uniformly positive bi-Ricci curvature or uniformly positive Ricci curvature, we have \(R^{h}_{1j1j}\geq 0\) for every j=2,…,n and either
for some R0>0. Therefore, if k≤1, we get
Since A is trace-free, we have
thus
Choose
We get
If n≤5, we have
Moreover, there exists C>0, such that
Therefore, there exists C>0, such that
for every smooth function φ such that φ(0)=φ(a)=0. Integrating by parts we obtain
Choosing φ(s)=sin(πs a−1), s∈[0,a] one has
i.e.
We conclude that the length (in the metric g) of the geodesic \(\widetilde{\gamma}(s)\) is finite and this gives a contradiction. Therefore (Mn,g) must be compact and this concludes the proof of Theorem 1.2. □
Proof of Corollary 1.3
If M is stable, by Theorem 1.2 it must be compact. Moreover there exists u>0 satisfying
Integrating over M we get a contradiction, since Rich>0 on M. Equivalently, one can use f≡1 in the stability inequality (1.1) to get a contradiction. □
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Almgren, F.J. Jr.: Some interior regularity theorems for minimal surfaces and an extension of Bernstein’s theorem. Ann. Math. (2) 84, 277–292 (1966)
Bombieri, E., De Giorgi, E., Giusti, E.: Minimal cones and the Bernstein problem. Invent. Math. 7, 243–268 (1969)
Cao, H.-D., Shen, Y., Zhu, S.: The structure of stable minimal hypersurfaces in
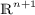 . (English summary). Math. Res. Lett. 4(5), 637–644 (1997)
. (English summary). Math. Res. Lett. 4(5), 637–644 (1997)
Chen, Q.: Curvature estimates for stable minimal hypersurfaces in
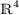 and
and 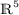 . (English summary). Ann. Glob. Anal. Geom. 19(2), 177–184 (2001)
. (English summary). Ann. Glob. Anal. Geom. 19(2), 177–184 (2001)
Cheng, X.: One end theorem and application to stable minimal hypersurfaces. Arch. Math. 90, 461–470 (2008)
Chodosh, O., Li, C.: Stable minimal hypersurfaces in
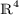 . Acta Math. (2024) To appear
. Acta Math. (2024) To appear
Chodosh, O., Li, C.: Stable anisotropic minimal hypersurfaces in R4. Forum Math. Pi 11, e3 (2023)
Chodosh, O., Li, C., Stryker, D.: Complete stable minimal hypersurfaces in positively curved 4-manifolds (2022). https://arxiv.org/abs/2202.07708v1
Colding, T.H., Minicozzi, W.P.: II, A Course in Minimal Surfaces. Graduate Studies in Mathematics, vol. 121. Am. Math. Soc., Providence (2011)
De Giorgi, E.: Una estensione del teorema di Bernstein (Italian). Ann. Sc. Norm. Super. Pisa, Cl. Sci. (3) 19, 79–85 (1965)
do Carmo, M., Peng, C.K.: Stable complete minimal surfaces in
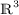 are planes. Bull. Am. Math. Soc. (N.S.) 1(6), 903–906 (1979)
are planes. Bull. Am. Math. Soc. (N.S.) 1(6), 903–906 (1979)
do Carmo, M., Peng, C.K.: Stable complete minimal hypersurfaces. In: Proceedings of the 1980 Beijing Symposium on Differential Geometry and Differential Equations (Beijing, 1980), vol. 1, 2, 3, pp. 1349–1358. Sci. Press Beijing, Beijing (1982)
Elbert, M.F., Nelli, B., Rosenberg, H.: Stable constant mean curvature hypersurfaces. Proc. Am. Math. Soc. 135(10), 3359–3366 (2007)
Fleming, W.H.: On the oriented Plateau problem. Rend. Circ. Mat. Palermo (2) Suppl. 11, 69–90 (1962)
Fischer-Colbrie, D.: On complete minimal surfaces with finite Morse index in three-manifolds. Invent. Math. 82, 121–132 (1985)
Fischer-Colbrie, D., Schoen, R.: The structure of complete stable minimal surfaces in 3-manifolds of nonnegative scalar curvature. Commun. Pure Appl. Math. 33(2), 199–211 (1980)
Hardt, R., Simon, L.: Area minimizing hypersurfaces with isolated singularities. J. Reine Angew. Math. 362, 102–129 (1985)
Nelli, B., Soret, M.: Stably embedded minimal hypersurfaces (English summary). Math. Z. 255(3), 493–514 (2007)
Pogorelov, A.V.: On the stability of minimal surfaces. Dokl. Akad. Nauk SSSR 260(2), 293–295 (1981). (Russian)
Qian, Z.: Estimates for weighted volumes and applications. Quart. J. Math. Oxford Ser. (2) 48(190), 235–242 (1997)
Schoen, R., Simon, L., Yau, S.T.: Curvature estimates for minimal hypersurfaces. Acta Math. 134, 275–288 (1975)
Schoen, R., Yau, S.T.: Complete three-dimensional manifolds with positive Ricci curvature and scalar curvature. In: Seminar on Differential Geometry. Ann. of Math. Stud., vol. 102, pp. 209–228. Princeton Univ. Press, Princeton (1982)
Shen, Y., Ye, R.: On stable minimal surfaces in manifolds of positive bi-Ricci curvatures. Duke Math. J. 85, 109–116 (1996)
Simons, J.: Minimal varieties in Riemannian manifolds. Ann. Math. (2) 88, 62–105 (1968)
Acknowledgements
The first and the second authors are members of the GNSAGA, Gruppo Nazionale per le Strutture Algebriche, Geometriche e le loro Applicazioni of INdAM. The third author is member of GNAMPA, Gruppo Nazionale per l’Analisi Matematica, la Probabilità e le loro Applicazioni of INdAM. The authors thank Douglas Stryker for useful comments regarding Theorem 1.2.
Funding
Open access funding provided by Politecnico di Milano within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to the memory of Cinzia Coatti
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Catino, G., Mastrolia, P. & Roncoroni, A. Two Rigidity Results for Stable Minimal Hypersurfaces. Geom. Funct. Anal. 34, 1–18 (2024). https://doi.org/10.1007/s00039-024-00662-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00039-024-00662-1



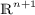 . (English summary). Math. Res. Lett. 4(5), 637–644 (1997)
. (English summary). Math. Res. Lett. 4(5), 637–644 (1997)
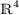 and
and 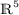 . (English summary). Ann. Glob. Anal. Geom. 19(2), 177–184 (2001)
. (English summary). Ann. Glob. Anal. Geom. 19(2), 177–184 (2001)
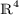 . Acta Math. (2024) To appear
. Acta Math. (2024) To appear
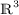 are planes. Bull. Am. Math. Soc. (N.S.) 1(6), 903–906 (1979)
are planes. Bull. Am. Math. Soc. (N.S.) 1(6), 903–906 (1979)